ЯКОБИ МНОГОЧЛЕНЫ, спец. система многочленов последовательно возрастающих степеней. Для и = 0,1,2... Я. м. Р_п ^{(а, 6)} (х) могут быть определены формулой:

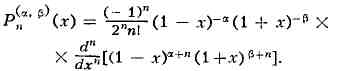
Я. м. ортогональны на отрезке [ -1,1] относительно веса (1 - я')° (1 + л)^е (см. Ортогональные многочлены). Введены К. Якоби (опубл. в 1859). Частными случаями Я. м. являются многочлены Лежандра (при а = (3 = 0), многочлены Чебышева первого рода (при а = |3 = = -½) и второго рода (при а = |3 = = ½), ультрасферич. многочлены (при а = |3). В свою очередь Я. м. являются частным случаем гипергеометрической функции. Дифференциальное уравнение для у = Р_n^{(а, b)}(х):

(1 + х²)у" + [b - а - (а + b + 2) x] y' + + n (а + b + n + 1)y = 0.

ЯКOБИ СИМВОЛ, обозначение

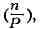
являющееся обобщением Лежандра символа в случае составного модуля Р. Введён К. Якоби (1837). См. Квадратичный вычет.  

ЯКOБИ ТЕЛЕГРАФНЫЙ АППАРАТ, 1) телеграфный аппарат синхронного действия с непосредственной (без расшифровки) индикацией в приёмнике передаваемых букв и цифр. Изобретён Б. С. Якоби в 1845. 2) Первый буквопечатающий телеграфный аппарат; изобретён Б. С. Якоби в 1850. Впервые применённый принцип согласованной (синхронной) работы передатчика и приёмника лёг в основу действия всех последующих телегр. аппаратов.

ЯКОБИАН, функциональный определитель |a_ik|₁ⁿ с элементами a_ik = дy_i/дх_k, где y_i = f_i (x₁, ...,x_n), 1 =<i= < п,- функции, имеющие непрерывные частные производные в нек-рой области Д; обозначение:

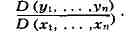
Введён К.Якобы (1833, 1841). Если, напр., п = 2, то система функций y₁ = f₁(x₁, x₂), y₂ = f₂ (x₁, х₂) (1), задаёт отображение области Д, лежащей на плоскости x₁, х₂, на часть плоскости y1, y2. Роль Я. для этого отображения во многом аналогична роли производной для функции одной переменной. Напр., абсолютное значение Я. в нек-рой точке М равно коэфф. искажения площадей в этой точке (т. е. пределу отношения площади образа окрестности точки М к площади самой окрестности, когда размеры окрестности стремятся к нулю). Я. в точке М положителен, если отображение (1) не меняет ориентации в окрестности точки М, н отрицателен в противоположном случае. Если Я. не обращается в нуль в области & и ф (y1, у2) - функция, заданная в области &1 (образе 7), то

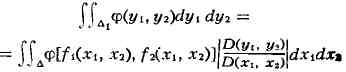
(формула замены переменных в двойном интеграле). Аналогичная формула имеет место для кратных интегралов. Если Я. отображения (1) не обращается в нуль в области Д, то существует обратное отображение

x₁ = Ф₁ (y₁, y₂), x₂ = Ф₂(y₁, y₂), причём

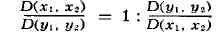
(аналог формулы дифференцирования обратной функции). Это утверждение находит многочисленные применения в теории неявных функций. Для возможности явного выражения в окрестности точки М (x₁^(O), ..., x_n⁽⁰⁾, y₁⁽⁰⁾, ..., y_m⁽⁰⁾) функций y₁, ..., у_т, неявно заданных уравнениями

F_k(x₁, ...,х_n, y₁, . . . , у_т) = 0, (2) 1 <= k<= m, достаточно, чтобы координаты точки М удовлетворяли уравнениям (2), функции F_k имели непрерывные частные производные и Я.

был отличен от нуля в точке М.

Лит.: Кудрявцев Л. Д., Математическпй анализ, 2 изд., т. 2, М., 1973; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971.