ЭЛЛИПС, линия пересечения круглого конуса с плоскостью, встречающей одну его полость (рис. 1). Э. может быть также определён как геометрич. место точек М плоскости, для к-рых сумма расстояний до двух определ. точек F₁ и F₂ (фокусов Э.) этой плоскости есть величина постоянная. Если выбрать систему координат хОу так, как указано на рис. 2 OF₂ = с, то уравнение Э. примет вид:

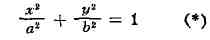
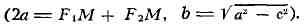
Э.- линия второго порядка; она симметрична относительно осей АВ и CD; точка О - центр Э.- является его центром симметрии; отрезки АВ = 2а и CD = 2b называются соответственно большой и малой осями Э.; число е = с/а<1 - эксцентриситет Э. (при е = О, то есть при а = b, Э. есть окружность). Прямые, уравнения к-рых х = -а/е и х = ale, наз. директрисами Э.; отношение расстояния точки Э. до ближайшего фокуса к расстоянию до ближайшей директрисы постоянно и равно эксцентриситету. Точки А, В, С, D пересечения Э. с осями Ох и Оу наз. его вершинами. См. также Конические сечения.

ЭЛЛИПС ИНЕРЦИИ в сопротивлении материалов, графич. изображение, используемое для вычисления осевых и центробежных моментов инерции плоской фигуры (напр., поперечного сечения стержня) относительно осей, проходящих через её центр тяжести. При построении Э. и. его полуоси, численно равные гл. радиусам инерции фигуры, совмещаются с её гл. центр, осями.

ЭЛЛИПСОИД (от эллипс и греч. eidos - вид), замкнутая центральная поверхность второго порядка. Э. имеет центр симметрии О (см. рис.) и три оси симметрии, к-рые наз. осями Э. Точки пересечения координатных осей с Э. наз. его вершинам и. Сечения Э. плоскостями являются эллипсами (в частности, всегда можно указать круговые сечения Э.). В надлежащей системе координат уравнение Э. имеет вид:

ЭЛЛИПТИЧЕСКАЯ ГЕОМЕТРИЯ, то же, что Римана геометрия.

ЭЛЛИПТИЧЕСКАЯ ТОЧКА поверхности, точка, в к-рой полная кривизна поверхности положительна. В окрестности Э. т. поверхность расположена по одну сторону от своей касат. плоскости.

ЭЛЛИПТИЧЕСКИЕ ГАЛАКТИКИ, гигантские звёздные системы, имеющие форму эллипсоида. Э. г., как правило, не содержат космич. пыли. См. Галактики.

ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ, интегралы вида 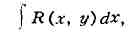где R(x, y) - рациональная функция х и

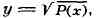
а Р(х) - многочлен 3-й или 4-й степени без кратных корней. Под Э. и. первого рода понимают интеграл

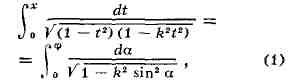
иод Э. л. второго рода - интеграл

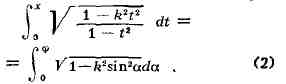
где h - модуль Э. и., О < k < 1 (х = sin<p, t = sinct). Интегралы в левых частях равенств (1) и (2) наз. Э. и. в нормальной форме Якоби, интегралы в правых частях - Э. и. в нормальной форме Лежандра. При х = 1 или ф = л/2 Э. и.наз. полными и обозначаются, соответственно, через

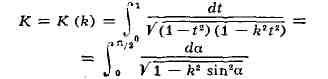
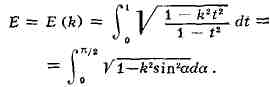
Своё назв. Э. и. получили в связи с задачей вычисления длины дуги эллипса и - asina, v = bcos а (а < b). Длина дуги эллипса выражается формулой

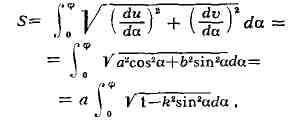
где

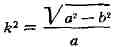
- эксцентриситет эллипса. Длина дуги четверти эллипса равна Е(к). Функции, обратные Э. и., наз. эллиптическими Функциями.

ЭЛЛИПТИЧЕСКИЕ КООРДИНАТЫ, координаты, связанные с семейством  

Функции	Периоды	Нули	Полюсы
sn z	4Кт+ 2iK'n	2mK+2iK'n	2тК +
СnZ	4К + (2К + 2iK')n	(2т+1)K + 2iК'п	+(2n+ 1)iK'
dn z	2Кт + 4iК'п	(2т + 1)K + (2п+ 1)iK

софокусных эллипсов и гипербол (см. Софокусные кривые). Э. к. точки М и её декартовы координаты х, у связаны соотношениями .т = с сbm cos v, y = c shusintt.

ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ, траектории, к-рые может описывать материальная точка (или центр масс тела) при движении под действием силы ньютонианского тяготения. В поле тяготения Земли, если пренебречь сопротивлением среды, Э. т. будет в 1-м приближении траектория центра масс тела, к-рому вблизи поверхности Земли сообщена начальная скорость vo<v->, где

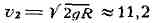
км сек - втооая космическая скорость (R - радиус Земли, g - ускорение силы тяжести).

ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ, функции, связанные с обращением эллиптических интегралов. Э. ф. применяются во мн. разделах математики и механики как при теоретич. исследованиях." тек и для численных расчётов.

Подобно тому как трнгонометрич. функция и = sinx является обратной по отношению к интегралу

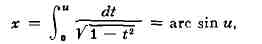
так обращение нормальных эллинтич. интег" ралов 1-го рода

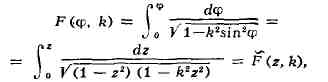
где г = sin ф, k - модуль эллпптич. интеграла, порождает функции: Ф = am г - амплитуда г (эта функция не является Э. ф.) и со = sn г = sin (am z) - синус амплитуды. Функции en z - косинус амплитуды и dn г - дельта амплитуды определяются формулами

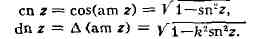
Функции sn z, en г, dn z называют Э. ф. Я к о б и. Они связаны соотношением sn²z + cn² z = k²sn²z + dn²z = 1.

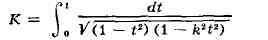
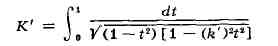
-полный нормальный эллиптич. интеграл 1-го рода и 4JC - основной период Э. ф. sn г. В отличие от однопериодич. функции sin х, функция sn z - двоякопериодическая. Её второй основной период равен 2гК', где 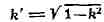- дополнительный модуль. Периоды, нули и полюсы Э. Ф. Якоби приведены в таблице, где тип - любые целые числа.

Э. ф. Веберштрасса сг(х) может быть определена как обратная нормальному вллиптич. интегралу Вейерштрасса 1-го рода

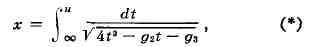
где параметры д₂ и д₃ - наз. инвариантами о (я:). При этом предполагается, что нули e1, e2 и e3 многочлена 4t³ - gt² - g₃ различны между собой (в противном случае интеграл (*) выражался бы через элементарные функции). Э. ф. Вейерштрасса {?(x) связана с Э. ф. Якоби следующими соотношениями:

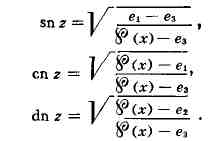
Любая мероморфная двоякопериодическая функция f(i) с периодами ш₁ и ш₂, отношение к-рых мнимо, т. е. f(z + mш₁ + mш₂) = А(z)при m, п = 0, ± 1, ±2, ... и

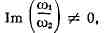
является Э. ф. Для построения Э. ф., а также численных расчётов применяют сигма-функции и тэта-функции.

Изучению Э. ф. предшествовало накопление знаний об эллиптич. интегралах, систематич. изложение теории к-рых дал А. Лежандр. Основоположниками теории Э. ф. являются Н. Абель (1827) и К. Якоби (1829). Последний дал развёрнутое изложение теории Э. ф., назв. его именем. В 1847 Ж. Лиувилль опубл. изложение основ общей теории Э. ф., рассматриваемых как мероморфные двоякопериодические функции. Представление Э. ф. через ^-функцию, а также ?-, а-функции дано К. Вейерштрассом в 40-х гг. 19 в. (две последние не являются Э. ф.).

Лит.: Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968; Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968; Уиттекер Э. Т., Ватсон Д ж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963; Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Эллиптические и автоморфные функции. Функции Ламе и Матье, пер. с англ., М., 1967.