ЧИСЕЛ ТЕОРИЯ, наука о целых числах. Понятие целого числа, а также арифметич. операций над числами известно с древних времён и является одной из первых матем. абстракций.

Особое место среди целых чисел, т. е. чисел ..., -3, -2, -1, 0, 1, 2, 3, ..., занимают натуральные числа - целые положительные числа 1, 2, 3,...- их свойства и операции над ними. Все натуральные числа, большие единицы, распадаются на 2 класса: к 1-му классу относятся числа, имеющие ровно два натуральных делителя, именно единицу и самого себя, ко 2-му - все остальные. Числа 1-го класса стали называть простыми, а 2-го - составными. Свойства простых чисел и их связь со всеми натуральными числами изучались Евклидом (3 в. до н. э.). Если выписывать простые числа подряд, то можно заметить, что относительная плотность их убывает: на первый десяток их приходится 4, т. е. 40%, на сотню - 25, т. е. 25%, на тысячу - 168, т. е. ж 17%, на миллион - 78 498, т. е. == 8%, и т. д., однако их бесконечно много (Евклид).

Среди простых чисел попадаются пары таких, разность между к-рыми равна двум (т. н. простые близнецы), однако конечность или бесконечность таких пар не доказана.

Евклид считал очевидным, что с помощью умножения только простых чисел можно получить все натуральные числа, причём каждое натуральное число представимо в виде произведения простых чисел единственным образом (с точностью до порядка множителей). T. о., простые числа образуют мультипликативный базис натурального ряда. Первыми задачами о простых числах были такие: как часто они расположены в натуральном ряде и как далеко они отстоят друг от друга. Изучение распределения простых чисел привело к созданию алгоритма (правила), позволяющего получать таблицы простых чисел. Таким алгоритмом является Эратосфена решето (3 в. до н. э.). Евклид в "Началах" указал способ нахождения общего наибольшего делителя двух чисел (Евклида алгоритм), следствием к-рого является теорема об однозначном разложении натуральных чисел на простые сомножители.

Вопрос о целочисленных решениях различного вида уравнений также восходит к древности. Простейшим уравнением в целых числах является линейное уравнение

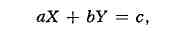
где а, b и с - попарно взаимно простые целые числа. С помощью алгоритма Евклида находится решение уравнения аХ + bY =1, из к-рого затем получаются все решения первоначального уравнения. Другим уравнением в целых числах является уравнение X² + Y² = Z² (решение X = 3, Y = 4, Z = 5 связано с именем Пифагора), все целочисленные решения к-рого выписаны в "Началах" (кн. X, предложение 29)

X = г² - q²Y = 2rq, Z = г² + q² где r и q - целые числа. Евклиду было известно также и уравнение аХ² + 1 = = Y², названное впоследствии Пелля уравнением. В "Началах" (кн. X, предложение 9) Евклид показал, как находить все его решения, исходя из наименьшего, для случая а = 1. Систематическое изложение теории известных к тому времени уравнений в целых числах дано Диофантом в его "Арифметике" (сер. 3 в. н. э.). Эта книга сыграла большую роль в дальнейшем развитии той части Ч. т., к-рая занимается решением уравнений в целых числах, называемых теперь диофантовыми уравнениями.

Следующий этап в развитии Ч. т. связан с именем П. Ферма, к-рому принадлежит ряд выдающихся открытий в теории диофантовых уравнений и в теории, связанной с делимостью целых чисел. Им была выдвинута гипотеза, получившая название Ферма великая теорема, и доказана теорема, известная как Ферма малая теорема, к-рая играет важную роль в теории сравнений и её позднейших обобщениях. Продолжая исследования Ферма по теории делимости чисел, Л. Эйлер доказал теорему, обобщающую малую теорему Ферма. Ему принадлежат также и первые доказательства великой теоремы Ферма для показателя n = 3.

К нач. 18 в. в науке о целых числах накопилось много фактов, позволивших создать стройные теории и общие методы решения задач Ч. т.

Л. Эйлер был первым из математиков, кто стал создавать общие методы и применять др. разделы математики, в частности математический анализ, к решению задач Ч. т. Исследуя вопрос о числе решений линейных уравнений вида

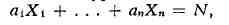
где a₁, ...,a_n - натуральные числа, в целых неотрицат. числах X₁, ..., X_n, Л. Эйлер построил производящую функцию Ф(z) от переменной z, коэффициенты к-рой при разложении по степеням z равняются числу решений указанного уравнения. Функция Ф(z) определяется как формальное произведение рядов

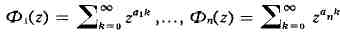
т. е. Ф(z) = Ф₁(z) ... Ф_k(z), каждый иг к-рых сходится при |z| < 1 и имеет достаточно простой вид, являясь суммой членов бесконечной геометрич. прогрессии:

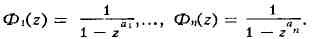
Следовательно,

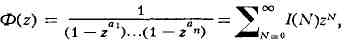
причем I(N) - число решении изучаемого уравнения. Метод производящих функций Эйлера послужил истоком кругового метода Харди-Литлвуда, далеко идущим развитием к-рого, в свою очередь, явился метод тригонометрических сумм

И. M. Виноградова.

Другой проблемой Ч. т., стимулировавшей создание мощного метода, была проблема простых чисел. Л. Эйлер, доказывая теорему Евклида о бесконечности числа простых чисел, рассмотрел произведение по всем простым числам р:

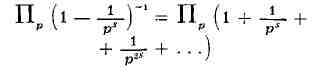
при s > 1. Это произведение сходится, и если его раскрыть, то в силу однозначности разложения натуральных чисел на простые сомножители получается, что оно равняется сумме ряда 1/n^sоткуда следует тождество Эйлера:

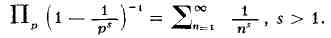
Так как при s=1 ряд справа расходится (гармонический ряд), то из тождества Эйлера следует теорема Евклида. Эта идея Л. Эйлера легла в основу позднейших теорий дзета-функции. JI. Эйлеру и X. Гольдбаху принадлежат первые постановки аддитивных (т. е. связанных со сложением) задач с простыми числами. К сер. 19 в. в основном было построено здание Ч. т., что связано с именами К. Гаусса, Ж. Лагранжа, А. Лежандра, П. Дирихле, П. Jl. Чебыгиева, Ж. Лиувилля, Э. Куммера.

К. Гаусс создаёт теорию сравнений, называемую иначе арифметикой остаточных классов, с помощью к-рой были доказаны теорема о том, что простое число является суммой двух квадратов тогда и только тогда, когда оно имеет вид 4n+1, и теорема о представимости каждого натурального числа суммой четырёх квадратов целых чисел. Кроме того, теория сравнений привела к важным понятиям теоретико-числового характера и тригонометрич. суммы. Простейшим характером является Лежандра символ.

К. Гаусс изучил свойства квадратичных вычетов и невычетов. Основной теоремой в этом круге вопросов является т. н. к в а д р а т и чный закон взаимности, при доказательстве к-рого К. Гаусс рассмотрел конечные суммы вида

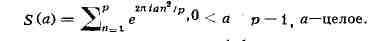
Суммы такого вида и их обобщения стали называть тригонометрическими, т. к. в силу формулы Эйлера e^tф = cosф+-isinф они могут быть представлены в виде суммы синусов и косинусов.

К. Гаусс, а затем П. Дирихле, продолжая исследования Л. Эйлера, создали теорию квадратичных форм, другими словами,- теорию о представлении натуральных чисел формами вида ах²+2bху+су², где a, b, с - целые числа.

К. Гаусс и П. Дирихле первыми стали рассматривать проблему о количестве целых точек в областях на плоскости. К. Гаусс доказал, что число целых точек в круге X²+Y²<=R² равно лR² +O(R), а П. Дирихле, в свою очередь, доказал, что число целых точек с положительными координатами под гиперболой xy = N равно N(1nN+2С-1)+О(N)^1/2, где С - Эйлера постоянная. Обобщения этих двух предложений, а также нахождение наилучших возможных остатков в написанных формулах (проблема целых точек в круге Гаусса и проблема делителей Дирихле) послужили источником большой главы Ч. т.

Теоремы о бесконечности числа простых чисел в арифметич. прогрессиях частного вида, таких, как 4k ±1, 6k±l, были известны давно, однако только П. Дирихле удалось доказать общую теорему о бесконечности числа простых чисел в прогрессиях вида

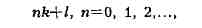
где k (разность прогрессии) и l (первый её член) взаимно просты. Он рассмотрел аналог эйлерова произведения по всем простым числам вида

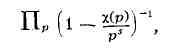
где x(p) удовлетворяет условиям: не равна тождественно нулю, периодическая x(n+k)=x(n) с периодом k, вполне мультипликативная, т. е. x(nm) =x(n)x(m) при любых целых nи т. Эту функцию назвали характером Дирихле. С помощью характеров Дирихле можно "вырезать" арифметич. прогрессии. Для каждого натурального k существует ф(k) характеров Дирихле ф(k) - Эйлера функция), причём если рассмотреть сумму чисел x(n) по всем возможным характерам , отвечающим k, то она будет равна ф(k), если n при делении на k даёт остаток 1, в противном случае - равна О. При s>1 получается аналог тождества Эйлера:

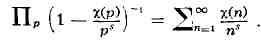
Ряд справа в этом равенстве называется рядом Дирихле. Изучая поведение таких рядов при s->1+0 Дирихле доказал свою теорему о бесконечности числа простых чисел в арифметич. прогрессии.

Характеры Дирихле играют важную роль как в самой Ч. т., так и в др. разделах математики (алгебре, топологии и др.), а ряды Дирихле составляют большую главу в современной теории функций.

Новый подход к проблеме распределения простых чисел предложен П. Л. Чебышевым. Обозначим через л(Х) число простых чисел, не превосходящих X. Теорема Евклида утверждает, что л(Х)->+оо при X->+оо.

П. Jl. Чебышев доказал более точный закон стремления к бесконечности л(Х):

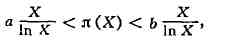
где а>¹/_гlп2, b<2ln2, и утверждение, что если существует предел

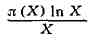
при Х->oо, то этот предел равен 1.П, Л. Чебышеву принадлежит и др. открытие в теории простых чисел. С помощью вычислений было замечено, что в интервале (X, 2X), Х>=2, лежит простое число; эту гипотезу назвали постулатом Бертрана. П. Л. Чебышев доказал (1852) эту гипотезу, причём он получил более точный результат, уменьшив длину рассматриваемого интервала. Тем самым вместе с вопросом о простых близнецах, т. е. о наименьшем значении разности p_n+1 - p_n, возник и стал решаться вопрос об оценке сверху этой разности.

Изучение неопределённых уравнений, и в первую очередь уравнения Ферма, привело к созданию нового раздела Ч. т. - теории алгебраических чисел. Э. Куммер, пытаясь доказать теорему Ферма, пришел к равенству
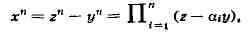где a₁ ~ корни n-й степени из единицы. Рассматривая числа вида z+a_iy, где z и у - целые, как "новые целые числа", Э. Куммер построил арифметику целых чисел алгебраического числового поля, порождённого a_i, т. е. множества чисел, к-рое получается из a_i путём применения к нему всех четырёх арифметич. операций. Если бы в таком поле выполнялась теорема о единственности разложения целых чисел на простые сомножители, то тогда записанное выше равенство давало бы противоречие. Однако это не всегда так. Э. Куммер, чтобы сохранить справедливость этой теоремы, ввёл т. н. идеальные множители. Возник ряд проблем, решение к-рых привело к алгебраич. теории чисел с большим количеством новых понятий и результатов.

Вместе с изучением свойств целых чисел возникло и стало развиваться новое направление Ч. т., изучающее арифметику числовой прямой. Уже Л. Эйлер отмечал, что корни квадратные из целых чисел и логарифмы целых чисел принципиально отличаются друг от друга. Последнее обстоятельство обрело точную математич. формулировку после работ Ж. Лиуэилля (1844), к-рый ввёл понятия алгебра и ческих чисел н трансценденпгных чисел. Оказывается, алгебраич. числа "плохо" приближаются рациональными дробями. Ж. Лиувилль доказал, что если алгебраич. число является корнем уравнения степени п, то, приближаясь к нему дробями вида P/Q, где P u Q - целые взаимно простые числа, подойти существенно ближе чем Q^-nк нему нельзя (теорема Л н у в и л л я). Отсюда сразу следует существование бесконечного числа неалгебранч. чисел, к-рые стали называть трансцендентными. Однако вопрос об алгебраичности и трансцендентности конкретных чисел труден, и первыми были такие вопросы о классич. постоянных л и е. В кон. 19 - нач. 20 вв. Ч. т. продолжала развиваться по многим направлениям, причем для решения отдельных задач создавались общие методы, применимые к широкому кругу задач, иногда далеко удалённых от первоначальных. Часто созданные здесь методы и понятия дают толчок развитию новых направлений.

Теория алгебраич. чисел разделилась на два направления; одно изучает конкретные числа, доказывая их трансцендентность, другое изучает степень приближения алгебраич. чисел рациональными или алгебраическими. В первом направлении общие методы были созданы Ш. Эрмитпом (1873), доказавшим трансцендентность числа е, н нем. математиком Ф. Линдеманом (1882), доказавшим трансцендентность числа л и тем самым решившим задачу о квадратуре круга. Во втором - А. Туэ (1909) был предложен метод, с помощью к-рого он доказал, что в неравенстве Лиувилля к алгебраич. числу нельзя подойти существенно ближе чем Q^-п/2. Следствием этого явилась теорема Туэ о конечности числа решений в целых числах х и у уравнения

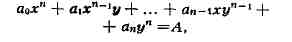
где a₀, a₁,..., a_n, A - целые числа, n>=3.

Дальнейшее изучение простых чисел привело к новому методу в Ч. т., связанному с функцией E(s). Б. Риман доказал, что дзета-функция E(s) аналитически продолжается на всю плоскость комплексного переменного, является аналитической в каждой точке плоскости, за исключением s=1, где она имеет полюс первого порядка с вычетом, равным 1, удовлетворяет функциональному уравнению

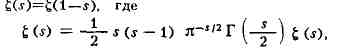
Г(s) - гамма-функция, и имеет бесконечно много нулей в полосе О <= Res=1 (эти нули называют нетривиальными, а полосу -критической). Он установил тесную связь между нетривиальными нулями Е(s) и асимптотич. поведением л(х). Изучение асимптотич. формулы для функции Чебышева

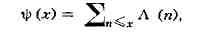
где d(n)= lnp, если n=p^kи d(n)=0, если n<>p^k, эквивалентно такой же задаче для функции л(х). Функция Y(x) может быть выражена через интеграл от производящей функции -

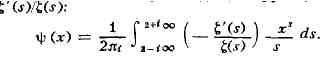
Б. Риман высказал гипотезу, что все нетривиальные нули E(s) лежат на прямой Res =½, из чего следует, что

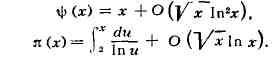
Из справедливости любой из последних формул следует гипотеза Римана. По аналогичной схеме были изучены L-ряды Дирихле, В 1896 Ш. Ла Балле Пуссен и Ж. Адамар доказали, что дзета(s)<>0 в области Res>=l, откуда следовала формула (асимптотический закон распределения простых чисел)

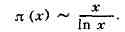
Кроме этого, Ш. Ла Валле Пуссен доказал, что дзета(s)<>0 в области

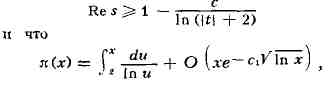
где с и c₁ - положительные постоянные. Такой же результат был получен им и для простых чисел в арифметич. прогрессиях: если л(х, k, l) - число простых чисел вида kn+l, п<=х, k и l - взаимно простые числа, то

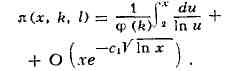
Метод получения асимптотич. формул для л(х), Y(s), л(х, k, I), названный методом комплексного интегрирования, нашёл многочисленные применения. Основой этого метода служит формула

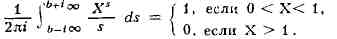
Теория квадратичных форм, начатая работами Л. Эйлера, К. Гаусса, П. Дирихле, продолжала своё развитие в работах A. H. Коркина, E. И. Золотарёва и А. А. Маркова. В частности, A. H. Коркин и E. И, Золотарёв доказали теорему: переменным любой положительной кватернарной квадратичной формы определителя D можно придать такие целые значения, что значение формы не будет превосходить величины

(4D)^1/4, и существуют такие формы, минимумы

к-рых равны (4D)^1/4. Примером такой формы является следующая:

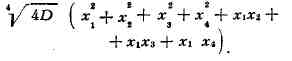
Исследования А. А. Маркова относились к изучению минимумов бинарных квадратичных форм положительного определителя и привели к целому ряду новых открытий.

Проблемы целых точек в областях на плоскости получили своё дальнейшее развитие в трудах Г. Ф. Вороного, создавшего (1903) метод, с помощью к-рого доказано, что остаточный член в асимптотич. формуле Дирихле для числа целых точек под гиперболой имеет порядок корня кубического из главного члена. Позднее (1906) метод Вороного был перенесён В. Серпиньским на проблему Гаусса целых точек в круге с тем же результатом. В это же время были предприняты попытки найти решения аддитивных проблем Ч. т. и, в частности, решить Варинга проблему. В 1909 она была решена Д. Гильбертом.

Второе, третье и четвёртое десятилетия 20 в. были исключительно богаты новыми идеями и методами в Ч. т. Г. Вейль, решая задачи, связанные с устойчивостью Солнечной системы, пришёл к понятию равномерного распределения дробных долей целочисленных функций: дробные доли действительнозначной функции FOc) равномерно распределены на [0,1) при x= 1,2,3.,.., если число попаданий дробных долей F(x) на любой интервал из [0,1) пропорционально длине этого интервала. Он доказал, что для равномерности распределения дробных долей F(x) необходимо и достаточно выполнение соотношения:

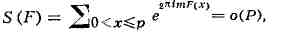
при любом фиксированном |m|>0, и получил нетривиальные оценки |S(F)| в случае, когда F(x) - многочлен, старший коэффициент к-рого есть иррациональное число. И. M. Виноградов, изучая распределение значений символа Лежандра на отрезках малой длины по сравнению с модулем, доказал (1914) неравенство

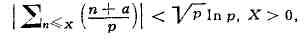
из к-рого следует, что квадратичных вычетов и невычетов на любом отрезке, длина к-рого чуть больше (p)^1/2 ln р, асимптотически поровну. Кроме того, он высказал гипотезу, что это будет верно при Х>р^E, где E>0 - сколь угодно малое число. В 1917 И. M. Виноградов доказал, что число целых точек в области 0<y<=f(x), а<х<=b, при определённых ограничениях на порядок роста второй производной f(x), равно площади этой области с точностью до слагаемого порядка корня кубического из главного члена. Позднее чешским математиком В. Ярником установлено, что точность этой формулы при сделанных предположениях относительно f(x) нельзя существенно улучшить.

Норвежским математиком В. Вруном доказаны (1919) теоремы, к-рые в определённом смысле приближались к проблеме простых близнецов и проблеме Эйлера. А именно, им доказана бесконечность числа nap u₁ и u₂, таких, что u₂ - u₁= 2 и число простых делителей u₁ и u₂ не превосходит девяти; а также разрешимость уравнения u₁+ u₂ = 2N, с теми же условиями на u₁и u₂.

Г. Харди и Дж. Литлвуд опубликовали (1922 - 23) серию мемуаров под общим названием "Partitio Numerorum", в к-рых развили общий метод решения аддитивных задач Ч. т., получивший впоследствии название "кругового". Этот метод (на примере решения проблемы Варинга) состоит в следующем: пусть

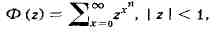
тогда

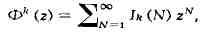
где I_k(N) - число решений уравнений Варинга, к-рое находят по формуле

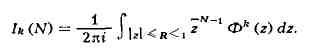
Г. Харди и Дж. Литлвуд изучали последний интеграл при R -> 1-0. Окружность интегрирования определённым образом разбивается на "большие" и "малые" дуги (отчего и получил название метод), при этом интегралы по "большим" дугам дают главный член асимптотической формулы для I_k(N), а по "малым" - остаточный. T. о. получают асимптотич. формулу величины

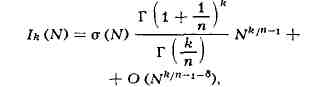
где q(N) - нек-рый "особый ряд"; q(N)>= с >0, б > 0 и k >= (п - 2) 2^n-1+ 5. С помощью этого метода Г. Харди и Дж. Литлвуд получили следующие результаты: дали новое решение проблемы Варинга, причём в форме более точной, чем это было у Д. Гильберта; дали условное решение проблемы Гольдбаха; сформулировали и выписали гипотетические формулы для количества решений большого числа уравнений с простыми числами.

В нач. 30-х гг. 20 в. И. M. Виноградовым был найден т. н. метод тригонометрич. сумм, позволивший решить многие проблемы Ч. т. Так, занимаясь проблемой Варинга, И. M. Виноградов обнаружил (1929), что результат Харди - Литлвуда будет значительно проще, если вместо производящих рядов рассматривать тригонометрич. суммы вида

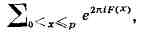
где F(x) - действительная функция, и пользоваться соотношением

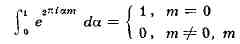
Тогда I_k(N) в проблеме Варинга запишется так:

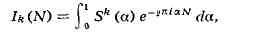
где

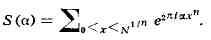
Далее интервал интегрирования [0,1] разбивается рациональными несократимыми дробями вида a/b, 0<=a< b <= t, t- параметр, зависящий от N, на подынтервалы подобные "большим" и "малым" дугам кругового метода. Интервалы, отвечающие дробям с малыми знаменателями, и сумма интегралов по ним дают главный член асимптотич. формулы для I_k(N). Другие интервалы отвечают "малым" дугам; для них И. M. Виноградов оценивает |S(a)| методом Вейля и получает остаточный член. К тригонометрич. суммам сводятся и др. задачи Ч. т.: распределение дробных долей функций, целые точки в областях на плоскости и в пространстве, порядок роста дзета-функции в критич. полосе п др. Причём главным в таких задачах является вопрос о возможно более точной оценке модуля тригонометрич. суммы. И. M. Виноградов предложил два метода оценок тригонометрич. сумм. Первый метод (1934) дал возможность получить новые оценки сумм Вейля. Следствием этого явились современные оценки, выведена асимптотич. формула в проблеме Варинга при k>=4n² ln п, доказано, что для разрешимости уравнения Варинга при N >= N_o(n) достаточно не более 3п ln п -11n слагаемых, получен новый остаточный член в асимптотич. формулах для пи(х) и пси(x) (И. M. Виноградов, 1957) порядка

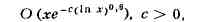
получено решение проблемы Гильберта - Камке (К. К. Марджанишвили, 1953).

Второй метод Виноградова (1937) позволил оценить такие тригонометрич. суммы, в к-рых суммирование ведётся по простым числам:

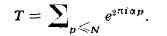
Это привело к доказательству асимптотич. формулы для числа представлений нечётного числа суммой трёх простых, из к-рой следовало, что все достаточно большие нечётные числа являются суммой трёх простых. Тем самым была решена Гольдбаха проблема. Этот метод привёл к решению др. общих задач Ч. т., напр, проблемы Варинга в простых числах, проблемы распределения квадратичных вычетов и невычетов в последовательностях вида p+а, где p принимает значения простых чисел.

Развитие идей А. Туэ (построение вспомогательного многочлена, с высокой кратностью корня) и Д. Пойа (США) (целая аналитич. функция, принимающая в целых положительных точках целые значения и растущая медленнее 2^Y|S| , Y < 1, является многочленом) привело А. О. Гельфонда и нем. математика T. Шнейдера (1934) к решению 7-й проблемы Гильберта, утверждающей трансцендентность чисел вида a^B, a не равно 0,1, B - алгебраич. число степени >=2. К. Зигель доказал ряд теорем о трансцендентности значений функций типа е^x (т. н. E-функции) в алгебраич. точках.

В алгебраич. Ч. т. доказан ряд теорем, обобщающих теоремы теории целых чисел на целые числа алгебраич. числовых полей; нек-рые из них привели и к чисто арифметич. результатам, сюда, в частности, относится теория представлений чисел полными и неполными разложимыми формами (простейшей из таких задач является уравнение Пелля). Развита также теория решений сравнений от двух и более переменных, из к-рой, напр., следует, что сравнение F (х, у) = 0 (mod p), где F - абсолютно неприводимый многочлен, имеет P + O(p)^1/2 решений (теорема Хассе - Вейля).

Начиная с конца 40-х гг. и по наст, время (1978) в Ч. т. появилось много работ в самых различных направлениях. Исследования ведутся как в классич. областях, так и в новых. Сов. математиками Б. H. Делоне и Д. К. Фаддеевым полностью исследовано диофантово уравнение х³ - ау³ = 1 (1940). В теории дзета-функции Римана А. Сельберг (Норвегия, 1942) доказал, что конечная доля всех нулей E(s) лежит на критич. прямой Re s = ½_. Ю. В. Линник доказал, что наименьшее простое число в арифметич. прогрессии с разностью k не превосходит k^c, с - постоянная, и разработал дисперсионный метод (1958 - 1961), с помощью к-рого вывел асимптотич. формулу для числа представлений натурального N суммой простого и двух квадратов (проблема Харди - Литлвуда); этим же методом он получил асимптотич. формулу для числа решений неопределённого уравнения вида p - а = ху, p <=N, ху <= N, а - фиксированное целое (проблема простых делителей Титчмарша). Метод тригонометрич. сумм Виноградова получил дальнейшее развитие в работах самого И. M. Виноградова и его учеников. Безуспешные попытки доказать гипотезу Римана привели к ряду методов, к-рые обходят её и в то же время позволяют решить определённые задачи Ч. т., выводимые из этой гипотезы. Сюда относится проблема оценки разности p_n+1- p_n = дельта n, к-рая сведена к оценке числа нулей дзета-функции в прямоугольниках вида q <= Re s <=1, q > ½, | Im s |<= T. Из таких "плотностных" теорем и границы нулей E(s), полученной на основе метода Виноградова, следует, что p_n+1- p_n = О (р_n^0,6). К подобного рода результатам пришли и в теории распределения простых чисел в арифметич. прогрессиях и её применениях к аддитивным задачам с простыми числами.

В теории трансцендентных чисел англ. математик К. Рот (1955) усилил метод Туэ и доказал, что алгебраич. число не может быть приближено рациональной дробью P/Q существенно точнее, чем Q^-2-E, E > О - произвольно мало; англ. математик А. Бейкер (1966) получил оценку снизу линейной формы логарифмов алгебраич. чисел, что привело к эффективному доказательству теоремы Туэ о конечности решений уравнения

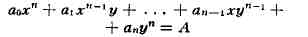
- целое. (указываются границы этих решений) и к эффективному усилению теоремы Лиувилля о приближении алгебраич. чисел рациональными дробями. Большое количество проблем Ч. т. ещё не решено (сюда относятся проблемы простых близнецов, бесконечности простых чисел вида n² + 1, целых точек в круге и под гиперболой, распределения нулей дзета-функции, трансцендентность чисел n² + е и постоянной Эйлера и мн. др.).

Лит.: Виноградов И. M., Основы теории чисел, 8 изд., M., 1972; его же, Метод тригонометрических сумм в теории чисел, M., 1971; его же, Особые варианты метода тригонометрических сумм, M., 1976; Карацуба А. А., Основы аналитической теории чисел, M., 1975; Боревич З. И., Шафаревич И. Р., Теория чисел, 2 изд., M., 1972; Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., M., 1971; Чандрасек, Харан К., Введение в аналитическую теорию чисел, пер. с англ., M., 1974; X а с с е Г., Лекции по теории чисел, пер. с нем., M., 1953; Дирихле П. Г. Л., Лекции по теории чисел, пер. с нем., M.- Л., 1936; Титчмарш E. К., Теория дзета-функции Римана, пер. с англ., M., 1953; В е н к о в Б. А., Элементарная теория чисел, М.-Л., 1937.

А. А. Карацуба.