ХАРАКТЕР в математике, функция спец. вида, применяемая в чисел теории и теории групп.

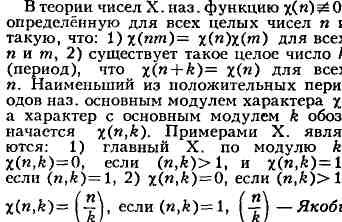
символ, k> 1 - нечётное натуральное число. X. степени q по модулю k наз. X., равный единице для чисел а, для к-рых разрешимо сравнение x^q = a(modk) (см. Степенной вычет). Такие X. играют важную роль в теории алгебраич. чисел. Многие вопросы теории чисел (напр., вопрос о распределении простых чисел)

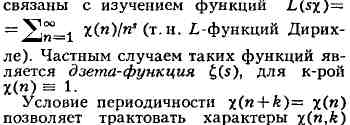
при фиксированном k>l как функции, заданные на приведённой системе вычетов по модулю k, рассматриваемой как группа по умножению, и удовлетворяющие там функциональному уравнению:

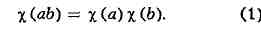
Такая трактовка понятия X. позволяет непосредственно перенести его на любую конечную коммутативную группу G. При этом, если п - порядок, е - единица, а - произвольный элемент группы

ность была сообщена Л. С. Понтрягиным на широкий класс групп и применена к решению важных проблем топологии (т. н. проблем двойственности для компактов).

Лит.: Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; Чудаков Н. Г., Введение в теорию L-функций Дирихле, М. - Л., 1947; Л е н г С., Алгебра, пер. с англ., М., 1968; Боревич З. И., III а ф а р е в и ч И. Р., Теория чисел, 2 изд., М., 1972.

ХАРАКТЕР литературный, образ человека, очерченный с известной полнотой и индивидуальной определённостью, через к-рый раскрываются как обусловленный данной обществ.-ист. ситуацией тип поведения (поступки, мысли, переживания, речевая деятельность), так и присущая автору нравственно-эстетич. концепция человеческого существования. Художественный X. являет собой органич. единство общего, повторяющегося и индивидуального, неповторимого; объективного (социально-психологич. реальность человеческой жизни, послужившая прообразом для лит. Х.)и субъективного (осмысление и оценка прообраза автором). В результате X. в иск-ве предстаёт "новой реальностью", художественно "сотворённой" личностью, к-рая, отображая реальный человеческий тип, идеологически проясняет его. Именно концептуальность лит. образа человека отличает понятие X. в литературоведении от значений этого термина в психологии, философии, социологии.

Представление о X. лит. героя создаётся посредством внеш. и внутр. "жестов" (в т. ч. речи) персонажа, его внешности, авторскими и иными характеристиками, местом и ролью персонажа в развитии сюжета. Соотношение в пределах произведения X. и обстоятельств, являющихся художеств, воспроизведением социально-ист., духовно-культурной и природной среды, составляет художеств, ситуацию. Противоречия между человеком и обществом, между человеком и природой, его "земной участью", а также внутр. противоречия человеческих X. воплощаются в конфликтах художественных.

Воспроизведение X. в его многоплановости и динамике - специфич. свойство художеств, лит-ры в целом (и большинства театр, и кинематографич. жанров на словесно-сюжетной основе). Обращение к изображению X. знаменует выделение лит-ры как иск-ва из синкретич., "долитературной" религиозно-публицистич. словесности "библейского" или ср.-век. типа. Само понятие X. формируется в Др. Греции, где впервые вполне осуществилось выделение лит.-художеств, творчества в особую область духовной культуры.

Однако у древних понимание X. как лит. категории отличалось от современного: поскольку в раскрытии идейного содержания главенствовал сюжет (событие), персонажи различались прежде всего не своими X., а своей ролью в изображаемых событиях. В новое время утверждается иное соотношение X. и сюжета: не факты, а "...характеры действующих лиц, благодаря которым факты осуществились, заставляют поэта избрать предпочтительнее то, а не другое событие. Только характеры священны для него" (Лессинг Г. Э., Гамбургская драматургия, М.-Л., 1936, с. 92). Понимание самостоятельного идейно-художеств. значения X. персонажа возникает уже в антич. литературе; напр., в "Параллельных жизнеописаниях" Плутарха герои сравниваются и по типу "судьбы", и по типу X. Подобная характерологическая двумерность доминирует вплоть до 18 в. (по Д. Дидро - соотношение прирождённого "нрава" и "общественного положения").

В рамках данного многовекового периода особо выделяются две эпохи: лит-pa Возрождения и классицизма. Ренессансный X. теряет очертания определ. "нрава", растворяясь в естественной родовой стихии человеческой "природы" (герой мог самовольно, как бы актёрствуя, менять типы поведения). При этом соотнесение общечеловеческого в X. героя с его ситуативной функцией - судьбой - выявляло неадекватность герою его социально-ист. судьбы (предвосхищение характерологич. принципа реализма 19-20 вв.: "Человек или больше своей судьбы, или меньше своей человечности",- М.М. Бахтин, "Вопросы литературы", 1970, № 1, с. 119). У Шекспира мн. действующие лица предстали и в "третьем измерении" - носителями индивидуального самосознания. Классицизм, возвратившись к жёсткой статичности X., одновременно сосредоточил внимание на самосознании личности, совершающей выбор между "долгом" и "чувством". Но воспринимаемая на "фоне" долга и безличной страсти личность в лит-ре классицизма не самоценна, она лишь средство соотнесения двух параллельных рядов всеобщности.

На всех этих стадиях духовного и лит. развития X. понимался как внеист., универсальная и самотождественная данность человеческой природы, как "...абстракт, присущий отдельному индивиду" (Маркс К., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 3, с. 3). В романтизме, провозгласившем самоцельность и автономность личности, возвысившем её как над психология, "природой", так и над социальной судьбой, сложилось новое понимание X. - как тождественного внутр. миру личности. Наконец, воссоздание индивидуального X. как исторически неповторимого взаимоотношения личности и среды стало открытием критич. реализма 19 в. (романтич. традицию продолжили символисты и экзистенциалисты), активность личности, её ответственность за свой духовный мир и судьбы других людей.

В теории новое понимание художеств. X. было выдвинуто Гегелем: X. - "... цельная человеческая индивидуальность...", в к-рой раскрываются те или иные "...всеобщие субстанциальные силы действия"; X. является "подлинным средоточием" изображения, поскольку он объединяет в себе всеобщность и индивидуальность "...в качестве моментов своей целостности". X. должен обнаруживаться во всём богатстве своих индивидуальных особенностей, а не быть "...игралищем лишь одной страсти...", ибо в таком случае он "... выступает как существующий вне себя..."; он должен быть "...целым самостоятельным миром, полным, живым человеком, а не аллегорической абстракцией какой-нибудь одной черты характера" ("Эстетика", т. 1, М., 1968, с. 244-46). Эта теория, опиравшаяся на художеств. достижения прошлого, во многом предвосхищала практику последующей реалистич. лит-ры, где присутствует саморазвивающийся X. - незавершённая и незавершимая, "текучая" индивидуальность, определяемая её непрерывным взаимодействием с исторически конкретными обстоятельствами.

Послегегелевская лит. теория, опиравшаяся на реалистич. иск-во, настойчиво подчёркивала значение индивидуально-конкретного в X., но главное - выдвинула и разработала проблему его "концептуальное", установила необходимость "присутствия" авторского идеологич. понимания в изображении X. В реалистич. лит-ре 19-20 вв. X. действительно воплощают различные, порой противоположные авторские концепции человеческой личности. У О. Бальзака первоосновой индивидуальности выступает понимаемая в духе антропологизма общечеловеческая природа, а её "текучесть" объясняется незавершимостью внешних воздействий среды на первооснову, мерой к-рых и "измеряется" индивидуальность личности. УФ. М. Достоевского индивидуальность воспринимается на фоне детерминизма обстоятельств как мера личностного самоопределения, когда X. героя остаётся неисчерпаемым средоточием индивидуальных возможностей. Иной смысл "незавершённости" X. у Л. Н. Толстого: потребность "ясно высказать текучесть человека, то, что он, один и тот же, то злодей, то ангел, то мудрец, то идиот, то силач, то бессильнейшее существо" (Полн. собр. соч., т. 53, 1953, с. 187), объясняется стремлением открыть в индивидуальности, отчуждаемой от других людей обществ, условиями жизни, общечеловеческое, родовое, "полного человека".

У представителей "нового романа" намечается отказ от художеств, индивидуальности в пользу безличной психологии (как следствия отчуждения и конформизма), для воспроизведения которой X. начинает играть служебную роль "подпорки".

Творчество писателей социалистического реализма, наследуя характерологич. достижения предшествующих направлений и прежде всего реалистов 19 в., утверждает новое "видение" детерминирующих обстоятельств: социально-историч. и политич. действительность в её революц. развитии, в связи с чем социально-психологич. индивидуальность X. в их произведениях сгущается в индивидуальность конкретно-историческую. В лит-ре 60-70-х гг. 20 в. акцентируется нравств.

Лит.: Гегель, Эстетика, т. 1, М., 1968, с. 244-53; Социалистический реализм и классическое наследие. (Проблема характера). Сб. ст., М., 1960; Проблема характера в современной советской литературе, М.-Л., 1962; Бочаров С. Г., Характеры и обстоятельства, в кн.: Теория литературы, [кн. 1], М., 1962; Бахтин М. М., Проблемы поэтики Достоевского, 3 изд., М., 1972, с. 78 - 129; его же, Эпос и роман, в его кн.: Вопросы литературы и эстетики, М., 1975; Лихачев Д. С., Человек в литературе древней Руси, [2 изд.]. М., 1970; Гинзбург Л., О психологической прозе, [Л.], 1971; А в е р и н ц е в С. С., Плутарх и античная биография, М., 1973.

В. И. Тюпа.

ХАРАКТЕРИСТИКА в математике, 1) целая часть десятичного логарифма.

2) Понятие теории дифференциальных уравнений с частными производными.

X. дифференциального уравнения 1-го порядка

нек-рая функция двух переменных. Обратно, чтобы найти интегральную поверхность, проходящую через заданную кривую (см. Коши задача), достаточно построить геом. место X., пересекающих эту кривую. Задача Коши имеет одно и только одно решение, если заданная кривая не является X. Понятие X. обобщается на случай дифференциального уравнения 1-го порядка с числом независимых переменных, большим двух.

X. дифференциального уравнения 2-го порядка

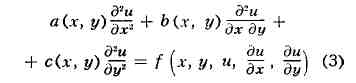
были введены Г. Монжем (1784, 1795) как линии, вдоль к-рых удовлетворяется обыкновенное дифференциальное уравнение

ady² - bdxdy + cdx² = 0. (4)

Если уравнение (3) принадлежит к гиперболич. типу, то получаются два семейства

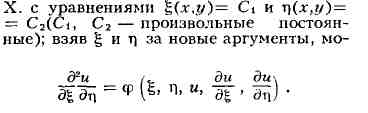
Для уравнения (3) параболич. типа эти семейства совпадают; если выбрать ар-

Значения решения и вдоль X. и значения ди/дх и ди/ду в к.-л. её точке полностью определяют значения этих производных вдоль всей линии [на этом основан т. н. метод X. решения краевых задач для уравнения (3)]; для других линий такой связи нет. С другой стороны, значения и, ди/дх и ди/ду, заданные на линии, не являющейся X., определяют значения решения вблизи этой линии; для X. же это не так. Если два решения уравнения (3) совпадают по одну сторону от нек-рой линии и различны по другую, то эта линия непременно является X.

Если коэффициенты уравнения (3) зависят от и, ди/дх а ди/ду (квазилинейный случай), то X., определяемые из уравнения (4), будут разные для разных решений. Имеются определения X. и для уравнений и систем уравнений с частными производными любого порядка.

Лит. см. при ст. Уравнения математической физики.

ХАРАКТЕРЙСТИКА в технике, взаимосвязь между зависимыми и независимыми переменными, определяющими состояние технич. объекта (процесса, прибора, устройства, машины, системы), выраженная в виде текста, таблицы, матем. формулы, графика и т. п. Напр., зависимости тока от электрич. напряжения на участке электрич. цепи (см. Вольтамперная характеристика), расхода топлива автомобилем от пройденного им пути и состояния дороги, громкости и качества звучания громкоговорителя от частоты, времени перемагничивания ферритового сердечника от величины намагничивающего поля.

X. по методике определения подразделяют на детерминированные (статические, динамические) и статистические; по виду аналитич. зависимости - на линейные и нелинейные; по назначению - на эксплуатационные, настроечные и т. д. Статич. X. наз. зависимость между выходной и входной величинами технич. системы в установившихся состояниях. Динамические X. (частотные, импульсные и др.) отражают реакции изучаемой системы ня к.-л. типовые возмущающие воздействия: напр., частотная X. отражает зависимость амплитуды и фазы периодич. сигнала на выходе системы от амплитуды и фазы входного гармонич. сигнала при изменении только его частоты; импульсная X. - зависимость изменения во времени сигнала на выходе системы от воздействия входного единичного импульса. В наиболее полной форме динамич. X. содержатся в динамич. матем. модели объекта, напр., в виде дифференциальных уравнений. Статистич. X. (оценки) применяют к объектам, поведение к-рых во времени меняется случайным образом. К статистич. X. относятся, напр., дисперсия, автокорреляционная функция, спектральная плотность и т. п.

Линейными наз. все X., к-рые могут быть с заданной точностью аппроксимированы выражением вида у = ах + b, где у - выходное воздействие, х - входное воздействие изучаемой системы, а и b -постоянные коэфф. Все остальные X. - нелинейные; среди них выделяют линеаризуемые X., к-рые по частям с известной точностью аппроксимируются указанным выше выражением (см. Линеаризация).

А. В. Кочеров.

ХАРАКТЕРИСТИЧЕСКАЯ КРИВАЯ, одна из важнейших характеристик фотографич. материала, выражающая зависимость (при оговорённых условиях экспонирования и проявления) между оптической плотностью полученного на материале почернения фотографического и десятичным логарифмом экспозиции (наз. также количеством освещения), вызвавшей это почернение. См. ст. Сенситометрия (рис. 1) и лит. при ней.

ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ в математике, 1) то же, что собственная функция. 2) X. ф. множества А (в соврем. терминологии - индикатор А) - функция f(x), определённая на нек-ром множестве Е, содержащем множество А, и принимающая значение f(x)=1, если х принадлежит множеству А, и значение f(x)=0, если х не принадлежит ему. 3) В теории вероятностей X. ф. fx(t) случайной величины X определяется как математическое ожидание величины е^itX. Это определение для случайных величин, имеющих плотность вероятности рх(х), приводит к формуле

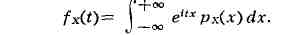
Напр., для случайной величины, имеющей нормальное распределение с параметрами а и о, X. ф. равна

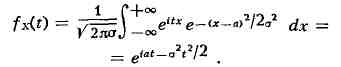
Свойства X. ф.: каждой случайной величине X соответствует определённая X. ф. fx(t); распределение вероятностей для X однозначно определяется по fx(t); при сложении независимых случайных величин соответствующие X. ф. перемножаются; при надлежащем определении понятия "близости" случайным величинам с близкими распределениями соответствуют X. ф., мало отличающиеся друг от друга, и, обратно, близким X. ф. соответствуют случайные величины с близкими распределениями. Указанные свойства лежат в основе применений X. ф., в частности к выводу предельных теорем теории вероятностей. Впервые аппарат, по существу равнозначный X. ф., был использован П. Лапласом (1812), но вся сила метода X. ф. была показана А. М. Ляпуновым (1901), получившим с его помощью свою известную теорему.

Понятие X. ф. может быть обобщено на конечные и бесконечные системы случайных величин (т. е. на случайные векторы и случайные процессы).

Теория X. ф. имеет много общего с теорией Фурье интеграла.

Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973.

ХАРАКТЕРИСТИЧЕСКИЕ СПЕКТРЫ, линейчатые рентгеновские спектры, вызванные электронными переходами на внутр. оболочки (слои) атомов. Длины волн X. с. лежат в интервале от 10~² или до 5-10 нм и, согласно Мозли закону, зависят от атомного номера элемента. Они не обнаруживают периодич. закономерностей, присущих оптич. спектрам, что объясняется сходным строением внутр. электронных оболочек всех элементов.

X. с. возникают при возбуждении атомов рентгеновскими фотонами или ускоренными электронами. При этом выбивается один из внутр. электронов, напр., с К-оболочки атома, и в ней появляется вакансия, к-рая заполняется при переходе электрона с L-, М- или более высоко лежащей оболочки с испусканием рентгеновского фотона определённой частоты. Совокупность линий, возникающих при переходах электронов с вышележащих оболочек на К-, L.- и т. д. оболочки, наз., соответственно, К-, L- и т. д. сериями. Внутри серии линии принято обозначать индексами а, (3, 7 и т. д. Напр., линия перехода L->К обозначается К* (см. рис. 1 в ст. Рентгеновские спектры). Дискретность, присущая X. с. испускания, проявляется и в спектрах поглощения рентгеновских лучей (см. рис.).

Зависимость коэффициента поглощения ц от частоты излучения v для Pt. Показаны К-, L-, М-и N- серии спектра поглощения рентгеновского излучения.

X. с. используют для исследований структуры материалов (см. Рентгеновский структурный анализ, Рентгенография материалов, Рентгеновская топография), а также в спектральном анализе рентгеновском.

А. В. Колпаков.

ХАРАКТЕРИСТИЧЕСКИЕ ЧАСТОТЫ, одинаковые или мало отличающиеся друг от друга частоты колебаний определённых групп атомов в различных молекулах; соответствуют определённым хим. связям (напр., С - Н, С - С, С = С, С-С1 и др.). Устойчивость X. ч. связана с сохранением динамич. свойств одинаковых групп атомов в разных молекулах. Во мн. случаях можно теоретически рассчитать, обладает ли определённая хим. группа X. ч. Интенсивности спектральных линий, соответствующих X. ч. определённой хим. группы в различных молекулах, часто имеют близкие значения. Наличие X. ч. в молекулярных спектрах позволяет делать выводы о строении молекул и имеет большое значение в спектральном анализе. По изменению интенсивностей X. ч. можно судить о скорости хим. процессов.

Лит.: М а я н ц Л.С., Теория it расчет колебаний молекул, М., I960; Колебания молекул, 2 изд., М., 1972; Свердлов Л.М., К о в н е р М.А., Крайнев Е.П., Колебательные спектры многоатомных молекул, М., 1970; Б е л л а м и Л.Д., Инфракрасные спектры сложных молекул, пер. с англ., 2 изд., М., 1963; Применение спектроскопии в химии, пер. с англ., М., 1959.

Л.Ф. Уткина.

ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА (матем.), то же, что собственные значения.

ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН, многочлен, стоящий в левой части характеристического уравнения.

ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ в математике, 1) Х. у. матрицы - алгебр. ур-ние вида

из диагональных элементов. Этот определитель представляет собой многочлен относительно X - характеристический многочлен. В раскрытом виде X. у. записывается так:

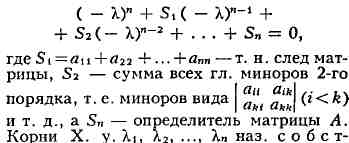
венными значениями матрицы А. У действительной симметричной матрицы, а также у эрмитовой матрицы все Хи действительны, у действительной кососимметричной матрицы все X* чисто мнимые числа; в случае действительной ортогональной матрицы, а также унитар-

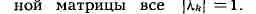
X. у. встречаются в самых разнообразных областях математики, механики, физики, техники. В астрономии при определении вековых возмущений планет также приходят к X. у.; отсюда и второе название для X. у. - вековое уравнение.

2)Х. у. линейного дифференциального уравнения с постоянными коэффициентами

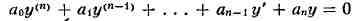
- алгебр. ур-ние, к-рое получается из да ного дифференциального ур-ния пос. замены функции y и её производных с ответствующими степенями величины т. е. ур-ние

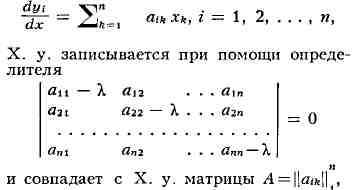
составленной из коэфф. ур-ний данной системы.