УПРАВЛЕНИЯ АВТОМАТИЗИРОВАННАЯ СИСТЕМА (АСУ), совокупность экономико-математич. методов, технич. средств (ЭВМ, средств связи, устройств отображения информации, передачи данных и т. д.) и организационных комплексов, обеспечивающих рациональное управление сложным объектом (напр., предприятием, технологич. процессом). Наиболее важная цель построения всякой АСУ - резкое повышение эффективности управления объектом (производственным, административным и т. д.) на основе роста производительности управленческого труда и совершенствования методов планирования и гибкого регулирования управляемого процесса. В СССР АСУ создаются на основе гос. планов развития нар. х-ва.

Основные принципы. Разработка АСУ, порядок их создания и направления эффективного использования базируются на след. принципах (впервые сформулированных В. М. Глушковым).

Принцип новых задач. АСУ должны обеспечивать решение качественно новых управленческих проблем, а не механизировать приёмы управления, реализуемые неавтоматизированными методами. На практике это приводит к необходимости решения многовариантных оптимизационных задач на базе экономико-математич. моделей большого объёма (масштаба). Конкретный состав подобных задач зависит от характера управляемого объекта. Напр., для машиностроит. и приборостроит. предприятий обычно наиболее важными оказываются задачи оперативно-календарного и объёмно-календарного планирования. Решающий эффект достигается в том случае, когда осуществляется точное согласование во времени всех сменных заданий как производственных, так и обеспечивающих (напр., на материально-технич. снабжение и др.), определяются оптимальные объёмы партий продукции и производится оптимизация загрузки оборудования. Аналогичные задачи возникают в стр-ве. В ряде случаев на первый план выдвигаются задачи технич. подготовки произ-ва, управления проектно-конструкторскими работами. На транспорте важнейшее значение приобретают оптимизация маршрутов и расписаний движения, а также погрузочно-разгрузочных работ. В системах управления отраслью первостепенное значение имеют оптимальное планирование работы предприятий, точное согласование сроков взаимных поставок, а также проблемы перспективного развития отрасли и задачи прогнозирования.

Принцип системного подхода к проектированию АСУ. Проектирование АСУ должно основываться на системном анализе как объекта, так и процессов управления им. Это означает необходимость определения целей и критериев эффективности функционирования объекта (вместе с системой управления), анализа структуры процесса управления, вскрывающего весь комплекс вопросов, к-рые необходимо решить для того, чтобы проектируемая система наилучшим образом соответствовала установленным целям и критериям. Этот комплекс охватывает вопросы не только технич., но также экономич. и организац. характера. Поэтому внедрение АСУ даёт принципиально новые возможности для коренного усовершенствования системы экономических показателей и экономического стимулирования.

Принцип первого руководителя. Разработка требований к системе, а также создание и внедрение АСУ возглавляются осн. руководителем соответствующего объекта (напр., директором завода, нач. главка, министром).

Принцип непрерывного развития системы. Осн. идеи построения, структура и конкретные решения АСУ должны позволять относительно просто настраивать систему на решение задач, возникающих уже в процессе эксплуатации АСУ в результате подключения новых участков управляемого объекта, . расширения и модернизации технич. средств системы, её инфор-мационно-математич. обеспечения и т. д. Математическое обеспечение АСУ строится таким образом, чтобы в случае необходимости можно было легко менять не только отд. программы, но и критерии, по к-рьш ведётся управление.

Принцип единства информационной базы. На машинных носителях информации накапливается (и постоянно обновляется) информация, необходимая для решения не какой-то одной или неск. задач, а всех задач управления. При этом в т. н. основных (генеральных) массивах исключается неоправданное дублирование информации, к-рое неизбежно возникает, если первичные информационные массивы создаются для каждой задачи отдельно. Осн. массивы образуют информац. модель объекта управления. Напр., на уровне предприятий осн. массивы должны содержать самую подробную информацию обо всех элементах произ-ва: кадровые данные на всех работающих; сведения об осн. фондах (земле, помещении, оборудовании со всеми характеристиками, необходимыми для принятия решений по их использованию, перераспределению и т. п.); данные о запасах, включая запасы на промежуточных складах и незавершённое произ-во; информацию о состоянии оборудования; нормативы (трудовые и материальные) и технологич. маршруты (последовательности производств. операций, необходимых для изготовления деталей, узлов и готовых изделий); планы (включая заявки на материально-технич. снабжение); цены и расценки; сведения о текущем состоянии банковских счетов предприятия и др. Система обработки первичных документов, а также система автоматич. датчиков должны быть организованы таким образом, чтобы данные о любом изменении, происходящем на предприятии, в минимально короткий срок вводились в ЭВМ, а затем автоматически или по указанию оператора периодически распределялись по осн. массивам и при этом чтобы сохранялось состояние готовности выдать любую информацию об объекте. В случае необходимости из осн. массивов оперативно формируются производные массивы, ориентированные на те или иные производства, изделия или комплексы задач. Производные массивы в таком случае являются вторичными.

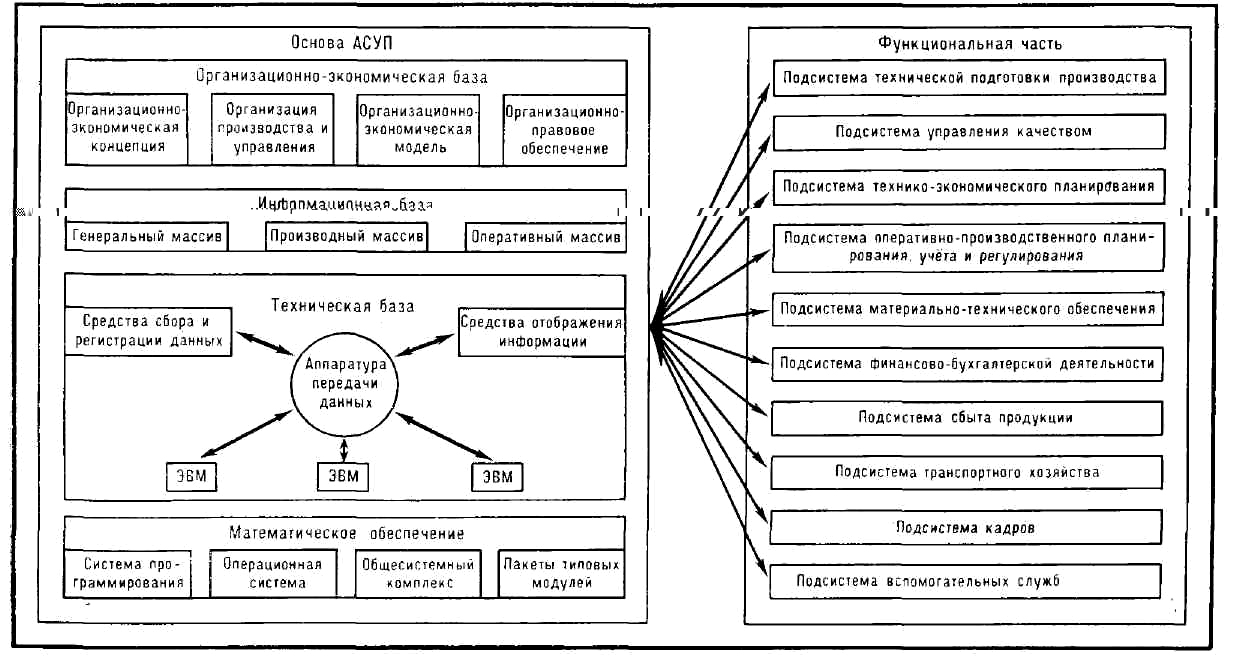
Структурная схема автоматизированной системы управления предприятием:  

Принцип комплексности задач и рабочих программ. Большинство процессов управления взаимосвязаны и поэтому не могут быть сведены к простому независимому набору отд. задач. Напр., задачи материаль-но-технич. снабжения органически связаны со всем комплексом задач оперативно-календарного и объёмно-календарного планирования; задание на материально-технич. снабжение составляется исходя из задач планирования произ-ва, а при срывах в снабжении (по срокам и по номенклатуре) возникает необходимость трансформации планов. Раздельное решение задач планирования и материально-технич. снабжения может значительно снизить эффективность АСУ. Принцип комплексности задач и рабочих программ характерен практически для всех классов автоматизированных систем обработки данных (проектирования, испытаний и др.).

Принцип согласования пропускной способности различных звеньев системы. Скорость обработки данных в различных сопряжённых контурах системы должна быть согласована таким образом, чтобы избежать информац. заторов (когда возникает объективная возможность потери данных) или больших информац. пробелов (приводящих к неэффективному использованию нек-рых элементов АСУ). Напр., не имеет смысла увеличивать скорость выполнений арифметич. операций ЦВМ, если при решении конкретных задач АСУ "узким местом" в системе является ввод данных или обмен информацией между внешней памятью и центральным процессором.

Принцип типовости. Разрабатывая технич. комплекс, системное математич. обеспечение, рабочие программы и связанные с ними формы и состав информац. массивов, исполнитель обязан стремиться к тому, чтобы предлагаемые им решения подходили возможно более широкому кругу заказчиков. Необходимо в каждом случае определять разумную степень типизации, при к-рой стремление к широкому охвату потребителей не приведёт к существ. усложнению типовых решений. Типизация решений способствует концентрации сил, что необходимо для создания комплексных АСУ.

В зависимости от целевого назначения АСУ можно разделить на два больших класса: АСУ объектами, предусматривающие управление объектом в целом (по всем функциям), и функциональные АСУ, обеспечивающие автоматизацию той или иной функции управления для широкого класса объектов. АСУ объектами по типу управляемого объекта делятся на АСУ технологич. процессами, АСУ цехами, АСУ предприятиями (напр., заводами, НИИ, КБ) - АСУП, АСУ отраслями народного хозяйства (напр., пром-стью, связью, транспортом) - ОАСУ и т. д. К функциональным АСУ относят, напр., автоматизированную систему плановых расчётов, автоматизированную систему материально-технич. снабжения, автоматизированную систему статистич. учёта и т. д.

Состав АСУ

АСУ состоит из основы и функциональной части. Обобщённая структурная схема АСУ (на примере АСУП) представлена на рис.

Основу АСУ составляют информац. база, технич. база, математич. обеспечение, организационно-экономич. база. Основа - общая часть для всех задач, решаемых АСУ.

Информационная база АСУ - размещённая на машинных носителях информации совокупность всех данных, необходимых для автоматизации управления объектом или процессом. Обычно информац. база делится на три массива: генеральный, производный и оперативный. Конструкция массивов и их полей (способы размещения на носителях, особенности взаимосвязи данных внутри массива, конкретная компоновка данных и т. д.) определяется типом АСУ и общими характеристиками объектов, для к-рых она предназначается. Однако целесообразно сохранять типовое конструктивное построение информац. базы для общего класса объектов (напр., для машиностроит. предприятий). Генеральный массив объединяет данные, являющиеся общими для всех задач, размещение к-рых отвечает универсальной структуре, не ориентированной на выполнение к.-л. одной функции управления. Генеральный массив для крупного объекта содержит сотни миллионов символов, занимает большие объёмы запоминающих устройств и не всегда удобен для использования в каждой конкретной задаче, требующей для своего решения специализированной информации. Эта проблема осложняется при мультипрограммной обработке данных и недостаточно ёмких оперативных запоминающих устройствах, предполагающих хранение многих массивов в машинных архивах (лентотеках, картотеках), функционально разобщённых с процессорами. В связи с этим в реально функционирующих АСУ возникает необходимость формирования производных массивов, отражающих специфику структуры объекта, особенности выполняемых в каждый период функций, частоту повторяемости различных задач и ряд др. факторов, связанных с текущей работой системы. Все производные массивы, как правило, формируются из генерального массива. Всякое устойчивое изменение характеристик обслуживаемого объекта должно быть отражено в генеральном массиве. Оперативный массив охватывает текущую информацию, а также промежуточные результаты вычислений. В нём же размещается первичная информация о состоянии обслуживаемого объекта, поступающая периодически по каналам связи или записанная на автономных носителях (перфолентах, перфокартах, магнитных лентах и т. д.). Обработанные и обобщённые данные могут затем вноситься в производный и генеральный массивы либо непосредственно выдаваться потребителю.

Техническая база АСУ включает средства обработки, сбора и регистрации, отображения и передачи данных, а также исполнительные механизмы, непосредственно воздействующие на объекты управления (напр., автоматич. регуляторы, датчики и т. д.), обеспечивающие сбор, хранение и переработку информации, а также выработку регулирующих сигналов во всех контурах автоматизированного управления произ-вом. Осн. элементы технич. базы - ЭВМ, к-рые обеспечивают накопление, хранение и обработку данных, циркулирующих в АСУ. ЭВМ позволяют оптимизировать параметры управления, моделировать произ-во, подготавливать предложения для принятия решения. Обычно выделяют два класса ЭВМ, используемых в АСУ: информационно-расчётные и учётно-регулирующие. Информационно-расчётные ЭВМ находятся на высшем уровне иерархии управления (напр., в координационно-вычислит. центре завода) и обеспечивают решение задач, связанных с централизованным управлением объектом по осн. планово-экономическим, обеспечивающим и отчётным функциям (технико-экономич. и оперативно-производств. планирование, материально-технич. снабжение, сбыт продукции и т. д.). Они характеризуются высоким быстродействием, наличием системы прерываний, слоговой обработкой данных, переменной длиной слова, мультипрограммным режимом работы и т. д., а также широким набором и большим объёмом запоминающих устройств (оперативных, буферных, внешних, односторонних и двусторонних, с произвольным и последовательным доступом). В СССР в 70-х гг. в качестве типовых информационно-расчётных ЭВМ для АСУ принята единая система ЭВМ (ЕС ЭВМ). Учётно-регулирующие ЭВМ, как правило, относятся к нижнему уровню управления. Они размещаются обычно в цехах или на участках и обеспечивают сбор информации от объектов управления (станков, складов и т. д.), первичную переработку этой информации, передачу данных в информационно-расчётную ЭВМ и получение от неё директивно-плановой информации, осуществление локальных расчётов (напр., расписания работы каждого станка и рабочего, графика подачи комплектующих изделий и материалов, группировки деталей в партии, режимов обработки и т. д.) и выработку управляющих воздействий на объекты управления при отклонении режимов их функционирования от расчётных. Особенность учётно-регулирующих ЭВМ - хорошо развитая система автоматич. сопряжения с большим числом источников информации (датчиков, регистраторов) и регулирующих устройств. Их вычислит. часть менее развита, поскольку первично обработанная информация передаётся в ЭВМ верхнего уровня для дальнейшего использования и длит. хранения. Примеры учётно-регулирующих ЦВМ - "Днепр" и М-6000.

Средства сбора и регистрации данных при участии человека включают различные регистраторы произ-ва, с помощью к-рых осуществляются сбор и регистрация данных непосредственно на рабочих местах (напр., в цехе, на участке, станке), а также датчики (темп-ры, количества изготовленных деталей, времени работы оборудования и т. д.), фиксаторы нарушений установленного технологич. и организац. ритма (отсутствие заготовок, инструмента, материалов, неправильная наладка станков, отсутствие трансп. средств для отправки готовой продукции и т. д.). Напр., типовыми регистраторами производства являются устройства РИ-7501 (цеховой регистратор) и РИ-7401 (складской регистратор).

Средства отображения информации предназначены для представления результатов обработки информации в удобном для практич. использования виде. К ним относятся различные печатающие устройства, пишущие машины, терминалы, экраны, табло, графопостроители, индикаторы и т. п. Эти устройства, как правило, непосредственно связаны с ЭВМ или с регистраторами производства и выдают либо регулярную (регламентную), либо эпизодическую (по запросу или в случае аварийной ситуации) справочную, директивную или предупредит. информацию.

Аппаратура передачи данных осуществляет обмен информацией между различными элементами АСУ (между регистраторами производства и ЭВМ, между координационно-управляющим центром и цеховыми ЭВМ и т. д.), а также между АСУ и смежными управления уровнями (напр., между АСУП и ОАСУ, между территориальными вычислительными центрами).

К технич. базе АСУ относят также средства оргтехники (копировально-множительную технику, картотеки, диктофоны и т. д.), а также вспомогат. и контрольно-измерит. средства, обеспечивающие нормальное функционирование осн. технич. средств в требуемых режимах.

Математическое обеспечение АСУ - комплекс программ регулярного применения, управляющих работой технич. средств и функционированием информац. базы и обеспечивающих взаимодействие человека с технич. средствами АСУ. Математич. обеспечение условно можно подразделить на систему программирования, операционную систему, общесистемный комплекс и пакеты типовых модулей.

Система программирования обеспечивает трансляцию программы решения задачи, выраженной на удобном для человека формализованном языке, на машинный язык, её отладку, редактирование и включение в пакет программ для обработки. В систему программирования входят описания языков программирования, комплекс трансляторов, библиотека стандартных подпрограмм, программы редактирования связей, наборы программ, осуществляющих преемственность (программную) ЭВМ различных типов. Кроме того, система программирования обычно содержит в своём составе набор программ, облегчающих взаимодействие пользователя с машиной и позволяющих системе программирования развиваться в зависимости от характера задач, решаемых потребителем. В качестве типовых языков программирования для АСУ в СССР приняты алгол-68, фортран, кобол ,универсальный язык высшего уровня ПЛ-1, а также машинно-ориентированные языки типа "Ассемблера".

Операционные системы обеспечивают функционирование всех устройств ЭВМ в требуемых режимах и выполнение необходимой последовательности заданий на реализацию различных процедур управления. Операционные системы, как правило, являются неотъемлемой составной частью тех вычислит. средств, к-рые входят в состав АСУ. Однако в ряде случаев при проектировании АСУ приходится расширять операционные системы для обеспечения спец. системных требований (напр., при подключении к системе специфичных для управляемого процесса регистраторов и систем отображения, при организации диалоговых режимов между терминалами и центр. вычислит. комплексом). В этой связи очень важной составной частью операционной системы АСУ является т. н. генератор систем. Это - программа, к-рая не входит в состав активной части управляющих программ и не связана непосредственно с процессом вычислений, но с помощью к-рой можно автоматически генерировать комплекс управляющих программ для системы любой конфигурации. Такой метод оказывается особенно эффективным при использовании ЭВМ в широком диапазоне АСУ на различных уровнях и на различных объектах, когда состав ЭВМ и состав решаемых задач может быть существенно различным.

Общесистемный комплекс охватывает набор программ, управляющих работой вычислит. системы и периферийных устройств (регистраторов, средств отображения результатов обработки данных и т. д.). Этот комплекс содержит программы совместной работы неск. ЭВМ, комп-лексируемых по различным уровням запоминающих устройств, программы обслуживания каналов связи, дистанц. решения задач в режиме разделения времени, разграничения доступа к информац. массивам и др. К общесистемным комплексам относят также информационно-поисковые системы, осуществляющие целенаправленный поиск требуемых массивов (или формирование необходимых массивов из фрагментов данных), их редактирование и выдачу потребителю в заданной форме (либо передачу этих массивов в запоминающее устройство для использования очередными рабочими программами). К ним же относят программы обслуживания средств. работающих в реальном масштабе времени, а также обслуживания терминальных устройств и средств отображения информации.

Пакеты типовых прикладных модулей (стандартных подпрограмм) могут использоваться в различных комбинациях при решении той или иной функциональной задачи. Типовыми, напр., являются прикладные модули сортировки данных, статистич. обработки информации, обработки сетевых графиков планирования и управления, моделирования реальных процессов и др. К математич. обеспечению АСУ часто относят также программы функционального анализа системы, обеспечивающие удобство эксплуатации и совершенствования системы.

Под организационно-экономической базой понимается совокупность экономич. принципов, методов организации произ-ва и управления, схем взаимодействия задач управления на основе правовых документов. Сюда входят организационно-экономич. состав и способы формирования технико-экономич. показателей управляемого объекта, а также осн. принципы повышения эффективности его функционирования и место АСУ в общей системе планирования, учёта и регулирования; организация произ-ва, труда и управления, определяющая рациональную структуру объекта (цеха, отдела и т. д.), порядок реализации технологич. маршрутов, наиболее благоприятные условия работы, сохраняющие высокую работоспособность рабочих и служащих, а также научно обоснованную систему управления объектом, чёткие положения о всех подразделениях, их подчинённости, обязанностях сотрудников и их ответственности; организационно-экономич. модель, предусматривающая построение схемы взаимодействия осн. задач АСУ, структуры информац. потока, а также методич. обеспечение порядка реализации задач и использования результатов их решения; организационно-правовое обеспечение (правовые основы и нормы создания и использования АСУ, правовой статус циркулирующей в АСУ информации, а также права и ответственность должностных лиц). Кроме того, организационно-экономич. база включает методич. и инструктивные материалы, определяющие влияние АСУ на осн. показатели функционирования объекта, оценку эффективности и пути дальнейшего развития АСУ.

Функциональная часть АСУ состоит из набора взаимосвязанных программ для реализации конкретных функций управления (планирование, финансовобухгалтерскую деятельность и др.). Все задачи функциональной части базируются на общих для данной АСУ информац. массивах и на общих технич. средствах. Включение в систему новых задач не влияет на структуру основы и осуществляется посредством типового для АСУ информац. формата и процедурной схемы. Функциональную часть АСУ принято условно делить на подсистемы в соответствии с осн. функциями управления объектом. Подсистемы в свою очередь делят на комплексы, содержащие наборы программ для решения конкретных задач управления в соответствии с общей концепцией системы. Состав задач функциональной части АСУ определяется типом управляемого объекта, его состоянием и видом выполняемых им заданий. Напр., в АСУ предприятием часто выделяют следующие подсистемы: технич. подготовки произ-ва; управления качеством продукции; технико-экономич. планирования; оперативно-производств. планирования; материально-технич. обеспечения; сбыта продукции; финансово-бухгалтерской деятельности; планирования и расстановки кадров; управления транспортом; управления вспомогат. службами. Деление функциональной части АСУ на подсистемы весьма условно, т. к. процедуры всех подсистем тесно взаимосвязаны и в ряде случаев невозможно провести чёткую границу между различными функциями управления (напр., между технико-экономич. планированием, оперативно-производств. планированием и материально-технич. обеспечением). Выделение подсистем используется для удобства распределения работ по созданию системы и для привязки к соответствующим организац. звеньям объекта управления. Структура функциональной части АСУ зависит от схемы процедур управления, определяющей взаимосвязь всех элементов управления и охватывающей автоматизированные, частично механизированные и ручные процедуры. Функциональная часть более мобильна, чем основа, и допускает изменение состава и постановки задач при условии обеспечения стандартного сопряжения с базовыми элементами системы.

Перспективным направлением развития АСУ является создание Общегосударственной автоматизированной системы управления (ОГАС), предусматривающей взаимную связь управления всеми административными, пром. и др. объектами страны с целью обеспечения оптимальных пропорций развития нар. х-ва СССР, выработки напряжённых сбалансированных плановых заданий и их безусловного выполнения. Технич. базой ОГАС станет Единая гос. сеть вычислительных центров, осуществляющая информац. и функциональную координацию работы всех вычислит. центров страны.

Лит.: Глушков В. М., Введение в АСУ, 2 изд., К., 1974; Жимери н Д. Г., Мясников В. А., Автоматизированные и автоматические системы управления, М., 1975.

И. А. Данильченко.

УПРАВЛЕНИЯ НАРОДНЫМ ХОЗЯЙСТВОМ ИНСТИТУТ (ИУНХ), высшее учебное научно-методич. учреждение по повышению квалификации руководящих работников нар. х-ва в области совр. методов управления, организации про-из-ва и планирования. Учреждено при Гос. комитете Сов. Мин. СССР по науке и технике (1970). Слушатели ИУНХ - лица с высшим образованием из числа руководителей гос. комитетов, общесоюзных, союзно-респ. мин-в и ведомств, крупных производств. объединений и предприятий. В институте обучаются также слушатели из социалистических стран. Срок обучения (с отрывом от производства) 3 мес. В составе института (1975): научно-методический отдел, 4 кафедры (социально-экономич. наук; экономико-математич. методов планирования, управления и прогнозирования; автоматизированных систем управления; социо-логич. и психологич. аспектов управления), проблемная н.-и. лаборатория экономико-математич. методов и исследования операций, учебно-вычислит. центр. Ин-т осуществляет методич. руководство и координацию деятельности системы институтов повышения квалификации руководящих работников нар. х-ва в области науч. методов управления, подготавливает и издаёт учебную и методич. литературу. В 1972-75 коллективом преподавателей ин-та подготовлена серия из 8 книг "Наука и управление", где освещены актуальные проблемы теории и практики управления.

В. Г. Шорин.

УПРАВЛЕНИЯ СИСТЕМА С ПЕРЕМЕННОЙ СТРУКТУРОЙ (СПС), нелинейная система автоматич. управления, состоящая из совокупности непрерывных подсистем (наз. структурами) с определённым правилом перехода в процессе функционирования от одной структуры данной совокупности к другой. В СПС устройство управления содержит ключевые элементы, к-рые разрывают или восстанавливают связи между функциональными элементами системы, изменяя тем самым каналы передачи воздействий и обеспечивая переход от одной структуры системы к другой (рис. 1). Такой принцип построения устройства управления существенно расширяет возможности управления вследствие использования полезных свойств каждой из структур и, кроме того, позволяет получить новые свойства, не присущие ни одной из них.

Особенности СПС можно пояснить на примере простейшей системы автоматич. управления (САУ), поведение (движение) к-рой описывается дифференциальным ур-нием

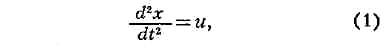
где х - управляемая величина, и - управляющее воздействие, t - время. Пусть в САУ (1) возможна реализация лишь положительной (и = вx, Р = const > 0) и отрицательной (и = -ах, а = const>0) обратной связи (а и в - коэфф. передачи цепи обратной связи). При положит. обратной связи движение САУ описывается

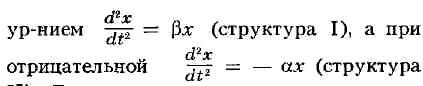
II). Для наглядного представления поведения (движения) САУ строят её фазовые портреты (см. Фазовой плоскости метод) для структуры I (рис. 2, а) и структуры II (рис. 2, б).

Задача состоит в том, что требуется выбрать такое управление и из класса возможных управлений, при к-ром система обладает асимптотич. устойчивостью. Из анализа фазовых портретов системы следует, что ни положит., ни отрицат. обратная связь порознь не решает поставленной задачи. Поэтому в соответствии с методами СПС реализуют следующее правило изменения структур:

Фазовый портрет такой системы изображён на рис. 2, в; из анализа портрета следует, что изображающая точка из произвольного начального положения попадает на прямую s = 0, проходящую через начало координат, в окрестности к-рой фазовые траектории направлены навстречу друг другу и, следовательно, изображающая точка не может покинуть эту прямую. Траектория 5 = 0 не принадлежит ни одной из структур (I или II), поэтому, согласно (2), за счёт переключения управления и в системе происходит смена структур теоретически с бесконечной частотой. Такой режим движения наз. скользящим, а за ур-ние движения принимается ур-ние прямой 5 = 0:

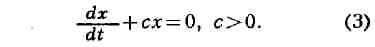
Все решения ур-ния (3) стремятся к нулю при t-> оо, т. е. поставленная задача решена. Существенно, что движение системы в скользящем режиме не зависит от характеристик объекта управления и коэфф. обратной связи, качество переходного процесса определяется только выбором параметра с.

Рассмотренный пример показывает, что посредством сочетания неприемлемых порознь структур и за счёт использования скользящих режимов можно синтезировать СПС, обладающие рядом положит. свойств, в частности апериодич. устойчивостью и параметрич. инвариантностью. С помощью СПС решается широкий круг задач теории управления, напр. задачи высококачеств. воспроизведения задающего воздействия при инвариантности к параметрич. и внеш. возмущениям, многосвязного регулирования, оптимизации и др.

Лит.: Емельянов С. В., Системы автоматического управления с переменной структурой, М., 1967; Системы с переменной структурой и их применение в задачах автоматизации полёта, М., 1968; Теория систем с переменной структурой, М., 1970; Уткин В. И., Скользящие режимы и их применения в системах с переменной структурой, М., 1974.

Б. З. Голембо, С. К. Коровин.

УПРАВЛЕНИЯ УРОВНИ, относит. градации совокупностей элементов управления сложной системы, сгруппированных и выделенных в соответствии с иерархическим принципом. Элементы управления разных уровней взаимосвязаны и имеют чёткое подчинение. В иерархич. системах управления каждое подразделение (подсистема) решает задачи только своего уровня; исходная информация для принятия решения и выработки управляющих воздействий передаётся снизу вверх, а управляющая информация (воздействия) - сверху вниз. Напр., в цифровой вычислительной машине (ЦВМ) работу отд. устройств (запоминающего устройства, печатающего устройства и др.) координирует (в соответствии с заданной программой вычислений) центр. управляющее устройство, одним из элементов к-рого является пульт управления ЦВМ (высший У. у.). Местные устройства управления (низший У. у.) по командам центр. устройства управления вырабатывают (в соответствии с собственным алгоритмом функционирования) сигналы на выполнение отд. операций, к-рые в совокупности представляют собой вычислит. процесс. В автоматизированных системах управления технологич. процессами (АСУТП) автоматич. регуляторы, управляющие работой исполнит. механизмов и рабочих машин, и измерительные преобразователи (датчики), осуществляющие контроль за ходом технологич. процесса, составляют низший У. у. Контрольно-измерительная информация с датчиков поступает на пульт управления диспетчера или в управляющую ЭВМ (высший уровень), к-рые оценивают правильность выполнения рабочих операций и вырабатывают команды, поступающие на элементы низшего У. у. (см. Управление в технике). В более сложных системах, напр. в автоматизированных системах управления отраслью (ОАСУ) и предприятием (АСУП), в единых энергосистемах выделяют 3 и более
 

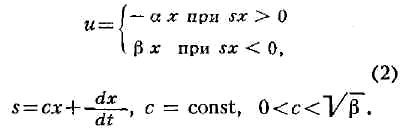
Разделение функции управления по У. у. в сложных системах позволяет ограничить круг задач, решаемых каждым подразделением, упорядочить распределение информации между элементами управления, упростить отчётность и сократить число разновидностей документации, улучшить качество принимаемых решений.

Лит. см. при ст. Сложная система.

УПРАВЛЕНЧЕСКОЙ РЕВОЛЮЦИИ ТЕОРИЯ, теория "революции управляющих", одна из технократических теорий совр. бурж. социаль-но-экономич. мысли, выдвигающая тезис о якобы произошедшем устранении власти капиталистов-собственников над корпорациями и банками и переходе её в руки специалистов-управляющих, технократов и бюрократов. Использует для обоснования этого тезиса переход к акц. форме предприятий и новую роль управ-ленч. и инженерно-организационных наук в капиталистич. произ-ве. Является составной частью "народного капитализма" теории. Ряд её положений сформулирован в 30-е гг. 20 в. в работах Г. Минса и А. Берли (США) в виде теорий корпоративной революции и контроля менеджеров. Сформировалась как концепция в 40-е гг. в работах амер. экономистов Дж. Бёрнхема (теория новой собственности и нового господствующего класса) и П. Друкера (теория нового общества, теория функций управления). В конце 60-70-х гг. пропагандируется Дж. Гэлбрейтом (теория техноструктуры, теория новой корпорации). Использована в работах Л. Блюма (Франция), Дж. Стрейчи (Великобритания), К. Реннера (Австрия), югосл. ревизиониста М. Джиласа и др. для затушёвывания коренного различия между капитализмом и социализмом.

В 3-м томе "Капитала" К. Маркс показал, что в акционерных обществах происходит не только отделение ведущего произ-во "функционирующего капиталиста" (собственника лишь части капитала) от остальных капиталистов-собственников, ссужающих свой капитал, но и отделение наёмных служащих, управляющих произ-вом (но не владеющих "...капиталом ни под каким титулом..."), от функционирующих капиталистов (см. К. Маркс и Ф. Энгельс, Соч., 2 изд., т. 25, ч. 1, с. 427). Он отметил двойственный характер этого "...многочисленного класса промышленных и торговых управляющих...", к-рые, с одной стороны, непосредственно эксплуатировали рабочих (функция надзора) и, с другой стороны, трудились сами (функция инженерно-технич. комбинирования и кооперирования труда) и получали зарплату за продажу своей "...особо обученной рабочей силы" (там же, с. 428, см. также с. 425-26). Уже в 19 в. это породило используемые совр. У. р. т. процессы абсолютного в пределах известных границ распоряжения чужим капиталом и чужой собственностью, частного произ-ва без контроля частной собственности, упразднения капитала как частной собственности в рамках самого капиталистического способа произ-ва (см. там же, с. 479, 482).

Исследованные К. Марксом процессы резкого повышения значения управления и акц. собственности получили особое развитие в 20 в. Однако сторонники У. р. т., подробно излагая именно эти явления, рассматривают их как якобы кардинально меняющие саму сущность экономич., социального и политич. строя капиталистич. общества. У. р. т. затушёвывает тот факт, что возникновение в 20 в. многочисленного и влиятельного слоя высшего управленч. персонала было оборотной стороной процесса развития монополий капиталистических и распространения в начале 20 в. контроля финансового капитала над сотнями тысяч предприятий, банков и контор, превратившего прежних их собственников в рядовых акционеров, отстранённых от управления. Адм. власть верхушки управляющих внутри этих предприятий и банков стала не препятствием, а организационной основой для контроля крупнейших собственников капитала над всей экономикой, причём "элита управляющих" вошла влиятельной составной частью в финансовую олигархию, получая невиданно высокие доходы.

Становление массового поточно-конвейерного произ-ва (в США - в 1914-50, в Зап. Европе и Японии - в 1950-70), во многом связанного с развитием и превращением в непосредственную производительную силу ряда управленч. и инженерно-организационных наук (операционный анализ, теория принятия решений, контроль качества, управление запасами, эргономика, инж. физиология и т. д.), ещё более укрепило положение управляющих, наладивших систему эксплуатации сложной рабочей силы. Вместе с тем У. р. т. маскирует процесс классовой поляризации среди численно выросшего в результате научно-технической революции инженерно-управленч. состава. Параллельно с обуржуазиванием его верхнего и среднего слоев резко усилилась пролетаризация осн. массы пром. инженеров, осуществляющих преим. функцию научно-технич. налаживания и поддержания производственных процессов, управления техникой, обучения и переобучения рабочих на произ-ве и т. д. Этот массовый слой наёмных работников стал объектом эксплуатации со стороны капитала и втягивается в пролетарские формы классовой борьбы, опровергая положение о новом господствующем классе, выдвинутое создателями У. р. т. Вновь проявилось первенствующее положение крупных собственников акц. капитала по отношению даже к высшим управляющим корпораций. Относительное совпадение в 50-60-х гг. гл. критериев успешного управления, выражающегося в устойчивом росте масштабов произ-ва, его эффективности и прибыльности, и успешного накопления капитала-собственности, оцениваемого по проценту прироста курса акций, ослабляло вмешательство акционеров в вопросы управления. В 70-е гг. расширение произ-ва происходило в условиях падения курса акций, и их собственники, представителями к-рых становятся различные банки, фирмы и фонды, через менеджеров этих организаций начали выражать недовольство деятельностью управляющих, производить персональные изменения в высшем управленч. составе и диктовать решения многих узловых управленч. проблем. Капиталистич. собственность (и власть капиталистов-собственников) не исчезла, как это утверждают сторонники У. р. т. В форме гигантских акц. компаний она приспосабливается к новым условиям произ-ва, став коллективной и анонимной капиталистич. собственностью.

Лит.: Ирибаджаков Н., Современ" ные критики марксизма, М., 1962; Гвишиани Д. М., Социология бизнеса, М., 1962; его же, Организация и управление, 2 изд., М., 1972; Меньшиков С. М., Миллионеры п менеджеры, М., 1965; Гэлбрейт Дж., Новое индустриальное общество, пер. с англ., М., 1969; Курс для высшего управленческого персонала, сокр. пер. с англ., М., 1970; Беглов И. И., США: собственность и власть, М., 1971; Вег1е А. А., Меаns С. С., The modern corporation and private property, N. Y., 1932; Burnham J., The managerial revolution, N. Y., 1941; Drucker P. F., Concept of the corporation, N. Y., 1946; его же, Technology, management and society, N. Y., 1970; его же, The new markets, and other essays, N. Y., 1971; Renner K., Die neue Welt und der Sozialismus, Salzburg, 1946.

Ю. А. Васильчук.

УПРАВЛЯЕМОСТЬ судна, способность судна двигаться по заданной траектории; одно из мореходных качеств судна. В У. различают устойчивость на курсе - возможность судна следовать прямолинейно, и поворотливость - способность изменять направление движения под воздействием органов управления (обычно руля, иногда поворотной насадки гребного винта, крыльчатого движителя). На отклонённом от прямого положения руле возникает поперечная сила, поворачивающая судно и смещающая его вбок; при этом судно движется по криволинейной траектории, кривизной к-рой оценивают его поворотливость (см. Циркуляция судна). У. зависит от формы и размеров руля и формы подводной части корпуса судна. Для улучшения У. при малых скоростях иногда применяют подруливающее устройство, активный руль (руль с гребным винтом) и т. д.

УПРАВЛЯЕМЫЙ РАЗРЯДНИК, ионный прибор с холодными электродами, в к-ром электрич. разряд между осн. электродами возбуждается под действием импульса напряжения, приложенного к управляющему (поджигающему) электроду. Различают У. р. с тремя электродами (тригатроны, или тригитроны) и с четырьмя (крайтроны). В тригатронах управляющий электрод расположен между основными или в полости одного из них. В крайтронах четвёртый электрод используют для получения т. н. подготовит. разряда (пропускается ток в неск. десятков мка от высоковольтного источника постоянного тока через ограничительный резистор), стабилизирующего время запаздывания осн. разряда по отношению к моменту подачи поджигающего импульса. Электроды У. р. изготовляют из тугоплавких металлов и их сплавов и заключают в стеклянный, металлостеклянный или металлокерамич. корпус (рис. 1), заполняемый газом под давлением 10-10³ кн/м². В У. р., наз. вакуумными искровыми реле (ВИР), или спрайтронами, внутр. пространство разрядника откачивают до высокого вакуума; искровой разряд, возникающий первоначально в вакууме, поддерживается затем в парах металлов, из к-рых сделаны электроды (см. также Искровой разрядник).

У. р. применяют в импульсной технике (в качестве быстродействующих коммутаторов, или переключателей), а также в устройствах защиты электрич. цепей и оборудования от перенапряжений и токовых перегрузок. Посредством У. р. можно коммутировать ток от десятков а до десятков ка при напряжении от сотен в до сотен кв и длительности импульсов от десятых долей мксек до неск. мсек. Их долговечность составляет до 10³ пробоев при токе неск. десятков ка и до 10⁷ при токе неск. ка. Обычно У. р. работают в режиме одиночных импульсов или импульсов с частотой следования до неск. десятков гц. Для повышения частоты следования импульсов до неск. кгц при напряжении неск. кв применяют многокамерную конструкцию У. р. (рис. 2).

От др. коммутирующих приборов аналогичного назначения (напр., импульсных тиратронов) У. р. отличаются отсутствием накала, мгновенной готовностью к работе, устойчивостью к перегрузкам, малыми габаритами и массой, простотой конструкции.

В. В. Никитин, Л. М. Тихомиров.

УПРАВЛЯЕМЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС, случайный процесс, вероятностные характеристики к-рого можно изменять с помощью управляющих воздействий. Осн. цель теории У. с. п.- отыскание оптимальных (или близких к ним) управлений, доставляющих экстремум заданному критерию качества. В простейшем случае управляемых марковских цепей одна из матем. постановок задачи

нахождения оптимального управления формулируется след. образом. Пусть

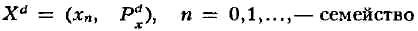
однородных марковских цепей с конечным числом состояний Е - {0,1,...,N} и матрицами переходных вероятностей

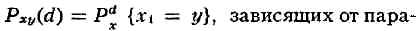
метра d, принадлежащего нек-рому множеству управляющих воздействий D. Набор функций а = {a₀(х₀),a₁(х₀,х₁),...} со значениями в D называют стратегией, а каждую из функций а_n = а_n(x₀,..., х_п) - управлением в момент времени п.

Каждой стратегии а отвечает управляемая

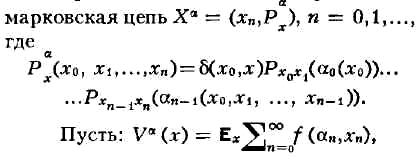
где функция f(d, х)5>= 0 и f(d,0) = 0 (если точка {0} является поглощающим состоянием и f(d,x) = 1, d принадлежит D,x = 1,...,N, то V^а(x) есть матем. ожидание времени попадания из точки х в точку 0). Функцию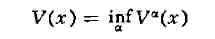

наз. ценой, а стратегию а* - оптимальной, если V^а*(x) = V(x) для всех х принадлежит Е.

При довольно общих предположениях о множестве D устанавливается, что цена V(x) удовлетворяет след. уравнению оптимальности (уравнению Белл-мана):

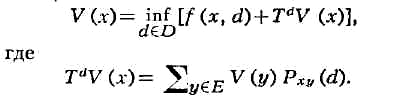
В классе всех стратегий наибольший интерес представляют т. н. однородные марковские стратегии, характеризуемые одной функцией а(х) такой, что а_n(х₀, ..., х_n)=а(х_п) при всех n = 0, 1, ...

След. критерий оптимальности (или достаточное условие оптимальности) может быть использован для проверки того, что данная однородная марковская стратегия является оптимальной: пусть существуют функции а* = а*(х) и V* = V*(x) такие, что для любого d принадлежащего D 0 = f(x, a*(x)) + L^а*V*<=f(x,d)+L^dV*(x)

(L^d = T^d - 1,1 - единичный оператор), тогда V* является ценой (V* = V) и стратегия а* = а*(х) является оптимальной.

Лит.: Xовард Р.-А., Динамическое программирование и марковские процессы, пер. с англ., М. 1964.

А. Н. Ширяев.

УПРАВЛЯЕМЫЙ ТЕРМОЯДЕРНЫЙ СИНТЕЗ, процесс слияния лёгких атомных ядер, происходящий с выделением энергии при высоких темп-рах в регулируемых, управляемых условиях. Скорости протекания термоядерных реакций малы из-за кулоновского отталкивания (см. Кулона закон) положительно заряженных ядер. Поэтому процесс синтеза идёт с заметной интенсивностью только между лёгкими ядрами, обладающими малым положит. зарядом и только при высоких темп-рах, когда кинетич. энергия сталкивающихся ядер оказывается достаточной для преодоления кулоновского потенциального барьера. В природных условиях термоядерные реакции между ядрами водорода (протонами) протекают в недрах звёзд, в частности во внутр. областях Солнца, и служат тем постоянным источником энергии, к-рый определяет их излучение. Сгорание водорода в звёздах идёт с малой скоростью, но гигантские размеры и плотности звёзд обеспечивают непрерывное испускание огромных потоков энергии в течение миллиардов лет (подробнее см. Термоядерные реакции). С несравненно большей скоростью идут реакции между тяжёлыми изотопами водорода (дейтерием ²Н и тритием ³Н) с образованием сильно связанных ядер гелия:

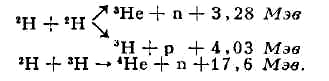
Именно названные реакции представляют наибольший интерес для проблемы У. т. с. В особенности привлекательна вторая реакция, сопровождающаяся большим энерговыделением и протекающая со значит. скоростью. Тритий радиоактивен (период полураспада 12,5 лет) и не встречается в природе. Следовательно, для обеспечения работы предполагаемого термоядерного реактора, использующего в качестве ядерного горючего тритий, должна быть предусмотрена ввзможность воспроизводства трития. С этой целью рабочая зона рассматриваемой системы может быть окружена слоем лёгкого изотопа лития, в к-ром будет идти процесс воспроизводства

⁶Li + n->³H + ⁴Не.

Вероятность (эффективное поперечное сечение) термоядерных реакций быстро возрастает с темп-рой, но даже в оптимальных условиях остаётся несравненно меньше эффективного сечения столкновений атомных. По этой причине реакции синтеза должны происходить в полностью ионизованной плазме, нагретой до высокой темп-ры, где процессы ионизации и возбуждения атомов отсутствуют и дейтон-дейтонные или дейтон-тритонные столкновения рано или поздно завершаются ядерным синтезом.

Удельная мощность термоядерного реактора находится путём умножения числа ядерных реакций, происходящих ежесекундно в единице объёма рабочей зоны реактора, на энергию, выделяющуюся при каждом акте реакции.

Критерий Лоусона. Применение законов сохранения энергии и числа частиц позволяет выяснить нек-рые предъявляемые к реактору синтеза общие требования, не зависящие от к.-л. особенностей технологич. или конструктивного характера рассматриваемой системы. На рис. 1 изображена принципиальная схема работы реактора. Установка произвольной конструкции содержит чистую водородную плазму с плотностью п при темп-ре Т. В реактор вводится топливо, напр. рав-нокомпонентная смесь дейтерия и трития, уже нагретая до необходимой темп-ры. Внутри реактора инжектируемые частицы время от времени сталкиваются между собой и происходит их ядерное взаимодействие. Это полезный процесс; одновременно, однако, из реактора уходит энергия за счёт электромагнитного излучения плазмы и из рабочей зоны ускользает нек-рая доля "горячих" (обладающих высокой энергией) частиц, к-рые не успели испытать ядерные взаимодействия. Пусть г - ср. время удержания частиц в реакторе; смысл величины т таков: за время в 1 сек из 1 см³ плазмы в среднем уходит n/т частиц каждого знака. В стационарном режиме в реактор надо ежесекундно инжектировать такое же число частиц (в расчёте на единицу объёма). Для покрытия энергетич. потерь подводимое топливо должно подаваться в зону реакции с энергией, превышающей энергию потока ускользающих частиц. Эта дополнит. энергия должна компенсироваться за счёт энергии синтеза, выделяющейся в зоне реакции, а также за счёт частичной рекуперации в стенках и оболочке реактора электромагнитного излучения и корпускулярных потоков. Примем для простоты, что коэфф. преобразования в электрич. энергию продуктов ядерных реакций, электромагнитного из.-лучения и частиц с тепловой энергией одинаков и равен n. Величину n часто наз. коэфф. полезного действия (кпд). В условиях стационарной работы системы и при нулевой полезной мощности уравнение баланса энергии в реакторе имеет вид:

ню*(Po + Pr+Pt) = Pr+Pt, (1)

где Р₀ - мощность ядерного энерговыделения, Рr - мощность потока излучения и Pt - энергетич. мощность потока ускользающих частиц. Когда левая часть написанного равенства делается больше правой, реактор перестаёт расходовать энергию и начинает работать как термоядерная электростанция. При написании равенства (1) предполагается, что вся рекуперированная энергия без потерь возвращается в реактор через инжектор вместе с потоком подводимого нагретого топлива. Величины Ро, Рr и Pt известным образом зависят от темп-ры плазмы, и из ур-ния баланса легко вычисляется произведение

где f(T) для заданного значения кпд ню и выбранного сорта топлива есть вполне определённая функция темп-ры. На рис. 2 приведены графики f(T) для двух значений ню и для обеих ядерных реакций. Если величины пт, достигнутые в данной установке, расположатся выше кривой f(T), это будет означать, что система работает как генератор энергии. При n = 1/3 энергетически выгодная работа реактора в оптимальном режиме (минимум на кривых рис. 2) отвечает условию ("критерий Лоусона"):

реакции (d, d):nт10¹⁵ см^-3*сек;

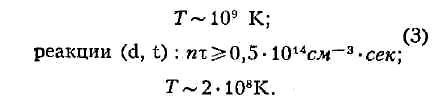
Т. о., даже в оптимальных условиях, для наиболее интересного случая - реактора, работающего на равнокомпонентной смеси дейтерия и трития, и при весьма оптимистических предположениях относительно величины ню необходимо достижение температур ~2*10⁸К. При этом для плазмы с плотностью ~ 10¹⁴ см^-3 должны быть обеспечены времена удержания порядка секунд. Конечно, энергетически выгодная работа реактора может происходить и при более низких температурах, но за это придётся "расплачиваться" увеличенными значениями т.

Итак, сооружение реактора предполагает: l) получение плазмы, нагретой до температур в сотни миллионов градусов; 2) сохранение плазменной конфигурации в течение времени, необходимого для протекания ядерных реакций. Исследования по У. т. с. ведутся в двух направлениях - по разработке квазистационарных систем, с одной стороны, и устройств, предельно быстродействующих, с другой.

У. т. с. с магнитной термоизоляцией. Рассмотрим сначала первый вариант. Энергетич. выход на уровне 10⁵квт/м³ достигается для (d, t) реакций при плотности плазмы ~ 10¹⁵ см^-3 и темп-ре ~ 10⁸К. Это означает, что размеры реактора на 10⁶ - 10⁷ квт (таковы типичные мощности совр. больших электростанций) должны быть в пределах 10-100 м³, что вполне приемлемо. Основной вопрос состоит в том, каким способом удерживать горячую плазму в зоне реакции. Диффузионные потоки частиц и тепла при указанных значениях п и Т оказываются гигантскими и любые материальные стенки непригодными. Основополагающая идея, высказанная в 1950 в Советском Союзе и США, состоит в использовании принципа магнитной термоизоляции плазмы. Заряженные частицы, образующие плазму, находясь в магнитном поле, не могут свободно перемещаться перпендикулярно к силовым линиям поля. В результате коэффициенты диффузии и теплопроводности поперёк магнитного поля, в случае устойчивой плазмы, очень быстро убывают с возрастанием напряжённости поля и, напр., при полях ~ 10⁵гс уменьшаются на 14-15 порядков величины против своего "незамагниченного" значения для плазмы с указанной выше плотностью и темп-рой. Т. о., применение достаточно сильного магнитного поля в принципе открывает дорогу для проектирования реактора синтеза.

Исследования в области У. т. с. с магнитной термоизоляцией делятся на три осн. направления: 1) открытые (или зеркальные) магнитные ловушки; 2) замкнутые магнитные системы; 3) установки импульсного действия.

В открытых ловушках уход частиц из рабочей зоны поперёк силовых линий на стенки установки затруднён; он происходит либо в ходе процесса "замагниченной" диффузии (т. е. очень медленно), либо путём перезарядки на молекулах остаточного газа (см. Перезарядка ионов). Уход плазмы вдоль силовых линий также замедлен областями усиленного магнитного поля (т. н. "магнитными зеркалами" или "пробками"), размещёнными на открытых концах ловушки. Заполнение ловушек плазмой обычно производится путём инжекции плазменных сгустков или отдельных частиц, обладающих большой энергией. Дополнительный нагрев плазмы может быть осуществлён с помощью адиабатического сжатия в нарастающем магнитном поле (подробнее см. Магнитные ловушки).

В системах замкнутого типа (токамак, стелларатор) уход частиц на стенки тороидальной установки поперёк продольного магнитного поля также затруднён и происходит за счёт замагниченной диффузии и перезарядки. Нагревание плазменного шнура в токамаке на начальных стадиях процесса осуществляется протекающим по нему кольцевым током. Однако по мере повышения темп-ры джоу-лев нагрев становится всё менее эффективным, т. к. сопротивление плазмы быстро падает с ростом темп-ры. Для нагревания плазмы св. 10⁷К применяются методы нагрева высокочастотным электромагнитным полем и ввод энергии с помощью потоков быстрых нейтральных частиц.

В установках импульсного действия (Z-пинч и 0-пинч) нагревание плазмы и её удержание осуществляются сильными кратковременными токами, протекающими через плазму. При одновременном нарастании тока и магнитного давления плазма отжимается от стенок сосуда, чем обеспечивается её термоизоляция. Повышение темп-ры происходит за счёт джоулева нагрева, адиабатического сжатия плазменного шнура и, по-видимому, в результате турбулентных процессов при развитии неустойчивости плазмы (подробнее см. Пинч-эффект).

Самостоятельное направление образуют исследования горячей плазмы в высокочастотных (ВЧ) полях. Как показали опыты П. Л. Капицы, в водороде и гелии при достаточно высоком давлении удаётся получить в ВЧ полях свободно парящий плазменный шнур с электронной темп-рой ~ 10⁵К. Система допускает замыкание шнура в кольцо и наложение дополнит. продольного магнитного поля.

Успешная работа любой из перечисленных установок возможна только при условии, что исходная плазменная структура оказывается макроскопически устойчивой, сохраняя заданную форму в течение всего времени, необходимого для протекания реакции. Кроме того, в плазме должны быть подавлены микроскопические неустойчивости, при возникновении и развитии к-рых распределение частиц по энергиям перестаёт быть равновесным и потоки частиц и тепла поперёк силовых линий резко возрастают по сравнению с их теоретич. значениями. Именно в направлении стабилизации плазменных конфигураций развивались осн. исследования магнитных систем начиная с 1950, и эта работа всё ещё не может считаться полностью завершённой.

Сверхбыстродействующие системы У. т. с. с инерциальным удержанием.

Трудности, связанные с магнитным удержанием плазмы, можно в принципе обойти, если сжигать ядерное горючее за чрезвычайно малые времена, когда нагретое вещество не успевает разлететься из зоны реакции. Согласно критерию Лоусона, полезная энергия при таком способе сжигания может быть получена лишь при очень высокой плотности рабочего вещества. Чтобы избежать ситуации термоядерного взрыва большой мощности, нужно использовать очень малые порции горючего, исходное термоядерное топливо должно иметь вид небольших крупинок (диам. 1-2 мм), приготовленных из смеси дейтерия и трития, впрыскиваемых в реактор перед каждым его рабочим тактом. Гл. проблема здесь заключается в подведении необходимой энергии для разогрева крупинки горючего. В наст. время (1976) решение этой проблемы возлагается на применение лазерных лучей или интенсивных электронных пучков. Исследования в области У. т. с. с применением лазерного нагрева были начаты в 1964; использование электронных пучков находится на более ранней стадии изучения - здесь выполнены пока сравнительно немногочисленные эксперименты. Оценки показывают, что выражение для энергии W, к-рую необходимо подводить к установке для обеспечения работы реактора, имеет вид:

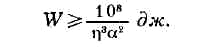
Здесь n - выражение общего вида для кпд устройства и а - коэфф. сжатия мишени. Как показывает написанное равенство, даже при самых оптимистических допущениях относительно возможного значения n величина W при а = 1 получается несоразмерно большой. Поэтому только в сочетании с резким увеличением плотности мишени (примерно в 10⁴ раз) по сравнению с исходной плотностью твёрдой (d, t) мишени можно подойти к приемлемым значениям W. Быстрое нагревание мишени сопровождается испарением её поверхностных слоев и реактивным сжатием внутр. зон. Если подводимая мощность определённым образом программирована во времени, то, как показывают вычисления, можно рассчитывать на достижение указанных коэфф. сжатия. Другая возможность состоит в программировании радиального распределения плотности мишени. В обоих случаях необходимая энергия снижается до 10⁶ дж, что лежит в пределах технич. осуществимости, учитывая стремительный прогресс лазерных устройств.

Трудности и перспективы. Исследования в области У. т. с. сталкиваются с большими трудностями как чисто физич., так и технич. характера. К первым относится уже упомянутая проблема устойчивости горячей плазмы, помещённой в магнитную ловушку. Правда, применение сильных магнитных полей спец. конфигурации подавляет потоки частиц, покидающих зону реакции, и позволяет получить в ряде случаев достаточно устойчивые плазменные образования. Электромагнитное излучение при используемых значениях п и Т плазмы и возможных размерах реактора свободно покидает плазму, но для чисто водородной плазмы эти энергетич. потери определяются только тормозным излучением электронов и в случае (d, t) реакций перекрываются ядерным энерговыделением уже при темп-pax выше 4*10⁷К.

Вторая фундаментальная трудность связана с проблемой примесей. Даже малая добавка чужеродных атомов с большим Z, к-рые при рассматриваемых темп-pax находятся в сильно ионизованном состоянии, приводит к резкому увеличению интенсивности сплошного спектра, к появлению линейчатого спектра и возрастанию энергетич. потерь выше допустимого уровня. Требуются чрезвычайные усилия (непрерывное совершенствование вакуумных установок, использование тугоплавких и труднораспыляемых металлов в качестве материала диафрагм, применение спец. устройств для улавливания чужеродных атомов и т. д.), чтобы содержание примесей в плазме оставалось ниже допустимого уровня. Точнее - "летальная" концентрация, исключающая возможность протекания термоядерных реакций, напр. для примеси вольфрама или молибдена, составляет десятые доли процента.

На рис. 3 на диаграмме (nт; T) указаны параметры, достигнутые на различных установках к сер. 1976. Ближе всего к области, где оказывается удовлетворённым критерий Лоусона и может протекать самоподдерживающаяся термоядерная реакция, располагаются установки типа токамак и системы с лазерным нагревом. Было бы, однако, ошибочным на основании имеющихся данных делать категорические заключения о типе того устройства, к-рое будет положено в основу термоядерного реактора будущего. Слишком быстрыми темпами происходит развитие данной области технич. физики, и мн. оценки могут измениться на протяжении ближайшего десятилетия.

Огромное значение, к-рое придаётся исследованиям в области У. т. с., объясняется рядом причин. Нарастающее загрязнение окружающей среды настоятельно требует перевода пром. производства планеты на замкнутый цикл, когда возникает минимум отходов. Но подобная реконструкция пром-сти неизбежно связана с резким возрастанием энергопотребления. Между тем ресурсы минерального топлива ограничены и при сохранении существующих темпов развития энергетики будут исчерпаны на протяжении ближайших десятилетий (нефть, горючие газы) или столетий (уголь). Конечно, наилучшим вариантом было бы использование солнечной энергии, но низкая плотность мощности падающего излучения сильно затрудняет радикальное решение этой проблемы. Переход энергетики в глобальном масштабе на ядерные реакторы деления ставит сложные проблемы захоронения огромных радиоактивных отходов (альтернатива: выброс радиоактивных отходов в космос). По имеющимся оценкам, радиоактивная опасность установок на У. т. с. должна оказаться на три порядка величины ниже, чем у реакторов деления. Если говорить о далёких прогнозах, то оптимум следует искать в сочетании солнечной энергетики и У. т. с.

Лит.: Тамм И. Е., Теория магнитного термоядерного реактора, ч. 1, в сб.: Физика плазмы и проблема управляемых термоядерных реакций, т. 1, М., 1958; Сахаров А. Д., Теория магнитного термоядерного реактора, ч. 2, там же; Арцимович Л. А., Управляемые термоядерные реакции, М., 1963; Капица П. Л., Свободный плазменный шнур в высокочастотном поле при высоком давлении, "Журнал экспериментальной и теоретической физики", 1969, т. 57, в. 6(12); его же, Термоядерный реактор со свободно парящим в высокочастотном поле плазменным шнуром, там же, 1970, т. 58, в. 2; Роуз Д., Управляемый термоядерный синтез. (Результаты и общие перспективы), "Успехи физических наук", 1972, т. 107, в. 1, с. 99; Лукьянов С. Ю., Горячая плазма и управляемый ядерный синтез, М., 1975; Лазеры и термоядерная проблема, под ред. Б. Б. Кадомцева, М., 1974; Ribe F. L.. Fusion reactor systems, "Reviews of Modern Physics", 1975, v. 47, № 1; Fuгth H. P., Tokamak Research, "Nuclear Fusion", 1975, v. 15, № 3; Ashbу D. E., Laser fusion, "Journal of the British Nuclear Energy Society", 1975, № 4.

С. Ю. Лукьянов.

Рис. 3. Параметры, достигнутые на различных установках для изучения проблемы управляемого термоядерного синтеза к середине 1976. Т-10 - установка токамак Института атомной энергии им. И. В. Курчатова, СССР; PLT - установка токамак Принстонской лаборатории, США; Алкатор - установка токамак Массачусетсского технологического института, США; TFR - установка токамак в Фонтене-о-Роз, Франция; ПР-6-открытая ловушка Института атомной энергии им. И. В. Курчатова, СССР; 2ХПВ - открытая ловушка Ливерморской лаборатории, США; 6-пинч (Сциллак) - установка Лос-Аламосской лаборатории, США; Стелларатор "Ураган-1" - установка Украинского физико-технического института, СССР; Лазер-импульсные системы с лазерным нагревом, СССР, США.  

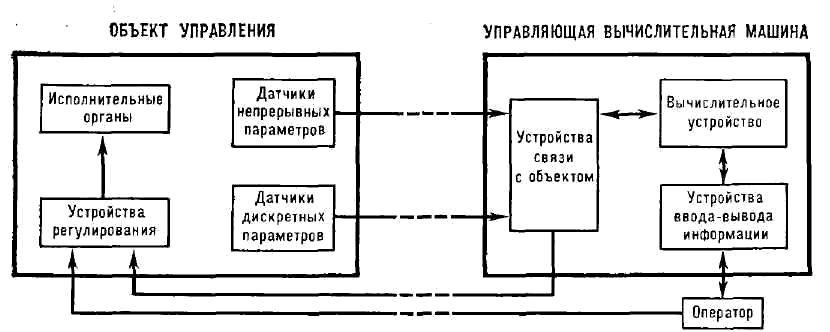
УПРАВЛЯЮЩАЯ МАШИНА, упpавляющая вычислительная машина (УВМ), вычислит. машина, включённая в контур управления технич. объектами (процессами, машинами, системами). УВМ принимают и обрабатывают информацию, поступающую в процессе управления, и выдают управляющую информацию либо в виде текста, таблицы, графика, отпечатанных на бумаге или отображаемых на экране дисплея, либо в виде сигналов (воздействий), подаваемых на исполнит. органы объекта управления (см. рис.). Гл. цель применения УВМ - обеспечение оптимальной работы объекта управления. Управление с помощью УВМ строится на основе математич. описания поведения объектов (см. Алгоритмизация процессов, Математическая модель). Отличит. особенность УВМ - наличие в них наряду с осн. устройствами, входящими в состав всех ЭВМ (процессором, памятью и др.), комплекса устройств связи с объектом. К этому комплексу относятся устройства, осуществляющие ввод в процессор данных (получаемых от датчиков величин, характеризующих состояние управляемого объекта), устройства, обеспечивающие выдачу управляющих воздействий на исполнит/ органы, а также различные преобразователи сигналов, устройства отображения информации.  

Различают УВМ универсальные (общего назначения) и специализированные. К специализированным относятся УВМ, ориентированные на решение задач в системах, управляющих заранее определённым небольшим набором объектов (процессов). К универсальным относят УВМ, к-рые по своим технич. параметрам и возможностям могут быть использованы практически в любой системе управления. По способу представления информации УВМ делят на цифровые (см. Цифровая вычислительная машина), аналоговые (см. Аналоговая вычислительная машина) и гибридные - цифроаналоговые. Цифровые УВМ превосходят аналоговые по точности управления, но уступают им в быстродействии. В гибридных УВМ цифровые и аналоговые вычислит. устройства работают совместно, что позволяет в макс, степени использовать их достоинства.

УВМ является центр. звеном в системах автоматического управления (САУ). Она осуществляет обработку информации о текущих значениях физ. величин, характеризующих объект, и об их изменении, а также вырабатывает управляющие сигналы, обеспечивающие заданные режимы его работы. В автоматизированных системах управления (АСУ) технологич. процессами УВМ обычно работает в режиме советчика, выдавая оператору сведения о состоянии объекта управления и рекомендации по оптимизации процесса управления, или (реже) в режиме непосредств. управления. По назначению и области использования УВМ подразделяются на промышленные, аэрокосмические, транспортные и др.

Появление УВМ связано с разработкой бортовых вычислит. машин для военной авиации в начале 50-х гг. Так, напр., одна из первых бортовых УВМ - "Диджитак" (США, 1952) предназначалась для автоматич. управления полётом и посадкой самолёта, для решения задач навигации и бомбометания. В ней использовалось около 260 субминиатюрных электронных ламп и 1300 полупроводниковых диодов. УВМ занимала объём 150 дм³ при массе 150 кг. В середине 50-х гг. были разработаны первые бортовые УВМ на транзисторах, а в начале 60-х гг. - первые бортовые УВМ на интегральных микросхемах, в т. ч. неск. моделей со сравнительно высокими вычислит. возможностями. Примером такой УВМ может служить "УНИВАК-1824" (США, 1963), состоящая из арифметико-логич. устройства, запоминающего устройства, блока ввода-вывода данных и блока питания; объём, занимаемый УВМ, 4,1 дм³, масса 7 кг, потребляемая мощность 53 вт (при этом не требовалась система охлаждения или вентиляции); эта УВМ собрана на 1243 интегральных микросхемах. В начале 60-х гг. УВМ применяли в системах управления непрерывными технологич. процессами (пример - УВМ RW-300, США, включённая в контур управления технологич. процессами произ-ва аммиака). В такой системе управления воздействия, вырабатываемые УВМ, преобразовывались из цифровой формы в аналоговую и в виде электрич. сигналов поступали на регуляторы исполнит. механизмов. Непосредств. цифровое управление непрерывным технологич. процессом впервые было применено в 1962 в СССР (в системе управления "Автооператор" на Лисичанском химкомбинате) и в Великобритании (в системе управления "Аргус-221" на содовом з-де в г. Флитвуд). Для управления непрерывными технологич. процессами в СССР в 60-х гг. были разработаны вычислит. машины "Днепр", "Днепр-2", ВНИИЭМ-1, ВНИИЭМ-3, УМ-I-HX и др. В середине 60-х гг. появилась тенденция к переходу от выпуска единичных моделей УВМ к выпуску управляющих вычислительных комплексов (УВК), к-рые строятся по агрегатному принципу. УВК представляет собой набор вычислит. средств, средств связи с объектом и оператором, внутренней и внешней связи. Пример УВК - комплекс М-6000, входящий в агрегатированную систему средств вычислит. техники (АСВТ), разработанную в СССР (серийный выпуск с 1969). Конструктивно АСВТ представляет собой набор модулей, из к-рых компонуют различные по структуре и назначению УВК. В основном это комплексы для сбора и первичной обработки информации при управлении различными технологич. процессами, науч. экспериментами и т. п. УВК М-6000 состоит из универсального цифрового процессора, устройств ввода-вывода данных, агрегатных модулей сбора и выдачи аналоговой и дискретной информации, агрегатных модулей для организации внутренней связи и связи с др. комплексами. На базе АСВТ создаются многоуровневые АСУ пром. предприятием. На нижнем уровне такой системы используются относительно простые УВМ (напр., микропрограммный автомат М-6010 и машина централизованного контроля М-40), выполняющие функции непосредств. управления технологич. процессом. На среднем уровне при помощи УВК (напр., УВК М-6000 и М-400) решаются более сложные задачи управления, связанные с оптимизацией группы технологич. процессов. Эти УВК, в свою очередь, имеют связь с центр. звеном системы, к-рое решает задачи управления работой всей системы в целом, в т. ч. задачи учёта и планирования произ-ва. На этом уровне обычно используются большие УВК (напр., М-4030 и М-7000).

Одно из направлений развития УВМ - их агрегатирование на основе функциональных модулей, отвечающих требованиям единства входных и выходных параметров, стандартных информационных связей между модулями и унифицированного математического обеспечения. При этом появляется реальная возможность компоновки (по заказу пользователя) вычислит. системы нужной структуры. Пример - вычислит. система Хьюлетт - Паккард-9600 (США), предназначенная для различных измерений и автоматич. регулирования, к-рая уже частично реализует это направление развития УВМ. Основа этой системы - функциональный унифицированный модуль, представляющий собой микропрограммный процессор, агрегатируемый с другими функциональными модулями. Для централизованного автоматич. управления группами территориально разобщённых объектов используют т. н. распределённые системы управления, к-рые включают центр обработки данных, оснащённый высокопроизводительными ЭВМ, центральные и периферийные системы управления, объединённые унифицированными системами связи. Использование в центре обработки данных высокопроизводительной ЭВМ позволяет обрабатывать информацию, поступающую от центральных систем управления (к-рые работают в реальном масштабе времени), а также осуществлять дистанционный ввод задач в центральные системы управления. Последние связаны с центром обработки данных и с периферийными системами, осуществляющими непосредств. управление объектами.

Большое внимание при создании совр. УВМ уделяется повышению надёжности их функционирования при одноврем. снижении стоимости, массы и габаритов, а также повышению надёжности средств получения информации, её преобразования и выдачи.

Лит.: Каган Б. М., Каневский М. М., Цифровые вычислительные машины и системы, 2 изд., М., 1973.

Г. Р. Воскобойников, М. А. Данилъченко, М. И. Никитин.

УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ, сигнал, поступающий на объект управления (регулирования) от задающего устройства или регулятора и влияющий на управляемую (регулируемую) величину объекта. В системах автоматического управления (САУ) У. в. изменяется таким образом, чтобы управляемая величина соответствовала заданию (в следящих системах, в системах стабилизации и программного управления) пли достигала нек-рого оптимального либо экстремального значения (в системах оптимального управления, экстремальное

Структурная схема системы управления непрерывным процессом с помощью управляющей вычислительной машины.

регулирования, самонастраивающихся системах и др.). В системах регулирования автоматического (САР) У. в. зависит от закона регулирования и определяется свойствами объекта регулирования, характером действующих на САР задающих и возмущающих воздействий и др. По числу У. в. различают одно- и многомерные объекты управления. В многомерных объектах каждое из У. в. может влиять на одну или неск. управляемых величин. что затрудняет управление объектом. Поэтому одна из важных задач, к-рая решается при создании САУ (САР), - устранение или ослабление влияния У. в. на все управляемые (регулируемые) величины, за исключением одной (см. Автономность).

УПРАВЛЯЮЩЕЕ УСТРОЙСТВО ЦВМ, устройство управления, часть вычислительной машины, координирующая работу всех её устройств, предписывая им те или иные действия в соответствии с заданной программой. У. у. вырабатывает управляющие сигналы, обеспечивающие требуемую последовательность выполнения операций, контролирует работу машины в различных режимах, обеспечивает взаимодействие человека-оператора с ЦВМ. Структура У. у. определяется типом ЦВМ и применяемым способом управления вычислит. процессом. При синхронном управлении ЦВМ на выполнение любой из операций отводится заранее определённое время; в таких ЦВМ, как правило, используется одно У. у., наз. центральным, к-рое синхронизирует работу машины в целом. При асинхронном способе управления начало выполнения очередной операции определяется завершением предыдущей операции. В асинхронных ЦВМ каждое устройство машины (арифметическое, запоминающее и др.) часто имеет своё местное У. у. В этом случае центральное У. у. вырабатывает только осн. сигналы управления, задающие режим работы для местных У. у., к-рые в соответствии с этими сигналами организуют функционирование своих устройств.

Различают У. у. с жёстко заданной и с произвольной программами управления. В первом случае все возможные сочетания управляющих сигналов и временные соотношения между ними неизменны и определяются структурой и конструкцией ЦВМ. Изменение порядка вычислений требует схемных преобразований в У. у. Поэтому жёстко заданная программа используется чаще всего в специализированных вычислительных машинах.

У. у. с произвольной программой универсально и позволяет формировать программу решения задачи непосредственно перед её реализацией. Произвольная программа управления используется в универсальных цифровых машинах. Наиболее эффективны У. у. с мультипрограммным управлением, допускающим одноврем. решение неск. задач и независимую связь ЦВМ со мн. потребителями. Мультипрограммирование обеспечивается либо неск. У. у., каждое из к-рых обслуживает одну из программ, выполняемых ЦВМ, либо временным разделением выполнения неск. программ, осуществляемым одним У. у., к-рое переключается с одной программы на другую в результате последоват. опроса пользователей (абонентов) или вследствие принудит. прерывания со стороны абонента в соответствии с заданным приоритетом. Получили также распространение микропрограммные У. у., в к-рых каждой машинной операции соответствует набор сигналов, составляющих микрокоманду; микрокоманды хранятся в постоянной памяти ЦВМ (см. Микропрограммное управление). При этом для всех операций выбираются оптимальные наборы управляющих сигналов и в соответствии с ними строятся рабочие микропрограммы.

Тенденции развития У. у. связаны с повышением их производительности и расширением логич. возможностей, позволяющих, напр., произвольно (или с нек-рыми ограничениями) задавать структуру команд, длину слова и т. д. Допускается изменение структуры машины, совместная работа неск. ЦВМ и т. д.

Лит.: Каган Б. М., Каневский М. М., Цифровые вычислительные машины и системы, 2 изд., М., 1973.

И. А. Данильченко.

УПРОЧНЕНИЕ в технологии металлов, повышение сопротивляемости материала заготовки или изделия разрушению или остаточной деформации.

У. характеризуется степенью У. - показателем относительного повышения значения заданного параметра сопротивляемости материала разрушению или остаточной деформации по сравнению с его исходным значением в результате упрочняющей обработки, а также (в ряде случаев) глубиной У. (толщиной упрочнённого слоя). У. обычно сопровождается снижением пластичности. Поэтому практически выбор способа и оптимального режима упрочняющей обработки определяется макс. повышением прочности материала при допустимом снижении пластичности, что обеспечивает наибольшую конструкционную прочность.

У. материала в процессе его получения может быть вызвано термин., радиац. воздействиями, легированием и введением в металлич. или неметаллич. матрицу (основу) упрочнителей - волокон, дисперсных частиц и др. (см. Композиционные материалы).

У. материала заготовок и изделий достигается механич., термич., химич. и др. воздействиями, а также комбинированными способами (химико-термич., термомеханич. и др.). Наиболее распространённый вид упрочняющей обработки - поверхностное пластическое деформирование (ППД) - простой и эффективный способ повышения несущей способности и долговечности деталей машин и частей сооружений, в особенности работающих в условиях знакопеременных нагрузок (оси, валы, зубчатые колёса, подшипники, поршни, цилиндры, сварные конструкции, инструменты и т. п.). В зависимости от конструкции, свойств материала, размеров и характера эксплуатационных нагрузок деталей применяются различные виды ППД: накатка и раскатка роликами и шариками, обкатка зубчатыми валками, алмазное выглаживание, дорнование, гидроабразивная, вибрационная, дробеструйная и др. способы обработки. Часто ППД, кроме У., значительно уменьшает шероховатость поверхности, повышает износостойкость деталей, улучшает их внеш. вид (упрочняюще-отделочная обработка). У. при термической обработке металлов обеспечивается, в частности, при закалке с последующим отпуском. Улучшению прочностных свойств значительно способствуют и определённые виды термо-механич. обработки (в т. ч. горячий и холодный наклёп). У. химико-термич. воздействием может осуществляться путём азотирования, цианирования, цементации, диффузионной металлизации (насыщением поверхности детали алюминием, хромом и др. металлами).

У. обеспечивается также применением электрофизических и электрохимических методов обработки: ультразвуковой, электроэрозионной, магнитоимпульсной, электрогидравлической, электроннолучевой, фотоннолучевой, анодно-химиче-ской, электроискровой, а также воздействием взрывной волны, лазера и др. Упрочняющая обработка может быть поверхностной (напр., пластич. деформирование с возникновением поверхностного наклёпа), объёмной (напр., изотер-мич. закалка) и комбинированной (напр., термич. обработка с последующим ППД). Объёмная и поверхностная упрочняющая обработки могут вестись последовательно неск. методами.

Лит.: Гуляев А. П., Металловедение, 4 изд., М., 1966; Прочность металлов при циклических нагрузках, М., 1967; Папшев Д. Д., Упрочнение деталей обкаткой шариками, М., 1968; Елизаветин М. А., Сатель Э. А., Технологические способы повышения долговечности машин, 2 изд., М., 1969; Кудрявцев И. В., Поверхностный наклеп для повышения прочности и долговечности деталей машин, 2 изд., М., 1969; Данилевский В. В., Технология машиностроения, 3 изд., М., 1972; Картавов С. А., Технология машиностроения, К., 1974.

Д. Л. Юдин.

УПРУГАЯ ДЕФОРМАЦИЯ, деформация, к-рая исчезает при снятии нагрузки. Для этого деформация не должна превосходить нек-рого предела, наз. пределом упругости; в противном случаев теле наблюдаются остаточные деформации.

УПРУГАЯ ЛИНИЯ в сопротивлении материалов, условное название кривой, по к-рой изгибается ось балки (бруса) под действием нагрузки (под осью балки понимается линия, соединяющая центры тяжести её поперечных сечений). Зная уравнение У. л. и используя дифференциальные зависимости теории изгиба, можно для любого сечения балки определить не только величину прогиба, но и угол поворота, изгибающий момент и поперечную силу. Уравнение У. л. находят из т. н. приближённого дифференциального уравнения оси изогнутой балки, для решения к-рого используют как аналитич., так и графоаналитич. способы. Последний особенно удобен, когда достаточно найти прогибы или углы поворота в отд. точках балки, в этом случае исключается необходимость в получении аналитич. выражения для У. л.

Лит. см. при ст. Сопротивление материалов.

УПРУГАЯ МУФТА, устройство для соединения по длине двух вращающихся частей машины (обычно валов), компенсирующее относит. смещение их осей и удары при включении. Упругий элемент У. м. может быть металлическим (напр., витая пружина) и неметаллическим (напр., резиновое кольцо). См. также Муфта,

УПРУГИЕ ВОЛНЫ, упругие возмущения, распространяющиеся в твёрдой, жидкой и газообразной средах. Напр., волны, возникающие в земной коре при землетрясениях, звуковые и ультразвуковые волны в жидкостях и газах и др. При распространении У. в. происходит перенос энергии упругой деформации в отсутствии потока вещества, к-рый имеет место только в особых случаях, напр. при акустическом ветре. Всякая гармонич. У. в. характеризуется амплитудой и частотой колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферич., цилиндрич. волны). В жидкостях и газах, к-рые обладают упругостью объёма, но не обладают упругостью формы, могут распространяться лишь продольные волны разрежения - сжатия, где колебания частиц среды происходят в направлении её распростране-

где К - модуль всестороннего сжатия, р - плотность среды. Пример таких У. в.- звуковые волны (см. Звук).

В однородной изотропной бесконечно протяжённой твёрдой среде могут распространяться У. в. только двух типов - продольные и сдвиговые. В продольных движение частиц параллельно направлению распространения волны, а деформация представляет собой комбинацию всестороннего сжатия (растяжения) и чистого сдвига. В сдвиговых волнах движение частиц перпендикулярно направлению распространения волны, а деформация является чистым сдвигом. Фазо-

(G- модуль сдвига). На границе твёрдого полупространства с вакуумом, жидкостью или газом могут распространяться поверхностные Рэлея волны, являющиеся комбинацией неоднородных продольных и сдвиговых волн. амплитуды к-рых экспоненциально убывают при удалении от границы.

В ограниченных твёрдых телах (пластина, стержень), представляющих собой твёрдые волноводы акустические, распространяются нормальные волны. Каждая из них является комбинацией неск. продольных и сдвиговых волн, к-рые распространяются под острыми углами к оси волновода и удовлетворяют (в совокупности) граничным условиям: отсутствию механич. напряжений на поверхности волновода. Число нормальных волн в пластине или стержне определяется их толщиной или диаметром d, частотой нормальных волн f и модулями упругости среды. При увеличении fd число п нормальных волн, возможных в волноводе, возрастает; fd->бесконечности, n->бесконечности. Нормальные волны распространяются с дисперсией скоростей (см. Дисперсия звука): при изменении fd от критич. значений до бесконечности фазовые скорости нормальных волн, как правило, уменьшаются от бесконечности до c_t, а групповые скорости возрастают от нуля до c_t. От величины fd сильно зависит также распределение смещений и напряжений в волне по поперечному сечению волновода.

В бесконечной пластине существуют два типа нормальных волн: волны Лэмба и сдвиговые нормальные волны. Плоская волна Лэмба характеризуется двумя составляющими смещений, одна из к-рых параллельна направлению распространения волны, другая перпендикулярна граням пластины. По характеру распределения смещений относительно ср. плоскости пластины волны Лэмба делятся на симметричные и антисимметричные. Частный случай симметричной волны Лэмба - продольная волна в пластине, а антисимметричной - изгибная волна. В плоской сдвиговой нормальной волне смещения параллельны граням пластины и одновременно перпендикулярны направлению распространения волны. Простейший вид такой волны - нормальная волна нулевого порядка, в к-рой смещения одинаковы во всех точках поперечного сечения пластины.

В цилиндрич. стержнях могут распространяться нормальные волны продольного, изгибного и крутильного типа, причём если толщина стержня мала по сравнению с длиной волны, то в нём может распространяться только по одной нормальной волне каждого типа.

В анизотропных средах (кристаллах) свойства У. в. и возможность её существования зависят от класса кристалла и направления распространения. В частности, чисто продольные и чисто сдвиговые волны могут распространяться только в кристаллах определённых симметрии (см. Симметрия кристаллов) и по определённым направлениям, как правило, совпадающим с направлением кристаллографич. осей. В общем случае в кристалле по любому направлению всегда распространяются У. в. с тремя различными скоростями: одна квазипродольная и две квазипоперечные волны, в к-рых преобладают соответственно продольные или поперечные смещения.

Из-за внутреннего трения и теплопроводности среды распространение У. в. сопровождается её затуханием с расстоянием (см. Поглощение звука). Если на пути У. в. имеется к.-л. препятствие (отражающая стенка, вакуумная полость и т. д.), то происходит дифракция волн на этом препятствии. Частный случай дифракции - отражение и преломление У. в. на плоской границе двух полупространств.

В У. в. напряжения пропорциональны деформациям (т. е. удовлетворяется Гука закон). Если амплитуда деформации в волне столь велика, что напряжение превосходит предел упругости вещества, то при прохождении волны в веществе появляются пластич. деформации и её наз. упруго-пластической волной. В жидкости и газе аналогичную волну наз. волной конечной амплитуды.

Лит.: Ландау Л. Д., Лифшиц Е. М., Теория упругости, 3 изд., М., 1965 (Теоретич. физика, т. 7); Кольский Г., Волны напряжения в твердых телах, пер. с англ., М., 1955; Морз Ф., Колебания и звук, пер. с англ., М. -Л., 1949; БреховскихЛ. М., Волны в слоистых средах, 2 изд., М., 1973; Викторов И. А., Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике, М., 1966.

И. А. Викторов.

УПРУГОЕ ОСНОВАНИЕ, основание сооружения, деформируемость к-рого учитывается при расчёте опирающейся на него конструкции. Понятием "У. о." пользуются гл. обр. при решении задач по расчёту гибких фундаментов зданий и сооружений на грунтовых основаниях. В соответствующих расчётах используют различные теоретич. положения, описывающие свойства грунтов, - гипотезу коэфф. жёсткости основания (коэфф. постели), теорию линейно-деформируемой среды (теорию упругости), комбинированные расчётные модели основания.

УПРУГОЕ РАССЕЯНИЕ микрочастиц, процесс столкновения (рассеяния) частиц, при к-ром их внутр. состояния остаются неизменными, а меняются лишь импульсы. См. Рассеяние микрочастиц.

УПРУГО-ПЛАСТИЧЕСКАЯ ВОЛНА, упругая волна, амплитуда деформации в к-рой столь велика, что напряжение превосходит предел упругости вещества и при её прохождении возникают пластич. деформации. Скорость распространения таких волн зависит от величины деформации. В стержне, по к-рому прошла У.-п. в., сохраняются остаточные деформации; по их распределению можно судить о динамических механических характеристиках материала.

УПРУГОСТИ МОДУЛИ, величины, характеризующие упругие свойства материала. См. Модули упругости.

УПРУГОСТИ ТЕОРИЯ, раздел механики, в к-ром изучаются перемещения, деформации и напряжения, возникающие в покоящихся или движущихся упругих телах под действием нагрузки. У. т.- теоретич. основа расчётов на прочность, деформируемость и устойчивость в строит. деле, авиа- и ракетостроении, машиностроении, горном деле и др. областях техники и промышленности, а также в физике, сейсмологии, биомеханике и др. науках. Объектами исследования методами У. т. являются разнообразные тела (машины, сооружения, конструкции и их элементы, горные массивы, плотины, геологич. структуры, части живого организма и т. п.), находящиеся под действием сил, температурных полей, радиоактивных облучений и др. воздействий. В результате расчётов методами У. т. определяются допустимые нагрузки, при к-рых в рассчитываемом объекте не возникают напряжения или перемещения, опасные с точки зрения прочности или недопустимые по условиям функционирования; наиболее целесообразные конфигурации и размеры сооружений, конструкций и их деталей; перегрузки, возникающие при динамич. воздействии, напр. при прохождении упругих волн; амплитуды и частоты колебаний конструкций или их частей и возникающие в них динамич. напряжения; усилия, при к-рых рассчитываемый объект теряет устойчивость. Этими расчётами определяются также материалы, наиболее подходящие для изготовления проектируемого объекта, или материалы, к-рыми можно заменить части организма (костные и мышечные ткани, кровеносные сосуды и т. п.). Методы У. т. эффективно используются и для решения нек-рых классов задач теории пластичности (в методе по-следоват. приближений).

Физические законы упругости материалов, надёжно проверенные экспериментально и имеющие место для большинства материалов, по крайней мере при малых (а иногда и очень больших) деформациях, отражают взаимно однозначные зависимости между текущими (мгновенными) значениями напряжений о и деформаций Е, в отличие от законов пластичности, в к-рых напряжения зависят от процесса изменения деформаций (при одних и тех же деформациях, достигнутых путём различных процессов, напряжения различны). При растяжении цилиндрич. образца длины l, радиуса r, с площадью поперечного сечения F имеет место пропорциональность между растягивающей силой Р, продольным удлинением образца dl и поперечным удлинением dr, к-рая выражается равенствами: c₁ = Ee₁, e₂ =- ve₁, где c₁ = P/F - нормальное напряжение в поперечном сечении, e₁ = dl/1 - относит. удлинение образца, e₂ = dr/r- относит. изменение поперечного размера; Е - модуль Юнга (модуль продольной упругости), v - Пуассона коэффициент. При кручении тонкостенного трубчатого образца касат. напряжение т в поперечном сечении вычисляется по значениям площади сечения, его радиуса и приложенного крутящего момента. Деформация сдвига у определяемая по наклону образующих, связана с т равенством т=Gу, где G - модуль сдвига.

При испытаниях образцов, вырезанных из изотропного материала по разным направлениям, получаются одни и те же значения Е, G и v. В среднем изотропны многие конструкционные металлы и сплавы, резина, пластмассы, стекло, керамика, бетон. Для анизотропного материала (древесина, кристаллы, армированные бетон и пластики, слоистые горные породы и др.) упругие свойства зависят от направления. Напряжение в любой точке тела характеризуется шестью величинами - компонентами напряжений: нормальными напряжениями c_xx, c_yy, c_гг и касательными напряжениями c_xy, c_уг, c_zx, причём c_xy = c_yx и т. д. Деформация в любой точке тела также характеризуется шестью величинами - компонентами деформаций: относительными удлинениями e_xx, e_yy, e_zz и сдвигами e_xy, e_yz, e_zх, Причём e_xy = e_ух и т. д..

Осн. физ. законом У. т. является обобщённый Тука закон, согласно к-рому нормальные напряжения линейно зависят от деформаций. Для изотропных материалов эти зависимости имеют вид:

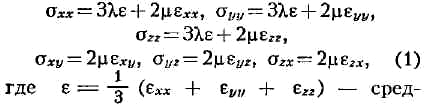
няя (гидростатическая) деформация, лямбда и мю = G - Ламе постоянные. Т. о., упругие свойства изотропного материала характеризуются двумя постоянными ч и м или к.-н. выраженными через них двумя модулями упругости.

Равенство (1) можно также представить в виде

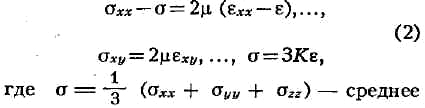
(гидростатич.) напряжение, К - модуль всестороннего сжатия.

Для анизотропного материала 6 зависимостей между компонентами напряжений и деформаций имеют вид:

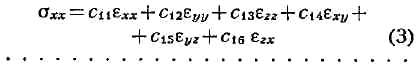
Из входящих сюда 36 коэфф. c_ij, наз. модулями упругости, 21 между собой независимы и характеризуют упругие свойства анизотропного материала. Для нелинейного упругого изотропного материала в равенствах (2) всюду вместо ц входит коэфф. Ф(е_u)/3e_u, а соотношение c = ЗKе заменяется равенством c = f(e) где величина e_u наз. интенсивностью деформации, а функции Ф и f, универсальные для данного материала, определяются из опытов. Когда Ф(е_u) достигает нек-рого критич. значения, возникают пластич. деформации. Законы пластичности при пропорциональном возрастании нагрузок или напряжений (простое нагружение) имеют тот же вид, но с др. значениями функций Ф и f (законы теории малых упруго-пластич. деформаций), а при уменьшении напряжений (разгрузке) имеют место соотношения (1) или (2), в к-рых вместо c_ij и e_ij подставляются их приращения (разности двух текущих значений).

Математическая задача У. т. при равновесии состоит в том, чтобы, зная действующие внеш. силы (нагрузки) и т. н. граничные условия, определить значения в любой точке тела компоненты напряжений и деформаций, а также компоненты и_х, и_у, и_г вектора перемещения каждой частицы тела, т. е. определить эти 15 величин в виде функций от координат х, у, z точек тела. Исходными для решения этой задачи являются дифференциальные ур-ния равновесия:

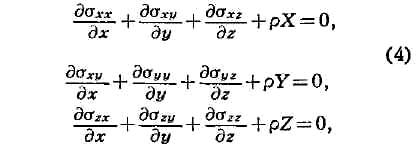
где р - плотность материала, XYZ - проекции на координатные оси действующей на каждую частицу тела массовой силы (напр., силы тяжести), отнесённые к массе этой частицы.

К трём ур-ниям равновесия присоединяются 6 равенств (1) в случае изотропного тела и ещё 6 равенств вида: e=du_x/dx,..., 2e_xy =du_x/dy+ди_y/dx ,..., (5) устанавливающих зависимости между компонентами деформаций и перемещений.

Когда на часть S₁ граничной поверхности тела действуют заданные поверхностные силы (напр., силы контактного взаимодействия), проекции к-рых, отнесённые к единице площади, равны F_x, F_v, F_z, а для части S₂ этой поверхности заданы перемещения её точек ф_x, ф_v, ф_z, граничные условия имеют вид:

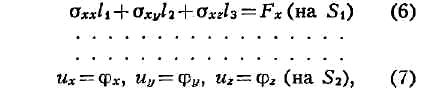
где l₁, l₂, l₃ - косинусы углов между нормалью к поверхности и координатными осями. Первые условия означают, что искомые напряжения должны удовлетворять на границе S₁ трём равенствам (6), а вторые - что искомые перемещения должны удовлетворять на границе S₂ равенствам (7); в частном случае может быть ф_х = ф_y = ф_z = 0 (часть поверхности S₂ жёстко закреплена). Напр., в задаче о равновесии плотины массовая сила - сила тяжести, поверхность S₂ подошвы плотины неподвижна, на остальной поверхности S₁ действуют силы: напор воды, давление различных надстроек, трансп. средств и т. д.

В общем случае поставленная задача представляет собой пространственную задачу У. т., решение к-рой трудно осуществимо. Точные аналитич. решения имеются лишь для нек-рых частных задач: об изгибе и кручении бруса, о контактном взаимодействии двух тел, о концентрации напряжений, о действии силы на вершину конич. тела и др. Т. к. ур-ния У. т. являются линейными, то решение задачи о совместном действии двух систем сил получается путём суммирования решений для каждой из систем сил, действующих раздельно (принцип линейной суперпозиции). В частности, если для к.-н. тела найдено решение при действии сосредоточенной силы в к.-л.,произвольной точке тела, то решение задачи при произвольном распределении нагрузок получается путём суммирования (интегрирования). Такие решения, наз. Грина функциями, получены лишь для небольшого числа тел (неограниченное пространство, полупространство, ограниченное плоскостью, и нек-рые др.). Предложен ряд аналитич. методов решения пространственной задачи У. т.: вариационные методы (Ритца, Бубнова-Галёркина, Кастильяно и др.), метод упругих потенциалов, метод Бетти и др. Интенсивно разрабатываются численные методы (конечно-разностные, метод конечных элементов и др.). Разработка общих метедов решений пространственной задачи У. т.- одна из наиболее актуальных проблем У. т.

При решении плоских задач У. т. (когда один из компонентов перемещения равен нулю, а два других зависят только от двух координат) широкое применение находят методы теории функций комплексного переменного. Для стержней, пластин и оболочек, часто используемых в технике, найдены приближённые решения мн. практически важных задач на основе нек-рых упрощающих предположений. Применительно к этим объектам специфич. интерес представляют задачи об устойчивости равновесия (см. Устойчивость упругих систем).

В задаче термоупругости определяются напряжения и деформации, возникающие вследствие неоднородного распределения темп-ры. При матем. постановке этой задачи в правую часть первых трёх ур-ний (1) добавляется член-(З лямбда +  2мю)аТ, где а - коэфф. линейного теплового расширения, T(x₁,x₂,x₃) - заданное поле темп-ры. Аналогичным образом строится теория электромагнитоупругости и упругости подвергаемых облучению тел.

Большой практич. интерес представляют задачи У. т. для неоднородных тел. В этих задачах коэфф. Ч, м в ур-нии (1) являются не константами, а функциями координат, определяющими поле упругих свойств тела, к-рое иногда задают статистически (в виде нек-рых функций распределения). Применительно к этим задачам разрабатываются статистич. методы У. т., отражающие статистич. природу свойств поликристаллич. тел.

В динамич. задачах У. т. искомые величины являются функциями координат и времени. Исходными для матем. решения этих задач являются дифференциальные ур-ния движения, отличающиеся от ур-ний (4) тем, что правые части вместо нуля содержат инерционные члены pd²u_x/dt² и т. д. К исходным ур-ниям должны также присоединяться ур-ния (1), (5) и, кроме граничных условий (6), (7), ещё задаваться начальные условия, определяющие, напр., распределение перемещений и скоростей частиц тела в начальный момент времени. К этому типу относятся задачи о колебаниях конструкций и сооружений, в к-рых могут определяться формы колебаний и их возможные смены, амплитуды колебаний и их нарастание или убывание во времени, резонансные режимы, динамич. напряжения, методы возбуждения и гашения колебаний и др., а также задачи о распространении упругих волн (сейсмич. волны и их воздействие на конструкции и сооружения, волны, возникающие при взрывах и ударах, термоупругие волны и т. д.).

Одной из совр. проблем У. т. является матем. постановка задач и разработка методов их решения при конечных (больших) упругих деформациях.

Экспериментальные методы У. т. (метод многоточечного тензометрирования, поляризационно-оптический метод исследования напряжений, метод муаров и др.) позволяют в нек-рых случаях непосредственно определить распределение напряжений и деформаций в исследуемом объекте или на его поверхности. Эти методы используются также для контроля решений, полученных аналитич. и численными методами, особенно когда решения найдены при к.-н. упрощающих допущениях. Иногда эффективными оказываются экспериментально-теоретич. методы, в к-рых частичная информация об искомых функциях получается из опытов.

Лит.: Ляв А., Математическая теория упругости, пер. с англ., М. - Л., 1935; Лейбензон Л. С., Курс теории упругости, 2 изд., М.-Л., 1947; Мусхелишвили Н. И., Некоторые основные задачи математической теории упругости, 5 изд., М., 1966; Трёхмерные задачи математической теории упругости, Тб., 1968; Лурье А. И., Теория упругости, М., 1970; Стретт Дж. В. (лорд Рэлей), Теория звука, пер. с англ., т. 1 - 2, М., 1955; Теория температурных напряжений, пер. с англ., М., 1964; Снеддон И. Н., Берри Д. С., Классическая теория упругости, пер. с англ., М., 1961; Тимошенко С. П., Гудьер Дж. Н., Теория упругости, пер. с англ., М., 1975.

А. А. Ильюшин, В. С. Ленский.

УПРУГОСТЬ, свойство макроскопич. тел сопротивляться изменению их объёма или формы под воздействием механич. напряжений. При снятии приложенного напряжения объём и форма упруго деформированного тела восстанавливаются.

У. тел обусловлена силами взаимодействия атомов, из к-рых они построены. В твёрдых телах при темп-ре абс. нуля в отсутствии внеш. напряжений атомы занимают равновесные положения, в к-рых сумма всех сил, действующих на каждый атом со стороны остальных, равна нулю, а потенциальная энергия атома минимальна. Кроме сил притяжения и отталкивания, зависящих только от расстояния (рис. 1) между атомами (центр. силы), в многоатомных молекулах и макроскопич. телах действуют также угловые силы, зависящие от т. н. валентных углов между прямыми, соединяющими данный атом с различными его соседями (рис. 2). При равновесных значениях валентных углов угловые силы также уравновешены. Энергия макроскопич. тела зависит от межатомных расстояний и валентных углов, принимая миним. значение при равновесных значениях этих параметров.

Под действием внеш. напряжений атомы смещаются из своих равновесных положений, что сопровождается увеличением потенциальной энергии тела на величину, равную работе внеш. напряжений по изменению объёма и формы тела. После снятия внеш. напряжений конфигурация упруго деформированного тела с неравновесными межатомными расстояниями и валентными углами оказывается неустойчивой и самопроизвольно возвращается в равновесное состояние, точнее, атомы колеблются около равновесных положений. Запасённая в теле избыточная потенциальная энергия превращается в кинетич. энергию колеблющихся атомов, т. е. в тепло. Пока отклонения межатомных расстояний и валентных углов от их равновесных значений малы, они пропорциональны действующим между атомами силам, подобно тому как удлинение или сжатие пружины пропорционально приложенной силе. Поэтому тело можно представить как совокупность атомов-шариков, соединённых пружинами, ориентации к-рых фиксированы др. пружинами (рис. 2). Константы упругости этих пружин определяют модули упругости материала, а упругая деформация тела пропорциональна приложенному напряжению, т. е. определяется Тука законом, к-рый является основой упругости теории и сопротивления материалов.

При конечных темп-pax (ниже температур плавления) даже без приложения и снятия внеш. напряжений атомы совершают малые тепловые колебания около положений равновесия Это приводит к тому, что модули упругости материала зависят от темп-ры, но не меняет существа рассмотренных явлений.

В жидкости тепловые колебания имеют амплитуду, сравнимую с равновесным расстоянием r₀, вследствие чего атомы легко меняют своих соседей и не сопротивляются касат. напряжениям, если они прикладываются со скоростью, значительно меньшей скорости тепловых колебаний. Поэтому жидкости (как и газы) не обладают упругостью формы.

В газообразном состоянии ср. расстояния между атомами или молекулами значительно больше, чем в конденсированном. Упругость газов (паров) определяется тепловым движением молекул, ударяющихся о стенки сосуда, ограничивающего объём газа.

Лит.: Фейнман Р., Лейтон Р., Сэн дс М., Фейнмановские лекции по физике, [в.] 7, М., 1966, гл. 38, 39; Смирнов А. А., Молекулярно-кинетическая теория металлов, М., 1966, гл. 2; Френкель Я. И., Введение в теорию металлов, 4 изд., Л., 1972, гл. 2.

А. Н. Орлов.

УПРУГОСТЬ ВОДЯНОГО ПАРА в атмосфере, парциальное давление водяного пара, находящегося в воздухе; выражается в мбар или мм рт. ст. (1 мбар = 10²н/м²). У. в. п. зависит от количества водяного пара в единице объёма и является одной из характеристик влажности воздуха. У. в. п. у земной поверхности может быть около нуля (в Антарктиде, зимой в Якутии, иногда в пустынях) и до 30-35 мбар вблизи экватора. С высотой У. в. п. быстро убывает - в 2 раза в нижних 1,5 км и почти до нуля на верхней границе тропосферы.

УПРУГОСТЬ НАСЫЩЕНИЯ в метеорологии, упругость водяного пара, максимально возможная при данной темп-ре. Она тем больше, чем выше темп-pa воздуха. По достижении У. н. начинается конденсация водяного пара. Над переохлаждённой водой У. н. больше, чем над льдом при тех же темп-pax; над выпуклой водяной поверхностью больше, а над вогнутой меньше, чем над плоской. У. н. при темп-ре 30 °С не превышает 42,4 мбар, при темп-ре О °С - 6,1 мбар, а при -20 °С равна 1,27 мбар над водой и 1,03 мбар над льдом (1 мбар = 10² н/м²).

УПРЯЖЬ, сбруя, приспособления для запряжки лошадей или др. упряжных животных (вол, верблюд, олень, собака и др.) с целью управления ими на работах в повозках и с.-х. орудиях, под въюком, а также в верховой езде. У. для лошади в зависимости от вида запряжки подразделяют на одноконную и пароконную, дуговую и бездуговую. В одноконную дуговую У. входят хомут с гужами и супонью, седёлка с подпругой, чересседельник, подбрюшник, дуга, шлея, уздечка с удилами и поводьями, вожжи; в одноконную бездуговую - хомут с гужевыми мочками, за к-рые крепят постромки, вместо гужей ремённые горты, скрепляющие хомут с оглоблями. Пароконная У. для дышловой вапряжки состоит из хомутов, нагрудных ремней, постромок, шлей, уздечек с удилами и парных вожжей. В нек-рых запряжках хомут заменяют шоркой. Осн. часть сбруи верховых лошадей - седло. Воловая парная У. представляет собой деревянное ярмо, надеваемое на шею и прикрепляемое к дышлу. Верблюжья У. состоит из уздечки, вожжей и шлейки. Оленья и собачья У. в нартах - шлейка с одной постромкой; управляют оленями шестом или одной вожжой. В собачьих У. вожжей нет. Неправильно изготовленная или плохо подогнанная У. вызывает намины и повреждения кожи животного, что снижает его работоспособность,

С. В. Афанасьев.

УПСАЛА (Upsala), ледник в Патагонских Андах. Дл. 60 км, шир. до 8 км, пл. 250 км² (крупнейший в Андах). Спускается на Ю. с Юж. Патагонского ледяного поля в сев. рукав оз. Лаго-Архентино.

УПСАЛА (Uppsala), город в Швеции. Адм. ц. лена Упсала. 136 тыс. жит. (1974). Крупный пром. и культурный центр.

Машиностроение, полиграфич., керамич., пищ. пром-сть. Старейший в Швеции ун-т (осн. в 1477). Музей К. Линнея, к-рый жил и похоронен в У. Совр. У., первоначально называвшаяся Эстра-Арос (Ostra-Aros), по-видимому, уже в 12 в. была поселением гор. типа. В 1273 стала резиденцией архиепископа, с 1280 наз. У. До 1719 в У. проходили важнейшие гос. собрания, коронации швед. королей. В 14-18 вв. У. - центр внутр. торговли, место общешвед. ярмарки. В кон. 19 - нач. 20 вв.- оплот консервативных сил Швеции. Город сохранил фрагменты ср.-век. планировки. Памятники архитектуры - готич. собор, крупнейший в Скандинавии (1260-1435), романская церковь Бондчюрка (12 в.), замок (с 1540, арх. Г. Васа, Ф. Парр), барочный "Густавианум" (1620; до 19 в. - центр. здание ун-та, ныне музей), ампирные постройки (б-ка ун-та, 1819-26, арх. К.Ф. Сундвалль, и др.). К С. от У. - Старая У. (в 1-м тыс. н. э. - языческий культовый центр), где сохранились многочисл. курганы и фрагменты древнейшего в Швеции собора (ок. 1100), включённые в церковь 13 в. В У. имеется Дисагорден (архит. музей на открытом воздухе).

Лит.: Liljeroth E., Brunius Т., Ett bildverk om Uppsala, Malmo, 1954.

УПСАЛЬСКИЙ УНИВЕРСИТЕТ (Universitet i Uppsala), старейший и один из крупнейших ун-тов Швеции. Осн. в 1477 архиепископом Якобом Ульфсоном. В 18 в. в У. у. преподавал медицину и естествознание К. Линней, астрономию - А. Цельсий. В составе У. у. (1974) 7 ф-тов: права, обществ. наук, теологии, мед., искусств (отделения - историко-философское и лингвистич.), фармацевтич., естеств. наук (отделения - матем.-физич., биолого-географич. и химич.). При ун-те - ботанич. сад и музей (осн. К. Линнеем), астрономич. обсерватория (осн. А. Цельсием), ин-т славяноведения (осн. в 1950-х гг.), собрание историко-архивных документов (в т. ч. коллекция древнеегип. папирусов), В б-ке ун-та (осн. в 1620) св. 1,5 млн. тт. В 1974/75 уч. г. в У. у. обучалось 20 тыс. студентов, работало 600 преподавателей, в т. ч. 180 профессоров.

УПТАР, посёлок гор. типа в Магаданской обл. РСФСР, подчинён Магаданскому горсовету. Расположен на Колымской трассе, в 42 км к С. от Магадана. Лесозавод, з-д стройматериалов, перевалочная база Колымской ГЭС.

УПУЩЕННАЯ ВЫГОДА, в гражд. праве разновидность убытков, к-рые должник обязан возместить кредитору при неисполнении или ненадлежащем исполнении обязательства, причинении внедоговор-ного вреда. По сов. праву это доходы, к-рые кредитор получил бы, если бы обязательство было исполнено должником. Они подлежат возмещению, исключая случаи, указанные в законе. Так, если социалистич. орг-ция, принявшая на себя по договору обязанность передать имущество в безвозмездное пользование, не предоставляет это имущество, она должна в соответствии со ст. 344 ГК РСФСР возместить контрагенту лишь те убытки, к-рые связаны с произведёнными им расходами, утратой или повреждением его имущества (напр., затратами по оборудованию помещения для станков, к-рые социалистич. орг-ция обязалась передать по договору безвозмездного пользования имуществом).

УПЫРЬ, мифологический образ у славянских народов. См. Вампир.

У ПЭЙ-ФУ (1878-1939), китайский воен. и политич. деятель. Один из лидеров чжилийской клики милитаристов, к-рая в 1920-24 контролировала пекинское пр-во. Пользовался поддержкой англ. и амер. империалистов, выдвигавших его на роль "объединителя" Китая. Учинил кровавую расправу над участниками Пекин-Ханькоуской стачки 1923. В период Северного похода 1926-27 войска У. П.-ф. были разбиты Нац.-революц. армией, после чего он сошёл с политич. арены.

УР (шумер. Урим), древний город-государство на месте совр. городища Тель-Мукайяр, в 20 км к Ю.-З. от г. Насирия в Ираке. Первое поселение на месте У. возникло в кон. 5-го тыс. до н.э., когда здесь была распространена расписная керамика типа эль-обейдской культуры. В 4-м тыс., в период Урука, произошло становление У. как города. В 25 в. до н. э., в период I династии Ура (правители Месанепада, Аанепада и др.), представлял собой сильное гос-во. В течение 24-22 вв. (с небольшими перерывами) был подчинён соседним городам-гос-вам Лагашу, Умме, Уруку, затем царству Аккада, кутиям. Ок. 21 в. стал столицей "царства Шумера и Аккада" (III династия Ура). При царе Ур-Намму (21 в.) были созданы, возможно, самые древние в Двуречье писаные законы. Для этого периода истории У. характерно наличие больших царских х-в с фактически рабовладельч. эксплуатацией подневольных работников. Создавались идеологич. основы деспотия, царской власти (единая система пантеона, учение о вечности "царственности" и т. д.). Четыре следующих царя III династии Ура (Шульги, Амар-Суэн, Шу-Суэн, Ибби-Суэн) были обожествлены при жизни. Гос-во III династии Ура пало ок. 2000 до н. э. в ходе войны с аморитами и Эламом. У. оставался важным торг.-ремесл. центром, находясь под властью вавилонского (с 18 по 6 вв.) и ахеменидского (с 6 в.) царств. К кон. 4 в. до н. э. У. пришёл в упадок. У. раскапывался англ. учёными Д. Тейлором в 1854, Р. Кэмпбелл-Томпсоном в 1918, Г. Р. Холлом в 1919-22 и особенно широко - англо-амер. экспедицией под рук. Ч. Л. Вулли в 1922-34. Наиболее многочисл. и интересные памятники, вскрытые раскопками, датируются временем правления в У. I и III династий. Ко времени правления I династии (25 в. до н. э.) относятся 16 царских (?) гробниц, в к-рых были найдены многочисл. образцы роскошной утвари (из золота, серебра, алебастра, ляпис-лазури, обсидиана и др. материалов, иногда - с применением мозаичной техники). У. времени III династии (21 в. до н. э.) представлял собой в плане неправильный овал, окружённый кирпичной стеной. Среди сохранившихся фрагментарно кирпичных зданий этого времени - остатки дворца, храмового комплекса, в центре к-рого находился четырёхъярусный зиккурат, и др. сооружений. О художеств. культуре У. см. также в ст. Вавилоно-ассирийская культура.

Лит.: Тюменев А. И., Государственное хозяйство древнего Шумера, М. - Л., 1956; Вулли Л., Ур халдеев, пер. с англ., М., 1961; Gadd С. J., The history and monuments of Ur, L., 1929; Ur excavations, v. 1 - 5, 8 - 10, Oxf.- L., 1927 - 62; Ur excavations texts, [V. 1-6], L., 1928-63.

Н. М. Дьяконов.

УРАБА (Uraba), залив Карибского м., у берегов Колумбии, юж. часть Дарьенского зал. Дл. 87 км. Глубины 25-54 м. В У. впадает р. Атрато. Порт Турбо.

УРАВА, город в Японии, на о. Хонсю. Адм. центр префектуры Сайтама. Город-спутник Токио. 324 тыс. жит. (1974). Металлообработка и машиностроение; хим., текст. пром-сть. Ун-т.

УРАВНЕНИЕ в математике, аналитическая запись задачи о разыскании значений аргументов, при к-рых значения двух данных функций равны. Аргументы, от к-рых зависят эти функции, наз. обычно неизвестными, а значения неизвестных, при к-рых значения функций равны,- решениями (корнями); о таких значениях неизвестных говорят, что они удовлетворяют данному У. Напр., Зх - 6 = 0 является У. с одним неизвестным, а х = 2 есть его решение; х² + у² = 25 является У. с двумя неизвестными, а х = 3, у = 4 есть одно из его решений. Совокупность решений данного У. зависит от области М значений, допускаемых для неизвестных. У. может не иметь решений в М, тогда оно наз. неразрешимым в области М. Если У. разрешимо, то оно может иметь одно или несколько, или даже бесконечное множество решений. Напр., У. х⁴ - 4=0 неразрешимо в области рацио-нальных чисел, но имеет два решения:

х₁= 2^1/2 , х₂ = - 2^1/2 в области действительных чисел и четыре решения: x₁ = 2^1/2,

x₂= - 2^1/2, х₃ =i*2^1/2, x₄ = - i*2^1/2 в области комплексных чисел. У. sinx = О имеет бесконечное множество решений: x_k = kn(k = 0,± 1, ± 2,...) в области действительных чисел. Если У. имеет решениями все числа области М, то оно наз. тождеcтвом в области М. Напр., У. х =(х²)^1/2является тождеством в области неотрицательных чисел и не является тождеством в области действительных чисел.

Совокупность У., для к-рых требуется найти значения неизвестных, удовлетворяющие одновременно всем этим У., наз. системой У.; значения неизвестных, удовлетворяющих одновременно всем У. системы,- решениями системы. Напр., х+2y= 5, 2х + у - z = 1 является системой двух У. с тремя неизвестными; одним из решений этой системы является x = 1, y = 2, z = 3.

Две системы У. (или два У.) наз. равносильными, если каждое решение одной системы (одного У.) является решением др. системы (другого У.), и наоборот, причём обе системы (оба У.) рассматриваются в одной и той же области (см. Равносильные уравнения). Напр., У. x - 4 = 0 и 2х - 8=0 равносильны, т. к. решением обоих У. является лишь х = 4. Всякая система У. равносильна системе вида f_k(x₁, х_г, ..., x_n)=0, где k = 1, 2, ... Процесс разыскания решений У. заключается обычно в замене У. равносильным. В нек-рых случаях приходится заменять данное У. другим, для к-рого совокупность решений шире, чем у данного У. Решения нового У., не являющиеся решениями данного У., наз. посторонними решениями (см. Посторонний корень).

Напр., возводя в квадрат У. (х - 3)^1/2 = = - 2, получают У. х - 3 = 4, решение к-рого х = 7 является посторонним для исходного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних решений (напр., возведение У. в квадрат), то все полученные решения преобразованного У. проверяют подстановкой в исходное У. Наиболее изучены У., для к-рых функции f_k являются многочленами от переменных x₁,. x₂, ..., x_n,- алгебраические У. Напр., алгебраич. У. с одним неизвестным имеет вид:

a₀ xⁿ+a₁x^n-1+a_n = 0 (a₀ не равно 0);(*)

число п наз. степенью У. Решение алгебраич. У. было одной из важнейших задач алгебры в 16-17 вв., когда были получены формулы и методы решения алгебраич. У. 3-й и 4-й степеней (см. Алгебра, Кардана формула) (правила решения алгебраич. У. 1-й и 2-й степеней были известны ещё в глубокой древности). Для корней У. 5-й и высших степеней общей формулы не существует, поскольку эти У., вообще говоря, не могут быть решены в радикалах (Н. Абель, 1824). Вопрос о разрешимости алгебраич. У. в радикалах привёл (ок. 1830) Э. Галуа к общей теории алгебраич. У. (см. Галуа теория).

Каждое алгебраич. У. всегда имеет хотя бы одно решение, действительное или комплексное. Это составляет содержание т. н. основной теоремы алгебры, строгое доказательство к-рой впервые было дано К. Гауссом в 1799. Если а. - решение У. (*), то многочлен аохⁿ + + a₁x^n-1+ ... + а_п делится на х - а. Если он делится на (х - а)^k, но не делится на (х -a)^k+1, то решение а имеет кратность k. Число всех решений У. (*), если каждое считать столько раз, какова его кратность, равно п.

Если f(x) - трансцендентная функция, то У. f(x) = 0 наз. трансцендентным (см., напр., Кеплера уравнение), причём в зависимости от вида f(x) оно наз. тригонометрическим У., логарифмическим У., показательным У. Рассматриваются также иррациональные У., то есть У., содержащие неизвестное под знаком радикала. При практич. решении У. обычно применяются различные приближённые методы решения У.

Среди систем У. простейшими являются системы линейных У., то есть У., в к-рых f_k суть многочлены первых степеней относительно x₁, x₂, ..., х_n (см. Линейное уравнение).

Решение системы У. (не обязательно линейных) сводится, вообще говоря, к решению одного У. при помощи т. н. исключения неизвестных (см. также Результант).

В аналитической геометрии одно У. с двумя неизвестными интерпретируется при помощи кривой на плоскости, координаты всех точек к-рой удовлетворяют данному У. Одно У. с тремя неизвестными интерпретируется при помощи поверхности в трёхмерном пространстве. При этой интерпретации решение системы У. совпадает с задачей о разыскании точек пересечения линий, поверхностей и т. д. У. с большим числом неизвестных интерпретируются при помощи многообразий в n-мерных пространствах.

В теории чисел рассматриваются неопределённые У., то есть У. с несколькими неизвестными, для к-рых ищутся целые или же рациональные решения (см. Диофантовы уравнения). Напр., целые решения У. х² + у² = z²имеют вид х = т² - n²; у = 2 тп; z = т² + п², где т и п - целые числа.

С наиболее общей точки зрения, У. является записью задачи о разыскании таких элементов нек-рого множества А, что F(a) = Ф(а), где F и Ф - заданные отображения множества А в множество В. Если множества А и В являются множествами чисел, то возникают У. рассмотренного выше вида. Если А я В - множества точек в многомерных пространствах, то получаются системы У., если же А и В - множества функций, то в зависимости от характера отображения могут получаться также дифференциальные уравнения, интегральные уравнения и др. виды У. Наряду с вопросами нахождения решения У. в общей теории У. различного вида изучаются вопросы существования и единственности решения, непрерывной зависимости его от тех или иных данных и т. д.

Термин "У." употребляется (в отличном от указанного выше смысле) и в др. естественных науках, см., напр., Уравнение времени (в астрономии), Уравнение состояния (в физике), Уравнения химические, Максвелла уравнения в электродинамике, Кинетическое уравнение Больц-мана в теории газов.

УРАВНЕНИЕ ВРЕМЕНИ, разность между средним и истинным солнечным временем; равна разности прямых восхождений истинного и среднего Солнца.

Часто У. в. определяют как разность истинного и среднего времени; в этом случае оно имеет противоположный знак, что нужно иметь в виду при пользовании справочниками.

У. в. непрерывно меняется. Это обусловлено тем, что истинное солнечное время, измеряемое часовым углом истинного Солнца, течёт неравномерно вследствие, во-первых, неравномерности движения Земли по орбите и, во-вторых, наклона эклиптики к экватору. Поэтому У. в. получается в результате сложения двух волн приблизительно синусоидальной формы и почти равной амплитуды (см. рис.). Одна из этих волн имеет годичный, другая - полугодичный периоды. Четыре раза в году, а именно: ок. 16 апр., 14 июня, 1 сент. и 25 дек. У. в. равно нулю и достигает 4 раза наибольшего значения (по абсолютной величине): ок. 12 февр. + 14,3 мин, 15 мая -3,8 мин, 27 июля + 6,4 мин и 4 ноября - 16,4 мин. С помощью У. в. может быть найдено среднее местное солнечное время, если известно истинное солнечное время, определённое по наблюдениям Солнца, напр. с помощью солнечных часов; при этом пользуются формулой:

m = m₀ +n,

где т - среднее время, т₀ - истинное время, n - У. в. Значения У. в. на каждый день даются в астрономич. ежегодниках и календарях. См. Время.

УРАВНЕНИЕ СОСТОЯНИЯ, связывает давление р, объём V и температуру Т физически однородной системы в состоянии равновесия термодинамического: f(p, V, T)= 0. Это уравнение наз. термическим У. с., в отличие от калорического У. с., определяющего внутреннюю энергию системы U как функцию к.-л. двух из трёх параметров р, V, Т. Термич. У. с. позволяет выразить давление через объём и темп-ру р = p(V, Т) и определить элементарную работу бА = pбV при бесконечно малом расширении системы бV. У. с. является необходимым дополнением к термодина-мич. законам, к-рое делает возможным их применение к реальным веществам. Оно не может быть выведено с помощью одних только законов термодинамики, а определяется или рассчитывается теоретически на основе представлений о строении вещества методами статистической физики. Из первого начала термодинамики следует лишь существование калорич. У. с., а из второго начала термодинамики - связь между термич. и калорич. У. с. (дU/дV)_T = T(дp/дT)v - р, откуда вытекает, что для идеального газа внутр. энергия не зависит от объёма (дU/дV)_Т = 0. Термодинамика показывает, что для вычисления как термич., так и калорич. У. с., достаточно знать любой из потенциалов термодинамических в виде функции своих параметров. Напр., если известна Гельмгольцева энергия F как функция Г и V, то У. с. находят дифференцированием:

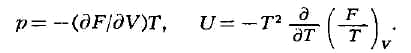
Примерами У. с. для газов может служить Клапейрона уравнение для идеального газа pv=RT, где R - газовая постоянная, v - объём 1 моля газа;

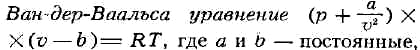
зависящие от природы газа и учитывающие влияние сил притяжения между молекулами и конечность из объёма, в и-риальное У. с. для неидеального газа рv/RT = 1 + B(T)/v + C(T)/v² + ..., где В(Т), С(T)... - 2-й, 3-й и т. д. вириальные коэфф., зависящие от сил взаимодействия между молекулами (см. Газы). Это уравнение является наиболее надёжным и теоретически обоснованным У. с. для газов и позволяет объяснить многочисленные экспериментальные результаты на основании простых моделей межмолекулярного взаимодействия. Были предложены также различные эмпирич. У. с., основанные на экспериментальных данных о теплоёмкости и сжимаемости. У. с. неидеальных газов указывает на существование критич. точки (с параметрами p_k, V_k,, T_k), в к-рой газообразная и жидкая фазы становятся идентичными (см. Критическое состояние). Если У. с. представить в виде приведённого У. с., т. е. в безразмерных переменных р/рк, V/V_k, Т/Т_k, то при не слишком низких темп-pax это уравнение мало меняется для различных веществ (закон соответственных состояний).

Для равновесного излучения, или фотонного газа, У. с. определяется Планка законом излучения для средней плотности энергии.

Для жидкостей из-за сложности учёта всех особенностей взаимодействия молекул пока не удалось теоретически получить общее У. с. Уравнение Ван-дер-Ваальса хотя и применяют для качественной оценки поведения жидкостей, но оно по существу неприменимо ниже критич. точки, когда возможно сосуществование жидкой и газообразной фаз. У. с., хорошо описывающее свойства ряда простых жидкостей, можно получить из приближённых теорий жидкого состояния типа теории свободного объёма или дырочной теории (см. Жидкость). Знание распределения вероятности взаимного расположения молекул (парной корреляционной функции) принципиально позволяет вычислить У. с. жидкости, но эта задача очень сложна и полностью ещё не решена даже с помощью вычислит. машин.

Для твёрдых тел термич. У. с. определяет зависимость модулей упругости от темп-ры и давления. Оно может быть получено на основании теории теплового движения в кристаллах, рассматривающей фононы и их взаимодействие, но пока общего У. с. для твёрдых тел не найдено.

Для магнитных сред элементарная работа при намагничивании равна бА = -HбM, где М - магнитный момент, Н - напряжённость магнитного поля. Следовательно, зависимость М = М(Н,Т) представляет собой магнитное У. с.

Для электрически поляризуемых сред элементарная работа при поляризации равна бА = -ЕбР, где Р - поляризация, Е - напряжённость электрич. поля, следовательно, У. с. имеет вид Р = Р(Е, Т).

Лит.: Хилл Т., Статистическая механика, пер. с англ., М., 1960; Вукалович М. П., Новиков И. И., Уравнение состояния реальных газов, М. -Л., 1948; Мейсон Э., СперлингТ., Вириальное уравнение состояния, пер. с англ., М., 1972; Лейбфрид Г., Людвиг В., Теория ангармонических эффектов в кристаллах, пер. с англ., М., 1963. См. также лит. при статьях Статистическая физика и Термодинамика.

Д. Н. Зубарев.

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ, дифференциальные уравнения с частными производными, а также нек-рые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т. д.), к к-рым приводит математич. анализ физич. явлений. Для теории У. м. ф. характерна постановка задач в таком виде, как это необходимо при исследовании физич. явления. Круг У. м. ф. с расширением области применения математич. анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У. м. ф. уравнения и задачи более общего вида, чем те, к-рые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физич. истолкование (см. Математическая физика).

Классификация уравнений математической физики. Значит. часть У. м. ф. составляют линейные уравнения с частными производными 2-го порядка общего вида:

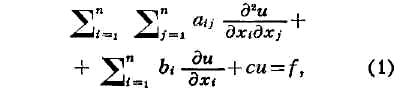
где все коэфф. а_ij(а_ij= а_ji), b_i, с и правая часть f представляют собой заданные функции независимых переменных x₁, x₂, ..., х_п(п>=2), а и - искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно X) уравнения

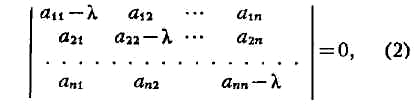
и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все п корней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных п - 1 корней, - к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, - к параболическому типу. Если коэффициенты ац постоянны, то уравнение (1) принад-

лежит к определённому типу независимо от значений аргументов; если же эти коэффициенты зависят от x₁, ..., х_n, то и корни уравнения (2) зависят от x₁, ..., х_n, а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в к-рых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболич. уравнения занимают промежуточное положение между эллиптическими и гиперболическими).

Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.

Основные примеры уравнений математической физики. Волновое уравнение:

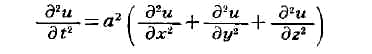
- простейшее уравнение гиперболич. типа, а также соответствующие неоднородные уравнения (в правой части к-рых добавлены известные функции) - телеграфное уравнение и т. д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболич. типа во многом аналогичны свойствам приведённых простейших таких уравнений.

Лапласа уравнение:

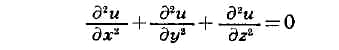
- простейшее уравнение эллиптич. типа и соответствующее неоднородное уравнение - Пуассона уравнение. Уравнения и системы эллиптич. типа появляются обычно при анализе стационарных состояний.

Теплопроводности уравнение:

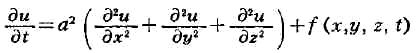
- простейший пример уравнения параболич. типа. Уравнения и системы параболич. типа появляются обычно при анализе процессов выравнивания.

Первым примером уравнений смешанного типа явилось т. н. уравнение Трикоми:

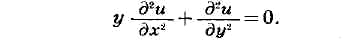
Для этого уравнения полуплоскость y>0(-оо < х < oo ) служит зоной эллиптичности, полуплоскость у<0 - зоной гиперболичности, а прямая у = 0 - зоной параболичности.

Ряд задач матем. физики приводит к интегральным уравнениям различных типов. Так, напр., интегральные уравнения Вольтерра возникают в тех задачах физики, в к-рых существует предпочтительное направление изменения независимого переменного (напр., времени, энергии и т. д.). В задаче о крутильных колебаниях возникает нек-рое интегро-дифференциалъное уравнение.

Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У. м. ф. много усилий было затрачено на отыскание их общего решения. Уже Ж. Д'Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л. Эйлером (1770), П. Лаплас предложил (1773) "каскадный метод", дающий общее решение нек-рых др. линейных однородных гиперболич. уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значит, класса уравнений, для к-рых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось, что при анализе физич. процессов У. м. ф. обычно появляются вместе с дополнительными условиями, характер к-рых коренным образом влияет на направление исследования решения (см. Краевые задачи, Коши задача).

Широкое распространение получили методы приближённого решения краевых задач, в к-рых задача сводится к решению системы алгебраических (обычно линейных) уравнений (см. Ритца и Галёркина методы, Сеток метод). При этом за счёт увеличения числа неизвестных в системе можно достичь любой степени точности приближения.

Лит.: Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; Годунов С. К., Уравнения математической физики, М., 1971; Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.