ТЕРМИЧЕСКИЕ КОЭФФИЦИЕНТЫ, величины, характеризующие изменение к.-л. параметра, входящего в термич. уравнение состояния термодинамич. системы (объёма V, давления р), в зависимости от др. параметра (давления р, темп-ры Т) в определённом термодинамич. процессе. Различают изотермич. коэфф. сжатия (изотермич. сжимаемость)

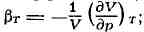
адиабатный коэффициент сжатия (адиабатическая сжимаемость)

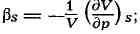
изохорный коэффициент давления

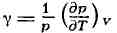
и изобарный коэфф. расширения (коэфф. объёмного расширения)

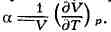
ТЕРМИЧЕСКИЕ НАПРЯЖЕНИЯ, напряжения, возникающие в связи с изменением теплового состояния тел при их нагреве, охлаждении, а также длительном пребывании при повышенной или пониженной темп-ре. Пример Т. н. - напряжения, возникающие при закалке стальных деталей; в этом случае Т. н. представляют собой сочетание напряжений, обусловленных изменением удельного объёма стали при её мартенситном превращении в процессе закалки, и температурных напряжений, вызванных быстрым охлаждением. Действие Т. н., напр., разрушение (растрескивание) при закалке, может проявляться не в момент изменения теплового состояния (охлаждения), а спустя нек-рое время (иногда спустя неск. сут) в результате постепенного накопления напряжений, возникающих при изменении удельных объёмов структурных составляющих.

ТЕРМИЧЕСКИЙ АНАЛИЗ, совокупность методов определения температур, при к-рых происходят процессы, сопровождающиеся либо выделением тепла (напр., кристаллизация из жидкости), либо его поглощением (напр., плавление, термическая диссоциация).

Визуальный метод Т. а. состоит в наблюдении и измерении темп-ры первого появления (исчезновения) неоднородности (напр., выпадения кристаллов, исчезновения мути в системе двух несмешивающихся жидкостей) в изучаемой среде при её охлаждении (или нагревании). Он применим только к прозрачным легкоплавким объектам. Гораздо более общим является метод построения кривых "время -темп-pa". Нагревая (охлаждая) изучаемый объект, измеряют через небольшие промежутки времени его темп-ру; результаты измерений изображают графически, откладывая время по оси абсцисс, а темп-ру - по оси ординат. При отсутствии превращений кривая нагревания (охлаждения) идёт плавно; превращения отражаются появлением на кривой изломов или горизонтальных участков ("остановок"). Наиболее точен дифференциальный метод Т. а., по к-рому нагревание (охлаждение) исследуемого объекта ведут вместе и в одних и тех же условиях с веществом-эталоном, к-рое в условиях опыта не имеет превращений. В этом случае на одном и том же графике записывают и кривую "время - темп-ра", и кривую "время - разность темп-р" объекта и эталона. Эта разность появляется при любом превращении исследуемого объекта, протекающем с поглощением (выделением) тепла. О характере превращений судят по виду простой кривой нагревания (охлаждения), а по дифференциальной кривой точно определяют темп-ру превращения. Для записи кривых нагревания и охлаждения используют самопишущие приборы (пирометр H. С. Курнакова), электронные (автоматич.) потенциометры, оптич. пирометры.

С помощью Т. а. решается задача получения количеств, характеристик (напр., фазовый состав, теплота реакций) при нагревании (охлаждении) исследуемых объектов. Т. а. широко применяется при изучении сплавов металлов и др. сплавов, а также минералов и др. геологич. пород (см. Термический анализ минералов).

Лит.: Ц у р и н о в Г. Г., Пирометр H. С. Курнакова, М., 1953; Берг Л. Г., Введение в термографию, М., 1961; Труды I совещания по термографии, М.- Л., 1955; Труды II совещания по термографии, Казань, 1961; Труды III совещания по термографии, Рига, 1962.

С.А.Погодин.

ТЕРМИЧЕСКИЙ АНАЛИЗ МИНЕРАЛОВ, исследование минеральных систем посредством термического анализа. В приложении к минералам и горным породам термич. анализ впервые был применён франц. учёным А. Л. Ле Шателье (1886). Т. а. м. проводят обычно в комплексе с др. методами (напр., сочетание термич. и термогравиметрич. анализа позволяет совместно с -термич. кривой регистрировать изменения массы вещества при нагревании). Т. а. м.- надёжный и удобный метод диагностирования мн. минералов; особенно ценен при расшифровке механич. минеральных тонкодисперсных смесей (глин, бокситов, железных и марганцевых руд, цем. сырья, карбонатных пород, почв, илов и т. д.). Количеств. оценка содержания минералов в породе осуществляется сопоставлением площадей или высот, соответствующих термич. эффектам, температурных пиков и т. д. на изучаемой и эталонной термограммах. Т. а. м. широко применяют при исследовании механизма и кинетики фазовых переходов и хим. реакций, происходящих в минералах при нагревании; при этом особое внимание обращается на определение тепловых эффектов и энергий активаций хим. реакций с участием минералов. С помощью Т. а. м. решаются также более общие геологические задачи: корреляция осадочных пород при составлении сводных геологических разрезов, выяснение закономерностей фациальной приуроченности минералов, установление минеральных парагенезисов в региональном масштабе и т. д.

Лит.: Термический анализ минералов и горных пород, Л., 1974; Differential thermal analysis, ed. R. C.Mackenzie, v. 1-2, L., 1970-72.

Г.О. Пилоян.

ТЕРМИЧЕСКИЙ УДАР, тепловой удар, одноразовое высокоскоростное (десятки, сотни градусов в 1 сек) п неоднородное изменение темп-ры тела. Обычно к Т. у. относят случаи быстрого нагрева, но Т. у. можно считать и резкое охлаждение (напр., при попадании холодной струи жидкости на нагретую стеклянную посуду). При Т. у., вызываемом кратковременным скоростным поверхностным нагревом, разрушение во мн. случаях происходит не на стадии нагрева, а при последующем охлаждении, протекающем тоже с большой скоростью. Определяющим показателем Т. у. является возникновение за весьма короткое время (доли сек) температурного градиента и обусловленных им деформаций и напряжений, приводящих к формоизменению, нарушениям сплошности (трещинообразованию) и в предельном случае к разрушению.

При Т. у. в условиях быстрого нагрева тела его внешние слои расширяются, а более глубокие, остающиеся ненагретыми, препятствуют расширению. В более разогретых слоях возникают напряжения сжатия, в менее нагретых - растяжения. Когда напряжения достигают пределов прочности на сжатие или растяжение, материал разрушается. У большинства материалов сопротивление сжатию выше сопротивления растяжению, поэтому разрушение происходит в зоне действия напряжений растяжения, т. е. трещина возникает в менее нагретых слоях и затем распространяется после прекращения нагрева на весь объём. Так разрушаются при Т. у. керамика, стекло и др. хрупкие и малотеплопроводные материалы. Действие Т. у. на металлы и сплавы в большинстве случаев ограничивается изменением формы. Вследствие высокой теплопроводности температурные градиенты при быстром нагреве в металлах и сплавах не достигают величины, необходимой для того, чтобы вызвать напряжения, превышающие прочность материала. Кроме того, в металлах и сплавах благодаря присущей им значительной пластичности температурные напряжения в большинстве случаев не выходят за пределы текучести. Т. у. наиболее опасен для материалов, имеющих высокий коэфф. теплового расширения, низкую теплопроводность, высокий модуль упругости, широкий диапазон предела прочности и низкую пластичность. Действие Т. у. усиливается при наличии резких изменений сечения (отверстия, выточки и пр.), концентрирующих тепловые напряжения и затрудняющих пластич. деформацию.

H. М. Скляров.

ТЕРМИЧЕСКИЙ ЭКВАТОР, параллель с наиболее высокой средней многолетней темп-рой воздуха у земной поверхности. В янв. Т. э. совпадает с геогр. экватором (ср. темп-pa воздуха ок. 26 °С), в июле смещается к 20-25° с. ш. (ср. темп-ра воздуха ок. 28 °С), а ср. годовое его положение ок. 10° с. ш. Смещение Т. э. к С. от географического обусловлено большим развитием суши в тропиках Сев. полушария, прогревающейся сильнее, чем океанич. воды.

ТЕРМИЧЕСКОЕ БУРЕНИЕ, способ бурения с использованием в качестве бурового инструмента термобура или плазмобура (см. Плазменное бурение). Разработан в кон. 40-х гг. 20 в. в США, с сер. 50-х гг. применяется в СССР. Большой вклад в изучение физ. основ и разработку технич. средств Т. б. внесли сов. учёные А. В. Бричкин, Р. П. Каплунов, И. П. Голдаев, А. П. Дмитриев, А. В. Ягупов.

Твёрдая среда (горная порода, бетон, лёд) при Т. б. разрушается в режимах хрупкого шелушения и плавления; при хрупком шелушении от нагреваемой до темп-ры 300-600 °С поверхности забоя отделяются небольшие твёрдые частицы (1-20 мм). Причина разрушения - термич. напряжения, вызванные неравномерным прогревом поверхностного слоя среды; режим шелушения характерен для гранитов, песчаников, безрудных и железистых кварцитов.

При режиме плавления разрушаемая среда, нагреваясь, переходит из твёрдого состояния в жидкое (расплав). Продукты разрушения выносятся из скважины газовым потоком; в режиме плавления разрушаются бетон, лёд и нек-рые горные породы (сланцы, базальты, габбро). Применение Т. б. целесообразно только в породах, склонных к хрупкому термич. шелушению. Это определяется комплексом их физ. свойств (тепловые, упругие, прочностные), получивших назв. критерия термобуримости. Скважина бурится обычно с макс, линейной скоростью при минимально допустимом её диаметре, к-рый определяется диаметром термоинструмента. Чистая скорость Т. б. в породах, склонных к хрупкому шелушению, 4-25 м/ч. Достоинство Т. б.- возможность расширения в любой части скважины до 300-500 мм; для этого термоинструмент протягивается на заданном участке предварительно пробуренной скважины со скоростью 10-20 м/ч, обычно по схеме "снизу-вверх". Т. б. применяется только на открытых горных работах из-за наличия в газовых струях высокотоксичных и ядовитых газов (СО, окислы азота и т. д.). При разработке пром. плазмобуров с использованием в качестве плазмообразующего газа водяного пара (что обеспечивает их работу без выхода вредных газов) не исключена возможность применения Т. б. и в подземных условиях.

Совершенствование Т. б. может быть достигнуто благодаря использованию комбинаций различных видов физ. воздействий (механич., ультразвуковое и т. д.) с тепловым, что позволяет увеличить термодинамич. параметры газовых струй и уменьшить темп-ру хрупкого шелушения.

Лит.: Огневое бурение взрывных скважин, М., 1962; Ягупов А. В., Тепловое разрушение горных пород и огневое бурение, М., 1972; Дмитриев А. П., Г о н ч ар о в С. А., Я н ч е н к о Г. А., Термоэлектрофизическое разрушение горных пород, ч. 2, М., 1975.

К.И. Наумов, Г.А. Янченко.

ТЕРМИЧЕСКОЕ СОПРОТИВЛЕНИЕ, тепловое сопротивление, способность тела (его поверхности или к.-л. слоя) препятствовать распространению теплового движения молекул. Различают полное Т. с.-величину, обратную коэфф. теплопередачи, поверхностное Т. с.-величину, обратную коэфф. теплоотдачи, и Т. с. слоя, равное отношению толщины слоя к его коэфф. теплопроводности. Т. с. сложной системы (напр., многослойной тепловой изоляции) равно сумме Т. с. её частей. Т. с. численно равно температурному напору, необходимому для передачи единичного теплового потока (равного 1 em/м²) к поверхности тела или через слой вещества; выражается в м² - К/вт.

ТЕРМИЯ (от греч. therme - тепло, жар), вышедшая из употребления единица кол-ва теплоты, равная кол-ву теплоты, необходимому для нагревания воды массой 1 т от 14,5 до 15,5 °С. 1 Т. равна 10⁶ кал, 3° (см. Калория).

ТЕРМО... (от греч. therme - тепло, жар), часть сложных слов, указывающая на отношение их к теплоте, темп-ре (напр., термодинамика, термометр, термопара).

ТЕРМОАБРАЗИЯ (от термо... и абразия), сочетание процессов теплового и механич. разрушения берегов водоёмов при воздействии волноприбоя на участках побережья, сложенных мёрзлыми горными породами, содержащими большое кол-во подземных ледяных тел. Др. факторами, определяющими интенсивность Т., являются темп-pa воды и энергия волноприбойных процессов - основные условия размыва и выноса рыхлого материала, слагающего береговые уступы.

ТЕРМОАНЕМОМЕТР, прибор для измерения скорости потока жидкости или газа от 0,1 м/сек и выше, принцип действия к-рого осн. на зависимости между скоростью потока v и теплоотдачей проволочки, помещённой в поток и нагретой электрич. током. Осн. часть Т.- мост измерительный (рис.), в одно плечо к-рого включён чувствит. элемент в виде нити из никеля, вольфрама или из платины длиной 3-12 мм и диаметром 0,005-0,15 мм, укреплённой на тонких электропроводных стержнях. Кол-во тепла, передаваемое нагретой проволочкой потоку жидкости (газа), зависит от физ. характеристик движущейся среды, геометрии и ориентации проволочки. С увеличением темп-ры проволочки чувствительность Т. увеличивается. Благодаря малой инерционности, высокой чувствительности, точности и компактности Т. широко применяется при изучении неустановившихся движений и течений в пограничном слое вблизи стенки, для определения направления скорости потока (двух- и трёхниточные Т.) и гл. обр. турбулентности возд. потоков. Т. пользуются для зондирования потоков как при обычных давлениях, так и при больших разрежениях.

Принципиальная схема термоанемометра.

Лит.: Горлин С. М., Слезингер И. И., Аэромеханические измерения, М., 1964; П о п о в С. Г., Измерение воздушных потоков, М.- Л., 1947.

ТЕРМОБАРОКАМЕРА, см. Барокамера.

ТЕРМОБАТИГРАФ, батитермограф судовой, прибор для регистрации на ходу судна распределения темп-ры воды по глубине. Корпус Т., имеющий обтекаемую форму, снабжён хвостовым оперением для стабилизации положения прибора при его погружении в воду. Т. опускается с борта судна на стальном тросе. Датчиком темп-ры воды в Т. служит термоанемометрич. система (см. Термоанемометр). Она представляет собой длинный медный капилляр, намотанный на каркас хвостового оперения прибора. Один конец капилляра запаян, другой соединён с неподвижным концом манометрич. спиральной пружины. Капилляр и пружина заполнены внутри толуолом. При изменении темп-ры изменяется объём толуола, а в связи с этим и давление внутри манометрич. системы. Поэтому свободный конец манометрич. пружины раскручивается при повышении темп-ры на угол, пропорциональный величине изменения темп-ры, и соответственно скручивается при понижении темп-ры. Стрелка, припаянная к свободному концу манометрич. пружины, записывает темп-ру на закопчённой стеклянной пластинке, к-рая по мере погружения прибора в воду передвигается гидростатич. датчиком глубины. В качестве датчика глубины служат герметизированные силъфоны, Совр. Т. позволяет записывать темп-ру воды с точностью 0,1° и выше. Т. используются при произ-ве океанографич. исследований, а также на судах рыбопромысловой разведки.

Термобатиграф: 1 - корпус прибора, внутри которого помещён датчик глубины; 2 - капилляр датчика температуры; 3 - хвостовое оперение; 4 - трос.

Лит.: Руководство по гидрологическим работам в океанах и морях, Л., 1967; Д ер ю г и н К. К., Степанюк И. А., Морская гидрометрия, Л., 1974.

ТЕРМОБУР, устройство для направленного разрушения твёрдых минеральных сред за счёт теплового и механич. воздействий сверхзвуковой, высокотемпературной газовой струи (одной или нескольких). Сконструирован и работает по принципу реактивного двигателя. В камеру сгорания пбдаётся обычно в распылённом виде горючее (дизельное топливо, керосин, бензин, метан, природный газ и др.), где смешивается с окислителем (как правило, кислород и сжатый воздух) и сгорает. Продукты сгорания выбрасываются наружу через сопло Лаваля, что увеличивает скорость их истечения до 1500-2000 м/сек. Термодинамич. параметры газовых струй уменьшаются по мере удаления от среза сопла Т. На расстоянии порядка 100-200 мм Т. с возд. окислителем имеют по оси струи темп-ру торможения 1700-2000 К и коэфф. теплоотдачи от газа к породе 3500-4500 вт/м²- град, с кислородным окислителем соответственно 2400-2700 К и 4000-5000 вт/м² • град. Применяют водяное, возд. и комбинированное (воздушно-водяное) охлаждение Т. При водяном и комбинированном охлаждении использованная вода обычно служит для подавления и улавливания пыли. Т. подразделяются на одно- и многосопловые; по размерам - на ручные и станковые. Ручные Т. используются при бурении шпуров, вторичном дроблении негабаритов, резке и обработке штучного камня. Их диаметр 20-50 мм, дл. 150-350 мм, расход горючего 10-15 кг/ч. Станковые Т. применяются для бурения и расширения скважин на спец. станках. Их диаметр 100-160мм, дл. 400-800мм, расход горючего 100-120 кг/ч. Повышение эффективности работы Т. ведётся в направлении повышения термодинамич. параметров газовых струй, упрощения конструкции, повышения износостойкости рабочих частей, создания конструкций для комбинированного воздействия на разрушаемую среду: "нагрев + охлаждение", "нагрев + механическое воздействие" и др.

Схема воздушного термобура: 1- магистраль для подачи горючего; 2 - магистраль для подачи воды; 3 - форсунка; 4 - сопла Лаваля; 5 - камера сгорания; 6 - винтовая нарезка для воды; 7 - сопловой аппарат; 5 - башмак.

Лит.: Ягупов А. В., Тепловое разрушение горных пород и огневое бурение, М., 1972; Дмитриев А. П., Гончаров С. А., Я н ч е н к о Г. А., Термоэлектрофизическое разрушение горных пород, ч. 2, М., 1975.

К. И. Наумов, А. П. Дмитриев, Г. А. Янченко.

ТЕРМОГЕННЫЕ БАКТЕРИИ (от термо... и греч. -genes - рождающий), бактерии, выделяющие в процессе роста значит, кол-во тепла. К Т. б. относятся бактерии, способные расти при высоких темп-pax (см. Термофильные организмы). Размножаясь в скоплениях органич. вещества (навоз, торф, сено и др.), Т. б. вызывают его нагревание до 70-80 °С, что может привести к самовозгоранию сена, торфа и т. п.

ТЕРМОГИГРОГРАФ, прибор для непрерывной регистрации темп-ры и относительной влажности воздуха на одной ленте. Т. состоит из биметаллич. термографа и волосного гигрографа.

ТЕРМОГЛУБОМЕР, прибор для определения глубины, на к-рую погружены океанографич. приборы в море. Т. представляет собой глубоководный термометр опрокидывающийся, резервуар к-рого не защищён от гидростатич. давления. При погружении Т. в море его резервуар сжимается водой и часть ртути вытесняется в капилляр. Т. о., длина столбика ртути в капилляре Т. определяется не только темп-рой воды, но и гидростатич. давлением, величина к-рого пропорциональна глубине погружения прибора. По разности показаний Т. и погружаемого вместе с ним глубоководного термометра, защищённого от внеш. давления, вычисляют глубину погружения океанографич. приборов.

Лит.: Руководство по гидрологическим работам в океанах и морях, Л., 1967; Дерюгин К.К., Степанюк И. А., Морская гидрометрия, Л., 1974.

ТЕРМОГРАММА, лента термографа с непрерывной записью темп-ры за сутки, неделю и т. д.

ТЕРМОГРАФ (от терло... и ...граф), прибор для непрерывной регистрации темп-ры воздуха, воды и др. Чувствит. элементом Т. может служить биметаллич. пластинка, термометр жидкостной или термометр сопротивления. В метеорологии наиболее распространён Т., чувствит. элементом к-рого является изогнутая биметаллич. пластинка 1 (рис.), деформирующаяся при изменении темп-ры. Перемещение её конца передаётся стрелке 3, к-рая чертит кривую на разграфлённой ленте. 1 мм записи по вертикали соответствует около 1 °С. По времени полного оборота барабана Т. подразделяются на суточные и недельные. Работа Т. контролируется по ртутному термометру.

Термограф: 1 - биметаллическая пластинка; 2 - передаточные рычаги; 3 - стрелка; 4 - барабан.

Лит.: Стернзат М. С., Метеорологические приборы и наблюдения, Л., 1968.

ТЕРМОГРАФИЯ (от термо... и ...графия), 1) в широком смысле слова Т. - производимая различными способами регистрация теплового поля объектов, т. е. поля их инфракрасного (ИК) излучения (см., напр., Инфракрасная фотография, Тепловидение). 2) В узком значении Т.- оперативный способ копирования и размножения рукописных, печатных и др. чёрно-белых штриховых материалов. Светлые участки оригинального материала меньше нагреваются при ИК-облучении, чем тёмные, т. к. они слабее поглощают ИК-излучение. Благодаря этому копировальный материал, приведённый в контакт с оригиналом при ИК-облучении последнего, испытывает те или иные изменения на более нагретых участках и не испытывает их на менее нагретых. Чаще всего таким изменением служит разложение введённых в копировальный материал солей металлов (напр., железа), в результате чего металл восстанавливается и темнеет в местах, контактировавших с более нагретыми участками оригинала. Достоинства Т. - быстрота и простота; вместе с тем разрешающая способность Т. невелика, а цветные детали почти не передаются.

См. также Термокопирование, Термокопировальный аппарат.

Лит.: Ш о р М. И., Светочувствительные бумаги и их применение, М., 1968; С л у ц к и й А. А., Шеберстов В. И., Копировальные процессы и материалы репрографии и малой полиграфии, М., 1971.

А. Л. Картужанский.

ТЕРМОДИНАМИКА, наука о наиболее общих свойствах макроскопич. систем, находящихся в состоянии термодинамич. равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундаментальных принципов (начал), к-рые являются обобщением многочисл. наблюдений и выполняются независимо от конкретной природы образующих систему тел. Поэтому закономерности в соотношениях между физ. величинами, к к-рым приводит Т., имеют универсальный характер. Обоснование законов Т., их связь с законами движения частиц, из к-рых построены тела, даётся статистической физикой. Последняя позволяет выяснить и границы применимости Т.

Равновесные и неравновесные состояния. Равновесным является такое состояние изолированной системы, в к-рое она переходит по истечении, строго говоря, бесконечно большого промежутка времени. Практически равновесие достигается за конечное время (время релаксации), к-рое зависит от природы тел, их взаимодействий, а также и от характера исходного неравновесного состояния. Если система находится в состоянии равновесия, то в равновесии находятся и отдельные её макроскопич. части. При неизменных внешних условиях такое состояние не меняется со временем. Следует подчеркнуть, что неизменность во времени не является достаточным признаком равновесности состояния. Напр., помещённый в термостат участок электрич. цепи, по к-рому течёт постоянный ток, находится в неизменном (стационарном) состоянии практически неограниченное время. Однако это состояние неравновесно: протекание тока сопровождается необратимым превращением энергии электрич. тока в теплоту, отводимую в термостат, в системе имеется градиент темп-ры. В стационарном неравновесном состоянии могут находиться и все т. н. открытые системы.

Равновесное состояние полностью характеризуется небольшим числом физ. параметров. Прежде всего, это температура, равенство значений к-рой для всех частей системы является необходимым условием термодинамич. равновесия. (Существование темп-ры - параметра, единого для всех частей системы, находящейся в равновесии, часто наз. нулевым началом Т.) Состояние однородных жидкости или газа полностью фиксируется заданием любых двух из трёх величин: темп-ры Т, объёма V и давления р. Связь между р, V и Т характерна для каждой данной жидкости (газа) и наз. уравнением состояния (напр., Клапейрона уравнение для идеального газа или Ван-дер-Ваалъса уравнение). В более сложных случаях для полной характеристики равновесного состояния могут понадобиться и др. параметры (напр., концентрации отдельных составляющих смеси газов, напряжённость электрич. поля, магнитная индукция).

Обратимые (квазистатические) и необратимые процессы. В процессе перехода из одного равновесного состояния в другое, к-рый может происходить под влиянием различных внешних воздействий, система проходит через непрерывный ряд состояний, не являющихся, вообще говоря, равновесными. Для реализации процесса, приближающегося по своим свойствам к равновесному, необходимо, чтобы он протекал достаточно медленно. Но сама по себе медленность процесса ещё не является достаточным признаком его равновесности. Так, процесс разрядки компенсатора через большое сопротивление или дросселирование (см. Джоуля-Томсона эффект), при к-ром газ перетекает из одного сосуда в другой через пористую перегородку под влиянием перепада давлений, могут быть сколь угодно медленными и при этом существенно неравновесными процессами. Равновесный процесс, представляя собой непрерывную цепь равновесных состояний, является обратимым - его можно совершить в обратном направлении, и при этом в окружающей среде не останется никаких изменений. Т. даёт полное количественное описание обратимых процессов, а для необратимых процессов устанавливает лишь определённые неравенства и указывает направление их протекания.

Первое начало термодинамики. Существуют два принципиально различающихся способа изменения состояния системы: первый связан с работой системы по перемещению на макроскопич. расстояния окружающих тел (или работой этих тел над системой); второй - с сообщением системе теплоты (или с отводом теплоты) при неизменном расположении окружающих тел. В общем случае переход системы из одного состояния в другое связан с сообщением системе нек-рого количества теплоты Д Q и совершением системой работы Д Л над внешними телами. Как показывает опыт, при заданных начальном и конечном состояниях Д Q и Д Л существенно зависят от пути перехода. Другими словами, эти величины являются характеристиками не отдельного состояния системы, а совершаемого ею процесса. Первое начало термодинамики утверждает, что если система совершает термодинамич. цикл (т. е. возвращается в конечном счёте в исходное состояние), то полное количество теплоты, сообщённое системе на протяжении цикла, равно совершённой ею работе.

Первое начало Т. представляет собой по существу выражение закона сохранения энергии для систем, в к-рых существенную роль играют тепловые процессы. Энергетич. эквивалентность теплоты и работы, т. е. возможность измерения их количеств в одних и тех же единицах и тем самым возможность их сравнения была доказана опытами Ю.Р. Майера (1842) и особенно Дж. Джоуля (1843). Первое начало Т. было сформулировано Майером, а затем в значительно более ясной форме Г. Гельмголъцем (1847). Приведённая выше формулировка первого начала равнозначна, очевидно, утверждению о невозможности вечного двигателя 1-го рода.

Из первого начала следует, что в случае незамкнутого процесса (когда система не возвращается в исходное состояние) разность

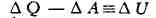
хотя и не равна, вообще говоря, нулю, но во всяком случае не зависит от пути перехода между данными состояниями. Действительно, произвольный процесс в обратном направлении образует с каждым из прямых процессов замкнутый цикл, для к-рого указанная разность обращается в нуль. Т. о., Д U представляет собой приращение величины 17, имеющей в каждом состоянии вполне определённое значение, или, как говорят, являющейся функцией состояний системы. Эта величина наз. внутренней энергией (или просто энергией) системы. Т. о., из первого начала Т. вытекает, что существует характеристич. функция состояния системы - её энергия. Если речь идёт об однородном теле, к-рое способно совершать работу только при изменении объёма, то

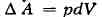
и бесконечно малое приращение (дифференциал) V равно

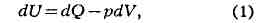
где dQ - бесконечно малое приращение теплоты, не являющееся, однако, дифференциалом к.-л. функции. При фиксированном объёме (dV = 0) вся сообщаемая телу теплота идёт на приращение внутренней энергии, и поэтому, в частности, теплоёмкость тела при постоянном объёме cv = (dU/dT)_v. Вводя другую функцию состояний H = U+pV (энтальпию), дифференциал к-рой

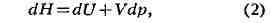
можно получить выражение для теплоёмкости, изменяемой пои постоянном давлении:

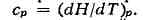
В случае идеального газа, к-рый описывается уравнением состояний Клапейрона

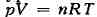
(я - число молей газа в объёме V, R - газовая постоянная), как свободная энергия, так и энтальпия определённой массы газа зависят только от Т, что подтверждается, напр., отсутствием охлаждения в процессе Джоуля-Томсона. Поэтому для идеального газа

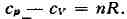
Второеначало термодинамики. Запрещая вечный двигатель 1-го рода, первое начало Т. не исключает возможности создания такой машины непрерывного действия, к-рая была бы способна превращать в полезную работу практически всю подводимую к ней теплоту (т. н. вечный двигатель 2-го рода). Однако весь опыт по конструированию тепловых машин, имевшийся в нач. 19 в., указывал на то, что кпд этих машин (отношение затраченной теплоты к полученной работе) всегда существенно меньше единицы: часть теплоты неизбежно рассеивается в окружающую среду. С. Карно первым показал (1824), что это обстоятельство имеет принципиальный характер, т. е. любая тепловая машина должна содержать помимо нагревателя (источника теплоты) и рабочего тела, совершающего термодинамич. цикл (напр., пара), также и холодильник, имеющий темп-ру, обязательно более низкую, чем темп-pa нагревателя. Второе начало термодинамики представляет собой обобщение вывода Карно на произвольные термодинамич. процессы, протекающие в природе. Р. Клаузиус (1850) дал 2-му началу следующую формулировку: теплота не может самопроизвольно перейти от системы с меньшей темп-рой к системе с большей темп-рой. Независимо в несколько иной форме этот принцип высказал У. Томсон (Кельвин) в 1851: невозможно построить периодически действующую машину, вся деятельность к-рой сводилась бы к поднятию нек-рого груза (совершению механич. работы) и соответствующему охлаждению теплового резервуара. Несмотря на качественный характер этого утверждения, оно приводит к далеко идущим количественным следствиям.

Прежде всего оно позволяет определить макс, кпд тепловой машины. Если машина работает на основе Карно цикла, то на протяжении изотермич. контакта с нагревателем (Т = Т i) рабочее тело получает количество теплоты ДQ₁, а на другом изотермич. участке цикла, находясь в контакте с холодильником (Т = Т₂), отдаёт ему количество теплоты ДQ₂. Отношение 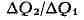должно быть одним и тем же у всех машин с обратимым циклом Карно, у к-рых одинаковы соответственно темп-ры нагревателей и холодильников, и не может зависеть от природы рабочего тела. Если бы это было не так, то машину с большей величиной указанного отношения можно было бы заставить работать в обратном направлении (поскольку циклы обратимы), приводя её в действие с помощью машины с меньшей величиной отношения. Эта комбинированная машина обладала бы тем свойством, что в ней теплота от холодильника передавалась бы нагревателю без совершения работы. Согласно 2-му началу Т. 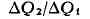это невозможно, и поэтому отношение  у обеих машин должно быть одинаковым. В частности, оно должно быть тем же, что и в случае, когда рабочим телом является идеальный газ. Здесь это отношение легко может быть найдено, и, т. о., оказывается, что для всех обратимых циклов Карно

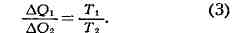
Это выражение наз. пропорцией Карно. В результате для всех машин с обратимым циклом Карно кпд максимален и равен
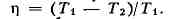
В случае, если цикл необратим, то кпд оказывается меньше этой величины. Необходимо подчеркнуть, что пропорция Карно и кпд цикла Карно имеют указанный вид только в том случае, если темп-pa измерена в абс. температурной шкале. Пропорция Карно положена в основу определения абс. температурной шкалы (см. Температурные шкалы). Следствием 2-го начала Т. (пропорции Карно) является существование энтропии как функции состояний. Если ввести величину S, изменение к-рой при изотермич. обратимом сообщении системе количества теплоты 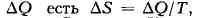то полное приращение S в цикле Карно будет равно нулю; на адиабатич. участках цикла ДS = 0 (т. к. ДQ = 0), а изменения на изотермич. участках компенсируют друг друга. Полное приращение S оказывается равным нулю и при осуществлении произвольного обратимого цикла, что доказывается разбиением цикла на последовательность бесконечно тонких циклов Карно (с малыми изотермич. участками). Отсюда следует (как и в случае внутренней энергии), что энтропия S является функцией состояния системы, т. е. изменение энтропии не зависит от пути перехода. Используя понятие энтропии, Клаузиус (1876) показал, что исходная формулировка 2-го начала Т. полностью эквивалентна следующей: существует функция состояния системы, её энтропия S, приращение к-рой при обратимом сообщении системе теплоты равно лов внутренней энергии и энтальпии:

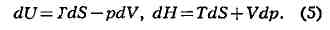
Отсюда видно, что естественными независимыми параметрами состояния для функций [7 и H являются соответственно пары S, V и S, р. Если же вместо энтропии в качестве независимого параметра используется темп-pa, то для описания системы более удобны свободная энергия (Гельмголъцева энергия, или изохорно-изотермич. потенциал) F = U - TS (для переменных Т и V) и термодинамич. потенциал G = H - TS для переменных Тир (Гиббсова энергия, или изобарно-изотермич. потенциал), диффепенциалы к-рых равны

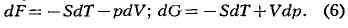
Функции состояний U, H, F и G наз. потенциалами термодинамическими системы для соответствующих пар независимых переменных. Метод термодинамич. потенциалов (Дж. Гиббс, 1874-1878), основанный на совместном применении 1-го и 2-го начал Т., позволяет получить ряд важных термодинамич. соотношений между различными физ. свойствами системы. Так, использование независимости вторых смешанных производных от порядка дифференцирования приводит к связи между теплоёмкостями Ср и cv, коэфф. теплового расширения (дV/дТ)p, и изотермич. коэфф. сжатия (ду/др)r

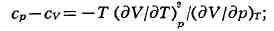
к соотношению между изотермич. и адиабатич. коэфф. сжатия (dV/dp)_s = = (Cp/Cv)(дV/дp)r и т. п. Из условия, что изолированная система в равновесном состоянии обладает макс, значением энтропии, вытекает условие минимальности термодинамич. потенциалов в равновесном состоянии по отношению к произвольным малым отклонениям от равновесия при фиксированных значениях соответствующих независимых переменных. Это приводит к важным неравенствам (условиям устойчивости), в частности (dpldV)_s <(др/дУ)г < 0, Ср > c_v > 0 (см. Устойчивость термодинамическая). Третье начало термодинамики. Энтропия определяется согласно 2-му началу Т. дифференциальным соотношением (4), т. е. определяется с точностью до постоянного слагаемого, к-рое хотя и не зависит от темп-ры, но могло бы быть различным для разных тел в состоянии равновесия. Соответствующие неопределённые слагаемые существуют и у термодинамич. потенциалов. В. Нернст (1906) на основе своих электрохимич. исследований пришёл к выводу, что эти слагаемые должны быть универсальными: они не зависят от давления, агрегатного состояния и других характеристик вещества. Этот новый, следующий из опыта принцип обычно наз. третьим началом термодинамики или тепловой теоремой Нернста. М. Планк (1911) показал, что оно равносильно условию: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения к абсолютному нулю темп-ры, поскольку универсальную константу в энтропии можно положить равной нулю. Из 3-го начала Т. следует, в частности, что коэфф. теплового расширения, изохорный коэфф. давления (др/дТУ и удельные теплоёмкости Ср и cv обращаются в нуль при Т - "0. Необходимо отметить, что 3-е начало T. и вытекающие из него следствия не относятся к системам, находящимся в т. н. заторможённом состоянии. Примером такой системы является смесь веществ, между к-рыми возможны хим. реакции, но они заторможены - скорость реакций при низких темп-pax очень мала. Другим примером может служить быстро замороженный раствор, к-рый при низкой темп-ре должен был бы расслоиться на фазы, но процесс расслоения при низких темп-pax практически не происходит. Такие состояния во многих отношениях подобны равновесным, однако их энтропия не обращается в нуль при Т = 0.

Применение термодинамики. Важными областями применения T. являются теория равновесия химического и теория фазового равновесия, в частности равновесия между разными агрегатными состояниями и равновесия при расслоении на фазы смесей жидкостей и газов. В этих случаях в процессе установления равновесия существенную роль играет обмен частицами вещества между разными фазами, и при формулировке условий равновесия используется понятие химического потенциала. Постоянство хим. потенциала заменяет условие постоянства давления, если жидкость или газ находятся во внешнем поле, напр, поле тяжести. Методы Т. эффективно применяются при изучении тех явлений природы, в к-рых существенную роль играют тепловые эффекты. В Т. принято выделять разделы, относящиеся к отдельным наукам и к технике (химич. Т., технич. Т. и т. д.), а также к различным объектам исследования (Т. упругих тел, Т. диэлектриков, магнетиков, сверхпроводников, плазмы, излучения, атмосферы, воды и др.).

Выяснение статистич. природы энтропии привело к построению термодинамич. теории флуктуации (А. Эйнштейн, 1910) и к развитию термодинамики неравновесных процессов.

Лит.: Зоммерфельд А., Термодинамика и статистическая физика, М., 1955; Леонтович М. А., Введение в термодинамику, 2 изд., М.- Л., 1952; Ландау Л. Д., Л и ф ш и ц Е. М., Статистическая физика, 2 изд., М., 1964 (Теоретическая физика, т. 5); Второе начало термодинамики Сб., М.- Л., 1934; Эпштейн П. С. Курс термодинамики, пер. с англ., М.- Л. 1948; Ван-дер-Ваальс И. Д., Констамм Ф., Курс термостатики, пер. с нем. М., 1936; Кубо Р., Термодинамика, пер с англ., М., 1970; Термодинамика. Терминология. Сб., М., 1973.

Г. М. Элиашберг.

ТЕРМОДИНАМИКА НЕРАВНОВЕСНЫХ ПРОЦЕССОВ, общая теория макроскопич. описания неравновесных процессов. Она наз. также неравновесной термодинамикой или термодинамикой необратимых процессов. Классич. термодинамика изучает термодинамич. (обратимые) процессы. Для неравновесных процессов она устанавливает лишь неравенства, к-рые указывают возможное направление этих процессов. Осн. задача Т. н. п.- количественное изучение неравновесных процессов, в частности определение их скоростей в зависимости от внешних условий. В Т. н. п. системы, в к-рых протекают неравновесные процессы, рассматриваются как непрерывные среды, а их параметры состояния - как полевые переменные, т. е. непрерывные функции координат и времени. Для макроскопич. описания неравновесных процессов применяют след, метод: систему представляют состоящей из элементарных объёмов,

при реальных (необратимых) адиабатич. процессах энтропия возрастает, достигая макс, значения в состоянии равновесия. Термодинамические потенциалы. Определение энтропии позволяет написать след, выражения для дифференции, к-рые всё же настолько велики, что содержат очень большое число молекул. Термодинамическое состояние каждого выделенного элементарного объёма характеризуется темп-рой, давлением и др. параметрами, применяемыми в термодинамике равновесных процессов, но зависящими от координат и времени. Количественное описание неравновесных процессов при таком методе заключается в составлении ур-ний баланса для элементарных объёмов на основе законов сохранения массы, импульса и энергии, а также ур-ния баланса энтропии и феноменологич. ур-ний рассматриваемых процессов. Методы Т. н. п. позволяют сформулировать для неравновесных процессов 1-е и 2-е начала термодинамики; получить из общих принципов, не рассматривая деталей механизма молекулярных взаимодействий, полную систему ур-ний переноса, т. е. ур-ния гидродинамики, теплопроводности и диффузии для простых и сложных систем (с хим. реакциями между компонентами, с учётом электромагнитных сил и т. д.).

Закон сохранения массы в Т. н. п. Для многокомпонентной системы скорость изменения массы /г-й компоненты в элементарном объёме равна потоку массы в этот объём РИС/., где ρ - плотность, a Vn-скорость компоненты. Поток в бесконечно малый элемент объёма, приходящийся на единицу объёма, есть дивергенция с обратным знаком, следовательно, ур-ние баланса массы k-u компоненты имеет вид

Для суммарной плотности

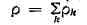
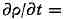
закон сохранения имеет аналогич. вид 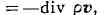где v-гидродинамич. скорость среды, зависящая от координат и времени. Для концентрации к.-л. компоненты

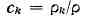
закон сохранения массы

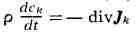
позволяет определить диффузионный поток
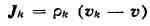(здесь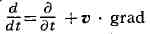
- полная производная по времени).

Закон сохранения импульса в Т. н. п. Изменение импульса элементарного объёма может происходить за счёт сил, вызванных градиентом внутренних напряжений в среде Paj, и внешних сил FI. Закон сохранения импульса, применённый к гидродинамич. скорости, позволяет получить основные ур-ния гидродинамики (Навье-Стокса уравнения):

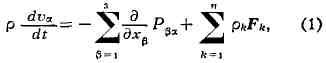
где и, - декартовы компоненты скорости v, а РЗ" - тензор напряжений. Закон сохранения энергии для элементарных объёмов представляет собой первое начало термодинамики в Т. н. п. Здесь приходится учитывать, что полная удельная энергия складывается из удельной кинетич., удельной потенциальной энергии в поле сил Ft,' и удельной внутренней энергии и, к-рая представляет собой энергию теплового движения молекул и среднюю энергию молекулярных взаимодействий. Для и получается ур-ние баланса, аналогичное (1), из к-рого следует, что скорость изменения плотности импульса на одну частицу dpu/dt определяется дивергенцией плотностей потоков внутренней энергии puv и теплоты Jq, а также работой внутренних напряжений

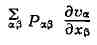
и внешних сил

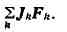
Уравнение баланса энтропии. В Т. н. п. принимается, что энтропия элементарного объёма s (локальная энтропия) является такой же функцией от внутренней энергии и, удельного объёма v = 1/p и концентрации си, как и в состоянии полного равновесия, и, следовательно, для неё справедливы обычные термодинамич. равенства. Эти положения вместе с законами сохранения массы, импульса и энергии позволяют найти уравнение баланса энтропии:

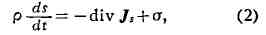
где а - локальное производство энтропии на единицу объёма в единицу времени, J_s-плотность потока энтропии, к-рый выражается через плотности теплового потока, диффузионного потока и ту часть тензора напряжений, к-рая связана с неравновесными процессами (т. е. через тензор вязких напряжений Пар).

Энтропия (в отличие от массы, энергии и импульса) не сохраняется, а возрастает со временем в элементе объёма вследствие необратимых процессов со скоростью а; кроме того, энтропия может изменяться вследствие втекания или вытекания её из элемента объёма, что не связано с необратимыми процессами. Положительность производства энтропии (а > о) выражает в Т. н. п. закон возрастания энтропии (см. Второе начало термодинамики).

Производство энтропии а определяется только необратимыми процессами (напр., диффузией, теплопроводностью, вязкостью) и равно

где Ji - поток (напр., диффузионный поток Jk, тепловой поток J_q, тензор вязких напряжений П-<э), а Х< - сопряжённые им термодинамич. силы, т. е. градиенты термодинамич. параметров, вызывающих отклонение от равновесного состояния. Для получения в Т. н. п. замкнутой системы ур-ний, описывающих неравновесные процессы, потоки физ, величин при помощи феноменология, ур-ний выражают через термодинамич. силы.

Феноменологические уравнения. Т. н. п. исходит из того, что при малых отклонениях системы от термодинамич. равновесия возникающие потоки линейно зависят от термодинамич. силы и описываются феноменологич. ур-ниями типа

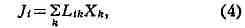
где Lift - кинетич. (феноменологич.) коэфф., или коэфф. переноса. В прямых процессах термодинамич. сила X* вызывает поток Jh, напр, градиент темп-ры вызывает поток теплоты (теплопроводность), градиент концентрации - поток вещества (диффузию), градиент скорости -поток импульса (определяет вязкость), электрическое поле - электрич. ток (электропроводность). Такие процессы характеризуются кинетич. коэфф., пропорциональными коэфф. теплопроводности, диффузии, вязкости, электропроводности. Последние обычно также наз. кинетич. коэфф. или коэфф. переноса. Термодинамич. сила Х_k может вызывать также поток J< при i ^ k; напр., градиент темп-ры может вызывать поток  вещества в многокомпонентных системах (термодиффузия, или Соре эффект), а градиент концентрации - поток теплоты (диффузионный термоэффект, или Дюфура эффект). Такие процессы наз. перекрёстными или налагающимися эффектами; они характеризуются коэфф
.
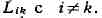
С учётом феноменологич. ур-ний производство энтропии равно

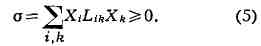
В стационарном состоянии величина o минимальна при заданных внешних условиях, препятствующих достижению равновесия (Пригожина теорема). В состоянии равновесия термодинамического o = 0. Одной из основных теорем Т. н. п. является Онсагера теорема, устанавливающая свойство симметрии кинетич. коэффициентов в отсутствие внешнего магнитного поля и вращения системы как целого: L_ik = L_ki.

Т. н. п. в гетерогенных системах. В рассмотренных выше примерах термодинамич. параметры были непрерывными функциями координат. Возможны неравновесные системы, в к-рых термодинамич. параметры меняются скачком (преры-вные, гетерогенные системы), напр, газы в сосудах, соединённых капилляром или мембраной. Если темп-ры Т и химические потенциалы ц газов в сосудах не равны (Т1 > Т₂ и Hi > ц₂), то термодинамич. силы

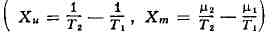
вызывают потоки массы и энергии (Jm = L₁₁Xm + L₁₂Xu, Ju = L₂₁Хm + L₂₂Xu) между сосудами. T. н. п. в этом случае объясняет возникновение термомолекулярной разности давлений и термомолекулярного эффекта. В этом примере потоки и термодинамич. силы - скаляры; такие процессы наз. скалярными. В процессах диффузии, теплопроводности, термодиффузии и эффекте Дюфура потоки и термодинамич. силы - векторы, поэтому они наз. векторными процессами. В вязком потоке, при сдвиговой вязкости, термодинамич. силы и потоки - тензоры, поэтому этот процесс наз. тензорным. В изотропной среде линейные соотношения могут связывать термодинамические силы и потоки лишь одинаковой тензорной размерности (теорема П. Кюри), в этом случае феноменологические уравнения сильно упрощаются.

T. н. п. даёт теоретич. основу для исследования открытых систем, позволяет объяснить многие неравновесные явления в проводниках, напр, термоэлектрические явления, гальваномагнитные явления и термомагнитные явления. Статистич. обоснование законов Т. н. п. и получение выражений для кинетич. коэфф. через параметры строения вещества входит в задачу неравновесной статистич. термодинамики, к-рая относится к Т. н. п. как статистическая термодинамика к термодинамике.

Лит.: Гроот С. Р. д е, Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Пригожий И., Введение в термодинамику необратимых процессов, пер. с англ., М., 1960; Денбиг К., Термодинамика стационарных необратимых процессов, пер. с англ., М., 1954; X а а з е Р., Термодинамика необратимых процессов, пер. с нем., М., 1967; Д ь я р м а т и И., Неравновесная термодинамика. Теория поля п вариационные принципы, пер. с англ., М., 1974.

Д. H. Зубарев.

ТЕРМОДИНАМИКА ХИМИЧЕСКАЯ, раздел физической химии, рассматривающий термодинамич. явления в области химии, а также зависимости термодинамич. свойств веществ от их состава и агрегатного состояния. Т. x. тесно связана с термохимией, учением о равновесии химическом и учением о растворах (в частности, электролитов), теорией электродных потенциалов, с термодинамикой поверхностных явлений.

Т. x. базируется на общих положениях и выводах термодинамики и прежде всего - на первом начале термодинамики и втором начале термодинамики. Первое начало и важнейшее его следствие - Тесса закон служат основой термохимии. При термохимич. расчётах большую роль играют теплоты образования веществ, значения к-рых для каждого из реагентов позволяют легко вычислить тепловой эффект реакции; для органич. веществ подобную роль играют теплоты сгорания. Наряду с измерениями тепловых эффектов различных процессов (см. Калориметрия) используются и определение энергии связи между атомами на основе спектральных данных, и различные приближённые закономерности. Первое начало термодинамики лежит в основе Кирхгофа уравнения, выражающего температурную зависимость теплового эффекта хим. реакции. Второе начало термодинамики служит основой учения о равновесии, в частности химического. Его применение к изучению хим. реакции впервые было дано в работах Дж. Гиббса, А. Л. Потылицына, Г. Гелъмгольиа, Я. Вант-Гоффа, А. Л. Ле Шателъе. В Т. x. второе начало позволяет установить, как изменение внешних условий (напр., темп-ры, давления) влияет на равновесие и, следовательно, какими они должны быть, чтобы рассматриваемый процесс мог совершаться самопроизвольно (т. е. без затраты работы извне) в нужном направлении и с оптимальными результатами.

В Т. x. для определения характеристик процесса применяют различные термодинамич. функции. Наряду с энтропией S, изменением к-рой наиболее просто характеризуются процессы в изолированных системах, широко используют потенциалы термодинамические, позволяющие получить характеристики процессов при различных условиях их проведения. Так как химические реакции обычно происходят при постоянных темп-ре Т, давлении р или объёме V, то наибольшее практич. значение приобрели две функции:

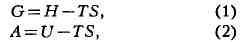
где G - гиббсова энергия, А - гельмголъцева энергия, H - энтальпия и U -внутренняя энергия. На основе (1) и (2) записываются зависимости:

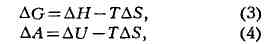
где ДН и Д[/- соответственно изобарный и изохорный тепловые эффекты реакции. Самопроизвольные процессы, происходящие при условии р, T = const, возможны лишь в направлении уменьшения G; пределом их протекания, т. е. условием равновесия, служит достижение минимального значения G. Ход процессов, происходящих при V, Т= const, прослеживается по изменению А. Знак и величина ДО (ДА) определяются соотношением между членами уравнения (3) или (4): тепловым эффектом ДН(Д[7) и т. н. энтропийным фактором ГД5; относительное значение первого возрастает с понижением темп-ры, для второго - с её повышением.

В T. x. важна роль химических потенциалов, т. к. любой переход вещества из одной фазы в другую (напр., при растворении) возможен лишь в направлении их выравнивания. Условием равновесия служат одинаковые значения хим. потенциала каждого компонента во всех фазах системы. Из этих условий выводится фаз правило, являющееся фундаментальным обобщением, описывающим равновесие в любой гетерогенной системе. В Т. x. большое значение имеют различные соотношения, выводимые из общих положений термодинамики. К их числу относятся: действующих масс закон; ур-ние изотермы реакции, характеризующее зависимость ДО(ДЛ) от концентраций (активностей) и парциальных давлений (фугитивностей) реагентов и выражающее величину максимальной работы реакции; ур-ние изобары (изохоры) реакции, характеризующее влияние темп-ры на хим. равновесие, и т. д.

Для расчётов равновесий существенное значение имеют т. н. стандартные состояния веществ. Если все реагенты находятся в этих состояниях, то справедливо соотношение

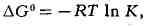
где G - стандартная гиббсова энергия, R - газовая постоянная, К - константа равновесия; объединение (3) с (5) даёт соотношение

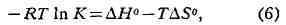
позволяющее по стандартным энтропиям и теплотам образования рассчитать разнообразные равновесия (хим. взаимодействие, фазовые равновесия в одно- и многокомпонентных системах, диссоциация электролитов, в частности комплексных соединений, и т. д.). Для расчёта хим. равновесий важно третье начало термодинамики (см. также Нернста теорема). С его помощью можно найти энтропию вещества в данных условиях на основании результатов калориметрич. определений - по температурной зависимости его теплоёмкости (от темп-р, близких к абс. нулю, до данной темп-ры), по температурам фазовых переходов и теплотам фазовых переходов (в соответствующем интервале темп-р). Затем по значениям S каждого реагента (5„р₀д. и SHCX. - энтальпии продуктов реакции и исходных веществ) легко вычислить Д5(Е5прод.- Д5„_с....) для реакции.

Важное место в Т. x. принадлежит квантовомеханич. расчётам термодинамич. свойств и характеристик процессов (напр., теплот образования); методами статистич. термодинамики можно вычислить значение различных термодинамич. функций на основе спектральных данных, связывая последние со структурой молекул (см. Статистическая физика).

Из других направлений Т. x. большая роль принадлежит термодинамике растворов. Хотя общая теория растворов не разработана, однако введение понятия активности существенно облегчило использование термодинамич. ур-ний (при наличии соответствующих экспериментальных данных).

Выводы и методы Т. x., связанные с термохимией, учением о хим. равновесии, свойствами растворов и т. д., широко используются и в смежных отраслях знаний (физика, теплоэнергетика, геология, геохимия, биология и др.), и при решении проблем прикладного характера (хим., нефтехим.,металлургич., топливная и др. отрасли пром-сти), способствуя теоретич. обоснованию и практич. осуществлению проектируемых, вновь вводимых и интенсификации ранее осуществлённых процессов.

С сер. 20 в. получили развитие термодинамика неравновесных процессов и термодинамика высокотемпературных хим. реакций.

Лит.: Курс физической химии, 2 изд., М., 1969; Ерёмин Е. H., Основы химической термодинамики, М., 1974; Карапетьянц М.X., Химическая термодинамика, 3 изд., М., 1975; Пригожий И., Д е ф э н Р., Химическая термодинамика, пер. с англ., Новосиб., 1966; Glasstone S., Thermodynamics for chemists, N. Y., 1947; Aston J., Fritz J., Thermodynamics and Statistical Thermodynamics, N. Y.-L., 1959; Lewis G., R a п d a l l М., Thermodynamics, 2 ed., N. Y. - L.-Toronto, 1961. См. также лит. при ст. Термодинамика.

М. X. Карапетьянц.