ТЕЙЛОРА РЯД, степенной ряд вида

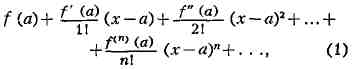
где f(x) - функция, имеющая при x = а производные всех порядков. Во многих практически важных случаях этот ряд сходится к f(x) на нек-ром интервале с центром в точке а:

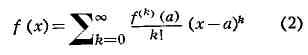
(эта формула опубликована в 1715 Б. Тейлором). Разность R_n(x) = f(x) - S_n(x), где S_n(x) - сумма первых п + 1 членов ряда (1), наз. остаточным членом Т. р. Формула (2) справедлива, если lim Rn(x) = 0. Т. р. можно представить n->... в виде

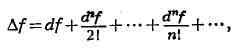
применимом и к функциям многих переменных.

При а = 0 разложение функции в Т. р. (исторически неправильно называемый в этом случае рядом Маклорена; см. Маклорена ряд) принимает вид:

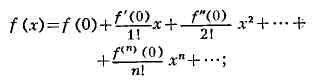
в частности:

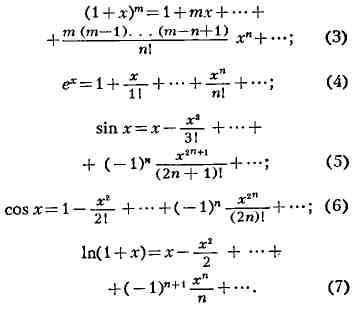
Ряд (3), являющийся обобщением на случай дробных и отрицательных показателей формулы бинома Ньютона, сходится: при -l<x<l, если т<-1; при - l<x-.S 1, если- 1<т<0;при- Isjxs; 1, если т>0. Ряды (4), (5) и (6) сходятся при любых значениях x, ряд (7) сходится при -l<xs? 1.

Функция f(z) комплексного переменного z, регулярная в точке а, раскладывается в Т. р. по степеням z - а внутри круга с центром в точке а и с радиусом, равным расстоянию от а до ближайшей особой точки функции f(z). Вне этого круга Т. р. расходится, поведение же его на границе круга сходимости может быть весьма сложным. Радиус круга сходимости выражается через коэффициенты Т. р. (см. Радиус сходимости).

Т. р. является мощным аппаратом для исследования функций и для приближённых вычислений. См. также Тейлора формула.

Лит.: Хинчин А. Я., Краткий курс математического анализа, М., 1953; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.

ТЕЙЛОРА ФОРМУЛА, формула

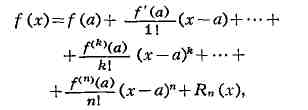
изображающая функцию f(x), имеющую n-ю производную f⁽ⁿ⁾ (a) в точке x = а, в виде суммы многочлена степени п, расположенного по степеням x-а, и остаточного члена R_n(x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x-а)" [т. е. R_n(x) = а_п(х)(х-а)ⁿ, где a_n(x)->0 при x->а]. Если в интервале между а и x существует (n + 1 )-я производная, то R_n(x) можно представить в видах:

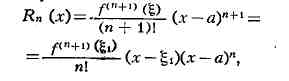
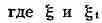- какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф., имеет в точке а соприкосновение не ниже n-ro порядка с графиком функции f(x). Т. ф. применяют для исследования функций и для приближённых вычислений.

Лит.: Хинчин А. Я., Краткий курс математического анализа, М., 1953; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969.