СТЬЮДЕНТА РАСПРЕДЕЛЕНИЕ с f степенями свободы, распределение отношения Т = X/Y независимых случайных величин X и Y, где X подчиняется нормальному распределению с математич. ожиданием ЕХ = 0 и дисперсией DX = 1, a fY² имеет "биквадрат" распределение с f степенями свободы. Функция распределения Стьюдента выражается интегралом

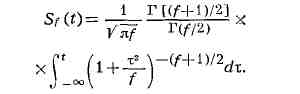
Если Х₁, ..., Х_N - независимые случайные величины, одинаково нормально распределённые, причём ЕХ₁ = а и DX₁ = о² (i = 1,...,n), то при любых действительных значениях а и о>0 отношение

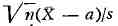
подчиняется С. р. с f = п - 1 степенями свободы (здесь

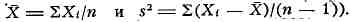
Это было впервые (1908) использовано для решения важной задачи классич. теории ошибок У. Госсетом (Англия), писавшим под псевдонимом Стьюдент (Student). Суть этой задачи заключается в проверке гипотезы а = = а₀ (а₀ = заданное число, дисперсия а² предполагается неизвестной). Гипотезу а = а0 считают не противоречащей результатам наблюдений X₁, ...,Х_n,если справедливо неравенство  

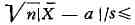
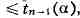
в противном случае гипотеза а = ао отвергается (т. н. критерий Стьюдента). Критическое значение t=t_n-1(a) представляет собой решение уравнения S_n-1(t)=1-a/2, a - заданный значимости уровень (0 < а<½) Если проверяемая гипотеза a = ао верна, то критерий Стьюдента, соответствующий критическому значению t_n-1(a), может её ошибочно отвергнуть с вероятностью a.

С. р. используется для решения мн. др. задач математич. статистики (см. Малые выборки, Ошибок теория, Наименьших квадратов метод).

Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.