СТОКСА ЗАКОН, закон, определяющий силу сопротивления F, испытываемую
твёрдым шаром при его медленном поступательном движении в неограниченной вязкой
жидкости: F = б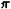
 rv, где
rv, где  - коэфф. вязкости
жидкости, г - радиус шара и
- коэфф. вязкости
жидкости, г - радиус шара и  - его скорость. Эта формула
выведена Дж. Г. Стоксом в 1851. С. з. справедлив лишь для малых Рейнольдса
чисел Re << 1. Им пользуются в коллоидной химии, молекулярной физике
и метеорологии. По С. з. можно определить скорость осаждения мелких капель
тумана, коллоидных частиц, частиц ила и других мелких частиц. Предельную
скорость
- его скорость. Эта формула
выведена Дж. Г. Стоксом в 1851. С. з. справедлив лишь для малых Рейнольдса
чисел Re << 1. Им пользуются в коллоидной химии, молекулярной физике
и метеорологии. По С. з. можно определить скорость осаждения мелких капель
тумана, коллоидных частиц, частиц ила и других мелких частиц. Предельную
скорость 
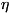
 падения шарика малых размеров в вязкой жидкости находят по формуле
падения шарика малых размеров в вязкой жидкости находят по формуле
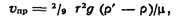
где 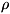 и
и 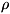 - плотность жидкости и вещества шарика, g - ускорение
свободного падения. С. з. применяется в вискозиметрии для определения
коэфф. вязкости очень вязких жидкостей (см. тадже Вискозиметр).
- плотность жидкости и вещества шарика, g - ускорение
свободного падения. С. з. применяется в вискозиметрии для определения
коэфф. вязкости очень вязких жидкостей (см. тадже Вискозиметр).
Лит.:
Лойцянский Л. Г., Механика жидкости и газа, 3 изд., M., 1970, §
92.
СТОКСА ПРАВИЛО, Стокса закон, утверждает, что длина волны
фотолюминесценции больше, чем длина волны возбуждающего света. Установлено Дж.
Г. Стоксом в 1852. С. п. выполняется не всегда, во MH. случаях в спектре
фотолюминесценции наблюдаются антистоксовы линии, длины волн к-рых короче
возбуждающей. Более широкую область применения С. п. имеет в формулировке нем.
физика Э. Ломмеля: максимум спектра люминесценции сдвинут по отношению к
максимуму спектра поглощения в сторону более длинных волн. Согласно С. п.,
энергия фотонов люминесценции меньше энергии фотонов возбуждающего света (см.
также ст. Люминесценция). Лит. см. при ст. Люминесценция.
СТОКСА ПРОБЛЕМА, задача об определении внешнего гравитационного поля
планеты по её внешней уровенной поверхности S, массе внутри S и угловой
скорости вращения около нек-рой оси. Дж. Г. Стоке доказал разрешимость
этой задачи и дал приближённое решение для сжатого сфероида с относит, ошибкой
порядка квадрата его сжатия как первой краевой задачи теории потенциала. Точное
решение С. п. для эллипсоида получено итал. учёным П. Пиццетти и M. С. Молоденским.
Произвольной форме S соответствуют краевое условие
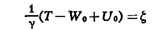
и уравнение относительно 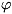 :
:
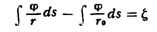
при условии
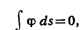
где 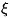 - высота S над отсчётным эллипсоидом S0, содержащим
заданную массу; возмущающий потенциал
- высота S над отсчётным эллипсоидом S0, содержащим
заданную массу; возмущающий потенциал
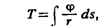
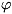 - плотность простого слоя на S, Wo - потенциал силы тяжести в
начале счёта
- плотность простого слоя на S, Wo - потенциал силы тяжести в
начале счёта 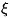 на пересечении S и S0, Uo - то же
на So,
на пересечении S и S0, Uo - то же
на So, 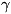 - сила тяжести в поле эллипсоида, г -, расстояние
между элементом ds и точкой на S с высотой
- сила тяжести в поле эллипсоида, г -, расстояние
между элементом ds и точкой на S с высотой 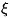 , T0 - то
же между ds и точкой, являющейся началом счёта
, T0 - то
же между ds и точкой, являющейся началом счёта 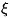 . Оси вращения
S и So совпадают. Уравнение для
. Оси вращения
S и So совпадают. Уравнение для 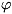 можно заменить системой линейных
алгебраич. уравнений. Определение
можно заменить системой линейных
алгебраич. уравнений. Определение 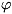 решает задачу, именуемую С. п.
Изложенное решение пригодно и в том случае, когда S - неуровенная и
решает задачу, именуемую С. п.
Изложенное решение пригодно и в том случае, когда S - неуровенная и 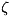 -
высота квазигеоида (см. Геоид).
-
высота квазигеоида (см. Геоид).
Лит.: Молоденский M. С., Еремеев В. Ф., Юркина M. И., Методы
изучения внешнего гравитационного поля и фигуры Земли, M., 1960 (Tp. Центр. н.-и. ин-та геодезии, аэросъемки и картографии, в. 131); Stokes G. G., On attractions and on
Clairaut's theor&m, "Cambridge and Dublin mathematical journal",
1849, v. 4.
М.И. Юркина.
CTОKCA ФОРМУЛА, формула преобразования криволинейного интеграла по
замкнутому контуру L в поверхностный интеграл по поверхности 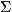 , ограниченной контуром L. С. ф. имеет вид:
, ограниченной контуром L. С. ф. имеет вид:
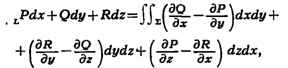
причём направление обхода контура L должно быть согласовано с
ориентацией поверхности 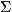 . В векторной форме С. ф.
приобретает вид:
. В векторной форме С. ф.
приобретает вид:
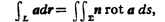
где а = Pi + Qj + Rk, dr - элемент контура L, ds - элемент
поверхности 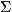 ,
,
и - единичный вектор внешней нормали к этой поверхности. Физич. смысл С. ф.
состоит в том, что циркуляция векторного поля по контуру L равна потоку вихря
поля через поверхность 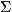 . С. ф. предложена Дж. Г. Стоксом
в 1854.
. С. ф. предложена Дж. Г. Стоксом
в 1854.
В гидромеханике формулой Стокса иногда называют Стокса закон.