СТАТИСТИКА ТОРГОВЛИ, отрасль экономической статистики, изучающая
количеств, закономерности массовых явлений в области товарного обращения, к-рые
характеризуют продвижение товаров нар. потребления из сферы производства в
сферу потребления.
В дореволюц. России С. т. по существу не было. Статистические наблюдение и
публикация ограничивались в основном данными биржевых оборотов и внеш.
торговли. Не было и прямых статистич. данных о внутр. торговле (о торг. сети,
кадрах, оптовом, розничном товарообороте и т. п.).
В СССР товарное обращение средств произ-ва изучает статистика
материально-технического снабжения и сбыта. Статистика заготовок характеризует
движение части с.-х. продуктов в сфере обращения.
Осн. источники С. т. - отчётность гос. и кооп. торг, орг-ций и предприятий, а
также единовременные обследования и переписи, посвящённые гл. обр.
характеристике качеств, состояния материальной базы торговли и эффективности
новых форм обслуживания покупателей.
Центр, раздел С. т.- статистика товарооборота. Статистика оптового
товарооборота изучает обеспечение розничной торговли товарами нар. потребления,
контролирует выполнение планов использования товарных ресурсов по важнейшим
товарам нар. потребления (в этих целях разрабатываются балансы распределения
товарных ресурсов), осуществляет контроль поставок товаров по рыночному фонду
торгующим орг-циям, а также отгрузок товаров из районов произ-ва в районы
потребления. Составляется также сводный отчётный баланс товарного обеспечения
розничного товарооборота. Статистика розничного товарооборота гос. и кооп.
торговли изучает заключит, этап товарного обращения, т. е. продажу товаров
населению. Ведёт учёт выполнения гос. плана розничного товарооборота, изучает
объём и динамику продажи отд. товаров. Является важным источником изучения
роста потребления и благосостояния трудящихся. По СССР, союзным республикам и
областям систематически исчисляются индексы розничного товарооборота в
фактических (Igp=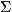 q1p1 /
q1p1 / 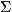 q0p0) и неизменных ценах (lg
=
q0p0) и неизменных ценах (lg
= 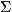 q1p0 /
q1p0 /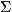 q0p0)
как в целом, так и в расчёте на душу населения. Наряду с этим С. т. изучает
обороты колх. торговли на основе систематич. наблюдения колх. рынков в более
чем 250 городах и рабочих посёлках.
q0p0)
как в целом, так и в расчёте на душу населения. Наряду с этим С. т. изучает
обороты колх. торговли на основе систематич. наблюдения колх. рынков в более
чем 250 городах и рабочих посёлках.
Тесно связана со статистикой товарооборота статистика товарных запасов,
определяющая их объём и состав в товаро-проводящей сети. Её осн. показатели:
обеспеченность товарооборота товарными запасами в днях (отношение объёма
запасов на определённое число к однодневному товарообороту), скорость
товарооборота (отношение товарооборота за нек-рый период к среднему товарному
запасу за этот же период) и продолжительность одного оборота в днях (отношение
среднего товарного запаса к однодневному товарообороту). Статистика товарных
запасов является важным источником изучения степени удовлетворения спроса
населения на отдельные товары и соответствия предлагаемых товаров спросу.
Важный раздел С. т.- статистика гос. розничных цен, характеризующая их
динамику при помощи индекса цен. Изучает средние цены товаров, их структуру и
динамику. Особо исчисляются индексы цен колх. торговли - на основе массовой
регистрации цен с.-х. товаров на 25-е число каждого месяца. Индексы цен
определяются по формуле агрегатного индекса с весами текущего периода
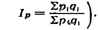
Статистика издержек обращения
и рентабельности торг. орг-ций даёт сведения
об общей сумме издержек обращения в оптовой и розничной торговле, обществ.
питании и на складах долгосрочного хранения овощей, картофеля и фруктов. На
основе единой номенклатуры статей изучается состав издержек обращения по видам
товаров. Сравнивая издержки обращения с товарооборотом, определяют
относительный уровень издержек обращения (отношение их суммы к товарообороту) - осн. показатель для изучения динамики издержек обращения и сравнения их уровня
по отд. торг, орг-циям. Статистич. анализ направлен на выявление осн. факторов,
определяющих динамику издержек обращения, и на поиски резервов снижения их
относительного уровня, что является гл. предпосылкой повышения рентабельности в
торговле (последняя определяется как отношение чистой прибыли к товарообороту).
Статистика материальной базы торговли изучает динамику, состав, размещение и
технич. оснащение оптовой и розничной торг, сети и сети обществ, питания. Один
из её качеств, показателей - обеспеченность населения розничной торг. сетью, исчисляемый как отношение мощности предприятий (торг. площадь, число
мест) на 10 тыс. человек населения. С. т. изучает также труд в торговле: численность
и состав работников торговли, производительность и оплату их труда.
Система показателей и методы сов. С. т. получили широкое применение в ряде
социалистич. стран. Постоянной комиссией СЭВ по статистике приняты
согласованные осн. показатели и унифицирована методология статистики розничного
товарооборота (товарная классификация, методы группировок, методология расчёта
индексов и пр.).
В капиталистич. странах осн. источниками С. т. являются переписи (цензы)
оптовой и розничной торговли, характеризующие торг. сеть, товарооборот,
товарные запасы и торг. персонал. Текущая (конъюнктурная) статистика
представлена индексами оптового и розничного товарооборота, товарных запасов и
цен, исчисляемыми гл. обр. на основе выборочных наблюдений.
Лит.:
Ряузов H. H., Tительбаум H. П., Статистика торговли, 5
изд., M., 1968.
H. H. Ряузов.
СТАТИСТИКА ТРАНСПОРТА, в СССР отрасль экономической статистики, объектом
изучения к-рой является трансп. система, включающая как отд. виды транспорта
общего пользования - ж.-д., морской, речной, автомобильный, воздушный и
трубопроводный, так и транспорт необщего пользования - ведомств, подъездные
пути, флот и автомобильный транспорт (см. Промышленный транспорт).
В СССР осн. источник данных С. т. - сплошной текущий учёт и основанная
на нём периодич. отчётность трансп. предприятий, а также спец. статистич.
обследования сплошного и несплошного характера (напр., ежегодная перепись
вагонов, обследование скорости доставки грузов). В С. т. выделяются след,
разделы: статистика перевозок; эксплуатационная; осн. фондов и технич.
вооружённости; труда; материально-технического снабжения; финансов.
Статистика перевозок исследует продукцию транспорта - перемещение грузов и
пассажиров. Перевозки грузов характеризуются след, показателями: отправлено,
прибыло, перевезено (т); грузооборот (т*км); ср. дальность
перевозки (км), ср. густота перевозок (т), ср. продолжительность (сут)
и скорость доставки грузов (км/сут); межрайонный (по ж.-д.
транспорту - и междудорожный) обмен и трансп. баланс районов страны по отд.
грузам. Аналогичные показатели, за нек-рым исключением, определяются и по пасс,
перевозкам. Эти показатели - общие для всей трансп. системы. Совокупная
(приведённая) продукция на всех видах транспорта, кроме воздушного,
определяется суммированием грузооборота и пассажирооборота.
Объект эксплуатационной С. т.- наличный парк подвижных перевозочных средств,
их работа и использование. Объём работы подвижного состава выражается
эксплуатационным грузооборотом (т*км, нетто и брутто), пробегом.
Сопоставлением объёмных показателей и затрат времени подвижного состава в
различных сочетаниях определяются показатели использования перевозочных
средств: среднесуточная производительность единицы перевозочных средств
(двухосного условного вагона, локомотива, тонны грузоподъёмности или лошадиной
силы мощности), среднесуточный пробег, ср. технич. и участковая (коммерческая) скорости
движения перевозочных средств. Кроме того, на отд. видах транспорта
определяются свойственные только им показатели: доля порожнего пробега вагонов,
ср. время оборота и показатели нагрузки грузового вагона, ср. вес и состав
поезда - на ж.-д. транспорте; чистая производительность речного судна (за время
хода с грузом), ср. продолжительность оборота баржи за рейс - на речном
транспорте и др.
Материально-техническая база изучается С. т. на основе натурального и
стоимостного выражения осн. средств с целью оценки использования производств,
фондов транспорта, исследования пропорциональности развития отд. элементов
трансп. системы и соответствия уровня технич. базы транспорта развитию нар.
х-ва. Для решения этих задач особо важное значение имеет паспортизация технич.
средств и единая классификация осн. фондов в нар. х-ве. Важнейшие показатели -
протяжённость путей сообщения и инвентарные парки подвижного состава.
Статистика труда на транспорте изучает численность, состав и движение
рабочей силы; использование рабочего времени и производительность труда; фонд
заработной платы и ср. заработную плату работников. В этом разделе С. т.
специфичным является измерение затрат труда работников, непосредственно
связанных с осуществлением перевозочного процесса, а также оценка уровня
производительности труда эксплуатац. контингента.
В статистике материально-технического снабжения особое значение имеют
показатели абсолютного и удельного расхода энергетич. ресурсов на перевозки, т.
к. на транспорте топливо и электроэнергия - осн. виды материальных затрат.
Финансовая статистика исследует доходы, расходы, доходность и себестоимость
перевозок, а также общую рентабельность работы отд. видов транспорта. Доходы в
основном учитываются по моменту и месту их получения, кроме ж.-д. транспорта,
где доходы отд. дорог от перевозок в прямом сообщении определяются расчётным
путём в процессе разработки сведений о перевозках. В анализе расходов и прибыли
используются данные бухгалтерского учёта.
На совр. этапе строительства материально-технической базы коммунизма перед
С. т. стоят задачи исследования закономерностей и пропорциональностей развития
трансп. системы как отрасли материального произ-ва, выявления степени
удовлетворения потребностей нар. х-ва и населения в перевозках, создания единой
системы С. т.
Организация С. т. в других социалистических странах во многом идентична С.
т. в СССР. Вопросы методологии исчисления показателей С. т. в 60- 70-е гг. 20
в. неоднократно обсуждались на совещаниях экспертов по статистике в рамках СЭВ
и ООН.
В капиталистических странах С. т. характеризует в основном перевозки,
протяжённость путей сообщения и доходы отд. видов транспорта.
Лит.:
Исторический очерк развития учреждений и работ ведомства путей
сообщения по статистике и карте путей сообщения в 1798-1898 гг., СПБ, 1898;
Кочетов И. В., Железнодорожная статистика, 2 изд., M., 1953; Лебедев E. П.,
Транспортная статистика, 2 изд., M., 1964; Транспорт и связь СССР. Статистич.
сб., M., 1972.
Я. П. Леонова, Э. А. Свиридова,
СТАТИСТИКА ТРУДА, отрасль экономической статистики, изучающая
количеств, закономерности массовых явлений в области воспроизводства трудовых
ресурсов и эффективности их использования. С. т. разрабатывает и
анализирует показатели занятости, организации и условий труда, качеств, состава
работающих (распределение их по полу, возрасту, образованию, профессиям и др.),
производительности труда, механизации труда, использования рабочего
времени, оплаты труда и нек-рые показатели уровня жизни трудящихся
[номинальные (денежные) и реальные доходы населения, потребление
материальных благ и услуг, использование внерабочего времени, в т. ч.
свободного времени]. Богатейший материал для изучения труда и положения трудящихся
дали К. Маркс, Ф. Энгельс и В. И. Ленин. Маркс и Энгельс разработали важнейшие
вопросы всеобщей статистики рабочего класса. В трудах Ленина отражено
возникновение и развитие науч. С. т.
В дореволюц. России не было единой системы гос. статистики. Нек-рые
показатели по труду разрабатывались отд. ведомствами, фаб.-зав. инспекторами и
исследователями. В работах прогрессивных деятелей освещались стачечная борьба,
заработки и штрафы, рабочий день, жилищные условия. После Окт. социалистич.
революции 1917 в СССР создана С. т. как самостоят. отрасль в единой системе гос. статистики.
В СССР система показателей С.
т. предусматривает: 1) изучение занятости, т. е. степени вовлечения населения в
обществ. произ-во, исследование воспроиз-ва,
распределения и использования трудовых ресурсов страны на всех стадиях обществ,
воспроизводства и выявление неиспользованных трудовых ресурсов. 2)
Определение и анализ численности и состава занятых в нар. х-ве по профессиям и
должностям, по их роли в производств, процессе, квалификации, стажу
работы, полу, возрасту и др. признакам; исследование перераспределения труда по
отраслям нар. х-ва и терр. страны в результате технич. прогресса; разработку и
анализ показателей подготовки квалифицированных рабочих кадров и повышения
квалификации работающих, а также численности специалистов с высшим и средним
специальным образованием, занятых в нар. х-ве; изучение движения работающих по
приёму и увольнению; разработку и анализ показателей, характеризующих
использование рабочего времени. 3) Измерение и анализ уровня, динамики
производительности труда и факторов его роста как показателей эффективности
обществ, произ-ва; определение увеличения объёма произ-ва в результате
повышения производительности труда. 4) Исчисление и анализ фонда, уровня и
динамики заработной платы во взаимной связи с показателями
производительности труда и объёма производства; изучение дифференциации оплаты
труда по профессиям, квалификации трудящихся и по терр. страны; определение
доли фондов материального поощрения в оплате труда; исследование
моральных и материальных стимулов труда. 5) Изучение уровня жизни трудящихся
при помощи показателей доходов и расходов различных социально-экономич. групп
трудящихся и исследование закономерностей влияния уровня и динамики доходов
семей на их потребление.
Исходной информацией С. т. служит первичный учёт личного состава и
заработной платы на предприятиях, в учреждениях и орг-циях. На её основе
составляется месячная (предприятиями осн. производств, отраслей), квартальная и
годовая отчётность. Большую роль в информац. обеспечении С. т. играют переписи
населения, единовременные обследования по труду и заработной плате, а также
выборочные бюджетные обследования семей рабочих, служащих и колхозников.
С. т. в других социалистических странах централизована и в рамках СЭВ
развивается в направлении взаимного обмена информацией и проведения совместных
работ. Для достижения сопоставимости показателей по труду проводится
работа по унификации методологических положений по осн. показателям статистики
труда (трудовые ресурсы, численность рабочих и служащих, рабочее время,
классификация отраслей по сферам приложения труда, уровень доходов и объём
потребления материальных благ и услуг). Разрабатываются и совершенствуются
работы по междунар. сравнению уровня производительности труда и принципам международного
социалистического разделения труда.
С. т. в капиталистических странах до 20-х гг. 20 в. основывалась на
эпизодических обследованиях. Кризисы и безработица 30-х гг. повысили интерес к
С. т., которая начинает базироваться на более систематич. информации. После 2-й
мировой войны 1939-45 С. т. получает дальнейшее развитие, однако статистич.
материалы по труду собираются и разрабатываются по различной методологии как
правительств. органами, так и различными ин-тами, поэтому для публикуемых
показателей по труду характерно отсутствие полноты, достоверности и
сопоставимости. В нач. 70-х гг. наблюдалась унификация показателей и методов С.
т. Однако фальсификаторские тенденции в буржуазной С. т. не ослабевают, а
усиливаются в связи с инфляцией, ростом цен и безработицы, трудовыми
конфликтами и др. пороками капиталистич. общества. Фальсификация, в частности,
выражается в преуменьшении числа безработных, забастовок, потерь рабочего
времени и случаев производств, травматизма, а также в преувеличении реальной
заработной платы за счёт завышения номинальной заработной платы и
потребительских цен.
Лит.: С т р у м и л и н С. Г., Избр. произведения, т. 1(с. 171 - 81),
т. 2 (с. 310-22, 407-10), т. 3 (с. 7-507), т. 4 (с. 29-37, 44-67, 310-36). т. 5
(с. 230-44, 338-51, 364-381), M., 1963-64; Минц Л. E., Проблемы баланса труда и
использования трудовых ресурсов в СССР, M., 1967; Еремина H. M., M а р ш а л о
в а В. П., Статистика труда, 2 изд., M., 1971; Шевченко H. H., Кошелюк С. A.,
Heлюбнн H. И., Статистика труда, M., 1972. См. также лит. при ст.
Статистика.
H. M. Ерёмина.
СТАТИСТИКА ФИНАНСОВ, отрасль экономической статистики, предметом
изучения к-рой являются закономерности и массовые процессы, происходящие в
области финансов, ден. обращения и кредита. Осн. задачами сов. С. ф. являются
сбор, обработка и анализ показателей, характеризующих финанс. отношения в нар.
х-ве, наблюдение за ходом выполнения финанс. планов. Сов. С. ф. подразделяется
на статистику гос. бюджета, банковскую статистику, статистику сберегательного
дела, гос. социального страхования, а также статистику финансов предприятия и
отраслей нар. х-ва.
Статистика гос. бюджета рассматривает структуру и динамику доходов и
расходов бюджетов (гос., респ. и местных), даёт характеристику финанс.
процессов в развитии экономики и культуры страны. Банковская статистика
разрабатывает систему статистич. показателей, характеризующих кредитные и
расчётные отношения банков с предприятиями, а также ден. обращения в стране. В
число этих показателей входят объём и структура выданных ссуд, объекты кредита,
своевременность возврата ссуд, оборачиваемость и динамика ссудной
задолженности, объём и распределение расчётных операций по способам расчётов,
денежная масса в стране и др.
Статистика сберегат. дела изучает состояние сети сберегат. касс, динамику и
структуру сбережений населения, выявляет тенденции их изменения по территории
страны и во времени. Осн. её показатели: сеть, объём вкладов и численность
вкладов в группировке по ряду признаков, средний срок хранения вкладов,
операции по гос. займам и ден.-вещевым лотереям, по кассовому обслуживанию
населения, предприятий и орг-ций, показатели, характеризующие деятельность
сберегат. касс, и др.
Статистика гос. страхования изучает объём и источники образования страховых
фондов и данные о выплатах страховых возмещений и страховых сумм в группировке
по ряду признаков (по территории, видам страхования, типам хозяйств и др.). В
статистике социального страхования наряду с другими учитываются показатели
частоты, тяжести и опасности страховых событий, даётся характеристика бюджета
социального страхования и обеспечения.
Большое значение в С. ф. имеют показатели, характеризующие финанс. деятельность
отд. предприятий и орг-ций, целых отраслей и всего нар. х-ва (прибыль,
рентабельность, фонды экономич. стимулирования, оборачиваемость оборотных
средств, платежи в бюджет и др.). В связи с осуществляемой в стране экономич.
реформой роль финанс. статистики предприятий и орг-ций возрастает, а система её
показателей и методы их анализа совершенствуются. Характерна интеграция финанс.
показателей с др. показателями деятельности предприятий и орг-ций (см. Техпромфинплан
предприятия). Важным разделом С. ф. является разработка показателей
отчётных финанс. балансов нар. х-ва СССР, республик, отраслей, предприятий.
Составная часть финансовых балансов - отчётный баланс ден. доходов и расходов
населения.
Осн. источником данных С. ф. являются материалы бухгалтерской и статистич.
отчётности, регулярно разрабатываемые в соответствии с инструкциями ЦСУ СССР и
Мин-ва финансов СССР. Данные сплошного наблюдения дополняются материалами
выборочного наблюдения.
С. ф. СССР развивается в тесной связи с С. ф. др. социалистич. стран, в
частности стран - членов СЭВ. Совместную работу в области С. ф. (регулярно и по
единому плану) социалистич. страны осуществляют через постоянные комиссии СЭВ
по статистике и финансам.
Осн. источником данных С. ф. капиталистич. стран являются сведения
бухгалтерских балансов предприятий и материалы различных обследований финанс.
органов, финанс. отчёты корпораций, а также переписи (цензы) коммерч.
учреждений, к-рые проводятся один раз в 5 лет и реже. Др. источник - материалы,
собираемые и публикуемые гос. финанс. службами (в США, напр., федеральным
резервным управлением), преим. на выборочной основе. Ценным источником сведений
являются также биржевые сообщения и публикации (курсы валют, курсы акций).
Материалы, характеризующие результаты финанс. деятельности частных компаний
(основной и наиболее важный раздел С. ф.), собираются на урезанной основе
(закон коммерческой тайны) и поэтому не дают полного представления о
результатах их деятельности.
При сопоставлениях показателей С. ф. различных капиталистич. стран эти
показатели пересчитываются по единой методологии. Большое значение имеет также
пересчёт сопоставимых нац. показателей в единую валюту. Международный
валютный фонд и Международный банк реконструкции и развития - осн.
орг-ции, занимающиеся междунар. С. ф. Большое внимание С. ф. уделяют также
статистич. службы ООН.
Лит.: Карпенко Б. И., Финансовая статистика, M., 1929; Лившиц Ф. Д.,
Банковская статистика с основами общей теории, 2 изд., M., 1948; P я у з о в H.
H., Ш о р Ю. Л., Статистика в кредитных учреждениях, M., 1973; Статистика
финансов, под ред. П. П. Маслова, M., 1974.
В. M. Симчера.
СТАТИСТИЧЕСКАЯ ГИПОТЕЗА, предположительное суждение о вероятностных
закономерностях, к-рым подчиняется изучаемое явление. Как правило, С. г.
определяет значения параметров закона распределения вероятностей или его вид.
С. г. называется простой, если она определяет единственный закон распределения;
в ином случае С. г. называется сложной и может быть представлена как нек-рый
класс простых С. г. Напр., гипотеза о том, что распределение вероятностей
является нормальным распределением с математическим ожиданием а =
а0 и нек-рой (неизвестной) дисперсией 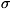 2
будет сложной, составленной из простых гипотез а = ао,
2
будет сложной, составленной из простых гипотез а = ао, 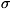 2
=
2
= 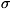 2 (ао и
2 (ао и 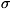 20 - заданные
числа). См. Статистическая проверка гипотез.
20 - заданные
числа). См. Статистическая проверка гипотез.
СТАТИСТИЧЕСКАЯ ЛИНГВИСТИКА, дисциплина, изучающая количеств,
закономерности естественного языка, проявляющиеся в текстах. В основе С. л.
лежит предположение, что нек-рые численные характеристики и функциональные
зависимости между ними, полученные для ограниченной совокупности текстов,
характеризуют язык в целом или его функциональные стили (публицистический,
научный, художественный и т. п.). Практически важной и наиболее изученной
числовой характеристикой является относит, частота употребления различных
лингвистических единиц (букв, фонем, слогов, слов, синтаксич. конструкций), их
классов (напр., гласных, согласных, частей речи) и сочетаний (напр.,
последовательностей из 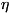 букв). Данные о частоте слов (иногда
словосочетаний) отражаются в частотных словарях. Важную роль в С. л.
играет функциональная зависимость, приближённо описывающая связь между частотой
слова и его номером (рангом) в последовательности по убыванию частот - Ципфа -
Мандельброта закон. С. л. изучает также зависимости между частотой и длиной
слова (в числе слогов), числом его значений и возрастом. Накопленные данные
используются для выявления особенностей стиля отдельных авторов, атрибуции
текстов, дешифровки исторических письменностей, для решения задач стенографии,
теории связи, а также информатики. С. л. при получении численных
характеристик использует методы математической статистики и нек-рые
методы теории информации (для определения энтропии и избыточности языка, см.
Информации теория), а для установления связи между наблюдаемыми характеристиками и
выбора наиболее существенных из них - метод математич. моделей, базирующихся на
понятиях теории вероятностей (см. Вероятностей теория) и математической
лингвистики. Возможно более широкое понимание С. л. как использования
методов статистики для проверки лингвистич. гипотез, к-рые могут носить и
качественный характер.
букв). Данные о частоте слов (иногда
словосочетаний) отражаются в частотных словарях. Важную роль в С. л.
играет функциональная зависимость, приближённо описывающая связь между частотой
слова и его номером (рангом) в последовательности по убыванию частот - Ципфа -
Мандельброта закон. С. л. изучает также зависимости между частотой и длиной
слова (в числе слогов), числом его значений и возрастом. Накопленные данные
используются для выявления особенностей стиля отдельных авторов, атрибуции
текстов, дешифровки исторических письменностей, для решения задач стенографии,
теории связи, а также информатики. С. л. при получении численных
характеристик использует методы математической статистики и нек-рые
методы теории информации (для определения энтропии и избыточности языка, см.
Информации теория), а для установления связи между наблюдаемыми характеристиками и
выбора наиболее существенных из них - метод математич. моделей, базирующихся на
понятиях теории вероятностей (см. Вероятностей теория) и математической
лингвистики. Возможно более широкое понимание С. л. как использования
методов статистики для проверки лингвистич. гипотез, к-рые могут носить и
качественный характер.
Лит.: Головин Б. H., Язык и статистика, M., 1971; Фрумкина P. M.,
Статистические методы и стратегия лингвистического исследования, "Изв. АН
СССР. Серия литературы и языка", 1975, т. 34, №2; Штейнфельдт Э.А.,
Частотный словарь современного русского языка, Таллин, 1963; Herdan G., The
advanced theory of language as choice and chance, B., 1966; M u l l e r Ch.,
Initiation a la statistique linguistique, P., 1968.
M. В. Арапов.
СТАТИСТИЧЕСКАЯ МЕХАНИКА, то же, что статистическая физика.
СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ, система приёмов в математической
статистике, предназначенных для проверки соответствия опытных данных
нек-рой статистической гипотезе. Процедуры С. п. г. позволяют принимать
или отвергать статистические гипотезы, возникающие при обработке или
интерпретации результатов измерений во многих практически важных разделах пауки
и производства, связанных с экспериментом. Правило, по к-рому принимается или
отклоняется данная гипотеза, паз. статистическим критерием. Построение критерия
определяется выбором подходящей функции T от результатов наблюдений,
к-рая служит мерой расхождения между опытными и гипотетическими значениями. Эта
функция, являющаяся случайной величиной, наз. статистикой критерия, при этом
предполагается, что распределение вероятностей T может быть вычислено
при допущении, что проверяемая гипотеза верна. По распределению статистики T
находится значение То, такое, что если гипотеза верна, то
вероятность неравенства T > Т0равна 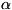 ,
где
,
где 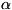 - заранее заданный значимости уровень. Если в конкретном
случае обнаружится, что T > T0, то гипотеза отвергается,
тогда как появление значения T <=T0не противоречит
гипотезе.
- заранее заданный значимости уровень. Если в конкретном
случае обнаружится, что T > T0, то гипотеза отвергается,
тогда как появление значения T <=T0не противоречит
гипотезе.
Пусть, напр., требуется проверить гипотезу о том, что независимые результаты
наблюдений х ,...,х
,...,х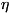 подчиняются нормальном распределению со
средним значением а = ао и известной дисперсией
подчиняются нормальном распределению со
средним значением а = ао и известной дисперсией 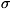 2.
При этом предположении среднее арифметическое х = (хt + ... + хn)/п
результатов наблюдений распределено нормально со средним а = ао
к дисперсией (
2.
При этом предположении среднее арифметическое х = (хt + ... + хn)/п
результатов наблюдений распределено нормально со средним а = ао
к дисперсией (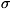 2/n, а величина корень n(
х-а0 )/v распределена нормально с параметрами (0,1). Полагая T
= корень n (| х - а0 | ) /
2/n, а величина корень n(
х-а0 )/v распределена нормально с параметрами (0,1). Полагая T
= корень n (| х - а0 | ) / 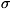 , можно найти
связь между То и
, можно найти
связь между То и 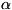 по таблицам нормального
распределения. Напр., при гипотезе а = ао событие T > 1,96
имеет вероятность
по таблицам нормального
распределения. Напр., при гипотезе а = ао событие T > 1,96
имеет вероятность 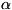 = 0,05. Правило, рекомендующее считать, что
гипотеза а = аоневерна, если T > 1,96, будет
приводить к ложному отбрасыванию этой гипотезы в среднем в 5 случаях из 100, в
к-рых она верна. Если же T <= 1,96, то это ещё не означает, что
гипотеза подтверждается, т. к. указанное неравенство с большой вероятностью
может выполняться при а, близких к ао. Следовательно,
при использовании предложенного критерия можно лишь утверждать, что результаты
наблюдений не противоречат гипотезе а = ао. При выборе
статистики T всегда явно или неявно учитывают гипотезы, конкурирующие с
гипотезой а = ао. Напр., если заранее известно, что a
>= а0, т. е. отклонение гипотезы а = а0 влечёт
принятие гипотезы а > а0, то вместо T следует взять
T1=корень n (х-а)/
= 0,05. Правило, рекомендующее считать, что
гипотеза а = аоневерна, если T > 1,96, будет
приводить к ложному отбрасыванию этой гипотезы в среднем в 5 случаях из 100, в
к-рых она верна. Если же T <= 1,96, то это ещё не означает, что
гипотеза подтверждается, т. к. указанное неравенство с большой вероятностью
может выполняться при а, близких к ао. Следовательно,
при использовании предложенного критерия можно лишь утверждать, что результаты
наблюдений не противоречат гипотезе а = ао. При выборе
статистики T всегда явно или неявно учитывают гипотезы, конкурирующие с
гипотезой а = ао. Напр., если заранее известно, что a
>= а0, т. е. отклонение гипотезы а = а0 влечёт
принятие гипотезы а > а0, то вместо T следует взять
T1=корень n (х-а)/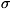 Если дисперсия
Если дисперсия 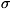 2
неизвестна, то вместо данного критерия для проверки гипотезы а = а0 можно
воспользоваться т. н. критерием Стьюдента, основанным на статистике корень n(х-а0) / s к-рая включает несмещённую оценку
дисперсии
2
неизвестна, то вместо данного критерия для проверки гипотезы а = а0 можно
воспользоваться т. н. критерием Стьюдента, основанным на статистике корень n(х-а0) / s к-рая включает несмещённую оценку
дисперсии
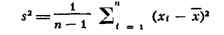
и подчинена Стьюдента распределению с п - 1 степенями свободы
(подобную задачу см. в ст. Математическая статистика, табл. 1a). Такого
рода критерии наз. критериями согласия и используются как для проверки гипотез
о параметрах распределения, так и гипотез о самих распределениях (см.
Непараметрические методы).
При решении вопроса о принятии или отклонении к.-л. гипотезы H0
с помощью любого критерия, основанного на результатах наблюдения, могут быть
допущены ошибки двух типов. Ошибка "первого рода" совершается тогда,
когда отвергается верная гипотеза H0. Ошибка "второго
рода" совершается в том случае, когда гипотеза На принимается, а на
самом деле верна не она, а к.-л. альтернативная гипотеза H. Естественно
требовать, чтобы критерий для проверки данной гипотезы приводил возможно реже к
ошибочным решениям. Обычная процедура построения наилучшего критерия для
простой гипотезы заключается в выборе среди всех критериев с заданным уровнем
значимости 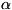 (вероятность ошибки первого рода) такого, к-рый
приводил бы к наименьшей вероятности ошибки второго рода (или, что то же самое,
к наибольшей вероятности отклонения гипотезы, когда она неверна). Последняя
вероятность (дополняющая до единицу вероятность ошибки второго рода) наз.
мощностью критерия. В случае, когда альтернативная гипотеза H простая,
наилучшим будет критерий, к-рый имеет наибольшую мощность среди всех других
критериев с заданным уровнем значимости а (наиболее мощный критерий).
Если альтернативная гипотеза H сложная, напр, зависит от параметра, то
мощность критерия будет функцией, определённой на классе простых альтернатив,
составляющих H, т. е. будет функцией параметра. Критерий, имеющий
наибольшую мощность при каждой альтернативной гипотезе из класса H, наз.
равномерно наиболее мощным, однако следует отметить, что такой критерий
существует лишь в немногих спец. ситуациях. В задаче проверки гипотезы о
среднем значении нормальной совокупности а = ао против
альтернативной гипотезы а > а0 равномерно наиболее мощный
критерий существует, тогда как при проверке той же гипотезы против альтернативы
a <> ао его нет. Поэтому часто ограничиваются поиском
равномерно наиболее мощных критериев в тех или иных спец. классах
(инвариантных, несмещённых критериев и т. п.).
(вероятность ошибки первого рода) такого, к-рый
приводил бы к наименьшей вероятности ошибки второго рода (или, что то же самое,
к наибольшей вероятности отклонения гипотезы, когда она неверна). Последняя
вероятность (дополняющая до единицу вероятность ошибки второго рода) наз.
мощностью критерия. В случае, когда альтернативная гипотеза H простая,
наилучшим будет критерий, к-рый имеет наибольшую мощность среди всех других
критериев с заданным уровнем значимости а (наиболее мощный критерий).
Если альтернативная гипотеза H сложная, напр, зависит от параметра, то
мощность критерия будет функцией, определённой на классе простых альтернатив,
составляющих H, т. е. будет функцией параметра. Критерий, имеющий
наибольшую мощность при каждой альтернативной гипотезе из класса H, наз.
равномерно наиболее мощным, однако следует отметить, что такой критерий
существует лишь в немногих спец. ситуациях. В задаче проверки гипотезы о
среднем значении нормальной совокупности а = ао против
альтернативной гипотезы а > а0 равномерно наиболее мощный
критерий существует, тогда как при проверке той же гипотезы против альтернативы
a <> ао его нет. Поэтому часто ограничиваются поиском
равномерно наиболее мощных критериев в тех или иных спец. классах
(инвариантных, несмещённых критериев и т. п.).
Теория С. п. г. позволяет с единой точки зрения трактовать выдвигаемые
практикой различные задачи математич. статистики (оценка различия между
средними значениями, проверка гипотезы постоянства дисперсии, проверка гипотезы
независимости, проверка гипотез о распределениях и т. п.). Идеи последовательного
анализа, применённые к С. п. г., указывают на возможность связать решение о
принятии или отклонении гипотезы с результатами последовательно проводимых
наблюдений (в этом случае число наблюдений, на основе к-рых по определённому
правилу принимается решение, не фиксируется заранее, а определяется в ходе
эксперимента) (см. также Статистические решения).
Лит.: Крамер Г., Математические методы статистики, пер. с англ.,2
изд., M., 1975; Л е м а и Э., Проверка статистических гипотез, пер. с англ.,
M., 1964.
А. В. Прохоров.
СТАТИСТИЧЕСКАЯ РАДИОФИЗИКА, раздел радиофизики, посвящённый изучению
флуктуационных явлений при генерации, излучении, распространении и приёме
радиоволн. В более широком смысле С. р. охватывает исследования стати стич.
закономерностей в колебательных и волновых процессах (когерентность, проблемы
взаимодействия сигналов и шумов в нелинейных системах и т. п.). Практич.
значение С. р. связано с тем, что в системах радиолокации, радионавигации,
радиосвязи и др. флуктуации играют важную и во многих случаях определяющую
роль на осн. этапах передачи информации.
Электрич. флуктуации, обусловленные фундаментальными физич. процессами в веществе,
являются причиной возникновения флуктуационных напряжений и токов в
радиоприёмных устройствах (см. Флуктуации электрические). Флуктуацпонные
токи и напряжения, неизбежные в реальных генераторах колебаний, определяют
предельно достижимые монохроматичность и стабильность частоты генератора
радиопередающих устройств. Флуктуационные явления при распространении
радиоволн в атмосфере связаны с тем, что показатель преломления тропосферы
и 'ионосферы испытывает нерегулярные изменения, носящие флуктуационный
характер. Идеи и методы С. р. проникают в оптику.
Лит.: P ы т о в С. M., Введение в статистическую радиофизику, M.,
1966; Вандер-Зил А., Флуктуации в радиотехнике и физике, пер. с англ., M.,
1958; Малахов A. H., Флуктуации в автоколебательных системах, M., 1968; Татарский В. И., Распространение волн в турбулентной атмосфере, M., 1967.
С. А. Ахманов.
СТАТИСТИЧЕСКАЯ CУMMA, величина, обратная нормирующему множителю
канонического Гиббса распределения в квантовой статистической физике.
В классич. статистич. физике такая величина наз. статистическим интегралом.
С. с. (статистич. интеграл) позволяет вычислить все потенциалы
термодинамические.
СТАТИСТИЧЕСКАЯ ТЕРМОДИНАИKA равновесная, раздел статистической
физики, дающий статистическое обоснование законов термодинамики на
основе статистич. механики Дж. У. Гиббса и посвящённый вычислениям
термодинамич. характеристик системы (потенциалы термодинамические, уравнение
состояния) на основе законов взаимодействия составляющих систему частиц.
Неравновесная С. т. даёт статистич. обоснование термодинамики неравновесных
процессов (уравнений переноса энергии, импульса, массы) и позволяет
получить выражения для входящих в уравнения коэффициентов (кинетич. коэфф., или
коэфф. переноса) на основе законов взаимодействия и движения частиц системы.
СТАТИСТИЧЕСКАЯ ФИЗИКА, раздел физики, задача к-рого - выразить свойства
макроскопич. тел, т. е. систем, состоящих из очень большого числа одинаковых
частиц (молекул, атомов, электронов и т. д.), через свойства этих частиц и взаимодействие
между ними.
Изучением макроскопич. тел занимаются и др. разделы физики - термодинамика,
механика сплошных сред, электродинамика сплошных сред. Однако при решении
конкретных задач методами этих дисциплин в соответствующие уравнения всегда входят
неизвестные параметры или функции, характеризующие данное тело. Так, для
решения задач гидродинамики необходимо знать уравнение состояния жидкости или
газа, т. е. зависимость плотности от темп-ры и давления, теплоёмкость жидкости,
её коэфф. вязкости и т. п. Все эти зависимости и параметры можно, разумеется,
определять экспериментально, поэтому методы, о к-рых идёт речь, наз.
феноменологическими. Статистическая же физика позволяет, по крайней мере в
принципе, а во многих случаях и фактически, вычислить все эти величины, если
известны силы взаимодействия между молекулами. T. о., С. ф. использует сведения
о "микроскопическом" строении тел - о том, из каких частиц они
состоят, как эти частицы взаимодействуют, поэтому её называют микроскопической
теорией.
Если в какой-то момент времени заданы координаты и скорости всех частиц тела
и известен закон их взаимодействия, то, решая уравнения механики, можно было бы
найти эти координаты и скорости в любой последующий момент времени и тем самым
полностью определить состояние исследуемого тела. (Для простоты изложение
ведётся на языке классич. механики. Но и в квантовой механике ситуация
та же: зная начальную волновую функцию системы и закон взаимодействия
частиц, можно, решая Шрёдингера уравнение, найти волновую функцию,
определяющую состояние системы во все будущие моменты времени.) Фактически,
однако, такой путь построения микроскопич. теории невозможен, т. к. число
частиц в макроскопич. телах очень велико. Напр., в 1 см3
газа при темп-ре 0 0C и давлении в 1 атм содержится примерно 2,7
·1019 молекул. Невозможно решить такое число уравнений, а начальные
координаты и скорости всех молекул всё равно неизвестны.
Однако именно большое число частиц в макроскопич. телах приводит к появлению
новых - статистических -закономерностей в поведении таких тел. Это поведение в
широких пределах не зависит от конкретных начальных условий - от точных
значений начальных координат и скоростей частиц. Важнейшее проявление этой
независимости - известный из опыта факт, что система, предоставленная самой
себе, т. е. изолированная от внеш. воздействий, с течением времени приходит в
нек-рое равновесное состояние (термодинамическое, или статистическое,
равновесие), свойства к-рого определяются только такими общими характеристиками
начального состояния, как число частиц, их суммарная энергия и т. п. (см.
Равновесие термодинамическое). В дальнейшем речь будет идти главным образом о С. ф.
равновесных состояний.
Прежде чем сформулировать теорию, описывающую статистич. закономерности,
следует разумно ограничить сами требования к теории. Именно, задачей теории
должно являться вычисление не точных значений различных физ. величин для
макроскопич. тел, а ср. значений этих величин по времени. Рассмотрим, напр.,
молекулы, находящиеся в нек-ром выделенном в газе достаточно большом -
макроскопическом - объёме. Число таких молекул с течением времени будет
меняться из-за их движения, и его можно было бы найти точно, если были бы
известны все координаты молекул во все моменты времени. В этом, однако, нет
необходимости. Изменение числа молекул в объёме будет носить характер
беспорядочных колебаний - флуктуации - относительно нек-рого ср. значения. При
большом числе частиц в объёме эти колебания будут малы по сравнению со ср.
числом частиц, так что для характеристики макроскопич. состояния достаточно
знать именно это ср. значение.
Для уяснения характера статистич. закономерностей рассмотрим ещё один
простой пример. Пусть в нек-рый сосуд помещено большое число зёрен двух сортов,
каждого сорта поровну, и содержимое сосуда тщательно перемешано. Тогда на
основании повседневного опыта можно быть уверенным, что во взятой из сосуда
пробе, содержащей всё ещё большое число зёрен, будет обнаружено примерно равное
число зёрен каждого сорта независимо от того, в каком порядке засыпались зёрна
в сосуд. На этом примере хорошо видны два важных обстоятельства, обеспечивающих
применимость статистич. теории. Во первых, необходимость большого числа зёрен
как во всей "системе" - сосуде с зерном, так и в выбранной для опыта
"подсистеме" - пробе. (Если Проба состоит всего из двух зёрен, то
нередко оба будут одного сорта.) Во-вторых, ясно, что существ, роль играет
сложность движения зёрен при перемешивании, обеспечивающая их равномерное
распределение в объёме сосуда.
Функция распределения. Рассмотрим систему, состоящую из N частиц,
для простоты считая, что частицы не имеют внутр. степеней свободы. Такая
система описывается заданием 6N переменных - 3N координат q1
и 3N импульсов PI частиц [совокупность этих переменных сокращённо
будет обозначаться (p,q)]· Вычислим ср. значение по интервалу времени t
нек-рой величины F (р, q), являющейся функцией этих координат и
импульсов. Для этого разобьём интервал (О, 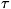 ) на s равных малых
отрезков
) на s равных малых
отрезков  t0(а = 1,2,... .... s). Тогда по
определению
t0(а = 1,2,... .... s). Тогда по
определению
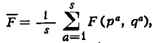
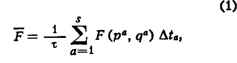
где qa и рa - значения координат и
импульсов в моменты времени ta. B пределе s-> бесконеч.
сумма переходит в интеграл:
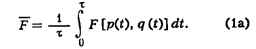
Понятие функции распределения ес-теств. образом возникает, если рассмотреть
пространство 6N измерений, на осях к-рого отложены значения координат и
импульсов частиц системы; оно наз. фазовым пространством. Каждому значению
времени ? соответствуют определённые значения всех q к р, т. е. нек-рая
точка в фазовом пространстве, изображающая состояние системы в данный момент
времени t. Разобьём всё фазовое пространство на элементы, размер к-рых мал по
сравнению с характерными для данного состояния системы значениями q и р,
но ещё настолько велик, что в каждом из них находится много точек,
изображающих состояние системы в различные моменты времени t. Тогда число таких
точек в элементе объёма будет примерно пропорционально величине этого объёма dpdq.
Если обозначить коэффициент пропорциональности через sw(p, q), то
это число для элемента с центром в нек-рой точке (р, q) запишется в
виде:
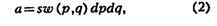
где dpdq = dp1dq1dp2dq2...dp3Ndq3N-
объём выбранного элемента фазового пространства. Cp. значение (1) с учётом малости
этих элементов объёма можно
переписать как F= (1/s) интегралFda, т.е.
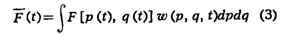
(интегрирование по координатам производится по всему объёму системы, по
импульсам - от -беск. до +беск.). функция w(p, q, t) носит название
функции распределения по координатам и импульсам частиц. Поскольку полное число
выбранных точек равно s, функция w удовлетворяет условию нормировки:
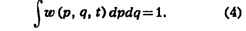
Из (3) и (4) видно, что wdpdq можно рассматривать как вероятность
системе находиться в элементе dpdq фазового пространства.
Введённой таким образом функции распределения можно дать и др. истолкование.
Для этого будем рассматривать одновременно большое число одинаковых систем и
примем, что каждая точка в фазовом пространстве изображает состояние одной
такой системы. Тогда усреднение по времени в (1) - (1a) можно понимать как
усреднение по совокупности этих систем, или, как говорят, по статистическому
ансамблю.
Проведённые до сих пор рассуждения носили чисто формальный характер, т. к.
нахождение функции распределения, согласно (2), требует знания всех р и q
во все моменты времени, т. е. решения уравнений движения с соответствующими
начальными условиями. Осн. положением С. ф. является, однако, утверждение о
возможности определить эту функцию из общих соображений для системы,
находящейся в состоянии термодинамич. равновесия. Прежде всего можно показать,
исходя из сохранения числа систем при движении, что функция распределения
является интегралом движения системы, т. е. остаётся постоянной, если р и
q меняются в соответствии с уравнениями движения (см. Лиувилля теорема).
При движении замкнутой системы не меняется её энергия, поэтому все точки в
фазовом пространстве, изображающие состояние системы в разные моменты времени,
должны лежать на нек-рой "гиперповерхности", соответствующей
начальному значению энергии E. Уравнение этой поверхности имеет вид: Н(р,
q) = Е, где H (р, q) - энергия системы, выраженная через координаты
и импульсы, т. е. её функция Гамильтона. Далее, движение системы из многих
частиц носит крайне запутанный характер. Поэтому с течением времени точки,
описывающие состояние, распределятся по поверхности постоянной энергии
равномерно, подобно тому как равномерно распределяются зёрна при перемешивании
в сосуде в упомянутом выше примере (см. также Эргодическая гипотеза). Такое
равномерное распределение по изоэнергетич. поверхности описывается функцией
распределения вида:
w(p,q) = A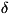 [H(p,q)-E], (5) где
[H(p,q)-E], (5) где 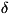 [Н (р,
q) - E] - дельта-функция, отличная от нуля только при H=E, т. е. на
этой поверхности, А - постоянная, определяемая из условия нормировки
(4). Функция распределения (5), наз. микроканонической, позволяет вычислять ср.
значения всех физ. величин по формуле (3), не решая уравнений движения.
[Н (р,
q) - E] - дельта-функция, отличная от нуля только при H=E, т. е. на
этой поверхности, А - постоянная, определяемая из условия нормировки
(4). Функция распределения (5), наз. микроканонической, позволяет вычислять ср.
значения всех физ. величин по формуле (3), не решая уравнений движения.
При выводе выражения (5) предполагалось, что единственная сохраняющаяся при
движении системы величина, от к-рой зависит w,- это энергия системы.
Разумеется, сохраняются также импульс и момент импульса, но эти величины можно
исключить, предположив, что рассматриваемое тело заключено в неподвижный ящик,
к-рому частицы могут отдавать импульс и момент.
Фактически обычно рассматриваются не замкнутые системы, а макроскопич. тела,
являющиеся макроскопически малыми частями, или подсистемами, к.-л. замкнутой
системы. Функция распределения для подсистемы будет отлична от (5), но не будет
зависеть от конкретного характера остальной части системы - т. н. термостата.
Поэтому функцию распределения подсистемы можно определить, считая, напр., что
термостат состоит просто из N частиц идеального газа, координаты и
импульсы к-рых будем обозначать через Q и P, в отличие от обозначений q
и р для подсистемы, тогда микроканонич. распределение:
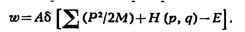
Здесь H (р, q) - функция Гамильтона подсистемы, M - масса
частицы газа, а суммирование производится по всем составляющим импульсов всех
частиц термостата. Чтобы найти функцию распределения для подсистемы, нужно
проинтегрировать это выражение по координатам и импульсам частиц термостата.
Если затем учесть, что число частиц в термостате много больше, чем в подсистеме,
и устремить N -> беск. , считая, что отношение E/N постоянно и
равно 3/2 kГ, то для функции распределения подсистемы
получится выражение:
w(p, q) = е[F-H(p,q)]/kT.(6)
Величина T в этой формуле имеет смысл темп-ры, k = 1,38 ·10~16
эрг/град - постоянная Больцмана. [Условие E/F -> 3/2
kT для газа в термостате соответствует, как и должно быть, формуле (13)
для идеального газа; см. ниже.] Нормировочный коэффициент eF/KT определяется
из условия нормировки (4):
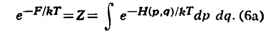
Распределение (6) наз. каноническим распределением Гиббса, или просто
каноническим распределением (см. Гиббса распределение), а величина Z -
статистич. интегралом. В отличие от микроканонич. распределения, энергия
системы в распределении Гиббса не задана. Состояния системы сосредоточены в
тонком, но конечной толщины слое вокруг энергетич. поверхности, соответствующей
ср. значению энергии, что означает возможность обмена энергией с термостатом. В
остальном в применении к определённому макроскопич. телу оба распределения
приводят по существу к одним и тем же результатам. Разница лишь в том, что при
использовании микроканонич. распределения все ср. значения оказываются
выраженными через энергию тела, а при использовании канонич. распределения - через
темп-ру.
Если тело состоит из двух невзаимодействующих частей 1 н 2 с функциями
Гамильтона H1н H2, то для всего тела H =
H1 + Н2 и, согласно (6), функция распределения тела
разбивается на произведение функций распределения для каждой из частей, так что
эти части оказываются статистически независимыми. Это требование вместе с
теоремой Лиувилля можно положить в основу вывода распределения Гиббса, не
обращаясь к микроканонич. распределению.
Формула (6) справедлива для систем, к-рые описываются классич. механикой.
В квантовой механике энергетич. спектр системы конечного объёма дискретен.
Вероятность подсистеме находиться в состоянии с энергией En даётся
формулой, аналогичной (6):
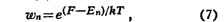
причём условие нормировки 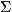 nwn=
1 можно переписать в виде:
nwn=
1 можно переписать в виде:
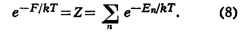
Величина Z наз. статистической суммой системы; сумма в выражении (8) берётся
по всем состояниям системы. Для системы, с достаточной точностью описывающейся
классич. механикой, в формуле (8) можно перейти от суммирования по состояниям к
интегрированию по координатам и импульсам системы. При этом на каждое квантовое
состояние приходится в фазовом пространстве "клетка" (или
"ячейка") объемом (2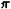 h)3N, где h - Планка
постоянная. Иными словами, суммирование по
h)3N, где h - Планка
постоянная. Иными словами, суммирование по 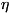 сводится к интегрированию
по dpdq/(2
сводится к интегрированию
по dpdq/(2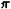 h)3N. Следует также учесть, что ввиду
тождественности частиц в квантовой механике при их перестановке состояние
системы не меняется. Поэтому, если интегрировать по всем
h)3N. Следует также учесть, что ввиду
тождественности частиц в квантовой механике при их перестановке состояние
системы не меняется. Поэтому, если интегрировать по всем 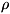 и q, необходимо
поделить интеграл на число перестановок из N частиц, т. е. на N
Окончательно классич. предел для статистич. суммы имеет вид:
и q, необходимо
поделить интеграл на число перестановок из N частиц, т. е. на N
Окончательно классич. предел для статистич. суммы имеет вид:
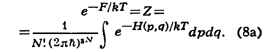
Он отличается множителем от чисто классич. условия нормировки (6а), что
приводит к дополнит, слагаемому в F.
Приведённые формулы относятся к случаю, когда число частиц в подсистеме
задано. Если выбрать в качестве подсистемы определённый элемент объёма всей
системы, через поверхность к-рого частицы могут покидать подсистему и
возвращаться в неё, то вероятность нахождения подсистемы в состоянии с энергией
En и числом частиц Nn даётся формулой
большого канонического распределения Г и б бса:
Wn=е(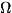 -En-
-En- Nn)/kT, (9)
Nn)/kT, (9)
в к-рой дополнит, параметр  - химический потенциал, определяющий
ср. число частиц в подсистеме, а величина
- химический потенциал, определяющий
ср. число частиц в подсистеме, а величина 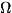 определяется
из условия нормировки [см. формулу (11)].
определяется
из условия нормировки [см. формулу (11)].
Статистическое истолкование термодинамики. Важнейший результат С. ф. -
установление статистич. смысла термодинамич. величин. Это даёт возможность
вывести законы термодинамики из осн. представлений С. ф. и вычислять
термодинамич. величины для конкретных систем. Прежде всего термодинамич. внутренняя
энергия отождествляется со ср. энергией системы. Первое начало
термодинамики получает тогда очевидное истолкование как выражение закона
сохранения энергии при движении составляющих тело частиц.
Далее, пусть функция Гамильтона системы зависит от нек-рого параметра  (координаты стенки сосуда, в к-рый заключена система, внешнего
поля и т. п.). Тогда производная дН/
(координаты стенки сосуда, в к-рый заключена система, внешнего
поля и т. п.). Тогда производная дН/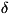
 будет обобщённой
силой, соответствующей этому параметру, а величина (dH/d
будет обобщённой
силой, соответствующей этому параметру, а величина (dH/d )d
)d после усреднения даёт механич. работу, совершаемую над системой
при изменении этого параметра. Если продифференцировать выражение E = интеграл Hwdpdq для ср. энергии E системы с
учётом формулы (6) и условия нормировки, считая переменными
после усреднения даёт механич. работу, совершаемую над системой
при изменении этого параметра. Если продифференцировать выражение E = интеграл Hwdpdq для ср. энергии E системы с
учётом формулы (6) и условия нормировки, считая переменными  и Г и
учитывая, что величина F тоже является функцией от этих переменных, то
получится тождество:
и Г и
учитывая, что величина F тоже является функцией от этих переменных, то
получится тождество:
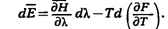
Согласно сказанному выше, член, содержащий d , равен ср.
работе dA, совершаемой над телом. Тогда последний член есть получаемое
телом тепло. Сравнивая это выражение с соотношением представляющим собой
объединённую запись первого и второго начал термодинамики (см. Второе начало
термодинамики) для обратимых процессов, находим, что T в (6)
действительно равна абс. темп-ре тела, а пролзводная dF/дТ - взятой с
обратным знаком энтропии S. Это означает, что F есть свободная
энергия тела, откуда выясняется её статистич. смысл.
, равен ср.
работе dA, совершаемой над телом. Тогда последний член есть получаемое
телом тепло. Сравнивая это выражение с соотношением представляющим собой
объединённую запись первого и второго начал термодинамики (см. Второе начало
термодинамики) для обратимых процессов, находим, что T в (6)
действительно равна абс. темп-ре тела, а пролзводная dF/дТ - взятой с
обратным знаком энтропии S. Это означает, что F есть свободная
энергия тела, откуда выясняется её статистич. смысл.
Особое значение имеет статистич. истолкование энтропии, к-рое следует из
формулы (8). Формально суммирование в этой формуле производится по всем
состояниям с энергией En, но фактически ввиду малости
флуктуации энергии в распределении Гиббса существенно лишь относительно
небольшое их число с энергией вблизи ср. энергии. Число этих существенных
состояний  n естественно определить поэтому, ограничив
суммирование в (8) интервалом
n естественно определить поэтому, ограничив
суммирование в (8) интервалом  n, заменив En на
ср. энергию E и вынося экспоненту из-под знака суммы. Тогда сумма
даст
n, заменив En на
ср. энергию E и вынося экспоненту из-под знака суммы. Тогда сумма
даст  n и (8) примет вид:
n и (8) примет вид:
е-(F-E)/kT
=  n
n
С др._стороны, согласно термодинамике, F=E - TS, что даёт связь
энтропии с числом микроскопич. состояний  n в данном
макроскопич. состоянии, иначе говоря, - со статистическим весом макроскопич.
состояния, т. е. с его вероятностью:
n в данном
макроскопич. состоянии, иначе говоря, - со статистическим весом макроскопич.
состояния, т. е. с его вероятностью:
S = k1n n. (10) При темп-ре абс. нуля любая система
находится в определённом у с н о в н о м состоянии, так что
n. (10) При темп-ре абс. нуля любая система
находится в определённом у с н о в н о м состоянии, так что  n =
1, S=O. Это утверждение выражает собой третье начало термодинамики. Здесь
существенно, что для однозначного определения энтропии нужно пользоваться
именно квантовой формулой (8); в чисто классич. статистике энтропия определена
только с точностью до произвольного слагаемого. Смысл энтропии как меры
вероятности состояния сохраняется и по отношению к произвольным - не
обязательно равновесным - состояниям. В состоянии равновесия энтропия имеет максимальное
возможное в данных внешних условиях значение. Это означает, что равновесное
состояние является состоянием с максимальным статистич. весом, наиболее
вероятным состоянием. Процесс перехода системы из неравновесного состояния в
равновесное есть процесс перехода из менее вероятных состояний в более
вероятные; это выясняет статистич. смысл закона возрастания энтропии, согласно
к-рому энтропия замкнутой системы может только увеличиваться.
n =
1, S=O. Это утверждение выражает собой третье начало термодинамики. Здесь
существенно, что для однозначного определения энтропии нужно пользоваться
именно квантовой формулой (8); в чисто классич. статистике энтропия определена
только с точностью до произвольного слагаемого. Смысл энтропии как меры
вероятности состояния сохраняется и по отношению к произвольным - не
обязательно равновесным - состояниям. В состоянии равновесия энтропия имеет максимальное
возможное в данных внешних условиях значение. Это означает, что равновесное
состояние является состоянием с максимальным статистич. весом, наиболее
вероятным состоянием. Процесс перехода системы из неравновесного состояния в
равновесное есть процесс перехода из менее вероятных состояний в более
вероятные; это выясняет статистич. смысл закона возрастания энтропии, согласно
к-рому энтропия замкнутой системы может только увеличиваться.
Формула (8), связывающая свободную энергию F со статистич. суммой, является
основой для вычисления термодинамич. величин методами С. ф. Она используется, в
частности, для построения статистич. теории электрич. и магнитных свойств
вещества. Напр., для вычисления магнитного момента тела в магнитном поле
следует вычислить статистич. сумму и свободную энергию. Магнитный момент т тела
даётся тогда формулой:
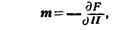
где H - напряжённость внеш. магнитного поля.
Аналогично (8) условие нормировки в большом канонич. распределении (9)
определяет термодинамический потенциал 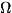 , согласно
формуле:
, согласно
формуле:
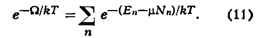
Этот потенциал связан со свободной энергией соотношением: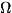 =
F-
=
F- N
N
Приложения С. ф. к изучению тех или иных свойств конкретных систем сводятся
по существу к приближённому вычислению статистич. суммы с учётом специфич.
свойств системы.
Во многих случаях эта задача упрощается применением закона
равнораспределения по степеням свободы, утверждающего, что теплоёмкость C0
(при постоянном объёме  ) системы взаимодействующих
материальных точек - частиц, совершающих гармоннч. колебания, равна cv
= k(l/2 + n)
) системы взаимодействующих
материальных точек - частиц, совершающих гармоннч. колебания, равна cv
= k(l/2 + n)
где l - общее число постулат, и вращат. степеней свободы, n - число
колебат. степеней свободы. Доказательство закона основано на том, что функция
Гамильтона H такой системы имеет вид: H = = K(pi)+
U(qm), где кинетич. энергия К - однородная квадратичная
функция от l + n импульсов pi, a потенц. энергия U
- квадратичная функция от 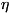 колебат. координат qm.
B статистич. интеграле Z (8а) интегрирование по колебат. координатам ввиду
быстрой сходимости интеграла можно распространить от -бескон. до бескон.
Сделав после этого замену переменных pi= корень Tpi' ,qm
=
колебат. координат qm.
B статистич. интеграле Z (8а) интегрирование по колебат. координатам ввиду
быстрой сходимости интеграла можно распространить от -бескон. до бескон.
Сделав после этого замену переменных pi= корень Tpi' ,qm
=
= корень Tqт', находим, что Z зависит от темп-ры
как Тl/2+n, так что свободная энергия F= - kT (1/2 + п)
(InT+ const). Отсюда следует приведённое выше выражение для теплоёмкости,
поскольку Cv = - Td2F/dT2. Отклонения от
закона равнораспределения в реальных системах связаны прежде всего с квантовыми
поправками, т. к. в квантовой С. ф. этот закон несправедлив. Существуют также
поправки, связанные с негармоничностью колебаний.
Идеальный газ. Простейшим объектом исследования С. ф. является идеальный
газ, т. е. газ настолько разреженный, что можно пренебречь взаимодействием
между его молекулами. Термодинамич. функции такого газа можно вычислить до
конца. Энергия газа равна просто сумме энергий отдельных молекул. Этого,
однако, ещё недостаточно, чтобы считать молекулы полностью независимыми.
Действительно, в квантовой механике, даже если силы взаимодействия между
частицами отсутствуют, существует определённое влияние одинаковых
(тождественных) частиц друг на друга, если он:; находятся в близких
квантовомеханич. состояниях. Это т. н. обменное взаимодействие. Им можно
пренебречь, если на одно состояние приходится в среднем много меньше одной
частицы, что во всяком случае имеет место при достаточно высокой темп-ре газа;
такой газ наз. невырожденным. Фактически обычные газы, состоящие из атомов и
молекул, невырождены при всех темп-pax (при к-рых они ещё газообразны). Для
невырожденного идеального газа функция распределения распадается на
произведение функций распределения для отдельных молекул. Энергия молекулы
одноатомного газа во внешнем поле с потенциальной энергией U(r) равна р2/2М
+ + U(r). Интегрируя (6) по координатам r(х, у, г) и импульсам P(рх,
рy, pz) всех молекул, кроме одной, можно найти число молекул dN, импульсы
к-рых лежат в интервалах dpx, dpy, dрz, а
координаты - в интервалах dx, dy, dz:
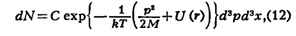
где d3p = dpxdpydpz, d3x
= dxdydz. Эта формула наз. распределением Максвелла - Больцмана (см. Болъцмана
статистика). Если проинтегрировать (12) по импульсам, то получится формула
для распределения частиц по координатам во внешнем поле, в частности в поле
тяготения - барометрическая формула. Распределение же по скоростям в
каждой точке пространства совпадает с Максвелла распределением.
Статистич. сумма идеального газа также распадается на произведение
одинаковых членов, соответствующих отдельным молекулам. Для одноатомного газа
суммирование в (8) сводится к интегрированию по координатам и импульсам, т. е.
сумма заменяется на интеграл по d3pd3x/(2 h)3в
соответствии с числом ячеек [с объёмом (2
h)3в
соответствии с числом ячеек [с объёмом (2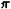 h)3] в фазовом
пространстве одной частицы. Свободная энергия N атомов газа равна:
h)3] в фазовом
пространстве одной частицы. Свободная энергия N атомов газа равна:
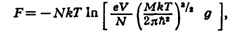
где g - статистич. вес осн. состояния атома, т. е. число состояний,
соответствующее его нижнему энергетич. уровню, V - объём газа (здесь е - основание
натуральных логарифмов). При высоких темп-pax g = (2J + 1)(2L + 1), где J
- величина спина, a L - момента орбитального атома (в
единицах h). Из выражения для свободной энергии следует, что уравнение
состояния идеального газа, т. е. зависимость его давления (P) от
плотности числа частиц (N/V) и температуры, имеет вид: PV = NkT. Внутр.
энергия одноатомного газа и его теплоёмкость при постоянном объёме оказываются
равными:
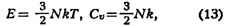
а его хим. потенциал:
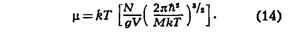
Характерно, что даже для невырожденного (т. е. с достаточной точностью
подчиняющегося классич. механике) газа выражения для свободной энергии и хим. потенциала содержат постоянную Планка
h. Это, в конечном счёте, обусловлено отмеченной ранее связью энтропии с
понятием числа квантовых состояний.
В случае двухатомных и многоатомных газов вклад в термодинамич. функции
вносят также колебания и вращение молекул. Этот вклад зависит от того,
существенны ли эффекты квантования колебаний и вращения молекулы. Расстояние
между колебат. уровнями энергии имеет порядок  Еk = h?, где
Еk = h?, где  - характерная частота колебаний, а расстояние между первыми вращат. уровнями
энергии порядка
- характерная частота колебаний, а расстояние между первыми вращат. уровнями
энергии порядка  Ев = h2/2l, где l - момент
инерции вращающегося тела, в данном случае молекулы. Классич. статистика
справедлива, если темп-pa достаточно высока, так что
Ев = h2/2l, где l - момент
инерции вращающегося тела, в данном случае молекулы. Классич. статистика
справедлива, если темп-pa достаточно высока, так что
kT> E.
E.
В этом случае в соответствии с законом равнораспределения вращение вносит в
теплоёмкость постоянный вклад, равный ½k на каждую вращат. степень
свободы; в частности, для двухатомных молекул этот вклад равен k. Колебания
же вносят в теплоёмкость вклад, равный k на каждую колебат. степень
свободы (так что колебат. теплоёмкость двухатомной молекулы равна k). Вдвое
больший вклад колебательной степени свободы по сравнению с вращательной связан
с тем, что при колебаниях атомы в молекуле имеют не только кинетическую, но и
потенциальную энергию. В обратном предельном случае kТ<h молекулы
находятся в своём осн. колебательном состоянии, энергия к-рого не зависит от
температуры, так что колебания вообще не вносят вклада в теплоёмкость. То же
относится к вращению молекул при условии kT <h2/21. По мере
повышения темп-ры появляются молекулы, находящиеся в возбуждённых колебат. и
вращат. состояниях, и эти степени свободы начинают давать вклад в теплоёмкость
- как бы постепенно "включаются", стремясь при дальнейшем повышении
темп-ры к своему классич. пределу. T. о., учёт квантовых эффектов позволил
объяснить экспериментально наблюдаемую зависимость теплоёмкости газов от
темп-ры. Значения величины h2/2kl, характеризующей
"вращательный квант", для большинства молекул порядка неск. градусов
или десятков градусов (85 К для H2, 2,4 К для O2,15 К для
HCl).
молекулы
находятся в своём осн. колебательном состоянии, энергия к-рого не зависит от
температуры, так что колебания вообще не вносят вклада в теплоёмкость. То же
относится к вращению молекул при условии kT <h2/21. По мере
повышения темп-ры появляются молекулы, находящиеся в возбуждённых колебат. и
вращат. состояниях, и эти степени свободы начинают давать вклад в теплоёмкость
- как бы постепенно "включаются", стремясь при дальнейшем повышении
темп-ры к своему классич. пределу. T. о., учёт квантовых эффектов позволил
объяснить экспериментально наблюдаемую зависимость теплоёмкости газов от
темп-ры. Значения величины h2/2kl, характеризующей
"вращательный квант", для большинства молекул порядка неск. градусов
или десятков градусов (85 К для H2, 2,4 К для O2,15 К для
HCl).
Рис. 1. Зависимость вращательной Свр (а) и колебательной
Скол (б) частей теплоёмкости двухатомного газа (в единицах классических
значений теплоёмкости) от температуры T.
В то же время характерные значения величины h /k для
"колебат. кванта" порядка тысяч градусов (6100 К для H2,
2700 К для O2, 4100 К для HCl). Поэтому вращат. степени свободы
включаются при гораздо более низких темп-pax, чем колебательные. На рис. 1
изображены температурная зависимость вращательной (а) и колебательной
(б) теплоёмкостей для двухатомной молекулы (вращат. теплоёмкость построена для
молекулы из разных атомов).
/k для
"колебат. кванта" порядка тысяч градусов (6100 К для H2,
2700 К для O2, 4100 К для HCl). Поэтому вращат. степени свободы
включаются при гораздо более низких темп-pax, чем колебательные. На рис. 1
изображены температурная зависимость вращательной (а) и колебательной
(б) теплоёмкостей для двухатомной молекулы (вращат. теплоёмкость построена для
молекулы из разных атомов).
Неидеальный газ. Важное достижение С. ф. - вычисление поправок к
термодинамическим величинам газа, связанных с взаимодействием между его
частицами. С этой точки зрения уравнение состояния идеального газа является
первым членом разложения давления реального газа по степеням плотности числа
частиц, поскольку всякий газ при достаточно малой плотности ведёт себя как
идеальный. С повышением плотности начинают играть роль поправки к уравнению
состояния, связанные с взаимодействием. Они приводят к появлению в выражении
для давления членов с более высокими степенями плотности числа частиц, так что
давление изображается т. н. вириальным рядом вида:
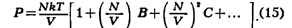
Коэффициенты В, С и т. д. зависят от темп-ры и наз. вторым, третьим и т. д.
вириальными коэффициентами. Методы С. ф. позволяют вычислить эти коэффициенты,
если известен закон взаимодействия между молекулами газа. При этом коэффициенты
В, С,... описывают одновременное взаимодействие двух, трёх и большего
числа молекул. Напр., если газ одноатомный и потенциальная энергия
взаимодействия его атомов U(r), то второй вириальный коэффициент равен
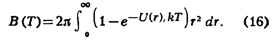
По порядку величины В равен r0, где rо-
характерный размер атома, пли, точнее, радиус действия межатомных сил. Это означает,
что ряд (15) фактически представляет собой разложение по степеням безразмерного
параметра Nr3/V, малого для достаточно разреженного газа.
Взаимодействие между атомами газа носит характер отталкивания на близких
расстояниях и притяжения па далёких. Это приводит к тому, что В > О
при высоких темп-pax и В<0 при низких. Поэтому давление реального
газа при высоких темп-pax больше давления идеального газа той же плотности, а
при низких - меньше. Так, напр., для гелия при T = 15,3 К коэффициент В
= = - 3*10-23 см3, а при T = 510 К В =
1,8 *10"23 см3. Для аргона B = = -7,1 *10-23
см3 при T = 180 К и В = 4,2 *10-23см3
при T = 6000 К. Для одноатомных газов вычислены значения вириальных
коэффициентов, включая пятый, что позволяет описывать поведение газов в
достаточно широком интервале плотностей (см. также Газы).
Плазма. Особый случай неидеального газа представляет собой плазма
- частично или полностью ионизованный газ, в к-ром поэтому имеются свободные
электроны и ионы. При достаточно малой плотности свойства плазмы близки к
свойствам идеального газа. При вычислении же отклонений от идеальности существенно, что электроны и ионы взаимодействуют
электростатически по закону Кулона. Кулоновские силы медленно убывают с
расстоянием, и это приводит к тому, что уже для вычисления первой поправки к
термодинамич. функциям необходимо учитывать взаимодействие не двух, а сразу
большого количества частиц, поскольку интеграл во втором вириальном
коэффициенте (16), описывающий парное взаимодействие, расходится на больших
расстояниях г между частицами. В действительности под влиянием кулоновских сил
распределение ионов и электронов в плазме изменяется таким образом, что поле
каждой частицы экранируется, т. е. быстро убывает на нек-ром расстоянии, наз.
дебаевским радиусом. Для простейшего случая плазмы, состоящей из электронов и
однозарядных ионов, дебаевский радиус T0 равен:
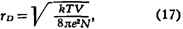
где N - число электронов, е - заряд электрона. Все частицы,
находящиеся внутри дебаевского радиуса, принимают участие во взаимодействии
одновременно. Это приводит к тому, что первая поправка к давлению
пропорциональна не (N/V)2, как в обычном газе, а более низкой
степени плотности - (N/V)3/2. Количественный расчёт основан на том,
что остальные частицы распределены в поле выбранного электрона или иона
согласно распределению Больцмана. В результате уравнение состояния с учётом
первой поправки имеет вид:
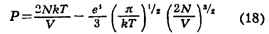
(т. к. число электронов равно числу ионов, полное число частиц равно 2N).
Такого же рода поправки возникают и в термодинамич. функциях электролитов, в
к-рых имеются свободные ионы растворённых веществ.
Жидкости. В отличие от газа, связанные с взаимодействием члены в
уравнении состояния жидкости не малы. Поэтому свойства жидкости сильно зависят
от конкретного характера взаимодействия между её молекулами. В теории жидкости
вообще отсутствует малый параметр, к-рый можно было бы использовать для
упрощения теории. Невозможно получить к.-л. аналитич. формулы для термодинамич.
величин жидкости. Одним из способов преодоления этой трудности является
изучение системы, состоящей из сравнительно небольшого числа частиц - порядка неск.
тысяч. В этом случае, используя ЭВМ, можно провести прямое решение уравнений
движения частиц и определить таким способом ср. значения всех характеризующих
систему величин без дополнит, предположений. При этом можно исследовать также и
процесс приближения такой системы к состоянию равновесия. Можно также найти
статистич. интеграл для такой системы из небольшого числа частиц путём
вычисления на ЭВМ интегралов в осн. формуле для статистич. интеграла (обычно
при этом используется Монте-Карло метод). Полученные обоими способами
результаты имеют, однако, малую точность в приложении к реальным жидкостям
из-за малого числа частиц в системе.
Ещё один способ построения теории жидкости основан на использовании функций
распределения молекул. Если проинтегрировать функцию распределения  системы
по импульсам всех частиц и по координатам всех частиц, кроме одной, получится
одночастичная пространств, функция распределения f1(r). Если
проинтегрировать
системы
по импульсам всех частиц и по координатам всех частиц, кроме одной, получится
одночастичная пространств, функция распределения f1(r). Если
проинтегрировать  по импульсам всех частиц и по координатам всех
частиц, кроме двух, получится двухчастичная функция распределения f2(rt,
г2), всех частиц, кроме трёх,- трёхчастичная функция
распределения fз(r1, r2, r3) и т. д.
Двухчастичная функция распределения является непосредственно наблюдаемой физ.
величиной - через неё выражается, напр., упругое рассеяние рентгеновских лучей
и нейтронов в жидкости. Считая, что функция распределения всей системы даётся
распределением Гиббса (6), можно получить интегральное соотношение, выражающее
двухчастичную функцию через трёхчастичную и потенциал взаимодействия между
частицами. В теории жидкости это точное соотношение дополняется нек-рыми
приближёнными, выражающими трёхчастичную функцию через двухчастичную
(одночастичная функция в однородной жидкости сводится к постоянной). В
результате получается уравнение для двухчастичной функции, к-рое решается
численно. Дополнит, соотношения находятся на основании правдоподобных физ.
соображений и носят интерполяционный характер, так что основанные на них теории
могут претендовать лишь на качеств, описание свойств жидкости. Тем не менее
даже такое качеств, описание имеет важное значение, поскольку в нём проявляется
общность законов С. ф. (см. также Жидкость).
по импульсам всех частиц и по координатам всех
частиц, кроме двух, получится двухчастичная функция распределения f2(rt,
г2), всех частиц, кроме трёх,- трёхчастичная функция
распределения fз(r1, r2, r3) и т. д.
Двухчастичная функция распределения является непосредственно наблюдаемой физ.
величиной - через неё выражается, напр., упругое рассеяние рентгеновских лучей
и нейтронов в жидкости. Считая, что функция распределения всей системы даётся
распределением Гиббса (6), можно получить интегральное соотношение, выражающее
двухчастичную функцию через трёхчастичную и потенциал взаимодействия между
частицами. В теории жидкости это точное соотношение дополняется нек-рыми
приближёнными, выражающими трёхчастичную функцию через двухчастичную
(одночастичная функция в однородной жидкости сводится к постоянной). В
результате получается уравнение для двухчастичной функции, к-рое решается
численно. Дополнит, соотношения находятся на основании правдоподобных физ.
соображений и носят интерполяционный характер, так что основанные на них теории
могут претендовать лишь на качеств, описание свойств жидкости. Тем не менее
даже такое качеств, описание имеет важное значение, поскольку в нём проявляется
общность законов С. ф. (см. также Жидкость).
Химическое равновесие. Большое значение имеет
предоставляемая С. ф. возможность вычисления констант хим. равновесия,
определяющих равновесные концентрации реагирующих веществ. Термодинамич. теория
приводит к условию равновесия в виде равенства нулю нек-рой линейной комбинации
хим. потенциалов этих веществ. В случае реакции между газами хим. потенциалы
определяются формулами, аналогичными формуле (14) для одноатомного газа, и
константу равновесия можно вычислить, если известна теплота реакции. В
выражения для хим. потенциалов входит постоянная Планка, поэтому квантовые
эффекты существенны даже для реакций между классич. газами. Важным частным
случаем формул хим. равновесия является Саха формула, определяющая
равновесную степень ионизации газа. (Подробнее см. Равновесие химическое.)
Вырожденные газы. Если понижать темп-ру газа при
постоянной плотности, начинают проявляться квантовомеханические эффекты,
связанные со свойствами симметрии волновых функций системы одинаковых частиц.
Газ "вырождается" (см. Вырожденный газ). Для частиц с полуцелым
спином волновая функция должна менять знак при перестановке любой пары частиц.
Это, в частности, приводит к тому, что в одном квантовом состоянии не может
находиться болвше одной частицы (Паули принцип). Количество частиц с
целым спином в одном состоянии может быть любым, но требуемая в этом случае
неизменность волновой функции при перестановке частиц и здесь приводит к
изменению статистич. свойств газа. Частицы с полуцелым спином описываются
статистикой Ферми - Дирака; их называют фермионами. К фермионам
относятся, напр., электроны, протоны, нейтроны, атомы дейтерия, атомы лёгкого
изотопа гелия 3He. Частицы с целым спином - бозоны - описываются
статистикой Бозе - Эйнштейна. К ним относятся атомы водорода, атомы 4He,
кванты света - фотоны.
Пусть ср. число частиц газа в единице объёма с импульсами, лежащими в
интервале d3p, есть npgd3pl(2 h)3,
так что пр - число частиц в одной ячейке фазового
пространства (g = 2J + 1, где J - спин частицы). Тогда из
распределения Гиббса следует, что для идеальных газов фермионов (верхний знак)
и бозонов (нижний знак):
h)3,
так что пр - число частиц в одной ячейке фазового
пространства (g = 2J + 1, где J - спин частицы). Тогда из
распределения Гиббса следует, что для идеальных газов фермионов (верхний знак)
и бозонов (нижний знак):
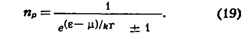
В этой формуле  = р2/2М -
энергия частицы с импульсом
= р2/2М -
энергия частицы с импульсом  ,
,  - хим. потенциал,
определяемый из условия постоянства числа частиц (N) в системе:
- хим. потенциал,
определяемый из условия постоянства числа частиц (N) в системе:
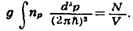
Формула (19) переходит в формулу распределения Больцмана (12) при kT>
(h2/M)(N/V)⅔; левая сторона этого неравенства
делается порядка правой при таких темп-pax, при к-рых длина волны де Бройля частиц,
движущихся с тепловой скоростью, становится порядка ср. расстояния между ними.
T. о., вырождение сказывается при темп-pax тем более низких, чем меньше
плотность числа частиц в газе (и чем больше масса частицы M).
В случае фермионов, как и должно быть, np<= 1. Это
приводит к тому, что частицы газа фермионов (ферми-газа) и при T = О
обладают отличными от нуля импульсами, поскольку в состоянии с нулевым
импульсом может находиться только одна частица. Точнее, при T = Q для
ферми-газа пр = 1 внутри Ферми поверхности - сферы в
импульсном пространстве с радиусом pF =(6 2/g)1/3h(N/V)1/3
, а вне этой "ферми-сферы" пр = О. При конечных,
но низких темп-pax прменяется от 1 внутри сферы до нуля вне сферы
постепенно, причём ширина переходной области порядка MkT/pF. Величина
пр для ферми-газа как функция от энергии
2/g)1/3h(N/V)1/3
, а вне этой "ферми-сферы" пр = О. При конечных,
но низких темп-pax прменяется от 1 внутри сферы до нуля вне сферы
постепенно, причём ширина переходной области порядка MkT/pF. Величина
пр для ферми-газа как функция от энергии  изображена схематически на рис. 2 (
изображена схематически на рис. 2 ( 0
=
0
=  F 2/2М). При изменении темп-ры газа
меняется состояние частиц только в этом переходном слое, и теплоёмкость
ферми-газа при низких темп-pax пропорциональна T и равна:
F 2/2М). При изменении темп-ры газа
меняется состояние частиц только в этом переходном слое, и теплоёмкость
ферми-газа при низких темп-pax пропорциональна T и равна:
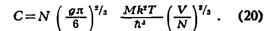
Рис. 2. Функция распределения Ферми - Дирака.
В бозе-газе при T = O все частицы находятся в состоянии с нулевым импульсом.
При достаточно низких темп-рах в состоянии с р = 0 находится конечная
доля всех частиц; эти частицы образуют т. н. бозе-эйнштейновский конденсат.
Остальные частицы находятся в состояниях с  <> O,
причём их число определяется формулой (19) с
<> O,
причём их число определяется формулой (19) с  = О. При темп-ре Tc = [(3,3/g⅔)*(h/kM)] * (N/V)⅔ в
бозе-газе происходит фазовый переход (см. ниже). Доля частиц с нулевым
импульсом обращается в нуль, Базе - Эйнштейна конденсация исчезает.
Кривая зависимости теплоёмкости от темп-ры имеет в точке T0 излом.
Распределение частиц по импульсам при T > Тс даётся
формулой (19), причём
= О. При темп-ре Tc = [(3,3/g⅔)*(h/kM)] * (N/V)⅔ в
бозе-газе происходит фазовый переход (см. ниже). Доля частиц с нулевым
импульсом обращается в нуль, Базе - Эйнштейна конденсация исчезает.
Кривая зависимости теплоёмкости от темп-ры имеет в точке T0 излом.
Распределение частиц по импульсам при T > Тс даётся
формулой (19), причём  < О. Схематически функции распределения
Максвелла, Ферми-Дирака и Бозе- Эйнштейна (приТ>Tс) изображены
на рис. 3.
< О. Схематически функции распределения
Максвелла, Ферми-Дирака и Бозе- Эйнштейна (приТ>Tс) изображены
на рис. 3.
Рис. 3. Сравнение функций распределения Максвелла (M), Ферми-Дирака (Ф.- Д.)
и Бозе - Эйнштейна (Б.- Э.). По оси ординат отложено число частиц на одно
состояние с энергией  .
.
Особым случаем применения статистики Бозе - Эйнштейна является равновесное
электромагнитное излучение, к-рое можно рассматривать как газ, состоящий из
фотонов. Энергия фотона связана с его импульсом соотношением 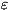 = h
= h = рс, где с - скорость света в
вакууме. Число фотонов не является заданной величиной, а само определяется из
условия термодинамич. равновесия, поэтому их распределение по импульсам даётся
формулой (19) с
= рс, где с - скорость света в
вакууме. Число фотонов не является заданной величиной, а само определяется из
условия термодинамич. равновесия, поэтому их распределение по импульсам даётся
формулой (19) с  = О (причём
= О (причём 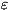 = рс).
Распределение энергии в спектре излучения получается умножением числа
фотонов на энергию
= рс).
Распределение энергии в спектре излучения получается умножением числа
фотонов на энергию 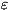 , так что плотность энергии
в интервале частот d
, так что плотность энергии
в интервале частот d равна пр (h
равна пр (h 3d
3d )/
)/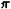 2c3,
причем пр берётся при
2c3,
причем пр берётся при 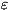 = h
= h .
T. о. получается формула Планка для спектра равновесного (чёрного) излучения
(см. Планка закон излучения).
.
T. о. получается формула Планка для спектра равновесного (чёрного) излучения
(см. Планка закон излучения).
Кристаллическая решётка. Применение С. ф. к вычислению термодинамич. функций
кристаллич. решётки основано на том, что атомы в решётке совершают малые
колебания около своих положений равновесия. Это позволяет рассматривать решётку
как совокупность связанных гармонич. осцилляторов. В такой системе могут
распространяться волны, характеризующиеся своим законом дисперсии, т. е.
зависимостью частоты  от волнового вектора k. B
квантовой механике эти волны можно рассматривать как совокупность т. н.
элементарных возбуждений, или квазичастиц, - фононов, обладающих
энергией h
от волнового вектора k. B
квантовой механике эти волны можно рассматривать как совокупность т. н.
элементарных возбуждений, или квазичастиц, - фононов, обладающих
энергией h и квазиимпульсом hk. Осн. отличие квазиимпульса от
импульса состоит в том, что энергия фонона является периодич. функцией
квазиимпульса с периодом, по порядку величины равным h/a, где
и квазиимпульсом hk. Осн. отличие квазиимпульса от
импульса состоит в том, что энергия фонона является периодич. функцией
квазиимпульса с периодом, по порядку величины равным h/a, где 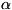 - постоянная решётки. Функция распределения фононов по квазиимпульсам даётся
формулой распределения Бозе - Эйнштейна (19) с
- постоянная решётки. Функция распределения фононов по квазиимпульсам даётся
формулой распределения Бозе - Эйнштейна (19) с  = О. При этом
= О. При этом 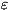 = h?. T. о., знание зависимости
= h?. T. о., знание зависимости  (k) позволяет
вычислить теплоёмкость решётки. Эту зависимость можно определить из опытов по
неупругому рассеянию нейтронов в кристалле (см. Нейтронография) или
вычислить теоретически, задавая значения "силовых констант",
определяющих взаимодействие атомов в решётке. При низких темп-рах существенны
только фононы с малой частотой, соответствующие квантам обычных звуковых волн,
для к-рых связь (а с k линейна. Это приводит к тому, что теплоёмкость
кристаллич. решётки пропорциональна T3. При высоких же темп-рах можно
пользоваться законом равного распределения энергии по степеням свободы, так что
теплоёмкость не зависит от темп-ры и равна 3Nk, где N - число атомов в
кристалле.
(k) позволяет
вычислить теплоёмкость решётки. Эту зависимость можно определить из опытов по
неупругому рассеянию нейтронов в кристалле (см. Нейтронография) или
вычислить теоретически, задавая значения "силовых констант",
определяющих взаимодействие атомов в решётке. При низких темп-рах существенны
только фононы с малой частотой, соответствующие квантам обычных звуковых волн,
для к-рых связь (а с k линейна. Это приводит к тому, что теплоёмкость
кристаллич. решётки пропорциональна T3. При высоких же темп-рах можно
пользоваться законом равного распределения энергии по степеням свободы, так что
теплоёмкость не зависит от темп-ры и равна 3Nk, где N - число атомов в
кристалле.
Металлы. В металлах вклад в термодинамич. функции дают также электроны
проводимости. Состояние электрона в металле характеризуется квазиимпульсом, и,
т. к. электроны подчиняются статистике Ферми - Дирака, их распределение по
киазиимпульсам даётся формулой (19). Поэтому теплоёмкость электронного газа, а
следовательно, и всего металла при достаточно низких темп-рах пропорциональна T.
Отличие от фермигаза свободных частиц состоит в том, что поверхность Ферми,
около к-рой сосредоточены "активные" электроны, уже не является
сферой, а представляет собой нек-рую сложную поверхность в пространстве квазиимпульсов.
Форму поверхности Ферми, равно как и зависимость энергии от квазпимпульса
вблизи этой поверхности, можно определять экспериментально, гл. обр. исследуя
магнитные свойства металлов, а также рассчитывать теоретически, используя т. н.
модель квазипотенциала. В сверхпроводниках (см. Сверхпроводимость) возбуждённые
состояния электрона отделены от ферми-поверхности щелью конечной ширины, что
приводит к экспоненц. зависимости электронной теплоёмкости от темп-ры. В
ферромагнитных и антиферромагнитных веществах вклад в термодинамич. функции
дают также колебания магнитных моментов - спиновые волны.
В диэлектриках и полупроводниках при T = О свободные электроны
отсутствуют. При конечных темп-рах в них появляются заряж. квазичастицы -
электроны с отрицат. зарядом и (в равном числе) "дырки" с положит,
зарядом. Электрон и дырка могут образовать связанное состояние - квазичастицу,
наз. экситоном. Др. тип экситона представляет собой возбуждённое
состояние атома диэлектрика, перемещающееся в кристаллич. решётке.
Методы квантовой теории поля в С. ф. При решении задач квантовой С. ф.,
прежде всего при исследовании свойств квантовых жидкостей, электронов в
металлах и магнетиков, важное значение имеют методы квантовой теории поля,
введённые в С. ф. сравнительно недавно. Осн. роль в этих методах играет функция
Грина G макроскопич. системы, аналогичная функции Грина в квантовой теории
поля. Она зависит от энергии 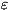 и импульса р, закон
дисперсии квазичастиц
и импульса р, закон
дисперсии квазичастиц 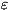 (
(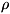 ) определяется
из уравнения:
) определяется
из уравнения:
[G (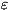 , р)]-1 = 0, (21)
, р)]-1 = 0, (21)
т. е. энергия квазичастицы определяется полюсом функции Грина. Существует
регулярный метод вычисления функций Грина в виде ряда по степеням энергии
взаимодействия между частицами. Каждый член этого ряда содержит многократные
интегралы по энергиям и импульсам от функций Грина невзаимодействующих частиц и
может быть изображён графически в виде диаграмм, аналогичных Фейнмана
диаграммам в квантовой электродинамике. Каждая из этих диаграмм имеет
определённый физический смысл, что позволяет отделить в бесконечном ряду члены,
ответственные за интересующее явление, и просуммировать их. Существует также
диаграммная техника для вычисления темп-рных функций Грина, позволяющих
вычислять термодинамич. величины непосредственно, без введения квазичастиц.
Упомянутые в разделе о жидкости методы, использующие многочастичные функции
распределения квазнчастнц, во многих отношениях близки к методам квантовой
теории поля. Использование этих функций всегда основано на приближённом
"расцеплении" - выражении функции более высокого порядка через
функции более низкого.
Фазовые переходы. При непрерывном изменении внешних параметров (напр.,
давления или темп-ры) свойства системы могут при нек-рых значениях параметров
измениться скачкообразно, т. е. происходит фазовый переход. Фазовые переходы делятся
на переходы первого рода, сопровождающиеся выделением скрытой теплоты перехода
и скачкообразным изменением объёма (к ним относится, напр., плавление), и
переходы второго рода, в к-рых скрытая теплота и скачок объёма отсутствуют
(напр., переход в сверхпроводящее состояние). Статистич. теория фазовых
переходов составляет важную, но ещё далёкую от завершения область С. ф.
Наибольшую трудность для теоретич. исследования представляют при этом свойства
вещества вблизи линии фазового перехода второго рода и вблизи критической
точки фазового перехода первого рода. С матем. точки зрения термодинамич.
функции системы имеют здесь особенности. Вблизи этих точек происходят
своеобразные критические явления. В то же время здесь аномально
возрастают флуктуации, и рассмотренные выше приближённые методы С. ф.
оказываются неприменимыми. Поэтому важную роль играет небольшое число точно
решаемых моделей, в к-рых есть переходы (напр., т. н. модель Йзинга).
Флуктуации. В основе С. ф. лежит тот факт, что физ. величины, характеризующие
макроскопич. тела, с большой точностью равны своим ср. значениям. Это равенство
является всё же приближённым, в действительности все величины испытывают малые
беспорядочные отклонения от ср. значений - фчуктуации. Существование флуктуации
имеет большое принципиальное значение, т. к. прямо доказывает статистнч.
характер термодинамич. закономерностей. Кроме того, флуктуации играют роль
шума, мешающего физ. измерениям и ограничивающего их точность. Флуктуации
нек-рсш величины х около её ср. значения х характеризуются ср.
квадратом флуктуации
( х)2 = (х-х)2 = х2 - х2.
х)2 = (х-х)2 = х2 - х2.
В подавляющем большинстве случаев величина х испытывает флуктуации
порядка корень ( х)2, существенно большие флуктуации
встречаются крайне редко. Знание функции распределения системы позволяет
вычислить ср. квадрат флуктуации точно так же, как н ср. значение любой физ.
величины. Малые флуктуации термодинамич. величин можно вычислить, используя
статистич. истолкование энтропии. Согласно (10), вероятность неравновесного
состояния системы с энтропией S пропорциональна eslk. Это
приводит к формуле
х)2, существенно большие флуктуации
встречаются крайне редко. Знание функции распределения системы позволяет
вычислить ср. квадрат флуктуации точно так же, как н ср. значение любой физ.
величины. Малые флуктуации термодинамич. величин можно вычислить, используя
статистич. истолкование энтропии. Согласно (10), вероятность неравновесного
состояния системы с энтропией S пропорциональна eslk. Это
приводит к формуле
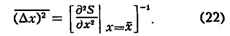
Напр., ср. квадраты флуктуации объёма и темп-ры тела равны:
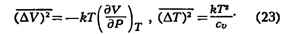
Из этих формул видно, что относит. флуктуации объёма и флуктуации темп-ры обратно пропорциональны корень N, где N - число частиц
в теле. Это и обеспечивает малость флуктуации для макроскопич. тел. Связь
между флуктуациями различных величин хi, хк характеризуется
функцией  хi
хi хк. Если
флуктуации величин хi и хк статистически
независимы, то
хк. Если
флуктуации величин хi и хк статистически
независимы, то  хi
хi хк =
хк =  хi*
хi* хк= 0.
хк= 0.
Под хi и хкможно понимать и значения
одной и той же величины, напр, плотности, в различных точках пространства.
Тогда эта функция имеет смысл пространственной корреляционной функции. С
увеличением расстояния между точками корреляционная функция стремится к нулю
(обычно экспоненциально), т. к. флуктуации в далёких точках пространства
происходят независимо. Расстояние, на к-ром эта функция существенно убывает,
наз. корреляционным радиусом.
Временной ход флуктуации и спектральное распределение флуктуационного шума
описываются временной корреляционной функцией  (t), в к-рой
усредняются флуктуации величины, взятые в различные моменты времени t:
(t), в к-рой
усредняются флуктуации величины, взятые в различные моменты времени t:
 (t1-t2) =
(t1-t2) =  х (t1)
х (t1) х(t2).
х(t2).
Важную роль в теории флуктуации играет т. н. флуктуационно-диссипативная
теорема, связывающая флуктуации в системе с изменением её свойств под влиянием
определённых внешних воздействий. Простейшее соотношение такого рода можно
получить, рассматривая флуктуации гармонич. осциллятора с потенц.
энергией 1/2 m o2 (х - х)2, где
т - масса осциллятора, соо - его собств. частота. Вычисление с помощью
формулы (22) даёт: (
o2 (х - х)2, где
т - масса осциллятора, соо - его собств. частота. Вычисление с помощью
формулы (22) даёт: ( х)2 = kT/т
х)2 = kT/т o2.
С др. стороны, если на осциллятор действует сила f, ср. значение х
смещается на величину
o2.
С др. стороны, если на осциллятор действует сила f, ср. значение х
смещается на величину  х = = f/m
х = = f/m o2,
так что
o2,
так что

и флуктуация х действительно связана с возмущением под влиянием силы
f. В общем случае флуктуационно-диссипативная теорема применима, если для х существует
"обобщённая сила" f, к-рая входит в оператор энергии системы
(гамильтониан; см. Квантовая механика) в виде члена -fx, где х
- квантовоме-ханнч. оператор, соответствующий величине х. Включение
силы f приведёт к изменению ср. значения х на величину 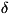
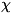 ,
причём, если f зависит от времени как е-1
,
причём, если f зависит от времени как е-1 t,
это изменение можно записать в виде:
t,
это изменение можно записать в виде:
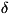 х =
х =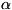 (
( ) f;
) f;
комплексная величина 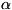 (
( ) наз. обобщённой
восприимчивостью системы. Теорема утверждает, что фурье-образ корреляционной
функции
) наз. обобщённой
восприимчивостью системы. Теорема утверждает, что фурье-образ корреляционной
функции
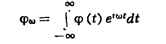
выражается через 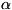 след, образом:
след, образом:
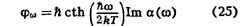
(Im означает мнимую часть функции). Частным случаем (25) является Найквиста
формула.
С. ф. неравновесных процессов. Всё большее значение приобретает кинетика
физическая - раздел С. ф., изучающий процессы в системах, находящихся в
неравновесных состояниях. Здесь возможны две постановки вопроса. Во-первых,
можно рассматривать систему в нек-ром неравновесном состоянии и следить за её
переходом в состояние равновесия. Во-вторых, можно рассматривать систему,
неравновесное состояние к-рой поддерживается внеш. условиями, напр, тело, в
к-ром задан градиент темп-ры, протекает электрич. ток и т. п., или тело,
находящееся в переменном внеш. поле.
Если отклонение от равновесия мало, неравновесные свойства системы
описываются т. н. кинетическими коэффициентами. Примерами таких коэффициентов
являются коэффициенты вязкости, теплопроводности и диффузии,
электропроводность металлов и т. п. Эти величины удовлетворяют принципу
симметрии кинетич. коэффициентов, выражающему симметрию уравнений механики
относительно изменения знака времени (см. Онсагера теорема). В силу
этого принципа, напр., электропроводность кристалла описывается симметричным тензором.
Описание сильно неравновесных состояний, а также вычисление кинетич.
коэффициентов производятся с помощью кинетического уравнения. Это уравнение
представляет собой интегро-дифференциальное уравнение для одночастичной
функции распределения (в квантовом случае - для одночастичной матрицы
плотности, или статистического оператора). Такое замкнутое, т. е. не
содержащее др. величин, уравнение невозможно получить в общем виде. При его
выводе необходимо использовать малые параметры, имеющиеся в данной конкретной
задаче. Важнейшим примером является кинетическое уравнение Болъцмана, описывающее
установление равновесия в газе за счёт столкновений между молекулами. Оно
справедливо для достаточно разреженных газов, когда длина свободного пробега
велика по сравнению с расстояниями между молекулами. Конкретный вид этого уравнения
зависит от эффективного сечения рассеяния молекул друг на друге. Если это
сечение известно, уравнение можно решать, разлагая искомую функцию по
ортогональным полиномам (см. Ортогональная система функций). Таким
способом можно вычислить кинетич. коэффициенты газа, исходя из известных
законов взаимодействия между молекулами. Уравнение Больцмана учитывает только
парные столкновения между молекулами и описывает только первый неисчезающий
член разложения этих коэфф. по плотности газа. Удалось найти и более точное
уравнение, учитывающее также тройные столкновения, что позволило вычислить
следующий член разложения.
Особую проблему представляет вывод кинетич. уравнения для плазмы. Из-за
медленного убывания кулоновских сил с расстоянием даже при рассмотрении парных
столкновений существенно экранирование этих сил остальными частицами.
Неравновесные состояния твёрдых тел и квантовых жидкостей можно при низких
темп-pax рассматривать как неравновесные состояния газа соответствующих
квазичастиц. Поэтому кинетич. процессы в таких системах описываются кинетич.
уравнениями для квазичастиц, учитывающими столкновения между ними и процессы их
взаимного превращения.
Новые возможности открыло применение в физ. кинетике методов квантовой
теории поля. Кинетич. коэффициенты системы можно выразить через её функцию
Грина, для к-рой существует общий способ вычисления с помощью диаграмм. Это
позволяет в ряде случаев получить кинетич. коэффициенты без явного
использования кинетич. уравнения и исследовать неравновесные свойства системы,
даже когда не выполняются условия применимости кинетич. уравнения.
Основные вехи развития С. ф. С. ф. целиком основана на представлениях
об атомном строении материи. Поэтому начальный период развития С. ф. совпадает
с развитием атомистич. представлений (см. Атомизм). Развитие С. ф. как
раздела теоретич. физики началось в сер. 19 в. В 1859 Дж. Максвелл определил
функцию распределения молекул газа по скоростям. В 1860-70 P. Клаузиус ввёл
понятие длины свободного пробега и связал её с вязкостью и теплопроводностью
газа. Примерно в то же время Л. Болъцман обобщил распределение Максвелла
на случай, когда газ находится во внеш. поле, доказал теорему о распределении
энергии по степеням свободы, вывел кинетич. уравнение, дал статистич.
истолкование энтропии и показал, что закон её возрастания является следствием
кинетич. уравнения. Построение классической С. ф. было завершено к 1902 в
работах Дж. Гиббса. Теория флуктуации была развита в 1905-06 в работах
M. Смолуховского и А. Эйнштейна. В 1900 M. Планк вывел
закон распределения энергии в спектре излучения чёрного тела, положив начало
развитию как квантовой механики, так и квантовой С. ф. В 1924 Ш. Базе нашёл
распределение по импульсам световых квантов и связал его с распределением
Планка. А. Эйнштейн обобщил распределение Бозе на газы с заданным числом
частиц. Э. Ферми в 1925 получил функцию распределения частиц,
подчиняющихся принципу Паули, а П. A. M. Дирак установил связь этого
распределения и распределения Бозе - Эйнштейна с математич. аппаратом квантовой
механики. Дальнейшее развитие С. ф. в 20 в. шло под знаком приложения её
основных принципов к исследованию конкретных проблем.
Лит.:
Классические труды: Б о л ь ц м а н Л., Лекции по теории газов, пер. с
нем., M., 1956; его же, Статьи н речи, [пер. с нем.], M., 1970; ГиббсДж. В.,
Основные принципы статистической механики, пер. с англ., М.- Л., 1946.
Учебники: A н с е л ь м А. И., Основы статистической физики и
термодинамики, M., 1973; Л е о н т о в и ч M. А., Статистическая физика, M.- Л.,
1944; Ландау Л. Д., Лифшиц E. M., Теоретическая физика, т. 5, 2 изд., M., 1964;
Майер Дж., Гепперт M а й e p M., Статистическая механика, пер. с англ., M., 1952; К и т т е л ь
Ч., Квантовая теория твердых тел, пер. с англ., M., 1967; X и л л Т.,
Статистическая механика. Принципы и избранные приложения, пер. с англ., M.,
1960; Хуан г К., Статистическая механика, пер. с англ., M., 1966.
Литература по
специальным вопросам:
Абрикосов А. А., Горьков Л. П., Дзялошинский И. E., Методы квантовой теории
поля в статистической физике, M., 1962; Боголюбов H. H., Проблемы динамической
теории в статистической физике, М.-Л., 1946; Гуревич Л. Э., Основы физической
кинетики, Л.- M., 1940; Силин В. П., Введение в кинетическую теорию газов, M.,
1971; Физика простых жидкостей. Сб., пер. с англ., M., 1971.
Л. П.
Питаевский.
СТАТИСТИЧЕСКИЕ ГРУППИРОВКИ, метод группировок, метод обработки и
анализа статистич. данных, при к-ром изучаемая совокупность явлений
расчленяется на однородные по отд. признакам группы и подгруппы и каждая из них
характеризуется системой статистич. показателей. Конкретное выражение С. г.
находят в групповых и комбннац. таблицах (см. Таблицы статистические).
Метод группировок - гл. метод статистич. изучения обществ, явлений; служит
предпосылкой для использования различных статистич. приёмов и методов анализа,
напр, для использования различных обобщающих показателей, в т. ч. средних
величин.
В дореволюц. рус. статистике, в особенности земской статистике, был
накоплен богатейший опыт группировок различных объектов, довольно подробно
разработаны групповые и комбинац. таблицы. Однако науч. обоснование теоретич.
вопросов применения методов группировок получило только в трудах В. И. Ленина,
к-рый высоко оценивал познават. ценность и практич. значимость метода
группировок. О комбинац. таблицах Ленин писал: "Можно сказать без всякого
преувеличения, что они внесли бы целый переворот в науку об экономике
земледелия" (Полн. собр. соч., 5 изд., т. 24, с. 281). Принципиально
важное значение имеют ленинские указания о предварит. политэкономич.
анализе существа закономерностей и характеристике типов явлений до начала
экспериментов с группировкой материалов исследования.
Кроме анализа структуры совокупности (см.
Совокупность статистическая), метод
группировок применяется при характеристике типов явлений и изучении
взаимосвязей между различными признаками или факторами. Примерами С. г.,
выражающих структуру совокупности, служит группировка населения по возрастным
группам (с годичными и, чаще, пятилетними интервалами), группировка предприятий
по их размерам (табл. 1).
Табл. 1.- Группировка промышленных предприятий СССР по численности рабочих
(1973, % к итогу)
|
|
|
|
Среднегодовая численность пром. -производств, персонала
|
Среднегодовая стоимость пром. -производств, осн. фондов
|
Предприятия, состоящие на самостоятельном балансе (без
электростанций, электросетей и теплосетей)
|
|
|
|
|
В том числе предприятия со среднегодовой численностью
рабочих:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Укрупняя группы или устанавливая неравномерные интервалы, можно выяснить
качеств, различия между отд. группами, а затем и определить техникоэкономич.
или социально-экономич. типы объектов (предприятий, X-B). Так, в С. г. населения
по возрасту, кроме простого хронологич. принципа, применяют специальные группы:
женщины в возрасте 16-54 лет и мужчины в возрасте 16-59 лет, в этом случае
статистика имеет возможность перейти к вычислению нар.-хоз. показателя - трудовых
ресурсов страны. Известная условность в определении границ интервалов (в
различных странах они различаются между собой) не имеет принципиального значения. От
детальной количеств, группировки предприятий и X-B можно перейти к выделению
неск. осн. качеств, групп - мелкие, средние, крупные, а затем к выяснению ряда
общих экономич. проблем, напр, процесса концентрации произ-ва и роста его
эффективности, производительности труда. Блестящий пример глубокого анализа
(проведённого с помощью С. г.) сложного характера закономерностей и связей
между величиной х-ва и его интенсивностью и производительностью имеется в
работе Ленина "Новые данные о законах развития капитализма в
земледелии" (там же, т. 27, с. 129-227).
Наиболее сложная задача метода группировок заключается в выделении и
развёрнутой характеристике типов (т. н. типологическая С. г.)
социально-экономич. явлений, к-рые представляют собой выражение форм определ.
обществ, процесса, существ, особенностей, общих для MH. единичных явлений.
Ленин всесторонне, комплексно использовал метод группировок в своём анализе
расслоения крестьянства, показав процесс формирования осн. классов в дореволюц.
России, в зап.-европ. деревне и в с. х-ве США.
Сов. статистика имеет большой опыт типологич. С. г.: напр., баланс
народного хозяйства СССР предполагает сложную и разветвлённую систему С.
г.; группировка классового состава населения (табл. 2); группировка осн.
производств, фондов по социально-экономич. видам х-ва; группировка совокупного
общественного продукта и др.
В бурж. статистике группировки используются недостаточно, а в случаях
применения они большей частью строятся на неправильных основаниях, не
способствуют характеристике действительного положения вещей в капиталистич.
странах, напр, группировка с.-х. предприятий по размерам земельной площади
приукрашивает положение мелкого произ-ва в с. х-ве; группировка населения по
занятиям не раскрывает действительную классовую структуру буржуазного общества
и т. д.
Социально-экономич. особенности социалистич. общества ставят новые задачи
перед С. г. Метод группировок применяется при анализе выполнения нар.-хоз.
планов, выяснении причин отставания отд. предприятий и отраслей, выявлении
неиспользованных резервов (напр.,
Табл. 2. - Классовый состав населен и я CCC P, %
|
|
|
|
|
Всё население (включая неработающих членов семей)...
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Колхозное крестьянство и кооперированные кустари
|
|
|
|
Крестьяне - единоличники и некооперированные кустари ...
|
|
|
|
Буржуазия, помещики, торговцы н кулаки ...
|
|
|
|
С. г. предприятий по степени выполнения планов, степени рентабельности). С.
г. предприятий по степени автоматизации и механизации, электровооруженности
труда и по др. технико-экономич. признакам важны для характеристики
внедрения достижений научно-технич. прогресса в произ-во.
Лит. см. при ст. Статистика.
T. В. Рябушкин.
СТАТИСТИЧЕСКИЕ ОЦЕНКИ, функции от результатов наблюдений,
употребляемые для статистического оценивания неизвестных параметров
распределения вероятностей изучаемых случайных величин. Напр., если X1,
..., Xn - независимые случайные величины, имеющие одно и то
же нормальное распределение с неизвестным средним значением а, то
функции - среднее арифметическое результатов наблюдений
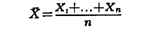
и выборочная медиана  =
=  (Х
(Х ,.... Xn)
являются возможными точечными С. о. неизвестного параметра а. В качестве
С. о. к.-л. параметра
,.... Xn)
являются возможными точечными С. о. неизвестного параметра а. В качестве
С. о. к.-л. параметра 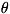 естественно выбрать функцию
естественно выбрать функцию 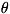 *(Х
*(Х ,
.., Xn) от результатов наблюдений Xi, ..., Xn, в нек-ром
смысле близкую к истинному значению параметра. Принимая к.-л. меру
"близости" С. о. к значению оцениваемого параметра, можно сравнивать
различные оценки по качеству. Обычно мерой близости оценки к истинному значению
параметра служит величина среднего значения квадрата ошибки (выражающаяся через математическое ожидание оценки Е
,
.., Xn) от результатов наблюдений Xi, ..., Xn, в нек-ром
смысле близкую к истинному значению параметра. Принимая к.-л. меру
"близости" С. о. к значению оцениваемого параметра, можно сравнивать
различные оценки по качеству. Обычно мерой близости оценки к истинному значению
параметра служит величина среднего значения квадрата ошибки (выражающаяся через математическое ожидание оценки Е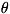
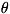 *
и её дисперсию D
*
и её дисперсию D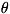 Q*). В классе всех несмещённых опенок (для
к-рых E
Q*). В классе всех несмещённых опенок (для
к-рых E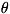
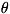 * =
* = 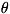 ) наилучшими с этой точки зрения
будут оценки, имеющие при заданном
) наилучшими с этой точки зрения
будут оценки, имеющие при заданном 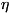 минимальную возможную
дисперсию при всех
минимальную возможную
дисперсию при всех 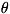 . Указанная выше оценка X для
параметра а нормального распределения является наилучшей несмещённой
оценкой, поскольку дисперсия любой другой несмещенной оценки а* параметра
а удовлетворяет неравенству Daa* > DaX
=
. Указанная выше оценка X для
параметра а нормального распределения является наилучшей несмещённой
оценкой, поскольку дисперсия любой другой несмещенной оценки а* параметра
а удовлетворяет неравенству Daa* > DaX
= 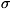 2/п, где
2/п, где 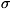 2 - дисперсия
нормального распределения. Если существует несмещённая оценка с минимальной
дисперсией, то можно найти и несмещённую наилучшую оценку в классе функций,
зависящих только от достаточной статистики. Имея в виду построение С. о.
для больших значений п, естественно предполагать, что вероятность
отклонений
2 - дисперсия
нормального распределения. Если существует несмещённая оценка с минимальной
дисперсией, то можно найти и несмещённую наилучшую оценку в классе функций,
зависящих только от достаточной статистики. Имея в виду построение С. о.
для больших значений п, естественно предполагать, что вероятность
отклонений  * от истинного значения параметра
* от истинного значения параметра  ,
превосходящих к.-л. заданное число, будет близка к нулю при n -> бескон..
С. о. с таким свойством называются состоятельными оценками. Несмещённые оценки,
дисперсия к-рых стремится к нулю при n->бескон., являются
состоятельными. Поскольку скорость стремления к пределу играет при этом важную
роль, то асимптотич. сравнение С. о. производят по отношению их асимптотич.
дисперсий. Так, среднее арифметическое X в приведённом выше примере -
наилучшая и, следовательно, асимптотически наилучшая оценка для параметра а,
тогда как выборочная медиана
,
превосходящих к.-л. заданное число, будет близка к нулю при n -> бескон..
С. о. с таким свойством называются состоятельными оценками. Несмещённые оценки,
дисперсия к-рых стремится к нулю при n->бескон., являются
состоятельными. Поскольку скорость стремления к пределу играет при этом важную
роль, то асимптотич. сравнение С. о. производят по отношению их асимптотич.
дисперсий. Так, среднее арифметическое X в приведённом выше примере -
наилучшая и, следовательно, асимптотически наилучшая оценка для параметра а,
тогда как выборочная медиана  , представляющая собой также несмещённую
оценку, не является асимптотически наилучшей, т. к.
, представляющая собой также несмещённую
оценку, не является асимптотически наилучшей, т. к.
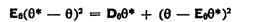
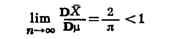
(тем не менее использование  имеет также положительные стороны: напр.,
если истинное распределение не является в точности нормальным, а несколько
отличается от него, дисперсия X может резко возрасти, а дисперсия
имеет также положительные стороны: напр.,
если истинное распределение не является в точности нормальным, а несколько
отличается от него, дисперсия X может резко возрасти, а дисперсия  остаётся почти той же, т. е.
остаётся почти той же, т. е.  обладает свойством, наз.
"прочностью"). Одним из распространённых общих методов получения С.
о. является метод моментов, к-рый заключается в приравнивании определённого
числа выборочных моментов к соответствующим моментам теоретич. распределения,
к-рые суть функции от неизвестных параметров, и решении полученных уравнений
относительно этих параметров. Хотя метод моментов удобен в практич. отношении,
однако С. о., найденные при его использовании, вообще говоря, не являются
асимптотически наилучшими. Более важным с теоретич. точки зрения представляется
максимального правдоподобия метод, который приводит к оценкам, при
некоторых общих условиях асимптотически наилучшим. Частным случаем последнего
является наименьших квадратов метод. Метод С. о. существенно дополняется
оцениванием с помощью доверительных границ.
обладает свойством, наз.
"прочностью"). Одним из распространённых общих методов получения С.
о. является метод моментов, к-рый заключается в приравнивании определённого
числа выборочных моментов к соответствующим моментам теоретич. распределения,
к-рые суть функции от неизвестных параметров, и решении полученных уравнений
относительно этих параметров. Хотя метод моментов удобен в практич. отношении,
однако С. о., найденные при его использовании, вообще говоря, не являются
асимптотически наилучшими. Более важным с теоретич. точки зрения представляется
максимального правдоподобия метод, который приводит к оценкам, при
некоторых общих условиях асимптотически наилучшим. Частным случаем последнего
является наименьших квадратов метод. Метод С. о. существенно дополняется
оцениванием с помощью доверительных границ.
Лит.: К е н д а л л M., Стьюарт А., Статистические выводы и связи,
пер. с англ., M., 1973; Крамер Г., Математические методы статистики, пер. с
англ., 2 изд., M., 1975.
А. В. Прохоров.
СТАТИСТИЧЕСКИЕ РАСЧЁТЫ, исчисление на основе имеющихся статистич.
данных новых показателей, расширяющих и обогащающих возможности анализа и
познания социально-экономич. явлений и процессов. С. р. можно подразделить на 2
группы: расчёты отд. показателей и комплексные расчёты систем показателей. К
первой группе относятся: расчёты относит, показателей (напр., показателей
выполнения плана, структуры совокупности, соотношения отд. её частей, динамики,
сравнения и интенсивности развития); расчёты средних величин (напр., ср.
заработной платы, ср. выработки на одного работающего, ср. урожайности и т.
п.); исчисление отд. статистич. характеристик (напр., ср. ошибки выборки, дисперсии,
вариационных коэффициентов); расчёты статистич. индексов; расчёты
недостающих показателей на основе балансовых уравнений, интерполяции в рядах
динамики; расчёты сводных показателей в социально-экономич. статистике
(напр., совокупного общественного продукта, национального дохода и др.).
Вторую группу составляют комплексные С. р., воссоздающие какой-либо процесс
или состояние социально-экономич. явления. В них применяются методы статистических
группировок, построение индексных систем, теория корреляции и др.
статистич. приёмы анализа. Непревзойдённые примеры глубоко научных С. р.
содержатся в трудах В. И. Ленина. В работе " Развитие капитализма в
России" на основе массового статистич. материала, собранного земской
статистикой и научно обработанного Лениным с помощью метода группировок,
доказано развитие капитализма в России: в пореформенной русской деревне
происходил процесс классовой дифференциации, выделялись 3 различных
социально-экономических типа крест. х-в: пролетарское и полупролетарское,
живущие гл. обр. или наполовину продажей рабочей силы; середняцкие, источник
существования к-рых - собственное мелкое х-во, и зажиточные, эксплуатирующие
наёмных рабочих. По расчётам В. И. Ленина, удельный вес этих типов крест. х-в в
кон. 19 в. в России составлял соответственно 50, 30 и 20%. В этой же работе дан
классич. пример С. р. социальной структуры населения России по материалам
переписи населения в 1897 с использованием данных переписи населения 1890 в
Петербурге и материалов земской статистики. В. И. Ленин установил, что
численность пролетариата в России в 1897 составляла "...не менее 22-х
миллионов" (Полн. собр. соч., 5 изд., т. 3, с. 505, прим.). В
социалистическом х-ве С. р. находят применение в балансовых работах (см.
Балансовый метод в планировании, Балансовый метод в статистике), прежде всего в
расчётах, связанных с построением баланса народного хозяйства СССР, баланса
основных фондов, финансового баланса, баланса трудовых ресурсов, баланса
межотраслевого произ-ва и распределения обществ, продукта; при
сопоставлении показателей между странами в междунар. сравнениях; при
исчислении различных сводных показателей и коэфф. и т. д. Большую группу
составляют С. р. по прогнозированию численности населения и др. показателей
социально-экономич. статистики на длит, период времени. Следует назвать также
расчёты по распространению на генеральную совокупность результатов выборочного
наблюдения и оценки их достоверности. Примером С. р. может служить
математич. обработка данных межотраслевого баланса нар. х-ва. Для произ-ва
комплексных С. р. применяются экономикоматематич. методы и электронно-вычислит.
машины.
Лит.: Эйдельман M. Р., Межотраслевой баланс общественного продукта,
M., 1966: Курс экономической статистики, под ред А. И. Петрова, 4 изд . M-,
1967; Курс демографии, под ред. А. Я. Боярского, M., 1967; Ряузов H. H., Общая
теория статистики, 2 изд., M., 1971.
H. H. Ряузов.
СТАТИСТИЧЕСКИЕ РЕШЕНИЯ, общее название решений, принимаемых на основе
результатов наблюдений к.-л. явления, подчиняющегося вероятностным
закономерностям (см. Вероятность), к-рые известны лишь частично. Напр.,
при обеззараживании воды хлорированием количество добавляемого хлора должно
зависеть от среднего числа 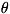 бактерий в единице объёма. Однако
само
бактерий в единице объёма. Однако
само 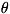 неизвестно и оценивается по результатам X1, X2,
...,Xn подсчёта численности бактерий в
неизвестно и оценивается по результатам X1, X2,
...,Xn подсчёта численности бактерий в 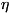 независимо выбранных
единицах объёма воды, при допущении (в простейшей модели), что X1
при z = 1, ...,n имеют Пуассона распределение с неизвестным
средним значением (математическим ожиданием)
независимо выбранных
единицах объёма воды, при допущении (в простейшей модели), что X1
при z = 1, ...,n имеют Пуассона распределение с неизвестным
средним значением (математическим ожиданием) 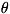 . Поэтому С.
р.- решение о количестве добавляемого хлора-будет функцией от к.-л. статистической
оценки
. Поэтому С.
р.- решение о количестве добавляемого хлора-будет функцией от к.-л. статистической
оценки 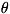 * параметра
* параметра 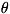 . Последняя должна
выбираться с учетом нежелательных последствий как недооценки
. Последняя должна
выбираться с учетом нежелательных последствий как недооценки 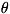 (недостаточное обеззараживание воды), так и завышенной оценки
(недостаточное обеззараживание воды), так и завышенной оценки 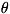 (ухудшение вкуса воды от чрезмерного добавления хлора). Точную математич.
формулировку понятий, касающихся С. р. и способов их сравнения, рассматривает статистических
решений теория.
(ухудшение вкуса воды от чрезмерного добавления хлора). Точную математич.
формулировку понятий, касающихся С. р. и способов их сравнения, рассматривает статистических
решений теория.
Ю. В. Прохоров.
СТАТИСТИЧЕСКИЕ СБОРНИКИ, справочные издания, содержащие цифровую
информацию о развитии нар. х-ва, его отраслей и подразделений. Различаются по
назначению (ежегодники, справочники, юбилейные издания, бюллетени и т. п.),
объёму (полные и краткие), охвату данных (общеэкономич. и отраслевые, по всей
стране или по республикам, р-нам), ведомственной принадлежности, форме (книги и
журналы) и периодичности издания (десятилетние, годовые, квартальные, месячные,
разовые и др.). Независимо от назначения С. с. охватывают характеристику
(состояние и развитие) территории и населения, науки и научно-технич.
прогресса, пром-сти и её отраслей, с. х-ва, строительства, транспорта и связи,
торговли, финансов и кредита, внешних связей, образования и культуры,
здравоохранения, труда и быта, материального благосостояния и развития нар.
х-ва в целом. Разработка схем и методологии С. с.- неотъемлемая часть статистики
как науки, а их составление и публикация - важный раздел в деятельности (в
странах социализма - плановой) статистич. организаций (в СССР - ЦСУ СССР и его
органов в республиках и на местах). В России систематич. издания С. с.
осуществлялись с 19 в. ("Статистический Временник Российской
империи", 1866-94, н "Ежегодник России", 1905-18). В 1924 в СССР
вышел первый С. с. по нар. х-ву. В 1925 он был дополнен новым материалом и
издан под назв. "Народное хозяйство Союза CCP в цифрах". Это был
первый опыт отражения в статистич. публикациях системы показателей развития
нар. х-ва СССР. С 1956 ежегодно (кроме 1958) выпускается С. с. "Народное
хозяйство СССР", а с 1957 - С. с. о развитии нар. х-ва отдельно по каждой
союзной республике, по краям и областям.
Ежегодники являются осн. разновидностью С. с. и в др. странах (издаются в
126 странах, в т. ч. во всех странах СЭВ). Важнейшими С. с. ООН и её
специализированных учреждений с 1946 являются: "Статистический
ежегодник" ("Statistical yearbook"), "Демографический
ежегодник" ("Demografic yearbook"), "Ежегодник по
статистике международной торговли" ("Yearbook of international trade
statistics"), "Ежегодник ООН" ("Yearbook of the United
Nations") и др. Продовольственная и с.-х. организация ООН (ФАО) издаёт
"Ежегодник по статистике продовольствия и сельского хозяйства"
("Yearbook of food and agricultural statistics"), а также ежегодники
по статистике рыболовства и лесного хозяйства; Организация Объединённых Наций
по вопросам образования, науки и культуры (ЮНЕСКО) издаёт "Международный
ежегодник по образованию" ("International
yearbook of education") и общий статистический ежегодник
("Statistical yearbook"). Свои ежегодники издают и мн. др.
междунар. организации.
В. M. Симчера.
СТАТИСТИЧЕСКИЙ АНАЛИЗ МНОГОМЕРНЫЙ, в широком смысле - раздел математической
статистики, объединяющий методы изучения статистич. данных, относящихся к
объектам, к-рые характеризуются неск. качественными или количественными
признаками. Наиболее разработана часть С. а. м., основанная на допущении, что
результаты отдельных наблюдений независимы и подчинены одному и тому же
многомерному нормальному распределению (обычно именно к этой части
применяют термин С. а. м. в узком смысле). Иными словами, результат Xj наблюдения
с номером j можно представить вектором
Хj = (Хj1, Xj2, ...,Xjs),
где случайные величины Xjn имеют математическое
ожидание  k, дисперсию
k, дисперсию 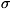 2k,
а коэффициент корреляции между Xjk и Xji равен
ры. Вектор математич. ожиданий
2k,
а коэффициент корреляции между Xjk и Xji равен
ры. Вектор математич. ожиданий  = (
= ( 1,
...,
1,
...,  s) и ковариационная матрица
s) и ковариационная матрица 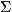 с
элементами
с
элементами 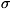 k,
k, 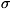 i, pki,k,
l = 1, ...,s, являются основными параметрами, полностью определяющими
распределение векторов X1, ..., Xn - результатов
i, pki,k,
l = 1, ...,s, являются основными параметрами, полностью определяющими
распределение векторов X1, ..., Xn - результатов  независимых
наблюдений. Выбор многомерного нормального распределения в качестве основной
математич. модели С. а. м. отчасти может быть оправдан след, соображениями: с
одной стороны, эта модель приемлема для большого числа приложений, с другой -
только в рамках этой модели удаётся вычислить точные распределения выборочных
характеристик. Выборочное среднее
независимых
наблюдений. Выбор многомерного нормального распределения в качестве основной
математич. модели С. а. м. отчасти может быть оправдан след, соображениями: с
одной стороны, эта модель приемлема для большого числа приложений, с другой -
только в рамках этой модели удаётся вычислить точные распределения выборочных
характеристик. Выборочное среднее
X = 1/n(X1 + ... + Xn) и выборочная ковариационная матрица
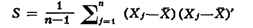
[где (Xj - X)' обозначает транспонированный вектор (Xj
- X), см. Матрица] суть оценки максимального правдоподобия
соответствующих параметров совокупности. Распределение X нормально ( ,1/n
,1/n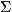 ), а совместное распределение элементов ковариационной матрицы S,
т. н. распределение Уишарта, является естественным обобщением "хи-квадрат"
распределения и играет значит. роль в С. а. м.
), а совместное распределение элементов ковариационной матрицы S,
т. н. распределение Уишарта, является естественным обобщением "хи-квадрат"
распределения и играет значит. роль в С. а. м.
Ряд задач С. а. м. более или менее аналогичен соответствующим одномерным
задачам (напр., задача проверки гипотез о равенстве средних значений в двух
независимых выборках). Другого типа задачи связаны с проверкой гипотез о
независимости тех или иных групп компонент векторов Xj, проверкой
таких специальных гипотез, как гипотеза сферической симметрии распределения Xjи
т. д. Необходимость разобраться в сложных взаимосвязях между компонентами случайных
векторов Xj ставит новые проблемы. В целях сокращения числа
рассматриваемых случайных признаков (уменьшения размерности) или сведения их к
независимым случайным величинам применяются метод главных компонент и метод
канонических корреляций. В теории главных компонент осуществляется переход от
векторов Xj к векторам Yj = (Yj1,...,Yjr).
При этом, напр., Yj выделяется максимальной дисперсией среди всех
нормированных линейных комбинаций компонент Xi; Yj2 имеет наибольшую
дисперсию среди всех линейных функций компонент Xi, не коррелированных с YJ1
и т. д. В теории канонич. корреляций каждое из двух множеств случайных
величин (компонент Xj) линейно преобразуется в новое множество т. н.
канонич. величин так, что внутри каждого множества коэффициенты корреляции
между величинами равны О, первые координаты каждого множества имеют
максимальную корреляцию, вторые координаты имеют наибольшую корреляцию из
оставшихся координат и т. д. (упорядоченные т. о. корреляции наз.
каноническими). Последний метод указывает максимальную корреляцию линейных
функций от двух групп случайных компонент вектора наблюдения. Выводы методов
главных компонент и канонич. корреляций помогают понять структуру изучаемой
многомерной совокупности. Сходным целям служит и факторный анализ, в схеме
к-рого предполагается, что компоненты случайных векторов Xj являются
линейными функциями от нек-рых ненаблюдаемых факторов, подлежащих изучению. В
рамках С. а. м. рассматривается и проблема дифференциации двух или большего
числа совокупностей по результатам наблюдений. Одна часть проблемы заключается
в том, чтобы на основе анализа выборок из неск. совокупностей отнести новый
элемент к одной из них (дискриминация), другая - в том, чтобы внутри
совокупности разделить элементы на группы, в определённом смысле максимально
отличающиеся друг от друга.
Лит.: Андерсон Т., Введение в многомерный статистический анализ, пер.
с англ., M., 1963; Кеndall M. G., Stuart A., The advanced
theory of statistics,  . 3,
L., 1966; Dempster A. P., Elements of continuons multivariate analysis, L.,
1969.
. 3,
L., 1966; Dempster A. P., Elements of continuons multivariate analysis, L.,
1969.
А. В. Прохоров.
СТАТИСТИЧЕСКИЙ АНАЛИЗ СЛУЧАЙНЫХ ПРОЦЕССОВ, раздел математич.
статистики, посвящённый методам обработки и использования статистич. данных,
касающихся случайных процессов (т. е. функций X(t) времени t,
определяемых с помощью нек-рого испытания и при разных испытаниях могущих в зависимости от случая принимать различные значения). Значение x(t) случайного
процесса X(t), получаемое в ходе одного испытания, наз. реализацией (иначе -
наблюдённым значением, выборочным значением или траекторией) процесса X(t);
статистич. данные о X(t), используемые при статистич. анализе этого процесса,
обычно представляют собой сведения о значениях одной или неск. реализаций x(t)
в течение опреде^ ленного промежутка времени или же о значениях каких-либо
величин, связанных с процессом X(t) (напр., о наблюдённых значениях процесса
Y(t), являющегося суммой X(t) и нек-рого "шума" N(t), созданного
внешними помехами и ошибками измерения значений x(t)). Весьма важный с
точки зрения приложений класс задач С. а. с. п. представляют собой задачи
обнаружения сигнала на фоне шума, играющие большую роль при радиолокации. С
математич. точки зрения эти задачи сводятся к статистической проверке
гипотез: здесь по наблюдённым значениям нек-рой функции требуется
заключить, справедлива ли гипотеза о том, что функция эта является реализацией
суммы шума N(t) и интересующего наблюдателя сигнала X(t), чти же справедлива
гипотеза о том, что она является реализацией одного лишь шума N(t).- В случаях,
когда форма сигнала X(t) не является полностью известной, задачи обнаружения
часто включают в себя и задачи статистической оценки неизвестных параметров
сигнала; так, напр., в задачах радиолокации очень важна задача об оценке
времени появления сигнала, определяющего расстояние до объекта, породившего
этот сигнал. Задачи статистич. оценки параметров возникают и тогда, когда по
данным наблюдений за значениями процесса X(t) в течение определённого
промежутка времени требуется оценить значения каких-то параметров распределения
вероятностей случайных величин X(t) или же, напр., оценить значение в
фиксированный момент времени t = t1 самого процесса X(t) (в предположении,
что t1 лежит зл пределами интервала наблюдений за этим процессом)
или значение y(t1) какого-либо вспомогат. процесса Y(t).
статистически связанного с X(t) (см. Случайных процессов прогнозирование). Наконец,
ряд задач С. а. с. п. относится к числу задач на непарачетрические методы статистики;
так обстоит дело, в частности, когда по наблюдениям за течением процесса X(t)
требуется оценить нек-рые функции, характеризующие распределения вероятностей
значений этого процесса (напр., плотность вероятности величины Х(t), или
корреляционную функцию EX(t)X(s) процесса X(t), или, в случае стационарного
случайного процесса X(t), его спектральную плотность f( )).
)).
При решении задач С. а. с. п. всегда требуется принять те или иные
специальные предположения о статистнч. структуре процесса X(t), т. е. как-то
ограничить класс рассматриваемых случайных процессов. Очень ценным с точки
зрения С. а. с. п. является допущение о том, что рассматриваемый процесс X(t)
является стационарным случайным процессом; при этом допущении, зная значения
единственной реализации x(t) в течение промежутка времени 0 <= t
<= T, можно уже получить целый ряд статистич. выводов о вероятностных
характеристиках процесса Х(t). В частности, среднеарифметнч. значение
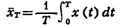
в случае стационарного случайного процесса X(t) при весьма широких условиях
является состоятельной оценкой математич. ожидания EX(t) = т (т. е. XT
сходится при Т-> бескон. к истинному значению оцениваемой величины т);
аналогично этому выборочная корреляционная функция
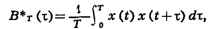
где  >0, при широких условиях является состоятельной оценкой
корреляционной функции
>0, при широких условиях является состоятельной оценкой
корреляционной функции
B( ) = EX(t) X (t +
) = EX(t) X (t + 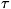 ).
).
Однако Фурье преобразование функции В*Т(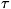 )- так
называемая периодограмма IT (
)- так
называемая периодограмма IT ( ) процесса X(t) -
уже не представляет собой состоятельной оценки спектральной плотности f(
) процесса X(t) -
уже не представляет собой состоятельной оценки спектральной плотности f( ), являющейся преобразованием Фурье функции В(
), являющейся преобразованием Фурье функции В(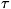 ); при
больших значениях T периодограмма 1Т (
); при
больших значениях T периодограмма 1Т ( ) ведёт
себя крайне нерегулярно и при T -> бескон. она не стремится ни к
какому пределу. Поэтому С. а. с. п. включает в себя ряд специальных приёмов
построения состоятельных оценок спектральной плотности f(
) ведёт
себя крайне нерегулярно и при T -> бескон. она не стремится ни к
какому пределу. Поэтому С. а. с. п. включает в себя ряд специальных приёмов
построения состоятельных оценок спектральной плотности f( ) по
наблюдённым значениям одной реализации стационарного процесса X(t), большинство
из к-рых основано на использовании сглаживания периодограммы процесса по
сравнительно узкой области частот
) по
наблюдённым значениям одной реализации стационарного процесса X(t), большинство
из к-рых основано на использовании сглаживания периодограммы процесса по
сравнительно узкой области частот  .
.
При исследовании статистич. свойств оценок вероятностных характеристик
стационарных случайных процессов очень полезными оказываются дополнительные
допущения о природе X(t) (напр., допущение о том, что все конечномерные распределения
значений процесса X(t) являются нормальными распределениями вероятностей).
Большое развитие получили также исследования по С. а. с. п., в к-рых
предполагается, что изучаемый процесс X(t) является марковским процессом того
или иного типа, или компонентой многомерного марковского процесса, или
компонентой многомерного процесса, удовлетворяющего определённой системе
стохастических дифференциальных уравнений.
Лит.: Дженкинс Г., Ватте Д., Спектральный анализ и его приложения,
игр. с англ.,в. 1 - 2, M., 1971 -72; Хеннан О., Анализ временных рядов, пер. с
англ., M., 1964; его же, Многомерные временные ряды, пер. с англ., M., 1974;
Лчпцер Р. Ш., Ширяев A. H., Статистика случайных процессов (нелинейная
фильтрация и смежные вопросы), M., 1974.
A. M. Яглом.
СТАТИСТИЧЕСКИЙ АНСАМБЛЬ, совокупность сколь угодно большого числа
одинаковых физ. систем многих частиц ("копий" данной системы),
находящихся в одинаковых макроскопич. состояниях; при этом микроскопич.
состояния системы могут принимать все возможные значения, совместимые с
заданными значениями макроскопич. параметров, определяющих её макроскопич.
состояние. Примеры С. а.- энергетически изолированные системы при заданном
значении полной энергии (микроканонический ансамбль), системы в контакте
с термостатом заданной темп-ры (канонический ансамбль), системы в
контакте с термостатом и резервуаром частиц (большой канонический ансамбль). С.
а.- осн. понятие статистической физики, позволяющее применить методы
теории вероятностей.
СТАТИСТИЧЕСКИЙ ВЕС, в квантовой механике и квантовой статистике -
число различных квантовых состояний с данной энергией, т. е. кратность
состояния. Если энергия принимает непрерывный ряд значений, под С. в. понимают
число состояний в данном интервале энергий. В классич. статистике С. в. наз.
величину элемента фазового объёма системы. См. Статистическая физика.
СТАТИСТИЧЕСКИЙ ИНСТИТУТ международный, занимается развитием и
усовершенствованием статистич. методов и их применением в различных областях
знаний. Основан в 1885. Организационная работа С. и. выполняется Постоянным
бюро, к-рое находится в Гааге. В составе С. и. (сер. 70-х гг.) св. 700
действительных членов более чем из 70 стран (в т. ч. из СССР и др. социалистич.
стран), специалисты в области социально-экономич. и математич. статистики, а
также руководители нац. статистич. учреждений и орг-ций. Каждые 2 года С. и.
проводит сессии, на к-рых заслушиваются и обсуждаются науч. сообщения по
проблемам различных отраслей статистики. Первая сессия состоялась в Риме в
1887, 40-я - в 1975 в Варшаве. Материалы сессий С. и. печатаются в
"Бюллетенях института". Статьи по отд. проблемам статистики (в
основном математической) и текущая информация о науч. жизни публикуются в журн.
"Международное статистическое обозрение" ("International
statistical review", с 1933). До 1-й мировой войны 1914-18 С. и. был
центром междунар. статистики, занимался сбором и обработкой статистич. данных
отд. стран, готовил рекомендации по сопоставимости данных. В 1919-33 он
осуществлял эту деятельность параллельно с органами Лиги Наций. С
созданием статистич. аппарата ООН С. и. полностью переключился на вопросы
статистич. теории и методологии. Ин-т готовит кадры статистиков для
развивающихся стран. В 70-е гг. сформировались 3 ассоциации как автономные
секции С. и.: Междунар. ассоциация по применению статистики в физич. науках,
Междунар. ассоциация муниципальных статистиков, Междунар. ассоциация
специалистов по выборочному методу.
Лит.: Рябушкин Т., Международная статистика, M., 1965.
T. В.
Рябушкин.
СТАТИСТИЧЕСКИЙ ОПЕРАТОР, матрица плотности, оператор, с помощью
к-рого можно вычислить ср. значение любой физ. величины в квантовой статистической
физике и, в частности, в квантовой механике. С. о. описывает
состояние системы, не основанное на полном (в смысле квантовой механики) наборе
данных о системе (смесь состоянии).
СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ МЕТОД, метод вычислительной и прикладной
математики, основанный на моделировании случайных величин и построении
статистич. оценок для искомых величин; то же, что Монте-Карло метод. Принято
считать, что С. и. м. возник в 1944, когда в связи с работами по созданию
атомных реакторов амер. учёные Дж. фон Нейман и С. Улам начали широко применять
аппарат теории вероятностей для решения прикладных задач с помощью ЭВМ. Первоначально
С. и. м. использовался гл. обр. для решения сложных задач теории переноса
излучения и нейтронной физики, где традиционные численные методы оказались мало
пригодными. Затем его влияние распространилось на больший класс задач
статистич. физики, очень разных по своему содержанию. С. и. м. применяется для
решения задач теории игр, теории массового обслуживания и математич. экономики,
задач теории передачи сообщений при наличии помех и т. д. Для решения
детерминированной задачи по С. и. м. прежде всего строят вероятностную модель,
представляют искомую величину, напр, многомерный интеграл, в виде математич.
ожидания функционала от случайного процесса, к-рый затем моделируется на ЭВМ.
Хорошо известны вероятностные модели для вычисления интегралов, для решения
интегральных уравнений 2-го рода, для решения систем линейных алгебраич.
уравнений, для решения краевых задач для эллиптич. уравнений, для оценки
собственных значений линейных операторов и т. д. Выбором вероятностной модели
можно распорядиться для получения оценки с малой погрешностью. Особую роль в
различных приложениях С. и. м. играет моделирование случайных величин с
заданными распределениями. Как правило, такое моделирование осуществляется
путём преобразования одного или нсск. независимых значений случайного числа а,
распределённого равномерно в интервале (0,1). Последовательности
"выборочных" значений 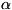 обычно получают на ЭВМ с помощью
теоретико-числовых алгоритмов, среди к-рых наибольшее распространение получил
"метод вычетов". Такие числа наз. "псевдослучайными", они
проверяются статистич. тестами и решением типовых задач. Если в расчёте по С.
и. м. моделируются случайные величины, определяемые реальным содержанием
явления, то расчёт представляет собой процесс "прямого
моделирования". Такой расчёт неэффективен, если изучению подлежат редкие
события, т. к. реальный процесс содержит о них мало информации. Эта
неэффективность обычно проявляется в слишком большой величине вероятностной
погрешности (дисперсии) случайных оценок искомых величин. Разработано много
способов уменьшения дисперсии указанных оценок в рамках С. и. м. Почти все они
основаны на модификации моделирования с помощью информации о "функции
ценности" значений случайных величин относительно вычисляемых величин. С.
и. м. оказал и продолжает оказывать существенное влияние на развитие др.
методов вычислительной математики (напр., на развитие методов численного
интегрирования) и при решении MH. задач успешно сочетается с др. вычислит,
методами и дополняет их. Более специальные математич. вопросы, связанные с С.
и. м., см. в ст. Статистическое моделирование.
обычно получают на ЭВМ с помощью
теоретико-числовых алгоритмов, среди к-рых наибольшее распространение получил
"метод вычетов". Такие числа наз. "псевдослучайными", они
проверяются статистич. тестами и решением типовых задач. Если в расчёте по С.
и. м. моделируются случайные величины, определяемые реальным содержанием
явления, то расчёт представляет собой процесс "прямого
моделирования". Такой расчёт неэффективен, если изучению подлежат редкие
события, т. к. реальный процесс содержит о них мало информации. Эта
неэффективность обычно проявляется в слишком большой величине вероятностной
погрешности (дисперсии) случайных оценок искомых величин. Разработано много
способов уменьшения дисперсии указанных оценок в рамках С. и. м. Почти все они
основаны на модификации моделирования с помощью информации о "функции
ценности" значений случайных величин относительно вычисляемых величин. С.
и. м. оказал и продолжает оказывать существенное влияние на развитие др.
методов вычислительной математики (напр., на развитие методов численного
интегрирования) и при решении MH. задач успешно сочетается с др. вычислит,
методами и дополняет их. Более специальные математич. вопросы, связанные с С.
и. м., см. в ст. Статистическое моделирование.
Лит.: Метод Монте-Карло в проблеме переноса излучений, M., 1967;
Метод статистических испытаний (Метод Монте-Карло), M., 1962; Решение прямых и
некоторых обратных задач атмосферной оптики методом Монте-Карло, Нопосиб.,
1968; E р м е к о в С. M., Метод Монте-Карло и смежные вопросы, M., 1971; M и х
а й л о в Г. А., Некоторые вопросы теории методов Монте-Карло, Новосиб., 1974.
Г.
И. Марчук.
СТАТИСТИЧЕСКИХ РЕШЕНИЙ ТЕОРИЯ, часть математической статистики и
игр теории, позволяющая единым образом охватить такие разнообразные
задачи, как статистическая проверка гипотез, построение статистических
оценок параметров и доверительных границ для них, планирование
эксперимента и др. В основе С. р. т. лежит предположение, что распределение
вероятностей F наблюдаемой случайной величины Xr принадлежит пек-рому
априори данному множеству 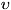 Осн. задача С. р. т. состоит в
отыскании наилучшего статистич. решения или решающего правила (функции) а =
d(x), позволяющего по результатам наблюдении х над X судить
об истинном (но неизвестном) распределении F. Для сравнения достоинств
различных решающих правил вводят в рассмотрение функцию потерь W[F,d(x)], представляющую
убыток от принятия решения d(x) (из заданного множества D), когда
истинное распределение есть F. Естественно было бы считать решающее правило d*
= d*(x) наилучшим, если средний риск r(F,d*) = MFW[F,d(X)]
(MF - усреднение по распределению F) не превышает r(F,d) для
любого Fe g и любого решающего правила d = d(x). Однако такое
"равномерно наилучшее" решающее правило в большинстве задач
отсутствует, в связи с чем наибольший интерес в С. р. т. представляет отыскание
т. н. минимаксных и бейесовских решений. Решение d = d(x) наз.
минимаксным, если
Осн. задача С. р. т. состоит в
отыскании наилучшего статистич. решения или решающего правила (функции) а =
d(x), позволяющего по результатам наблюдении х над X судить
об истинном (но неизвестном) распределении F. Для сравнения достоинств
различных решающих правил вводят в рассмотрение функцию потерь W[F,d(x)], представляющую
убыток от принятия решения d(x) (из заданного множества D), когда
истинное распределение есть F. Естественно было бы считать решающее правило d*
= d*(x) наилучшим, если средний риск r(F,d*) = MFW[F,d(X)]
(MF - усреднение по распределению F) не превышает r(F,d) для
любого Fe g и любого решающего правила d = d(x). Однако такое
"равномерно наилучшее" решающее правило в большинстве задач
отсутствует, в связи с чем наибольший интерес в С. р. т. представляет отыскание
т. н. минимаксных и бейесовских решений. Решение d = d(x) наз.
минимаксным, если
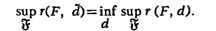
Решение d = а(х)наз. бейесовским (относительно заданного априорного
распределения я на множестве Jf), если для всех решающих правил d
R ( , d) <= R (
, d) <= R ( , d), где
, d), где
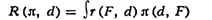
между минимаксными и бейесовскими решениями существует тесная связь,
заключающаяся в том, что в весьма широких предположениях о данных задачи
минимаксное решение является бейесовским относительно "наименее
благоприятного" априорного распределения  .
.
Лит.: Вальд А., Статистические решающие функции, в сб.: Позиционные
игры, M., 1967; Л е м а н Э., Проверка статистических гипотез, пер. с англ.,
M., 1964.
A. H. Ширяев.
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ, численный метод решения математич.
задач, при к-ром искомые величины представляют вероятностными характеристиками
к.-л. случайного явления, это явление моделируется, после чего нужные характеристики
приближённо определяют путём статистической обработки "наблюдений"
модели. Напр., требуется рассчитать потоки тепла в нагреваемой тонкой металлич.
пластине, на краях к-рой поддерживается нулевая темп-pa. Распределение тепла
описывается тем же уравнением, что и расплывание пятна краски в слое жидкости
(см. Теплопроводность, Диффузия). Поэтому моделируют плоское броуновское
движение частиц "краски" по пластине, следя за их положениями в
моменты k , k = 0, 1, 2, ... Приближённо принимают, что за малый
интервал
, k = 0, 1, 2, ... Приближённо принимают, что за малый
интервал  частица перемещается на шаг h равновероятно во всех
направлениях. Каждый раз направление выбирается случайным образом, независимо
от всего предыдущего. Соотношение между
частица перемещается на шаг h равновероятно во всех
направлениях. Каждый раз направление выбирается случайным образом, независимо
от всего предыдущего. Соотношение между 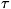 и h определяется
коэффициентом теплопроводности. Движение начинается в источнике тепла и
кончается при первом достижении края (наблюдается налипание "краски"
на край). Поток Q(C) тепла через участок С границы измеряется
количеством налипшей краски. При общем количестве N частиц согласно больших
чисел закону такая оценка даёт случайную относительную ошибку порядка
1/корень N (и система-тич. ошибку порядка h из-за дискретности выбранной
модели).
и h определяется
коэффициентом теплопроводности. Движение начинается в источнике тепла и
кончается при первом достижении края (наблюдается налипание "краски"
на край). Поток Q(C) тепла через участок С границы измеряется
количеством налипшей краски. При общем количестве N частиц согласно больших
чисел закону такая оценка даёт случайную относительную ошибку порядка
1/корень N (и система-тич. ошибку порядка h из-за дискретности выбранной
модели).
Искомую величину представляют математическим ожиданием числовой
функции f от случайного исхода  явления: Ef (
явления: Ef ( )
= интеграл f(
)
= интеграл f( )dP,
)dP, 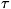 . е. интегралом по вероятностной мере
P (см. Мера множества'). На оценку Ef(
. е. интегралом по вероятностной мере
P (см. Мера множества'). На оценку Ef( ) = [f(
) = [f( 1))
+ +... + f (
1))
+ +... + f ( N)]/N, где
N)]/N, где  1,
...,
1,
...,  N - смоделированные исходы, можно смотреть как на
квадратурную формулу для указанного интеграла со случайными узлами сой и случайной
погрешностью RN. Обычно принимают |RN| <=3 * корень DfIN,
считая большую погрешность пренебрежимо маловероятной; дисперсия Df может
быть оценена в ходе наблюдений (см. Ошибок теория).
N - смоделированные исходы, можно смотреть как на
квадратурную формулу для указанного интеграла со случайными узлами сой и случайной
погрешностью RN. Обычно принимают |RN| <=3 * корень DfIN,
считая большую погрешность пренебрежимо маловероятной; дисперсия Df может
быть оценена в ходе наблюдений (см. Ошибок теория).
В разобранном выше примере f( ) = = 1, когда траектория кончается
на С; иначе f(
) = = 1, когда траектория кончается
на С; иначе f( ) = О. Дисперсия Df = = [1-Q(C)]Q(C) <=
1/4. Интеграл берётся по пространству ломаных со звеньями постоянной длины; он
может быть выражен через кратные интегралы.
) = О. Дисперсия Df = = [1-Q(C)]Q(C) <=
1/4. Интеграл берётся по пространству ломаных со звеньями постоянной длины; он
может быть выражен через кратные интегралы.
Проведение каждого "эксперимента" распадается на две части:
"розыгрыш" случайного исхода  и последующее
вычисление функции f(
и последующее
вычисление функции f( ). Когда пространство всех исходов и вероятностная
мера P слишком сложны, розыгрыш проводится последовательно в несколько
этапов (см. пример). Случайный выбор на каждом этапе проводится с помощью
случайных чисел, напр, генерируемых к.-л. физич. датчиком; употребительна также
их арифметич. имитация - псевдослучайные числа (см. Случайные и
псевдослучайные числа). Аналогичные процедуры случайного выбора
используются в математич. статистике и теории игр.
). Когда пространство всех исходов и вероятностная
мера P слишком сложны, розыгрыш проводится последовательно в несколько
этапов (см. пример). Случайный выбор на каждом этапе проводится с помощью
случайных чисел, напр, генерируемых к.-л. физич. датчиком; употребительна также
их арифметич. имитация - псевдослучайные числа (см. Случайные и
псевдослучайные числа). Аналогичные процедуры случайного выбора
используются в математич. статистике и теории игр.
С. м. широко применяется для решения на ЭВМ интегральных уравнений, напр,
при исследовании больших систем. Они удобны своей универсальностью, как
правило, не требуют большого объёма памяти. Недостаток - большие случайные
погрешности, слишком медленно убывающие при увеличении числа экспериментов.
Поэтому разработаны приёмы преобразования моделей, позволяющие понижать разброс
наблюдаемых величин и объём модельного эксперимента.
Лит.: Метод статистических испытаний (Метод Монте-Карло), M., 1962;
Ермаков С. M., Метод Монте-Карло и смежные вопросы, M., 1971.
H. H. Ченцов.
СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ, см. Выборочное наблюдение, Наблюдение
сплошное.
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ, совокупность способов, употребляемых в математической
статистике для приближённого определения неизвестных распределений
вероятностей (или к.-л. их характеристик) по результатам наблюдений. В наиболее
распространённом случае независимых наблюдений их результаты образуют
последовательность X1, X2, ...,Xn, ... (1) независимых случайных
величин (или векторов), имеющих одно и то же (неизвестное) распределение
вероятностей с функцией распределения F(х). Часто предполагают, что
функция F(х) зависит неизвестным образом от одного или нескольких параметров и
определению подлежат лишь значения самих этих параметров [напр., значительная
часть теории, особенно в многомерном случае, развита в предположении, что
неизвестное распределение является нормальным распределением, у которого
все параметры или к.-л. часть их неизвестны (см. Статистический анализ
многомерный)]. Два осн. вида С. о.- т. н. точечное оценивание и оценивание
с помощью доверительных границ. В первом случае в качестве приближённого
значения для неизвестной характеристики выбирают к.-л. одну функцию от
результатов наблюдений, во втором - указывают интервал значений, с высокой
вероятностью "накрывающий" неизвестное значение этой характеристики.
В более общих случаях интервалы, образуемые доверительными границами
(доверительные интервалы), заменяются более сложными доверительными
множествами.
О С. о. функции распределения F(.r) см. Непараметрические методы в
математич. статистике; о С. о. параметров см. Статистические оценки.
Разработаны также методы С. о. и для случая, когда результаты наблюдений (1)
зависимы, и для случая, когда индекс 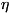 заменяется непрерывно
меняющимся аргументом (, т. е. для случайных процессов. В частности,
широко используется С. о. таких характеристик случайных процессов, как
корреляционная функция и спектральная функция. В связи с задачами регрессионного
анализа был развит новый метод С. о.- стохастическая аппроксимация. При
классификации и сравнении способов С. о. исходят из ряда принципов (таких, как
состоятельность, несмещённость, инвариантность и др.), к-рые в их наиболее общей
форме рассматривают в Статистических решений теории.
заменяется непрерывно
меняющимся аргументом (, т. е. для случайных процессов. В частности,
широко используется С. о. таких характеристик случайных процессов, как
корреляционная функция и спектральная функция. В связи с задачами регрессионного
анализа был развит новый метод С. о.- стохастическая аппроксимация. При
классификации и сравнении способов С. о. исходят из ряда принципов (таких, как
состоятельность, несмещённость, инвариантность и др.), к-рые в их наиболее общей
форме рассматривают в Статистических решений теории.
Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2
изд., M., 1975; Рао С. Р., Линейные статистические методы и их применения, пер.
с англ., M., 1968.
Ю.В.Прохоров.
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ, см. Равновесие статистическое.
СТАТИЧЕСКАЯ БАЛАНСИРОВКА, см. Балансировка.
СТАТИЧЕСКАЯ НАГРУЗКА в строительной механике, нагрузка, величина,
направление и место приложения к-рой изменяются столь незначительно, что при
расчёте сооружения их принимают не зависящими от времени и поэтому пренебрегают
влиянием сил инерции, обусловленных такой нагрузкой. Примеры С. н.- собственно
вес сооружения, снеговая нагрузка и т. п.
СТАТИЧЕСКАЯ СИСТЕМА РЕГУЛИРОВАНИЯ, система автоматич. регулирования,
в к-рой погрешность в установившемся состоянии в общем случае не равна
нулю и зависит от величины нагрузки на объект. На рис. 1 представлена схема
одноконтурной С. с. р., состоящей из объекта регулирования и устройства
управления, куда входят измерительный преобразователь, регулятор и исполнительный
механизм.
Рис. 1. Функциональная схема одноконтурной статической системы
регулирования: OP - объект регулирования; УУ - устройство управления; ИП -
первичный измерительный преобразователь (датчик); CP - статический регулятор;
БЗР - блок формирования закона регулирования; ИМ - исполнительный механизм.
На объект регулирования действуют управляющее воздействие xi(t) и
внешние возмущения f(t). Регулируемая величина объекта регулирования x(t)
преобразуется измерит, преобразователем в сигнал x*(t), к-рый
подаётся на регулятор, где сравнивается с заданным значением управляющего
воздействия g(t), в результате чего образуется сигнал
рассогласования  (t) = g(t) - - x *(t). Далее в регуляторе
задаётся зависимость между
(t) = g(t) - - x *(t). Далее в регуляторе
задаётся зависимость между  (t) и управляющей величиной регулятора x1(t)-
формируется закон регулирования. Для статич. пропорционального регулятора x1
= kp ·
(t) и управляющей величиной регулятора x1(t)-
формируется закон регулирования. Для статич. пропорционального регулятора x1
= kp · , где kp - коэфф. передачи
(усиления) регулятора.
, где kp - коэфф. передачи
(усиления) регулятора.
Как правило, статич. регуляторы относительно просты, экономичны,
малоинерционны, поэтому их целесообразно использовать в системах автоматич.
регулирования пром. установок. На рис. 2 изображена простейшая С. с. р. уровня
жидкости в сосуде. В случае, напр., увеличения расхода жидкости уровень её в
сосуде понижается, изменяется положение поплавка и задвижка поднимается,
увеличивая приток жидкости. Установившееся состояние наступает тогда, когда
расход жидкости равен притоку, что соответствует нек-рому уровню, отличному от
первоначального.
Рис. 2. Простейшая статическая система регулирования: T1 -
входная труба; З - задвижка; P - рычажная система; П - поплавок; С - сосуд с
жидкостью; T2- выходная труба.
Лит. см. при ст. Регулирование автоматическое. А. В. Кочеров.
СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ СИСТЕМА в строительной механике,
геометрически неизменяемая система (конструкций), в к-рой реакции связей
(усилия в опорных закреплениях, стержнях и т. п.) не могут быть определены с
помощью одних ур-ний статики (см. Строительная механика), а требуется
совместное рассмотрение последних с дополнит, ур-ниями, характеризующими
деформации системы. Необходимый и достаточный признак С. н. с.-наличие т. н.
лишних (избыточных) связей, к-рые можно удалить, не нарушая геометрич.
неизменяемости системы. Число дополнит, ур-ний, равное числу лишних связей
(лишних неизвестных), наз. степенью статич. неопределимости системы.
В элементах С. н. с. (в отличие от статически определимых) могут возникать
усилия, вызванные осадкой опор, темп-рными воздействиями, усадкой материала,
неточностью сборки или изготовления и т. п. Распределение усилий в С. н. с.
зависит не только от нагрузки, но и от соотношения поперечных размеров отд.
элементов, а если эти элементы изготовлены из различных материалов, то и от
соотношения их модулей упругости. Если в статически определимых системах
разрушение хотя бы одной связи приводит к выходу из строя всего сооружения, то
С. н. с. после потери одной или даже всех лишних связей сохраняют свою несущую
способность (геометрич. неизменяемость). В этом смысле С. н. с. более надёжны,
чем статически определимые.
Осн. методы расчёта С. н. с.- метод сил и метод перемещений, в к-рых за
исходные (лишние) неизвестные принимаются соответственно усилия или
перемещения. Метод, основанный на выборе одной части неизвестных в виде усилий,
а другой - в виде перемещений, наз. смешанным. Гл. трудность при расчёте С. н.
с. с высокой степенью статич. неопределимости заключается в необходимости
составления и решения систем ур-ний с большим числом неизвестных; применение
ЭВМ даёт возможность полностью автоматизировать трудоёмкий процесс расчёта.
Лит.: Расчёт сооружений с применением вычислительных машин, M., 1964;
Киселев В. А., Строительная механика, 2 изд. M., 1969. Г. Ш. Подольский
СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ СИСТЕМА в строительной механике, система
конструкций, в к-рой реакции всех связей (усилия в опорных закреплениях,
стержнях и т. п.) при любой нагрузке могут быть определены с помощью ур-ний
статики (см. Строительная механика). С. о. с. содержит только те связи,
к-рые необходимы для обеспечения её геометрич. неизменяемости. В отличие от статически
неопределимых систем в С. о. с. осадка опор, температурные воздействия,
неточности сборки или изготовления и т. п. не влияют на распределение и
величину усилий; последние не зависят также от физико-механич. характеристик
материала и поперечных размеров элементов системы.
СТАТОБЛАСТЫ (от греч. statos - стоящий, неподвижный и blastos -
зародыш, росток), покоящиеся зимние почки у пресноводных беспозвоночных
животных - мшанок, С. развиваются внутри брыжейки желудка (т. н.
канатика) и являются внутренними почками, в отличие от наружных, за счёт к-рых
образуются колонии. С. имеет плотную наружную оболочку, иногда с
крючкоподобными выростами. С. обычно чечевицеобразной формы. При отмирании
осенью материнского организма С. выпадают из его тела и благодаря имеющимся у
них воздушным камерам плавают в толще воды. !Весной оболочка С. лопается, и из
него выходит молодая мшанка - родоначальница новой колонии.
СТАТОЛИТЫ (от греч. statos - стоящий и Hthos - камень), 1) то же, что
отолиты. 2) Мелкие подвижные крахмальные зёрна, находящиеся в клетках чехлика
корня, верхушек колеоптилей злаков и др. растущих частях растений; при
изменении направления оси органа они опускаются книзу и, оказывая давление на
цитоплазму, вызывают геотропич. изгиб органа. С. расходуются растением при
сильном голодании, напр, при продолжит, затемнении. Клетки, в к-рых имеются С.,
наз. статоцистами.
СТАТОР (англ, stator, от лат. sto - стою) электромашины, неподвижная
часть электрнч. машины, выполняющая функции магнитопровода н несущей
конструкции. С. состоит из сердечника и станины. Сердечник изготовляют из
изолированных лаком листов электротехнич. стали (толщиной 0,35-0,5 мм), собираемых
в пакеты и укрепляемых в литом или сварном корпусе - станине. В пазы,
выштампованные в сердечнике, укладывается статорная обмотка. Во избежание
значит, вихревых токов (и, соответственно, потерь) проводник обмотки С.
составляют из ряда параллельно соединённых изолированных жил, к-рые в машинах
большой мощности сплетают (транспонируют). В линейных двигателях сердечник
статора развёрнут в линию.
Лит.: К о с т е н к о M. П., Пиотровский Л. M., Электрические машины,
3 изд., ч. 1-2, Л., 1972-73.
СТАТОР ГИДРОТУРБИНЫ, фундаментная часть гидротурбины, предназначенная
для передачи нагрузки от массы гидроагрегата и давления воды на здание ГЭС. С.
г. устанавливается внутри спиральной камеры гидротурбины. С. г. с
бетонной спиральной камерой выполняется из отд. колонн с фланцами в торцах для
укрепления (бетонирования) в выходной части камеры. Колонны С. г. профилируются
так, чтобы поток из камеры, проходя через статор, не менял своей крутки
(отношения тангенциальной составляющей скорости к меридиональной). С. г. со
стальной спиральной камерой имеет верхний и нижний пояса, к к-рым жёстко
крепятся установленные в его проточной части колонны. Нижний пояс С. г.
бетонируется. Для крупных турбин С. г. обычно выполняются сварными.
СТАТОРЕЦЕПТОРЫ (от греч. statos - стоящий, неподвижный и рецепторы),
специализированные чувствительные нервные окончания - рецепторы,
реагирующие на изменение положения тела в пространстве. У низших беспозвоночных
С. расположены в слуховых пузырьках, или статоцистах (см. Равновесия
органы). У рыб и нек-рых земноводных С. располагаются в органах боковой
линии (см. Боковые органы). У позвоночных животных и человека функцию С.
выполняют вестибулярный аппарат и зрения органы, экстерорецепторы
кожных покровов, проприорецепторы мышц, сухожилий, суставов и связок.
СТАТОСКОП (от греч. statos - стоящий 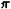 skopeo - смотрю), прибор
дтя регистрации изменений высоты полета летательного аппарата по измеряемой
разности атмосферного давления и давления внутри прибора. Предназначен гл. обр.
для аэрофотосъёмки при создании карт. Наибольшее применение имеет С. в
виде жидкостного дифференциального барометра, состоящего из 2 одинаковых
автоматически переключающихся манометрич. систем. По фиксируемому различию в
уровнях спирта в манометрич. трубках, давлению и температуре воздуха на высоте
полёта вычисляют барометрич. высоты точек фотографирования и их изменения с
точностью порядка 0,5-1,0 м.
skopeo - смотрю), прибор
дтя регистрации изменений высоты полета летательного аппарата по измеряемой
разности атмосферного давления и давления внутри прибора. Предназначен гл. обр.
для аэрофотосъёмки при создании карт. Наибольшее применение имеет С. в
виде жидкостного дифференциального барометра, состоящего из 2 одинаковых
автоматически переключающихся манометрич. систем. По фиксируемому различию в
уровнях спирта в манометрич. трубках, давлению и температуре воздуха на высоте
полёта вычисляют барометрич. высоты точек фотографирования и их изменения с
точностью порядка 0,5-1,0 м.
Лит.: Аржанов Е.П., ИльинВ.Б., Аэрофотосъёмочное оборудование, M.,
1972.
СТАТОЦИСТЫ (от греч. status - стоящий и kystis - пузырь), 1) слуховые
пузырьки, органы равновесия беспозвоночных, имеющие вид ямки или погружённого
под наружный покров тела пузырька, а также колбообразного выпячивания покрова
(у медуз и мор. ежей). Внутри С. находится одно или неск. твёрдых образований -
статолитов, или отолитов. При изменении положения тела отолиты
перемещаются, раздражая чувствит. клетки С. От них нервный импульс передаётся
по нервным волокнам в центр, нервную систему, вызывая ответную реакцию
организма, ведущую к восстановлению равновесия. См. также Равновесия органы.
2) Клетки растений, в к-рых образуются мелкие подвижные крахмальные зёрна,-
статолиты. С. находятся в чехлике корня, верхушках колеоптилей злаков и
в др. растущих частях растений.
СТАТСКИЙ СОВЕТНИК в России, гражд. чин 5-го класса по Табели о
рангах, соответствовал должности вице-директора департамента, вице-губернатора,
председателя казённой палаты и др. С 1856 давал право на личное дворянство,
ранее - на потомственное. Титуловался "ваше высокородие". Для
производства в чин С. с. был установлен срок службы в 5 лет со времени
получения предыдущего чина. Действительный С. с.- гражд. чин 4-го класса,
соответствовал должности директора департамента, губернатора и градоначальника,
давал право на потомственное дворянство. Титуловался "ваше
превосходительство". Для производства в чин действительного С. с. был
установлен срок службы в 10 лет со времени получения предыдущего чина. В 1903
было 3113 действительных С. с. Чин С. с. упразднен декретом Сов. власти 10(23)
нояб. 1917 об уничтожении сословий и чинов (см. Чиновничество).
СТАТС-СЕКРЕТАРЬ (нем. Staatssekretar,
англ. Secretary of
State, франц. Secretaire
d'État), 1) в Герм, империи (1871-1918) - имперский министр, непосредственно
подчинённый рейхсканцлеру; 2) в ФРГ и нек-рых др. странах - высшее должностное
лицо в аппарате министерства, ближайший помощник министра, в т. ч. по
поддержанию контактов пр-ва с парламентом, его фракциями и комитетами
(парламентский С.-с.); 3) официальный титул нек-рых министров (в
Великобритании, США) или руководителей ведомств при премьер-министре (во
Франции); 4) в ГДР - должностное лицо в ранге первого зам. министра или главы
спец. правительств, ведомства (секретариата); 5) в Венгрии - руководитель
общегос. органа (напр., Венгерского нац. банка, Центр, статистич. управления),
подчинённого Совету Министров (в отличие от министра, С.-с. не входит в состав
пр-ва).
СТАТУС (от лат. status - состояние, положение), правовое положение
гражданина либо юридич. лица. См. также в ст. Субъект права.
СТАТУС социальный, соотносительное положение (позиция) индивида или
группы в социальной системе, определяемое по ряду признаков, специфичных для
данной системы (экономических, профессиональных, этнических и др.). Люди,
обладающие одним и тем же С., обнаруживают ряд сходных личностных черт,
обозначаемых как "социальный тип" личности. В зависимости от того,
занимает ли человек данную позицию благодаря наследуемым признакам (раса,
социальное происхождение и т. п.) или благодаря собств. усилиям (образование,
заслуги), различаются соответственно "предписанный" и
"достигаемый" С. Каждый С. может сравниваться с другим по тому или
иному признаку, соотносимому с господствующей системой ценностей, приобретая
таким образом определ. социальный престиж.
Бурж. социологи, исследуя проблему С., опираются в значит, мере на теорию M.
Вебера, к-рый, противопоставляя свои взгляды историч. материализму,
утверждал, что стратификация общества определяется не только экономическими
(доступ к обществ, богатству) и политическими (власть, право), но и социальными
(престиж) показателями. По Веберу, С. (он употреблял термин Stand, к-рый
обозначает не только положение вообще, но и сословие) - это общность
людей, основанная на специфич. стиле жизни, включающем набор привычек,
ценностей, верований, представлений о чести и др. психологич. моменты. Каждому
стилю жизни соответствует более или менее высокая оценка (почёт), и люди,
добиваясь такой оценки, усваивают определ. нормы и представления. Так,
разбогатевший буржуа стремится копировать стиль жизни аристократии, и его дети
могут усвоить презрит, отношение к экономич. предпринимательству. В бурж.
социологии предпринимаются попытки эмпирически установить совокупность
объективных свойств (пол, возраст, этнич. принадлежность, образование, род
занятия, собственность и др.), на основе к-рой возникают статусные группы с
определ. "стилем жизни". Подобные концепции С. игнорируют классовые
отношения как реальную основу С., социальных различий.
Понятие С. применяется также в качестве соотносительного с понятием роли
социальной', С. обозначает совокупность прав и обязанностей, а роль -
дпнамич. аспект С., т. е. определ. поведение. В бурж. социологии и социальной
психологии это значение понятия С. психологизируется, т. к. сводится по
существу к представлениям индивида о собств. позиции или представлениям других
о его позиции.
Марксистско-ленинское учение о классах позволяет исследовать членение
общества на различные классы, социальные группы и слои, определять
фундаментальные основы С. людей. В социалистич. обществе, где отсутствуют
антагонистич. классы, наиболее существ, признаками С. отд. групп являются
профессия, квалификация (образование) и, следовательно, заработная плата, а
также семейно-возрастные и локально-территориальные различия. С. человека тем
выше, чем полезнее для общества его деятельность, чем больше его трудовые
усилия и заслуги.
Лит.: Ленин В. И., Что такое "друзья народа" и как они
воюют против социал-демократов?, Полн. собр. соч., 5 изд., т. 1; Социология в
СССР, т. 1-2, M., 1965; Человек и его работа, M., 1967: Кон И. С., Социология
личности, M., 1967; Щ е п а н ь с к и й Я., Элементарные понятия социологии, пер.
с польск., M., 1969; Социальные проблемы труда и производства, M-, 1969; А и т
о в H. А., Технический прогресс и движение рабочих кадров, M., 1972; Гордон Л.
А., К л о п о в Э. В., Человек после работы, M., 1972; Linton R., The study
of man, N. Y.-L., 1936; Parsons T., The social system, [2 ed.], Glencoe, 1952.
Cм. также лит. при ст. Классы, Социальная стратификация, Социальный престиж.
В. Б. Ольшанский.
СТАТУС-КВО (лат. status quo, букв.- положение, в к-ром), в междунар.
праве термин, применяемый для обозначения к.-л. существующего или
существовавшего на определ. момент фактич. или правового положения, о
восстановлении или сохранении к-рого идёт речь. В междунар. правовой практике
употребляется также термин "status quo ante bellum" - положение,
существовавшее перед началом войны.
СТАТУТ (позднелат. statutum, от лат. statuo - постановляю, решаю), 1)
положение, устав, определяющий порядок организации и деятельности отд.
внутригос. и междунар. орг-ций, напр. Статут Международного суда ООН (1945).
2) Уставы, фиксировавшие правовое положение ср.-век. городов и внутригор.
объединений (цехи, купеч. гильдии и др.). Гор. С.- записи гор. привилегий,
регулировавших внутр. орг-цию городов и их отношения с сеньорами. Цеховые С.
(иногда наз. цеховыми уставами) - основанные на обычном праве своды правил,
регламентировавших деятельность цехов; ценный ист. источник. 3) Положение о
чём-либо, напр. С. ордена, определяющий порядок награждения данным
орденом, его описание. 4) Некоторые законодат. акты парламента в
Великобритании, напр. Вестминстерский статут 1931; в США - нек-рые акты
конгресса.
СТАТУТЫ О РАБОЧИХ, Рабочее законодательство, законы и постановления,
устанавливавшие уровень зарплаты наёмных рабочих, продолжительность рабочего
дня и т. д.; действовали в ряде стран Европы в 14-19 вв. Первый С. о р. (1349)
был издан в Англии после стихийного повышения зарплаты, связанного с нехваткой
рабочих рук после чумы 1348-49; под страхом тюрьмы предписывал всем людям в
возрасте от 12 до 60 лет, не имеющим собственной земли и др. средств к жизни,
наниматься на работу за плату, принятую до чумы. Целью С. о р. было обеспечить
феодалов и гор. верхушку с помощью внеэкономич. принуждения дешёвой рабочей
силой. С переходом к пром. капитализму действие С. о р. прекратилось. В
Великобритании были официально отменены в 1813.
Лит.: Маркс К., Капитал, т. 1, Маркс К. и Энгельс Ф., Соч., 2 изд., т.
23, с. 280-82, 748-50; Роджерс Т., История труда и заработной платы в Англии с
XIII по XIX век, пер. с англ., СПБ, 1899.
СТАТУЯ (лат. statua), один из основных видов скульптуры, скульптурное
изображение человеческой фигуры или
животного (реже к.-л. фантастич. существа), обычно помещённое на постамент. T.
н. конная С. изображает всадника верхом. Небольшие С., служащие для украшения
интерьеров, называются статуэтками.
СТАТХАУДЕР, стадхаудер (голл. stadhouder, от stad - место, город и
houder - обладатель, держатель), наместник (штатгальтер) государя из
Бургундской, а затем Габсбургской династий в Нидерландах в 15-16 вв.; после
Нидерландекой бурж. революции 16 в.- глава исполнит, власти в республике
Соединённых провинций (до кон. 18 в )
СТАТЬИ КОНФЕДЕРАЦИИ (Thearticles of Confederation), первая
конституция США. Принята в нояб. 1777, вступила в силу в 1781, действовала до
1789. С. к. закрепили революц. завоевания, достигнутые в ходе Войны за
независимость в Северной Америке 1775-83, и определили респ. форму гос.
устройства б. англ, колоний в Сев. Америке, провозгласив образование
конфедерации и вечный союз штатов.
СТАТЬЯ, 1) один из основных жанров журналистики. Общие отличит,
признаки С.: осмысление и анализ значит, явления (или группы явлений),
аргументированные обобщения и выводы, подтверждающие выдвинутую концепцию,
идею. В зависимости от целевого назначения С. могут быть пропагандистскими,
проблемными, критическими, научными и т. д. В практике парт.-сов. печати
сложились, кроме того, особые виды С.- директивные (см. Передовая статья), С.,
обобщающие передовой опыт, и др. 2) Раздел офиц. юридич. акта, документа
(напр., С. закона, С. междунар. договора).
Лит.: Жанры советской газеты, M., 1972.
СТАУНИНГ (Stauning) Торвальд (26.10. 1873, Копенгаген, - 3.5.1942, там
же), датский политический и гос. деятель. С 1896 член, в 1910-42 пред. С.-д.
партии Данин (СДПД). В 1905-42 деп. ригсдага от СДПД, в 1910-29 (исключая
1924-26) пред, фракции СДПД в ригсдаге. В 1913, 1916-18, 1920 входил в пр-во. В
годы 1-й мировой войны 1914-18 выступал как социал-шовинист (см. В. И. Ленин,
Полн. собр. соч., т. 30, с. 193-95). В 1924-26, 1929-40, 1940-42
премьер-министр. При пр-ве С. были установлены дипломатич. отношения Дании с
Сов. Союзом (1924), проведён ряд социальных реформ (в 30-е гг.), предоставлены в
то же время значит. экономич. выгоды агр. буржуазии. После оккупации Дании
фаш. Германией (апр. 1940) С.- активный сторонник сотрудничества с
гитлеровцами.
СТАФИЛИНЫ (Staphylinidae), коротконадкрылы, семейство жуков. Тело
обычно узкое, удлинённое (1,5-40 мм); надкрылья короткие, не покрывают
3-5 сегментов брюшка; голова, грудь и брюшко подвижно сочленены между собой.
Личинки С. подвижные, с хорошо развитыми ногами. Более 30 тыс. видов;
распространены широко, в СССР - св. 2 тыс. видов. С., ведут скрытный образ
жизни - под камнями, в лесной подстилке, под корой, в грибах, в гнёздах
млекопитающих и птиц, муравейниках, нередко в навозе и на падали; личинки - там
же или в почве. Большинство С.- хищники, питающиеся насекомыми, их
личинками, мелкими клещами и т. п., или сапрофаги; немногие растительноядны;
отдельные виды - второстепенные вредители с.-х. культур. С. рода Paederus
содержат в крови ядовитые вещества и при раздавливании на коже человека
вызывают местное воспаление.
СТАФИЛОКОККИ (от греч. staphyle - виноградная гроздь и кокки) (Staphylococcus),
род шаровидных бактерий; клетки С. (диам. 0,6-0,8 мкм) спор не образуют,
грамположительны, неподвижны. Размножаются делением в разл. плоскостях;
образующиеся новые клетки остаются соединёнными друг с другом и образуют скопления,
похожие на гроздь винограда, но могут располагаться также поодиночке и попарно.
С. хорошо растут на мясопептонном агаре, картофеле и др. Отдельные виды С.
могут сбражнвать разл. углеводы и спирты с образованием кислот. С. могут
образовывать ряд токсич. продуктов: гемолизнн - растворяющий эритроциты
человека, лейкоцитин - растворяющий лейкоциты, фпбринолизин - растворяющий
сгустки фибрина. С. патогенны, т. к. вызывают нагноение ран, абсцессы,
фурункулы, ангины, воспалительные заболевания кожи, ссптич. состояния;
золотистые С., образующие энтеротоксин, могут быть причиной тяжёлых пищевых
отравлений. Выделяют С. из гноя, с поверхности здоровой кожи и слизистых
оболочек, из комнатной пыли.
А. А. Имшенецкий.
СТАФИЛОКОККОВ КРОЛИКОВ, инфекционная болезнь, характеризующаяся
образованием локальных гнойных очагов, сепсисом и вызываемая стафилококками.
Источник возбудителя инфекции - больные кролики. Заражение происходит при
повреждении кожи и слизистых оболочек. С. к. проявляется в форме пиодермии (у
новорождённых крольчат), абсцессов, гнойного мастита, пододерматита, септицемии
или септикопиемни. Диагноз ставят на основании клинич. признаков и
бактериологпч. исследований. Лечение - антибиотики и др. апимикробные
средства. Профилактика и меры борьбы: систематич. клинич. осмотр животных,
выбраковка, убой или изоляция больных, дезинфекция помещений, соблюдение сан.
условий содержания животных.
Лит.: Болезни кроликов, 2 изд., M., 1974.
В. С. Слугин.
СТАФИЛОКОККОЗ ПТИЦ, микрокок к о з птиц, инфекционная болезнь всех
видов птиц, вызываемая стафилококками. С. п. регистрируется во мн. странах
мира. Источник возбудителя инфекции - больные птицы; факторы передачи - корм,
подстилка, вода. Болезнь может передаваться трансовариально (через яйцо). При
остром течении С. п. у кур - понос, угнетение, воспаление суставов, птицы
погибают на 2-6-е сут; для хронич. течения характерны хромота, потеря
аппетита, сильная жажда, прекращение яйцекладки; птицы погибают через 10-14 сут.
У цыплят возможны дерматиты. У индеек С. п. протекает в виде септицемии,
воспаления суставов и сухожилий, у уток и гусей - оститов, тен довагинитов,
паралича конечностей. Диагноз ставят на основании бактериологич. исследования.
Лечение - антибиотики. Профилактика и меры борьбы: соблюдение вет.-сан. правил
при заготовке яиц и суточных цыплят, при инкубации; убой больных и
подозрительных по заболеванию птиц, дезинфекция помещений.
Лит.: Бессарабов Б. Ф., Стафилококкоз птиц, в кн.: Болезни
сельскохозяйственных птиц, M., 1970.
Б. Ф. Бессарабов.
СТАФФ (Staff) Леопольд (14.11.1878, Львов, - 31.5.1957, Скаржиско-Каменна), польский поэт. Окончил Львовский ун-т (1901). В первом сб.
"Сны о могуществе" (1901), следуя символистским исканиям "Молодой
Польши", С. выступил в то же время против декаданса. Сб-кам "Цветущая
ветвь" (1908), "Улыбки мгновений" (1910), "В тени
меча" (1911) свойственны ориентация на классицистич. традиции, интерес к
культуре античности и Возрождения, воспевание вечных этич. и эстетич.
ценностей, совершенство стиха. В годы 1-й мировой войны 1914-18 жил в Харькове,
где написал сб. гражд. лирики "Радуга слез и крови" (1918). В сб-ках
"Высокие деревья" (1931), "Цвет мёда" (1936) С., воспевая
природу, вместе с тем развенчивает обществ, систему 30-х гг. Трагизм фаш. оккупации
отразился в сб. "Мёртвая погода" (1946). Послевоенную лирику С.
отличает стремление к простоте, непосредственности поэтич. выражения
общечеловеческих чувств ("Лозина", 1954; "Девять муз",
1958). Переводчик Микеланджело, И. В. Гёте, P. Роллана и др. Вице-президент
Польской академии лит-ры (1934-39). Гос. пр. ПНР (1927, 1937, 1951).
Соч.: Wiersze zebrane, t. 1 - 5, Warsz., 1955: в рус. пер.- Стихи, M., 1973.
Лит.: БогомоловаН.А., Л. Стафф, в кн.: История польской литературы,
т. 2, M., 1969; Б р и т а н и ш с к и и В., Классик неоклассического века,
"Вопросы литературы", 1972, № 9; M а с i e j e w s k a I., L. Staff. Lwcwski okres tworczosci, Warsz.,
1965; её же, L. Staff. Warszawski okres
tworczosci, Warsz., 1973. K w a t k о ws k i J., U podstaw liryki L. Staffa, Warsz.,
1966.
H. А. Богомолова.
СТАФФАЖ (нем. Staffage, от staffieren - украшать картины фигурами),
фигуры людей и животных, изображаемые в произведениях пейзажной живописи для
оживления вида н имеющие второстепенное значение. С. получил распространение в
16-17 вв., когда пейзажисты часто включали в свои произведения религ. и
мифологич. сцены. Нередко С. вписывался в картины не автором пейзажа, а другим
художником.
СТАФФОРД (Stafford) Томас (р. 17.9. 1930, Уэтерфорд, шт. Оклахома),
лётчик-космонавт США, бригадный генерал ВВС. По окончании Воен.-мор. академии
США (1952) получил степень бакалавра наук. Служил в ВВС, летал на
истребителях-перехватчиках. В 1959, окончив школу лётчиков-испытателей на
авиац. базе Эдуарде (шт. Калифорния), стал одним из руководителей школы по подготовке
пилотов для аэрокосмич. исследований на этой же базе. Один из авторов
"Справочника пилота по лётным испытаниям характеристик летательных
аппаратов" и "Аэродинамического справочника по лётным испытаниям
характеристик летательных аппаратов". С 1962 в группе космонавтов Нац.
управления по аэронавтике и исследованию космич. пространства США. Совм. с У. Ширра
15-16 дек. 1965 осуществил полёт в космос на космич. корабле
"Джемини-6" (2-й пилот). Полёт продолжался 25 ч 51 мин (17
витков вокруг Земли). Совм. с Ю. Сернаном 3-6 июня 1966 совершил полёт в
качестве командира космич. корабля "Джемини-9". За 72 ч 21 мин
корабль сделал 45 оборотов вокруг Земли, пролетев более 1,8 млн. км. Во
время полёта было осуществлено сближение корабля "Джемини-9" с
ракетой-мишенью. Совм. с Дж. Янгом и Ю. Сернаном 18-26 мая 1969 совершил
в качестве командира космич. корабля "Аполлон-10" облёт Луны с
выходом 21 мая на орбиту искусств, спутника Луны (ИСЛ). В отделившейся от
космич. корабля лунной кабине С. с Сернаном приблизились на 15 км к
поверхности Луны, затем орбита была изменена. После 8 ч полёта лунная
кабина состыковалась с космич. кораблём на орбите ИСЛ (общее время пребывания
на орбите ИСЛ 61 ч 40 мин), и был пройден обратный путь к Земле. В
полёте выполнялась отработка систем космич. корабля и велись науч. наблюдения.
Полёт продолжался 192 ч 3 мин. 15-25 июля 1975 совм. с Д. Слейтоном
и В. Брандом совершил полёт в космос по программе ЭПАС в качестве
командира космич. корабля "Аполлон". В полёте, длившемся 217 ч 28
мин, дважды была совершена стыковка с сов. космич. кораблём
"Союз-19" и выполнено неск. науч.-технич. экспериментов. За 4 рейса в
космос налетал 517 ч 43 мин. С 1975 нач. авиац. базы Эдуарде.
Г.Л. Назаров.
СТАФФОРД (Stafford) Уильям (1.3. 1554, Рочфорд,
Эссекс, - 16.11.1612, Лондон), английский экономист, представитель раннего меркантилизма.
Предполагаемый автор (авторство оспаривается) памфлета "Краткое
изложение некоторых обычных жалоб различных наших соотечественников",
опубл. в 1581 под инициалами W. S. По мнению автора памфлета, написанного с
позиций защиты активного регулирования денежного обращения, фальсификация денег
и их отлив за границу вызывают рост цен и ухудшают материальное положение
народа. Решение экономич. проблем С. видел в запрещении вывоза золота и
серебра, в регламентации торговли с целью ограничения импорта. Выступая за
развитие отечеств, пром-сти, он полагал, что это приведёт к уменьшению
зависимости от импорта и тем самым к улучшению ден. баланса страны.
А. А.
Хандруев.
СТАФФОРД (Stafford), город (адм. округ) в Великобритании, в графстве
Стаффордшир, на р. Трент. 113,2 тыс. жит. (1973). Ж.-д. узел. Центр
электротехнической пром-сти. В 18-19 вв. С. был одним из важнейших центров
англ, нар. иск-ва. Здесь изготовлялись (из каменной массы) покрытые соляной
глазурью "стаффордширские фигурки" (животные, птицы, солдаты, моряки,
герои нар. легенд и целые сценки - бытовые, религ. или связанные с к.-л.
политич. событием). Для произв. 19 в. характерно широкое использование гипсовых
форм и надглазурной росписи. Илл. см. также т. 17, табл. XXII
"Стаффордширокая фигурка" из каменной массы с соляной глазурью.
Конец 18 в. Музей Виктории и Альберта. Лондон.
СТАФФОРДШИР (Staffordshire), графство в Великобритании, в басе. р.
Трент, частью на равнине Мидленд, частью в предгорьях Пеннин. Пл. 3 тыс. км2.
Нас. 984,6 тыс. чел. (1973). Главный город - Стаффорд.
СТАХАНОВ Алексей Григорьевич [р. 21.12.1905 (3.1.1906), дер. Луговая
Орловской губ.], новатор угольной пром-сти, Герой Социалистического Труда
(1970). Чл. КПСС с 1936. В 1927 С. начал работать на шахте "Центральная -
Ирмино" в Кадиевке (Донбасс) тормозным, затем коногоном, отбойщиком, с
1933 - забойщиком на отбойном молотке. В 1935 окончил на шахте курсы
забойщиков. В ночь с 30 на 31 авг. 1935 С. установил рекорд, добыв за смену (5 ч
45 мин) 102 m угля, что соответствовало 14 нормам. Такой высокой
производительности труда С. достиг благодаря овладению техникой и разделению
труда забойщика и крепильщика. Это позволило ему одному произвести отбойку угля
в нескольких уступах. 19 сент. 1935 С. установил новый рекорд, дав 227 га угля
в смену. Трудовой подвиг С. встретил горячий отклик в Донбассе, а затем по всей
стране, вылившись в Стахановское движение. В 1936-41 учился в
Промакадемии в Москве. В 1941-42 начальник шахты № 31 в Караганде. В 1943-57
работал в Мин-ве угольной пром-сти СССР. В 1957-59 заместитель управляющего
трестом "Чистяковантрацит", с 1959 помощник гл. инженера
шахтоуправления № 2/43 треста "Торезантрацит"; с 1974 С. на пенсии.
Деп. Верх. Совета СССР 1-го созыва. Награждён 2 орденами Ленина, орденом
Трудового Красного Знамени и медалями.
Соч.: Рассказ о моей жизни, [M.], 1938; Шахтёры. M., 1938 (совм. с В.
Хмара); Возродим родной Донбасс, [M.], 1944.
T. Стаффорд.
СТАХАНОВСКОЕ ДВИЖЕНИЕ, массовое движение новаторов социалистич.
производства в СССР - передовых рабочих, колхозников, инженерно-технич.
работников за повышение производительности труда на базе освоения новой
техники. Возникло во 2-й пятилетке, в 1935, как новый этап социалистического
соревнования. С. д. было подготовлено всем ходом социалистич.
строительства, успехами индустриализации страны, ростом культурно-технич.
уровня и материального благосостояния трудящихся. Большинство стахановцев вышло
из числа ударников (см. Ударничество). "Стахановским" движение
названо по имени его зачинателя - забойщика шахты "Центральная -
Ирмино" (Донбасс) А. Г. Стаханова, добывшего за смену 102 т угля
при норме 7 т. Рекорд Стаханова был вскоре перекрыт его последователями.
Наибольшей выработки в Донбассе достиг H. А. Изотов, добывший 1 февр.
1936 на шахте № 1 "Кочегарка" (Горловка) 607 т угля за смену. С. д.,
поддержанное и возглавленное Коммунистич. партией, за короткое время охватило
все отрасли пром-сти, транспорт, стр-во, с. х-во и распространилось по всему
Сов. Союзу. Зачинателями С. д. были в автомоб. пром-сти A. X. Бусыгин, в
обувной - H. С. Сметанин, в текст. - E. В. и M. И. Виноградовы, в
станкостроит. - И. И. Гудов, в лесной - В. С. Мусинский, на ж.-д. транспорте -
П. Ф. Кривонос, в с. х-ве - П. H. Ангелина, К. А. Борин, M. С. Демченко
и др. 14-17 нояб. 1935 состоялось Первое Всесоюзное совещание стахановцев в
Кремле, к-рое подчеркнуло выдающуюся роль С. д. в социалистич. строительстве. В
дек. 1935 пленум ЦК ВКП(б) специально обсуждал вопросы развития пром-сти и
транспорта в связи со С. д.
В резолюции пленума подчёркнуто: "Стахановское движение означает
организацию труда по-новому, рационализацию технологических процессов,
правильное разделение труда в производстве, освобождение квалифицированных
рабочих от второстепенной подготовительной работы, лучшую организацию рабочего
места, обеспечение быстрого роста производительности труда, обеспечение
значительного роста заработной платы рабочих и служащих" ("КПСС в
резолюциях...", 8 изд., т. 5, 1971, с. 232).
В соответствии с решениями Декабрьского пленума ЦК ВКП(б) была организована
широкая сеть производств.-технич. обучения, для передовиков созданы курсы
мастеров социалнстич. труда. Состоявшиеся в 1936 отраслевые производств.-технич.
конференции пересмотрели проектные мощности предприятий, были повышены нормы
выработки. В 1936 проводились стахановские пятидневки, декады, месячники в
масштабе целых предприятий. Создавались стахановские бригады, участки, цехи,
достигавшие устойчивой высокой коллективной выработки.
Развернувшееся С. д. способствовало значит, росту производительности труда.
Так, если за годы 1-й пятилетки (1929-32) производительность труда в пром-сти
СССР выросла на 41%, то за годы 2-й пятилетки (1933-37) на 82%. С новой силон
творческая инициатива новаторов проявилась в годы Великой Отечественной войны
1941-45. Использовались такие стахановские методы, как многостаночное
обслуживание, совмещение профессий, скоростная технология производства и
строительства. Стахановцам принадлежала инициатива движения
"двухсотников" (две нормы и более за смену), а затем
"тысячников" (1000% нормы), создания "фронтовых бригад".
Опыт С. д. сохранил своё значение и в послевоенный период, когда в условиях
непрерывного роста экономики и культуры возникли новые формы социалистич.
соревнования. Характерное для развитого социалистич. общества в СССР движение
за коммунистич. отношение к труду (см. Коллективы и ударники
коммунистического труда) использует методы высокопроизводит. труда
стахановцев с целью повышения эффективности социалистич. производства.
Лит.: В. И. Ленин, КПСС о социалистическом соревновании. [Сб ], M.,
1973: Первое всесоюзное совещание рабочих и работниц-стахановцев, 14 - 17
ноября 1935 г. Стенографический отчет, M., 1935: О дальнейшем улучшении
организации социалистического соревнования Постановление Центрального Комитета
КПСС, M , 1972; Социалистическое соревнование в СССР. 1918 - 1964, M., 1965; E
в с т а ф ь е в Г, H., Социалистическое соревнование - закономерность и движущая
сила экономического развития советского общества, M., 1952; Г е р ш б е р г С.
Р., Руководство Коммунистической партии движением новаторов промышленности
(1935 - 1941), M., 1956.
С.
P. Гершберг.
СТАХИБОТРИОТОКСИКОЗ, отравление животных (лошадей, кр. рог. скота,
овец, свиней) при поедании грубых растит, кормов, пораженных токсич. грибом
Stachybotrys alternans. Токсич. вещества гриба воздействуют на центр, нервную
систему и стенки кровеносных сосудов. Нарушаются кровообращение, минеральный
обмен, возникают очаги распада тканей в кишечнике и др. изменения. Для С.
характерны быстрота распространения и массовость поражения. Общие признаки
болезни для всех видов животных - повышение темп-ры тела, потеря аппетита,
образование язв на коже губ, отёки; у лошадей - слюнотечение, колики, у
рогатого скота - носовое истечение, поносы с примесью крови, у свиней - в
малошёрстных участках кожи кровоизлияния, иногда язвы. Больные нередко
погибают. Лечение результативно лишь в начале болезни (адсорбирующие,
дезинфицирующие, вяжущие средства, антибиотики и др.). Профилактика: соблюдение
агротехнич. правил уборки и хранения грубых (сено, солома) кормов. Поражённые
грибом корма сжигают.
A. H. Спесивцева.
СТАХИОЗА, дигалактозилсахароза, невосстанавливающий резервный углевод
(тетрасахарид) растений, состоящий из двух остатков галактозы, остатка глюкозы
и остатка фруктозы. Впервые выделена в 1890 из корневища чистеца
(Stachys tuberifera); обнаружена более чем в 100 видах растений, в т. ч. в
представителях семейств бобовых, розоцветных, губоцветных и др. Богатым её
источником служат также соевая мука, неочищенный свекловичный сахар. В клетках
растений С. может служить и донором, и акцептором галактозильного остатка в
реакциях обмена углеводов (трансгликозилировании).
СТАХИС, употребляемое в цветоводстве название видов растений рода чистец.
СТАЦИОНАР (от лат. stationarius - стоящий на месте, неподвижный), 1)
лечебное учреждение, имеющее постоянные койки для больных (в отличие от
поликлиник); больница. 2) В широком смысле - постоянно действующее учреждение,
напр., библиотека, театр и др. (может быть передвижным). 3) Неподвижное
основание, фундамент к.-л. машины, сооружения.
СТАЦИОНАРНАЯ ТОЧКА (или кривая), точка (кривая), в к-рой дифференциал
функции (вариация функционала) обращается в нуль. Для функции одного
переменного у - f(x) касательная в С. т. к графику функции параллельна
оси Ox, касательная плоскость к поверхности z = f(x, у) в С. т.
функции двух переменных f(x, у) параллельна плоскости хОу.
СТАЦИОНАРНОГО ДЕЙСТВИЯ ПРИНЦИП, один из вариационных принципов
механики; то же, что наименьшего действия принцип.
СТАЦИОНАРНОЕ СОСТОЯНИЕ в физике, состояние физ. системы, при к ром
нек-рые существенные для характеристики системы величины (разные в разных
случаях) не меняются со временем. Напр., состояние потока жидкости стационарно,
если скорость движения (и др. характеристики) остаётся в каждой точке
пространства неизменной. В квантовой механике С. с. наз. состояние, в
к-ром энергия имеет определённое (и не меняющееся со временем) значение. О С.
с. в термодинамике см. Открытые системы, Пригожина теорема. Состояние
системы наз. квазистационарным, если величины, при постоянстве к-рых оно было
бы стационарным, медленно меняются со временем. При этом соотношения между
разными свойствами системы остаются приблизительно такими же, как и в С. с.
СТАЦИОНАРНЫЙ ДВИГАТЕЛЬ, двигатель, постоянно закреплённый на
фундаменте и передающий энергию машинам, имеющим постоянное расположение.
Используется гл. обр. для привода генераторов электрич. тока.
СТАЦИОНАРНЫЙ ИСКУССТВЕННЫЙ СПУТНИК ЗЕМЛИ, спутник, движущийся в
экваториальной плоскости Земли по круговой орбите с угловой скоростью, равной
угловой скорости вращения Земли. С. и. с. З. постоянно "висит" над
одной и той же точкой земного экватора. Это свойство С. и. с. З. используется
при создании систем связных искусств, спутников Земли (см. Связи спутник). Высота
С. и. с. З. над земной поверхностью ок. 35 800 км.
Орбиту С. и. с. З. иногда наз. стационарной орбитой.
СТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС, важный спец. класс случайных
процессов, часто встречающийся в приложениях теории вероятностей к
различным разделам естествознания и техники. Случайный процесс X(t) наз.
стационарным, если все его вероятностные характеристики не меняются с течением
времени t (так что, напр., распределение вероятностей величины X(O при
всех t является одним и тем же, а совместное распределение вероятностей
величин Х(t1) и X(t2) зависит только от
продолжительности промежутка времени t2 - t2, т.
е. распределения пар величин {X(t1), X(t2)} и {X(t1
+ s}, X(t2+ s)} одинаковы при любых t1, t2
и s и т. д.).
Схема С. с. п. с хорошим приближением описывает многие реальные явления,
сопровождающиеся неупорядоченными флуктуациями. Так, напр., пульсации силы тока
или напряжения в электрич. цепи (электрич. "шум") можно рассматривать
как С. с. п., если цепь эта находится в стационарном режиме, т. е. если все её
макроскопич. характеристики и все условия, вызывающие протекание через неё
тока, не меняются во времени; пульсации скорости в точке турбулентного течения
представляют собой С. с. п., если не меняются общие условия, порождающие
рассматриваемое течение (т. е. течение является установившимся), и т. д. Эти и
другие примеры С. с. п., встречающиеся в физике (в частности, гео- и
астрофизике), механике и технике, стимулировали развитие исследований в области
С. с. п.; при этом существенными оказались также и нек-рые обобщения понятия С.
с. п. (напр., понятия случайного процесса со стационарными приращениями
заданного порядка, обобщённого С. с. п. и однородного случайного поля).
В математяч. теории С. с. п. осн. роль играют моменты распределений
вероятностей значений процесса X(t). являющиеся простейшими числовыми
характеристиками этих распределений. Особенно важны моменты первых двух
порядков: среднее значение С. с. п. EX(t) = т - математич. ожидание
случайной величины X(t) и корреляционная функция С. с. п. ЕХ(t1)Х (t2)
= B(t1-t2)-математич. ожидание произведения X(t1)X(t2)
(просто выражающееся через дисперсию величин Х(t1) и коэффициент
корреляции между X(t1) и Х(t2); см. Корреляция). Во
многих математич. исследованиях, посвящённых С. с. п., вообще изучаются только
те их свойства, к-рые полностью определяются одними лишь характеристиками т и
В(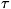 ) (т. н. корреляционная теория С. с. п.). В этой связи случайные
процессы X(t), имеющие постоянное среднее значение EX(t) = т и
корреляционную функцию В(t2, t1) = = ЕХ(t1)
Х(t2), зависящую только от t2 - t1, часто
наз. С. с. п. в широком смысле (а более частные случайные процессы, все
характеристики к-рых не меняются с течением времени, в таком случае наз. С. с.
п. в узком смысле).
) (т. н. корреляционная теория С. с. п.). В этой связи случайные
процессы X(t), имеющие постоянное среднее значение EX(t) = т и
корреляционную функцию В(t2, t1) = = ЕХ(t1)
Х(t2), зависящую только от t2 - t1, часто
наз. С. с. п. в широком смысле (а более частные случайные процессы, все
характеристики к-рых не меняются с течением времени, в таком случае наз. С. с.
п. в узком смысле).
Большое место в математич. теории С. с. п. занимают исследования,
опирающиеся на разложение случайного процесса X(O и его корреляционной функции
B(t2 - t1) - B(t) в интеграл Фурье, или Фурье-Стилтьеса
(см. Фурье интеграл). Осн. роль при этом играет теорема Хинчина,
согласно к-рой корреляционная функция С. с. п. X(t) всегда может быть
представлена в виде
где F( ) - монотонно неубывающая функция
) - монотонно неубывающая функция  (а интеграл справа - это интеграл Стилтьеса); если же В(
(а интеграл справа - это интеграл Стилтьеса); если же В( )
достаточно быстро убывает при |
)
достаточно быстро убывает при | |->бескон. (как это чаще всего и
бывает в приложениях при условии, что под X(t) понимается на самом деле
разность X(t) - т), то интеграл в правой части (1) обращается в обычный
интеграл Фурье:
|->бескон. (как это чаще всего и
бывает в приложениях при условии, что под X(t) понимается на самом деле
разность X(t) - т), то интеграл в правой части (1) обращается в обычный
интеграл Фурье:
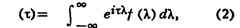
где f( ) = F'(
) = F'( ) - неотрицат.
функция. Функция F(
) - неотрицат.
функция. Функция F( ) наз. спектральной функцией С. с. п. X(t), а
функция f(
) наз. спектральной функцией С. с. п. X(t), а
функция f( ) [в случаях, когда имеет место равенство (2)] -
его спектральной плотностью. Из теоремы Хинчина вытекает также, что сам процесс
X(t) допускает спектральное разложение вида
) [в случаях, когда имеет место равенство (2)] -
его спектральной плотностью. Из теоремы Хинчина вытекает также, что сам процесс
X(t) допускает спектральное разложение вида
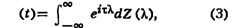
где Z( )- случайная функция с некоррелированными приращениями,
а интеграл справа понимается как предел в среднем квадратичном соответствующей
последовательности интегральных сумм. Разложение (3) даёт основание
рассматривать любой С. с. п. X(t) как наложение некоррелированных друг с другом
гармонич. колебаний различных частот со случайными амплитудами и фазами; при
этом спектральная функция F(
)- случайная функция с некоррелированными приращениями,
а интеграл справа понимается как предел в среднем квадратичном соответствующей
последовательности интегральных сумм. Разложение (3) даёт основание
рассматривать любой С. с. п. X(t) как наложение некоррелированных друг с другом
гармонич. колебаний различных частот со случайными амплитудами и фазами; при
этом спектральная функция F( ) и спектральная плотность f(
) и спектральная плотность f( ) определяют распределение средней энергии входящих в состав X(t)
гармонич. колебаний по спектру частот
) определяют распределение средней энергии входящих в состав X(t)
гармонич. колебаний по спектру частот  (в связи с чем в
прикладных исследованиях функция f(
(в связи с чем в
прикладных исследованиях функция f( ) часто наз. также энергетич.
спектром или спектром мощности С. с. п. X(t)
) часто наз. также энергетич.
спектром или спектром мощности С. с. п. X(t)
Выделение понятия С. с. п. и получение первых относящихся к нему математич.
результатов являются заслугой E. E. Слуцкого и относятся к кон. 20-х и
нач. 30-х гг. 20 в. В дальнейшем важные работы по теории С. с. п. были
выполнены А. Я. Хинчиным, A. H. Колмогоровым, Г. Крамером, H.
Винером и др.
Лит.: Слуцкий E. E., Избр. тр., M., 1960; X и н ч и н А. Я., Теория
корреляции стационарных стохастических процессов, "Успехи математических
наук", 1938, в. 5, с. 42 - 51; Розанов Ю. А., Стационарные случайные
процессы, M., 1963; Прохоров Ю. В., Розанов Ю. А., Теория вероятностей.
(Основные понятия. Предельные теоремы. Случайные процессы), 2 изд., M., 1973;
Гихман И. И., Скороход А. В., Теория случайных процессов, т. 1,М., 1971; X е н
н а н Э., Многомерные временные ряды, пер. с англ., M., 1974.
A. M. Яглом.
СТАЦИЯ (от лат. static - стояние, место, местопребывание) (биол.), 1)
местообитание популяции. 2) Часть местообитания, используемая животным
или видом животных либо в ограниченный период, либо для одной определённой
функции. Различают С. дневные и ночные, сезонные, С. размножения, питания, С.
переживания неблагоприятных условий и, наконец, С. расселения (при наступлении
благоприятных условий).
СТАЧКА, см. Забастовка.
СТАШЕК (Stasek) Антал [псевд.; наст. имя Антонин Земан (Zeman)]
(22.7. 1843, с. Станов, близ Йилемнице, - 9.10. 1931, Прага), чешский писатель.
Окончил Краковский ун-т (1866). Работал адвокатом. Посещал Россию (1874-75,
1889, 1897). Пропагандист демократич. рус. культуры в Чехии. В романтич. стихах
60-70-х гг. воспевал борцов за нац. освобождение Чехии, участников Революции
1848. Затем обратился к реалистич. прозе, поев, жизни и борьбе чеш. трудящихся:
романы "В мутном водовороте" (1900), "В пограничье" (1908),
"О сапожнике Матоуше и его друзьях" (1927, рус. пер. 1954). В
3-томном собрании повестей и небольших романов "Мечтатели наших гор"
(1895) С. рисует суровую и безрадостную жизнь жителей Подкрконошского края,
мечтающих о счастье и справедливости. В ряде произведений 20-х гг. дал картины
страшных последствий 1-й мировой войны 1914-18. Автор "Воспоминаний"
(1926) о политич. и лит. жизни Чехии. С. стремился раскрыть в своих книгах движение
обществ, жизни, сочетая реалистич. повествование с элементами фантазии и
романтизма.
Соч.: Vybrane spisy, sv. 1
- 10, Praha, 1955-64.
Лит.:
Очерки истории чешской литературы XIX-XX вв., M., 1963; PoIak K., О Antalu Staskovi, Praha, 1951;
Dejiny ceske literatury, dl. 3, Praha, 1961.
Л. С.
Кишкин.
СТАШИЦ (Staszic, Staszyc) Станислав (ноябрь 1755, Пила, - 20.1.1826,
Варшава), польский общественный деятель, идеолог Просвещения, публицист,
учёный. Выходец из бурж. семьи. В 1779 принял духовный сан. Учился в духовной
семинарии в Познани, затем в Лейпцигском и Гёттингенском ун-тах. В 1787 опубл.
анонимно "Размышлелия над жизнью Яна Замойского", содержавшие критику
социального и политич. строя Речи Посполитой, формулировавшие программу реформ,
имевших антифеод, характер. Эти идеи развиты С. в трактате
"Предостережение Польше" (1790), оказавшем большое влияние на
деятельность Четырёхлетнего сейма 1788-92. В 1800 участвовал в Варшаве в
создании Об-ва друзей наук (с 1808 его президент). Сыграл значит, роль в
развитии нар. просвещения, горнодобывающей пром-сти в Королевстве Польском (в
1816-24 С.- глава департамента пром-сти и ремёсел). Исследования С. в области
геологии обобщены им в труде "О геологии Карпат и других гор и равнин
Польши" (1815). Основное филос. соч. С. поэма "Род человеческий"
(1819-20) - энциклопедия польск. Просвещения. В духе франц. просветителей С.
объясняет историю человечества как этап развития природы, специфику той или
иной историч. эпохи он связывает с господствующим видом собственности. В 1816 основал
в Хрубешове крест, об-во, к-рому передал в вечное владение свои земли.
Соч. в рус. пер.: Избр. произв. прогрессивных польских мыслителей, т. 1, M.,
1956, с. 101-290; Избранное, M., 1957.
Лит.: Нарский И. С., Философия польского просвещения, M., 1958; Осиповa E. В., Философия польского просвещения, M., 1961.
И.С.Миллер.
СТАШКОВ Николай Иванович [2(15).4. 1907 - 26.1.1943], один из
организаторов партиз. движения на Украине в годы Великой Отечеств, войны
1941-45, Герой Сов. Союза (2.5.1945, посмертно). Чл. КПСС с 1931. Род. в Одессе
в семье рабочего. В 1920 в рядах Красной Армии участвовал в боях под Каховкой и
Перекопом. С 1927 слесарь на Днепропетровском з-де "Спартак". В
1933-35 на комсомольской работе в MTC. В 1938-41 служил в Красной Армии. С авг.
1941 1-й секретарь подпольного Днепропетровского обкома КП(б)У. 28 июля 1942
арестован нем.-фаш. оккупантами; после жестоких пыток расстрелян. В
Днепропетровске на аллее С. установлена стела с его барельефом.
Лит.: К и з я Л. E. и Клоков В. И., Украина в пламени народной войны,
в сб.: Советские партизаны, M., 1961; Рашев П. H., Днепропетровские
подпольщики, в сб.: Герои подполья, в. 2, M., 1968.
СТАЯ, временная группа рыб или птиц, обычно одного вида, находящихся
в сходном биологич. состоянии, активно поддерживающих взаимный контакт и
координирующих свои действия; С. состоит из особей, к-рые выполняют ряд важных
жизненных функций, будучи членами той или иной С. на протяжении большой части
своей жизни. В отличие от стада, в С. отсутствует распознавание одних
животных другими (нет вожаков, доминирующих и подчинённых особей). С. может
состоять из особей одного или разных видов, разного пола и возраста.
Образование С. характерно для мн. рыб (напр., сельдевых, макрелевых и
анчоусовых) и птиц (напр., гусеобразных, журавлино-образных и воробьиных).
Птицы образуют С. преим. вне периода гнездования. Биологич. значение С. зависит
от состояния животных и окружающих условий. Пребывание в С. помогает
разыскивать корм и ловить добычу, защищаться от хищников, а птицам также при
выборе места ночёвки, при ориентации и навигации во время миграции животных.
Для рыб и птиц образование С., по-видимому, имеет значение и для улучшения
гидродинамич. и аэродинамич. условий движения в воде или в воздухе
соответственно. Напр., построение С. у птиц - клин (журавли), шеренга (утки),
рыхлая масса (голуби, воробьиные) (см. Перелёты птиц). Величина и форма
С., а также расстояние между отдельными особями изменчивы, что является
приспособлением к различным условиям среды. В С. между особями существуют
разные формы сигнализации (у рыб - преим. зрительной, а у птиц также
акустической). Закономерности стайного поведения рыб широко используются в
промысловом рыболовстве.
В литературе термин "С." применяется также к семейным группам
(напр., С. волков, дельфинов).
Д. В. Радаков, В. Э. Якобы.
СТВИРИ, гудаствири, грузинский духовой музыкальный инструмент, род волынки.
СТВОЛ, мощно развитый стебель древесных растений, к-рый значительно
толще и выше боковых ветвей. У деревьев с моноподиальным ветвлением С.- главная
ось, развивающаяся из конуса нарастания проростка; у деревьев с симподиальным
ветвлением - система боковых осей разных порядков, последовательно сменяющих
друг друга.
СТВОЛ в пожарной технике, приспособление для создания и направления
струй воды, пены, порошка и др. огнетушащих веществ. Устар. назв. С.-
брандспойт. С. простейшей конструкции представляет собой трубу с насадком на
конце, от типа к-рого зависит вид струи. С. позволяют получать сплошные и
распылённые струи, а также перекрывать поток без отключения питающего
устройства. Струю пены получают из 1- 6%-ного водяного раствора
пенообразователя, распыляемого насадком в кожухе, где капли смешиваются с
воздухом, эжектрируемым за счёт энергии струи. Производительность С. 1-200 кг/сек
огнетушащего вещества. С. подразделяются на ручные (производительность
менее 13 кг/сек) и лафетные. Лафетные С. бывают стационарными
(закрепляются на крыше автомобиля, палубе катера, вышке и т. п.), возимыми и
переносными. Ручными С. комплектуются пожарные автомобили, мотопомпы,
внутренние пожарные краны. К рукавным линиям С. подсоединяются с помощью
быстросмыкаемых головок.
СТВОЛ ШАХТНЫЙ, вертикальная или наклонная горная выработка, имеющая
выход на земную поверхность и предназначенная для вскрытия месторождений и
обслуживания подземных работ. Различают главные и вспомогательные С. ш. Главный
ствол располагается на центр, площадке шахты и предназначается в основном для
подъёма на поверхность полезного ископаемого (угля, руды и т. п.);
вспомогательный ствол - для транспортирования людей, пустых пород,
оборудования, материалов. Вспомогательный ствол может быть также вентиляционным
- для подачи в шахту свежего воздуха (т. н. воздухоподающий ствол) или выдачи
отработанного. Такие стволы могут располагаться на центральной пром. площадке и
на флангах шахтного поля (фланговые стволы). С. ш. оборудуют скипами, клетями,
рельсовым или конвейерным транспортом, а в период стр-ва - бадьями.
Верхняя часть С. ш., выходящая на земную поверхность, наз. устьем (иногда
воротником); нижняя (ниже горизонта околоствольного двора) - зумпфом.
Поперечное сечение шахтных стволов бывает круглым, иногда - прямоугольным, реже
- эллиптическим. Диаметр вертикальных С. ш. достигает 9 м, глубина 3-3,5 км. Наклонные стволы имеют прямоугольную, арочную, круглую формы.
Стенки стволов закрепляют бетоном, железобетоном и металлич. или
железобетонными тюбингами; в крепких устойчивых породах - набрызг-бетоном.
Армировка С. ш. включает обычно металлич. горизонтальные элементы (расстрелы) и
вертикальные элементы (проводники), обеспечивающие плавное движение скипов и
клетей. Сооружают С. ш. с помощью буровзрывных работ, бурильных установок и
стволопроходческих агрегатов.
Разновидность С. ш.- слепой ствол - вертикальная горная выработка, не
имеющая непосредственного выхода на поверхность и предназначенная в основном
для подъёма полезного ископаемого с нижних горизонтов шахты на верхние.
Ю.
И. Свирский.
СТВОЛОВЫЕ КЛЕТКИ, клетки, входящие в состав постоянно обновляющихся
тканей животных и способные развиваться в различных направлениях, в пределах
тканевой дифференцировки. Подробнее см. Камбиальные клетки.
СТВОЛОПРОХОДЧЕСКАЯ БУРОВАЯ УСТАНОВКА, установка для проведения
вертикальных шахтных стволов и скважин большого диаметра бурением с
поверхности.
Рис. 1. Бурение ствола установкой УЗТМ-8,75.
Основана на принципе роторного (установки УЗТМ и Щепотьева - Иванова),
колонкового (УКБ) или реактивно-турбинного бурения (РТБ). Установками типа УЗТМ
(рис. 1) бурят стволы диам. 7,5 и 8,75 м на глубину до 600 м. Рабочий
инструмент - шарошечные пилот-долота и расширители. Наиболее экономично их
использование в обводнённых неустойчивых породах и плывунах. Скорость проходки
до 50 м в месяц. Установками пробурено 5 стволов всего ок. 1500 м (1974).
Установка УКБ-3,6 (рис. 2) бурит стволы диам. 3,6 м на глуб. до 700 м
с извлечением керна вые. до 5,3 м. В слабых породах
применяется шарошечная приставка для сплошного разбуривания при обратной
промывке. Скорость бурения до 150 м в месяц. Установкой пробурено 4
ствола на глуб. 2000 м (1974). Установка Щепотьеиа - Иванова базируется
на серийном нефтебуровом оборудовании; пилотдолото имеет диам. 600 мм, комплекс
расширителей - от 900 до 2400 мм. Применяется в мягких и средней
крепости породах на глуб. до 300 м. Скорость бурения до 50 м в
месяц. Установками пробурено св. 70 стволов всего 20 000 м (1974).
Установка реактивно-турбинного бурения РТБ (рис. 3) имеет два и более
агрегатированных турбобуров. Установкой бурят за один проход ствол диам. от 2
до 5 м. Применяются в мягких, средней крепости и отчасти крепких породах
на глубину 1000 м и более. Скорость бурения 100 м в месяц.
Установками пробурено св. 160 стволов, всего ок. 100 км (1974).
В Зап. Европе для проходки стволов диам. до 8,5 м на глуб. до 750 м
в сложных гидрогеологич. условиях применяется роторная буровая установка де
Boойса (Нидерланды), работающая по принципу последоват. расширения ствола с
извлечением породы через бурильные трубы эрлифтом. В США в 60-х гг. получили
распространение (пробурено св. 100 км) роторные установки, к-рыми
проводят стволы диам. от 1,5 до 4 м. В установках используют тяжёлое
нефтебуровое и спец. наземное оборудование, трубы, многошарошечные долота,
расширители, грузы. Кроме обратной промывки, применяется система обратной
продувки воздухом.
Прообраз стволопроходческого бурового агрегата создал в 1894 Хонигман
(Германия). В 1938 К. H. Щепотьевым и В. П. Ивановым сконструирован комплекс
расширителей лопастного и шарошечного типа, позволивший бурить скважины диам.
до 2,4 м при помощи оборудования для роторного бурения нефтяных скважин.
В 1941 Г. И. Маньковский, Ш. X. Оганезов и Ф. Д. Мещеряков создали буровую
установку на основе нефтяного оборудования; этими установками в годы Великой
Отечеств, войны 1941- 1945 пройдено ок. 30 стволов диам. до 5 м и
глубиной до 110 м в сложных горно-геологич. условиях Челябинского и
Подмосковного угольных бассейнов. В 1965 была создана буровая установка
УЗТМ-7,5 (позднее УЗТМ-8,75). В 1947 Г. И. Булахом был сконструирован
колонковый шарошечный бур, что позволило в 1956 под рук. M. H. Кудрякова
создать установку УКБ-3,6. В 1960 P. А. Иоаннесяном, M. T. Гусманом и Г. И.
Булахом предложены и испытаны первые забойные агрегаты и установки РТБ.
Рис. 2. Буровая установка УКБ-3,6.
Рис. 3. Установка РТБ.
Лит.: Ф е д ю к и н В. А-, Проходка шахтных стволов н скважин
бурением, M , 1959; Малевич H. А., Комплексы оборудования для проходки и
бурения вертикальных стволов, M., 1960; M а н ь к о в с к н й Г. И., Специальные
способы сооружения стволов шахт, M., 1965; Реактивно-турбинное бурение, M.,
1967.
Г. И. Булах.
СТВОЛОПРОХОДЧЕСКИЙ АГРЕГАТ, комбайн для сооружения вертикальных
шахтных стволов. Применяется в породах не выше средней крепости (коэфф.
крепости до 8, по шкале M. M. Протодьяконова). Совмещает процессы механич.
разрушения пород, погрузку горной массы в подъемные сосуды, возведение
постоянного крепления ствола, водоотлив, наращивание ставов труб и т. д. Представляет
собой трёхэтажный металлич. каркас с размещенным на нём оборудованием (рис.). С
помощью С. а. типа ПД в СССР в Карагандинском угольном басе, пройдено 4 шахтных
ствола общей глуб. св. 2150 м и один ствол в Донбассе на глуб. св. 520 м.
При этом темпы проходки, достигнутые на агрегатах, составили в Караганде
133 м ч в Донбассе 175 м готового ствола в месяц и были
установлены мировые рекорды по производительности труда проходчиков
соответственно 13,23 и 12,7 м3 готового ствола на человека в смену.
Агрегат обслуживают 3 человека в смену.
Создание С. а.- качественно новый этап в развитии техники сооружения шахтных
стволов, т. к. позволяет в 5-6 раз повысить производительность труда рабочих,
устранить тяжёлый физич. труд, обеспечить высокую степень безопасности ведения
горных работ и улучшить санитарно-гигиенич. условия. Первый С. а. создан в СССР
(1952).
Стволопроходческий агрегат типа ПД-2: 1 - каркас; 2 - механизм гидрораспора; 3 - двухдисковый планетарный исполнительный орган; 4 - пневматический
эжектор для уборки горной массы; 5 - редуктор главного привода; 6 - телескопические
валы; 7 - пульт управления; 8 - механизм перегрузки; 9 - подъёмный со суд; 10
- опалубка; 11 - телескопический механизм для наращивания труб.
А. С. Банк.
СТВОЛОПРОХОДЧЕСКИЙ КОМПЛЕКС, совокупность машин и механизмов,
предназначенных для выполнения осн. технологич. операций при проходке
вертикальных стволов буровзрывным способом. В СССР распространение получили С.
к. типа КС-2у (рис. 1). В стволах диам. до 7 м применяются одногрейферные
погрузочные машины КС-2у/40 с грейфером ёмкостью 0,65 м3 или КС-1м с
грейфером ёмкостью 1,0-1,25 м3; в стволах больших диаметров
применяются двухгрейферные машины с грейферами ёмкостью 0,65-1 м3. В
С. к. входит бурильная установка типа БУКС, подвешиваемая вместо грейфера на тельфер
породопогрузочной машины, к-рой осуществляется групповое бурение шпуров,
саморазгружающиеся бадьи для выдачи погруженной породы на поверхность и
металлич.передвижная опалубка. При наиболее распространённой совмещённой
технологич. схеме проходки стволов опалубка устанавливается на забое.
Среднетехнич. скорости проходки по этой схеме составляют 100-120 м в
месяц.
Рис. 1. Стволопроходческий комплекс типа КС-2у:
1 - проходческий полок; 2
- монорельс; 3 - породопогрузочная машина типа КС; 4 - грейфер
5 - бурильная установка БУКС; 6 - проходческая бадья; 7 -
передвижная опалубка.
Рис. 2. Стволопроходческий комплекс КС-1м/6,2:
1 - металлический щит; 2 -
натяжной полок; 3 - каретка с породопогрузочной машиной КС-1м; 4 -
опалубка; 5 - балкон опалубки; 6 - опускное пикотажное кольцо.
Для скоростного прохождения стволов в устойчивых породах применяется С. к.
типа КС-1м/6,2 (рис. 2), рассчитанный на параллельно-одновременное производство
работ по выемке породы и возведение крепи. При использовании этого комплекса
достигнуты скорости проходки ствола 401,3 м/мес.
Д. И. Малиованов.
СТВОР в гидротехнике, участок реки, на к-ром расположены сооружения гидроузла,
образующие его напорный фронт. С. обычно выбирают в 2 этапа. Вначале
намечают район створа (в соответствии с общей схемой водохозяйственного
использования данной реки), затем определяют ось с т в ор а, практически
понимая под нею полосу нек-рой ширины, к-рая, пересекая реку и долину, в плане
может быть прямолинейной (перпендикулярной берегам реки), криволинейной или
ломаной. Выбор оптимального С. осуществляется технико-экономич. сопоставлением
различных вариантов с учётом климатических, топографических, гидрологических,
инженерно-геологических и строительных условий.
CTBOP гидрометрический, обозначенный на местности створ, совпадающий
с направлением поперечного сечения водного потока (реки), в к-ром измеряются
расходы воды и наносов. С. г. располагается перпендикулярно среднему
направлению течения на прямолинейном участке с более или менее правильным
корытообразным устойчивым дном. На этом участке не должно быть перекатов,
островов и впадающих в реку притоков, к-рые могут вызвать явления, нарушающие
однообразие течения. С. г. должен контролировать весь поток (главное русло, протоки
и рукава, пойму). Расходы воды, измеренные в С. г., относятся к уровням воды,
одновременно измеренным на уровнемере (водомерной рейке, самописцем),
расположенном в С. г. или поблизости от него.
СТВОРНЫЕ ЗНАКИ, ориентиры, расположенные на одной прямой (в створе),
для указания направления движения судна или самолёта, обозначения к.-л. рубежа.
С. з.- щиты, башни, ажурные мачты-устанавливают на открытой местности и
окрашивают в цвета, контрастирующие с окружающим фоном. В необходимых случаях
С. з. оборудуют электрич. осветит, устройствами, включающимися обычно
автоматически. Для указания фарватера на берегу устраивают обычно 2-3 С. з.,
перед посадочной полосой - от 10 и более. Места расположения С. з. указываются
на морских или топографических картах и в лоциях.
В. И. Кулаков.
СТЕАРИН (франц. stearine, от греч. stear - жир, сало), технич.
стеариновая к-та, смесь высших жирных карбоновых K-T (гл. обр. стеариновой и
пальмитиновой). С.- полупрозрачная масса белого или желтоватого цвета, жирная
на ощупь, Гпл 53-65 °С (в зависимости от сорта), плотность 0,92 г/см3
(20 0C). Получают дистилляцией гидролизатов животных жиров (с
последующей кристаллизацией и отжимом) или гидрированием ненасыщенных к т
растительных масел. С. используют в произ-ве свечей (обычно в смеси с
парафином); о других областях применения см. в ст. Стеариновая кислота.
СТЕАРИНОВАЯ КИСЛОТА, октадекановая кислота, CH3(CH2)16COOH,
одноосновная насыщенная карбоновая кислота алифатич. ряда. Бесцветные
кристаллы, tпл 69,6 0C,tкип 376,1 0С;
нерастворима в воде, растворима в эфире. С. к. является одной из наиболее
распространённых в природе высших жирных кислот; глицериды С. к.-
главная составная часть многих жиров и масел, из к-рых её выделяют гидролизом
(обычно в виде стеарина - смеси С. к. и пальмитиновой кислоты). С. к.
можно получить дробным осаждением или дистилляцией из стеарина, гидрированием олеиновой
кислоты и др. способами. Щелочные соли С. к. являются мылами. Применяют
С. к.: очищенную - в органич. синтезе, аналитич. химии (для определения Ca, Mg,
Li), технич.- как диспергатор ингредиентов и активатор вулканизации в
производстве резины. Стеараты натрия, лития, кальция, свинца и др. металлов
используют как компоненты пластичных смазок, С. к. и её эфиры - при получении
косметических средств.
СТЕАТИТОВАЯ КЕРАМИКА, изделия и материалы,
применяемые как изоляторы в высоковольтной и высокочастотной технике;
изготовляется на основе минерала стеатита (разновидность талька). С.к.
характеризуется значит, прочностью при статич. изгибе - до 190 Мн/м2 (1900
кгc/см2), диэлектрич. проницаемость колеблется в пределах
5,5-7, диэлектрич. потери (при частоте 1 Мгц и темп-ре 20 0C)
(3-25)*10-4. Изделия из С.к. формуют методами керамич. технологии
(прессование, литьё под давлением и др.) и обжигают при темп-ре 1200-1300° С.
Произ-во изделий из С. к., особенно крупных размеров, сопряжено с трудностями,
обусловленными узким интервалом спекания (10-40 0C). Недостаток С.
к.-склонность к "старению" при длительной эксплуатации.
СТЕАТОПИГИЯ (от греч. stear, род. падеж steatos - жир и pyge -
огузок, ягодицы), сильное развитие подкожного жирового слоя у человека на
ягодицах (в области большой ягодичной мышцы). Наиболее выражена С. у женщин
нек-рых южноафр. народов, гл. обр. у бушменов и готтентотов. У
этих народов, а также у зулу С. считается признаком женской красоты.
Причина возникновения С. окончательно не выяснена.
СТЕБЕЛЬ (caulis), осевой орган высших растений, вместе с листьями
составляющий побег; служит для передвижения воды и веществ между корнями
и листьями, для увеличения ассимилирующей поверхности растения путём ветвления
и упорядоченного расположения листьев, а также цветков и плодов; может
участвовать в накоплении воды и запасных питат. веществ, в фотосинтезе. Участки
С., от к-рых отходят боковые органы (ветви, листья и др.), наз. узлами, участки
между узлами - междоузлиями. С. бывают травянистыми и деревянистыми; главный С.
древесных растений наз. стволом. Форма С. разнообразна: цилиндрич.
(наиболее распространена), трёхгранная (осоки), четырехгранная (губоцветные),
многогранная, уплощенная (кактусы) и др. По положению в пространстве различают
С. прямостоячие, лежачие, ползучие, лазающие и др.; надземные и подземные (см.
рис. 2). Длина С. от 1-1,5 мм (пресноводная вольфия) до 200-300 м (тропич.
пальмы-ротанги), диаметр от долей мм (мхи) до 10-11 м (баобаб,
секвойя). С. растёт в длину за счёт деятельности верхушечной меристемы побега,
составляющей конус нарастания. Кроме верхушечного роста, у некрых
растений в основании междоузлий происходит ещё интеркалярный (вставочный) рост
(напр., у злаков).
В С. выделяют анатомо-топографические зоны: наружную - эпидермис, внутреннюю
- центральный цилиндр, или стелу, и расположенную между ними зону первичной
коры, внутр. паренхимный слой к-рой превращён в эндодерму. Последняя
граничит с периферич. зоной стелы (представленной паренхимной или механической
тканями) - перициклом (у нек-рых растений его нет). Большая часть стелы
состоит из проводящих тканей, флоэма находится снаружи от ксилемы. У
лиственных мхов в центре С. расположен "проводящий пучок", элементы
к-рого лишь внешне сходны с проводящими элементами флоэмы и ксилемы. У
сосудистых растений формированию проводящих тканей предшествует развитие прокамбия.
У плаунов ксилема разделена на лентовидные тяжи, окружённые флоэмой,
сердцевины нет. У хвощей закрытые коллатеральные пучки с т. н. каринальной
полостью вместо ксилемы располагаются вокруг центр, воздушной полости. У
папоротников проводящие ткани кольцом окружают сердцевину. В С. семенных
растений встречаются пучковый и сплошной типы строения проводящей системы,
пересечённой радиально расходящимися паренхимными сердцевинными лучами.
Рис. 1. Анатомическое строение стебля цветковых растений:
I - общий вид
проводящей системы стебля с причленившимся трёхпучковым листовым следом;
II -
строение стебля в области трехлакунного узла, III - однолакунного, IV - многолакунного;
V - пальмовый тип прохождения пучков в стебле однодольных растений; VI -
строение соломины злаков; VII - строение стебля бигнонии с вдающимися в
древесину участками луба; VlII - строение стебля вистарии, утолщение
которого обусловлено несколькими камбиями; 1 - сердцевина; 2 - стела; 3
- листовой след; 4 - пучки листового следа; 5 - листовые
прорывы; 6 - флоэмные волокна; 7 - ксилема; 8 -
камбий пучковый; 9
- флоэма; 10 - стебель; 11 -
влагалище листа; 12 - закрытые
коллатеральные пучки; 13 - ассимиляционная паренхима; 14 - воздушная
полость; 15 - сосуды ксилемы; 16 - механическая ткань; 17 - сердцевинные
лучи; 18 - перидерма; 19 - первичная кора; 20
- древесина; 21
- луб.
Рис. 2. Типы стеблей по положению в пространстве·
1 - прямостоячий; 2 - наклонный;
3 - изогнутый; 4 - дуговидный; 5
- поникающий, 6 -
лежачий; 7
-ползучий, укореняющийся в узлах; 8 - восходящий; 9 - коленчато-восходящий;
10 - изломанный; 11 -
извилистый; 12, 13 - вьющиеся; 14 -
цепляющийся;
15 - лазающий; 16 - всползающий; 17 - вплетающийся; 18
- свисающий;
19 - плавающий; 20 - всплывающий; 21 - погружённый в толщу
воды.
Наружная часть прокамбия дифференцируется в первичную флоэму, на периферии
к-рой нередко развиваются механич. волокна, внутренняя - в первичную ксилему.
Между проводящими тканями остаётся слой клеток, образующих камбий, к-рый
откладывает наружу элементы вторичной флоэмы - луба, внутрь - вторичной ксилемы
- древесины, обусловливая утолщение стелы.
Строение С. в зоне узлов отличается от строения средней части междоузлия
наличием листовых и веточных лакун (прорывов). У двудольных (см. рис. 1) часты
трёхлакунные узлы (яблоня), реже встречаются однолакунные (сирень) и
многолакунные (бузина). Наиболее активное вторичное утолщение свойственно
многолетним древесным растениям, во вторичной древесине к-рых (а иногда и в
лубе) можно видеть границы годичных приростов. С возрастом вследствие развития
перидерм первичная кора, а позднее и наружная часть луба отмирают, образуя корку.
Для большинства однодольных (см. рис. 1, V) характерен пальмовый тип
прохождения закрытых коллатеральных пучков, обусловливающих их диффузное
расположение на поперечных срезах. Лишь у некоторых злаков со С.-соломиной, у
традесканции и диоскореи имеется тенденция к круговому расположению пучков.
Вторичное утолщение свойственно только древовидным лилейным (алоэ, драцена), у
к-рых в перицикле или первичной коре формируется меристема, образующая
концентрич. пучки и межпучковую (часто одревесневающую) паренхиму. См. также Стелярная
теория.
Лит.: Серебряков И. Г., Морфология вегетативных органов высших
растений, M., 1952; Мейер К. И., Морфогения высших растений, M., 1958; И м с
А., Морфология цветковых растений, пер. с англ., M., 1964; Ботаника, под ред.
Л. В. Кудряшова, т. 1, M., 1966; Эсау К., Анатомия растений, пер. с англ., M.,
1969.
Л. И. Лотова.
СТЕБЕЛЬЧАТОГЛАЗЫЕ МОЛЛЮСКИ, отряд наземных брюхоногих моллюсков из
подкласса лёгочных моллюсков. Глаза расположены на вершине второй пары
щупалец (отсюда назв.).
СТЕБЛЁВ, посёлок гор. типа в Корсунь-Шевченковском р-не Черкасской
обл. УССР. Расположен на р. Рось (приток Днепра), в 20 км от ж.-д. ст.
Корсунь (на линии Фастов - Цветково). Хл.-бум. ф-ка. Мемориально-литературный
музей И. С. Нечуй-Левицкого.
СТЕБЛЕВОЙ МОТЫЛЁК, кукурузный мотылёк [Ostrinia (Pyrausta)
nubilalis], бабочка сем. огнёвок, многоядный вредитель растений. Тело дл. 13-15
мм, крылья в размахе 27- 32 мм; самки крупнее самцов. Передние
крылья самок от бледно-жёлтых до светло-коричневых, поперёк 2 тёмные
зигзагообразные линии; задние более светлые, со светлой серединной перевязью. У
самцов крылья более тёмные. Гусеницы дл. до 25 мм, светло-серые, иногда
коричневые с тёмной полосой вдоль спины. Распространён в Европе, Азии, Америке;
в СССР - в степной и лесостепной зонах Европ. части, на Ю. Сибири, Д. Востоке и
в Cp. Азии. Гусеницы С. м. повреждают ок. 230 видов гл. обр. крупностебельных
растений, наиболее часто кукурузу, коноплю, просо, сорго, хмель, несколько реже
картофель, подсолнечник, кенаф, канатник и др. Самки откладывают яйца на нижнюю
сторону листьев; гусеницы проникают за влагалища и в черенки листьев, соцветия,
стебли; их дальнейшее питание и развитие происходит внутри стеблей (отсюда
назв.), а на кукурузе - и внутри початков.
Стеблевой мотылёк:
1 - самка; 2 - самец; 3 - гусеница; 4 - яйца
на листе конопли.
У повреждённых растений ухудшаются условия питания, переламываются и усыхают
стебли, соцветия, что значительно снижает урожай зелёной массы, семян, а у
лубяных культур - и волокна.
Меры борьбы: агротехнич. фи-тосанитарные мероприятия; выпуск яйцееда
трихограммы (70-100 тыс. на 1 га) в 2 приёма в начале массовой откладки
яиц и через 10 сит; использование устойчивых сортов. Применение химич.
метода затруднено из-за скрытого образа жизни гусениц.
Лит.: Хомякова В. О., Кукурузный мотылек, Л. -M., 1962; Поспелове.
M., Арсентьева M. В., ГруздевТ. С., Защита растений, Л., 1973.
СТЕБЛЕВЫЕ НЕМАТОДЫ (Ditylenchus), род круглых червей, или нематод,
сем. Tylenchidae. Тело длинное, тонкое, заострённое. Длина взрослых С. н.
0,8-1,5 мм, толщина 0,02-0,03 мм. Цикл развития С. н. происходит
в тканях растений. Наиболее опасны С. н. картофеля (D. destructor) и С. н. D.
dipsaci, к-рая поражает лук, чеснок, пастернак, петрушку, помидоры, клевер,
зерновые.
Рис. 1. Луковица лука-севка, поражённая нематодой Ditylenchus dipsaci.
С. н. поражают луковицы клубни, корневища и стебли. При отмирании
заражённого растения С.н. либо уходят в почву и активно отыскивают нового
хозяина, либо остаются в тканях старого. Меры борьбы: возвращение на прежнее
место в севообороте культур, поражаемых С. н., не чаще 1 раза в 3 года.
Рис. 2. Клубень картофеля, сильно заражённый стеблевой нематодой картофеля.
Лит.: Кирьянова
Е. С. и Кралль Э. Л., Паразитические нематоды растений
и меры борьбы с ними, т. 2, Л., 1971.
СТЕБЛИН-КАМЕНСКИЙ Михаил Иванович [р. 29.8(11.9).1903, Петербург],
советский филолог-скандинавист, доктор филологич. наук (1948). Окончил ЛГУ
(1939). Основатель (1958) кафедры сканд. филологии ЛГУ, проф. (с 1950). Осн.
труды по языкознанию посвящены диахрония, фонологии, историч. и теоретич.
грамматике сканд. языков, проблемам общего языкознания: "Древнеисландский
язык" (1955), "Грамматика норвежского языка" (1957),
"Очерки по диахронической фонологии скандинавских языков" (1966),
"Спорное в языкознании" (1974). Исследования С.-К. по др.-исл. лит-ре
раскрывают сущность ср.-век. сознания: "Исландская литература" (1947),
"Мир саги" (1971) и др. Подготовил к печати др.-исл. памятники:
"Исландские саги" (1956), "Старшая Эдда" (1963),
"Младшая Эдда" (1970), "Исландские саги" (1973). Почётный
доктор Стокгольмского (1969) и Рейкьявикского (1971) университетов.
Соч.: История скандинавских языков, М.- Л., 1953; Культура Исландии, Л.,
1967.
Лит.: Лихачев Д., Сага об Исландии, "Новый мир", 1967,
№
12; Б е р к о в с к и й H., Мир саги, "Вопросы литературы", 1971, № 8;
Скандинавский сборник, т. 18, Тал., 1973 (номер посвящен M И.
Стеблин-Каменскому).
О. А. Смирницкая.
СТЕБНИК, посёлок гор. типа в Львовской обл. УССР. Подчинён
Дрогобычскому горсовету. Ж.-д. станция на линии Трускавец - Самбор. 18 тыс.
жит. (1975). Калийный завод.
СТЕБНИЦКИЙ Иероним Иванович [30.9(12.10). 1832, Волынская губ., -
29.1(10.2).1897, Петербург], русский геодезист, чл.-корр. Петерб. АН (1878),
генерал от инфантерии. В 1852 окончил Ин-т корпуса инженеров путей сообщения.
Начальник Кавк. военно-топографич. отдела (с 1867) и Военно-топографич. отдела
Гл. штаба (с 1886). С 1860 проводил работы по триангуляции и картографированию
Кавказа, Закаспийской обл., М.Азии и руководил обработкой триангуляции и
нивелирований.
СТЕБС (Stubbs) Уильям (21.6.1825, Нэрсборо, Йоркшир, - 22.4.1901, Каддесдон близ Оксфорда), английский историк-медиевист; епископ Оксфордский (с
1888). По политическим взглядам консерватор, в методологич. отношении близок к
позитивизму. Труды С. посвящены конституц. истории Англии и истории английской
церкви. Ист. концепция С. преследовала цель доказать древние традиции и
исключит. достоинства англ. парламентского строя, к-рый по С. сформировался в
борьбе между древними демократич. учреждениями англо-саксов и сильной нормандской
государственностью. С. был активным участником издания серии источников
("Rolls series"), в к-рой опубликовал 19 тт. англ. хроник 11-15 вв.
Соч.: The constitutional
history of England, V. 1 - 3, Oxf., 1874-78; Registrum sacrum anglicanum, Oxf.,
1858; Select charters and other illustrations of English constitutional
history, 2 ed., Oxf., 1874.
Лит.: Гутнова Е. В., Историография истории средних веков, M., 1974
(см. Указат. имен).
СТЕБУТ Иван Александрович [31.1 (12.2). 1833, Великие Луки, ныне Псковской
обл., - 20.10.1923, Москва], русский учёный-агроном. В 1854 окончил Горы-Горецкий
земледельч. ин-т (ныне Белорусская с.-х. академия), с 1860 проф. там же. В
1865-94 проф. Петровской земледельч. и лесной академии в Москве (ныне Моск.
с.-х. академия им. К. А. Тимирязева), возглавил первую в России кафедру
растениеводства; на организованной им опытной станции академии проводил большую
работу по изучению агротехники полевых культур. Пропагандировал внедрение
достижений агрономич. науки в практику с. х-ва. Автор работы "Основы
полевой культуры и меры к её улучшению в России" (в. 1-2, 1873-79) и
соавтор "Настольной книги сельских хозяев" (т. 1-3, 1875-80).
Выступал в защиту женского с.-х. образования в России. При участии С.
разработано и утверждено Положение о с.-х. опытных учреждениях (1901-02).
Редактор (1869-70) журн. -"Русское сельское хозяйство".
Соч.: Избр. соч., т. 1 - 2, M., 1956-57 (лит.).
Лит.: Балашев Л. Л., Иван Александрович Стебут, M., 1966.
СТЕВЕН (Steven) Христиан Христианович [19(30).1.1781, Фридрихсгамн,
ныне г. Хамина, Финляндия, - 18(30).4.1863, Симферополь], русский ботаник и
энтомолог, почётный чл. Петерб. АН (1849; чл.-корр. 1815). По национальности
швед. Окончил Медико-хирургич. академию в Петербурге (1799). Инспектор
шелководства на Кавказе (1800), пом. старшего инспектора (1806), гл. инспектор
шелководства и с. х-ва на юге России (1826-51). В 1812 организовал Никитский
ботанический сад в Крыму и был его директором до 1824. Осн. труды посвящены
флоре Крыма и Кавказа, систематике семенных растений и насекомых.
Лит.: Станков С. С., Христиан Христианович Стевен. (1781 - 1863), M.,
1940.
СТЕВИН (Stevin) Симон (1548, Брюгге,- 1620, Гаага), нидерландский
учёный и инженер. С 1583 преподавал в Лейденском ун-те. В 1592 получил место
инженера, а затем суперинтенданта по воен. и финанс. вопросам у Морица
Оранского. В 1600 организовал инж. школу при Лейденском ун-те, где читал
лекции по математике. Работа С. "Десятина" (De Thiende, 1585)
посвящена десятичной системе мер и десятичным дробям, к-рые С. ввёл в
употребление (в Европе).
В механике С. дал доказательство закона равновесия тела на наклонной
плоскости, основанное на невозможности вечного движения, сформулировал правила
равновесия трёх сил, образующих замкнутый треугольник. С. принадлежат также
работы по гидростатике, навигации, технич. и военно-инж. вопросам.
Соч.: The principal works
of Simon Stevin, v. 1-5, Amst., 1955-66; в рус. пер.- Начала гидростатики, в
сб.: Начала гидростатики. Архимед. Стэвин. Галилей. Паскаль, М. -Л., 1932.
Лит.:
Steichen M., Memoire sur Ia vie et
les travaux de Simon Stevin, Brux., 1846; D e р a u R., Simon Stevin, Brux., 1942.
И.
Д. Рожанский.
СТЕГАЛЬНЫЙ ЧЕРЕП (от греч. stege - крыша), анапсидный, или стегокротафический, череп (от греч. krotaphos - висок), в к-ром покровные кости
образуют сплошной щит с отверстиями лишь для ноздрей и глаз. Характерен для
костных рыб, древних земноводных и наиболее примитивных пресмыкающихся (илл.
см. т. 5, стр. 107, рис. 1, A). В процессе эволюции у типичных наземных позвоночных
в крыше черепа в височной области (позади глазниц) образуются височные окна,
разделённые скуловыми дугами, или височными дугами. В результате
увеличивается место для челюстной мускулатуры, а С. ч. превращается в
зигальный, или зигокротафический (от греч. zygoma - скуловая дуга). При
редукции скуловых дуг у змей височная область становится обнажённой; такой
череп наз. гимнокротафическим (от греч. gymnos - голый). У безногих
земноводных кости крыши черепа вторично разрастаются, перекрывая височные окна,-
вторично С. ч. Редукция С. ч. может осуществляться также путём утраты части
покровных костей (особенно в глазничной области).
Л. П. Татаринов.
СТЕГОЗАВРЫ (Stegosauria), подотряд птицетазовых динозавров. Жили
в юре и начале мела. Ранние С.- сцелидозавры, по-видимому, ходили преим. на
задних ногах, более поздние - вторично вернулись к передвижению на 4 ногах. С.
были громадными (дл. до 6 м) растительноядными животными с относительно
маленькой головой. Спина и хвост сверху были усажены мощными костными шипами,
защищавшими тело от нападения крупных хищников - карноэавров; их
появлением, вероятно, был вызван переход С. к четвероногому хождению, при к-ром
уменьшалась уязвимая поверхность тела. С., судя по строению зубов, были
исходным стволом для остальных четвероногих птицетазовых динозавров начиная с анкилозавров.
Остатки С. известны из Сев. Америки, Зап. Европы, Сев. и Вост. Африки.
Сообщения о находках С. в Азии оказались ошибочными.
СТЕГОЦЕФАЛЫ (Stegocephalia), ископаемые земноводные, крыша черепа
к-рых образовывала сплошной покров, а туловище нередко было покрыто костными
щитками. Жили в девоне - триасе. С. противопоставляли совр., или
"голым", земноводным. T. к. нек-рые С. (напр., лепоспондилы) ближе
к совр. земноводным, большую часть С. включают в надотряд лабиринтодонтов и
назв. "С." больше не применяют.
СТЕЙНБЕК (Steinbeck) Джон Эрнст (27.2.1902, Салинас, шт. Калифорния,-
20.12.1968, Нью-Йорк), американский писатель. Учился на биологич. ф-те
Станфордского ун-та. В молодости сменил ряд профессий. В раннем творчестве
разделял романтич. иллюзии о возможности бегства от бурж. общества (роман
"Чаша господня", 1929), тяготел к изображению причудливых типов
провинц. и сел. Америки (циклы рассказов "Райские пастбища", 1932, "Рыжий
пони", 1933). В 30-е гг. сложился как писатель острой социальной
проблематики (роман "В схватке с сомнительным исходом", 1936, повесть
"О мышах и людях", 1937, рус. пер. 1963). Герои С. трагичны своей
обездоленностью и непониманием причин преследующих их жизненных крушений.
Вершина творчества С. роман "Гроздья гнева" (1939, рус. пер. 1940), в
центре к-рого судьба согнанных с земли фермеров, кочующих по стране в поисках
работы. Через тяжкие испытания герои приходят к сознанию того, что они -
частица страдающего и борющегося народа. В 40-с гг. отступил от традиций
пролет, и революц. лит-ры (романы "Консервный ряд", 1945;
"Заблудившийся автобус", 1947; "К Востоку от рая", 1952).
Новый взлёт творчество С. пережило в нач. 60-х гг. Роман "Зима тревоги
нашей" (1961, рус. пер. 1962) и кн. очерков "Путешествие с Чарли в
поисках Америки" (1962, рус. пер. 1965) с тревогой поведали о разрушении
личности в мире мещанских стандартов, в атмосфере обманчивого процветания. В
годы войны во Вьетнаме выступил с оправданием агрессии США. Нобелевская пр. (1962).
С о ч.: The long
valley, L., 1964; The moon is down, N. Y., 1964; в рус. пер.- Жемчужина.
Квартал Тортилья Флэт, M., 1963.
Лит.: Мендельсон M. О., Современный американский роман, M., 1964;
Fontenrose J., J. Steinbeck..., N. Y., 1964; M oore H. Т., The novels of J.
Steinbeck, 2 ed.. Port
Washington (N. J.), [1968]; Steinbeck's literary dimension: a guide to
comparative studies, Metuchen (N. J.), 1973; Hayashi T., A new Steinbeck
bibliography 1929 - 1971, Metuchen (N. Y.), 1973.
A. M. Зверев.
Дж. Э. Стейнбек.
СТЕЙНИЦ (Steinitz) Вильгельм (14.5. 1836, Прага, - 12.8.1900,
Нью-Йорк), первый чемпион мира по шахматам (1886-1894), шахматный теоретик.
Учился в Венском политехнич. институте. В 1862-83 жил в Лондоне, с 1883 - в
США. Чемпионом мира официально провозглашён после победы в матче с И.
Цукертортом (1886). В 80-х гг. 19 в. разработал теорию позиционной игры в
шахматах. Крупнейшие успехи С.- победы в матчах с А. Андерсеном (1866), M. И. Чигориным (1889, 1892), И. Гунсбергом (1890-91), Э. С.
Шифферсом (1896) и в международных турнирах: Вена, 1873 и 1882 (совм. с Ш. А.
Винавером); Нью-Йорк, 1894. В 1894 С. проиграл матч на первенство мира Э.
Ласкеру.
Лит.: Л е в и д о в M. Ю., Стейниц, Ласкер, M., 1936; H е
й ш т а д т
Я. И., Первый чемпион мира, M., 1971.
СТЕЙНЛЕН (Steinlen) Теофиль Александр (10.11.1859, Лозанна, - 14.12.
1923, Париж), французский график. Уроженец Швейцарии. Окончил художеств, школу
в Лозанне. С 1882 жил в Париже. Работал в основном в технике литографии.
Сотрудничал в соцналистич. журналах, иллюстрировал книги (напр., сб. А. Брюана
"На улице", 1888). Следуя традициям О. Домье, С. лаконично и
остро показывал социальное неравенство, ужасы войны, революц. борьбу народа
("Стачка", 1898, илл. см. т. 14, табл. XLI, стр. 560-561;
"Освободительница", 1903; "Беженцы", офорт, 1916). Работал
также как карикатурист и мастер плаката, обращался к живописи.
В поел. годы жизни С. был активным участником журнала "Кларте",
сотрудничал в "Юманите".
Илл. см. также на вклейке, табл. XXXVIII.
Лит.: Калитина H., Стейнлен, M., 1959; Стейнлен. [Альбом. Авт.- сост.
В. Tyрова], M., 1960; Contat-Mercanton L.,
Steinlen, Berne. 1959.
T. Стейнлен. Автопортрет. Литография. 1905.
"СТЕЙТ БАНК ОФ ИНДИЯ", см. Государственный банк Индии.
СТЕКА, стек (итал. stecca), основной инструмент при лепке. С.
имеют вид небольших (и часто изогнутых) деревянных, костяных или металлич.
палочек с расширяющимися концами в форме прямой, закруглённой либо скошенной
лопаточки, ланцета и пр. С. бывают односторонними и двусторонними.
Распространены также проволочные С.- кольца различной кривизны на деревянных
ручках.
СТЕККЕТТИ (Stecchetti) Лоренцо (1845-1916), итальянский поэт; см. Гуэррини
О.
СТЕКЛО, твёрдый аморфный материал, полученный в процессе
переохлаждения расплава. Для С. характерна обратимость перехода из жидкого
состояния в метастабильное, неустойчивое стеклообразное состояние. При
определённых температурных условиях кристаллизуется. С. не плавится при
нагревании подобно кристаллич. телам, а размягчается, последовательно переходя
из твёрдого состояния в пластическое, а затем в жидкое. По агрегатному
состоянию С. занимает промежуточное положение между жидким и кристаллическим
веществами. Упругие свойства делают С. сходным с твёрдыми кристаллич. телами, а
отсутствие кристаллографич. симметрии (и связанная с этим изотропность)
приближает к жидким. Склонность к образованию С. характерна для мн. веществ
(селен, сера, силикаты, бораты и др.).
С. наз. также отд. группы изделий из С., напр, строительное С., тарное С.,
химико-лабораторное С. и др. Изделия из С. могут быть прозрачными или
непрозрачными, бесцветными или окрашенными, люминссцировать под воздействием,
напр., ультрафиолетового и 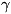 -излучения, пропускать или поглощать
ультрафиолетовые лучи и т. д. Наибольшее распространение получило неорганич.
С., характеризующееся высокими механич., тепловыми, хим. и др. свойствами. Осн.
масса неорганич. С. выпускается для строительства (гл. обр. листовое) и для
изготовления тары. Эти виды продукции получают преим. из С. на основе двуокиси
кремния (силикатное С.); применение находят также и др. кислородные (оксидные)
С., в состав к-рых входят окислы фосфора, алюминия, бора и т. д. К
бескислородным неорганическим С. относятся С. на основе халькогенидов мышьяка
(As2S3), сурьмы (Sb2Se3) и т. д.,
галогенидов бериллия (BeF2) и т. д. (см. также Полупроводники
аморфные).
-излучения, пропускать или поглощать
ультрафиолетовые лучи и т. д. Наибольшее распространение получило неорганич.
С., характеризующееся высокими механич., тепловыми, хим. и др. свойствами. Осн.
масса неорганич. С. выпускается для строительства (гл. обр. листовое) и для
изготовления тары. Эти виды продукции получают преим. из С. на основе двуокиси
кремния (силикатное С.); применение находят также и др. кислородные (оксидные)
С., в состав к-рых входят окислы фосфора, алюминия, бора и т. д. К
бескислородным неорганическим С. относятся С. на основе халькогенидов мышьяка
(As2S3), сурьмы (Sb2Se3) и т. д.,
галогенидов бериллия (BeF2) и т. д. (см. также Полупроводники
аморфные).
По назначению различают: строительное стекло (оконное, узорчатое,
стеклянные блоки н т. д.), тарное стекло, стекло техническое (кварцевое
стекло, светотехническое стекло, стеклянное волокно и т. д.), сортовое
стекло и т. д. Вырабатываются С., защищающие от ионизирующих излучений, С.
индикаторов проникающей радиации, фотохромные С. с переменным
светопропусканием, С., применяемое в качестве лазерных материалов, увиолевое
стекло, пеностекло, растворимое С. и др. Растворимое С., содержащее ок. 75%
SiO2, 24% Na2O и др. компоненты, образует с водой клейкую
жидкость (жидкое С.); используется как уплотняющее средство, напр, для
изготовления силикатных красок, конторского клея, в качестве диспергаторов и
моющих средств, для пропитки тканей, бумаги и пр. Хим. состав нек-рых видов С.
приведён в таблице.
Физико-химические свойств а С. Свойства С. зависят от сочетания входящих в
их состав компонентов. Наиболее характерное свойство С.- прозрачность
(светопрозрачность оконного С. 83-90%, а оптического стекла - до
99,95%). С. типично хрупкое тело, весьма чувствительное к механич.
воздействиям, особенно ударным, однако сопротивление сжатию у С. такое же, как
у чугуна.
Для повышения прочности С. подвергают упрочнению (закалка, ионный обмен, при
к-ром на поверхности С. происходит замена ионов, напр, натрия, на ионы лития
или калия, хим. и термохим. обработка и др.), что ослабляет действие
поверхностных микротрещин (трещины Гриффитса), возникающих на поверхности С. в
результате воздействия окружающей среды (темп-pa, влажность и пр.) и являющихся
концентраторами напряжений, и позволяет повысить прочность С. в 4-50 раз.
Обычно для устранения влияния микротрещин применяют стравливание или сжатие
поверхностного слоя. При стравливании дефектный слой растворяется плавиковой
к-той, а на обнажившийся бездефектный слой наносится защитная плёнка, напр, из
полимеров. При закалке поверхностный слой сжимается, что препятствует раскрытию
трещин. Плотность С. 2200-8000 кг/м3, твёрдость по
минералогич. шкале 4,5-7,5, микротвёрдость 4-10 Гн/м2, модуль
упругости 50-85 Гн/м2. Предел прочности С. при сжатии равен
0,5-2 Гн/м2, при изгибе 30-90 Мн/м2, при
ударном изгибе 1,5-2 кн/м2. Теплоёмкость С. 0,3-1 кдж/кг *К,
термостойкость 80° - 1000 °С, температурный коэфф. расширения (0,56-12)·109
1/К. Коэфф. теплопроводности С. мало зависит от его хим. состава и равен 0,7
-1,3 вт/(м *К). Коэфф. преломления 1,4-2,2, электрич. проводимость 10-8
- 10-18ом -1 -см1, диэлектрич.
проницаемость 3,8-16.
Технология С. Произ-во С. состоит из след, процессов: подготовки
сырьевых компонентов, получения шихты, варки С., охлаждения стекломассы,
формования изделий, их отжига и обработки (термической, химической,
механической). К гл. компонентам относят стеклообразующие вещества (природные,
напр. SiO2, и искусственные, напр. Na2CO3), содержащие
основные (щелочные и щёлочноземельные) и кислотные окислы. Главный компонент
большинства промышленных С. - кремнезём (кремния двуокись), содержание
к-рого в С. составляет от 40 до 80% (по массе), а в кварцевых и кварцоидных от
96 до 100%. В стекловарении обычно в качестве источника кремнезёма используют
кварцевые стекольные пески, которые в случае необходимости обогащают. Сырьём,
содержащим борный ангидрид, являются борная кислота, бура и др. Глинозём
вводится с полевыми шпатами, нефелином и т. д.; щелочные окислы - с
кальцинированной содой и поташом; щёлочноземельные окислы - с мелом, доломитом
и т. п. Вспомогат. компоненты - соединения, придающие то или иное свойство,
напр. окраску, ускоряющие процесс варки и т. д. Напр., соединения марганца,
кобальта, хрома, никеля используются как красители, церия, неодима, празеодима,
мышьяка, сурьмы - как обесцвечиватели и окислители, фтора, фосфора, олова,
циркония - как глушители (вещества, вызывающие интенсивное светорассеяние); в
качестве осветлителей применяют хлорид натрия, сульфат и нитрат аммония и др.
Все компоненты перед варкой просеиваются, сушатся, при необходимости
измельчаются, смешиваются до полностью однородной порошкообразной шихты, к-рая
подаётся в стекловаренную печь.
Процесс стекловарения условно разделяют на несколько стадий:
силикато-образование, стеклообразование, осветление, гомогенизацию и охлаждение
("студку").
При нагревании шихты вначале испаряется гигроскопическая и химически
связанная вода. На стадии силикатообразования происходит термическое разложение
компонентов, реакции в твёрдой и жидкой фазе с образованием силикатов, к-рые
вначале представляют собой спекшийся конгломерат, включающий и не вступившие в
реакцию компоненты. По мере повышения темп-ры отд. силикаты плавятся и,
растворяясь друг в друге, образуют непрозрачный расплав, содержащий значит,
количество газов и частицы компонентов шихты. Стадия силикатообразования
завершается при 1100-1200 0C.
На стадии стсклообразования растворяются остатки шихты и удаляется пена -
расплав становится прозрачным; стадия совмещается с конечным этапом силикатообразования и протекает при темп-ре 1150-1200 0C. Собственно
стсклообразованием называют процесс растворения остаточных зёрен кварца в
силикатном расплаве, в результате чего образуется относительно однородная
стекломасса. В обычных силикатных С. содержится ок. 25% кремнезёма, химически
не связанного в силикаты (только такое С. оказывается пригодным по своей хим.
стойкости для практич. использования). Стеклообразование протекает значительно
медленнее, чем силикатообразование, оно составляет ок. 90% от времени,
затраченного на провар шихты и ок. 30% от общей длительности стекловарения.
Обычная стекольная шихта содержит ок. 18% химически связанных газов (CO2,
SО2, O2 и др.). В процессе провара шихты эти газы в основном
удаляются, однако часть их остаётся в стекломассе, образуя крупные и мелкие
пузыри.
Состав некоторых промышленных стёкол
На стадии осветления при длит. выдержке при темп-ре 1500-1600 °С уменьшается
степень пересыщения стекломассы газами, в результате чего пузырьки больших
размеров поднимаются на поверхность стекломассы, а малые растворяются в ней.
Для ускорения осветления в шихту вводят осветлители, снижающие поверхностное
натяжение стекломассы; стекломасса перемешивается спец. огнеупорными мешалками
или через неё пропускают сжатый воздух или др. газ.
Одновременно с осветлением идёт гомогенизация - усреднение стекломассы по
составу. Неоднородность стекломассы обычно образуется в результате плохого
перемешивания компонентов шихты, высокой вязкости расплава, замедленности
диффузионных процессов. Гомогенизации способствуют выделяющиеся из стекломассы
газовые пузыри, к-рые перемешивают неоднородные микроучастки и облегчают
взаимную диффузию, выравнивая концентрацию расплава. Наиболее интенсивно
гомогенизация осуществляется при механич. перемешивании (наибольшее распространение
эта операция получила в произ-ве оптич. С.).
Последняя стадия стекловарения - охлаждение стекломассы ("студка")
до вязкости, необходимой для формования, что соответствует темп-ре 700- 1000 0C.
Гл. требование при "студке" - непрерывное медленное снижение темп-ры
без изменения состава и давления газовой среды; при нарушении установившегося
равновесия газов образуется т. н. вторичная мошка (мелкие пузыри).
Процесс получения нек-рых С. отличается специфическими особенностями. Напр.,
плавка оптического кварцевого С. в электрических стекловаренных печах ведётся
сначала в вакууме, а в конце плавки - в атмосфере инертных газов под давлением.
Произ-во каждого типа С. определяется технологической нормалью.
Формование изделий из стекломассы осуществляется механич. способом
(прокаткой, прессованием, прессовыдуванием, выдуванием и т. д.) на стеклоформующих
машинах. После формования изделия подвергают термич. обработке (отжигу).
В результате отжига (выдержки изделий при темп-ре, близкой к темп-ре
размягчения С.) и последующего медленного охлаждения происходит релаксация
напряжений, появляющихся в С. при быстром охлаждении. В результате т. н.
закалки в С. возникают остаточные напряжения, обеспечивающие его повышенную
механич. прочность, термостойкость и специфический (безопасный) характер
разрушения в сравнении с обычным С. (закалённые С. применяют для остекления
автомобилей, вагонов и т. п. целей).
Историческая справка. В природе существует природное С.- перлит, обсидиан
(см. Вулканическое стекло).
Появление искусств. С. обычно связывают с развитием гончарства. При
обжиге на изделие из глины могла попасть смесь соды и песка, в результате чего
на поверхности изделия образовалась стекловидная плёнка-глазурь. Произ-во С.
началось в 4-м тыс. до н. э. (Др. Египет, Передняя Азия).
Первоначально получались непрозрачные С., с помощью к-рых имитировали
поделочные камни (малахит, бирюзу и т. д.). Постепенно состав С. менялся,
количество окислов щелочных металлов с 30% (по массе) уменьшилось до 20%; в С.
вводились окислы свинца и олова; для окрашивания стали добавлять соединения
марганца и кобальта. Во 2-м тыс. до н. э. в Египте С. варили в глиняных
горшочках - тиглях ёмкостью ок. 0,25 л.
Коренные изменения в технологии стеклоделия произошли на рубеже нашей эры,
когда были решены две важнейшие проблемы стеклоделия - изготовление прозрачного
бесцветного С. и формование изделий выдуванием. Получение прозрачного С. стало
возможным в результате усовершенствования стекловаренных печей, что позволило
повысить темп-ру варки и надёжно воспроизводить условия хорошего осветления
стекломассы. Стеклодувная трубка, изобретённая в 1 в. до н. э., оказалась
универсальным инструментом, с помощью к-рого стало возможным создавать простые,
доступные всем предметы обихода, напр., посуду. Первым науч. трудом по
стеклоделию считают вышедшую во Флоренции в 1612 книгу монаха Антонио Нери, в
к-рой были даны указания об использовании окислов свинца, бора и мышьяка для
осветления С., приведены составы цветных С. Во 2-й пол. 17 в. нем. алхимик И. Кункель
опубликовал соч. "Экспериментальное искусство стеклоделия", он же
изобрёл способ получения золотого рубина. В 1615 в Англии стали применять для
нагрева стеклоплавильных печей уголь, что повысило температуру в печи. С начала
17 в. во Франции был предложен способ отливки зеркальных С. на медных плитах, с
последующей прокаткой; в то же время был открыт метод травления С. смесью
плавикового шпата и серной к-ты, освоено произ-во оконного и оптич. С. Существ,
роль в создании основ стеклоделия сыграли рус. учёные: M. В. Ломоносов, Э. Г.
Лаксман, С. П. Петухов, А. К. Чугунов, Д. И. Менделеев, В. E. Тищенко.
До кон. 19 в. в стеклоделии преобладал ручной труд, и только со 2-й пол. 20
в. произ-во всех видов массового С. (оконное, тарное и др.) было механизировано
и автоматизировано, а ручные методы сохранились лишь при изготовлении
художеств. С. и нек-рых сортовых изделий (см. также Стекольная промышленность).
H. M. Павлушкин.
Художественное С. включает в себя витражи, смальтовые мозаики,
сосуды художественные, архит. детали, декоративные композиции, скульптуру
(обычно малых форм), светильники, искусств, драгоценности (бижутерия). В
древнем мире произ-во С. было особенно развито в Египте (эпоха Птолемеев, 4 - 1
вв. до н. э.), Сирии, Финикии, Китае.
Стеклянный светильник для мечети, покрытый эмалью и золочением (Сирия). Ок.
1309-10. Виктории и Альберта музей. Лондон.
Как правило, в иск-ве древнего мира изделия из С. (небольшие вазочки, чаши,
блюдца, бусы, серьги, амулеты, печати) изготовлялись посредством прессования в
открытых глиняных формах или путём навивания стекломассы на палочку; такое С.
обычно было непрозрачным, а по цвету - зелёным, голубым, бирюзовым. Изобретение
способа свободного выдувания С. с помощью трубки, а также повышение темп-ры его
варки дали эллинистическим и др.-рим. мастерам возможность получать
тонкостенные (иногда двухслойные) более прозрачные и однородные по массе
изделия относительно крупных размеров.
С 6 в. центры художеств, стеклоделия сосредоточились в Византии, где
процветала выделка цветного непрозрачного стекла для посуды и смальт. В
ср.-век. Зап. Европе эпохи готики важнейшей областью иск-ва,
стимулировавшей развитие вкуса к художеств. С., было изготовление витражей.
Среди ср.-век. стран мусульм. Востока в 12-14 вв. произ-вом стеклянных изделий
с эмалевыми росписями славилась Сирия.
В 15-16 вв. ведущее значение в декоративно-прикладном иск-ве Европы
приобрело венецианское стекло. С изобретением в 17 в. более твёрдого
кальциевого С. и развитием техники гравировки центр художеств. стеклоделия
переместился в Чехию (см. Чешское стекло). С 1770-х гг. (первоначально в
Англии) стало широко применяться С., полученное на основе окиси свинца
(хрусталь или флинтгласс), гл. способом обработки к-рого явилось т. н.
алмазное гранение, выявляющее способность хрусталя преломлять или отражать
свет. Начиная с 18 в. интенсивно развивается а. произ-во искусственных
драгоценных камней. На рубеже 19-20 вв. к художеств. С. обращаются специалисты
по декоративно-прикладному иск-ву (Э. Галле, О. Даум, Э. Руссо во Франции, Й.
Хофман в Австрии, Л. К. Тиффани в США); в их изделиях, нередко отличающихся
стремлением к ассоциативному сопоставлению художественных и природных, преим. растительных
форм, преобладали черты стиля "модерн". Для совр. художеств.
С. характерно необычайное разнообразие техник и стилевых тенденций; увлечение
изысканными, подчёркнуто фантастич. конфигурациями и усложнённо-орнаментальной
обработкой поверхностей сосуществует с тяготением к аскетически-строгим
решениям, выделяющим в качестве важнейших элементов образа простоту форм и
прозрачность неукрашенного С.
В Др. Руси стеклоделие получило, значит, развитие уже в домонгольский период
(выделка украшений, сосудов, смальты для мозаик). Прерванное татаромонг.
нашествием, произ-во художеств. С. возродилось в 17 в., когда в 1635 был
основан первый в России стекольный завод. Огромный вклад в произ-во цветного С.
(гл. обр. для мозаик, бижутерии и архит. облицовки) внёс M. В. Ломоносов,
создавший в 1753 Усть-Рудицкую ф-ку. Важнейшую роль в развитии рус. стеклоделия
сыграл Имп. хрустальный и стекольный з-д в Петербурге (заложенный Петром I в
нач. 18 в. под Москвой и к сер. 18 в. вместе с Ямбургскими з-дами переведённый
в Петербург). В 18 в. были основаны также Гусевской хрустальный завод и Дятьковский
хрустальный завод. Для рус. иск-ва 18 в. было характерно гутное С.,
изготовлявшееся путём свободного выдувания и лепки на небольших купеч. заводах
(изделия из такого С., часто тёмные по тону, расписывались эмалевыми красками),
и прозрачное светлое С., декорируемое в основном с помощью гравировки и
выпускавшееся Имп. заводом и наиболее крупными частными предприятиями; на этих
же заводах с сер. 18 в. производилось много изделий из молочного С. По проектам
крупнейших зодчих (A. H. Воронихина, Ч. Камерона, M. Ф. Казакова, H. А. Львова,
К. И. Росси, T. де Томона) на Имп. заводе выполнялись (в стиле классицизма) детали
осветит, арматуры, мебели и архит. декора. С кон. 18 в. здесь же были освоены
варка свинцового хрусталя и алмазное гранение, для к-рого в нач. 19 в. типичен
особый рисунок, подражающий бриллиантовой огранке ("русский
камень"). К сер. 19 в. в русском художеств. С. возникает увлечение
гигантскими размерами изделий (сборные хрустальные канделябры, вазы, детали
архит. декора); в кон. 19 в. развивается имитационное направление (подражание
камню, фарфору, дереву и металлу), распространяются влияния стиля
"модерн".
B.C. Муратов. "Конь". Хрусталь. 1968.
В СССР интенсивное произ-во художеств. С. начинается с кон. 1930-х гг.
Ведущую роль в развитии сов. художеств, стеклоделия сыграла скульптор В. И.
Мухина (см. Ленинградский завод художественного стекла). В 50-60-е гг.
художеств, лаборатории появились почти на всех крупных сов. заводах сортовой
посуды. Среди видных мастеров декоративно-прикладного иск-ва, работавших на
заводах СССР в 60-70-е гг., - Г. А. Антонова, А. А. Аствацатурьян, А. Г.
Балабин, С. M. Бескинская, M.-T. В.Грабарь, О. И. Гущин, Ю. В. Жульев, А. Д.
Зельдич, X. Кырге, Л. M. Митяева, В. С. Муратов, В. С. Мурахвер, M. А.
Павловский, С. Раудвеэ, E. И. Рогов, Б. А. Смирнов, В. А. Филатов, В. Я.
Шевченко, Л. О. Юрген, E. В. Яновская. В сов. художеств. С. выделяется неск.
направлений: ленинградская школа (бесцветный и цветной хрусталь строгих форм с
алмазной гранью), владимирское С. (использование традиций рус. гутного С.),
украинское С. (традиции укр. гутного С., яркая полихромия), прибалтийская школа
(слабо окрашенное прессованное С. с тонкой гравировкой). В 60- 70-е гг.плодотворно
развивается витраж, широкое распространение получают создание хрустальных
фонтанов и различных декоративных установок из С. и металла, изготовление
изделий (в т. ч. гобеленов из стеклоткани) для украшения интерьеров.
Н. В.
Воронов.
Илл. см. на вклейках - к стр. 121 и табл. XXXIII-XXXV.
Лит.: Петухов С. П., Стеклоделие, СПБ, 1898; Безбородов M. А., Очерки
по истории русского стеклоделия, M., 1952; Евстропьев К. С., Торопов H.А.,
Химия кремния и физическая химия силикатов, M., 1950; Качалов H., Стекло, M.,
1959; Батанова E. И., Воронов H. В., Советское художественное стекло, [M.,
1964]; Бартенев Г. M., Строение и механические свойства неорганических стекол,
M., 1966; Технология стекла, 4 изд., M., 1967; Шелковников Б., Русское
художественное стекло, Л., 1969; Aппен А. А., Химия стекла, 2 изд., Л., 1974; P о у с о н Г., Неорганические стеклообразующие системы, пер. с англ., M.,
1970; Pожанковский В. Ф., Стекло и художник, M., 1971; Воронов H. В., Paчук
E. Г., Советское стекло, [Л.], 1973; "Journal of glass studies!·, с 1959
(изд. продолж.); Grover R. and L., Contemporary art glass, N. Y., [1975].
"СТЕКЛО И КЕРАМИКА", ежемесячный научно-технич. и
производств, журнал, орган Мин-ва пром-сти строит, материалов СССР. Начал
издаваться в Ленинграде в 1925; с 1927 издаётся в Москве. В 1925-38 выходил под
названием "Керамика и стекло", в 1938- 1940 - "Стекольная
промышленность", в 1944-47 - "Стекольная и керамическая
промышленность". Освещает вопросы технологии, экономики и организации
производства всех видов стекла и тонкой керамики. Тираж (1975) 10 тыс. экз.
СТЕКЛО ОРГАНИЧЕСКОЕ, технич. название оптически прозрачных твёрдых
материалов на основе органич. полимеров (полиакрилатов, полистирола,
поликарбонатов, сополимеров винилхлорида с метилметакрилатом и др.). В пром-сти
под "органич. стеклом" обычно понимают листовой материал, получаемый
полимеризацией в массе (блоке) метилметакрилата (см. Полиметилметакрилат). Реакцию
осуществляют в формах, собранных из листов силикатного стекла, стали или алюминия;
между листами помещают эластичные прокладки, толщина к-рых определяет толщину
листа С. о. Чтобы избежать дефектов в листе, вызываемых значит, усадкой (~23%)
реакционной массы, процесс проводят след, способами: вначале получают т. н.
форполимер (сиропообразную жидкость с вязкостью 50-200 мн*сек/м2,
или спз), к рую затем заливают в форму и полимеризуют, или
полимеризуют в форме раствор полиметилметакрилата в мономере (т. н.
сироп-раствор). Пластификаторы, красители, замутнители, стабилизаторы или др.
компоненты (в зависимости от назначения С. о.) вводят в форполимер или
сироп-раствор, смесь тщательно перемешивают, вакуумируют и фильтруют, заливают
в герметизируемые формы, к-рые помещают в камеры с циркулирующим тёплым
воздухом или в ванны с тёплой водой (условия изотермические). По окончании
полимеризации листы С. о. извлекают из форм и подвергают окончат, обработке.
С. о. можно перерабатывать вакуум и пневмоформованием, штампованием; его
можно обрабатывать механически, склеивать и сваривать. С. о. применяют как
конструкционный материал в авиа-, автомобиле- и судостроении, для остекления
парников и теплиц, куполов, окон, веранд и декоративной отделки зданий, для
изготовления деталей приборов и инструментов, протезов - в медицине, линз и
призм - в оптике, труб - в пищ. пром-сти и др.
С. о. различных марок производится в СССР; за рубежом выпускается под назв.
плексиглас (США, ФРГ, Франция), перспекс (Великобритания), к л а р е к с
(Япония).
СТЕКЛОБЛОК, стеклянный блок, строит, изделие с герметичной полостью,
изготовляемое формованием (из стекломассы) и последующим свариванием двух
составляющих элементов (полублоков). Выпускаются С. светорассеивающие и
светонаправляющие, из бесцветного и окрашенного стекла, квадратного и
прямоугольного сечений, уголковые и др. Светорассеивающий и светонаправляющий
эффекты достигаются нанесением на поверхность С. (при формовании) спец.
рифлений и узоров. Размеры С. от 200 X 200 до 400 X 400 мм, толщина
80-100 мм. Применяются для заполнения световых проёмов в наружных стенах
и дня устройства светопрозрачных покрытий и перегородок. С. создают мягкое
освещение, обладают высокими декоративными качествами, огнестойкостью, тепло- и
звукоизолирующей способностью. Коэфф. пропускания света С. (%): бесцветных
50-60, цветных 35-40; коэфф. рассеяния света 25-30%.
СТЕКЛОВ Владимир Андреевич [28.12. 1863 (9.1.1864), H. Новгород, ныне
Горький, - 30.5.1926, Крым, похоронен в Ленинграде], советский математик, акад.
(1912; чл.-корр. 1902). В 1919-26 вице-президент АН СССР. В 1887 окончил Харьковский
ун-т, где учился у A. M. Ляпунова. В 1889-1906 работал на кафедре
механики в Харьковском ун-те, сначала в качестве ассистента, затем
приватдоцента (с 1891) и проф. (с 1896). В 1893-1905 был преподавателем
теоретической механики Харьковского технологич. ин-та. В 1894 защитил
магистерскую диссертацию "О движении твердого тела в жидкости" (изд.
1893), а в 1902 - докторскую диссертацию "Общие методы решения основных
задач математической физики" (изд. 1901). В 1906 С. перешёл на работу в
Петерб. ун-т. Вёл большую общественную и научно-организац. работу, особенно в
последние годы жизни. По его инициативе организован при АН Физико-математич.
ин-т (в 1921), директором к-рого он состоял до конца своей жизни. В 1926 имя С.
было присвоено Физико-математич. ин-ту, к-рый в 1934 разделился на два ин-та
(один из них - Математич. ин-т АН СССР сохранил имя С.).
Осн. направления науч. творчества С.- приложения математич. методов к
вопросам естествознания; большая часть его работ относится к математич. физике.
С. получил ряд существенных результатов, касающихся осн. задач теории
потенциала. Для функций, обращающихся в нуль на границе области, С. вывел
функциональное неравенство типа неравенства Пуанкаре с точной константой.
Большинство работ С. посвящено вопросам разложения функций в ряды по наперёд
заданным ортогональным системам функций, обычно к таким системам
приводят краевые задачи математич физики
B. А. Стеклов.
В основе этих исследований лежит введенное С. понятие замкнутости системы
ортогональных функций С. вплотную подошел к понятию гильбертова пространства. При
исследовании вопросов разложений в ряды С. развил асимптотич. методы, среди
к-рых - метод получения асимптотич. выражений для классич ортогональных
многочленов, называемый методом Лиувилля - Стеклова. Установленные С. теоремы о
разложимости в обобщенный ряд Фурье весьма близки к т. н. теоремам
"равносходимости" С. ввел особый метод сглаживания функций, к-рый
затем получил большое развитие (см. Стеклова функция). С. - автор ряда
работ по математич. анализу, в частности, по теории квадратурных формул, а также
по теории упруюсти и гидромеханике. С. известен как историк математики, философ и
писатель. Ему принадлежат книги научно-биографич. характера о M. В. Ломоносове и Г.
Галилее, очерки и статьи о жизни и деятельности П. Л. Чебышева, H. И.
Лобачевского, M. В. Остроградского, A. M. Ляпунова, А. А. Маркова, А. Пуанкаре, Дж.
Томсона и др., работа по философии "Математика и ее значение для
человечества" (1923), а также книга "В Америку и обратно.
Впечатления" (1925).
Лит.: Памяти В. А. Стеклова. Сб.
ст., Л., 1928 (лит.), Смирнов В. И. Памяти
Владимира Андреевича Стеклова, "Тр. Математического института им. В. А.
Стеклова", 1964, т. 73; Игнациус Г. И., Владимир Андреевич Стеклов, M., 1967; Владимиров В. С. Маркуш И. И. Академик В. А. Стеклов, M 1973 (лит.).
В. С. Владимиров.
СТЕКЛОВ (Ю. Невзоров) Юрий Михайлович (наст. фам. Нахамкис) [15(27) 8
1873 - 15 9 1941], участник революционного движения в России с 1888, сов. гос
деятель, историк, публицист. Чл. Коммунистич. партии с 1893. Род. в Одессе в мелкобурж. семье. В 1894 арестован, сослан в Якутскую обл., в 1899 бежал за
границу. Входил в с.-д. лит. группу "Борьба", сотрудничал в марксистском журн. "Заря". Участник Революции 1905-07 в России, в 1910 выслан за
границу, входил в Парижскую секцию большевиков. Был лектором в партийной
школе в Лонжюмо. В 1909-1914 сотрудничал в большевистских газ. "Социал-демократ", "Звезда", "Правда", журн. "Просвещение",
участвовал в работе с.-д. фракции 3-й и 4-й Госдум. С 1914 работал в России. Во
время Февр. революции 1917 избран чл. Исполкома Петрогр. совета, занимал позицию революционного
оборончества, от к-рой позднее отказался, один из редакторов газ.
"Новая жизнь". Участник Окт. революции 1917. С окт. 1917 до 1925 редактор
газ. "Известия ВЦИК". С 1925 на журналистской, адм. и науч. работе. С 1929
зам. пред. Ученого к-та при ЦИК СССР. Работы "Интернационал 1864-1914"
(ч. 1-2, 1918), "Карл Маркс. Его жизнь и деятельность (1818-1883)"
(1918), "Борцы за социализм" (ч. 1-2, 1923-1924) сыграли известную
роль в популяризации марксизма в первые годы Сов власти. По истории росс. революц.
движения наиболее значит. монографии "Н. Г. Чернышевский. Его жизнь и
деятельность" (т. 1-2, 1928) и "М. А. Бакунин. Его жизнь и деятельность
(1814-1876)" (т. 1-4, 1920-27). Работы, написанные на большом фактич.
материале, вместе с рядом др. статей по российскому революц. движению, в целом
сохраняют свое значение, несмотря на отд. ошибочные положения и оценки.
Делегат 7, 8, 10, 12, 13-го съездов партии. Был чл. Президиума ВЦИК, чл. ЦИК
СССР.
С о ч.: Избранное, M., 1973; Воспоминания и публицистика. M., 1965 (бнбл.
указатель).
Лит.: Л е н и н В. И.,
Полн. собр. соч., 5 изд. (см. Справочный том, ч. 2, с.
475); Очерки истории исторической науки в СССР, т. 4, M., 1966.
СТЕКЛОВА ФУНКЦИЯ, функция, определяемая для данной функции f(x) paвенством
где h настолько мало, что интервал (х, х + h) лежит в области
определения функции f(x) C 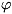 применяются для сглаживания данной
функции, т. к. если функция f(x) непрерывна, то Ф(х, h) имеет на
одну производную больше, чем f(х). При этом lim Ф(х, h) =f(x), то
есть С.
применяются для сглаживания данной
функции, т. к. если функция f(x) непрерывна, то Ф(х, h) имеет на
одну производную больше, чем f(х). При этом lim Ф(х, h) =f(x), то
есть С. 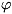 могут применяться для приближения непрерывных
функций более гладкими. Если функция f(x) интегрируема, то функция Ф(х,
h) непрерывна. С.
могут применяться для приближения непрерывных
функций более гладкими. Если функция f(x) интегрируема, то функция Ф(х,
h) непрерывна. С. 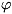 введены В. А. Стекловым в
1903 и применялись им для решения мн. вопросов в математич. физике С
введены В. А. Стекловым в
1903 и применялись им для решения мн. вопросов в математич. физике С 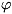 могут быть определены и для неск. переменных.
могут быть определены и для неск. переменных.