СООБЩЕНИЕ в теории информ а ц и и, всякий носитель информации. При этом теория информации интересуется лишь количеств, стороной информации, содержащейся в С. Понятие С. в теории информации имеет существенно вероятностный характер: каждый источник информации (или источник С.) задаётся перечислением возможных С. и соответствующих им вероятностей. Пусть х₁, х₂, ..., х_n - возможные С., а р₁, р₂, ..., р_п- соответствующие вероятности. Тогда количество информации в С. Xi принимают равным log₂ 1/p₁. Среднее количество информации в С. данного источника (его энтропия), т. е. сумма

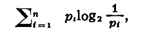
является важнейшей характеристикой источника. Именно величина энтропии определяет возможности передачи и хранения С., производимых источником.

Пример. Пусть источником С. являются результаты N последовательных измерений с точностью до 0,1 нек-рой физ. величины, равномерно распределённой в интервале от нуля до единицы. Тогда, если указывать только число десятых (с недостатком), возможными результатами отд. измерения будут числа 0,1,...,9. Вероятность появления каждого из них равна 0,1. С. в данном примере представляются N-членными последовательностями цифр. Вероятность каждого С. равна (0,1)^N. Количество информации в каждом С. и энтропия источника равны Nlоg₂ 10 = 3,32N двоичных единиц. Можно сказать, что источником С. в этом примере является случайная последовательность десятичных знаков (цифр) длины N. Именно такую форму случайных последовательностей знаков (или более общим образом - форму случайных процессов) имеют источники С., рассматриваемые в теории информации.

При изучении конкретных типов С., таких, как письменная речь, телеграфные, телефонные или телевизионные сигналы, обычно строится та или иная приближённая вероятностная модель источника С. Так, с достаточной для целей теории информации точностью в качестве модели русской письменной речи может быть принята т. н. сложная цепь Маркова. Для непрерывных С. в качестве моделей используются стационарные случайные процессы. Построение подобных моделей опирается на обширные статистич. данные, касающиеся рассматриваемых процессов.

Ю. В. Прохоров.

СООБЩЕНИЯ ВОЕННЫЕ (BOCO), сухопутные, водные и воздушные пути, подготовленные и оснащённые необходимыми средствами для обеспечения всех видов воинских перевозок в мирное и воен. время. В состав BOCO входят жел. и автомоб. дороги, судоходные участки внутр. водных путей, мор. и возд. пути, станции, порты, пристани, аэродромы, площадки для погрузки, выгрузки и перегрузки войск и материальных средств. Для мед. и материального обеспечения перевозимых войск на путях сообщения развёртываются санитарно-контрольные, дезинфекционные пункты, пункты мед. помощи, средства водоснабжения. С. в. всегда играли значит, роль в войнах. С увеличением численности вооруж. сил, развитием их технич. оснащённости и расширением масштабов воен. действий значение путей сообщения и объём воинских перевозок резко возросли. Напр., во время Великой Отечеств, войны 1941-45 воинские перевозки по жел. дорогам СССР составили св. 443 тыс. поездов (ок. 20 млн. вагонов), в т. ч. св. 55% оперативных и ок. 45% снабженческих перевозок. По внутр. водным путям было перевезено св. 4 млн. военнослужащих, 4500 танков, 10 тыс. орудий; по возд. путям - ок. 3 млн. военнослужащих и св. 300 тыс. т воинских грузов; автомоб. транспортом - 625 млн. т грузов.

Взаимодействие с трансп. учреждениями по вопросам подготовки и использования путей сообщения в интересах вооруж. сил в мирное и воен. время осуществляют органы BOCO.

В. А. Феклин.

СООБЩЕСТВО (La Communaute), Французское сообщество, политическое и экономич. объединение Франции, её владений (заморские департаменты и территории) и ряда независимых государств Африки - б. франц. колоний. Образовано по инициативе Франции в 1958 взамен распавшегося Французского Союза (провозглашён в 1946). Формально в компетенцию С. входят внеш. политика, оборона, финансовая система, использование стратегич. сырья, а также наблюдение за органами юстиции, высшим образованием, внеш. транспортом и средствами связи. Глава С.- президент Франции.  

СООБЩЕСТВО (биол.), то же, что биоценоз.  

СООСАЖДЕНИЕ, переход в осадок примесей (микрокомпонентов), сопутствующий осаждению основного вещества (макрокомпонента) из раствора, расплава или пара, содержащих несколько веществ. С. происходит тогда, когда раствор (пар) пересыщен в отношении вещества, образующего осадок, или расплав переохлаждён. С. начинается лишь по истечении т. н. латентного периода; длительность его можно менять от микросекунд до десятков часов, изменяя исходное пересыщение (переохлаждение), интенсивность перемешивания, чистоту и темп-ру среды, из к-рой выделялся осадок. С. протекает в две стадии: оно начинается с захвата примеси в ходе роста частиц осадка при его выделении и завершается перераспределением её между осадком и средой. На первой стадии примесь захватывается поверхностью растущих частиц (поверхностное С.) и их объёмом (объёмное С.). Если растущие частицы имеют кристаллнч. структуру, то при объёмном С. примесь локализуется на участках твёрдой фазы с совершенной структурой (сокристаялизация) и вблизи структурных дефектов (окклюзия, межкристаллитный захват и дислокационный захват). Нек-рые сведения о первой стадии обобщены правилом Гана. Важнейшей количеств, характеристикой первой стадии С. является эффективный (практический) коэффициент распределения примеси между осадком и средой К, равный отношению средней концентрации примеси в осадке к средней её концентрации в среде. При описании сокристаллизации используют также эффективный коэффициент сокристаллизац и и, равный произведению К на отношение средней концентрации кристаллизующегося вещества в среде к плотности твёрдой фазы. Если псресыщение среды мало и осаждение происходит очень медленно, то эффективный коэффициент распределения (сокристаллизации) не меняется в ходе С. и равен коэффициенту равновесного распределения Кравн. При быстром осаждении растущие частицы захватывают неравновесное кол-во примеси, к-рая обычно неоднородно распределена по объёму твёрдой фазы. При этом величина К, как правило, монотонно растёт по мере возрастания скорости осаждения, если К_равн<1, и уменьшается при К_равн>1, приближаясь к единице при исключительно быстром осаждении.

На второй стадии С. уменьшается концентрация дефектов в объёме осадка и его частицы укрупняются. При этом примесь, захваченная на первой стадии, частично или полностью возвращается в среду. Происходит выравнивание концентрации примеси в различных участках твёрдой фазы, в результате чего кристаллы приобретают равновесный состав, зависящий только от состава и темп-ры среды. При этом коэффициент К изменяется до значения К_равн. Опытные данные о равновесной сокристаллизации обобщены Хлопина законом. Закономерности С. лежат в основе гидрометаллургии, кристаллизационных и сублимационных методов разделения и очистки веществ (напр., дробной кристаллизации и зонной плавки), методов получения твёрдых тел с заданным содержанием активатора (для радиоэлектроники, оптической пром-сти). С. используют в аналитической химии и радиохимии для концентрирования вешеств. Применяя С., можно обнаружить и выделить микрокомпонент при концентрациях до 10^-10-10^-12 г-ион/л.

Лит.: C т а р и к И. E., Основы радиохимни, 2 изд., Л., 1969; Мелихов И. В., Меркулова M. С., Сокристаллизация, M., 1975.

П. В. Мелихов. 

СООСНАЯ ГИДРОТУРБИНА, осевая гидротурбина с двумя рабочими колёсами, одно из к-рых укреплено на полом валу, а другое - на валу, проходящем внутри полого. К валам рабочих колёс (они вращаются в разные стороны) могут подсоединяться валы роторов двух расположенных один за другим генераторов или валы ротора и контрротора (см. Контрроторный агрегат). В С. г. поток из подвода поступает последовательно в рабочие колёса, а затем в отсасывающую трубу. T. к. С. г. значительно сложнее, чем поворотно-лопастные гидротурбины и радиально-осевые гидротурбины, применения в гидроэнергетике они не нашли.

СООТВЕТСТВЕННЫЕ СОСТОЯНИЯ, состояния различных веществ, соответствующие одинаковым значениям приведённых параметров состояния (напр., темп-ры, давления, плотности). Приведёнными параметрами состояния наз. отношения параметров состояния к параметрам приведения - чаще всего к значениям параметров критического состояния: критич. темп-ры Т_к, давления p_k, плотности 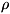_k или удельного объёма v_k·

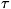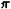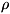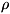
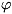Согласно закону соответственных состояний ур-ние состояния, записанное в приведённых параметрах (приведённое уравнение состояния), одинаково для различных веществ, т. е. для разных веществ одинаковым значениям, напр, приведённой темп-ры ( = T/T_k ) и приведённого давления ( = /), соответствует одно и то же значение приведённого удельного объёма ( = /v), а на кривой сосуществования жидкости и газа одним и тем же значениям приведённой темп-ры соответствует одно и то же значение приведённого давления, теплоты испарения, поверхностного натяжения и т. д. Закон С. с. справедлив лишь при достаточно высоких темп-pax, когда несущественны квантовые эффекты, и для тех веществ, у к-рых зависимость энергии межмолекулярного взаимодействия от расстояния имеет одинаковый характер. Практически поведение всех веществ отклоняется от закона С. с., однако в рамках отдельных групп веществ с близкими формами потенциала межмолекулярного взаимодействия эти отклонения часто относительно невелики и носят систематич. характер, что позволяет осуществлять расчёт свойств малоизученных веществ на основе закона С. с.

Лит.: Ландау Л. Д., Лифшиц E. M., Статистическая физика, 2 изд., M., 1964 (Теоретическая физика, т. 5); Г и р ш ф е л ь д е р Дж., К е р т и с с Ч., Б е р д Д., Молекулярная теория газов и жидкостей, пер. с англ., M., 1961; Рид Р., Шервуд Т., Свойства газов и жидкостей, пер. с англ., M., 1964.

С. П. Малышенко.

СООТВЕТСТВИЯ ПРИНЦИП, постулат квантовой механики, требующий совпадений её физ. следствий в предельном случае больших квантовых чисел с результатами классич. теории. В С. п. проявляется тот факт, что квантовые эффекты существенны лишь при рассмотрении микрообъектов, когда величины размерности действия сравнимы с постоянной Планка п. Если же квантовые числа, характеризующие состояние физич. системы (напр., орбитальное квантовое число /), велики, то величиной h можно пренебречь и система с высокой точностью подчиняется классич. законам. С формальной точки зрения, С. п. означает, что в пределе h -> О квантово-механич. описание физич. объектов должно быть эквивалентно классическому.

Часто под С. п. понимают след, более общее положение. Любая новая теория, претендующая на более глубокое описание физич. реальности и на более широкую область применимости, чем старая, должна включать последнюю как предельный случай. Так, релятивистская механика (см. Относительности теория) в пределе малых скоростей (v<c, где с - скорость света в вакууме) переходит в классическую. Формально переход осуществляется при с стремится к бескон.

Когда основные аксиомы теории уже сформулированы, С. п. представляет в основном иллюстративный интерес, подчёркивая преемственность теоретич. построений. В ряде случаев С. п. помогает развить приближ. методы решения задач. Напр., если в данной конкретной физич. проблеме ft можно считать малой величиной, то это равносильно т. н. к в азиклассическому приближению в квантовой механике. При этом нерелятивистское волновое Шрёдингера уравнение в пределе h-> О приводит к классич. ур-нию Гамильтона - Якоби. Однако в период возникновения новой теоретич. дисциплины, когда её принципы во многом ещё не ясны, С. п. имеет самостоятельное эвристич. значение.

С. п. был выдвинут H. Бором в 1923 (в т. н. старой квантовой теории, предшествующей квантовой механике) в связи с проблемой спектров излучения и поглощения атомов. Впоследствии, когда была создана последоват. квантовая механика, особенности атомных спектров были объяснены на более глубокой основе, причём существенные черты матем. аппарата определялись С. п.

Значение С. п., однако, далеко выходит за рамки квантовой механики. Им широко пользуются в квантовой электродинамике, теории элементарных частиц и, без сомнения, он войдёт составной частью в любую новую теоретич. схему.

Лит.: Бор H., Три статьи о спектрах и строении атомов, пер. с нем., M.- П., 1923; Блохинцев Д. И., Основы квантовой механики, 3 изд., M., 1961; Шифф Л., Квантовая механика, пер. с англ., M., 1957.

О. И. Завьялов.

СООТВЕТСТВИЯ ПРОИЗВОДСТВЕННЫХ ОТНОШЕНИЙ ХАРАКТЕРУ И УРОВНЮ РАЗВИТИЯ ПРОИЗВОДИТЕЛЬНЫХ СИЛ ЗАКОН, всеобщий экономический закон развития общества, действующий в различных формациях общественно-экономических. Выражает взаимодействие производительных сил- основы развития произ-ва и производственных отношений - их обществ, формы. Показывает зависимость производств, отношений от уровня и характера развития производит, сил и обратную зависимость. Этот закон впервые был открыт и обоснован К. Марксом. В кн. "К критике политической экономии" он писал, что в "... общественном производстве своей жизни люди вступают в определенные, необходимые, от их воли не зависящие отношения - производственные отношения, которые соответствуют определенной ступени развития их материальных производительных сил" (M арке К. и Энгельс Ф., Соч., 2 изд., т. 13, с. 6).

В единстве производит, сил и производств, отношений определяющая роль принадлежит производит, силам. Уровень их развития непосредственно обусловливает способ производства материальных благ. Так, первобытнообщинный способ произ-ва основывался на относительно неразвитых средствах производства, к-рые не позволяли отдельному работнику трудиться самостоятельно. Для произ-ва необходимых жизненных благ члены первобытной общины должны были трудиться сообща. Коллективное ведение хозяйства и незначит. размеры произведённого продукта вызывали уравнительное распределение жизненных средств среди всех членов общины. Совершенствование орудий труда привело к обособлению людей в трудовой деятельности, появлению частной собственности на средства произ-ва, к разделению общества на классы. Новые орудия труда позволяли отдельному работнику произвести больше жизненных средств, чем это было необходимо для обеспечения его жизнедеятельности. Возник прибавочный продукт, складывались производств, отношения рабовладельч. или феодального способа произ-ва.

Характерной чертой антагонистич. формации в период их разложения является опережение производит, силами производств, отношений; господствующая форма присвоения начинает тормозить развитие производит, сил. Так, при капитализме выступает антагонистическое, т. е. неустранимое в процессе эволюции данной совокупности производств, отношений, противоречие между обществ, характером произ-ва и частной формой присвоения. В период становления этого способа произ-ва оно было скрыто, частная форма присвоения результатов эксплуатации наёмных рабочих стимулировала развитие производит, сил. Капиталисты были заинтересованы в создании и совершенствовании машин и технологии произ-ва, т. к. рост производительности труда обеспечивал увеличение массы прибавочной стоимости. Но машинное производство, явившись средством увеличения массы прибавочной стоимости, стало и материальной основой периодич. кризисов перепроизводства (см. Экономические кризисы). Первый кризис показал, что дальнейшее развитие производит, сил в рамках совокупности капиталистич. производств, отношений возможно только посредством уничтожения части произведённого продукта. Обществ, производит, силы, т. о., вступают в противоречие с частной формой присвоения. Капиталистич. форма присвоения, порождающая анархию обществ, произ-ва, накопление богатства на одном полюсе и нищеты на другом, перестаёт соответствовать уровню и характеру развития производит, сил. Для их всестороннего развития требуется не модификация отд. элементов совокупности капиталистич. производств, отношений, а её ликвидация. Особенно ярко несоответствие между производит, силами и капиталистич. производств, отношениями проявляется в условиях империализма. "Эпоха капиталистического империализма,- подчёркивал В. И. Ленин,- является эпохой созревшего и перезревшего капитализма, стоящего накануне своего крушения, назревшего настолько, чтобы уступить место социализму" (Поли. собр. соч., 5 изд., т. 27, с. 116). Назревшее противоречие разрешается в результате социалистич. революции. Пришедший к политич. власти пролетариат в союзе с крестьянством ликвидирует частную собственность капиталистов и устанавливает общественную собственность на средства произ-ва, создавая для управления обществ. произ-вом соответствующие органы. В этих условиях объективно формируется совокупность социалистич. производств, отношений, среди к-рых основным является планомерное соединение ассоциированных производителей с обобществлёнными средствами произ-ва. Новые отношения собственности на средства произ-ва отвечают обществ, характеру производит, сил.

В социалистич. странах закон соответствия учитывается коммунистическими и рабочими партиями в процессе строительства нового общества, в определении перспектив его развития. Так, в СССР перевод предприятий пром-сти, строительства, транспорта, связи, торговли, с. х-ва на новые условия планирования и экономич. стимулирования был обусловлен возросшими масштабами обществ, произ-ва, необходимостью развития инициативы коллективов предприятий для совершенствования процесса произ-ва и повышения его эффективности. Изменение форм управления обществ, производством стало основой для приведения в соответствие производит, сил и производств, отношений.

Господство общественной собственности на средства произ-ва исключает перерастание несоответствия отдельных элементов социалистических производств, отношений уровню и характеру производительных сил в антагонистический конфликт и предполагает всестороннее использование действия этого закона в процессе перехода от социализма к коммунизму.

Лит.: Маркс К., К критике политической экономии, Маркс К. и Энгельс Ф., Соч., 2 изд., т. 13, с. 6-7; Маркс К. и Энгельс Ф., Манифест Коммунистической партии, там же, т. 4, с. 429; Ленин В. И., Империализм, как высшая стадия капитализма, Полн. собр. соч., 5 изд., т. 27, с. 385-406; его же, Оппортунизм и крах II Интернационала, там же, т. 26, с. 116; Программа Коммунистической партии Советского Союза, M., 1974, с. 21; Об улучшении управления промышленностью, совершенствовании планирования и усилении экономического стимулирования промышленного производства. Постановление пленума ЦК КПСС 27-29 сентября 1965 г., в кн.: КПСС в резолюциях и решениях съездов, конференций и пленумов ЦК, т. 8, M., 1972.

H. В. Московченко.

СОПЕЛЬ, сопилка (укр.), дудка (белорус.), духовой музыкальный инструмент, род деревянной продольной флейты со свистковым устройством. Дл. 350-400 мм. Имеет 5-6 боковых отверстий для изменения высоты извлекаемых звуков. Практически звукоряд диатонический.

СОПИКОВ Василий Степанович (1765, Суздаль, - 1818, Петербург), русский библиограф, книговед, один из основоположников отечеств, библиографии. В 1788 открыл в Петербурге книжную лавку с публичной "библиотекой для чтения" и издавал каталоги имевшейся лит-ры. Переводил французских просветителей (Вольтера, Марешаля, Монтескье), занимался издат. деятельностью. В 1811 поступил помощником библиотекаря в петерб. Публичную библиотеку, где совместно с И. А. Крыловым проделал большую работу по созданию фонда рус. книги. Осн. труд С.- "Опыт российской библиографии" (ч. 1-5, 1813-21, последняя часть подготовлена к печати В. Г. Анастасевичем; переиздан с доп. в 1904-06 В. H. Рогожиным), представляющий собой свод данных о 13249 произведениях печати, изданных на рус. и церк.-слав. языках в России и за рубежом от возникновения слав, книгопечатания до нач. 19 в. Первый том открывается "Предуведомлением", в к-ром С. изложил теоретич. суждения по вопросам библиографии, подчеркнув её воспитат. и просветит, роль, охарактеризовал методич. принципы своего труда. С. отмечал рецензии на отд. книги, давал аннотации, применял условные обозначения для рекомендуемых книг и таким образом впервые придал библиографич. указателю критич. и рекомендат. характер. В "Опыте" приведены также сведения о древних славянских типографиях.

Лит.: Здобнов H. В., История русской библиографии до начала XX века, 3 изд., M., 1955, с. 174-84.

А.С. Мыльников.

СОПКА, 1) в геоморфологии и геологии - общее название холмов и гор с округлой вершиной в Казахстане, Забайкалье и на Д. Востоке СССР; на Камчатке и Курильских о-вах С. наз. вулканы (Ключевская С., Авачинская С.), в Крыму и на Кавказе - грязевые вулканы. 2) В археологии - высокие (до 4 л и выше) курганы округло-конич. формы, погребальные памятники словен новгородских гл. обр. 9-10 вв. Распространены в басс. оз. Ильмень и pp. Ловать, Волхов, Мета; на С.-В. доходят до Белого оз., на З. - до р. Великой.

СОПЛО, специально спрофилированный закрытый канал, предназначенный для разгона жидкостей или газов до заданной скорости и придания потоку заданного направления. Служит также устройством для получения газовых и жидкостных струй. Поперечное сечение С. может быть прямоугольным (плоские С.), круглым (осесимметричные С.) или иметь произвольную форму (пространств. С.). В С. происходит непрерывное увеличение скорости  жидкости или газа в направлении течения - от начального значения _o во входном сечении С. до наибольшей скорости = _a на выходе. В силу закона сохранения энергии одновременно с ростом скорости  в С. происходит непрерывное падение давления и темп-ры от их начальных значений р₀ ,T₀ до наименьших значений р_а, Т_а в выходном сечении. T. о., для реализации течения в С. необходим нек-рый перепад давления, т. е. выполнение условия р₀>р_а. При увеличении T₀ скорость во всех сечениях С. возрастает в связи с ростом начальной потенциальной энергии. Пока скорость течения невелика, малы и соответствующие изменения давления и темп-ры в С., поэтому свойство сжимаемости (способность жидкости или газа изменять свой объём под действием перепада давления или изменения темп-ры) ещё не проявляется, и изменением плотности среды 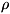 в направлении течения можно пренебречь, считая её постоянной. В этих условиях для непрерывного увеличения скорости С. должно иметь сужающуюся форму, т. к. в силу уравнения неразрывности pvF = const площадь F поперечного сечения С. должна уменьшаться обратно пропорционально росту скорости. Однако при дальнейшем увеличении начинает проявляться сжимаемость среды, плотность её уменьшается в направлении течения. Поэтому постоянство произведения трёх множителей pvF в этих новых условиях зависит от темпа падения 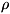 с ростом . При <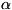, где а - местная скорость распространения звука в движущейся среде, темп падения плотности газа отстаёт от темпа роста скорости, поэтому для обеспечения разгона, т. е. увеличения v, F нужно уменьшать (рис. I),. несмотря на падение плотности (дозвуковое С.). Но при разгоне до скоростей >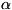падение плотности происходит быстрее, чем рост скорости, поэтому в сверхзвуковой части необходимо увеличивать площадь F (сверхзвуковое С.).

Рис. 1. Схема дозвукового сопла.

Рис. 2. Схема сверхзвукового сопла (сопла Лаваля).

T. о., сверхзвуковое С., наз. также соплом Лаваля, имеет вначале сужающуюся, а затем расширяющуюся форму (рис. 2). Изменение скорости вдоль С. определяется законом изменения площади его поперечного сечения F по длине С.

Давление в выходном сечении дозвукового С. всегда равно давлению р_с в окружающей среде, куда происходит истечение из С. (p_a = р_с), т. к. любые отклонения в величине давления представляют собой возмущения, к-рые распространяются внутрь С. со скоростью, равной скорости звука, и вызывают перестройку потока, ведущую к выравниванию давлений в выходном сечении С. При возрастании PO и неизменном р_с скорость а в выходном сечении дозвукового С. сначала увеличивается, а после того как р₀ достигнет нек-рой определённой величины, _a становится постоянной и при дальнейшем увеличении р_ане изменяется. Такое явление наз. кризисом течения в С. После наступления кризиса средняя скорость истечения из дозвукового С. равна местной скорости звука (Va - а) и наз. критич. скоростью истечения. Дозвуковое С. превращается в звуковое С. Все параметры газа в выходном сечении С. также наз. в этом случае критическими. Для дозвуковых С. с плавным контуром критич. отношение давлений при истечении воздуха и др. двухатомных газов (р₀/р_с)_КР = 1,9.

В сверхзвуковом С. критическим наз. его наиболее узкое сечение. Относит, скорость _a/a в выходном сечении сверхзвукового С. зависит только от отношения площади выходного сечения F_a к площади его критич. сечения F_KP и в широких пределах не зависит от изменений давления р₀перед С. Поэтому, изменяя с помощью механич. устройства площадь критич. сечения F_KP при неизменной площади F_a, можно изменять _a/a. На этом принципе основаны используемые в технике регулируемые С. с переменной скоростью газа в выходном сечении. Давление в выходном сечении сверхзвукового С. может быть равно давлению в окружающей среде (р_а= р_с), такой режим течения наз. расчётным, в противном случае - нерасчётным. В отличие от дозвукового С., возмущения

давления при р_а<>р_с, распространяющиеся со скоростью звука, относятся сверхзвуковым потоком и не проникают внутрь сверхзвукового С., поэтому давление р_ане уравнивается с р_c. Нерасчётвые режимы характеризуются образованием волн разрежения в случае р_а>р_с или ударных волн в случае р_а < р_c Когда поток проходит через систему таких волн вне С., давление становится равным р_c. При большом избытке давления в атмосфере над давлением в выходном сечении С. ударные волны могут перемещаться внутрь С., и тогда нарушается непрерывное увеличение скорости в сверхзвуковой части С. Сильное падение давления и темп-ры газа в сверхзвуковом С. может приводить, в зависимости от состава текущей среды, к различным физико-химич. процессам (химич. реакции, фазовые превращения, неравновесные термодинамич. переходы), к-рые необходимо учитывать при расчёте течения газа в С.

С. широко используются в технике (в паровых и газовых турбинах, в ракетных и воздушно-реактивных двигателях, в газодинамических лазерах, в магнитно-газодинамич. установках, в аэродинамических трубах и на газодинамич. стендах, при создании молекулярных пучков, в химич. технологии, в струйных аппаратах, в расходомерах, в дутьевых процессах и мн. др.). В зависимости от технич. назначения С. возникают специфич. задачи расчёта С.: напр., в С. аэродинамич. труб необходимо обеспечить создание равномерного и параллельного потока газа в выходном сечении, требования к С. ракетных двигателей заключаются в получении наибольшего импульса газового потока в выходном сечении С. при его заданных габаритных размерах. Эти и др. технич. задачи привели к бурному развитию теории С., учитывающей наличие в газовом потоке жидких и твёрдых частиц, неравновесных химич. реакций, переноса лучистой энергии и др., что потребовало широкого применения ЭВМ для решения указанных задач, а также для разработки сложных экспериментальных методов исследования С.

Лит.: Абрамович Г. H., Прикладная газовая динамика, 3 изд., M., 1969; С т е рнин Л. E., Основы газодинамики двухфазных течений в соплах, M., 1974.

С. Л. Вишневецкий.

СОПЛОВОЙ АППАРАТ, элемент паровой или газовой турбины; состоит из расположенных по окружности спрофилированных сопловых (направляющих) лопаток, в каналах между к-рыми происходит расширение пара (газа) и превращение его потенциальной энергии в кинетическую. Лопатки С. а. либо крепятся в неподвижных дисках (диафрагмах), либо устанавливаются непосредственно в корпусе турбины. Пар в С. а. приобретает значит, скорость, после чего поступает на рабочие лопатки турбины, где кинетич. энергия струи пара превращается в механич. энергию вращающегося ротора. В зависимости от скорости пара на выходе различают дозвуковые и сверхзвуковые С. а. См. также Сопло.

СОПЛОДИЕ у растений (infructestentia), совокупность плодов, развившихся из цветков целого соцветия и сросшихся как бы в один плод. С. образуются у инжира, свёклы, ананаса, шелковицы (тутовое дерево) и др. Часто С. считают только те, к-рые опадают с материнского растения целиком, вместе с разросшейся осью (инжир, свёкла). В быту С. иногда наз. плодом или семенем.

СОПОЛИМЕРИЗАЦИЯ, полимеризация, в к-рой участвуют два или более мономера различных типов.

СОПОЛИМЕРЫ, полимеры, макромолекулы к-рых содержат мономерные звенья неск. типов. В регулярных С. различающиеся звенья распределяются в определённой периодичности. Простейшие примеры - С. стирола с малеиновым ангидридом и нек-рых олефинов с SO₂, построенные по принципу ...ABABAB... (А и В - мономерные звенья различных типов). Более сложные регулярные последовательности чередования звеньев характерны, напр., для различных аминокислотных остатков в нек-рых белках, напр, глицин-пролин-оксипролин в коллагене. В нерегулярных С. распределение звеньев случайное, что характерно для многих синтетич. С. В нуклеиновых кислотах и большинстве белков нерегулярные последовательности звеньев задаются соответствующим кодом и определяют биохимич. и биологич. специфичность соответствующих соединений.

С., в к-рых звенья каждого типа образуют достаточно длинные непрерывные последовательности (блоки), сменяющие друг друга в пределах макромолекулы, наз. блоксополимерами. К внутр. (неконцевым) звеньям макромолекулярной цепи одного химич. состава могут быть присоединены одна или неск. цепей др. состава. Такие С. наз. привитыми.

Сочетая в одной макромолекуле химич. звенья самых различных типов, можно создавать материалы с заранее заданным комплексом свойств. T. о., синтез С.- один из наиболее эффективных путей модификации свойств высокомолекулярных соединений.

Лит.: Энциклопедия полимеров, т. 1 - 2, M., 1972 - 74.

В. А. Кабанов.

СОПОР (от лат. sopor - оцепенение, вялость), глубокое угнетение сознания при сохранении рефлексов. Больной в С. пассивен, безучастен, хотя и способен реагировать на некоторые сильные внеш. раздражители - оклик, настойчивые повторные приказы и т. д. Наблюдается при черепно-мозговой травме, нарушениях мозгового кровообращения, воспалит, и токсич. поражениях мозга и т. д. При углублении этого прекоматозного состояния сознание полностью утрачивается, развивается кома.

СОПОСТАВИМОСТЬ в статист и-к е, необходимое условие для сравнения статистич. показателей и их анализа. С. требует единства методологии расчёта показателей, единиц измерения, полноты охвата наблюдением явления, территориальных границ и др. условии сравнимости показателей. Несопоставимость статистических данных по методологии расчёта особенно часто встречается при сравнениях статистических показателей различных стран. Например, стоимости нац. дохода в СССР и США непосредственно несопоставимы не только потому, что они выражены в разных валютах, но и по той причине, что нац. доход в СССР и США исчисляется по разной методологии. В статистике одной страны такая несопоставимость также может возникнуть, если изменяется методология расчёта к.-л. статистич. показателя. Различия в методологии расчёта, приводящие к нарушению С. статистич. показателей, можно устранить соответствующим пересчётом с целью приведения показателей в сопоставимый по методологии расчёта вид. Сложнее, когда несопоставимость вызвана отсутствием чётком методологии и ненаучной организацией статистического наблюдения. В. И. Ленин в работе "К вопросу о нашей фабрично-заводской статистике" (1898) показал, что статистика промышленности России 2-й пол. 19 в. приводила из года в год несопоставимые данные о числе фабрик и заводов, т. к. в рус. статистике не было чётко определено, какие предприятия следует относить к разряду фабрик. В результате в число фабрик включались и мелкие заведения, причём в последующие годы их включалось всё меньше. Создавалось неверное впечатление, что число фабрик в России сокращалось, но в действительности, как показал Ленин, приведя данные в сопоставимый вид, оно увеличивалось.

С. нарушается в результате изменения охвата явления нерепрсзентативным статистич. наблюдением. Напр., в статистике колх. рынков до 1940 наблюдение велось по 71 крупному городу, а в послевоен. годы - по 264 городам, поэтому для соблюдения С. индексы товарооборота ц цен колх. рынка исчисляются: при сравнении с 1940 - по 71 городу, а с 1960 - по 264. С. нарушается при изменении терр. границ. Вследствие этого возникает проблема пересчёта статистич. показателей за старые годы в новых границах.

Нарушение С. происходит также в результате изменения единиц измерения. Так, в связи с изменением масштаба цен в СССР статистич. данные, выраженные в рублях, начиная с 1961 стали несопоставимы со статистич. данными до 1961, что потребовало соответствующего пересчёта данных за прошлые годы. Изменение цен приводит к несопоставимости ряда стоимостных показателей в динамике (продукция, нац. доход и т. д.). Поэтому производится пересчёт их в сопоставимые цены.

Нск-рые сложные статпстич. показатели непосредственно несопоставимы, т. к. на них влияет разная структура явления. Для сравнительной характеристики уровня смертности в различных странах, напр., не всегда пригодны общие коэффициенты смертности, т. к. на них влияет возрастная структура населения, к-рая в нек-рых случаях может резко различаться. При этом для С. коэффициент смертности исчисляется по одной и той же стандартной структуре населения.

Проблема С. возникает и при расчёте относительных и ср. величин в статистике. Так, процент выполнения плана можно исчислить при условии, если показатели фактич. выполнения и показатели плана относятся к одинаковому кругу предприятий, темпы динамики - если показатели даны за равные отрезки времени, среднюю заработную плату - если фонд заработной платы строго соответствует численности рабочих.

H. H. Ряузов.

СОПОСТАВИМЫЕ ЦЕНЫ, цены к.-л. определённого года (на к.-л. определённую дату), условно принимаемые за базу при сопоставлении в ден. выражении объёма произ-ва, товарооборота и др. экономич. показателей за разные периоды. Планы развития нар. х-ва СССР и отчёты об их выполнении содержат стоимостные показатели, исчисленные в С. ц. Разновидность С. ц. - неизменные цены. В качестве С. ц. применялись оптовые цены на 1 янв. 1952, на 1 июля 1955 и на 1 июля 1967. В зависимости от целей экономич. исследования в качестве С. ц. могут служить и совр. цены, в к-рые пересчитываются данные за предыдущие годы. С 1976 в планировании и учёте в качестве С. ц. применяются оптовые цены и тарифы на 1 янв. 1975, а в с. х-ве - ср. цены с.-х. продукции за 1973.

СОПОТ (Sopot), город в Польше, в Гданьском воеводстве, на берегу Гданьского зал. Балтийского м. Входит в агломерацию Трёхградье (наряду с гг. Гдыня и Гданьск). 50,7 тыс. жит. (1974). Машиностроение, кож. и пищ. пром-сть. 3 факультета Гданьского ун-та. Приморский климатич. курорт. Лето тёплое (ср. темп-pa июля 18 ⁰C), зима очень мягкая (ср. темп-pa февраля -1,5 ⁰C); осадков 650 мм в год. Леч. средства: аэрогелиотерапия, морские купания (с сер. июня до нач. сентября), торфогрязелечение и др. Мелкопесчаный пляж (длина св. 3 км, ширина ок. 200 м). Лечение заболеваний опорно-двигательного аппарата, периферич. нервной системы, гинекологич., анемий и др. Санатории, водогрязелечебница, дома отдыха, пансионаты, отели. Проводится Междунар. фестиваль эстрадной песни.

Лит.: Krzyzanowski L., GdanskSopot-Gdynia, Warsz., 1973.

СОПОЦКИН, посёлок гор. типа в Гродненском р-не Гродненской обл. БССР, в 27 км к С.-З. от Гродно. Лесозавод. Совхоз по откорму крупного рогатого скота.

СОПОЧАНИ (Сопопани, Sopocani), монастырь на Ю. Сербии, близ г. Нови-Пазар; памятник ср.-век. сербского иск-ва. Основан королём Урошем I. Сохранилась церковь св. Троицы (1264-65), однонефная постройка рашской школы, отличающаяся стройностью и композиц. цельностью (открытый притвор и башня зап. фасада - кон. 13 в.; боковые пристройки в виде пониженных нефов - нач. 14 в.). Церковь частично разрушена в кон. 14 в. ив 17 в. (реставрирована в 1929, 1948-56). В центр, нефе - первоклассные фрески (ок. 1265), отличающиеся спокойной величественностью и лиризмом образов, чистым и светлым колоритом, в боковых пристройках - фрески кон. 13 в., нач. 14 в. и 16-17 вв.

Лит.: R j у р и h В., Сопопани, Београд, 1963.

СОПРАНО (итал. soprano, от sopra - над), 1) самый высокий певческий голос. Диапазон: до¹ - до (ре - фа)³. Необходимое качество С. - хорошо развитый т. н. головной регистр. С. обладают обычно женщины и дети. В хоре особенно красиво звучат голоса мальчиков (т. н. дискантистов). В 16-18 вв. было широко распространено пение кастратов-певцов (наз. также сопранистами). Существует 3 осн. разновидности женских С.: драматическое, лирическое и колоратурное. Бывает также лирико-драматическое и лирико-колоратурное С. Драматич. С. отличается силой звучания на всём диапазоне, плотным нижним регистром; лирич. С. свойственны мягкость тембра, гибкость и большая выразительность в кантилене; для колоратурного С. характерны подвижность в исполнении фиоритур, пассажей и т. п., прозрачность тембра, лёгкость и свобода звучания в верхнем регистре. 2) Самая высокая партия в хоре. 3) Высокие по регистру разновидности нек-рых муз. инструментов.

СОПРИКАСАЮЩАЯСЯ ОКРУЖНОСТЬ в точке M кривой l, окружность, имеющая с l в точке M касание порядка п>=2 (см. Соприкосновение). Если кривизна кривой / в точке M равна нулю, то С. о. вырождается в прямую. T. к. порядок касания / и С. о. в точке M не ниже двух, то С. о. воспроизводит ход кривой вблизи точки касания с точностью до малых 3-го порядка по сравнению с размерами участка кривой. На рисунке изображено обычное (порядок касания кривой и С. о. равен двум) взаимное расположение кривой п её С.о.: кривая пронизывает С. о. в точке соприкосновения. Радиус С. о. наз. радиусом кривизны кривой / в точке M, а центр С.о.- центром кривизны. Если кривая / плоская и задана уравнением у = f(x), то радиус С. о. определяется формулой:

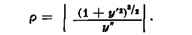
Если кривая l - пространственная и задана уравнениями х = х(и), у = у(и), z = z(u), то радиус С. о. определяется формулой:

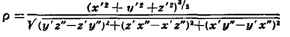
(здесь штрихи означают дифференцирование по параметру и).

Иногда С. о. наз. соприкасающимся кругом. См. также Дифференциальная геометрия.

Лит.: Рашевский П. К., Курс дифференциальной геометрии, 4 изд., M., 1956.

СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ в точке Мкривой l, плоскость, имеющая с l в точке M касание порядка n>=2 (см. Соприкосновение). С. п. может быть также определена как предел переменной плоскости, проходящей через три точки кривой /, когда эти точки стремятся к точке M. С механич. точки зрения С. п. может быть охарактеризована как плоскость ускорений: при произвольном движении материальной точки по кривой / вектор ускорения лежит в С. п. Обычно кривая, кроме исключит, случаев, пронизывает свою С. п. в точке соприкосновения (см. рис.). Если кривая / задана уравнениями x = х(и), у = и(и), z = z(u), то уравнение С. п. имеет вид:

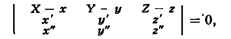
где X, Y, Z - текущие координаты, а х, у, z, х', и', z', x", у", z" вычисляются в точке соприкосновения; если все три коэффициента при X, У, Z в уравнении С. п. исчезают, то С. п. делается неопределённой (может совпадать с любой плоскостью, проходящей через касательную). См. также Дифференциальная геометрия.

Лит.: Рашевский П. К., Курс дифференциальной геометрии, 4 изд., M., 1956.

СОПРИКАСАЮЩАЯСЯ СФЕРА в точке М кривой /, сфера, имеющая с / в точке M касание порядка n>=З (см. Соприкосновение). С. с. может быть также определена как предел переменной сферы, проходящей через четыре точки кривой /, когда эти точки стремятся к точке M. Если радиус кривизны кривой I в точке M равен р, а 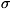 - кручение, то формула для вычисления радиуса С. с. имеет вид:

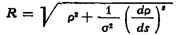
№- дифференциал дуги кривой /).

Лит.: P а ш е в с к и и П. К., Курс дифференциальной геометрии, 4 изд., M 1956

СОПРИКАСАЮЩИЙСЯ КРУГ в дифференциальной геометрии, см. Соприкасающаяся окружность.

СОПРИКОСНОВЕНИЕ кривой q с кривой /вданной точке M, геометрическое понятие, означающее, что q имеет с I в точке M касание максимального порядка по сравнению с любой кривой из нек-рого заранее данного семейства кривых {q}, включающего q. Порядок касания кривых q я I считается равным и, если отрезок QL есть величина 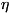 + 1 порядка малости по отношению к отрезку MK (см. рис., где отрезок QL перпендикулярен к общей касательной кривых q и I в точке M). Таким образом, среди всех кривых семейства {q} C. с кривой / имеет та кривая, к-рая наиболее тесно прилегает к / (для неё отрезок QL имеет максимальный порядок малости). Кривая семейства {q}, к-рая имеет С. с кривой / в данной её точке M, называется соприкасающейся кривой данного семейства в указанной точке кривой /. Напр., соприкасающейся окружностью в точке M кривой / является окружность, к-рая в этой точке имеет с / максимальный порядок касания по сравнению с любой другой окружностью.

Аналогично вышеизложенному определяется понятие соприкосновения поверхности q, принадлежащей данному семейству поверхностей {q}, с какой-нибудь кривой / (или с поверхностью) в нек-рой её точке M (в этих случаях порядок касания определяется также аналогично предыдущему; следует только вместо касательной прямой MK, изображённой на рисунке, рассматривать касательную плоскость поверхности q в точке M). См. Соприкасающаяся плоскость, Соприкасающаяся сфера.

Лит.: Ла Балле-Пуссен Ш. Ж., Курс анализа бесконечно малых, пер. с франц., т. 2, Л.- M., 1933; Ильин В. А., П о з н я к Э. Г., Основы математического анализа, 3 изд., ч. 1, M., 1971.

СОПРОТИВЛЕНИЕ АКТИВНОЕ электрическое, величина, характеризующая сопротивление цепи (её участка) переменному току, обусловленное необратимым превращением электрической энергии в др. формы энергии (преим. в тепловую); выражается отношением активной мощности, поглощаемой на участке цепи, к квадрату действующего

Вначения тока на этом участке; измеряется в омах. На участках цепи, содержащих проводники большого поперечного сечения, С. а. больше электрического сопротивления при постоянном токе (из-за поверхностного эффекта, см. Скин-эффект, и потерь в магнитном поле на вихревые токи и гистерезис).

СОПРОТИВЛЕНИЕ АКУСТИЧЕСКОЕ, характеристика, вводимая при рассмотрении колебаний акустических систем, равная отношению звукового давления к объёмной колебательной скорости. Активное и реактивное С. а. образуют комплексный импеданс акустический.

СОПРОТИВЛЕНИЕ ЁМКОСТНОЕ, величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью цепи (её участка); измеряется в омах. В случае синусоидального тока С. ё. х_с выражается в виде отношения 1/С, где  - угловая частота тока, С - ёмкость цепи. С. ё. равно отношению амплитуды напряжения на зажимах цепи, имеющей ёмкостный характер (обладающей малыми индуктивностью и сопротивлением активным; такую цепь можно считать эквивалентной конденсатору электрическому), к амплитуде тока в ней. Если (<>0, изменение напряжения на конденсаторе вызывает изменение заряда на его обкладках; в силу этого в цепи конденсатора непрерывно течёт зарядный (разрядный) ток. В процессе перезарядки конденсатора электрич. энергия периодически передаётся от источника тока электрич. полю конденсатора и затем обратно, причём средняя за период мощность равна нулю, поэтому С. ё. наз. реактивным.

СОПРОТИВЛЕНИЕ ИНДУКТИВНОЕ, величина, характеризующая сопротивление, оказываемое переменному току индуктивностью цепи (её участка); измеряется в омах. В случае синусоидального тока С. и. x_L выражается в виде произв. L, где  - угловая частота тока, L - индуктивность цепи. С. и. равно отношению амплитуды напряжения на зажимах цепи, имеющей индуктивный характер (обладающей малым сопротивлением активным и достаточно большой индуктивностью; такую цепь можно считать эквивалентной индуктивности катушке), к амплитуде тока в ней. При постоянном токе в катушке ( = О) С. и. равно нулю. Когда через катушку протекает переменный ток, электрич. энергия передаётся от источника тока магнитному полю катушки и затем обратно, причём средняя за период мощность равна нулю, поэтому С. и. наз. реактивным.

СОПРОТИВЛЕНИЕ МАГНИТНОЕ, характеристика магнитной цепи. См. Магнитное сопротивление.

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ, наука о прочности и деформируемости элементов (деталей) сооружений и машин. Осн. объекты изучения С. м.- стержни и пластины, для к-рых устанавливаются соответств. методы расчёта на прочность, жёсткость и устойчивость при действии статич. и динамич. нагрузок. С. м. базируется на законах и выводах теоретической механики, но, помимо этого, учитывает способность материалов деформироваться под действием внешних сил. Физико-механич. характеристики (предел текучести, предел прочности, модуль упругости ц т. п.), необходимые для оценки прочности и деформативности материалов, определяются при помощи испытательных машин и спец. измерительных приборов - тензометров. При испытаниях обеспечиваются требуемые условия загружения и высокая точность измерения деформаций испытываемых образцов материалов. Наиболее характерно испытание на растяжение образцов, представляющих собой стержни круглого сечения или полосы с сечением в виде узкого прямоугольника. По результатам этих испытаний строится т. и. диаграмма растяжения-сжатия. Располагая диаграммой испытания и пользуясь разработанными в С. м. методами расчёта, можно предсказать, как будет вести себя реальная конструкция, изготовленная из того же материала.

Основное содержание и методы С. м. При деформации твёрдого тела под нагрузкой изменяется взаимное расположение его микрочастиц, вследствие чего в теле возникают внутр. напряжения. В С. м. определяются наибольшие напряжения в элементах сооружений или деталях машин. Они сравниваются с нормативными величинами, т. е. с напряжениями, к-рые можно допустить, не опасаясь повреждения или разрушения этих элементов (деталей). Проверке подлежат также деформации тела и перемещения его отд. точек. Помимо необходимой прочности, конструкция должна быть также устойчивой, т. е. обладать способностью при малых случайных кратковременных воздействиях, нарушающих её равновесие, лишь незначительно отклоняться от исходного состояния. Выполнение этого требования зависит от внешних сил, геометрии элемента (детали) и от физических констант материала.

Для расчёта элементов конструкций в С. м. разрабатываются приближённые инж. методы, использующие кинематич. и статич. гипотезы, к-рые в большинстве случаев оказываются достаточно близкими к действительности. При выводе расчётных формул для определения напряжений и перемещений производится схематизация рассчитываемого элемента сооружения, его опорных закреплений и действующей нагрузки, иначе говоря, создаётся расчётная схема (модель) объекта.

При построении общей теории расчёта в С. м. рассматриваются т. н. идеализированные тела со свойствами, лишь приближённо отражающими поведение реальных объектов. Тела считаются однородными (со свойствами, одинаковыми во всех точках), сплошными (без пустот), обладающими упругостью (способностью восстанавливать свои размеры после снятия нагрузки), изотропными (с одинаковыми упругими свойствами по всем направлениям). На основе изучения простейших деформаций - растяжения-сжатия, кручения, изгиба в С. м. выводятся формулы, позволяющие для каждого из этих видов деформаций определять напряжения, перемещения и деформации в отд. точках тела. При наличии одновременно двух или неск. простейших деформаций, протекающих в упругой стадии (для к-рой справедлива линейная зависимость между напряжением и деформациями), напряжения и деформации, найденные отдельно для каждого вида, суммируются.

Mн. материалы (напр., бетон) обладают свойством ползучести (см. Ползучесть материалов), вследствие к-рой деформации могут возрастать со временем при неизменной нагрузке. В С. м. устанавливаются законы развития ползучести и время, в течение к-рого она заметно проявляется, а также рассматривается воздействие на стержень ударной нагрузки, при к-рой возникают динамические напряжения; последние определяются по приближённым формулам, выведенным на основе ряда допущений. При расчёте элементов сложной формы, для к-рых аналитич. формулы вывести не удаётся, применяют экспериментальные методы (напр., оптический, лаковых покрытий, муаровых полос и др.), позволяющие получать наглядную картину распределения деформаций по поверхности исследуемого элемента (детали) и вычислять напряжения в его отд. точках. Наибольшую трудность представляет определение т. н. остаточных напряжений, к-рые могут возникать в элементах конструкций, не несущих нагрузки (напр., при сварке или в процессе прокатки стальных профилей).

Одна из важных задач С. м. состоит в создании т. н. теорий прочности, на основе к-рых можно проверить прочность элементов в сложном напряжённом состоянии, исходя из прочностных характеристик, полученных опытным путём для простого растяжения-сжатия. Существует ряд теорий прочности; в каждом отд. случае пользуются той из них, к-рая в наибольшей степени отвечает характеру нагружения и разрушения материала.

Историческая справка. История С. м., как и многих др. наук, неразрывно связана с историей развития техники. Зарождение науки о С. м. относится к 17 в.; её основоположником считается Галилей, к-рый впервые обосновал необходимость применения аналитич. методов расчёта взамен эмпирич. правил. Важным шагом в развитии С. м. явились экспериментальные исследования P. Гука (60-70-е гг. 17 в.), установившего линейную зависимость между силой, приложенной к растянутому стержню, и его удлинением (закон Гука). В 18 в. большой вклад в развитие аналитич. методов в С. м. был сделан Д. Бернулли, Jl. Эйлером и Ш. Кулоном, сформулировавшими важнейшие гипотезы и создавшими основы теории расчёта стержня на изгиб и кручение. Исследования Эйлера в области продольного изгиба послужили основой для создания теории устойчивости стержней и стержневых систем. T. Юнг ввёл (1807) понятие о модуле упругости при растяжении и предложил метод его определения.

Важный этап в развитии С. м. связан с опубликованием (в 1826) Л. Навъе первого курса С. м., содержавшего систематизированное изложение теории расчёта элементов конструкций и сооружений. Принципиальное значение имели труды А. Сен-Венана (2-я пол. 19 в.). Им впервые были выведены точные формулы для расчёта на изгиб кривого бруса и сформулирован принцип, согласно к-рому распределение напряжений в сечениях, отстоящих на некотором расстоянии от места приложения нагрузки, не связано со способом её приложения, а зависит только от равнодействующей этой нагрузки.

Большие заслуги в развитии С. м. принадлежат рус. учёным M. В. Остроградскому, исследования к-рого в области С. м., строит, механики, математики и теории упругости приобрели мировую известность, и Д. И. Журавскому, впервые установившему (1855) наличие касат. напряжений в продольных сечениях бруса и получившему формулу для их определения (эта формула применяется и в совр. практике инж. расчётов). Всеобщее признание получили исследования Ф. С. Ясинского, разработавшего (1893) теорию продольного изгиба в упругой стадии и за её пределами (рекомендации Ясинского послужили основой для разработки совр. нормативных документов в СССР и за рубежом).

В нач. 20 в. расширение масштабов применения железобетонных и стальных конструкций, появление сложных машин и механизмов обусловили быстрое развитие науки о С. м. Были опубликованы классич. учебники С. П. Тимошенко по С. м. и строительной механике, труды A. H. Динника по продольному изгибу, устойчивости сжатых стержней и др.

Дальнейшему совершенствованию методов С. м. способствовало создание в СССР ряда н.-и. учреждений для проведения исследований в области расчета конструкций. Появились новые разделы С. м. Большое влияние на развитие С. м. оказали труды H. M. Беляева в области пластич. деформаций, А. А. Ильюшина по теории пластичности, Ю. H. Работнова и А. Р. Ржаницына по теории ползучести. Значит, вкладом в науку о С. м. явилась созданная В. 3. Власовым теория расчёта тонкостенных стержней и оболочек. Важные фундаментальные исследования выполнены сов. учёными H. И. Безуховым, В. В. Болотиным, А. Ф. Смирновым, В. И. Феодосьевым и др.

Современные тенденции развития науки о С. м. Одна из важнейших задач С. м. - установление причин и характера разрушения материалов, требующее всестороннего теоретич. и экспериментального изучения процессов, происходящих в микрообъёмах тела, в частности характера возникновения и развития трещин. Установлено существование таких (предельных) напряжений, превышение к-рых влечёт за собой прогрессирующий рост уже появившихся трещин, приводящий в конечном счёте к разрушению тела. Если напряжения меньше указанного предела, то тело, имеющее трещины, находится в состоянии трещиноустойчивости. В нек-рых случаях под действием нагрузки разрушения в микроэлементах распространяются на весь объём тела (особенно при высоких темп-рах). Исследование этих вопросов требует создания нового важного раздела механики деформируемого тела - механики разрушения. Ещё недостаточно изучен ряд вопросов т. н. усталостной прочности материалов, в частности прочность элементов (деталей) машин при их длительном циклическом нагружении.

В связи с появлением новых конструкционных материалов (напр., пластмасс, лёгких сплавов) возникла необходимость создания теорий прочности, отражающих специфич. свойства этих материалов. Совр. технологич. процессы (напр., с применением высоких давлений) позволяют получать материалы с весьма высокой прочностью, поведение к-рых под нагрузкой недостаточно изучено и требует целенаправленных исследований.

Лит.: Тимошенко С. П., История науки о сопротивлении материалов с краткими сведениями из истории теории упругости и теории сооружений, M., 1957; Работнов Ю. H., Сопротивление материалов,M., 1962; Феодосьев В. И., Сопротивление материалов, M.. 1974; Сопротивление материалов, M., 1975. Под редакцией А. Ф. Смирнова.

СОПРОТИВЛЕНИЕ ОМИЧЕСКОЕ, прежнее название предельного значения сопротивления активного при =0, где  - частота переменного тока. Термином "С. о." подчёркивается выполнение Ома закона, т. е. наличие линейной зависимости между током и напряжением.

СОПРОТИВЛЕНИЕ РЕАКТИВНОЕ электрическое, величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью и индуктивностью цепи (её участка); измеряется в омах. В случае синусоидального тока при последоват. соединении индуктивного и ёмкостного элементов цепи С. р. выражается в виде разности сопротивления индуктивного и сопротивления ёмкостного: х = L-1/С

где  - угловая частота тока, L к С - индуктивность и ёмкость цепи; С. р. равно отношению амплитуды напряжения на зажимах цепи, обладающей малым сопротивлением активным, к амплитуде тока в ней. В цепи, обладающей только С. р., при протекании переменного тока происходит передача энергии источника тока электрическому или магнитному полю, создаваемому соответственно ёмкостным или индуктивным элементом цепи, и затем обратно, причём средняя за период мощность равна нулю. Наличие у цепи С. р. вызывает сдвиг фаз между напряжением и током. В цепях несинусоидального тока С. р. различно для отд. гармонич. составляющих тока.

СОПРОТИВЛЕНИЕ ЭЛЕКТРИЧЕСКОЕ, см. Электрическое сопротивление.

СОПРОТИВЛЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ, полное электрическое сопротивление, величина, характеризующая сопротивление цепи электрич. току; измеряется в омах. В случае синусоидального переменного тока С. э. ц. выражается отношением амплитуды напряжения на зажимах цепи к амплитуде тока в ней и равно Z =кор(r²+x²), где г - сопротивление активное, х - сопротивление реактивное. При несинусоидальном переменном токе С. э. ц. определяется отдельно для каждой k-той гапмонич. составляющей:

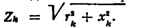
СОПРОТИВЛЕНИЯ ЭЛЕКТРИЧЕСКОГО ИЗМЕРИТЕЛИ, электро- и радиоизмерит. приборы для измерения активного сопротивления электрич. цепи (см. Омметр, Мегомметр, Мост измерительный, Заземления измеритель).

СОПРЯЖЕНИЕ КОНТУРОВ, обеспечение согласованного изменения резонансных частот колебательных контуров к.-л. устройства (напр., супергетеродинного радиоприёмника), перестраиваемых посредством одной ручки настройки. При настройке супергетеродинного приёмника на определённый сигнал резонансная частота контуров входной цепи и усилителя радиочастоты f₀ устанавливается равной частоте принимаемого радиосигнала f_c, а резонансная частота контура гетеродина f_r - такой, чтобы промежуточная частота (равная обычно разности частот fо и fr) совпадала с резонансной частотой контуров усилителя промежуточной частоты. Для С. к. преим. используют метод, при к-ром во всех перестраиваемых контурах применяют одинаковые конденсаторы переменной ёмкости, но в контор гетеродина, частота к-рого должна отличаться от f₀ , дополнительно включают постоянные конденсаторы, наз. конденсаторами сопряжения (см. рис.). Получаемые в этом случае зависимости частот f₀ и f_r от угла поворота ручки настройки несколько отличаются от требуемых, т. е. С. к. является лишь приближённым (однако с достаточной степенью точности) В совр. (сер. 70-х гг.) приёмниках при С. к. в качестве конденсаторов переменной ёмкости используют конденсаторы с механич. изменением ёмкости либо варакторы (варикапы).

Принципиальная схема одного из контуров, содержащихся во входной цепи и в усилителе радиочастоты, и контура гетеродина: L и Lr - катушки индуктивности контуров; С - конденсаторы переменной ёмкости; C₁, С₂, С₃ - конденсаторы сопряжения; f₀ и f_r - резонансные частоты контуров; пунктир означает, что ёмкости конденсаторов изменяются при помощи одной ручки настройки.

Лит.: Радиоприемные устройства, под ред В. И. Сифорова, M., 1974; Чистяков H. И., Сидоров В. M., Радиоприемные устройства, M., 1974.

В. M. Сидоров.

СОПРЯЖЕНИЕ СВЯЗЕЙ, один из важнейших видов внутримолекулярного взаимного влияния атомов и связей в органич. соединениях; обусловлено взаимодействием электронных систем атомов (прежде всего валентных электронов, см. Валентность). Главный признак сопряжения - распределение по всей сопряжённой системе электронной плотности, создаваемой р- и п-электронами. Такими системами являются: чередующиеся простая и кратные связи - двойные или тройные; см. Простая связь, Кратные связи (п, п-сопряжение, как, напр., в бутадиене, I; здесь и далее жирными штрихами, а также точками выделена сопряжённая система); кратная связь и атом со свободной электронной парой (р,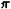-сопряжение, напр, в винилхлориде, II); кратная связь и способная к сопряжению простая связь (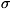, я-сопряжение, например в хлормеркурацетальдегиде, III); две способные к сопряжению простые связи (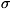, 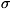-сопряжение, например в этанолмеркурвлориде, IV). Такая классификация сопряжённых систем предложена в начале 50 х гг. 20 в. A. H. Несмеяновым.

CH₂=CH-CH = CH₂

I

CH₂ = CH-Cl

II

ClHg-CH₂-CH=O

III

ClHg-CH₂-CH₂-OH

IV

Общая особенность всех сопряжённых систем - "растекание" электронной плотности р- и 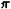-электронов (см. Сигма- и пи-связи) по всей сопряжённой системе - определяет их физ. и хим. свойства. Так, простые связи приобретают нек-рую "двоесвязность", выражающуюся, в частности, в уменьшении их длины. Напр., в бутадиене длина центральной С - С-связи 1,46 А вместо обычной 1,54 А. С. с. проявляется также, напр., в УФ- и ИК-спектрах, дипольных моментах. Наиболее характерная хим. особенность сопряжённых систем - способность вступать в реакции не только с участием одной кратной связи, но и всей сопряжённой системы как единого целого. Примером может служить, напр., присоединение к бутадиену хлористого водорода:

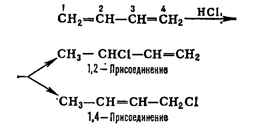
Количество образующихся продуктов 1,2-и 1,4-присоединения зависит от природы сопряжённой системы, от реагента и условий реакции. Сопряжение снижает внутр. энергию молекул и, следовательно, делает их более устойчивыми: величина энергии сопряжения колеблется между неск. единицами и десятками ккал/моль (напр., для бутадиена 3,6 ккал/моль, для бензола 35 ккал/моль; 1 ккал/моль = = 4,19 кож/моль).

Истинное распределение электронной плотности в сопряжённых системах нельзя выразить простейшими структурными формулами. Их строение более точно передаётся наборами предельных структур (см. Мезомерия, Резонанса теория), формулами с пунктирными ("полуторными") связями или с изогнутыми стрелками, указывающими направление сдвига электронов, напр.:

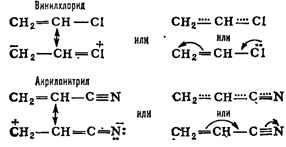
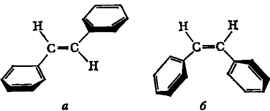
Для проявления С. с. необходимо, чтобы участвующие в нём электронные системы находились в одной плоскости. Если структура молекулы не допускает этого, то говорят о пространственных препятствиях сопряжению. Так, у транс-стильбена (а), по данным УФ-спектров, обнаруживается более сильное сопряжение, чем у цис-стильбена (6), у к-рого бензольные ядра не могут разместиться в одной плоскости с двойной связью:

СОПРЯЖЁННЫЕ ГИПЕРБОЛЫ, две гиперболы, к-рые в одной и той же системе прямоугольных координат при одних и тех же значениях а и b определяются уравнениями:

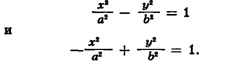
С. г. имеют общие асимптоты и общий основной прямоугольник (см. рис.).

СОПРЯЖЁННЫЕ ДИАМЕТРЫ линии второго порядка, два диаметра, каждый из к-рых делит пополам хорды этой кривой, параллельные другому. С. д. играют важную роль в общей теории линий второго порядка. При параллельном проектировании эллипса в окружность его С. д. проектируются в пару взаимно перпендикулярных диаметров окружности.

СОПРЯЖЁННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, понятие теории дифференциальных уравнений. Уравнением, сопряжённым с дифференциальным уравнением

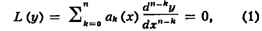
наз. уравнение

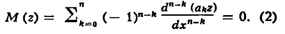
Соотношение сопряжённости взаимно. Для С. д. у. имеет место тождество

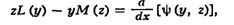
где 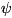(у, z) - билинейная форма относительно у, z и их производных до (п - 1)-го порядка включительно. Знание k интегралов сопряжённого уравнения позволяет понизить на k единиц порядок данного уравнения. Если

y₁, y₂, . . . , y_п(3) - фундаментальная система решений уравнения (1), то фундаментальная система решений уравнения (2) даётся формулами

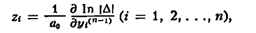
где  - определитель Вроньского (см. Вронскиан) системы (3). Если для уравнения (1) заданы краевые условия, то существуют сопряжённые с ними краевые условия для уравнения (2) такие, что уравнения (1) и (2) с соответствующими краевыми условиями определяют сопряжённые дифференциальные операторы (см. Сопряжённые операторы). Понятие сопряжённости обобщается также на системы дифференциальных уравнений и на уравнения с частными производными.

СОПРЯЖЁННЫЕ ОПЕРАТОРЫ, понятие операторов теории. Два ограниченных линейных оператора T и T* в гильбертовом пространстве наз. сопряжёнными, если для всех векторси xи у из H справедливо соотношение (Tx, у) = = (x, Т*у). Напр., если

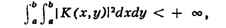
то оператору

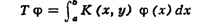
сопряжен оператор

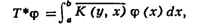
где K(x, у) - функция, комплексно сопряжённая с K(x, у). Если оператор T не ограничен и его область определения Dm всюду плотна (см. Плотные и неплотные множества), то С. о. определяется; на множестве тех векторов у, для к-рых можно найти такой вектор у*, что равенство (Tx, у) = (х, у*) справедливо для всех х принадлежит D_m; при этом полагают Т*у=у*. Понятие сопряжёплостп обобщается также на операторы в др. пространствах.

СОПРЯЖЁННЫЕ РЕАКЦИИ, такие реакции химические, к-рые протекают только совместно и при наличии хотя бы одного общего реагента. Реакция (А + В -> продукты), индуцирующая (вызывающая) прохождение др. реакции, называется первичной, а индуцируемая ею, или сопряжённая ей (А + С -> продукты),- вторичной. Реагент А, участвующий в обеих реакциях, называется актором, реагент В, взаимодействие к-рого с А индуцирует вторичную реакцию,- индуктором, а реагент С - акцептором. Индукторы в С. р., в отличие от катализаторов (в каталитич. реакциях), расходуются.

Примером С. р. может служить совместное окисление окиси углерода и водорода: 2H₂ + O₂ = 2H₂O и 2CO + + O₂ = 2CO₂. Вторая реакция в отсутствие водорода не идёт до очень высоких темп-р, при добавлении же в систему H₂ она становится легко осуществимой. В качестве количественной характеристики для С. р. используют фактор индукции /, равный отношению количеств прореагировавших акцептора и индуктора, выраженных в молях (грамм-молекулах) или грамм-эквивалентах; в данном примере l =n_co /n_н2.

Осн. черты механизма и кинетич. особенностей С. р. были установлены при исследовании окислительных реакций в растворах H. А. Шиловым. В основе явления сопряжения реакций, или xимической индукции, лежит образование промежуточных веществ, возникающих при первичной реакции и осуществляющих перенос индуктивного влияния первичной реакции на вторичную. Как правило, С. р. относятся к цепным реакциям - вслед за образованием под действием индуктора первичного радикала развивается цепь превращений молекул акцептора уже без участия молекул индуктора. Во многих случаях С. р. близки к автокаталитическим реакциям (см. Автокатализ).

Лит. см. при ст. Кинетика химическая.

СОПРЯЖЁННЫЕ ТОЧКИ в оптике, пары точек, в каждой из к-рых одна является по отношению к оптич. системе объектом, вторая - его изображением; при этом согласно обратимости теореме объект и изображение могут взаимно меняться местами. Понятие С. т. вполне строго применимо лишь к идеальным (безаберрационным) оптич. системам в их параксиальных областях (см. Параксиальный пучок лучей). Для реальных систем оно представляет собой широко используемое приближение.

СОПРЯЖЁННЫЕ ФУНКЦИИ, функции и(х, у), v(x, у) двух переменных х и у, связанные в нек-рой области D условиями Коши - Римана (см. Коши-Римана уравнения):

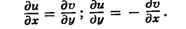
При определённых условиях, напр, при непрерывности частных производных первого порядка, С. ф. и 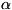являются соответственно действительной и мнимой частью иск-рой аналитич. функции f(x + iy). Они удовлетворяют в области D уравнению Лапласа

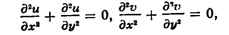
т. е. являются гармоническими функциями. Заданием функции, гармонической в односвязной области D [напр., и(х, у)] однозначно (с точностью до постоянного слагаемого) определяется сопряжённая с ней гармонич. функция v(x, у), а тем самым и аналитич. функция f(x+iy). Напр., если

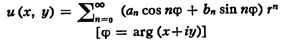
- гармоническая функция в нек-ром круге |x + iy| = r < R, то С. ф.

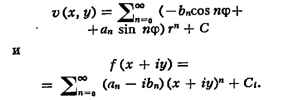
Значения С. ф. на круге r = 1 являются периодич. функциями аргумента . Они раскладываются в тригонометрич. ряды вида

называемые сопряжёнными тригонометрич. рядами.