СОБСТВЕННОЕ ВРЕМЯ в теории относительности, время, измеряемое часами
в собственной системе отсчета движущегося тела, т. е. часами, жестко
связанными с телом (покоящимися относительно него и находящегося в том же
месте). Время протекания к. л. процесса, измеряемое наблюдателем вне тела, в к-ром
происходит процесс, зависит от относит скорости наблюдателя и тела. При
измерениях вдали от тяготеющих тел можно пользоваться частной (специальной)
теорией относительности (см. Относительности теория). Если измерения
производятся в нек-рой инерциалъной системе отсчета ("лабораторной
системе"), а тело движется относительно нее с постоянной скоростью  , то
промежуток С. в.
, то
промежуток С. в. 
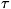 связан с промежутком времени
связан с промежутком времени  t наблюдателя соотношением
t наблюдателя соотношением 
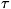 =
= t кор (1 - v2/c2),
где с - скорость света в вакууме, если
t кор (1 - v2/c2),
где с - скорость света в вакууме, если  меняется со временем, то
для конечного интервала времени t1, t2 С. в.
меняется со временем, то
для конечного интервала времени t1, t2 С. в.
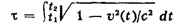
При наличии полей тяготения следует пользоваться общей теорией относительности (см.
Тяготение). С. в. процесса в поле тяготения течет тем медленнее с
точки зрения наблюдателя вне поля, чем сильнее гравитац поле, т е чем больше
модуль гравитац. потенциала 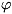 (потенциал
(потенциал 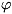 отрицателен, вне поля полагают
отрицателен, вне поля полагают 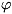 = О). Для не слишком снльных полей, когда |
= О). Для не слишком снльных полей, когда | 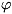 |/с2<1,
С. в.
|/с2<1,
С. в. 
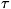 по неподвижным часам в точке с потенциалом
по неподвижным часам в точке с потенциалом 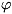 связано с временем
связано с временем  t неподвижного
наблюдателя вне поля соотношением
t неподвижного
наблюдателя вне поля соотношением 
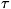 = (1 - |
= (1 - |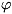 |/c2)
|/c2) t.
t.
Как видно из формул, С. в. всегда меньше времени, измеренного в любой др
системе отсчета.
И. Ю. Кобзарев.
СОБСТВЕННОСТЬ, исторически развивающиеся обществ отношения, к рые
характеризуют распределение (присвоение) вещей как элементов материального
богатства общества между различными лицами (отд. индивидуумами, общественными
группами, классами, гoc-вом) Совокупность вещей, принадлежащих данному субъекту
(собственнику), составляет объект С., или имущество соответствующего лица,
поэтому отношения С. наз. также имущественными отношениями. Будучи
законодательно урегулированы гoc-вом, они приобретают форму права
собственности, к-рое включает полномочия собственника владеть, пользоваться
и распоряжаться имуществом (см. Владение, Пользование, Распоряжение).
Во всяком обществе важнейшее значение имеет С на средства произ-ва, к-рая
определяет и характер С на предметы потребления. Такая связь обусловлена тем,
что процессу обществ. произ-ва принадлежит решающая роль в экономич. жизни
общества. "Всякое распределение предметов потребления есть всегда лишь
следствие распределения самих условии производства. Распределение же последних
выражает характер самого способа производства" (M а р к с К., см. Маркс К.
и Энгельс Ф., Соч., 2 изд., т. 19, с. 20). Отношения С. носят объективный характер.
Хотя на поверхности явлений С представляется в виде предметов, принадлежащих к. л. лицам, понятие ее нельзя сводить к вещественному содержанию или к
отношению человека к вещи, как это делают бурж идеологи, стремясь доказать
вечность капиталистич. С. Марксистско-ленинская теория рассматривает С. как
определенное социальное отношение между людьми, обществ классами, к-рое
развивается в соответствии с изменениями социально-экономич условий жизни
общества. С. характеризует положение отд социальных групп в произ-ве и
взаимоотношения между ними.
Подобно другим обществ отношениям, С. и регулирующие ее правовые нормы имеют историч.
характер. "В каждую историческую эпоху собственность развивалась различно и
при совершенно различных общественных отношениях" (Mарке К., там же, т. 4,
с. 168). Каждая общественно экономич. формация характеризуется специфич. формами С., соответствующими определенному состоянию и уровню производит сил. Исторически
первой формой была коллективная, общинная С. (см. Община, Первобытнообщинный
строй), к-рая основывалась на совместном труде и социальном равенстве
членов общины. В результате длительного историч. процесса, сопровождавшегося
развитием производит. сил и переходом от коллективного труда и общего х-ва к
индивидуальному, парцеллярному труду и обособленным друг от друга мелким х-вам,
происходило разложение общины и возникновение частной С. (см. К. Маркс, там же, т. 19, с. 419). Скот, инвентарь и другое движимое имущество, а затем и земля
превратились в объекты исключительной С. отд. семей. Первоначально частная С.
покоилась на собственном труде семьи. Но с течением времени происходивший
на основе прогресса производит сил процесс роста имущественного неравенства,
лишения отд. семей земли привел к появлению частной С., основанной на присвоении
результатов чужого труда. Возникает эксплуатация человека человеком, общество
раскалывается на классы эксплуататоров и эксплуатируемых (см. Рабовладельческий
строй, Феодализм, Kaпитализм). Рабовладельческая форма С. покоилась на
присвоении труда раба, к-рый, как и др. средства произ-ва, сам был объектом С. рабовладельца. Основу феод. частной С. составляет С на землю и эксплуатация лично зависимых,
крепостных крестьян В отличие от раба, крепостной был участником отношений С.,
поскольку владел мелким зем. участком и средствами произ-ва, необходимыми для
его обработки. Для феодализма характерна такая форма С., при к-рой земля не
принадлежала исключительно отд. лицу. Взаимные отношения как внутри класса
феодалов (сеньоров, вассалов), так и его связи с непосредственными
производителями строились на личном господстве и подчинении. Это была не
свободная и полная частная С. на землю, а условная, ограниченная отношениями
личного господства и подчинения земельная собственность, с к-рой
непосредственно связывалась политич. и военная власть класса феодалов.
В недрах феодализма возникли и отношения С., не связанные с прикреплением
производителей к земле. Кроме мелкой частной С. свободных крестьян, существовала
отделившаяся от зем. С. и свободная от крепостной зависимости С. гор.
ремесленников, изготовлявших продукты для продажи С. развитием производит. сил и товарного
производства возникает капиталистическая, или бурж. С., к-рая существенно
отличается от предшествовавших форм С. она основана на полном отделении
непосредственных производителей от материальных условий их труда. Возникновение
ее связано с экспроприацией сел. населения. В результате появилась крупная частная
С. на землю и вместе с нею масса формально свободных, но не имеющих ничего,
кроме собственных рабочих рук, людей.
Бурж. частная С. основана на капиталистич. товарном произ-ве, формальном
равенстве и формальной свободе частных лиц как субъектов С. В противоположность
частной С. мелких товаропроизводителей основу капиталистич. частной С. составляет
безвозмездное присвоение овеществленных результатов чужого труда, эксплуатация
человека человеком в форме присвоения прибавочной стоимости.
С перерастанием капитализма в монополистич. и особенно в государственно
монополистический капитализм отношения бурж. С. претерпели существенную
эволюцию. Господство монополии привело к превращению акц формы организации
капиталистич. произ-ва в господствующую. Все большее значение приобретают
ассоциированные (коллективные) формы бурж. С. (капиталистич. С. определенной
группы крупнейших акционеров). Коллективные формы бурж. С. не изменили ее капиталистич. эксплуататорского характера, рабочий класс по-прежнему отделен от
средств произ-ва. Ассоциированная С. остаётся поэтому по своему содержанию
капиталистической. Это С. крупнейших капиталистов, объединившихся в
монополистич. союзы, к-рые охватывают пром. корпорации, банки, транспортные,
торг, и др. компании, господствующие в экономич. жизни совр. бурж. общества.
Научно-технич. революция в странах капитализма определила наряду с
дальнейшим развитием ассоциированных форм С. усиливающуюся тенденцию к
повышению роли гос. капиталистич. С. Эта форма существенно отличается от
классич. частной С. и от ассоциированной бурж. С. тем, что её непосредственным
субъектом является гос-во, защищающее интересы господствующего класса. Она
выражает слияние монополий и бурж. гос-ва, играет роль орудия перераспределения
прибавочной стоимости и нац. дохода в пользу частных монополий и отраслей
экономики, расширение к-рых в данный момент соответствует классовым интересам
крупной буржуазии. Степень участия совр. гос-ва в процессе обществ, воспроиз-ва
проявляется в его доле в нац. доходе. На рубеже 60- 70-х гг. в развитых странах
капитализма она колебалась: от 25 и 35% для Японии и США до 38, 42 и 48%
соответственно в Италии, Великобритании и Франции. В тех странах, где гос-во
контролирует более или менее значит, часть производств, аппарата, оно
превратилось по сути в гл. функционирующего капиталиста (см. табл.).
Удельный вес государственных предприятий в экономике стран Западной Европы
(кон. 60-х гг.), %
Капиталистич. национализация С. осуществляется в интересах улучшения
условий накопления капитала, поддержания наиболее эффективного функционирования
капиталистич. предприятий, прежде всего в отраслях инфраструктуры. Быстро
развивающийся процесс капиталистич. огосударствления, имеющий целью подчинить
гос. сектор упрочению капиталистич. системы, тесно связав его с частными
монополиями, характерен для бурж. общества в эпоху гос.-монополистич.
капитализма. Усиливая обобществление произ-ва, этот процесс вместе с тем сужает
сферу прямого господства монополий, наглядно демонстрируя обречённость
частнособственнич. основ капиталистич. строя, создаёт материальные предпосылки
для перехода к социализму. Коммунистич. и рабочие партии капиталистич. стран
исходят из того, что национализация под давлением и при систематич. контроле
рабочего класса создаёт условия для подрыва экономич. и политич. господства
финанс. олигархии, облегчает пролетариату борьбу
за завоевание политич. власти. Отношения С. в условиях гос.-монополистич.
капитализма представляют собой исторически последние формы, покоящиеся на
эксплуатации человека человеком. В силу присущих капиталистич. способу произ-ва
противоречий, и прежде всего усиливающегося противоречия между обществ,
характером произ-ва и капиталистич. формой присвоения, они полностью
исчерпывают себя. В ходе социалистич. революции возникает высшая обществ, форма
С. - социалистическая (всенародная и кооперативная собственность).
Глубокие социальные сдвиги внутри мирового капиталистич. х-ва вызвали
появление совр. переходных форм С., к-рые на данном этапе, как правило, нельзя
отнести ни к последовательно капиталистическому, ни к полностью социалистич.
типу. Они характерны для развивающихся стран, ставших на путь самостоятельного
экономич. и политич. развития. В нек-рых из них гос. С., с одной стороны,
содержит нарождающиеся элементы социалистич. отношений, с другой - сохраняет
элементы капиталистич. или докапиталистич. производств, отношений (см.
Государственный капитализм).
Но при всём многообразии существующих конкретных форм С. всеобщей тенденцией
совр. ступени развития общества является переход от капиталистич. и
докапиталистич. отношений С. к социалистическим и развитию последних в
коммунистич. С.
Вопрос о С. как в теории, так и на практике всегда прямо или косвенно
отражал интересы соответствующих классов. В своё время буржуазия провозгласила
величайшим злом феод. С. Утвердившаяся в результате бурж. революций капиталистич.
частная С. изображалась её идеологами как самая справедливая, отвечающая
естественным правам человека. Капиталистич. С. по сравнению с феодальной была
прогрессивной, поскольку ускоряла рост обществ, произ-ва и материального
богатства и благодаря этому, несмотря на резко выраженное имуществ. неравенство
людей, способствовала развитию экономики и культуры общества. Это прогрессивное
для своего времени значение бурж. С. получило философское и экономич.
обоснование в произведениях таких мыслителей, как Дж. Локк, А. Смит, Д.
Рикардо, П. Гольбах, Ф. Кенэ и Г. Гегель. Но все
они рассматривали бурж. частную С. как вечное условие социального прогресса. С
ростом ассоциированных и гос. форм частной С. в условиях совр. капитализма
идеологи монополистич. капитала уже не говорят о вечности и справедливости
частной С. Они пытаются, создавая теории гос-ва всеобщего благоденствия (см.
"Государства всеобщего благоденствия теория"), индустриального общества,
конвергенции двух мировых систем (см. Конвергенции теория и т. п.),
изобразить новейшие формы капиталистич. С. как отрицающие всё то, что связано с
частно-собственнич. бурж. системой. Пропагандируя тезис т. н. диффузии С.,
бурж. экономисты пытаются доказать, что в условиях совр. капитализма происходит
возрастание числа мелких акционеров, к-рые оказывают определяющее влияние на
деятельность крупных монополий. В действительности, практикуемая крупнейшими
корпорациями продажа акций наиболее квалифицированным рабочим и служащим не означает "диффузии собственности", т. к. подавляющая
масса совокупного акц. капитала остаётся в С. незначит. верхушки общества
(подробнее см. в ст. "Народного капитализма" теория). Такой
поворот от безусловной апологии частной С. к вынужденному признанию её историч.
ограниченности свидетельствует о глубоком кризисе бурж. мировоззрения,
отражающем усиливающийся кризис капиталистич. способа произ-ва в целом.
Марксизм, не отрицая прогрессивности капитализма и бурж. С. для определённой
историч. эпохи, научно доказал путём анализа противоречий капиталистич. способа
произ-ва неизбежность гибели частнособственнич. системы и перехода к новому,
социалистич. обществу, к новой экономич. структуре произ-ва и соответствующей
ей обществ, форме С. (см. Coциалистическая собственность).
Лит.:
Маркс К., Формы, предшествующие капиталистическому
производству. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 46, ч. 1; его же,
Капитал, т. 1, 1л. 24, т. 3, гл. 31, 47, там же, т. 23, т. 25. ч. 1 - 2;
Энгельс Ф., Происхождение семьи, частной собственности и государства, там же,
т. 21; Ленин В. И., Развитие капитализма в России, Полн. собр. соч., 5 изд., т.
3; его же" Империализм, как высшая стадия капитализма, там же, т. 27;
Материалы XXIV съезда КПСС, M., 1971; Колганов M. В., Собственность в
социалистическом обществе, M., 1953; Тюльпанов С. И., Очерки политической
экономии. (Развивающиеся страны), M., 1969; Столяров П., Вопросы теории
и исторического развития форм собственности в работах К. Маркса, К., 1970;
Политическая экономия современного монополистич. капитализма, 2 изд., т. 1, M.,
1975, гл. 16; Ш кредов В., Метод исследования собственности в
"Капитале" К. Маркса, M., 1973; Государственная собственность и
антимонополистическая борьба в странах развитого капитализма, M., 1973.
В. П. Шкредов.
СОБСТВЕННЫЕ ВЕКТОРЫ линейного преобразования, векторы, к-рые при этом
преобразовании не меняют своего направления, а только умножаются на скаляр.
Напр., С. в. преобразования, составленного из вращений вокруг нек-рой оси и
сжатия к перпендикулярной ей плоскости, служат векторы, направленные по этой
оси. Координаты х1, х2, ..., хn С. в.
линейного преобразования 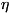 -мерного пространства с матрицей преобразования
||aik|| удовлетворяют системе однородных линейных уравнений
-мерного пространства с матрицей преобразования
||aik|| удовлетворяют системе однородных линейных уравнений 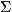 nk=iаikхk =
nk=iаikхk =  1 (i = 1,2,...,
1 (i = 1,2,...,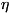 ), где
), где  - одно из собственных значений этой
матрицы. Если матрица преобразования самосопряжённая (см. Самосопряжённая
матрица), то С. в. - взаимно перпендикулярны. При самосопряжённом
преобразовании сфера переходит в эллипсоид, гл. осями к-рого являются С. в.
преобразования.
- одно из собственных значений этой
матрицы. Если матрица преобразования самосопряжённая (см. Самосопряжённая
матрица), то С. в. - взаимно перпендикулярны. При самосопряжённом
преобразовании сфера переходит в эллипсоид, гл. осями к-рого являются С. в.
преобразования.
СОБСТВЕННЫЕ ДВИЖЕНИЯ ЗВЁЗД, видимые угловые перемещения звёзд по
небесной сфере за год. С. д. з. являются следствием как действительных (т. н.
пекулярных) перемещений звёзд в пространстве, так и кажущихся (т. н.
параллактических) смещений, представляющих собой отражение движения Солнечной
системы (вместе с Землёй) в пространстве. Периодич. изменение положения звёзд с
годовым периодом (годичный параллакс) вследствие движения Земли вокруг
Солнца в С. д. з. не входит. Знание С. д. з. важно при построении
фундаментальных систем сферических
координат (фундаментальных звёздных каталогов), опирающихся на точные
положения звёзд, а также при изучении кинематики звёздных систем (совместно с
лучевыми скоростями и параллаксами). Обычно С. д. з. не превышают по величине
сотых долей угловой секунды, редко достигая десятых долей и ещё реже целых
секунд дуги. Наибольшее собств. движение - 10",27 имеет звезда Барнарда
9,7 звёздной величины, находящаяся в созвездии Змееносца.
В древности звёзды считались неподвижно укреплёнными на небосводе. Но уже
китайский астроном И Син (683-727 н. э.), сравнивая полученные
взаиморасположения звёзд в созвездии Стрельца с наблюдениями предшественников,
высказал предположение об изменении угловых расстояний между звёздами со
временем. В 16 в. Дж. Бруно утверждал, что, как и все тела во Вселенной,
звёзды участвуют в непрерывном движении и изменении. Впервые С. д. з. обнаружил
Э. Галлей (1718) у трёх ярких звёзд: Альдебарана, Сириуса и Арктура, из
сопоставления совр. ему координат с координатами в Альмагесте Птолемея. В 1742
Дж. Брадлей высказал предположение, что С. д. з. представляют собой
отражение движения Солнца в пространстве. В кон. 18 - нач. 19 вв. начали
появляться каталоги С. д. з. В последующие годы было показано, что пекулярные
движения звёзд, а следовательно и С. д. з., следует считать беспорядочными с
известной осторожностью, в движении звёзд в пространстве имеются общие
закономерности (движение звёзд скоплений, галактическое вращение).
Определение С. д. з. из-за малости их величины сопряжено с большими
трудностями и требует значит, времени для проведения наблюдений. Визуальный
метод определений С. д. з. основан на сравнении экваториальных координат звёзд,
полученных на меридианных инструментах в разные годы, как правило, на разных
обсерваториях. Однако при таких определениях трудно учитывать все ошибки
используемых каталогов, причём практически невозможно наблюдать звёзды слабее
десятой звёздной величины. Фотографич. метод, удобный для массового определения
С. д. з., основан на сравнении двух или более астрофотографий изучаемой области
неба, разделённых промежутком времени, достаточным, чтобы смещения изображений
звёзд на фотографиях могли быть измерены уверенно. Фотографич. метод позволяет
определять С. д. з. с точностью, в среднем равной ±0,003". К 70-м гг. 20
в. известны собственные движения более чем 250 000 звёзд. Примером каталогов С.
д. з. являются каталоги Астрономического об-ва (ACK) и каталог Смитсоновской
астрофизической обсерватории (АО) (см. Звёздные каталоги).
С. д. з., полученные визуальным методом, относятся к инерциальной системе
координат, определяемой положениями звёзд, содержащихся в использованном
фундаментальном каталоге. При фотографич. же определениях собственные движения
определяются относительно небольшой группы т. н. опорных звёзд в исследуемой
области, среднее движение к-рых принимается равным нулю. Для перехода к
инерциальной системе координат (эта операция паз. абсолютизацией координат)
полагают, что среднее движение совокупности опорных звёзд является
параллактическим и вычисляют его из статистич. соображений, либо для этой цели
используют изображения галактик, объектов, практически неподвижных на небесной
сфере.
Лит.: Паренаго П. П., Курс звёздной астрономии, 3 изд , M., 1954.
В.
В. Подобед.
СОБСТВЕННЫЕ ЗНАЧЕНИЯ линейного преобразования или оператора А, числа  , для к-рых существует ненулевой вектор x такой, что Ax
=
, для к-рых существует ненулевой вектор x такой, что Ax
=  x; вектор x наз. собственным вектором. Так, С.
з. дифференциального оператора L(y) с заданными краевыми условиями
служат такие числа
x; вектор x наз. собственным вектором. Так, С.
з. дифференциального оператора L(y) с заданными краевыми условиями
служат такие числа  , при к-рых уравнение L(y) =
, при к-рых уравнение L(y) =  у имеет ненулевое решение, удовлетворяющее этим краевым
условиям. Напр., если оператор L(y) имеет вид у", то его С.
з. при краевых условиях y(0) = = y(л) = О служат числа вида
у имеет ненулевое решение, удовлетворяющее этим краевым
условиям. Напр., если оператор L(y) имеет вид у", то его С.
з. при краевых условиях y(0) = = y(л) = О служат числа вида  n
= n2, где n - натуральное число, т. к. уравнению - у"
= п2у с указанными краевыми условиями удовлетворяют
функции yn= sin nx; если же
n
= n2, где n - натуральное число, т. к. уравнению - у"
= п2у с указанными краевыми условиями удовлетворяют
функции yn= sin nx; если же  n<>
п2ни при каком натуральном п, то уравнению - у"
=
n<>
п2ни при каком натуральном п, то уравнению - у"
=  у при тех же краевых условиях удовлетворяет
только функция у(х) = 0. К изучению С. з. линейных операторов приводят
MH. задачи математики, механики и физики (аналитической геометрии и алгебры,
теории колебаний, квантовой механики и т. д.).
у при тех же краевых условиях удовлетворяет
только функция у(х) = 0. К изучению С. з. линейных операторов приводят
MH. задачи математики, механики и физики (аналитической геометрии и алгебры,
теории колебаний, квантовой механики и т. д.).
С. з. матрицы А = ||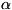 ik|| (i, k - =
1,2,...,и) называют С. з. соответствующего ей линейного преобразования
ik|| (i, k - =
1,2,...,и) называют С. з. соответствующего ей линейного преобразования 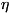 -мерного
комплексного пространства. Их можно определить также как корни определителя
матрицы А -
-мерного
комплексного пространства. Их можно определить также как корни определителя
матрицы А -  E (где E - единичная матрица), т. е.
корни уравнения
E (где E - единичная матрица), т. е.
корни уравнения
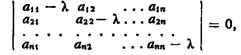
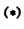
называемого характеристическим уравнением матрицы. Эти числа
совпадают для подобных матриц А и B-1AB (где В - неособенная
матрица) и характеризуют поэтому свойства линейного преобразования, не
зависящие от выбора системы координат. Каждому корню  f
уравнения (*) отвечает вектор x1 <> 0 (собственный
вектор) такой, что Ax1 = =
f
уравнения (*) отвечает вектор x1 <> 0 (собственный
вектор) такой, что Ax1 = =  1x1.Если
все С. з. различны, то множество собственных векторов можно выбрать за
базис векторного пространства. В этом базисе линейное преобразование
описывается диагональной матрицей
1x1.Если
все С. з. различны, то множество собственных векторов можно выбрать за
базис векторного пространства. В этом базисе линейное преобразование
описывается диагональной матрицей

Каждую матрицу А с различными С. з. можно представить в виде C-1 C. Если А - самосопряжённая матрица, то её С. з.
действительны, собственные векторы ортогональны, а матрицу С можно выбрать
унитарной (см. Унитарная матрица). Модуль каждого С. з. унитарной
матрицы равен 1. Сумма С. з. матрицы равна сумме её диагональных элементов, т.
е. следу её матрицы. Знание С. з. матрицы играет важную роль в исследовании
сходимости некоторых приближённых методов решения систем линейных уравнений.
См. также Собственные функции.
C. Если А - самосопряжённая матрица, то её С. з.
действительны, собственные векторы ортогональны, а матрицу С можно выбрать
унитарной (см. Унитарная матрица). Модуль каждого С. з. унитарной
матрицы равен 1. Сумма С. з. матрицы равна сумме её диагональных элементов, т.
е. следу её матрицы. Знание С. з. матрицы играет важную роль в исследовании
сходимости некоторых приближённых методов решения систем линейных уравнений.
См. также Собственные функции.
СОБСТВЕННЫЕ ИМЕНА, слова или словосочетания, называющие, в отличие от
нарицательных имён, единичное или собирательное лицо или объект в его
цельности и единственности, индивидуализирующие его, однозначные для него вне
зависимости от контекста. Общим отличительным признаком С. и. (если пренебречь
нек-рыми семантич. особенностями отд. групп) служит денотативный характер их
значения (см. Знак языковой). Центром класса, наиболее
"подлинными" С. и. являются имена личные (см. Ономастика); все
С. и. генетически - нарицательные имена, чёткой границы между ними нет (ср.
этнонимы, товарные знаки); С. и. с ясной и затемнённой внутр. формой
употребляются одинаково (Новгород, Москва). В системе отношений с др. единицами
словаря С. и. занимают изолированное место. Языковая информация их меньше, а
культурная - значительно больше, чем нарицательных. В разных науках, изучающих
С. и. (лингвистика, логика, философия, мифология и др.), объём класса и его
определение не совпадают.
Для мифолого-символич. сознания, сводящего язык к набору имён и считающего
С. и. словами, наиболее точно выполняющими функцию именования, они стоят в
центре онтологии языка. В ряде антич. и ср.-век. теорий они признавались
знаками, связанными с сущностью именуемого, символически причастными его
глубинной тайне. Имманентное (не фонетич. или графич.) имя, истолкованное по
аналогии с идеями Платона, рассматривалось как корень индивидуального бытия.
Это учение было возрождено и развито в 20 в. (П. А. Флоренский, С. H. Булгаков,
M. Хайдеггер). Крайним выражением его является отождествление имени с именуемым
или приписывание мистич. свойств имязвучию или имяначертанию. представление о
конденсации в имени мощи именуемого, из чего исходят словесная магия и табу.
Ему противостоят рационалистические воззрения, идущие от Демокрита,
обосновавшего произвольность (условность) природы всякого имени. К. Маркс
считал, что название какой-либо вещи не имеет ничего общего с её природой.
Лингвисты и логики, развивающие это направление, считают С. и.
немотивированными знаками, одним из способов обозначения точек пространственно-временной
действительности; они могут быть заменены другими знаками (переименование),
номерами (как улицы в Нью-Йорке), алгебраич. символами. Выбор С. и. и объём их
класса определяют экстрасемиотич. причины (напр., списки канонич. личных имён в
христианстве или мусульманстве); связь между именем и именуемым существует не в
реальной действительности, а лишь в сознании именующих.
Лит.: Волошинов В. H., Марксизм и философия языка, Л., [1929];
Булгаков С. H., Философия имени, Париж, [1953]; Суперанская А. В., Обшая теория
имени собственного, M., 1973; Никонов В. А., Имя и общество, M., 1974.
Ю. M.
Ядельштейн.
СОБСТВЕННЫЕ КОЛЕБАНИЯ, свободные колебания, колебания в механич.,
электрич. или к.-л. другой физич. системе, совершающиеся при отсутствии
внешнего воздействия за счёт первоначально накопленной энергии (вследствие
наличия начального смещения или начальной скорости). Характер С. к.
определяется гл. обр. собственными параметрами системы (массой, индуктивностью,
ёмкостью, упругостью). В реальных системах вследствие рассеяния энергии С. к.
всегда затухающие, а при больших потерях они становятся апериодическими.
Подробнее см. в статье Колебания.
СОБСТВЕННЫЕ НУЖДЫ ЭЛЕКТРОCTAHЦИИ, комплекс вспомогательного электрич.
оборудования электростанции, обеспечивающего бесперебойную работу её
осн. агрегатов (паровых котлов, турбогенераторов, ядерных реакторов или гидротурбин).
В состав С. н. э. входят: силовая и осветительная электросети станции,
аккумуляторные установки, аварийные источники электропитания, электродвигатели
всех механизмов - насосов (водяных, нефтяных, масляных и т. д.), вентиляторов,
а на наиболее распространённых тепловых электростанциях - также
механизмов разгрузки железнодорожных вагонов, подачи топлива, угледробления и
пылеприготовления.
Электроприёмники С. н. э. подразделяют на группы в соответствии с
требованиями бесперебойной работы. К группе наиболее ответственных (НО) относят
электроприемпики, выход из строя к-рых приводит к нарушению нормального режима
работы станции или к аварии. На ТЭС это - электродвигатели питательных насосов
паровых котлов, на АЭС - системы управления и защиты реактора, механизмы
расхолаживания реактора, на ГЭС - механизмы, обеспечивающие циркуляцию масла и
воды в системах смазки и охлаждения, механизмы закрытия дроссельных затворов
напорных трубопроводов. Организация работы НО электроприёмников предусматривает
их надёжное резервирование, обеспечивающее высокую надёжность устройств
С. н. э. Затраты электроэнергии на работу С. н. э. составляют (в % от общего
кол-ва электроэнергии, вырабатываемой станцией) от 0,2 на ГЭС большой мощности
до 12 на АЭС с газовым теплоносителем.
Лит.: Б а п т и д а н о в Л. H., Тарасов В. И., Электрооборудование
электрических станций п подстанций, 3 изд., т. 1 - 2, M.-Л., 1959-60;
Электротехнический справочник, 4 изд., т. 2, кн. 1, M., 1972.
Б. А.
Князевский,
СОБСТВЕННЫЕ ФУНКЦИИ, понятие математич. анализа. При решении многих
задач: математич. физики (в теории колебаний, теплопроводности и т. д.)
возникает необходимость в нахождении не равных тождественно нулю решений
однородных линейных дифференциальных уравнений L(y) =  y,
удовлетворяющих тем или иным краевым условиям. Такие решения называют С. ф.
задачи, а соответствующие значения
y,
удовлетворяющих тем или иным краевым условиям. Такие решения называют С. ф.
задачи, а соответствующие значения  - собственными
значениями. Если дифференциальное уравнение с соответствующими краевыми
условиями самосопряжённое (см. Самосопряжённое дифференциальное уравнение), то
его собственные значения действительны, а С. ф., соответствующие различным
собственным значениям, ортогональны. Если дифференциальное уравнение
рассматривается на конечном отрезке и его коэффициенты не имеют на этом отрезке
особенностей, то множество С. ф. счётно (задача имеет дискретный спект р);
знание С. ф. и соответствующих собственных значений позволяет тогда при нек-рых
условиях получить решение задачи в виде ряда по С. ф. (см. Фурье метод). Если
же уравнение рассматривается на бесконечном промежутке или его коэффициенты
имеют особенности (напр., если коэффициент при старшей производной обращается в
нуль), может существовать континуум С. ф., и вместо разложения в ряд получается
разложение в интеграл по С. ф., аналогичное представлению в виде Фурье интеграла.
В этом случае говорят, что задача имеет непрерывный спектр. Многие
специальные функции (ортогональные многочлены и др.) служат С. ф.
нек-рых уравнений. В теории интегральных уравнений С. ф. ядра K(X, у) называют
функцию, удовлетворяющую при нек-ром значении
- собственными
значениями. Если дифференциальное уравнение с соответствующими краевыми
условиями самосопряжённое (см. Самосопряжённое дифференциальное уравнение), то
его собственные значения действительны, а С. ф., соответствующие различным
собственным значениям, ортогональны. Если дифференциальное уравнение
рассматривается на конечном отрезке и его коэффициенты не имеют на этом отрезке
особенностей, то множество С. ф. счётно (задача имеет дискретный спект р);
знание С. ф. и соответствующих собственных значений позволяет тогда при нек-рых
условиях получить решение задачи в виде ряда по С. ф. (см. Фурье метод). Если
же уравнение рассматривается на бесконечном промежутке или его коэффициенты
имеют особенности (напр., если коэффициент при старшей производной обращается в
нуль), может существовать континуум С. ф., и вместо разложения в ряд получается
разложение в интеграл по С. ф., аналогичное представлению в виде Фурье интеграла.
В этом случае говорят, что задача имеет непрерывный спектр. Многие
специальные функции (ортогональные многочлены и др.) служат С. ф.
нек-рых уравнений. В теории интегральных уравнений С. ф. ядра K(X, у) называют
функцию, удовлетворяющую при нек-ром значении  уравнению
уравнению
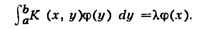
Всякое симметрическое непрерывное ядро имеет С. ф. В этом случае всякая
функция, представимая в виде
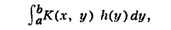
может быть разложена в ряд по С. ф. Если ядро имеет особенности или задано в
бесконечной области, то может также возникнуть непрерывный спектр. Наиболее
общим образом С. ф. можно определить как собственные векторы линейных
операторов в линейных функциональных пространствах. В квантовой механике С. ф.
оператора, отвечающего к.-л. физич. величине (см. Операторы в квантовой
теории), соответствуют состояниям системы, в к-рых данная физич. величина имеет
определённое значение.
Иногда С. ф. называют также фундаментальными функциями, характеристич.
функциями и т. д.