СИНУСОВ ТЕОРЕМА, теорема тригонометрии, устанавливающая соотношения между сторонами а, b, с произвольного треугольника и синусами противолежащих им углов А, В, С. Содержание С. т. заключается в равенствах:

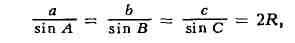
где R - радиус описанного круга.

СИНУСОВ УСЛОВИЕ в оптике должно соблюдаться, чтобы оптич. система, исправленная в отношении сферической аберрации, давала неискажённое (безаберрационное) изображение у' малого линейного элемента у, расположенного

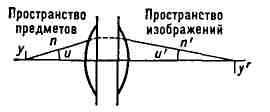
на оптической оси системы и перпендикулярного этой оси (рис.). С. у. выражается формулой sin u/sin и' = В(бетта)n'/n, где и и и' - углы, образуемые с оптич. осью лучом, проходящим через находящиеся на оси точки предмета и соответственно его изображения; п и п' - преломления показатели сред по обе стороны оптич. системы; В = у'/у - линейное увеличение оптическое системы.

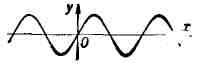
СИНУСОИДА, график функции у = = sin x; плоская кривая (см. рис.), изображающая изменение синуса в зависимости от изменения его аргумента (угла). С. пересекает ось Ох в точках 180 ° k (или пk); в точках вида 90° + 360° k (или п/2 + 2пk) имеет максимумы, а в точках -90° + 360 ° k (или - п/2 + 2пk) - минимумы (k = О, ±1, ...).

 Часто С. называют кривую, определяемую уравнением у = A sin (wх + ф_о), к-рая получается из кривой у = sin x растяжением (в w раз) по оси Оx, растяжением (в А раз) по оси Оу и сдвигом (на -ф_о/w). Число А наз. амплитудой, со - круговой частотой, Фо - начальной фазой. С. имеет большое значение в теории колебаний.

СИНУСОИДАЛЬНЫЕ КОЛЕБАНИЯ, колебания, при к-рых изменения колеблющейся величины происходят по синусоиде;, то же, что гармонические колебания.

СИНУСОИДАЛЬНЫЕ СПИРАЛИ, синус-спирали, кривые, уравнения к-рых в полярной системе координат имеют вид

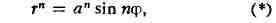
где п - рациональное число. Частными случаями С. с. являются окружность, прямая, равнобочная гипербола, лемниската, кардиоида, парабола (см. Линия) (соответственно при п = 1, -1, -2, 2, 1/2 , -1/2). Логарифмическую спираль можно рассматривать как нек-рый предельный случай С. с. при п = 0 [хотя уравнение (*) теряет при этом смысл], разделяющей С. с., лежащие в конечной части плоскости, от С. с., имеющих бесконечные ветви. Проекция центра кривизны любой точки С. с. на радиус-вектор этой точки делит его в отношении п : 1 (считая от полюса). При равномерном вращении радиус-вектора С. с. вокруг полюса касательная равномерно вращается вокруг точки касания. Поэтому С. с. наз. также кривыми пропорционального изгиба. При натуральном и С. с. состоит из п лепестков, лежащих в углах

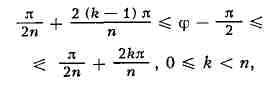
касаясь в начале координат сторон угла. Углы

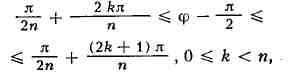
не содержат точек С. с., отличных от начала координат. Если вписать в круг радиуса а •2-¹1п правильный n-угольник P₁, P₂, ..., Р_п, то множество точек, произведение расстояний к-рых до точек P₁, Р₂, ..., Р_n равно аⁿ/2, является С. с. Площадь одного лепестка С. с. равна

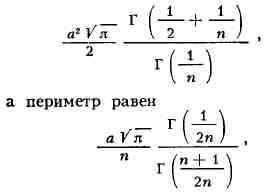
где Г(х) - гамма-функция. При натуральном п С. с. имеет п осей симметрии. Если п = 1/q, то кривая симметрична относительно полярной оси, причём каждая из половин кривой имеет вид спирали, начинающейся в точке r = а, ф = п/2 и после оборота на угол qп/2 приходящей в полюс. С. с. при п = p/q является алгебраической кривой (см. Алгебраическая геометрия), обладающей р осями симметрии, наклонёнными к вертикальной оси под углами 2пqk/p, 0 <=k<p. Изучение С. с. с отрицательными значениями п сводится к изучению С. с. с положительными п при помощи преобразования инверсии. С. с. применяются в нек-рых вопросах механики, геодезии и др.