САМОСОПРЯЖЁННАЯ МАТРИЦА (матем.), матрица, совпадающая со своей сопряжённой, т. е. такая, что а_ik= а_ki, где а - число, комплексно сопряжённое с а. Если элементы С. м. действительны, то она симметрическая (см. Симметрическая матрица). С. м. имеет действительные собственные значения Л₁, Л₂, ..., Л_n и соответствует линейному преобразованию в комплексном га-мерном пространстве, сводящемуся к растяжениям в [Л_i| раз по п взаимно перпендикулярным направлениям и зеркальным отражениям в плоскостях, ортогональных тем из этих направлений, для к-рых Л_i<0. Билинейную форму вида

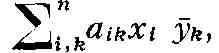
коэффициенты к-рой образуют С. м., называют эрмитовой формой. Всякая матрица может быть записана в виде А₁ + iА₂, где A₁ и А₂ суть С. м., а также в виде AU, где А является С. м., a U - унитарная матрица. Если А а В суть С. м., то АВ является С. м. тогда и только тогда, когда А и В перестановочны.

САМОСОПРЯЖЁННОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ, уравнение, имеющее те же решения, что и сопряжённое с ним (см. Сопряжённые дифференциальные уравнения). Обыкновенное С. д. у. чётного порядка 2т имеет вид

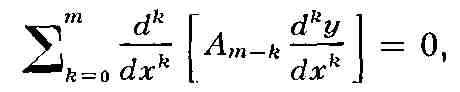
а нечётного порядка 2т - 1 имеет вид

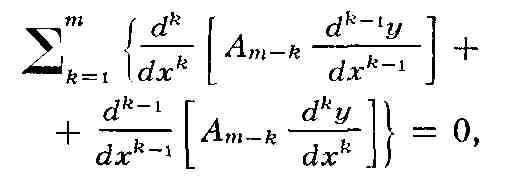
где A_i - функции от .т. Понятие С. д. у. играет большую роль в теории дифференциальных уравнений, обыкновенных и с частными производными. При нек-рых краевых условиях левая часть С. д. у. определяет самосопряжённый дифференциальный оператор. Наиболее важны в приложениях С. д. у. второго порядка.

САМОСОПРЯЖЁННЫЙ ОПЕРАТОР оператор, совпадающий со своим сопряжённым (см. Сопряжённые операторы); иначе называется эрмитовым. Теория С. о. возникла как обобщение теории интегральных уравнений с симметрич. ядром, самосопряжённых дифференциальных уравнений, симметрич. матриц и т. д. Примерами С. о. могут служить оператор умножения на независимое переменное в пространстве функций, заданных на всей числовой прямой и имеющих интегрируемый квадрат, оператор дифференцирования

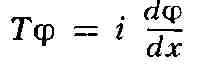
в том же пространстве и т. д.

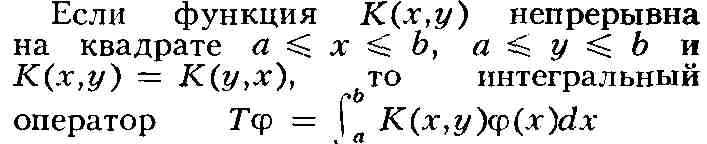
самосопряжён. Спектр С. о. (см. Спектр оператора) лежит на действительной оси. В квантовой механике физич. величинам соответствуют С. о., спектр к-рых даёт возможные значения этих величин. С. о. может быть в известном смысле представлен в виде интеграла, являющегося пределом линейных комбинаций попарно ортогональных проекционных операторов с действительными коэффициентами. См. Спектральный анализ линейных операторов, Операторов теория.