РЫЧАГ, простейший механизм, позволяющий меньшей силой уравновесить большую; представляет- собой твёрдое тело, вращающееся вокруг неподвижной опоры. Основное свойство Р. (любой формы) выражается равенством Ph₁ = Qh₂ (см. рис.), где Р и О - приложенные силы, h₁ и h₂ - расстояния по перпендикулярам, опущенным из точки опоры Р. на линии действия сил (плечи сил). Если опора располагается между точками приложения сил, то это Р. 1-го рода (рис., а). Если же обе силы приложены с одной стороны опоры, то это Р. 2-го рода (рис., б). Для равновесия Р. 1-го рода силы должны быть направлены в одну сторону, а для равновесия Р. 2-го рода - в разные стороны. Теория равновесия Р. под действием сил тяжести была дана Архимедом, а общее условие равновесия Р. П. Вариньоном в 1687. Часто Р. используют в качестве простейшего подъёмного приспособления.

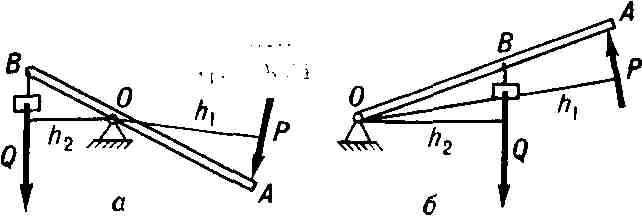
Рычаг 1-го (а) и 2-го (б) рода.

РЫЧАЖНЫЙ МЕХАНИЗМ, механизм, состоящий из звеньев, соединённых между собой в низшие кинематические пары. Р. м. бывают плоские и пространственные. В плоских Р. м. звенья соприкасаются по окружности (шарниры, вращат. пары) и по линии (постулат, пары). В пространств. Р. м. звенья соединяются по цилиндрич. или сферич. поверхностям (вращат. пары) и по плоскости (постулат, пары). Часто в технич. лит-ре Р. м. называют стержневыми шарнирными механизмами. К ним относят также кулисные и кривошипно-ползунные механизмы. Р. м. проще в изготовлении, прочнее и более износостойки, чем кулачковые и зубчатые механизмы, поэтому Р. м. применяют для передачи больших усилий в прессах, ковочных машинах, двигателях внутр. сгорания, погрузчиках и т. п.

Лит. см. при статье Механизм.

РЫЧКОВ Николай Петрович (1746-1784), русский путешественник. Сын П. И. Рычкова. В 1760-67 на воен. службе. С 1768 принимал участие в экспедиции Петерб. АН, возглавлявшейся П. С. Палласом; в 1769-70 объехал Казанскую, Оренбургскую, Уфимскую, Вятскую и Пермскую губ. и составил их описание, к-рое содержит сведения о природе, древних городищах, обычаях и др. В 1771 участвовал в экспедиции по терр. Зап. и Сев. Казахстана.

Соч.: Журнал или дневные записки путешествия по разным провинциям Российского государства 1769 и 1770 годов, ч. 1 - 2, СПБ, 1770 - 72; Дневные записки путешествия в Кпргиз-Кайсацкой степи в 1771 году, СПБ, 1772.

РЫЧКОВ Пётр Иванович [1(12).10.1712, Вологда, - 15(26).10.1777, Екатеринбург, ныне Свердловск], русский учёный, автор трудов по географии, экономике, истории. Род. в купеческой семье. Первый чл.-корр. Петерб. АН (1759). С 30-х гг. служил в Оренбургском крае; в 1734-37 участвовал в Оренбургской экспедиции под рук. И. К. Кирилова, затем В. Н. Татищева. Осн. труд "Топография Оренбургская..." (2 чч., 1762), являющийся пояснительным текстом к составленным в 1755 И. Красильниковым картам Оренбургской губ. и представляющий одну из первых региональных сводок, где дано подробное историч. и географич. описание края. Эта работа имела большое значение для зарождения в России экономич. географии. Р. принадлежат также работы по истории, экономике, этнографии народов Поволжья, Урала, Прикаспия.

Лит.: М и л ь к о в Ф. Н., П. И. Рычков. Жизнь и географические труды, М., 1953.

РЫШКАНЫ, посёлок гор. типа, центр Рышканского р-на Молд. ССР. Расположен на р. Копочанка (приток р. Реут), в 22 км от ж.-д. ст. Дрокия (на линии Окница - Бельцы-Слободзея). 12 тыс. жит. (1973). З-ды: сыродельный, эфирномасличных культур, стройматериалов. Совхоз-техникум эфирномасличной и табачной пром-сти.

РЭДУЛЕСКУ (Radulescu) Ион Элиаде (1802-1872), румынский поэт; см. Элиаде-Рэдулеску И.

РЭКЕТИР, рекетир (англ, racketeer, от racket - шантаж), в США - шантажист, вымогатель, гангстер.

РЭЛЕЙ, Рейли (Rayleigh) Джон Уильям (12.11.1842, Лэнгфорд-Гров, графство Эссекс,- 30.6.1919, Тирлинг-Плейс, близ г. Уитем), английский физик, один из основоположников теории колебаний. Чл. Лондонского королев, об-ва (1873). Фамилия до получения титула лорда Рэлея (1873) - Стретт (Strutt). Окончил Кембриджский ун-т (1865); после смерти Дж. Максвелла (1879) стал проф. этого ун-та и директором Кавендишской лаборатории. С 1887 проф. Британского королев, ин-та (Лондон). Диапазон науч. интересов Р. очень широк: акустика, теория колебаний, оптика, электричество и др. области физики. Р. исследовал акустич. колебания (колебания струн, стержней, пластинок и др.). В 1873 он сформулировал ряд фундаментальных теорем линейной теории колебаний, позволяющих делать качеств, заключения о собственных частотах колебат. систем, и разработал количеств, метод возмущений для нахождения собств. частот колебат. системы, мало отличающейся от простой системы с известными собств. частотами. Р. впервые указал на специфичность нелинейных систем, способных совершать незатухающие колебания без периодического воздействия извне, и на особый характер этих колебаний (наз. впоследствии автоколебаниями). Он объяснил различие групповой и фазовой скоростей и получил формулу для групповой скорости (формула Р.). Он рассмотрел также задачу сложения многих колебаний со случайными фазами и получил функцию распределения для результирующей амплитуды - т. н. Рэлея распределение. Метод, разработанный при этом Р., надолго определил дальнейшее развитие теории случайных процессов. В теории упругих волн Р. рассмотрел вопросы дифракции, рассеяния и поглощения волн, давление звука, исследовал волны конечной амплитуды и особый вид поверхностных волн (Рэлея волны). Работы Р. по теории колебаний систематизированы им в фундаментальном труде" Теория звука" (2тт., 1877-78, 2 изд. 1894-96), в к-ром впервые отчётливо проявился единый подход к изучению колебат. и волновых процессов, имеющих различную природу. Эти идеи Р. легли в основу совр. теории колебаний.

Дж. У. Рэлей.

В 1900 Р. вывел один из законов излучения абсолютно чёрного тела (см. Рэлея-Джинса закон); эта работа имела большое значение для возникновения теории квантов. Р. заложил основы теории молекулярного рассеяния света. Установив обратную пропорциональность интенсивности рассеянного света 4-й степени длины волны (Рэлея закон), он объяснил голубой цвет неба. В 1879 Р. создал теорию разрешающей способности оптич. приборов. В 1894 совм. с У. Рамзаем открыл аргон. Имя Р. получили многие физич. понятия, законы, приборы (диск Рэлея, интерферометр Рэлея, рэлеевское рассеяние света, Рэлея закон намагничивания и др.). Нобелевская пр. (1904).

Соч.: Scientific papers, v. 1 - 6, Camb., 1899 -1920; в рус. пер.- Волновая теория света, М.- Л., 1940; Теория звука, т. 1 - 2, 2 изд., М., 1955.

Лит.: S t r u t t R. J., The life of John William Strutt, 3 rd Baron Rayleigh, L., 1924; Schucter A., John William Strutt, baron Rayleigh (1842 - 1919), "Proc. of Royal Society", A., 1921, v. 98, №695.

РЭЛЕЙ, редко употребляемая единица удельного акустического сопротивления в СГС системе единиц (см. Импеданс акустический). Названа в честь англ, физика Дж. У. Рэлея. 1 Р. равен удельному акустич. сопротивлению среды, при к-ром звуковое давление 1 дин/см² вызывает колебательную скорость частиц среды 1 см/сек. 1 Р.=1дин*сек/см³=-10н*сек/м³.

РЭЛЕЯ ВОЛНЫ, упругие возмущения, распространяющиеся в твёрдом теле вдоль его свободной границы и затухающие с глубиной. Их существование было предсказано Дж. У. Рэлеем в 1885. Примеры Р. в.- волны на земной поверхности, возникающие при землетрясениях; ультразвуковые волны, применяемые для контроля поверхностного слоя различных деталей и образцов и т. д. Толщина слоя локализации Р. в. составляет (1-2Д, где ~k - длина волны. На глубине А плотность энергии в волне ~ 0,05 плотности у поверхности. Движение частиц в Р. в. происходит по эллипсам, большая полуось к-рых перпендикулярна поверхности твёрдого тела, а малая - параллельна направлению распространения волны. Фазовая скорость Р. в. меньше фазовых скоростей продольных и сдвиговых волн и равна групповой скорости.

В анизотропных средах структура и свойства Р. в. зависят от типа анизотропии и направления распространения волн, причём имеются такие среды, напр, кристаллы триклинной системы, в к-рых Р. в. вообще не могут существовать. Иногда под Р. в. понимают поверхностные волны более общего типа, возникающие на границе твёрдого тела с жидкостью и на границе системы твёрдых или жидких слоев с твёрдым полупространством.

Лит.: Кольский Г., Волны напряжения в твердых телах, пер. с англ., М., 1955; Ландау Л. Д., ЛифшицЕ. М., Теория упругости, 3 изд., М., 1965 (Теоретическая физика, т. 7); В и к т о р о в И. А., физические основы применения ультразвуковых волн Рэлея и Лэмба в технике, М., 1966.

РЭЛЕЯ ДИСК, прибор для измерения силы звука; подробнее см. Диск Рэлея.

РЭЛЕЯ ЗАКОН, гласит, что интенсивность I рассеиваемого средой света обратно пропорциональна 4-й степени длины волны Л. падающего света (1 ~ Л^-4 ) в случае, когда среда состоит из частиц-диэлектриков, размеры к-рых много меньше Я. Установлен Дж. У. Рэлеем в 1871. См. также Рассеяние света.

РЭЛЕЯ ЗАКОН НАМАГНИЧИВАНИЯ, установленная Дж. У. Рэлеем (1887) зависимость намагниченности J (ила магнитной индукции В) ферромагнетиков от напряжённости магнитного поля Н в слабых полях (когда напряжённость поля, действующего на образец, много меньше коэрцитивной силы, Н_с). Р. з. н. может быть выражен следующими формулами: а) для кривой первого намагничивания J = н_обрН±RH² (см. Намагничивания кривые), где и_06Р - обратимая магнитная восприимчивость, к-рая характеризует обратимую линейную часть процесса, R - постоянная Рэлея, характеризующая необратимые нелинейные процессы намагничивания; б) для восходящих и нисходящих петель гистерезиса |дельта J| = н_обр |дельта Н| + R |дельтаН|²/2„ где |дельта J| и |дельта Н| - абс. величины приращений J и Н. Р. з. н. выполняется не только вблизи размагниченного состояния (J = О, Н = 0), но и при др. исходных значениях J или В, лишь бы значение Н и его изменение дельта Н были бы малыми по сравнению с Н_с (Н, дельта Н " Н_c). При этом параметры н_обр и R, конечно, меняются. Вблизи размагниченного состояния Иобр совпадает с обратимой начальной магнитной восприимчивостью н_а и обусловлена обратимыми смещениями границ между доменами (см. Намагничивание). При исходных J не равно 0 и Н не равно 0 значение н_обр не равно н_а, но н_обр и в этом случае определяется обратимыми процессами смещения доменных границ. Параметр R характеризует необратимые смещения доменных границ. Область применимости Р. з. н. для различных ферромагнетиков может составлять от неск. мэ (ферриты) до неск. э (перминвары).

Лит.: Вонсовский С. В., Магнетизм. М., 1971.

О. В. Росницкий.

РЭЛЕЯ РАСПРЕДЕЛЕНИЕ, распределение вероятностей случайной величины X, характеризующееся плотностью

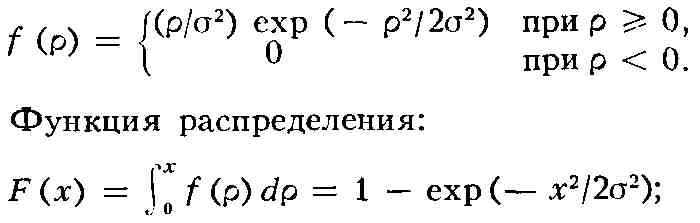
математическое ожидание:

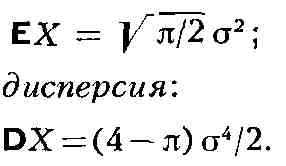
Максимальное значение плотности равно

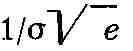
и достигается при х = а (на рис. даны графики плотности

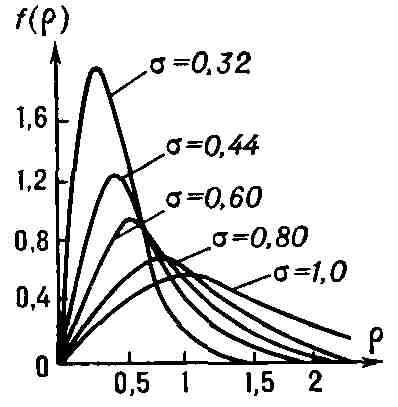
Р. р. при различных а). Р. р. встречается в применениях теории вероятностей, напр, к радиотехнике. Введено Дж. У. Рэлеем (1880) в связи с задачей сложения гармонич. колебаний со спиральными фазами.

РЭЛЕЯ ТЕОРЕМА, см. Взаимности реакций принцип.

РЭЛЕЯ - ДЖИНСА ЗАКОН ИЗЛУЧЕНИЯ, закон, выражающий распределение энергии в спектре абсолютно чёрного тела в зависимости от темп-ры. Р. - Д. з. и. может быть записан в виде:

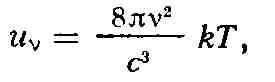
где u_v - плотность излучения, соответствующая частоте V, с - скорость света, Т - абс. темп-pa, k - Болъцмана постоянная.

Р.- Д. з. и. был выведен в 1900 Дж. У. Рэлеем из классич. представлений о равномерном распределении энергии по степеням свободы. В 1905-09 Дж. Джине, применив методы классич. статистич. механики к стационарным волнам в полости, пришёл к той же формуле, что и Рэлей. Р.- Д. з. и. хорошо согласуется с экспериментом лишь для малых v (в длинноволновой области спектра). С ростом v энергия излучения по Р.- Д. з. и. должна неограниченно расти, достигая чрезвычайно больших значений в далёкой ультрафиолетовой и ещё более коротковолновой областях спектра (т. н. ультрафиолетовая катастрофа), но это противоречит опыту. Распределение энергии в спектре абсолютно чёрного тела, справедливое для всего спектра, получается только на основе квантовых представлений (см. Планки закон излучения). Р.- Д. з. и. является частным случаем закона Планка для малых v; его применяют вместо закона Планка при рассмотрении достаточно длинноволнового излучения и в тех случаях, когда не требуется высокая точность вычислений.

Лит.: П л а н к М., Теория теплового излучения, пер. с нем., М. - Л., 1935; Ш п о л ь с к н й Э. В., Атомная физика, 5 изд., т. 1, М., 1963.

РЭЛИ, Роли, Рэлей (Ralegh, Raleigh) Уолтер (ок. 1552, Хейс-Бартон, Девоншир, - 29.10.1618, Лондон), английский политич. деятель, поэт, историк. В молодости сражался на стороне гугенотов во Франции и участвовал в борьбе Нидерландов против исп. господства (1577). Учился в Оксфордском ун-те. В 1580 один из руководителей англ. карательной экспедиции против Ирландии. В 80-е гг. фаворит Елизаветы Тюдор, активный сторонник её внутр. и внеш. политики. В 1583-85 предпринял попытку основать в Сев. Америке англ. колонию ("Виргиния"). В 1585 занял пост управляющего рудниками, внце-адмирала и лорда-наместника Девона н Корнуолла. В 1588 участвовал в разгроме испанской "Непобедимой армады". В 1595 совершил плавание в район р. Ориноко (Юж. Америка), к-рое описал в кн. "Открытие обширной богатой и прекрасной Гвианской империи..." (1596, рус. пер. 1963). Обвинённый в причастности к заговору против вступления Якова I Стюарта на англ. престол, был приговорён к смерти, а затем (без отмены приговора) заключён в Тауэр (1604). В тюрьме занимался химич. опытами, написал трактат о кораблестроении и "Историю мира.,.", к-рую довёл до 130 до н. э.

В 1616 представил Якову план разработки золотых рудников в Гвиане; был освобождён из тюрьмы и назначен руководителем эскадры. Экспедиция, в ходе к-рой произошло вооруж. столкновение с испанцами, закончилась неудачно. После возвращения в Англию был казнён на основании приговора 1603.

Р.- идеолог буржуазии и нового дворянства эпохи первоначального накопления капитала, сторонник сотрудничества королевской власти с парламентом, способного, по его мнению, обеспечить интересы предпринимательских кругов, один из первых глашатаев колониальной экспансии. Пользовался у современников репутацией "материалиста" и "атеиста", резко критиковавшего догматику и организационные принципы христ. церкви. Типичный деятель английского Возрождения, Р. известен также как автор поэтических произведений и политических трактатов.

Соч.: The works, v. 1-8, Oxf., 1829.

Лит.: Hume М., Sir Walter Raleigh, L., 1897; W i 1 1 i a m s N. L., Sir Walter Raleigh, Phil., 1963; Bradbrook M. C., School of night, N. Y., 1965.

В. М. Карев.

РЭНГА (нанизанные строфы), жанр японской поэзии, был в моде в 15-16 вв. В создании Р. участвовало неск. поэтов (чаще трое), каждый по очереди сочинял по строфе в соответствии с образами только предыдущей строфы. Получалась цепь строф по форме танка, но длиннее, до 100 и 1000 строф. Классич. Р. чаще всего - пейзажная лирика; её сочинение, как и танка, подчинялось строгим правилам. Рядом с ней развивалась шуточная Р. (хайкай рэнга), свободная в выборе тем и образов; из первой строфы шуточной Р. возник жанр трёхстишия хокку, или хайку.

Лит.: Басе, Лирика, М., 1964; Григорьева Т. и Логунова В., Японская литература, М., 1964; Литература Востока в средние века, т. 1, М., 1970; Конрад Н. И., Очерки японской литературы, М., 1973; его же, Японская литература, М., 1974.

РЭТСКИЙ ЯРУС (от лат. Raetia, Rhaetia - назв. древней области в Альпах), верхний ярус триасовой системы [см. Триасовая система (период)]. Выделен в 1858 нем. геологом К. В. Гюмбелем. В типовом разрезе (Ретийские Альпы) сложен внизу переслаиванием мергелей и известняков (кессенская фация), вверху известняками и доломитами (дахштейнская фация). До 1963 франц. геологи относили Р. я. к основанию юрской системы. Нек-рые исследователи (нем. геологи Ф. Фабрициус, М. Урлихс, И. Видман, австр.- X. Цапфе, Л. Кристин) подвергают сомнению самостоятельность Р. я., считая его фацией норийского яруса. Отложения Р. я. развиты в Евразии, Гренландии, Сев. Америке, на о. Тимор, в Н. Зеландии.

РЮГЕН (Rugen), остров в Балтийском м., на С. ГДР. Пл. 926 км². Нас. с прилегающими мелкими островами 86,2 тыс. чел. (1971). Берега низкие, сильно расчленённые, с многочисл. косами, пересыпями, дюнами. Рельеф - всхолмлённая равнина с грядами конечных морен, перекрывающих известняки. выс. до 161 м. Б. ч. поверхности распахана (рожь, овёс, картофель, сах. свёкла). На В. и в центре - массивы буковых лесов. Молочное животноводство. Рыболовство (сельдь, угорь). Осн. порт - Засниц (близ к-рого - добыча мела). Приморские курорты (Бинц, Зеллин и др.). С материком соединён ж. д. и шоссе, проходящими по дамбе дл. 2,5 км и мосту. Между гг. Засниц (ГДР) и Треллеборг (Швеция) - паромная переправа.

Лит.: Oehler H., Mit offenen Augen durchs Rugenland, Schwerin, [1971].

РЮД (Rude) Франсуа (4.1.1784, Дижон,- 3.11.1855, Париж), французский скульптор, представитель романтизма. Учился у живописца Ф. Девожа в Дижоне (с 1798), а также у скульпторов Э. Голля и П. Картелье в Париже (с 1807). В период реставрации Бурбонов эмигрировал в Бельгию (1815-27), в Брюсселе сблизился с Ж. Л. Давидом, оказавшим на Р. сильное влияние. Вернувшись во Францию, исполнил ряд работ, навеянных антич. мифологией ("Меркурий, завязывающий сандалию", бронза, 1827, Лувр, Париж). В 1833-36 Р. создал своё крупнейшее произв.- монументальный рельеф "Марсельеза" ("Выступление добровольцев в 1792 году"; камень) Триумфальной арки на площади де Голля (б. Этуаль) в Париже (илл. см. на вклейке, табл. XV стр. 128-129). Революционный подъём народа воплощён Р. в обобщённых и вместе с тем глубоко жизненных образах, особенно в полной страстного порыва аллегорической женской фигуре. Рельеф отличается ритмической цельностью и динамикой композиции, богатой пластической разработкой фигур. Автор мн. скульпт. памятников, в т. ч. исполненного порывистого движения памятника маршалу Нею (бронза, 1852-53) на площади Обсерватории в Париже. Известен как тонкий рисовальщик.

Лит.: Drouot H., Une carriere. Francois Rude, Dijon, 1958.

РЮДБЕРГ (Rydberg) Абрахам Виктор (18.12.1828, Иёнчёпинг, - 21.9.1895, Юрсхольм, близ Стокгольма), шведский писатель. В романе-фельетоне с авантюрным сюжетом "Вампир" (1848) и др. сказались демократич. симпатии автора. Романтизм Р. наиболее полно выразился в повести "Сингуалла" (1857, рус. пер. 1904)- о любви рыцаря и цыганки. В ист. романах "Корсар в Балтийском море" (1857), "Последний афинянин" (1859, рус. пер. 1901) и "Оружейник" (1891) романтич. интрига сочетается с полемич. заострённостью против фанатизма и нетерпимости церкви. В лирич. стихах Р., продолжая романтич. традиции, обратился к совр. тематике. Выступал как переводчик и автор лекций по истории философии и культуры. В 1886-89 опубл. "Исследования в области германской мифологии".

Соч.: Kulturhistoriska forelasningar, bd 1 - 6, Stockh., 1903-06; Skrifter, bd 1 - 12, Stockh., 1945-46.

Лит.: Warburg K., Viktor Rydberg. En levnadsteckning, bd 1 - 2, Stockh., 1900; В ii s s о w H., V. Rydberg's historische Romane, Braunschweig, 1929; L i n d b e r g e r O., Prometeustanken hos Viktor Rydberg, del 1 - 2, Stockh., 1938; Granlid H., Nya grepp i Rydbergs lyrik, Stockh., 1973.

А. А. Мацевич.

PЮИСДАЛЬ (Ruysdael, Ruijsdael), семья голландских живописцев 17 в.; см. Рёйсдал С. и Рёйсдал Я.

РЮЙШ (Ruysch) Фредерик (1638-1731), голландский анатом; см. Рейс Ф.

РЮКЮ, Нанеси, архипелаг островов в Японии, между о-вами Кюсю и Тайвань, отделяет Вост.-Китайское м. от открытой части Тихого ок. Вытянут дугообразно с С.-В. на Ю.-З. приблизительно на 1200 км. Состоит из 6 групп островов (Осуми, Токара, Амами, Окинава, Мияко и Яэяма; 2 последние часто объединяют под назв. Сакисима), включающих в совокупности 98 о-вов пл. ок. 4,8 тыс. кл² (в япон. источниках назв. "Р" часто относят только к среднему и юго-зап. звеньям островной дуги, состоящим из 55 о-вов пл. 2,4 тыс. км²). Наиболее крупные о-ва - Окинава и Амамиосима. Нас. ок. 1,2 млн. чел. (1970, оценка). Юго-вост. полоса о-вов сложена гл. обр. закарстованными известняками мезокайнозоя; в осевой зоне на поверхность часто выходит палеозойский складчатый фундамент; на С.-З. распространены вулканич. породы (имеется 3 действующих и неск. потухших вулканов). В рельефе преобладают плато и низкогорья (выс. 300-500 м), а также низкие береговые террасы. Наибольшая выс. 1935 м (на о. Яку). К Ю. от 29° с. ш. вдоль берегов местами протягиваются полосы коралловых рифов. Месторождения фосфоритов и кам. угля. Климат на С.- субтропический, на Ю.- тропический, муссонный (осадков 2000-3500 мм в год), с частыми тайфунами в авг.- сент. Ср. темп-ра янв. 14-18 ^оС, июля 27-28 ^оС. Склоны гор юж. о-вов местами покрыты тропич. лесами с пальмами и орхидеями; на сев. о-вах сохранились леса из камелий, магнолий, камфарного лавра, дуба. Посевы риса, батата, сах. тростника. Рыболовство, выделка шёлковых тканей и изделий из лака. Осн. город - Наха на о. Окинава. Вывоз ананасов.

Ю. К. Ефремов.

РЮКЮСЦЫ, этнографическая группа японцев.

РЮМ, рогатый жаворонок (Eremophila alpestris), птица сем. жаворонков.

РЮПЕЛ (Rupel), река в Бельгии, прав, приток Шельды. Образуется слиянием pp. Нет, Диль и Сенна, бассейны к-рых охватывают значит, часть Вост. Бельгии. Длина от места слияния 12 км, пл. басс. 6,5 тыс. км. Ср. расход воды ок. 50 м³/сек (повышенная водность зимой и весной). Канализована, судоходна для судов водоизмещением до 2 тыс. т. Подвержена действию мор. приливов выс. до 4-4,5 м, во время к-рых доступна для мор. судов. Вблизи устья -крупные верфи.

"РЮРИК", русский крейсер. Построен в Петербурге, вступил в строй в 1895. Водоизмещение 11 930 т, скорость 19 узлов (35 км/ч), вооружение: 4 орудия 203-мм, 16 орудий 152-мм, 6 орудий 120-мм, 10 орудий 47-мм, 12 орудий 37-мм, 6 торпедных аппаратов; экипаж св. 800 чел. В 1904 входил в состав Владивостокского отряда крейсеров. В ходе русско-японской войны 1904-05 1(14) авг. 1904 во время боя в Корейском проливе слабо бронированный "Р." в начале боя получил серьёзные повреждения и потерял управление. Попытка командующего эскадрой контр-адмирала К. П. Иессена прикрыть "Р." и отвлечь противника была безуспешной. Окружённый 4 японскими лёгкими крейсерами, "Р." в течение 2 часов героически сражался с врагом; было убито 150 чел., в т. ч. командир и старший офицер, и ок. 280 ранено. Принявший командование лейтенант К. Иванов, ввиду угрозы захвата корабля противником, приказал открыть кингстоны и "Р." был затоплен. Из воды японцами было подобрано 625 чел., в т. ч. 230 раненых.

РЮРИКОВ Борис Сергеевич [20.3(2.4). 1909, Женева,- 21.5.1969, Москва], советский критик, литературовед, публицист. Чл. КПСС с 1932. Окончил историко-филологич. ф-т Горьковского пед. ин-та (1932). Печатался с кон. 20-х гг. Работал в газ. "Правда", "Литературной газете" (в 1953-55 гл. редактор), в аппарате ЦК КПСС, гл. редактором журн. "Иностранная литература" (1963-69). Статьи Р., посвящённые актуальным проблемам марксистско-ленинской и революционно-демократической эстети ки, искусства социалистич. и критич. реализма, вошли в его сб-ки "Литература и жизнь" (1953), "О богатстве искусства" (1956), "Коммунизм, культура и искусство" (1964), "В. И. Ленин и вопросы литературы" (1970) и др. Выступления Р. отличались партийностью, полемич. Остротой, непримиримостью к бурж. идеологии и догматич. вульгаризаторству. Награждён орденом Ленина, 4 др. орденами, а также медалями.

Соч.: Н. Г. Чернышевский, 2 изд., М., 1961; О русских классиках. [Вступ. ст. И. Черноуцана], М., 1972; Реальный гуманизм. Статьи. [Вступ. от. Б. Сучкова], М., 1972.

Лит.: П е р ц о в В., Не только объяснять, но и изменять!, "Новый мир", 1956, № 7; Зельдович М., Пафос современности, "Вопросы литературы", 1961, № 7; Иезуитов А., В. И. Ленин и вопросы литературы, там же, 1972, № 4; Дмитрнев В., Гуманизм знания и действия, "Иностранная литература", 1973, № 1.

В. А. Калашников.

РЮРИКОВИЧИ, князья - потомки киевского вел. князя Игоря, считавшегося, по летописному известию, сыном Рюрика (см. Рюрик - Синеус-Трувор). Р. стояли во главе Древнерус. гос-ва (поэтому в ист. лит-ре его называли иногда "Империей Рюриковичей") и крупных и мелких княжеств периода феод, раздробленности. В 12-13 вв. некоторые Р. назывались также по именам родоначальников ответвлений рода Р.- Мономаховичи (Мономашичи), Ольгови-чи и др. Моск. вел. князья и цари являлись потомками владимиро-суздальских Мономаховичей. Последний царь Р.- Фёдор Иванович - умер в 1598. С образованием Рус. централизованного гос-ва мн. Р., утратив удельные владения, составили высший слой моск. служилых людей ("княжата"). В 17 в. часть Р. постепенно слилась с представителями верхушки нетитулованного дворянства и вместе с ними занимала господствующее положение среди придворной знати 17-19 вв. (напр., потомки черниговских князей - Р.: Барятинские, Волконские, Горчаковы, Долгоруковы, Оболенские, Одоевские, Репнины, Щербатовы и др.). Др. часть Р., обеднев, смешалась со средним и даже мелким дворянством, и нек-рые из них при этом потеряли княжеский титул.

Лит.: Власьев Г. А., Потомство Рюрика. Материалы для составления родословий, т. 1,ч. 1 - 3, СПБ, 1906 - 07; В a u m g а r t е n N., Genealogie et mariages occidentaux des Rurikides russes du X-е au XIII-e siecle, Roma, 1928; его же, Genealogies des branches regnantes de Rurikides du XIII-е au XVI-е siecle, Roma, 1934.

РЮРИКОВО ГОРОДИЩЕ, древнее городище, расположенное в 2 км от Новгорода, на правом берегу р. Волхова, в пределах с. Городище. Первоначально наз. просто Городище; Р. г.- назв. позднее, возникшее в нач. 19 в. под влиянием летописной легенды о Рюрике. Раскопки, проведённые в 1928, 1935 и 1965 новгородской археол. экспедицией, обнаружили на Р. г. три культурных слоя: эпохи неолита, раннего железного века и русский (с 12 в.). На Р. г. неоднократно находили свинцовые печати 12-15 вв. с именами князей, бояр, посадников, наместников. Эти находки связаны с существованием здесь в 12-13 вв. укреплённой княжеской усадьбы, где поселились князья, к-рым после народных восстаний 12 в. было запрещено жить в Новгороде. В 14-15 вв. здесь жили великокняжеские наместники.

РЮРИК-СИНЕУС-ТРУВОР, по рус. летописным преданиям, три брата-конунга, предводителя варяжских дружин, якобы призванные "из-за моря" новгородскими славянами с целью прекращения междоусобиц в Новгороде и основавшие Др.-рус. гос-во. Согласно этой версии, Рюрик сел в Новгороде, Синеус - в Белоозере, Трувор - в Изборске. Быстрая смерть среднего и младшего братьев сделала Рюрика полновластным правителем Новгородской земли. Нек-рые учёные отождествляют его с Рёриком Датским, совершавшим во главе варяжской дружины набеги на страны Зап. Европы (до 860). Существует мнение, что Синеуса и Трувора не существовало, а известие о них - результат неправильно прочитанного рус. летописцем иностр. текста, к-рый сообщает, что Рюрик пришёл в землю славян со своим домом ("сине-хус") и верной дружиной ("тру-воринг" ).

Рюрик правил сначала в Ладоге. Он не был призван "из-за моря", а захватил в 862 власть в Новгороде, воспользовавшись внутр. усобицами. Это вызвало восстание против варягов во главе с Вадимом Храбрым. Рюрик казнил Вадима и его "советников", другие новгородцы бежали в Киев. Легенда о "призвании" варягов, сложившаяся в Новгороде или Ладоге в 11 в., была использована при редактировании "Повести временных лет" в нач. 12 в. для объяснения происхождения и прославления правящей рус. княжеской династии, основателем к-рой стали считать Рюрика. Эта версия легла в основу антинауч. норманской теории. Легенда о создании Рюриком Др.-рус. гос-ва опровергается многочисл. данными источников, к-рые говорят о складывании государственности славян задолго до 9 в. и о становлении Др.-рус. гос-ва вследствие внутреннего обществ, развития.

Лит.: М а в р о д и н В. В., Древняя Русь, М., 1946; Греков Б. Д., Киевская Русь, М.. 1953; К у з ь м и н А. Г., К вопросу о происхождении варяжской легенды, в сб.: Новое о прошлом нашей Родины, М., 1967.

В. И. Буганов.

РЮСТЕНБУРГ (Rustenburg), город в ЮАР, в пров. Трансвааль. 33 тыс. жит. (1969). Ж.-д. веткой, соединён с магистралью Претория - Йоханнесбург. Центр крупных разработок платины, хромитов, также никеля. Таб. ф-ки, пищ. предприятия. В р-не Р. - возделывание цитрусовых, табака, хлопчатника.

РЮТБЁФ (Rutebeuf) (ок. 1230, Шампань,- 1285, Париж), французский поэт и драматург. Писал сатирич. стихи, отражавшие жизнь ср.-век. города, песни о крестовых походах, жития святых, фаблио, религ. драмы. Р. клеймил пороки дворянства, корыстолюбие гор. верхушки, лицемерие духовенства. Для сцены Р. написал "Миракль о Теофиле" (ок. 1261; рус. пер. под назв. "Действо о Теофиле" А. А. Блока, 1907) - человеке, продавшем душу дьяволу.

Соч.: Œuvres completes, t. 1-2, P., 1959 - 60; в рус. пер., в кн.: Хрестоматия по зарубежной литературе. Литература средних веков, М., 1953.

Лит.: История французской литературы, т. 1, М.- Л., 1946, с. 161-63; Lafeuille G., Rutebeuf. Р., [1966]; S е г р е г А., Rutebeuf, poete satyrique, P., 1969; R e g a 1 a d о N. F., Poetic Patterns in Rutebeuf, New Haven - L., 1970.

А. Л. Михайлов.

PЮTИ (Ryti) Ристо (3.8.1889, Хуйттинен, - 25.10.1956, Хельсинки), финский политич. и гос. деятель. По образованию юрист. В 1921-22, 1922-24 мин. финансов. Один из лидеров бурж. Прогрессивной партии Финляндии. В 1939-40 премьер-мин., в 1940-44 президент. Способствовал вовлечению Финляндии во 2-ю мировую войну 1939-45 на стороне фаш. Германии против СССР. В 1946 по процессу виновников войны осуждён спец. фин. судом на 10 лет тюремного заключения. В 1949 помилован "по состоянию здоровья".

РЮТИМЕЙЕР (Rutimeyer) Людвиг (26.2.1825, Биглен, близ г. Берн,- 26.11. 1895, Базель), швейцарский палеонтолог, проф. Базельского ун-та (с 1855), чл.-корр. Петерб. АН (1882). Осн. труды об ископаемых млекопитающих и о происхождении домашних животных. Р.- один из первых палеонтологов, принявших учение Ч. Дарвина. Признавая роль естественного отбора как фактора эволюции, Р. допускал, особенно применительно к эволюции человека, стремление к совершенствованию.

Лит.: Давиташвили Л. Ш., Развитие идей и методов в палеонтологии после Дарвина, М.- Л., 1940.

РЮФИСК (Rufisque), город на Атлантич. побережье Сенегала, к В. от Дакара, фактически его пригород. 60 тыс. жит. (1967). Ж.-д. ст. Маслоб., кожевенно-обув., цем., хим. пром-сть.

РЮЭЙ-МАЛЬМЕЗОН (Rueil-Malmaison), город во Франции, в деп. О-де-Сен, зап. пригород Парижа. 63 тыс. жит. (1968). Машиностроение, металлообработка, литейное произ-во.

РЮЭМЯ (Ryoma) Маури (20.11.1911 - 28.11.1958, Хельсинки), деятель финского рабочего движения. По профессии врач. В нач. 1930-х гг. вступил в С.-д. партию Финляндии. В 1936-39 редактор радикального общественно-политич. журн. "Сойхту" ("Soihtu"). Один из основателей (нач. 1940) и первый пред. Об-ва мира и дружбы с Сов. Союзом. После запрета об-ва (кон. 1940) арестован; освобождён в 1944 после выхода Финляндии из 2-й мировой войны 1939-45. С 1944 чл. компартии Финляндии (КПФ). В 1945-58 чл. ЦК и Политбюро ЦК КПФ. В 1936-37 и 1945-58 деп. парламента. В 1944-58 зам. пред, об-ва "Финляндия - Советский Союз".

РЮЭФ (Rueff) Жак Леон (р. 23.8.1896, Париж), французский экономист, чл. Франц. академии (1964) и Академии моральных и политич. наук (1944). Получил образование в Политехнич. школе. В 20-40-е гг. ген. инспектор в Мин-ве финансов, сотрудник аппарата Лиги Наций, финанс. советник франц. посольства в Лондоне, директор Казначейства в Мин-ве финансов, зам. управляющего Банком Франции, гос. советник. В послевоен. годы участвовал в работе ООН, верховных органов Европ. объединения угля и стали и европ. сообществ. Проф. ряда уч. заведений Франции. Сторонник экономич. либерализма, количеств, и металлистич. теорий денег. В своих экономич. работах отстаивает принципы свободной конкуренции.

Соч.: Des sciences physiques aux sciences morales, P., 1921; Theorie des phenomenes monetaires, P., 1927; L'ordre social, v. 1 - 2, P., 1945; The age of inflation, Chi., 1964; Le lancinant probleme de la balance des paiements, P., 1965; Le peche monetaire de 1'Occident, ГР.], 197,1.

В.И. Кузнецов.

РЯБАЯ МОГИЛА, курган на зап. берегу р. Прут, близ устья р. Калмацуй, в р-не к-рого 17(28) июня 1770 во время рус.-тур. войны 1768-74 рус. армия под команд. ген. П. А. Румянцева (38- 39 тыс. чел., 115 орудий) нанесла поражение тур.-тат. войскам крымского хана Каплан-Гирея (до 70 тыс. чел.). Наступление рус. войск с фронта и флангов создало угрозу окружения противника, к-рый обратился в бегство.

РЯБИНА (Sorbus), род листопадных деревьев или кустарников сем. розоцветных. Листья очередные от непарноперистых до лопастных и цельных. Цветки в щитковидных соцветиях. Плоды 2- 5-гнёздные, яблоковидные. Ок. 50 (по др. данным, ок. 100) видов, распространённых в умеренном поясе Сев. полушария. Наибольшее значение имеет Р. обыкновенная (S. aucuparia) - дерево или кустарник с гладкой серой корой. Листья у неё непарноперистые, цветки белые, плоды шаровидные, красные, служат кормом для птиц. В пределах СССР встречается в Европ. части и на Кавказе; разводится как декоративное и ради плодов, используемых в кондитерском и ликёрно-водочном произ-ве; применяется в медицине. На С.-В. Европ. части и в Сибири растёт Р. сибирская (S. sibirica), используемая так же, как и Р. обыкновенная. Р. садовую (S. domestica), растущую в Крыму, на юге Зап. Европы и в Средиземноморье, разводят в садах. Виды с простыми цельными или лопастными листьями нередко выделяют в самостоят. роды. Распространённую в культуре черноплодную рябину (родом из Сев. Америки), как правило, относят к особому роду а р о н и я.

М. Э. Кирпичников.

Рябина обыкновенная: а - ветка с цветками; б - ветка с плодами; в - цветок; г - плод в разрезе.

РЯБИНИНЫ, сказители рус. былин. Трофим Григорьевич Р. (1791, дер. Гарницы Петрозаводского у. Олонецкой губ., - 1885, дер. Серёдка того же уезда и губ., ныне Заонежского р-на Карел. АССР), принадлежал к эпикам строгой, выдержанной школы исполнения, следовал традициям героич. трактовки образов и сюжетов. От него записывали былины П. Н. Рыбников и А. Ф. Гильфердинг. Его сын - Иван Трофимович Р. [1844, дер. Серёдка,- 2(15).2.1909, дер. Гарницы], широкую известность приобрёл в 90-х гг., когда выступал с исполнением былин во мн. городах России и за границей. В текстах его былин заметны варьирования и отступления от традиции. Пётр Иванович Рябинин-Андреев [27.5(9.6).1905, дер. Гарницы, - 3.2.1953, Петрозаводск], сын сказителя Ивана Герасимовича Р., пасынка Ивана Трофимовича Р. Первые записи от него произведены в 1926; неоднократно выступал с исполнением былин в Петрозаводске, Москве, Ленинграде. Пел былины со значит. отступлением от традиции, иногда создавал внефольклорные стилизаторские произв., т. н. новины. Значение былинного творчества Р. для науки очень велико.

Тексты и лит.: Л я ц к и й Е., Сказитель Иван Трофимович Рябинпн н его былины. Этнографический очерк, М., 1895; Соколов Б. М., Сказители, М., [1925]; Былины П. И. Рябннина-Андреева, Петрозаводск, 1940; Былины Ивана Герасимовича Рябиннна-Андреева, Петрозаводск, 1948; Былины Севера. [Подгот. текста и коммент. А. М. Астаховой], т. 2, М.- Л., 1951; Астахова А. М., Сказители былин, их художественное мастерство, в кн.: Русское народное поэтическое творчество, т. 2, кн. 2, М.- Л., 1956; её же, Былины, М.- Л., 1966; Chetteoui W., Un rapsode russe Rjabinin le pere, P., 1942.

В. П. Аникин.

РЯБИННИК, птица рода дроздов.

РЯБИННИК (Sorbaria), род листопадных кустарников сем. розоцветных. выс. от 40 см до 3-6 м. Листья непарноперистосложные с остающимися прилистниками, светло- или тёмно-зелёные, осенью жёлтые или карминовые, б. ч. с линейными, заострёнными, двоякопильчатыми, сидячими листочками. Цветки мелкие, 5-членные, белые или розовые, в крупных конечных пирамидальных метёлках. Плод - многолистовка из 5 сросшихся у основания листовок, раскрывающихся по брюшному шву. 10 видов, в Азии; в СССР 4 вида - в Ср. Азии, Сибири, на Д. Востоке. Р. р я б н н о л и с т н ы й (S. sorbifolia) растёт в Сибири, на Д. Востоке, в Китае, Корее, Монголии и Японии по берегам горных и лесных рек, окраинам болот часто густыми зарослями. Р. разводят в садах и парках для устройства живых изгородей, закрепления берегов и откосов.

Лит.: Деревья и кустарники СССР, т. 3, М.- Л., 1954.

РЯБКИ (Pterocletes), подотряд птиц отряда голубеобразных. Дл. тела 23- 40 см. Крылья, приспособленные к быстрому полёту, длинные и острые. Цевка оперённая, задний палец короткий или отсутствует. Оперение плотное, кожа толстая - защита от перегрева, а у саджи - и от морозов. Окраска песочных или рыжеватых тонов. 1 сем. - Pteroclidae с 3 родами: собственно Р. (12 видов), саджа (1 вид) и тибетская саджа (1 вид). Распространены в сухих степях и пустынях юго-зап. Европы, Африки и Азии. Питаются Р. семенами трав и кустарников. Гнездятся на земле. В безводных местах летают на водопои, приносят воду птенцам в зобу или намокших перьях брюшка. В кладке обычно 3 яйца, насиживают оба пола. Птенцы вылупляются зрячими, покрытыми густым пухом, их кормят отрыжкой из зоба. В СССР 2 вида собственно Р., живущих в Юж. Казахстане и Ср. Азии: белобрюхий P. (Pterocles alchata), предпочитающий песчаные пустыни, и чернобрюхий P. (P. orientalis) - обитатель щебнистых предгорий. Оба вида перелётны. Р.- объект охоты.  

Рябки: 1 - чернобрюхий; 2 - белобрюхий.

Лит.: Птицы Советского Союза, под ред. Г. П. Дементьева и Н. А. Гладкова, т. 2, М., 1951.

А. П. Иванов.

РЯБУХА, инфекционная болезнь табака и махорки, вызываемая бактерией Pseudomonas tabacum и характеризующаяся появлением гл. обр. на листьях, иногда на чашелистиках и коробочках, многочисленных (диам. до 2 см) бледно-жёлтых (хлоротических) пятен. Поражённые участки в сухую погоду подсыхают, во влажную загнивают, что нередко приводит к продырявливанию листьев. Возбудитель проникает в растение через устьица и в местах повреждения тканей; сохраняется в пыли, приставшей к семенам, парниковому инвентарю, осевшей в сушильных сараях, а также в несгнивших остатках урожая. Р. снижает урожай на 40-50%; заготовит, цены на поражённые листья табака уменьшаются па 80%. Меры борьбы: влажное протравливание семян; дезинфекция парникового инвентаря; опрыскивание рассады в фазе 2 настоящих листочков бордоской жидкостью; выращивание устойчивых сортов; внесение калийных удобрений; зяблевая вспашка.

Лит.: Грушевой С. Е., Болезни табака и система мероприятий по борьбе с ними, М., 1950; Леонов И. П.. Петренко А. Г., Псарев Г. М.. Пособие для табаководов, М., 1968.

С. Е. Грушевой.

РЯБУШИНСКИЕ, русские промышленники и банкиры. Выходцы из крестьян Калужской губ., где в сер. 19 в. П. М. и В. М. Рябушинские имели неск. небольших текст, фабрик. В 1869 Р. купили хл.-бум. предприятия в Вышнем Волочке. Одновременно они занимались кредитными операциями. Сыновья П. М. Рябушинского приобрели предприятия в льняной, стекольной, бумажной и полиграфич. пром-сти, а в годы 1-й мировой войны 19^4-18 - в лесопромышленной и металлообрабатывающей; начали строить автомоб. з-д. В 1900 заняли руководящее положение в Харьковском поземельном банке. В 1902 был создан банкирский дом братьев Р., реорганизованный в 1912 в Моск. банк. Р. принадлежала ведущая роль в крупнейших предпринимательских орг-циях России (Об-во фабрикантов хл.-бум. пром-стн, Моск. биржевой к-т, Военно-пром. к-т, Всеросс. союз торговли и пром-сти и др.). Они входили в руководящую группу партии "прогрессистов" и издавали газ. "Утро России". Из 8 братьев Р. наибольшую известность приобрёл Павел Павлович Р. (1871-1924), ставший накануне Окт. революции 1917 признанным лидером росс, контрреволюц. буржуазии. Он был одним из организаторов и руководителей корниловщины, калединщины и воен. интервенции в Сов. Россию. Контрреволюц. деятельность продолжал в эмиграции.

Лит.: Л а в е р ы ч е в В. Я., Монополистический капитал в текстильной промышленности (1900-1917 гг.), М., 1963; его же, Всероссийский союз торговли и промышленности, в сб.: Исторические записки, т. 70, М., 1961.

РЯБУШКИН Андрей Петрович [17(29).10.1861, с. Станичная Слобода, ныне Воронежская обл.,- 27.4(10.5). 1904, усадьба Дидвино, близ ст. Любань, ныне Ленингр. обл.], русский живописец. Сын крестьянина-иконописца. Учился в Московском уч-ще живописи, ваяния и зодчества (1875-82) у В. Г. Перова и И. М. Прянишникова и в петерб. АХ (1882-90). Жил в Петербурге. Писал жанровые картины, поев, в основном праздничной, обрядовой стороне крест, быта ("Крестьянская свадьба в Тамбовской губернии", 1880, Третьяковская гал.; "Чаепитие", 1903, частное собр., Москва), сцены из истории России (гл. обр. 17 в.), трактуя их в камерно-бытовом плане ["Русские женщины XVII столетия в церкви", 1899, "Свадебный поезд в Москве (XVII столетие)", 1901, обе-Третьяковская гал.; "Едут", 1901, Рус. музей, Ленинград]. Оставаясь в целом верным традициям рус. живописи 2-й пол. 19 в. (убедительно передавая обстановку, костюмы, пейзаж), Р. вместе с тем нередко прибегал к обобщению форм, придавал своим композициям динамику и нек-рую плоскостность. Декоративной красочностью, навеянной нар. творчеством, введением орнаментальных и архит. мотивов он стремился подчеркнуть нац. характер изображаемого. Работал также как иллюстратор.

А. П. Р я б у ш к и н. "Едут". 1901. Русский музей. Ленинград.

Лит.: А. П. Рябушкин. [Альбом. Предисл. Е. Б. Муриной], М., 1961; Суздалев П. К., Рябушкин, М., 1961; М а с а л и н а Н. В., А. П. Рябушкин, М., 1966.

РЯБУШКИН Тимон Васильевич [р. 30.12.1914 (12.1.1915), Воронеж], советский экономист, чл.-корр. АН СССР (1966). Чл. КПСС с 1942. Окончил Ин-т нар.-хоз. учёта в Воронеже (1936). В 1948-53 зам. нач., нач. отдела статистич. методологии ЦСУ СССР; гл. редактор Госстатиздата. В 1954-61 зав. сектором экономич. статистики Ин-та экономики АН СССР. В 1961-70 зав. сектором статистики, зам. директора Ин-та экономики мировой социалистич. системы АН СССР. С 1970 зав. отделом демографии и статистики Центр, экономико-математич. ин-та. В 1948-61 представитель СССР в статистич. комиссии и комиссии по народонаселению ООН. С 1958 чл. Междунар. статистич. ин-та, в 1961-65 и с 1973 вице-президент этого ин-та. Осн. труды в области политич. экономии и статистики. В них рассматриваются проблемы баланса нар. х-ва, экономико-статистич. методы анализа пропорций в нар. х-ве и взаимосвязи его элементов, методы сопоставления статистич. данных в междунар. плане, исследуются закономерности развития мирового социалистич. х-ва. Под редакцией Р. издана книга "В. И. Ленин и современная статистика" (т. 1-3, 1970-73). Награждён орденом Трудового Красного Знамени.

Соч.: Очерки по экономической статистике, М., 1950; Статистические методы изучения народного хозяйства, М., 1957; Проблемы экономической статистики, М., 1959; Международная статистика, М., 1965; Темпы и пропорции развития народного хозяйства социалистических стран, М., 1966; Экономическая статистика, М.. 1966; В. И. Ленин и статистика, М., 1971.

РЯБЦЕВ Константин Иванович [14(26).5. 1879 - 29.7.1919, Харьков], русский контрреволюц. деятель, полковник (1917), правый эсер. Из крестьян Костромской губ. На воен. службе с 1900, окончил Тбилисское пех. уч-ще (1904) и Академию Генштаба (1912). Во время 1-й мировой войны 1914-1918 на штабных должностях. С июля 1917 нач. штаба Моск. воен. округа, выступал против корниловщины, в сент. 1917 был назначен командующим войсками Моск. воен. округа. Во время Окт. вооруж. восстания 1917 в Москве возглавил контрреволюц. силы, оказавшие упорное сопротивление восставшим рабочим и солдатам. 2(15) нояб. смещён с должности Военно-революц. к-том и уехал в Харьков. В июне 1919 при занятии Харькова белогвардейцами был арестован и расстрелян за выступление против ген. Корнилова и недостаточно активную борьбу с большевиками в окт. 1917.

РЯБЧИК (Tetrastes bonasia), птица семейства тетеревиных отр. куриных. Дл. тела 35-37 см, весит 350-500 г. Крылья короткие, тупые. Взлетает с шумом, летает лишь на небольшие расстояния. Ниж. часть цевки и пальцы голые. Оперение рыжевато-серое с пестринами, у Р., обитающих в Сибири,- более чистого серого тона. Распространён в Европе и Азии; в СССР - в лесной зоне от Карпат до Сахалина; в лесах Кавказа и Камчатки отсутствует. Р. живут оседло, совершая лишь короткие кормовые кочёвки. Селятся отд. парами в сырых захламлённых хвойных (елово-пихтовых) или смешанных лесах. Гнёзда на земле; в кладке 6- 10 яиц, насиживает самка ок. 3 недель. Птенцы достигают размеров взрослых Р. через 6 недель после вылупления. Первое время они питаются насекомыми, потом растит, кормом. Зимой Р. кормятся на деревьях серёжками берёзы, ольхи и др., ночуют в снегу. Осн. корма летом: зелёные части растений, ягоды, семена и насекомые. Р. - ценная промысловая птица.

Рябчик: 1 - самец; 2 - самка.

РЯБЧИК (Fritillaria), род луковичных растений сем. лилейных. Луковица округлая, чаще из 2-4 мясистых чешуи; стебель облиственный, листорасположение очередное или мутовчатое. Цветки обычно крупные, одиночные или по нескольку на верхушке стебля; околоцветник из 6 листочков с нектарниками у основания, колокольчатый или кубаревидный, беловатый, жёлтый, оранжевый, коричневатый, нередко с шахматным рисунком. Плод - 6-гранная, иногда крылатая коробочка. Ок. 100 видов, в умеренных областях обоих полушарий. В СССР около 30 видов, чаще на Кавказе и в Ср. Азии, а также в Европ. части (лесостепь и степь), Зап. Сибири и на Д. Востоке, на лугах, в степях, среди кустарников, по склонам гор в субальпийском и альпийском поясах. Все виды Р. декоративны, цветут весной; наиболее известны Р. шахматный (F. meleagris) и Р. императорский (F. imperialis).

РЯВАЛА, прибрежная земля (мааконд) в Сев. Эстонии (ныне Харьюский р-н Эст. ССР), состоявшая из трёх терр. объединений (кихелькондов). Центром Р. в 11 -13 вв. была крепость, известная под назв. Колывань или Линданисе. Под дат. властью Р. была объединена с землёй Харью под назв. Харьюмаа (Гарриен). От названия земли Р. происходит старое название Таллина - Ревель (Reval).

Лит.: История Эстонской ССР, т. 1, Тал., 1961; Johansen P., Die Estlandlisteden Liber census Daniae, Kph.- Reval, 1933.

РЯД, бесконечная сумма, напр, вида

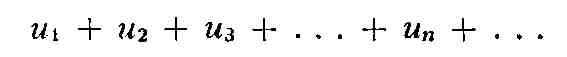
или, короче,

Одним из простейших примеров Р., встречающихся уже в элементарной математике, является сумма бесконечно убывающей геометрич. прогрессии

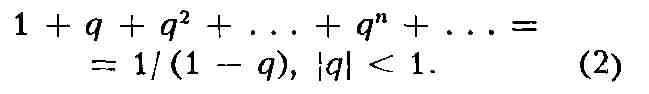
Р. широко используются в математике и её приложениях как в теоретич. исследованиях, так и при приближённых численных решениях задач. Многие числа могут быть записаны в виде специальных Р., с помощью к-рых удобно вычислять их приближённые значения с нужной точностью. Напр., для числа я имеется Р.

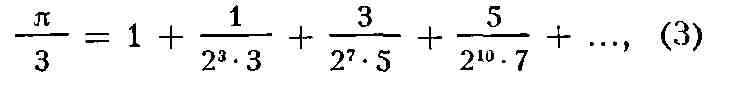
для основания е натуральных логарифмов - Р.

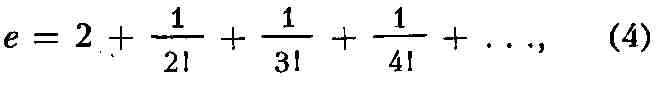
а для натурального логарифма 1n2 - ряд

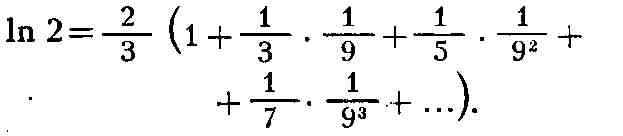
Метод разложения в Р. является эффективным методом изучения функций. Он применяется для вычисления приближённых значений функций, для вычисления и оценок интегралов, для решения всевозможных уравнений (алгебраических, дифференциальных, интегральных) и т. п.

При численных расчётах, когда Р. заменяется конечной суммой его первых слагаемых, полезно иметь оценку получаемой при этом погрешности (оценку "скорости сходимости" Р.)- При этом целесообразно использовать Р., у к-рых эти погрешности достаточно быстро стремятся к нулю с возрастанием номера п. Напр., в случае Р. (4) оценка указанной погрешности имеет вид 0 < е - s_n< <\1п|п.

Одни и те же величины могут выражаться через суммы различных рядов. Так, для числа я, кроме Р. (3), имеются и другие Р., напр.

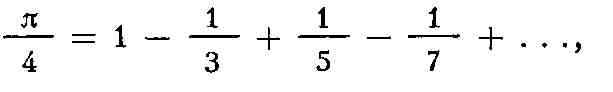
однако он сходится значительно "медленнее" Р. (3), и потому его невыгодно использовать для приближённого вычисления числа я. Существуют методы преобразования Р., иногда улучшающие скорость сходимости Р.

На бесконечные суммы не переносятся все свойства конечных сумм. Напр., если взять Р.

и сгруппировать подряд его члены по два, то получим (1 - 1)+ (1 - 1) + ... = 0; при другом же способе группировки 1 - (1 - 1) - (1 - 1) - ... = 1. Поэтому следует дать чёткое определение того, что называется бесконечной суммой, и, определив это понятие, проверить, справедливы ли для таких сумм закономерности, установленные для конечных сумм. Доказывается, что для бесконечного числа слагаемых при определённых условиях сохраняются законы коммутативности и ассоциативности сложения, дистрибутивности умножения относительно сложения, правила почленного дифференцирования и интегрирования и т. п.

Числовые ряды. Формально Р. (1) можно определить как пару числовых (действительных или комплексных) последовательностей {и_п} и {S_п} таких, что Sn = U₁ + ... + и_п, п = 1,2,... Первая последовательность иаз. последовательностью членов Р., а вторая - последовательностью его частичных сумм [точнее s_n наз. частичной суммой n-го порядка Р. (1)]. Р. (1) называется сходящимся, если сходится последовательность его частичных сумм {s_n}. В этом случае предел

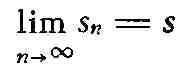
называется суммой Р. и пишется

Т. о., обозначение (1) применяется как для самого Р., так и для его суммы (если он сходится). Если последовательность частичных сумм не имеет предела, то Р. называется расходящимся. Примером сходящегося Р. является Р. (2), расходящегося - Р. (5). Каждый Р. однозначно определяет последовательность его частичных сумм, и обратно: для любой последовательности {s_n} имеется и притом единственный Р., для к-рого она является последовательностью его частичных сумм, причём члены и_п этого Р. определяются по формулам u₁ = S₁, ..., u_п+1 = = S_п+1 - S_п, ..., п = 1,2,... В силу этого изучение Р. эквивалентно изучению последовательностей.

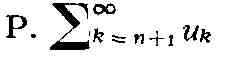
называется остатком

порядка п Р. (1). Если Р. сходится, то каждый его остаток сходится, а если какой-либо остаток Р. сходится, то и сам Р. также сходится. Если остаток порядка п Р. (1) сходится и его сумма равна r_п то s = s_n + r_п. Если Р. (1) и Р.

сходятся, то сходится и Р.

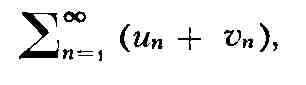
называемый суммой рядов (1) и (6), причём его сумма равна сумме данных Р. Если Р. (1) сходится и X - комплексное число, то Р.

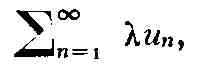
называемый произведением Р. на число X, также сходится и

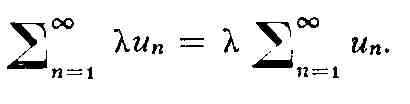
Условие сходимости Р., не использующее понятия его суммы (в случаях, когда, напр., сумма Р. неизвестна), даёт критерий Коши: для того чтобы Р. (1) сходился, необходимо и достаточно, чтобы для любого e > 0 существовал такой номер п_e, что при любом n >= n_е и любом целом р >=0 выполнялось неравенство

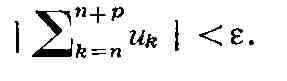
Отсюда следует, что если Р. (1) сходится, то

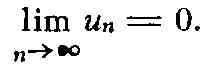
Обратное неверно: я-й член т. н. гармонического ряда

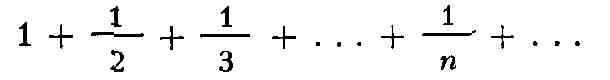
стремится к нулю, однако этот Р. расходится.

Большую роль в теории Р. играют Р. с неотрицательными членами. Для того чтобы такой Р. сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху. Если же он расходится, то

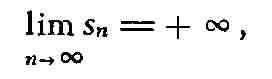
поэтому в этом случае пишут:

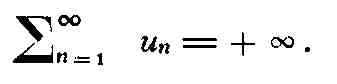
Для Р. с неотрицательными членами имеется ряд признаков сходимости.

Интегральный признак сходимости: если функция f (x) определена при всех х >= 1, неотрицательна и убывает, то Р.

сходится тогда и только тогда, когда сходится интеграл

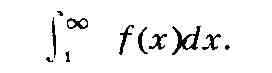
С помощью этого признака легко устанавливается, что Р.

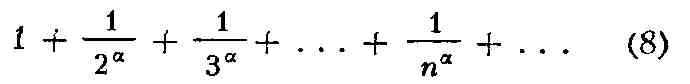
сходится при а > 1 и расходится при а =< 1.

Признак сравнения: если для двух Р. (1) и (6) с неотрицательными членами существует такая постоянная с > 0, что 0 =< u_п =< cv_n, то из сходимости Р. (6) следует сходимость Р. (1), а из расходимости Р. (1) - расходимость Р. (6). Обычно для сравнения берётся Р. (8), а в заданном Р. выделяется главная часть вида А/п^a. Таким методом сразу получается, что Р. с к-м членом

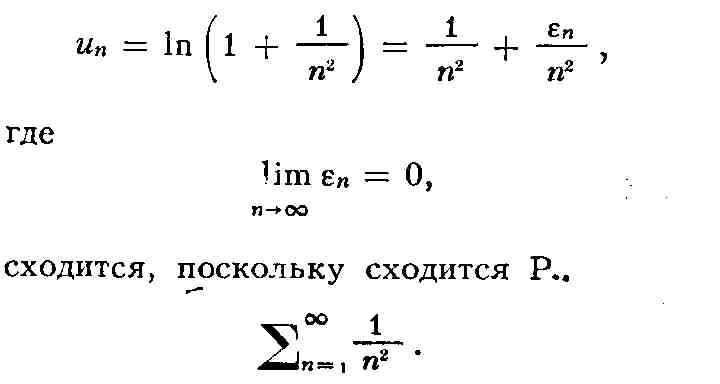
Как следствие признака сравнения получается следующее правило: если

то при l < 1 Р. (1) сходится, а при l > 1 Р. расходится. При l=1 как в случае признака Д'Аламбера, так и в случае признака Коши существуют и сходящиеся и расходящиеся Р.

Важный класс Р. составляют абсолютно сходящиеся ряды: Р. (1) называется абсолютно сходящимся, если сходится Р.

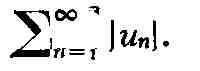
Если Р. абсолютно сходится, то он и просто сходится. Р.

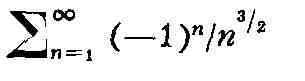
абсолютно сходится, а Р.

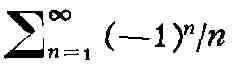
сходится, но не абсолютно. Сумма абсолютно сходящихся Р. и произведение абсолютно сходящегося Р. на число являются также абсолютно сходящимися Р. На абсолютно сходящиеся Р. наиболее полно переносятся свойства конечных сумм. Пусть

- Р., составленный из тех же членов, что и Р. (1), но взятых, вообще говоря, в другом порядке. Если Р. (1) сходится абсолютно, то Р. (9) также сходится и имеет ту же сумму, что и Р. (1). Если Р. (1) и Р. (6) абсолютно сходятся, то Р., полученный из всевозможных попарных произведений u_mv_n членов этих Р., расположенных в произвольном порядке, также абсолютно сходится, причём если сумма этого Р. равна s, а суммы Р. (1) и (6) равны соответственно s₁и s₂, то s = s₁s₂, т. е. абсолютно сходящиеся Р. можно почленно перемножать, не заботясь о порядке членов. Признаки сходимости для Р. с неотрицательными членами применимы для установления абсолютной сходимости рядов.

Для Р., не абсолютно сходящихся (такие Р. называют также условно сходящимися), утверждение о независимости их суммы от порядка слагаемых неверно. Справедлива теорема Римана: посредством надлежащего изменения порядка членов данного не абсолютно сходящегося Р. можно получить Р., имеющий наперёд заданную сумму, или расходящийся Р. Примером условно сходящегося Р. может служить Р.

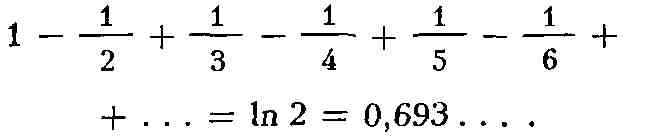
Если в этом Р. переставить члены так, чтобы за двумя положительными следовал один отрицательный:

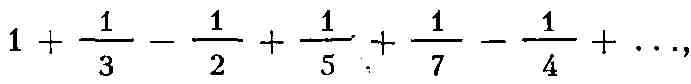
то его сумма увеличится в 1,5 раза. Существуют признаки сходимости, применимые к не абсолютно сходящимся Р. Напр., признак Лейбница: если

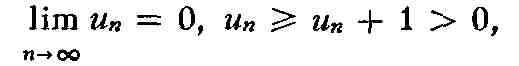
то знакочередующийся Р.

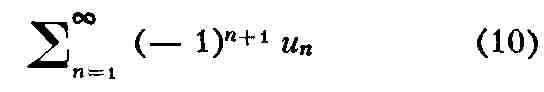
сходится. Более общие признаки можно получить, напр., с помощью преобразования Абеля для Р., представимых в виде

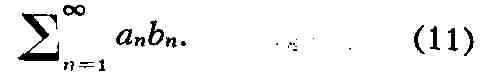
Признак Абеля: если последовательность {а_п} монотонна и ограничена, а Р.

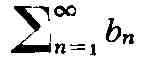
сходится, то Р. (11) также сходится. Признак Дирихле: если последовательность {а_n} монотонно стремится к нулю, а последовательность частичных сумм Р.

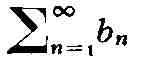
ограничена, то Р. (11) сходится. Напр., по признаку Дирихле Р.

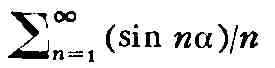
сходится при всех действительных а. Иногда рассматриваются Р. вида

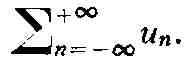
Такой Р. называется с х од я щ и м с я, если сходятся Р.

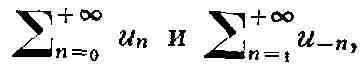
сумма этих Р. называется суммой исходного Р.

Р. более сложной структуры являются кратные ряды, т. е. Р. вида

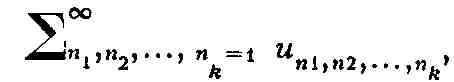
где u_n1,n₂,...,n_k - заданные числа (вообще говоря, комплексные), занумерованные k индексами п₁, n₂, ...,n_k, каждый из к-рых независимо от других пробегает натуральный ряд чисел. Простейшие из Р. этого типа - двойные ряды.

Для нек-рых числовых Р. удаётся получить простые формулы для величины или оценки их остатка, что весьма важно, напр., при оценке точности вычислений, проводимых с помощью Р. Напр., для суммы геометрич. прогрессии (2)

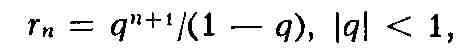
для Р. (7) при сделанных предположениях

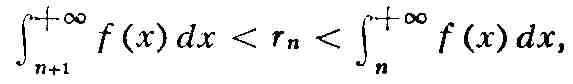
а для Р. (10)

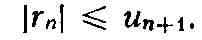
С помощью нек-рых специальных преобразований иногда удаётся "улучшить" сходимость сходящегося Р. В математике используются не только сходящиеся Р., но и расходящиеся. Для последних вводятся более общие понятия суммы Р. (см. Суммирование рядов и интегралов). Так, напр., расходящийся Р. (5) можно просуммировать определённым способом к 'Ь-

Функциональные ряды. Понятие Р. естественным образом обобщается на случай, когда членами Р. являются функции и_n= u_п(х) (действительные, комплексные или, более общо, функции, значения к-рых принадлежат какому-то метрич. пространству), определённые на нек-ром множестве Е. В этом случае ряд

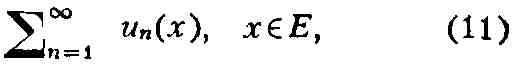
наз. функциональным.

Если Р. (11) сходится в каждой точке множества Е, то он называется сходящимся на множестве Е.

Пример: Р.

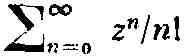
сходится на всей комплексной плоскости. Сумма сходящегося Р. непрерывных, напр., на нек-ром отрезке, функций не обязательно является непрерывной функцией. Условия, при к-рых на функциональные Р. переносятся свойства непрерывности, дифференцируемое™ и интегрируемости конечных сумм функций, формулируются в терминах равномерной сходимости Р. Сходящийся Р. (11) называется равномерно сходящимся на множестве Е, если во всех точках Е отклонение частичных сумм Р.

при достаточно больших номерах п от суммы Р.

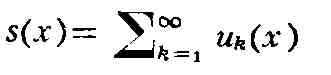
не превышает одной и той же сколь угодно малой величины, точнее, каково бы ни было наперёд заданное число е > 0, существует такой номер п_e, что

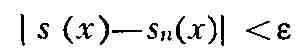
для всех номеров п >= n_Еи всех точек х принадлежит Е. Это условие равносильно тому, что

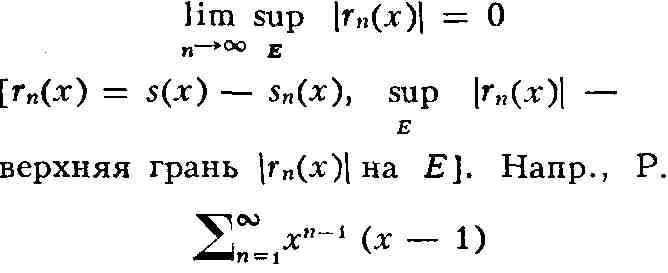
равномерно сходится на отрезке [0, q] при 0 < q < 1 и не сходится равномерно на отрезке [О, 1].

Критерий Коши: для того чтобы Р. (11) равномерно сходился на множестве Е, необходимо и достаточно, чтобы для любого е>0 существовал такой номер' п_е, что для всех номеров п>=n_е, р>=0 и всех точек х принадлежит Е выполнялось неравенство

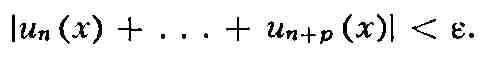
Признак Вейерштрасса: если существует такой сходящийся числовой Р.

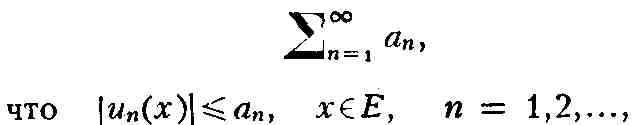
то Р. (11) равномерно сходится на Е.

Сумма равномерно сходящегося Р. непрерывных на нек-ром отрезке (или, более общо, на нек-ром топологическом пространстве) функций является непрерывной на этом отрезке (пространстве) функцией. Сумма равномерно сходящегося Р. интегрируемых на нек-ром множестве функций является интегрируемой на этом множестве функцией, и Р. можно почленно интегрировать. Если последовательность частичных сумм Р. интегрируемых функций сходится в среднем к нек-рой интегрируемой функции, то интеграл от этой функции равен сумме Р. из интегралов от членов Р. Интегрируемость в этих теоремах понимается в смысле Римана или Лебега. Для интегрируемых по Лебегу функций достаточным условием возможности почленного интегрирования Р. с почти всюду сходящейся последовательностью частичных сумм является равномерная оценка их абсолютных величин нек-рой интегрируемой по Лебегу функцией. Если члены сходящегося на нек-ром отрезке Р. (11) дифференцируемы на нём и Р. из их производных сходится равномерно, то сумма Р. также дифференцируема на этом отрезке и Р. можно почленно дифференцировать .

Понятие функционального Р. обобщается и на случай кратных Р. В различных разделах математики и её приложениях широко используется разложение функции в функциональные Р., прежде всего в степенные ряды, тригонометрические ряды и, более общо, в Р. по специальным функциям некоторых операторов.

К понятию бесконечных сумм подошли ещё учёные Др. Греции, у них уже встречалась сумма членов бесконечной геометрич. прогрессии с положительным знаменателем меньшим единицы. Как самостоятельное понятие Р. вошёл в математику в 17 в. И. Ньютон и Г. Лейбниц систематически использовали Р. для решения уравнений как алгебраических, так и дифференциальных. Формальная теория Р. успешно развивалась в 18 - 19 вв. в работах Я. и И. Бернулли, Б. Тейлора, К. Маклорена, Л. Эйлера, Ж. Д'Аламбера, Ж. Лагранжа и др. В этот период использовались как сходящиеся, так и расходящиеся Р., хотя не было полной ясности в вопросе о законности действий над ними. Точная теория Р. была создана в 19 в. на основе понятия предела в трудах К. Гаусса, Б. Болъцано, О. Коши, П. Дирихле, Н. Абеля, К. Вейерштрасса, Г. Римана и др.

Лит.: М а р к у ш е в и ч А. И. , Ряды. Элементарный очерк, 3 изд., М., 1957; Ильин В. А., П о з н я к Э. Г., Основы математического анализа, 3 изд., ч. 1 - 2, М., 1971-73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1 - 2. М., 1973; Никольский С. М., Курс математического анализа, т. 1 - 2, М., 1973; Бахвалов Н. С. , Численные методы, М., 1973.

Л.Д. Кудрявцев.

РЯД, таксономическая категория, применяемая в ботанике; то же, что серия.

РЯД АКТИВНОСТЕЙ, то же, что ряд напряжений.

РЯД НАПРЯЖЕНИЙ (реже - ряд активностей), последовательность расположения металлов и их ионов в порядке возрастания стандартных электродных потенциалов в растворах электролитов. Электродом сравнения обычно служит стандартный водородный электрод. В странах электродному потенциалу принято давать знак, одинаковый со знаком заряда электрода из данного металла по отношению к стандартному водородному электроду (в США принято давать обратный знак). Наибольшие отрицательные потенциалы характерны для щелочных металлов (ок.-3 в), за. ними следуют щёлочноземельные металлы и т. д.; наиболее положительные потенциалы имеют благородные металлы (ок. + 1,5 в; численные значения см. в ст. Металлы, табл. 2 и 3). В Р. н. часто включают неметаллы, ионы и нек-рые хим. соединения. Наиболее распространённые металлы расположены в Р. н. в след, последовательности: Li, К, Са, Na, Mg, Al, Mn, Zn, Fe, Co, Ni, Sn, Pb, H₂, Cu, Hg, Ag, Au (см. там же). Место каждого элемента в Р. н. несколько условно, т. к. величина электродного потенциала зависит от темп-ры и состава раствора, в к-рый погружены электроды, в частности от активности (или концентрации) ионов данного вещества в электролите. Большое значение имеет состояние поверхности электрода (гладкая, шероховатая), в особенности наличие на ней окисной защитной плёнки (см. Пассивирование). Р. н., обычно приводимый в уч. лит-ре, относится к водным растворам при темп-ре 25 ^оС, давлении газов 1 атм и при активности ионов, участвующих в электрохим. реакции, равной 1. При изменении концентраций и растворителя последовательность веществ в Р. н. может изменяться, особенно для веществ, близко расположенных в этом ряду.

Важнейшие следствия, вытекающие из Р. н. и широко используемые в хим. практике; 1) каждый металл способен вытеснять (замещать) из растворов солей все другие металлы, стоящие в Р. н. правее данного металла; 2) все металлы, расположенные в Р. н. левее водорода, способны вытеснять его из кислот; 3) чем дальше расположены друг от друга два металла в Р. н., тем большее напряжение может давать построенный из них гальванический элемент. Р. н. составляется на основе термодинамических характеристик электрохимических процессов, поэтому он позволяет судить лишь о принципиальной возможности этих процессов; реальное же их осуществление во многом определяется кинетическими факторами.

Лит.: Курс физической химии (под общ. ред. Я. И. Герасимова), т. 2, 2 изд., М., 1973, гл. 20; П о л и н г Л., Общая химия, пер. с англ., М., 1974, гл. XV.

М. Е. Ерлыкина.

РЯДОВИЧИ, 1) в Др. Руси лица, заключившие с феодалом договор (ряд), ставивший их в определённую экономич. и личную зависимость. Сведения о социальном положении Р. скудны. Р., в частности, могли быть низшими агентами феод, администрации. 2) В 14-17 вв. Р. назывались члены торг. корпораций, владельцы лавок в торг, рядах, а также жители рядков - торгово-ремесленных поселений.

Лит.: Греков Б. Д., Крестьяне на Руси с древнейших времен до XVII в., 2 изд., кн. 1, М., 1952, с. 162-65; Черепнин Л. В., Из истории формирования класса феодально-зависимого крестьянства на Руси, в сб.: Исторические записки, т. 56, [M.J, 1956, с. 260: Зимин А. А., Холопы на Руси, М., 1973.

РЯДОВКА (Tricholoma), род шляпочных пластинчатых грибов. Шляпка с центр. сплошной ножкой, как правило без покрывала. Пластинки слегка приросшие к ножке. Споры бесцветные, в массе белые. Св. 100 видов. Большинство - микоризообразователи. Плодоносят пре-им. осенью, иногда в больших кол-вах, напр. Р. серая (Т. portentosum), Р. бело-бурая (Т. albobrunneum). Съедобны; нек-рые ядовиты, напр. Т. pardinum, T. sulphureum.

РЯДОВОЙ ПОСЕВ, обычный сплошной посев, размещение семян на поле рядками с междурядьями от 10 до 25 см. Наиболее распространённый способ посева зерновых культур. При Р. п. семена высевают в бороздки, образуемые сошниками сеялки, и равномерно заделывают рыхлой почвой на заданную глубину. Это обеспечивает дружные всходы и развитие растений, одновременное созревание урожая. Недостаток Р. п.- чрезмерная сближенность растений в рядке и относительно большое расстояние между рядками.

РЯДОК, в 15-17 вв. торгово-ремесленное поселение, центр погоста или волости на терр. Новгородской земли. Расположенные на водных путях Р. представляли собой тип поселения, переходный от сельского к городскому. В Р. жили торговцы, ремесленники, занимавшиеся также сельским хозяйством. Нек-рые Р. (Тихвин, Повенец, Валдай, Вышний Волочёк и др.) в 17 в. превратились сначала в посады, затем в города (см. также Рядовичи).

Лит.: С е р б и н а К. Н., Очерки из социально-экономической истории русского города. Тихвинский посад в XVI-XVIII вв., М.-Л., 1951; Данилова Л. В., Очерки по истории землевладения и хозяйства в Новгородской земле в XIV - XV вв., М., 1955; Тихомиров М. Н., Россия в XVI ст., М., 1962, с. 291-93.

РЯДЫ ДИНАМИКИ, статистические ряды, характеризующие изменение (развитие) социально-экономич. явлений во времени. Напр., данные, о произ-ве электроэнергии в СССР за период 1928-73 представляют Р. д.

Производство электроэнергии в СССР, млрд. квт•ч

1928	1932	1937	1940	1950	1960	1970	1973
5,0	13,5	36,2	48,3	91,2	292	741	915

Последовательно расположенные во времени статистич. данные наз. уровнями Р. д. Они должны быть сопоставимы между собой, особенно в территориальном разрезе, по кругу охватываемых объектов, методике расчёта, критической дате, структуре. Уровни Р. д. могут характеризовать величину явлений за нек-рые отрезки времени (интегральные Р. д.) или на определённую дату (моментные Р.д.). Анализ Р. д. состоит в определении скорости и интенсивности развития рассматриваемого явления, нахождении осн. тенденции его развития (тренда), измерении колеблемости уровней, установлении связи с развитием др. явлений, проведении сравнительного анализа развития разных стран или районов. Для анализа Р. д. определяются статистич. показатели: абс. приросты, темпы роста и прироста, ср. уровни ряда, ср. абс. приросты, ср. темпы роста и прироста. Абсолютным приростом наз. разность между последующим и предыдущим уровнями, а темпом роста - их отношение. Темп прироста составит разность между темпом роста и 1 (в коэффициенте) или 100% . Средний уровень ряда для интервальных рядов определяется как средняя арифметическая, а для моментных рядов - по формуле:

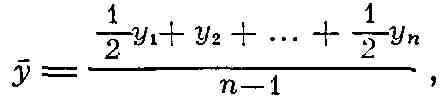
где у - средний уровень, у₁ - начальный, а У_n - конечный, п - число уровней. Средний абсолютный прирост определяется как частное от деления абсолютного прироста за весь период на число единиц времени в периоде. Средний темп роста вычисляется как средняя геометрич. темпов роста за отд. отрезки времени или как корень, степень к-рого определяется числом периодов, а под корнем берётся темп роста за весь период.

Определение тренда ведётся выравниванием статистическим. Колеблемость уровней Р. д. измеряется средней из квадратов отклонений фактич. уровней от тренда. Для установления связи развития данного явления с другими пользуются методом корреляции Р. д., отличающимся от обычного возможностью автокорреляции, авторегрессии, переменной корреляции и временного лага. Для сравнит. анализа разных стран (районов) часто используется приведение к одному основанию, состоящее в определении темпов роста для двух или более стран за одинаковые отрезки времени. Сравнительный анализ развития лучше вести с расчётом показателей на душу населения. Всесторонний анализ Р. д. позволяет выявить закономерности развития отражаемых в них явлений.

Г. С. Кильдшиев.