РОЛЛЯ ТЕОРЕМА, теорема математич. анализа, впервые высказанная М. Роллем (1690): если функция f (x) непрерывна на отрезке а=<х=<b, имеет внутри его определённую производную, а на концах принимает равные значения f(a)=f(b), то её производная f'(x) по меньшей мере один раз обратится в нуль в интервале (а, б), т. е. существует такое с (где а<с<b), что f (с) = 0. Как следствие получается, что между двумя последоват. 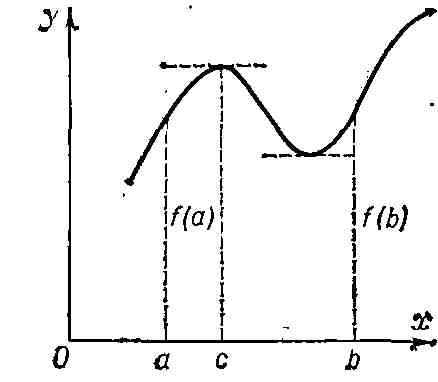корнями функции имеется хотя бы один корень её производной. Геометрически Р. т. очевидна (см. рис.). См. также Дифференциальное исчисление.