РИМАНА СФЕРА, одно из возможных геометрич. изображений совокупности комплексных чисел, введённое Б. Риманом. Комплексное число

z = х + iy = r (cos Ф + i sin Ф) = re^iФ

можно изображать точками на плоскости (комплексной числовой плоскости) с декартовыми координатами х, у или полярными r, Ф. Для построения Р. с. проводится сфера, касающаяся комплексной числовой плоскости в начале координат; точки комплексной числовой плоскости отображаются на поверхность сферы с помощью стереографической проекции. В этом случае каждое комплексное число изображается соответствующей точкой сферы; последняя и наз. сферой Римана. Число О изобразится при этом юж. полюсом Р. с.; числа с одинаковым аргументом ф = const (лучи комплексной числовой плоскости) изобразятся меридианами, а числа с одинаковым модулем r = const (окружности комплексной числовой плоскости) - параллелями Р. с. Сев. полюсу Р. с. не соответствует никакая точка комплексной числовой плоскости. В целях сохранения взаимной однозначности соответствия между точками комплексной числовой плоскости и Р. с. на плоскости вводят "бесконечно удалённую точку", к-рую считают соответствующей сев. полюсу и обозначают z=бесконечности. Т. о., на комплексной числовой плоскости имеется одна бесконечно удалённая точка, в отличие от проективной плоскости.

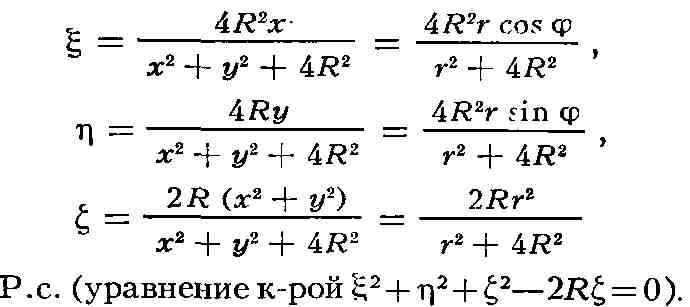
РИМАНОВА ГЕОМЕТРИЯ, многомерное обобщение геометрии на поверхности, представляющее собой теорию римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка сравнительно с размерами области). Р. г. получила своё название по имени Б. Римана, к-рый заложил её основы в 1854.

Понятие о римановой геометрии. Гладкая поверхность в евклидовом пространстве, рассматриваемая с точки зрения измерений, производимых на ней, оказывается двумерным пространством, геометрия к-рого (т. н. внутренняя геометрия), будучи приближённо евклидовой в малом (в окрестности любой точки она совпадает с точностью до малых высшего порядка с геометрией касательной плоскости), точно не является евклидовой; к тому же, как правило, поверхность неоднородна по своим геометрич. свойствам. Поэтому внутр. геометрия поверхности и есть не что иное, как Р. г. двух измерений, а сама поверхность есть двумерное риманово пространство.

Так, при измерениях на участках земной поверхности, малых в сравнении с размерами земного шара, можно с успехом применять обычную планиметрию, однако результаты измерений на больших участках обнаруживают существенное отклонение от законов планиметрии. Перенесение этих понятий на многомерные пространства приводит к общей Р. т. В основе Р. г. лежат три идеи. Первая идея - признание того, что вообще возможна геометрия, отличная от евклидовой,- была впервые развита Н. И. Лобачевским; вторая - это идущее от К. Ф. Гаусса понятие внутр. геометрии поверхностей и её аналитич. аппарат в виде квадратичной формы, определяющей линейный элемент поверхности; третья идея - понятие об и-мерном пространстве, выдвинутое и разработанное в 1-й пол. 19 в. рядом геометров. Риман, соединив и обобщив эти идеи (в лекции "О гипотезах, лежащих в основании геометрии", прочитанной в 1854 и опубликованной в 1867), ввёл общее понятие о пространстве как непрерывной совокупности любого рода однотипных объектов, к-рые служат точками этого пространства (см. Геометрия, раздел Обобщение предмета геометрии, Пространство в математике), и перенёс на эти пространства представления об измерении длин малыми шагами.

После опубликования работ Римана его идеи привлекли внимание ряда математиков, к-рые развивали дальше аналитич. аппарат Р. г. и устанавливали в ней новые теоремы геометрич. содержания. Важным шагом было создание итал. геометрами Г. Риччи-Курбастро и Т. Леви-Чивита на рубеже 20 в. т. н. тензорного исчисления, к-рое оказалось наиболее подходящим аналитич. аппаратом для разработки Р. г. Решающее значение имело применение Р. г. в создании А. Эйнштейном общей теории относительности, к-рое было триумфом не только абстрактной геометрии, но и идей о связи геометрии и физики, выдвинутых Лобачевским и Риманом. Это привело к бурному развитию Р. г. и её разнообразных обобщений. В наст, время Р. г. вместе с её обобщениями представляет собой обширную область геометрии, к-рая продолжает успешно развиваться, причём особое внимание уделяется вопросам глобального характера.

Определение риманова пространства. К строгому определению риманова пространства можно подойти следующим образом. Положение точки n-мерного многообразия определяется п координатами х¹, x², . . ., хⁿ. В евклидовом n-мерном пространстве расстояние между любыми двумя точками X, Y в надлежаще выбранных координатах выражается формулой

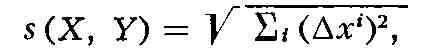
где дельта хⁱ - разности координат точек X, Y. Соответственно в римановом пространстве в окрестности каждой точки А могут быть введены координаты х¹,...,хⁿтак, что расстояние между точками X, Y, близкими к А, выражаются формулой

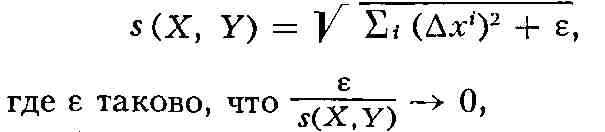
когда X, Y приближаются к А. Отсюда следует, что в произвольных координатах расстояние между близкими точками (хⁱ) и (xⁱ+dxⁱ), или, что то же самое, дифференциал длины дуги кривой, задаётся выражением

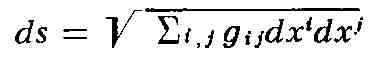
(здесь коэффициенты g_ij = д_ij(х¹, ..., хⁿ) суть функции координат), к-рое наз. линейным элементом риманова пространства. Т. о., риманово пространство R можно аналитически определить как re-мерное многообразие, в к-ром в каждой точке задана дифференциальная квадратичная форма

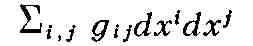
(она наз. также метрической формой, или просто метрикой, R и является по своему определению положительно определённой). Возможность преобразования координат обусловливает то, что одно и то же риманово пространство в разных координатах имеет разные выражения метрич. формы, однако её величина (вследствие своего геометрич. смысла как квадрата элемента длины дуги) при преобразовании координат должна оставаться неизменной :

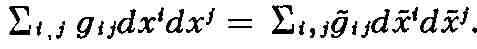
Это приводит к определённому закону преобразования коэффициентов g_ij как компонент дважды ковариантного тензора (см. Тензорное исчисление); он наз. метрическим тензором риманова пространства.

Каждой точке А риманова пространства R сопоставляется т. н. касательное евклидово пространство Е_A, в к-рое отображается нек-рая окрестность U точки А так, что относительное искажение расстояний стремится к нулю при приближении к точке А. Аналитически это сводится к введению вблизи нек-рой точки А₀пространства Е_A таких координат, что в них квадрат линейного элемента ds²₀ евклидова пространства Е_Aвыражается в точке АО такой же формой сумма_i,jg_ij(А)dxⁱdx^j, какой выражается квадрат линейного элемента риманова пространства ds² в точке А. Т. о., в пренебрежении малыми выше первого порядка окрестность точки в римановом пространстве можно заменять окрестностью точки касательного пространства.

Простейшие понятия римановой геометрии. 1)Длина дуги s кривой xⁱ - xⁱ(t) (iⁱ=1, . . ., п, t₁=<t=<t₂) в римановом пространстве R определяется как интеграл

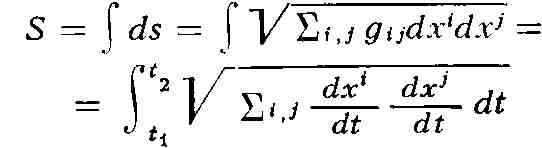
вдоль этой кривой (что соответствует как бы измерению длин "малым масштабом", как отметил ещё Риман). Если любые две точки пространства R соединимы кривой, то R становится метрическим пространством: расстояние р (Х, У) между двумя точками определяется как точная нижняя грань длин кривых, соединяющих эти точки, и наз. внутренней метрикой риманова пространства R.

2) Угол между двумя исходящими из одной точки А кривыми определяется как угол между касательными векторами к кривым в точке А.

3) О б ъ ё м V n-мерной области G риманова пространства определяется по формуле:

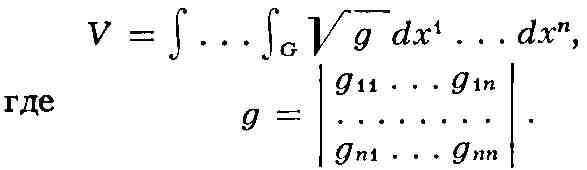
Геодезические. Линии, к-рые в достаточно малых областях являются кратчайшими из всех кривых с теми же концами, наз. геодезическими, они играют роль прямых в римановом пространстве R. По определению, они являются экстремалями функционала

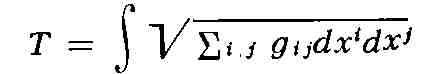
(см. Вариационное исчисление) и удовлетворяют уравнениям:

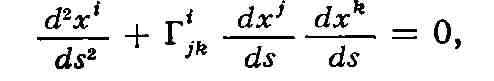
где Гⁱ_jk - т. н. Кристоффеля символы, выражающиеся через компоненты метрич. тензора g_ij и их первые производные. Через каждую точку риманова пространства в любом направлении проходит геодезическая; любые две точки А, В достаточно малой области можно соединить кратчайшей [длина её будет равна внутр. расстоянию р (А, В) между этими точками], и притом единственной, однако единственность может нарушаться, если точки достаточно удалены друг от друга (напр., полюсы сферы соединимы бесконечным множеством дуг больших кругов, являющихся кратчайшими).

Представляет интерес (для описания периодич. движений в механич. задаче многих тел, например) оценка числа v замкнутых геодезических пространства R; эта задача (поставленная Ж. А. Пуанкаре в 1905 в связи с нек-рыми вопросами небесной механики), несмотря на усилия многих математиков, ещё далека от завершения, наилучший результат: v>=2, если R односвязно.

Соприкасающееся пространство. Между римановым пространством R и касательным к нему евклидовым пространством в окрестности V нек-рой точки А можно установить такое соответствие, при к-ром оба пространства будут совпадать с точностью до малых выше второго порядка. Для этого проводят из точки А геодезические во всех направлениях и каждой из них в касательном пространстве сопоставляют луч соответствующего направления, а затем устанавливают такое соответствие этих лучей и геодезических, при к-ром длины дуг геодезических и соответствующих им лучей равны. В достаточно малой окрестности такое соответствие будет взаимно однозначным; если ввести в касательном пространстве декартовы координаты х¹, . . ., хⁿ и приписать их значения соответствующим точкам окрестности U, то между линейными элементами ds риманова и ds₀евклидова пространств будет такая связь:

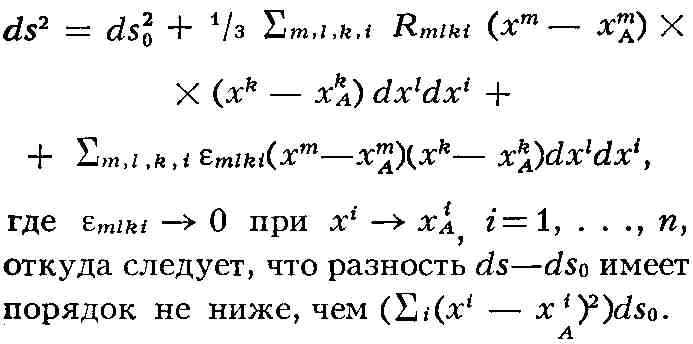
Евклидово пространство, поставленное в такое соответствие с римановым, и называется соприкасающимся (в отличие от обычного касательного пространства). Добиться более высокого порядка совпадения за счёт специального выбора соответствия между римановым и евклидовым пространствами в общем случае уже невозможно. Поэтому коэффициенты R_mlki характеризуют отличие риманова пространства от евклидова; они являются компонентами т. н. тензора кривизны (или тензора Римана - Кристоффеля), определяемого по формуле

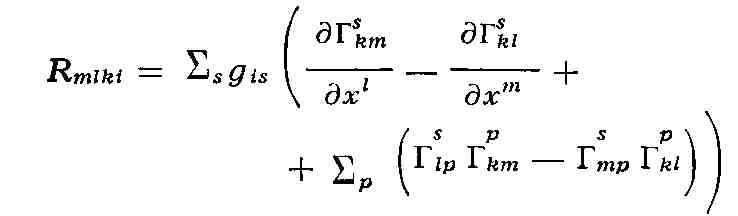
лишь через g_ik и их производные до второго порядка.

Тождественное обращение в нуль тензора кривизны необходимо и достаточно для того, чтобы пространство в окрестности каждой точки совпадало с евклидовым (в целом оно может отличаться от него своим строением, подобно тому как боковая поверхность цилиндра отличается от плоскости).

Параллельное перенесение. Для всякой гладкой кривой L риманова пространства существует отображение её окрестности U_Lв евклидово пространство E_L, при к-ром оно оказывается соприкасающимся во всех точках кривой L. Образ кривой L в пространстве E_L наз. развёрткой L' этой кривой на евклидово пространство (для поверхности F в евклидовом пространстве соприкасающееся евклидово пространство вдоль кривой L можно интерпретировать как развёрнутую на плоскость огибающую семейства плоскостей, касательных к F вдоль L). Вектор (и любой тензор) параллельно переносится вдоль кривой L, если параллельно переносится соответствующий вектор (тензор) в евклидовом пространстве E_L, соприкасающемся с римановым вдоль этой кривой. Аналитически параллельное перенесение вектора aⁱ вдоль кривой xⁱ = xⁱ(f) определяется дифференциальным уравнением

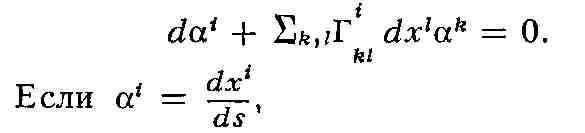
определить как кривые, вдоль к-рых касательный к ним вектор переносится параллельно, т. е. развёртка геодезической - прямая, что углубляет их сходство с прямыми. Результат параллельного перенесения вектора из точки А в точку В зависит, как правило, от кривой АВ, вдоль к-рой происходит перенесение,- в этом отсутствии "абсолютного параллелизма" наглядно проявляется отличие риманова пространства от евклидова.

Геодезическая кривизна (первая кривизна) кривой L в точке М оценивает её отклонение от геодезической L₀, касающейся L в точке М, и определяется следующим образом. Пусть касательный вектор к L в точке М параллельно перенесён в точку М' и образует там угол ср с касательной к L в точке М; пусть s - длина дуги ММ' кривой L. При стремлении М' к М существует предел

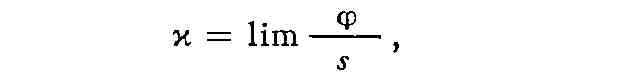
к-рый и наз. геодезической кривизной кривой L в точке М. Аналитически геодезическая кривизна кривой хⁱ = xⁱ(s), параметризованной длиной дуги, определяется формулами:

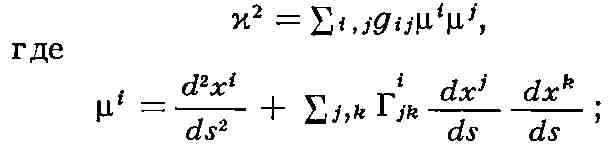
таким образом, геодезическая кривизна кривой L совпадает с (первой) кривизной её развёртки L, а геодезические линии во всех точках имеют нулевую геодезическую кривизну.

Для кривой L в римановом пространстве R определяются также вторая и т. д. кривизны и имеют место соотношения, аналогичные обычным формулам Френе (см. Дифференциальная геометрия) для кривых евклидова пространства.

Риманова кривизна. Пусть М - точка риманова пространства, F - двумерная поверхность xⁱ = xⁱ(u, v), проходящая через М, L - простой замкнутый контур на F, проходящий через М, а - площадь участка поверхности, ограниченного контуром L. Пусть произвольный вектор аⁱ, касательный к поверхности F (т. е. линейно выражающийся через векторы дхⁱ/дu, дхⁱ/дv) перенесён параллельно по L.

Тогда составляющая перенесённого вектора, касательная к F, окажется повёрнутой по отношению к аⁱ на угол ф (положительное направление отсчёта углов должно совпадать с направлением обхода L). При стягивании L в точку М существует предел

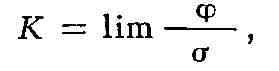
наз. кривизной риманова пространства (римановой кривизной) в данной точке в направлении двумерной поверхности; К зависит не от поверхности, а лишь от её направления в точке М, т. е. от направления двумерной плоскости касательного евклидова пространства, содержащей векторы дхⁱ/дu, дхⁱ/дv Риманова кривизна К связана с тензором кривизны формулой:

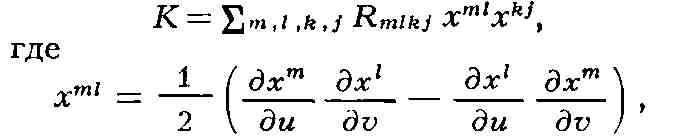
причём параметры и, v выбраны так, что площадь параллелограмма, построенного на векторах дхⁱ/дu, дхⁱ/дv, равна 1.

В двумерном случае К совпадает с полной кривизной (Theorema egregium К. Ф. Гаусса, 1827), при этом для области G, ограниченной простой замкнутой кривой Г, имеющей геодезическую кривизну и, справедлива т. н. формула Гаусса - Бонне:

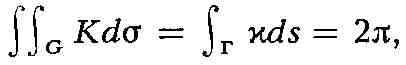
в частности, для треугольника, образованного отрезками геодезических

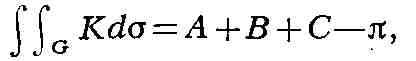
где А, В, С - величины углов треугольника. Для замкнутого (т. е. без границы) двумерного риманова пространства R его эйлерова характеристика х(R) пропорциональна интегралу римановой кривизны :

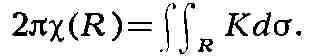
Эта формула обобщена на случай четно-мерного замкнутого риманова пространства, в к-ром интегрируется нек-рая функция компонент тензора кривизны.

Если в каждой точке риманова пространства кривизна не зависит от направления двумерной поверхности, то она не меняется и от точки к точке, т. е. пространство имеет постоянную кривизну. Представляют интерес также (в частности, для описания механич. систем с циклич. координатами) римановы пространства со специальной структурой тензора кривизны; они суть обобщение пространств постоянной кривизны и имеют достаточно обширную группу движений. Таковы, напр., симметрические пространства, характеризующиеся тем, что их тензор кривизны не меняется при параллельном перенесении, субпроективные пространства, характеризующиеся спец. координатной системой, в к-рой геодезические описываются линейными ур-ниями, и др. Риманова кривизна играет важную роль в геометрич. приложениях Р. г., тем более, что на всяком многообразии можно ввести нек-рую риманову метрику. Так, напр., топологич. строение полных римановых пространств (т. е. пространств, в к-рых всякая геодезическая бесконечно продолжаема) зависит от свойств его кривизны: всякое полное односвязное n-мерное риманово пространство гомеоморфно n-мерному евклидову пространству, если его кривизна во всех точках и по всем направлениям неположительна и гомеоморфна n-мерной сфере единичного радиуса, если его кривизна К удовлетворяет неравенствам

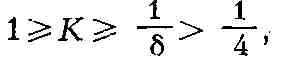
где о - нек-рая постоянная. От величины кривизны полного риманова пространства R зависит и его диаметр d - точная верхняя грань расстояний между точками R, определяемых внутр. метрикой R: напр.,

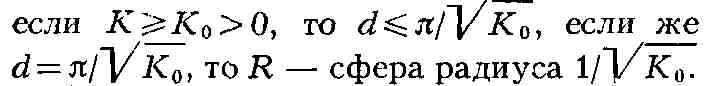
Метрическая связность. Параллельное перенесение вдоль кривой L с концами А, В задаёт изометричное (т. е. сохраняющее расстояния) преобразование т_i касательного пространства Е_Aв точке Л в касательное пространство Е_B в точке А. Дифференциал преобразования т.; в точке А, т. е. главная линейная часть изменения т_i при переходе из А(хⁱ) в близкую точку А(х¹ + dx¹), определяет нек-рый геометрич. объект, наз. римановой связностью, ассоциированной с данным параллельным перенесением. Аналитически эта связность выражается системой линейных дифференциальных форм

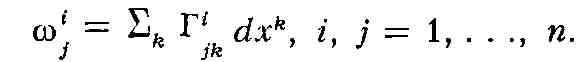
Однако в римановом пространстве R можно определить и другие связности, такие, что ассоциированные с ними параллельные перенесения также сохраняют метрич. тензор; они наз. метрическими связностями и определяются аналогичными коэффициентами Гⁱ_jk , но уже не симметричными по индексам j, k и не выражающимися (подобно символам Кристоффеля) только через тензор g_ij и его производные. Отличие метрич. связности от римановой оценивается т. н. тензором кручения:

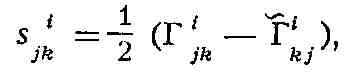
геометрический смысл к-рого иллюстрируется следующим образом. Рассмотрим в двумерном римановом пространстве метрической связности малый треугольник, образованный отрезками геодезических длины а, Ь, с и углами А, В, С. Тогда главная часть проекции кручения в точке А на сторону АВ равна отношению величины с-acos В-b cos А к площади треугольника, а главная часть проекции кручения на перпендикуляр к АВ -величине a sin В-b sin А, делённой на площадь треугольника. Т. о., в римановом пространстве нулевого кручения имеют место теоремы косинусов и синусов обыкновенной тригонометрии с точностью до величин, малых в сравнении с площадью треугольника.

Кривые, касательный вектор к к-рым переносится вдоль них параллельно, наз. геодезическими соответствующей связности; они совпадают с римановыми геодезическими, если тензор

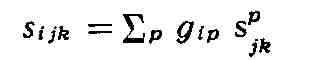
кососимметричен по всем индексам.

М наз. римановым подпространством пространства R.

Достаточно малая область га-мерного риманова пространства R может быть погружена в евклидово пространство достаточно большой размерности N (т. е. допускает сохраняющее длины отображение на подмногообразие этого пространства). Известно, что N=<[(m(m+1))/2]+m вопрос о минимальном значении N в общем случае ещё не решён, однако если коэффициенты метрич. формы дц пространства R являются аналитич. функциями (т. е. разлагаются в сходящиеся степенные ряды), то N=<[(m(m+1))/2]+m. Относительно задачи погружения в целом (представляющей интерес для физики калибровочных полей) известно ещё меньше.

Наиболее подробно исследованы погружения двумерных римановых пространств. Так, напр.: 1) двумерное полное риманово пространство положительной кривизны К погружается в виде замкнутой выпуклой поверхности (овалоида) в трёхмерное риманово пространство кривизны не меньшей К [проблема Г. Вейля (1916), решённая нем. математиком X. Леви (1937) и А. Д. Александровым (1941) для погружения в евклидово пространство и А. В. Погореловым (1957) для риманова пространства], причём любые два погружения, имеющие общую точку и общее соприкасающееся пространство в ней, совпадают [т. е. овалоид однозначно определён своей метрикой, нем. математик С. Э. Кон-Фоссен (1927), А. В. Погорелое (1948)]. 2) Двумерное полное риманово пространство отрицательной кривизны К=<К₀<0 не допускает погружения в виде регулярной поверхности [сов. математик Н. В. Ефимов (1963), частный случай плоскости Лобачевского (К = - 1) разобран Д. Гильбертом (1901)]. 3) Двумерное риманово пространство, гомеоморфное тору, допускает погружение в четырёхмерное евклидово пространство [сов. математик Э. Г. Позняк (1973)].

Приложения и обобщения римановой геометрии. 1) Поскольку Р. г. определяется заданием дважды ковариантного симметричного тензора, постольку всякую физич. задачу, сводящуюся к изучению такого тензорного поля, можно формулировать как задачу Р. г. В частности, к тензорным полям такого типа относятся различные физич. величины, характеризующие упругие, оптич., термодинамические, диэлектрические, пьезомагнитные и др. свойства анизотропных тел. При этом симметрия коэффициентов дц является отражением одного из фундаментальных физич. законов - закона взаимности. Так, задача о теплопроводности анизотропного тела, решённая ещё Риманом (1861), явилась первым приложением Р. г.

2) Рассмотрение конфигурационного пространства в механике системы с n степенями свободы позволило представить в ясной геометрич. форме ряд механич. задач. Так, напр., траектории свободного (т. е. в отсутствии обобщённых сил) движения голономной механич. системы с кинетич. энергией

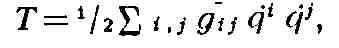
где qⁱ - обобщённые скорости, являются геодезическими соответствующего n-мерного риманова пространства с метрич. тензором дц. О нек-рых др. фактах упоминалось выше. Аналогичную интерпретацию получает и движение в поле сил, имеющих потенциал (см. Герца принцип). 3) В приложениях Р. г. к механике и физике важную роль играют дополнит, структуры, согласующиеся в том или ином смысле с метрикой риманова пространства. Так, напр.,

а) физич. представлениям об упругой сплошной среде с непрерывным распределением источников внутр. напряжений соответствует риманово пространство с нек-рой метрич. связностью: параллельное перенесение, соответствующее ей, определяет т. н. естественное состояние среды вдоль кривой, а кручение отождествляется с плотностью дислокаций,

б) римановы пространства с почти комплексной структурой (определяется полем один раз ковариантного и один раз контравариантного тензора Jⁱ_k, такого, что

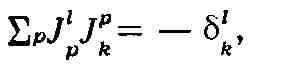
где S - Кронекера символ) используются квантовой механикой для описания наблюдаемых и состояний систем многих частиц; в) привлечение понятия т. н. конформной связности, т. е. связности риманова пространства, при к-рой результат параллельного перенесения метрич. тензора дц пропорционален ему самому, позволило смоделировать нек-рые из т. н. Бора постулатов, в частности избранные (или "разрешённые") орбиты движения электронов в атоме - кривые, вдоль к-рых метрич. тензор сохраняется.

4) Развитие Р. г. в связи с общей теорией относительности (см. Тяготение) и механикой сплошных сред породило различные обобщения её предмета, главнейшими из к-рых являются т. н. псевдоримановы пространства. Таково, напр., согласно теории тяготения, многообразие событий (многообразие пространства - времени) - четырёхмерное пространство с заданной на нём зна-конеопределённой невырожденной квадратичной формой

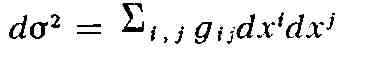
(коэффициенты такой "метрики", допускающей мнимые расстояния, как раз и характеризуют поле тяготения, играя роль потенциальных функций). Эта форма в каждой точке пространства событий может быть приведена к виду

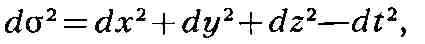
где х, у, z - пространственные координаты, t - время. Физически такие, т. н. локально галилеевы, системы отсчёта являются свободно падающими в поле тяготения. Однако ввести такую систему на всём многообразии невозможно (поскольку наличие поля тяготения математически выражается в кривизне псевдориманова пространства).

Другой путь обобщения Р. г. связан с рассмотрением более общих законов определения расстояний, задаваемых в виде линейного элемента ds (см. Финслерова геометрия), и более общих законов параллельного перенесения, а также с отказом от требований регулярности.

Лит.: Риман Б., Соч., пер. с нем., М.- Л., 1948; Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; Эйзенхарт Л. П., Риманова геометрия, пер. с англ., М., 1948; С х о у т е н Я. А., Тензорный анализ для физиков, пер. с англ., М., 1965; Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971.

А. Д. Александров, Ю. Ф. Борисов.