РИККАТИ (Riccati) Якопо Франческо (28.5.1676, Венеция, - 15.4.1754, Тревизо), итальянский математик. Учился в Падуе. С 1747 жил в Венеции. Осн. труды Р. относятся к интегральному исчислению и дифференциальным уравнениям. Автор исследований об интегрируемости в элементарных функциях одного типа дифференциального уравнения 1-го порядка - т. н. специального Риккати уравнения. Известен также инженерной деятельностью; руководил постройкой речных плотин.

Соч.: Opere..., v. 1-4, Lucca, 1761 - 65.

Лит.: Cantor M., Vorlesungen über Geschichte der Mathematik, 2 Aufl., Bd 3, Lpz., [1901].  

РИККАТИ УРАВНЕНИЕ, обыкновенное дифференциалъное уравнение 1-го порядка вида

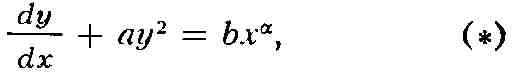
где а, б, а - постоянные. Это уравнение впервые исследовалось Я. Риккати (1724); отдельные частные случаи рассматривались раньше. Д. Бернулли установил (1724-25), что уравнение (*) интегрируется в элементарных функциях, если а = -2 или а = -4k/(2k-1), где k - целое число. Как доказал Ж. Лиувилль (1841), при других значениях а решение уравнения (*) нельзя выразить в квадратурах от элементарных функций; общее решение его может быть записано с помощью цилиндрических функций. Дифференциальное уравнение

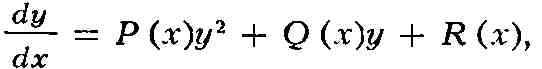
где Р(х), Q(x), R(x)- непрерывные функции, наз. общим Р. у. [в отличие от него уравнение (*) наз. специальным Р. у.]. При Pi(.r)=0 общее Р. у. является линейным дифференциальным уравнением, при R(x)=0 - т. н. Бернулли уравнением, к-рые интегрируются в конечном виде. Изучены также другие случаи интегрируемости общего Р. у.

Лит.: Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 4 изд., М., 1971.