ПФАФФА УРАВНЕНИЯ, уравнения вида X₁dx₁ + X₂dx₂+... + X_nx_n = 0, (1) где X₁, Х₂, ..., Х_n - заданные функции независимых переменных x₁, x₂, ..., х_п. Изучались И. Ф. Пфаффом. (1814-15). Решение ур-ния (1) состоит из соотношений

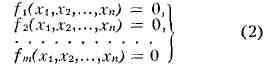
таких, что ур-ние (1) является следствием их и соотношений df₁ = 0, df₂ = 0, ..., df_m = 0. Соотношения (2) определяют интегральное многообразие П. у. (1). Если через каждую точку n-мерного пространства x₁, х₂, ..., х_n проходит (п - 1)-мерная интегральная гиперповерхность, т. е. если ур-ние (1) интегрируется одним соотношением, содержащим одну произвольную постоянную, то оно наз. вполне интегрируемым. В случае трёх независимых переменных х, у, z П. у. может быть записано в виде где Р = Р (х, у, z), Q = Q (х, у, z), R = R (х, у, z). Геометрически решение ур-ния (1') означает нахождение кривых в пространстве х, у, z, ортогональных в каждой своей точке векторному полю (Р, Q, R), т. е. таких кривых, нормальная плоскость к к-рым в каждой точке содержит вектор поля. Такие кривые являются интегральными кривыми ур-ния (1'). Если задать одно соотношение Ф (х, у, z) = О произвольно, т. е. искать интегральные кривые на произвольной гладкой поверхности, то из ур-ния (1') и соотношения

Ф_xdx + Ф_у dy + Ф_z dz = О

находятся, напр., dy/dx и dz/dx как функции х, у, г, и задача сводится к интегрированию системы двух обыкновенных дифференциальных ур-ний первого порядка. Решая ее, находят двупараметрич. семейство кривых, из к-рого выделяют однопараметрич. семейство интегральных кривых ур-ния (1'), лежащих на заданной поверхности Ф (х, у, z) = 0. Это семейство интегральных кривых может рассматриваться как пересечение заданной поверхности и однопараметрич. семейства поверхностей Ф₁ (х, у, z, c)=0, т. е. общее решение П. у. (1') состоит из двух соотношений Ф (х, у, z) = 0 и Ф₁ (х, у, 2, с) = 0, из к-рых первое произвольно, а второе определяется по первому. П. у. (1') интегрируется одним соотношением F (х, у, z, с) = 0, т. е. является вполне интегрируемым, если выполняется условие интегрируемости

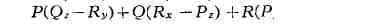
тождественно относительно х, у, z. Геометрически это значит, что существует однопараметрич. семейство интегральных поверхностей П. у. (1'), ортогональных в каждой точке векторному полю {Р, Q, К}. Любая кривая на интегральной поверхности является интегральной кривой П. у. (1').

Tеория П. у. обобщена на случай систем П. у., играющих особо важную роль в приложениях. П. у. и системы П. у. встречаются в механике неголономных систем, т. к. неголономные связи суть П. у. между виртуальными перемещениями, а также в термодинамике.

Лит.: Рашевский П. К., Геометрическая теория уравнений с частными производными, М. - Л., 1947; Степанов В. В., Курс дифференциальных уравнений, 8 изд., М.. 1959; Goursat Е., Leçons sur le probleme de Pfaff, P., 1922.