ПРЕДЕЛ, одно из осн. понятий математики. П.- постоянная, к к-рой неограниченно приближается нек-рая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие П. числовой последовательности, с помощью к-рого могут быть определены понятия П. функции, П. последовательности точек пространства, П. интегральных сумм.

Предел последовательности. Пусть задана последовательность действит. чисел х_п, п = 1, 2, . . . Число а называется пределом этой последовательности, если для любого числа е>0 существует такой номер n_е, что для всех номеров п>=п_с выполняется неравенство \х_п-а|<е. В этом случае пишется

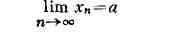
(lim - первые буквы латинского слова limes), или

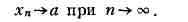
Если последовательность имеет П., то говорят, что она сходится. Так, последовательность 1/n, n = 1, 2,..., сходится и имеет своим П. число 0. Не всякая последовательность имеет П., напр., последовательность 1, -1, 1, . . ., (-1)ⁿ⁺¹, ... не имеет П. Последовательность, не имеющая П., наз. расходящейся. На геометрич. языке существование у последовательности П., равного а, означает, что каждая окрестность точки а содержит все члены данной последовательности, за исключением, быть может, их конечного числа.

Для П. последовательностей имеют место формулы

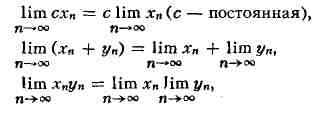
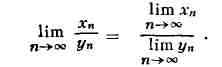
Эти формулы справедливы в предположении, что П., стоящие в их правых частях, существуют, причём в формуле для П. частного х_п/у_п надо ещё допол-

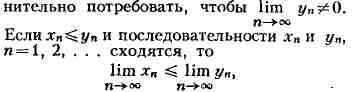
т. е. при предельных переходах нестрогие неравенства сохраняются (но из x_п<y_п

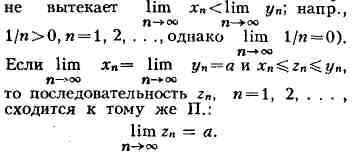
Последовательность а_п, и = 1, 2, . . ., сходящаяся к нулю, называется бесконечно малой. Последовательность сходится к к.-л. числу тогда и только тогда, когда разность между членами последовательности и этим числом является бесконечно малой последовательностью (т. о., общее понятие П. последовательности сводится к понятию бесконечно малой). Так, напр., последовательность ⁴/₂, ⅔, ¾, ...,n/(n+1),... имеет своим П. единицу, поскольку разность 1-n/(n+l) = l/(n+l), и = 1, 2,... является бесконечно, малой последовательностью.

Всякая возрастающая (убывающая) последовательность, ограниченная сверху (соответственно снизу), сходится. Напр., если для заданного числа а обозначить чеоез а_п ппиближённое значение его

возрастающей ограниченной сверху последовательности является последовательность длин периметров правильных многоугольников, вписанных в данную окружность, к длине к-рой сходится эта последовательность.

Для того чтобы сходилась произвольная последовательность х_п, необходимо и достаточно, чтобы она удовлетворяла критерию Кош и: для любого числа е>0 существует такой номер N_e, что для всех номеров m>=Ne и n>=N_e выполняется неравенство |х_п-x_m|<е.

Если последовательность х_п, и = 1,2,..., такова, что для числа e>0 существует такой номер п_eчто для всех номеров n>=n_e выполняется неравенство |x_п|>е, то последовательность х_п наз. бесконечно большой и пишется

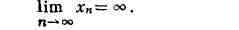
Если же при этом для любого е>0 существует такой номер n_е, что х_п>е (соответственно х_п<-е) для всех n^n_t.

собой разумеется, что бесконечно большие последовательности не являются сходящимися в смысле данного выше определения этого понятия. На бесконечные П. переносятся далеко не все свойства конечных П. Напр., последовательности х_п = п и y_n = sin [(nп)/2 -n] бесконечно большие, а последовательность x_n + y_п, n = 1, 2, ..., ограниченная и к тому же расходящаяся.

Частичные пределы. Верхний и нижний пределы. П. (конечный и бесконечный) к.-л. подпоследовательности наз. частичным пределом последней. Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность (теорема Больцано - Вейерштрасса), а из всякой неограниченной - бесконечно большую. В множестве всех частичных П. последовательности всегда имеется как наибольший, так и наименьший (конечный или бесконечный). Наибольший (соответственно наименьший) частичный П. последовательности х_п, п = 1, 2, ..., наз. её верхним (соответственно нижним)

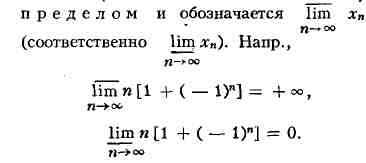
Последовательность имеет конечный или бесконечный П. тогда и только тогда, когда её верхний П. совпадает с нижним, при этом их общее значение и является её П. Конечный верхний П. последовательности можно также определить как такое число а, что при любом б>0 существует бесконечно много членов последовательности, больших, чем а-е, и лишь не более, чем конечное число членов, больших, чем а + е.

Предел функции. Пусть функция f, принимающая действит. значения, определена в нек-рой окрестности точки х₀, кроме, быть может, самой точки х₀. Функция f имеет П. в точке х₀, если для любой последовательности точек х_п, n = 1, 2, . . ., x_n не= x₀, стремящейся к точке х₀, последовательность значений функции f(x_n,) сходится к одному и тому же числу А, к-рое и наз. пределом функции f в точке х₀(или при х->x₀), при этом пишется

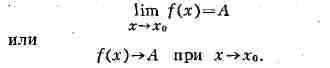
В силу этого определения на П. функций переносятся свойства П. суммы, произведения и частного последовательностей, а также сохранение неравенств при предельном переходе.

Определение П. функции можно сформулировать и не прибегая к понятию П. последовательности: число А наз. пределом функции f в точке x₀, если для любого числа е>0 существует такое число б>0, что для всех точек х не= х₀, удовлетворяющих условию |х-x₀|<б, х не= х₀, выполняется неравенство |t(x)-A\<e.

Все основные элементарные функции: постоянные, степенная функция х^a, показательная функция а^x, тригонометрические функции sin х, cos х, tg х и ctg х и обратные тригонометрические функции arc sin х, arc cos х, arc tg x и arc ctg x во всех внутренних точках своих областей определения имеют П., совпадающие с их значениями в этих точках. Но это не всегда бывает так. Функция

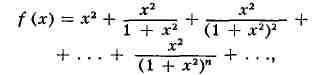
являющаяся суммой бесконечной геометрич. прогрессии со знаменателем q = l/(l + x²), 0<<7<1, в точке х = 0 имеет П., равный 1, ибо /(*)=1 + лг² при х^О. Этот П. не совпадает со значением функции f в нуле: f(0)-Q. Функция же

Примером функций, всегда имеющих П., являются монотонные функции. Так, если функция f определена на интервале (а, b) н не убывает, то в каждой точке х, а<х<b, она имеет конечный П. как слева, так и справа; в точке а П. справа, к-рый конечен тогда и только тогда, когда функция f ограничена снизу, а в точке b П. слева, конечный в том и только в том случае, когда функция ограничена сверху. В общем же случае стремление к П. может носить разный, необязательно монотонный характер. Напр.,

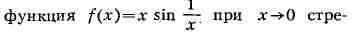
мится к нулю, бесконечное число раз переходя от возрастания к убыванию и обратно.

Т. н. внутренний критерий (критерий К о ш и) существования П. функции в точке состоит в следующем: функция f имеет в точке x₀ П. в том и только

означает, что для любого е>0 существует такое б>0, что для всех х, удовлетворяющих условию х<-б, выполняется неравенство f(x)>е.

Расширение понятия предела функции. Если функция f определена на нек-ром множестве Е числовой прямой и точка х₀ такова, что в любой её окрестности имеются точки множества Е, то аналогично данному выше определению П. функции, заданной в нек-рой окрестности точки х₀, кроме, быть может, самой точки х₀, определяется понятие предела функции по множеству Е

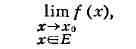
для этого следует лишь в определении П. всегда дополнительно требовать, чтобы точка х принадлежала множеству Е : х принадлежит  Е П. последовательности х_п, п = 1, 2, ..., является при таком определении понятия П. частным случаем П. функции по множеству, а именно функции f, определённой на множестве натуральных чисел п формулой f(n)=x_n, n = 1, 2, ... .

Функция, равная нулю при рациональных х и единице при иррациональных, не имеет П. при x->0, однако по множеству рациональных чисел она при x->0 имеет П., равный нулю. Понятие П. числовой функции по множеству переносится и на функции многих переменных. В этом случае можно говорить, в частности, о П. в данном направлении, о П. по данной кривой, по данной поверхности и т. д. Кроме того, для функций многих переменных возникает понятие повторного предела, когда предельный переход совершается последовательно по разным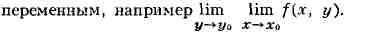 

Распространяется понятие П. и на функции, к-рые могут принимать не только действительные, но и комплексные значения.

Предел интегральных сумм. Ещё одно важное понятие П. возникает при определении интеграла. Пусть, напр., функция f определена на отрезке [а, b]. Совокупность {xi} таких точек xi, что

суммой функции f. Число А является пределом интегральных сумм и наз. определённым интегралом:

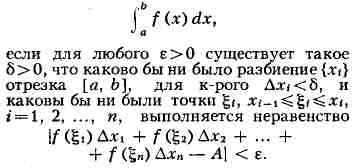
Понятие П. интегральных сумм может быть введено и с помощью П. последовательности.

Обобщения понятия предела. Ввиду разнообразия употребляемых в математике спец. видов понятия П. естественно возникло стремление включить их как частный случай в то или иное общее понятие П. Напр., можно ввести понятие П., обобщающее как понятие П. функции, так и понятие П. интегральных сумм. Система S непустых подмножеств некоторого множества Е наз. направлением, если для каждых двух подмножеств А и В этой системы выполняется одно из включений Лей или ВсЛ и пересечение всех множеств из S пусто. Пусть на множестве Е задана числовая функция f. Число а наз. пределом функции f по направлению S, если для любого е>0 существует такое множество А из S, что во всех его точках выполняется неравенство |f(x)-а|<е. При определении П. функции f в точке х₀ за направление следует взять совокупность всех окрестностей этой точки с достаточно малыми радиусами за вычетом самой точки х₀. При определении П. интегральных сумм функции f, заданной на отрезке [a, b], следует рассмотреть множество Е, элементами к-рого являются всевозможные разбиения отрезка [а, b] с выбранными в них точками R_i. Подмножества Е_п множества Е, отвечающие разбиениям, длины Дxi отрезков к-рых не превышают т), образуют направление. П. интегральных сумм (к-рые, очевидно, являются функциями, определёнными на множестве Е) по указанному направлению является интеграл.

Понятие П. обобщается на более широкие классы функций, напр. на функции, заданные на частично упорядоченных множествах, или на функции, являющиеся отображениями одного пространства (метрического или, более общо, топологического) на другое. Наиболее полно задача определения П. решается в топологии и означает в общем случае, что нек-рый объект, обозначенный f(x), меняющийся при изменении др. объекта, обозначенного через х, при достаточно близком приближении объекта х к объекту х₀сколь угодно близко приближается к объекту А. Основным в такого рода понятиях П. является понятие близости объектов х и х₀, f(x) и А, к-рые нуждаются в математич. определении. Только после того как это будет сделано, высказанному определению П. можно будет придать чёткий смысл и оно станет содержательным. Различные понятия близости и изучаются, в частности, в топологии.

Встречаются, однако, понятия П. др. природы, не связанные с топологией, напр. понятие П. последовательности множеств. Последовательность множеств An, n = 1, 2, ..., наз. сходящейся, если существует такое множество А, наз. её пределом, что каждая его точка принадлежит всем множествам А_п, начиная с нек-рого номера, и каждая точка из объединения всех множеств А_п, не принадлежащая Л, принадлежит лишь конечному числу А„.

Историческая справка. К понятию П. вплотную подошли ещё др.-греч. учёные при вычислении площадей и объёмов нек-рых фигур и тел с помощью исчерпывания метода. Так, Архимед, рассматривая последовательности вписанных и описанных ступенчатых фигур и тел, с помощью метода исчерпывания доказывал, что разность между их площадями (соответственно объёмами) может быть сделана меньше любой наперёд заданной положит. величины. Включая в себя представление о бесконечно малых, метод исчерпывания являлся зародышем теории П. Однако в явном виде в др.-греч. математике понятие П. не было сформулировано, не было создано и к.-л. основ общей теории.

Новый этап в развитии понятия П. наступил в эпоху создания дифференциального и интегрального исчислений. Г. Галилей, И. Кеплер, Б. Кавальеры, Б. Паскаль и др. широко используют при вычислении площадей и объёмов "неделимых" метод, метод актуальных бесконечно малых, т. е. таких бесконечно малых, к-рые, по их представлению, являются неизменными величинами, не равными нулю и вместе с тем меньшими по абсолютной величине любых положит. конечных величин. Продолжает в этот период применяться и развиваться и метод исчерпывания (Григорий из Сен-Винцента, П. Гульдин, X. Гюйгенс и др.). На основе интуитивного понятия П. появляются попытки создать общую теорию П. Так, И. Ньютон первый отдел первой книги ("О движении тел") своего труда "Математические начала натуральной философии" посвящает своеобразной теории П. под назв. "Метод первых и последних отношений", к-рую он берёт за основу своего флюксий исчисления. В этой теории Ньютон взамен актуальных бесконечно малых предлагает концепцию "потенциальной" бесконечно малой, к-рая лишь в процессе своего изменения становится по абсолютной величине меньше любой положит. конечной величины. Точка зрения Ньютона была существенным шагом вперёд в развитии представления о П. Понятие П., намечавшееся у математиков 17 в., в 18 в. постепенно всё больше анализировалось (Л. Эйлер, Ж. Д'Аламбер, Л. Карно, братья Бернулли и др.) и уточнялось. В этот период оно служило лишь для попыток объяснить правильность дифференциального и интегрального исчисления и ещё не являлось методом разработки проблем математич. анализа.

Совр. теория П. начала формироваться в нач. 19 в. в связи с изучением свойств различных классов функций, прежде всего непрерывных, а также в связи с попыткой доказательства существования ряда осн. объектов математич. анализа (интегралов функций действительных и комплексных переменных, сумм рядов, алгебраических корней и более общих уравнений и т. п.). Впервые в работах О. Коши понятие П. стало основой построения математич. анализа. Им были получены осн. признаки существования П. последовательностей, осн. теоремы о П. и, что очень важно, дан внутренний критерий сходимости последовательности, носящий теперь его имя. Наконец, он определил интеграл как П. интегральных сумм и изучил его свойства, исходя из этого определения. Окончательно понятие П. последовательности и функции оформилось на базе теории действит. числа в работах Б. Больцано и К. Вейерштрасса. Из дальнейших обобщений понятия П. следует отметить понятия П., данные в работах С. О. Шатуновского (опубл. в 1923), амер. математиков Э. Г. Мура и Г. Л. Смита (1922) и франц. математика А. Картана (1937).

Лит.: Александров П. С., Введение в общую теорию множеств и функций, М.- Л., 1948; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., т. 1-2, М., 1971 - 73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1 - 2, М., 1970; Никольский С. М., Курс математического анализа, т. 1 - 2, М., 1973; Смирнов В. И., Курс высшей математики, 22 изд., т. 1, М., 1967.

Л. Д. Кудрявцев.

ПРЕДЕЛЬНАЯ РАВНИНА, почти равнина, то же, что пенеплен.

ПРЕДЕЛЬНАЯ ТОЧКА множества А, такая точка § пространства, сколь угодно близко от к-рой имеются отличные от g точки множества Л, т. е. в любой окрестности к-рой содержится бесконечное множество точек из Л. Характеристическим свойством П. т. множества Л является существование по крайней мере одной сходящейся к ней последовательности различных точек множества Л. П. т. множества Л не обязана ему принадлежать. Так, напр., всякая точка числовой прямой является П. т. для множества Л рациональных её точек: ко всякому как рациональному, так и иррациональному числу можно подобрать сходящуюся к нему последовательность различных рациональных чисел. Не всякое бесконечное множество имеет П. т. - таково, напр., множество всех целых чисел. Однако всякое бесконечное и ограниченное множество любого евклидова пространства имеет по крайней мере одну П. т.

Лит.: Александров П. С., Введение в общую теорию множеств и функций, М. - Л., 1948.

ПРЕДЕЛЬНАЯ ЭФФЕКТИВНОСТЬ КАПИТАЛА (англ. marginal efficiency of capital), термин бурж. политич. экономии, означающий ожидаемую норму прибыли на дополнит. капитал. Это понятие наиболее чётко сформулировано Дж. М. Кейнсом (Великобритания) и получило распространение в работах представителей кейнсианства. По Кейнсу, П. э. к.-первое определяющее, к-рым руководствуется капиталист при решении вопроса об инвестициях, т. к. их размер зависит от той нормы прибыли, к-рую он рассчитывает получить. Вторым определяющим выступает процентная ставка на капитал. Капиталист проводит сравнение между П. э. к. и нормой процента. Инвестирование осуществляется лишь в том случае, если процентная ставка на капитал ниже нормы прибыли, ожидаемой от капиталовложений. Чем больше разрыв между этими показателями, тем сильнее побуждение капиталиста к инвестированию. Т. о., объём текущих инвестиций зависит от соотношения между П. э. к. и нормой процента: повышение нормы процента вызывает понижение П. э. к. и уменьшение инвестиций, понизившаяся норма процента и повысившаяся доступность кредита, наоборот, вызывают рост инвестиций. Кейнс исходит из предположения, что предприниматель расширяет свои инвестиции до тех пор, пока П. э. к. не снизится до уровня нормы процента. Однако такое предположение несостоятельно. Во-первых, Кейнс считает, что предприниматель применяет только ссудный капитал. В действительности же самая возможность использования ссудного капитала обусловлена наличием собственного капитала. Поэтому вопрос о норме процента имеет подчинённое значение для предпринимателя. Во-вторых, Кейнс признаёт распространённый в бурж. политич. экономии закон убывающей производительности капитала, согласно к-рому с увеличением вложения каждой дополнит. единицы капитала его производительность или эффективность снижается. Однако Кейнс не отвечает на вопрос, почему с увеличением применяемого в произ-ве капитала норма прибыли должна снижаться и почему в конечном счёте она должна снизиться до нормы процента.

Теория П. э. к. Кейнса является вульгарным истолкованием имеющейся в капиталистич. действительности и вскрытой ещё К. Марксом тенденции нормы прибыли к понижению (см. Тенденции нормы прибыли к понижению закон). Кейнс назвал эту тенденцию снижением П. э. к. и связал её с избыточным предложением капитала. По Кейнсу, рост инвестиций приводит к созданию новых капитальных благ, конкурирующих со старыми. Расширение выпуска продукции, считает он, неминуемо должно привести к снижению цен, что уменьшит ожидаемую прибыль. Такое явление может продолжаться до тех пор, пока норма процента не превысит П. э. к. Если же норма процента упадёт до нуля, капиталы будут непрерывно предлагаться до тех пор, пока они не насытят до предела рынок. В этом случае возникнут избыточные капиталы, не находящие применения, и норма прибыли катастрофически снизится. Т. о., Кейнс даёт искажённый анализ тенденции нормы прибыли к понижению, сохраняющей свою силу и в условиях монополистич. капитализма. В его толковании не проводится чёткого различия между нормой и массой прибыли, превратно объясняются причины, вызывающие снижение нормы прибыли, неправильно показывается влияние этого понижения на капиталистич. накопление.

Лит.: Кейнс Дж. М., Общая теория занятости, процента и денег, пер. с англ., М., 1948; Хаберлер Г., Процветание и депрессия, пер. с англ., М., 1960; Блюмин И. Г., Критика буржуазной политической экономии, т. 2, М., 1962.

С. С. Носова.

ПРЕДЕЛЬНО-ДОПУСТИМАЯ КОНЦЕНТРАЦИЯ (ПДК), максимальное количество вредного вещества в единице объёма (воздуха, воды или др. жидкостей) или веса (напр., пищ. продуктов), к-рое при ежедневном воздействии в течение неограниченно продолжит. времени не вызывает в организме к.-л. патологич. отклонений, а также неблагоприятных наследств. изменений у потомства. Для установления ПДК используют расчётные методы, результаты биол. экспериментов, а также материалы динамич. наблюдений за состоянием здоровья лиц, подвергшихся воздействию вредных веществ. Уровни ПДК одного и того же вещества различны для разных объектов внеш. среды (напр., в СССР для свинца и его неорганических соединений ПДК в воде водоёмов хозяйственно-питьевого назначения - 0,1 мг/л, в воздухе производственных помещений - 0,01 мг/м³, в атм. воздухе - 0,007 мг/м³). В СССР при нормировании ПДК учитывают воздействие вещества на людей любого возраста (в т. ч. и больных) в течение всей жизни, а также др. факторы (напр., влияние на общий сан. режим водоёма, возможности возникновения неприятных запахов в окружающем воздухе и т. д.). Правилами по охране поверхностных вод определены раздельные ПДК для водоёмов хоз.-питьевого и рыбопромыслового назначения. Установлено, что принятые уровни ПДК веществ в атм. воздухе, рассчитанные на охрану здоровья человека, в ряде случаев недостаточны для охраны зелёных насаждений; совр. гигиеной разрабатываются нормативы ПДК, учитывающие вредные влияния соответств. веществ и на зелёные насаждения. Уровни ПДК включены в ГОСТы, сан. нормы и др. нормативные документы, обязательные для исполнения на всей терр. СССР; их учитывают при проектировании технологич. процессов, оборудования, очистных устройств и пр. Санитарно-эпидемиологическая служба в порядке сан. надзора систематически контролирует соблюдение нормативов ПДК в воде водоёмов хоз.-питьевого водопользования (см. Санитарная охрана водоёмов), атм. воздухе (см. Санитарная охрана воздушного бассейна) и в воздухе производственных помещений: контроль за состоянием водоёмов рыбопромыслового назначения осуществляют органы рыбнадзора.

В зарубежных социалистич. странах перечень нормируемых веществ и уровни их ПДК аналогичны нормативам в СССР. В нек-рых капиталистич. странах также установлены ПДК для отдельных вредных веществ в водоёмах хоз.-питьевого водопользования, атм. воздухе и воздухе рабочих помещений. Однако, по мнению сов. учёных-гигиенистов, количество нормируемых веществ является недостаточным, а уровни их ПДК в большинстве случаев завышены.

А. М. Сточик.

ПРЕДЕЛЬНОЕ СОСТОЯНИЕ в строительной технике, состояние строит. конструкции или основания здания (сооружения), при к-ром они перестают удовлетворять эксплуатац. требованиям. Понятием "П. с." пользуются при расчёте конструкций по методу того же названия, разработанному в СССР и введённому Строительными нормами и правилами (СНиП) в 1955. По сравнению с ранее применявшимися методами (по допускаемым напряжениям и по разрушающим нагрузкам) метод расчёта по П. с. является более совершенным; он отличается полнотой оценки несущей способности и надёжности конструкций благодаря учёту вероятностных свойств действующих на конструкции нагрузок и сопротивлений этим нагрузкам, особенностей работы отд. видов конструкций, а также пластич. свойств материалов.

В методе расчёта по П. с. вместо ранее применявшегося единого коэфф. запаса прочности используют неск. независимых коэфф., каждый из к-рых имеет определ. значение в обеспечении надёжности конструкции и гарантии от возникновения П. с. Осн. из них: коэффициент безопасности по материалу (и грунту), учитывающий статистич. изменчивость прочностных свойств материалов (грунтов), а также нек-рые др. факторы, исключающие или сильно затрудняющие возможность статистической оценки, напр. отличие сопротивлений материалов в конструкциях от определяемых испытаниями контрольных образцов; коэффициент перегрузки, учитывающий возможное отклонение величин нагрузок от исходных (нормативных) значений из-за изменчивости нагрузок и отступления от условий нормальной эксплуатации; коэффициент условий работы, учитывающий особенности действит. работы элементов конструкций, оснований, а также зданий и сооружений в целом, не отражаемые непосредственно в расчётах; коэффициент надёжности, учитывающий степень капитальности зданий и сооружений, а также значимость последствий наступления тех или иных П. с.

Различают П. с., при к-рых конструкция становится непригодной к нормальной эксплуатации, и П. с., при к-рых она полностью утрачивает несущую способность. Пригодность к нормальной эксплуатации обычно определяется требованиями жёсткости, ограничениями осадок, трещиностойкостью и т. д. Потеря несущей способности может проявляться в виде хрупкого, вязкого, усталостного разрушения материала, изменения конфигурации конструкции, а также потери устойчивости её формы, положения и т. д. Осн. цель расчёта по П. с.- предотвратить их возникновение в течение всего срока службы здания (сооружения).

Метод расчёта по П. с. получил широкое распространение в СССР, странах - членах СЭВ и странах, входящих в Международную орг-цию по стандартизации и Европ. к-т по бетону. В СССР этот метод применяется также при расчёте некоторых маш.-строит, конструкций, например металлич. конструкций мостовых, подвесных и башенных грузоподъёмных кранов.

Лит.: Строительные нормы и правила, ч. 2, раздел А, гл. 10. Строительные конструкции и основания. Основные положения проектирования, М., 1972; Балдин В. А. [и др.], К выходу СНиП II - А. 10 - 71, "Строительная механика и расчет сооружений", 1972, № 4.

А. А. Бать, В. А. Отставнов.

ПРЕДЕЛЬНОЙ ПОЛЕЗНОСТИ ТЕОРИЯ, бурж. теория, пытающаяся дать объяснение процессам ценообразования в условиях капиталистич. х-ва. Возникла в последней трети 19 в. в противовес теории трудовой стоимости К. Маркса. Разрабатывалась У. С. Джевонсом (Великобритания), Л. Вальрасом (Швейцария), К. Менгером, Э. Бём-Баверком (Австрия). Бурж. экономисты не могли примириться с тем, что марксистская теория не только даёт объяснение процессам ценообразования, но и вскрывает источник капиталистич. эксплуатации в виде прибавочной стоимости и тем самым показывает основу непримиримых противоречий между двумя осн. классами капиталистич. общества. Конкретно-историч. условия, способствовавшие возникновению и развитию П. п. т., были связаны с вовлечением в сферу действия капиталистич. рынка новых территорий и сфер х-ва. Усиление рыночных отношений затушёвывало производств. основу ценообразования и способствовало бурж. фетишизации рыночных процессов.

Методологии П. п. т. присущи: 1) субъективно-психологический взгляд на действующие в рыночном х-ве механизмы, в основу к-рых кладутся оценки агентов рыночного х-ва (продавца, покупателя), а не объективные процессы, формирующие в конечном счёте психологич. оценки этих агентов. 2) Потребительский подход к объяснению сил, воздействующих на формирование цены. В этом П. п. т. коренным образом отличается от классич. бурж. политич. экономии, рассматривавшей стоимость в качестве основы цены, и связывавшей эту категорию с процессами произ-ва и трудовыми затратами в ходе произ-ва, хотя часто объяснения классиков бурж. политич. экономии страдали эклектизмом и не вскрывали единого источника стоимости, заключённого в затратах абстрактного труда. На место категории стоимости П. п. т. ставит категорию полезности, выводя последнюю из процессов потребления. В этом едином источнике формирования цен, исходящем из потребления, из полезности, состоит монизм П. п. т. 3) Априорно-дедуктивный метод построения теории. П. п. т. исходит из ограниченного набора постулатов, имеющих характер очевидности с точки зрения "здравого смысла", и, пользуясь ими, стремится к построению теории, не противоречащей законам формальной логики. Однако коренным пороком такого метода является отсутствие практич. проверки теоретич. конструкции.

К числу осн. постулатов П. п. т. относятся Госсена законы. Процесс установления цены на рынке наиболее подробно описывается в работах представителей австрийской школы (Менгера, Ф. Визера, Бём-Баверка). На основе взаимоотношений т. н. рыночных пар (продавец - покупатель) пока на рынке оценки полезности товара со стороны продавца ниже, чем оценки покупателя, обмен идёт беспрепятственно. Это способствует вовлечению в обмен продавцов с более высокой оценкой полезности товара и покупателей с более низкой оценкой. Процесс обмена продолжается до тех пор, пока не встречается т. н. предельная пара, чьи субъективные оценки полезности, выраженные в деньгах, совпадают. Субъективная оценка полезности товара этой последней пары продавец - покупатель и есть та предельная полезность, к-рая определяет рыночную цену товара. Это -цена равновесия, определяющая в дальнейшем течение всех сделок на рынке. Апологетич. сущность П. п. т. состоит в том, что она выводит проблему измерения и соизмерения цен из области обществ.-производств, отношений в область субъективно-психологич. оценок. Непротиворечивость П. п. т. оказывается мнимой, поскольку оценки полезности носят конкретно-историч. характер и зависят от сложившейся в тот или иной период структуры цен. Т. о. возникает порочный логический круг: цены - полезности - цены. Полезность и предельная полезность есть не что иное, как свойства потребительной стоимости (см. Товар). Между тем потребительные стоимости невозможно соизмерить непосредственно. Соизмерению они подвергаются в той мере, в какой они являются носителями стоимости, т. е. определённого количества абстрактного труда, выраженного в единицах общественно необходимого рабочего времени. В марксистской лит-ре даётся также критика модификаций

П. п. т. (метода кривых безразличия, теории выявленных предпочтений).

Лит.: Hilferding R., Böhm Bawerks Marx-Kritik, "Marx - Studien", Bd 1, W., 1904; Блюмин И. Г., Критика буржуазной политической экономии, т. 1, М., 1962; Козлова К., Энтов Р., Теории цены, М., 1972.

Ю. Б. Кочеврин.

ПРЕДЕЛЬНОЙ ПРОИЗВОДИТЕЛЬНОСТИ ТЕОРИЯ, см. в ст. Производительности теории.

ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ теории вероятностей, общее назв. ряда теорем вероятностей теории, указывающих условия возникновения тех или иных закономерностей в результате действия большого числа случайных факторов. Исторически первые П. т.- теорема Бернулли (1713) и теорема Лапласа (1812) - относятся к распределению отклонений частоты появления нек-рого события Е при п независимых испытаниях от его вероятности р(0<р<1). Частотой называется отношение т/га, где т - число наступлений события Е при п испытаниях (точные формулировки см. в ст. Бернулли теорема и Лапласа теорема). С. Пуассон (1837) распространил эти теоремы на случай, когда вероятность рц наступления Е в k-м испытании может зависеть от k, описав предельное поведение при n-> бесконечности распределения отклонений частоты т/п от среднего арифметического р вероятностей p_k(1<=k<=n):

(см. Больших чисел закон). Если обозначить через x_k, случайную величину, принимающую значение, равное единице при появлении события Е в k-миспытании, и значение, равное нулю при его непоявлении, то т можно представить в виде суммы

т = X₁ + Х₂ + . . . + Х_n,

что позволяет рассматривать перечисленные теоремы как частные случаи общих П. т., относящихся к суммам независимых случайных величин (закона больших чисел и центральной предельной теоремы).

Закон больших чисел. Пусть X₁,X₂, ... , Х_п, ... (*) - к.-л. последовательность независимых случайных величин, s_n - сумма первых га из них
s_n = X, + Х₂ + . . . + Х_п, А_n и В²_n - соответственно математическое ожидание

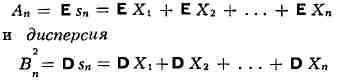
суммы s_n. Говорят, что последовательность (*) подчиняется закону больших чисел, если при любом е>0 вероятность неравенства
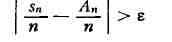стремится к нулю при n-> бесконечности.

Широкие условия приложимости закона больших чисел найдены впервые П. Л. Чебышевым (в 1867) (см. Больших чисел закон). Эти условия затем были обобщены А. А. Марковым (старшим). Вопрос о необходимых и достаточных условиях приложимости закона больших чисел был окончательно решён А. Н. Колмогоровым (1928). В случае, когда ве-

личины х_n имеют одну и ту же функцию распределения, эти условия, как показал А. Я. Хинчин (1929), сводятся к одному: величины X" должны иметь конечные математич. ожидания.

Центральная предельная теорема. Говорят, что к последовательности (*) применима центральная предельная теорема, если при любых Z₁ и Z₂ вероятность неравенства

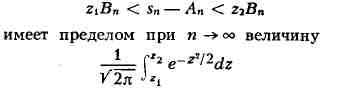
(см. Нормальное распределение). Довольно общие достаточные условия применимости центральной предельной теоремы были указаны Чебышевым (1887), но и в его доказательстве обнаружились пробелы, восполненные лишь позже Марковым (1898). Решение вопроса, близкое к окончательному, было получено А. М. Ляпуновым (1901). Точная формулировка теоремы Ляпунова такова: пусть

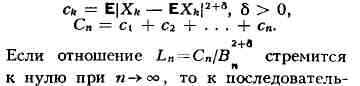
ности (*) применима центральная предельная теорема. Окончат. решение вопроса об условиях приложимости центральной предельной теоремы получено в основных чертах С. Н. Бернштейном (1926) и дополнено В. Феллером (1935). Из др. направлений работ в области П. т. можно отметить следующие.

1) Начатые Марковым и продолженные Бернштейном и др. исследования условий приложимости закона больших чисел и центральной предельной теоремы к суммам зависимых величин.

2) Даже в случае последовательности одинаково распределённых случайных величин можно указать простые примеры, когда суммы имеют в пределе распределение, отличное от нормального (речь идёт о невырожденных распределениях, т. е. о распределениях, не сосредоточенных целиком в одной точке). В работах сов. математиков А. Я. Хинчина, Б. В. Гне-денко, франц. математиков П. Леви, В. Дёблина и др. полностью изучены как класс возможных предельных распределений для сумм независимых случайных величин, так и условия сходимости распределений сумм к тому или иному предельному распределению.

3) Значит. внимание уделяется т. н. локальным П. т. Пусть, напр., величины х_п принимают лишь целые значения. Тогда суммы s_n принимают также только целые значения и естественно поставить вопрос о предельном поведении вероятностей Р_n(т) того, что s_n=m (где т - целое). Простейшим примером локальной П. т. может служить локальная теорема Лапласа (см. Лапласа теорема)

4) П. т. в их классич. постановке описывают поведение отд. суммы s_n с возрастанием номера n. Достаточно общие П. т. для вероятностей событий, зависящих сразу от неск. сумм, получены впервые Колмогоровым (1931). Так, напр., из его результатов следует, что при весьма широких условиях вероятность неравенства

имеет пределом величину

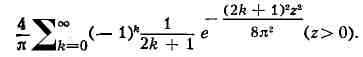
5) Перечисленные выше П. т. относятся к суммам случайных величин. Примером П. т. иного рода могут служить П. т. для членов вариационного ряда. Эти П. т. подробно изучены сов. математиками Б. В. Гнеденко и Н. В. Смирновым.

6) Наконец, к П. т. относят также и теоремы, устанавливающие свойства последовательностей случайных величин, имеющие место с вероятностью, равной единице (см., напр., Повторного логарифма закон).

Лит.: Гнеденко Б. В., Колмогоров А. Н., Предельные распределения для сумм независимых случайных величин, М. - Л., 1949; Ибрагимов И. А., Линник Ю. В., Независимые и стационарно связанные величины, М., 1965; Прохоров Ю. В., Розанов Ю. А., Теория вероятностей. Основные понятия. Предельные теоремы. Случайные процессы, 2 изд., М., 1973.

Ю. В. Прохоров.

ПРЕДЕЛЬНЫЕ УГЛЕВОДОРОДЫ, то же, что насыщенные углеводороды.

ПРЕДЕЛЬНЫЙ ЦИКЛ системы дифференциальных уравнений 2-го порядка

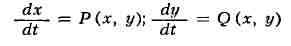
- замкнутая траектория в фазовом пространстве хОу, обладающая тем свойством, что все траектории, начинающиеся в достаточно узкой кольцеобразной её окрестности, неограниченно приближаются к этой траектории или при t -> + бесконечность (устойчивый П. ц.), или при t -> - бесконечности (неустойчивый П. ц.), или часть из них при t->+бесконечности, а остальные - при t-> -бесконечности (полуустойчивый П. ц.). Напр., система

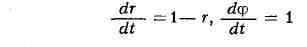
(r и ф - полярные координаты), общее решение к-рой r = 1-(1-r₀)е^-t, ф=ф_о + t (где r₀=>0), имеет устойчивый П. ц. r = 1 (см. рис.). Понятие П. ц. переносится также на систему n-го порядка. С механич. точки зрения устойчивый П. ц. соответствует устойчивому перио-дич. режиму системы. Поэтому разыскание П. ц. имеет важное значение в теории нелинейных колебаний.

Лит.: Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 3 изд., М., 1970; Андронов А. А., Витт А. А., Xаикин С. Э., Теория колебаний, 2 изд., М., 1959.

ПРЕДИВИНСК, посёлок гор. типа в Болыпемуртинском р-не Красноярского края РСФСР. Расположен на правом берегу Енисея, в 183 км ниже Красноярска. Леспромхоз.

ПРЕДИКАТ (от позднелат. praedicatum-сказанное), то же, что свойство; в узком смысле - свойство отд. предмета, напр, "быть человеком", в широком смысле -свойство дары, тройки, вообще и-ки предметов, напр., "быть родственником". П. в широком смысле наз. также отношениями.

Исторически понятие о П. явилось следствием логич. анализа высказываний естеств. языка, т. е. выяснения их логич. структуры, выяснения того, какой логикой может быть выражен (формализован) смысл этих высказываний. Идея выделения логич. структуры речи, в отличие от грамматической, для нужд логич. дедукции принадлежит Аристотелю. В аристотелевской и в последующей "традиционной" логике П. понимался в узком смысле как один из двух терминов суждения, а именно тот, в к-ром нечто говорится о предмете речи - субъекте. Форма сказывания - предикативная связь - сводилась при этом к атрибутивной связи, т. е. выражала "присущность" предмету нек-рого признака. Аристотель выделял 4 типа признаков, способных играть роль П.: родовые, видовые, собственные и случайные. Это т. н. предикабилии - типы сказуемых.

Логич. анализ фраз естеств. языка на том уровне представлений о логич. дедукции, к-рый был характерен для аристотелевской (и традиционной) логики, ограничивался, т. о., для выражения смысла высказываний логикой одноместных П. (логикой свойств в узком смысле). Это существенно ослабляло "выразительные возможности" логики и служило препятствием для адекватной формализации тех объективных связей между предметами, к-рые, будучи мыслимыми в виде отношений (свойств в широком смысле) между соответствующими понятиями, лежат в основе логич. правильности умозаключений об отношениях - осн. умозаключений в науке. Устранение указанного препятствия и усиление выразительных средств формализма совр. логики связано, в частности, с восходящей к работе Г. Фреге "Исчисление понятий" (1879) новой трактовкой П. Главная идея этой трактовки - рассмотрение отношения предикации как частного случая функциональной зависимости. Это обеспечивает более ёмкое, чем аристотелевское, отображение смысловой структуры фраз естеств. языка в формализме субъектно-предикатного типа и одновременно дальнейшее развитие самого этого формализма на пути сближения языков логики и математики.

Основой для "функциональной" точки зрения на П. служат в естественных и в искусственных (точных) языках выражения вида повествовательных предложений, содержащие неопределённые термины - неопределённые имена предметов: переменные (параметры) в записи утверждений в математич. языке, напр. х+2 = 4; слова "нечто", "некто", "кто-либо" и пр., играющие в естественном языке роль переменных в выражениях типа: "Некто человек", "Кто-то любит кого-то", "Если кто-либо человек, то он смертен" и т. п. Записав эти выражения нек-рым единым способом, напр. заменяя неопределённые термины пробелами, аналогично тому, как это делается в опросных бланках, "- + 2 = 4", "-человек", "- любит -", "Если - человек, то - смертен", или же принимая запись с помощью переменных в качестве основной, "х+2 = 4", "х человек", "х любит у", "Если х человек, то х смертен", легко заметить нечто общее между ними. Во-первых, наличие неопределённых терминов делает эти и подобные им выражения, вообще говоря, неопределёнными как в смысле того, что в них утверждается, так и в смысле их истинностного значения; во-вторых, всякое подходящее указание на область значений неопределённых терминов и одновременная квантификация или замена неопределённых терминов их значениями преобразует соответствующие выражения в осмысленные высказывания. В совр. логике выражения, имеющие вид повествовательных предложений и содержащие неопределённые термины, получили общее назв. пропозициональных функций, или, сохраняя традиц. термин, П. Как и числовые функции, П. являются соответствиями. Неопределённые термины играют в них обычную роль аргументов функции, но, в отличие от числовых функций, значениями П. служат высказывания. В общем случае, отвлекаясь от к.-л. определённого языка и сохраняя только функциональную форму записи, П. от п переменных (от п неопредел, терминов) выражают формулой P(x₁, . . ., х_п), где п>=0. При n = 0 П. совпадает с высказыванием, при n=1 П. будет свойством в узком смысле (1-местным П.), при п = 2 - свойством "пары" (2-местным П., или бинарным отношением), при и = 3 - свойством "тройки" (3-местным П., или тернарным отношением) и т. д. Выражения: "x + 2 = 4", "х человек", "х любит у", "х сын у и z" служат соответственно примерами 1-местного, 2-местного и 3-местного П. Они преобразуются в высказывания либо при надлежащей подстановке, напр. "2 + 2 = 4", "Сократ - человек", "Ксантиппа любит Сократа", "Софрониск - сын Ксантиппы и Сократа", либо при связывании переменных кванторными словами, напр. "СУЩЕСТВУЕТ х(х + 2 = 4)" (существует число, к-рое в сумме с 2 даёт 4), "СУЩЕСТВУЕТ х (х - человек)" (существуют люди), "Vх СУЩЕСТВУЕТ у СУЩЕСТВУЕТ z(х сын у и z)" (каждый является сыном по крайней мере двух родителей) и т. п., имея в виду, что области значений переменных в первом случае -числа, во втором - живые существа, в третьем - люди. (Подробнее о квантификации см. Квантор.)

Членение предложения на субъект и П., характерное для традиционной логики, вообще говоря, не совпадало с грамматич. членением предложения на подлежащее и сказуемое: для приведения выражений обычной речи к виду силлогистич. аргументов требовалось определённое преобразование этих выражений, изменяющее, как правило, форму сказываемости. Трактовка П. как пропозициональных функций, связанная с отождествлением синтаксич. роли подлежащих и дополнений на основе их принадлежности к общему семантич. типу объектов из области определения (значений аргументов) пропозициональной функции, явилась дальнейшим отходом в логике от собственно лингвистич. точки зрения на П. Тем не менее, в рамках, напр., прикладной логики П. естественно рассматривать и как лингвистич. понятие, точнее как лингвистич. конструкцию, несущую "неполное сообщение", к-рая в чистой логике описывается понятием пропозициональной функции.

В современной теоретико-множественной ("классической") логике принято более абстрактное, чем приведённое выше, истолкование П., основанное на отождествлении высказываний и их истинностных значений, что в рамках этой логики допустимо, хотя и не обязательно. П. можно тогда понимать только как логич. функцию, заданную теоретико-множественно, т. е. 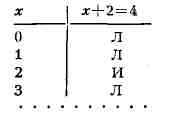как отображение Dⁿв {И, Л}, где п - число аргументов функции, D - область их значений, Dⁿ-n-кратное прямое произведение этой области, а {И, Л} -множество истинностных значений функции. К примеру, если значения переменной х выражения x+ 2 = 4 определены в множестве натуральных чисел, то соответствующая функция задана таблицей:

Выбор той или иной трактовки понятия П. не произволен, в частности он определяется методологич. позицией - конструктивистской, интуиционистской или классической. Но при этом речь идёт по существу не о претензии той или иной трактовки на единственно правильное описание некой "единой сущности", именуемой П., а о соглашении употреблять термин - "П." в том или ином подходящем к данному случаю его значении. Об исчислении П. см. Логика предикатов.

Лит.: Марков А. А., О логике конструктивной математики, М., 1972; Новиков П. С., Элементы математической логики, 2 изд., М., 1973; Клини С. К., Математическая логика, пер. с англ., М., 1973.

М. М. Новосёлов.

ПРЕДИКАТ, 1) логическое сказуемое. 2) Грамматическое сказуемое.

ПРЕДИКАТИВНОСТЬ, синтаксич. категория, формирующая предложение; относит содержание предложения к действительности и тем самым делает его единицей сообщения (высказывания). П. представляет собой единство двух синтаксич. категорий - времени грамматического и наклонения. В П. иногда включают категорию лица, однако она выражает собственно синтаксич. отношения между словами и принадлежит иному уровню организации предложения. В двусоставных предложениях носитель П.-сказуемое, в односоставных - их гл. член. П. отличается от т. н. субъективной модальности, на базе к-рой складываются оценочные значения, заключающие отношение говорящего к сообщаемому. К П. не относятся негация (отрицание) и целевая установка говорящего на передачу или поиски информации (повествовательность - вопросительность).

ПРЕДКАВКАЗЬЕ, территория, расположенная к северу от Большого Кавказа и ограниченная с севера Кумо-Манычской впадиной, с запада Азовским м. и Керченским прол., с востока Каспийским м. Протяжённость с З.-С.-З. на В.-Ю.-В. более 900 км, шир. до 300 км. Большая часть П. относится к эпигерцинской (Скифской) платформе, в низовьях Кубани и Терека - впадины, относящиеся к краевому прогибу Альпийской геосинклинальной области. В Западном П. выделяются Кубано-Приазовская низм., Прикубанская наклонная равнина (южнее ниж. Кубани), дельта Кубани и примыкающий к ней Таманский п-ов. В Среднем Предкавказье - возвышенности: Ставропольская (до 831 м), Терско-Сунженская (Сунженский хр. до 926 м), между ними - поднимающиеся среди равнины куполовидные горы-лакколиты Минераловодской группы (г. Бештау - 1402 м, Машук - 992 м, Железная - 851 м и др.). В Восточном П.- Терско-Кумская низменность.

Зап. и Среднее П. - важный земледельческий р-н, в Вост. П.- полупустынные пастбища. Во многих р-нах П. известны нефт. (Русский Хутор, Малгобек-Вознесенское и др.) и газовые (Северо-Ставропольское, Майкопское, Ленинградское и др.) месторождения.

Н. А. Гвоздецкий.

ПРЕДКАМЕРА, форкамера, аванкамера, полость в головке цилиндра двигателя внутреннего сгорания, соединённая с надпоршневым пространством (камерой сгорания) одним или неск. каналами. П., в к-рую поступает и где частично сгорает топливо, предназначается для организации в камере сгорания газовых потоков, улучшающих смесеобразование. Объём П. составляет обычно 25-30% объёма осн. камеры сгорания. См. также Предкамерный двигатель.

ПРЕДКАМЕРНЫЙ ДВИГАТЕЛЬ, двигатель внутр. сгорания, в к-ром смесеобразование улучшается с помощью предкамеры. В П. д. топливо (или рабочая смесь) подаётся сначала в предкамеру, где частично сгорает. При воспламенении паров топлива давление в предкамере повышается, в результате чего смесь нагретого топлива и продуктов сгорания поступает в надпоршневое пространство (камеру сгорания). Сгорание топлива по мере его выбрасывания из предкамеры в камеру сгорания обеспечивает равномерное нарастание давления в цилиндре, благодаря предкамере двигатель работает более мягко.

П. д. дизеля устойчиво работают без дымления в широком диапазоне частот вращения вала, давление впрыска у них меньше, чем у др. типов дизелей. Одно из важных достоинств таких П. д. - нетребовательность к сорту применяемого топлива; к недостаткам П. д. следует отнести затруднённый пуск, т. к. для самовоспламенения топлива требуется хороший прогрев предкамеры. Для облегчения пуска П. д. используют электрич. свечи накаливания, служащие для подогрева воздуха в предкамере.

У бензиновых П. д. на 6-8% (по массе) ниже расход топлива, кол-во токсичных компонентов в отработавших газах меньше, однако хуже стабильность и надёжность работы на нек-рых режимах.

ПРЕДКОВ КУЛЬТ, см. Культ предков.

ПРЕДКРЫЛОК, добавочная несущая поверхность (крылышко), расположенная в носовой части крыла самолёта; увеличивает подъёмную силу крыла, что улучшает устойчивость и уменьшает посадочную скорость самолёта. Может быть неподвижным и подвижным (убирающимся). Выпуск и убирание П. производятся автоматически (при изменении угла атаки крыла) или по команде из кабины пилота с помощью гидро-, пневмо-и электроприводов. Улучшение указанных свойств может быть достигнуто также отклоняемым носком крыла. См. также Механизация крыла.

ПРЕДЛИСТ, профилл, мелкие редуцированные листья близ основания боковых ветвей. У двудольных растений два П., у однодольных - один, обычно двукилеватый, что указывает на его образование путём срастания двух П. (признак, свидетельствующий о вторичности однодольных). В области соцветия и боковых цветков П. наз. прицветнич-ками.

ПРЕДЛОГ, разряд служебных слов (или служебная часть речи), употребляемых во мн. языках (напр., индоевропейских, семитских) для выражения различных отношений между зависимыми и гл. членами словосочетания (зависимый член - обычно существительное или местоимение). П. всегда предшествуют зависимому члену. Выступая только в роли показателя синтаксич. связи между членами предложения, П. членами предложения не являются. П. делятся на первообразные (простые по составу, отличаются многозначностью выражаемых с их помощью отношений - рус. "без", "над", "в", "к", "о" и др.) и производные (связаны по строению и происхождению с полнозначными словами: наречные - "вблизи", "навстречу", "сбоку"; отымённые - "в области", "в целях"; отглагольные - "благодаря", "включая").

ПРЕДЛОЖЕНИЕ, одна из основных категорий синтаксиса, противопоставленная слову и словосочетанию по формам, значению и функциям. В широком смысле - это любое (от развёрнутого синтаксич. построения - в письм. тексте от точки до точки - до отд. слова или словоформы) высказывание (фраза), являющееся сообщением о чём-либо и рассчитанное на слуховое (в произнесении) или зрительное (на письме) восприятие. В узком, собственно грамматич., смысле П. - это имеющая в своей основе спец. абстрактный образец (модель) особая синтаксич. конструкция, организованная по законам данного языка и специально предназначенная для того, чтобы быть сообщением. В зависимости от цели сообщения П. могут быть повествовательными, вопросительными или побудительными (возможны и другие, более частные классификации).

П. может быть простым или сложным. Простое П. как элементарная синтаксич. конструкция (т. н. нераспространённое) состоит из двух (реже - более) форм слов (конституирующих компонентов), объединённых друг с другом специфическим, существующим только в П. синтаксич. отношением (т. н. предикативным), либо из одной формы слова (напр., "Ученик пишет"; "Воды прибывает"; "Простить значит забыть"; "Ночь"; "Светает"). П. могут быть распространены (т.н. распространённые предложения) по правилам присловных связей - согласования, управления, примыкания, либо словоформами, распространяющими П. в целом (напр., "Для неё простить значит забыть"; "На Камчатке сейчас уже ночь"), либо причастными, деепричастными и др. оборотами и спец. распространяющими формами слов, союзными сочетаниями и др.

Элементарный отвлечённый образец, по к-рому строится нераспространённое П., может быть представлен символически, напр. формула N1-Vf передаёт конструкцию нераспространённого П. типа "Ученик пишет" (N1: лат. nomen - имя, 1 - именит. падеж; Vf - verbum finitum - спрягаемая форма глагола). Такая абстрагированная конструкция наз. отвлечённым образцом П. или его моделью, формулой, структурной схемой. Эти схемы классифицируются по разным основаниям (односоставные - двусоставные, свободные и ограниченные со стороны лексико-семантич. состава, имеющие или не имеющие парадигматич. свойства и др.). Каждый язык имеет свою систему структурных схем. Отд. схемы в разных языках могут совпадать, но системы в целом всегда различаются. Для индоевроп. языков характерны т. н. двусоставные структурные схемы, содержащие сказуемое, т. е. глагол в личной форме (или форму др. слова в той же позиции), и подлежащее, т. е. форму именит. падежа имени (или инфинитив в той же позиции). Сказуемое как компонент схемы всегда обозначает осуществляющийся во времени признак (действие, состояние, свойство, качество), а подлежащее-субъект, т. е. носителя или производителя этого признака (при распространении П. значение субъекта может перемещаться и сосредоточиваться в распространяющейся словоформе). Индоевроп. языкам принадлежат и многие другие модели, в т. ч. односоставные (состоящие или из одного компонента, или двукомпонентные, но не членящиеся на подлежащее и сказуемое). Структурные схемы лежат в основе построенных по их образцу конкретных предложений, напр. П. "Ученик пишет", "Наступила ночь", "Теплится надежда" построены по схеме N1- Vf; "Сын - рабочий", "Москва - столица", "Ель - дерево" - по схеме N1 - N1 и т. д. Структурная схема лишена интонации. Но каждое П., построенное по той или иной схеме, и все его формы и модификации (синтаксич. изменения) обязательно имеют определённую интонацию (интонац. контур). П. совмещает в одной грамматич. форме неск. значений разной степени абстракции. Во-первых, сама структурная схема П. имеет отвлечённое значение, общее для всех структурных схем, т. н. предикативность. Значение предикативности, заложенное в схеме, переносится в конкретное П. и модифицируется в парадигме П., т. е. в разных его формах, выражающих значения реальности и ирреальности. Однако в конкретных П. на значение предикативности накладывается новое, иного качества значение, идущее от позиций, т. е. от компонентов схемы и от их отношений, а также от лексич. семантики слов, заполнивших эти позиции (напр., "Ученик пишет" - субъект - его активное действие; "Гром гремит" - субъект - его наличие, существование; "Светает" - наличие бессубъектного состояния и т. д.). Такие значения относятся к семантич. структуре П. Предложения, имеющие разную грамматич. организацию, но одинаковую семантич. структуру, в нек-рых исследованиях рассматриваются как трансформы, т. е. преобразования одного в другое, напр. "Наступает вечер" - "Вечереет"; "Гремит гром" - "Гром"; "Сын учится" -"Сын - учащийся" и т. п.

Третий вид значения предложения - распределение функциональной нагрузки его членов - выражается актуальным членением предложения.

Сложное П.- объединение двух (или более) простых П. средствами союзов, союзных слов или союзных частиц (в сочетании с определённой интонацией, а часто также и при поддержке лексики) в некое новое синтаксич. образование, части к-рого вступают друг с другом в определённые синтаксич. отношения. При этом одна из частей может претерпевать существенные структурные изменения либо вообще иметь такую формальную организацию, к-рая простому П. не свойственна. В зависимости от того, какие средства связывают части сложного П., эти П. делятся на сложносочинённые (с взаимно независимыми частями) и сложноподчинённые (с "главной" и "придаточной" частью); однако внутр. отношения частей и в том, и в др. случае часто оказываются не совпадающими с формальной организацией сложного П., и семантич. типы сложносочинённых и сложноподчинённых П. перекрещиваются.

И в рус., и в зап.-европ. лингвистике П. и его компоненты долгое время изучались как категории, совпадающие с логич. суждением и его частями (нем. учёный К. Беккер, рус. учёные Н. И. Греч, Ф. И. Буслаев) либо с психологич. актом коммуникации (Ф. Ф. Фортунатов, А. А. Шахматов). В изучении П. как собственно языковой, синтаксич. категории, имеющей свои формальные и смысловые (содержательные) характеристики, сложилось неск. направлений, связанных: 1) с учением о П. как о сложной неодноуровневой структуре, одновременно репрезентирующей собою неск. ступеней языковой абстракции (чеш. учёные В. Матезиус, М. Докулил, Ф. Данеш); 2) с теорией порождающей грамматики и трансформац. синтаксиса [амер. учёные Н. Хомский, 3. Харрис, Д. Ворт, нем. (ГДР) учёный Р. Ружичка]; 3) с разными учениями о П. как о синтагматич. цепи связей и отношений, об "аранжировке слов" (нем. учёный И. Рис; амер. учёный Л. Блумфилд; голл. учёный А. де Гроот; франц. учёный Л. Теньер; сов. учёный А. М. Мухин); 4) с анализом П. прежде всего как единицы значения (дат. учёный О. Есперсен; сов. учёный Л. В. Щерба), в 60-70-е гг. - в аспекте теории "глубинных и поверхностных структур" и "препозитивной номинации" (англ. учёный А. Гардинер; нем. учёный У. Вайнрайх; сов. учёные В. Г. Гак, Н. Д. Арутюнова). Активно исследуются парадигматич. связи и отношения П., организующие их в определённые системы (Д. Ворт, чеш. учёные П. Адамец, В. Грабе; сов. учёные Н. Ю. Шведова, Т. П. Ломтев).

Лит.: Виноградов В. В., Основные вопросы синтаксиса предложения, в сб.: Вопросы грамматического строя, М., 1955; Пешковский А. М., Интонация и грамматика, в его кн.: Избранные труды, М., 1959; Курилович Е., Основные структуры языка: словосочетание и предложение, в его кн.: Очерки по лингвистике, М., 1962; Мельничук А. С., Аспекты общей теории предложения как единицы речи, в кн.: Проблемы языкознания, М., 1967; Мухин А. М., Структура предложений и их модели, М., 1968; Грамматика современного русского литературного языка, М., 1970; Общее языкознание, ч. 2 - Внутренняя структура языка, М., 1972; Шведова Н. Ю., О соотношении грамматической и семантической структуры предложения, в кн.: Славянское языкознание, М., 1973; Ries I., Was ist ein Satz?, в сб.: Beiträge zur Grundlegung der Syntax, H. 3, Prag, 1931; Danes F., A three-level approach to syntax, "Travaux linguistiques de Prague", 1966, v. 1.

Н. Ю. Шведова.

ПРЕДЛОЖЕНИЕ в логике, см. в ст. Высказывание.

ПРЕДЛОЖЕНИЕ в музыке, составная часть периода, отграниченная каденцией. Самостоят. значение приобретает в незамкнутой гл. партии сонатной формы; порою выполняет функции периода. См. Музыкальная форма.

ПРЕДМЕТ ТРУДА, см. в ст. Средства производства.

ПРЕДМЕТ УЧЕБНЫЙ, дисциплина учебная, дидактически обоснованная система знаний, умений и навыков, отобранных из соответствующей отрасли науки, техники, искусства, производств, деятельности и др. для изучения в уч. заведении. Содержание П. у. определяется учебной программой, перечень (состав) П. у. для различных типов общеобразоват. школы, специальностей (специализаций) в спец. уч. заведениях, взаимосвязи и последовательность изучения П. у. - учебным планом. Различают П. у. общеобразовательные или общенаучные (основы наук - во всех типах ср. школы; обществ, науки, иностр. языки, высшая математика, физика и т. п. - в высшей школе) и специальные, определяющие профиль подготовки специалиста. К общенаучным П. у. относят также общетехнич. дисциплины, изучаемые в технич. уч. заведениях,- детали машин, сопротивление материалов, гидравлика и др. См. также Средняя общеобразовательная школа, Профессионально-техническое образование, Среднее специальное образование, Высшее образование и статьи об отдельных отраслях спец. образования, напр. Биологическое образование, Металлургическое образование.

М. М. Михайлов.

ПРЕДМЕТИЗАЦИЯ произведений печати, метод многоаспектной аналитико-синтетич. обработки произведений печати по содержанию, заключающийся в отборе и обозначении (как правило, в условной словесной форме) предметов, их свойств и отношений. Под предметом понимается любой объект мысли, описываемый или упоминаемый в тексте, к-рый может быть интересен читателю (потребителю). В качестве предметизируемого объекта чаще всего выступает издание в целом (книга, брошюра, журнал и т. п.) или его части (главы, параграфы, страницы, статьи и т. д.).

Объектами П. могут быть не только произведения печати, но и любые другие носители информации, а также информац. запросы. При анализе текста и формулировке предметных рубрик принимаются во внимание конкретные условия использования метода П. и особенности предметизируемого документа (напр., при П. книги в целом для каталога учитываются не только её содержание, но также форма и назначение - читательское и целевое).

Практич. приёмы и правила применения метода П. составляют содержание как общей методики П. (разрабатываемой для всех видов документов независимо от их тематики), так и частных методик, определяемых спецификой объекта П. и конкретными информационно-поисковыми задачами (напр., П. мед. лит-ры, П. авторефератов диссертаций и т. п.).

Метод П. широко используется при составлении предметных каталогов, вспо-могат. предметных указателей, предметных указателей литературы и других информационно-поисковых систем. Общность языков предметных рубрик и дескрипторных языков, установленная в информатике, позволяет рассматривать П. как вид индексирования.

Лит.: Кругликова В. П., Предметизация произведений печати, М., 1967; Михайлов А. И., Чёрный А. И., Гиляревский Р. С., Основы информатики, 2 изд., М., 1968.

Э. Л. Призмент.

ПРЕДМЕТНАЯ ОБЛАСТЬ, область объектов, универсум рассуждения, универсум рассмотрения, или просто универсум, класс (множество) объектов, рассматриваемых в пределах данного контекста. Под контекстом здесь может пониматься отд. рассуждение или выражающая его фраза, или совокупность фраз, фрагмент науч. теории или теория в целом. Напр., в теории чисел П. о. служит натуральный ряд (множество целых неотрицат. чисел), в математич. анализе -множество действит. чисел, в ботанике - множество всех растений (точнее, растит. видов), а в исчислении предикатов или логике классов - любая фиксированная непустая область. П. о., наз. также универсальным множеством, противопоставляется в логике и теории множеств т. н. пустому множеству (классу, области), не содержащему ни одного предмета рассматриваемого вида и являющемуся её дополнением. Общепринятое представление о П. о. именно как о фиксированной области объекта (согласно к-рому, напр., в теории чисел дополнением к множеству чётных чисел служит множество нечётных чисел, а вовсе не "множество всех мыслимых объектов, не являющихся чётными числами", в каковое должен был бы входить, напр., и данный экземпляр энциклопедии, и вообще "всё на свете", кроме чётных чисел) идёт от Дж. Венна; оно сменило господствовавшую до того (исходившую от Г. Фреге) концепцию "универсальной" П. о., приводящую к парадоксам.

Лит. см. при ст. Логика предикатов. Аксиоматическая теория множеств.

ПРЕДМЕТНО-КУРСОВАЯ СИСТЕМА ОБУЧЕНИЯ, предусматривает возможность сдачи студентами (уч-ся) в течение уч. года зачётов и экзаменов по предметам данного и следующих курсов (при соблюдении последовательности изучения дисциплин, основанной на их преемственности и взаимосвязи). Принята в СССР в высшем заочном образовании, при этом по возможности сохраняются принципы курсовой системы обучения, к-рая применяется на дневных и вечерних ф-тах (отделениях) вузов. В нек-рых уч. заведениях ряда зарубежных стран организация уч. процесса носит характер П.-к. с. о.

ПРЕДМЕТНЫЙ КАТАЛОГ, см. в ст. Каталог библиотечный.

ПРЕДМЕТЫ ПОТРЕБЛЕНИЯ, продукты труда для непроизводственного, прежде всего личного, потребления. К П. п. относятся материальные блага, используемые населением для удовлетворения своих потребностей. По назначению среди П. п. выделяют: продукты питания; одежду и обувь; жилища; топливо, осветительные материалы, воду, газ и электроэнергию, применяемые для бытовых нужд; мебель, хозяйственные вещи; книги, журналы; предметы культурно-бытового назначения длит. пользования; предметы для спорта, гигиены, медикаменты. П. п. являются все материальные блага, к-рые потребляются в учреждениях сферы обслуживания, включая здания и сооружения этой сферы, а также в отраслях, удовлетворяющих общественные потребности (управление, наука, оборона).

Мн. продукты труда могут служить как для непроизводственного, так и для производительного потребления. Так, мука, используемая для выпечки хлеба на хлебозаводе, сахар, идущий на приготовление кондитерских изделий, фрукты, из к-рых изготовляют консервы, и т. п. выступают в этих случаях как средства произ-ва.

Специфич. предметы потребления - услуги.

В. Ф. Майер.

ПРЕДМОСТНОЕ УКРЕПЛЕНИЕ, предмостная позиция, тет де-пон, оборонительная позиция, создаваемая с целью прикрытия (обороны) мостовой переправы. Передний край обороны обычно выбирается на удалении, исключающем ведение по переправе арт. огня противника; фланги позиции упираются в реку. На водной преграде подготавливаются верховая и низовая брандвахты, предохраняющие переправу от разрушения плавучими минами и брандерами.

ПРЕДНИЗОЛОН, синтетич. лекарств, средство из группы гормональных препаратов, обладающее противовоспалит. и антиаллергич. действием. Применяют в таблетках, растворе для инъекций и мазях при ревматизме, артритах, нек-рых заболеваниях почек, бронхиальной астме и др.

ПРЕДОПРЕДЕЛЕНИЕ, религ. представление об исходящей от воли божества детерминированности этич. поведения человека и отсюда его "спасения" или "осуждения" в вечности. Особое значение приобретает в монотеистич. религиях, поскольку с точки зрения последоват. монотеизма всё существующее определяется в конечном счёте волей бога. При этом концепция П. вступает в противоречие с учением о свободе воли и ответственности человека за его вину, без к-рого оказывается невозможной религ. этика. Это обусловило возникновение споров о П. в иудаизме, исламе, христианстве. Сообщая о существовании в Иудее трёх направлений, историк Иосиф Флавий (1 в.) характеризует ессеев как сторонников доктрины о П., саддукеев - как сторонников учения о свободной воле, а фарисеям приписывает компромиссную позицию. В исламской теологии 8-9 вв. шла острая полемика между джабаритами, учившими об абсолютном П., и кадаритами, отстаивавшими свободу воли. В христианстве концепция П. была сформулирована Августином в борьбе с пелагианством: благодать не может быть заслужена и обусловлена лишь свободным произволом божества. Повышенный интерес к проблеме П. характерен для религ. индивидуализма Реформации - для М. Лютера и особенно для Ж. Кальвина, развившего учение об абсолютном П. - кальвинизм.

С. С. Аверинцев.

ПРЕДОХРАНИТЕЛЬНАЯ МУФТА, муфта, служащая для разъединения валов или вала с сидящей на нём деталью при недопустимом увеличении передаваемого момента (перегрузке) или скорости вращения, т. е. предохраняющая машину от поломки в случае нарушения нормального режима работы. Различают: П. м. предельного момента с разрушающимися элементами, обычно срезными штифтами, подлежащими замене после срабатывания П. м.; кулачковые, шариковые и др. муфты зацепления, к-рые удерживаются во включённом состоянии пружинами, пока возрастающий момент не создаёт силы, способной преодолеть усилие пружины; фрикционные, в к-рых давление между поверхностями трения создаётся пружинами, отрегулированными на передачу предельного момента. Функции предохранения машины от перегрузки выполняют часто др. муфты, напр., гидродинамические. П. м., ограничивающие скорость вращения, выполняют обычно центробежными.

ПРЕДОХРАНИТЕЛЬНЫЕ BЗРЫBЧАТЫЕ ВЕЩЕСТВА, антигризутные взрывчатые вещества, предназначены для проведения взрывных работ в подземных условиях, когда возможно образование взрывоопасных смесей природного газа или горючей пыли с воздухом. Содержат гл. обр. аммиачную селитру, тротил или нитроэфиры. Особые свойства П. в. в. обусловлены тем, что в их состав вводятся в значит. кол-вах (от 12 до 75% по массе) компоненты (хлориды калия, натрия, аммония), ингибирующие окисление метана и др. горючих веществ и понижающие темп-ру взрыва. Действие хлоридов усиливается при использовании их в тонкоизмельчённом виде или, в случае их образования в процессе взрыва, в результате ионного обмена между солями (напр., между хлоридом аммония и калиевой селитрой). Предохранит, свойства выше у селективно-детонирующих П. в. в., содержащих 10% нитроглицерина и 90% ионообменных солей (в шпурах с прочными стенками они детонируют с полным выделением энергии, в открытом заряде детонирует только нитроглицерин, благодаря чему выделяемая энергия и темп-ра продуктов взрыва очень малы и не опасны в отношении воспламенения газа).

В СССР в общей классификации взрывчатых веществ, включающей шесть классов, П. в. в. выделены в III - VI классы (к первым двум классам относятся не-предохранительные взрывчатые вещества, применяемые на открытых разработках и в шахтах, не опасных по скоплению газа и пыли). Скорость детонации П. в. в. III класса (аммониты АП-4ЖВ, АП-5ЖВ, ПЖВ-20 и победит ВП-4) составляет 3,6-4,6 км/ceк, удельная теплота взрыва ок. 200 Эж/г; к VI классу относится угленит № 7 со скоростью детонации 1,6-1,8 км/сек и удельной теплотой взрыва ок. 90 дж/г. Применение каждого класса П. в. в. строго регламентировано определёнными условиями подземных горных работ. См. также Взрывчатые вещестеа.

Лит.: Дубнов Л. В., Бахаревич Н. С., Романов А. И., Промышленные взрывчатые вещества, М., 1973.

Л. Г. Болховитинов.

ПРЕДОХРАНИТЕЛЬНЫЙ КЛАПАН, устройство, обеспечивающее безопасность оборудования, работающего при высоком давлении жидкости, газа или пара, в тех случаях, когда превышение давления сверх установленного рабочего может вызвать повреждение этого оборудования. П. к. устанавливают на паровых котлах, ресиверах для сжатого воздуха, различном технологич. оборудовании и трубопроводах, работающих под давлением. При повышении в системе давления сверх допустимого П. к. открывается и автоматически сбрасывает избыток рабочей среды, предотвращая аварию. По достижении допустимого давления П. к. автоматически закрывается. Область обязат. применения, установки и обслуживания П. к. в СССР определена спец. правилами (см. Котлонадзор). П. к. разделяются на грузовые и пружинные. В грузовых П. к. затвор нагружается грузом непосредственно (для низких давлений) или через рычажное устройство. В пружинных П. к. давлению среды на затвор противодействует сила пружины.

Г. Г. Мирзабеков.

ПРЕДПАРЛАМЕНТ [офиц. назв. со 2(15) окт. 1917 - Временный совет Российской республики], совещательный орган при бурж. Временном правительстве. Образован на заседании президиума Демократического совещания 20 сент. (3 окт.) 1917. Первонач. назв. - Всероссийский демократич. совет. Общее число членов определялось в 313 (из расчёта 15% от каждой фракции и группы Демократич. совещания). Образованное 25 сент. (8 окт.) новое коалиц. Врем. пр-во ограничило права и функции П. и изменило его состав; в П. включались также представители т. н. цензовых, т. е. бурж.-помещичьих, орг-ций и учреждений (партии кадетов, торгово-пром. объединений и др.). Число членов увеличилось до 555. По неполным данным, в него вошли 135 эсеров, 92 меньшевика, 30 нар. социалистов, 75 кадетов; большевики получили 58 мандатов. Разоблачая контрреволюц. сущность П., В. И. Ленин писал, что его единств. назначение - отвлечь рабочих и крестьян от растущей революции (см. Поли. собр. соч., 5 изд., т. 34, с. 260). 5(18) окт. ЦК РСДРП(б) принял решение о выходе большевиков из П. 7(20) окт. председателем П. был избран эсер Н. Д. Авксентьев. В тот же день, выступив с декларацией, в к-рой заявлялось, что большевики не имеют ничего общего с "правительством народной измены" и с "советом контрреволюционного попустительства", члены большевистской фракции покинули П.

24 окт. (6 нояб.) в П. с заявлением о "состоянии восстания" в Петрограде выступил А. Ф. Керенский. Стремясь расколоть революц. силы и предотвратить революцию, меньшевики и эсеры провели резолюцию (за - 123 голоса, против - 102, при 26 воздержавшихся), в к-рой наряду с требованием подавления восстания обращалось внимание пр-ва на необходимость немедленного издания декрета "о передаче земель в ведение земельных комитетов и решительного выступления во внеш. политике с предложением союзникам провозгласить условия мира и начать мирные переговоры". Днём 25 окт. (7 нояб.) революц. войска окружили Мариинский дворец, П. был распущен.

Лит.: Ленин В. И., Поли. собр. соч., 5 изд., т. 34, с. 257-63, 342-46, 347-50; Славин Н. Ф., Октябрьское вооруженное восстание и Предпарламент, в сб.: Ленин в Октябрьское вооруженное восстание в Петрограде, М., 1964.

ПРЕДПЛЕЧЬЕ у человека, анатомич. отдел верхней конечности, между плечом и кистью. Костная основа П. - лучевая и локтевая кости, соединяющиеся между собой верхним и нижним лучелоктевыми суставами, что делает возможным вращат. движения вокруг оси, проходящей вдоль локтевой кости. Кости П. служат местом прикрепления мышц, приводящих в движение плечо, кисть и пальцы. В межмышечных промежутках П. проходят глубокие сосуды и нервы - лучевая и локтевая артерии и вены, лучевой, локтевой и срединный нервы. В подкожной клетчатке П. расположены поверхностные нервы и вены. При травмах П., помимо повреждения мягких тканей, возможны закрытые или открытые переломы одной или обеих костей П. (чаще - нижнего суставного конца лучевой кости).

ПРЕДПЛЮСНА, анатомич. область стопы человека.

ПРЕДПОРОЖНЫЙ, посёлок гор. типа в Оймяконском р-не Якут. АССР. Расположен на прав, берегу Индигирки. Добыча золота.

ПРЕДПОСЕВНАЯ ОБРАБОТКА ПОЧВЫ, совокупность приёмов механич. воздействия на почву (боронование, культивация, перепашка и др.), выполняемых в определённой последовательности перед посевом сельскохозяйственных культур. Задача П. о. п. - максимально сохранить влагу в почве, очистить поле от сорняков, разрыхлить почву, заделать удобрения, создать влажный слой на глубине заделки семян.

П. о. п. под яровые культуры начинается ранней весной с боронования зяби (покровного боронования), цель к-рого выровнять и разрыхлить поверхность почвы, чтобы предотвратить капиллярное испарение влаги. Оно проводится выборочно по мере наступления физич. спелости почвы - сначала на лёгких по механич. составу почвах, на юж. склонах и повышенных местах. На хорошо вспаханных осенью почвах лёгкого механич. состава применяют лёгкие бороны и шлейфы, на глинистых заплывающих почвах - тяжёлые бороны. Для лучшего выравнивания и рыхления почвы боронование проводят поперёк вспашки или по диагонали, часто в неск. следов. Под рано высеваемые культуры (овёс, ячмень, пшеница и др.) после покровного боронования проводят культивацию зяби; одновременно почву выравнивают бороной или шлейфом. Под поздно высеваемые культуры (просо, кукуруза, гречиха и др.) вслед за покровным боронованием дополнительно проводят глубокую культивацию (на тяжёлых почвах на глуб. 10-12 см, на средних - на глуб. 8-10 см) с одновременным боронованием, что обеспечивает эффективное уничтожение многолетних сорняков. После этого участок культивируют на глубину заделки семян. В зоне избыточного и достаточного увлажнения почву весной иногда перепахивают.

Приёмы П. о. п., их последовательность в зависимости от природных и сложившихся погодных условий осени, зимы и весны могут видоизменяться. Напр., предпосевная культивация зяби под посев ранних культур необходима, когда весной зябь сильно уплотнена. Если почва рыхлая, а весна засушливая, то лучшие результаты даёт обработка почвы тяжёлыми боронами. При возделывании мелкосемянных культур в систему П. о. п. включают прикатывание почвы гладкими катками одновременно с предпосевной культивацией.

П. о. п. под озимые культуры проводится при паровой обработке почвы (см. Пар).

Лит.: Земледелие, под ред. С. А. Воробьева, 2 изд., М., 1972.

В. И. Румянцев.

ПРЕДПОСЕВНОЙ ПОЛИВ, полив поля перед посевом для увлажнения верх. слоя почвы в целях получения дружных всходов и лучшего развития растений в первый период вегетации.

ПРЕДПОЧКА, орган выделения у зародышей низших позвоночных; то же, что пронефрос.

ПРЕДПРИНИМАТЕЛЬСКИЙ ДОХОД, часть средней прибыли, остающаяся у пром. или торгового (функционирующего) капиталиста после уплаты процента за банковскую ссуду. П. д. возникает на основе движения ссудного капитала. Стремясь извлечь максимум прибыли, пром. капиталисты наряду с использованием собственных капиталов прибегают также к использованию заёмных средств. Получив капитал в ссуду, функционирующий капиталист покупает средства произ-ва и рабочую силу и путём эксплуатации наёмных рабочих извлекает прибавочную стоимость, к-рая выступает в форме прибыли. Эта прибыль распадается на П. д., присваиваемый функционирующим капиталистом-заёмщиком, и процент, присваиваемый ссудным капиталистом-кредитором. Деление прибыли на процент и П. д. маскирует капиталистич. эксплуатацию и искажает действит. природу этих частей прибавочной стоимости. Создаётся видимость, будто процент выступает как результат собственности на капитал, а не произ-ва, а П. д.- как результат деятельности функционирующего капиталиста по надзору и управлению пром. или торг. предприятием, а не присвоения неоплаченного труда рабочих. Выдавая видимость за сущность, буржуазные экономисты в апологетических целях изображают П. д. как разновидность "заработной платы" капиталиста.

Между функционирующими и ден. капиталистами идёт ожесточённая борьба за делёж прибыли. Первые заинтересованы в наиболее низком уровне процента, а вторые - в более высоком. В то же время обе группы капиталистов противостоят рабочему классу, ибо в эксплуатации его непосредственно заинтересованы те и другие. Это обусловливает коренную общность классовых интересов: и денежные и функционирующие капиталисты заинтересованы в увеличении прибавочной стоимости, т. е. в усилении эксплуатации наёмного труда. Т. о., П. д. выражает непосредственно отношения между функционирующими и ден. капиталистами, а в конечном счёте - осн. производств, отношение бурж. общества между трудом и капиталом.

ПРЕДПРИЯТИЕ СОЦИАЛИСТИЧЕСКОЕ, см. Социалистическое государственное производственное предприятие.

ПРЕДРАК, патологич. изменения, предшествующие возникновению злокачественной опухоли. Понятие о П. первоначально сформировалось по отношению к наиболее доступному для клинич. наблюдений кожному раку. Позже были описаны П. нижней губы, молочных желез, шейки матки, желудка и т. д. Исследования в области экспериментальной онкологии показали, что различные по клинич. проявлениям предраковые состояния представляют единый в своей основе патологич. процесс, к-рому присущи определённые закономерности. В советской онкологии принято различать 3 стадии П. Стадия неравномерной диффузной гиперплазии - ткань сохраняет своё нормальное строение, однако число её структурных элементов (клеток, волокон и др.) увеличивается. Стадия очаговых пролифератов - в общей массе размножающихся клеток появляются участки (очаги), в к-рых деление клеток происходит особенно интенсивно. Стадия относительно доброкачественной опухоли - очаги размножающихся клеток всё больше утрачивают сходство с исходной тканью, всё резче обособляются, но не проявляют тенденции к инвазивному росту, т. е. врастанию в здоровую ткань и её разрушению. Первая стадия ещё не является П. в строгом смысле слова, 2-я стадия -наиболее закономерный этап П., 3-я стадия не обязательна - рак может развиться, минуя её. П. может подвергнуться регрессии или надолго остановиться в своём развитии.  

Лит.: Ш а б а д Л. М., Предрак в экспериментально-морфологическом аспекте, М., 1967.

Таблица XVII

К ст. Потсдам. 1. Общий вид города. В центре - церковь Николайкирхе (1830-37, архитектор К. Ф. Шинкель; купол 1834-49, архитекторы Ф. Л. Персиус и Ф. А. Штюлер). 2. Ансамбль Сан-Суси. "Павильон с драконами". (1770). 3. Ансамбль Сан-Суси. Дворец Коммёнс (1765-69, архитекторы К. фон Гонтард и Ж. Леже). 4. Ратуша (ныне Дом культуры им. Ханса Мархвицы). 1753. Архитектор И. Боуман. 5. Бранденбургские ворота. 1770. 6. Ансамбль Сан-Суси. Новый дворец (1763-69, архитекторы И. Г. Бюринг, Г. Л. Мангер и К. фон Гонтард). 7. Ансамбль Сан-Суси. Новые палаты (1771-74). 8-10. Дворец Сан-Суси. 1745-47: 8. Западная часть колоннады. 9. Библиотека (декор И. А. Наля). 10. Музыкальный салон (декор И. М. Хоппенхаупта). 11. Дворец Цецилиенхоф. 1913-16. Зал, где проходили заседания.

Таблица XVIII

К ст. Почтовые марки. Советские марки. 1 - 5. Стандартные марки: 1. Выпуск 1922. 2. "Золотой стандарт", 1923. 3. Выпуск 1924-31. 4. Выпуск 1939. 5. Выпуск 1966. 6. Марка памяти В. И. Ленина, выпущенная 28 января 1924. 7-9, 15-22. Тематические марки. 10-14. Специализированные марки: 10. Доплатная марка, 1925. 11-12. Марки с надпечаткой нового номинала. 13-14. Почтово-благотворительные марки.

Таблица XIX

К ст. Почтовые марки. 1-3. Первые марки: 1. Английская марка "Чёрный пенни". 1840. 2. Французская марка. 1850. 3. Русская марка. 1858. 4. Русская марка с портретом Петра 1. 1913. 5. Первая марка Советской России. 1918. 6-25. Марки разных стран: 6. Болгария. 7. Монгольская Народная Республика. 8. Чехословацкая Социалистическая Республика. 9. ГДР. 10. Демократическая Республика Вьетнам. 11. Венгрия. 12. Румыния. 13. КНДР. 14. Индия. 15. Польша. 16. Куба. 17. Югославия. 18. США. 19. Италия. 20. Алжирская Народная Демократическая Республика. 21. Исландия. 22. Бельгия (только для корреспонденции, сдававшейся в почтовые вагоны). 23. Уругвай. 24. Канада. 25. Австрия (для посылки газет). 26. Марка ООН.

Таблица XX

К ст. Прага. 1. Общий вид центральной части Праги, на втором плане - Градчаны. 2. Перед Малой площадью. 3. Вацлавская площадь. 4. Староместская площадь. В центре - памятник Яну Гусу. 5. Мелантрихова улица. 6. Улица Ленина. 7. В саду Кинских.

Таблица XXI

К ст. Прага. 1. Южная башня собора св. Вита. 14-16 вв. 2. Собор св. Вита. 1344-1929. 3. Староместская башня Карлова моста. Ок. 1370-90. 4. Староместская ратуша (14-17 вв.) и Тынская церковь (14 в.). 5. Архиепископский дворец. 1767. 6. Собор св. Креста. 18 в. 7. Театр им. Б. Сметаны. Конец 19 в. 8. Национальный театр. 1868-81. Архитектор И. Зитек. 9. Институт макромолекулярной химии. 1964-65. Архитектор К. Прагер.

Таблица XXII

К ст. Пракситель. 1. Пракситель (?). "Гермес с младенцем Дионисом". Ок. 340 до н. э. Музеи Олимпии. 2. "Отдыхающий сатир". Капитолийские музеи. Рим. 3. "Артемида из Габий". Лувр. Париж. 4. Статуя юноши, найденная в море близ Марафона. Бронза. Ок. 330 до н. э. Национальный археологический музей. Афины. Фрагмент. 5. "Афродита Книдская" из Тралл (современный Айдын, Турция). Античное собрание. Берлин. Фрагмент. 6. Статуя "Аполлона Ликейского", найденная на афинской агоре. Слоновая кость. Музей Агоры. Афины. Фрагмент. (1-3, 5, 6 - мрамор; 2-6 - античные копии или скульптуры круга Праксителя.)

Таблица XXIII

К ст. Примитивизм. 1. П. Гоген. "Желтый Христос". 1889. Галерея Олбрайта. Буффало. 2. П. Клее. "Акробатический номер". 1923. 3. М. Ф. Ларионов. "Офицерский парикмахер". 1909. 4. П. Пикассо. "Танцовщица". 1907-08. 5. X. Пинпин. "Джона Брауна везут на казнь". 1942. Пенсильванская академия изящных искусств. Филадельфия. Фрагмент. 6. А. Руссо. Автопортрет. 1890-96. Национальная галерея. Прага. 7. Н. Пиросманашвили. "Кутёж пяти торговцев". 1909. Музей искусств Грузинской ССР. Тбилиси. 8. И. Генералич. "Похороны Штефа Халачека": 1934. Современная галерея Югославской академии наук и искусств. Загреб. (2-4 - частные собрания.)

Таблица XXIV

К ст. Приморский край. 1. Побережье Японского моря в районе Снхота Алинского заповедника. 2. В горах Сихотэ-Алинь. 3. Река Артёмовна. 4. Обогатительная фабрика Краснореченского горно-обогатительного комбината. 5. Ханкайский район. Уборка риса в совхозе "Авангард", 6. Находка. Судоремонтный завод. 7-8. Владивосток: 7. Железнодорожный вокзал. 8. Встреча китобойной флотилии.  

ПРЕДРАССУДОК, букв. - мнение, предшествующее рассудку, усвоенное некритически, без размышления. П. называются иррациональные компоненты обществ, и индивидуального сознания - суеверия, связанные с религией, и предубеждения. Предубеждение - это неблагоприятная социальная установка к к.-л. явлению; не основанное на критически проверенном опыте, стереотипное и эмоционально окрашенное, оно тем не менее весьма устойчиво и плохо поддаётся изменению под влиянием рациональной информации. Особенно живучи нац. и расовые предубеждения. Предубеждения существуют и в др. сферах обществ. психологии.

Как всякий социально-психологич. стереотип, этнич. предубеждения имеют двоякие корни - социально-экономические и психологические. Этнич. предубеждения, чувства расовой и нац. вражды коренятся в объективных условиях жизни общества, ставящих людей во враждебные отношения друг к другу. Недоверие и подозрительность к "чужаку" заложены уже в этноцентризме первобытного мышления, кругозор к-рого по необходимости ограничен рамками своего собств. рода и племени. "Мы" определяется через соотнесение и противопоставление каким-то другим - "Они". С развитием обмена, межплеменного общения представления людей о др. этнич. общностях усложняются, однако содержание и эмоциональная окраска этих представлений всегда отражают конкретную историю взаимоотношений соответствующих групп. Нейтральные или дружеств. отношения порождают нейтральные или положительные стереотипы; зависимая, подчинённая группа с более низким уровнем цивилизации вызывает к себе снисходительно-пренебрежительное отношение, наделяется чертами детской наивности и интеллектуальной неполноценности (типичный образ "туземца" в колониальном фольклоре 19 в.); группа-конкурент, напротив, воспринимается как враждебная и опасная, её представители наделяются чертами агрессивности, коварства, моральной ненадёжности. Соответствующие стереотипы прочно закрепляются в массовом сознании и освящаются религией. В условиях классовоантагонистич. общества этнич. предубеждения не только стихийно вырастают из недр массовой психологии как специфическая, хотя и искажённая форма символизации социальных конфликтов, но и сознательно распространяются и пропагандируются реакц. классами в целях разобщения трудящихся, отвлечения их внимания от коренных социальных проблем. Поэтому необходимые предпосылки ликвидации всех нац. и расовых предубеждений - уничтожение классов и эксплуатации человека человеком, широкая воспитат. работа в условиях социалистич. общества.

Однако предубеждения - не только социальный, но и психологич. феномен. Один и тот же по своему объективному содержанию стереотип в одном случае является просто средством приспособления к социальной ситуации (напр., расистские установки в обществе, в к-ром расовое неравенство является нормой), а в другом - защитным механизмом личности, к-рая проецирует на "чужака" свои собств. неосознаваемые качества. Психологич. трактовка нац. и иных предубеждений, если она претендует заменить социально-историческую, классовый анализ, реакционна и несостоятельна. Однако изучение диалектики когнитивных (познавательных), эмоциональных и волевых компонентов предубеждения или соотношения социальной установки и реального поведения имеет важное значение для выработки эффективных способов воспитания.

И. С. Кон.

ПРЕДРОМАНТИЗМ, преромантизм, комплекс идейно-стилевых тенденций в зап.-европ. лит-ре 2-й пол. 18 - нач. 19 вв. и изобразит. иск-ве кон. 18 - нач. 19 вв.; генетически предвосхищая романтизм, П. сохраняет преемственность нек-рых мотивов и идей лит-ры сентиментализма (апелляция к "чувству", апология "естественного" существования, поэтизация "мирной" природы и др.), однако это идеологически разные течения: в рамках сентиментализма осуществляется критика рационализма Просвещения, тогда как П.- начало его полного и бескомпромиссного отрицания. "Зыбкая", переходная природа П. находит подтверждение в творч. судьбах "предромантиков", часто относимых либо уже к романтизму (У. Блейк), либо ещё к сентиментализму (Ж. А. Бернарден де Сен-Пьер). Связанный с выдвижением третьего сословия, П. проникнут пафосом самоопределения и утверждения личности ("Влюблённый дьявол" Ж. Казота; в известной мере произв. маркиза де Сада). В предреволюц. годы франц. П. обретает гражданственное антифеод. звучание.

Наиболее характерно и полно П. развился в Англии. Констатируя кризис просветит. сознания, англ. П. демонстративно реставрирует "старину" (мистификации Т. Чаттертона, Дж. Макферсо-на), обращается к нар. творчеству (песни и баллады Т. Перси, А. Рамзей и др.), создаёт "готический роман" (А. Радклиф и др.). Поэтизируя душевную стихию, углубляясь в неё, англ. П. переносит акцент на перипетии индивидуальной человеческой судьбы. В русле увлечения средневековьем лежит и возрождение интереса к "варварскому" У. Шекспиру как образцу истинной поэзии ("Мысли об оригинальном творчестве", 1759, Э. Юнга). Критика бурж. прогресса выразилась в "кладбищенской поэзии" Юнга ("Жалоба, или Ночные думы", 1742-45), в меланхолич. "Элегиях" (1751) Т. Грея. П. проявился также в лит-pax США, Венгрии, Италии, Испании. В России П. не получил законченного выражения; синкретизм рус. лит-ры кон. 18 в. (одновременное присутствие различных идейно-художеств. тенденций) свёл его к отд. мотивам в поэзии Г. Р. Державина, Н. И. Гнедича, В. А. Жуковского.

В сфере изобразительного искусства П. гораздо органичнее переходит в собственно романтизм. Здесь он также отмечен стремлением к индивидуализации образов, тяготением к драматич. мотивам, островыразительной художеств. форме и нередко обладает гражданств. звучанием.

В. А. Харитонов.

ПРЕДРОСТОК, нитчатое или пластинчатое образование у мхов, на к-ром возникают побеги - гаметофоры, несущие половые органы; то же, что протонема.

ПРЕДСЕДАТЕЛЬ ПРЕЗИДИУМА ВЕРХОВНОГО СОВЕТА СССР, лицо, возглавляющее Президиум Верховного Совета СССР. Организует и направляет работу Президиума, созывает и ведёт его заседания, представительствует от имени Президиума в отношениях с др. гос. органами, вручает ордена и медали СССР, грамоты о присвоении почётных званий СССР, осуществляет от имени Президиума Верх. Совета СССР представительство СССР во внеш. сношениях, принимает верительные грамоты и отзывные грамоты дипломатич. представителей иностр. гос-в. За подписью председателя (совместно с секретарём Президиума) публикуются законы и пост. Верх. Совета СССР и Указы Президиума Верх. Совета СССР. В необходимых случаях функции председателя могут выполняться его заместителями. В союзных и автономных республиках также избираются председатели Президиумов Верховных Советов.

ПРЕДСЕДАТЕЛЬ СОВЕТА МИНИСТРОВ СССР, глава правительства СССР-Совета Министров СССР. Назначается Верховным Советом СССР на 1-й сессии каждого очередного созыва. Ему поручается сформировать правительство, состав к-рого вносится на утверждение Верх. Совета СССР. Пред. Сов. Мин. СССР руководит всей деятельностью пр-ва СССР, представляет его в отношениях со всеми гос. и обществ. орг-циями, организует выполнение принятых пост. и распоряжений и контроль за их выполнением, отчитывается перед Верх. Советом СССР за деятельность пр-ва и т. д. По поручению Президиума Верх. Совета СССР может представлять СССР во внеш. сношениях. За подписью Пред. Совета Мин. СССР издаются пост. и распоряжения пр-ва СССР. Верх. Советы союзных и авт. республик образуют свои пр-ва - Советы Министров, во главе с пред. Совета Министров соответств. республики.

ПРЕДСЕДАТЕЛЬ СУДА, в СССР лицо, возглавляющее судебный орган. Пред. краевого, обл. (гор.) суда, суда авт. области и нац. округа избирается на 5 лет при выборах состава суда, к-рый он возглавляет, на сессии соответствующего Совета депутатов трудящихся. Пред. Верх. суда СССР, Верх. судов союзных и авт. республик избираются на сессии Верх. Совета СССР, Верх. Советов союзных и авт. республик. В районе, где избрано неск. нар. судей, районный Совет депутатов трудящихся (а в городе, не имеющем районного деления,- гор. Совет) утверждает председателя районного (гор.) суда из числа избранных нар. судей.

П. с. председательствует в судебных заседаниях, руководит обобщением судебной практики, ведёт организац. работу. П. с., за исключением пред. районного (гор.) нар. суда, принадлежит право истребования дел и принесения протестов на незаконные или необоснованные приговоры, решения и определения, вступившие в законную силу.

ПРЕДСЕДАТЕЛЬСТВУЮЩИЙ В СУДЕБНОМ ЗАСЕДАНИИ, в СССР лицо, непосредственно руководящее ходом судебного заседания от имени всего состава суда. Закон устанавливает, кто может быть П. в с. з., а также, регламентирует его права и обязанности. Так, в заседании районного (гор.) нар. суда председательствует пред. этого суда или нар. судья, а в заседаниях иного суда - пред. суда, его заместитель или член суда. П. в с. з. не имеет к.-л. прав, к-рыми не обладают др. судьи. Он обязан принять все предусмотренные законом меры для всестороннего, полного и объективного исследования обстоятельств дела и установления истины, а также для воспитательного воздействия процесса; обеспечить надлежащий порядок в судебном заседании. Руководит совещанием судей при вынесении приговора или решения, при голосовании подаёт свой голос последним.

ПРЕДСТАВИТЕЛЬ ВЛАСТИ, по сов. праву должностное лицо, наделённое правами и обязанностями по осуществлению функций органов гос. власти или гос. управления, в соответствии с к-рыми он вправе давать обязательные для исполнения указания гражданам, учреждениям и орг-циям. Такими полномочиями обладают, например, работники органов милиции, гос. сан. инспекции, гос. пожарного надзора. Для деятельности П. в. характерно использование в первую очередь методов убеждения, но в определённых случаях возможно применение меры принуждения. П. в. в пределах своей компетенции обязан действовать в строгом соответствии с законом.

ПРЕДСТАВИТЕЛЬСТВО, в гражд. праве совершение одним лицом (представителем) ог имени и в интересах др. лица (представляемого), на основании определённых полномочий, сделок или иных юридически значимых действий, к-рые непосредственно создают, изменяют и прекращают гражд. права и обязанности представляемого. П. необходимо в случаях, когда лицо не может в силу ряда обстоятельств (отсутствия времени, недостатка квалификации и т. д.) самостоятельно осуществить свои гражданские (в основном имущественные) права и обязанности.

По сов. праву представителями могут быть как дееспособные граждане, так и юридич. лица. Не допускается совершение через представителя юридич. действий, к-рые могут быть совершены только лично (напр., подписание завещания, регистрация брака). П. возникает в силу доверенности, на основании закона (напр., П. родителей от имени несовершеннолетних детей в качестве законных представителей), адм. акта (напр., опекун представительствует от имени подопечного на основании решения исполкома соответств. Совета депутатов трудящихся о назначении опеки).

ПРЕДСТАВЛЕНИЕ, образ предметов, воздействовавших на органы чувств человека, восстанавливаемый по сохранившимся в мозгу следам при отсутствии этих предметов и явлений, а также образ, созданный усилиями продуктивного воображения, высшая форма чувственного отражения в виде наглядно-образного знания. В отличие от восприятия, П. поднимается над непосредств. данностью единичных объектов и связывает их с общим началом, с понятием. П. осуществляется в двух формах - в виде воспоминания и воображения. Если восприятие относится только к настоящему, то П. одновременно относится и к настоящему, и к прошлому.

П. есть вспоминающее созерцание, спецификой к-рого является промежуточность между созерцающим и мыслящим сознанием. Без воспоминания было бы невозможно узнавание: "...так называемое воспоминание в собственном смысле слова есть отнесение образа к созерцанию и притом в качестве подведения непосредственного единичного созерцания под то, что по своей форме является общим, под представление, имеющее то же самое содержание" (Гегель, Соч., т. 3, М., 1956, с. 257).

С помощью воображения создаются П. и мысленные ситуации, непосредственно не воспринимающиеся в целом в действительности. Чем реальнее отражение в П., тем продуктивнее его регулятивная и стимулирующая деятельность во всех видах человеческого творчества.

Восприятие и П. не есть независимые силы или способности сознания. Они образуют неразрывное единство. При этом П. является синтезом многих чувственных впечатлений. Характеризуя диалектику взаимоотношения П. и мышления, В. И. Ленин писал: "Представление ближе к реальности, чем мышление? И да, и нет. Представление не может схватить движения в целом, например, не схватывает движения с быстротой 300 000 км в 1 секунду, а мышление схватывает и должно схватить" (Полн. собр. соч., 5 изд., т. 29, с. 209).

Лит. см. при ст. Воображение.

А. Г. Спиркин.

ПРЕДСТАРЧЕСКИЕ ПСИХОЗЫ, пресенильные психозы, инволюционные психозы, группа психических болезней, возникающих на 5-6-м десятилетии жизни. Причина П. п. неизвестна; обычно им предшествуют психич. травмы или соматич. заболевания. Чаще наблюдаются у женщин в период климакса и менопаузы. Мн. психиатры не признают самостоятельность П. п. и считают их проявлением др. психич. болезней (шизофрении, маниакально-депрессивного психоза, сосудистых психозов). Осн. формы П. п.: пресенильная депрессия (инволюционная меланхолия) и пресенильный бред (инволюционный параноид, см. Паранойя; пресенильный бред ущерба). Для пресенильной депрессии характерны тоскливое настроение, тревожное возбуждение и бред самообвинения; течение длительное с исходом в состояние однообразного тревожно-подавленного настроения. Пресенильный бред проявляется подозрительностью, бредовыми идеями ущерба, ревности, отравления, к-рые имеют будничное, обыденное содержание (бред "малого размаха") и направлены на ближайшее окружение больного (соседи, родственники); характерна бредовая активность в виде "защитных" и "разоблачительных" действий. Лечение: психотропные средства.

Лит.: Жислин С. Г., Очерки клинической психиатрии, М., 1965, с. 181; Wеitbгесht H., Psychiatric im Grundriss, В., 1963. М. И. Фатьянов.

ПРЕДСТАТЕЛЬНАЯ ЖЕЛЕЗА, простата, непарная железа мужского полового аппарата. Расположена в малом тазу, между дном мочевого пузыря и ампулой прямой кишки; плотно охватывает шейку пузыря и задний отдел мочеиспускат. канала. Длина П. ж. 4-4,5 см, ширина 2-3,5 см, толщина 1,7-2,5 см; весит 17-28 г. П. ж. образована 30-50 отд. дольками (желёзками) разной величины, залегающими в плотной соединительнотканной основе с большим кол-вом гладких мышечных волокон. Выводные протоки П. ж. открываются в простатич. отделе мочеиспускат. канала. Кровоснабжение осуществляется через нижние пузырные и средние прямокишечные артерии, венозный отток - в систему внутр. подвздошной вены. Лимфатич. сосуды идут к лимфатич. узлам таза. П. ж. иннервируется подвздошным нервом. Секрет П. ж. играет важную роль в обеспечении жизнедеятельности сперматозоидов в семенной жидкости (разжижение семени, увеличение его объёма). Наиболее часто встречающиеся заболевания - простатит, опухоли (напр., аденома предстательной железы) и камни П. ж.

ПРЕДУПРЕЖДАЮЩАЯ ОКРАСКА, вид покровительственной окраски и формы, при к-рой несъедобные животные обладают яркой, обычно пёстрой, окраской. Такие животные хорошо заметны благодаря контрастным сочетаниям цветов (чёрного, красного, белого; оранжевого, белого, чёрного и т. д.). Из насекомых П. о. обладают клопы-солдатики, жуки (божьи коровки, бронзовки, листоеды, нарывники), бабочки (пестрянки, медведицы, геликониды) и др. Среди позвоночных животных П. о. присуща некоторым рыбам, саламандрам, жабам жерлянкам, птицам (дронго), млекопитающим (американский скунс). Заметность животных с П. о.- их преимущество, поскольку они, будучи узнанными, не подвергаются нападению со стороны хищников. П. о. способствует выживаемости вида в борьбе за существование и является результатом действия естественного отбора. См. также Мимикрия.

ПРЕДУСТАНОВЛЕННАЯ ГАРМОНИЯ, понятие, введённое в философию Г. Лейбницем (1695) для объяснения всеобщей взаимосвязи и согласованности в мире. Согласно учению о П. г., развитому Лейбницем в 1696, субстанциальные элементы мира - монады, будучи чисто психич. сущностями, не могут физически взаимодействовать друг с другом; однако развитие каждой из них находится в изначально предустановленном богом соответствии с развитием всех др. монад и мира в целом. Благодаря этой сущностной гармонии возникает также гармония в явлениях (физич. детерминизм) и гармония между сущностью и явлением (согласие между конечными и действующими причинами, между душой и телом). Теория П. г. была направлена против окказионализма Н. Малъбранша и картезианского дуализма (см. Картезианство), в рамках деизма в ней отстаивалась имманентная закономерность природных процессов.

Лит.: Еislеr R., Kritische Untersuchung des Begriffes der Weltharmonie..., В., 1895; Belaval Y., L'idee d'harmonie chez Leibniz, "Studium Generate", 1966, Jg. 19, H. 9. См. также лит. при ст. Лейбниц.

Г. Г. Майоров.

ПРЕЕМСТВЕННОСТЬ, связь между явлениями в процессе развития, когда новое, снимая старое, сохраняет в себе нек-рые его элементы. П. есть одно из проявлений диалектики отрицания отрицания закона и перехода количественных изменений в качественные. П. носит объективный и всеобщий характер, проявляясь в природе, обществе и познании. Применительно к обществу различают две стороны П.: передачу социальных и культурных ценностей от поколения к поколению, от формации к формации и усвоение этих ценностей каждым новым поколением, каждой новой социальной системой. П. - особый механизм "памяти общества", к-рый осуществляет накопление и хранение культурной информации прошлого, на основе к-рой создаются новые ценности. П. может быть непрерывной, когда культурные ценности прошлого постоянно функционируют в жизни общества, и прерывной, когда к.-л. ценности на время исчезают из культурного обихода. П. обозначает также всю совокупность действия традиций, воспроизводящих нормы социального поведения, характерные для исторически прошедшей обществ. реальности. При этом следует различать наследование подлинных ценностей культуры и сохранение пережитков прошлого. Марксизм-ленинизм выступает как против левацко-анархич. отрицания культуры прошлого, так и некритич. отношения к ней. На принципе П. основаны все социальные институты обучения и воспитания. О П. в биологии см. ст. Наследственность.

В. А. Кругликов.

ПРЕЖИХОВ ВОРАНЦ (Prezihov Voranc) (псевд.; наст, имя и фам. Ловро Кухар, Lovro Kuhar) (10.8.1893, Котле, - 18.2.1950, Марибор), словенский писатель. Сын крестьянина. Чл. компартии Югославии с 1920. Один из организаторов Народно-освободит. фронта во время 2-й мировой войны 1939-45. Печатался с 1909. Успех П. В. принесли новеллы из крест. жизни, составившие цикл "Самородки" (1940). Три романа П. В., написанные в тюрьмах и эмиграции, - широкие полотна из истории словенского народа ("Добердоб", 1929, опубл. 1940, рус. пер. 1962; "Пожганица", 1939; "Ямница", 1941, опубл. 1945). Автор сб. очерков "Битва на чужой земле" (1946) и др.

Соч.: Zbrano delo, knj. 1-2, Ljubljana, 1962-64; в рус. пер.- Ландыши, М., 1959.

Лит.: Рябова Е. И., К характеристике "социального реализма" в словенской литературе, в сб.: Формирование социалистического реализма в литературах западных и южных славян, М., 1963; Prezihov Zbornik, Maribor, 1957.

ПРЕЗЕНТИЗМ (от англ, present - настоящее время, современность), термин, применяемый в литературе для обозначения субъективно-идеалистич. направления в бурж. методологии истории 20 в., рассматривающего ист. науку не как отражение объективных, имевших место в прошлом явлений, а лишь как выражение идеологии, отношений современности. Абсолютизируя тот реальный факт, что любая картина прошлого предполагает определённую совр. перспективу, П. в принципе отвергает возможность объективной истины в ист. познании. Наиболее широкое распространение П. получил в США в 20-40-е гг., будучи тесно связан с философией прагматизма.

ПРЕЗЕРВАТИВ (франц. preservatif, от позднелат. praeservo - предохраняю), кондом, одно из противозачаточных средств. Мужской П. представляет собой чехол из тонкой резины, в к-ром остаётся сперма после эякуляции; женские П. (резиновые или металлические колпачки) вводятся во влагалище и защищают шейку матки от проникновения сперматозоидов .

ПРЕЗЕРВЫ, пресервы (отпозднелат. praeservo - предохраняю), нестерилизуемые рыбные консервы в острой заливке.

ПРЕЗИДЕНТ (от лат. praesidens, род. падеж praesidentis - сидящий впереди, во главе), 1) в ряде общественных и науч. учреждений, организаций и др. (в т. ч. и международных) - выборный руководитель, председатель (напр., президент АН СССР, президент Междунар. совета науч. союзов, президент Междунар. академии астронавтики, президент Об-ва дружбы СССР - Франция). 2) Глава гос-ва в странах с республиканской формой правления. В т. н. парламентарных республиках (Италия, Индия, ФРГ, Турция, Ливан) П. избирается на установленный конституцией срок либо парламентом, либо особой коллегией, основу к-рой составляет парламент. В президентских республиках П. избирается внепарламентским путём: посредством прямых (Франция, Панама, Парагвай, Колумбия, Коста-Рика, Боливия) или косвенных (США, Аргентина) выборов. В президентских республиках П. обладает обширными фактич. полномочиями, т. к. он соединяет в своих руках функции главы гос-ва и главы пр-ва. Конституции парламентарных республик формально наделяют П. широкими полномочиями, но фактически они осуществляются премьер-министром, что закрепляется установлением института контрасигнатуры. В социалистич. гос-вах (ЧССР, ФНРЮ, ДРВ, КНДР) главой государства также является П., избираемый высшими представительными органами. Президент Кубинской Республики избирается Советом Министров.

ПРЕЗИДЕНТИ-ПРУДЕНТИ (Presidents Prudente), город на Ю.-В. Бразилии, в шт. Сан-Паулу. 105,4 тыс. жит. (1970). Ж.-д. станция. Узел автодорог. Пищ. (мясо-молочная, маслоб., рисоочистительная), деревообр., кож.-обув., текст, пром-сть; произ-во керамики. Торг. центр с.-х. района.

ПРЕЗИДИУМ (от лат. praesidium, букв.- защита; переносное значение -председательство), группа лиц, коллегия, избранная для руководства собранием, совещанием или как постоянный руководящий орган партийных, науч. и др. общественных организаций.

ПРЕЗИДИУМ ВЕРХОВНОГО СОВЕТА СССР, орган гос. власти в СССР. Избирается Верховным Советом СССР на совместном заседании обеих палат на первой сессии каждого очередного созыва из числа депутатов на весь срок полномочий Верх. Совета (см. Верховный Совет СССР). Президиум Верх. Совета СССР состоит из председателя, 15 его заместителей (по одному от каждой союзной республики), секретаря и 20 членов. Во всей своей деятельности Президиум подотчётен Верх. Совету СССР. Осн. полномочиями Президиума Верх. Совета СССР, согласно Конституции СССР, являются: издание указов; толкование действующих законов СССР; роспуск Верх. Совета СССР на основании ст. 47 Конституции СССР и назначение новых выборов; проведение по своей инициативе или по требованию одной из союзных республик всенародного опроса (референдума), отмена пост. и распоряжений Сов. Мин. СССР и Сов. Мин. союзных республик в случае их несоответствия закону; по представлению пред. Сов. Мин. СССР освобождение от должности и назначение министров СССР (в период между сессиями Верх. Совета СССР) с последующим внесением на утверждение Верх. Совета СССР; учреждение орденов и медалей СССР и награждение ими; установление почётных званий СССР и присвоение их; осуществление права помилования; назначение и смещение высшего командования Вооруж. Сил СССР; установление воинских званий, дипломатич. рангов и др. спец. званий; объявление общей и частичной мобилизации; объявление состояния войны в случае воен. нападения на СССР или в случае необходимости выполнять междунар. договорные обязательства во взаимной обороне от агрессии; ратификация и денонсация междунар. договоров СССР, представление Верх. Совета СССР (в период между его сессиями) в сношениях с парламентами иностр. гос-в; назначение и отзыв полномочных представителей СССР в иностр. гос-вах; приём верительных и отзывных грамот аккредитованных при нём дипломатич. представителей иностр. гос-в; объявление в отд. местностях или по всему СССР воен. положения в интересах обороны СССР или обеспечения обществ. порядка и гос. безопасности. Президиум решает также вопросы приёма в сев. гражданство, лишения его или добровольного выхода из сов. гражданства. Президиумы Верх. Советов имеются также в союзных и авт. республиках; функции их определяются конституциями соответствующих республик.

ПРЕЗИДИУМ СУДА, в СССР коллегиальный орган в краевых, обл., гор. судах, судах авт. областей и нац. округов, республик, осуществляющий функции суд. надзора. Состоит из пред, данного суда, его заместителей и членов суда. Состав П. с. утверждается исполкомом соответств. Совета депутатов трудящихся, а Президиум Верх. судов союзных и авт. республик - Президиумами Верх. Советов этих республик.

Президиумы Верх. суда АССР, краевого, обл., гор. суда, суда авт. областей и нац. округов рассматривают дела по протестам на кассационные определения коллегий этих судов, на вступившие в законную силу приговоры, решения и определения районных (гор.) нар. судов и на пост. нар. судей о предании суду. Президиум Верх. суда союзной республики рассматривает дела по протестам на приговоры, решения, определения, пост. любого суда республики (включая определения своих судебных коллегий, вынесенные в кассационном или надзорном порядке), а также на приговоры решения и определения коллегий Верх. суда республики, слушавшего дела по первой инстанции.

При рассмотрении дел в П. с. участие прокурора обязательно.

ПРЕЗИДИУМ ЦК КПСС, руководящий парт, орган, избиравшийся пленумом ЦК КПСС для руководства работой ЦК между пленумами. Впервые образован пленумом ЦК КПСС 16 окт. 1952 в соответствии с Уставом КПСС, утверждённым 19-м съездом партии (1952), вместо Политбюро ЦК ВКП(б). В соответствии с постановлением 23 го съезда партии 8 апр. 1966 вновь создано Политбюро ЦК КПСС.

ПРЕЗИНДЖАНТРОП (букв. - предшествующий зинджантропу: лат. рrае - перед, впереди), условное название высшего примата, кости к-рого были открыты Л. Лики в 1960 в ущелье Олдовай (Танзания). Назван так потому, что находка была сделана в слое более древнем, чем слой, содержавший кости зинджантропа. Абс. древность П. св. 2 млн. лет. Вместе с П. были найдены оббитые гальки, что побудило нек-рых исследователей считать его человеком и назвать Homo habilis (человек умелый). Другие учёные рассматривают П. как представителя австралопитеков (Australopithecus habilis).

ПРЕЗУМПТИВНЫЙ ЗАЧАТОК (от позднелат. praesumptivus - предполагаемый, ожидаемый) в эмбриологии, клеточный материал, из к-рого в процессе зародышевого развития образуется зачаток того или иного органа (презумптивные нервная пластинка, хорда, эпидермис и др.). Положение П. з. определяют при помощи маркировки. Для ряда хордовых животных созданы карты П. з. на стадии ранней гаструлы (рис.). У нек-рых червей и моллюсков положение П. з. прослежено до стадий раннего дробления.

Карта относительного положения и размеров презумптивных зачатков на поверхности ранней гаструлы у земноводных. Вид со спинной стороны. Презумптивный материал: 1 - головной эктодермы; 2 - энтодермы; 3 - сомитов; 4 - эпидермиса; 5 - нервной пластинки; 6 - хорды; 7 - боковой мезодермы; 8 - спинная губа бластопора; ан - анимальный полюс; вег - вегетативный полюс.

ПРЕЗУМПЦИЯ НЕВИНОВНОСТИ (от лат. praesumptio - предположение), в праве положение, согласно к-рому обвиняемый не считается виновным, пока его вина не будет доказана в установленном законом порядке. Цель П. н. в сов. уголовном процессе - охрана прав личности, осуществление конституционного права обвиняемого на защиту, ограждение невиновного от незаконного и необоснованного привлечения к уголовной ответственности и осуждения. Как и всякое предположение, П. н. может быть отвергнута, но только путём доказывания установленными процессуальным законом средствами и лишь при помощи доказательств, относящихся к делу и допустимых законом.

П. н. впервые была провозглашена в Декларации прав человека и гражданина 1789 в начале Великой франц. революции: "каждый предполагается невиновным, пока не установлено обратное" (ст. 9). В законодательстве совр. бурж. гос-в и в бурж. науке уголовного процесса принцип П. н. обычно прокламируется. Однако в судебной практике бурж. гос-в доминирует, напротив, презумпция виновности, что особенно чётко проявляется при уголовном преследовании прогрессивных деятелей. Тем не менее П. н. в этих странах - средство борьбы против необоснованных обвинений, когда против таких обвинений выступают широкие круги трудящихся, прогрессивной общественности .

Принцип П. н. закреплён в Декларации прав человека, принятой Ген. Ассамблеей ООН 10 дек. 1948, а также в Междунар. пакте о гражданских и политических правах 1966.

Истинный смысл и реальное содержание П. н. обрела только в социалистич. уголовном процессе. Этот принцип закреплён в УПК Польши (1970), ГДР (1968) и др. социалистических стран. Он выражен во многих положениях Основ уголовного судопроизводства Союза ССР и союзных республик (1958): никто не может быть привлечён в качестве обвиняемого, иначе как на основаниях и в порядке, установленном законом (ст. 4); никто не может быть признан виновным и подвергнут в связи с этим уголовному наказанию, иначе как по приговору суда (ст. 7); суд, прокурор, следователь, лицо, производящее дознание, не вправе перелагать обязанность доказывания на обвиняемого, т. е. обвиняемый не обязан доказывать свою невиновность; запрещается домогаться показаний обвиняемого путём насилия, угроз и иных незаконных мер (ст. 14); виновность обвиняемого в совершении преступления подлежит доказыванию при расследовании и разбирательстве дела в суде (ст. 15); предание обвиняемого суду не предрешает вопроса о его виновности (ст. 36); обвинительный приговор не может быть основан на предположениях и постановляется лишь при условии, если в ходе судебного разбирательства виновность подсудимого в совершении преступления доказана (ст. 43). Положение П. н. об истолковании всех неустранимых сомнений в пользу подсудимого закреплено пост. пленума Верх. суда СССР от 30 июня 1969 "О судебном приговоре". Все эти нормы в их совокупности в полной мере обеспечивают фактическое применение П. н.

Лит.: Теория доказательств в советском уголовном процессе, 2 изд., М., 1973, гл. V; Полянский Н. Н., Доказательства в иностранном уголовном процессе, М., 1946; Строгович М. С., Курс советского уголовного процесса, т. 1, М., 1968, гл. V, X.

ПРЕЙЛИ, город, центр Прейльского р-на Латв. ССР. Расположен в 18 км от ж.-д. ст. Аглона (на линии Даугавпилс - Резекне) и в 204 км к Ю.-В. от Риги. Крахмальный, сыродельный и льнообр. з-ды, произ-во швейных изделий.

ПРЁЙСИШ-ЭЙЛАУ, прежнее (до 1946) название г. Багратионовск Калининградской обл. РСФСР. Во время русско-прусско-французской войны 1806-1807 в районе П.-Э. 26-27 янв. (7-8 февр.) 1807 произошло сражение между рус. и франц. войсками. 4(16) янв. рус. армия под команд, ген. Л. Л. Беннигсена начала наступление от Бялы на З. с целью разбить изолированные левофланговые корпуса (М. Нея и Ж. Бернадота) наполеоновской армии. Из-за нерешительности Беннигсена этого достигнуть не удалось. Наполеон собрал войска с зимних квартир (до 70 тыс. чел.) и перешёл в наступление от Алленштейна (совр. Ольштын) на С. с целью отрезать рус. армию (78 тыс. чел., в т. ч. 8 тыс. пруссаков) от сообщений с Россией. Под прикрытием арьергарда ген. П. И. Багратиона гл. силы рус. войск отошли на позицию северо-восточнее П.-Э., где произошло двухдневное кровопролитное сражение. Попытка Наполеона обойти лев. крыло рус. войск была сорвана их упорной обороной. Потери составили по 26-36 тыс. чел. с каждой стороны. Активные боевые действия продолжались до мая 1807.

ПРЕЙСКУРАНТ (нем. Preiskurant, от Preis - цена и франц. courant - текущий), систематизированный сборник цен (тарифов) по группам и видам товаров и услуг. В СССР издаются отдельно П. оптовых, розничных и закупочных цен, тарифов на услуги транспорта, предприятий бытового и коммунального обслуживания. В П. приводится наименование изделия (продукции) по стандарту или технич. условиям (ТУ), присвоенная марка (шифр, модель, артикул), номер стандарта или ТУ с указанием, кем и когда они утверждены, краткая технич. характеристика изделия (продукции), единица измерения и цена. На товары, реализуемые по поясным ценам (мясо-молочные продукты, яйцо, сахар, хлеб и др.), цены даются по каждому поясу.(см. Дифференцирование цен). В П., содержащих большой ассортимент товаров, последние группируются по разделам.

Госкомитет цен СССР утверждает общесоюзные П. оптовых цен на осн. массу продукции производственно-технич. назначения (топливо, электроэнергию, чёрные и цветные металлы, продукцию химич. пром-сти и т. д.), на важнейшие товары нар. потребления (ткани, обувь, трикот. изделия, радиотовары, хлеб, сахар, мясо, молоко, рыба и др.) независимо от подчинённости предприятий, изготовляющих эти товары. Госкомитеты цен союзных республик утверждают респ. П. на товары производств, назначения, выпускаемые предприятиями респ. мин-в и ведомств, а также на большую группу товаров нар. потребления (швейные изделия, мебель, посуду и т. д.). Сов. Мин. авт. республик, краевые (обл.) исполкомы и горисполкомы городов респ. подчинения утверждают П. розничных цен на мн. товары хоз. назначения, овощи и фрукты, тарифы на бытовые и коммунальные услуги Контроль за соблюдением действующих П. осуществляют органы ценообразования и нар. контроля.

Н. М. Орлов.

ПРЕЙСКУРАНТНЫЕ ЦЕНЫ, цены, включаемые в спец. сборник - прейскурант. Устанавливаются на продукцию серийного или массового произ-ва, как правило, без указания срока их действия. В СССР прейскурантные розничные цены применяются при продаже товаров через гос. и кооперативную розничную торговлю. По этим же ценам, за вычетом торг, скидок, производятся расчёты поставщиков с торгующими предприятиями и орг-циями. Прейскурантные оптовые цены на товары производств. назначения применяются при расчётах поставщиков с предприятиями и организациями-покупателями. К ним могут быть установлены надбавки (скидки), если поставляемая продукция изготовляется по требованию заказчика с отступлениями от действующих стандартов и технич. условий. Соблюдение П. ц. обязательно для всех поставщиков продукции и торгующих орг-ций.

ПРЕКАРИЙ (лат. precarium, от preces - просьба), в рим. и ср.-век. праве пользование землёй, предоставляемой собственником на более или менее длит. срок по обращённой к нему письменной просьбе. Утратив свойственные рим. П. право собственника требовать возвращения данного в пользование владения и необходимость возобновлять прекарный договор каждые 5 лет, П. получил широкое распространение в странах Зап. Европы в раннее средневековье. Различают неск. видов П.: precaria data (данный), при к-ром собственник земли предоставлял просителю в П. свою землю; precaria oblata (предоставленный) - наиболее распространённый вид П., при к-ром собственник земли (обычно - мелкий, нередко крестьянин) дарил её церкви или светскому магнату и затем получал её обратно уже в качестве П. (к таким дарениям мелких собственников часто вынуждали покушения на их собственность со стороны крупных землевладельцев); если верховный собственник земли добавлял к такому П. свой зем. участок, возникали precaria remuneratoria (букв.-П. с вознаграждением). Условия П. различны: от обязательства уплачивать небольшой чинш до несения барщины. П. в раннее средневековье давался пожизненно, часто с правом передачи по наследству (обычно до третьего поколения). Последствия заключения пре-карного договора были различны. Для представителей феод, слоев П. создавал отношения, приближающиеся к бенефицию. Крестьян прекарный договор приводил, хотя и медленным путём, к втягиванию в различные формы феод. зависимости, вплоть до полного закрепощения (неуплата чинша в срок могла привести к окончат. превращению земли прекариста в тяглый надел).

ПРЕКОРДИЛЬЕРЫ, складчато-глыбовые горные хребты на С.-З. Аргентины (пров. Ла-Риоха, Сан-Хуан и Мендоса), между 68° з. д. и Андами. Вые. до 5000 м. Хребты разделены глубокими впадинами. Климат тропический и субтропический, засушливый. На вост. склонах ксерофильные леса, на выровненных гребнях сухие степи, на зап. склонах сухие кустарники; во впадинах орошаемое земледелие (садоводство, виноградарство).

ПРЕКОС (франц. ргёсосе, от лат. ргаесох - ранний, скороспелый), порода тонкорунных овец мясо-шёрстного направления продуктивности. Выведена во Франции в кон. 19 в. скрещиванием маток породы рамбулье с баранами лейстерской породы и в Германии скрещиванием нем. мериносов с баранами англ. длинношёрстных пород. Овцы крупные, складок кожи на шее и туловище, как правило, нет. Бараны весят 100-110 кг, нек-рые 115 кг и более. Настриг шерсти с баранов 8-10 кг, максимальный 14 кг, с маток - 3,8-4,2 кг, максимальный 10 кг. Шерсть 58-60-го качества, дл. 7-10 см. Выход мытой шерсти 45-50%. Плодовитость до 150 ягнят на 100 маток. Животные скороспелы, требовательны к условиям кормления и содержания, не приспособлены для разведения в засушливых районах. Распространена порода во Франции, ФРГ, ГДР, СФРЮ, ЧССР, СРР, ПНР, Италии, странах Сев. Африки. В СССР П. завозили в 1926 - 31 из Германии; разводят в центр, районах РСФСР, Башк. АССР, Тэт. АССР, лесостепи и Полесье УССР, БССР и др.

ПРЕКРАСНОЕ, категория эстетики, характеризующая явления, обладающие высшей эстетич. ценностью. Как эстетич. ценность П. отличается от нравственных и теоретич. ценностей (добра, истины) тем, что оно связано с определённой чувственной формой и обращается к созерцанию или воображению; в отличие от утилитарно-полезного, восприятие П. носит бескорыстный характер.

Для древнейшего эстетич. сознания П. мыслилось как неотъемлемое свойство мира, космоса. Для пифагореизма П. есть гармония, внутренне присущая вещам, источник к-рой усматривался в мистически понимаемых количеств. отношениях. По Гераклиту, "прекраснейший строй мира" и "прекраснейшая гармония" являются результатом единства и борьбы противоположностей. Гераклит говорит также об относительности П.: "...Самая прекрасная обезьяна безобразна по сравнению с родом людей" (Платон, "Гиппий Больший", 289А). По Сократу, относительность П. обусловлена тем, что чвсе хорошо и прекрасно по отношению к тому, для чего оно хорошо приспособлено" (Ксенофонт, Воспоминания о Сократе, III, 8,5). Платон проводит чёткое различие между тем, ччтб прекрасно" и тем, "что такое прекрасное" (Гиппий Больший, 287 Е), т. е. между сущностью П. и его проявлениями. Сущность П. Платон трактует как вечную, безотносительную, божеств. идею, от к-рой зависит существование всех прекрасных явлений (см. "Пир", 211 А - В). Человек же, "видя здешнюю красоту, вспоминает красоту истинную" ("федр", 249 D).

Отвергая теорию платоновских чидей", Аристотель полагает, что должно быть единым "прекрасное и бытие прекрасного" ("Метафизика", VII, 6 1031 в). В соответствии с этим Аристотель рассматривает П. как объективное свойство самой действительности, как проявление её закономерностей: "...самые главные формы прекрасного, это - порядок < в пространстве >, соразмерность и определенность..." (там же, XIII, 3, 1078а 34); в живой природе П. связано с целесообразностью (см. "О частях животных", 645а).

Объективно-идеалистич. понимание П. развивается в эстетич. учениях неоплатонизма и христианства. Согласно Плотину, П. в телах возникает благодаря приобщению к высшей красоте, исходящей от Единого (см. "Эннеады", 1, 6, 1-9). Августин писал, что бог сотворил "прекрасные разнообразные формы, блестящие и приятные цвета" ("Исповедь", X, 34). Фома Аквинский, усматривая конечный источник П. в боге, условиями П. считал целостность, или совершенство, должную пропорцию, или созвучие, и ясность (см. "Summa theologiae" I, qu. 39, art. 8).

Мыслители эпохи Возрождения были убеждены в объективности П., к-рое определяется Л. Б. Алъберти как "...строгая соразмерная гармония всех частей, объединяемых тем, чему они принадлежат..." ("Десять книг о зодчестве", т. 1, М., 1935, с. 178). Для Леонардо да Винчи и других теоретиков и практиков искусства Возрождения гармонически и многосторонне развитый человек - высшая мера П.

Классицизм трактовал П. и его оценку рационалистично и нормативно. В эпоху Просвещения эстетика вычленяется в самостоят. дисциплину (у А. Баумгартена) именно как "наука о прекрасном". Анализ П. у просветителей связан с их поисками гармонических обществ, связей, преодолевающих противоречия совр. цивилизации. П. рассматривается как посредствующее звено между разумом и чувствами, отвлечённым долгом и естеств. влечениями, как "свобода в явлении" (Ф. Шиллер), как единство правды и идеала в иск-ве (Д. Дидро, Г. Э. Лессинг). Дидро, считая, что "...восприятие отношений есть основа прекрасного", различает "реально прекрасное" и "прекрасное, которое мы воспринимаем", или "относительно прекрасное" (см. Избр. произв., М., 1951, с. 382, 378). Англ. сенсуалистич. эстетика 18 в. детально исследовала психологию восприятия и переживания П. (Ф. Хатчесон, Г. Хом, Э. Бёрк). Абсолютизация субъективной стороны П. привела к идеалистич. отрицанию его объективности в эстетич. воззрениях Д. Юма и И. Канта. По мнению Канта, "эстетическое свойство" - что, что в представлении об объекте чисто субъективно..." (Соч., т. 5, М., 1966, с. 188) и "...суждение вкуса не познавательное суждение..." (там же, с. 210). Предмет может считаться прекрасным, если отношение к нему будет незаинтересованным, если он без понятия представляется как объект всеобщего "необходимого удовольствия" и если он воспринимается как обладающий "формой целесообразности" "без представления о цели" (там же, с. 245, 240). Г. Гегель цри исследовании П. отвергает кантовское "...ошибочное представление о существовании прочной противоположности между субъективным мышлением и объективными предметами..." (Соч., т. 12, М., 1938, с. 61). Для Гегеля П. объективно как "чувственная видимость идеи" (там же, с. 115). Поскольку же в природе идея проявляется лишь смутно, то и П. в ней несовершенно. Только искусство, по Гегелю, способно осуществить необходимое для истинно П. полное соответствие идеи и образа; П. в искусстве и есть идеал. Ценнейшее достижение гегелевской эстетики - диалектич. подход к изучению П. и понимание историч. развития П., хотя и на объективно-идеалистич. основе.

Материалистич. эстетика 18-19 вв. доказывала объективность П., рассматривая его как свойства, качества, отношения самой материальной действительности. "Под красотой я понимаю, - писал Э. Бёрк (Великобритания) в кн. "Философское исследование происхождения наших идей о возвышенном и прекрасном",- качество или качества тел, благодаря которым они (тела. - Ред.) вызывают любовь или подобную страсть". Н. Г. Чернышевский выступил против упрощённой трактовки этой объективности у Бёрка, критикуя его за то, что тот принял "прекрасное и возвышенное прямо за качества самих тел, производящих на нас такие впечатления" (Полн. собр. соч., т. 2, 1949, с. 136). Согласно Чернышевскому, "прекрасное есть жизнь" и "прекрасно то существо, в котором видим мы жизнь такою, какова должна быть она по нашим понятиям" (там же, с. 10).

В бурж. эстетике кон. 19-20 вв. проблема П. рассматривается с идеалистич. позиций. Согласно субъективно-идеалистич. теории вчувствования (Р. Фишер, Т. Липпс, Верной Ли и др.), П. образуется проецированием на предмет человеческого чувства. По определению Дж. Сантаяны (США) "...красота есть наслаждение, рассматриваемое как качество вещи" ("Тhе sense of beauty", N. Y., 1955, p. 51). Для Б. Кроче П.- "адекватность выражения" (см. "Эстетика как наука о выражении и как общая лингвистика", ч. 1, М., 1920, с. 106). В эстетике прагматизма П. трактуется как качество "опыта" в идеалистическом его понимании; Дж. Дьюи (США) сводит П. к "обозначению характерной эмоции" ("Art as experience", N. Y., 1934, p. 129). Ряд представителей совр. бурж. эстетики стирает границы между П. и безобразным.

Марксистская эстетика раскрыла закономерную связь между П. и трудовой деятельностью человека, на основе к-рой вообще возникло его эстетич. отношение к миру. К. Маркс отмечает, что "...человек формирует материю также и по законам красоты", поскольку он в практическом созидании предметного мира утверждает себя в своей общественно-человеческой сущности и, в отличие от животного, "производит универсально... будучи свободен от физической потребности...", "...свободно противостоит своему продукту", умеет производить по мерам любого вида и всюду умеет прилагать к предмету соответствующую меру (см. К. Маркс и Ф. Энгельс, Из ранних произв., 1956, с. 566). Многообразные явления природы и обществ, жизни обладают свойством П. в той мере, в какой они в своей конкретно-чувств. целостности выступают как общественно-человеческая ценность, свидетельствующая об утверждении человека в действительности, предметно воплощающая свободное развитие человека и общества. Поэтому восприятие и переживание П. вызывает бескорыстную любовь, чувство радости и ощущение свободы.

Определ. закономерности (правильность, симметричность, гармония, ритм, пропорциональность, "целесообразность", мера в звуковых и цвето-световых отношениях), характеризующие внеш. облик явлений, стали обладать эстетич. значимостью, поскольку через познание и использование их человек материально и духовно утверждает себя в мире. Свойством П. обладает сам человеческий труд как свободная, творческая, общественно значимая деятельность, доставляющая наслаждение "...игрой физических и интеллектуальных сил" (Маркс К., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 23, с. 189), а также её результаты, несущие на себе "отпечаток" большого мастерства и высокой культуры. В продуктах человеч. деятельности П. выступает как проявление и, следовательно, как свидетельство целесообразности и совершенства.

Значение П. для человека и общества носит духовно-практич. характер. Восприятие П. бескорыстно, т. е. чуждо вульгарному утилитаризму, но это не есть "незаинтересованность". Напротив, переживание П. потому и бескорыстно, что в нём сливаются личные и обществ. интересы, человек ощущает себя лично причастным к обществ. значению П. Т. о., эстетич. отношение к П. имеет и этич. аспект, соответствующий единству эстетич. и нравств. ценностей.

П. в искусстве - его художеств. ценность - обусловлено правдивым отражением жизни (красота истины), выражением гуманистических идеалов, а также мастерством, создающим форму, гармонически соответствующую содержанию.

П. как ценность, в к-рой выражено объективное эстетич. значение явлений, осваивается через субъективные эстетич. оценки, сквозь призму вкусов и идеалов людей. Важнейшей задачей эстетич. воспитания является формирование и развитие способности человека воспринимать подлинную ценность П.

В сов. лит-ре по эстетике проблема П.-предмет дискуссии, в центре к-рой соотношение в П. объективного и субъективного, природного и общественного.

Лит.: Ванслов В. В., Проблема прекрасного, М., 1957; Дмитриева Н. А., О прекрасном, М., 1960; Эстетическое. Сб. ст., М., 1964; Крюковский Н., Логика красоты, [Минск, 1965]; Лосев А. Ф., Шестаков В. П., История эстетических категорий, [М.], 1965; Природа и функции эстетического, [М.], 1968; Борев Ю., Эстетика, М., 1969; Столович Л. Н., Категория прекрасного и общественный идеал, М., 1969; Каган М. С., Лекции по марксистско-ленинской эстетике, 2 изд., Л., 1971; Philosophies of beauty..., sel. and ed. by E. F. Carritt, Oxf.. [1962].

Л. Н. Столович.

ПРЕКРАЩЕНИЯ ТОЧКА (матем.), особая точка кривой, в к-рой кривая обрывается. Напр., начало координат (рис.) является П. т. для кривой у=хlnх [т. к. функция lnх не определена (в области действительных чисел) при х < 0].

ПРЕКУЛЕ, город в Клайпедском р-не Литовской ССР. Расположен на р. Миния. Ж.-д. станция (на линии Клайпеда -Советск). Маслосыродельный и кафельный з-ды.

ПРЕЛОГ (Prelog) Владимир (р. 23.7. 1906, Сараево, Югославия), швейцарский химик-органик. После окончания Пражского технологич. ин-та (1928) работал в Праге в Лаборатории синтеза тонких хим. веществ. В 1935 вернулся в Югославию, где преподавал органич. химию в Загребском ун-те. В 1941 после оккупации Югославии фаш. войсками П. переехал в Швейцарию. Работал в Федеральной высшей технич. школе в Цюрихе; там в 1957 принял от Л. Ружички его Лабораторию органич. химии - один из крупных центров изучения химии природных соединений и физиологически активных веществ. П. принадлежат работы по стереохимии и разработке совр. методов исследования сложных органич. соединений, в т. ч. ряда практически важных антибиотиков. Иностр. чл. АН СССР (1966).

ПРЕЛОМЛЕНИЕ ВОЛН, изменение направления распространения волны, обусловленное переходом её из одной среды в другую, отличающуюся от первой значением скорости распространения волн в ней. См. Волны, Преломление света.

ПРЕЛОМЛЕНИЕ СВЕТА, изменение направления распространения оптического излучения (света) при его прохождении через границу раздела двух сред. На протяжённой плоской границе раздела однородных изотропных непоглощающих (прозрачных) сред с преломления показателями n₁ и п₂ П. с. определяется следующими двумя закономерностями: преломлённый луч лежит в плоскости, проходящей через падающий луч и нормаль (перпендикуляр) к поверхности раздела; углы падения ф и преломления Х (рис.) связаны Снелля законом преломления: n₁ sin ф = n₂sin X. П. с. сопровождается и отражением света, при этом сумма энергий преломлённого и отражённого пучков лучей (количеств. выражения для них следуют из Френеля формул) равна энергии падающего пучка. Их относит, интенсивности зависят от угла падения, значений n₁ и n₂ и поляризации света в падающем пучке. При нормальном падении отношение ср. энергий преломлённой и упавшей световых волн равно 4n₁ n₂/(n₁+n₂)²; в существенном частном случае прохождения света из воздуха (п₁с большой точностью = 1) в стекло с n₂ = 1,5 оно составляет 96%. Если n₁ >n₂ и угол падения ф>=arcsin (n₂/n₁ ), П. с. не происходит. и вся энергия, принесённая на границу раздела падающей световой волной, уносится отражённой волной (явление полного внутреннего отражения). При любых ф, кроме ф = 0, П. с. сопровождается изменением состояния поляризации света [наиболее сильным при т. н. угле Брюстера ф = arctg(n₂/n_t), см. Брюстера закон], что используют для получения линейно-поляризованного света (см. Стопа в оптике). Зависимость П. с. от поляризации падающих лучей наглядно проявляется при двойном лучепреломлении в оптически анизотропных средах. В поглощающих средах П. с. формально можно описать, используя те же выражения, что и для непоглощающих сред, но рассматривая п как комплексную величину (мнимая часть к-рой характеризует поглощение света средой; см., напр., Металлооптика). X при этом также становится комплексным и теряет простой смысл угла преломления, к-рый он имеет для непоглощающих сред. В общем случае п среды зависит от длины волны X света; поэтому при преломлении немонохроматич. света составляющие его лучи с различными X идут по разным направлениям (дисперсия света). На законах П. с. основано устройство линз и мн. оптич. приборов, служащих для изменения направления световых лучей и получения изображений оптических.

Ход лучей света при преломлении на плоской поверхности, разделяющей две прозрачные среды. Пунктиром обозначен отражённый луч. Угол преломления х больше угла падения Ф; это указывает, что в данном случае происходит преломление из оптически менее плотной 1-й среды в более оптически плотную 2-ю (n₁< <n₂). п- нормаль к поверхности раздела.

Лит.: Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973.

Н. А. Войшвилло.

ПРЕЛОМЛЕНИЯ ПОКАЗАТЕЛЬ относительный двух сред n₂₁ безразмерное отношение скоростей распространения оптического излучения -света (реже - излучения радиодиапазона) в 1-й (v₁) и во 2-й (v₂) средах: n₂₁=v₁/v₂. В то же время относительный П. п. есть отношение синусов угла падения а и угла преломления В излучения на границе раздела этих сред: п₂₁ = sin а/sinВ (см. Преломление света). Если 1-й средой служит вакуум (в к-ром скорость света с = 3-10¹⁰ см/сек), то П. п. среды относительно него наз. абсолютным: п = c/v. Относительный П. п. есть отношение абс. П. п. сред: n₂₁ = п₂/п₁.

П. п. зависит от длины волны X (частоты v) излучения (см. Дисперсия света). С диэлектрической проницаемостью е и магнитной проницаемостью п. соелы её абс. П. п. связан выражением

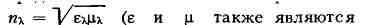
функциями X). Абс. II. п. среды определяется поляризуемостью составляющих её частиц (см. Клаузиуса-Моссотти формула, Лоренц-Лоренца формула, Поляризуемость атомов, ионов и молекул, Рефракция молекулярная), а также структурой среды и её агрегатным состоянием. Для сред, обладающих оптической анизотропией (естественной или индуцированной), П. п. зависит от направления распространения излучения и его поляризации (см. Поляризация света). Типичными анизотропными средами являются мн. кристаллы (см. Кристаллооптика). Среды, поглощающие излучение, описывают комплексным П. п. и = п(1 + г'и), где член, содержащий только п, как обычно, соответствует направленному пропусканию, а и = kХ/4п характеризует поглощение (fe - поглощения показатель среды; см. также Металлооптика, Поглощение света).

В диапазоне видимого света П. п. для слабо поглощающих (прозрачных) твёрдых тел меняется от 1,3 до 4,0; для жидкостей - от 1,2 до 1,9; для газов (при нормальных условиях) - от 1,000035 (Не) до 1,000702 (Хе).

ПРЕЛЮДИЯ, прелюд (позднелат. praeludium, от лат. praeludo - играю предварительно, на пробу, делаю вступление), инструментальная музыкальная пьеса, преим. сольная. Первоначально П. представляла собой небольшое вступление к к.-л. муз. пьесе, исполнявшееся на лютне, струнном клавишном инструменте или органе. Для П., в особенности ранней, характерны импровизационность, свободное развёртывание, фигурационная разработка материала, применение от начала до конца единого типа фактуры, сближающее её с жанром этюда. Такие пьесы часто носили и др. названия, напр., преамбула, интрада, ричеркар, фантазия и т. п. С 18 в. П. стали создаваться и как самостоят. пьесы гл. обр. для струнного клавишного инструмента; в то же время, прежде всего в творчестве И. С. Баха, сложился устойчивый малый цикл прелюдия - фуга. Бах утвердил также тип большого цикла прелюдий и фуг, охватывающий все мажорные и минорные тональности (1-й и 2-й тома "Хорошо темперированного клавира"). Подобные циклы создавались и впоследствии ("24 прелюдии и фуги" Шостаковича для фп.). Возник и цикл только прелюдий, также во всех тональностях (произв. Ф. Шопена, А. Н. Скрябина, К. Дебюсси, Д. Б. Кабалевского и др.).

ПРЕМИАЛЬНЫЕ СИСТЕМЫ ЗАРАБОТНОЙ ПЛАТЫ, см. в ст. Заработная плата.

ПРЕМИИ ГОСУДАРСТВЕННЫЕ, см. Государственные премии СССР.

ПРЕМИИ ИМЕНИ В. И. ЛЕНИНА, см. в ст. Ленинские премии.

ПРЕМИКСЫ (от лат. ргае - вперёд, предварительно и misceo - смешиваю), обогатительные смеси биологически активных веществ микробиол. и хим. синтеза, применяемые для повышения питательности комбикормов и улучшения биол. действия их на организм с.-х. животных. Различают П. витаминные, минеральные, витаминно-терапевтические и др. В состав П. входят: наполнитель (продукт, способный растворять и удерживать активные вещества) - овсяная мука, отруби, травяная мука, жмыхи, дрожжи и др.; биол. активные вещества - витамины, микроэлементы, аминокислоты, химико-терапевтич. препараты и др. П. производят на специализированных з-дах или на спец. линиях комбикормовых предприятий. Вырабатываются для животных разных видов, возрастов и направлений продуктивности.

ПРЕМИРОВАНИЕ на социалистических предприятиях в СССР, главная форма материального поощрения работников за личные или коллективные успехи в труде. В 1919 В. И. Ленин писал, что "премии будут недопустимы при системе полного коммунизма, но в переходную эпоху от капитализма к коммунизму обойтись без премий нельзя..." (Полн. собр. соч., 5 изд., т. 38, с. 98). Опыт строительства социализма и материально-технич. базы коммунизма подтвердил жизненность и необходимость этой формы поощрения.

П. осуществляется из двух источников: из фонда материального поощрения (см. Фонды экономического стимулирования) и из фонда заработной платы (см. Заработная плата). В отличие от тарифной ставки и должностного оклада, образующих основную, относительно постоянную часть заработной платы, премия представляет собой дополнительную, переменную её часть. Роль П. возросла в условиях экономич. реформы, когда на хозрасчётных предприятиях из прибыли создаются фонды материального поощрения. Размер премий зависит от личного трудового вклада работника, степени выполнения предприятием количественных и качественных показателей плана.

Наиболее распространено текущее П. Это - осн. форма материального поощрения рабочих и служащих, обусловленная системой оплаты труда. Осуществляется в соответствии с положениями о П., которые разрабатываются на предприятиях или в организациях на основе Типового положения о премировании работников пром. предприятий, переведённых на новую систему планирования и экономич. стимулирования, утверждённого Гос. комитетом Сов. Мин. СССР по вопросам труда и заработной платы и Президиумом ВЦСПС 4 февр. 1967. Администрация по согласованию с фабрично-заводским местным комитетом самостоятельно решает вопрос о выборе большинства показателей и условий П., определяет размер премий и круг премируемых лиц. Используются различные количественные и качественные показатели. Напр., текущее П. рабочих, направленное на улучшение количественных показателей, производится за выполнение и перевыполнение производств. планов, нормированных заданий, технически обоснованных норм выработки, снижение трудоёмкости и т. д. Среди показателей П. рабочих за улучшение качества продукции и работ часто используются такие, как бездефектное изготовление продукции, снижение потерь от брака, выполнение или перевыполнение плановых заданий по сорту, марке продукции. Рабочие премируются также за экономию материальных ценностей, улучшение результатов хоз. деятельности бригады, участка, цеха и др. показатели. Текущее П. работников аппарата управления предприятия производится за выполнение и перевыполнение планов по реализации продукции (или прибыли), заданий по росту производительности труда и повышению удельного веса продукции высшей категории качества, рентабельности. Инженерно-технич. работники (ИТР) и служащие цехов премируются по одному или неск. показателям, в числе к-рых могут быть выполнение и перевыполнение планов по объёму произ-ва и качеству продукции, производительности труда, снижению себестоимости и т. д.

Важное условие орг-ции П. - периодич. пересмотр и повышение уровня показателей, при достижении к-рого выплачивается премия. Несоблюдение этого требования ослабляет стимулирующую роль П. и может привести к превращению премии в простую надбавку к заработной плате. Совершенствование системы П. должно учитывать степень влияния данного работника на рост производительности труда и эффективности произ-ва.

Размер премий рабочим и служащим устанавливается с учётом их вклада в общие результаты труда. Величина премий из фонда материального поощрения не ограничивается. Премии, выплачиваемые рабочим из фонда заработной платы, не должны превышать 40% сдельного заработка или тарифной ставки (60% у нек-рых категорий рабочих в электротехнич., угольной, хим. пром-сти, чёрной металлургии). Полное или частичное лишение отд. работников премий допускается за производств. упущения, прогул, в случаях привлечения к адм. или уголовной ответственности, а также как мера обществ. воздействия за хулиганство.

Среди осн. направлений использования фонда материального поощрения - П. работников по итогам внутризаводского социалистич. соревнования, а также отличившихся при выполнении особо важных производств. заданий. Из того же источника выплачиваются вознаграждения работникам за общие результаты работы предприятия по итогам года, размер к-рых зависит от личного вклада каждого работника в выполнение и перевыполнение плановых показателей, а также от продолжительности непрерывного стажа работы на данном предприятии.

Для решения отд. задач, имеющих нар.-хоз. значение, используются различные виды премий рабочим и служащим, к-рые выплачиваются из спец. фондов предприятий: за создание и внедрение новой техники, поставку продукции на экспорт, выпуск предметов широкого потребления из отходов произ-ва, лучшие результаты по итогам социалистич. соревнования.

П. служит не только материальным, но и моральным поощрением. П. рассматривается как признание заслуг работника и имеет большое воспитат. значение. В социалистич. соревновании П. обеспечивает более полное сочетание материальных и моральных стимулов к труду (см. ст. Материальное и моральное стимулирование).

Роль премиальной части заработной платы значительно возросла в условиях хоз. реформы и в др. социалистич. странах. Во многих из них осн. принципы П. и макс. размеры премий устанавливаются централизованно. Предприятия самостоятельно решают вопросы выбора показателей и условий П., определяют его сроки и порядок, а также круг премируемых. Кроме фонда заработной платы, для П. используются такие поощрит, фонды, как фонд дополнит. материального стимулирования (Болгария), единый премиальный фонд (ГДР), фонд участия в прибылях (Венгрия), премиальный фонд ИТР и служащих и фонд предприятия (Румыния), фонд вознаграждения (ЧССР).

Лит.: Ленин В. И., Проект программы РКП(б), Полн. собр. соч., 5 изд., т. 38; его же, Постановление о работе замов (заместителей председателя СНК и СТО), там же, т. 45; его же, Ответ на замечания, касающиеся работы замов (заместителей председателя СНК), там же; Материалы XXIV съезда КПСС, М., 1971; Сухаревский Б. М., Стимулирование производства я экономика социализма. (Вопросы теории и практики), М., 1968; Шкурко С. И., Материальное стимулирование в новых условиях хозяйствования, М., 1970; [Егизарян Г. А., Хейфец Л. С.], Проблемы материального стимулирования в промышленности, М., 1970; Материальное поощрение работников промышленных предприятии, М., 1973.

Л. С. Хейфец.

ПРЕМИЯ (от лат. praemium - награда), одна из форм поощрения за успехи, достигнутые в труде, на науч. поприще, в литературе, искусстве и др. общественно полезной деятельности.

В СССР учреждены Ленинские премии, Государственные премии СССР и союзных республик, премии Ленинского комсомола, а также Международные Ленинские премии "За укрепление мира между народами*. Гос. премии учреждены и в ряде других социалистич. стран (напр., П. им. Димитрова в Болгарии, П. им. Кошута в Венгрии, П. им. Готвальда в Чехословакии, Нац. П. в ГДР, Гос. П. в Польше и Румынии). Гос. П. имеются и в нек-рых бурж. гос-вах (напр., во Франции, Италии). Всемирный конгресс сторонников мира присуждает Международные премии мира.

П. в области науки. Традиция присуждения почётных П. за крупные науч. труды, открытия и изобретения начала складываться в 18 в. В 1714 в Великобритании была учреждена П. за нахождение точного метода определения долготы на море (части её были выплачены только в 1765 наследникам Т. Майера - за лунные таблицы, Л. Эйлеру - за разработку вопросов лунной теории, Дж. Харрисону - за усовершенствование хронометра). В 18 в. П. за успешное решение задач, выдвинутых на спец. конкурсы, присуждали ведущие академии наук: франц. АН (с 1720), Прусская АН в Берлине (с 1746), Петерб. АН (в соответствии с уставом 1747), Баварская АН (с 1756). Позднее П. за науч. исследования стали учреждать нек-рые учёные, богатые меценаты, науч. и др. об-ва, фонды, редакции науч. журналов и т. д.

В России до 1917 большинство П. за науч. труды присуждала АН, в их числе Демидовская П. (в 1832-64, по мн. отраслям), П. им. К. М. Бэра (с 1867, анатомия, гистология, эмбриология и др.), Ломоносовская (с 1866, по мн. отраслям), им. В. Я. Буняковского (с 1878, математический анализ), им. Г. П. Гельмерсена (с 1879, геология, палеонтология и др.), им. Ф. Ф. Брандта (с 1896, зоогеография и др.), им. К. Д. Ушинского (с 1901, воспитательная психология). П. за науч. труды и решение конкурсных задач присуждали также гос. ведомства (напр., Гл. артиллерийское управление учредило в 1845 Большую Михайловскую П. за труды и изобретения по артиллерии), науч. об-ва (напр., Петерб. об-во естествоиспытателей с 1889 присуждало П. им. К. Ф. Кесслера за труды по зоологии; Казанское физико-математическое об-во с 1897 - международную П. им. Н. И. Лобачевского за труды по математике), учебные заведения (напр., с 1854 П. Михайловской артиллерийской академии, с 1838 П. им. акад. И. Ф. Буша Медико-хирургич. академии).

В СССР, кроме Ленинских премий и Гос. премий, учреждены П. имени выдающихся рус. и сов. учёных. АН СССР присуждает П. имени: Д. И. Менделеева (учреждена в 1934, химия и хим. технология), И. П. Павлова (1934, физиология), А. О. Ковалевского (1940, эмбриология), К. А. Тимирязева (1941, физиология растений и др.), С. А. Чаплыгина (1942, механика), В. И. Вернадского (1943, биогеохимия и др.), С. В. Лебедева (1944, химия и технология синтетич. каучука и др.), В. Л. Комарова (1944, ботаника и др.), П. Л. Чебышева (1944, математика), И. И. Мечникова (1945, микробиология и др.), А. Н. Баха (1946, биохимия), А. Е. Ферсмана (1945, минералогия и др.), Ф. А. Бредихина (1946, астрономия), А. П. Карпинского (1946, геология и др.), В. В. Докучаева (1946, почвоведение), Н. И. Лобачевского (1947, геометрия), Е. С. Фёдорова (1947, кристаллография), В. Г. Белинского (1947, лит. критика, теория и история лит-ры), П. П. Аносова (1948, металлургия и др.), Н. Д. Зелинского (1949, химия и химия нефти), М. В.Ломоносова (1956, физика), А. М. Бутлерова (1956, органич. химия), И. М. Сеченова (1956, общая физиология), Н. Г. Чернышевского (1956, общественные науки), А. С. Попова (1959, радиотехника и электроника), Н. И. Вавилова (1965, генетика и др.), Г. В. Плеханова (1969, философия), А. С. Пушкина (1969, рус. яз. и лит-ра) и др. АМН СССР присуждает П. имени: Н. Н. Бурденко (1946, нейрохирургия и др.), Н. Ф. Филатова (1947, педиатрия); с 1958 - П. имени: С. П. Боткина (внутренние болезни), В. М. Бехтерева (неврология и др.), В. П. Воробьёва (нормальная анатомия), Н. П. Кравкова (фармакология и токсикология), Г. Ф. Ланга (сердечно-сосудистая патология), Н. И. Пирогова (хирургия); А. Л. Мясникова (1967, кардиология), Н. Н. Петрова (1967, онкология) и др. ВАСХНИЛ присуждает П. по земледелию, агропочвоведению и агрохимии; растениеводству и селекции; защите растений; животноводству, ветеринарии; гидротехнике, мелиорации и водному х-ву; лесоводству и агролесомелиорации и др. П. присуждают также нек-рые науч. об-ва (напр., Географич. об-во СССР - П. им. С. И. Дежнёва, 1948, за лучшие труды по географии Сев.-Вост. Азии), ун-ты (напр., МГУ - П. им. М. В. Ломоносова, 1945, по мн. отраслям). П. имени выдающихся учёных установлены в союзных республиках, напр. Гос. П. Тадж. ССР им. Ибн Сины (1967).

В др. социалистич. странах также учреждены П. имени выдающихся обществ. деятелей и учёных, напр. в ГДР - П. им. Ф. Энгельса за труды по истории, П. им. Р. Вирхова за труды по медицине; в Польше - П. им. М. Склодовской-Кюри за труды по физике, П. им. О. Ланге за труды по экономике.

Среди междунар. П. за науч. труды и открытия ведущее место занимают Нобелевские премии. Учреждены также др. международные научные П.; лауреатами их являются и советские учёные. Напр., Международная академия астронавтики с 1961 присуждает премию Гутгенхеймов (в числе её лауреатов М. В. Келдыш, космонавты А. Г. Николаев, В. И. Севастьянов); междунар. П. учреждена А. Галабером в 1958 (присуждена Ю. А. Гагарину, В. В. Николаевой-Терешковой; сов. учёным А. А. Штернфельду, А. Г. Масевич; АН СССР за создание науч. станции "Луна-16"). Спец. комитет Междунар. математич. конгресса присуждает молодым математикам Филдсовскую П. (один из её лауреатов - С. П. Новиков). П. фонда Э. Бальзана, учреждённой в 1962, отмечены труды А. Н. Колмогорова. В Италии в 1954 учреждена междунар. П. по коммуникациям им. X. Колумба (один из её лауреатов - АН СССР), в 1958 - П. им. М. Панетти за труды в области механики (этой П. награждён Н. И. Мусхелишвили).С 1956 П. присуждает амер. комитет "Атом для мира" (лауреат 1963 - В. И. Векслер). Имеются междунар. П., присуждаемые за труды, способствующие развитию сотрудничества между двумя странами (напр., сов. и инд. учёным с 1968 присуждается П. им. Дж. Неру).

Во Франции наиболее авторитетные нац. науч. П. присуждает франц. АН: им. Ж. Кювье (учреждена в 1839, естествознание, зоология, геология), им. Ж. Ж. Ф. Лаланда (1802, астрономия), им. П. А. Чихачёва (1890, археология, география и геология Азии). В Италии высшей науч. наградой считается Нац. П. президента республики (по мн. отраслям); учреждены также П. им. А. Фельтринелли (1949, по мн. отраслям) и др. Одной из видных науч. П. в США является П. Нац. АН (естественные, точные и технические науки). Ряд нац. П. присуждается и иностр. учёным. В др. странах, напр. в Великобритании, ФРГ, практикуется выдача спец. денежных П. вместе с медалями, присуждаемыми за лучшие науч. труды. Так, Лондонское королев. об-во вместе с медалью им. Г. Копли (учреждена в 1731) с 1957 выдаёт лауреату П. им. Д. Яффе; П. выдаются при награждении медалями им. Э. Резерфорда, им. Ч. Дарвина и др.

П. в области литературы и искусства. Практика присуждения П. и призов в области иск-ва (ранее всего - музыкального) сложилась ещё в Др. Греции, где награждались участники Олимпийских игр, лучшие музыканты Пифийских игр и др. состязаний (в т. ч. и театральных). В ср. века П. и призы присуждались победителям рыцарских турниров, муз. фестивалей, соревнований трубадуров, миннезингеров, театральных зрелищ и др.

В 19 в. П. в области лит-ры и иск-ва стали присуждаться различными обществами, редакциями журналов. Так, в дореволюц. России АН (1881) была учреждена лит. П. им. А. С. Пушкина (среди лауреатов - А. Н. Майков, Я. П. Полонский, С. Я. Надсон, И. А. Бунин, А. П. Чехов); Об-во рус. драматических писателей и оперных композиторов учредило П. им. А. С. Грибоедова (присуждена А. Н. Островскому, Л. Н. Толстому, А. М. Горькому и др.). Крупнейшей муз. П. были Глинкинские П., учреждённые в 1884 известным издателем М. П. Беляевым за лучшие муз. произведения, созданные рус. композиторами (первые лауреаты - М. А. Балакирев, А. П. Бородин, П. И. Чайковский, Н. А Римский-Корсаков, Ц. А. Кюи, А. К. Лядов).

В СССР деятели литературы и искусства награждаются Ленинскими премиями, Гос. премиями СССР и союзных республик, премиями Ленинского комсомола, кроме того, учреждены спец. П. по литературе, музыкальные П., П. в области театрального искусства, кинематографии и т. д. В союзных республиках учреждены спец. гос. П. и П. комсомола в этой области, в т. ч.: в РСФСР - лит. П. им. М. Горького, им. Н. К. Крупской, им. К. С. Станиславского (за драматургич. произведения и театральные спектакли), им. М. И. Глинки (в области музыки), им. братьев Васильевых (в области киноискусства), им. И. Е. Репина (изобразит. иск-во), им. В. И. Баженова (архитектура); в УССР - им. Т. Г. Шевченко (лит-pa и др. виды иск-ва), лит. П. им. Павла Тычины, Максима Рыльского, Леси Украинки, Николая Островского; в БССР - лит. П. им. Янки Купалы, Якуба Коласа (за произведения лит-ры и иск-ва для детей), им. П. Н. Лепешинского (в области журналистики и в области музыки), комсомола Белоруссии и др.; в Узб. ССР - П. им. Хамзы (по всем видам иск-ва), П. комсомола Узбекистана, лит. П. им. Ниязи и др.; в Груз. ССР - П. комсомола Грузии и П. им. Шота Руставели (по всем видам иск-ва); в Арм. ССР - премия ЦК комсомола (для поощрения творческой молодёжи), П. им. А. Хачатуряна (для композиторов) и им. А. Даниэлян (для исполнителей); в Казах. ССР - лит. П. им. Абая и муз. П. им. К. Байсеитовой и им. Курмангазы, П. комсомола Казахстана (по всем видам иск-ва); в Азерб. ССР - лит. П. им. М. Ф. Ахундова и муз. П. им. У. Гаджибекова; в Туркм. ССР - П. им. Махтумкули и П. комсомола Туркменистана (по всем видам иск-ва); в Кирг. ССР - П. им. Токтогу-ла Сатылганова (по всем видам иск-ва); в Молд. ССР - П. комсомола Молдавии им. Бориса Главана (по всем видам иск-ва); в Тадж. ССР - П. им. Абу Абдулло Рудаки (по всем видам иск-ва); в Литов. ССР - П. комсомола Литвы (по всем видам иск-ва), лит. П. им. Жемайте и им. П. Зибертаса; в Латв. ССР - П. комсомола Латвии (по всем видам иск-ва), лит. П. им. Э. Вейденбаума; в Эст. ССР - П. комсомола Эстонии (по всем видам иск-ва), лит. П. им. Юхана Смуула и др. Премии по лит-ре и иск-ву имеются также в ряде авт. республик. Кроме того, П. в области отд. видов иск-ва учреждены творческими союзами, напр. Союзом журналистов СССР - П. за лучшие произведения года, опубликованные в печати, переданные по радио и телевидению, П. им. М. И. Ульяновой за лучшую постановку массовой работы в редакциях городских, районных и многотиражных газет. Моск. гор. орг-ция Союза журналистов СССР учредила П. за лучшие произведения в области междунар. журналистики.

П. по лит-ре и иск-ву присуждаются и в зарубежных гос-вах. Старейшая из них - Римская премия, учреждённая в 1803 Академией иск-в в Париже (присуждается выпускникам художеств. уч. заведений по итогам спец. конкурсов). Лауреатами Римской П. были композиторы Ж. Галеви, Г. Берлиоз, Ж. Визе, Ж. Массне, К. Дебюсси и др.

В ГДР учреждена лит. П. им. И. Бехера, в Румынии - им. Василе Александрии др. Широко известны такие лит. П., как Пулицеровская (США), Гонкуровская и П. Франц. академии (Франция), премия Джеймса Тейта Блейка (Великобритания), премия Виареджо, Лучано (Италия), им. Сервантеса (Испания), П. им. Бюхнера и П. им. Гёте города Франкфурта-на-Майне (ФРГ) и др., муз. П. "Мендельсоновская стипендия" (Великобритания), П. изд-ва "Рикорди" (Италия) и др.

Существуют междунар. П. в области лит-ры и иск-ва, напр. П. "Лотос" Ассоциации писателей Азии и Африки, премия Ханса К. Андерсена Междунар. совета по книгам для детей и юношества, Междунар. П. издателей и др.

Распространение получили различные междунар. и нац. муз. конкурсы, кинофестивали, выставки и т. д., на к-рых победителям присуждаются П. и призы. Наиболее известны П. Междунар. московского кинофестиваля (3 золотых приза), П. "Золотой Лев св. Марка" и П. "Серебряный Лев св. Марка" Междунар. кинофестиваля в Венеции, Гран при Междунар. конкурса балета в Москве, "Золотая пальмовая ветвь" Каннского кинофестиваля, П. "Хрустальный глобус" Междунар. кинофестиваля в Карлови-Вари, П. "Оскар" Амер. академии киноискусства и наук, П. междунар. выставок и конкурсов по изобразит. иск-ву в Венеции, Сан-Паулу, Любляне, Кракове, Братиславе и др. Учреждены П. Междунар. союза архитекторов (им. Л. П. Аберкромби, О. Перре, им. Ж. Чуми), П. ЮНЕСКО за лучшие студенческие работы в области архитектуры и др.

Лит.: Корнеев С. Г., Советские ученые - почетные члены иностранных научных учреждений, М., 1973; Копелевич Ю. X., Возникновение научных академий, Л., 1974.

Премчанд.

ПРЕМЧАНД (псевд.; наст. имя Дханпатрай Шривастав) (31.7.1880, Ламхи, близ Бенареса, - 8.10. 1936, Бенарес), индийский писатель и публицист. Писал на урду и хинди языках. Работал учителем и школьным инспектором . Творчество П. развивалось под воздействием инд. нац.-освободит. движения. Первый сб. рассказов "Любовь к родине", опубликованный в 1909, был сожжён английскими властями. В романах П. "Обитель любви" (1922), "Арена" (1925, рус. пер. 1967), "Поле битвы" (1932, рус. пер. 1958), "Жертвенная корова" (1936, рус. пер. 1956), в сб-ках "Семь лотосов" (1917), "Ратный путь" (1932) запечатлены политич. пробуждение масс, их борьба за социальные права и освобождение родины. П. обличал колониальный и феод, произвол, ср.-век. косность и религ. фанатизм. Острая критика колониализма навлекла на него гонения властей. Злободневные политич. и социальные проблемы сочетались у П. с психологич. глубиной характеристик действующих лиц. Писатель-демократ, П. видел в народе гл. силу общества и боролся за утверждение гуманистич. идеалов, восхищался успехами социалистич. строительства в СССР. П.- основоположник критич. реализма в лит-pax урду и хинди. Большую роль в укреплении позиций реалистич. и демократич. лит-ры в Индии сыграли публицистика П. и его журналы "Ханс" (1930-1936) и "Джагаран" (1932-1934). П. - один из основателей Ассоциации прогрессивных писателей Индии (1936), оказавшей значит, влияние на инд. лит-ры.

Соч.: Манасаровар, т. 1-8, Бенарес, 1953 - 56; Гуптадхан, т. 1 - 2, Аллахабад, 1962; Вивидх прасанг, т. 1 - 3, Аллахабад, 1962; в рус. пер.- Колодец тхакура, М., 1955; Змеиный камень, М., 1957; Рассказы. Нирмала, М., 1958; Растрата, М., 1961; Ратный путь. Рассказы, М., 1969.

Лит.: Балин В., Премчанд-новеллист, Л., 1973; Премчанд. Биобиблиографич. указатель, М., 1962; Раджешвар Гуру, Премчанд. Эк адхъяян, Бхопал, 1958; Камар Раис, Премчанд ка танкиди мутала, Алигарх, 1959; Амритрай, Премчанд. Калам ка сипахи, Аллахабад, 1962; МаdanGopal, Munshi Premchand. A literary biography, N. Y., 1964.

В. И. Балин.

ПРЕМЬЕР, премьерша (от франц. premier - первый), актёр (актриса), занимающий первое или одно из первых мест в труппе, играющий главные (первые) роли.

ПРЕМЬЕРА (от франц. premiere - первая), первое публичное платное представление нового (или возобновлённого) спектакля, эстрадной, цирковой программы, кинофильма, телефильма и др. Под словом "П." часто подразумевается репертуарная новинка.

ПРЕМЬЕР-МАЙОР, штаб-офицерский чин в русской армии, введённый Петром I в 1711. П.-м. являлся первым заместителем командира полка. Чин П.-м. упразднён в 1797.

ПРЕМЬЕР-МИНИСТР, в ряде совр. бурж. гос-в глава правительства, по общему правилу назначаемый главой гос-ва. П.-м. назначает и отстраняет от должности министров, руководит повседневной деятельностью пр-ва, возглавляет адм. аппарат. Как правило, П.-м.- лидер партии, располагающей большинством в парламенте, или лидер партийной коалиции, руководит парламентской фракцией большинства. В нек-рых странах (напр., в ФРГ) глава пр-ва называется канцлером.

ПРЕНАЙ, город, центр Пренайского р-на Литовской ССР. Расположен на лев. берегу р. Нямунас, в 32 км к Ю. от Каунаса. Швейная ф-ка, молочный и скипидарный з-ды; леспромхоз.

ПРЕНИТ [от имени голл. полковника Прена (Prehn), обнаружившего этот минерал на мысе Доброй Надежды], минерал из подкласса слоистых алюмосиликатов хим. состава Са₂А[AlSi₃O₁₀](OH)₂ с небольшой примесью Fe, замещающего Аl. Кристаллизуется в ромбич. системе. Ясно образованные кристаллы редки. Обычно имеют призматич. таблитчатый облик. Распространён гл. обр. в виде почковидных агрегатов с радиально-волокнистым строением. Цвет зеленовато-жёлтый, серый. Тв. по минералогич. шкале 6,5; плотность 2800-2950 кг/м³. П. - обычный гидротермальный минерал, выполняющий пустоты основных эффузивных пород совместно с цеолитами, кальцитом, эпидотом и др.; образуется также при разложении плагиоклазов в габбро и диабазах, а также в метаморфизованных породах (скарнах).

ПРЕНИЯ СУДЕБНЫЕ, в судебном процессе самостоят. часть судебного разбирательства, в к-рой участники процесса подводят итог проведённого судом исследования обстоятельств дела и высказывают предложения о том, как оно должно быть разрешено. В сов. уголовном процессе П. с. включают речи обвинителей (см. Обвинение), гражд. истца, гражд. ответчика или их представителей, защитника, общественного защитника или подсудимого, если защитник в суд. заседании не участвует, а по делам т. н. частного обвинения, кроме того, потерпевшего (или его представителя). По законодательству нек-рых союзных республик (напр., УПК УССР, ст. 318) потерпевший участвует в П. с. по всем делам, по к-рым не выступает гос. или обществ. обвинитель. Продолжительность П. с. временем не ограничена, но председательствующий вправе остановить выступающих, если они касаются обстоятельств. не имеющих отношения к делу. После речей участники П. с. могут обменяться репликами (по одной реплике каждый, причем право последней реплики принадлежит защитнику, а при его отсутствии подсудимому). В гражд. процессе в П. с. выступают истец, ответчик, их представители и третьи лица. Прокурор участвует в П. с. по гражд. делу, только если он сам возбудил дело (в иных случаях он даёт заключение после П. с.).

ПРЕНСАЛАТИНА (ПЛ; Prensa Latina), латиноамер. информац. агентство - акционерное об-во лат.-амер. стран, осн. в 1959. Находится в Гаване. ПЛ снабжает информацией прессу Кубы и др. стран Лат. Америки. Отделения и корреспондентские пункты ПЛ имеются в большинстве стран Лат. Америки, в странах Европы и Африки. Имеет соглашения об обмене информацией с ТАСС и др. агентствами социалистич. стран, а также с рядом агентств др. стран. Издаёт бюллетени лат.-амер. новостей на исп. и англ. языках.

ПРЕНЦЛАУ (Prenzlau), город в ГДР, в округе Нёйбранденбург, на сев. берегу озера Унтер-Иккер, при выходе из него р. Иккер. 22,8 тыс. жит. (1973). Машиностроение, произ-во арматуры, пищ. (сахарная и др.), деревообр. пром-сть.

ПРЕОБРАЖЕНИЕ, посёлок гор. типа в Лазовском р-не Приморского края РСФСР. Расположен на берегу Японского м., в 163 км к Ю.-В. от ж.-д. ст. Сергеевка. Рем.-эксплуатационная база.

ПРЕОБРАЖЕНСКАЯ Ольга Ивановна [1881 (по др. данным, 1884), Москва, - 31.10.1971, там же], русская советская киноактриса и кинорежиссёр, засл. деят. иск-в РСФСР (1935). Училась в студии Моск. Художеств, театра (1905-06), затем работала в провинциальных театрах. В 1913 дебютировала в кино. Роли: Лиза ("Дворянское гнездо" по Тургеневу), Наташа Ростова ("Наташа Ростова" по "Войне и миру" Л. Н. Толстого), княгиня Вера ("Гранатовый браслет" по Куприну) - все в 1915. С 1916 кинорежиссёр; первый фильм поставила совм. с В. Р. Гардиным - "Барышня-крестьянка" (по Пушкину); последующие режиссёрские работы: "Каштанка" (1926, по Чехову), "Аня" (1927). Совместно с И. К. Правовым поставила фильмы "Бабы рязанские" (1927), "Последний аттракцион" (1929), "Тихий Дон" (1931, по Шолохову), "Вражьи тропы" (1935), "Степан Разин" (1939), "Парень из тайги" (1941). В 20-е гг. преподавала в Гос. киношколе (ныне ВГИК).

ПРЕОБРАЖЕНСКАЯ Софья Петровна [14(27).9.1904, Петербург, - 21.7.1966, Ленинград], русская советская певица (меццо-сопрано), нар. арт. СССР (1955). Окончив Ленингр. консерваторию (класс И. В. Ершова), в 1928 дебютировала на сцене Ленингр. театра оперы и балета им. Кирова, где работала до 1959. Обладала сильным голосом, редким по красоте тембра и широте диапазона. Партии: Марфа ("Хованщина" Мусоргского), Иоанна, Графиня ("Орлеанская дева", "Пиковая дама" Чайковского; Гос. пр. СССР, 1946), Любаша ("Царская невеста" Римского-Корсакова), Азучена ("Трубадур" Верди), Груня ("Броненосец "Потёмкин"" Чишко), Ефросинья ("Семья Тараса" Кабалевского; Гос. пр. СССР, 1951). Вела концертно-исполнит. деятельность (вокальный цикл "Песни и пляски смерти" Мусоргского). В 1949-53 проф. Ленингр. консерватории. Награждена 2 орденами, а также медалями.

Лит.: Ольховский Е., Софья Петровна Преображенская, Л., 1950; Трайнин В., Софья Петровна Преображенская, Л., 1972.

ПРЕОБРАЖЕНСКИЙ Борис Сергеевич [15(27).6.1892, Москва, - 7.12.1970, там же], советский оториноларинголог, акад. АМН СССР (1950), Герой Социалистич. Труда (1962). В 1914 окончил мед. ф-т Моск. ун-та. В 1936-41 проф. 3-го Моск. мед. ин-та, с 1941 зав. кафедрой болезней уха, горла и носа 2-го Моск. мед. ин-та. Осн. труды по проблемам ангины и хронич. тонзиллита, тугоухости и глухоты, повреждений уха, горла и носа, аллергии в оториноларингологии, истории медицины. Разработал классификацию школьной тугоухости; предложил и усовершенствовал технику нек-рых операций, ряд мед. инструментов. Создал школу оториноларингологов. Один из организаторов Всесоюзного науч. об-ва оториноларингологов, почётный чл. Чехосл. науч. об-ва им. Я. Пуркине, чл. Интернац. к-та оториноларингологов, Венг. ассоциации мед. об-в. Награждён 5 орденами Ленина, а также медалями.

Соч.: Глухонемота, М., 1933; Военно-травматические повреждения уха, горла, носа, М., 1944; Болезни уха, горла и носа, 7 изд., М.,_1968 (совм. с Я. С. Тёмкиным и А. Г. Лихачёвым); Ангина, хронический тонзиллит и сопряжённые с ним заболевания, М., 1970 (совм. с Г. Н. Поповой).

Лит.: Памяти Б. С. Преображенского, "Вестник оториноларингологии", 1971, №2.

ПРЕОБРАЖЕНСКИЙ Евгений Николаевич [9(22).6.1909, с. Благовещенье, ныне Кирилловского р-на Вологодской обл., - 29.10.1963, Москва], советский военачальник, генерал-полковник авиации (1951), Герой Сов. Союза (13.8.1941). Чл. КПСС с 1940. Род. в семье сел. учителя. В Сов. Армии с 1927. Окончил Военно-морское авиац. уч-ще (1930) и курсы усовершенствования начсостава при Военно-возд. инж. академии (1933). Во время Великой Отечеств. войны 1941-45 командир авиаполка и бригады (1941-43) на Балт. флоте. В авг. 1941 участвовал в нанесении первых бомбовых ударов по воен. объектам Берлина с о. Сааремаа (Эст. ССР), а затем в обороне Ленинграда. Нач. штаба (апр. 1943 - сент. 1944) и командующий ВВС (сент. 1944 - апр. 1945) Сев. флота, зам. команд. ВВС Тихоокеанского флота (1945-46). С февр. 1946 команд. ВВС флота, с февр. 1950 команд, авиацией ВМФ. С 1962 воен. консультант группы ген. инспекторов Мин-ва обороны СССР. Награждён 3 орденами Ленина, 5 орденами Красного Знамени, орденами Суворова 2-й степени, Красной Звезды и медалями, а также орденом КНДР.

ПРЕОБРАЖЕНСКИЙ Николай Александрович (р. 27.11.1918, Москва), советский оториноларинголог, чл.-корр. АМН СССР (1974). Чл. КПСС с 1959. В 1941 окончил 1-й Моск. мед. ин-т. С 1963 проф., с 1972 зав. кафедрой болезней уха, горла и носа этого ин-та. Осн. труды по проблемам заболеваний органов слуха, ангины и хронич. тонзиллита; разработал методы мобилизации стремени при отосклерозе и отите, предложил протезы для реконструкции звукопроводящей системы среднего уха, ряд мед. инструментов. Ленинская пр. (1964) за совершенствование и внедрение в практику слухоулучшающих операций у больных отосклерозом. Пред. Всесоюзного науч. об-ва оториноларингологов (1968), почётный чл. Итал. об-ва оториноларингологов и шейно-лицевых хирургов (1973). Награждён орденом Отечеств, войны 2-й степени и медалями.

Соч.: Отосклероз, 2 изд., М., 1965 (совм. с К. Л. Хиловым); Стапедэктомия и стапедопластика при отосклерозе, М., 1973 (совм. с О. К. Патякиной).

ПРЕОБРАЖЕНСКИЙ Павел Иванович [1(13).1.1874. ныне Крестецкий р-н Новгородской обл.,-10.9.1944, Москва], советский геолог, специалист в области га-лургии, доктор геолого-минералогич. наук (1935). Окончил Горный ин-т в Петербурге (1900). Работал старшим геологом Геол. к-та (1913-18 и 1924-39), проф. Пермского ун-та (1923-24), сотрудником Ин-та галургии (1939-43), зам. директора Ин-та горно-химич. сырья (1943-1944). Проводил геол. исследования в Ленско-Витимском и Байкальско-Ленском золотоносных р-нах (1901-16). Основные труды связаны с изучением соляных месторождений СССР. П. - первооткрыватель крупнейшего в мире Соликамского месторождения калийных и магниевых солей (1925) и первого промышленного месторождения нефти в Приуралье - Верхнечусовские городки (1929). В честь П. назван минерал из группы водных боратов - преображенскит Mg₃BioO₁₈ -4,5H₂O. Награждён 2 орденами.

Соч.: Соликамское калийное месторождение, Л., 1933.

Лит.: Дзенс-Литовский А. И., Татаринов П. М., Эдельштейн Я. С., Памяти проф. П. И. Преображенского, "Природа", 1946, № 3.

ПРЕОБРАЖЕНСКИЙ ПРИКАЗ, центр. гос. учреждение России в кон. 17 - нач. 18 вв. Создан Петром I в 1686 в подмосковном с. Преображенском для управления Преображенским и Семёновским полками; использовался царём в борьбе за власть против царевны Софьи. С 1695 стал называться П. п.; ведал охраной порядка в Москве, расследовал особо важные суд. дела и др. С 1697 получил исключит. право следствия и суда по политич. преступлениям. Находился в непосредств. ведении царя. Известным ограничением функций П. п. было учреждение Тайной канцелярии (1718-26), к-рая рассматривала дела чрезвычайной важности (дело царевича Алексея и др.). Деятельность П. п. была направлена на подавление антикрепостнич. выступлений народа (до 70% всех дел), борьбу с противниками преобразований Петра I. Упразднён в апр. 1729. Начальники (судьи) П. п.: кн. Ф. Ю. Ромодановский (1686-1717), кн. И. Ф. Ромодановский (1718-29).

Лит.: Голикова Н. Б., Политические процессы при Петре I, M., 1957.

ПРЕОБРАЗОВАНИЕ, одно из осн. понятий математики, возникающее при изучении соответствий между классами геометрич. объектов, классами функций и т. п. Напр., при геометрич. исследованиях часто приходится изменять все размеры фигур в одном и том же отношении, увеличивать радиусы кругов на одну и ту же величину, вообще сопоставлять фигурам к.-л. класса другие, получаемые из них по определённым правилам. При решении дифференциальных ур-ний операционными методами (см. Операционное исчисление) заменяют данные функции другими, преобразованными функциями, и т. д. Такие соответствия и наз. П. Точнее, преобразованием называется соответствие, в силу к-рого каждому элементу х некоторого множества X сопоставляется вполне определённый элемент у нек-рого другого множества У. Логически понятие П. совпадает с понятиями функция, отображение, оператор. Термин "П." чаще употребляют в геометрии и функциональном анализе, при этом обычно считают соответствие между х и у - f(x) взаимно однозначным.

Геометрические преобразования. В геометрии чаще всего рассматриваются точечные П., при к-рых каждой точке нек-рого многообразия (линии, поверхности, пространства) ставится в соответствие другая точка того же многообразия. Иными словами, точечное П. является отображением многообразия на себя. При точечном П. каждая фигура (прообраз), рассматриваемая как совокупность точек, преобразуется в новую фигуру, называемую образом первоначальной. Если точечное П. взаимно однозначно, то можно определить обратное П. (см. Отображение). Точечное П. наз. тождественным, если при нём образ каждой точки совпадает с прообразом. Если ограничиться для определённости точечными П. плоскости, то такие П. могут быть заданы аналитически формулами: х' = f (х, у), у' = ф (х, у), где х, у - координаты прообраза, а х'. у' - координаты образа в одной и той же системе координат.

Многие важные классы точечных П. образуют группу, т. е. вместе с любыми двумя П. содержат их произведение (результат последовательного применения), а вместе с каждым П. содержат обратное П. Наиболее важные примеры групп точечных П. плоскости таковы:

1) группа вращений плоскости вокруг начала координат:

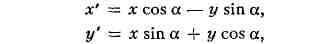
где а - угол поворота.

2) Группа параллельных переносов, при к-рых все точки смещаются на один и тот же вектор ai + bj:

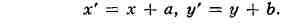
3) Группа движений, состоящая из П., не изменяющих расстояния между точками и ориентации плоскости:

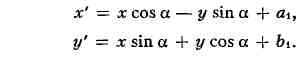
См. также Движение в геометрии.

4) Группа движений и зеркальных отражений, состоящая из П., не изменяющих расстояния между точками плоскости. Совокупность движений и зеркальных отражений, совмещающих нек-рую фигуру с собой, наз. группой симметрии этой фигуры. Эта группа определяет свойства симметрии фигуры. Напр., группа симметрии правильного тетраэдра состоит из 4! = 24 П., переставляющих между собой его вершины.

5) Группа П. подобия, порождаемая П. движения, зеркального отражения и гомотетии.

6) Группа аффинных П., состоящая из взаимно однозначных отображений плоскости на себя, при к-рых прямые переходят в прямые:

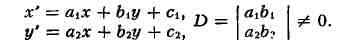
Если c₁ = с₂, то П. наз. центро-аффинным, а если D = 1, то - экви-аффинным; экви-аффинные П. не изменяют площади фигур. См. также Аффинные преобразования.

7) Группа проективных П., состоящая из взаимно однозначных П. расширенной плоскости (дополненной бесконечно удалённой прямой), при к-рых прямые линии переходят в прямые:

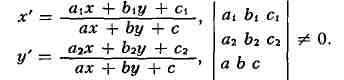
Из этой записи видно, что прямая ах + bу + с = 0 переходит при этом П. в бесконечно удалённую прямую. См. также Проективное преобразование.

8) Группа круговых П. (или П. обратными радиусами-векторами), порождаемая П. движения, зеркального отражения, подобия и инверсий. Если точки плоскости изобразить комплексными числами, то П. этой группы запишутся в виде:

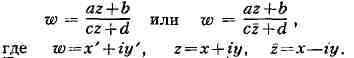
Т. о., они совпадают с дробно-линейными преобразованиями (см. Дробно-линейные функции). П. этой группы обладают круговым свойством, т. е. переводят совокупность прямых и окружностей на плоскости в себя. Они обладают также свойством конформности (см. Конформное отображение). П. плоскости, обладающее круговым свойством, принадлежит всегда группе круговых П.

Группы 1-7 являются линейными группами, т. к. они переводят прямые линии в прямые. При этом группы 1 и 2 являются подгруппами группы 3, каждая следующая группа (4, 5, 6, 7) содержит в себе предыдущую как часть. Группы 1-6 можно охарактеризовать как совокупность проективных П., оставляющих неизменным нек-рый образ на расширенной плоскости. Напр., аффинные П. являются П., оставляющими на месте бесконечно удалённую прямую. Группа 8 является примером нелинейной группы, т. к. при П. этой группы прямые линии могут перейти в окружности. П. групп 1-8 являются бирациональными преобразованиями, т. е. такими П., при к-рых х' и у' рационально выражаются через х и у и обратно.

Наряду с точечными П., при к-рых устанавливается соответствие между точками, в геометрии применяются П. фигур, при к-рых устанавливается соответствие между самими фигурами. Напр., в нек-рых задачах геометрии заменяют все окружности окружностями же, увеличивая их радиус на определённую величину. Этим определяется П. многообразия окружностей в себя. Рассматриваются также П., изменяющие природу элементов, т. е. переводящие точки в линии, линии в точки и т. д. Напр., можно поставить в соответствие каждой точке М(х, у) прямую их' + vy' = 1, где и и v - нек-рые функции от х и у. Если и и v дробно-линейно зависят от х и у.

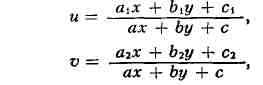
то имеет место общее проективное П. точек плоскости в прямые плоскости. Если при этом b₁= а₂, с₁ = -а, с₂ = -b, то получается полярное П. относительно нек-рой линии второго порядка (см. Полюсы и поляры). В частности, когда и = х и т' = у, получается полярное П. относительно окружности х² + у² = 1. При этом каждой точке на плоскости (х,у) соответствует прямая на плоскости (х',у'). Кривой Г на плоскости (х, у) соответствует семейство прямых, касающихся нек-рой кривой Г' (или проходящих через одну и ту же точку). Этим устанавливается соответствие между кривыми плоскости (х, у), рассматриваемыми как множество своих точек, и кривыми плоскости (х',у'), рассматриваемыми как огибающие своих касательных. Более общими являются П., задаваемые формулой F(x,y,x',y') = 0. Если задать х и у, то эта формула определяет нек-рую кривую на плоскости (х',у'), а если задать х' и у', то определяется кривая на плоскости (х,у). Этим устанавливается соответствие точек одной плоскости двухпараметрич. множеству кривых другой плоскости. Указанное соответствие можно распространить до соответствия между кривыми одной плоскости, рассматриваемыми как множество своих точек, и кривыми другой плоскости, рассматриваемыми как огибающие соответствующего семейства кривых. При этом П. касающиеся друг друга кривые одной плоскости переходят в касающиеся друг друга кривые другой плоскости. Поэтому описанные П. наз. контактными П., или П. прикосновения (см. Прикосновения преобразования).

Аналогично П. плоскости определяются П. многомерных (в частности, трёхмерных) пространств. Для каждой из разобранных выше групп П. плоскости имеется трёхмерный аналог, получающийся из неё увеличением числа преобразуемых переменных. Так, группе 1 соответствует группа ортогональных преобразований, группе центро-аффинных П.- группа невырожденных линейных преобразований и т. д. Примером группы П. четырёхмерного пространства является группа Лоренца (см. Лоренца преобразования), играющая важную роль в теории относительности. П. многомерных пространств используются в анализе при вычислении кратных интегралов, так как позволяют свести заданную область интегрирования к более простой области.

Как для групп П. плоскости, так и для групп П. многомерных пространств можно определить понятие близости П., позволяющее образовать непрерывные группы П. (см. Непрерывная группа).

Для каждой из групп П. существуют свойства фигур, не изменяющиеся при П. соответствующей группы. Эти свойства являются, как говорят, инвариантами относительно данной группы П. Так, при преобразованиях группы движений инвариантно расстояние между двумя точками, при аффинных П. - параллельность прямых, отношение площадей двух фигур, при проективных П. - двойное отношение AB/AD : CB/CD точек А, В, С, D, лежащих на одной прямой. Каждой группе П. соответствует своя область геометрич. исследований, изучающая свойства фигур, остающихся инвариантными при П. этой группы (см. Эрлангенская программа). В соответствии с этим различают метрич. свойства фигур, аффинные свойства, проективные свойства и т. д. Вообще говоря, чем шире группа, тем теснее связаны эти инвариантные свойства с фигурой. Наиболее общими являются свойства фигур, остающиеся инвариантными при любых топологич. П. (т. е. любых взаимно однозначных и непрерывных П.). К ним относятся размерность, связность, ориентируемость (см. Топология).

Особенно важную роль играют П. при установлении новых и при обобщении ранее известных теорем. Если в формулировку нек-рой теоремы, доказанной для фигуры F, входят лишь свойства фигуры, инвариантные относительно нек-рой группы П., то теорема сохраняет свою силу для всех фигур, получаемых из F П. этой группы (как говорят, гомологичных или эквивалентных F относительно этой группы). Это свойство П. особенно важно, если среди эквивалентных между собой фигур имеется такая, к-рая обладает в нек-рых отношениях наиболее простыми свойствами. Так, ряд теорем проективной геометрии был установлен впервые для окружности, а потом перенесён на любые невырожденные конич. сечения (все невырожденные конич. сечения эквивалентны окружности относительно группы проективных П.). При решении геометрии, задач на построение часто используют П., для того чтобы привести фигуры в наиболее удобные для решения положения.

Преобразования функций. Существ. значение имеет также теория групп П. для теории аналитич. функций. Там рассматриваются классы функций, не изменяющихся при П., образующих некоторую группу (см. Автоморфные функции).

Понятие П. играет важную роль и в функциональном анализе, где рассматриваются П. одного множества функций в другое. К таким П. относятся, напр., Фурье преобразование, Лапласа преобразование и др. При этих П. каждой функции f ставится по определённому правилу в соответствие другая функция ф. Например, преобразование Фурье имеет вид:

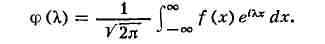
Оно, как и преобразование Лапласа, относится к классу интегральных П., определяемых формулами вида:

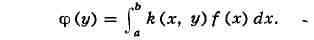
В ряде случаев П. позволяют заменить операции над функциями более простыми операциями над их образами (напр., дифференцирование - умножением на независимую переменную), что облегчает решение ур-ний.

Мн. ур-ния можно записать в виде f = Af, где f - искомая функция, а А - символ П. В этом случае задача решения уравнения может быть истолкована как задача нахождения функции, не изменяющейся при П. Эта точка зрения, называемая принципом неподвижной точки, позволяет в ряде случаев устанавливать существование и единственность решения (см. Сжатых отображений принцип).

Лит.: Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971; Клейн Ф., Высшая геометрия, пер. с нем., М.- Л., 1939; его ж е, Элементарная математика с точки зрения высшей. Лекции..., пер. с нем., 2 изд., т. 2, М. - Л., 1934; Адамар Ж., Элементарная геометрия, пер. с франц., 4 изд., ч. 1, М.,1957.