ПРАКТИЧЕСКАЯ АСТРОНОМИЯ, раздел астрометрии, посвящённый учению об астрономич. инструментах и способах определения из астрономических наблюдений времени, географических координат и азимутов направлений. В зависимости от условий, в к-рых решаются задачи П. а., она подразделяется на геодезическую астрономию, мореходную астрономию и авиационную астрономию. Способы П. а. основываются на правилах сферической астрономии и использовании звёздных каталогов, составлением к-рых занимается фундаментальная астрометрия.

П. а. возникла в глубокой древности под влиянием задач хоз. жизни человеческого общества.

Применяемые в П. а. инструменты позволяют измерять углы в горизонтальной и вертикальной плоскостях и фиксировать моменты прохождения светил через вертикалы и альмукантараты. Среди этих инструментов: универсальный инструмент, зенит-телескоп, вертикальный круг, переносной пассажный инструмент, зенитная фотографич. труба, мореходный и авиац. секстанты и др. (см. Астрономические инструменты и приборы). Для измерения времени служат кварцевые часы и морские хронометры. При определении долгот используется аппаратура для приёма радиосигналов времени.

В П. а. применяются след, способы определения местного времени s (что равносильно определению поправки часов и), широты фи, долготы лямбда и азимута А направления на земной предмет. (Ниже использованы обозначения: а — азимут, z — зенитное расстояние, a — прямое восхождение, б — склонение, t — часовой угол небесного светила, s — местное время, Т — показания часов в момент наблюдений.)

1) Определение и и фи по измерениям z светила g. Из параллактического треугольника PZсигма (Р — полюс мира, Z — зенит, сигма— место светила; рис. 1) следует, чтo

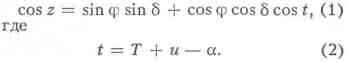
Найдя в астрономич. каталоге а и 5 наблюдаемого светила и измерив его зенитное расстояние z в момент Т, из ур-ний (1) и (2) можно вычислить поправку часов u, если известна фи, или вычислить фи, если известна и. Если неизвестны миф, то решение ур-ний (1) и (2) ведут способом последовательных приближений или наблюдают две звезды: одну вблизи меридиана, другую — вблизи первого вертикала. Полученные две системы ур-ний (1) и (2)

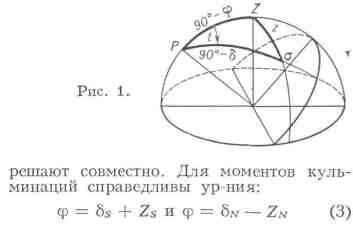
(индексы S и N обозначают светила, кульминирующие, соответственно, к югу и северу от зенита). Т. к. измерить z строго в меридиане нельзя, то измеряют его вблизи меридиана, вводя при вычислениях необходимую поправку.

2) Определение и и фи по наблюдениям пар звёзд на равных зенитных расстояниях z. В 1874 рус. геодезист Н. Я. Цингер предложил способ определения и по наблюдениям моментов прохождения двух звёзд через один и тот же альмукантарат (см. Цингера способ). Звёзды наблюдаются вблизи первого вертикала: одна — на востоке, другая на западе, симметрично относительно меридиана. Аналогичный способ для определения ф по наблюдениям пары звёзд на равных зенитных расстояниях вблизи меридиана предложил в 1887 рус. путешественник М. В. Певцов (см. Певцова способ). Оба способа характеризуются простотой наблюдений и высокой точностью получаемых результатов.

3) Совместное определение u и фи. Сов. учёные В. В. Каврайский (1924—36) и А. В. Мазаев (1943—45) предложили способы совместного определения u и фи (см. Каврайского способ и Мазаева способ). По способу Каврайского наблюдаются четыре звезды на попарно равных зенитных расстояниях z; по способу Мазаева — серия звёзд в альмукантарате с г = 45° или z = 30°.

4) Определение ф по способу Талькотта. Этот способ, предложенный в 1857 амер. геодезистом А. Талькоттом, основан на измерении малой разности зенитных расстояний двух звёзд, кульминирующих по разные стороны от зенита (см. Талькотта способ). Полусумма правых и левых частей равенств (3) даёт:

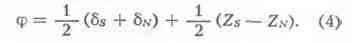
Звёзды выбираются так, чтобы разность их зенитных расстояний была в пределах диаметра рабочей части поля зрения трубы, т. е. не превышала 10—15', а разность прямых восхождений отличалась бы на 5—20 мин (при наблюдениях обеих звёзд в верхней кульминации). Для наблюдений труба зенит-телескопа или универсального инструмента устанавливается на среднее зенитное расстояние пары в азимуте 0° для наблюдения звезды, кульминирующей к югу от зенита, и 180° — к северу от него. Величина Zs — Z_N измеряется окулярным микрометром. Способ нашёл широкое применение, в частности на междунар. станциях, изучающих движение земных полюсов.

5) Определение и и ф из наблюдений на зенитной фотографич. трубе. В нек-рых обсерваториях для служб времени и служб широты определяют и и ф из совместных наблюдений на фотографич. зенитных трубах. Изображение звезды фиксируется на движущейся с её скоростью фотографич. пластинке с маркировкой на ней моментов времени. Звёзды наблюдают в узкой зенитной зоне, ограниченной рабочей частью поля зрения трубы. Ось инструмента постоянно направлена в зенит, что контролируется ртутным горизонтом.

6) Определение и пассажным инструментом. Этот способ широко применяется в практике служб времени и при высокоточных определениях долгот. Наблюдаются моменты прохождений серии звёзд через меридиан с регистрацией их или контактным микрометром, или с помощью фотоумножителей. Поправки определяются по формуле

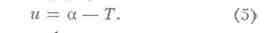
Подобный способ применительно к универсальному инструменту предложил рус. геодезист Н. Д. Павлов (1912). В нек-рых случаях определение и производится по наблюдению прохождений звёзд в вертикале Полярной (способ Деллена).

7) Определение лямбда. Восточная долгота места наблюдения связана со всемирным временем S и местным s соотношением:

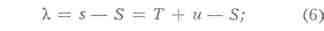
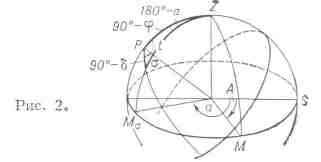
и — определяется одним из изложенных выше способов, a S — путём приёма радиосигналов времени, транслируемых в течение суток многими радиостанциями. 8) Определение А. Наиболее распространённый способ основан на измерении универсальным инструментом горизонтального угла между направлениями на Полярную М_сигма (рис. 2) и земной предмет М и вычислении азимута Полярной в момент наблюдения s. Для этого служит соотношение:

 

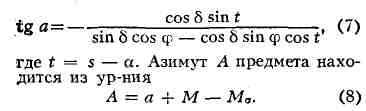
В геодезии, практике часто применяется способ определения азимута, основанный на наблюдениях моментов прохождения звёзд с большими z (50°-70°) вблизи меридиана.

9) Определение ср и X способом высотных линий положений, предложенным амер. моряком Т. Сомнером в 1843 (см. Сомнера способ). В мореходной и авиац. астрономии, где требуется меньшая точность, но большая быстрота в определении ф и X, широко применяется способ высотных линий положения, сущность к-рого ясна из рис. З. Находясь в точке то, географич. координаты к-рой необходимо определить, измеряют зенитное расстояние z₁ небесного светила о₁ (с координатами а₁ и б₁) и вычисляют географич. координаты проекции СУММА₁), светила на поверхность Земли - т. н. географич. места светила -по формулам ф1= б; Х₁=а₁ - S (долгота восточная). Окружность радиуса z₁ с центром в 2₄ проходит на глобусе через точку т. Измерив z₂ другого светила, проводят другую окружность радиусом z₂ с центром в СУММА₂; в одной из двух точек пересечения этих окруж-Лостей расположена искомая точка т (выбор нужной точки не представляет затруднений, т. к. приближённое место наблюдения бывает известно). На практике пользуются не глобусом, а картой, прочерчивая на ней отрезки кривых, отождествляемые с дугами окружности вблизи их пересечений. Эти отрезки наз. высотными линиями положений или линиями Сомнера (см. Позиционная линия).

Рис. 3.

Все проблемы П. а. имеют большое значение для астрономии, геодезии, геофизики. Определения ф, X. и А необходимы для ориентирования триангуляционных сетей, служащих опорой для картографич. работ и для изучения фигуры Земли. Изучение изменяемости ф привело к установлению периодич. и вековых движений земных полюсов. Переопределение долгот обсерваторий в разные эпохи доставляет необходимые данные для изучения дрейфа континентов.

Лит.: Блажко С. Н., Курс практической астрономии, 3 изд., М.- Л., 1951; Белобров А. П., Мореходная астрономия, Л., 1954; Воробьев Л. М., Астрономическая навигация летательных аппаратов, М., 1968.

В. П. Щеглов.

ПРАМБАНАН (Prambanan), населённый яункт в Индонезии, в центр. части о. Ява; (расположен у юж. подножия вулкана Мерапи, в долине, где сохранились ср.- век. постройки. Среди них: буддийский храм чанди Каласан (осн., возможно, в 778; позднее перестроен; нынешний облик - сер. 9 в.), чанди Сари (8-9 вв.), буддийские храмовые комплексы чанди Севу (1-я пол. 9 в.) и чанди Плаосан (сер. 9 в.), индуистский храмовый комплекс Лара Джонгранг ("Стройная дева" -по нар. прозвищу статуи богини Дурги в главном храме; 2-я пол. 9 в. или нач. 10 в.). Илл. см. т. 10, стр. 253, вклейка к стр. 249.

Лит.: Groneman I., The Hindu ruins in the plain of Parambanan, Semarang, 1901; Bernet Kempers A., Tjandi Kalasan dan Sari, Djakarta, 1954; Petundjuk singkat tentang tjandi Lara Djonggrang, Jogjakarta, [1955].

ПРАМНЕК, Прамниекс Эдуард Карлович (31.12.1899 - 29.7.1938), советский парт, и гос. деятель. Чл. Коммунистич. партии с 1917. Род. в Яун-раунской вол. (ныне Цесисский р-н Латв. ССР) в семье батрака. С 1913 работал каменщиком. Вёл революц. работу среди молодёжи Раунской вол. В 1919-21 служил в Красной Армии - на политич. работе в латыш. стрелк. полках, участвовал в боях на Зап. и Юж. фронтах, в подавлении Кронштадтского контрреволюц. мятежа 1921. В 1921-24 учился в Коммунистич. ун-те народов Запада, затем в Коммунистич. ун-те им. Я. М. Свердлова. С 1924 на парт, работе в Н. Новгороде (ныне Горький). В 1929 секретарь Вятского губкома и окружкома партии. В 1930-34 2-й секретарь, в 1934-1937 1-й секретарь Горьковского крайкома и обкома ВКП(б). С 1937 секретарь Донецкого обкома КП(б)У, чл. Политбюро ЦК. Делегат 14-17-го съездов ВКП(б), на 17-м съезде избирался канд. в чл. ЦК. Чл. ВЦИК и ЦИК СССР. Деп. Верх. Совета СССР 1-го созыва.

ПРАМОНОТЕИЗМА ТЕОРИЯ (от пра... и монотеизм), учение, по к-рому первоначальной формой религии в истории человечества был культ единого бога, а анимистич., фетишистские, политеистич. и др. отклоняющиеся от монотеизма культы, заполняющие всю историю религии, появились как следствие забвения людьми данного им богом откровения. П. т. базируется на иудейско-христиан-ском догмате божественного откровения и подкрепляется извращённо толкуемыми этнографич. данными. В лит-ре по этнографии и истории религий П. т. особенно активно пропагандировалась австр. като-лич. патером В. Шмидтом. Начиная с 1912 он выпускал многотомную серию "Происхождение идеи бога" (12-й том вышел посмертно в 1955), посвящённую обоснованию П. т. этнографич. материалами. Обилие неправильных истолкований этнографич. данных и наличие прямых фальсификаций в этом соч. неоднократно устанавливалось учёными. После смерти Шмидта даже его ученики, группирующиеся вокруг журнала "Anthropos", предприняли ревизию П. т. и фактически отказались от неё, постулируя в качестве первичной формы религии не прамонотеизм, а пратеизм (см. Теизм).

Лит.: Крывелев И. А., Крушение теории прамонотеизма, "Вопросы философии", 1960, № 7.

И. А. Крывелев.

ПРАМУДЬЯ АНАНТА ТУР (Pramoedya Anantae Toer) (p. 1925), индонезийский писатель и обществ, деятель; см. Тур Прамудъя Ананта.

ПРАНГОС (Prangos), род растений сем. зонтичных. Крупные многолетние травы с многократно пернсторассечёнными листьями. Лепестки жёлтые, с загнутой внутрь верхушкой. Плоды крупные, с крылатыми рёбрами. Ок. 35 (по др. данным, до 50) видов в Средиземноморье, Зап., Ср. и Центр. Азии и в Гималаях.

Прангос кормовой..

В СССР 18 видов, растущих преим. по сухим горным склонам. П. кормовой, или юган (P. pabularia), широко распространён в Ср. Азии, где часто образует обширные заросли. Имеет 2 различные по химич. составу формы: сладкий юган (его листья в сене хорошо поедаются скотом) и горький юган. Виды П. содержат (гл. обр. в корнях) кумарин и его производные. Иногда П. включают в род кахрис (Cachrys).

ПРАНДТЛЬ (Prandtl) Людвиг (4.2.1875, Фрейзинг, Бавария, - 15.8.1953, Гёттинген), немецкий учёный в области механики, один из основателей экспериментальной аэродинамики. Окончил Высшее политехнич. уч-ще в Мюнхене. Проф. Высшего технич. уч-ща в Ганновере (с 1901), Гёттингенского ун-та (с 1904), директор Ин-та гидроаэродинамики кайзера Вильгельма в Гёттингене (1925-47). Осн. труды по теории упругости и пластичности, гидроаэромеханике, газовой динамике и динамич. метеорологии. В 1904 ввёл представление о пограничном слое и объяснил сопротивление формы при обтекании тела отрывом пограничного слоя (см. Отрывное течение). Создал теорию самолётного крыла конечного размаха, разработал методы упрощённого решения соответствующих уравнений, исследовал крыло с наивыгоднейшим распределением циркуляции, рассмотрел случай нестационарного решения (совм. с Бирнбаумом), ввёл чёткое понятие индуцированного сопротивления, дал формулу для его определения и т. д. Изучал турбулентное течение в трубах, турбулентность свободной атмосферы, переход от ламинарного течения к турбулентному, исследовал сверхзвуковое истечение газов и паров под давлением и разработал линеаризованную теорию крыла в дозвуковом потоке сжимаемого газа. Именем П. названы уравнения, понятия, приборы. Основал школу в прикладной гидроаэромеханике.

Л. Прандтль.

Соч.: Führer durch die Stromungslehre, 4 Aufl., Braunschweig, 1956; Gesammelte Abhandlungen zur angewandten Mechanik, Hydro- und Aerodynamik, Tl 1-3, В., 1961; в рус. пер.-Гидроаэромеханика, 2 изд., М., 1951.

Лит.: Ackeret J., Ludwig Prandtl, "Zeitschrift fiir Angewandte Mathematik und Physik", 1954, v. 5; Лойцянский Л. Г., Механика жидкости и газа, 3 изд., М., 1970.

И. Д. Рожанский.

ПРАНДТЛЯ ТРУБКА, Пито-Прандтля трубка, прибор для одновременного измерения полного и статич. давления в потоке жидкости или газа. Представляет собой Пито трубку, усовершенствованную Л. Прандтлем, к-рый совместил измерение полного и статич. давления в одном приборе. См. Трубки гидрометрические.

ПРАНДТЛЯ ЧИСЛО, один из подобия критериев тепловых процессов в жид-

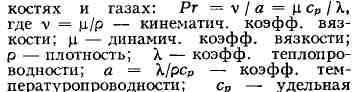
теплоёмкость среды при постоянном давлении.

Названо по имени Л. Прандтля.

П. ч.- физич. характеристика среды и зависит только от её термодинамич. состояния. У газов П. ч. с изменением темп-ры практически не изменяется (для двухатомных газов Рr =~ 0,72, для трёх-и многоатомных Рr =~ от 0,75 до 1). У неметаллич. жидкостей П. ч. изменяется с изменением темп-ры тем значительнее, чем больше вязкость жидкости (напр., для воды при 0 °С Рr = 13,5, а при 100 °С Рr = 1,74; для трансформаторного масла при 0 °С Рr = 866, при 100 °С Рr = 43,9 и т. д.). У жидких металлов Рr << 1 и не так сильно изменяется с темп-рой (напр., для натрия при 100 °С Рr = 0,0115, при 700 °С Рr = = 0,0039).

П. ч. связано с др. критериями подобия - Пекле числом Ре и Рейнольдса числом Re соотношением Рr = Pe/Re.

С. Л. Вишневецкий.