ПОВЕРХНОСТЕЙ ТЕОРИЯ, раздел дифференциальной геометрии, в к-ром изучаются свойства поверхностей (см. Дифференциальная геометрия, Поверхность). В классич. П. т. рассматриваются свойства поверхностей, неизменные при движениях. Одна из осн. задач классич. П. т. - задача измерений на поверхности. Совокупность фактов, получаемых при помощи измерений на поверхности, составляет внутреннюю геометрию поверхности. К внутр. геометрии поверхности относятся такие понятия, как длина линии, угол между двумя направлениями, площадь области, а также геодезические линии, геодезии, кривизна линии и др. Внутр. геометрию определяет первая осн. квадратичная форма поверхности

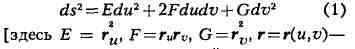
радиус-вектор переменной точки поверхности, и, v - её криволинейные координаты], выражающая квадрат дифференциала дуги линии на поверхности. Именно, если известны функции Е = E(u,v), F = F(u,v), G = G(u,v), то, зная внутр. уравнения линии и = u(t), v = v(t) и интегрируя ds, можно определить длину этой линии; кроме того, существуют формулы, к-рые при данных Е, F, G выражают угол между двумя линиями и площадь области по внутр. уравнениям этих линий и по внутр. уравнению контура области. Изучение пространственного строения окрестности точки на поверхности производится при помощи второй осн. квадратичной формы поверхности

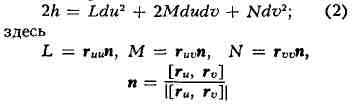
- единичный вектор нормали к поверхности. Величина h с точностью до малых более высокого порядка относительно du, dv равна расстоянию от точки М' поверхности с координатами и + du, v + dv до касательной плоскости у в точке М с координатами и, v, причём расстояние берётся со знаком + или -в зависимости от того, с какой стороны от у расположена точка М'. Если форма (2) знакоопределённая, то поверхность в достаточно малой окрестности точки М располагается по одну сторону от касательной плоскости -у, и в этом случае точка М поверхности наз. эллиптической (рис. 1). Если форма (2) знакопеременная, то поверхность в окрестности точки М располагается по разные стороны от плоскости ч, и точка М тогда наз. гиперболической (рис. 2). Если форма (2) знакоопределённая, но принимает нулевые значения (при не равных одновременно нулю du и dv), то точка М наз. параболической (на рис. 3 показан один из примеров строения поверхности в окрестности па-раболич. точки).

Рис. 1.

Рис. 2.

Рис. 3.

Более точная характеристика пространственной формы поверхности может быть получена с помощью исследования геометрич. свойств линий на поверхности. Пусть М - нек-рая точка поверхности S и и - единичный вектор нормали к поверхности в М. Линия (L) пересечения S с плоскостью, проходящей через п в на-

дои кривизны в данной точке наз. главными кривизнами, а соответствующие направления на поверхности - главными направлениями. Кривизна произвольного нормального сечения в данной точке связана простым соотношением с гл. кривизнами (см. Эйлера формулы). Если гл. кривизны в точке М различны, то в этой точке существуют два различных гл. направления. Линии, направления к-рых в каждой точке являются главными, наз. линиями кривизны. Направления, в к-рых нормальная кривизна равна нулю, наз. асимптотическими, а линии, имеющие в каждой точке асимптотич. направление, - асимптотическими линиями. Поверхность, состоящая из эллиптич. точек (напр., сфера), не имеет асимптотич. линий. Поверхность, состоящая из гиперболич. точек, имеет два семейства асимптотич. линий (напр., две системы прямолинейных образующих однополостного гиперболоида). Поверхность, состоящая из парабо-лич. точек, имеет одну систему асимптотич. линий - систему прямолинейных образующих. Дальнейшее изучение свойств произвольных линий на поверхности (в первую очередь кривизн линий) тесно связано с кривизнами нормальных сечений. Кривизна k в данной точке М произвольной линии Г может быть вычислена по формуле:

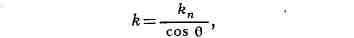
где Rn - кривизна нормального сечения L в точке М в направлении касательной к Г, а в - угол между гл. нормалями к Г и L в этой точке (см. Мёнъе теорема). Поверхности, между точками к-рых можно установить такое взаимно однозначное соответствие, что длины соответствующих линий равны, наз. и з о м е т р и ч н ы м и. Изометричные поверхности имеют одинаковую внутр. геометрию, но их пространственное строение может быть различным и гл. кривизны в соответствующих точках у них могут быть также различными (напр., окрестность точки на плоскости изометрична нек-рой окрестности точки на цилиндре, но имеет иную пространственную структуру). Однако произведение К гл. кривизн ¹/R₁ и ¹/R₂ в точке М не меняется при изометричных преобразованиях поверхности (теорема Гаусса, 1826) и может служить внутр. мерой искривлённости поверхности в данной точке. Величина X наз. полной (или гауссовой) кривизной поверхности в точке М и выражается соотношением:

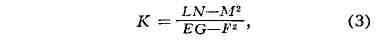
к-рое наз. формулой Гаусса (полная кривизна в соответствии с теоремой Гаусса может быть выражена только через коэффициенты первой квадратичной формы и их производные). Приведённая выше классификация точек регулярной поверхности может быть сопоставлена со значениями полной кривизны: в эллиптич. точке кривизна положительна, в гиперболической - отрицательна и в параболической - равна нулю.

Во мн. вопросах П. т. рассматривается др. характеристика искривлённости поверхности - т. н. средняя кривизна, равная полусумме гл. кривизн поверхности. Так, напр., одним из объектов исследований П. т. являются минимальные поверхности, ср. кривизна к-рых в каждой точке равна нулю.

Важное значение в П. т. имеет вопрос о возможности изгибания поверхности: можно ли утверждать, что данная поверхность будет изгибаемой? Математически этот вопрос формулируется след, образом: возможно ли включить данную регулярную поверхность в однопараметрич. семейство изометричных неконгруэнтных регулярных поверхностей (конгруэнтные поверхности - поверхности, совмещаемые движением). Достаточно малые куски поверхностей положительной и отрицательной кривизны допускают непрерывные изгибания. Существуют поверхности с точкой уплощения (т. е. точкой, где все нормальные кривизны равны нулю), сколь угодно малая окрестность к-рой не допускает изгибания. Последний результат установлен сов. геометром Н. В. Ефимовым. Кроме самой возможности изгибания, рассматриваются и изгибания спец. типов.

Задача изгибания поверхностей тесно связана с задачей определения поверхности по заданным осн. квадратичным формам, получившей полное решение в работах нем. математика К. Гаусса, рус. математика К. М. Петерсона, итал. математиков Г. Майнарди и Д. Кодацци и франц. математика О. Бонне. Поскольку значение полной кривизны К поверхности может быть выражено через коэффициенты первой квадратичной формы, то уравнение (3) является одним из соотношений, связывающих коэффициенты первой (1) и второй (2) форм. Другие два соотношения

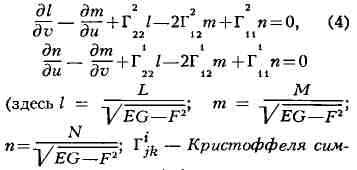
волы второго рода) были установлены в 1853 К. М. Петерсоном. Справедливо и обратное утверждение - если коэффициенты двух форм, одна из к-рых положительно-определённая, удовлетворяют уравнениям (3) и (4), то существует определённая с точностью до движения и зеркального отражения поверхность, для к-рой указанные формы будут первой и второй квадратичными формами.

К числу наиболее важных проблем П. т. относится проблема разыскания признаков, к-рые позволяют по заданным двум осн. квадратичным формам поверхности (в произвольных координатах) установить, относится ли поверхность к данному классу поверхностей или нет. Для решения этой общей проблемы, как и мн. др. проблем П. т., используются методы тензорного исчисления.

С нач. 20 в. в П. т. появляется новое направление, в к-ром исследуется поверхность "в целом" по данным свойствам окрестностей её точек. Напр., Л. Г. Шнирельманом и Л. А. Люстерником было доказано существование трёх замкнутых геодезических на регулярных замкнутых поверхностях, гомеоморфных сфере. Продолжение гладких поверхностей иногда приводит к появлению на них особенностей. Напр., всякая развёртывающаяся поверхность, не являющаяся цилиндрической, при продолжении доходит до ребра (или острия в случае конуса). Рассмотрение поверхностей во всём их протяжении и с особенностями (т. е. отказ от требований дифференцируемое) потребовало изобретения принципиально новых методов исследования поверхностей и привлечения методов из др. разделов математики. Развитие П. т. в этом направлении привело к созданию содержательных разделов геометрии. Так, напр., глубокие и принципиально новые результаты были получены А. Д. Александровым и А. В. Погореловым в теории выпуклых поверхностей. Александровым был предложен новый метод исследования выпуклых поверхностей, основанный на приближении выпуклых поверхностей выпуклыми многогранниками.

Рассмотренные свойства поверхностей не меняются при любых изометрич. преобразованиях всего пространства, т.е. они относятся к т. н. метрической П. т. Изучают также свойства поверхностей, инвариантные по отношению к к.-л. другой группе преобразований пространства, напр, группе аффинных или проективных преобразований. Аффинная П. т. рассматривает свойства поверхностей, неизменные при эквпаффинных преобразованиях (аффинных преобразованиях, сохраняющих объём). Проективная П. т. рассматривает проективно-инвариантные свойства поверхностей.

Лит.: Р а ш е в с к и й П. К., Курс дифференциальной геометрии, 4 изд., М., 1956; Н о р д е н А. П., Теория поверхностей, М., 1956; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1 - 2, М.-Л., 1947-48; Бляшке В., Дифференциальная геометрия и геометрические основы теории относительности Эйнштейна, пер. с нем., т. 1, М.- Л., 1935; Александров А.Д., Внутренняя геометрия выпуклых поверхностей, М.- Л., 1948; ПогореловА. В., Внешняя геометрия выпуклых поверхностей, М., 1969; Фиников С. П., Проективно-дифференцпальная геометрия, М.- Л., 1937; Широков П. А., Широков А. П., Аффинная дифференциальная геометрия, М., 1959; В 1 a s с h k e W., Vorlesungen über Differential geometrie, Bd 2, В., 1923; Bianchi L., Lezioni di geometria differenziale, 3 ed., t. 1-2, Bologna, 1937; D a r b о u x G., Lecons sur la theorie generate des surfaces, 2 ed., t, 1-4, P., 1924-25.

Э. Г. Позняк.

ПОВЕРХНОСТИ ВРАЩЕНИЯ, поверхности, образуемые вращением плоской кривой вокруг прямой (о с н П. в.), расположенной в плоскости этой линии. Примером П. в. может служить сфера (к-рую можно рассматривать как поверхность, образованную вращением полуокружности вокруг её диаметра). Линии пересечения П. в. с плоскостями, проходящими через её ось, наз. мер и-дианами; линии пересечения П. в. с плоскостями, перпендикулярными оси, - параллелями. Если по оси П. в. направить ось Ог прямоугольной системы координат Oxyz, то параметрич. уравнения П. в. можно записать след. образом:

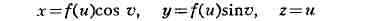
[здесь f(u) - функция, определяющая форму меридиана, a v - угол поворота плоскости меридиана].

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА, поверхности, декартовы прямоугольные координаты точек к-рых удовлетворяют алгебраическому уравнению 2-й степени:

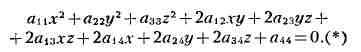
Уравнение (*) может и не определять действительного геометрич. образа, но для сохранения общности в таких случаях говорят, что оно определяет м н и м у ю П. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из 17 приведённых ниже канонических видов, каждому из к-рых соответствует определённый класс П. в. п. Среди них выделяют пять осн. типов поверхностей. Именно,

При исследовании общего уравнения П. в. п. важное значение имеют т. н. осн. инварианты - выражения, составленные из коэффициентов уравнения (*) и не меняющиеся при параллельном переносе и повороте системы координат. Напр., если

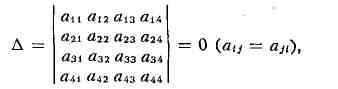
то уравнение (*) определяет вырожденные П. в. п.: конусы и цилиндры второго порядка и распадающиеся П. в. п.; если определитель

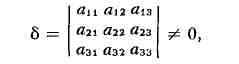
то поверхность имеет единств, центр симметрии (центр П. в. п.) и наз. центральной поверхностью. Если 5 = 0, то поверхность либо не имеет центра, либо имеет бесконечно много центров.

Для П. в. п. установлена аффинная и проективная классификация. Две П. в. п. считают принадлежащими одному аффинному классу, если они могут быть переведены друг в друга нек-рым аффинным преобразованием (аналогично определяются проективные классы П. в. п.). Каждому аффинному классу соответствует один из 17 канонических видов уравнения П. в. п. Проективные преобразования позволяют установить связь между различными аффинными классами П. в. п. Это объясняется тем, что при этих преобразованиях исчезает особая роль бесконечно удалённых элементов пространства. Напр., эллипсоиды и двуполостные гиперболоиды, различные с аффинной точки зрения, принадлежат одному проективному классу П. в. п.

Лит.: Александров П. С., Лекции по аналитической геометрии..., М., 1968; Ильин В. А., Позняк Э. Г., Аналитическая геометрия, 2 изд., М., 1971; Е ф и м о в Н. В., Квадратичные формы и матрицы, 5 изд., М., 1972.

А. Б. Иванов.

ПОВЕРХНОСТИ ВЫРАВНИВАНИЯ, участки земной поверхности со сглаженным рельефом различного генезиса, формирующиеся в условиях преобладания экзогенных процессов над эндогенными. П. в. характерны как для платформенных, так и для складчатых областей. Различают П. в. денудационного происхождения (см. Денудационные поверхности, Пенеплен, Педиплен, Педимент), а также абразионные, абразионно-аккумулятивные и денудационно-эрозионные. Денудационные П. в., как правило, сочленяются с аккумулятивными морскими и аллювиальными равнинами, к-рые могут считаться элементами сложных полигенетических (денудационно-аккумулятивных) П. в.

Возраст П. в. соответствует периоду наиболее полной планации рельефа, к-рый обычно прерывается интенсивным поднятием, приводящим к расчленению поверхности. Выделение П. в., изучение их строения и определение возраста - основной метод установления этапов гео-морфологич. истории крупных территорий. Наряду с большим теоретич. значением анализ П. в. представляет значит, практич. интерес, поскольку с П. в. связан ряд полезных ископаемых (бокситы, железные руды и др.). В целях систематизации и обобщения данных о П. в. территории Сов. Союза составлена "Карта поверхностей выравнивания и кор выветривания СССР" в масштабе 1 : 2 500 000 (гл. ред. И. П. Герасимов, А. В. Сидоренко, 1972).

Лит.: Проблемы поверхностей выравнивания, М., 1964.

ПОВЕРХНОСТНАЯ ИОНИЗАЦИЯ, термическая десорбция (испарение) положительных (положительная П. и.) или отрицательных (отрицательная П. и.) ионов с поверхностей твёрдых тел. Чтобы эмиссия ионов при П. и. была стационарной, скорость поступления на поверхность соответствующих ионам атомов, молекул или радикалов (за счёт диффузии этих частиц из объёма тела или протекающей одновременно с П. и. адсорбции) должна равняться суммарной скорости десорбции ионов и нейтральных частиц. П. и. происходит и при собственном испарении твёрдых тел, напр/, тугоплавких металлов.

Взаимодействие частиц с поверхностями отображают кривыми типа показанной на рис. 1. Переход с кривой для нейтральных частиц А на кривую для ионов А⁺ на расстоянии х -> БЕСКОНЕЧНОСТЬ от поверхности соответствует ионизации частицы с переводом освободившегося электрона в твёрдое тело.

Рис. 1. Потенциальные кривые взаимодействия систем поверхность твёрдого тела - нейтральная частица (А) и поверхность - положительный ион (А⁺); х - удаление от поверхности; U(x) - энергия связи частицы с поверхностью. Расстояние х_р соответствует равновесному состоянию частицы у поверхности, а глубины "потенциальных ям" lt и l₀ равны теплотам десорбции иона и нейтральной частицы соответственно. Разность lt -l₀ в данном случае равна разности энергии ионизации eV нейтральной частицы (V - её ионизационный потенциал, е - заряд электрона) и работы выхода поверхности еф.

Рис. 2. Характерные зависимости степени поверхностной ионизацшт а в стационарных процессах от температуры Т: 1 - для случая, когда теплота десорбции иона lt меньше теплоты десорбции нейтральной частицы 1о; 2 - в случае, когда lt- > 1о. Т₀ - температурный порог поверхностной ионизации.

Требуемая для этого энергия равна e(V - ф); V - ионизационный потенциал частицы, еф -работа выхода тела, е - заряд электрона. Выражение а через эти величины приводит к Ленгмюра - Саха уравнению, причём для положит. П. и. (lt+ - 1о) = e(V -ф), a для отрицат. П. и. (lt- - 1о) = е(ф-S), где е S -энергия сродства к электрону частицы. П. и. наиболее эффективна (а велико) для частиц с lt<l₀ или ф>V и S > ф; а для них уменьшается с ростом Т. При обратных неравенствах П. и. усиливается с возрастанием Т (рис. 2).

lt и l₀ зависят on N - обычно lt растёт, a 1₀ падает с увеличением N. Если при Т> То соблюдается условие эффективной П. и. (lt<l₀и vi>>vo), то при Т = То знак (lо - lt) меняется, а а начинает скачкообразно падать до малых значений. Т₀ наз. температурным порогом П. и.

Внешнее электрическое поле Е, ускоряющее ионы с поверхности, снижает величину lt. При Е<10⁷ в/см это снижение Дl = е*КОРЕНЬ(еЕ) = 3,8- 10-^4*КОРЕНЬ(Е) эв (Е должно быть выражено в в/см). Соответственно растёт а. Если li<l₀ и vi>v₀, Е при стационарной П. и. уменьшает N и То. Так, T₀ для атомов Cs на W с 1000 °К при Е = 10⁴в/см снижается до 300 °К при Е = 10⁷ в/см. Это даёт основание рассматривать явления десорбции и испарения ионов электрич. полем при низких Т как П. и. Совр. экспериментальная техника позволяет наблюдать П. и. частице V =<10в и S=>0,6 в. С помощью электрич. поля эти пределы могут быть существенно расширены.

Приведённые выше закономерности П. и. справедливы (подтверждены опытом) для однородных поверхностей. Однако на практике чаще приходится иметь дело с неоднородными поверхностями, на к-рых l₀, lt, ф и N неодинаковы на различных участках. В таких случаях указанные зависимости а от Т к Е сохраняются для нек-рых усреднённых значений l₀, lt и ф.

П. и. широко используется в ионных источниках различного назначения, в чувствит. детекторах частиц, для компенсации объёмного заряда электронов в термоэлектронных преобразователях, перспективна для создания плазменных двигателей, а также лежит в основе мн. методов изучения физико-химич. характеристик поверхностей твёрдых тел и взаимодействующих с ними частиц.

Лит.: Зандберг Э. Я., Ионов Н.И., Поверхностная ионизация, М., 1969.

Н. И. Ионов.

ПОВЕРХНОСТНАЯ МОРЕНА, обломочный материал, залегающий на поверхности ледника. Образуется за счёт падения на ледник обломков горных пород со склонов долины, а также путём вытаивания его из толщи самого льда.

ПОВЕРХНОСТНАЯ СИЛА в механике, сила, приложенная к точкам поверхности тела. Пример П. с.- атмосферное давление на поверхность тела.

ПОВЕРХНОСТНАЯ ЭНЕРГИЯ в термодинамике, избыток энергии в тонком слое вещества у поверхности соприкосновения тел (фаз) по сравнению с энергией вещества внутри тела. Полная П. э. складывается из работы образования поверхности, т. е. работы, необходимой для преодоления сил межмолекулярного (или межатомного) взаимодействия при перемещении молекул (атомов) из объёма фазы в поверхностный слой, и теплового эффекта, связанного с этим процессом. В соответствии с тер-модинамич. зависимостями удельная полная П. э.
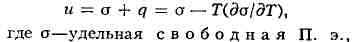тождественно равная для подвижных жидкостей поверхностному натяжению, q - скрытая теплота (связанная энергия) единицы площади поверхности, Т-абс. температура и дСИГМА/дТ - удельная поверхностная энтропия, имеющая обычно отрицательную величину. Свободная П. э. с ростом темп-ры уменьшается, тогда как полная П. э. неполярных (неассоциированных) жидкостей остаётся постоянной, а полярных - несколько возрастает. Так, для воды при 0, 20 и 100 ⁰С значения и соответственно равны 117, 120 и 129 мдж/м² или эрг/см². С приближением к критической температуре различие в составе и свойствах контактирующих фаз сглаживается, поверхность раздела фаз исчезает и П. э. обращается в нуль. П. э. влияет на мн. физико-хим. свойства твёрдых тел и жидкостей. Особенно возрастает её роль в высокодисперсных коллоидных системах, где поверхность раздела фаз предельно велика.

Лит. см. при ст. Поверхностное натяжение и Поверхностные явления.

Л. А. Шиц.

ПОВЕРХНОСТНАЯ ЭРОЗИЯ, смыв поверхностного слоя почвы в результате действия ливневых дождей и талых вод. См. Эрозия, Поверхностный сток.

ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА, вещества, способные накапливаться (сгущаться) на поверхности соприкосновения двух тел, называемой поверхностью раздела фаз, или межфазной поверхностью. На межфазной поверхности П.-а. в. образуют слой повышенной концентрации - адсорбционный слой (см. также Мономолекулярный слой).

Любое вещество в виде компонента жидкого раствора или газа (пара) при соответствующих условиях может проявить поверхностную активность, т. е. адсорбироваться под действием межмолекулярных сил на той или иной поверхности (см. Адсорбция), понижая её свободную энергию. Однако поверхностно-активными обычно называются лишь те вещества, адсорбция к-рых из растворов уже при весьма малых концентрациях (десятые и сотые доли %) приводит к резкому снижению поверхностного натяжения.

Типичные П.-а. в.- органич. соединения дифильного строения, т. е. содержащие в молекуле атомные группы, сильно различающиеся по интенсивности взаимодействия с окружающей средой (в наиболее практически важном случае - водой). Так, в молекулах П.-а. в. имеются один или неск. углеводородных радикалов, составляющих олео-, или липофильную, часть (она же - гидрофобная часть молекулы), и одна или неск. полярных групп - гидрофильная часть (см. также Гидрофильность и гидрофобность). Слабо взаимодействующие с водой олеофильные (гидрофобные) группы определяют стремление молекулы к переходу из водной (полярной) среды в углеводородную (неполярную). Гидрофильные группы, наоборот, удерживают молекулу в полярной среде или, если молекула П.-а. в. находится в углеводородной жидкости, определяют её стремление к переходу в полярную среду. Т. о., поверхностная активность П.-а. в., растворённых в неполярных жидкостях, обусловлена гидрофильными группами, а растворённых в воде - гидрофобными радикалами.

По типу гидрофильных групп П.-а. в. делят на ионные, или ионогенные, и н е и о н н ы е, или неионогенные. Ионные П.-а. в. диссоциируют в воде на ионы, одни из к-рых обладают адсорбционной (поверхностной) активностью, другие (противоионы) - адсорбционно неактивны. Если адсорбционно активны анионы, П.-а. в. наз. анионными, или анионоактивными, в противоположном случае - катионными, или катионоактивными. Анионные П.-а. в.- органич. кислоты и их соли, катионные - основания, обычно амины различной степени замещения, и их соли. Нек-рые П.-а. в. содержат и кислотные, и основные группы. В зависимости от условий они проявляют свойства или анионных, или катионных П.-а. в., поэтому их наз. а м ф о т е р н ы м и, или амфолитными, П.-а. в.

Все П.-а. в. можно разделить на две категории по типу систем, образуемых ими при взаимодействии с растворяющей средой. К одной категории относятся ми-целлообразующие П.-а. в., к другой -не образующие мицелл. В растворах мицеллообразующих П.-а. в. выше критической концентрации мицеллообразования (ККМ) возникают коллоидные частицы (мицеллы), состоящие из десятков или сотен молекул (ионов). Мицеллы обратимо распадаются на отдельные молекулы или ионы при разбавлении раствора (точнее, коллоидной дисперсии) до концентрации ниже ККМ. Таким образом, растворы мицеллбобразующих П.-а. в. занимают промежуточное положение между истинными (молекулярными) и коллоидными растворами (золями), поэтому их часто наз. полуколлоидными системами. К мицеллообразующим П.-а. в. относят все моющие вещества (см. Моющие средства, Моющее действие, Мыла), эмульгаторы, смачиватели, диспергаторы и др.

В мировом произ-ве П.-а. в. большую часть составляют анионные вещества. Среди них можно выделить следующие основные группы: карбоновые кислоты, а также их соли, алкилсульфаты (сульфоэфиры), алкилсульфонаты и алкил-арилсульфонаты, пр. продукты. Наиболее распространены натриевые и калиевые мыла жирных и смоляных к-т; нейтрализованные продукты сульфирования высших жирных к-т, олефинов, алкилбензолов. Второе место по объёму промышленного произ-ва занимают неионные П.-а. в.- эфиры полиэтиленгликолей. Большинство неионных П.-а. в. получают присоединением окиси этилена к алифа-тич. спиртам, алкилфенолам, карболовым к-там, аминам и др. соединениям с реакционноспособным атомом водорода. Ассортимент П.-а. в. чрезвычайно велик. Приведённые ниже данные (1971) позволяют видеть соотношение объёмов произ-ва П.-а. в. различных типов.  

Поверхностно-активные вещества	тыс . m	%
Анионные	2480	62
Неионные	1160	29
Катионные и пр.	360	9
Всего	4000	100

Мировое произ-во П.-а. в. постоянно возрастает, причём доля неионных и катионных веществ в общем выпуске всё время увеличивается. В зависимости от назначения и хим. состава П.-а. в. выпускают в виде твёрдых продуктов (кусков, хлопьев, гранул, порошков), жидкостей и полужидких веществ (паст, гелей). Особое внимание всё больше и больше уделяется произ-ву П.-а. в. с линейным строением молекул, к-рые легко подвергаются биохим. разложению в природных условиях и не загрязняют окружающую среду.

П.-а. в. находят широкое применение в пром-сти, с. х-ве, медицине, быту. Важнейшие области потребления П.-а. в.: произ-во мыл и моющих средств для тех-нич. и санитарно-гигиенич. нужд; текстильно-вспомогат. веществ, т. е. веществ, используемых для обработки тканей и подготовки сырья для них; лакокрасочной продукции. П.-а. в. используют во мн. технологич. процессах хим., нефтехим., химико-фармацевтич., пищевой пром-сти. Их применяют как присадки, улучшающие качество нефтепродуктов, как флотореагенты при флотационном обогащении полезных ископаемых (см. Флотация); компоненты гидроизоляционных и антикоррозионных покрытий и т. д. П.-а. в. облегчают механич. обработку металлов и др. материалов, повышают эффективность процессов диспергирования жидкостей и твёрдых тел. Незаменимы П.-а. в. как стабилизаторы высококонцентрированных дисперсных систем (суспензий, паст, эмульсий, пен). Кроме того, они играют важную роль в биологич. процессах и вырабатываются для "собственных нужд" живыми организмами. Так, поверхностной активностью обладают вещества, входящие в состав жидкостей кишечно-желудочного тракта и крови животных, соков и экстрактов растений.

Лит.: Шварц А., Перри Д ж., Б е р ч Д ж., Поверхностноактивные вещества и моющие средства, пер. с англ., М., 1960; Ребиндер П. А., Поверхностно-активные вещества и их применение, "Журнал Всесоюзного химического общества им. Д. И. Менделеева", 1959, т. 4, № 5; его же, Поверхностные и объемные свойства растворов поверхностно-активных веществ, там же, 1966, т. 11, № 4; е г о же, Взаимосвязь поверхностных и объёмных свойств растворов поверхностноактивных веществ, в сб.: Успехи коллоидной химии, М., 1973; Коллоидные поверхностноактивные вещества, пер. с англ., М., 1966; Nonionic surfactans, ed. М. J. Schick, N. Y., 1967. См. также лит. при ст. Моющие средства.

Л. А. Шиц.

ПОВЕРХНОСТНОЕ ДАВЛЕНИЕ, плоское давление, двумерное давление, сила, действующая на единицу длины границы (барьера), разделяющей чистую поверхность жидкости и поверхность той же жидкости, покрытую адсорбционным слоем поверхностно-активного вещества. П. д. имеет молекулярно-кинетическую природу; оно направлено в сторону чистой поверхности и определяется разностью поверхностных натяжений чистой жидкости и жидкости с адсорбционным монослоем.

ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ, важнейшая термодинамическая характеристика поверхности раздела фаз (тел), определяемая как работа обратимого изотермического образования единицы площади этой поверхности. В случае жидкой поверхности раздела П. н. правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз. Применительно к легкоподвижным поверхностям оба определения равнозначны, но первое предпочтительнее, т. к. имеет более ясный физ. смысл. П. н. на границе двух конденсированных фаз обычно наз. межфазным натяжением. Работа образования новой поверхности затрачивается на преодоление сил межмолекулярного сцепления (когезии) при переходе молекул вещества из объёма тела в поверхностный слой. Равнодействующая межмолекулярных сил в поверхностном слое не равна нулю (как в объёме тела) и направлена внутрь фазы с большей ко-гезией. Таким образом, П. н.- мера не-компенсированности межмолекул ярных сил в поверхностном (межфазном) слое или, что то же, избытка свободной энергии в поверхностном слое по сравнению со свободной энергией в объёмах соприкасающихся фаз. В соответствии с определениями П. н. его выражают в дж/м² или н/м (эрг/см² или дин/см).

Благодаря П. н. жидкость при отсутствии внешних силовых воздействий принимает форму шара, отвечающую минимальной величине поверхности и, следовательно, наименьшему значению свободной поверхностной энергии. П. н. не зависит от величины и формы поверхности, если объёмы фаз достаточно велики по сравнению с размерами молекул; при повышении темп-ры, а также под действием поверхностно-активных веществ оно уменьшается. Расплавы металлов имеют наибольшее среди жидкостей П. н., напр., у платины при 2000 °С оно равно 1820 дин/см, у ртути при 20 °С -484. П. н. расплавленных солей значительно меньше - от неск. десятков до 200-300. П. н. воды при 20 °С - 72,8, а большинства органич. растворителей -в пределах 20-60. Самое низкое при комнатной темп-ре П. н. - ниже 10 - имеют нек-рые фторуглеродные жидкости.

В общем случае многокомпонентных систем в соответствии с термодинамич. ур-нием Гиббса при адсорбции изменение П. н.

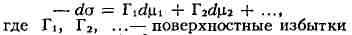
компонентов i, i, ..., т. е. разность их концентраций в поверхностном слое и объёме раствора (или газа), a dм₁, dм₂,... -изменения химии, потенциалов соответствующих компонентов (знак "минус" показывает, что П. н. при положительной адсорбции уменьшается). Разницей в П. н. чистой жидкости и жидкости, покрытой адсорбционным монослоем, определяется поверхностное давление.

На легкоподвижных границах жидкость - газ (пар) или жидкость - жидкость П. н. можно непосредственно измерить мн. методами. Так, широко распространены способы определения П. н. по массе капли, отрывающейся от конца вертикальной трубки (сталагмометра); по величине максимального давления, необходимого для продавлива-ния в жидкость пузырька газа; по форме капли (или пузырька), лежащей на плоской поверхности, и т. д. Экспериментальное определение П. н. твёрдых тел затруднено из-за того, что их молекулы (или атомы) лишены возможности свободного перемещения. Исключение составляет пластическое течение металлов при темп-pax, близких к точке плавления. Ввиду анизотропии кристаллов П. н. на разных гранях кристалла различно. Понятия П. н. и свободной поверхностной энергии для твёрдых тел не тождественны. Дефекты кристаллич. решётки, гл. обр. дислокации, рёбра и вершины кристаллов, границы зёрен поликристаллич. тел, выходящие на поверхность, вносят свой вклад в свободную поверхностную энергию. П. н. твёрдых тел обычно определяют косвенно, исходя из межмолекулярных и межатомных взаимодействий. Величиной и изменениями П. н. обусловлены мн. поверхностные явления, особенно в дисперсных системах (см. также Капиллярные явления).

Л. А. Шиц.

В живых организмах П. н. клетки - один из факторов, определяющих форму целой клетки и её частей. Для клеток, обладающих жёсткой или полужёсткой поверхностью (мн. микроорганизмы, инфузории, клетки растений и т. д.), значение П. н. невелико. У клеток, лишённых прочной надмембранной структуры (большинство клеток животных, нек-рые простейшие, сферопласты бактерий), П. н. в основном определяет конфигурацию (клетки, находящиеся во взвешенном в жидкости состоянии, приобретают форму, близкую к сферической). Форма клетки, прикреплённой к к.-л. субстрату или к др. клеткам, зависит преим. от др. факторов - цитоскелета, образуемого микротрубочками, контактных структур и т. д. Полагают, что локальные изменения П. н. существенны в таких явлениях, как фагоцитоз, пиноцитоз, гаструляция. Определение П. н. клетки - сложная экспериментальная задача; обычно П. н. клетки не превышает неск. дин/см (10^-3 н/м).

А. Г. Маленков.

Лит.: Адам Н. К., Физика и химия поверхностей, пер. с^англ., М.- Л.,1947; Surface and colloid science, ed. E. Matijevic, v. 1, N. Y.- [a. o.], 1969. См. также лит. при ст. Поверхностные явления.

ПОВЕРХНОСТНОЙ ВОЛНЫ АНТЕННА, бегущей волны антенна, отличающаяся тем, что фазовая скорость электромагнитной волны, к-рая распространяется вдоль антенны, меньше фазовой скорости распространения плоской волны в свободном пространстве, а амплитуда поля в направлении нормали к антенне убывает по экспоненциальному закону (такую волну наз. поверхностной). Замедляющую структуру П. в. а. выполняют в виде ребристой металлич. поверхности (см. рис. 19 в ст. Антенна, т. 2, с. 63) либо в виде плоской металлич. поверхности, покрытой слоем диэлектрика. Поверхностная волна обычно возбуждается рупорной антенной или электрич. вибратором. Осн. достоинством П. в. а. является то, что конструктивно она может быть выполнена в виде вставки, практически не выступающей из несущей поверхности, что очень важно при установке таких антенн на летат. аппаратах. П. в. а. применяют гл. обр. в радиоустройствах, работающих на сантиметровых и дециметровых волнах.

ПОВЕРХНОСТНЫЕ ВОЛНЫ, упругие волны, распространяющиеся вдоль свободной поверхности твёрдого тела или вдоль границы твёрдого тела с другими средами и затухающие при удалении от границы. Простейшими и вместе с тем наиболее часто встречающимися на практике П. в. являются Рэлея волны.

О П. в., возникающих и распространяющихся по свободной поверхности жидкости или на поверхности раздела двух несмешивающихся жидкостей, см. Волны на поверхности жидкости.

ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ, выражение особых свойств поверхностных слоев, т. е. тонких слоев вещества на границе соприкосновения тел (сред, фаз). Эти свойства обусловлены избытком свободной энергии поверхностного слоя, особенностями его структуры и состава. П. я. могут иметь чисто физ. характер или сопровождаться хим. превращениями; они протекают на жидких (легкоподвижных) и твёрдых межфазных границах. П. я., связанные с действием поверхностного натяжения и вызываемые искривлением жидких поверхностей раздела, наз. также капиллярными явлениями. К ним относятся капиллярное всасывание жидкостей в пористые тела, капиллярная конденсация, установление равновесной формы капель, газовых пузырей, менисков. Свойства поверхности контакта двух твёрдых тел или твёрдого тела с жидкой и газовой средами определяют условия таких явлений, как адге-зия, смачивание, трение. Молекулярная природа и свойства поверхности могут коренным образом изменяться в результате образования поверхностных мономолекулярных слоев или фазовых (полимолекулярных) плёнок. Такие изменения часто происходят вследствие физич. процессов (адсорбции, поверхностной диффузии, растекания жидкости) или химич. взаимодействия компонентов соприкасающихся фаз. Любое "модифицирование" поверхностного (межфазного) слоя обычно приводит к усилению или ослаблению молекулярного взаимодействия между контактирующими фазами (см. Лиофильностъ и лиофобность). Физ. или хим. превращения в поверхностных слоях сильно влияют на характер и скорость гетерогенных процессов - коррозионных, каталитических, мембранных и др. П. я. отражаются и на типично объёмных свойствах тел. Так, уменьшение свободной поверхностной энергии твёрдых тел под действием адсорбционно активной среды вызывает понижение их прочности (см. Ребиндера эффект). Особую группу составляют П. я., обусловленные наличием в поверхностном слое электрич. зарядов: электроадгезионные явления, электрокапиллярные явления, электродные процессы. Физ. или хим. изменения в поверхностном слое проводника или полупроводника существенно сказываются на работе выхода электрона. Они также влияют на П. я. в полупроводниках (поверхностные состояния, поверхностную проводимость, поверхностную рекомбинацию), что отражается на эксплуатационных характеристиках полупроводниковых приборов (солнечных батарей, фотодиодов и др.). П. я. имеют место в любой гетерогенной системе, состоящей из двух или неск. фаз. По существу весь материальный мир -от космич. объектов до субмикроскопич. образований - гетерогенен. Как гомогенные можно рассматривать системы лишь в ограниченных объёмах пространства. Поэтому роль П. я. в природных и технологич. процессах чрезвычайно велика. Особенно важны П. я. в коллоидно-дисперсных (микрогетерогенных) системах, где межфазная поверхность наиболее развита. С П. я. связана сама возможность возникновения и длит, существования таких систем. К П. я. в дисперсных системах сводятся основные проблемы коллоидной химии. Во взаимосвязи броуновского движения и П. я. протекают все процессы, приводящие к изменению размеров частиц высокодисперсной фазы (коагуляция, коалесценция, пептизация, эмульгирование). В грубо-дисперсных и макрогетерогенных системах на первый план выступает конкуренция поверхностных сил и внешних механич. воздействий. П. я., влияя на величину свободной поверхностной энергии и строение поверхностного слоя, регулируют зарождение и рост частиц новой фазы в пересыщенных парах, растворах и расплавах, взаимодействие коллоидных частиц при формировании разного рода дисперсных структур. На глубину и направление процессов, обусловленных П. я., часто решающим образом влияют поверхностно-активные вещества, меняющие в результате адсорбции структуру и свойства межфазных поверхностей. Основы совр. термодинамики П. я. созданы американским физикохимиком Дж. Гиббсом. В трудах советских учёных П. А. Ребиндера, А. Н. Фрумкина, Б. В. Дерягина, А. В. Думанского получили развитие теоретич. представления о природе и молекулярном механизме П. я., имеющие важное практич. значение.

Использование П. я. в производственной деятельности человека позволяет интенсифицировать существующие технологич. процессы. П. я. в значительной мере определяют пути получения и долговечность важнейших строительных и конструкционных материалов; эффективность добычи и обогащения полезных ископаемых; качество и свойства продукции, выпускаемой химической, текстильной, пищевой, химико-фармацевтической и мн. другими отраслями пром-сти. Большое значение имеют П. я. в металлургии, производстве керамики, металлокерамики, полимерных материалов (пластических масс, резины, лакокрасочных продуктов). Для техники важны такие П. я., как смазочное действие, износ, контактные взаимодействия, структурные изменения в поликристаллич. и композиционных материалах, а также электрич. и электрохимич. процессы и явления на поверхностях твёрдых тел. Познание П. я. в живой природе позволяет сознательно влиять на биологич. процессы с целью повышения продуктивности с. х-ва, развития микробиологич. пром-сти, расширения возможностей медицины и ветеринарии.

Л. А. Шиц.

В биологии П. я. играют важную роль прежде всего на клеточном, субклеточном и молекулярном уровнях организации живых систем. Различные биологические мембраны отграничивают клетку от внешней среды и обеспечивают её микрогетерогенность. На мембранах клетки и внутриклеточных органелл (митохондрий, пластид и др.) происходят фундаментальные для жизни процессы: рецепция экзо- и эндогенных биологически активных веществ (гормонов, медиаторов, антигенов, феромонов и т. д.); ферментативный катализ (мн. ферменты встроены в мембраны, образуя многоферментные каталитич. ансамбли); преобразование химич. энергии в осмотическую работу; окислительное фосфорилирование, т. е. сопряжение процессов окисления с накоплением энергии в макроэргических соединениях. Особенности взаимодействия поверхностей ответственны за агрегацию клеток, их прикрепление к живым и неживым субстратам (в т. ч. образование тромба при повреждении стенки сосуда, сорбция вирусов на клетках и т. п.). Функционирование важнейших ферментных систем (напр., ансамбля дыхательных ферментов) - пример гетерогенного катализа. Адсорбция соответствующих физиологически активных веществ на поверхностях лежит в основе "распознавания" своих и чужих макромолекул (см. Иммунология, Компетенция, Хеморецепция), наркоза, передачи нервного импульса. В целом П. я. в живых системах отличаются от таковых в неживой природе гораздо большей химич. специфичностью, взаимной согласованностью во времени и пространстве. Напр., рецепция гормона на поверхности клетки вызывает конформационный переход (см. Конформация) ряда компонентов мембраны, что обусловливает изменение её проницаемости и гетероката-литич. активности. Это, в свою очередь, вызывает многочисленные физико-хи-мич. и биохимич. сдвиги в клетке, что в совокупности и определяет её реакцию на воздействие.

По мере эволюции роль П. я. в процессах жизнедеятельности возрастает. Так, более древний механизм обеспечения клеток энергией - гликолиэ - осуществляется ферментами цитоплазмы, лишь частично закреплёнными на структурах эндоплазматической сети; эволюционно более поздний и экономичный путь получения энергии - дыхание - осуществляется за счёт гетерокаталитич. систем (см. Окисление биологическое). У одноклеточных организмов питание происходит путём заглатывания целых макромолекул и их последующего расщепления внутри клетки (см. Пиноцитоз); у высших - существенную роль играет пристеночное (контактное) пищеварение, когда ферментативный гидролиз макромолекул пищи происходит на внешней поверхности клетки и координирован с последующим транспортом продуктов расщепления в клетку. См. также Проницаемость биологических мембран.

А. Г. Маленков.

Лит.: Мелвин-Хьюз Э. А., Физическая химия, пер. с англ., кн. 2, М., 1962, с. 807; Курс физической химии, под ред. Я. И. Герасимова, 2 изд., т. 1, М.- Л., 1969; Успехи коллоидной химии, под ред. П. А. Ребиндера и Г. И. Фукса, М., 1973; Гиббс Д ж. В., Термодинамические работы, пер. с англ., М.- Л., 1958; Р у с а н о в А. И., Фазовые равновесия и поверхностные явления. Л., 1967; Межфазовая граница газ - твёрдое тело, пер. с англ., М., 1970; Дерягпн Б. В., Кротова Н. А., Смилга В. П., Адгезия твёрдых тел, М., 1973; 3имон А. Д., Адгезия жидкости и смачивание, М., 1974; Семенченко В. К., Поверхностные явления в металлах и сплавах, М., 1957; Recent progress in surfase science, ed by J. F. Danielli [a. o.], v. 1-5, N. Y.- L., 1964-72. См. также лит. при статьях Коллоидная химия, Поверхностное натяжение. Васильев Ю. М., Маленков А. Г., Клеточная поверхность и реакции клеток, Л., 1968; П а с ы н с к и й А. Г., Биофизическая химия, 2 изд., М., 1968; Surface phenomena in chemistry and biology, L.- [a. o.], 1958; Surface chemistry of biological systems, N. Y.- L., 1970.

ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ, интеграл от функции, заданной на к.-л. поверхности. К П. и. приводит, напр., задача вычисления массы, распределённой по поверхности S с переменной поверхностной плотностью f(M). Для этого разбивают поверхность на части s₁, s₂, ..., s_n и выбирают в каждой из них по точке M_t. Если эти части достаточно малы, то их массы приближённо равны f(Mi)si, а масса всей поверхности будет

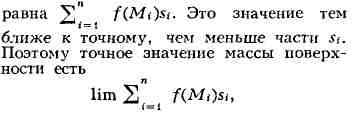
где предел берётся при условии, что размеры всех частей s (и их площади) стремятся к нулю. К аналогичным пределам приводят и другие задачи физики. Эти пределы наз. П. и. первого рода от функции f(M) по поверхности S и обозначают

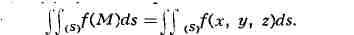
Их вычисление приводится к вычислению двойных интегралов (см. Кратный интеграл).

В нек-рых задачах физики, напр, при определении потока жидкости через поверхность S, встречаются пределы аналогичных сумм с той лишь разницей, что вместо площадей самих частей стоят площади их проекций на три координатные плоскости. При этом поверхность S предполагается ориентированной (т. е. указано, какое из направлений нормалей считается положительным) и площадь проекции берётся со знаком + или -в зависимости от того, является ли угол между положительным направлением нормали и осью, перпендикулярной плоскости проекций, острым или тупым. Пределы сумм такого вида наз. П. и. второго рода (или П. и. по проекциям) и обозначают

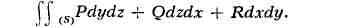
В отличие от П. и. первого рода, знак П. и. второго рода зависит от ориентации поверхности S.

М. В. Остроградский установил важную формулу, связывающую П. и. второго рода по замкнутой поверхности S с тройным интегралом по ограниченному ею объёму V (см. Остроградского формула). Из этой формулы следует, что если функции Р, Q, R имеют непрерывные частные производные и в объёме V выполняется тождество

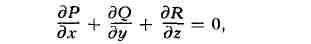
то П. и. второго рода по всем поверхностям, содержащимся в V и имеющим один и тот же контур, равны между собой. В этом случае можно найти такие функции P₁, Q₁, R₁, что

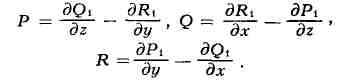
Стокса формула выражает криволинейный интеграл по замкнутому контуру через П. и. второго рода по ограниченной этим контуром поверхности.

Лит.: Никольский С. М., Курс математического анализа, т. 2, М., 1973; Ильин В. А.,Позняк Э. Г., Основы математического анализа, ч. 2, М., 1973; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 2, М., 1973.

ПОВЕРХНОСТНЫЙ СЛОЙ, тонкий слой вещества близ поверхности соприкосновения двух фаз (тел, сред), отличающийся по свойствам от веществ в объёме фаз. Особые свойства П. с. обусловлены сосредоточенным в нём избытком свободной энергии (см. Поверхностная энергия, Поверхностное натяжение), а также особенностями его строения и состава. П. с. на границе конденсированных фаз часто наз. межфазным слоем. Толщина П. с. зависит от разности плотностей фаз, интенсивности и типа межмолекулярных взаимодействий в граничной зоне, темп-ры, давления, хим. потенциалов и др. термодинамич. параметров системы. В одних случаях она не превышает толщины мономолекулярного слоя, в других - достигает десятков и сотен молекулярных размеров. Так, П. с. жидкостей вблизи критич. температур смешения могут иметь толщину 1000 А (100 нм) и более. П. с., образованный молекулами (или ионами) адсорбированного вещества, наз. адсорбционным слоем. Особенно резко изменяются состав и свойства П. с. при адсорбции поверхностно-активных веществ. Адсорбционное, хемосорбционное и хим. воздействия на П. с. твёрдого тела могут вызвать его лиофилизацию или лиофобизацию (см. Лиофильность и лиофобность), привести к понижению его прочности (см. Ребиндера эффект) или, наоборот, повысить механич. характеристики. Состояние П. с. различных конструкционных, радиотех-нич. и др. материалов сильно отражается на их эксплуатационно-технич. и технологич. характеристиках. Со свойствами П. с. связаны многообразные поверхностные явления в окружающем нас мире.

Л. А. Шиц.

ПОВЕРХНОСТНЫЙ СТОК, процесс перемещения воды по земной поверхности под влиянием силы тяжести. П. с. делится на склоновый и русловой. Склоновый сток образуется за счёт дождевых и талых вод, происходит на поверхности склона вне фиксированных путей. Русловой сток проходит по определённым линейным направлениям - в руслах рек, днищах оврагов и балок. В формировании руслового П. с. иногда принимают участие также подземные воды и грунтовые воды. П. с. характеризуется объёмом воды, стекающей по поверхности (модуль стока), выраженным в л /сек км² или слоем мм в год или за к.-л. другой период. В СССР наименьший модуль стока в засушливых р-нах равнин Ср. Азии - 0-1 л/сек км², наибольший в горах Зап. Кавказа - до 125 л/сек км². П. с. изменчив во времени: при ср. годовом модуле стока в басс. р. Ворскла 2,1 л/сек км², макс. модуль весеннего половодья 220 л/сек км²; в Приморье, где модуль ср. стока составляет 8-15 л/сек км², макс. модули ливневого стока достигают 600-700 (и даже более 1000 л/сек км²).

К. Г. Тихоцкий.

ПОВЕРХНОСТЬ, одно из основных геометрич. понятий. При логич. уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.

1) В школьном курсе геометрии рассматриваются плоскости, многогранники, а также нек-рые кривые поверхности. Каждая из кривых П. определяется специальным способом, чаще всего как множество точек, удовлетворяющих нек-рым условиям. Напр., П. шара - множество точек, отстоящих на заданном расстоянии от данной точки. Понятие "П." лишь поясняется, а не определяется. Напр., говорят, что П. есть граница тела или след движущейся линии.

2) Математически строгое определение П. основывается на понятиях топологии. При этом основным является понятие простой поверхности, к-рую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям). Более точно, простой П. наз. образ гомеоморфного отображения (т. е. взаимно однозначного и взаимно непрерывного отображения) внутренности квадрата (см. Гомеоморфизм). Этому определению можно дать аналитическое выражение. Пусть на плоскости с прямоугольной системой координат и и v задан квадрат, координаты внутренних точек к-рого удовлетворяют неравенствам 0 < u < 1, 0<v<l. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул

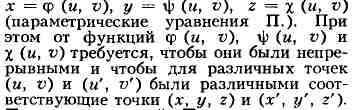
примером простои 11. является полусфера. Вся же сфера не является простой П. Это вызывает необходимость дальнейшего обобщения понятия П. Поверхность, окрестность каждой точки к-рой есть простая П., наз. правильной. С точки зрения топологич. строения, П. как двумерные многообразия разделяются на неск. типов: замкнутые и открытые, ориентируемые и неориентируемые и т. д. (см. Многообразие).

В дифференциальной геометрии исследуемые П. обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это - условия гладкости П., т. е. существования в каждой точке П. определённой касательной плоскости, кривизны и т. д. Эти требования сводятся к тому, что функ-

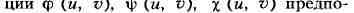
лагаются однократно, дважды, трижды, а в нек-рых вопросах - неограниченное число раз дифференцируемыми или даже аналитическими функциями. Кроме того, требуется, чтобы в каждой точке хотя бы один из определителей

был отличен от нуля (см. Поверхностей теория).

В аналитич. геометрии и в алгебраич. геометрии П. определяется как множество точек, координаты к-рых удовлетворяют определённому виду уравнений:

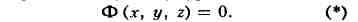
Таким образом, определённая П. может и не иметь наглядного геометрич. образа. В этом случае для сохранения общности говорят о мнимых П. Напр., уравнение

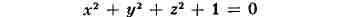
определяет мнимую сферу, хотя в действительном пространстве нет ни одной точки, координаты к-рой удовлетворяют такому уравнению (см. также Поверхности второго порядка). Если функция

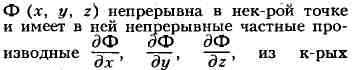
хотя бы одна не обращается в нуль, то в окрестности этой точки П., заданная уравнением (*), будет правильной.