ПИ, Пи , буква греческого алфавита, применяемая в математике для обозначения определённого иррационального числа, именно - отношения длины окружности к диаметру. Это обозначение (вероятно, от греч. Пиеpiфepеa - окружность, периферия) стало общепринятым после работы Л. Эйлера, относящейся к 1736, однако впервые оно было употреблено англ. математиком У. Джонсом (1706). Как и всякое иррациональное число, Пи представляется бесконечной непериодической десятичной дробью:

Пи = 3, 141 592 653589 793 238 462 643... Нужды практич. расчётов, относящихся к окружности и круглым телам, заставили уже в глубокой древности искать для Пи приближений с помощью рациональных чисел. Древнеегипетские вычисления (2-е тыс. до н. э.) площади круга соответствуют приближённому значению Пи ~ 3 или, более точному, Пи ~

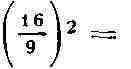
= 3,16049 ... Архимед (3 в. до н. э.), сравнивая окружность с правильными вписанными и описанными многоугольниками, нашёл, что Пи заключается между

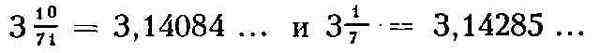
(последним из этих приближений до сих пор пользуются при расчётах, не требующих большой точности). Китайский математик Цзу Чун-чжи (2-я пол. 5 в.) получил для я приближение 3,1415927, вновь найденное в Европе значительно позднее (16 в.); это приближение даёт ошибку лишь в 7-м десятичном знаке. Поиски более точного приближения Пи продолжались и в дальнейшем, напр. аль-Каши (1-я пол. 15 в.) вычислил 17 десятичных знаков Пи , голл. математик Лудольф ван Цейлен (нач. 17 в.) - 32 десятичных знака. Для практич. надобностей, однако, достаточно знать неск. десятичных знаков числа я и простейших выражений, содержащих я; в справочниках обычно даются приближённые значения для я, 1/ Пи и Пи ², lg Пи с 4-7 десятичными знаками.

Число я появляется не только при решении геометрич. задач. Со времени Ф. Виета (16 в.) разыскание пределов нек-рых арифметич. последовательностей, составляемых по простым законам, приводило к эхому же числу Пи . Примером может служить ряд Лейбница (1673-74):

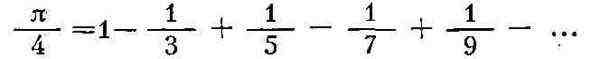
Этот ряд сходится очень медленно. Существуют значительно быстрее сходящиеся ряды, пригодные для вычисления Пи . Так, напр., формула

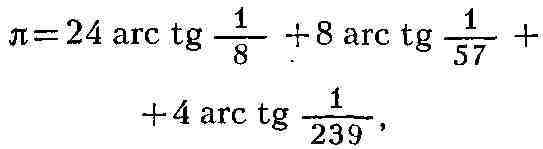
где значения арктангенсов вычисляются с помощью ряда

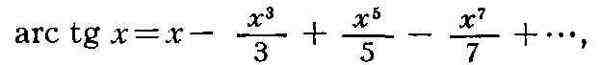
была использована (1962) для вычисления с помощью ЭВМ ста тысяч десятичных знаков числа Пи . Такого рода вычисления приобретают интерес в связи с понятием случайных и псевдослучайных чисел. Статистическая обработка указанной совокупности знаков Пи показывает, что она обладает многими чертами случайной последовательности.

Возможность чисто аналитического определения числа Пи имеет принципиальное значение и для геометрии. Так, в неевклидовой геометрии Пи также участвует в нек-рых формулах, но уже не как отношение длины окружности к диаметру (это отношение в неевклидовой геометрии вовсе не является постоянным). Средствами анализа, среди к-рых решающую роль сыграла замечательная формула Эйлера e^{2 Пи i} = 1 (е - основание натуральных логарифмов, см. Неперово число;

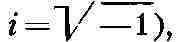
была окончательно выяснена и арифметич. природа числа Пи.

В кон. 18 в. И. Ламберт и А. Лежандр установили, что Пи - число иррациональное, а в 1882 нем. математик Ф. Линдеман доказал, что оно трансцендентно, т. е. не может удовлетворять никакому алгебраич. уравнению с целыми коэффициентами. Теорема Линдемана окончательно установила невозможность решения задачи о квадратуре круга с помощью циркуля и линейки.

Лит.: О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). С приложением истории вопроса..., пер. с нем., 3 изд., М.-Л., 1936; Shanks D., Wrench J. W., Calculation of Пи to 100 000 decimals, "Mathematics of Computation", 1962, v. 16, № 77.