ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ, движение точки (или тела) по отношению к подвижной системе отсчёта, перемещающейся определённым образом относительно нек-рой другой, основной системы отсчёта, условно наз. неподвижной. Скорость точки в О. д. наз. относит, скоростью v_ОТ, а ускорение - относит, ускорением w_ОТ. Движение всех точек подвижной системы относительно неподвижной наз. в этом случае переносным движением, а скорость и ускорение той точки подвижной системы, через к-рую в данный момент времени проходит движущаяся точка,- переносной скоростью Спер и переносным ускорением w_пер. Наконец, движение точки (тела) по отношению к неподвижной системе отсчёта наз. сложным или абсолютным, а скорость и ускорение этого движения - абс. скоростью v_а и абс. ускорением w_а. Напр., если с пароходом связать подвижную систему отсчёта, а с берегом - неподвижную, то для шара, катящегося по палубе парохода, движение по отношению к палубе будет О. д., а по отношению к берегу - абсолютным. Соответственно скорость и ускорение шара в первом движении будут v_ОТ И w_ОТ, а во втором - v_а И w_a.

Движение же всего парохода по отношению к берегу будет для шара переносным движением, а скорость и ускорение той точки палубы, к-рой в данный момент касается шар, будут v_пер и w_пер (шар рассматривается как точка). Зависимость между этими величинами даётся в классич. механике равенствами:

v_а = v_от + v_пер, w_а = w_от +w_пер+w_кор, (1)

где w_кор - Кориолиса ускорение. Формулами (1) широко пользуются в кинематике при изучении движения точек и тел.

В динамике О. д. наз. движение по отношению к неинерциальной системе отсчёта, для к-рой законы механики Ньютона несправедливы. Чтобы ур-ния О. д. материальной точки сохранили тот же вид, что и в инерциальной системе отсчёта, надо к действующей на точку силе взаимодействия с другими телами F присоединить т. н. переносную силу инерции J_пep = - mw_пep и Кориолиса силу инерции J_кор = - mw_кор, где m - масса точки. Тогда

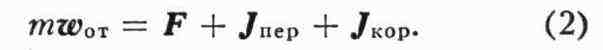
При О. д. системы материальных точек аналогичные ур-ния составляются для всех точек системы. Этими уравнениями пользуются для изучения О. д. под действием сил различных механич. устройств (в частности, гироскопов), устанавливаемых на подвижных основаниях (кораблях, самолётах, ракетах), а также для изучения движения тел по отношению к Земле в случаях, когда требуется учесть её суточное вращение.

Лит. см. при статьях Кинематика и Дикалика.

С. М. Торг.

ОТНОСИТЕЛЬНОЕ ОТВЕРСТИЕ, отношение диаметра действующего отверстия объектива к его фокусному расстоянию. Квадрат О. о. определяет освещённость в плоскости изображения и часто наз. светосилой объектива.

ОТНОСИТЕЛЬНОЕ ПЕРЕНАСЕЛЕНИЕ, относительный избыток рабочего населения при капитализме по сравнению со спросом на рабочую силу со стороны капиталистов. См. статьи Промышленная резервная армия труда, Безработица, Всеобщий закон капиталистического накопления .

ОТНОСИТЕЛЬНОЕ УХУДШЕНИЕ ПОЛОЖЕНИЯ ПРОЛЕТАРИАТА, см. в ст. Абсолютное и относительное ухудшение положения пролетариата.

ОТНОСИТЕЛЬНОСТИ ПРИНЦИП, один из наиболее фундаментальных физ. законов, согласно к-рому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе, находящейся в состоянии равномерного прямолинейного движения. Состояние движения или покоя определяется здесь по отношению к произвольно выбранной инерциалъной системе отсчёта; физически эти состояния полностью равноправны. Эквивалентная формулировка О. п.: законы физики имеют одинаковую форму во всех инерц. системах отсчёта. О. п. вместе с постулатом о независимости скорости света в вакууме от движения источника света легли в основу специальной (частной) теории относительности А. Эйнштейна (см. Относительности теория).

И. Ю. Кобзарев.

ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ, физическая теория, рассматривающая пространственно-временные свойства физ. процессов. Закономерности, устанавливаемые О. т., являются общими для всех физ. процессов, поэтому часто о них говорят просто как о свойствах пространства-времени. Как было установлено А. Эйнштейном, эти свойства зависят от гравитац. полей (полей тяготения), действующих в данной области пространства-времени. Свойства пространства-времени при наличии полей тяготения исследуются в общей теории относительности (ОТО), наз. также теорией тяготения. В частной теории относительности рассматриваются свойства пространства-времени в приближении, в к-ром эффектами тяготения можно пренебречь. Логически частная О. т. есть частный случай ОТО, откуда и происходит её название. Исторически развитие теории происходило в обратном порядке; частная О. т. была сформулирована Эйнштейном в 1905, окончательная формулировка ОТО была дана им же в 1916. Ниже излагается частная О. т., наз. в литературе также теорией относительности Эйнштейна, просто О. т., или специальной теорией относительности (история её возникновения изложена в последнем разделе).

Основные черты теории относительности

Явления, описываемые О. т. и называемые релятивистскими (от лат. relatio - отношение), проявляются при скоростях движения тел, близких к скорости света в вакууме с=(2,997924562±0,000000011)X10¹⁰см/сек. При таких скоростях (называемых релятивистскими) зависимость энергии Е тела от его скорости v описывается уже не формулой классич. механики Е_кин = mv²/2, а релятивистской формулой

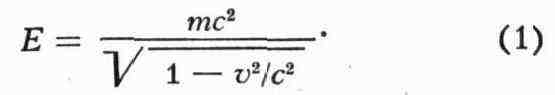
Масса т, входящая в эту формулу, в О. т. наз. также массой покоя. Из (1) видно, что энергия тела стремится к бесконечности при скорости v, стремящейся к с, поэтому если масса покоя не равна нулю, то скорость тела всегда меньше с, хотя при Е " тс² она может стать сколь угодно близкой к с. Это непосредственно наблюдается на ускорителях протонов и электронов, в которых частицам сообщаются энергии, много большие тс², и поэтому они движутся со скоростью, практически равной с. Со скоростью света всегда движутся частицы, масса покоя к-рых равна нулю (фотоны - кванты света, нейтрино). Скорость с является предельной скоростью передачи любых взаимодействий и сигналов из одной точки пространства в другую.

Существование предельной скорости вызывает необходимость глубокого изменения обычных пространственно-временных представлений, основанных на повседневном опыте. Рассмотрим след, мысленный опыт. Пусть в вагоне, движущемся со скоростью v относительно полотна жел. дороги, посылается световой сигнал в направлении движения. Скорость сигнала для наблюдателя в вагоне равна с. Если бы длины и времена, измеряемые любым наблюдателем, были одинаковы, то выполнялся бы закон сложения скоростей классич. механики и для наблюдателя, стоящего у полотна, скорость сигнала была бы равна с + v, т. е. была бы больше предельной. Противоречие устраняется тем, что в действительности с точки зрения наблюдателя, относительно к-рого физич. система движется со скоростью v, все процессы в этой системе замедляются в корень из 1-v²/с² раз (это явление наз. замедлением времени), продольные (вдоль движения) размеры тел во столько же раз сокращаются и события, одновременные для одного наблюдателя, оказываются неодновременными для другого, движущегося относительно него (т. н. относительность одновременности). Учёт этих эффектов приводит к закону сложения скоростей, при к-ром предельная скорость оказывается одинаковой для всех наблюдателей.

Характерное для О. т. явление замедления времени может принимать огромные масштабы. В опытах на ускорителях и в космических лучах образуются распадающиеся (нестабильные) частицы, движущиеся со скоростью, близкой к скорости света. В результате замедления времени (с точки зрения земного наблюдателя) времена их распада и, следовательно, проходимые ими (от рождения до распада) расстояния увеличиваются в тысячи и десятки тысяч раз по сравнению с теми, к-рые частицы пролетали бы, если бы эффект замедления времени отсутствовал.

Из релятивистской формулы для энергии следует, что при малых скоростях (м<<с) энергия тела равна

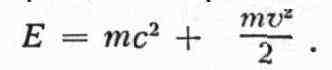
Второй член справа есть обычная кинетич. энергия, первый же член показывает, что покоящееся тело обладает запасом энергии Е₀=тс², наз. энергией покоя (т.н. принцип эквивалентности энергии и массы, или принцип эквивалентности Эйнштейна).

В ядерных реакциях и процессах превращений элементарных частиц значит, часть энергии покоя может переходить в кинетич. энергию частиц. Так, источником энергии, излучаемой Солнцем, является превращение четырёх протонов в ядро гелия; масса ядра гелия меньше массы четырёх протонов на 4,8•10^-26 г, поэтому при каждом таком превращении выделяется 4,3•10^-5 эрг кинетич. энергии, уносимой излучением. За счёт излучения Солнце теряет в 1 сек 4•10⁷ т своей массы.

О. т. подтверждена обширной совокупностью фактов и лежит в основе всех совр. теорий, рассматривающих явления при релятивистских скоростях. Уже последоват. теория электромагнитных, в частности оптических, явлений, описываемых классич. электродинамикой (см. Максвелла уравнения), возможна только на основе О. т. Теория относительности лежит также в основе квантовой электродинамики, теорий сильного и слабого взаимодействий элементарных частиц. Законы движения тел при релятивистских скоростях рассматриваются в релятивистской механике, к-рая при скоростях v"с переходит в классическую механику Ньютона. Квантовые законы движения релятивистских микрочастиц рассматриваются в релятивистской квантовой механике и квантовой теории поля.

Принцип относительности и другие принципы инвариантности

В основе О. т. лежит принцип относительности, согласно к-рому в физич. системе, приведённой в состояние свободного равномерного и прямолинейного движения относительно системы, условно наз. "покоящейся", для наблюдателя, движущегося вместе с системой, все процессы происходят по тем же законам, что и в "покоящейся" системе. Говорят, что движущаяся система получается из "покоящейся" преобразованием движения и что принцип относительности выражает инвариантность (независимость) законов природы относительно преобразований движения.

Справедливость принципа относительности означает, что различие между состояниями покоя и равномерного прямолинейного движения не имеет физич. содержания. Если физич. система В движется равномерно и прямолинейно (со скоростью V) относительно системы А, то с тем же правом можно считать, что А движется относительно В (со скоростью-V). Термин "принцип относительности" связан с тем, что если преобразованию движения подвергнуть систему движущихся тел, то все относительные движения этих тел останутся неизменными.

Наряду с принципом относительности из опыта известны и др. принципы инвариантности, или, как ещё говорят, симметрии, законов природы. Любой физич. процесс происходит точно так же если осуществить его в любой др. точке пространства; эта симметрия выражает равноправие всех точек пространства, однородность пространства; если систему, в к-рой происходит процесс, повернуть на произвольный угол; эта симметрия выражает равноправие всех направлений в пространстве, изотропию пространства; если повторить процесс через нек-рый промежуток времени; эта симметрия выражает однородность времени.

Т. о., имеет место инвариантность законов природы по отношению к четырём типам преобразований: 1) переносу в пространстве, 2) вращению в пространстве, 3) сдвигу во времени, 4) преобразованию движения. Симметрии 1-4 выполняются точно только в изолированной от внешних воздействий системе, т. е. если можно пренебречь воздействием на систему внешних факторов; для реальных систем они справедливы лишь приближённо.

Изучение свойств преобразований 1-2 составляет предмет евклидовой геометрии трёхмерного пространства, если рассматривать её как физич. теорию, описывающую пространств, свойства физич. объектов (при этом под переносом следует понимать преобразование параллельного переноса).

При скоростях тел v, сравнимых со скоростью с, обнаруживается тесная связь и матем. аналогия между преобразованиями 1, 3 и 2, 4. Это даёт основание говорить об О. т., в к-рой все преобразования 1-4 следует рассматривать совместно, как о геометрии пространства-времени. Содержанием О. т. является рассмотрение свойств преобразований 1-4 и следствий из соответствующих принципов инвариантности. Математически О. т. является обобщением геометрии Евклида - геометрией четырёхмерного Минковского пространства.

Принцип относительности был известен (и справедлив) в классич. механике, но свойства преобразований движения при v<<c и при v~c различны; при v<<c релятивистские эффекты исчезают и преобразования движения переходят в преобразования инвариантности, справедливые для классич. механики (преобразования Галилея; см. Галилея принцип относительности). Поэтому различают релятивистский принцип относительности, обычно наз. принципом относительности Эйнштейна, и нерелятивистский принцип относительности Галилея.

Осн. понятие О. т. - точечное событие, т. е. нечто, происходящее в данной точке пространства в данный момент времени (напр., световая вспышка, распад элементарной частицы). Это понятие является абстракцией - реальные события всегда имеют нек-рую протяжённость в пространстве и во времени и могут рассматриваться как точечные только приближённо. Любой физический процесс есть последовательность событий (С)-C₁, С₂, ..., С_n, ... . Справедливость симметрии 1-4 означает, что наряду с последовательностью (С) законы природы допускают существование бесконечного числа др. последовательностей (С*), к-рые получаются из (С) соответствующим преобразованием и различаются положением событий в пространстве и времени, но имеют одинаковую с (С) внутр. структуру. Напр., в случае симметрии 4 процесс (С) можно наглядно описать как происходящий в стоящем на земле самолёте, а процесс (С*)- как такой же процесс, происходящий в самолёте, летящем с постоянной скоростью (относительно земли); различным скоростям и направлениям движения соответствуют различные последовательности (С*). Преобразования, переводящие одну последовательность событий в другую, наз. активными (в отличие от пассивных преобразований, к-рые связывают координаты одного и того же события в двух системах отсчёта; см. ниже). Совокупность этих преобразований должна удовлетворять определённым свойствам. Прежде всего последоват. применение любых двух преобразований должно представлять собой одно из возможных преобразований [напр., переход от системы (1) к системе (2), а затем от системы (2) к системе (3) эквивалентен переходу (1)-(3)]. Кроме того, для каждого преобразования должно существовать обратное преобразование, так что последоват. применение обоих преобразований даёт тождественное (единичное) преобразование, являющееся одним из возможных преобразований системы. Это означает, что совокупность рассматриваемых преобразований (1-4) должна составлять группу в математич. смысле. Эта группа наз. группой Пуанкаре (назв. предложено Ю. Вигнером). Преобразования группы Пуанкаре носят универсальный характер: они действуют одинаково на события любого типа. Это позволяет считать, что они описывают свойства пространства-времени, а не свойства конкретных процессов. Свойства преобразований Пуанкаре могут быть описаны различными способами (так же, как можно описывать различными способами свойства движений в трёхмерном пространстве); наиболее простое описание получается при использовании инерциалъных систем отсчёта и связанных с ними часов. Роль инерц. систем отсчёта (и. с. о.) в О. т. такая же, как роль прямоугольных декартовых координат в геометрии Евклида.

Инерциальные системы отсчёта

С той степенью точности, с какой свойства данной области пространства-времени описываются частной О. т., можно ввести и. с. о., в к-рых описание пространственно-временных закономерностей О. т. принимает особенно простую форму. Под системой отсчёта в этом случае можно подразумевать жёсткую систему твёрдых тел (или её мысленное продолжение), по отношению к к-рой определяются положения событий, траектории тел и световых лучей. Любая система отсчёта, движущаяся относительно данной и. с. о. равномерно и прямолинейно без вращения, также будет инерциальной, а система отсчёта, вращающаяся или движущаяся ускоренно, уже не будет и. с. о. Следовательно, и. с. о. образуют выделенный класс систем отсчёта. В и. с. о. справедлив закон инерции, т. е. свободная (не испытывающая воздействий др. тел) частица движется в и. с. о. прямолинейно и (при принятой синхронизации часов; см. ниже) равномерно. Требование выполнения закона инерции может быть принято как определение и. с. о. Первый закон Ньютона может рассматриваться при этом как утверждение о существовании таких систем отсчёта. Все и. с. о. равноправны; это равноправие является непосредственным выражением принципа относительности.

Степень инерциалыгости системы отсчёта зависит от свойств гравитац. полей, действующих в рассматриваемой области пространства-времени. Количеств, критерии применимости частной О. т. и инерциальности систем отсчёта рассматриваются в ОТО.

В области пространства-времени, в к-рой справедлива частная О. т., можно пользоваться и неинерц. системами отсчёта (так же, как можно пользоваться криволинейными координатами в геометрии Евклида), но при этом описание свойств пространства-времени оказывается более сложным.

В данной и. с. о. необходимо определить способ измерения времени и координат. В и. с. о. трёхмерная пространств, геометрия- евклидова, если прямые определить, напр., как траектории световых лучей, а расстояния измерять твёрдыми масштабами. Поэтому в данной и. с. о. можно ввести декартовы прямоугольные координаты х, у, z. Для определения времени t события можно принять, что в той точке, где оно произошло, находятся часы, покоящиеся в данной и. с. о. Если события происходят в разных точках А, В, то для сравнения их времён нужно синхронизировать часы в A и В, т. е. определить значение того, что часы в Л и В показывают одинаковое время. Обычное определение таково: пусть в момент t_A по часам в A посылается сигнал в В, а в момент его прибытия в В посылается такой же сигнал из В в Л; если сигнал пришёл в Л в момент t'_A, то принимается, что сигнал пришёл в В в момент t_в = (t_А + t'_А)/2 и соответственно устанавливаются часы в В. При таком определении времена распространения сигнала из Л в В и из В в А одинаковы и равны (t'_А - t_А)/2. Сигналами могут служить световые вспышки, звуковые сигналы (если среда, в к-рой они распространяются, покоится по отношению к данной системе отсчёта), выстрелы из двух одинаковых орудий, установленных в Л и В, и т. д., требуется лишь, чтобы условия передачи сигнала из Л в В и из В в Л были одинаковыми. Целесообразность такого определения времени связана с тем, что в любой и. с. о. отсутствует к.-л. физически выделенное направление; описанная процедура синхронизации часов симметрична относительно Л и В и поэтому не вносит анизотропии в способ описания. Отсутствие выделенного направления проявляется в том, что синхронизация любыми сигналами приводит к одному и тому же результату; к такому же результату приводит медленный (с v << с) перенос часов из Л в В. При практич. измерениях времён и координат используются многочисл. косвенные методы, при условии, что они дают такой же результат, как и описанные выше процедуры. В любой другой и. с. о. координаты и время измеряются с помощью таких же масштабов и часов, синхронизируемых таким же способом. Заранее не очевидно, что времена, определённые таким образом в двух различных и. с. о., будут одними и теми же, и они действительно оказываются различными. После того как синхронизация произведена, могут измеряться скорости частиц и сигналов в данной и. с. о., в частности скорость распространения световых сигналов. Скорость света в любой и. с. о. всегда равна с.

Преобразования Лоренца

Рассмотренные выше активные преобразования непосредственно связаны с пассивными преобразованиями, описывающими связь между координатами и временем данного события в двух различных и. с. о. В силу принципа относительности безразлично, сообщить ли телу скорость V по отношению к данной и. с. о. L или перейти к системе отсчёта L', движущейся со скоростью V относительно L,- закон преобразования координат и времени должен быть одним и тем же.

Вследствие справедливости симметрии 1-4, преобразования, связывающие координаты и времена событий х, у, z, t и х', у', z', t', измеренные в двух и. с. о. L и L', должны быть линейными. Из симметрии 1-4 и требования, чтобы преобразования составляли группу, можно получить вид этих преобразований. Если система отсчёта L' движется относительно L со скоростью V, то при надлежащем выборе осей координат и начал отсчёта времени в L и Z' (оси х и х' совпадают и направлены по V, оси у и у', г и г' соответственно параллельны, начала координат О и О' совпадают при t = 0 и часы в L' установлены так, что при t = 0 часы в О' показывают время f = 0) преобразования координат и времени имеют вид:

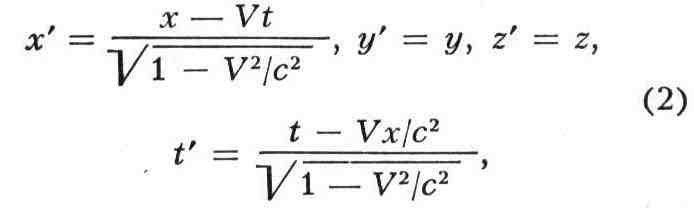
где с - произвольная постоянная, имеющая смысл предельной скорости движения (равной скорости света в вакууме). Эта постоянная может быть определена из любого эффекта О. т. (напр., замедления времени распада быстрого я-мезона). Справедливость кинематики и динамики, основанных на преобразованиях (2), подтверждена неисчислимой совокупностью экспериментальных фактов.

Преобразования Лоренца (2) вместе с преобразованиями вращения вокруг начала координат образуют группу Лоренца; добавление к ней сдвигов во времени t' = t + а и в пространстве х' = х + b (где а, Ь - произвольные постоянные размерности времени и длины) даёт группу Пуанкаре.

Из принципа относительности вытекает, что физич. законы должны иметь одинаковую форму во всех и. с. о.; следовательно, они должны сохранять свой вид при преобразованиях Лоренца. Это требование наз. принципом (постулатом) релятивистской инвариантности, или лоренц-инвариантности (лоренц-ковариантности), законов природы.

Из преобразований Лоренца вытекает релятивистский закон сложения скоростей. Если частица или сигнал движется в L по оси х со скоростью и, то в момент tx = vt и скорость частицы v' = = x'/t', измеряемая в системе L', равна:

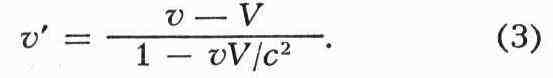
Эта формула отражает осн. черту релятивистской кинематики - независимость скорости света от движения источника. Действительно, если скорость света, испущенного покоящимся в нек-рой и. с. о. L источником, есть с, v = с, то из закона сложения скоростей (2) получаем, что измеренная в и. с. о. L' скорость света v' также равна с. Так как направление оси х произвольно, то отсюда следует независимость скорости света от движения источника. Это свойство скорости света однозначно определяет вид преобразований Лоренца: постулировав независимость скорости света от движения источника, однородность пространства и времени и изотропию пространства, можно вывести преобразования Лоренца.

Особая роль скорости света в О. т. связана с тем, что она является предельной скоростью распространения сигналов и движения частиц, достигаемой при энергии частицы, стремящейся к бесконечности, или массе, стремящейся к нулю; если бы масса покоя то фотона оказалась хотя и очень малой, но отличной от нуля (экспериментально установлено, что m_y < 4*10^-21 т_e, где т_e - масса электрона), то скорость света была бы меньше предельной. Чтобы предельная скорость вообще могла существовать, она не должна зависеть от движения источника частиц.

Из преобразований Лоренца легко получить осн. эффекты О. т.: относительность одновременности, замедление времени, сокращение продольных размеров движущихся тел. Действительно, события 1, 2, одновременные в одной и. с. о. L : t₁ = t₂ и происходящие в разных точках х\, х₂, оказываются неодновременными в другой и. с. о. L':t₁'-t₂'=(х₂-х₁)*V/c²*на корень из(1-V/c²) не равно 0. Далее, когда часы, покоящиеся в Z. в точке х = 0, показывают время t, то время t' по часам в L', пространственно совпадающим с часами в Z, в этот момент времени, есть

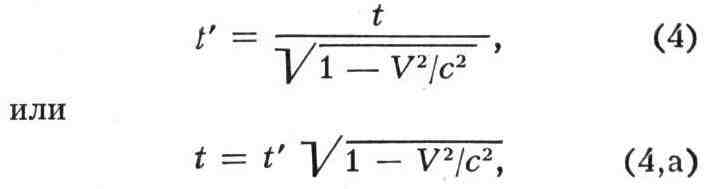
т. е. с точки зрения наблюдателя в L' часы в L отстают. В силу принципа относительности отсюда следует, что с точки зрения наблюдателя в L' все процессы в L. замедлены в такое же число раз.

Легко получить также, что размеры l всех тел, покоящихся в L, оказываются при измерении в L' сокращёнными

в корень из(1 - V²/c²) раз в направлении V:

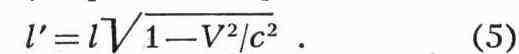
В частности, продольный диаметр сферы, движущейся со скоростью v относительно L', будет при измерении в L' в корень из (1-v²/с²)раз короче, чем поперечный. (Заметим, что это сокращение не обнаружилось бы на мгновенной фотографии сферы: из-за различного запаздывания световых сигналов, приходящих от разных точек сферы, её видимая форма остаётся прежней.)

Для и. с. о. пространственно-временные эффекты, определяемые преобразованиями Лоренца, относительны: с точки зрения наблюдателя в L замедляются все процессы и сокращаются все продольные масштабы в L'. Однако это утверждение несправедливо, если хотя бы одна из систем отсчёта неинерциальна. Если, напр., часы 1 перемещаются относительно L из Л в В со скоростью с, а потом из В в Л со скоростью - v, то они отстанут по сравнению с покоящимися в А часами 2 в корень из (1-v²/c²) раз; это можно обнаружить прямым сравнением, так что эффект абсолютен. Он должен иметь место для любого процесса; напр., близнец, совершивший путешествие со скоростью v, вернётся в корень из (1-v²/c²) раз более молодым, чем его брат, остававшийся неподвижным в и. с. о. Это явление, получившее назв. "парадокса близнецов", в действительности не содержит парадокса: система отсчёта, связанная с часами 1, не является ннерциаль-ной, т. к. эти часы при повороте в В испытывают ускорение по отношению к инерциальной системе; поэтому часы 1 и 2 неравноправны.

При малых скоростях v преобразования Лоренца переходят в преобразования Галилея х'=х-vt, у'=у, z'=z, t'=t, к-рые описывают связь между картинами различных наблюдателей, известную из повседневного опыта: размеры предметов и длительность процессов одинаковы для всех наблюдателей.

Преобразования Пуанкаре оставляют инвариантной величину, наз. интервалом S_AB между событиями Л, В, к-рая определяется соотношением:

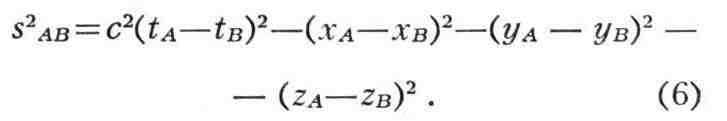
Математически инвариантность s аналогична инвариантности расстояния при преобразованиях движения в евклидовой геометрии. Величины ct, х, у, z можно рассматривать как четыре координаты события в четырёхмерном пространстве Минковского: x⁰ = ct, х¹ = х, х² = у, х³ = z, к-рые являются компонентами четырёхмерного вектора.

Если вместо х⁰ ввести мнимую координату x⁴ = ix⁰ = ict, то произвольное преобразование Пуанкаре можно записать в виде, полностью аналогичном формуле, описывающей вращения и сдвиги в трёхмерном пространстве.

Вследствие того, что квадраты разностей временных и пространств, координат входят в (6) с разными знаками, знак s² может быть различным; геометрия такого пространства отличается от евклидовой и наз. псевдоевклидовой. В такой геометрии интервалы разделяются на три типа: s²<0, s²>О и s²=0. Интервалы первого и второго типа наз. соответственно времени-подобными н пространственноподобными. Если s²>=0, знак t_A-t_Bне зависит от системы отсчёта. Это тесно связано с принципом причинности. Действительно, если s²>=0 и (для определённости) t_A<t_B, то события Л и В могут быть связаны сигналом, распространяющимся со скоростью v=<с, т. е. Л может быть причиной В. Обычные представления о причинности требуют тогда, чтобы в любой системе отсчёта событие В следовало за событием Л. Инвариантность условия s²=0 непосредственно выражает инвариантность скорости света. Если s²<О, то знак t_A - t_Bможет быть различным в разных и. с. о. Однако это не противоречит причинности, т. к. такие события не могут быть связаны никаким взаимодействием.

Если s²<0, то существует такая система отсчёта, в к-рой события А и В одновременны; в этой системе s²=-l², где l - обычное расстояние. При s² > О существует система отсчёта, в к-рой события А и В происходят в одной точке.

В классич. физике требование инвариантности законов физики относительно преобразований Лоренца означает, что любые физич. величины должны преобразовываться как скаляры, векторы или тензоры в пространстве Минковского. Правила вычислений с такими величинами даются тензорным исчислением. Использование тензорного исчисления позволяет записывать законы физики в таком виде, что их лоренц-инвариантность становится непосредственно очевидной.

Законы сохранения в теории относительности и релятивистская механика

В О. т., так же как в классич. механике, для замкнутой физич. системы сохраняется импульс р и энергия Е, Трёхмерный вектор импульса вместе с энергией образует четырёхмерный вектор импульса-энергии с компонентами Е/с, р, обозначаемый как (E;с,р). При преобразованиях Лоренца остаётся инвариантной величина E²- (cp)² = m²c⁴, (7) где от - масса покоя частицы. Из требований лоренц-инвариантности следует, что зависимость энергии и импульса от скорости имеет вид

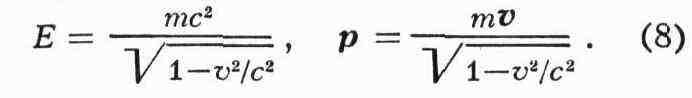
Энергия и импульс частицы связаны соотношением р = Ev/с². Это соотношение справедливо также для частицы с нулевой массой покоя; тогда v = с и р = Е/с. Такими частицами, по-видимому, являются фотоны (у) и электронные и мюонные нейтрино. Из (8) видно, что импульс и энергия частицы с m не равно 0 стремятся к бесконечности при v -> с.

Обсуждалась возможность существования объектов, движущихся со скоростью, большей скорости света (т. н. тахионов). Формально это не противоречит лоренц-инвариантности, но приводит к серьёзным затруднениям с выполнением требования причинности.

Масса покоя т не является сохраняющейся величиной. В частности, в процессах распадов и превращений элементарных частиц сумма энергий и импульсов частиц сохраняется, а сумма масс покоя меняется. Так, в процессе аннигиляции позитрона и электрона е⁺+е^-->2у сумма масс покоя изменяется на 2 m_е .

В системе отсчёта, в к-рой тело покоится (такая система отсчёта наз. собственной), его энергия (энергия покоя) есть Е_о = тс². Если тело, оставаясь в покое, изменяет своё состояние, получая энергию в виде излучения или тепла, то из релятивистского закона сохранения энергии следует, что полученная телом энергия ДЯ связана с увеличением его массы покоя соотношением дельта Е = дельта mc². Из этого соотношения, названного Эйнштейном принципом эквивалентности массы и энергии, следует, что величина E₀ = mс² определяет максимальную величину энергии, к-рая может быть "извлечена" из данного тела в системе отсчёта, в к-рой оно покоится.

Для движущегося тела величина

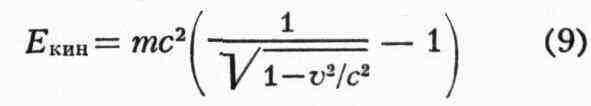
определяет его кинетич. энергию. При v<<с (9) переходит в нерелятивистское выражение Е_кин=mv²/2, при этом импульс равен р = mv. Из определения E_кин следует, что для любого процесса в изолированной системе выполняется равенство:

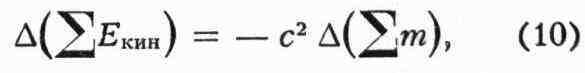
согласно к-рому увеличение кинетич. энергии пропорционально уменьшению суммы масс покоя. Это соотношение широко используется в ядерной физике; оно позволяет предсказывать энерговыделение в ядерных реакциях, если известны массы покоя участвующих в них частиц. Возможность протекания процессов, в к-рых происходит превращение энергии покоя в кинетич. энергию частиц, ограничена др. законами сохранения (напр., законом сохранения барионного заряда, запрещающим процесс превращения протона в позитрон и у-квант). Иногда вводят массу, определяемую как

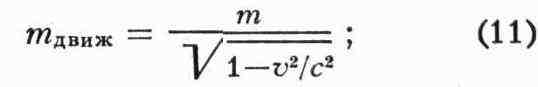
при этом связь между импульсом и энергией имеет тот же вид, что и в ньютоновской механике: р = m_движv. Определённая таким образом масса отличается от энергии тела лишь множителем 1/с². (В теоретич. физике часто выбирают единицы измерения так, что с = 1, тогда E = m_движ)

Осн. уравнения релятивистской механики имеют такой же вид, как второй закон Ньютона и уравнение энергии, только вместо нерелятивистских выражений для энергии и импульса используются выражения (8):

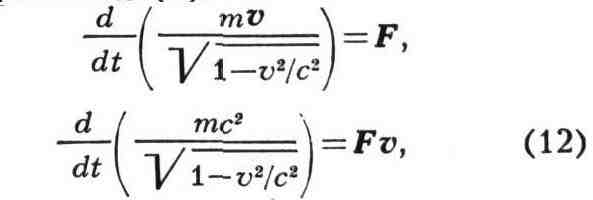
где F - сила, действующая на тело. Для заряженной частицы, движущейся в электромагнитном поле, F есть Лоренца сила.

Теория относительности и эксперимент

Предположения о точечных событиях, справедливости принципа относительности, однородности времени и однородности и изотропии пространства с неизбежностью приводят к О. т. При этом абстрактно допустим предельный случай, соответствующий с = бесконечности, однако такая возможность исключена экспериментально: доказано с огромной точностью (см. ниже), что предельная скорость с есть скорость света в вакууме (её значение дано в начале статьи).

Каковы границы применимости О. т.? Отклонения от пространственно-временной геометрии О. т., связанные с гравитацией, наблюдаемы и рассчитываются в ОТО; никаких др. ограничений применимости О. т. пока не обнаружено, хотя неоднократно высказывались подозрения, что на очень малых расстояниях (напр., ~10^-17 см) понятие точечного события, а следовательно, и О. т. могут оказаться неприменимыми (см., напр., Квантование пространства-времени).

Предположение о лоренц-инвариантности и точечности событий (означающей локальность взаимодействий) лежит в основе всех совр. теорий, в к-рых существен релятивизм. Справедливость квантовой электродинамики электронов и мюонов, а следовательно, и О. т. установлена вплоть до расстояний 10^-15 см. При энергиях порядка масс этих частиц согласие квантовой электродинамики с опытом установлено с относит, точностью, несколько лучшей, чем 10^-5; с точностью того же порядка должна быть справедлива и механика О. т.

Релятивистские законы сохранения применяются при исследованиях превращений элементарных частиц, вызванных сильным, слабым и электромагнитным взаимодействиями; отсутствие противоречий подтверждает справедливость этих законов. Всё, что известно о названных взаимодействиях, согласуется с представлением об их лоренц-инвариантности.

Предположение о невозможности сверхсветовых сигналов, вытекающее из О. т., лежит в основе дисперсионных методов, широко используемых в теории сильных взаимодействий (см. также Квантовая теория поля); их успех демонстрирует справедливость осн. представлений О. т.

Одним из наиболее ярких подтверждений справедливости релятивистской инвариантности явилось предсказание на её основе существования античастиц и их последующее открытие (см. Дирака уравнение, Античастицы).

Требование лоренц-инвариантности взаимодействий приводит при очень общих предположениях к т. н. СРТ-теореме, устанавливающей связь между свойствами частиц и античастиц. Эта связь выполняется на опыте для всех известных взаимодействий.

Неоднократно ставились опыты по прямой проверке осн. черт кинематики О. т. Независимость скорости света от движения источника проверена с наилучшей точностью в 1964 в опытах [Европ. центр ядерных исследований (ЦЕРН, Швейцария)], в к-рых использовались у-кванты от распада л°-мезона; при скорости Пи°v= 0,9997с относит, точность совпадения скорости Y-кванта с с составляла 10^-4. Релятивистское замедление времени измерено в широком интервале скоростей с помощью поперечного Доплера эффекта и непосредственно по распадам элементарных частиц с точностью 1-5% . Неоднократно проверялась также формула т_движ= m*корень из (l-v²/c²) наилучшая достигнутая точность - 5-10^-4 (В. Мейер и др., 1963).

История частной теории относительности

Хотя О. т. в логич. смысле проста, путь, приведший к ней, был сложным. Справедливость принципа относительности для механических явлений и его связь с явлением инерции были поняты после появления теории Н. Коперника: отсутствие видимых проявлений движения Земли с неизбежностью приводило к заключению, что общее движение системы не сказывается на происходящих в ней механических явлениях. Уже в 16 в. это поясняли, описывая эксперименты на движущемся корабле. Классич. изложение принципа относительности было дано в 1632 Г. Галилеем: "Заставьте теперь корабль двигаться с любой скоростью и тогда (если только движение будет равномерным и без качки в ту и другую сторону) во всех ... явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли .корабль или стоит неподвижно" (Галилей Г., Диалог о двух главнейших системах мира: птолемеевой и коперниковой, М.- Л., 1948, с. 147). Принцип относительности широко использовался X. Гюйгенсом для решения задач механики.

Полная система законов движения для любой механич. системы была дана И. Ньютоном в "Началах" (1687). Ньютон, установив, что законы механики не могут быть справедливыми в любой системе отсчёта, ввёл понятия абс. пространства и абс. времени; по существу это были для него система отсчёта и временная переменная t, для к-рых выполнялись законы движения. Вопрос об измерении времени в механике Ньютона был простым, т. к. любые равномерно движущиеся часы годились для измерения t. Более сложным был вопрос об абс. пространстве. В механике Ньютона выполнялся принцип относительности. Согласно формулировке Ньютона, "относительные движения друг по отношению к другу тел, заключённых в каком-либо пространстве, одинаковы, покоится ли это пространство или движется равномерно и прямолинейно без вращения" ("Математические начала натуральной философии", см. Крылов А. И., Собр. трудов, т. 7, 1936, с. 49). Поэтому нельзя было отличить покоящуюся в абсолютном пространстве систему отсчёта от равномерно движущейся. Переход от одной и. с. о. к другой в механике Ньютона описывался преобразованиями х' = х - vt, t' = t, наз. сейчас преобразованиями Галилея. Такая форма преобразований казалась очевидной, т. к. не сомневались в том, что длины предметов должны быть одинаковыми в любой системе отсчёта, а время единым. Эта уверенность подтверждалась инвариантностью законов Ньютона относительно преобразований Галилея. Столь же несомненным казалось то, что для оптич. явлений принцип относительности несправедлив. Уже в 17 в. широко использовалось представление о заполняющей пространство среде - эфире. Среди мн. функций, приписывавшихся эфиру, была передача световых возмущений. В нач. 19 в. была разработана оптика Т. Юнга - О. Френеля, в к-рой скорость света относительно эфира считалась константой, не зависящей от движения источника. Отсюда следовало нарушение принципа относительности, т. к. для наблюдателя, движущегося в эфире со скоростью v навстречу световому лучу, скорость света должна была бы равняться с + v (эфирный ветер). Такой эфирный ветер должен был бы возникать, в частности, из-за орбитального движения Земли (со скоростью 30 км/сек). Поиски эфирного ветра затруднялись, однако, тем, что уже по теории Френеля эффекты порядка v/c (~10^-4 для орбитального движения Земли) должны отсутствовать в широком классе опытов.

Проблема эфира заняла одно из центр, мест в физике после построения Дж. Максвеллом теории электромагнитного поля, в к-рой эфир стал носителем не только световых волн, но и электрич. и магнитных полей. Попытки обнаружения эфирного ветра были сделаны А. Майкельсоном (1881) и А. Майкельсоном и Э. Морли (1887), искавшими эффект порядка v²/c², и дали отрицат. результат (см. Майкелъсона опыт). Возникла проблема согласования опыта Майкельсона с оптикой и электродинамикой, основанными на представлении об эфире. Наиболее очевидными казались объяснения, базирующиеся на гипотезе полного увлечения эфира движущимися телами. Оптич. и электромагнитные теории, использовавшие эту гипотезу, обсуждались (Дж. Г. Стоке, Г. Герц), но они оказались либо внутренне противоречивыми, либо не описывали всей совокупности экспериментальных фактов. Наиболее успешной была электродинамика X. Лоренца, в основе к-рой лежало представление о неподвижном эфире и к-рая, на первый взгляд, была несовместима с принципом относительности. В 1892 Лоренц (ранее англ, физик Дж. Фицджеральд, 1889) заметил, что отрицат. результат опыта Майкельсона объясняется, если продольные размеры всех тел сокращаются в корень из (1-v²/c²) раз при движении тел относительно эфира со скоростью v. Это сокращение (т. н. Лоренца - Фицджеральда сокращение) Лоренц объяснял изменением действующих в телах электромагнитных сил при движении тела через эфир. В 1895 Лоренц, рассматривая соответствие между движущейся и неподвижной относительно эфира системами тел, ввёл (в приближении v/c) понятие "местного времени" t'=t-(v/c)(x-vt) и доказал, что эффекты движения относительно эфира отсутствуют в порядке v/c.

Ситуация наталкивала на мысль о необнаружимости движения относительно эфира. Такой вывод сделал А. Пуанкаре, к-рый начиная с 1895 выражал убеждение, что движение относительно эфира необнаружимо принципиально. В 1900-е гг. при обсуждении электромагнитных явлений он начал пользоваться термином "принцип относительности", формулируя его как невозможность обнаружения движения относительно эфира. В нач. 1900-х гг. был проведён ряд опытов, подтвердивших, что движение Земли не влияет на электромагнитные, в частности на оптические, явления. [К этому вопросу возвращались и после создания О. т.; в 1963, напр., отсутствие эфирного ветра проверено в опытах, к-рые могли бы обнаружить эфирный ветер в неск. м/сек (Д. Чампней и др.).] Проблема согласования этого факта с электродинамикой Максвелла - Лоренца стала насущной.

Объяснение невозможности обнаружить абс. движение в рамках представлений об эфире и связанной с ним привилегированной системе отсчёта было дано Лоренцом и Пуанкаре в 1904-05. Предполагая, что уравнения электродинамики Лоренца (см. Лоренца - Максвелла уравнения) справедливы в системе координат, покоящейся относительно эфира, они сделали вывод, что все тела при движении в эфире испытывают лоренц-фицджеральдовское сжатие, а происходящие в них движения изменяются определённым образом, но эти изменения в силу их универсальности необнаружимы для наблюдателя, движущегося вместе с телом. Преобразования, названные Пуанкаре преобразованиями Лоренца, описывали связь между пространственно-временными координатами для процессов в двух телах, одно из к-рых двигалось, а другое покоилось относительно эфира. (Ранее близкие преобразования применил нем. физик В. Фохт; правильные преобразования нашёл впервые Дж. Лармор в 1900.)

В завершающей работе Пуанкаре (поступившей в печать 23 июля 1905) содержался разработанный математич. анализ релятивистских преобразований, интерпретировавшихся в описанном выше смысле. Было показано, что преобразования Лоренца образуют группу, оставляющую инвариантным интервал х²+y²+z²-c²t²; были найдены преобразования для потенциалов электромагнитного поля, плотностей тока и заряда, установлена инвариантность действия для электромагнитного поля, показано, что группа Лоренца является группой инвариантности уравнений электродинамики. Лоренц и Пуанкаре видели также универсальный характер лоренц-инвариантности, к-рую они формулировали как требование, чтобы все силы и массы преобразовывались так же, как электромагнитные.

Ещё в 1904 Пуанкаре, перечисляя принципы классич. физики, дал общую и полную формулировку принципа относительности: "Законы природы должны быть одинаковы как для неподвижного наблюдателя, так и для наблюдателя, находящегося в состоянии равномерного и прямолинейного движения, так что не существует и не может существовать способа обнаружить, находимся мы в состоянии такого движения или нет" ("Bulletin des sciences mathematiques", 1904, v. 25, ser. 2, p. 302).

Для того чтобы убедиться, что постулат относительности в такой форме выполним, был необходим последовательный анализ измерения пространственно-временных координат в произвольной и. с. о. Важный шаг в этом направлении был сделан Пуанкаре ещё в 1900, когда он заметил, что синхронизация часов светом в системе отсчёта, движущейся относительно эфира, даёт местное время Лоренца в приближении v/c. Последовательно такой анализ уже с совр. точки зрения был сделан Эйнштейном.

В работе, направленной в печать 30 июня 1905, Эйнштейн изложил совершенно новую точку зрения на проблему принципа относительности. Он сделал вывод, что из невозможности обнаружить абс. движение следует равноправие всех и. с. о. Эйнштейн отказался от представления об эфире и стал рассматривать поле в пустоте как новый вид физического объекта, не нуждающийся в механическом носителе (эфире). Это было революционным шагом, означавшим резкий разрыв с господствовавшими в физике того времени взглядами. Равноправие всех и. с. о. логически требовало признания полного равноправия пространственно-временных координат, измеряемых в любой и. с. о. Эйнштейн дал последовательный анализ физич. содержания понятий времени и координат события, исходя из того, что координаты в каждой и. с. о. измеряются стандартными масштабами, а время- часами, синхронизированными светом, и поставил и разрешил вопрос о связи пространственных и временных координат, измеренных в разных и. с. о. Эта связь должна была быть такой, чтобы электродинамика Максвелла - Лоренца, находившаяся в согласии с обширной совокупностью фактов, была справедлива в любой и. с. о. Из уравнений Максвелла - Лоренца вытекает, что скорость света в вакууме не зависит ни от направления распространения света, ни от движения источника. Т. о., в них неявно содержались и принятая Эйнштейном синхронизация часов светом и универсальное постоянство скорости света. Дав явное определение синхронизации часов и сформулировав 2 постулата -

"1. Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения состояния относятся.

2. Каждый луч света движется в „покоящейся" системе координат с определённой скоростью V, независимо от того, испускается ли этот луч света покоящимся или движущимся телом" (Собр. научных трудов, т. 1, М., 1965, с. 10), - из к-рых следовала независимость скорости света от движения источника для любой и. с. о., Эйнштейн нашёл связь между пространственно-временными координатами события, измеряемыми в различных и. с. о. Полученные преобразования, математически тождественные преобразованиям Лоренца, приобрели, т. о., в работе Эйнштейна новое физич. содержание, а требование лоренц-инвариантности законов природы стало очевидным следствием и выражением равноправия всех и. с. о.

Анализ содержания релятивистских преобразований привёл Эйнштейна к заключению о необходимости изменения складывавшихся в течение столетий представлений об абсолютности длины, времени и одновременности; отказ от них позволил установить относит, характер сжатия Лоренца - Фицджеральда и др. явлений, рассматривавшихся ранее как "реальные" эффекты, вызванные движением тела относительно эфира.

Т. о., Эйнштейном было дано полное решение проблемы относительности и построена О. т. как физич. теория пространства-времени, основанная на представлении об относит, характере релятивистских явлений и относительности времени. Найденное Эйнштейном объединение принципа относительности с относительностью одновременности получило назв. "принцип относительности Эйнштейна".

Открытие относительности одновременности было завершением развития идеи относительности, в начале к-рого стояла теория Н. Коперника. Из теории Коперника следовала относительность "места в пространстве"; Эйнштейн сделал аналогичный вывод для понятия "момента времени". Вместо них осн. понятием теории стало понятие события - оно абсолютно в том смысле, что два совпадающих события остаются таковыми для любого наблюдателя.

В 1905-06 Эйнштейн, применив принцип относительности, установил связь между массой и энергией, а вскоре М. Планк (1906) нашёл релятивистские выражения для энергии и импульса электрона, не прибегая к гипотезам о его структуре (использовавшимся ранее в работах Лоренца и Пуанкаре), и тем самым завершил программу "релятивизации" классич. электродинамики. В 1906 Планк ввёл термин "теория относительности". В 1907-08 Г. Минковский указал, что О. т. может рассматриваться как геометрия пространства-времени; в его работах был развит совр. четырёхмерный аппарат теории. К 1910 построение О. т. в основном завершается, но её воздействие на развитие теоретич. физики только начинается.

Появление теории относительности Эйнштейна оказало существ, влияние на развитие революции в физике, происходившей в нач. 20 в. О. т. была первой физич. теорией, продемонстрировавшей, что представления, основанные на повседневном опыте, казавшиеся очевидными и отождествлявшиеся с истинами "здравого смысла", могут оказываться неприменимыми при переходе в новые области опыта. О. т. стала первой "не наглядной" науч. теорией. Революционизировав мышление физиков, О. т. подготовила почву для ещё более далеко идущего отказа от "непосредственно очевидных" представлений, потребовавшегося для создания квантовой механики.

О. т. оказала большое непосредственное воздействие на всё последующее развитие физики. Так, успех релятивистской кинематики при объяснении Комп-тона эффекта стал одним из центр, аргументов в пользу корпускулярной природы фотона (1922); использование преобразований Лоренца привело Л. де Бройля (1924) к соотношению Л=h/р (где Л - длина волны, связанной с движущейся частицей, h - Планка постоянная; см. Волны де Бройля); релятивистская инвариантность послужила ключом к открытию Клейна - Гордона уравнения (1926) и Дирака уравнения (1928). Принцип релятивистской инвариантности сыграл решающую роль в развитии квантовой теории поля; с ним связаны такие её достижения, как установление связи между спином и статистикой (В. Паули, 1940) и создание метода перенормировок в квантовой электродинамике (1949). В совр. физике принцип релятивистской инвариантности продолжает играть решающую роль.

Лит.: Классические труды: Принцип относительности, М.- Л., 1935; Эйнштейн А., Собр. науч. трудов, т. 1 - 4, М., 1965 - 67. Учебники и монографии: Паули В., Теория относительности, пер. с англ., М.- Л., 1947; Ландау Л. Д., Л и ф ш и ц Е. М., Теория поля, 6 изд., М., 1973 (Теоретическая физика, т. 2); Мандельштам Л. И., Лекции по оптике, теории относительности и квантовой механике, М., 1972; Тейлор Э. Ф., У и л е р Д ж. А., Физика пространства-времени, пер. с англ., М., 1969; У га р о в В. А., Специальная теория относительности, М., 1968; Фейнма^н Р., Лейтон Р., С э н д с М., Фейнмановские лекции по физике, [пер. с англ.], в. 2, М., 1965; Ф о к В. А., Теория пространства, времени и тяготения, 2 изд., М., 1961. Популярная литература: Б о р н М., Эйнштейновская теория относительности, пер. с англ., М., 1964; Л а н д а у Л. Д., Р у м е р Ю. Б., Что такое теория относительности, К., 1965; Фейнман Р. П., Характер физических законов, пер. с англ., М., 1968. Обзоры: Вайскопф В., Видимая форма быстродвижущихся тел, "Успехи физических наук", 1964, т. 84, в. 1, с. 183; Блохинцев Д. И., Обоснованность специальной теории относительности опытами в области физики высоких энергий, там же, 1966, т. 89, в. 2, с. 185 - 99; Шмидт-Отт В. Д., Некоторые новые измерения в связи с доказательством справедливости специальной теории относительности, там же, 1968, т. 96, в. 3, с. 519 - 27. История: Вавилов С. И., Экспериментальные основания теории относительности, М.- Л., 1928; Л а у э М., История физики, пер. с нем., М., 1956; Франкфурт У. И., Френк А. М., Оптика движущихся тел, М., 1972.

И. Ю. Кобзарев.

ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ в статистике, количественные характеристики отношения двух сравниваемых между собой показателей. О. в. получаются в результате деления одного из показателей на другой, принятый за базу сравнения. О. в. выражаются в коэффициентах (кратных отношениях), процентах, промиллях и т. д., а в нек-рых случаях - именованными числами (напр., число жителей на 1 км²). В. И. Ленин в своих работах использовал О. в. для анализа статистич. данных по с. х-ву, пром-сти и др. отраслям.

В СССР О. в. применяются для определения уровня выполнения плана, измерения динамики развития обществ, явлений, выяснения их структуры, степени распространения, сравнения между собой различных объектов. В соответствии с этим О. в. подразделяются на след, виды: О. в. выполнения плана, динамики, структуры, координации, интенсивности и сравнения. О. в. выполнения плана - отношение фактич. величины показателя к плановой за тот же период. О. в. динамики - результат отношения уровня показателя за сравниваемый период к его уровню за один из предшествующих периодов (напр., темп роста общего объёма продукции пром-сти СССР в 1972 по сравнению с 1940 составлял 1365%, а по сравнению с 1971 - 106,5%). О. в. структуры рассчитываются как отношение частей или групп совокупности ко всей совокупности (напр., удельный вес произ-ва средств произ-ва в общем объёме продукции пром-сти составил в 1972 73,6%). О. в. координации характеризуют отношение частей одной совокупности между собой (напр., число вспомогат. рабочих на 100 производственных рабочих). О. в. интенсивности показывают степень развития или распространения явлений в данной среде; получаются как отношения разноимённых, но связанных между собой величин (напр., плотность населения - число жителей на 1 км²). О. в. сравнения представляют собой отношение одноимённых показателей по разным объектам (напр., произ-во чугуна составляло в 1972 в СССР 110% к произ-ву в США и 620% к произ-ву в Великобритании). О. в. используются в практике сов. статистики как важное средство анализа деятельности отд. предприятий, отраслей и всего нар. х-ва.

Лит.: Ленин В. И., Развитие капитализма в России, Полн. собр. соч., 5 изд., т. 3; К о з л о в Т. И., Овсненко В.Е., С м и р н с к и и В. И., Курс общей теории статистики, 2 изд., М., 1965; Общая теория статистики, под ред. Т. И. Козлова, 2 изд., M.I 1967.

С. Б. Ошерова.

ОТНОШЕНИЕ, фплос. категория, выражающая характер расположения элементов определённой системы и их взаимозависимости; эмоционально-волевая установка личности на что-либо, т. е. выражение её позиции; мысленное сопоставление различных объектов или сторон данного объекта.

Диалектич. материализм исходит из того, что О. носит объективный и универсальный характер. В мире существуют только вещи, их свойства и О., к-рые находятся в бесконечных связях и О. с др. вещами и свойствами. В. И. Ленин называет верной мысль Гегеля о том, что всякая конкретная вещь состоит в различных отношениях ко всему остальному (см. Полн. собр. соч., 5 изд., т. 29, с. 124). О. образуют системы различной степени сложности из соответствующих элементов, при этом одно и то же О. может быть в различных вещах (внутренние О.) или между различными вещами (внешние О.). Примером является любой закон как существенное О. между вещами, явлениями. И, наоборот, одна и та же вещь может вступать в бесконечно разнообразные О. с др. вещами, что характеризует множественность свойств у той или иной вещи. Любую вещь можно рассматривать как соотношение составляющих её элементов, с изменением к-рого меняется и сама вещь. Напр., различное расположение одних и тех же элементов в словах "кот" и "ток" делает эти слова различными. Вместе с тем любое О. характеризует именно те вещи, между к-рыми оно существует. Напр., О. "меньше" или "больше" характеризует величины; О. "южнее" - место расположения чего-либо по отношению к иному; О. "отец" - характер родства и т. п. Следовательно, О. может выступать в роли свойства, признака вещей. Вещь, взятая в разных О., выявляет разные и даже противоположные свойства. О. предметов и явлений друг к другу бесконечно многообразны (пространственные, временные, причинно-следственные, О. части и целого, формы и содержания, внешнего и внутреннего и др.). Особый тип О. составляют общественные отношения.

Науч. мышление раскрывает суть вещей, закономерность их возникновения и развития через выявление их О. с др. вещами. Характеризуя элементы диалектики, В. И. Ленин указывал на необходимость исследования О.: "Вся совокупность многоразличных отношений этой вещи к другим", "отношения каждой вещи... не только многоразличны, но всеобщи, универсальны. Каждая вещь (явление, процесс...) связаны с каждой; бесконечный процесс раскрытия новых сторон, отношений..." (там же, с. 202-03). В связи с возрастанием роли системноструктурных методов исследования категория О. приобретает всё большее значение в совр. науке.

А. Г. Спиркин.

О. в логике. В содержательных формулировках естественных языков О. выражается обычно сказуемыми предложений, имеющих более одного подлежащего (или одно подлежащее с дополнениями); в зависимости от числа этих подлежащих (и дополнений) их наз. членами, субъектами или элементами данного О.; различают двуместные (бинарные, двучленные) О. ("а меньше b", "Ока короче Волги", "рельсы параллельны между собой" и т. п.), трёхместные (тернарные, трёхчленные; "точка Л лежит между В и С", "5 есть сумма 2 и 3"), четырёхместные ("числа х₁, y₁, x₂ и y₂ пропорциональны"), вообще п-местные (n-арные, n-членные) О. Эти содержательные представления реализуются в точных терминах теории множеств (алгебры) и матем. логики; первое из этих уточнений отражает экстенсиональный (объёмный) аспект понятия О., второе - интенсиональный (смысловой, содержательный). В теоретико-множественных терминах бинарным (n-арным) О. наз. множество упорядоченных пар (соответственно упорядоченных к-ок) членов нек-рого множества (поля данного О.). Если упорядоченная пара (x, у) принадлежит нек-рому О. R, то говорят также, что х находится в О. R к у [символически: R(xy) или xRy]; множество первых элементов упорядоченных пар, входящих в О. R, составляет его область определения (отправлени я), множество вторых элементов - область значений (прибытия); аналогичные понятия вводятся и для многоместных О. Отношение, состоящее из пар (у, х), полученных перестановкой членов данного О. R пар (х, у), наз. обратным к К и обозначается через R^-1; область значений одного из этих взаимно-обратных О. [термин оправдан тем, что всегда (R^-1)^-1=R] служит областью определения другого, а область определения - областью значений. Поскольку О. являются частными случаями множеств, для них обычным образом вводятся теоретико-множественные операции, в частности объединение, пересечение и дополнение О. (см. Множеств теория). Рассмотрим нек-рые свойства и основные типы важнейшего (для приложений и теоретич. построений) класса О.- бинарных О.

Свойства бинарных О. Пусть К = (х, у). Если для любого х верно xRx, то R наз. рефлексивным (примеры: О. равенства чисел - каждое число равно самому себе, подобие треугольников и т. п.). Если для любого х xRy не имеет места (символически: xRy), то R наз. антирефлексивным, или иррефлексивным (напр., О. перпендикулярности прямых - никакая прямая не перпендикулярна самой себе). Если для любых не равных между собой х и у одно из них находится в отношении R к другому (т. е. выполнено одно из трёх соотношений xRy , х = у или yRx), то R наз. связанным (напр., О. <). Если для любых x и y из xRy следует yRx, то R наз. симметричным (напр., О. равенства = или О. неравенства ^). Если для любых х и y из xRy и xR^-1y следует х = у (т. е. R и R^-1 выполняются одновременно лишь для равных между собой членов), то R наз. антисимметричным (напр., О. =< и >= для любых объектов). Если для любых х и у из xRy следует хRy, то R наз. асимметричным (таковы, напр., О. < и > , поскольку никакой объект не больше и не меньше себя). Если для любых х, у и z из xRy и yRz следует xRz, то R наз. транзитивным (таковы, напр., О. = или <, но не не равно ). Можно было бы определить и др. свойства бинарных О., но нетрудно показать, что уже через эти свойства посредством логических операций определяются все прочие.

Типы отношений. Значит, часть приводимых ниже типов О. уже встречалась выше в примерах. Сочетание свойств рефлексивности, симметричности и транзитивности приводит нас к важнейшему типу О.- это О. типа равенства (тождества, эквивалентности). Нетрудно показать, что любое такое О. индуцирует (определяет) разбиение множества, на к-ром оно определено, на непересекающиеся классы - т. н. классы эквивалентности: элементы, связанные данным О., попадают в общий класс, не связанные- в различные. Т. о., элементы, попавшие в общий класс, в известном смысле неразличимы, что и определяет важность этого типа О.

Лит.: Тарский А., Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948; Ч ё р ч А., Введение в математическую логику, пер. с англ., т. 1, М., 1960; У е м о в А. И., Вещи, свойства и отношения, М., 1963; Ш р е й д е р Ю. А., Равенство, сходство, порядок, М., 1971.

Ю. А. Гастев.

ОТНОШЕНИЕ двух чисел, частное от деления первого числа на второе. О. двух однородных величин наз. число, получающееся в результате измерения первой величины, когда вторая выбрана за единицу меры. Если две величины измерены при помощи одной и той же единицы меры, то их О. равно О. измеряющих их чисел.

О. длин двух отрезков может выражаться рациональным или иррациональным числом. В первом случае отрезки наз. соизмеримыми, а во втором - несоизмеримыми. Математики древнего мира не знали иррациональных чисел; для них понятие О. двух отрезков не сводилось к понятию числа; не зависимая от понятия числа геометрич. теория О. величин играла у них самостоят, роль и заменяла в известном смысле теорию действительных чисел (см. Число). Действительно, по Евклиду, четыре отрезка а, b, а', b' составляют пропорцию а : b = а' : b', если для любых натуральных чисел т и п выполняется одно из соотношений ma = nb, та > nb, та < пb всякий раз одновременно с соответствующим соотношением та' = пb', та' > пb' или та' < пb'. В случае несоизмеримости а и b это означает, что разбиение всех рациональных чисел (х=т/п) на два класса по признаку а > xb или а < хb совпадает с разбиением по признаку а' > xb' или а' < xb'- в этом состоит идея современной теории дедекиндовых сечений. О двойном (иначе - сложном, ангармоническом) О. см. Двойное отношение.

ОТНОШЕНИЕ СМЕСИ, количество водяного пара в г на 1 кг сухого воздуха. См. также Влажность воздуха.

ОТНОШЕНИЕ ТИПА РАВЕНСТВА, отношение эквивалентности, понятие логики и математики, выражающее факт наличия одних и тех же признаков (свойств) у различных объектов. Относительно таких общих признаков эти различные объекты неразличимы (тождественны, равны, эквивалентны), так что любой из них с равным основанием может служить "представителем" того класса эквивалентности, к-рому принадлежат все объекты, находящиеся между собой в О. т. р. Отношения типа равенства обладают свойствами рефлексивности, симметричности и транзитивности, а также, в определённых условиях и в определённых границах, т. н. свойством замены, состоящим в том, что объекты, находящиеся между собой в таком отношении, могут выполнять одни и те же функции, а их имена (обозначающие их слова) можно подставлять одно вместо другого в различные предложения. См. Абстракции принцип, Отношение, Понятие, Равенство, Тождество, Эквивалентность.

ОТО... (от греч. us, род. падеж otos - ухо), часть сложных слов, указывающая на их отношение к уху, болезням уха (напр., оториноларинголог, отосклероз).

ОТОБРАЖЕНИЕ (матем.) множества Л в множество В, соответствие, в силу к-рого каждому элементу х множества А соответствует определённый элемент у - f(x) множества В, наз. образом элемента х (элемент х наз. прообразом элемента у). Иногда под О. понимают установление такого соответствия. Примерами О. могут служить параллельное проектирование одной плоскости на другую, стереографическая проекция сферы на плоскость. Геогра-фич. карта может рассматриваться как результат О. точек земной поверхности (или части её) на точки куска плоскости. Логически понятие "О." совпадает с понятиями функция, оператор, преобразование. Как средство исследования О. даёт возможность заменять изучение соотношений между элементами множества А изучением соотношений между элементами множества В, что в ряде случаев может оказаться проще. Так, параллельным проектированием можно отобразить параллелограмм в квадрат, центральным проектированием - любую линию второго порядка в окружность и т. д. Многие свойства остаются неизменными (инвариантными) при О. Так, при параллельном проектировании сохраняется параллельность прямых, отношение отрезков длин параллельных прямых и т. д.

Если каждый элемент множества В является образом элемента множества А, то О. наз. отображением А на множество В. Если каждый элемент из В имеет один и только один прообраз, то О. наз. взаимно однозначным. О. наз. непрерывным, если близкие элементы множества А переходят в близкие элементы множества В. Точнее это означает, что если элементы XL, Х₂, . . ., х_п, . . сходятся к х, то элементы f(X₁), f(x₂), . . ., f(X_n), . . . сходятся к f(x).

Каждой части Т множества А соответствует часть f(T) множества В, состоящая из образов точек этой части; она наз. образом Т. Если все точки части Q множества В являются образами точек из А, то совокупность всех точек х из А таких, что f(x) лежит в Q, наз. полным прообразом Q и обозначается f^-1 (Q). При взаимно однозначном О. полный прообраз каждого элемента множества В состоит из одного элемента множества А.

Взаимно однозначное О. имеет обратное О., сопоставляющее элементу у из В его прообраз f^-1(y). Взаимно однозначное О. наз. топологическим, или гомеоморфным, если как оно, так и обратное ему О. непрерывны. При гомеоморфных О. сохраняются лишь наиболее общие свойства фигур, как, напр., связность, ориентируемость, размерность и др. Так, квадрат и круг гомеоморфны, но квадрат и куб не гомеоморфны. Свойства фигур, не изменяющиеся при гомеоморфных О., изучаются в топологии. Если в множествах А и В имеются нек-рые соотношения и если эти соотношения сохраняются при О., то О. наз. изоморфным относительно этих соотношений (см. Изоморфизм). В математич. анализе большую роль играют О. одного множества функций на другое. Напр., дифференцирование может рассматриваться как О., при к-ром функции f(x) соответствует функция f'(x). Среди таких О. наиболее простыми являются О., при к-рых сумма функций переходит в сумму, а при умножении функции на число образ её умножается на то же число. Такие О. наз. линейными, их изучают в функциональном анализе. См. также Линейное преобразование, Операторов теория. В ряде случаев в множествах А и В можно ввести координаты, т. е. задавать каждую точку этих множеств системой чисел (x₁, . . ., x_п) и (y₁, . . ., y_n). Тогда О. задаётся системой функций у_k=f_k(x₁, . . . , х_n), 1=<k=<m. В большинстве встречающихся на практике случаев функции f₁, f₂, . . ., f_mдифференцируемые: тогда О. наз. дифференцируемым. Если О. дифференцируемо, т=п и якобиан О. отличен от нуля, то О. взаимно однозначно.

Дифференцируемые О. поверхностей на поверхности изучаются в дифференциальной геометрии. Имеются свойства, общие всем дифференциально-геометрическим О. Напр., на поверхности S всегда можно указать такую ортогональную сеть (см. Сети линий), к-рой на поверхности S' соответствует также ортогональная сеть. Эта теорема имеет важное значение в картографии.

Наиболее важны след, классы О. поверхностей. Изометрическое отображение, к-рое характеризуется тем, что всякая дуга, лежащая на S, имеет ту же длину, что и образ этой дуги на S'. При таких О. сохраняются площади фигур, а также углы между двумя направлениями, выходящими из одной точки (подробнее см. Дифференциалъная геометрия, Изгибание). Конформное отображение, при к-ром сохраняются углы между всякими двумя направлениями, выходящими из одной точки (см. Конформное отображение). Примером может служить стереографич. проекция. Сферическое отображение поверхности S на сферу состоит в том, что каждой точке М поверхности S ставится в соответствие такая точка М' сферы 2, чтобы нормали к S, проведённые соответственно в точках М и М', были параллельны. Более общим является О. двух произвольных поверхностей по параллельности нормалей. Геодезическое отображение поверхностей, при к-ром любой геодезической линии на поверхности S соответствует на S' линия также геодезическая. Геодезич. О. поверхности постоянной отрицательной кривизны на часть плоскости имеет большое значение для истолкования геометрии Лобачевского. Эквиареальное отображение поверхности на поверхность, при к-ром площади соответствующих друг другу фигур равны.

С точки зрения картографии, каждое из трёх О. кривой поверхности на плоскость - конформное, геодезическое и эквиареальное - имеет свои преимущества; удовлетворить сразу не только всем этим требованиям, но даже и к.-л. двум из них оказывается невозможным.

Лит.: Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; Бляшке В., Дифференциальная геометрия и геометрические основы теории относительности Эйнштейна, пер. с нем., ч. 1, М.- Л., 1935; Гильберт Д. и Конфоссен С., Наглядная геометрия, пер. с нем., 2 изд., М.- Л., 1951.

ОТОБРАЖЕНИЯ ИНФОРМАЦИИ УСТРОЙСТВО, дисплей, устройство вывода данных из ЦВМ, обеспечивающее представление информации (обычно результатов обработки вводимых данных) в форме, удобной для зрительного (визуального) восприятия человеком и принятия им решений (напр., в виде цифро-буквенного текста, плана, таблицы, графика, схемы, чертежа и т. д.). О. и. у. как оконечные устройства ЦВМ широко используются в системах передачи информации, в системах диагностики и машинного обучения, в науч. исследованиях и при конструировании мн. техннч. устройств, в автоматизированных системах управления и проектирования, сигнализации и контроля и т. п. системах "человек и машина". О. и. у. подразделяют на индивидуальные и коллективные.

В качестве индивидуальных применяют О. и. у., осн. элементом к-рых служит электроннолучевая трубка (ЭЛТ) (рис. 1).

Рис. 1. Схема устройства отображения на ЭЛТ: ЦП - центральный процессор вычислительной системы; ЗУ - вспомогательное запоминающее устройство; БУ - блок местного управления; ЭП - электронный прожектор; ОС -отклоняющая система.

Координаты часто воспроизводимых знаков (букв, цифр, обозначений, спец. символов и т. п.) хранятся во вспомогат. запоминающем устройстве; центр, процессор вычислит, системы выдаёт лишь адреса этих знаков, после чего знаки на экране воспроизводятся автоматически. Такое О. и. у. способно воспроизвести на экране текст книжной страницы за 0,02-0,05 сек. Чтобы изображение на экране не мерцало, его повторно воспроизводят (регенерируют) с частотой 20-50 раз в сек. Обмен информацией с центр, процессором происходит лишь тогда, когда требуется внести изменения в изображение или передать в процессор команды оператора. В таких О. и. у. оператор может, напр., при помощи светового карандаша стирать отд. знаки, строчки и участки текста, заменять элементы схемы, рисунка, может поворачивать (в плоскости экрана) изображение, изменять его масштаб.

Кроме обычных ЭЛТ, в О. и. у. используют знакопечагпающие электроннолучевые трубки, многолучевые трубки для синхронного отображения неск. быстроменяющихся величин, трубки с оптич. окном для совмещения сложного фона (напр., карты местности или чертежа), поступающего с диапроектора, с изображением, воспроизводимым электронным лучом, а также цвешые телевизионные трубки. Гл. недостаток О. и. у. на ЭЛТ - трудность их согласования с ЦВМ, требующего дополнит. оборудования.

Более удобны с точки зрения совместимости с ЦВМ т. н. плазменные панели. Такая панель состоит из трёх стеклянных пластин; средняя имеет отверстия (ячейки), заполненные смесью неона и азота, а на наружные нанесены шины выборки (параллельные полупрозрачные полоски золота) т. о., чтобы каждое отверстие оказалось расположенным между двумя взаимно перпендикулярными полосками. При подаче на шины управляющего напряжения (сигнала) газ в ячейках начинает светиться и это свечение сохраняется после снятия управляющего сигнала (разряд поддерживается постоянным напряжением). Для гашения элемента на выбранную пару шин подаётся сигнал противоположной полярности. Аналогично устроены матричные люминесцентные экраны (средняя пластина покрыта люминофором - точками размером ок. 0,25 мм²). Разрабатывают экраны на светодиодах и жидких кристаллах. Первые основаны на явлении свечения некоторых полупроводников (напр., фосфида и арсенида галия) под действием приложенного к ним напряжения, вторые - на изменении положения молекул в нек-рых искусств, органич. веществах под влиянием электрич. поля. Это ведёт к изменению прозрачности или цвета соответствующих участков экрана.

В О. и. у. коллективного пользования первичное изображение, полученное на промежуточном носителе - люминофоре электроннолучевой трубки, увеличивают и проецируют на экран. Достаточная разрешающая способность и яркость обеспечиваются в таких О. и. у. лишь при сравнительно небольших размерах экрана (пл. порядка 2,5 м²); при больших размерах экрана эти параметры ухудшаются. Заменив люминофор тонкой масляной плёнкой, находящейся под постоянным потенциалом, получают плёночный модулятор света (рис. 2). Под действием электронного луча на плёнке возникает заряд, деформирующий её поверхность,- первичное изображение оказывается рельефным. Свет мощной лампы отбрасывается зеркальными полосками отражателя на первичное изображение; отражаясь от неровностей поверхности масляной плёнки, свет несёт изображение рельефа, к-рое фокусируется объективом и проецируется на экран. Плёночный модулятор света обеспечивает высококачеств. многоцветные изображения на больших экранах (пл. до 200 м²). Перспективно применение термо-пластич. модуляторов света (аналогичных по устройству плёночным, но с первичным носителем в виде предварительно разогретого и приведённого в пластич. состояние материала) и лазерных О. и. у. (аналогичных О. и. у. на ЭЛТ, но с передачей цветного изображения тремя разноцветными лазерными лучами на большой экран) (см. Проекционное телевидение).

Рассмотренные О. и. у. дают двухмерные изображения. Однако в ряде случаев (напр., в системах посадки самолётов, при проектировании корпусов автомобилей и т. п.) предпочтительнее трёхмерная индикация. О. и. у. на электроннолучевой трубке, дополненное рядом устройств, может воспроизводить трёхмерные изображения в аксонометрической (или иной) проекции; невидимые наблюдателю линии стираются, изображение можно поворачивать, чтобы оператор мог осмотреть его с разных сторон. Не менее перспективно использование трёхмерных О. и. у., основанных на голографии. Новые возможности открывает объёмная индикация, при к-рой изображения формируются не на плоскости, а в объёме, заполненном газом (рис. 3). От внешних источников света в газовую среду направляют два луча; каждый из них изменяет энергетич. состояние молекул газа, в точке пересечения лучей возникает флюоресценция (свечение) газа. При быстром перемещении лучей появляется светящийся след, к-рый при многократном повторении воспринимается наблюдателем как законченное изображение.

Рис. 2. Схема устройства отображения с масляным модулятором света: ИС - источник света; К - конденсор; ОТ - отражатель; ОБ - объектив; З - зеркало; Э - экран; МП - масляная плёнка; ЭП - электронный прожектор; БУ - блок местного управления; ЦП - центральный процессор вычислительной системы.

Рис. 3. Схема устройства отображения с объёмной индикацией: ИС - источник света; К - конденсор; ОС - отклоняющая система; ЦП - центральный процессор вычислительной системы; ГО - газовый объём; ФТ - флюоресцирующая точка; БУ - блок местного управления.

Лит.: Пул Г., Основные методы и системы индикации, пер. с англ., Л., 1969; В е н д а В. Ф., Средства отображения информации, М., 1969; Темников Ф. Е., Афонин В. А., Дмитриев В. И., Теоретические основы информационной техники, М., 1971; Ч а ч к о А. Г.. Человек за пультом, М., 1974: Da vis S., Computer data displays, Englewood Cliffs (N. Y.), 1969.

А. Г. Чачко.

ОТОЛИТЫ (от ото... и греч. lithos - камень), статолиты, твёрдые образования, расположенные на поверхности механорецепторных клеток органа равновесия у ряда беспозвоночных и всех позвоночных животных. Происхождение, размер и строение О. варьируют у разных животных: они могут быть продуктом секреторной деятельности клеток или заносятся извне (напр., у рака О. служат песчинки); О. млекопитающих - обычно удлинённые (дл. до 10 мкм, шир. 1-3 мкм) кристаллы кальцита (СаСО₃). Смещение О. при изменении положения тела и влиянии ускорений вызывает механич. раздражение подлежащих волосковых рецепторных клеток и появление соответствующих сигналов, направляющихся в мозг. Действие О. наглядно показано в опытах с речным раком. При линьке животному заменяли песчинки железными опилками и помещали над ним магнит, к-рый притягивал опилки кверху. Рак принимал "верх" за "низ", переворачивался и плавал брюшком вверх. См. Вестибулярный аппарат, Равновесия органы.

О. Б. Ильинский.