ОРТОГОНАЛЬНАЯ МАТРИЦА порядка п, матрица

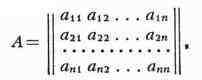
произведение к-рой на транспонированную матрицу А' даёт единичную матрицу, то есть АА' = Е (а следовательно, и А'А = Е). Элементы О. м. удовлетворяют соотношениям:

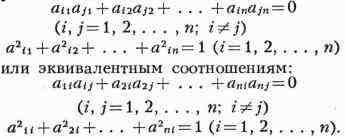
Определитель |А| О. м. равен +1 или - 1. При перемножении двух О. м. снова получается О. м. Все О. м. порядка п относительно операции умножения образуют группу, называемую ортогональной. При переходе от одной прямоугольной системы координат к другой коэффициенты а_ij в формулах преобразования координат

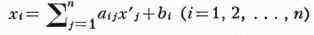
образуют О. м. См. также Унитарная матрица.

ОРТОГОНАЛЬНАЯ ПРОЕКЦИЯ, частный случай параллельной проекции, когда ось или плоскость проекций перпендикулярна (ортогональна) направлению проектирования.

ОРТОГОНАЛЬНАЯ СИСТЕМА ФУНКЦИЙ, система функций {ф_п(x)},п=1, 2, . . ., ортогональных с весом р (х) на отрезке [а, b], т. е. таких, что

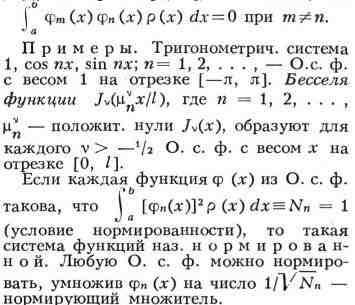
Систематич. изучение О. с. ф. было начато в связи с методом Фурье решения краевых задач ур-ний математич. физики. Этот метод приводит, напр., к разысканию решений Штурма - Лиувилля задачи для ур-ния [р(х)у']'+q(x)у=Лу, удовлетворяющих граничным условиям у(а)+hy'(a)=0, у(b)+Ну'(b)=0, где h и Н - постоянные. Эти решения - т. н. собственные функции задачи - образуют О. с. ф. с весом р (х) на отрезке [а, b].

Чрезвычайно важный класс О. с. ф.- ортогональные многочлены - был открыт П. Л. Чебышевым в его исследованиях по интерполированию способом наименьших квадратов и проблеме моментов. В 20 в. исследования по О. с. ф. проводятся в основном на базе теории интеграла и меры Лебега. Это способствовало выделению этих исследований в самостоят, раздел математики. Одна из осн. задач теории О. с. ф.- задача о разложении функции f(x) в ряд вида сумма С_пф_п(х), где {(ф_п(х)} - О. с. ф. Если положить формально f (х) = сумма С_пфп(х), где (ф_п(х)} - нормированная О. с. ф., и допустить возможность почленного интегрирования, то, умножая этот ряд на ф_п(x) p(x) и интегрируя от а до b, получим:

имеет наименьшее значение по сравнению с ошибками, даваемыми при том же п другими линейными выражениями вида

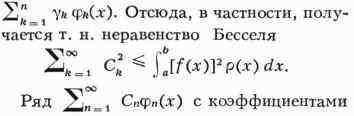
С_п, вычисленными по формуле (*), наз. рядом Фурье функции f (x) по нормированной О. с. ф. (ф_п(х)}. Для приложений первостепенную важность имеет вопрос, определяется ли однозначно функция f(x) своими коэффициентами Фурье. О. с. ф., для к-рых это имеет место, наз. полными, или замкнутыми. Условия замкнутости О. с. ф. могут быть даны в неск. эквивалентных формах. 1) Любая непрерывная функция f(x) может быть с любой степенью точности приближена в среднем линейными комбинациями функций ф_k(х), то есть lim_n->ооб_n =0 [в этом случае говорят, что ряд сумма^оо_n=1 С_пф_п(х) сходится в среднем к функции f(x)}. 2) Для всякой функции f(x), квадрат к-рой интегрируем относительно веса р (х), выполняется условие замкнутости Ляпунова - Стеклова:

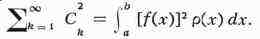
3) Не существует отличной от нуля функции с интегрируемым на отрезке [а, b] квадратом, ортогональной ко всем функциям ф_п(х), п = 1, 2, ....

Если рассматривать функции с интегрируемым квадратом как элементы гильбертова пространства, то нормированные О. с. ф, будут системами координатных ортов этого пространства, а разложение в ряд по нормированным О. с. ф.- разложением вектора по ортам. При этом подходе многие понятия теории нормированных О. с. ф. приобретают наглядный геометрич. смысл. Напр., формула (*) означает, что проекция вектора на орт равна скалярному произведению вектора и орта; равенство Ляпунова - Стеклова может быть истолковано как теорема Пифагора для бесконечномерного пространства: квадрат длины вектора равен сумме квадратов его проекций на оси координат; замкнутость О. с. ф. означает, что наименьшее замкнутое подпространство, содержащее все векторы этой системы, совпадает со всем пространством и т. д.

Лит.: Толстов Г. П., Ряды Фурье, 2 изд., М., 1960; Натансон И. П., Конструктивная теория функций, М.- Л., 1949; его же, Теория функций вещественной переменной, 2 изд., М., 1957; Джексон Д., Ряды Фурье и ортогональные полиномы, пер. с англ., М., 1948; К а ч м а ж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958.

ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ, линейное преобразование евклидова векторного пространства, сохраняющее неизменным длины или (что эквивалентно этому) скалярное произведение векторов. В ортогональном и нормированном базисе О. п. соответствует ортогональная матрица. О. п. образуют группу - т. н. группу вращений данного евклидова пространства вокруг начала координат. В трёхмерном пространстве О. п. сводится к повороту на нек-рый угол вокруг нек-рой оси, проходящей через начало координат О, если определитель соответствующей ортогональной матрицы равен +1. Если же этот определитель равен -1, то поворот дополняется зеркальным отражением относительно плоскости, проходящей через О и перпендикулярной оси поворота. В двумерном пространстве, т. е. в плоскости, О. п. определяет поворот на нек-рый угол вокруг начала координат О или зеркальное отражение относительно нек-рой прямой, проходящей через О. Используется О. п. при приведении к гл. осям квадратичной формы. См. также Матрица, Векторное пространство.

ОРТОГОНАЛЬНОСТЬ (греч. orthogonios - пря1тоугольный, от orthos - прямой и gonia - угол), обобщение (часто синоним) понятия перпендикулярности. Если два вектора в трёхмерном пространстве перпендикулярны, то их скалярное произведение равно нулю. Это позволяет обобщить понятие перпендикулярности, распространив его на векторы в любом линейном пространстве, в к-ром определено скалярное произведение, обладающее обычными свойствами (см. Гильбертово пространство), назвав два вектора ортогональными, если их скалярное произведение равно нулю. В частности, вводя скалярное произведение в пространстве комплекснозначных функций, заданных на отрезке [а, b] формулой

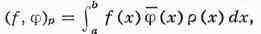
где р(х) >= 0, называют две функции f(x) и ф(x), Для которых (f, ф)_р = 0, то есть

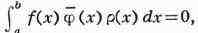
ортогональными с весом р(х). Два линейных подпространства наз. ортогональными, если каждый вектор одного из них ортогонален каждому вектору другого. Это понятие обобщает понятие перпендикулярности двух прямых или прямой и плоскости в трёхмерном пространстве (но не понятие перпендикулярности двух плоскостей). Термином ортогональные кривые обозначают кривые линии, пересекающиеся под прямым углом (измеряется угол между касательными в точке пересечения). См., напр., ортогональные траектории в ст. Изогональные траектории.

ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ, специальные системы многочленов (рп(х)}; п = 0, 1, 2, . . ., ортогональных с весом р(д-) на отрезке [", о] (см. Ортогональная система функций). Нормированная система О. м. обозначается через р_п(х), а система О. м., старшие коэффициенты к-рых равны 1,- через Р_п(х). В краевых задачах математич. физики часто встречаются системы О. м., для к-рых вес р(х) удовлетворяет дифференциальному ур-нию (Пирсона)

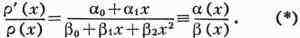
Многочлен Р_n(Х) такой системы удовлетворяет дифференциальному ур-нию

Наиболее важные системы О. м. (классические) относятся к этому типу; они получаются (с точностью до постоянного множителя) при указанных ниже а, b и р(х).

1) Якоби многочлены {Р_n^(Л,n)(х)} - при а = -1, b = 1 и р(л:) = (1-x)^Л (1 + х)ⁿ, Л > - 1, n > - 1. Специальные частные случаи многочленов Якоби соответствуют следующим значениям X и ц: Л = n - ультрасферические многочлены Р^(Л)_n(х) (их иногда называют многочленами Гегенбауэра); Л = n = -1/2, т. е. р(х)= 1/корень из (1-х²) - Чебышева многочлены 1-го рода_Т_n(х); Л = n = 1/2, т. е. р(х)= корень из (1-.x²) - Чебышева многочлены 2-го рода U_n(x); Л = n = 0, т. е. р(х) =1 - Лежандра многочлены Р_п(х). 2) Лагерра многочлены L_n(x) - при а = 0, b = + бесконечность и р(х) = е^-x (их наз. также многочленами Чебышева - Лагерра) и обобщённые многочлены Лагерра L^a_n(x) - при р(х) = х^aе^-x(а > - 1). 3) Эрмита многочлены Н_n(х) - при а = -бесконечность , b=+бесконечность и р(х)=е^-х (их наз. также многочленами Чебышева - Эрмита).

О. м. обладают многими общими свойствами. Нули многочленов р_п(х) являются действительными и простыми и расположены внутри [а, b]. Между двумя последоват. нулями многочлена р_n(х) лежит один нуль многочлена p_n+1(x). Многочлен р_n(х) может быть представлен в виде т. н. формулы Родрига

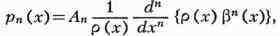
где A_n - постоянное, а b(х) см. формулу (*). Каждая система О. м. обладает свойствами замкнутости. Три последоват. О. м. p_n(x),p_n+1(x),p_n+2(x) связаны рекуррентным соотношением: р_n+2(x) = (x- a_n+2)p_n+1(x) - Л_n+1p_n(x), где а_n+2 и Л_n+1 след, образом выражаются через коэффициенты этих многочленов: если

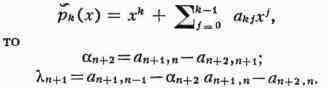
Общая теория О. м. построена П. Л. Чебышевым. Осн. аппаратом изучения О. м. явилось для него разложение интеграла

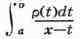
в непрерывную дробь с элементами вида х - осп и числителями Л_n-1. Знаменатели ф_п(х)/р_n(х) подходящих дробей этой непрерывной дроби образуют систему О. м. на отрезке [а, b] относительно веса р(х).

Приведённые выше классич. системы О. м. выражаются через гипергеометрическую функцию.

Лит.: Сеге Г., Ортогональные многочлены, пер. с англ., М., 1962; см. также лит. при ст. Ортогональная система функций.

В. И. Битюцков.

ОРТОГОНАЛЬНЫЕ ТРАЕКТОРИИ, см. в ст. Изогональные траектории.

ОРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ (от греч. orthos - прямой и grapho - пишу), одна из картографических проекций. О. п. относится к перспективным проекциям. Из-за значит, искажений в картографии не применяется.

ОРТОДОНТИЯ (от греч. orthos - прямой, правильный и odds, род. падеж odontos - зуб), раздел стоматологии, занимающийся изучением, лечением и предупреждением аномалий развития зубов и челюстно-лицевого скелета, к-рые зависят как от наследств, факторов, так и от условий роста и развития детского организма в зародышевом периоде и после рождения. Частые причины возникновения аномалий зубо-челюстной системы - нарушения обмена веществ, детские болезни, отрицательно влияющие на процессы формирования скелета, и др. Способств. факторами могут быть вредные привычки (сосание пальцев, злоупотребление сосками, затруднённое носовое дыхание и др.). Деформации зубо-челюстной системы ведут к нарушению функции органов пищеварения, дыхания и речи. Цель ортодонтич. лечения - создание лучшей в косметическом и функциональном отношении формы зубо-челюстной системы и нормализация развития детского организма. Лечение комплексное: применение спец. аппаратуры в сочетании с фармакологическим и физиотерапевтическим, иногда хирургич. и последующим логопедич. лечением. Плановая санация полости рта у детей дошкольного и школьного возраста.

Лит.: Калвелис Д. А., Ортодонтия, Л., 1964; Курляндский В. Ю., Ортопедическая стоматология. Атлас, т. 2. Ортодонтия, травматология, челюстное и лицевое протезирование, М., 1970.

А. А. Кузнецова.

ОРТОДРОМИЯ (от греч. orthos - прямой и dromos - бег, путь), кратчайшая линия между двумя точками на поверхности вращения. В кораблевождении и самолётовождении, где Земля принимается за шар, О. представляет собой дугу большого круга. В противоположность локсодромии, О. пересекает меридианы под разными углами.

ОРТОКЛАЗ (от греч. orthos - прямой и klasis - ломка, раскалывание), породообразующий минерал из группы полевых шпатов. Химич. состав K[AlSi₃O₈]. В качестве примеси содержит Na (до 8% Na₂O), реже Ва и в небольших кол-вах Fe, Ca, Rb, Cs и пр. Кристаллизуется в моноклинной системе. Кристаллы призматической формы. Характерны разнообразные двойники (см. Двойникование). Спайность совершенна, под углом 90° (отсюда и назв.), чем отличается от микроклина. Цвет светло-розовый, буровато-жёлтый, иногда красный; блеск стеклянный. Тв. по минералогической шкале 6-6,5; плотность 2550-2580 кг/м³. О.- один из важнейших породообразующих минералов магматич. горных пород; скопления крупных кристаллов О. характерны для пегматитовых жил. Часто образуется в процессе регионального и контактного метаморфизма. Используется в качестве сырья в стекольной и керамич. пром-сти.

ОРТОКУЗЕННЫЙ БРАК, форма брака; см. Кузенный брак.

ОРТОЛАМАРКИЗМ, одно из направлений неоламаркизма.

ОРТОМЕТРИЧЕСКАЯ ВЫСОТА (от греч. orthos - прямой, вертикальный и metreo - измеряю), см. в ст. Нивелирная высота.

ОРТОПЕДИЧЕСКИЕ АППАРАТЫ, ортопедическая техника, различные механич. приспособления и аппараты для лечения и предупреждения деформаций и повреждений опорно-двигательного аппарата человека. К О. а. относят повязки, шины, протезы, спец. аппараты. Различают неск. видов О. а. Фиксирующие О. а. предназначены для полного или частичного ограничения движений в суставе; к ним относят глухие гильзы (туторы), шарнирные аппараты (для сохранения определённой амплитуды движения в суставе) и др. Разгружающие О. а. служат для разгрузки больного участка переносом опоры на вышележащие здоровые участки конечности (аппараты Томаса и Воскобойниковой и др.). Коррегирующие О. а. используют для постепенного исправления деформаций; такими приспособлениями являются корсеты, шинно-гильзовые аппараты, ортопедич. обувь, супинаторы и пронаторы, к-рые коррегируют неправильное положение стопы. Компрессионно - дистракционные О. а. служат для исправления приобретённых или врождённых деформаций конечностей (напр., искривление, укорочение, ложные суставы); к ним относят аппараты Гудушаури, Илизарова, Сиваша, Волкова - Оганесяна и др.

Для рассечения костей при устранении деформаций и соединения костных фрагментов применяют долота, остеотомы, электрич. и пневматич.пилы,метод ультразвуковой резки и сварки костной ткани. При остеосинтезе используют стержни, гвозди, пластины, винты, при замещении дефектов суставов - полимерные изделия, металлич. эндопротезы.

Лит. см. при ст. Ортопедия.

М. В. Волков.

ОРТОПЕДИЯ [франц. orthopedic, от греч. orthos - прямой, правильный и paideia - воспитание (от pais, род. падеж paidos - дитя)], медицинская дисциплина, изучающая распознавание, предупреждение и лечение деформаций и повреждений опорно-двигательного аппарата человека. В СССР и нек-рых др. странах совм. с травматологией составляет единую мед. специальность, хотя каждая из них имеет свои историч. и специфич. особенности. Начало науч. О. было положено французским врачом Н. Андри (1658-1742), к-рый под этим названием издал двухтомный труд, посвящённый предупреждению и лечению деформаций тела у детей. Ещё в сочинениях Гиппократа имеются классические описания вывихов и переломов, косолапости, искривления позвоночника, а также нек-рых методов их лечения. Первая попытка выделить из хирургии учение об искривлениях тела принадлежала А. Паре, но только в кон. 18 в. появились спец. ортопедич. лечебные учреждения. Впервые в Европе (1814) стал применять гипс для фиксации сломанной конечности голландец Гендрихс и независимо от него рус. врач К. Гибенталь (1815). При становлении О. широко использовались консервативные методы лечения - редрессация, вытяжение конечностей при переломах, гипсовые повязки, массаж, гимнастич. упражнения (см. Лечебная физкультура, Механотерапия). По мере развития антисептики, асептики, наркоза, а в дальнейшем и рентгенографии, в О. стали применять и оперативные методы (остеотомия, остеосинтез, арт-родез, артропластика, пересадка мышц, сухожилий и т. д.). Значит, роль в разработке этих методов сыграли англ, хирург П. Потт, итал. - А. Скарпа, франц.- Г. Дюпюитрен, австр.- А. Лоренц, нем.- А. Гоффа и др.

В 1806 была опубликована книга Е. О. Myхина, Первые начала костоправ-ной науки, к-рая послужила толчком к развитию в России хирургии органов движения. Первая отечеств, науч. работа по О. (по тенотомии ахилова сухожилия) принадлежала Н. И. Пирогову (1840). Н. Эллинский издал руководство по десмургии (1834), Н. И. Студенский - "Курс ортопедии" (1885). В 1839 рус. врач И. В. Рклицкий произвёл первую поднадкостнич-ную резекцию кости. Ещё в 1791 И. П. Кулибин сконструировал совершенные по тому времени шинно-шарнирные протезы для ампутированных в бедре и голени; более усовершенствованные протезы этого типа изобрёл в 30-х гг. 19 в. и описал в 1855 Р. Черносвитов. Большой вклад в развитие русской О. внесли труды И. А. Бредихина о регенерации кости из надкостницы (1862); С. Ф. Феоктистова, разработавшего метод надкостничной ампутации (1863); экспериментальные работы Н. П. Никольского, способствовавшие прогрессу костно-пластич. хирургии (1870); Н. И. Носилова, предложившего метод остеосинтеза с помощью "русского замка" (1875); В. И. Кузьмина, осуществившего впервые (1893) внутрикостное скрепление фрагментов повреждённой кости стальными никелированными штифтами, и др. Впервые в России (1910) К. Ф. Вегнер применил метод постоянного скелетного вытяжения.

Эмблема ортопедии.

В 1900 в Воен.-мед. академии в Петербурге Г. И. Турнером были созданы первые в России кафедра О. и ортопедич. клиника. В 1906 там же был организован первый ин-т О., к-рый возглавил Р. Р. Вреден. В 1907 в Харькове был создан Медико-механич. ин-т (с 1966 Харьковский ин-т протезирования, травматологии и ортопедии им. М. И. Ситенко). Работы школы Турнера послужили началом углублённого клинич. изучения ортопедич. заболеваний, школы Вредена - активного хирургич. направления в О.; в Харькове разрабатывались ортопедические аппараты. Эти три направления и определили осн. линии развития рус. и сов. О.

Основоположником системы ортопедо-травматологич. помощи в СССР был Н. Н. Приоров, создавший в Москве (1921) Лечебно-протезный ин-т, реорганизованный в 1940 в Центр, ин-т травматологии и ортопедии, к-рому в 1971 присвоено имя Н. Н. Приорова. Этот ин-т - методич. центр для 19 н.-и. ин-тов травматологии и ортопедии, открытых в крупных городах СССР.

Достижение сов. О.- разработка системы мероприятий по профилактике и раннему лечению ортопедич. заболеваний уже с периода новорождённости (напр., врождённый вывих, косолапость и др.). Широко применяются новые методы остеосинтеза с использованием спец. компрессионных и компрессионно-дистракционных аппаратов (О. Н. Гудушаури, Г. А. Илизаров, К. М. Сиваш, М. В. Волков, О. В. Оганесян и др.). Сов. ортопеды впервые в мире разработали и внедрили в практику пластич. операции с применением консервированных гомотканей при замещении дефектов костей, суставов, сухожилий и мышц (М. В. Волков, А. С. Имамалиев, М. И. Панова и др.), методы аллопластич. замещения суставов, металлич. эндопротезы тазо-бедренного сустава (К. М. Сиваш), методы ультразвуковой резки и сварки костей, за что В. А. Поляков, М. В. Волков, Г. Г. Чемянов и др. удостоены Гос. пр. СССР (1972).

В 1925 на 17-м Росс, съезде хирургов впервые была выделена ортопедич. секция. В 1926 было организовано первое отечественное науч. об-во хирургов-ортопедов в Ленинграде, в 1932 - об-во ортопедов, травматологов и работников протезного дела в Москве. В 1963 создано Всесоюзное об-во травматологов и ортопедов.

Крупнейшие зарубежные ортопедич. учреждения: клиника ун-та г. Падуя, возглавляемая проф. К. Казуччо, в Риме - клиника проф. Дж. Монтичелли; в Париже - больница "Кошен" во главе с проф. М. Постелем; в США - крупнейшая клиника фонда Мейо (Сан-Франциско), ортопедич. отделением к-рой руководит Ф. Иергенсен.

В 1929 организовано Междунар. об-во ортопедич. хирургии и травматологии (сов. учёные входят в него с 1963). Проблемы О. освещаются в журн. "Ортопедия, травматология и протезирование" (Хар., с 1927); за рубежом издаются "Revue d'orthopedie" (Р., с 1890), "Zeitschrift fur orthopadische Chirurgie" (Stuttg., с 1891), "Journal, of bone and jonitstrgery" (Boston, с 1919) и др.

Лит.: Вреден Р. Р., Практическое руководство по ортопедии, Л., 1936; 3 а ц е п и н Т. С., Ортопедия детского и подросткового возраста, М., 1956; Ч а к л и н В. Д., Ортопедия, кн. 1 - 2, М., 1957; Хрупко И. Л., Основы ортопедии, Л., 1967; Многотомное руководство по ортопедии и травматологии, т. 1 - 2, М., 1967 - 68; Трубников В. Ф., Ортопедия и травматология, М., 1971 (лит.).

М. В. Волков.

ОРТОПТЕР (от греч. orthos- прямой, вертикальный и pteron - крыло), орнитоптер, у к-рого крылья движутся только вверх и вниз. Подъёмная сила в большинстве конструкций О. появляется благодаря изменению положения шарнирных створок, расположенных на крыльях: при движении крыльев вверх створки открываются, при движении вниз - закрываются.

ОРТОСТИХА (от греч. orthos - прямой, вертикальный и stichos - ряд, линия), прямой (продольный) ряд листьев на стебле (иногда боковых корней на гл. корне). При спиральном листорасположении число О. соответствует числу листьев в листовом цикле (спиральная линия между двумя листьями на одной О.); при мутовчатом - О. на побеге обычно вдвое больше, чем листьев в мутовке; при накрест супротивном - их 4. Ср. Парастиха.

Ортостиха (а-б); пунктиром обозначен листовой цикл.

ОРТО-ТОКОЙ, посёлок гор. типа в Иссык-Кульской обл. Кирг. ССР, подчинён Рыбачинскому горсовету. Расположен на р. Чу, в 20 км к Ю.-З. от ж.-д. станции Рыбачье (конечный пункт линии Луговая - Рыбачье). В 2 км выше О.-Т. на р. Чу построено (1960) Ортотокойское водохранилище (пл. 24 км²), воды которого используются для орошения.

ОРТОТРОПИЗМ (от греч. orthos - прямой и tropos - поворот, направление), ориентация растущих органов растений в сторону раздражителя (сила тяжести, источник света и др.) - О. положительный или от него - О. отрицательный. О. противоположен плагиотропизму, т. е. ориентации растущих органов растения под тем или другим углом к направлению раздражителя. Ортотропные органы (главный стебель или корень) имеют, как правило, радиально-симметричное строение. Однако в ходе развития растения нередко наблюдается изменение направления роста его органов. Понижение темп-ры, изменение светового режима, воздействия ростовых веществ в определённых дозах могут вызвать у побегов нек-рых растений смену О. плагиотропизмом, в результате чего образуются ползучие или стелющиеся формы растений. См. также Тропизмы.

ОРТОФОТОПЛАН, фотографич. план местности на точной геодезич. опоре, полученный путём аэрофотосъёмки с последующим преобразованием аэроснимков (из центральной проекции в ортогональную) на основе эффективного метода их дифференциального ортофототрансформирования, разработанного в сер. 60-х гг. 20 в. Последний, в отличие от известного метода трансформирования аэроснимков по зонам (см. Фотограмметрия), рассчитан на автоматизированное устранение искажений аэроснимка (обусловленных рельефом местности и отклонениями оси аэрофотоаппарата от вертикали при съёмке) путём последоват. проектирования трансформируемого изображения возможно малыми участками с помощью спец. приборов - ортофотопроекторов. Аэроснимки, преобразованные данным методом (т. н. ортофотоснимки), позволяют составить О. на любые р-ны, что существенно расширяет применение аэро-фотосъёмочных материалов при топографических, геологических и др. проектно-изыскательских работах.

Л. М. Гольдман.

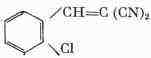
ОРТО - ХЛОРБЕНЗАЛЬМАЛОНОДИНИТРИЛ, бесцветные кристаллы, t_пл95°С, t_кип 310 ^оС (с разложением), хорошо растворяются в бензоле, ацетоне, ограниченно - в спирте, плохо - в воде. О.-х. получают взаимодействием о-хлорбензальдегида Сl₆H₄СНО с динитрилом малоновой к-ты CH₂(CN)₂ в присутствии катализаторов. О.-х. - отравляющее вещество, обладающее резким раздражающим действием на глаза и верхние дыхат. пути. Токсичность является в основном результатом блокирования сульфгидрильных групп нервных окончаний. Непереносимая концентрация в воздухе 5*10^-4 мг/л при экспозиции 1 мин, в больших концентрациях О.-х. раздражает кожу, особенно потную. В некоторых зарубежных странах О.-х. наз. отравляющим веществом "Си Эс" (CS).

ОРТОХРОМАТИЧЕСКИЕ МАТЕРИАЛЫ, чёрно-белые светочувствительные фотографические материалы, сенсибилизированные (обладающие добавочной светочувствительностью) к зелёным и жёлтым лучам. Фотографич. эмульсии, содержащие галогениды серебра, обладают т. н. собственной светочувствительностью в сине-фиолетовой области видимого спектра (длина волны 400-500 нм) и почти не чувствительны к зелёным, жёлтым и красным лучам. Для придания им светочувствительности в дополнительных спектральных областях в эмульсию вводят спец. добавки - красители-сенсибилизаторы (см. Сенсибилизация). Обусловленная ими светочувствительность наз. добавочной, или сенсибилизированной. О. м. обладают добавочной светочувствительностью к видимому свету с длиной волны 500-600 нм (в отличие от О. м., панхроматические материалы сенсибилизированы также к красным лучам с длиной волны 600-700 нм). При дневном свете добавочная светочувствительность О. м. составляет 25-30% от общей светочувствительности, при свете ламп накаливания - 50-60% . Выпускаются 2 вида О. м.: собственно О. м. с пониж. чувствительностью в сине-зелёной зоне и изоортохроматические материалы с равномерной чувствительностью ко всем лучам с длинами волн 400-580 нм. Поскольку О. м. не чувствительны к красным лучам, их обычно применяют для съёмки объектов, не содержащих красных деталей, для микрофотосъёмки, репродуцирования чёрно-белых изображений, рентгеновской съёмки с зелёного флуоресцирующего экрана и др. За проявлением изображения на О. м. можно следить при красном свете.

Л. Я. Крауш.