НЕОПРЕДЕЛЁННАЯ ФОРМА, понятие линейной алгебры. Квадратичную
форму
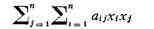
с действительными
коэффициентами aij наз. H. ф., если при действительных значениях
переменных она может принимать как положительные, так и отрицательные значения.
Линейным преобразованием переменных квадратичная H. ф. может быть приведена к
виду
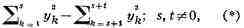
где s и t для заданной H. ф.
не зависят от способа её приведения к виду (*) (т. н. закон инерции
квадратичных форм). H. ф. х1 + у2 + z2 -C2t2
играет важную роль в относительности теории. Понятие H. ф.
встречается при изучении экстремумов функций многих переменных, в механике, в
аналитич. геометрии.
НЕОПРЕДЕЛЁННОЕ УРАВНЕНИЕ,
уравнение,
содержащее более одного неизвестного. Систему уравнений, в к-рой число
неизвестных больше числа уравнений, наз. неопределённой системой уравнений. H.
у. и неопределённые системы уравнений имеют, как правило, бесконечное число
решений. Термин "Н. у." употребляется в теории чисел, где
интересуются решениями H. у., удовлетворяющих тем или иным арифметич. условиям
(обычно ищут решения H. у. в целых или рациональных числах). Изучение таких
решений составляет предмет теории диофантовых уравнений.
НЕОПРЕДЕЛЁННОСТЕЙ
СООТНОШЕНИЕ, принцип
неопределённости, фундаментальное положение квантовой теории, утверждающее, что
любая физ. система не может находиться в состояниях, в к-рых координаты её
центра инерции и импульс одновременно принимают вполне определённые, точные
значения. Количеств, формулировка H. с.: если  x; - неопределённость значения
координаты х, а
x; - неопределённость значения
координаты х, а  px - неопределённость проекции
импульса на ось х, то произведение этих неопределённостей должно быть по
порядку величины не меньше постоянной Планка И. Аналогичные неравенства должны
выполняться для любой пары т. н. канонически сопряжённых переменных, напр. для
координаты у и проекции импульса ри на ось у, координаты
z и проекции импульса рz . Если под неопределённостями
координаты и импульса понимать среднеквадратичные отклонения этих физ. величин
от их ср. значений, то H. с. имеют вид:
px - неопределённость проекции
импульса на ось х, то произведение этих неопределённостей должно быть по
порядку величины не меньше постоянной Планка И. Аналогичные неравенства должны
выполняться для любой пары т. н. канонически сопряжённых переменных, напр. для
координаты у и проекции импульса ри на ось у, координаты
z и проекции импульса рz . Если под неопределённостями
координаты и импульса понимать среднеквадратичные отклонения этих физ. величин
от их ср. значений, то H. с. имеют вид:
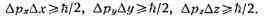
Ввиду малости h по сравнению
с макроскопич. величинами той же размерности действия H. с. существенны
в основном для явлений атомных (и меньших) масштабов и не проявляются при
взаимодействиях макроскопич. тел.
Из H. с. следует, что чем
точнее определена одна из входящих в неравенство величин, тем менее
определённым является значение другой. Никакой эксперимент не может привести к
одновременно точному измерению таких динамич. переменных; при этом
неопределённость в измерениях связана не с несовершенством экспериментальной
техники, а с объективными свойствами материи.
Принцип неопределённости,
открытый в 1927 В. Гейзенбергом, явился важным этапом в уяснении
закономерностей внутриатомных явлений и построении квантовой механики. Существенной
чертой микроскопич. объектов является их корпускулярно-волновая природа (см. Корпускулярно-волновой
дуализм). Состояние частицы полностью определяется волновой функцией. Частица
может быть обнаружена в любой точке пространства, в к-рой волновая функция
отлична от нуля. Поэтому результаты экспериментов по определению, напр,
координаты, имеют вероятностный характер. Это означает, что при проведении
серии одинаковых опытов над одинаковыми системами получаются каждый раз, вообще
говоря, разные значения. Однако нек-рые значения будут более вероятными, чем
другие, т. е. будут появляться чаще. Относительная частота появления тех или
иных значений координаты пропорциональна квадрату модуля волновой функции в
соответствующих точках пространства. Поэтому чаще всего будут получаться те
значения координаты, к-рые лежат вблизи максимума волновой функции. Если
максимум выражен чётко (волновая функция представляет собой узкий волновой
пакет), то частица "в основном" находится около этого максимума.
Тем не менее, нек-рый разброс в значениях координаты, нек-рая их
неопределённость (порядка полуширины максимума) неизбежны. Тот же вывод
относится и к измерению импульса.
T. о., понятия координаты и
импульса в классич. смысле не могут быть применены к микроскопич. объектам.
Пользуясь этими величинами при описании микроскопич. системы, необходимо внести
в их интерпретацию квантовые поправки. Такой поправкой и является H. с.
Несколько иной смысл имеет
H. с. для энергии E и времени t,  Е
Е t>h. Если система находится
в стационарном состоянии (т. е. в состоянии, к-рое при отсутствии внешних сил
не изменяется), то из H. с. следует, что энергию системы в этом состоянии можно
измерить лишь с точностью, не превышающей h/
t>h. Если система находится
в стационарном состоянии (т. е. в состоянии, к-рое при отсутствии внешних сил
не изменяется), то из H. с. следует, что энергию системы в этом состоянии можно
измерить лишь с точностью, не превышающей h/ t, где
t, где  t - длительность
процесса измерения. Причина этого - во взаимодействии системы с измерит,
прибором, и H. с. применительно к данному случаю означает, что энергию
взаимодействия между измерит, прибором и исследуемой системой можно учесть лишь
с точностью до h/
t - длительность
процесса измерения. Причина этого - во взаимодействии системы с измерит,
прибором, и H. с. применительно к данному случаю означает, что энергию
взаимодействия между измерит, прибором и исследуемой системой можно учесть лишь
с точностью до h/ t (в предельном случае мгновенного измерения возникающий
энергетич. обмен становится полностью неопределённым). Соотношение
t (в предельном случае мгновенного измерения возникающий
энергетич. обмен становится полностью неопределённым). Соотношение  E
E t>= h
справедливо также, если под
t>= h
справедливо также, если под  Е понимать неопределённость значения энергии
нестационарного состояния замкнутой системы, а под
Е понимать неопределённость значения энергии
нестационарного состояния замкнутой системы, а под  t - характерное
время, в течение к-рого существенно меняются ср. значения физ. величин в этой
системе.
t - характерное
время, в течение к-рого существенно меняются ср. значения физ. величин в этой
системе.
H. с. для энергии и времени
приводит к важным выводам относительно возбуждённых состояний атомов, молекул,
ядер. Такие состояния нестабильны, и из H. с. вытекает, что энергии
возбуждённых уровней не могут быть строго определёнными, т. е. обладают нек-рой
шириной (т. н. естественная ширина уровня). Если  t - ср. время жизни
возбуждённого состояния, то ширина его энергетич. уровня (неопределённость
энергии состояния) составляет
t - ср. время жизни
возбуждённого состояния, то ширина его энергетич. уровня (неопределённость
энергии состояния) составляет  E= h/
E= h/ t. Др. примером служит альфа-распад радиоактивного
ядра: энергетич. разброс
t. Др. примером служит альфа-распад радиоактивного
ядра: энергетич. разброс  E испускаемых
E испускаемых 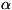 -частиц связан с временем
жизни
-частиц связан с временем
жизни  такого ядра соотношением
такого ядра соотношением  E=h/
E=h/ .
.
Лит.: Гейзенберг В., Шредингер Э.,
Дирак П., Современная квантовая механика, пер. с англ., М.- Л., 1934; Дирак П.,
Принципы квантовой механики, пер. с англ., M., 1960; Блохинцев Д. И., Основы
квантовой механики, 3 изд., M , 1961; Мандельштам Л. И., T а м м И. E.,
Соотношение неопределенности энергия - время в нерелятивистской квантовой
механике, в кн.: Мандельштам Л. И., Полн. собр. трудов, т. 2, М.- Л., 1947, с.
306; Крылов H. С., Ф о к В. А., О двух основных толкованиях соотношения
неопределенности для энергии в времени, "Журнал экспериментальной и
теоретической физики", 1947, т. 17, в. 2, с. 93.
О. И. Завьялов.
НЕОПРЕДЕЛЁННЫЕ ВЫРАЖЕНИЯ в математике, выражения, предел к-рых
не может быть найден путём непосредств. применения теорем о пределах. Типы H.
в.:
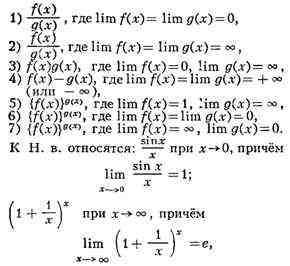
где е = 2,71828...- неперово
число. Указанные типы H.в. символически обозначают так: 1) 0/0, 2)oo/oo, 3)0·oo,
4)oo - oo, 5) 1°°, 6)0°, 7)oo°. Следует отметить, что данная функция может
являться H. в. при одних значениях аргумента и не являться таковым при других
(напр., выражение (sin x)/x при x-> не является H. в.). Не всякое H. в. имеет предел; так,
выражение
не является H. в.). Не всякое H. в. имеет предел; так,
выражение
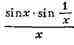
при х->0 не
стремится ни к какому пределу
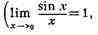
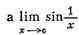
не существует).
Нахождение предела H. в. (в
случае, когда он существует) наз. иногда "раскрытием
неопределённости", или нахождением "истинного значения" H. в.
(второй термин устарел). Оно часто основывается на замене данной функции
другой, имеющей тот же предел, но не являющейся уже H. в. Иногда такая замена
достигается путём алгебраич. преобразований.
Так, напр., сокращая в
выражении
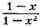
числитель и знаменатель на
1-х,
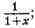
поэтому
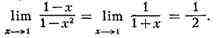
Для вычисления пределов H.
в. типов 1) и 2) часто оказывается полезной теорема (или правило) Лопиталя,
утверждающая, что в этих случаях
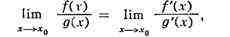
если f(x) и g(х) дифференцируемы
в окрестности (конечной или бесконечно удалённой) точки x0, за
возможным исключением самой точки x0, и второй предел
существует. Пользуясь этой теоремой, находим, напр., что
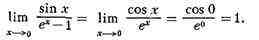
Иногда f'(x)/g'(x)-
вновь является H. в. вида 1)или 2); тогда теорема Лопиталя может быть применена
(при выполнении её условий) ещё раз и т. д. Однако это не всегда приводит к
цели; напр., применение теоремы Лопиталя к H. в.
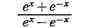
[f(x)=еx-е-x,
g(x)= еx-е-x],при
ничего не даёт. Может также случиться,
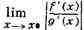
не существует, тогда как
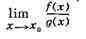
типа 1) или 2) всё же
существует; пример:
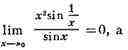
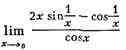
не существует. Мощным
средством нахождения пределов H. в. является разложение функций в ряды. Напр.,
так как
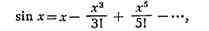
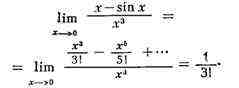
H. в. видов 3)-7) могут быть
сведены к одному из видов 1) или 2). Так, напр., при x-> /2 Н. в.
/2 Н. в.
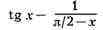
вида 4) преобразуется к виду
1):
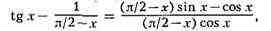
а последнее H. в. имеет
предал 0; H. в. вида 3) приводится к H. в. вида 1) или 2) преобразованием f(x)g(x)
=f(x)/h(x), или g(x)/k(x), где h(x)=1/g(x), k(x)=1/f(x)
Наконец, если через и(х) обозначить
логарифм H. в. видов 5), 6) и 7): u(x)=g(x)lnf(x), то и(х) является
H. в. вида 3), к-рое, как указано, сводится к H. в. вида 1) или 2). Так как {f(x)}g(x)
=еu(x), то, найдя предел и(х) (если он существует), можно
найти и предел данного H. в. Напр., для хxпри x->0
имеем
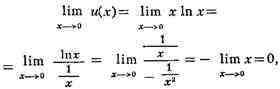
и, следовательно,
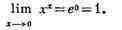
Лит.: Ильин В. А., Позняк Э. Г., Основы
математического анализа, 3 изд., ч. 1, M., 1971; К у д р я в ц е в Л. Д.,
Математический анализ, 2 изд., т. 1, М.„ 1973.
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ, общее выражение первообразной для
подынтегральной функции fix); обозначает
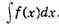
Напр.,
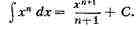
См. Интегральное
исчисление.
НЕОПРЕДЕЛЁННЫХ
КОЭФФИЦИЕНТОВ МЕТОД, метод,
применяемый в математике для отыскания коэффициентов выражений, вид к-рых
заранее известен. Так, напр., на основании теоретич. соображений дробь
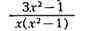
может быть представлена в
виде суммы
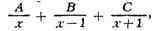
где А, В и С -
коэффициенты, подлежащие определению. Чтобы найти их, приравнивают второе
выражение первому:
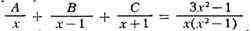
и, освобождаясь от
знаменателя и собирая слева члены с одинаковыми степенями х, получают: (A+B+C)x2
+(B-C)x-A=3x2-1
T. к. последнее равенство
должно выполняться для всех значений х, то коэффициенты при одинаковых
степенях х справа и слева должны быть одинаковыми. Т.о., получаются три
уравнения для определения трёх неизвестных коэффициентов: А + В + С = 3,
B-C=O, A = 1, откуда A=B=C = 1. Следовательно,
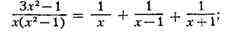
справедливость этого равенства
легко проверить непосредственно.
Пусть ещё нужно представить
дробь
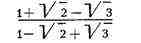
в виде
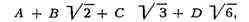
где A, B, C и D- неизвестные
рациональные коэффициенты. Приравниваем второе выражение первому
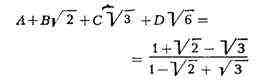
или, освобождаясь от
знаменателя, вынося, где можно, рациональные множители из-под знака корней и
приводя подобные члены в левой части, получаем:
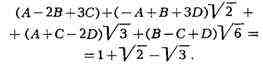
Но такое равенство возможно
лишь в случае, когда равны между собой рациональные слагаемые обеих частей и
коэффициенты при одинаковых радикалах. T. о., получаются четыре уравнения для
нахождения неизвестных коэффициентов А, В, С и D: А - 2В + 3C =
1, -А+В+3D=1, А+С-2D = -1, В-С+D=0, откуда А = О, В = -1/2,
С = 0, D = 1/2, т. е.
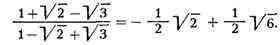
B приведенных примерах успех
H. к. м. зависел от правильного выбора выражений, коэффициенты к-рых
отыскивались. Если бы в последнем примере вместо выражения
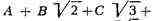
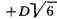
было взято выражение
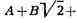
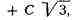
то, рассуждая, как и выше,
получили бы для трёх коэффициентов А, В и С четыре уравнения А -2B +
3C = 1, -А-В=1, А+С=-1, В-C=0, к-рым нельзя удовлетворить никаким
выбором чисел А, В и С. Особенно важны применения H. к. м. к задачам, в
к-рых число неизвестных коэффициентов бесконечно. К ним относятся задача деления
степных рядов, задача нахождения решения дифференциального уравнения в виде
степенного ряда и др. Пусть, напр., нужно найти решение дифференциального
уравнения у" + ху = О такое, что у = 0 и у' = 1 при х
= О. Из теории дифференциальных уравнений следует, что такое решение
существует и имеет вид степенного ряда
y =x + C2x2 + C3x3 + C4x4
+ C5x5 +···.
Подставляя это выражение
вместо у в правую часть уравнения, а вместо у" - выражение
2с2 + 3 · 2c3x
+ 4 · 3c4x2 + 5 · 4c5x3 +· · · ,
затем умножая на x и
соединяя члены с одинаковыми степенями х, получают
2с2 + 3 · 2с3х
+ ( 1 + 4 · 3c4x2 +(c2+5·4c5)x3+...=0
откуда при определении
неизвестных коэффициентов получается бесконечная система уравнений: 2с2
= О; 3·2с3 = О; 1 + 4· 3с4 =0; C2 + 5· 4с5
= О; ...
Решая последовательно эти
уравнения, находят:

Лит.: Смирнов В. И., Курс высшей
математики, т. 1, 23 изд., M., 1974; т. 2, 20 изд., M., 1967; Степанов В. В.,
Курс дифференциальных уравнений, 8 изд., M., 1959.