МОМЕНТ (лат. momentum - движущая сила, толчок, побудительное начало, от moveo - двигаю), математич. понятие, играющее важную роль в механике и теории вероятностей. Если на прямой линии расположена система материальных точек, массы к-рых соответственно равны ял, т₂, ..., (гт > 0), а абсциссы относительно нек-рого начала отсчёта О равны х\, х_г, ..., то м о м е н т о м порядка k этой системы относительно точки О наз. сумму

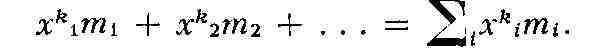
М. первого порядка в механике наз. статическим моментом, а М. второго порядка - моментом инерции. Если в выражении М. все абсциссы заменить их абс. значениями, то получатся т. н. абсолютны М. Точку с абсциссой (СУММА iXimi)l(СУММА imi) наз. центром данной системы масс. М., вычисленные относительно центра, наз. центральными. Центр. М. первого порядка для всякой системы равен нулю. Из всех М. инерции центральный является наименьшим. Неравенство Ч е б ы ш е в а: сумма масс, находящихся от точки О на расстоянии, большем а, не превышает М. инерции системы относительно О, разделённого на а².

Если распределение массы имеет плотность f(x)>=0, то М. порядка k наз. интеграл

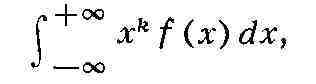
при условии его абс. сходимости. В случае произвольно распределённой массы, суммы в выражениях для М. заменяются интегралами Стилтьеса (см. Интеграл); именно таким путём и возник впервые интеграл Стилтьеса. Все упомянутые определения и теоремы при этом сохраняют силу.

В теории вероятностей роль абсцисс играют различные возможные значения случайной величины, а на места масс становятся соответствующие вероятности. М. первого порядка (к-рый здесь всегда является абсциссой центра, т. к. полная масса равна 1) наз. математическим ожиданием данной случайной величины, а центр. М. второго порядка - её дисперсией. В теории вероятностей чрезвычайно важную роль играет упомянутое неравенство Чебышева. В математич. статистике М. служат обычно осн. статистич. сводными характеристиками распределений.

Задача математич. анализа, состоящая в том, чтобы охарактеризовать свойства функции f(x) по свойствам последовательности её М.:

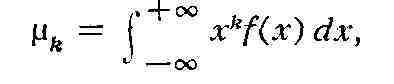
носит назв. проблемы моментов. Эта задача впервые рассматривалась П. Л. Чебышевым в 1874 в связи с исследованиями по теории вероятностей (попытка доказать центральную предельную теорему). Позже при исследовании этой задачи возникли новые мощные методы математич. анализа.

Лит.: Чебышев П. Л., Избр. труды, М., 1955; Марков А. А., Избр. труды, М., 1951; Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; Лоэв М., Теория вероятностей, пер. с англ., М., 1962.

МОМЕНТ ВРАЩАЮЩИЙ, см. Вращающий момент.

МОМЕНТ ИНЕРЦИИ, величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая равенством:

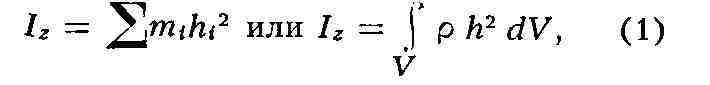
где mi - массы точек тела, hi - их расстояния от оси z, р - массовая плотность, V - объём тела. Величина I, является мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой М. и. можно также выразить через линейную величину k, наз. радиусом инерции, по формуле Ii = Mk², где М-масса тела. Размерность М. и.- L²M; единицы измерения  г/см².

Центробежным М. и. относительно системы прямоугольных осей х, у, г, проведённых в точке О, наз. величины, определяемые равенствами:

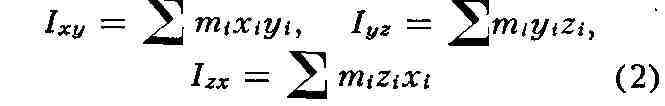
или же соответствующими объёмными интегралами. Эти величины являются характеристиками динамич. неуравновешенности масс. Напр., при вращении тела вокруг оси z от значений 1_хг и 1уг зависят силы давления на подшипники, в к-рых закреплена ось.

М. и. относительно параллельных осей z и г' связаны соотношением

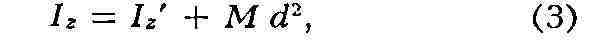
где z - ось, проходящая через центр масс тела, а а - расстояние между осями (теорема Гюйгенса).

М. и. относительно любой, проходящей через начало координат О оси О/ с направляющими косинусами а, (3, у находится по формуле:

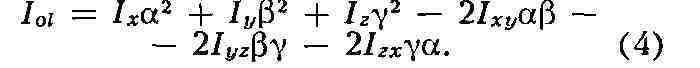
Зная шесть величин I_X, I_Y, I_Z, I_XY, I_YX, I_ZX, можно последовательно, используя формулы (4) и (3), вычислить всю совокупность М. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно-перпендикулярные оси, называемые главными осями инерции, для к-рых 1_ху = =I_YX = I_ZX, = 0. Тогда М. и. тела относительно любой оси можно определить, зная главные оси инерции и М. и. относительно этих осей.

М. и. тел сложной конфигурации обычно определяют экспериментально. Понятием о М. и. широко пользуются при решении многих задач механики и техники.

Лит.: Краткий физико-технический справочник, под общ. ред. К. П. Яковлева, т. 2, М., 1960, с. 94-101; Фаворин М. В., Моменты инерции тел. Справочник, М., 1970; Г е р н е т М. М., Р а т о б ы л ь с к и й В. Ф-, Определение моментов инерции, М., 1969; см. также лит. при ст. Механика.

С. М. Тарг.

МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ, кинетический момент, одна из мер механич. движения материальной точки или системы. Особенно важную роль М. к. д. играет при изучении вращательного движения. Как и для момента силы, различают М. к. д. относительно центра (точки) и относительно оси.

Для вычисления М. к. д. k материальной точки относительно центра О или оси z справедливы все формулы, приведённые для вычисления момента силы, если в них заменить вектор F вектором количества движения mv. Т. о., ko = [r-mv], где г - радиус-вектор движущейся точки, проведённый из центра О, a k, равняется проекции вектора ho на ось г, проходящую через точку О. Изменение М. к. д. точки происходит под действием момента m₀(F) приложенной силы и определяется теоремой об изменении М. к. д., выражаемой ур-нием dko/dt = mo(F). Когда m₀ (F) = 0, что, напр., имеет место для центр, сил, движение точки подчиняется площадей закону. Этот результат важен для небесной механики, теории движения искусств, спутников Земли, космич. летат. аппаратов и др.

Главный М. к. д. (или кинетич. момент) механич. системы относительно центра О или оси г равен соответственно геомет-рич. или алгебраич. сумме М. к. д. всех точек системы относительно того же

или ног значение момента инерции I_г, он может изменять угловую скорость со. Др. примером выполнения закона сохранения М. к. д. служит появление реактивного момента у двигателя с вращающимся валом (ротором). Понятие о М. к. д. широко используется в динамике твёрдого тела, особенно в теории гироскопа.

Размерность М. к. д.- L²MT^-1, единицы измерения - кг- V/сек, г*см²/сек. М. к. д. обладают также электромагнитное, гравитационное и др. физические поля. Большинству элементарных частиц присущ собственный, внутренний М. к. д.- спин. Большое значение М. к. д. имеет в квантовой механике.

Лит. см. при ст. Механика.

С. М. Тарг.

МОМЕНТ ОРБИТАЛЬНЫЙ, момент количества движения микрочастицы при её движении в силовом поле, обладающем сферич. симметрией. Назв. М. о." связано с наглядным представлением о движении атомного электрона в сферически симметричном поле ядра по определённой замкнутой орбите.

Согласно квантовой механике, М. о. Mi квантован, т. е. его величина, а также проекция на произвольно выбранную в пространстве ось (ось г) могут принимать лишь определённые дискретные значения:

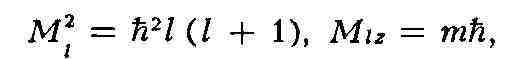
где ft - постоянная Планка, l = О, 1, 2, ... - азимутальное (орбитальное), р. m - I, l - 1, ..., -  магнитное квантовые числа. Классификация состояний микрочастиц по значениям l играет большую роль в теории атома и атомного ядра и в теории столкновений.

Лит. см. при статьях Атом, Ядро атомное, Рассеяние микрочастиц, Квантовая механика.

М. А. Ельяшевич.

МОМЕНТ СИЛЫ, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из осн. понятий механики. Различают М. с. относительно центра (точки) и относительно оси.

М. с. относительно центра О величина векторная. Его модуль Mo - Fh, где F - модуль силы, a h - плечо, т. е. длина перпендикуляра, опущенного из О на линию действия силы (см. рис.); направлен вектор М₀ перпендикулярно плоскости, проходящей через центр О и силу, в сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки (в правой системе координат). С помощью векторного произведения М. с. выражается равенством Л/о = [rF], где г - радиус-вектор, проведённый из О в точку приложения силы. Размерность М. с.- L²MT², единицы измерения - н-м, дин-см (1 н-м = - 10⁷ дин-см) или кгс-м.

М. с. относительно оси величина алгебраическая, равная проекции на эту ось

М. с. относительно любой точки О оси или же численной величине момента проекции Fxy силы F на плоскость ху, перпендикулярную оси 2, взятого относительнс точки пересечения оси с плоскостью. Т. е.

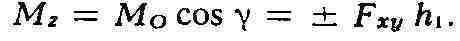
Знак плюс в последнем выражении берётся, когда поворот силы F с положит, конца оси z виден против хода часовой стрелки (тоже в правой системе). М. с. относительно осей х, у, z могут также вычисляться по формулам:

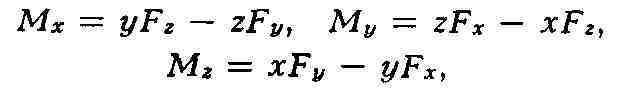
где Fx, Fy, Р_г - проекции силы F на оси; х,у, z - координаты точки А приложения силы.

Если система сил имеет равнодействующую, то её момент вычисляется по Вариньона теореме.

Лит. см. при ст. Механика.

С. М. Тарг.

МОМЕНТНЫХ НАБЛЮДЕНИЙ МЕТОД в статистике, фиксация наличия или отсутствия отд. элементов изучаемого процесса на определённые моменты времени без учёта продолжительности этих элементов. Является разновидностью выборочного наблюдения и применяется при изучении использования рабочего времени и эксплуатации производств, оборудования в пром-сти, покупательского спроса в розничной торговле, использования вагонного парка на ж.-д. транспорте. Позволяет также получить необходимую информацию для расчёта осн. характеристик процессов массового обслуживания (потока заявок в единицу времени и среднего уровня обслуживания). Метод является наиболее приемлемым для определения эффективности изменений в организации труда инж.-технич. работников и служащих. М. н. м. заключается в проведении наблюдений через случайные или постоянные интервалы времени с отметками о состоянии исследуемого объекта в тот или иной момент времени. Спец. регистраторы в течение рабочей смены по намеченному маршруту через определённые интервалы производят обход рабочих мест и фиксируют элементы рабочего или станочного времени ("работа" или "простой"). Число наблюдений рассчитывают по формуле:

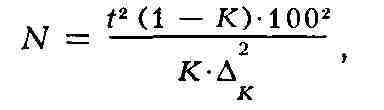
где К - коэфф. использования времени; Дк - заданная точность, т. е. предельная относит, ошибка при определении К с доверительной вероятностью 0,954 или 0,997; t - гарантийный коэфф. точности результатов моментного наблюдения. В условиях стабильного производств, процесса t - 1, тогда доверительная вероятность Фt = 0,954; в условиях нестабильного производств, процесса t = 3 и Ф (t) = 0,997. Количество обходов определяется путём деления числа записей на число рабочих мест или на количество установленного оборудования. Оценка результатов моментного наблюдения производится по формуле:

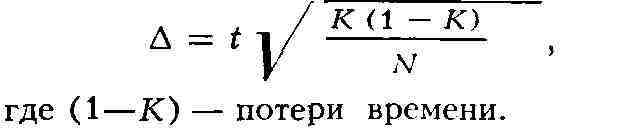
Лит.: Б а р н е с П., Выборочное изучение рабочего времени способом мгновенных наблюдений, в сб.: Применение статистических методов в производстве, М., 1963; Оноприенко Г. К., Выборочный анализ использования рабочего времени, М., 1968; Ильенкова С. Д., Резервы производства, М., 1973.

А. Г. Шифман.