МОДАЛЬНАЯ ЛОГИКА, область логики, посвящённая изучению модальностей, построению исчислений, в к-рых модальности применяются к высказываниям, наряду с логическими операциями, и сравнительному исследованию таких исчислений. "Модальные операторы" ("возможно", "необходимо" и др.) могут относиться как к высказываниям или предикатам, так и к словам, выражающим к.-л. действия или поступки. Интерес к проблемам М. л. обусловлен прежде всего естественной связью, с одной стороны, между модальностями типа "необходимо" и понятием "логического закона" (т. е. тождественно истинного высказывания к.-л. логич. системы), а с другой - между модальностями типа "возможно" и такими гносеологич. и общенауч. понятиями, как "(эффективно) осуществимо", "вычислимо" и т. п.

В классич. системах М. л. (для к-рых справедлив исключённого третьего прин-

нем.: sollen, konnen, wollen и др.); др. модальными словами (напр., рус.: "кажется", "пожалуй"; англ.: perhaps, likely); интонационными средствами. Различные языки грамматически по-разному выражают разные значения М. Так, англ, язык выражает значение ирреальной М. при помощи спец. наклонения (т. н. Subjunctive II, напр.: If you had come in time we should have been able to catch the train), в ягнобском языке формы настояще-будущего времени могут иметь модальные оттенки косвенного приказания, приглашения к действию, решимости сделать что-либо, допущения и др.

МОДЕЛЕЙ ТЕОРИЯ, раздел математики, возникший при применении методов математич. логики в алгебре. Ко 2-й пол. 20 в. М. т. оформилась в самостоят. дисциплину, методы и результаты к-рой находят применение как в алгебре, так и в др. разделах математики.

Осн. понятия М. т. - понятия алгебраич. системы, формализованного языка, истинности высказывания рассматриваемого языка в данной алгебраич. системе. Типичным примером алгебраич. системы является система натуральных чисел вместе с операциями сложения и умножения, отношением порядка и выделенными элементами 0,1. Простейшие высказывания об этой системе - выскамодальную операцию (используя к.-л. из этих эквивалентностей в качестве определения др. операции). Аналогично вводятся и др. модальные операции (не входящие в число логич. операций и не выразимые через низе).

Системы М. л. могут быть интерпретированы в терминах многозначной логики (простейшие системы - как трёхзначные: "истина", "ложь", "возможно"). Это обстоятельство, а также возможность применения М. л. к построению теории "правдоподобных" выводов указывают^ на её глубокое родство с вероятностной логикой.

Кроме рассматривавшихся выше "абсолютных" модальностей, в М. л. приходится иметь дело с т. н. относительными, т. е. связанными с к.-л. условиями ("Л возможно, если В", и т. п.); формализация правил обращения с ними не вызывает дополнит. трудностей и проводится с помощью аппарата ограниченных кванторов (с использованием предикатов, выражающих ограничит, условия, и логические операции материальной импликации).

Ю. А, Гастев.

МОДАЛЬНОСТЬ (от лат. modus - мера, способ), способ существования к.-л. объекта или протекания к.-л. явления (онтологическая М.) или же способ понимания, суждения об объекте, явлении или событии (гносеологическая, или логическая М.). Понятие М., введённое по существу ещё Аристотелем, перешло затем в классич. филос. системы. Слова (термины), выражающие различные модальные понятия, являются предметом рассмотрения и изучения лингвистики (см. Модальность в языкознании). Различие суждений по М., разрабатывавшееся в антич. логике учениками и комментаторами Аристотеля Теофрастом, Евдемом Родосским и др., уточнялось далее средневековыми схоластами. В логике и философии нового времени стало традиционным предложенное И. Кантом подразделение суждений на ассерторические (суждения действительности), аподиктические (суждения необходимости) и проблематические (суждения возможности); общепринятое следование суждения "происходит Л" из "необходимо А" и суждения "возможно А" из "происходит Л" стало основой разработки М. в совр. формальной (математической) логике. При этом М., относящиеся к высказываниям или предикатам, наз. а л е т и ч е с к и м и, а М., относящиеся к словам, выражающим действия и поступки,- деонтическими. М. делятся далее на абсолютные (безусловные) и относительные (условные) согласно обычному смыслу данных терминов. В совр. модальной логике и логической семантике к М. причисляются иногда понятия "истинно" и "ложно", а также "доказуемо", "недоказуемо" и "опровержимо".

Ю. А. Гастев.

МОДАЛЬНОСТЬ в языкознании, понятийная категория, выражающая отношение говорящего к содержанию высказывания, целевую установку речи, отношение содержания высказывания к действительности. М. может иметь значение утверждения, приказания, пожелания, допущения, достоверности, ирреальности и др. М. выражается различными грамматич. и лексич. средствами: спец. формами наклонений; модальными глаголами (напр., рус.: "может", "должен"; нем.: sollen, konnen, wollen и др.); др. модальными словами (напр., рус.: «кажется», «пожалуй»; англ.: perhaps, likely); интонационными средствами. Различные языки грамматически по-разному выражают разные значения М. Так, англ, язык выражает значение ирреальной М. при помощи спец. наклонения (т. н. Subjunctive II, напр.: If you had come in time we should have been able to catch the train), в ягнобском языке формы настояще-будущего времени могут иметь модальные оттенки косвенного приказания, приглашения к действию, решимости сделать что-либо, допущения и др.

МОДЕЛЕЙ ТЕОРИЯ, раздел математики, возникший при применении методов математич. логики в алгебре. Ко 2-й пол. 20 в. М. т. оформилась в самостоят, дисциплину, методы и результаты к-рой находят применение как в алгебре, так и в др. разделах математики.
Осн. понятия М. т. - понятия алгебраич. системы, формализованного языка, истинности высказывания рассматриваемого языка в данной алгебраич. системе. Типичным примером алгебраич. системы является система натуральных чисел вместе с операциями сложения и умножения, отношением порядка и выделенными элементами 0,1. Простейшие высказывания об этой системе - выска-  

и, значит, получается из простейших при помощи пропозициональных связок и кванторов.

В общем случае под алгебраической системой понимается непустое множество вместе с заданными на этом множестве совокупностями отношений и операций от конечного числа аргументов. Эти операции и отношения наз. основными в алгебраич. системе. Каждой такой операции и каждому такому отношению ставится в соответствие

пропозициональные связки и кванторы (см. ниже); набора символов, наз. предметными переменными, а также скобок и запятой. При этом каждому символу отношения или операции приписывается натуральное число, наз. местностью этого символа; оно равно числу аргументов той операции или того отношения, к-рым соответствует рассматриваемый символ. В число символов отношений включается специальный символ = для отношения равенства. Индуктивно определяются понятия терма и формулы. Предметные переменные являются термами.

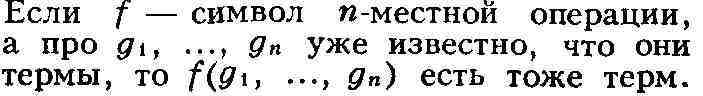
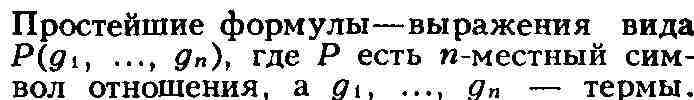
Более сложные формулы получаются из простейших с помощью конечного числа связываний их знаками кванторов и пропозициональных связок. Символы предметных переменных, встречающиеся в формуле, разделяются на свободные и связанные. Связанные те, к-рые находятся в области действия квантора по этому переменному, а остальные свободные. Напр., в формуле

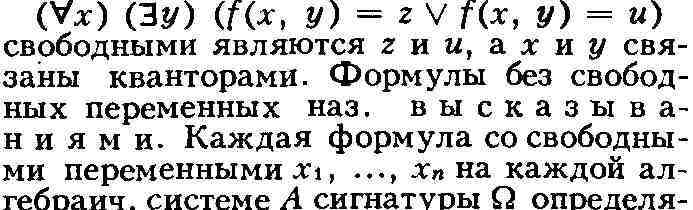
ет n-местное отношение. Напр., формула, записывающая утверждение, что числа и и v взаимно простые, определяет на натуральных числах отношение взаимной простоты, к-рое для пары (3, 5) истинно, а для пары (2, 4) ложно. Для простейших формул соответствующее отношение фактически задаётся самой системой А. Для более сложных формул соответствующее отношение определяется путём интерпретации кванторов и

этому определению, каждое высказывание в каждой алгебраич. системе соответствующей сигнатуры либо ложно, либо истинно. Например, если символу f ставится в соответствие операция сложения на натуральных числах, то формула

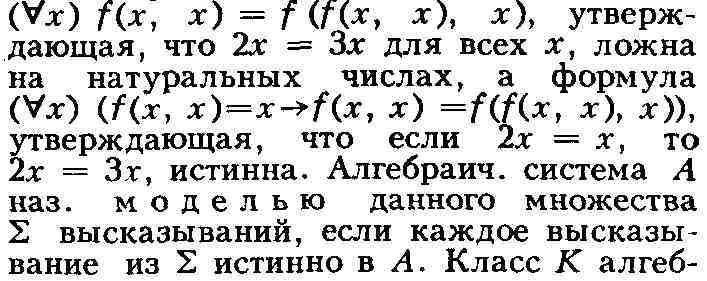
раич. систем наз. аксиоматизируемым, если К есть совокупность всех моделей нек-рого множества высказываний. Мн. важные классы алгебраич. систем, напр, классы групп, колец, полей, аксиоматизируемы.

Изучение общих свойств аксиоматизируемых классов - важная часть М. т. Во мн. случаях по форме высказываний

Фундаментальный результат М. т.-локальная теорема Мальцева (1936), согласно к-рой если каждая конечная подсовокупность совокупности Ʃ высказываний имеет модель, то и Ʃ имеет модель. А. И. Мальцев нашел многочисл. применения своей теоремы для доказательства т. н. локальных теорем алгебры. Важным фактом в теории аксиоматизируемых классов является теорема Лёвенхейма-Сколема: всякий аксиоматизируемый класс конечной или счётной сигнатуры, содержащий бесконечные системы, содержит и счётную систему. В частности, нельзя написать такую совокупность высказываний, все модели к-рой были бы изоморфны одной бесконечной алгебраич. системе, напр., полю комплексных чисел или кольцу целых чисел. Но тем не менее существуют аксиоматизируемые классы, все системы к-рых данной бесконечной мощности изоморфны .

Одной из важных конкретных совокупностей высказываний является совокупность, определяющая понятие множества. Это понятие описывается на языке 1-й ступени, сигнатура которого состоит из одного символа - символа бинарного отношения, интерпретируемого как "х есть элемент y". Существует несколько вариантов таких описаний, каждый из к-рых осуществляется при помощи своей совокупности высказываний. Эти совокупности наз. системами аксиом для теории множеств. Развитие М. т. показало, что нельзя выбрать такую систему аксиом для теории множеств, к-рая удовлетворила бы все потребности математики (см. также Аксиоматическая теория множеств).

Центральная часть совр. М. т.- это изучение элементарных теорий, т. е. теорий, описываемых на языке 1-й ступени. Однако постепенно всё возрастающее место отводится и изучению теорий, описываемых при помощи более богатых языков.

Историческая справка. Осн. понятия М. т. возникли в математике в 19 в., гл. обр. в работах по основаниям геометрии. К понятию модели данного множества высказываний вплотную подошёл Н. И. Лобачевский в работах по геометрии. В полной мере оно появилось в работах Э. Белътрами и Ф. Клейна, построивших модели геометрии Лобачевского. Совр. формулировки осн. понятий М. т. сложились в работах школ Д. Гильберта и А. Тарского. М. т. возникла в нач. 30-х гг. 20 в. в результате применения методов математич. логики в алгебре, одним из инициаторов к-рого был А. И. Мальцев.

Лит.: Мальцев А. И., Алгебраические системы, М., 1970; Робинсон А., Введение в теорию моделей и метаматематику алгебры, пер. с англ., М., 1967.

А. Д. Тайманов, М. А. Тайцлин.

МОДЕЛИ в биологии применяются для моделирования биологи ч. структур, функций и процессов на разных уровнях организации живого: молекулярном, субклеточном, клеточном, органно-системном, организменном и популяционно-биоценотическом. Возможно также моделирование различных биологич. феноменов, а также условий жизнедеятельности отдельных особей, популяций и экосистем. В биологии применяются в осн. три вида М.: биологические, физико-химические и математические (логико-математич.). Биологические М. воспроизводят на лабораторных животных определённые состояния или заболевания, встречающиеся у человека или животных. Это позволяет изучать в эксперименте механизмы возникновения данного состояния или заболевания, его течение и исход, воздействовать на его протекание. Примеры таких М.- искусственно вызванные генетич. нарушения, инфекционные процессы, интоксикации, воспроизведение гипертония, и гипоксич. состояний, злокачественных новообразований, гиперфункции или гипофункции нек-рых органов, а также неврозов и эмоциональных состояний. Для создания биологич. М. применяют различные способы воздействия на генетич. аппарат, заражение микробами, введение токсинов, удаление отдельных органов или введение продуктов их жизнедеятельности (напр., гормонов), различные воздействия на центр, и периферич. нервную систему, исключение из пищи тех или иных веществ, помещение в искусственно создаваемую среду обитания и мн. др. способы. Биологич. М. широко используются в генетике, физиологии, фармакологии.

Физико-химические М. воспроизводят физич. или химич. средствами биологич. структуры, функции или процессы и, как правило, являются далёким подобием моделируемого биологич. явления. Начиная с 60-х гг. 19 в. были сделаны попытки создания физико-химич. М. структуры и нек-рых функций клеток. Так, нем. учёный М. Траубе (1867) имитировал рост живой клетки, выращивая кристаллы CuSO₄ в водном растворе K₄[Fe(CN)₆]; франц. физик С. Ледюк (1907), погружая в насыщенный раствор К₃РО4 сплавленный СаС1₂, получил -благодаря действию сил поверхностного натяжения и осмоса - структуры, внешне напоминающие водоросли и грибы. Смешивая оливковое масло с разными растворимыми в воде веществами и помещая эту смесь в каплю воды, О. Бючли (1892) получал микроскопич. пены, имевшие внешнее сходство с протоплазмой; такая М. воспроизводила даже амебоидное движение. С 60-х гг. 19 в. предлагались также разные физич. М. проведения возбуждения по нерву. В М., созданной итал. учёным К. Маттеуччи и нем.- Л. Германом, нерв был представлен в виде проволоки, окружённой оболочкой из проводника второго рода. При соединении оболочки и проволоки с гальванометром наблюдалась разность потенциалов, изменявшаяся при нанесении на участок "нерва" электрич. "раздражения". Такая М. воспроизводила нек-рые биоэлектрич. явления при возбуждении нерва. Франц. учёный Р. Лилли на М. распространяющейся по нерву волны возбуждения воспроизвёл ряд явлений, наблюдаемых в нервных волокнах (ре-фрактерный период, "всё или ничего* закон, двустороннее проведение). М. представляла собой стальную проволоку, к-рую помещали сначала в крепкую, а затем в слабую азотную к-ту. Проволока покрывалась окислом, к-рый восстанавливался при ряде воздействий; возникший в одном участке процесс восстановления распространялся вдоль проволоки. Подобные М., показавшие возможность воспроизведения некоторых свойств и проявлений живого посредством физико-химических явлений, основаны на внешнем качественном сходстве и представляют лишь исторический интерес.

Позднее более сложные М., основанные на гораздо более глубоком количественном подобии, строились на принципах электротехники и электроники. Так, на основе данных электрофизиологич. исследований были построены электронные схемы, моделирующие биоэлектрические потенциалы в нервной клетке, её отростке и в синапсе. Построены также механич. машины с электронным управлением, моделирующие сложные акты поведения (образование условного рефлекса, процессы центр, торможения и пр.). Этим М. обычно придают форму мыши, черепахи, собаки (см. рис. 1-3). Такие М. также слишком упрощают явления, наблюдаемые в организме, и имеют большее значение для бионики, чем для биологии.

Рис. 1. Общий вид "черепахи" Института автоматики и телемеханики АН СССР.

Значит, большие успехи достигнуты в моделировании физико-химич. условий существования живых организмов или их органов и клеток. Так, подобраны растворы неорганич. и органич. веществ (растворы Рингера, Локка, Тироде и др.), имитирующие внутреннюю среду организма и поддерживающие существование изолированных органов или культивируемых вне организма клеток (см. Культуры тканей).

Рис. 2. "Мышь" К. Шеннона-автомат, моделирующий "обучение" при повторном прохождении лабиринта.

М. биологических мембран (плёнка из природных фосфолипидов разделяет раствор электролита) позволяют исследовать физико-химич. основы процессов транспорта ионов и влияние на него различных факторов. С помощью химич. реакций, протекающих в растворах в автоколебательном режиме, моделируют колебательные процессы, характерные для многих биологических феноменов, - дифференцировки, морфогенеза, явлений в сложных нейронных сетях и т. д.

Рис. 3. К. Шеннон пускает "мышь" в лабиринт.

Математические М. (математич. и логико-математич. описания структуры, связей и закономерностей функционирования живых систем) строятся на основе данных эксперимента или умозрительно, формализованно описывают гипотезу, теорию или открытую закономерность того или иного биология, феномена и требуют дальнейшей опытной проверки. Различные варианты подобных экспериментов выявляют границы применения математич. М. и дают материал для её дальнейшей корректировки. Вместе с тем "проигрывание" математич. М. биологич. явления на ЭВМ часто позволяет предвидеть характер изменения исследуемого биологич. процесса в условиях, трудно воспроизводимых в эксперименте. Матёматич. М. в отдельных случаях позволяет предсказать нек-рые явления, ранее не известные исследователю. Так, М. сердечной деятельности, предложенная голл. учёными ван дер Полом и ван дер Марком, основанная на теории релаксационных колебаний, указала на возможность особого нарушения сердечного ритма, впоследствии обнаруженного у человека. Из матёматич. М. физиология, явлений следует назвать также М. возбуждения нервного волокна, разработанную англ, учёными А. Ходжкином и А. Хаксли. На основе теории нервных сетей амер. учёных У. Мак-Каллока и У. Питса строятся логико-математич. модели взаимодействия нейронов. Системы дифференциальных и интегральных уравнений положены в основу моделирования биоценозов (В. Вольтерра, А. Н. Колмогоров). Марковская математич. М. процесса эволюции построена О. С. Кулагиной и А. А. Ляпуновым. И. М. Гельфандом и М. Л. Цетлиным на основе теории игр и теории конечных автоматов разработаны модельные представления об организации сложных форм поведения. В частности, показано, что управление многочисленными мышцами тела строится на основе выработки в нервной системе нек-рых функциональных блоков - синергий, а не путём независимого управления каждой мышцей. Создание и использование математич. и логико-математич. М., их совершенствование способствуют дальнейшему развитию математической и теоретической биологии.

Лит.: Моделирование в биологии. Сб. ст., пер. с англ., М., 1963; Новик И. Б., О моделировании сложных систем, М., 1965; Кулагина О. С., Ляпунов А. А., К вопросу о моделировании эволюционного процесса, в кн.: Проблемы кибернетики, в. 16, М., 1966; Модели структурно-функциональной организации некоторых биологических систем. [Сб. ст.], М., 1966; Математическое моделирование жизненных процессов. Сб. ст., М., 1968; Теоретическая и математическая биология, пер. с англ., М., 1968; Моделирование в биологии и медицине, Л., 1969; Б е й л и Н., Математика в биологии и медицине, пер. с англ., М., 1970; Управление и информационные процессы в живой природе, М., 1971; Эйген М., Молекулярная самоорганизация и ранние стадии эволюции, "Успехи физических наук^, 1973, т. 109, в. 3.

Е. Б. Бабский, Е. С. Геллер.

МОДЕЛИ в экономике используются начиная с 18 в. В "Экономических таблицах" Ф. Кенэ, к-рые К. Маркс назвал идеей "...бесспорно самой гениальной из всех, какие только выдвинула до сего времени политическая экономия" (М арке К. и Энгельс Ф., Соч., 2 изд., т. 26, ч. 1, с. 345), по существу была впервые сделана попытка формализации всего процесса обществ, воспроизводства. Огромное влияние на экономическую науку оказали схемы воспроизводства, созданные Марксом и развитые В. И. Лениным. Непосредственным следствием этого подхода явилась., теория межотраслевого баланса (см. Баланс межотраслевой).

Особенно широко М. употребляются в экономич. исследованиях начиная с сер. 20 в., когда возник ряд новых областей математики (см., напр., Операций исследование) и были созданы электронные вычислительные машины (ЭВМ). Экономико-матем. М. используют за рубежом такие учёные, как Л. Валърас, Дж. Нейман (создатель первой ЭВМ и один из основоположников игр теории и вообще матем. экономики), Дж. М. Кейнс, Р. Фриш, Я. Тинберген, П. Сэмюэлсон, К. Арроу, В. Леонтьев, а также Г. Дж. Данциг, Дж. Дебре, Т. Купманс, X. Ни-кайдо, М. Морисима, Р. Харрод, Дж. Хикс.

В СССР развитие метода М. в экономике связано прежде всего с именами Л. В. Канторовича (впервые в мировой науке сформулировал М. социалистич. экономики в виде матем. задачи линейного программирования), А. Л. Лурье, В. С. Немчинова, В. В. Новожилова, а также А. Г. Аганбегяна, А. Л. Вайнштейна, В. А. Волконского, Л. М. Дуд-кина, А. А. Макарова, В. Л. Макарова, С. М. Мовшовича, Ю. А. Олейника, В. Ф. Пугачёва, Е. Ю. Фаермана, Н. П. Федоренко, С. С. Шаталина.

Процесс экономич. исследования с помощью М. можно условно подразделить на ряд этапов. На первом этапе формулируется общая задача, в соответствии с к-рой фиксируется объект исследования (напр., мировая экономика в целом, экономика мирового капиталистич. и социалистич. х-ва, отд. страны, отрасли, предприятия, фирмы или определённый аспект функционирования экономич. систем: спрос и потребление, распределение доходов, ценообразование и т. п.). Далее выдвигаются требования к характеру исходной информации, к-рая может быть статистич. (получаемой в результате наблюдений за ходом экономич. процессов) или нормативной (коэффициенты затрат-выпуска, рациональные нормы потребления). Затем изучаются наиболее простые (исходные) свойства моделируемого объекта и выдвигаются гипотезы о характере его развития. Так, для решения ряда задач эффективного управления экономич. системой фундаментальное значение имеют такие свойства, как ограниченность в каждый момент времени материальных, трудовых и природных ресурсов, достигнутый уровень научно-технич. знаний общества, определяющий набор технологич. способов получения нужных продуктов из имеющихся ресурсов, а также многовариантность допустимых траекторий экономич. развития (диктующая задачу выработки критерия выбора наиболее эффективной траектории).

Информация, полученная на первом этапе, нужна для создания М. экономич. системы, к-рая и составляет содержание второго этапа. Для изучения различных аспектов функционирования экономич. систем используются разные М. Наиболее общие закономерности развития экономики исследуются при помощи нар.-хоз. М. (балансовых, оптимизационных, равновесных, игровых и др.). Для анализа и прогнозов динамики и соотношения различных синтетич. показателей (нац. дохода, занятости, процента на фонды, потребления, сбережений, инвестиций и т. п.) применяются макро-экономич. М., а исследование конкретных хоз. ситуаций производится с помощью микроэкономич. М. произ-ва, транспорта, торговли, снабжения и сбыта и т. п. Для исследования сложных экономич. систем используются преимущественно матёматич. М., ибо они лучше всего приспособлены для анализа простейших экономич. процессов (напр., на транспорте), - т. н. аналоговые М. (электрич., механич., гидравлич.). Начиная с 1960-х гг. большую известность приобрели т. н. имитационные М., используемые для изучения реальных процессов функционирования экономич. систем в тех случаях, когда их матёматич. анализ затруднён или невозможен (и в определ. степени заменяющие экспериментальное изучение экономич. систем), а также применяемые для обучения руководителей правилам наиболее эффективного ведения х-ва (т. н. деловые игры). Экономич. М. классифицируются по следующим осн. критериям: целям и задачам, объекту, применяемому аппарату исследования, характеру исходной информации. С точки зрения последнего критерия различаются статистич. и нормативные модели. Все эти классификации, разумеется, весьма условны, т. к. реальные М. могут занимать промежуточное положение (напр., часть информации задаётся нормативно, а часть из статистич. анализа поведения экономич. системы). Кроме того, более общие М. могут включать в себя частные. Напр., элементом М. нар. х-ва страны могут быть М. отраслей, предприятий и т. д. (субмодели), и наоборот, в локальные М. вводятся требования, вытекающие из анализа всей экономики.

На этапе построения матем. М. результаты эмпирич. исследования переводятся со специфич. языка исследуемого объекта на универсальный матем. язык, выбирается схема (конструкция) М., вводятся осн. переменные, параметры и функциональные зависимости. Затем полученная М. сопоставляется с уже имеющимися. Если оказывается, что М. данного класса достаточно хорошо изучены и существуют готовые методы их анализа, то можно решать соответствующую матем. задачу. В противном же случае возникает вопрос, нельзя ли так упростить предпосылки М., чтобы она не утратила существенных специфич черт исследуемого объекта, и в то же время подвести её под класс структур, уже изученных математикой. В свою очередь, построение М. с ещё не изученными свойствами стимулирует развитие новых матем. направлений.

Третий этап - матем. анализ М., служащий средством получения не только количественных, но и качественных выводов. (Здесь важно уяснить, на какие вопросы можно получить ответ с помощью М., а на какие - нет; типичная ошибка - попытка объяснить с помощью анализа М. круг явлений, выходящих за её пределы.) Качественные выводы, получаемые из анализа экономич. М., позволяют обнаружить неизвестные ранее свойства экономич. системы: её структуру, динамику развития, устойчивость, соотношения макроэкономич. параметров, свойства ценностных показателей и т. п. Напр., К. Маркс из своих схем воспроиз-ва получил соотношение между постоянным капиталом первого подразделения и переменным капиталом и прибавочной стоимостью второго подразделения. Ленинские схемы воспроизводства позволили установить, при каком характере технич. прогресса имеет место закон преимущественного роста произ-ва средств производства. На основе т. н. М. сбалансированного роста удалось выяснить асимптотические свойства эффективных экономич. траекторий - тенденцию к стационарному развитию с максимальным темпом. С помощью М. оптимального планирования исследуются теоре-тич. проблемы ценообразования.

К количественным выводам из экономич. М. относятся оптимальные планы развития тех или иных хоз. ячеек, прогнозы экономич. динамики, расчёты цен, уже сейчас дающие большой экономич. эффект. Соответствующие экономические М. являются важным элементом автоматизированных систем управления. Требования к разным М. различны. От теоретических (абстрактных) М. требуется отображение лишь самых общих свойств экономич. систем. С помощью математич. методов здесь доказывается существование эффективного (равновесного, оптимального) состояния (траектории) системы, а затем изучаются его свойства. Если возможно, определяется также алгоритм отыскания эффективного состояния (алгоритмом решения экономич. задачи часто служит отображение процессов, реально протекающих в моделируемом объекте). М., используемые для конкретных расчётов, имеют в качестве своей теоретич. базы абстрактные М. и результаты их анализа. Конкретные М. достаточно полно отражают специфич. особенности исследуемого объекта, ибо в противном случае расчёты, осуществляемые на их основе, не могут быть использованы на практике. Рассматриваемый этап завершается экономич. интерпретацией полученных результатов: математич. понятия переводятся на язык изучаемого объекта. Качественные результаты интерпретируются как свойства и закономерности развития экономич. системы, алгоритм - как механизм её планирования и функционирования, числовые результаты - как планы или прогнозы.

Прежде чем использовать полученные выводы в теории или на практике, необходимо провести четвёртый этап исследования "моделирования" - проверку полученных результатов. Здесь перед исследователем встают огромные трудности. Обычные способы естественных наук -эксперимент, сопоставление полученных результатов с характеристиками реальных процессов - применимы далеко не всегда. Напр., если программа развития хоз. объекта, полученная с помощью М., показывает возможности улучшения практики, то ещё не ясно, вызвано ли это действительно несовершенством существующих методов планирования, управления и стимулирования или тем, что в исходной М. не учтены нек-рые существенные условия, имеющие место в реальности, 'и намеченные улучшения неосуществимы. Поэтому особо важна теоретич. проверка правильности исходных предпосылок М., к-рую необходимо провести ещё на первом этапе исследования. Гораздо реже применяется эксперимент на объекте или на имитирующей его М. (напр., аналоговом устройстве), дающий возможность проверить результаты моделирования, т. к. это связано с большими затратами, а натурный эксперимент - ещё и с рядом трудностей социально-экономич. характера.

Последний, пятый этап - внедрение - должен приводить (в случае положительного исхода предшествующего этапа) к совершенствованию экономич. теории и методов управления экономич. процессами, цен, планов хоз. развития. В противном случае необходимо уточнить исходные предпосылки М., т. е. вновь пройти все перечисленные этапы. Т. о., исследование экономических систем с помощью М. носит конструктивный характер. В капиталистич. обществе М. дают определённый эффект, гл. обр. в пределах фирмы. Практическое же применение М. в масштабе всей страны существенно ограничено в силу присущих капитализму антагонистич. противоречий. В условиях же социализма открываются принципиально новые возможности использования М. для решения проблем планирования и управления всем нар. х-вом.

Использование М. в экономике имеет определённые границы применения: не вся информация об экономич. процессах может быть полностью формализована и не вся является доступной, не всякая М. поддаётся теоретич. анализу. Кроме того, даже самые совр. вычислительные средства не могут справиться с громадным объёмом вычислений, к-рые необходимо провести, чтобы решить нек-рые конкретные экономич. задачи. Поэтому применение М. должно дополняться др. методами, в т. ч. использованием опыта хоз. руководителей. В свою очередь, результаты расчётов, проведённых на основе М., могут оказать существенную помощь хоз. руководителям в деле управления.

Лит.: Маркс К. и Энгельс Ф., Соч., 2 изд., т. 23-25; Ленин В. И., По поводу так называемого вопроса о рынках, Поли, собр. соч., 5 изд., т. 1; е г о же, К характеристике экономического романтизма, там же, т. 2, К а н т о р о в и ч Л. В., Экономический расчёт наилучшего использования ресурсов, М., 1959; Новожилов В. В., Проблемы измерения затрат и результатов при оптимальном планировании, М., 1967; Нейман Д ж. фон. Морген-Штерн О., Теория игр и экономическое поведение, пер. с англ., М., 1970; Воспроизводство и экономический оптимум, М., 1972; Кунявский М. С., Отношения непосредственного производства при социализме, Минск, 1972; Лурье А. Л., Экономический анализ моделей планирования социалистического хозяйства, М., 1973; А г-row К., Hahn F., General competitive analisis, S. F., 1971.

Ю. В. Овсиенко.

МОДЕЛИ в языкознании, используются в структурной лингвистике при описании языка и его отд. аспектов (фонологич., грамматич., лексич. и др. систем) для уточнения лингвистич. понятий и связей между ними, что помогает выявить структуры, лежащие в основе бесконечного разнообразия языковых явлений (М. иногда называют сами эти структуры). В зависимости от области применения М. делятся на фонологич., морфологич., синтаксич., семантич. При построении М. используются средства и методы математич. лингвистики. В любой М. фиксируются: объекты, соответствующие данным непосредств. наблюдения,- множества звуков, слов, предложений; объекты, конструируемые исследователем для описания ("конструкты"), - заранее заданные строго ограниченные наборы категорий, признаков, элементарных смысловых структур и т. п.

Если исходный материал ("вход") при исследовании - звуки, слова, предложения, а результат ("выход") - категории и смысловые структуры, то М. наз. аналитической. Такова М. категории рода, дающая однозначное решение спорных вопросов. Принадлежность к грамматич. роду может определяться формой слова (напр., в рус. яз. слова, оканчивающиеся на "-а", обычно жен. рода, но этот признак не однозначен, ср. "папа"), значением (слова, обозначающие существа жен. пола, относятся к жен. роду, но и этот признак не однозначен, ср. в нем. яз. das Weib -"женщина" - ср. рода). В М. рода считается, что для каждого слова задана система его форм (напр., стол, стола, столу...) и известно, какие словоформы согласуются с данной словоформой (напр., этот стол, этого стола...). Два слова х (стол) и у (какаду) относятся к одному роду, если для любой формы х¹ слова х и любой словоформы г, согласуемой с х¹, найдётся форма у¹ слова у, согласуемая с г (этот какаду, этого какаду), причём обратное верно для любой формы у¹ слова у. Эта М. даёт возможность не только однозначно решать спорные вопросы, на и сопоставить категорию рода с категорией части речи (род оказывается "вложенным" в часть речи); установить, какие категории др. частей речи устроены изоморфно (аналогично) с родом существительного (напр., категория глагольного управления); сравнить категорию рода в рус. и др. индоевропейских языках с категорией грамматич. класса, напр, в языках банту. Т. о., аналитич. М. находят применение в типологии языков.

Если исходный материал-категории и элементарные смысловые структуры, а "выход" - нек-рые формальные построения, то М. называется синтетической, или порождающей (такие М. называют также порождающими грамматиками, см. Грамматика формальная, Математическая лингвистика). Порождающая М. воплощает в себе нек-рую гипотезу о внутреннем (недоступном прямому наблюдению) строении языка, к-рая затем проверяется путём сравнения множества выводимых в М. объектов с реальными языковыми фактами. Это позволяет классифицировать и оценивать М. по степени соответствия фактам языка и по степени раскрытия интуитивно ощущаемых закономерностей языка ("объяснительной силе"). Т. к. каждая М. описывает не весь язык, а нек-рую его область или даже отд. категорию, то точное описание языка предполагает одновременное использование разных М., относящихся как к одной области языка (напр., неск. дополняющих друг друга М. категорий части речи, падежа, рода), так и к разным областям.

Лит.: Апресян Ю. Д., Идеи и методы современной структурной лингвистики, М., 1966; Ревзин И. И-, Метод моделирования и типология славянских языков, М., 1967; Маркус С., Теоретико-множественные модели языков, пер. с англ., М., 1970; X о м с к и й Н., Аспекты теории синтаксиса, пер. с англ., М., 1972.

И. И. Ревзин.

МОДЕЛИЗМ спортивный, конструирование и постройка действующих и стендовых моделей летательных аппаратов, автомобилей, судов, локомотивов и др. средств транспорта для спортивных соревнований и демонстраций. См. Авиамоделизм, Автомодельный спорт, Судомодельный спорт.

МОДЕЛИРОВАНИЕ, исследование объектов познания на их моделях, построение и изучение моделей реально существующих предметов и явлений (живых и неживых систем, инженерных конструк-ций, разнообразных процессов - физических, химических, биологических, социальных) и конструируемых объектов (для определения, уточнения их характеристик, рационализации способов их построения и т. п.).

М. как познавательный приём неотделимо от развития знания. По существу, М. как форма отражения действительности зарождается в античную эпоху одновременно с возникновением научного познания. Однако в отчётливой форме (хотя без употребления самого термина) М. начинает широко использоваться в эпоху Возрождения; Брунеллески, Микеланджело и др. итал. архитекторы и скульпторы пользовались моделями проектируемых ими сооружений; в теоретич. же работах Г. Галилея и Леонардо да Винчи не только используются модели, но и выясняются пределы применимости метода М. Н.Ньютон пользуется этим методом уже вполне осознанно, а в 19-20 вв. трудно назвать область науки или её приложений, где М. не имело бы существ, значения; исключительно большую методологич. роль сыграли в этом отношении работы Кельвина, Дж. Максвелла, Ф. А. Кекуле, А. М. Бутлерова и др. физиков и химиков - именно эти науки стали, можно сказать, классич. "полигонами" методов М. Появление же первых электронных вычислит, машин (Дж. Нейман, 1947) и формулирование осн. принципов кибернетики (Н. Винер, 1948) привели к поистине универсальной значимости новых методов - как в абстрактных областях знания, так и в их приложениях. М. ныне приобрело общенаучный характер и применяется в исследованиях живой и неживой природы, в науках о человеке и обществе (см. Модели в биологии, Модели в экономике, Модели в языкознании, Ядерные модели).

Единая классификация видов М. затруднительна в силу многозначности понятия -"модель" в науке и технике. Её можно проводить по различным основаниям: по характеру моделей (т. е. по средствам М.); по характеру моделируемых объектов; по сферам приложения М. (М. в технике, в физических науках, в химии, М. процессов живого, М. психики и т. п.) и его уровням ("глубине"), начиная, например, с выделения в физике М. на микроуровне (М. на уровнях исследования, касающихся элементарных частиц, атомов, молекул). В связи с этим любая классификация методов М. обречена на неполноту, тем более, что терминология в этой области опирается не столько на "строгие" правила, сколько на языковые, научные и практич. традиции, а ещё чаще определяется в рамках конкретного контекста и вне его никакого стандартного значения не имеет (типичный пример - термин "кибернетическое" М.).

Предметным наз. М., в ходе к-рого исследование ведётся на модели, воспроизводящей осн. геометрич., физич., динамич. и функциональные характеристики "оригинала". На таких моделях изучаются процессы, происходящие в оригинале - объекте исследования или разработки (изучение на моделях свойств строит, конструкций, различных механизмов, транспортных средств и т. п.). Если модель и моделируемый объект имеют одну и ту же физич. природу, то говорят о физическом М. (см. Моделирование физическое). Явление (система, процесс) может исследоваться и путём опытного изучения к.-л. явления иной физич. природы, но такого, что оно описывается теми же математич. соотношениями, что и моделируемое явление. Напр., механич. и электрич. колебания описываются одними и теми же дифференциальными уравнениями; поэтому с помощью механич. колебаний можно моделировать электрические и наоборот. Такое "предметно-математическое" М. широко применяется для замены изучения одних явлений изучением других явлений, более удобных для лабораторного исследования, в частности потому, что они допускают измерение неизвестных величин (см. Моделирование аналоговое). Так, электрическое М. позволяет изучать на электрич. моделях механич., гидродинамич., акустич. и др. явления. Электрич. М. лежит в основе т. н. аналоговых вычислительных машин.

При знаковом М. моделями служат знаковые образования к.-л. вида: схемы, графики, чертежи, формулы, графы, слова и предложения в нек-ром алфавите (естеств. или искусств, языка) (см. Знак, Семиотика).

Важнейшим видом знакового М. является математическое (логико-математич.) М., осуществляемое средствами языка математики и логики (см. Математическая модель). Знаковые образования и их элементы всегда рассматриваются вместе с определ. преобразованиями, операциями над ними, которые выполняет человек или машина (преобразования математич., логич., химич. формул, преобразования состояний элементов цифровой машины, соответствующих знакам машинного языка, и др.). Совр. форма "материальной реализации" знакового (прежде всего, математического) М.- это М. на цифровых электронных вычислительных машинах, универсальных и специализированных. Такие машины - это своего рода "чистые бланки", на к-рых в принципе можно зафиксировать описание любого процесса (явления) в виде его программы, т. е. закодированной на машинном языке системы правил, следуя к-рым машина может "воспроизвести" ход моделируемого процесса.

Действия со знаками всегда в той или иной мере связаны с пониманием знаковых образований и их преобразований: формулы, матем. уравнения и т. п. выражения применяемого при построении модели науч. языка определ. образом интерпретируются (истолковываются) в понятиях той предметной области, к к-рой относится оригинал (см. Интерпретация). Поэтому реальное построение знаковых моделей или их фрагментов может заменяться мысленно-наглядным представлением знаков и (или) операций над ними. Эту разновидность знакового М. иногда наз. мысленным М. Впрочем, этот термин часто применяют для обозначения "интуитивного" М., не использующего никаких чётко фиксированных знаковых систем, а протекающего на уровне "модельных представлений". Такое М. есть непременное условие любого познавательного процесса на его начальной стадии.

По характеру той стороны объекта, к-рая подвергается М., уместно различать М. структуры объекта и М. его поведения (функционирования протекающих в нем процессов и т. п.). Это различение сугубо относительно для химии или физики, но оно приобретает чёткий смысл в науках о жизни, где различение структуры и функции систем живого принадлежит к числу фундаментальных методологич. принципов исследования, и в кибернетике, делающей акцент на М. функционирования изучаемых систем. При "кибернетическом" М. обычно абстрагируются от структуры системы, рассматривая её как "чёрный ящик", описание (модель) к-рого строится в терминах соотношения между состояниями его "входов" и "выходов" ("входы" соответствуют внешним воздействиям на изучаемую систему, "выходы" - её реакциям на них, т. е. поведению).

Для ряда сложных явлений (напр., турбулентности, пульсаций в областях отрыва потока и т. п.) пользуются стохастическим М., основанным на установлении вероятностей тех или иных событий. Такие модели не отражают весь ход отдельных процессов в данном явлении, носящих случайный характер, а определяют нек-рый средний, суммарный результат.

Понятие М. является гносеологич. категорией, характеризующей один из важных путей познания. Возможность М., т. е. переноса результатов, полученных в ходе построения и исследования моделей, на оригинал, основана на том, что модель в определённом смысле отображает (воспроизводит, моделирует) к.-л. его черты; при этом такое отображение (и связанная с ним идея подобия) основано, явно или неявно, на точных понятиях изоморфизма или гомоморфизма (или их обобщениях) между изучаемым объектом и нек-рым другим объектом "оригиналом" и часто осуществляется путём предварительного исследования (теоретического или экспериментального) того и другого. Поэтому для успешного М. полезно наличие уже сложившихся теорий исследуемых явлений, или хотя бы удовлетворительно обоснованных теорий и гипотез, указывающих предельно допустимые при построении моделей упрощения. Результативность М. значительно возрастает, если при построении модели и переносе результатов с модели на оригинал можно воспользоваться нек-рой теорией, уточняющей связанную с используемой процедурой М. идею подобия. Для явлений одной и той же физич. природы такая теория, основанная на использовании понятия размерности физич. величин, хорошо разработана (см. Моделирование физическое. Подобия теория). Но для М. сложных систем и процессов, изучаемых, напр., в кибернетике, аналогичная теория ещё не разработана, чем и обусловлено интенсивное развитие теории больших систем - общей теории построения моделей сложных динамич. систем живой природы, техники и социально-экономич. сферы.

М. всегда используется вместе с др. общенауч. и спец. методами. Прежде всего М. тесно связано с экспериментом. Изучение к.-л. явления на его модели (при предметном, знаковом М., М. на ЭВМ) можно рассматривать как особый вид эксперимента: "модельный эксперимент", отличающийся от обычного ("прямого") эксперимента тем, что в процесс познания включается "промежуточное звено" - модель, являющаяся одновременно и средством, и объектом экспериментального исследования, заменяющим изучаемый объект. Модельный эксперимент позволяет изучать такие объекты, прямой эксперимент над к-рыми затруднён, экономически невыгоден, либо вообще невозможен в силу тех или иных причин [М. уникальных (напр., гидротехнич.) сооружений, сложных пром. комплексов, экономич. систем, социальных явлений, процессов, происходящих в космосе, конфликтов и боевых действий и др.].

Исследование знаковых (в частности, матем.) моделей также можно рассматривать как нек-рые эксперименты ("эксперименты на бумаге", умственные эксперименты). Это становится особенно очевидным в свете возможности их реализации средствами электронной вычислит, техники. Один из видов модельного эксперимента - модельно-кибернетич. эксперимент, в ходе к-рого вместо " реального" экспериментального оперирования с изучаемым объектом находят алгоритм (программу) его функционирования, который и оказывается своеобразной моделью поведения объекта. Вводя этот алгоритм в цифровую ЭВМ и, как говорят, "проигрывая" его, получают информацию о поведении оригинала в определ. среде, о его функциональных связях с меняющейся "средой обитания".

Т. о., можно прежде всего различать "материальное" (предметное) и "идеальное" М.; первое можно трактовать как "экспериментальное", второе - как "теоретическое" М., хотя такое противопоставление, конечно, весьма условно не только в силу взаимосвязи и обоюдного влияния этих видов М., но и наличия таких "гибридных" форм, как "мысленный эксперимент". "Материальное" М. подразделяется, как было сказано выше, на физич. и предметно-математич. М., а частным случаем последнего является аналоговое М. Далее, "идеальное" М. может происходить как на уровне самых общих, быть может даже не до конца осознанных и фиксированных, "модельных представлений", так и на уровне достаточно детализированных знаковых систем; в первом случае говорят о мысленном (интуитивном) М., во втором - о знаковом М. (важнейший и наиболее распространённый вид его - логико-матем. М.). Наконец, М. на ЭВМ (часто именуемое "кибернетическим") является "предметно-математич. по форме, знаковым по содержанию".

М. необходимо предполагает использование абстрагирования и идеализации. Отображая существ, (с точки зрения цели исследования) свойства оригинала и отвлекаясь от несущественного, модель выступает как специфич. форма реализации абстракции, т. е. как нек-рый абстрактный идеализированный объект. При этом от характера и уровней лежащих в основе М. абстракций и идеализации в большой степени зависит весь процесс переноса знаний с модели на оригинал; в частности, существ, значение имеет выделение трёх уровней абстракции, на к-рых может осуществляться М.: уровня потенциальной осуществимости (когда упомянутый перенос предполагает отвлечение от ограниченности познавательно-практической деятельности человека в пространстве и времени, см. Абстракции принцип), уровня "реальной" осуществимости (когда этот перенос рассматривается как реально осуществимый процесс, хотя, быть может, лишь в некоторый будущий период человеч. практики) и уровня практич. целесообразности (когда этот перенос не только осуществим, но и желателен для достижения нек-рых конкретных познавательных или практич. задач).

На всех этих уровнях, однако, приходится считаться с тем, что М. данного оригинала может ни на каком своём этапе не дать полного знания о нём. Эта черта М. особенно существенна в том случае, когда предметом М. являются сложные системы, поведение к-рых зависит от значит, числа взаимосвязанных факторов различной природы. В ходе познания такие системы отображаются в различных моделях, более или менее оправданных; при этом одни из моделей могут быть родственными друг другу, другие же могут оказаться глубоко различными. Поэтому возникает проблема сравнения (оценки адекватности) разных моделей одного и того же явления, что требует формулировки точно определяемых критериев сравнения. Если такие критерии основываются на экспериментальных данных, то возникает дополнительная трудность, связанная с тем, что хорошее совпадение заключений, к-рые следуют из модели, с данными наблюдения и эксперимента ещё не служит однозначным подтверждением верности модели, т. к. возможно построение др. моделей данного явления, к-рые также будут подтверждаться эмпирич. фактами. Отсюда - естественность ситуации, когда создаются взаимодополняющие или даже противоречащие друг другу модели явления; противоречия могут "сниматься" в ходе развития науки (и затем появляться при М. на более глубоком уровне). Напр., на определ. этапе развития теоретич. физики при М. физич. процессов на "классическом" уровне использовались модели, подразумевающие несовместимость корпускулярных и волновых представлений; эта "несовместимость" была "снята" созданием квантовой механики, в основе к-рой лежит тезис о корпускулярно-волновом дуализме, заложенном в самой природе материи.

Другим примером такого рода моделей может служить М. различных форм деятельности мозга. Создаваемые модели интеллекта и психич. функций - напр., в виде эвристических программ для ЭВМ - показывают, что М. мышления как информационного процесса возможно в различных аспектах (дедуктивном - формально-логическом, см. Дедукция; индуктивном - см. Индукция; нейтрол отческом, эвристическом - см. Эвристика), для "согласования" к-рых необходимы дальнейшие логич., психологич., физиологич. эволюционно-генетич. и модельно-кибернетич. исследования.

М. глубоко проникает в теоретич. мышление. Более того, развитие любой науки в целом можно трактовать - в весьма общем, но вполне разумном смысле, - как "теоретическое М.". Важная позна-ват. функция М. состоит в том, чтобы служить импульсом, источником новых теорий. Нередко бывает так, что теория первоначально возникает в виде модели, дающей приближённое, упрощённое объяснение явления, и выступает как первичная рабочая гипотеза, к-рая может перерасти в "предтеорию" - предшественницу развитой теории. При этом в процессе М. возникают новые идеи и формы эксперимента, происходит открытие ранее неизвестных фактов. Такое "переплетение" теоретич. и экспериментального М. особенно характерно для развития физич. теорий (напр., молекулярно-кинетич. или теории ядерных сил).

М.- не только одно из средств отображения явлений и процессов реального мира, но и - несмотря на описанную выше его относительность - объективный практич. критерий проверки истинности наших знаний, осуществляемой непосредственно или с помощью установления их отношения к другой теории, выступающей в качестве модели, адекватность к-рой считается практически обоснованной. Применяясь в органич. единстве с др. методами познания, М. выступает как процесс углубления позна ния, его движения от относительно бедных информацией моделей к моделям более содержательным, полнее раскрывающим сущность исследуемых явлений действительности.

При М. более или менее сложных систем обычно применяют различные виды М. Примеры см. ниже в разделах о М. энергосистем и М. химич. реактивов.

Лит.: Гутенмахер Л. И., Электрические модели, М.- Л., 1949; К и р п и ч е в М. В., Теория подобия, М., 1953; Ляпунов А. А., О некоторых общих вопросах кибернетики, в кн.: Проблемы кибернетики, в. 1, М., 1958; Вальт Л. О., Познавательное значение модельных представлений в физике, Тарту, 1963; Г л у ш к о в В. М., Гносеологическая природа информационного моделирования, "Вопросы философии", 1963, № 10; Н о в и к И. Б., О моделировании сложных систем, М., 1965; Моделирование как метод научного исследования, М., 1965; Веников В. А., Теория подобия и моделирование применительно к задачам электроэнергетики, М., 1966; Ш т о ф ф В. А., Моделирование и философия, М.- Л., 1966; Чавчанидзе В. В., Гельман О. Я., Моделирование в науке и технике, М., 1966; Г а с т е в Ю. А., О гносеологических аспектах моделирования, в кн.: Логика и методология науки, М., 1967; Бусленко Н.П., Моделирование сложных систем, М., 1968; Морозов К. Е., Математическое моделирование в научном познании, М., 1969; Проблемы кибернетики, М., 1969; У е м о в А. И., Логические основы метода моделирования, М-, 1971; Налимов В. В., Теория эксперимента, М., 1971; Бирюков Б. В., Г е л л е р Е. С., Кибернетика в гуманитарных науках, М., 1973.

Б. В. Бирюков, Ю. А. Гастев, Е. С. Геллер.

Моделирование энергосистем. Поскольку энергосистема содержит множество отдельных элементов, соединённых определённым образом, то и модель системы должна воспроизводить все подлежащие исследованию отношения и связи внутри объекта, касающиеся взаимоотношений всех элементов или выделяемых групп элементов, рассматриваемых в этом случае как подсистемы. При М. энергосистем различают случаи, когда подобие устанавливается для всех элементов, влияющих на изучаемые функции, проявляющиеся как во времени, так и в пространстве (полное подобие), и случаи, когда устанавливается подобие только части процессов или изучаемых функций системы (неполное подобие), например, когда изучается изменение параметров процесса только во времени без рассмотрения соответствующих изменений в пространстве. Полное подобие и соответственно полное М. энергосистем реализуется преимущественно при изучении систем или отдельных элементов, действие к-рых существенно связано с распространением электромагнитной энергии в пространстве (конструирование и изучение работы таких элементов системы, как электрич. машины, трансформаторы, волноводы, протяжённые линии электропередачи и т. д.). Неполное М. обычно реализуется при изучении режимов энергетич. систем.

При физическом М. изучение конкретной энергосистемы заменяется изучением подобной энергосистемы др. размера (мощности, напряжения, частоты тока, протяжённости линий электропередачи, габаритов), но имеющей ту же физич. природу важнейших (в условиях данной задачи) элементов модели. В СССР и за рубежом широко распространены физич. модели энергосистем, содержащие электрич. машины, к-рые изображают в уменьшенном по мощности (до Vioooo-Vaoooo) и напряжению С'/юоо) масштабе реальную энергосистему с её регулирующими, защитными и др. устройствами. Физич. модели применяются для исследований электроэнер-гетич. систем в целом, линий электропередачи (обычно на повышенной частоте), устройств регулирования и защиты и т. д.

Физическое М. энергосистем применяется преимущественно для изучения и проверки осн. теоретич. положений, уточнения схем замещения и расчётных формул, проверки действия аппаратов, установок, новых схем защиты и способов передачи энергии, а также для определения общих характеристик электромагнитных, электромеханических и волновых процессов в системах, не имеющих точного математич. описания или находящихся в необычных условиях.

Примером аналогового М. энергосистем могут служить расчётные столы постоянного или переменного тока, иначе называемые расчётными моделями, на к-рых набор активных и реактивных сопротивлений изображает электрич. сеть, а источники питания - генераторы (станции), работающие в энергосистеме,- заменяются регулируемыми трансформаторами (модель переменного тока) или источниками постоянного тока, напр, аккумуляторами (модель постоянного тока). Действит. физич. процессы, происходящие в исследуемой системе, на такой модели не воспроизводятся. Сопротивления и эдс, составляющие в соответствии с принятыми расчётными уравнениями схему замещения изучаемой системы, могут изменяться (вручную или автоматически), отражая тем самым реальные изменения, происходящие в изучаемой системе. Значения электрич. напряжений, сил токов и мощностей, измеряемых в такой модели (схеме замещения) с определёнными допущениями, характеризуют реальный процесс в энергосистеме.

При М. энергосистем с использованием аналоговых вычислительных машин (напр., МН-7, МН-14, МПТ-10 и т. п.) также воспроизводятся нек-рые процессы, имеющие природу, отличную от природы процессов в энергосистеме, но описываемые формально точно такими же, как для энергосистемы, дифференциальными уравнениями.

Разновидностью аналоговых моделей являются аналого-физич. модели и цифроаналоговые или гибридные модели, объединяющие в одной установке аналоговую и физическую модели, аналоговую модель и элементы ЦВМ или специализированную ЦВМ. Существуют специализированные аналоговые модели, к-рые могут работать как в действительном, так и изменённом масштабе времени и применяться при быстром прогнозировании процессов, существенном для управления энергосистемой.

Аналоговое М. применяется для расчётов при таких схемах замещения, для к-рых нет надобности проводить проверку их физич. адекватности реальной системе, но необходимо исследовать влияние изменения отд. параметров элементов и начальных условий процессов в значительном диапазоне.

Математическое М. энергосистем практически реализуется составлением приспособленной для решения на ЦВМ системы уравнений, представленных в виде алгоритмов и программ, с помощью к-рых на ЦВМ получают численные характеристики процессов (в виде графика или таблицы), происходящих в изучаемой энергосистеме.

Математическое М. энергосистем широко применяется в проектных и эксплуатационных расчётах, оперирующих с заданными параметрами, изменяемыми при изучении конкурирующих вариантов, что особенно важно при технико-экономич. анализе, оптимизации, распределении токов, мощностей и напряжений в сложных энергосистемах. Отсутствие физич. наглядности в получаемых результатах заставляет особенно остро ставить вопрос о соответствии расчётов и действительности, т. е. об апробации составленных программ. Для выполнения программ, по к-рым ведутся расчёты энергосистем на ЦВМ, наиболее удобным является алгоритмич. язык фортран, применяемый в мировой энергетич. практике.

Лит.: Тетельбаум И. М., Электрическое моделирование, М., 1959; А з а р ь е в Д. И., Математическое моделирование электрических систем, М.- Л., 1962', Горушкин В. И., Выполнение энергетических расчетов с помощью вычислительных машин, М., 1962; Вопросы теории и применения математического моделирования, М., 1965; Применение аналоговых вычислительных машин в энергетических системах, 2 изд., М., 1970.

В. А. Веников.

Моделирование химических реакторов применяется для предсказания результатов протекания химико-технологических процессов при заданных условиях в аппаратах любого размера. Попытки осуществить масштабный переход от реактора малого размера к промышленному реактору при помощи физического М. оказались безуспешными из-за несовместимости условий подобия химич. и физич. составляющих процесса (влияние физич. факторов на скорость химич. превращения в реакторах разного размера существенно различно). Поэтому для масштабного перехода преимущественно использовались эмпирич. методы: процессы исследовались в последовательно увеличивающихся реакторах (лабораторная, укрупнённая, опытная, полупромышленная установки, пром. реактор).

Исследовать реактор в целом и осуществить масштабный переход позволило математическое М. Процесс в реакторе складывается из большого числа химич. и физич. взаимодействий на различных структурных уровнях - молекула, макрообласть, элемент реактора, реактор. В соответствии со структурными уровнями процесса строится многоступенчатая математич. модель реактора. Первому уровню (собственно химич. превращению) соответствует кинетич. модель, ур-ния которой описывают зависимость скорости реакции от концентрации реагирующих веществ, температуры и давления во всей области их изменений, охватывающей практические условия проведения процесса. Характер следующих структурных уровней зависит от типа реактора. Напр., для реактора с неподвижным слоем катализатора второй уровень - процесс, протекающий на одном зерне катализатора, когда существенны перенос вещества и перенос тепла в пористом зерне. Каждый последующий структурный уровень включает все предыдущие как составные части, напр., математич. описание процесса на одном зерне катализатора включает как уравнения переноса, так и кинетические. Модель третьего уровня включает, кроме того, уравнения переноса вещества, тепла и импульса в слое катализатора и т. д. Модели реакторов др. типов (с псевдоожиженным слоем, колонного типа с суспендированным катализатором и др.) также имеют иерархическую структуру.

С помощью математич. М. выбираются оптимальные условия проведения процесса, определяются необходимое количество катализатора, размеры и форма реактора, параметрич. чувствительность процесса к начальным и краевым условиям, переходные режимы, а также исследуется устойчивость процесса. В ряде случаев сначала проводится теоретич. оптимизация - определяются оптимальные условия, при к-рых выход полезного продукта наибольший, независимо от того, смогут ли они быть осуществлены, а затем, на втором этапе, выбирается инженерное решение, позволяющее наилучшим образом приблизиться к теоретич. оптимальному режиму с учётом экономич. и др. показателей. Для осуществления найденных режимов и нормальной работы реактора необходимо обеспечить равномерное распределение реакц. смеси по сечению реактора и полноту смешения потоков, различающихся составом и темп-рой. Эти задачи решаются физич. (аэрогидродинамич.) М. выбранной конструкции реактора.

М. Г. Слинько.

МОДЕЛИРОВАНИЕ АНАЛОГОВОЕ, один из важнейших видов моделирования, основанный на аналогии (в более точных терминах - изоморфизме) явлений, имеющих различную физич. природу, но описываемых одинаковыми матем. (дифференциальными, алгебраическими или к.-л. другими) уравнениями.

Простой пример - две системы, первая из к-рых имеющая механич. природу, состоит из оси, передающей вращение через пружину и маховик, погружённый частично в вязкую тормозящую жидкость, валу, жёстко связанному с маховиком. Вторая система - электрическая - состоит из источника электродвижущей силы, соединённого через катушку индуктивности, конденсатор и активное сопротивление со счётчиком электрич. энергии. Если подобрать значения индуктивности, ёмкости и сопротивления так, чтобы они определённым образом соответствовали упругости пружины, инерции маховика и трению жидкости, то эти системы обнаружат структурное и функциональное сходство (даже тождество), выражаемое, в частности, в том, что они будут описываться одним и тем же дифференциальным уравнением с постоянными коэффициентами вида

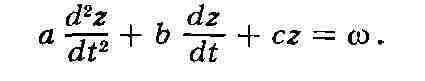
Это уравнение может служить "теоретич. моделью" обеих систем, любая же из них - "экспериментальной моделью" этого уравнения и "аналоговой моделью" друг друга. Эта аналогия лежит в основе электрич. моделирования механич. систем; электрич. модели гораздо более удобны для экспериментального исследования, нежели моделируемые механические. Другой традиционной областью применения М. а. является исследование процессов теплопроводности, основанное на электротепловой и гидротепловой аналогиях (в первой из них аналогами температурного поля в твёрдом теле и теплоёмкости служат соответственно поле электрич. потенциала в электропроводной среде и ёмкости нек-рых конденсаторов, во второй - темп-pa моделируется уровнем воды в вертикальных стеклянных сосудах, образующих гидравлич. модель, теплоёмкость элементарного объёма -площадью поперечного сечения этих сосудов, а тепловое сопротивление - гидравлич. сопротивлением соединяющих сосуды трубок). Для исследования лучистого (радиационного) переноса тепла часто применяют метод светового моделирования, при к-ром потоки теплового излучения заменяют подобными им потоками излучения светового. Таким путём определяют угловые коэффициенты излучения, а если оптические свойства (степень черноты и поглощательные способности) соответствующих поверхностей у модели и натуры тождественны, то и распределение тепловых потоков по поверхностям, входящим в систему лучистого теплообмена.

До создания цифровых электронных вычислительных машин в конце 1940-х гг. М. а. было основным способом "предметно-математич. моделирования" (см. об этом в ст. Моделирование) многих процессов, связанных с распространением электромагнитных и звуковых волн, диффузии газов и жидкостей, движения и фильтрации жидкостей в пористых средах, кручения стержней и др. (в связи с чем его часто называли тогда просто "математическим моделированием"), причём для каждой конкретной задачи моделирования строилась своя "сеточная" модель (основными её элементами служили соединённые в плоскую сеточную схему электрич. сопротивления различных видов), а аналоговые вычислительные машины позволяли проводить М. а. целых классов однородных задач. В настоящее время значение М. а. значительно уменьшилось, поскольку моделирование на ЭВМ имеет большие преимущества перед ним в отношении точности моделирования и универсальности. В достаточно фиксированных и специальных задачах свои преимущества (простота, а тем самым и дешевизна технич. выполнения) имеет и М. а. Употребительно также и совместное использование обоих методов (см. Гибридная вычислительная система).

МОДЕЛИРОВАНИЕ ФИЗИЧЕСКОЕ, вид моделирования, к-рый состоит в замене изучения нек-рого объекта или явления экспериментальным исследованием его модели, имеющей ту же физич. природу.

В науке любой эксперимент, производимый для выявления тех или иных закономерностей изучаемого явления или для проверки правильности и границ применимости найденных теоретич. путём результатов, по существу представ-

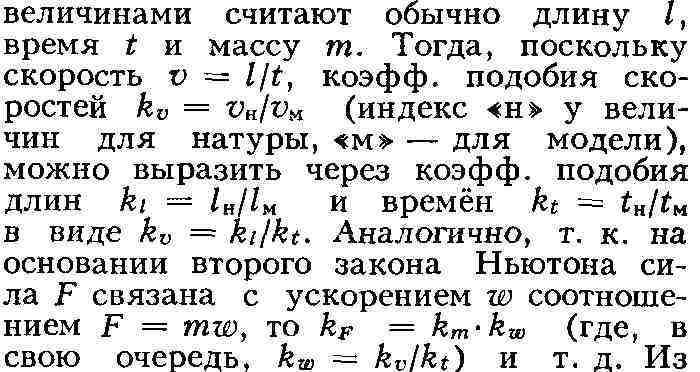
ляет собою моделирование, т. к. объектом эксперимента является конкретная модель, обладающая необходимыми фи-зич. свойствами, а в ходе эксперимента должны выполняться основные требования, предъявляемые к М. ф. В технике М. ф. используется при проектировании и сооружении различных объектов для определения на соответствующих моделях тех или иных свойств (характеристик) как объекта в целом, так и отдельных его частей. К М. ф. прибегают не только по экономич. соображениям, но и потому, что натурные испытания очень трудно или вообще невозможно осуществить, когда слишком велики (малы) размеры натурного объекта или значения других его характеристик (давления, темп-ры, скорости протекания процесса и т. п.).

В основе М. ф. лежат подобия теория и размерностей анализ. Необходимыми условиями М. ф. являются геометрич. подобие (подобие формы) и физич. подобие модели и натуры: в сходственные моменты времени и в сходственных точках пространства значения переменных величин, характеризующих явления для натуры, должны быть пропорциональны значениям тех же величин для модели. Наличие такой пропорциональности позволяет производить пересчёт экспериментальных результатов, получаемых для модели, на натуру путём умножения каждой из определяемых величин на постоянный для всех величин данной размерности множитель - коэффициент подобия.

Поскольку физич. величины связаны определёнными соотношениями, вытекающими из законов и ур-ний физики, то, выбрав нек-рые из них за основные, можно коэфф. подобия для всех других производных величин выразить через коэфф. подобия величин, принятых за основные. Напр., в механике основными наличия таких связей вытекает, что для данного физического явления некоторые безразмерные комбинации величин, характеризующих это явление, должны иметь для модели и натуры одно и то же значение. Эти безразмерные комбинации физич. величин наз. критериями подобия. Равенство всех критериев подобия для модели и натуры является необходимым условием М. ф. Однако добиться этого равенства можно не всегда, т. к. не всегда удаётся одновременно удовлетворить всем критериям подобия.

Чаще всего к М. ф. прибегают при исследовании различных механических (включая гидроаэромеханику и механику деформируемого твёрдого тела), тепловых и электродинамич. явлений. При этом число и вид критериев подобия для каждого моделируемого явления зависит от его природы и особенностей. Так, напр., для задач динамики точки (или системы материальных точек), где все ур-ния вытекают из второго закона Ньютона, критерием подобия является чи-

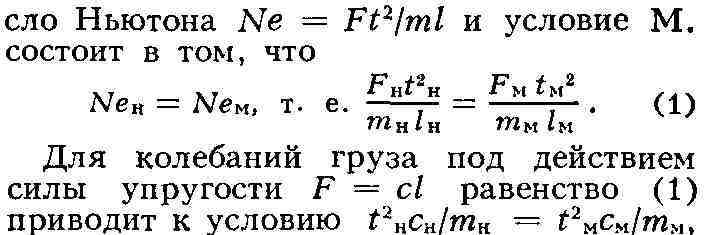
что, напр., позволяет по периоду колебаний модели определить период колебаний натуры; при этом явление не зависит от линейного масштаба (от амплитуды колебаний). Для движения в поле тяго-

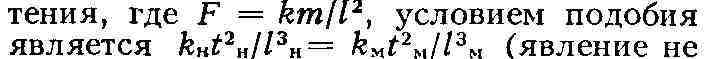
зависит от масс). При движении в одном и том же поле тяготения, напр. Солнца, k_Н = k п,, и полученное соотношение даёт третий закон Кеплера для периода обращения. Отсюда, считая одну из планет "моделью", можно, напр., найти период обращения любой др. планеты, зная её расстояние от Солнца.

Для непрерывной среды при изучении её движения число критериев подобия возрастает, что часто значительно усложняет проблему М. ф. В гидроаэромеханике основными критериями подобия являются Рейнолъдса число Re, Маха, число М, Фруда число Fr, Эйлера число Ей, а для нестационарных (зависящих от времени) течений ещё и Струхаля число St. При М. ф. явлений, связанных с переносом тепла в движущихся жидкостях и газах или с физико-химич. превращениями компонентов газовых потоков и др., необходимо учитывать ещё ряд дополнит, критериев подобия.

Создаваемые для гидроаэродинамич. моделирования экспериментальные установки и сами модели должны обеспечивать равенство соответствующих критериев подобия у модели и натуры. Обычно это удаётся сделать в случаях, когда для течения в силу его особенностей сохраняется лишь один критерий подобия. Так, при М. ф. стационарного течения несжимаемой вязкой жидкости (газа) определяющим будет параметр Re и необходимо выполнить одно условие

При аэродинамич. исследованиях увеличивать и_м в этом случае нельзя (нарушится условие несжимаемости), но можно увеличить р„, используя аэродинамические трубы закрытого типа, в к-рых циркулирует сжатый воздух.

Когда при М. ф. необходимо обеспечить равенство нескольких критериев, возникают значит, трудности, часто непреодолимые, если только не делать модель тождественной натуре, что фактически означает переход от М. ф. к натурным испытаниям. Поэтому на практике нередко прибегают к приближённому моделированию, при к-ром часть процессов, играющих второстепенную роль, или совсем не моделируется, или моделируется приближённо. Такое М. ф. не позволяет найти прямым пересчётом значения тех характеристик, к-рые не отвечают условиям подобия, и их определение требует соответствующих дополнит, исследований. Напр., при М. ф. установившихся течений вязких сжимаемых газов необходимо обеспечить равенство критериев Re и М и безразмерного числа и = Cp/Cv (Ср и Сv - удельные теплоёмкости газа при постоянном давлении и постоянном объёме соответственно), что в общем случае сделать невозможно. Поэтому, как правило, обеспечивают для модели и натуры лишь равенство числа М, а влияние на определяемые параметры различий в числах Re и Y. исследуют отдельно или теоретически, или с помощью др. экспериментов, меняя в них в достаточно широких пределах значения Re и и.

Для твёрдых деформируемых тел особенности М. ф. тоже зависят от свойств этих тел и характера рассматриваемых задач. Так, при моделировании равновесия однородных упругих систем (конструкций), механич. свойства к-рьцс определяются модулем упругости (модулем Юнга) Е и безразмерным Пуассона коэффициентом v, должны выполняться 3 условия подобия:

летворять первым двум из условий (3), что практически обычно неосуществимо. В большинстве случаев модель изготовляется из того же материала, что и

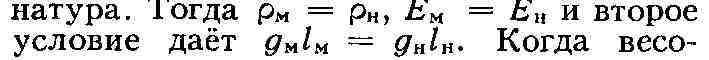
вые нагрузки существенны, для выполнения этого условия прибегают к т. н. центробежному моделированию, т. е. помещают модель в центробежную машину, где искусственно создаётся приближённо однородное силовое поле, по-

дель будет меньше требуемой этим условием, т. е. М. ф. не будет пол-ным и модель, как недогруженная, будет прочнее натуры. Это обстоятельство тоже можно учесть или теоретич. расчётом или дополнит, экспериментами.

Одним из видов М. ф., применяемым к твёрдым деформируемым телам, является поляризационно-оптический метод исследования напряжений, основанный на свойстве ряда изотропных прозрачных материалов становиться под действием нагрузок (т. е. при деформации) анизотропными, что позволяет исследовать распределение напряжений в различных деталях с помощью их моделей из прозрачных материалов.

При М. ф. явлений в др. непрерывных средах соответственно изменяются вид и число критериев подобия. Так, для пластичных и вязкопластичных сред в число этих критериев наряду с параметрами Фруда, Струхаля и модифицированным параметром Рейнольдса входят параметры Лагранжа, Стокса, Сен-Венана и т. д. При изучении процессов теплообмена тоже широко используют М. ф. Для случая переноса тепла конвекцией определяющими критериями подобия являются

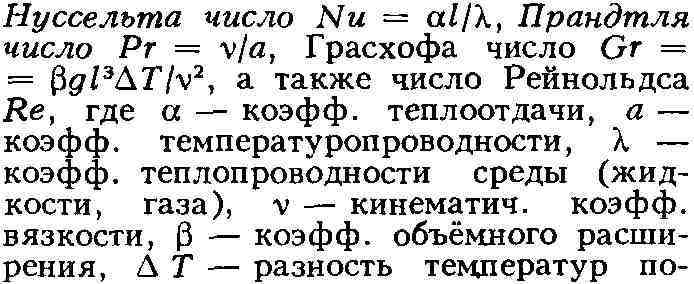
верхности тела и среды. Обычно целью М. ф. является определение коэфф. теплоотдачи, входящего в критерий Nu, для чего опытами на моделях устанавливают зависимость Nu от других критериев. При этом в случае вынужденной конвекции (напр., теплообмен при движении жидкости в трубе) становится несущественным критерий Gr, а в случае свободной конвекции (теплообмен между телом и покоящейся средой) - критерий Re. Однако к значит, упрощениям процесса М. ф. это не приводит, особенно из-за критерия Рг, являющегося физич. константой среды, что при выполнении условия Рг_а = Рг_Ипрактически исключает возможность использовать на модели среду, отличную от натурной. Дополнит, трудности вносит и: то, что физич. характеристики среды зависят от её темп-ры. Поэтому в большинстве практически важных случаев выполнить все условия подобия не удаётся; приходится прибегать к приближённому моделированию. При этом отказываются от условия равенства критериев, мало влияющих на процесс, а др. условиям (напр., подобие физич. свойств сред, участвующих в теплообмене) удовлетворяют лишь в среднем. На практике часто используют также т. н. метод локального теплового моделирования, идея к-рого заключается в том, что условия подобия процессов для модели и натуры выполняются только в той области модели, где исследуется процесс теплообмена. Напр., при исследовании теплоотдачи в системе однотипных тел (шаров, труб) в теплообмене на модели может участвовать лишь одно тело, на к-ром выполняют измерения, а остальные служат для обеспечения геометрич. подобия модели и натуры. В случаях переноса тепла теплопроводностью (кондукцией) критериями

ное время. При М. ф. таких процессов теплообмена удаётся в широких пределах изменять не только размеры модели, но и темп протекания процесса.

Однако чаще для исследования процессов переноса тепла теплопроводностью применяют моделирование аналоговое.

Электродинамическое моделирование применяется для исследования электромагнитных и электро-механич. процессов в электрич. системах. Электродинамич. модель представляет собой копию (в определённом масштабе) натурной электрич. системы с сохранением физич. природы основных её элементов. Такими элементами модели являются синхронные генераторы, трансформаторы, линии передач, первичные двигатели (турбины) и нагрузка (потребители электрич. энергии), но число их обычно значительно меньше, чем у натурной системы. Поэтому и здесь моделирование является приближённым, причём на модели по возможности полно представляется лишь исследуемая часть системы.

Особый вид М. ф. основан на использовании спец. устройств, сочетающих физич. модели с натурными приборами. К ним относятся стенды испытательные для испытания машин, наладки приборов и т. п., тренажеры для тренировки персонала, обучаемого управлению сложными системами или объектами, имитаторы, используемые для исследования различных процессов в условиях, отличных от обычных земных, напр., при глубоком вакууме или очень высоких давлениях, при перегрузках и т. п. (см. Барокамера, Космического полёта имитация).

М. ф. находит многочисленные приложения как при научных исследованиях, так и при решении большого числа практич. задач в различных областях техники. Им широко пользуются в строит, деле (определение усталостньгх напряжений, эксплуатационных разрушений, частот и форм свободных колебаний, виброзащита и сейсмостойкость различных конструкций и др.); в гидравлике и в гидротехнике (определение конструктивных и эксплуатационных характеристик различных гидротехнич. сооружений, условий фильтрации в грунтах, моделирование течений рек, волн, приливов и отливов и др.); в авиации, ракетной и космич. технике (определение характеристик летат. аппаратов и их двигателей, силового и теплового воздействия среды и др.); в судостроении (определение гидродинамич. характеристик корпуса, рулей и судоходных двигателей, ходовых качеств, условий спуска и др.); в приборостроении; в различных областях машиностроения, включая энергомашиностроение и наземный транспорт; в нефте- и газодобыче, в теплотехнике при конструировании и эксплуатации различных тепловых аппаратов; в электротехнике при исследованиях всевозможных электрич. систем и т. п.

Лит.: Седов Л. И., Методы подобия и размерности в механике, М., 1972; Г у х м а н А. А., Введение в теорию подобия, М., 1963; Э и г е н с о н Л. С., Моделирование, М., 1952; К и р п и ч е в М. В., М и х е е в М. А., Моделирование тепловых устройств, М. -Л., 1936; Ш н е й д е р П. Д ж., Инженерные проблемы теплопроводности, пер. с англ., М., 1960; Веников В. А., Иванов-Смоленский А. В., Физическое моделирование электрических систем, М.- Л., 1956.

С. М. Торг, С. Л. Вишневецкий, В. А. Арутюнов.

"МОДЕЛИСТ-КОНСТРУКТОР", ежемесячный популярный научно-технич. журнал ЦК ВЛКСМ. Издаётся с 1966 в Москве (с 1962 выходил как альманах "Юный моделист-конструктор"). Освещает вопросы научно-технич. творчества сов. молодёжи, рационализаторской работы, конструирования новой любительской техники, деятельности обществ, конструкторских бюро, клубов, кружков юных техников и др.; рассказывает об истории рус., сов. и зарубежной техники, о боевых подвигах сов. лётчиков, танкистов, моряков. Печатаются чертежи, описания и др. материалы для моделистов и конструкторов-любителей. Имеется раздел, поев, воен.-технич. видам спорта. Тираж (1974) 400 тыс. экз.

МОДЕЛЬ (Model) Вальтер (24.1.1891, Гентин, Вост. Пруссия,- 21.4.1945, близ Дуйсбурга), немецко-фашистский ген.-фельдмаршал (1944). В армии с 1909, участвовал в 1-й мировой войне 1914-18. С нояб. 1940 командовал 3-й танк. дивизией, с к-рой участвовал в нападении фаш. Германии на СССР. С окт. 1941 командир 41-го танк, корпуса, с янв. 1942 по нояб. 1943 (с перерывами) командующий 9-й армией на Вост. фронте. В февр.-марте 1944 командовал группой армий "Север", в апр.-июне 1944-группой армий "Сев. Украина", в июне-авг. 1944 - группой армий "Центр". Считался "мастером отступления", проводил тактику "выжженной земли", отличался особой жестокостью. В авг.-сент. 1944 командующий войсками Запада, а с сент. 1944 - группой армий "Б" (во Франции). В апр. 1945 войска М. были разгромлены в ходе Рурской операции 1945 и 18 апр. капитулировали, после чего М. застрелился.

МОДЕЛЬ (франц. modele, итал. modello, от лат. modulus - мера, мерило, образец, норма), 1) образец, служащий эталоном (стандартом) для серийного или массового воспроизведения (М. автомобиля, М. одежды и т. п.), а также тип, марка к.-л. изделия, конструкции. 2) Изделие (изготовленное из дерева, глины, воска, гипса и др.), с к-рого снимается форма для воспроизведения в др. материале (металле, гипсе, камне и др.). См. также Лекало, Литейная модель, Плаз, Шаблон. 3) Человек, позирующий художнику (натурщик), и вообще изображаемые объекты ("натура"). 4) Устройство, воспроизводящее, имитирующее (обычно в уменьшенном, "игрушечном" масштабе) строение и действие к.-л. др. устройства ("настоящего") в научных (см. ниже), практических (напр., в производств, испытаниях) или спортивных (см. Моделизм) целях.

МОДЕЛЬ (в широком понимании) -образ (в т. ч. условный или мысленный -изображение, описание, схема, чертёж, график, план, карта и т. п.) или прообраз (образец) к.-л. объекта или системы объектов ("оригинала" данной М.), используемый при определённых условиях в качестве их "заместителя" или "представителя". Так, М. Земли служит глобус, а М. различных частей Вселенной (точнее - звёздного неба) - экран планетария. В этом же смысле можно сказать, что чучело животного есть М. этого животного, а фотография на паспорте (или список примет и вообще любой перечень паспортных или анкетных данных)-М. владельца паспорта (хотя живописец, напротив, наз. М. именно изображаемого им человека). В математике и логике М. к.-л. системы аксиом обычно наз. совокупность объектов, свойства к-рых и отношения между к-рыми удовлетворяют данным аксиомам, в терминах к-рых эти объекты описываются.

Все эти примеры естественно делятся на 2 осн. группы: примеры первой группы выражают идею "имитации" (описания) чего-то "сущего" (некоей действительности, "натуры", первичной по отношению к М.); в остальных примерах, напротив, проявляется принцип "реального воплощения", реализации нек-рой умозрительной концепции (и здесь первичным понятием выступает уже сама М.). Иными словами, М. может быть системой и более высокого уровня абстракции, чем её "оригинал" (как в первом случае), и более низкого (как во втором). При различных же уточнениях понятия "М." средствами математики и логики в качестве М. и "оригиналов" выступают системы абстрактных объектов, для к-рых вообще, как правило, не имеет смысла ставить вопрос об относит, "старшинстве". (Более подробно о возможных классификациях М., исходящих, в частности, из характера средств построения М., см. в ст. Моделирование.)

В естеств. науках (напр., в физике, химии) следуют обычно первому из упомянутых пониманий термина, называя М. к.-л. системы её описание на языке нек-рой научной теории (напр., хим. или математич. формулу, уравнение или систему уравнений, фрагмент теории или даже всю теорию в целом). В таком же смысле говорят и о "моделях языка" (см. Модели в языкознании), хотя в наст, время всё чаще следуют второму пониманию, называя М. нек-рую языковую реальность, противопоставляя эту реальность её описанию - лингвистич. теории. Впрочем, оба понимания могут и сосуществовать; напр., релейно-контактные схемы используют в качестве "экспериментальных" М. формул (функций) алгебры логики, последние же, в свою очередь,- как "теоретические" М. первых.

Такая многозначность термина становится понятной, если учесть, что М. в конкретных науках так или иначе связываются с применением моделирования, т. е. с выяснением (или воспроизведением) свойств к.-л. объекта, процесса или явления с помощью др. объекта, процесса или явления - его "М." (типичные примеры: "планетарная" М. атома и концепция "электронного газа", апеллирующие к более наглядным - точнее, более привычным -механическим представлениям). Поэтому первое естественно возникающее требование к М.- это полное тождество строения М. и "оригинала". Требование это реализуется, как известно, в условии изоморфизма М. и "моделируемого" объекта относительно интересующих исследователя их свойств: две системы объектов (в интересующем нас сейчас случае -М. и "оригинал") с определёнными на них наборами предикатов, т. е. свойств и отношений (см. Логика предикатов) наз. изоморфными, если между ними установлено такое взаимно-однозначное соответствие (т. е. каждый элемент любой из них имеет единственного "напарника" из числа элементов др. системы), что соответствующие друг другу объекты обладают соответствующими свойствами и находятся (внутри каждой системы) в соответствующих отношениях между собой. Однако выполнение этого условия может оказаться затруднительным или ненужным, да и вообще настаивать на нём неразумно, поскольку никакого упрощения исследовательской задачи, являющейся важнейшим стимулом для моделирования, использование одних лишь изоморфных М. не даёт. Т. о., на след, уровне мы приходим к представлению о М. как об упрощённом образе моделируемого объекта, т. е. к требованию гомоморфизма М. "оригиналу". (Гомоморфизм, как и изоморфизм, "сохраняет" все определённые на исходной системе свойства и отношения, но, в отличие от изоморфизма, это отображение, вообще говоря, однозначно лишь в одну сторону: образы нек-рых элементов "оригинала" в М. оказываются "склеенными" - подобно тому, как на сетчатке глаза или на фотографии сливаются в одно пятно изображения близких между собой участков изображаемого предмета.) Но и такое понимание термина "М." не является окончательным и бесспорным: если мы преследуем цель упрощения изучаемого объекта при моделировании в к.-л. определённых отношениях, то нет никакого резона требовать, чтобы М. была во всех отношениях проще "оригинала" - наоборот, имеет смысл пользоваться любым, сколь угодно сложным арсеналом средств построения М., лишь бы они облегчали решение проблем, ставящихся в данном конкретном случае. Поэтому к максимально общему определению понятия "М." можно прийти, допуская сколь угодно сложные М. и "оригиналы" и требуя при этом лишь тождества структуры нек-рых "упрощённых вариантов" каждой из этих систем. Иными словами, две системы объектов А и В мы будем теперь называть М. друг друга (или моделирующими одна другую), если нек-рый гомоморфный образ А и нек-рый гомоморфный образ В изоморфны между собой. Согласно этому определению, отношение "быть М." обладает свойствами рефлексивности (т. е. любая система есть своя собственная М.), симметричности (любая система есть М. каждой своей М., т. е. "оригинал" и М. могут меняться "ролями") и транзитивности (т. е. модель модели есть М. исходной системы). Т. о., "моделирование" (в смысле последнего из наших определений понятия "М.") является отношением типа равенства (тождества, эквивалентности), выражающим "одинаковость" данных систем (относительно тех их свойств, к-рые сохраняются при данных гомоморфизмах и изоморфизме). То же, конечно, относится и к первоначальному определению М. как изоморфного образа "оригинала", в то время как отношение гомоморфизма (лежащее в основе второго из данных выше определений) транзитивно и антисимметрично (М. и "оригинал" не равноправны!), порождая тем самым иерархию М. (начиная с "оригинала") по понижающейся степени сложности.

М., применяемые в совр. научных исследованиях, впервые были в явном виде использованы в математике для доказательства непротиворечивости геометрии Лобачевского относительно геометрии Евклида (см. Неевклидовы геометрии, Аксиоматический метод). Развитый в этих доказательствах т. н. метод интерпретации получил затем особенно широкое применение в аксиоматической теории множеств. На стыке алгебры и математической логики сформировалась специальная дисциплина - моделей теория, в рамках которой под М. (или "алгебраич. системой") понимается произвольное множество с заданными на нём наборами предикатов и (или) операций - независимо от того, удаётся ли такую М. описать аксиоматич. средствами (нахождение таких описаний и является одной из осн. задач теории М.). Дальнейшую детализацию такое понятие М. получило в рамках логической семантики. В результате логико-алгебраич. и семантич. уточнений понятия "М." выяснилось также, что его целесообразно вводить независимо от понятия изоморфизма (поскольку аксиоматич. теории допускают, вообще говоря, и не изоморфные между собой М.).

В соответствии с различными назначениями методов моделирования понятие "М." используется не только и не столько с целью получения объяснений различных явлений, сколько для предсказания интересующих исследователя явлений. Оба эти аспекта использования М. оказываются особенно плодотворными при отказе от полной формализации этого понятия. "Объяснительная" функция М. проявляется при использовании их в пе-дагогич. целях, "предсказательная" -в эвристических (при "нащупывании" новых идей, получении "выводов по аналогии" и т. п.). При всём разнообразии этих аспектов их объединяет представление о М. прежде всего как орудии познания, т. е. как об одной из важнейших филос. категорий. Для использования этого понятия во всех разнообразных аспектах на совр. этапе развития науки характерно значит, расширение арсенала применяемых М. Введение в число параметров , описывающих изменяющиеся (развивающиеся) системы временных характеристик (или использование функций в математич. смысле этого слова в качестве первичных элементов М.), позволяет расширить понятие изоморфизма до т. н. изофункционализма и с его помощью отображать (моделировать) не только "жёстко заданные", неизменные системы, но и различные процессы (физ., хим., производств., экономич., социальные, биол. и др.). Это открывает широкие возможности использования в качестве М. программ для цифровых ЭВМ, "языки" к-рых можно рассматривать как "универсальные моделирующие системы". То же, конечно, относится и к обычным (естественным) языкам, причём и по отношению к языковым М. претензии на их непременный изоморфизм описываемым ситуациям оказываются несостоятельными и ненужными. К тому же предварит, учёт всех подлежащих "моделированию" параметров, нужный для буквального понимания термина "М.", введённого к.-л. точным определением, часто невозможен (что и обусловливает, кстати, потребность в моделировании), в силу чего особенно плодотворным опять-таки оказывается расширительное понимание термина "М.", основывающееся на интуитивных представлениях о "моделировании". Это относится ко всякого рода "вероятностным" М. обучения (см. также Программированное обучение), "М. поведения" в психологии, к типичным для кибернетики М. самоорганизующихся (самонастраивающихся) систем. Требование непременной формализации как предпосылки построения М. лишь сковывало бы возможности научных исследований. Весьма перспективным путём преодоления возникающих здесь трудностей представляется также введение различных ослаблений в формальные определения понятия "М.", в результате чего возникают "приближённые", "размытые" понятия "квазимодели", "почти М." и т. п. При этом для всех модификаций понятия "М." на всех уровнях его абстракции оно используется в обоих упомянутых выше смыслах, причём зачастую одновременно. Напр., "запись" генетической информации в хромосомах моделирует родительские организмы и в то же время моделируется в организме потомка.

Лит.: К л и н и С. К., Введение в метаматематику, пер. с англ., М., 1957, § 15; Э ш б и У. Р., Введение в кибернетику, пер. с англ., М., 1959, гл. 6; Л а х у т и Д. Г., Р е в з и н И. И., Финн В. К., Об одном подходе к семантике, "Философские науки", 1959, № 1; Моделирование в биологии. [Сб. ст.], пер. с англ., М., 1963; Вир С., Кибернетика и управление производством, пер. с англ., М., 1963; Чжао Юань-жен ь, Модели в лингвистике и модели вообще, в сб.: Математическая логика ц её применения, пер. с англ., М., 1965, с. 281-92; М и л-л е р Д ж., Галантер Ю., П р и б р а м К., Планы и структура поведения, пер. с англ., М., 1965; Г а с т е в Ю. А., О гносеологических аспектах моделирования, в сб.: Логика и методология науки, М., 1967, с. 211-18; К а р р и X. Б., Основания математической логики, пер. с англ., М., 1969, гл. 2 и 7;Хомский Н., Язык и мышление, пер. с англ., М.. 1972; С a map R., The logical syntax of language, L., 1937; К е т e n у J. G., A new approach to semantics, "Journal of Symbolic Logic", 1956, v. 21, № 1-2; G a s t e v У u. A., The role of.the isomorphism and homomorphism conceptions in methodology of deductive and empirical sciences, в сб.: Abstracts. IV International congress for logic, methodology and philosophy of science, Buc., [1971], p. 137-38.

Ю. А. Гастев.

МОДЕЛЬНЫЙ КОМПЛЕКТ, совокупность элементов литейной технологич. оснастки, предназначенной для образования внеш. контуров и внутр. полостей отливки в литейной форме.

В состав М. к. входят: литейные модели, модельные и протяжные плиты, стержневые ящики, модели частей литниковой системы, формовочные и контрольные шаблоны, кондукторы, сушильные плиты и др. оснастка. В М. к. включаются также и специализиров. опоки. В зависимости от технологии изготовления формы те или иные элементы могут отсутствовать.

Материалом для М. к. служат древесина, пластмасса, металл, гипс и др. Выбор материала определяется характером произ-ва, программой изготовления форм, требованиями к размерной точности и качеству поверхности отливки. В СССР по деревянным М. к. получают св. 60% отливок. Существует тенденция увеличения выпуска отливок по металлич. и пластмассовым М. к. Для отливок из всех сплавов М. к. изготовляют с учётом линейной усадки сплавов.

По прочности деревянные М. к. подразделяются на три класса. Класс прочности определяет конструкцию и качество изготовления М. к., что в свою очередь определяет точность его размеров и долговечность. По точности изготовления деревянные М. к. разбивают на три класса в зависимости от требуемого класса точности отливки; точность М. к. должна превышать требуемую точность отливки. В необходимых случаях быстро изнашиваемые части деревянных моделей армируют металлом. Износостойкость металлич. М. к. повышают преимущественно хромированием деталей. При изготовлении деревянных М. к. используют нормализованные элементы. Осн. оборудованием модельных цехов или участков являются деревообр. станки. Метал -лич. М. к. изготовляют в металломодельных отделениях инструментальных цехов или в металломодельных цехах. Крупные модельные произ-ва обслуживают неск. литейных цехов. Для изготовления форм и стержней из термореактивных материалов (оболочковые формы и стержни объёмные стержни, твердеющие в "горячих ящиках") применяется спец. металлич. оснастка (обычно из серого чугуна, выдерживающая нагрев до 400 °С.

М. к. хранят на специально оборудованных модельных складах при темпер. ок. 20 °С и относит, влажности воздуха 60%.

Лит.: Поляков Д. С., Таскин В. Л., Литейные модельные лекты, М., 1967; К л е б а н е р В. Я., Экономика и организация модельного производства, Л., 1968; Ложнчевский А. Изготовление литейных металлических моделей, М., 1969; Б а л а б и н В. В., Моделы производство, М., 1970; его же, Изготовленне деревянных модельных комплект в литейном производстве, 2 изд., М.

В. Л. Тарст.

МОДЕНА (Modena), город в Сев. Италии, в обл. Эмилия-Романья, на Падаской равнине, между притоками По, Панаро и Секкья. Адм. ц. провинц. Модена. 171,1 тыс. жит. (1971). Важн. транспортно-пром. центр. Произ-во спорт. автомобилей, автобусов, тракторов ж.-д. оборудов., с.-х. и типографск. машин, оборудования для пищ. пром-сти, хим., электротехнич., цем., литейная, табачная, пищ., кож.-обув. пром-сть. Ун-т.

В древности М.- этрусский город, со 183 до н. э.- рим. колония (Мутина Сражение при М. (43 до н. э.) решили исход Мутинской войны. Пришедший в упадок в период варварских нашествий М. возрождается в 8 в. н. э., став резиденцией епископов и графов. В 11 в. вошла в Ломбардскую лигу. В 12 в. добилась прав коммуны. В 12 в. в М. был основан ун-т. В 1288-1860 М. Haxодилась под властью рода д' Эсте (с перерывами: в 1306-36 вновь коммуна, в 1510-27 - под властью пап). С 15в. центр одноимённого герцогства, существовавшего до 1860 (с перерывом в 1797-1815, когда его терр. входила в гос-во создававшиеся в Италии в период франц. оккупации). В годы 2-й мировой войны 1939-45 (после оккупации Италии германскими войсками) в пров. М. развернулось Движение Сопротивления; силами Сопротивления М. была освобождена в апр. 1945.

Модена. Собор. 11 -13 вв.

Г. Модена.

Архит. памятники: романский собор (с 1099 по 13 в., мастер Ланфранко и др.), ренессансная церковь Сан-Пьетро (15 в.), барочное Палаццо Дукале (1634, арх. Б. Аванцини). Галерея, музей и собр. медалей Эсте (живопись итал. и исп. школ Возрождения и барокко).

Лит.: Elenco degli edifici monumental. Provincia di Modena, Roma, 1920; AmorthL., Modena capitale, Mil., 1967.

МОДЕНА (Modena) Густаво (13.2.1803, Венеция,-20.2.1861, Турин), итальянский актёр. Род. в актёрской семье. Получил юридич. образование в Падуанском ун-те. В 1824 начал сценич. деятельность. Выступал в труппах различных антрепренёров, был организатором собств. трупп. Героич., романтически приподнятое иск-во М. сложилось под влиянием идей нац. -осв ободит. движения в Италии 1-й пол. 19 в. Он участвовал в Болонском восстании 1831, был тесно связан с тайным республиканским об-вом "Молодая Италия" и его основателем Дж. Мадзини; стремился сделать театр орудием борьбы за свободу и независимость родины. Среди лучших ролей М.: Паоло ("Франческа да Римини" Пелли-ко), Адельгиз ("Адельгиэ" Мандзони), Брут, Саул, Филипп ("Брут", "Саул", "Филипп" Альфьери), Магомет ("Магомет" Вольтера). Творчество М. способствовало созданию итал. реалистич. школы актёрского иск-ва; он воспитал таких актёров, как А. Ристори, Э. Росси, Т. Сальвини. В 1859 оставил сцену. В 1888 изданы письма М., представляющие интерес для изучения театра.

Лит.: История западноевропейского театра, т. 3, М., 1963.

МОДЕРАДОС (исп. moderados, букв. - умеренные), испанская партия правых либералов, объединявшая часть дворянства и буржуазии в 1820-68. Образовавшееся во время Испанской революции 1820-23 пр-во М. (март 1820 - авг. 1822) декретировало ряд реформ (ликвидацию майоратов, закрытие части монастырей и др.), но проявило нерешительность в борьбе со сторонниками абсолютизма и вынуждено было уступить власть левым либералам (эксальтадос). После начала Карлистской войны регентша Мария Кристина передала власть (15 янв. 1834) руководителю правых либералов Ф. Мартинесу де ла Роса, к-рый в апр. 1834 издал Королев, статут -консервативную конституцию, воплотившую в себе политич. идеалы М. Развитие нар. движения привело в сент. 1835 к отставке правительства М. В 1840-е гг. партия М. активно выступала против демократич. реформ. В июле 1843 лидер М.- Р. М. Нарваэс совершил контрреволюционный переворот, положивший конец Испанской революции 1834-43. С началом в Испании революции 1868-74 партия М. прекратила своё существование.

МОДЕРАТО (итал. moderate, букв.- умеренно), обозначение умеренного темпа, среднего между аллегро и аллегретто.

МОДЕРАТОР (лат. moderator, от moderor - умеряю, сдерживаю), приспособление, предназначенное для приглушения звука в пианино и роялях. Состоит из деревянной планки, расположенной поперёк всех струн, и рычага управления.
"МОДЕРН", стиль "модерн" (франц. moderne - новейший, современный), одно из названий стилевого направления в европ. и амер. иск-ве кон. 19 -нач. 20 вв. В Бельгии, Великобритании и США оно известно как "новое иск-во" (Art Nouveau), в Германии - "югенд-стиль" (Jugendstil), в Австрии - "стиль Сецессиона" (Sezessionstil), в Италии -"стиль Либерти" ("stile Liberty"), в Испании - "модернизм" (modernismo). "M." возник в условиях кризиса бурж. культуры как один из видов неоромантич. протеста против антиэстетичности бурж. образа жизни, как реакция на господство позитивизма и прагматизма. Эстетика "М." развивала идеи символизма и эстетизма, "философии жизни" Ф. Ницше. "М.", по мысли ряда его теоретиков (бельгиец X. К. ван де Велде, опиравшийся на социалистич. утопии У. Морриса), должен был стать стилем жизни нового, формирующегося под его воздействием общества, создать вокруг человека цельную эстетически насыщенную пространств, и предметную среду, выразить духовное содержание эпохи с помощью синтеза иск-в, новых, нетрадиционных форм и приёмов, совр. материалов и конструкций. Наиболее последовательно "М." осуществил свои принципы в узкой сфере создания богатых индивидуальных жилищ. Но в духе "М.", стремившегося стать универсальным стилем своего времени, строились и многочисл. деловые, пром. и торг, здания, вокзалы, театры, мосты, доходные дома. "М." пытался преодолеть характерное для бурж. культуры 19 в. противоречие между художеств, и утилитарным началами, придать эстетич. смысл новым функциям и конструктивным системам, приобщить к иск-ву все сферы жизни и сделать человека частицей художеств, целого. Стремление изменить иск-вом мир в рамках капиталистич. общества было глубоко утопичным. Практически же "М." явился первым относительно цельным стилем художеств, оформления различных сфер бурж. быта.

"М." противопоставил эклектизму 19 в. единство, органичность и свободу развития стилизованной, обобщённой, ритмически организованной формы, назначение к-рой - одухотворить материально-вещную среду, выразить тревожный, напряжённый дух переломной эпохи. Период становления "М." (рубеж 19-20 вв.) отмечен нац.-романтич. увлечениями, интересом к ср.-век. и нар. иск-ву. Для этого этапа характерно возникновение художеств.-ремесленных мастерских (прообразами их были мастерские русского Севера".

Журнал "Мир искусства". 1904. "Модерн". Графика. Слева - Я. Т о р о п. Рекламный плакат. Цветная литография. Около 1897. В центре - И. X о ф м а н. Виньетка для журнала "Вер сакрум". 1898. Справа - И. Я. Б и л и б и н. Титульный лист к статье "Народное творчество У. Морриса, 1861.

и "Выставочное общество искусств и ремёсел", 1888, в Великобритании, часто противопоставлявших себя капиталистич. индустрии: "Объединённые художественно-ремесленные мастерские" (1897) и "Немецкие мастерские художественных ремёсел" (1899) в Германии; "Венские мастерские" (1903) в Австрии; мастерские в Абрамцеве (1882) и Талашкине (ок. 1900) в России. Зрелый "М." (кон. 1900-х и 1910-е гг.) приобрёл черты интернац. стиля, основанного на применении принципиально новых художеств, форм. Быстрому распространению "М." способствовали журналы "Revue blanche" (1891, Париж), "The Studio" (1893, Лондон), "The Yellow Book" (1894, Лондон), "Jugend" (1896, Мюнхен), "Deutsche Kunst und Dekoration" (1897, Дармштадт), "Ver Sacrum" (1898, Вена), "Mup искусства" (1898/99, Петербург).

В противоположность эклектизму с его интересом к достоверности воспроизведения отд. деталей ист. и нац. стилей "М." хотел возродить дух стилевого единства художеств, организмов, присущий ср.-век. или нар. иск-ву, общность и взаимовлияние всех видов иск-ва. Это предопределило появление нового типа художника-универсала, соединившего в одном лице архитектора, графика, живописца, проектировщика бытовых вещей и часто теоретика. Идея синтетич., цельного произведения иск-ва (Gesamtkunstwerk) ярче всего воплощена в архитектуре интерьеров, лучшие образцы к-рых отличаются ритмич. согласованностью линий и тонов, единством деталей декора и обстановки (обои, мебель, лепнина, панели, арматура светильников), целостностью однородного перетекающего пространства, усложнённого и расширенного зеркалами, многочисленными дверными и оконными проёмами, живописными панно.

Архитектура "М." была первым шагом в архит. развитии 20 в. Она искала единства конструктивного и художеств, начал, вводила свободную, функционально обоснованную планировку, применяла каркасные конструкции, разнообразные, в т. ч. новые, строит, и отделочные материалы (железобетон, стекло, кованый металл, необработанный камень, изразцы, фанера, холст). Свободно размещая в пространстве здания с различно оформленными фасадами, архитекторы "М." восставали против симметрии и регулярных норм градостроительства. Богатейшие возможности формообразования, предоставленные новой техникой, они использовали для создания подчёркнуто, индивидуализированного образного строя; здание и его конструктивные элементы получали декоративное и символически-образное осмысление. Наряду со стремлением к необычным живописным эффектам, динамикой и текучей пластичностью масс, уподоблением архит. форм органическим природным явлениям (постройки А. Гауди в Испании, В. Орта и X. К. ван де Велде в Бельгии, ф. О. Шехтеля в России) существовала и рационалистич. тенденция: тяготение к геометрической правильности больших, спокойных плоскостей, к строгости, порой даже пуризму (ряд построек И. Хофмана, И. Ольбриха в Австрии, Ч. Р. Макинтоша в Шотландии, поздние работы Шехтеля). Нек-рые архитекторы нач. 20 в. предвосхищали во многом функционализм, стремились выявить каркасную структуру здания, подчеркнуть тектонику масс и объёмов (ряд построек О. Вагнера в Австрии, П. Беренса в Германии, О. и Г. Перре во Франции).

"Модерн". Декоративно-прикладное искусство. 1. В. О р т а. Паркет в особняке Сольве в Брюсселе (фрагмент). 1895 -1900. 2. Э. Г и м а р. Ограда станции метрополитена в Париже. Кованое железо, роспись. Около 1900.

X. К. ван де Велде. Столовая. 1906.

Осн. средством выражения в стиле "М." является орнамент, к-рый не только украшает произведение, но и формирует его композиционную структуру. В интерьерах белы, архитекторов изящные линейные плетения, подвижные растит, узоры рассыпаны по стенам, полу и потолку, концентрируются в местах их сопряжения, объединяют архит. плоскости, активизируют пространство. Бесконечно текущие, то плавно, то взволнованно извивающиеся, чувственно-сочные линии декора несут духовно-эмоциональный и символич. смысл, сочетая изобразительное с отвлечённым, живое с неживым, одухотворённое с вещным.

У мастеров венского "М."- И. Хофмана, И. Ольбриха,- в работах шотл. группы "Четверо" во главе с Ч. Р. Макинтошем строго геометричный орнамент варьирует мотивы круга и квадрата. Несмотря на провозглашённый откав от подражания историч. стилям, художники "М." использовали линейный строй япон. гравюры, стилизованные растит, узоры эгейского иск-ва и готики, элементы декоративных композиций барокко, рококо, ампира.

Для "М." характерно взаимопроникновение станковых и декоративно-прикладных форм иск-ва. Орнамент "М.", во всех видах иск-ва структурно организующий плоскость, и своеобразный ритм его гибких линий сложились в графике. Литография, ксилография, иск-во книги достигли в этот период высокого подъёма. Среди ведущих графиков "М.": англичанин О. Бёрдсли, немцы Т. Т. Хейне, Г. Фогелер, швейцарец Ф. Валлоттон, голландец Я. Тороп, норвежец Э. Мунк, в России - А. Н. Бенуа, К. А. Сомов; мастера плаката - французы А. Тулуз-Лотрек, Э. Грассе, чех А. Муха, австриец К. Мозер. В живописи и скульптуре "М.", неразрывно связанный с символизмом, стремился создать самостоятельную художеств, систему, но был вместе с тем своего рода переходом от традиц. форм 19 в. к условному языку новейших европ. течений. В этом важным импульсом послужила деятельность т. н. понт-авенской школы во главе с П. Гогеном. Картины и панно "М." рассматривались как элементы интерьера, его пространственной и эмоциональной организации. Поэтому декоративность стала одним из гл. качеств живописи "М.". Характерно часто встречающееся в ней парадоксальное сочетание декоративной условности, орнаментальных ковровых фонов и вылепленных со скульпт. чёткостью и осязаемостью фигур и лиц первого плана (Г. Климт в Австрии, Ф. Кнопф в Бельгии, М. А. Врубель в России). Выразительность живописи достигалась сочетанием больших цветовых плоскостей ("набы" во Франции, Л. С. Бакст в России, Э. Мунк в Норвегии), тонко нюансированной монохромией (Врубель, Бенуа). Поэтика символизма обусловила интерес к символике линии и цвета, к темам мировой скорби, смерти, эротики, к миру тайны, сна, легенды, сказки. Динамика и текучесть формы и силуэта характерны для скульптуры (бельгиец Ж. Минне, немец Г. Обрист) и для произв. декоративно-прикладного иск-ва, уподобляющихся феноменам природы с их органич. внутр. силами (керамич. и жел. изделия А. Гауди; металлич. ограды метро Э. Гимара, стеклянные изделия Э. Галле, украшения Р. Лалика во Франции; стеклянные сосуды Л. К. Тиффани в США, мебель X. ван де Велде); тяготение к конструктивности, чистоте линий, лаконизму форм проявилось в мебели Ч. Р. Макинтоша, И. Хофмана, И. А. Фомина.

Илл. см. на вклейке, табл. XXV, XXVI (стр. 408-409).

Лит.: История русского искусства, т. 10, кн. 2, М., 1969; Русская художественная культура конца XIX - начала XX века (1895-1907), кн. 2, М., 1969; Борнеова Е. А., Каждая Т. П., Русская архитектура конца XIX - начала XX века, М., 1971; Всеобщая история архитектуры, т. 10, М., 1972; Кириченко Е., О закономерностях развития архитектуры, "Архитектура СССР", 1973, № 12; L e n n i n g Н. F., The Art Nouveau, Den Haag, 1951; S с h m u t z 1 e r R., Art Nouveau, N. Y., [1962]; Ноfstatter H. Die Geschichte der europäischen Jugendstilmalerei, Köln, [19631; Madsen S. Т., Jugendstil, Munch., 1967.

Т.Н. Володина.

МОДЕРНИЗАЦИЯ (франц. modernisation, от moderne - новейший, современный), изменение в соответствии с новейшими, современными требованиями и нормами, напр. М. (обновление) технич. оборудования, производств, процесса и т. п.

МОДЕРНИЗМ (франц. modernisme, от moderne - новейший, современный), главное направление бурж. иск-ва эпохи упадка. Первым признаком начинающегося падения художеств, культуры в наиболее развитых капиталистич. странах было академич. и салонное повторение прежних стилей, особенно наследия Ренессанса, превратившегося в школьную азбуку форм. Такое эпигонство заметно в иск-ве сер. и 2-й пол. 19 в. Однако на смену бессильному повторению традиц. форм приходит воинственное отрицание традиции - явление, аналогичное новым течениям в бурж. политике и философии. На место мещанской морали становится декадентский аморализм, на место эстетики бесплотных идеалов, извлечённых из художеств, культуры античности и Возрождения,- эстетика безобразия. Прежняя вера в "вечные истины" классовой цивилизации сменяется обратной иллюзией ложного сознания - релятивизмом, согласно к-рому истин столько же, сколько мнений, "переживаний", "экзистенциальных ситуаций", а в историч. мире -каждая эпоха и культура имеют свою неповторимую "душу", особое "видение", "коллективный сон", свой замкнутый стиль, не связанный никаким общим художеств, развитием с др. стилями, одинаково ценными и просто равными. М. исторически сложился под знаком восстания против высокой оценки классич. эпох, против красоты форм и реальности изображения в иск-ве, наконец, против самого иск-ва. Это абстрактное отрицание явл. наиболее общим принципом т. н. "авангарда". По словам теоретика М.-исп. философа Ортеги-и-Гасета, новое иск-во "состоит целиком из отрицания старого". Можно различно оценивать это движение, но существование определённой грани, отделяющей новый взгляд на задачи художника от традиц. системы художеств, творчества, общепризнано. Спорят лишь о том, где пролегает эта грань - в 60-80-х гг. 19 в., т. е. в эпоху франц. декадентства, или позднее, в эпоху кубизма (1907 -14). Лит-pa модернистского направления оценивает эту грань как величайшую "революцию в иск-ве". Марксистская лит-pa, напротив, уже в кон. 19 в. (П. Лафарг, Ф. Меринг, Г. В. Плеханов) заняла по отношению к М. отрицат. позицию, рассматривая егс как форму разложения бурж. культуры.

Эта оценка как бы противоречит двум фактам. Во-первых, основателями М. в 19 в. были поэты и художники большого таланта, создавшие произведения, способные сильно действовать на ум и чувство современников, несмотря на присутствие в их творческой деятельности мн. болезненных черт. Достаточна вспомнить Ш. Бодлера в поэзии, ван Гога в живописи. Существует громадная разница между их своеобразным иск-вом, как бы повисшим над пропастью, и теми последствиями, к-рыми были чреваты открытые ими возможности. Последствия эти были необходимым, хотя и абсурдным выводом из однажды принятых начал. Каждое поколение художников нового типа отворачивалось от своих продолжателей. Однако логика разложения иск-ва на почве М. действовала неотвратимо. Ценность художеств, произведений, созданных модернистскими школами, находится в обратном отношении к расстоянию от начала этого процесса. Разумеется, процесс упадка сам по себе носит неравномерный характер.

Во-вторых, оценке М. как явления упадочной бурж. идеологии противоречит, на первый взгляд, его- антибурж. тон. Уже в сер. 19 в. первые демонстрации модернистского новаторства носили ярко выраженный анархич. характер. Они вызывали ярость культурного мещанина как посягательство на его домашний очаг. Поэты-декаденты и основатели новых течений в живописи были нищими бунтарями, или, по крайней мере, аутсайдерами-одиночками, как наиболее влиятельный мыслитель этого направления Ф. Ницше. Но положение менялось от десятилетия к десятилетию, и совр. практика модернистского "авангарда" прочно вошла в экономич. и культурный быт капитализма. К сер. 20 в. громадная машина спекуляции и рекламы подчинила себе художеств, жизнь капиталистич. стран. Игра на выдвижении сменяющих друг друга модных школ сливается с общей лихорадочной стихией совр. капитализма. Массированная реклама создаёт ложные потребности, искусств, спрос на обществ, фантомы, обладание к-рыми, часто совершенно номинальное (напр., обладание траншеей, вырытой художником "земляного" направления в пустыне Невады), становится вывеской богатства. Парадоксально, что бунтарский характер М. при этом растёт, напр., в ч антиискусстве" 1960-х гг., связанном с движением "новых левых". Суть дела в том, что совр. бурж. идеология не могла бы сохранить своё владычество над умами без широкого развития внутренне присущего ей духовного анархизма как оборотной стороны традиц. системы обществ, норм. Антибурж. характер модернистских течений свидетельствует о кризисе этой системы, но, по признанию таких теоретиков "авангарда", как Г. Маркузе, весь этот бунт в иск-ве без особых трудностей "интегрируется" господств, системой.

И всё же М. не является простым созданием капиталистич. экономики и пропаганды. Это явление имеет глубокие корни в социальной психологии эпохи империализма. Первые признаки поворота к М. не случайно совпадают с началом "эры революции сверху" (Ф. Энгельс), то есть цезаризма Наполеона III и Бисмарка. Чем меньше выходов для свободной самодеятельности людей, чем больше скопившейся в обществе, не находящей себе разрядки массовой энергии, тем больше потребности в различных формах "отдушины" и "компенсации". Совр. эстетич. теории, объясняющие этой потребностью значение иск-ва вообще, несостоятельны, но они отчасти применимы к модернистским течениям, в к-рых мнимая свобода художника ломать реальные формы окружающего мира во имя своей творческой воли действительно является психологич. "компенсацией" полного безволия личности, подавленной громадными отчуждёнными силами капиталистич. экономики и гос-ва.

Судьба иск-ва выражает глубокое противоречие совр. бурж. цивилизации - господство громадной массы мёртвого абстрактного труда над миром конкретных потребит, ценностей и качественно различной работы людей, родственной иск-ву прежних эпох. По мере упадка творческой продуктивности былых времён художник всё более страдает от перегрузки мёртвым знанием готовых форм. Отсюда поиски формально нового, болезненный страх перед повторением того, что уже было, абстрактный культ "современности", неизвестный прежней истории иск-ва.

М. есть особая психотехника, посредством к-рой художник стремится преодолеть последствия омертвления культуры, замыкаясь в пределах своей профессии. Гл. смысл художеств, деятельности он видит не в изменении окружающего мира во имя обществ, идеала, а в изменении способа изображения или способа "видения" мира ("новая оптика" бр. Гонкур). "В недалёком будущем хорошо написанная морковь произведёт революцию",- говорит художник Клод в романе Э. Золя "Творчество". Так начинается серия формальных экспериментов, с помощью к-рых художник надеется подчинить своей воле поток уродливой "современности", а там, где это становится уже невозможным, примирение иск-ва с жизнью достигается отрицанием всех признаков реального бытия, вплоть до отрицания изобразительности вообще (абстрактное искусство), отрицания самой функции иск-ва как зеркала мира (•"поп-арт", "оп-арт", мини-арт, боди-арт и т. п.). Сознание отрекается от самого себя, стремясь вернуться в мир вещей, немыслящей материи.

Отсюда две черты всякого М.: гипертрофия субъективной воли художника в борьбе против враждебной ему реальности и падение идеальных границ субъекта под натиском бессмысленного хода вещей. Течения М. постоянно колеблются между крайностями бунта и восстановлением жёсткой "дисциплины" предков, абстрактным новаторством и возвращением к архаич. традиции, иррациональной стихией и культом мёртвого рационализма. В природе М. лежит постоянное изменение его условных знаков, но было бы ошибкой видеть в этом процессе только поиски новых форм. Ни деформацию реальности, ни полный отказ от её изображения в абстрактном иск-ве нельзя считать безусловными признаками М. Таким признаком является только бешеное движение рефлексии, отвергающей всякую остановку в постоянной смене моделей "современности". Одни и те же формы могут быть то отвергаемой пошлостью, то последним словом изысканного вкуса. Даже академич. приёмы и точное изображение реальности становятся символами модернистского иск-ва, если они взяты не в прямом и обычном смысле, а как условные знаки самоиронии больного сознания.

Во всём этом неизменно растёт раскол с "наивным реализмом" большинства людей, внутр. полемика против отображения действительности нашим глазом. В теории М. принцип отражения жизни считается устаревшей схемой, а в практике его иск-во теряет свои изобразит, черты, превращаясь в систему знаков, выражающих только позицию художника. И знаки эти должны быть как можно менее похожи на зрит, иллюзию. Так, в живописи, к-рая играет ведущую роль в процессе растущей модернизации художеств, жизни, вместо красок появляются песок, цемент, дёготь, а затем и реальные предметы как таковые. В поэзии слово теряет значение экрана для передачи духовного содержания, приобретая ценность материального факта - звукового воздействия. В музыке устраняется разница между муз. тоном и обычным шумом жизни.

Обществ. роль "авангарда" растёт в полном противоречии с действит. художеств, ценностью его творений. В качестве отдушины модернистское иск-во даёт придавленной обществ, духовной энергии род мнимого выхода. Противопоставление "авангарда" "массовой культуре" большинства выгодно господств, классу как одно из средств для разъединения нации. Социальная демагогия эпохи империализма приобретает т. о. важный козырь для разжигания ненависти тёмных масс к заумным интеллектуалам, грозящим духовному здравию народа. Авангардизм, выдвигающий на первый план негативную, анархич. сторону бурж. сознания, имеет два лица. С одной стороны, это ультралевые течения в иск-ве и философии, с другой - "правый радикализм", переходящий в прямое черносотенство.

Будучи явлением бурж. идеологии, М. выражает прежде всего настроения мелкобурж. слоя, страдающего от материального и духовного гнёта. Если разочарование в капитализме ведёт художника к участию в борьбе нар. масс, то есть надежда, что его модернистские предрассудки будут побеждены в общем подъёме демократии и социализма. Однако само по себе анархич. бунтарство не выходит за пределы бурж. горизонта. Вот почему лихорадочная активность футуристов и др. авангардистских течений в нач. Великой Окт. социалистич. революции вызвала решит, недовольство В. И. Ленина и он стремился вытеснить этот слой из образоват. учреждений Сов. власти, заменив его интеллигенцией более высокого уровня, к-рая вчера ещё была только нейтральна. Претензия модернистов от имени пролетариата "сбросить" устаревшую классику "с парохода современности" была осуждена ленинской партией и нар. депутатами в Советах. Подлинная культурная революция не имеет ничего общего с разрушением старой культуры и созданием модернистской "антикультуры ".

Когда началась Окт. революция 1917, воспоминания о подъёме демократич. реализма в России были ещё живы. Сегодня в капиталистич. странах мира сознание художника и его публики находится под давлением прочно сложившейся экономич. и культурной системы, враждебной реализму. Это делает обстановку борьбы за реалистич. иск-во, связанное с передовыми обществ, силами, особенно сложной. Однако наличие модернистских предрассудков в сознании художеств, интеллигенции не является препятствием для политич. союза с ней. Нельзя дифференцировать М. на хороший и плохой, но можно и нужно дифференцировать людей иск-ва по двум признакам - их политич. симпатиям и наличию в их творчестве действит. стремления к отказу от формалистич. "революций в иск-ве". Важно только понять, что участие в подобных - "революциях" не приближает художника к нар. движению, а удаляет от него. В таком понимании дела заложено решит, отличие марксистской эстетики от ревизионистского "марксизма 20 в." в духе Р. Гароди. Самое прочное сплочение художеств, интеллигенции с народом, столь необходимое для победы демократич. культуры во всём мире, может быть достигнуто только под знаменем социалистич. реализма.

Лит.: Ленин В. И., О литературе и искусстве. [Сб.J, 3 изд., М., 1967; Плеханов Г. В., Соч., т. 14, М., [6.r.]; Л у н а ч а р с к и и А. В., Об изобразительном искусстве, т. 1-2, М., 1967; Модернизм. Анализ и критика основных направлений, 2 изд., М., 1973; Theories of modern art, ed. H. B. Chipp, Berk. - Los Ang.- L., 1970.

Мих. Лифшиц.

МОДЕРНИЗМ, течение в католицизме, возникшее в кон. 19 - нач. 20 вв. Сторонники М., расходясь по ряду вопросов с позицией церкви, выступили с критикой нек-рых сторон учения и практики католич. церкви, выдвинули систему взглядов, направленную на приспособление католич. вероучения к совр. условиям обществ, жизни и к совр. уровню науки. Виднейшими представителями М. были во Франции - А. Луази, Л. Дюшен, М. Блондель, в Германии - Г. Шелль, в Великобритании - Дж. Тиррелл, в Италии - Р. Мурри, А. Фогаццаро и др. Осн. положения М.: религия создана человеком; библия - не боговдохновенная книга; Христос не был сыном бога, а был евр. Мессией, зачинателем религ. движения; следует различать вечную сущность христ. догм и конкретно-историч. формы их проявления, зависящие от развития общества; церковь должна отказаться от наиболее примитивных суеверий, от веры в чудеса, в дьявола, в загробные муки и т. п. (но при этом, разумеется, М. не отказался от веры в сверхъестественное). Нек-рые представители М. (напр., А. Луази) отвергали догмат о непогрешимости папы, о его верх, власти. В 1907 Ватикан осудил М. как "синтез всех ересей" декретом Пия X "Lamentabili" и энцикликой "Pascendi". Наиболее видные модернисты были отлучены от церкви; их соч. были включены в "Индекс запрещённых книг". В 1910 Ватикан ввёл антимодернистскую присягу для лиц, посвящаемых в очередной духовный сан, для профессоров католич. богословских ф-тов, служащих епископских курий и др.

Католич. церковь, осудившая М., со временем сама встала перед необходимостью учёта изменившихся в мире условий, эволюции сознания широких масс верующих, успехов науки и обществ, прогресса. Вопросы "обновления" были в центре внимания 2-го Ватиканского собора (1962-65), давшего толчок к дальнейшей модернизации церкви. Течения, аналогичные М., получили распространение (особенно после 2-й мировой войны 1939-45) и в др. религиях -православии, протестантизме, иудаизме, исламе и др. Их сторонники в целях укрепления сильно подорванных позиций религии требуют "обновления" догматики, культа, структуры и практики дерквей.

Лит.: Л е р у а Э., Догмат и критика, пер. с франц., [М.], 1915; Керенский В., Римско-католический модернизм, Хар., 1911; Ш е й н м а н М. М., Модернизм и модернизация в католицизме, в кн.: Ежегодник Музея истории религии и атеизма, М.- Л., 1958, т. 2; Беленький М., Иудаизм, М., 1966; Беликов и ч Л., Кризис современного католицизма, М., 1967; М ч е д л о в М., Эволюция современного католицизма, М., 1967; Бабосов Е., Научно-техническая революция и модернизация католицизма, Минск, 1971; К у р о ч к и н П., Эволюция современного русского православия, М., 1971; А ш и р о в Н., Эволюция ислама в СССР, М., 1972.

М. М. Шейнман.

МОДЕСТИН (Modestinus) Геренний (гг. рож д. и смерти неизв.), римский юрист 3 в. Ученик одного из крупнейших римских юристов Ульпиана. Занимал высшие гос. должности (в 226-44 префект). Имел в числе немногих право (т. н. jus respondendi) давать свои решения по гражд. спорам как бы от имени императора. В 426 законом о цитировании сочинениям 5 юристов, в т. ч. и сочинениям М., была придана обязат. юридич. сила. М. внёс существенный вклад в формулирование нек-рых вопросов юридич. доктрины и практики; известно 345 фрагментов из произв. М., включённых в состав Дигест.

МОДЕСТОВ Василий Иванович [24.1 (5.2). 1839, Валдайский у. Новгородской губ.,- 13(26).2.1907, Рим], русский историк и филолог, специалист в области античности. Доктор римской словесности, проф. с 1868. Окончил ист.-филологич. ф-т Петерб. ун-та (1860). Преподавал в Новороссийском ун-те в Одессе (1865-1867; 1889-93), в Казанском (1867-68), Киевском (1869-78), Петерб. (1886-89) ун-тах. Из работ по истории рим. лит-ры особый интерес представляют "Римская письменность в период царей" (1868), в к-рой автор выступал против скептич. направления в историографии Др. Рима, доказывая, что лат. письменность восходит ещё к дорим. эпохе, а также монография о Таците ("Тацит и его сочинения. Историко-литературное исследование", 1864) и полный перевод соч. Тацита (т. 1-2, 1886-87). С 1893 М. подолгу жил в Риме, занимался изучением археологии Италии. В работе "Введение в римскую историю" (ч. 1-2, 1902-09) он изложил систематич. историю древнейшей Италии на основании памятников материальной культуры, а также лингвистич. и историко-традиционных данных. Будучи блестящим публицистом, М. написал ряд работ по истории Германии, Франции, Италии кон. 19 в.

Соч.: Лекции по истории римской литературы, СПБ, 1888.

Лит.: А н у ч и н Д. Н., Труд проф. В. И. Модестова "Введение в римскую историю", "Древности. Труды Ими. Археологического об-ва", 1909, т. 22, в. 2; Бузескул В. П., Всеобщая история и ее представители в России в 19 и начале 20 в., ч. 1, Л., 1929.

МОДЖЕВСКИЙ, Моджевский-Ф р ы ч (Modrzewski-Frycz) Анджей (1503, Вольбуж,- 1572, там же), польский публицист, обществ, деятель. После окончания в 1519 Краковского ун-та секретарь канцлера Я. Лаского, а позднее королев, секретарь. Осн. произв.- "Об исправлении государства" (1551, доп. изд. 1554), где он отстаивал идеи равенства сословий перед законом, усиления центр, власти, смягчения крайностей крепостничества, создания нац. церкви, необходимости широкого просвещения, свободного от воздействия церкви,- было запрещено папской курией. Взгляды М. оказали влияние на польск. и европ. обществ, мысль.

Соч.: Dziela wszystkie, t. 1-5, Warsz., 1953-59; Index, Warsz., 1960.

Лит.: Польские мыслители эпохи Возрождения, М., 1960, с. 69-128; К a w e s k а-Gryczowa A., Rostkowska J., A. Frycz Modrzewski. Bibliografia, Wroclaw, 1962.

МОДЖЕЕВСКАЯ (Modrzejewska) Хелена (Елена) (12.10.1840, Краков,-8.4. 1909, Ньюпорт, Калифорния), польская актриса. Воспитывалась в монастыре. Брала частные уроки драматич. иск-ва. В 1865-69 выступала на сцене Краковского театра, в 1869-76 - в Варшаве (театры "Бельки" и "Розмаитости"). Гастролировала в Великобритании и США. Иск-во М. было органично, близко жизненной правде, отличалось романтич. одухотворённостью. Лучшие образы, созданные М., поднимались до высот подлинного трагизма: Мария Стюарт ("Мария Стюарт" Словацкого), Амалия ("Разбойники" Шиллера), Федра ("Федра" Расина). Всеобщим признанием пользовались её роли в пьесах У. Шекспира: Анна ("Ричард III"), леди Макбет ("Макбет") и др. Поэтич. обобщённость и покоряющая правда иск-ва помогли М. стать одной из лучших исполнительниц ролей в драмах С. Выспяньского.

X. М о д ж е е в с к а я в роли Марии Стюарт ("Мария Стюарт" Ю. Словацкого).

С о ч.: Wspomnienia i wrazenia, Krakow, 1957; Korespondencja, t. 1-2, Warsz., 1965 (Chtaoowski K.).

Лит.: Got J., Szczublewskl J., Helena Modrzejewska, Warsz., 1958; Т е r 1 е с k i Т., Pani Helena, L., [1962].

МОДЖОКЕРТО (Modjokerto), город в Индонезии, на В. о. Ява, близ г. Сурабая. 52 тыс. жит. (1961). Важный торгово-трансп. узел в долине р. Брантас. Пищевкусовая, преим. сах., и текст, пром-сть.

Близ М. в 1936 нидерл. учёным Г. Кёнигсвальдом найдена черепная коробка двух-трёхлетнего ребёнка ископаемого человека. Череп характеризуется нек-рыми примитивными чертами и малой ёмкостью мозговой полости (700 см³). Абсолютная древность находки из М.- 700 тыс. лет. Большинство исследователей считает, что это ребёнок ранних питекантропов.

МОДЖУЗ, М о в д ж у з Мирза Али (29.3.1873, Шебустар, Юж. Азербайджан,- 25.9.1934, Шахруд, Иран), азербайджанский поэт. Род. в семье купца. Учился в духовной школе. Первые стихи опубл. в Турции, куда переехал в 1889. Вернулся на родину в 1905. Под влиянием азерб. демократич. лит-ры, особенно Сабира, М. писал сатирич. стихи. Бесправие народа ("Родина", "Что ни день" и др.), его борьба против притеснителей, положение закрепощённой женщины ("Несчастные девушки" и др.) - осн. темы его творчества. М. воспевал В. И. Ленина ("Ленин"), Октябрьскую революцию 1917 ("Революция грянет", "Наконец" и др.). Произв. М. увидели свет лишь после смерти поэта.

Соч.: Шэирлэр, Бакы, 1955; в рус. пер.- Стихи. [Предисл. Г. Мамедали], Б., 1956, в кн.: Антология азербайджанской поэзии, т. 2, М., 1960, с. 244-58.

Лит.: О м а р о в а Л., М. А. Мовджуз Шабустари, "Изв. АН Азерб. ССР", 1955, № 5; е ё же, М. Эли Мечуз, Бакы, 1958.

Л. Г. Мкртчян.

МОДЗАЛЕВСКИИ Борис Львович [20.4(2.5}.1874, Тбилиси,- 3.4.1928, Ленинград], советский литературовед, чл.-корр. АН СССР (1918). Окончил Петерб. ун-т (1898). Один из создателей Пушкинского дома. Осн. труды, посвящённые А. С. Пушкину и людям его времени, отличаются широтой эрудиции, тщательностью историко-лит. и биографически-бытовых комментариев. Как автор и редактор участвовал в издании "Русского биографического словаря" (1900-1918), сб-ков "Пушкин и его современники" (в. 1-37, 1903-28); издал "Архив Раевских" (т. 1-5, 1908-15), "Архив декабриста С. Г. Волконского" (т. 1, 1918; изд. не закончено), дневник Пушкина (1923) и его письма (т. 1-2, 1926-28).

Соч.: Библиотека А. С. Пушкина. (Библиографическое описание), СПБ, 1910; А. П. Керн, [Л.], 1924; Пушкин под тайным надзором, 3 изд., Л., 1925: Роман декабриста Каховского, Л., 1926; Пушкин. [Сб. ст.], [Л.], 1929.

Лит.: Памяти Б. Л. Модзалевского. Биографические даты. Библиография трудов, М., 1928.

МОДЗИ, город в Японии, на сев. побережье о. Кюсю, у Симоносекского пролива, в префектуре Фукуока. С 1963 - в составе г. Китакюсю. Один из гл. портов страны; вместе с городом и портом Симоносеки образует объединённый порт Каммон.

МОДИЛЬЯНИ (Modigliani) Амедео (12.7.1884, Ливорно, - 25.1.1920, Париж), итальянский живописец и скульптор, представитель парижской школы. Учился в АХ во Флоренции. С 1906 жил в Париже. Испытал влияние творчества А. де Тулуз-Лотрека, П. Сезанна, П. Пикассо, а также афр. пластики. Как скульптор формировался под воздействием К. Брынкуши, тяготея к упрощённым геометризов. формам и удлинённым пропорциям ("Голова", известняк, 1913, Гал. Тейт, Лондон). Живописная манера М. с её декоративной плоскостностью, острой лаконичностью композиции, музыкальностью силуэтно-линейных ритмов, насыщенностью колорита определилась в нач. 1910-х гг. В своих, как правило, однофигурных картинах - портретах и ню - М. создавал особый мир образов, интимно-индивидуальных и вместе с тем схожих общей меланхолич. самоуглублённостью; их своеобразный тонко нюансированный психологизм, просветлённая поэтичность сочетаются с постоянным, подчас трагич. ощущением незащищённости человека в мире (портрет Л. Зборовского, 1917, Художеств, музей Сан-Паулу; "Эльвира", 1919, частное собрание, Берн; "Большая обнажённая", 1919, Музей совр. иск-ва, Нью-Йорк).

Илл. см. на вклейке к стр. 289, а также т. 11, табл. VI (стр. 48-49).

Лит.: Виленкин В. В., Амедео Модильяни, М., 1970; [Valsecchi M.], Amedeq Modigliani, Mil., 1955; S i с h e 1 P., Modigliani. A biography of Amedeo Modigliani, N. Y., 1967; I dipinti di Modigliani Mil., [1970].

В.А. Калмыков.

МОДИФИКАТОР (от позднелат. modifico - видоизменяю, меняю форму) металлов и сплавов, вещество, малые дозы к-рого существенно изменяют структуру и свойства обработанного им металла или сплава. Эффект от такой обработки наз. модифицированием.

Согласно классификации П. А. Ребиндера, М. делят на две группы. М. первого рода - поверхностно-активные вещества - адсорбируются на зародышах, возникающих на центрах кристаллизации, и тормозят их рост, в результате чего появляется большое кол-во новых зародышей, рост к-рых становится возможным из-за уменьшения концентрации М. на их поверхности. М. второго рода - т. н. М. инокулирующего действия - облегчают образование в расплаве центров кристаллизации, напр., коллоидных частиц, оказывающих влияние на зарождение кристаллов металлич. фаз при затвердевании. При появлении большого числа таких центров образуется повышенное кол-во мелких зёрен осн. фазы или мелких включений др. фаз. Иногда на этих центрах кристаллизуются фазы, иначе не выпадающие в материале.

М. обеих групп размельчают зёрна материала (включений), но М. первого рода усиливают переохлаждение расплавов при кристаллизации, а второго -уменьшают.

Лит.: Ребиндер П. А., Л и п м а н М. С., Физико-химические основы модификации металлов и сплавов малыми поверхностно активными примесями, в кн.: Исследования в области прикладной физико-химии поверхностных явлений, М.- Л., 1936. См. также лит. при ст. Модифицирование металлов и сплавов.

А. А. Жуков.

МОДИФИКАЦИИ в биологии, ненаследственные изменения признаков организма (его фенотипа), возникающие под влиянием изменившихся условий внешней среды. Модифицирующие факторы среды (ими могут быть темп-ра, освещение, режим питания и т. п.) через сдвиги во внутренней среде организма, напр., в уровне гормонов, воздействуют на организм в чувствит. периоды его развития, изменяя течение онтогенеза. Модификационная изменчивость - это изменения в пределах генотипически обусловленной нормы реакции. Гималайские кролики в зависимости от темп-ры среды могут менять окраску от чёрной на холоде, через горностаевую при умеренных темп-pax, до чисто белой при повышенных (рис. 1). Но та или иная окраска родителей крольчатами не наследуется, а наследуется лишь способность менять окраску в зависимости от темп-ры. В природе М., как правило, являются адаптивными реакциями организмов на воздействие тех или иных факторов среды. Так, у озёрного стрелолиста форма листьев зависит от того, где эти листья находятся: надводные - стреловидные, плавающие - сердцевидные с устьицами на верхней стороне, подводные листья - лентовидные (рис. 2). Неадаптивные М. часто представляют собой всевозможные нарушения развития, в крайнем выражении - уродства, морфологич. и физиологич. дефекты (см. Фенокопия, Морфозы).

Рис. 1. Изменение окраски гималайских кроликов в зависимости от температуры: 1 - выращенный при температуре св. 30 °С; 2 - при температуре ок. 25 °С; 3 - кролик, у которого участок кожи на левом бедре охлаждали ниже 25 °С.

Рис. 2. Изменение формы листьев на одном и том же экземпляре стрелолиста в зависимости от условий среды.

Эти М. возникают, как правило, в ответ на сильные внешние стимулы, действию к-рых особи данного вида в нормальных условиях жизни подвергаются очень редко.

М., в отличие от мутаций, не передаются по наследству и могут развиваться у особей данного поколения лишь при наличии условий, в к-рых они обычно возникают. Однако у одноклеточных, а изредка и у многоклеточных организмов встречаются т.н. длительные М., когда признаки, возникающие под влиянием условий внешней среды, сохраняются в течение неск. поколений и после исчезновения индуцирующего фактора. Этот тип М. обусловлен, по-видимому, изменениями относительно стабильных ауто-репродуцирующихся цитоплазматических структур. Являясь ненаследственными изменениями, М. прямого эволюционного значения не имеют. Если же формирующийся в результате М. фенотип имеет высокую адаптивную ценность, то он может фиксироваться в эволюции только путём отбора мутаций, закрепляющих данную М. и приводящих к утрате др. М. данного признака. См. также Изменчивость, Приобретённые признаки.

Лит.: Л о б а ш е в М. Е., Генетика, 2 изд., Л., 1967; Шмальгаузен И. И., Факторы эволюции, М., 1968.

Н. В. Тимофеев-Ресовский, , В. И. Иванов, В. А.Мглинец.

МОДИФИКАЦИЯ (позднелат. modificatio - изменение, от лат. modus - мера, вид, образ и facio - делаю), видоизменение, преобразование, появление новых свойств. Модификации - качественно различные состояния или разновидности чего-либо.

МОДИФИЦИРОВАНИЕ металлов и сплавов, введение в расплавленные металлы и сплавы модификаторов, небольшие количества к-рых резко влияют на кристаллизацию, напр, вызывают формирование структурных составляющих в округлой или измельчённой форме и способствуют их равномерному распределению в основной фазе. В результате М. сплавы приобретают более тонкую структуру, что улучшает их механич. свойства. М. применяется при произ-ве отливок из чугуна (см. Модифицированный чугун) и силуминов (см. Алюминиевые сплавы) др. М. отличается от микролегирования, при к-ром увеличение дозировки присадки приводит к обычному легированию (без явной границы между получаемыми эффектами). При М. увеличение дозировки присадки либо невозможно (из-за малой растворимости, летучести), либо неэффективно, либо вредно (перемодифицирование). Иногда при смешении двух различных расплавов наблюдается явление жидкого М. Эффект, подобный М., может быть получен при нек-рых физ. методах воздействия на жидкий металл, напр, при ультразвуковой обработке, наложении электромагнитного поля и др.

Лит.: Л е в и Л. И., Кантеник С. К., Литейные сплавы, М., 1967.

Л. Л. Жуков.

МОДИФИЦИРОВАННЫЙ ЧУГУН, чугун, в к-рый в жидком состоянии при определённых условиях введены модификаторы.

Модификаторы инокулирующего действия (ферросилиций, силикокальций, С, Аl, сплавы титана, циркония, нек-рых лантаноидов, бария, стронция) позволяют снизить в чугуне содержание Si и С без появления отбела, размельчают графит, в результате чего увеличивается кол-во перлита и улучшаются механич. свойства серого чугуна. Введение Sn, Pb, Р, Sb, N и др. модификаторов способствует получению перлитных серых чугунов. Введение Bi и повышение содержания S резко отбеливают чугун. В ковком чугуне нек-рые модификаторы связывают такие вредные примеси, как азот (в виде AlN, BN) и хром (в виде атомных сегрегации типа Sb₂Cr₃). Нек-рые модификаторы (магний, большинство лантаноидов, иттрий) при определённой их дозе вызывают выделение графита округлой формы, вследствие чего образуется чугун с шаровидным графитом, наз. в ы-сокопрочным. Такой вид модифицирования существенно увеличивает прочность чугуна и резко повышает его пластичность и вязкость. Осн. способы модифицирования: на жёлобе печей, в автоклавах, в спец. ковшах, напр., герметизированных, вдуванием, введением модификаторов через лигатуры или соли, в литниковых системах литейных форм.

Лит.: Г и р ш о в и ч Н. Г., Кристаллизация и свойства чугуна в отливках, М.- Л.. 1966.

А. А. Жуков.

МОДЛОНСКОЕ СВАЙНОЕ ПОСЕЛЕНИЕ, неолитическое поселение 2-й пол. 3-го тыс. до н. э. на р. Модлона, на терр. Кирилловского р-на Вологодской обл. РСФСР. Открыто и исследовалось А. Я. Брюсовым в 1938-40, 1945-57 и С. В. Ошибкиной в 1970. Открыты остатки четырёх домов на сваях и соединяющие их мостки. Найдены кам. и костяные орудия, керамич. и деревянная (украшенная резьбой и скульптурой) посуда, подвески из янтаря, шифера и кости. М. с. п. является инородным среди неолитич. культур севера Европ. части СССР. Стоянки этого типа во 2-й пол. 3-го тыс. до н. э. были распространены южнее - гл. обр. в Вост. Латвии; известны также в Псковской обл. и на верх. Волге.

Модлонское свайное поселение. Реконструкция жилища.

Лит.: Брюсов А. Я., Свайное поселение на р. Модлоне и другие стоянки в Чарозерском районе Вологодской области, в сб.: Материалы и исследования по археологии СССР, № 20, М., 1951.

МОДСЛИ (Maudsley) Генри [5.2.1835, близ г. Сетл, Йоркшир,- 23 (или 24). 1. 1918, Ваши Хит], английский психиатр и философ. В 1857 окончил Лондонский ун-т. Чл. Королев. мед. колледжа (1869). В 1869-79 проф. Лондонского ун-та, затем работал в психиатрич. больницах и созданном им в Лондоне психиатрич. госпитале. Основоположник эволюционного направления в психиатрии; последователь Ч. Дарвина, к-рый высоко ценил книгу М. "Физиология и патология души" (1867, рус. пер. 1871). Заложил основы детской психиатрии в Великобритании, внёс существенный вклад в развитие судебной психиатрии. В филос. взглядах был представителем позитивизма, стоял на позициях психофизиологич. параллелизма и переносил биологич. законы эволюции в область обществ.-ист. развития человека, оправдывал колон. политику, считал, что войны - "полезны человечеству" и т. п.

Соч.: Ogranic to human: psychological and sociological, L., 1916; в рус. пер.- Наследственность в здоровье и в болезни, СПБ, 1886; Ответственность при душевных болезнях, СПБ, 1875.

Лит.: Морозов В. М., Эволюционное направление в психиатрии, "Журнал невропатологии и психиатрии им. С. С. Корсакова", 1957, т. 57, в. 4.

МОДСЛИ (Maudslay) Генри (22.8.1771, Вулидж,- 14.2.1831, Ламбет, похоронен в Вулидже), английский механик. С 12 лет начал работать в мастерских Вулидж-ского арсенала. В 1797 построил токарно-винторезный станок с суппортом (механизированным на основе винтовой пары) и набором зубчатых колёс; тем самым внедрил в пром-сть идеи, разработанные А. К. Нартовым и др., и механизировал произ-во винтов и гаек. Дальнейшая механизация станков, осуществлённая М. и др., привела к машинному произ-ву деталей машин. В 1810 основал крупный маш.-строит, з-д, на к-ром было разработано много новых конструкций станков, паровых и др. машин. В 1815 создал станочную линию по произ-ву канатных корабельных блоков.

МОДУЛИ УПРУГОСТИ, величины, характеризующие упругие свойства материала. В случае малых деформаций, когда справедлив Гука закон, т. е. имеет место линейная зависимость между напряжениями и деформациями, М. у. представляют собой коэфф. пропорциональности в этих соотношениях. Одностороннему нормальному напряжению а, возникающему при простом растяжении (сжатии), соответствует в направлении растяжения модуль продольной упругости Е (модуль Юнга). Он равен отношению нормального напряжения а к относит, удлинению е, вызванному этим напряжением в направлении его действия: Е = σ/ε, и характеризует способность материала сопротивляться растяжению. Напряжённому состоянию чистого сдвига, при к-ром по двум взаимно перпендикулярным площадкам

териала сопротивляться изменению формы при сохранении его объёма. Всестороннему нормальному напряжению а, одинаковому по всем направлениям (возникающему, напр., при гидростатич. давлении), соответствует м о д у л ь объёмного сжатия К - объёмный модуль упругости. Он равен отношению величины нормального напряже

гости характеризует способность материала сопротивляться изменению егс объёма, не сопровождающемуся изменением формы. К постоянным величинам, характеризующим упругие свойства материала, относится также Пуассона

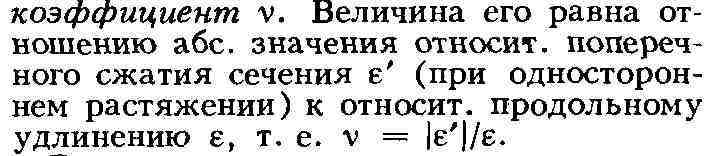
В случае однородного изотропного тела М. у. одинаковы по всем направлениям.

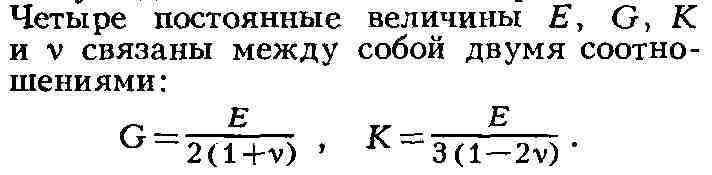
Следовательно, только две из них являются независимыми величинами и упругие свойства изотропного тела определяются двумя упругими постоянными. В случае анизотропного материала постоянные Е, G и v принимают различные значения в различных направлениях и величины их могут изменяться в широких пределах. Кол-во М. у. анизотропного материала зависит от структуры материала. Анизотропное тело, лишённое всякой симметрии в отношении упругих свойств, имеет 21 М. у. При наличии симметрии в материале число М. у. сокращается.

М. у. устанавливаются экспериментально-механич. испытанием образцов изучаемых материалов. М. у. не являются строго постоянными величинами для одного и того же материала, их значения меняются в зависимости от хим. состава материала, от его предварит. обработки (термич. обработка, прокат, ковка и др.). Значения М. у. также зависят от темп-ры материала.

Лит.: Фридман Я. Б., Механические свойства металлов, 2 изд., М., 1952.

МОДУЛОР, модулер, модюлор (франц. modulor), система пропорций, предложенная в 1940-х гг. франц. архитектором Ле Корбюзье и его сотрудниками. М. основывается на размерах и пропорциях человеческого тела (исходные величины - условный рост человека, его высота до солнечного сплетения и с поднятой рукой, принятые равными 183, 113 и 226 см), на золотом сечении и рядах Фибоначчи чисел. Введение М. преследовало цели внести в совр. архитектуру и художеств. конструирование модуль, осн. на измерении человека. М. последовательно использован в ряде построек самого Ле Корбюзье и оказал известное влияние на практику мировой архитектуры и особенно дизайна.

Лит.: Ле Корбюзье Ш. Э., Архитектура 20 века, пер. с франц., [МЛ, 1970; Le Corbusier Ch., Le modulor, Boulogne sur Seine, [1951].

МОДУЛЬ (от лат. modulus - мера) в архитектуре, условная единица, принимаемая для координации размеров частей здания или комплекса. В архитектуре разных народов в зависимости от особенностей строит, техники и композиции зданий за М. принимались разные величины. М. сооружения могут быть: одно из осн. его измерений (диаметр купола или стороны помещения в ср.-век. сводчатых постройках Европы и Ср. Азии), размер отд. элемента сооружения (диаметр колонны, ширина триглифа в ордерной антич. архитектуре) или размер строит, изделия (длина кирпича, бревна). В качестве М. используются также и непосредственно меры длины (фут, сажень, метр и др.), образуя т. н. линейный М.

Возникнув вследствие технич. необходимости, М. стал и одним из средств архит. композиции, к-рое используется для приведения в гармонич. соответствие размеров целого и его частей (напр., золотое сечение в антич. архитектуре, модулор в практике Ле Корбюзье). Однако применение М. никогда не означало механич. расчёта всех величин: в поисках выразит, соотношений архитекторы вносили в соразмерность частей поправки, учитывающие особенности зрительного восприятия. В архитектуре 2-й пол. 20 в., в связи с развитием методов сборного индустр. стр-ва, постоянные линейные М. получили особенно большое технич. значение как средство согласования планировочных и конструктивных элементов зданий, их унификации и стандартизации.

Осн. М. размером в 10 см, производные от него укрупнённые (3 М., 6 М., 12 М., 15 М., 30 М., 60 М.) и дробные М. вместе с правилами их применения составляют модульную систему. Они установлены сов., зарубежными и междунар. нормами и стандартами.

Лит.: ХазановД. Б., Модуль в архитектуре, в сб.: Вопросы теории архитектурной композиции, [в.] 2, М., 1958; Архитектура жилого комплекса, М., 1969.

Д. Б. Хазанов.

МОДУЛЬ в математике, 1)М. (или абс. величина) комплексного числа

исходящим из начала прямоугольной системы координат и имеющим конец в точке с координатами (х, у); длина этого вектора и есть М. комплексного числа г. 2) М. перехода от системы логарифмов при основании а к системе логарифмов при основании b есть число

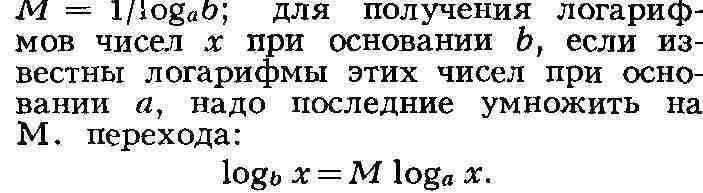
МОДУЛЬ в электронике, унифицированный функциональный узел, функционально законченный узел радиоэлектронной аппаратуры, оформленный конструктивно как самостоят. изделие. По конструкции М. разделяют на плоские, объёмные и объёмно-плоскостные, по типу электронных приборов - на транзисторные и ламповые. Чаще всего М. собирают на печатных платах. Технология изготовления М. допускает высокую степень автоматизации, что обеспечивает высокую надёжность М. в работе. М. могут быть отдельно настроены и проверены, что позволяет при ремонте производить их замену без дополнит, подстроек и регулировок. Применение М. (функционально-узловой метод конструирования) сокращает сроки проектирования, удешевляет проектирование и изготовление аппаратуры, упрощает её эксплуатацию и модернизацию.

Рис, 1. Плоский модуль - логическая ячейка узла электронной вычислительной машины: 1 - выводы; 2 - полупроводниковый диод; 3 - транзистор; 4 - конденсатор; 5 - печатная плата (основание модуля); 6 - резистор.

Рис. 2. Объёмный модуль (без кожуха)- усилитель звуковой частоты: 1 - верхняя печатная плата; 2 - резисторы; 3 - металлическая перемычка между печатными платами; 4 - конденсатор; 5 - нижняя печатная плата; 6 - выводы; 7 - транзистор.

Лит.: Гусев В. П., Технология радио-аппаратостроения, М., 1972.

МОДУЛЬ ВЫСОКОЭЛАСТИЧЕСКИЙ, мера сопротивления деформированию резин и др. каучукоподобных материалов, представляющая собой отношение напряжения а к обратимой деформации е. При малых е величина о пропорциональна е (линейная область механич. поведения материала), и поэтому здесь, по определению, М. в. аналогичен обычному модулю продольной упругости (модулю Юнга) или модулю сдвига (см. Модули упругости) в зависимости от того, при каком виде напряжённого состояния измеряется М. в. При больших Е (обычно наз. высокоэластическими) пропорциональность о и е нарушается, и под М. в. в этом случае понимают эквивалентную величину, зависящую от Е и по-прежнему определяемую как отношение а/е. М. в. обычно составляет от долей Мн/м² до неск. Мн/м² (от долей кгс/см² до десятков кгс/см²), тогда как, напр., для металлов и полимерных стёкол модуль Юнга достигает величин порядка 10⁵ или 10³ Мн/м² соответственно (10⁶ или 10⁴ кгс/см²). Теоретически М. в. должен возрастать с повышением темп-ры линейно, практически температурной зависимостью М. в. можно пренебречь. Для высокоэластич. состояния характерно отсутствие изменений объёма при растяжении, поэтому М. в., измеренный при сдвиге, составляет ⅓ М. в., определённого при одноосном растяжении.

Резкая разница значений М. в. каучукоподобных веществ и модуля Юнга кристаллич. тел и стёкол связаны с различием природы деформаций. Определяющим фактором в случае высокоэластич. деформации является гибкость полимерной цепи: деформация тела в целом осуществляется прежде всего путём изменения конформаций макромолекул (см. Высокоэластическое состояние). Упругая же деформация происходит вследствие изменения межатомных расстояний и валентных углов. Силы упругости, препятствующие таким изменениям, существенно больше, чем силы, необходимые для предотвращения упругого восстановления каучукоподобного тела. Абс. значения М. в. возрастают по мере усиления межмолекулярного взаимодействия полимерных цепей и увеличения густоты пространственной сетки хим. связей.

А.Я. Малкин.

МОДУЛЬ ЗУБЧАТОГО КОЛЕСА, геометрический параметр зубчатых колёс. Для прямозубых цилиндрич. зубчатых колёс модуль то равен отношению диа-

нормальный и осевой шаги по делительному цилиндру. Значения М. з. к. стандартизованы, что является основой для стандартизации др. параметров зубчатых колёс (геометрич. размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента (см. Зубчатая передача).

МОДУЛЬ РАССТОЯНИЯ, разность между видимой (то) и абсолютной (М) звёздными величинами небесного светила, применяемая в астрономии для описания расстояний до звёзд и звёздных систем. В то время как М зависит только от собственной светимости звезды, т зависит также и от расстояния г (в пс) до неё: т - М = 5 lg r - 5.

МОДУЛЬ ЮНГА, то же что, модуль продольной упругости Е; см. Модули упругости.

МОДУЛЬОН, м о д и л ь о н  (франц. modillon, от итал. modiglione), архитектурная деталь типа кронштейна, к-рая поддерживает выносную плиту венчающего карниза, преим. в ордерной архитектуре (см. Ордер архитектурный). Иногда М. играет лишь декоративную роль.

МОДУЛЯТОР в радиотехнике и дальней связи, устройство, осуществляющее модуляцию - управление параметрами высокочастотного электромагнитного переносчика информации в соответствии с электрич. сигналами передаваемого сообщения. М. является составной частью гл. обр. передающих устройств электросвязи и радиовещания. Переносчиком информации обычно служат гармонич. колебания или волны с частотой (наз. несущей или поднесущей) ~ 10⁴-10¹⁵ гц. В зависимости от того, какой параметр гармонич. колебаний или волн изменяется, различают амплитудную, частотную, фазовую или смешанную (напр., при однополосной передаче) модуляцию колебаний. Соответственно различны и виды М. При импульсно-кодовой модуляции переносчиком информации служит регулярная последовательность импульсов электрических, параметрами к-рых (амплитуда, ширина, частота или фаза повторений) управляют с помощью соответствующих типов импульсных М. Модулирующие электрич. сигналы передаваемого сообщения могут иметь самую разнообразную форму: от простых и медленных телеграфных посылок в виде точек и тире или колебаний звукового диапазона частот при передаче речи и музыки до сложных, быстро изменяющихся сигналов, применяемых в телевидении или в многоканальной проводной и радиорелейной связи. Часто в функцию М. входит также усиление модулирующих колебаний.

Непременное требование к модуляции состоит в том, что модулирующее колебание должно изменяться во времени значительно медленнее модулируемого. Поэтому в любом М. сочетаются взаимодействующие цепи модулируемых колебаний или волн с цепями модулирующего сигнала более низкой частоты. Определяющим в М. является управляющий элемент, посредством к-poro сигнал воздействует на параметры модулируемых колебаний или волн. Электронная лампа как универсальный управляющий элемент сохранилась к 1974 гл. обр. в М. мощных радиопередающих устройств (для них специально разработаны т. н. модуляторные лампы). При мощностях передатчиков <0,5 квт лампы успешно вытесняются транзисторами и др. полупроводниковыми приборами. В устройствах, работающих на СВЧ, наряду с полупроводниковыми приборами используются клистроны, лампы бегущей волны и др. О М. в оптич. диапазоне волн см. в ст. Модуляция света.

При амплитудной модуляции М. изменяет амплитуду генерируемых (или усиливаемых) колебаний с несущей частотой. В сеточном М. лампового радиопередатчика модулирующее напряжение воздействует на входную (сеточную) цепь генератора или усилителя высокочастотных колебаний, в анодном М.- на выходную (анодную) цепь генераторной лампы. Сеточный М. более экономичен, анодный же может обеспечить большую глубину модуляции при малых искажениях. В транзисторных радиопередатчиках базовый и коллекторный М. (рис. 1 а, 6) являются транзисторными аналогами соответственно сеточного и анодного ламповых М. Для получения амплитудно-модулиров. колебаний с подавленными колебаниями несущей частоты применяют т. н. балансный М. (см. Однополосная модуляция).

Рис. 1. Транзисторные амплитудные модуляторы: а - базовый: б - коллекторный; и_вч - напряжение модулируемых колебаний; Тр - низкочастотный трансформатор; С1 C2, L1 - конденсаторы и катушка индуктивности развязывающих цепей по высоким и низким частотам; R и R1 - резисторы делителя постоянного напряжения в цепи питания транзистора; Ек - напряжение, подаваемое на коллектор транзистора. Транзистор Т с резонансным контуром из катушки индуктивности L и конденсатора С образуют управляемый усилитель колебаний с несущей частотой, коэффициент усиления которого изменяется при изменении Uм.

Рис. 2. Варикапный частотный модулятор: В - варикап, ёмкость которого с индуктивностью катушки L образуют резонансный контур генератора на транзисторе Т; Е_в, Е_т - напряжения, подаваемые соответственно на варикап и транзистор; C1, С2 - конденсаторы развязывающих цепей; R, R1, R2 - резисторы в развязывающих цепях. Эффективной ёмкостью варикапа управляет модулирующее напряжение u_м.

Рис. 3. Волноводный импульсный модулятор сверхвысоких частот: 1 - радиоволновод; 2 - диодная камера; Д - переключательный диод или варикап, открывающий радиоволновод (импульс электромагнитной волны на выходе) при положительном "м и запирающий его (пауза на выходе) при отрицательном модулирующем напряжении ы_м.

При частотной модуляции и фазовой модуляции в качестве управляющего элемента в М. используются т. н. реактивные устройства, у к-рых эффективная ёмкость или индуктивность (или то и другое) изменяется под действием модулирующего сигнала. Реактивное устройство включается или непосредственно в резонансный контур задающего генератора, или в последующие фазовращающие цепи радиопередатчика. В ламповых М. такое устройство получило назв. реактивной лампы, в транзисторных - реактивного транзистора. Кроме того, в нек-рых транзисторных фазовых и частотных М. используют явление сдвига фазы генерируемых колебаний, зависящего при определённых режимах работы от значения постоянной составляющей коллекторного тока. Широкое применение в качестве реактивного управляющего элемента в М. находят варикапы (рис. 2). При импульсной модуляции в М. управляющими элементами также служат электронная лампа или полупроводниковый прибор, напр., варикап (рис. 3), к-рый запирает или отпирает волноводный тракт при посылках импульсного модулирующего напряжения различного знака.

Иногда М. входит в состав усилительных устройств, работающих в различных диапазонах частот -от звуковых до СВЧ. Магнитный усилитель имеет М. в виде насыщающегося дросселя электрического, индуктивностью к-рого управляет ток усиливаемого сигнала. В этом случае обычно модулируется переменный ток пром. частоты, более высокой по сравнению с частотами спектра сигналов - обычно команд в системах автоматики. В диэлектрическом усилителе М. представляет собой нелинейный конденсатор, ёмкостью к-рого управляет напряжение сигнала. М. является составной частью нек-рых параметрических усилителей.

Лит.: К у к к К. И., С о к о л и н с к и й В. Г., Передающие устройства многоканальных радиорелейных систем связи, М., 1968; М о д е л ь З. И., Радиопередающие устройства, М., 1971; Радиопередающие устройства, под ред. Б. П. Терентьева. М., 1972; Радиопередающие устройства на полупроводниковых приборах, под ред. Р. А. Валитова и И. А. Попова, М., 1973.

М. Д. Карасёв.

МОДУЛЯЦИЯ (от лат. modulatio - мерность, размеренность) в физике и технике, изменение по заданному закону во времени величин, характеризующих к.-л. регулярный процесс. М. вызывают внешним воздействием. Наибольшее практич. значение имеет М. электромагнитных колебаний радио- и оптич. диапазонов (см. Модуляция колебаний, Модуляция света). Работа всех электронных приборов основана на М. электронного потока. Так, в электронных лампах применяется М. плотности электронного потока, в кинескопах - М. интенсивности электронного пучка, бомбардирующего экран. В клистронах и др. электронных приборах СВЧ используют М. скорости электронов. М. широко применяется в измерительной технике; предварительная М. измеряемой величины позволяет повысить чувствительность аппаратуры и точность измерений.

МОДУЛЯЦИЯ в музыке, смена тональности со смещением тоники (тональная М.). В обычной функциональной М. связь тональностей устанавливает общий для них посредствующий аккорд, меняющий свою функцию при появлении гармонич. оборота, характерного для новой тональности. Решающее значение приобретает модулирующий аккорд с соответствующей альтерацией.

Особый вид функциональной М.- энгармоническая М. (см. Энгармонизм), в к-рой посредствующий аккорд оказывается общим для обеих тональностей благодаря энгармоническому переосмыслению его структуры. Такая М. легко связывает отдалённые тональности и часто производит впечатление неожиданного крутого модуляционного поворота.

Таблица XXV

К ст. "Модерн"-. 1. И. М. О л ь б р и х. Выставочное здание и "Свадебная башня" в Дармштадте. 1907-08. 2. В. Орта. Особняк в Брюсселе. Ок. 1900. 3. А. Г а у д и. Жилой дом Каса Батло в Барселоне. 1905-07. 4. А. Э н д е л л ь. "Пёстрый театр" в Берлине. 1901. 5. Лестница в особняке Рябушинского в Москве (1902-06, архитектор Ф. О. Шехтель). 6. Ф. О. Шехтель. Здание типографии "Утро России" в Москве. 1907. 7. И. М. О л ь б р и х. Универсальный магазин "Тиц" в Дюссельдорфе. 1908. 8. Ч. Р. Макинтош. Столовая на выставке в Берлине. 1906.

Таблица XXVI

К ст. "Модерн"-. 1. Л. С. Бакст. "Ужин". 1902. Русский музей. Ленинград. 2. Ф. Ходлер. "День". 1898-1900. Художественный музей. Берн. 3. ф. О. Ш е х т е л ь. Фонарь у входа в Московский Художественный театр. 1902. 4. X. в а н де В е л д е. Фолькванг-музей в Хагене (Германия). 1901-02 ("Фонтан коленопреклонённых" - мрамор, 1898, скульптор Ж. Минне). В. А. Г а у д и. Лестница в парке Гуэль в Барселоне. 1903. 6. Р. Л а л и к (Франция). Ваза. Стекло. Музей декоративных искусств. Париж. 7. Р. Л а л и к. Брошь. Серебро, жемчуг. Ок. 1900. Художественно-промышленный музей города Цюриха. 8. О. Делаэрш (Франция). Ваза. Керамика. Музей декоративных искусств. Париж.

Большое значение в М. имеют мелодич. связи аккордов, естественное голосоведение. Они могут играть ведущую роль в М., отстраняя на задний план функциональные связи аккордов и даже совсем их заменяя. Такая мелодико-гармонич. М. без общего аккорда наиболее характерна при непосредств. переходе в отдалённую тональность, в к-ром связующим звеном служит только модулирующий мелодически-подводящий аккорд. В одноголосном (или октавном) движении встречается мелодическая М. (как таковая, без гармонии), к-рая может идти и в далёкую тональность.

М. без всякой подготовки, с непосредств. утверждением новой тоники, наз. сопоставлением тональностей. Она обычно применяется при переходе к новому разделу формы, однако изредка встречается и внутри построения.

От тональной М. отличается ладовая М., в к-рой без смещения тоники происходит только перемена наклонения лада в одноимённой тональности (см. Наклонение в музыке).

Лит.: Р и м а н Г., Систематическое учение о модуляции..., пер. с нем., М., 1929; Римский-Корсаков Н. А., Учебник гармонии, Поли. собр. соч., т. 4, М., 1960; Т ю л и н Ю., Учебник гармонии, ч. 2, М., 1959.

Ю. Н. Тюлин.

МОДУЛЯЦИЯ КОЛЕБАНИЙ, медленное по сравнению с периодом колебаний изменение амплитуды, частоты или фазы колебаний по определённому закону. Соответственно различаются амплитудная модуляция, частотная модуляция и фазовая м о д у л я ц и я (рис. 1). При любом способе М. к. скорость изменения амплитуды, частоты или фазы должна быть достаточно малой, чтобы за период колебания модулируемый параметр почти не изменился.

Рис. 1. Схематическое изображение модулированных колебаний: а - немодулированное колебание; б - модулирующий сигнал; в - амплитудно-модулированное колебание; г - частотно-модулированное колебание; д - фазово-модулированное колебание.

М. к. применяется для передачи информации с помощью электромагнитных волн радио- или оптич. диапазонов. Переносчиком сигнала в этом случае являются синусоидальные электрич. колебания высокой частоты ю (несущая частота). Амплитуда, частота, или фаза этих колебаний, а в случае света и полязация, модулируются передаваемым сигналом (см. Модуляция света).

Рис. 2. Амплитудная модуляция синусоидальным сигналом, (О - несущая частота, О - частота модулирующих колебаний, Амакс и Амин - максимальное и минимальное значения амплитуды.

В простейшем случае модуляции амплитуды А синусоидальным сигналом модулированное колебание, изображённое на рис. 2, может быть записано в виде:

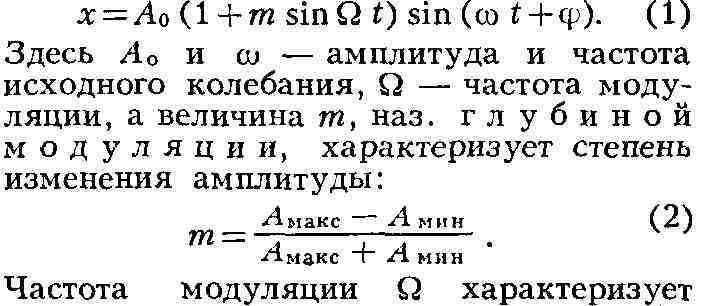
скорость изменения амплитуды колебаний. Эта частота должна быть во много раз меньше, чем несущая частота со. Модулированное колебание уже не является синусоидальным. Амплитудно-модулированное колебание представляет собой сумму трёх синусоидальных колебаний с частотами w, w+ Q и со - Q. Колебание частоты со наз. (в радиотехнике) несущим. Его амплитуда равна амплитуде исходного колебания Ло. Две остальные частоты наз. б о-ковыми частотами, или спутниками. Амплитуда каждого спутника равна mAо/2.

Т. о., любая передающая радиостанция, работающая в режиме амплитудной модуляции, излучает не одну частоту, а целый набор (спектр) частот. В простейшем случае М. к. синусоидальным сигналом этот спектр содержит лишь три составляющие - несущую и две боковые. Если же модулирующий сигнал не синусоидальный, а более сложный, то вместо двух боковых частот в модулированном колебании будут две боковые полосы, частотный состав к-рых определяется частотным составом модулирующего сигнала. Поэтому каждая передающая станция занимает в эфире определённый частотный интервал. Во избежание помех несущие частоты различных станций должны отстоять друг от друга на расстоянии, большем, чем сумма боковых полос. Ширина боковой полосы зависит от характера передаваемого сигнала: для радиовещания - 10 кгц, для телевидения - 6 Мгц. Исходя из этих величин, выбирают интервал между несущими частотами различных станций. Для получения амплитудно-модулированного колебания колебание несущей частоты со и модулирующий сигнал частоты Q подают на спец. устройство - модулятор.

В случае частотной модуляции синусоидальным сигналом частота колебаний меняется по закону:

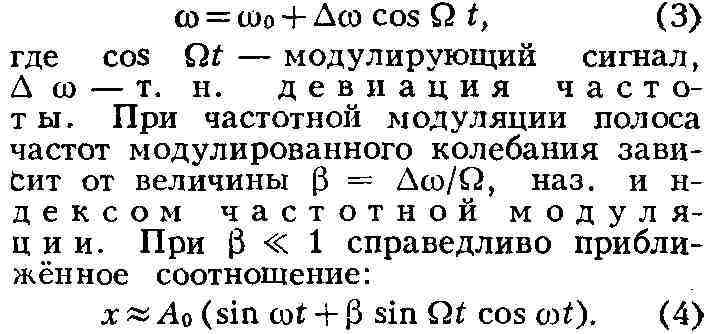
В этом случае частотно-модулированное колебание, так же как и амплитудно-модулированное, состоит из несущей частоты ю и двух спутников с частотами

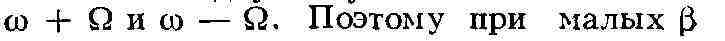
полосы частот, занимаемые амплитудно-модулированным и частотно-модулированным сигналами, одинаковы. При больших индексах B спектр боковых частот значительно увеличивается. Кроме колебаний с частотами w ± Q, появляются колебания, частоты к-рых равны w±2Q, w ± 3 Q и т. д. Полная ширина полосы частот, занимаемая частотно-модулированным колебанием с девиацией Дw и частотой модуляции О (с точностью, достаточной для практич. целей), может считаться равной 2Дw + 2Q. Эта полоса всегда шире, чем при амплитудной модуляции.

Преимуществом частотной модуляции перед амплитудной в технике связи является большая помехоустойчивость. Это качество частотной модуляции проявляется при B>>1, т. е. когда полоса частот, занимаемая частотно-модулированным сигналом, во много раз больше 2Q. Поэтому частотно-модулированные колебания применяются для высококачественной передачи сигналов в диапазоне ультракоротких волн (УКВ), где на каждую радиостанцию выделена полоса частот, в 15-20 раз большая, чем в диапазоне длинных, средних и коротких волн, на к-рых работают радиостанции с амплитудной модуляцией. Частотная модуляция применяется также для передачи звукового сопровождения телевизионных программ. Частотно-модулированные колебания могут быть получены изменением частоты задающего генератора (см. Радиопередатчик).

В случае фазовой модуляции модулированное колебание имеет вид:

х = Ао sin (wof + Д ф cos Qt). (5)

Если модулирующий сигнал синусоидальный, то форма модулированных колебаний и их спектральный состав для частотной и фазовой модуляции одинаковы. В случае несинусоидального модулирующего сигнала это различие чётко выражено.

В многоканальных системах связи в качестве переносчика информации используется не гармонич. колебание, а периодич. последовательность радиоимпульсов, каждый из к-рых представляет собой цуг колебаний высокой частоты (рис. 3). Периодич. последовательность таких импульсов определяется четырьмя основными параметрами: амплитудой, частотой следования, длительностью (шириной) и фазой. В соответствии с этим, возможны четыре типа импульсной модуляции: амплитудно-импульсная, частотно-импульсная, широтно-импульсная, фазово-импульсная (рис. 4). Импульсная модуляция обладает повышенной помехоустойчивостью по сравнению с модуляцией непрерывной синусоидальной несущей, зато полоса частот, занимаемая передающей радиостанцией с импульсной модуляцией, во много раз шире, чем при амплитудной модуляции (см. Импульсная модуляция, Импульсная радиосвязь).

Рис. 3. Радионмпульс.

Рис. 4. Различные виды импульсной модуляции: а - немодулированная последовательность радиоимпульсов; б - передаваемый сигнал; в - амплитудно-имлульсная модуляция; г - частотно-импульсная модуляция; д - широтно-импулъсная модуляция; е - фазово-импульсная модуляция.

Лит.: Харкевич А. А., Основы радиотехники, ч. 1, М., 1962; Гольдман С. Гармонический анализ, модуляция и шумы пер. с англ., М., 1951; Рыто в С. М. Модулированные колебания и волны, "Тр Физического ин-та АН СССР", 1940, т. 2 в 1.

В. Н. Парыгин