МНИМАЯ ЕДИНИЦА, число г, квадрат к-рого равен отрицательной единице;

МНИМАЯ СДЕЛКА, см. в ст. Сделка.

МНИМАЯ ЧАСТЬ комплексного числа z = х + iy, множитель у при мнимой единице г; М. ч. обозначается Im 2.

МНИМОЕ ИЗОБРАЖЕНИЕ предмета (воспринимается глазом как предмет) образуется пересечениями геометрич. продолжений световых лучей, прошедших через оптич. систему, в направлениях, обратных действит. ходу этих лучей. Подробнее см. Изображение оптическое.

МНИМОЕ КОРМЛЕНИЕ, предложенный И. П. Павловым (1890) метод исследования роли центр. нервной системы (ЦНС) в регуляции желудочной секреции, а также др. вопросов нейрофизиологии (напр., уровня глюкозы в крови, состояния пищевых депо, распределения воды в организме в условиях, когда поглощаемая пища или вода не поступает в желудочно-кишечный тракт). М. к., как и мнимое питьё, заключается в поглощении пищи (или жидкости) оперированным животным с перерезанным пищеводом, концы к-рого выведены наружу на шее и приживлены в коже (такая хронич. операция наз. эзофаготомией). Опыт обычно ставят на собаке, к-рой предварительно накладывают фистулу желудка (см. рис.). Через неск. минут после начала М. к. начинает выделяться желудочный сок, секреция к-рого не прекращается 2-3 часа, даже при кратковременном М. к. (если же продолжать М. к. неск. часов, то от собаки можно получить до 1 л чистого, т. е. не смешанного с пищей, сока, используемого для леч. целей). Как показал И. П. Павлов с сотрудниками, после двусторонней перерезки блуждающих нервов, по к-рым импульсы из ЦНС поступают к желудку, сокоотделение при М. к. отсутствует. Это подтверждает рефлекторный характер первой фазы сокоотделения, в ходе к-рой выделяется примерно ⁴/4 нормального кол-ва желудочного сока (т. н. запальный сок). См. также Желудок, Пищеварение.

Опыт мнимого кормления (схема).

Лит.: Павлов И. П., Поли. собр. соч., т. 5, М.- Л., 1952. О. М. Бенюмов.

МНИМЫЕ ЧИСЛА, числа вида х + iy, где i = КОРЕНЬ ИЗ (-1), х и у - действительные числа и у не= 0, т. е. комплексные числа, не являющиеся действительными; М. ч. вида iy наз. чисто мнимы м н (иногда только их наз. М. ч.). Термин "М. ч." возник, когда эти числа уже вошли в употребление, однако реальный смысл их ещё не был раскрыт.

МНИШЕК (Mniszech) Марина (ок. 1588-1614), политическая авантюристка, дочь польск. воеводы Ежи (Юрия) Мнншека, одного из организаторов интервенции против России в начале 17 в. Брак М. с самозванцем Лжедмитрием 1 давал возможность польско-литов. магнатам и католич. духовенству контролировать своего ставленника; в мае 1606 М. короновалась в Москве. За отказ от царского титула (после гибели Лжедмитрия I) отпущена на родину (июль 1608), но оказалась в Тушине, где признала Лжедмитрия II "спасшимся" мужем. После его смерти (дек. 1610) М. нашла покровителя в лице атамана И. М. Заруцкого, к-рый пытался поддержать кандидатуру её сына Ивана (род. в янв. 1611) на рус. престол. Вместе с Заруцким и сыном М. бежала в Астрахань, а затем (в мае 1614) на р. Яик (Урал), где они были выданы казаками рус. пр-ву. Заруцкий и сын М. были казнены в Москве, а М. умерла в заточении.

МНОГОАТОМНЫЕ СПИРТЫ, спирты жирного ряда с несколькими группами - ОН в молекуле; так же, как и др. многоатомные соединения, содержащие в молекуле более одной функциональной группировки, подразделяются на двухатомные (гликоли), трёхатомные (глицерины), четырёхатомные (тетриты), пятиатомные (пентиты), шестиатомные (гекситы) и т. д. Из спиртов, содержащих не менее четырёх групп - ОН, наибольшее значение имеют пентаэритрит C(CH₂OH)i и генетически связанные с моносахаридами пентиты (напр., ксилит, адонит, арабит) и гекситы (маннит, сорбит, дульцит и др.). М. с.- бесцветные кристаллич. вещества сладкого вкуса, легко растворимые в воде; многие из них синтезируются растениями; для каждого спирта известно большое число стереоизомеров. М. с. обладают всеми свойствами одноатомных спиртов (они легко, напр., этерифицируются и окисляются). Нитраты М. с. обладают взрывчатыми свойствами. М. с. в пром-сти получают обычно восстановлением соответствующих альдоз и кетоз; применяют в производстве полимеров (пентаэритрит, ксилит), взрывчатых веществ, используют в качестве заменителей сахара для больных диабетом (сорбит, ксилит), в косметич. и фармацевтич. пром-сти (как увлажнители, а эфиры М. с.- как эмульгаторы).

МНОГОБОРОДНИК (Polypogon), род растений сем. злаков. Однолетние или многолетние травы с плоскими листовыми пластинками. Соцветие - густая, б. ч. цилиндрич. щетинистая метёлка из мелких одноцветковых колосков. Колосковые чешуи почти равные, на спинке округлые, нижняя цветковая чешуя плёнчатая, с 5 жилками, без ости или с очень короткой остью. 8-10 (по др. данным, до 15) видов в умеренных (на юге), субтропич. и тропич. областях. В СССР - 3 однолетних вида на юге Европ. части, Кавказе, юге Зап. Сибири и в Ср. Азии; растут по сырым солончаковатым лугам, приречным пескам, солончакам и как сорняки в посевах. Молодые растения М. хорошо поедаются скотом.

МНОГОБОРЬЯ спортивные, установленные междунар. или гос. спортивными классификациями сочетания физич. упражнений в одном или неск. видах спорта. М. имеют целью выявление разносторонних психофизич. качеств и двигательных навыков спортсменов и физкультурников. Впервые соревнования в М.- пентатлон (бег, прыжки, метание копья и диска, борьба) были включены в программу др.-греч. Олимпийских игр в 708 до н. э. Существующие в совр. спортивной классификации М. в одном виде спорта условно подразделяются на 3 группы: неоднократное выполнение однородных упражнений (М. в акробатике, бобслее, прыжках в воду и на батуте, в парусном и санном спорте, фигурном катании и др.); выполнение однородных упражнений на разных дистанциях или из разных положений (в конькобежном спорте, стрельба из лука и др.); выполнение разных упражнений в разных условиях, на разных снарядах или дистанциях (в лёгкой атлетике, гимнастике, конном, воднолыжном, горнолыжном и парашютном спорте, тяжёлой атлетике, комплексном плавании и др.). М., состоящие из упражнений в разных видах спорта, условно подразделяются на выполняемые с одного старта (напр., биатлон) и с разных стартов (лыжное двоеборье, совр. пятиборье, комплекс ГТО и др.).

Особую группу М. составляют военные и военно-прикладные М., культивируемые в Вооружённых Силах СССР и организациях ДОСААФ. Военные М. впервые появились в отд. воинских частях после окончания Гражданской войны 1918-20, широкое распространение получили в Сов. Армии в период Великой Отечеств, войны 1941-45 как средство повышения боевой подготовки подразделений. С сер. 40-х гг. включаются в программы первенств воен. округов, с 50-х гг. в программы чемпионатов Вооружённых Сил СССР, спартакиад и чемпионатов Спортивного комитета дружественных армий (СКДА). В 1964 в Вооружённых Силах СССР введена Военно-спортивная классификация, в к-рую включены троеборье (стрельба, преодоление полосы препятствий, метание гранат), пятиборье (стрельба, гимнастика, плавание, кросс, фигурное вождение автомобиля), офицерские М. (летнее - стрельба, кросс, плавание, гимнастика; зимнее - стрельба, лыжные гонки, гимнастика) и др. Массовое развитие в СССР в 50-70-е гг. военно-технических видов спорта обусловило появление различных военно-спортивных М.: автомобильное, мотоциклетное, радиомногоборье, морское, подводное, летние военно-прикладные троеборье и пятиборье, малокалиберный биатлон, военизированная эстафета и др. Как правило, военно-спортивные М. включают упражнения из различных видов спорта, напр.: автомобильное - фигурное вождение автомобиля, соревнование на экономичность движения, кросс, стрельбу, метание гранаты; морское - греблю на морских ялах, парусные гонки на ялах, кросс, плавание, стрельбу. Все виды военно-прикладных М. включены в Единую всесоюзную спортивную классификацию. См. также Десятиборье, Пятиборье и статьи о видах спорта, например Лёгкая атлетика, Конькобежный спорт.

К. П. Жаров, Л. Л. Чистый.

МНОГОБУГОРЧАТЫЕ (Multituberculata), отряд вымерших млекопитающих. Жили с юры до среднего эоцена. Самые крупные из мезозойских млекопитающих (достигали величины сурка). М., подобно грызунам, имели по паре крупных резцов в верхней и нижней челюстях и крупные коренные зубы с многочисл. бугорками, расположенными правильными продольными рядами (отсюда назв.). По характеру питания и образу жизни, очевидно, были сходны с появившимися позднее грызунами; строение конечностей указывает на древесный образ жизни. Вероятно, были яйцекладущими, подобно совр. клоачным. Однако ряд черт строения сближает их с сумчатыми. Были распространены в Зап. Европе, Центр. Азии и Сев. Америке. М. - своеобразная боковая ветвь класса млекопитающих, не оставившая потомков.

МНОГОГЛАЗКИ, червонцы (Chrysophanus), род бабочек сем. голубянок.

МНОГОГЛАСИЕ, в рус. богослужении одновременное исполнение неск. различных песнопений, отличающихся как по тексту, так и по напеву. Возникло в нач. 16 в., когда был распет полный круг песнопений и мелодии из речитативных переросли в распевные, в связи с чем певческое исполнение всей церк. службы занимало очень много времени. На протяжении 16-17 вв. велась борьба с М., к-рое приводило к антихудожеств. смешению музыки песнопений и полной неразборчивости для слушателей их текстов . Полностью М. перестало применяться лишь в 1-й пол. 18 в.

Лит.: Преображенский А. В., Вопрос о единогласном пении в русской церкви XVII-ro века. Исторические сведения ц письменные памятники, [СПБ], 1904.

МНОГОГОЛОСИЕ, склад музыки, основанный на сочетании в одновременности неск. голосов; противостоит монодии. Различают неск. типов М.: гетерофонию, гомофонию и полифонию. Гетерофония характерна для различных нар. культур, в т. ч. русской (подголосочное М. рус. нар. песни); гомофония и полифония ведут своё происхождение от неё. Возможно сочетание в одновременности различных типов М.

МНОГОГРАННИК в трёхмерном пространстве, совокупность конечного числа плоских многоугольников, такая, что каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым (по этой стороне); от любого из многоугольников, составляющих М., можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь,- к смежному с ним, и т. д. Эти многоугольники наз. гранями, их стороны - рёбрами, а их вершины - вершинам и М.

Приведённое определение М. получает различный смысл в зависимости от того, как определить многоугольник. Если под многоугольником понимают плоские замкнутые ломаные (хотя бы и самопересекающиеся), то приходят к первому определению М. (вопросы, связанные с определяемыми таким образом М., будут рассмотрены в конце статьи). Осн. часть статьи построена на основе второго определения М., при к-ром его грани являются многоугольниками, понимаемыми как части плоскости, ограниченные ломаными. С этой точки зрения М. есть поверхность, составленная из многоугольных кусков. Если эта поверхность сама себя не пересекает, то она есть полная поверхность нек-рого геометрич. тела, к-рое также наз. М.; отсюда возникает третья точка зрения на М. как на геометрич. тела, причём допускается также существование у этих тел "дырок", т. е. что эти тела не односвязаны.

М. наз. выпуклым, если он весь лежит по одну сторону от плоскости любой его грани; тогда грани его тоже выпуклы. Выпуклый М. разрезает пространство на две части - внешнюю и внутреннюю. Внутренняя его часть есть выпуклое тело. Обратно, если поверхность выпуклого тела многогранная, то соответствующий М.- выпуклый.

Важнейшие теоремы общей теории выпуклых М. (рассматриваемых как поверхности) следующие.

Теорема Эйлера (1758): число вершин минус число рёбер плюс число граней выпуклого М. - эйлерова характеристика М. - равно двум; символически: в - р + г = 2.

Теорема Кош и (1812) (в современной форме): если два выпуклых М. изометричны друг другу (т. е. один М. может быть взаимно однозначно отображен), говорят, что он принадлежит этой голоэдрии (или входит в состав её сингонии), если этот класс не является подгруппой никакой голоэдрии, содержащейся в данной. Если взять плоскость, не проходящую через точку О, и подвергнуть её всем поворотам к.-н. кристаллографич. класса, то полученные плоскости ограничивают либо нек-рый изоэдр с центром в точке, либо бесконечное выпуклое призматическое тело, либо многогранный угол. Полученные тела наз. простыми формами кристаллов, в первом случае замкнутыми, во втором и третьем - открытыми. Две простые формы считают одинаковыми, если они имеют один и тот же комбинаторный тип, порождены одним и тем же кристаллографич. классом и повороты этого класса одинаковым образом связаны с формой. Существует 30 различных в этом смысле замкнутых форм и 17 открытых, каждая из них имеет вполне определённое название (см. Кристаллы).

Основываясь на первом (указанном в начале статьи) определении М., можно указать ещё четыре правильных невыпуклых многогранника (т. н. тела Пуансо), впервые найденных франц. математиком Л. Пуансо в 1809 (рис. 6-9, см. на вклейке, табл. XXIV, стр. 321). Доказательство несуществования других невыпуклых правильных М. дал франц.математик О. Коши в 1811. В этих М. либо грани пересекают друг друга, либо сами грани - самопересекающиеся многоугольники. Для изучения вопросов, связанных с площадями поверхностей и объёмами таких М., удобно пользоваться именно первым определением М.

Если у М. можно так ориентировать грани, чтобы каждое ребро в тех двух гранях, к-рые смежны по этому ребру, имело бы обратные направления, то его наз. ориентируемым, в противном случае - неориентируемым. Для ориентируемого М. (даже если он самопересекающийся и его грани - самопересекающиеся многоугольники) можно ввести понятия площади поверхности и величины объёма. Площадью ориентируемого М. наз. просто сумму площадей его граней (об определении площади самопересекающегося многоугольника см. Многоугольник). Для определения объёма надо заметить, что совокупность внутр. кусков граней М. разрезает пространство на определённое число связных кусков, из к-рых один по отношению к М. бесконечный (внешний), а остальные конечные (внутренние). Если из внешней по отношению к М. точки провести отрезок в к.-л. внутреннюю точку внутр. куска, то сумму "коэффициентов", тех внутр. кусков граней М., к-рые пересечёт этот отрезок, наз. коэффициентом рассматриваемого внутр. куска М. (она не зависит от выбора внешней точки О); такой коэффициент есть целое положительное, отрицательное число или нуль. Сумму обычных объёмов всех внутр. кусков М., умноженных на эти их коэффициенты, наз. объёмом М.

Можно рассматривать и и-мерные М. Нек-рые из указанных определений и теорем имеют я-мерное обобщение. В частности, найдены все выпуклые правильные М.; при п = 4 их оказалось 6, а при всех больших и всего три: обобщение тетраэдра, куба и октаэдра. В то же время, напр., неизвестны все четырёхмерные изоэдры и изогоны.

Примеры нерешённых задач теории многогранников.

1) Нем. математик Э. Штейниц дал примеры того, что не для всякого тополо-гич. типа сетки рёбер выпуклого М. существует М., к-рый можно описать вокруг шара; в общем виде задача не решена.

2) Параллелоэдры суть выпуклые основные области групп параллельных переносов, но до сих пор не определены основные типы стереоэдров, т. е. выпуклых основных областей произвольных (фёдоровских) дискретных групп движений.

3) Определение всех типов четырёхмерных изоэдров.

Лит.: Фёдоров Е. С., Начала учения о фигурах, СПБ, 1885; Александров А. Д., Выпуклые многогранники, М.- Л., 1950; Вороной Г. Ф., Собр. соч., т. 2, К., 1952; Bruckner M., Vielecke und Vielflache. Theorie und Geschichte, Lpz., 1900; S t e i n i t z V., Vorlesungen über die Theorie der Polyeder unter Einschluss der Elemente der Topologie..., В., 1934; Сохеter H. S. M., Regular polytopes, 2 ed., L.- N. Y., 1963.

Б.Н. Делоне.

МНОГОГРАННЫЙ УГОЛ, часть пространства, ограниченная одной полостью многогранной конической поверхности, направляющая к-рой - плоский многоугольник без самопересечений. Грани этой поверхности наз. гранями М. у., вершину - вершиной М. у. М. у. наз. правильным, если равны все его линейные углы и все его двугранные углы. Мерой М. у. является площадь, ограниченная сферическим многоугольником (см. рис.), полученным пересечением граней М. у., сферой с радиусом, равным единице, и с центром в вершине М. у. См. также Телесный угол.

МНОГОГРЕШНЫЙ Демьян Игнатович (ум. не ранее 1696), гетман Левобережной Украины в 1668-72. Выходец из народа. Активный участник Освободит, войны украинского народа 1648-54. В 1649 в чине генерального есаула подписал Зборовский договор 1649. Став гетманом, М. проводил политику, угодную зажиточному казачеству. В 1670 участвовал в подавлении восстания казацкой и крестьянской бедноты под рук. И. Дзиковского. В 1672 был обвинён в тайных связях с Турцией, арестован и сослан в Иркутск вместе с женой и детьми. В 1688 освобождён. В 1696 постригся в монахи.

МНОГОДВИГАТЕЛЬНЫЙ ЭЛЕКТРОПРИВОД, группа электродвигателей, объединённых общей системой управления и приводящих в движение отд. рабочие органы машины или установки (напр., прокатных станов, бумагоделательных машин, комбинированных металлообр. станков, шагающих экскаваторов и т. п.). См. Электропривод.

МНОГОДЕТНЫЕ МАТЕРИ, в трудовом законодательстве СССР - матери, имеющие 3 и более детей, для к-рых установлены определённые льготы. Женщинам, имеющим 2 детей, выплачивается единовременное пособие при рождении 3-го и каждого следующего ребёнка и ежемесячное пособие при рождении 4-го и каждого следующего ребёнка, начиная с достижения ребёнком одного года и до того времени, когда ему исполнится 5 лет. При назначении пособия учитываются как родные дети, так и усыновлённые, а также дети мужа и усыновлённые им дети, находящиеся на воспитании М. м. не позже чем с 12 лет (с учётом требований, установленных законом). М. м. предоставляются льготы по оплате содержания детей в детских садах и яслях (плата снижается на 25-50%, с учётом количества детей и общего заработка родителей). Для М. м. установлены также льготы в области пенсионного обеспечения. Так, женщины, родившие 5 и более детей и воспитавшие их до 8-летнего возраста, имеют право на пенсию по старости по достижении 50 лет и при стаже работы не менее 15 лет, если они не имеют права на пенсию по старости в более раннем возрасте. Для М. м. учреждены спец. ордена и медали: "Мать-героиня", "Материнская слава", "Медаль материнства". Женщинам, родившим и воспитавшим 10 детей, присваивается почётное звание "Мать-героиня" с вручением ордена "Мать-героиня" и грамоты Верховного Совета СССР. См. также Звания почётные, Медали СССР, Ордена СССР.

МНОГОДОМНЫЕ РАСТЕНИЯ, многобрачные, полигамные, цветковые растения, к-рые наряду с обоеполыми цветками имеют и однополые. На одном и том же растении могут быть обоеполые и мужские цветки (андромонэция, напр, у чемерицы); обоеполые и женские цветки (гиномонэция, напр. у смолевки н мн. растений сем. сложноцветных); как обоеполые, так и мужские и женские цветки (тримонэция, напр. у конского каштана). На одних экземплярах М. р. бывают обоеполые цветки, на других - мужские (андродиэция - у куропаточьей травы и др.) или женские (гинодиэция - у незабудок, мн. растений сем. губоцветных). Наконец, обоеполые, мужские и женские цветки могут быть на разных растениях (триэция - у ясеня, винограда). Между указанными типами имеются переходы. Многодомность у растений способствует перекрёстному опылению.

МНОГОЖЕНСТВО, см. Полигиния и Двоежёнство.

МНОГОЗАБОИНОЕ БУРЕНИЕ, сооружение буровых скважин, имеющих ответвления в виде резко искривлённых дополнительных стволов от осн. ствола скважины в пределах продуктивного пласта (нефти, газа и т. п.). М. б. применяется для добычи нефти и газа, а также при разведке твёрдых полезных ископаемых. М. б. целесообразно в сравнительно устойчивых продуктивных пластах мощностью 20 м и более, напр., в монолитных или с прослоями глин и сланцев нефтеносных песчаниках, известняках и доломитах, при глубинах 1500-2500 м и при отсутствии газовой шапки и аномально высоких пластовых давлений. М. б. сокращает число обычных скважин путём увеличения дренирующей поверхности эксплуатац. скважины (рис. 1). Для проведения таких скважин в СССР созданы мощные искривлённые турбобуры и электробуры, способы и средства для принудит, продвижения геофизич. приборов, разработаны технологич. приёмы и инструменты для забуривания и крепления ответвлений.

Рис. 1. Способы вскрытия пласта: 1 -обычная скважина; 2 - многозабойная скважина; 3 - продуктивный пласт нефти; 4 - резервуар для нефти.

Впервые М. б. осуществлено в США в шт. Техас (1930). Ответвления бурились специально спроектированными для этой цели шарнирными и в виде гибкого шланга бурильными трубами, к-рые приводились во вращение с земной поверхности. Недостаточная прочность таких труб и сложность технологии ограничили длину дополнит, стволов до 30 м. Новый принцип - использование забойных двигателей (турбобуров, электробуров) был впервые реализован в СССР по предложению А. М. Григоряна, В. А. Брагина и К. А. Царевича в 1948, когда этим методом были пробурены первые многозабойные скважины. Это позволило применить обычные высокопрочные бурильные трубы и увеличить длину дополнит, стволов до неск. сотен метров.

В нефтедобывающих районах СССР эксплуатируются скважины с 5-10 ответвляющимися стволами длиной по 150-300 м каждый. Благодаря этому приток нефти в несколько раз больше, чем в обычных скважинах (стоимость сооружения скважин возросла всего на 30-80%). Важное преимущество таких скважин перед обычными в возможности более полного извлечения нефти из залежей. Так, три многозабойные скважины с горизонтальными стволами, пробурённые в 1957 вблизи г. Борислава, давали в сутки по 28-15 т нефти на истощённой залежи, к-рая эксплуатировалась с 1914 и на к-рой суточные дебиты обычных скважин не превышали 0,1-2 т. Применяя методы М. б., можно бурить скважины строго заданного направления, что используется при ликвидации открытого газонефтяного фонтана (проведение спец. скважин для соединения со стволом фонтанирующей скважины).

Достижение в области М. б.- проведение разведочной скважины на Марковском нефт. месторождении (Иркутская обл.) в 1968 с протяжённостью горизонтального ствола 630 м, при глубине по вертикали 2250 м. Скважина бурилась с такой же скоростью, как и обычная вертикальная, и была дороже всего на 23%. Большая длина горизонтальных участков при М. б. дала возможность проводить скважины-гиганты (рис. 2) с охватом большой площади залежи и с высокими дебитами нефти (это особенно важно для разработки труднодоступных залежей, напр., при разработке шельфов, в заболоченных районах, в черте городов и т. п.).

Рис. 2. Многозабойно-горизонтальная скважина-гигант: 1 - плавучая буровая установка; 2 - трубы; 3 - устье скважины; 4 - основной ствол; 5 - ответвления; 6 - нефтеносный пласт.

В СССР (1974) М. б. успешно проведено неск. десятков скважин на нефть, разрабатывается и испытывается скоростное М. б. глубоких горизонтальных скважин большой протяжённости (неск. км).

Лит.: Григорян А. М., Вскрытие пластов многозабойными и горизонтальными скважинами, М., 1969.

Л. М. Григорян.

МНОГОЗНАЧНАЯ ЛОГИКА, раздел математической логики, изучающий математические модели логики высказываний. Эти модели отражают две осн. черты последней - множественность значений истинности высказываний и возможность построения новых, более сложных высказываний из заданных при помощи логич. операций, к-рые позволяют также по значениям истинности исходных высказываний устанавливать значение истинности сложного высказывания. Примерами многозначных высказываний являются суждения с модальным исходом ("да", "нет", "может быть") и суждения вероятностного характера, а примерами логич. операций - логич. связки типа "и", "или", "если..., то". В общем случае модели М. л. представляют собой обобщения алгебры логики. Важно отметить, что в алгебре логики высказывания принимают только два значения истинности ("да", "нет"), в связи с чем она в общем случае не может отразить всего многообразия логич. построений, встречающихся на практике. При достаточно широком толковании М. л. в неё иногда включают также логич. исчисления.

Исторически первыми моделями М. л. явились двузначная логика Дж. Буля (называемая также алгеброй логики), трёхзначная логика Я. Лукасевича (1920) и пг-значная логика Э. Поста (1921). Изучение этих моделей составило важный этап в создании теории М. л. М. л. обладает определённой спецификой, состоящей в рассмотрении задач и подходов, возникающих при исследовании М. л. с позиций матем. логики, теоретич. кибернетики и алгебры. Так, с позиций теоретич. кибернетики, модели М. л. рассматриваются как языки, описывающие функционирование сложных управляющих систем, компоненты к-рых могут находиться в нек-ром числе различных состояний; а с точки зрения алгебры, модели М. л. представляют собой алгебраич. системы, имеющие наряду с прикладным и чисто теоретич. интерес.

Построение моделей М. л. осуществляется по аналогии с построением двузначной логики. Так, индивид, высказывания логики, разбитые на классы с одним и тем же значением истинности, приводят к понятию множества Е - констант модели, к-рые фактически отождествляют все индивидуальные высказывания, заменяя их соответствующими значениями истинности; переменные высказывания - к переменным величинам xi, х₂, ..., к-рые в качестве значений принимают элементы из множества Я; логич. связки - к множеству М элементарных функций (операций), к-рые, как и их аргументы, принимают значения из Е. Сложные высказывания, построенные из индивидуальных и переменных высказываний, а также логич. связок, приводят к множеству <М> формул над М. Значение истинности из Е сложного высказывания является функцией от соответствующих значений истинности высказываний, входящих в данное сложное высказывание. В модели эта функция приписывается формуле, соответствующей данному сложному высказыванию; говорят также, что формула реализует эту функцию. Множество формул <М> приводит к множеству [М] функций, реализуемых формулами из <М> и называемых суперпозициями над М. Множество [М] наз. замыканием множества М. Задание конкретной модели М. л. считается эквивалентным указанию множеств Е, М, <М> и [Л/]; при этом говорят, что модель порождается множеством М. Эта модель наз. формульной моделью, а также m-значной логикой, где т обозначает мощность множества Е.

Своеобразие подхода матем. кибернетики к М. л. состоит в рассмотрении моделей М. л. как управляющих систем. Элементарные функции при этом являются элементами, производящими определённые операции, а формулы интерпретируются как схемы, построенные из элементов и также осуществляющие переработку входной информации в выходную. Такого рода управляющие системы, известные в кибернетике как схемы из функциональных элементов, широко используются в теоретич. и практич. вопросах кибернетики. Вместе с тем существует ряд задач логики и кибернетики, к-рый связан с изучением соответствий между множествами М и [М] и при к-ром роль множества <М> несколько затушёвывается, сводясь к способу определения второго множества по первому. В этом случае приходят к другой модели М. л., к-рая представляет собой алгебру, элементами к-рой являются функции, принимающие в качестве значений, как и их аргументы, элементы из Е. В качестве операций в этих алгебрах обычно используется спец. набор операций, эквивалентный в смысле соответствий М и [М] множеству формул, построенных из функций множества М, т. е. получению сложных функций из заданных путём подстановки одних функций вместо аргументов других.

К числу задач, характерных для формульной модели М. л., относится задача "об описании", т. е. вопрос об указании для заданного множества М₂ принадлежит и включает [Mi] всех формул из <Mi>, реализующих функции из М₂. Частным случаем такой задачи является важный вопрос матем. логики об указании всех формул, реализующих заданную константу, что, напр., для исчисления высказываний эквивалентно построению всех тождественно истинных высказываний. Пограничным вопросом между матем. логикой и алгеброй, примыкающим к задаче об описании, является задача о тождественных преобразованиях. В ней при заданном множестве М требуется выделить в нек-ром смысле простейшее подмножество пар равных (т. е. реализующих одну и ту же функцию) формул из <М>, позволяющее путём подстановки выделенных равных формул одной вместо другой получить из любой формулы все формулы, равные ей. Аналогичное место занимает один из важнейших вопросов для М. л.- т. н. проблема полноты, состоящая в указании всех таких подмножеств Mi заданного замкнутого, т. е. совпадающего со своим замыканием, множества М, для к-рых выполнено равенство [Mi] = М, т. е. имеет место свойство полноты Mi в М. Глобальной задачей для М. л. является описание структуры замкнутых классов данной модели М. л.

Характерный для теории управляющих систем вопрос о сложности этих систем естественно возникает и по отношению к формулам и функциям из М. л. Типичной при таком подходе является след, задача о сложности реализации. На множестве всех элементарных формул нек-рым способом вводится числовая мера (сложность формул), к-рая затем распространяется на множество всех формул, напр., путём суммирования мер всех тех элементарных формул, к-рые участвуют в построении заданной формулы. Требуется для заданной функции указать ту формулу (простейшую), к-рая реализует эту функцию и имеет наименьшую сложность, а также выяснить, как эта сложность зависит от нек-рых свойств рассматриваемой функции. Исследуются различные обобщения этой задачи. Широкий круг вопросов связан с реализацией функций формулами с наперёд заданными свойствами. Сюда относятся задача о реализации функций алгебры логики дизъюнктивными нормальными формами и связанная с этим задача о минимизации; а также задача о реализации функций формулами в нек-ром смысле ограниченной глубины (т. е. такими формулами, в к-рых цепочка подставляемых друг в друга формул имеет ограниченную длину, такое ограничение связано с надёжностью и скоростью вычислений).

Решения всех перечисленных задач существенно зависят от мощности множества Е и множества М, порождающего заданную модель М. л.

К числу наиболее важных примеров М. л. относятся конечнозначные логики (т. е. ги-значные логики, для к-рых т конечно). Среди них наиболее глубоко исследован случай т = 2. Важнейшим результатом здесь является полное описание структуры замкнутых классов и получение для них важной информации по задаче о сложности реализации. Установлено, что при m > 2 у конечнозначных логик возникает ряд особенностей, существенно отличающих их от двузначного случая. Таковы, напр., континуальность множества замкнутых классов (при m = 2 их счётное число), особенности решения задачи о сложности реализации и ряд других. Общим результатом для конечнозначных логик является эффективное решение задачи о полноте для замкнутых классов, содержащих все функции со значениями в Е. Решение остальных проблем для конечнозначных логик продвинуто в различной степени. Особая значимость конечнозначных логик связана ещё и с тем, что они позволяют описывать работу самых различных реальных вычислит, устройств и автоматов.

Примерами др. М. л. являются с ч ё т -нозначные и континуум- з н а ч н ы е логики (т. е. такие т-значные логики, для к-рых мощность т является, соответственно, счётной или континуальной). Эти модели играют важную роль в матем. логике, моделей теории и в математическом анализе. К М. л. иногда относят и такие алгебры функций, в к-рых запас операций несколько отличается от указанного. Как правило, это достигается путём сужения описанного запаса или введения в операции нек-рых функций рассматриваемой М. л.

Лит.: Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б., Функции алгебры логики и классы Поста, М., 1966; Яблонский С. В., Функциональные построения в fe-значной логике, "Тр. Матем. ин-та АН СССР", 1958, т. 51, с. 5-142.

В. Б. Кудрявцев.

МНОГОЗНАЧНАЯ ФУНКЦИЯ, функция, принимающая неск. значений для одного и того же значения аргумента. М. ф. появляются при обращении однозначных функций, повторяющих свои значения. Так, функция х² принимает каждое положительное значение дважды (при значениях аргумента, различающихся только знаком); обращение её даёт

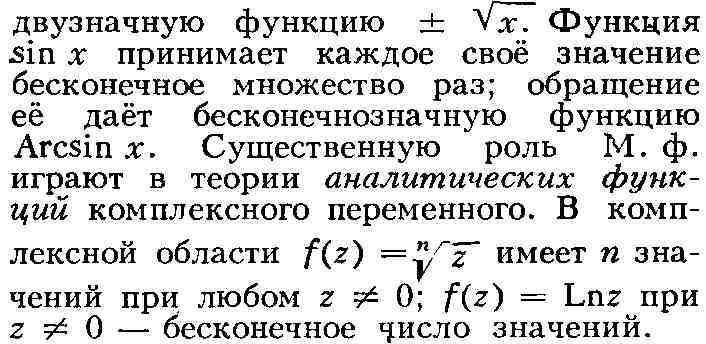
МНОГОЗНАЧНОСТЬ СЛОВА, полисемия, наличие у слова более чем одного значения, т. е. способность одного слова передавать различную информацию о предметах и явлениях внеязыковой действительности. Напр., у слова г о р л о 4 значения: передняя часть шеи; полость позади рта; верхняя суженная часть сосуда; узкий выход из залива, устье. Во многих языках, в том числе в русском, многозначные слова преобладают над однозначными. М. с. принято отграничивать от омонимии, т. к. значения многозначного слова связаны общими семантич. элементами (семантич. признаками) и образуют определённое семантич. единство (семантич. структуру слова). Различаются первичные и вторичные (производные) значения, к-рые иногда понимаются как прямые и переносные значения. Первичные значения, как правило, наименее контекстно обусловленны. Соотношение между первичными и вторичными значениями с течением времени может меняться. У разных типов слов существуют различные типы М. с., напр, относит. регулярная и нерегулярная М. с.- слова, обозначающие населённые пункты (город, деревня, село, посёлок и т. д.), могут иметь в рус. яз. также значение "жители данного насел, пункта", т. е. следуют определённой семантич. формуле, в то время как вторичные значения, напр. обозначения животных (лев, лиса и т. д.) в применении к людям индивидуальны. Особенности объединения значений в пределах одного слова во многом определяют своеобразие словарного состава каждого языка. Многозначными могут быть также грамматич. формы слова и синтаксич. конструкции.

Лит.: Виноградов В. В., Основные типы лексических значений слова, "Вопросы языкознания", 1953, № 5; А х м а н о в а О. С., Очерки по общей и русской лексикологии, М., 1957; Курилович Е., Заметки о значении слова, в его кн.: Очерки по лингвистике, пер. с польск., англ., франц., нем., М., 1962; Ullmann S., The principles, of semantics, 2 ed., Glasgow, 1959.

Д. Н. Шмелёв.

МНОГОЗУБ (Polyodon spathula), рыба семейства веслоносов отряда осетрообразных.

МНОГОЗУБЫЕ БЕЛОЗУБКИ (Suncus), род млекопитающих сем. землероек отряда насекомоядных. Длина тела 3-15 см, хвоста - 2,5-10 см. Представитель рода - малая белозубкa (S. etruscus) - самое маленькое млекопитающее. Ок. 20 видов. Распространены в Африке, Юж. Европе, Юж. Азии на В. до Филиппин и Н. Гвинеи. Отдельные виды обитают на лугах и в заболоченных местах, иногда селятся в постройках человека. Питаются гл. обр. насекомыми, нередко мясом, хлебом. Активны ночью. Размножаются круглый год. В помёте 2-5 детёнышей.

Малая белозубка

МНОГОКАМЕРНЫЙ РАКЕТНЫЙ ДВИГАТЕЛЬ, жидкостный ракетный двигатель (ЖРД) с неск. камерами и общими системами подачи топлива и управления. М. р. д. отличается от однокамерного той же тяги меньшими размерами (длиной), что позволяет выиграть в массе ракеты в целом; имеет преимущества в доводке камеры ракетного двигателя, однако конструкция его сложнее. Иногда неск. камерами снабжается твердотоп-ливный ракетный двигатель для ступенчатого изменения тяги.

МНОГОКАНАЛЬНАЯ СВЯЗЬ, система электросвязи, обеспечивающая одновременную и независимую передачу сообщений от неск. отправителей к такому же числу получателей. М. с. применяется для передачи по кабельным, радиорелейным и спутниковым линиям связи телефонных и телеграфных сообщений, данных телеметрии и команд телеуправления, телевизионных и факсимильных изображений, информации для ЭВМ, в автоматич. системах управления и т. д. Системы М. с. в сочетании с ком-мутац. системами явятся важнейшими составными частями единой автоматизированной системы связи.

Схема образования первичного группового тракта.

В основу построения систем М. с. положен принцип уплотнения линий связи. Наиболее распространено частотное уплотнение, при к-ром каждому каналу связи отводится определённая часть области частот, занимаемой трактом групповой передачи сообщений. В качестве стандартного канала принимается канал тональной частоты (ТЧ), обеспечивающий передачу речевого (телефонного) сообщения с эффективной полосой частот 300-3400 гц. С учётом защитных промежутков между каналами каждому из них отводится номинальная полоса частот 4 кгц. При построении М. с. с частотным уплотнением используется метод объединения стандартных каналов в стандартные групповые тракты. Вначале образуют первичный групповой тракт из 12 стандартных каналов, занимающий полосу частот 60-108 кгц (рис.). Для этого каждый канал посредством своего индивидуального преобразователя частоты (модулятора) переносится в соответствующую область полосы частот первичного тракта. Из 5 первичных групповых трактов аналогичным образом формируется вторичный и т. д. В практике встречаются системы М. с. на 12, 60, 120, 180, 300, 600, 900, 1920, 10 800 стандартных каналов. Такой метод не только существенно облегчает реализацию электрических фильтров, но также обеспечивает более широкие возможности унификации оборудования и др. технич. преимущества. Образование групповых трактов обеспечивает также передачу таких видов информации, к-рые требуют более широкой полосы частот, чем полоса частот стандартного канала: напр., при передаче звукового вещания с полосой частот 50-10 000 гц объединяются 3 стандартных канала, при передаче чёрно-белого и цветного телевиз. изображений используется полоса частот всего четвертичного тракта (900 стандартных каналов). Для передачи сообщений, требующих полосы частот более узкой, чем полоса частот стандартного канала ТЧ (напр., при уплотнении стандартного канала ТЧ низкоскоростными каналами передачи данных), последний с помощью аппаратуры уплотнения разделяют на 24-48 узкополосных каналов. При этом стандартный канал ТЧ становится уплотнённым каналом связи. Такое уплотнение часто наз. вторичным.

Основное достоинство систем М. с. с частотным уплотнением и однополосной модуляцией - экономное использование спектра частот; существенные недостатки - накопление помех, возникающих на промежуточных усилит, пунктах, и, как следствие, сравнительно невысокая помехоустойчивость. От последнего недостатка свободны системы с временным уплотнением и импульсно-кодовой модуляцией (см. Линии связи уплотнение, Импульсная радиосвязь). При построении М. с. большой мощности (по числу каналов) намечается тенденция одноврем. использования методов частотного и временного уплотнения. Теория и техника М. с. развиваются в направлении повышения помехоустойчивости передачи сообщений и эффективности использования линий связи.

Лит.: Назаров М. В., Кувшинов Б. И., Попов О. В., Теория передачи сигналов, М., 1970; Многоканальная связь, под ред. И. А. Аболица, М., 1971.

М. В. Назаров.

МНОГОКЛЕТОЧНЫЕ организмы, животные и растения, тело к-рых состоит из мн. клеток и их производных (различные виды межклеточного вещества). Характерный признак М.- качественная неравноценность слагающих их тело клеток, их дифференцировка и объединение в комплексы различной сложности (ткани, органы), выполняющие разные функции в целостном организме. Для М. характерно также индивидуальное развитие (онтогенез), начинающееся в большинстве случаев (исключая вегетативное размножение) с делений и дифференцировки одной клетки (половой клетки, споры или др.). Ср. Одноклеточные.

МНОГОКОВШОВЫЙ ЭКСКАВАТОР, экскаватор непрерывного действия, рабочий орган к-рого конструктивно объединяет несколько ковшей, перемещающихся по замкнутой траектории. По конструкции рабочего органа различают М. э. цепные и роторные; по способу экскавации - поперечного черпания (направление движения рабочего органа перпендикулярно к направлению движения машины) и продольного черпания (направление движения рабочего органа совпадает с направлением движения машины). Полноповоротные М. э. производят разработку забоев комбинированно, т. е. в поперечном, продольном и -"косом" направлениях.

М. э. используются для выемки пород, не подвергающихся предварительному рыхлению, т. к. только единичные конструкции М. э. могут работать не срезая стружку, а как погрузчики, заполняя ковш рыхлым (сыпучим) материалом на протяжении одной - двух длин ковша. М. э. применяются в комплексе с ж.-д. и конвейерным транспортом, консольными отвалообразователями, транс-портно-отвалъными мостами. См. также Роторный экскаватор. Цепной экскаватор .

Лит.: Домбровский Н. Г., Многоковшовые экскаваторы, М., 1972.

Ю. Д. Буянов.

МНОГОКОРЕННИК (Spirodela), род водных растений сем. рясковых. Включает 1 вид - М. обыкновенный (S. polyrrhiza) - многолетнее растение с округлым видоизменённым стеблем - листецом, плавающим на поверхности воды и несущим пучок мелких корней (отсюда назв.). Цветки однополые, без околоцветника, собраны в соцветие из 1 пестичного и 1 тычиночного цветков. Плод односемянный, невскрывающийся. М. цветёт очень редко; размножается ветвлением листеца. Произрастает в Сев. полушарии; в СССР - почти повсеместно, кроме Крыма и Ср. Азии, в стоячих и медленно текущих водах. Служит кормом для свиней, гусей, уток, кур.

МНОГОКРАТНОГО ЭКСПОНИРОВАНИЯ МЕТОД, метод комбинированной киносъёмки, основанный на совмещении в кадре неск. изображений с помощью последоват. съёмки различных объектов на одну и ту же киноплёнку. Для этого съёмочный аппарат должен иметь хорошую устойчивость изображения в кадровом окне, обратный ход для отмотки киноплёнки, счётчик метров и кадров отснятой киноплёнки. Многократным экспонированием получают изображения в кадрах, в к-рых одни объекты как бы просвечивают через другие (рис.). Эту особенность используют как изобразит, приём для показа воспоминаний, сновидений, а также для плавного перехода в кинофильме от одного монтажного плана или кадра к другому. Для предохранения определённых участков кадра от повторного экспонирования при М. э. м. применяется различного рода маскирование, напр, с использованием чёрного фона, неподвижных и подвижных масок. Маски и контрмаски нужной формы изготавливаются из плотной чёрной бумаги или тонкого картона и устанавливаются в спец. маскодержателе перед объективом аппарата. В простейшем варианте съёмки на чёрном фоне получают неск. изображений одного и того же объекта в разных участках кадра. Применение маски, неподвижной по отношению к кадровому окну аппарата, даёт возможность съёмки одного актёра в неск. ролях и соединения в кадре естеств. объекта с рисунком или макетом (см. Неподвижной маски метод). Широко применяются также подвижные, или блуждающие, маски, посредством к-рых при съёмке кинофильмов решаются сложные постановочные и изобразит, задачи (см. Блуждающей маски метод).

Б. Ф. Плужников.

Кадр из кинофильма "Александр Матросов", иллюстрирующий метод многократного экспонирования.

МНОГОКРАТНОЕ ТЕЛЕГРАФИРОВАНИЕ, метод последоват. временного линии связи уплотнения. Принцип М. т. заключается в том, что телеграфные передатчики или приёмники одной станции автоматически поочерёдно соединяются на короткие промежутки времени механич. или электронными распределителями через линию (канал) связи соответственно с телеграфными приёмниками или передатчиками др. станции. Число передатчиков (или приёмников) одной станции определяет кратность передачи. М. т. с использованием механнч. распределителей применялось до нач. 60-х гг. 20 в.; на проводных линиях связи оно постепенно вытеснено телеграфированием при помощи однократных стартстопных аппаратов благодаря появлению в 30-х гг. 20 в. частотного телеграфирования. М. т. с применением электронных распределителей получило распространение с сер. 60-х гг. 20 в. для временного уплотнения телефонных каналов и при передаче телеграмм по радиоканалам. См. также Многократный телеграфный аппарат.

В.В. Новиков.

МНОГОКРАТНЫЙ КООРДИНАТНЫЙ СОЕДИНИТЕЛЬ, коммутационное устройство релейного типа, используемое гл. обр. на городских, сельских, междугородных координатных автоматич. телефонных станциях и автоматич. телеграфных станциях. Соединитель наз. многократным, потому что в нём может быть одновременно осуществлено неск. (до 20) соединений, и координатным, потому что место каждого соединения определяется точкой пересечения подвижных вертикальных и горизонтальных реек.

Лит.: Кармазов М. Г., Метельский Г. Б., Автоматическая телефония, М., 1963; Автоматическая коммутация и телефония, под ред. Г. Б. Метельского, ч. 2, М., 1969.

Схема однократного телеграфирования: Эt ... , ЭБ - электромагниты приёмника; Е_п - источники питания клавиатуры передатчика.

МНОГОКРАТНЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ, применяется при многократном телеграфировании, в основном на радиотелеграфных линиях связи большой протяжённости; он состоит из распределителя с неск. секторами, передатчиков и приёмников для поочерёдной передачи и приёма знаков телеграмм. Изобретение в 1872 первого двукратного аппарата, получившего применение в проводной связи, принадлежит франц. инженеру Ж. Бодо. Принцип действия М. т. а. можно пояснить на примере однократного аппарата Бодо (рис.). Распределитель аппарата представляет собой диск из изоляц. материала с укреплёнными на нём металлич. кольцами. Внеш. кольцо распределителя разрезано на 10 изолиров. контактов, объединённых в 2 сектора. На станции А 5 контактов первого сектора соединены с передатчиком (его клавишами). К контактам второго сектора подключены 5 электромагнитов приёмника. На станции Б - наоборот, к контактам первого сектора подключены электромагниты приёмника, а к контактам второго-клавиши. Внутреннее кольцо соединено с линией связи. Щётки распределителей обеих станций вращаются синхронно и синфазно с частотой 200 об/мин, ограничиваемой инерционностью движущихся частей аппарата.

При вращении в первые пол-оборота щётки последовательно соединяют контакты клавиатуры станции А с электромагнитами приёмника станции Б, а во вторые пол-оборота - контакты клавиатуры станции Б с электромагнитами приёмника станции А. Нажатие клавишей на клавиатуре (в соответствии с комбинацией посылок передаваемого знака) телеграфист производит заранее, когда щётки находятся на секторе приёмника,- по звуковому сигналу, создаваемому тактовым электромагнитом. Посылки тока от клавиатуры станции А поступают на контакты первого сектора внеш. кольца распределителя и через его щётки, линию связи и щётки распределителя станции Б приходят на контакты внеш. кольца первого сектора и в электромагниты приёмника. Последний отпечатывает на бумажной ленте соответствующий знак. Эксплуатац. пропускная способность двукратного аппарата составляет ок. 2000 слов в 1 ч.

Усовершенствованные М. т. а. Бодо применялись до сер. 20 в. В 30-х гг. 20 в. были разработаны трёх-, шести-, девятикратные аппараты, что значительно увеличило пропускную способность телеграфных связей: до 20 000 слов в 1 ч в случае девятикратного аппарата. С 60-х гг. электромеханич. М. т. а. стали вытесняться электронными, снабжёнными устройствами для автоматич. обнаружения и исправления ошибок. Электронные М. т. а. производятся (1974) в СССР, Нидерландах, Швейцарии, ФРГ и др. странах.

В. В. Новиков.

МНОГОЛЕТНЕМЁРЗЛЫЕ ГОРНЫЕ ПОРОДЫ, породы, длительное время (не менее двух лет подряд) содержащие лёд и составляющие оси. массу мёрзлой зоны литосферы. Форма, размеры и взаимное расположение ледяных включений (криогенная текстура М. г. п.) определяются условиями осадконакопления и промерзания. М. г. п. могут включать также жидкую и газообразную фазы Н₂О, объём и распределение к-рых зависят от дисперсности минерального или органоминерального скелета пород и условий промерзания или протаивания. Присутствие льда в М. г. п. существенно влияет на их физич., механич. и фильтрационные свойства. Рыхлые и трещиноватые скальные горные породы благодаря промерзанию приобретают новые свойства (сцепление, прочность, непроницаемость и др.), к-рые имеют важное значение при использовании их в качестве стройматериалов, а также оснований и среды для инж. сооружений. М. г. п. создают специфич. условия, требующие особых решений при пром. и с.-х. освоении территории, строительстве, водоснабжении и др. мероприятиях. Науч. основы проектирования и строительства различных сооружений на М. г. п., их водной и тепловой мелиорации и решения др. прикладных задач рассматриваются в инж. геокриологии, разработанной гл. обр. в СССР (Н. А. Цытович, М.М. Крылов, В. Г. Гольдтман, Г. В. Порхаев, С. С. Вялов, К. Ф. Войтковский и др.). Значит, вклад в развитие инж. геокриологии внесли также зарубежные исследователи (швед. - Г. Бесков, амер. - С. Тейбер и К. Терцаги и др.).

Лит.: Основы геокриологии (мерзлотоведения), ч. 1-2, М., 1959; Д о с т о в а л о в Б. Н., Кудрявцев В. А., Общее мерзлотоведение, М., 1967; II Международная конференция по мерзлотоведению. Доклады и сообщения, в. 1 - 7, Якутск, 1973.

Г. И. Дубиков, А. А. Шарбатян.

МНОГОЛЕТНИЕ КОРМОВЫЕ ТРАВЫ посевные, травянистые растения с длительностью жизни более одного года, возделываемые на корм скоту. Годовой цикл жизни М. к. т. слагается из фаз: весеннее отрастание, кущение, колошение - бутонизация, цветение, плодоношение с повторным кущением, осенняя вегетация, зимний покой. Возделывают в основном растения сем. злаков (тимофеевка, лисохвост, житняк и др.) и бобовых (клевер, люцерна, эспарцет и др.). Чаще злаковые и бобовые травы высевают в смеси, что оказывает положительное влияние на качество корма и плодородие почвы. В связи с повторным кущением М. к. т. весьма целесообразно во 2-ю половину вегетации подкормить удобрениями. См. Кормовые травы.

МНОГОЛЕТНИКИ, многолетние растения, травянистые растения и полукустарники, зимующие более двух лет. Одни из них живут неск. лет, другие - до 20-30 и даже до 100 лет (напр., тау-сагыз). Достигнув определённого возраста, М. могут цвести и плодоносить каждый год (поликарпич. растения), в отличие от одно- и двулетников (монокарпич. растения), цветущих и плодоносящих один раз в жизни. У нек-рых из М. листья сохраняются круглый год (вечнозелёные растения). У большинства же в неблагоприятные периоды (зимой, в период засухи) листья и др. надземные органы отмирают, живыми у них остаются лишь подземные органы (корневища, клубни, луковицы, корни). У нек-рых же сохраняются частично и надземные побеги с почками возобновления (розетки, ползучие побеги, нижние части прямостоячих стеблей). Иногда деление растений на однолетники, двулетники и М. условно. Так, многолетнее растение тропиков клещевина (Ricinus communis) в условиях умеренного климата развивается как однолетник, а однолетнее растение равнин мятлик однолетний в горах развивается как многолетнее растение. Иногда М. наз. также деревья и кустарники.

Лит.: Серебряков И. Г., Морфология вегетативных органов высших растений, М., 1952; Ботаника, 7 изд., т. 1, М., 1966.

Л. В. Кудряшов.

МНОГОЛЕТНЯЯ КРИОЛИТОЗОНА, верхний слой земной коры, характеризующийся устойчивой в течение многих лет отрицательной или нулевой температурой, обеспечивающей круглогодичное и длительное (не менее двух лет подряд) сохранение подземного льда. Верх, часть М. к. слагают многолетне-мёрзлые горные породы и подземные ледяные тела, образующие мёрзлую зону литосферы, нижнюю - морозные горные породы и непромерзающие горизонты сильноминерализованных подземных вод. Формирование ледяных включений здесь может быть связано только с появлением пресных вод или слабоминерализованных растворов в естеств. или искусств, полостях. Эта часть М. к. преобладает в зонах затруднённого водообмена и выклинивается в зонах активного водообмена. Верх, граница М. к. в субгляциальных условиях проходит по поверхности раздела лёд - горные породы, а в субаэральных и субаквальных - по подошве сезонноталого или прогретого выше О °С слоя пород. На этой границе, непостоянной во времени и в пространстве, темп-ра ни разу в течение года не поднимается выше О °С. Отрицат. значения ср. годовой темп-ры земной поверхности (практически совпадающие со ср. годовой темп-рой пород у подошвы сезонноталого слоя) - необходимое условие возникновения М. к. При положит, ср. годовых темп-pax поверхности суши или шельфа М. к. может существовать только в деградирующем состоянии как реликт прошлых более суровых климатич. условий. Нижняя граница М. к. проходит по геоизотерме О °С, к-рая при изменении условий тепло- и влагообмена верх, слоя горных пород с поверхностью почвы, атмосферой и водоёмами постепенно изменяет своё положение, что обнаруживается только за достаточно большие промежутки времени. Глубина залегания нулевой изотермы от поверхности Земли колеблется от неск. м в умеренных широтах (на границах области распространения многолетнемёрзлых или охлаждённых горных пород) до неск. км в высоких широтах (св. 4 км в Антарктиде и 1,5 км в Субарктике).

КАРТА КРИОГЕННЫХ ОБРАЗОВАНИЙ (по И.Я.Баранову и П.А.Шумскому)

В Юж. полушарии М. к. распространена под ледниковым покровом Антарктиды и в её шельфовой зоне с отрицат. ср. годовой темп-рой морского дна, а также под ледниками и сезонноталыми почвами горных сооружений Юж. Америки, Африки и Австралии. В Сев. полушарии М. к. охватывает обширный субполярный пояс материков, расширяющийся с 3. на В. по мере усиления континен-тальности климата; горные сооружения островов и континентов, возвышающиеся над снеговой линией; значит, часть шельфа арктич. морей, а также горные породы под ледниковыми покровами и сезонноталыми почвами Гренландии, Исландии и островов Сев. Ледовитого океана. М.к. существует и под термокарстовыми озёрами, изобилующими на равнинах Арктики и Субарктики. Сплошность М. к. в высоких широтах нарушают сквозные и несквозные талики различного генезиса, в к-рых темп-pa пород хотя бы часть года положительна. В широкой полосе равнин вблизи совр. границы М. к. встречаются только отд. острова многолетнемёрзлых горных пород. В Зап.-Сибирской равнине южнее этой границы (при отсутствии многолетнемёрзлых горных пород в подпочвенном слое) на значит, глубине от поверхности (до 100 м и более) протягивается широкий (св. 400 км) и прерывистый клинообразный слой реликтовой М. к., к-рый раньше (по-видимому, до голоценового климатич. оптимума) сливался с активным слоем, а в совр. эпоху интенсивно протаивает сверху и снизу. Площадь распространения М. к. с учётом реликтовых мёрзлых слоев составляет более 25% терр. суши, включая 11% под ледниковыми покровами. На прилагаемой карте криогенных образований площади, занимаемые М. к., показаны тёмными видами штриховки.

Возникновение М. к. требует устойчивого положения суши в высоких широтах и на достаточной высоте над уровнем моря, а также определённого типа циркуляции атмосферы и океанич. вод. Формирование М. к. предшествует развитию поверхностного оледенения и охватывает большие по сравнению с последним площади. Особенно яркого выражения М.к. достигала при глобальных похолоданиях климата. Периоды агградации и деградации М. к. неоднократно повторялись на протяжении геол. истории Земли.

Термин М. к. предложен П. Ф. Швецовым в 1955. Организация систематич. исследований явлений М. к. начата в СССР в 1927 и связана с именем М. И. Сумгина. Значит, вклад в дальнейшее развитие учения о М. к. внесли советские учёные (Н. И. Толстихин, В. А. Кудрявцев, П. А. Шумский, И. Я. Баранов, Б. Н. Достовалов, А. И. Попов), а также амер. (С. Мюллер, Т. Л. Певе, А. Л. Уошберн, А. Лахенбрух), франц. и англ. (А. Кайо, Дж. Тейлор), швед. (Г. Бесков), канад. (Дж. Р. Маккей) и др. учёные.

Лит.: Сумгин М.И., Вечная мерзлота почвы в пределах СССР, 2 изд., М.-Л., 1937; Толстихин Н. И., Подземные воды мерзлой зоны литосферы, М.-Л., 1941; Шумский П. А., К р е н к е А. Н., Современное оледенение Земли и его изменения, "Геофизический бюллетень", 1964, N° 14; Баранов И. Я., Вечная мерзлота и ее возникновение в ходе эволюции Земли как планеты, "Астрономический журнал", 1966, т. 43, в. 4; Достовалов Б. Н., Кудрявцев В. А., Общее мерзлотоведение, М., 1967; Попов А. И., Мерзлотные явления в земной коре (Криолитология), М., 1967; II Международная конференция по мерзлотоведению.Доклады и сообщения, в. 1-7, Якутск, 1973; М u 1 1 е г S. W., Permafrost or permanently frozen ground and related engineering problems, Ann Arbor, 1947; Т е r z a g h i K., Permafrost, "Journal of the Boston Society of Civil Engineers", 1952, v. 39, № 1; С a i 1 1 e u x А., Т а у 1 о г G., Cryopedologie. Etude des sols geles, P., 1954; Proceedings, International Permafrost Conference, W., 1965.

А. А. Шарбатян.

МНОГОЛЕТНЯЯ МЕРЗЛОТА, то же, что вечная мерзлота. См. также Многолетняя криолитозона.

МНОГОМЕРНОЕ ПРОСТРАНСТВО, пространство, имеющее число измерений (размерность) более трёх. Обычное евклидово пространство, изучаемое в элементарной геометрии, трёхмерно; плоскости - двумерны, прямые - одномерны. Возникновение понятия М. п. связано с процессом обобщения самого предмета геометрии. В основе этого процесса лежит открытие отношений и форм, сходных с пространственными, для многочисл. классов математич. объектов (зачастую не имеющих геом. характера). В ходе этого процесса постепенно выкристаллизовалась идея абстрактного математического пространства как системы элементов любой природы, между к-рыми установлены отношения, сходные с теми или иными важными отношениями между точками обычного пространства. Наиболее общее выражение эта идея нашла в таких понятиях, как топологическое пространство и, в частности, метрическое пространство.

Простейшими М. п. являются и-мерные евклидовы пространства, где п может быть любым натуральным числом. Подобно тому, как положение точки обычного евклидова пространства определяется заданием трёх её прямоугольных координат, "точка" n-мерного евклидова пространства задаётся п "кооодина-

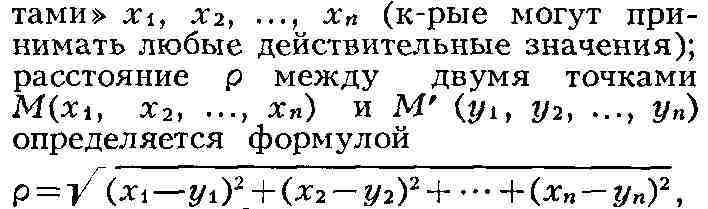
аналогичной формуле расстояния между двумя точками обычного евклидова пространства. С сохранением такой же аналогии обобщаются на случай и-мерного пространства и другие геом. понятия. Так, в М. п. рассматриваются не только двумерные плоскости, но и k-мерные плоскости (k < п), к-рые, как и в обычном евклидовом пространстве, определяются линейными уравнениями (или системами таких уравнений).

Понятие n-мерного евклидова пространства имеет важные применения в теории функций многих переменных, позволяя трактовать функцию п переменных как функцию точки этого пространства и тем самым применять геом. представления и методы к изучению функций любого числа переменных (а не только одного, двух или трёх). Это и было главным стимулом к оформлению понятия w-мерного евклидова пространства.

Важную роль играют и другие М. п. Так, при изложении физич. принципа относительности пользуются четырёхмерным пространством, элементами к-рого являются т. н. "мировые точки". При этом в понятии "мировой точки" (в отличие от точки обычного пространства) объединяется определённое положение в пространстве с определённым положением во времени (поэтому "мировые точки" и задаются четырьмя коорди-

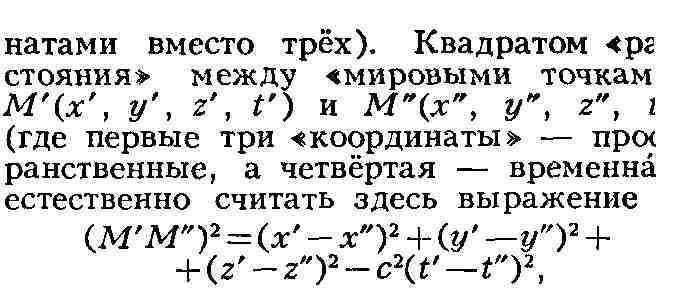
где с - скорость света. Отрицательное последнего члена делает это пространство "псевдоевклидовым".

Вообще й-мерным пространством на топологич. пространство, к-рое в каждой своей точке имеет размерность и. В на более важных случаях это означает, ч каждая точка обладает окрестность] гомеоморфной открытому шару п-мерного евклидова пространства.

Подробнее о развитии понятия М. г геометрии М. п., а также лит. см. в с Геометрия.

МНОГОМУЖЕСТВО, см. Полиандри.

МНОГОНОЖКИ (Myriapoda), общ; название 4 классов наземных членистоногих животных: губоногих, двупарноногих, симфил и пауропод; прежде считались одним классом. Тело М. состоит из головы и б. или м. длинного сегментированного туловища. Усиков 1 пар, ноги имеются на всех (или почти на всех туловищных сегментах. Ок. 11 тыс. видов; в СССР ок. 1000 видов. Обитают в почве, лесной подстилке, гнилой древесине. Питаются гниющими расти остатками (двупарноногие, симфилы мицелием грибов (пауроподы); нек-рые хищники (губоногие).

МНОГОНОЖКОВЫЕ (Polypodiaceae семейство растений из класса папоротников. Многолетники с ползучими ил иногда восходящими корневищами, покрытыми чешуйками. Листья перистьк дважды перистые, лопастные или цельные. Ок. 65 родов (до 1200 видов растут преимущественно в тропика где они часто развиваются как эпифиты. В СССР 5 видов М.: 1 дальневосточный из рода пиррозия (Pyrrosia) и из рода многоножка (Polypodium). Многоножка обыкновенная, или сладкий папоротник (P. vulgare), растёт в Европ. части СССР, на Кавказе, в Ср. Азии и Зап. Сибири; имеет сладковатое корневище. Мн. тропич. М. (Drynaria, Platycerium и др.) разводят в оранжереях и комнатах.

Лит.: Тахтаджян А. Л., Высшие растения, т. 1, М.- Л., 1956.

Многоножка обыкновенная.

МНОГООБРАЗИЕ, математич. понятие, уточняющее и обобщающее на любое число измерений понятия линии и поверхности, не содержащих особых точек (т. е. линии без точек самопересечения, концевых точек и т. п. и поверхности без самопересечений, краёв и т. п.).

Примером одномерного М. могут служить прямая, парабола, окружность, эллипс, вообще любая линия, у каждой точки к-рой существует окрестность, являющаяся взаимно однозначным и непрерывным (или, как говорят в топологии, гомеоморфным) образом интервала (внутр. части отрезка прямой). Интервал сам является одномерным М., отрезок же не является М. (так как концы его не имеют окрестностей указанного вида).

Примером двумерного М. может служить любая область на плоскости (напр., внутренность круга х² + y² < г²), сама плоскость, параболоид, сфера, эллипсоид, тор и т. п. Двумерные М. характеризуются тем, что у каждой их точки имеется окрестность, гомеоморфная внутренности круга. Это требование исключает, напр., из числа двумерных М. конич. поверхность (её вершина, в к-рой сходятся две её полости, не имеет требуемого вида окрестности). Однако выделяют спец. класс объектов, к-рые не удовлетворяют этому требованию, - т. н. многообразия с краем (напр., замкнутый круг х² + y² =< r²).

Примером трёхмерного М. может служить обычное евклидово пространство, а также любое открытое множество в евклидовом пространстве. Трёхмерные М. характеризуются тем, что у каждой их точки имеется окрестность, гомеоморфная внутренности шара.

М. разделяются на замкнутые и открытые (определение см. ниже). В случае одного измерения каждое замкнутое М. гомеоморфно окружности, а каждое открытое - прямой (на рис. 1 изображены одномерные М. и окрестности точки Р на каждом из них). В случае двух измерений уже замкнутые М. довольно разнообразны. Они распадаются на бесконечное число топологических типов: сфера - поверхность рода 0 (рис. 2, а), тор - поверхность рода 1 (рис. 2, б), "крендель" - поверхность рода 2 (рис. 2, в), вообще "сфера с п ручками"-поверхность рода п (на рис. 2, г изображена такая поверхность при п = 3). Этими примерами исчерпываются все топологич. типы замкнутых двумерных ориентируемых М. (см. также Ориентируемая поверхность). Существует ещё бесконечное число замкнутых двумерных неориентируемых М. - односторонних поверхностей, напр., проективная плоскость, т. н. односторонний тор (Клейна поверхность). Имеется и классификация открытых двумерных М. Полная классификация М. трёх измерений не найдена (1974) (даже для случая замкнутых М.).

Рис. 1. Одномерные многообразия.

Рис. 2. Примеры замкнутых двумерных многообразий.

Многообразием п измерений (или n-мерным многообразием) наз. всякое хаусдорфово топологическое пространство, обладающее след. свойством: каждая его точка имеет окрестность, гомеоморфную внутренности n-мерного шара, и всё пространство может быть представлено в виде суммы конечного или бесконечного (счётного) множества таких окрестностей. М. наз. замкнутым, если оно компактно (см. Компактность), в противном случае - открытым. Иногда к определению М. прибавляют ещё требование его связности: каждые две точки М. могут быть в нём соединены непрерывной дугой.

Введение в математику понятия М. любого (натурального) числа измерений п было вызвано весьма разнообразными потребностями геометрии, математич. анализа, механики и физики. Важность достаточной широты понимания М. как топологич. пространства основана на том, что точками так определённых М. могут быть объекты любой природы, напр., прямые, сферы, матрицы и т. д.

При надлежащем добавлении требований к определению М. устанавливается понятие гладкого, или дифференцируемого, многообразия. На гладком М. имеется возможность рассматривать дифференцируемые функции и дифференцируемые отображения в себя или в др. гладкие М. Гладкие М. имеют особенно большое значение в совр. математике, поскольку именно они наиболее широко используются в приложениях и смежных областях (напр., конфигурационные пространства и фазовые пространства в механике и физике). На гладких М. можно ввести метрику, превратив его в риманово пространство. Это позволяет строить дифференциальную геометрию на М. Напр., введя нек-рым образом метрику в конфигурационном пространстве механич. системы, можно истолковать траектории движения как геодезические линии в этом пространстве (см. Наименьшего действия принцип). М., для элементов к-рого определено (дифференцируемое) умножение, превращающее М. в группу, наз. группой Ли (см. Непрерывная группа).

Понятие М. играет большую роль в теории алгебраич. функций, непрерывных групп и т. Д. Во всех этих приложениях существенны свойства М., не изменяющиеся при топологич. преобразованиях,- т. н. топологические свойства. К ним относятся, напр., ориентируемость или неориентируемость М. (см. Ориентация). Изучение этих свойств является одной из важнейших задач топологии.

Лит.: А л е к с а н д р о в П. С. и Ефремович В. А., Очерк основных понятий топологии, М.- Л., 1936; Александров П. С., Комбинаторная топология, М.- Л., 1947; Л е н г С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967.

Н. В. Ефимов.

МНОГООСНЫЙ АВТОМОБИЛЬ, автомобиль, имеющий число осей более двух. Многоосными чаще всего выполняются грузовые автомобили и тягачи, реже автобусы и троллейбусы. М. а. благодаря распределению общего веса на большее число осей имеют, как правило, большую грузоподъёмность и повышенную проходимость по сравнению с двухосными. Недостатки М. а.- их повышенная стоимость н большие расходы на эксплуатацию.

Схемы многоосных автомобилей (ведущие колёса выделены чёрным цветом): а - МАЗ-537А (СССР). Татра-813 (ЧССР); б - БТР-бОП(СССР), ДАФ (Нидерланды); в - Панар-ЭБР (Франция); г - АЕК-Маммут (Великобритания): д - Скэммель-Самсон (Великобритания); е - СВАРЗ (СССР); ж - ЗИЛ-131 и Урал-375 (СССР); з - Альвис (Великобритания); и - КрАЗ-257 (СССР); к - Бюссинг-Суперкарго (ФРГ), ФИАТ-590НА (Италия); л - МАЗ-516 (СССР); м  - Икарус-180 (ВНР), Шкода-ШМ 16,5 (ЧССР).

Первая попытка создания М. а. относится к 1898; серийное произ-во началось в сер. 1920-х гг. на з-де "Рено" (Франция). В СССР выпуск М. а. (ЯГ-10) грузоподъёмностью 8 т начал Ярославский автомобильный (ныне моторный) з-д в 1932.

В зависимости от числа колёс принято характеризовать автомобили т. н. колёсной формулой, где первая цифра указывает на общее число колёс, а вторая  - на число ведущих колёс (считая сдвоенное колесо за одно). М. а. выполняются трёх- и четырёхосными, а в отд. случаях и пятиосными. М. а. первой группы (четырёхосные, рис., а - е) выпускаются в сравнительно небольших количествах и применяются в основном для геоло-

Краткая техническая характеристика многоосных автомобилей, выпускаемых в СССР

Марка автомобиля
 

Показатели	ЗИЛ-131	Урал-375Д	КамАЗ	КрАЗ-257	КрАЗ-255Б	МАЗ-516А	МАЗ-537А
Колёсная формула Грузоподъёмность, m  Снаряжённый вес, т  Мощность двигателя, кет (л. с.) Скорость, км/ч Контрольный расход топлива, л/100 км	6X6  3,5  6,46 110 (150)  80 40	6X6  4,5  8,4 132  (180) 75 48	6X4  8,0     154 (210)  80	6X4  12,0  11,13 176  (240) 70 36	6X6 7,5  11,95 176 (240)  70 40	6X2  14,5  8,8 132 (180)  85 30	8X8  15,0  22,5 386  (525) 60 125

горазведочных работ, в строительстве, в войсковых подразделениях. М. а. второй группы (трёхосные, рис., ж - м) более распространены и применяются для магистральных перевозок грузов; к ним относятся междугородные и сочленённые городские автобусы.

Машины повышенной проходимости (грузовые, спец. автомобили, тягачи, бронетранспортёры) выполняются со всеми ведущими колёсами. Краткие технич. характеристики М, а., выпускаемых в СССР, приведены в табл.

Развитие конструкций М. а. повышенной проходимости осуществляется за счёт создания сочленённых автомобилей с числом осей от 3 до 6; в дорожных М. а. намечается тенденция к более широкому использованию схем, показанных на рис., д, к и л (для грузовых автомобилей) и рис., кпм (для автобусов).

Лит.: Колесные автомобили высокой проходимости, М., 1967; Селиванов И. И., Автомобили и транспортные гусеничные машины высокой проходимости, М., 1967; Краткий автомобильный справочник, 6 изд., М., 1971.

Л. М. Шугуров.

МНОГОПЁРЫ (Polypterus), род рыб надотряда многопёрых. Тело вытянутое (дл. до 120 см), слабо сжатое с боков. Грудные плавники в основании имеют мясистую лопасть, спинной - из ряда плавничков, имеющих спереди по жёсткому лучу, брюшные - отнесены далеко назад. Тело покрыто ганоидной чешуёй.

Многопёр: 1 - взрослая форма; 2 - личинка.

Плавательный пузырь двойной, ячеистый, открывается с брюшной стороны и играет роль "лёгкого". М. поднимаются наверх и заглатывают воздух; лишённые возможности дышать атм. воздухом, М. гибнут через 2-3 ч, но и вне воды они жить не могут. 10 видов. Населяют тихие заводи рек и лагуны озёр Африки. Питаются мелкой рыбой и беспозвоночными. Нерест в июле - сентябре (в период дождей), икра мелкая (до 1-3 мм), сильно пигментирована. Из икры выходят личинки с наружными жабрами. Промысловое значение невелико; мясо вкусное. Нек-рые виды содержат в аквариумах.

Лит.: Никольский Г. В., Частная ихтиология, 3 изд., М., 1971; Жизнь животных, т. 4, ч. 1, М., 1971.

МНОГОПИЛЬНЫЙ СТАНОК, предназначается для распиловки и раскроя древесины и древесных материалов, в процессе резания участвуют одновременно или последовательно неск. пил. См. Круглопилъный станок, Ленточнопилъный станок, Лесопильная рама.

МНОГОПЛОДИЕ у человека, беременность, при к-рой одновременно развивается неск. плодов (см. Близнецы). Встречается относительно редко: двойня - одна на 80 родов, тройня - на 80², четверня - на 80³, пятерня - на 80⁴ родов; описаны случаи родов шестью и семью плодами. Предполагают, что причинами М. могут быть: одновременное оплодотворение двух яйцеклеток (двуяйцевая двойня); одна оплодотворённая яйцеклетка делится на две и больше частей, каждая из к-рых в дальнейшем развивается самостоятельно; одна оплодотворённая яйцеклетка имеет два ядра, и после деления из неё развиваются два самостоятельных зародыша.

М. чаще наблюдается у женщин, у к-рых в семье (или семье мужа) были многоплодные роды. Известен случай, когда женщина имела 11 беременностей, закончившихся 3 раза двойнями, 6 раз тройнями и 2 раза четвернями (всего 32 ребёнка), причём её муж был из двойни, а сама она из четверни.

Женщины при многоплодной беременности находятся под особым диспансерном наблюдением в консультации и в случае установления к.-л. осложнений госпитализируются для стационарного обследования и лечения. При нормальном течении беременности женщины с М. госпитализируются за две недели до предполагаемых родов. При М. чаще наблюдаются преждевременные роды, раннее или преждевременное отхождение околоплодных вод первого плода, первичная и вторичная слабость родовой деятельности, неправильное положение плодов и др. С целью профилактики кровотечений после родов применяют лекарственные средства, сокращающие матку.

М. у животных - см. Плодовитость .

Лит.: Кленицкий Я. С., Многоплодная беременность, в кн.: Многотомное руководство по акушерству и гинекологии, т. 3, кн. 1, М., 1964; Жорданиа И. Ф., Учебник акушерства, 4 изд., М., 1964; Малиновский М. С., Оперативное акушерство, [2 изд., М., 1967].

О. К. Никончик.

МНОГОПЛОДИЕ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ЖИВОТНЫХ, способность некоторых видов с.-х. животных давать в одном приплоде неск. детёнышей. Крупные животные (лошади, кр. рог. скот и др.) рождают обычно по одному детёнышу, двойни редки (у кобыл - 0,5%, у коров - 1-3% ), лишь в исключит, случаях регистрируется рождение кобылой 3-4 жеребят, коровой 3-7 телят и т. п. Более мелкие с.-х. животные чаще многоплодны. Наибольшим многоплодием отличается свинья, в помёте к-рой обычно 10-12 поросят, иногда до 32. Овцы, рождающие обычно одинцов, в 15-30% случаев приносят двоен. Нек-рые породы овец многоплодны; напр., романовская порода овец даёт за окот в среднем 2-3 ягнёнка, в отд. случаях до 8-9. Многоплодные пометы дают кролики - в среднем 5-6, до 18 крольчат.

Многоплодие зависит от числа яйцеклеток, оплодотворённых за один половой цикл, и является наследственно обусловленным. Оно меняется с возрастом (молодые и старые самки менее многоплодны), снижается при неполноценном кормлении, неудовлетворит. содержании, чрезмерной эксплуатации животных, перемещении их в резко изменённые климатич. условия, при систематич. применении близкородственного спаривания (кровосмешение) и отдалённой гибридизации, при к-рой иногда вообще утрачивается плодовитость. У животных, для к-рых типично одноплодие, напр, у кр. рог. скота, при рождении в двойне бычка и тёлочки в 85% случаев тёлки бесплодны (фримартины). Это происходит вследствие срастания сосудов плодовых оболочек эмбрионов и подавления гормонами бычков воспроизводит, сист. тёлочек. Многоплодные виды животных имеют защитные приспособления, предотвращающие такое срастание, поэтому самцы и самки многоплодных помётов плодовиты, по энергии роста и продуктивности не уступают потомкам одноплодных животных.

В овцеводстве для стимулирования многоплодия применяют иногда инъекцию сыворотки крови жеребых кобыл (СЖК), содержащей гонадостимулирующий гормон. Однако более надёжно использование наследств, обусловленности многоплодия и закрепление этого признака отбором, подбором, полноценным кормлением и хорошими условиями содержания животных многоплодных помётов. В плем. работе в свиноводстве, овцеводстве и др. отраслях животноводства многоплодие - один из важных селекционируемых признаков. См. Плодовитость.

Лит.: Повышение плодовитости сельскохозяйственных животных, под ред. Н. А. Флегматова, М., 1959; Падучева А. Л., Бойко Д. Ф., Гормональные методы повышения плодовитости сельскохозяйственных животных, М., 1965.

В. А. Эктов.

МНОГОПЛОДНИКОВЫЕ (Polycarpiсае), группа семейств или порядков двудольных свободнолепестных растений. Характеризуются признаками, к-рые оценивают как примитивные (неопределённое и часто спиральное или спирально-круговое расположение частей цветка, многочисл. нередко лентовидные тычинки и др.). Среди древних М. преобладают древесные формы с древесиной из трахеид (как у хвойных) или чаще из трахеид и сосудов с лестничной или простой перфорацией. К М. относят от 20 до 40 и более семейств; среди них наиболее типичные: магнолиевые, анноновые, винтеровые, лютиковые, нимфейные и др. Полагают, что М. ближе др. растений стоят к исходным предкам цветковых, а древнейшие М. дали начало остальным покрытосеменным.

Лит.: Тахтаджян А. Л., Происхождение и расселение цветковых растений, Л., 1970.

МНОГОПОЛЬЕ, устаревшее название севооборотов с 7-8 и более полями. М. в дореволюц. России, а также в сов. доколхозной деревне противопоставлялось отсталому паровому трёхполью, характерному для единоличного крест. хозяйства; переход к М. обычно был связан с введением в севооборот пропашных культур, многолетних трав и являлся прогрессивным мероприятием. См. Севооборот.

МНОГОПОЛЮСНИК, электрич. схема, к-рая может соединяться с др. схемами только в определённых, предназначенных для этой цели узлах, называемых полюсами. Представление отд. частей сложной электрич. схемы в виде М. во мн. случаях позволяет облегчить расчёты, т. к. при этом не определяются токи или напряжения во всех элементах, входящих в состав М., число к-рых может быть очень велико, а определяются только напряжения между полюсами и токи в полюсах М. Для решения мн. практич. задач этого бывает вполне достаточно. М. наз. активным, если он содержит внутри независимые источники энергии, действие к-рых взаимно не компенсируется. Если все полюса такого М. разомкнуть, то между всеми или нек-рыми полюсами будут напряжения, обусловленные наличием внутр. источников энергии. М., не содержащий независимых источников энергии, наз. пассивным. М. подразделяются на линейные и нелинейные. В линейных М. ток и напряжение связаны линейными зависимостями и для их расчёта применим принцип суперпозиции (принцип наложения); для нелинейных М. принцип суперпозиции не применим. М. наз. обратимыми или необратимыми в зависимости от того, подчиняются или не подчиняются они принципу взаимности. По числу полюсов М. называют трёхполюсниками, четырёхполюсниками и т. д.

МНОГОРЕЗЦОВЫЕ СУМЧАТЫЕ (Роlyprotodontia), подотряд сумчатых млекопитающих; большинством зоологов подотряд М. с. ныне не выделяется.

Многорядник копьевидный (Polystichum lonchitis).

МНОГОРЯДНИК (Polystichum), род папоротников сем. аспидиевых. Наземные корневищные растения, обычно с жёсткими кожистыми листьями. Сорусы (собрания спорангиев) округлые, б. ч. снабжённые щитовидным покрывальцем (индузием). Ок. 175 видов; распространены широко. В СССР 7-8 видов, растущих в лесах и на скалах. Нек-рые М. используют как декоративные растения в открытом грунте и в оранжереях. Размножаются спорами или корневищами.

МНОГОСВЯЗНАЯ ОБЛАСТЬ в математике, область, в к-рой существуют замкнутые кривые, не стягиваемые в пределах этой области в точку (см. Область в математике). На чертеже А есть односвязная область, В - М. о.; пунктиром изображена кривая, не стягиваемая в точку в пределах В.

МНОГОСОЮЗИЕ, полисиндетон (от греч. polysyndeton), такое построение предложения, когда все или почти все однородные члены связаны между собой одним и тем же союзом (чаще "и"), тогда как обычно в этом случае соединяются лишь два последних однородных члена предложения. М.-средство усилить впечатление общности перечисляемого. М. часто использовалось в рус. нар. песне (чаще с союзом "а").

МНОГОСТАНОЧНАЯ РАБОТА, технически обоснованное и организационно обеспеченное одновременное обслуживание неск. станков. Планомерное сочетание машинной работы на одних станках с ручной или машинно-ручной на других обеспечивает успешную эксплуатацию оборудования на участках многостаночного обслуживания. Большое распространение М. р. получила в различных отраслях пром-сти в период возникновения стахановского движения (в текст. пром-сти Е. В. и М. И. Виноградовы в 1935 обслуживали 40 станков, а затем 216 автоматов). Особо массовый характер многостаночное обслуживание приняло в 1939, в процессе развития социалистического соревнования М. р. вылилась в особую форму стахановского труда. Инициаторами движения многостаночников выступили стахановцы "Урал-машзавода" и Харьковского станкостроит. з-да (1939). Дальнейшее распространение М. р. получила во время Великой Отечеств, войны 1941-45, рабочие переходили на обслуживание двух и более станков, заменяя ушедших на фронт. В послевоен. период ускорение научно-технич. прогресса создаёт объективные предпосылки для широкого внедрения М. р. С появлением автоматич. устройств и поточных линий возникают реальные условия для изменения характера труда рабочего-многостаночника, превращения его в оператора, управляющего работой самостоят. участка автоматизированного произ-ва.

Распространению М. р. способствует развитие внутризаводской специализации, применение универсальной технологич. оснастки, повышение уровня централизации обслуживания рабочих мест, технологич. проектирование и совершенствование нормирования.

Многостаночное обслуживание - важный резерв роста производительности труда и экономии трудовых ресурсов. М. р. требует особенно высокой квалификации рабочих, заработок к-рых при обслуживании станков сверх установленных норм возрастает в зависимости от использования рабочего времени и оборудования, сложности работы или операции и условий труда. При этом тарифные ставки рабочих, применяемые для определения расценок на единицу изделия, увеличиваются в зависимости от количества единиц обслуживаемого сверх норм оборудования.

Опыт М.р. используется в других социалистических странах (например, в ПНР и СРР).

Лит.: Пруденский Г. А., Многостаночная работа и совмещение профессий, в кн.: Машиностроение. Энциклопедический справочник, т. 15, М., 1951; Опыт и меры по дальнейшему развитию многостаночного обслуживания, Свердловск, 1971.

П. А. Седлов.

МНОГОСТАНОЧНИКИ, см. Многостаночная работа.

МНОГОСТЕПЕННЫЕ ВЫБОРЫ, система выборов, при к-рой депутаты представит, органа или глава гос-ва избираются не непосредственно избирателями, а через т. н. выборщиков. В порядке М. в. (косвенных) избирается, напр., президент в США.

В СССР до принятия Конституции 1936 в порядке М. в. избирались высшие органы гос. власти. Напр., депутаты съезда Советов СССР избирались на губернских съездах Советов, а в тех союзных республиках, где не было губернских объединений,- на республиканских съездах Советов.

МНОГОСТОРОННИЕ РАСЧЁТЫ, система взаимных платежей по внешней торговле, кредитам, инвестициям, неторговым платежам, охватывающая трёх или более участников. Различные формы М.р. применяются в практике международных расчётов капиталистич. и социалистич. стран. Ведущей формой М.р. капиталистич. стран в совр. условиях являются расчёты в свободно конвертируемых валютах. Своеобразной формой М. р. является многосторонний клиринг, основанный на принципе переводи-мости средств по счетам участников расчётов. Примером такого клиринга может служить существовавшая в Великобритании в 1947-58 система "переводных счетов" в фунтах стерлингов. В практике М. р. капиталистич. стран известна и др. форма многостороннего клиринга - т. н. валютные клубы (напр., "Гаагский валютный клуб", "Парижский валютный клуб"), предусматривающая осуществление расчётов между его участниками в частично конвертируемых валютах.

Между социалистич. странами также широко применяются М. р. С 1964 расчёты между странами - членами СЭВ осуществляются в рамках системы М. р. в переводных рублях через Международный банк экономического сотрудничества (МВЭС).

Лит. см. при статьях Клиринг, Международные расчёты.

О. М. Шелков.

МНОГОСТУПЕНЧАТАЯ ТУРБИНА, газовая или паровая турбина, в к-рой расширение пара или газа от начального до конечного давления и преобразование его тепловой энергии в механич. работу осуществляется не в одной, а в ряде последовательно расположенных ступеней. Каждая ступень в принципе представляет собой элементарную турбину и состоит из неподвижного соплового аппарата и подвижных рабочих лопаток. В сопловом аппарате происходит расширение пара или газа, на рабочих лопатках - преобразование кинетич. энергии потока рабочего тела в работу вращения ротора турбины. Поскольку в каждой ступени используется только часть располагаемого перепада давления и тепла, скорости пара или газа в ней умеренные. Это позволяет получить хороший кпд при относительно невысокой частоте вращения ротора, что необходимо для непосредственного соединения турбины с приводимыми машинами (электрич. генераторами, компрессорами).

Число ступеней при проектировании М. т. выбирают с учётом заданных параметров рабочего тела, кпд и габаритных размеров турбины. С увеличением числа ступеней улучшается экономичность, т. к. тепловые потери предыдущей ступени используются в последующей, но растут размеры, масса и стоимость турбины. При небольшом (до 10-15) числе ступеней их размещают в одном корпусе (цилиндре), при большем (до 30-40) - в двух или трёх корпусах. Практически все турбины, кроме мелких вспомогательных, строят многоступенчатыми (см. Паровая турбина, Газовая турбина).

Лит.: Лосев С. М., Паровые турбины и конденсационные устройства. 10 изд., М.- Л., 1964; Ш л я х и н П. Н., Паровые и газовые турбины, М.- Л., 1966.

С. М. Лосев.

МНОГОТИРАЖНАЯ ПЕЧАТЬ, группа изданий советской прессы, выходящих в производственных и учебных коллективах (на предприятиях, в колхозах, вузах и т. д.) и отражающих в основном их трудовую деятельность. М. п. возникла как одно из выражений подлинно демократии, характера, народности сов. печати. Опыт активного участия трудящихся в выпуске в трудовых коллективах тысяч стенных газет привёл к появлению в 1922-25 первых печатных фабрично-заводских газет. Термин "М. п." отражал тот факт, что первые издания подобного типа создавались на основе стенных газет путём их тиражирования с помощью гектографа - печатного станка. Среди первых печатных заводских изданий были "Наша газета" (ныне "Мартеновка", з-д "Серп и Молот", Москва), "Погонялка" (ныне "Знамя", ф-ка "Трёхгорная мануфактура", Москва), "Светоч" (з-д "Светоч", Ленинград), "Гайка" (з-д "Профинтерн", Бежецк) и др. К нач. 1928 насчитывалось ок. 200 печатных газет трудовых коллективов. Они сыграли значительную роль в восстановлении пром-сти, в борьбе с недостатками на производстве и пережитками прошлого в сознании рабочих, с неграмотностью. М. Горький оценил это новое явление как "...одно из очень крупных достижений рабочего класса на его пути к новой культуре" ("О печати", 1962, с. 241). В годы 1-й пятилетки М. п. утверждается как массовый вид прессы: так, в 1933 существовало уже 2734 фабрично-заводские газеты. Значительную часть этих изданий - газеты новостроек пятилетки, среди них газеты "Даёшь трактор!" (Сталинградский тракторный з-д, газета награждена в 1932 орденом Ленина), "Днепрострой" (Днепрогэс), "Автогигант" (Горьковский автозавод) и др. В постановлении ЦК партии от 19 авг. 1932 "О фабрично-заводской печати" было подчёркнуто, что задачей газет является освещение жизни предприятия во всей её многогранности, помощь в организации политич. и производств, жизни коллектива, что осн. авторами газеты должны быть рабкоры. В 30-е гг. М. п. способствовала распространению передовых приёмов труда, развитию стахановского движения; газеты пропагандировали произведения сов. литературы, искусства, при многих из них создавались лит. объединения. Начало творческого пути ряда сов. писателей связано с М. п. Наряду с фабрично-заводскими газетами многотиражные издания стали выходить в крупнейших колхозах и совхозах, а также на транспорте, в вузах, производств, и творческих объединениях и т. д.

В 1972 выпускались 3852 многотиражные газеты (из них 955 колхозных) общий годовой тираж их св. 424 млн. экз.; периодичность этих изданий от 3-5 раз в неделю до 1 раза в месяц. Важнейшую их часть составляют производств, издания.

Совр. М. п., являясь средством социального управления и связи в коллективе, помогает в осуществлении задач, поставленных партией, всесторонне освещает деятельность предприятия, помогает контролировать ход трудового процесса, участвует в развёртывании социалистич. соревнования, способствует проявлению социальной активности трудящихся. М. п. играет важную роль в создании необходимого социально-психологического климата в коллективе, в выработке коммунистич. отношения к труду, норм поведения, пропагандирует революционные, боевые и трудовые традиции. Участие трудящихся в работе М. п. носит массовый, постоянный, организованный характер (общественные редколлегии, отделы, рабкоровские посты и т. д.). См. Рабселькоровское движение.

Издания, подобные сов. М. п., существуют и в др. социалистич. странах.

Лит.: Ю р о в Ю., Твоя заводская газета, М., 1960; Алексеева М. И., Газета в зеркале социологического анализа, Л., 1970.

Г. С. Вычуб.

МНОГОТОПЛИВНЫЙ ДВИГАТЕЛЬ, двигатель внутреннего сгорания, предназначенный для работы на различных нефтяных топливах, начиная от бензина и кончая дизельным топливом. Первые М. д. появились в 30-х гг. 20 в. в Германии. Они строились на базе карбюраторных двигателей, но имели раздельную подачу воздуха и топлива. Воздух поступал в цилиндры под действием разрежения, а топливо впрыскивалось насосом с давлением ок. 5 Мн/м* (50 кгс/см²). Пуск двигателя осуществлялся на бензине при помощи карбюратора, выключавшегося при нормальной работе. Смесь воспламенялась электрич. системой зажигания. В 40-е гг. получили развитие М. д., построенные на базе автомобильных дизельных двигателей. Топливо в них подавалось насосом под давлением ок. 21 Мн/м² (210 кгс/см²). При переходе с одного топлива на другое при помощи насоса подачи топлива устанавливался одинаковый расход топлива по массе, тем самым сохранялась та же мощность двигателя.

Применение М. д. на автомобилях и тракторах значительно расширяет их топливную базу. По сравнению с карбюраторными двигателями М. д. обладают лучшей топливной экономичностью, но уступают дизелям. К недостаткам М. д. относятся сложность конструкции и необходимость тщательного наблюдения за работой системы топливоподачи. М. д. получили широкое распространение за рубежом, особенно в ФРГ.

А. А. Сабинин.

МНОГОТОЧИЕ, знак препинания в виде трёх рядом поставленных точек; см. Знаки препинания.

МНОГОУГОЛЬНИК, замкнутая ломаная линия. Подробнее, М.- линия, к-рая получается, если взять п любых точек At, А?, ..., An и соединить прямолинейным отрезком каждую из них с последующей, а последнюю - с первой (см. рис. 1, а). Точки At, А₂, ••-, А_п наз. вершинами М., а отрезки AiA₂, А₂Аз, ..., An-t An, AnAt - его сторонами. Далее рассматриваются только плоские М. (т. е. предполагается, что М. лежит в одной плоскости). М. может сам себя пересекать (см. рис. 1, в), причём точки самопересечения могут не быть его вершинами.

Существуют и другие точки зрения на то, что считать М. Многоугольником можно наз. связную часть плоскости, вся граница к-рой состоит из конечного числа прямолинейных отрезков, наз. сторонами многоугольника. М. в этом смысле может быть и многосвязной частью плоскости (см. рис. 1, г), т. е. такой М. может иметь "многоугольные дыры". Рассматриваются также бесконечные М.- части плоскости, ограниченные конечным числом прямолинейных отрезков и конечным числом полупрямых.

Рис. 1. Дальнейшее изложение опирается на данное выше первое определение М.

Если М. не пересекает сам себя (см., напр., рис. 1, а и б), то он разделяет совокупность всех точек плоскости, на нем не лежащих, на две части - конечную (внутреннюю) и бесконечную (внешнюю) в том смысле, что если до точки принадлежат одной из этих частей, то их можно соединить друг с другом ломаной, не пересекающей М., а если разным частям, то нельзя. Несмотря на совершенную очевидность этого обстоятельства, строгий его вывод из аксиом геометрии довольно труден (т. н. теорема Жордана для М.). Внутренняя по отношению к М. часть плоскости имеет определённую площадь. Если М.- самопересекающийся, то он разрезает плоскость на определённое число кусков из к-рых один бесконечный (наз. внешним по отношению к М.), а остальные конечные односвязные (наз. внутренними причём граница каждого из них есть нек-рый самонепересекающийся М., стороны к-рого есть целые стороны или части сторон, а вершины - вершины или точки самопересечения данного М. Если каждой стороне М. приписать направление, т. е. указать, какую из двух определяющих её вершин мы будем считать её началом, а какую - концом, и притом так, чтобы начало каждой стороны было концом предыдущей, то получится замкнутый многоугольный путь, или ориентированный М. Площадь области, ограниченной самопересекающимся ориентированным М., считается положительной, если контур М. обходит эту область против часовой стрелки, т. е. внутренность М. остаётся слева от идущего по этому пути, и отрицательной -в противоположном случае. Пусть М.- самопересекающийся и ориентированный; если из точки, лежащей во внешней по отношению к нему части плоскости провести прямолинейный отрезок к точке, лежащей внутри одного из внутренних его кусков, и М. пересекает этот отрезок р раз слева направо и q раз справа налево, то число р - q (целое положительное, отрицательное или нуль) не зависит от выбора внешней точки и наз. коэффициентом этого куска. Сумма обычных площадей этих кусков, помноженных на их коэффициенты, считается "площадью" рассматриваемого замкнутого пути (ориентированного М.). Определяемая "площадь замкнутого пути играет большую роль в теории математич. приборов (планиметр и др.); оно получается там обычно в виде интеграла (в полярных координатах р, со) или §ydx (в декартовых координатах х, у), где конец радиус-вектора р или ординаты у один раз обегает этот путь.

Сумма внутр. углов любого самонепересекающегося М. с и сторонами равна (п - 2) 180°. М. наз. выпуклым (см. рис. 1, в), если никакая сторона М., будучи неограниченно продолженной, не разрезает М. на две части. Выпуклый М. можно охарактеризовать также следующим свойством: прямолинейный отрезок, соединяющий любые две точки плоскости, лежащие внутри М., не пересекает М. Всякий выпуклый М.- самонёпересекающийся, но не наоборот. Напр., на рис. 1, б изображён самонепересекающийся М., к-рый не является выпуклым, т. к. отрезок PQ, соединяющий нек-рые его внутр. точки, пересекает М.

Важнейшие М.: треугольники, в частности прямоугольные, равнобедренные, равносторонние (правильные); четырёхугольники, в частности трапеции, параллелограммы, ромбы, прямоугольники, квадраты. Выпуклый М. паз. правильным, если все его стороны равны и все внутр. углы равны. В древности умели по стороне или радиусу описанного круга строить при помощи циркуля и линейки правильные М. только в том случае, если число сторон М. равно т= 3-2n, 4-2n,5-2n, 3-5-2n, где и-любое положительное число или нуль. Нем. математик К. Гаусс в 1801 показал, что можно построить при помощи циркуля и линейки правильный М., когда число его сторон имеет вид: т = 2n-pi-p₂- ...-pit, где pi, p-2, ... РК -различные простые числа вида р - 2²' + 1 (s - целое положительное число). До сих пор известны только пять таких р : 3, 5, 17, 257, 65537. Из теории Галуа (см. Галуа теория) следует, что никаких др. правильных М., кроме указанных Гауссом, построить при помощи циркуля и линейки нельзя. Т. о., построение возможно при т = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, ... и невозможно при т = 7,9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33, ...

Рис. 2.

В приведённой ниже таблице указаны радиус описанной окружности, радиус вписанной окружности и площадь правильного и-угольника (для п = 3, 4, 5, 6, 8, 10), сторона к-рого равна k.

Начиная с пятиугольника существуют также невыпуклые (самопересекающиеся, или звездчатые) правильные М., т. е. такие, у к-рых все стороны равны и каждая следующая из сторон повёрнута в одном и том же направлении и на один и тот же угол по отношению к предыдущей . Все вершины такого М. также лежат на одной окружности. Такова, напр., пятиконечная звезда. На рис. 2 даны все правильные (как выпуклые, так и невыпуклые) М. от треугольника до семиугольника.

Лит. см. при ст. Многогранник.

МНОГОУГОЛЬНИК СИЛ, ломаная линия, которая строится для определения главного вектора (геом. суммы) данной системы сил. Чтобы построить М. с. для системы сил Fi, F₂, ..., F_n (рис., а), надо от произвольной точки а поочерёдно отложить в выбранном масштабе вектор ab, изображающий силу Fi, от его конца отложить вектор be, изображающий силу F₂, и т. д. и от конца т предпоследней силы отложить вектор тп, изображающий силу Fn (рис., б). Фигура а,b,с ... тп и наз. М. с. Вектор an, соединяющий в М. с. начало первой силы с концом последней, изображает геометрнч. сумму R данной системы сил. Когда точка п совпадает с а, М. с. наз. замкнутым; в этом случае R = 0. Правило М. с. может быть получено последовательным применением правила параллелограмма сил.

Построением М. с. пользуются при графич. решении задач статики для систем сил, расположенных в одной плоскости.

МНОГОУСТКИ, класс червей; то же, что моногенетические сосальщики.

МНОГОФОТОННЫЕ ПРОЦЕССЫ, процессы взаимодействия электромагнитного излучения с веществом, сопровождающиеся поглощением или испусканием (или тем и другим) нескольких электромагнитных квантов (фотонов) в элементарном акте.

Осн. трудность наблюдения М. п.- их чрезвычайно малая вероятность по сравнению с однофотонными процессами. В оптич. диапазоне до появления лазеров наблюдались только двухфотонные процессы при рассеянии света: резонансная флуоресценция (см. Люминесценция), релеевское рассеяние света, Мандельштама - Бриллюэна рассеяние и комбинационное рассеяние света. При резонансной флуоресценции (рис., а) атом или молекула поглощают в элементарном акте одновременно один фотон возбуждающего излучения hw1 и испускают один фотон hw₂ той же самой энергии. Рассеивающий атом при этом снова оказывается на том же самом уровне энергии E1. В элементарном акте бриллюэновского и комбинационного рассеяний в результате поглощения и испускания фотонов рассеивающая частица оказывается на уровне энергии, удовлетворяющем закону сохранения энергии для всего двухфотонного процесса в целом: увеличение энергии частицы Е₂ - Е1 равно разности энергий поглощённого и испущенного фотонов hw1 -hw₂ (рис., б). После появления лазеров стало возможным наблюдение процессов многофотонного возбуждения, когда в элементарном акте одновременно поглощается неск. фотонов возбуждающего излучения (рис., в). Так, при двухфотонном возбуждении атом или молекула одновременно поглощают два фотона hw1 и hw2 и оказываются в возбуждённом состоянии с энергией Е₂ = Е 1 + (hw1 + + hw₂) (см. Вынужденное рассеяние света, Нелинейная оптика).

Схемы квантовых переходов для двухфотонных процессов; а - в случае резонансной флуоресценции; б -комбинационного Рассеяния и рассеяния Мандельштама - Риллюэна; в - двухфотонного возбуждения.

Представление о М. п. возникло в квантовой теории поля для описания взаимодействия излучения с веществом. Это взаимодействие описывается через элементарные однофотонные акты поглощения и испускания фотонов, причём р-приближению теории возмущений соответствует элементарный акт с одновременным участием р фотонов; р-фотонный переход можно рассматривать как переход, происходящий в р этапов через р - 1 промежуточных состояний системы: сначала поглощается (или испускается) один фотон и система из состояния Ео переходит в состояние Е1, затем поглощается (или испускается) второй фотон и система оказывается в состоянии Е₂ и т. д.; наконец, в результате р элементарных однофотонных актов система оказывается в конечном состоянии Е1.

В случае М. п. с поглощением или вынужденным испусканием р фотонов одинаковой частоты со величина вероятности перехода пропорциональна числу фотонов этой частоты в степени р, т. е. интенсивности излучения в этой степени.

Вероятность М. п. с участием р фотонов отличается от вероятности М. п. с участием (р - 1) фотона множителем, к-рый в оптич. диапазоне для нерезонансных разрешённых дипольных электрич. переходов (см. Квантовые переходы)

тонов вероятность перехода резко уменьшается. В случае лазерных источников уже достигнуты столь большие плотности

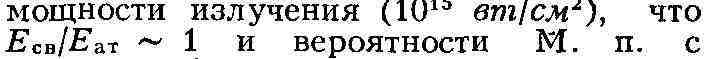
участием большого числа фотонов становятся сравнимыми с вероятностями однофотонных переходов.

Правила отбора для М. п. отличны от правил отбора для однофотонных. В системах с центром симметрии дипольные электрич. переходы с участием чётного числа фотонов разрешены только между состояниями с одинаковой чётностью, а с участием нечётного числа фотонов - между состояниями с разной чётностью. На новых правилах отбора для М. п. основано одно из наиболее принципиальных применений М. п.-многофотонная спектроскопия. Измерение спектров многофотонного поглощения позволяет оптич. методами исследовать энергетич. состояния, возбуждение к-рых запрещено из осн. состояния в однофотонных процессах.

В отличие от однофотонных процессов, закон сохранения энергии при М. п. может быть выполнен при результирующем переходе атома из более низкого в более высокое энергетич. состояние не только с поглощением, но и с испусканием отд. фотонов. Поэтому М. п. лежат в основе методов преобразования частоты излучения лазеров и создания новых перестраиваемых по частоте лазерных источников излучения (генераторов гармоник, генераторов комбинационных частот, параметрических генераторов света и т. п.). На основе М. п. возможно также создание перестраиваемых по частоте источников мощного оптического излучения.

Лит.: Бонч-Бруевич А. М., X о-довой В. А., Многофотонные процессы, "Успехи физических наук", 1965, т. 85, в. 1, с. 3 - 67; их же, Многофотонные процессы в оптическом диапазоне, "Изв. АН БССР, сер. физико-математических наук", 1965, № 4, с. 13-32.

В. А. Ходовой.

МНОГОЦВЕТНАЯ ПЕЧАТЬ, способ получения цветных отпечатков (репродукций) путём последовательного печатания на бумагу (или др. материал) с печатных форм на машине или станке. Цветные репродукции могут быть изготовлены любым способом печати (высоким, плоским и глубоким). Общим для всех способов является получение цветного оттиска определённым числом печатных красок, причём число печатных форм, с к-рых производится печатание, соответствует числу используемых красок.

Цветная полиграфич. репродукция появилась на заре печатания (оттиски с гравюр на дереве или металле раскрашивались от руки). М. п. начали применять после изобретения в кон. 18 в. литографии, когда для каждого цвета оригинала изготавливалась на литографском камне отд. печатная форма. Цветная литография получила название хромолитографии. Создание цветочувствительных фотографических слоев в конце 19 в, и др. достижения фотографической техники (более совершенная оптика, светофильтры, мощные источники света) привели к замене ручных способов изготовления печатных форм для цветной репродукции фотомеханическими способами.

Осн. задача М. п.- получить с помощью определённого кол-ва цветных красок на каждом участке оттиска цветные изображения, идентичные по цвету и рисунку данному участку оригинала. Исходя из теории трёхкомпонентности зрения, многообразие цветов на цветной репродукции достигается в результате трёхцветного синтеза, основанного на субтрактивном способе воспроизведения, т. е. на принципе образования цвета путём субтракции (вычитания) к.-л. лучей из состава белого света (см. Цветовые измерения). Любой цвет и, следовательно, любой многоцветный оригинал может быть воспроизведён тремя красками: пурпурной (синевато-красной), голубой (зеленовато-синей) и жёлтой. Каждая из этих красок имеет макс, поглощение в одной зоне спектра и максимум отражения в двух др. зонах. Из-за прозрачности красок при наложении их в равных кол-вах практически не получается чёрного цвета. Этот недостаток восполняется применением четвёртой краски - чёрной. Поэтому рекомендуется использовать не трёх-, а четырёхкрасочный синтез. Результаты цветового синтеза при М. п. зависят от цветового охвата комплекта (триады) красок, т. е. от предельного кол-ва цветовых тонов, которое может быть получено при их сочетании в разных кол-вах, а также от свойств поверхности применяемой бумаги (или др. материала). В тех случаях, когда осн. комплект красок не обеспечивает воспроизведения определённого цвета, сюжетно важного для данного оригинала, кроме осн. триады красок, применяют дополнительно ещё к.-л. цветную краску, напр, зелёную или фиолетовую, или "под золото".

Процесс получения цветной репродукции состоит из трёх осн. частей. Первая часть - аналитическая (или цветоделение) - может быть осуществлена фотографич. или электронным цветоделением. Вторая - переходная (или градационный процесс) - состоит в получении градаций цветоделённого изображения и включает изготовление цветоделённых полутоновых или растровых негативов и диапозитивов (см. Растр полиграфический) и печатных форм. Третья часть - синтетическая - состоит в получении цветных печатных оттисков.

Для М. п. применяются однокрасочные, двухкрасочные или многокрасочные машины. При использовании однокрасочных и двухкрасочных машин после одного печатного цикла получается одно-или двухкрасочный оттиск, а для получения четырёхкрасочного оттиска необходимо соответственно четыре или два раза повторять процесс печатания для наложения последующих красок. Наиболее перспективно использование многокрасочных машин, на к-рых производится печатание последовательно всех четырёх красок за один печатный цикл с одной или двух сторон бумажного листа.

Лит.: Попрядухин П. А., Печатные процессы, 2 изд., М., 1955 (Технология полиграфического производства, кн. 3); Синков Н. И., Технология изготовления фотомеханических печатных форм, М., 1963; З е р н о в В. А., Фотографические процессы в репродукционной технике, М., 196

А. Л. Попов.

МНОГОЦВЕТНИЦА (Nymphalis polchloros), дневная бабочка сем. нимф. лид. Крылья в размахе до 6 см, фестосчатые, красно-бурые с буровато-черным рисунком; вдоль тёмной краевой каймы проходит ряд голубых полулунных пя тен. Распространена в Европе и 3aп. Сибири. Бабочки выводятся во второй половине лета; зимуют оплодотворённые самки. Гусеницы чёрные с продольными жёлтыми полосами; развиваются в нек-рых лиственных деревьях, в т. ч. плодовых; живут выводками в рыхлых сплетённых листьях. М. - второстепенный вредитель плодовых деревьев.

МНОГОЧЛЕН, полином, выражение вида

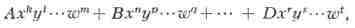
где x, y, ..., w — переменные, а А, В, ..., D (коэффициенты М.) и k, l, ..., t (показатели степеней — целые неотрицательные числа) — постоянные. Отд. слагаемые вида Ax^ky¹... w^m наз. членами М. Порядок членов, а также порядок множителей в каждом члене можно менять произвольно; точно так же можно вводить или опускать члены с нулевыми коэффициентами, а в каждом отд. члене — степени с нулевыми показателями. В случае, когда М. имеет один, два или три члена, его наз. одночленом, двучленом или трёхчленом. Два члена М. наз. подобными, если в них показатели степеней при одинаковых переменных попарно равны. Подобные между собой члены

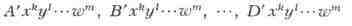
можно заменить одним (приведение подобных членов). Два М. наз. равными, если после приведения подобных все члены с отличными от нуля коэффициентами оказываются попарно одинаковыми (но, может быть, записанными в разном порядке), а также если все коэффициенты этих М. оказываются равными нулю. В последнем случае М. наз. тождественным нулём и обозначают знаком 0. М. от одного переменного х можно всегда записать в виде

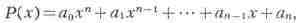
где а₀, a₁ ,..., an — коэффициенты.

Сумму показателей степеней к.-л. члена М. наз. степенью этого члена. Если М. не тождественный нуль, то среди членов с отличными от нуля коэффициентами (предполагается, что все подобные члены приведены) имеются один или несколько наибольшей степени; эту наибольшую степень наз. степенью М. Тождественный нуль не имеет степени. М. нулевой степени сводится к одному члену А (постоянному, не равному нулю). Примеры: xyz + х + у + z есть многочлен третьей степени, 2х + у — z + 1 есть многочлен первой степени (л и н е й н ы й М.), 5x² — 2x² — 3x² не имеет степени, т. к. это тождественный нуль. М., все члены к-рого одинаковой степени, наз. однородным М., или формой; формы первой, второй и третьей степеней наз. линейными, квадратичными, кубичными, а по числу переменных (два, три) двоичными (бинарными), тройничными (тернарными) (напр., х² + + y² + z² - ху - yz - xz есть тройничная квадратичная форма).

Относительно коэффициентов М. предполагается, что они принадлежат определённому полю (см. Поле алгебраическое), напр., полю рациональных, действительных или комплексных чисел. Выполняя над М. действия сложения, вычитания и умножения на основании переместительного, сочетательного и распределительного законов, получают снова М. Таким образом, совокупность всех М. с коэффициентами из данного поля образует кольцо (см. Кольцо алгебраическое) - кольцо многочленов над данным полем; это кольцо не имеет делителей нуля, т. е. произведение М., не равных 0, не может дать 0.

Если для двух многочленов Р(х) и Q(x) можно найти такой многочлен R(x), что Р = QR, то говорят, что Р делится на О; О наз. делителем, a R - частным. Если Р не делится на О, то можно найти такие многочлены Р(х) и S(x), что Р = QR + S, причём степень S(x) меньше степени Q(x).

Посредством повторного применения этой операции можно находить наибольший общий делитель Р и О, т. е. такой делитель Р и Q, к-рый делится на любой общий делитель этих многочленов (см. Евклида алгоритм). М., к-рый можно представить в виде произведения М. низших степеней с коэффициентами из данного поля, наз. приводимым (в данном поле), в противном случае -неприводимым. Неприводимые М. играют в кольце М. роль, сходную с простыми числами в теории целых чисел. Так, напр., верна теорема: если произведение PQ делится на неприводимый многочлен R, а Р на R не делится, то тогда О должно делиться на R. Каждый М. степени, большей нуля, разлагается в данном поле в произведение неприводимых множителей единств, образом (с точностью до множителей нулевой степени). Напр., многочлен х^л + 1, неприводимый в поле рациональных чисел, разлагается на два множителя

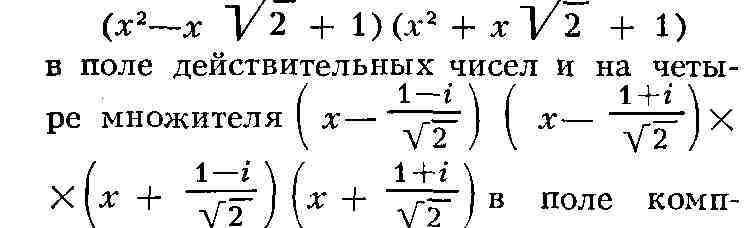
лексных чисел. Вообще каждый М. от одного переменного х разлагается в поле действительных чисел на множители первой и второй степени, в поле комплексных чисел - на множители первой степени (основная теорема алгебры). Для двух и большего числа переменных этого уже нельзя утверждать; напр., многочлен х³ + уz² + + z³ неприводим в любом числовом поле.

Если переменным х, у, ..., w придать определённые числовые значения (напр., действительные или комплексные), то М. также получит определённое числовое значение. Отсюда следует, что каждый М. можно рассматривать как функцию соответствующих переменных. Эта функция непрерывна и дифференцируема при любых значениях переменных; её можно характеризовать как целую рациональную функцию, т. е. функцию, получающуюся из переменных и нек-рых постоянных (коэффициентов) посредством выполненных в определённом порядке действий сложения, вычитания и умножения. Целые рациональные функции входят в более широкий класс рациональных функций, где к перечисленным действиям присоединяется деление: любую рациональную функцию можно представить в виде частного двух М. Наконец, рациональные функции содержатся в классе алгебраических функции.

К числу важнейших свойств М. относится то, что любую непрерывную функцию можно с произвольно малой ошибкой заменить М. (теорема Вейерштрасса; точная её формулировка требует, чтобы данная функция была непрерывна на к.-л. ограниченном, замкнутом множестве точек, напр., на отрезке числовой оси). Этот факт, доказываемый средствами математич. анализа, даёт возможность приближённо выражать М, любую связь между величинами, изучаемую в к.-л. вопросе естествознания и техники. Способы такого выражения исследуются в спец. разделах математики (см. Приближение и интерполирование функций, Наименьших квадратов метод).

В элементарной алгебре многочленом иногда наз. такие алгебраич. выражения, в к-рых последним действием является сложение или вычитание, напр.

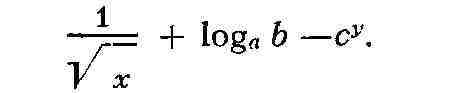
Лит.; К у р о ш А. Г., Курс высшей алгебры, 9 изд., М., 1968; Мишина А. П., Проскуряков И. В., Высшая алгебра, 2 изд., М., 1965.

А. И. Маркушевич.

МНОГОЩЕТИНКОВЫЕ ЧЕРВИ, п о л и х е т ы (Polychaeta), класс кольчатых червей. Дл. от 2 мм до 3 м. Тело - из множества, иногда до неск. сот, колец-сегментов, в каждом из к-рых повторяется комплекс внутр. органов. Туловищные сегменты снабжены примитивными конечностями - параподиями - с многочисл. щетинками (отсюда назв.). С параподиями часто связаны ветвистые придатки - жабры; у нек-рых М. ч. функцию жабр выполняет венчик щупалец на головном участке. Имеются глаза, иногда сложно устроенные, и органы равновесия (статоцисты). М. ч., как правило, раздельнополы; оплодотворение наружное. Развитие с метаморфозом, из яйца развивается личинка трохофора. Бесполое размножение путём почкования и живорождение редки. При созревании половых продуктов у нек-рых М. ч. (нереид, пололо и др.) происходят резкие морфологич. изменения (разрастаются параподии, появляются добавочные придатки и т. д.), червь всплывает на поверхность и здесь вымётывает половые продукты (т. н. эпитокия).

Многощетинковые черви: 1 - пескожил (Arenicola); 2 - Thelepus (в трубке, сложенной из песчинок): 3 - Serpula (в известковой трубке); 4 - Lepidonotus (спинная сторона прикрыта чешуйками, или элитрами); 5 - нереис; 6 ~ Tomopteris.

М. ч. живут в морях, лишь немногие-в пресных водах (напр., Manayunkia в Байкале). В классе ок. 70 сем. (св. 6 тыс. видов); в СССР не менее 700 видов. Большинство М. ч.- обитатели дна (встречаются на глубине до 10 тыс. м): свободно ползают по грунту или зарываются в ил; многие строят из песчинок или др. материалов разной формы трубки, к-рые никогда не покидают. Питаются детритом; мн. хищники, нередко комменсалы; паразиты - лишь как исключение. Нек-рым видам свойственно свечение (см. Биолюминесценция). М. ч. служат пищей для мн. рыб. В 1939-1941 из Азовского м. в Каспийское м. был перевезён М. ч. нереис, ставший осн. пищей осетровых рыб. Нек-рые крупные черви (пескожилы и др.) используются как наживка для рыбной ловли. Нек-рые виды наносят вред нар. хозяйству (участвуют в обрастании). К М. ч. относят архианнелид и сильно видоизменённых в связи с паразитизмом мизостомид. Ископаемые остатки М. ч. известны с кембрия.

Лит.: Руководство по зоологии, т. 2, М. - Л., 1940; Большой практикум по зоологии беспозвоночных, ч. 1, Л., 1941; Ушаков П. В., Многощетинковые черви дальневосточных морей СССР (Polychaeta), М.-Л., 1955; Жизнь животных, т. 1, М., 1968; Фауна СССР. Многощетннковые черви, т. 1, Л., 1972 (АН СССР. Зоологический нн-т. Нов. серия, № 102.

П. В. Ушаков.

МНОГОЭТАЖНЫЕ ЗДАНИЯ. Понятие "М. з." изменяется исторические зависимости от этажности гор. застройки, обусловленной социальными, экономич. и гра-достропт. требованиями. Жилые и обществ. М. з. начали широко распространяться в античных городах вследствие потребности в ускоренном стр-ве дешёвых жилищ для населения с низким доходом (напр., инсулы в Др. Риме), а позднее и в ср.-век. городах ввиду ограниченности их терр., защищённой гор. стенами (дома зажиточных горожан Европы с жильём, мастерскими и лавками в 1-2-х этажах и амбарами в остальных). В эпоху капитализма бурный рост городов и значительное удорожание гор. земельных участков вызвали резкое расширение стр-ва М. з., а совершенствование их инж. оборудования (в первую очередь появление лифта) позволило значительно поднять их высоту (16-этажный Монаднок-билдннг в Чикаго, 1891, арх. Д. X. Бёрнем и Дж. У. Рут). В кон. 19 - нач. 20 вв. в США появились М. з. в несколько десятков этажей (т. н. небоскрёбы), используемые для контор, банков, гостиниц, жилья. Построенный в 1930-31 в Нью-Йорке небоскрёб Эмпайр стейт билдинг (архит. фирма "Шрив, Лэмб и Хармон") насчитывает 102 этажа (вые. без телевизионной вышки, выстроенной в 1951,- ок. 380 м). Со 2-й пол. 1940-х гг., в связи с интенсивной урбанизацией, а. иногда и недостатком свободных территорий, М. з. получили широкое распространение во многих странах мира. Наряду с основным массовым строительством М. з. в 9-17 этажей возводятся т. н. высотные здания, часто многофункционального назначения (например, 100-этажный Джон Хэнкок билдинг в Чикаго, 1971, арх. Л. Скидмор, Н. А. Оуингс, Дж. О. Мерилл, где размещаются магазины, банк, гараж, конторы, жильё и др.). В условиях капиталистического градостроительства стихийная концентрация М. з. на ограниченной терр. и скопление значит, масс людей и трансп. средств приводят к разрушению функциональных, физико-гигиенич. и эстетич. качеств гор. среды (трансп. пробки, оглушающе шумные, узкие улицы, лишённые свежего воздуха, ощущение хаоса, к-рое создаёт вид тесной застройки разновысотными, нередко невыразительными по архитектуре М. з.).

В СССР и др. социалистич. странах М. з. размещаются обычно в соответствии с градостроит. требованиями, согласно ген. планам городов (в частности, в целях экономии территорий в центре города, особо ценных вследствие их насыщенности дорогостоящими коммуникациями, инж. оборудованием и пр.). В кон. 1940-х - нач. 1950-х гг. в Москве по единому градостроительному замыслу было построено 7 высотных зданий в 26-32 этажа (арх. В. Г. Гельфрейх, А. Н. Душкин, Б. С. Мезенцев, М. А. Минкус, А. Г. Мордвинов, Л. М. Поляков, Л. В. Руднев, Д. Н. Чечулин и др.). Сооружение этих зданий ускорило технич. прогресс в области строительства. Поставленные в ключевых местах столицы и увенчанные шпилями, они придали ей новый силуэт и масштабность. Для этих зданий характерны сложная композиция из разновысотных объёмов, обилие декора на фасадах и в интерьерах, низкий процент полезной площади. Стр-во М. з. индустриальными методами резко увеличилось в СССР во 2-й пол. 1960-х гг. (в 1973 - 20% от общего стр-ва жилых зданий). Наряду с осн. массой 9-17-этажных зданий воздвигаются и здания в 25 этажей и выше. Иногда М. з. образуют целые комплексы (напр., проспект Калинина в Москве, 1964-69, арх. М. В. Посохин, А. А. Мндоянц и др.; илл. см. т. 7, табл. XV, стр. 208-209). Единой классификации М. з. не существует. Критерием отнесения зданий к категории М. з. принято считать появление (в результате большой высоты) качественных изменений в их планировке, конструкции и техническом оснащении. В М. з. требуется обеспечение пожарной безопасности (повышенная огнестойкость конструкций, устройство незадымляемых лестниц, систем пожарного водопровода, дымоудаления и др.), конструктивной устойчивости под действием ветровых, в т. ч. динамич., нагрузок, усложняются лифтовое хозяйство и технич. оборудование. Конструктивная устойчивость жилых М. з. достигается гл. обр. за счёт поперечных несущих стен или связевого каркаса (в СССР преим. сборного железобетонного; см. Железобетонные конструкции и изделия, Крупнопанельные конструкции), в обществ, зданиях - в сочетании с т. н, ядром жёсткости (железобетонной коробкой, ограждающей собранные вместе лифтовые шахты, технич. коммуникации). В высотных зданиях за рубежом распространены ядрооболочковые конструкции, в к-рых "оболочка" - несущие фасадные ограждения решётчатого типа из стальных или предварительно напряжённых железобетонных элементов - соединяется перекрытиями с расположенным в центре "ядром", образуя единую систему большой жёсткости (две 110-этажные башни Центра междунар. торговли в Нью-Йорке, арх. М. Ямасаки и др., 1971-73). Из-за большого (порой отрицательного) влияния на традиц. облик старых городов огромных объёмов, повторения многих тысяч одинаковых фасадных элементов создать выразительное архит. решение М. з. очень сложно. Стремясь преодолеть сверхчеловеческий масштаб и однообразие, архитекторы вводят в композицию М. з. сопоставление разновысотных объёмов, иногда криволинейные очертания, ищут выразит, пропорции и силуэт, прибегают к ритмич. организации фасадных элементов (напр., группировка балконов и их ограждений или окон в композиции орнаментального характера), к эффектной отделке фасадов нержавеющей сталью, алюминием, бронзой, стеклом (напр., 38-этажное здание Сигрем-билдинг в Нью-Йорке, 1958, арх. Л. Мис ван дер РОЭ).

Лит.: Д ы х о в и ч н ы й Ю. А., Конструирование и расчет жилых и общественных зданий повышенной этажности, М., 1970; I Международный симпозиум. Многоэтажные здания. Сборник докладов. Москва -СССР. Октябрь 1971, М., 1972 (на рус. и англ, яз.); R a f e i n e r F., Hochhauser. Planting, Kosten, Bauausfuhrung, В., 1968.

А. И. Опочинская,

МНОЖЕСТВ ТЕОРИЯ, учение об общих свойствах множеств, преимущественно бесконечных. Понятие м н о ж е с т в а, или совокупности, принадлежит к числу простейших математических понятий; оно не определяется, но может быть пояснено при помощи примеров. Так, можно говорить о множестве всех книг, составляющих данную библиотеку, множестве всех точек данной линии, множестве всех решений данного уравнения. Книги данной библиотеки, точки данной линии, решения данного уравнения являются элементами соответствующего множества. Чтобы определить множество, достаточно указать характеристич. свойство элементов, т. е. такое свойство, к-рым обладают все элементы этого множества и только они. Может случиться, что данным свойством не обладает вообще ни один предмет; тогда говорят, что это свойство определяет пустое множество. То, что данный предмет х есть элемент множества М, записывают так: х е М (читают: х принадлежит множеству М).

Подмножества. Если каждый элемент множества А является в то же время элементом множества В, то множество А наз. подмножеством, или частью, множества В. Это записывают так: А ? В или В Э А. Т. о., подмножеством данного множества В является и само множество В. Пустое множество, по определению, считают подмножеством всякого множества. Всякое непустое подмножество А данного множества В, отличное от всего множества В, наз. правильной частью последнего.

Мощность множеств. Первым вопросом, возникшим в применении к бесконечным множествам, был вопрос о возможности их количественного сравнения между собой. Ответ на этот и близкие вопросы дал в кон. 70-х гг. 19 в. Г. Кантор, основавший М. т. как математич. науку. Возможность сравнительной количественной оценки множеств опирается на понятие взаимно однозначного соответствия между двумя множествами. Пусть каждому элементу множества А поставлен в соответствие в силу какого бы то ни было правила или закона некоторый определённый элемент множества В; если при этом каждый элемент множества оказывается поставленным в соответствие одному и только одному элементу множества Л, то говорят, что между множествами А и В установлено взаимно однозначное, или одно-однозначное, соответствие [сокращённо: (1 - 1)-соответствие]. Очевидно, между двумя конечными множествами можно установить (1 - 1)-соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В обобщение этого факта определяют количественную эквивалентность, или равномощность, двух бесконечных множеств как возможность установить между ними (1 - 1)-соответствие.

Ещё до создания М. т. Б. Больцано владел, с одной стороны, вполне точно формулированным понятием (1-1)-соответствия, а с другой стороны, считал несомненным существование бесконечностей различных ступеней; однако он не только не сделал (1-1 соответствие основой установления количественной равносильности множеств, но решительно возражал против этого. Больцано останавливало то, что бесконечное множество может находиться в (1-^-соответствии со своей правильной частью. Напр., если каждому натуральному числу п поставить в соответствие натуральное число 2п, то получим (1 - 1 ^соответствие между множеством всех натуральных и множеством всех чётных чисел. Вместо того чтобы в применении к бесконечным множествам отказаться от аксиомы: часть меньше целого, Больцано отказался от взаимной однозначности как критерия равномощности и, т. о., остался вне осн. линии развития М. т. В каждом бесконечном множестве М имеется (как легко доказывается) правильная часть, равномощная всему М, тогда как ни в одном конечном множестве такой правильной части найти нельзя. Поэтому наличие правильной части, равномощной целому, можно принять за определение бесконечного множества (Р. Дедекинд).

Для двух бесконечных множеств А и В возможны лишь следующие три случая: либо Л есть правильная часть, равномощная В, но в В нет правильной части, равномощной Л; либо, наоборот, в В есть правильная часть, равномощная Л, а в Л нет правильной части, равномощной В; либо, наконец, в А есть правильная часть, равномощная В, и в В есть правильная часть, равномощная Л. Доказывается, что в третьем случае множества Л и В равномощны (теорема Кантора-Бернштейна). В первом случае говорят, что мощность множества Л больше мощности множества В, во втором - что мощность множества В больше мощности множества Л. A priori возможный четвёртый случай - в Л нет правильной части, равномощной В, а в В нет правильной части, равномощной Л,- в действительности не может осуществиться (для бесконечных множеств).

Ценность понятия мощности множества определяется существованием неравно-мощных бесконечных множеств. Напр., множество всех подмножеств данного множества М имеет мощность большую, чем множеством. Множество, равномощное множеству всех натуральных чисел, наэ. счётным множеством. Мощность счётных множеств есть наименьшая мощность, к-рую может иметь бесконечное множество; всякое бесконечное множество содержит счётную правильную часть. Кантор доказал, что множество всех рациональных и даже всех алгебраич. чисел счётно, тогда как множество всех действит. чисел несчётно. Тем самым было дано новое доказательство существования т. н. трансцендентных чисел, т. е. действит. чисел, не являющихся корнями никакого алгебраич. уравнения с Целыми коэффициентами (и даже несчётность множества таких чисел). Мощность множества всех действительных чисел наз. мощностью континуума. Множеству всех действительных чисел равномощны: множество всех подмножеств счётного множества, множество всех комплексных чисел и, следовательно, множество всех точек плоскости, а также множество всех точек трёх- и вообще и-мерного пространства при любом п. Кантор высказал гипотезу (т.н. континуум-гипотезу): всякое множество, состоящее из действит. чисел, либо конечно, либо счётно, либо равномощно множеству всех действит. чисел; по поводу этой гипотезы и существенных связанных с нею результатов см. Континуума проблема.

Отображения множеств. В М. т. аналитич. понятие функции, геометрич. понятие отображения или преобразования фигуры и т. п. объединяются в общее понятие отображения одного множества в другое. Пусть даны два множества X

или значением данной функции для данного значения её аргумента х.

Примеры. 1) Пусть задан в плоскости с данной на ней прямоугольной системой координат квадрат с вершинами (0; 0), (0; 1), (1; 0), (1; 1) и осуществлена проекция этого квадрата, напр., на ось абсцисс; эта проекция есть отображение множества X всех точек квадрата на множество У всех точек его основания; точке с координатами (х; у) соответствует точка (х; 0).

2) Пусть X - множество всех действит. чисел; если для каждого действит. числа

(1 - 1 ) - соответствие между двумя множествами X и У есть такое отображение множества X в множество Y, при к-ром каждый элемент множества У является образом одного и только одного элемента множества X. Отображения примеров 2) и 3) взаимно однозначны, примера 1) - нет. Операции над множествами. С у м м о й, или объединением, двух, трёх, вообще произвольного конечного или бесконечного множества множеств наз. множество всех тех предметов, каждый из к-рых есть элемент хотя бы одного из данных множеств-слагаемых. Пересечением двух, трёх, вообще любого конечного или бесконечного множества множеств наз. множество всех элементов, общих всем данным множествам. Пересечение даже двух непустых множеств может быть пустым. Разностью между множеством В и множеством А наз. множество всех элементов из В, не являющихся элементами из А: разность между множеством В и его частью А наз. дополнением множества А в множестве В.

Операции сложения и пересечения множеств удовлетворяют условиям сочетательности и переместительности (см. Ассоциативность, Коммутативность). Операция пересечения, кроме того, распределительна по отношению к сложению и вычитанию. Эти действия обладают тем общим свойством, что если их производить над множествами, являющимися подмножествами одного и того же множества М, то и результат будет подмножеством множества М. Указанным свойством не обладает т. н. внешнее умножение множеств: внешним произведением множеств X и У наз. множество X XV всевозможных пял

ных множеств согласуется с умножением и возведением в степень натуральных чисел. Аналогично определяется сумма мощностей как мощность суммы попарно непересекающихся множеств с заданными мощностями.

Упорядоченные множества. Установитьв данном множестве X порядок - значит установить для нек-рых пар х', х" элементов этого множества какое-то правило предшествования (следования¹), выражае-

рассматриваемое вместе с каким-нибудь установленным в нём порядком, наз. "частично упорядоченным множеством"; иногда вместо "частично упорядоченное множество" говорят "упорядоченное множество" (Н. Бурбаки). Однако чаще упорядоченным множеством наз. такое частично упорядоченное множество, в к-ром порядок удовлетворяет след, дополнительным требованиям ("линейного порядка"): 1) никакой элемент не предшествует самому себе; 2) из всяких двух раз-

3) Всякое множество действит. чисел линейно упорядочено: меньшее из двух чисел считается предшествующим большему.

Два упорядоченных множества наз. подобными между собой, или имеющими один и тот же порядковый тип, если между ними можно установить (1 - 1)-соответствие, сохраняющее порядок. Элемент упорядоченного множества наз. первым, если он предшествует в этом упорядоченном множестве всем остальным элементам; аналогично определяется и последний элемент. Примеры: в упорядоченном множестве всех действит. чисел нет ни первого, ни последнего элемента; в упорядоченном множестве всех неотрицательных чисел нуль есть первый элемент, а последнего элемента нет; в упорядоченном множестве всех действительных чисел .г, удовлетворяющих неравенствам a <= x <= b, число а есть первый элемент, а число b - последний.

Упорядоченное множество называется вполне упорядоченным, если оно само и всякое его правильное подмножество имеют первый элемент. Порядковые типы вполне упорядоченных множеств наз. порядковыми, или ординальными, числами. Если вполне упорядоченное множество конечно, то его порядковое число есть обычное порядковое число элементарной арифметики. Порядковые типы бесконечных вполне упорядоченных множеств наз. трансфинитными числами.

Точечные множества. Теория точечных множеств, т. е. в первоначальном понимании слова - теория множеств, элементами к-рых являются действит. числа (точки числовой прямой), а также точки двух-, трёх- и вообще га-мерного пространства, основана Г. Кантором, установившим понятие предельной точки множества и примыкающие к нему понятия замкнутого множества и др. Дальнейшее развитие теории точечных множеств привело к понятиям метрического пространства и топологического пространства, изучением к-рых занимается общая топология. Наиболее самостоятельное существование ведёт дескриптивная теория множеств. Основанная франц. математиками Р. Бэром и А. Лебегом в связи с классификацией разрывных функций (1905), дескриптивная М. т. началась с изучения и классификации т. н. борелевских множеств (В-множеств). Борелевские множества определяются как множества, могущие быть построенными, отправляясь от замкнутых множеств, применением операций сложения и пересечения в любых комбинациях, но каждый раз к конечному или к счётному множеству множеств. А. Лебег показал, что те же множества - и только они - могут быть получены как множества точек, в к-рых входящая в Бэра классийикаиию действительная (Функ-

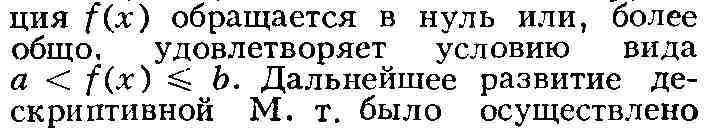
преимущественно рус. и польск. математиками, особенно московской школой, созданной Н. Н. Лузиным (П. С. Александров, М. Я. Суслин, М. А. Лаврентьев, А. Н. Колмогоров, П. С. Новиков). Александров доказал теорему (1916) о том, что всякое несчётное борелевское множество имеет мощность континуума. Аппарат этого доказательства был применён Суслиным для построения теории А -множеств, охватывающих как частный случай борелевские (или В-) множества (считавшиеся до того единств, множествами, принципиально могущими встретиться в анализе). Суслия показал, что множество, дополнительное к Л-множеству М, является само Л-множеством только в том случае, когда множество М - борелевское (дополнение к борелевскому множеству есть всегда борелевское множество). При этом Л-множества оказались совпадающими с непрерывными образами множества всех иррациональных чисел. Теория Л-множеств в течение неск. лет оставалась в центре дескриптивной М. т. до того, как Лузин пришёл к общему определению проективных множеств, которые могут быть получены, отправляясь от множества всех иррациональных чисел при помощи повторного применения операции вычитания и непрерывного отображения. К теории Л-множеств и проективных множеств относятся также работы Новикова и др. Дескриптивная М. т. тесно связана с исследованиями по основаниям математики (с вопросами эффективной определимости математич. объектов и разрешимости математич. проблем).

Значение М. т. Влияние М. т. на развитие совр. математики очень велико. Прежде всего, М. т. явилась фундаментом ряда новых математич. дисциплин (теории функций действительного переменного, общей топологии, общей алгебры, функционального анализа и др.).

Постепенно теоретико-множественные методы находят всё большее применение и в классич. частях математики. Напр., в области математич. анализа они широко применяются в качественной теории дифференциальных уравнений, вариационном исчислении, теории вероятностей и др.

Наконец, М. т. оказала глубокое влияние на понимание самого предмета математики или таких её больших отделов, как геометрия. Только М. т. позволила отчётливо сформулировать понятие изоморфизма систем объектов, заданных вместе со связывающими их отношениями, и привела к пониманию того обстоятельства, что каждая математич. теория в её чистой абстрактной форме изучает ту или иную систему объектов лишь "с точностью до изоморфизма", т. е. может быть без всяких изменений перенесена на любую систему объектов, изоморфную той, для изучения к-рой теория была первоначально создана.

Что касается М. т. в вопросах обоснования математики, т. е. создания строгого, логически безупречного построения математич. теорий, то следует иметь в виду, что сама М. т. нуждается в обосновании применяемых в ней методов рассуждения. Более того, все логич. трудности, связанные с обоснованием математич. учения о бесконечности (см. Бесконечность в математике), при переходе на точку зрения общей М. т. приобретают лишь большую остроту (см. Аксиоматическая теория множеств, Логика, Конструктивная математика, Континуум).

Лит.: Лузин Н. Н., Теория функций действительного переменного, 2 изд., М., 1948; Александров П. С., Введение в общую теорию множеств и функций, М.-Л., 1948; Хаусдорф Ф., Теория множеств, пер. с нем., М.- Л., 1937.

П. С. Александров.

МНОЖЕСТВЕННЫЕ ПРОЦЕССЫ, рождение большого числа вторичных сильно взаимодействующих частиц (адронов) в одном акте столкновения частиц при высокой энергии. М. п. характерны для столкновения адронов, однако в редких случаях они наблюдаются и при столкновениях др. частиц, если их энергия достаточна для рождения неск. адронов (напр., при электронных столкновениях на ускорителях со встречными пучками). При столкновениях адронов с энергией выше неск. Гэв М. п. доминируют над процессами одиночного рождения мезонов и упругого рассеяния частиц. Впервые М. п. наблюдались в космических лучах, однако тщательное их изучение стало возможным после создания ускорителей заряженных частиц высоких энергий. В результате исследований взаимодействия частиц космич. лучей с энергией до 10"- 10⁷ Гэв в лабораторной системе координат, а также частиц от ускорителей с энергией до ~ 10³ Гэв (встречные пучки) выявлены нек-рые эмпирич. закономерности М. п.

С наибольшей вероятностью в М. п. рождаются самые лёгкие адроны - пи-мезоны, составляющие 70-80% вторичных частиц. Значит, долю составляют также К-мезоны и гипероны (~ 10-20%) и нуклон-антинуклонные пары (порядка неск. процентов). Многие из этих частиц возникают от распада рождающихся резонансов.

Вероятность столкновения, сопровождаемого М. п. (эффективное сечение М. п.), при высоких энергиях почти не зависит от энергии сталкивающихся частиц (меняется не более чем на неск. десятков процентов при изменении энергии столкновения в 10⁴ раз). Приблизит, постоянство сечения М. п. привело к модели "чёрных шариков" для описания процессов столкновения адронов. Согласно этой модели, при каждом сближении адронов высокой энергии на расстояния, меньшие радиуса действия ядерных сил, происходит неупругий процесс множеств, рождения частиц; упругое рассеяние при этом носит в основном дифракционный характер (дифракция волн де Бройля частиц на "чёрном шарике"). Эта модель сыграла важную роль в развитии теории сильных взаимодействий (в частности, в установлении теоремы Померанчука о равенстве эффективных сечений взаимодействия частиц и античастиц при предельно высоких энергиях). С др. стороны, согласно квантовой теории поля, возможен медленный рост сечения М. п. с увеличением энергии Е, не быстрее, чем 1n² Е (теорема Фруассара).

Рис. 1. Фотография множественного рождения заряженных частиц, полученная в жидководородной пузырьковой камере "Мирабель", помещённой в пучок л-мезонов с энергией 50 Гэв на Серпуховском ускорителе.

Число частиц, рождающихся в различных актах столкновения адронов определённой энергии, сильно варьирует и в отдельных случаях оказывается очень большим (рис. 1). Ср. число вторичных частиц (п) (ср. множественность) медленно растёт с ростом энергии столкновения Е и практически не зависит от типа сталкивающихся адронов (рис. 2). При существующей точности измерений зависимость (п) от энергии одинаково хорошо описывается как логарифмической, так и степенной (типа Еv; v < 1) функцией от энергии, что затрудняет выбор между различными теоретич. моделями М. п., предсказывающими разные типы этой зависимости. Ср. множественность много меньш. максимально возможного числа вторичных частиц, к-рое определяется условием, что вся энергия столкновения в системе центра инерции (с. ц. и.) сталкивающихся частиц переходит в масс. покоя вторичных частиц. Так, при столкновении протонов с энергией 70 Гэв (от Серпуховского ускорителя) с протонами мишени могло бы рождаться до 70 я-мезонов, в действительности же ср. множественность заряженных частиц при этой энергии составляет 5-6 частиц. Это означает, что на создание массы покоя вторичных частиц идёт только небольшая часть энергии столкновения, т. е энергия тратится гл. обр. на сообщение осн. части генерированных частиц большой кинетич. энергии (большого импульса). В то же время характерной эмпирич. закономерностью М. п. является то, что поперечные (к оси соударения) компоненты p импульсов вторичных частиц как правило, малы. Ср. значение р составляет приблизительно 0,3-0,4 Гэв.

и почти постоянно в очень широкой области энергий. Поэтому вторичные частицы вылетают резко направленными и сужающимися по мере роста энергии потоками вдоль направления движения сталкивающихся частиц (в с. ц. и.- вперёд и назад, в лабораторной системе - по направлению движения налетающей частицы).

Изучение М. п. очень существенно для выяснения структуры адронов и построения теории сильных взаимодействий. В этом отношении особое значение имеют закономерности, установленные при изучении спец. класса М. п.- т. н. инклюзивных процессов, когда из большого числа М. п., происходящих при столкновениях адронов "а" и "b", отбираются события с рождением определённой частицы "с" независимо от того, какие др. частицы (X) и в каком количестве сопровождают рождение частицы "с". На важность изучения инклюзивных процессов указал в 1967 А. А. Логунов, установивший на основе квантовой теории поля предельные законы возрастания их сечения с ростом энергии (аналогичные

теореме Фруассара). При экспериментальном исследовании инклюзивных процессов на Серпуховском ускорителе (1968) и сравнении полученных данных с результатами опытов при более низких энергиях был обнаружен своеобразный закон подобия в микромире - т. н. масштабная инвариантность, или скейлинг (scaling). Масштабная инвариантность состоит в том, что вероятность рождения "инклюзивной" частицы "с" с определённым значением продольного импульса PL (проекции импульса на направление движения сталкивающихся частиц) является при разных энергиях столкновения универсальной функцией от переменной х = PL/РМАКС, где рмакс - максимально возможное (при данной энергии) значение продольного импульса частицы "с" (рис. 3). Т. о., продольные импульсы вторичных частиц растут пропорционально энергии столкновения. Указания на существование такого рода зависимости получались ранее при изучении космич. лучей. Она вытекала из того факта, что энергетич. спектр вторичной компоненты космич. лучей почти точно повторяет форму энергетич. спектра первичной компоненты (Г. Т. Зацепин и др.). Масштабная инвариантность имеет глубокий физич. смысл. Объяснение её на основе модельных представлений о составном строении адронов было предложено в 1969 Р. Фейнманом. (В 1963 на возможность такой закономерности указывал амер. физик К. У ил сон.)

Экспериментальные данные показывают, что масштабная инвариантность наблюдается при столкновениях не только элементарных частиц, но и атомных ядер при релятивистских энергиях.

Из-за отсутствия полной и последоват. теории сильных взаимодействий для объяснения эмпирич. закономерностей, обнаруженных в М. п., используются различные теоретич. модели. В статистико-гидродинамич. моделях [развитых в работах В. Гейзенберга, Э. Ферми, Л. Д. Ландау (1949-53) и др.] предполагается, что для сильно взаимодействующих частиц в течение короткого времени столкновения успевает установиться статистическое равновесие между образовавшимися в результате соударения частицами. Это позволяет рассчитать мн. характеристики М. п., в частности ср. множественность, к-рая должна расти с энергией по степенному закону Е" с показателем степени v < 1 (в теории Ферми - Ландау v = ¼. В др. классе моделей (итал. физики Д. Амати, С. Фубини, А. Стангеллини и др., сов. физики Е. Л. Фейнберг, Д. С. Чернавский и др.) считается, что рождение вторичных частиц происходит в "периферических" или "мультипериферических" взаимодействиях адронов, возникающих в результате обмена между ними виртуальным я-мезоном или др. частицей. С конца 60-х гг. для теоретич. анализа М. п. широко используется представление о том, что сильное взаимодействие при высоких энергиях осуществляется путём обмена особым состоянием - "реджеоном", являющимся как бы струёй частиц с монотонно меняющимся от частицы к частице импульсом (см. Сильные взаимодействия). Эти представления (развитые, в частности, сов. физиками В. Н. Грибовым, К. А. Тер-Мартиросяном и др.) позволяют количественно объяснить мн. закономерности М. п. Согласно "мультипериферическим" моделям и модели "реджеонов", ср. множественность должна расти пропорционально логарифму энергии столкновения.

Лит.: Мурзин В. С., Сарычев а Л. И., Множественные процессы при больших энергиях, М., 1974 (в печати); Беленький С. З., Ландау Л. Д., Гидродинамическая теория множественного образования частиц, "Успехи физических наук", 1955, т. 56, в. 3, с. 309; Ф е й н б е р г Е. Л., Множественная генерация адронов и статистическая теория, там же, 1971, т. 104, в. 4, с. 539; Feynman R., Very high-energy collisions of hadrons, "Physical Review Letters", 1969, v. 23, p. 1415; Е ж е л а В. В. [и др.], Инклюзивные процессы при высоких энергиях, "Теоретическая и математическая физика", 1973, т. 15, № 2; Тер-Мартиросян К. А., Процессы образования частиц при высокой энергии, в кн.: Материалы 6-й зимней школы по теории ядра и физике высоких энергий, ч. 2, Л., 1971, с. 334; Розенталь И. Л., Множественные процессы при больших энергиях, "Природа", 1973, № 12.

С.С. Герштейн.