МЕХАНИКА ТЕЛ ПЕРЕМЕННОЙ МАССЫ, раздел теоретич. механики, в к-ром изучаются движения материальных тел, масса которых изменяется во время движения. Основоположники М. т. п. м. - И. В. Мещерский и К. Э. Циолковский. Задачи М. т. п. м. выдвигаются развитием авиационной и ракетной техники, а также теоретич. механики.

Изменение массы тела (точки) во время движения может обусловливаться отделением (отбрасыванием) частиц или их присоединением (налипанием). При полёте совр. реактивных самолётов с воздушно-реактивными двигателями происходят одновременно как процессы присоединения, так и отделения частиц. Масса таких самолётов увеличивается за счёт частиц воздуха, засасываемых в двигатель, и уменьшается в результате отбрасывания частиц - продуктов горения топлива. Основное векторное дифференциальное ур-ние движения точки переменной массы для случая присоединения и отделения частиц (впервые полученное в 1904 Мещерским) имеет вид:

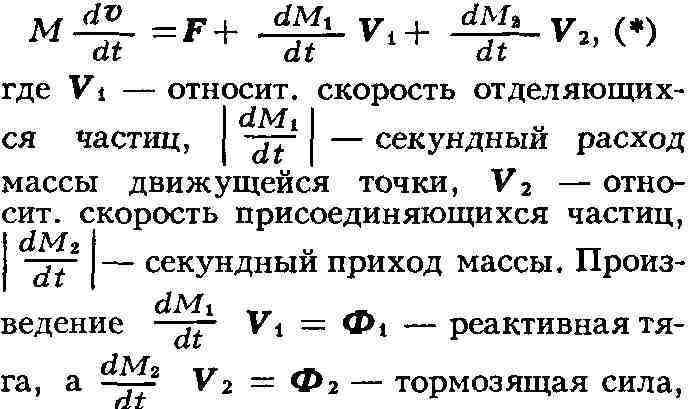
обусловленная присоединением частиц. Для совр. ракет ур-ние движения получается из (*) при условии Ф₂ = 0; оно было получено Мещерским в 1897.

В М. т. п. м. рассматриваются 2 класса задач: определение траекторий центра масс и определение движения тела переменной массы около центра масс. В ряде случаев можно найти траекторные характеристики движения центра масс, исходя из ур-ний динамики точки переменной массы. Изучение движения тел переменной массы около центра масс важно для исследования динамич. устойчивости реальных объектов (ракет, самолётов), их управляемости и манёвренности. К задачам М. т. п. м. относится также отыскание оптимальных режимов движения, т. е. определение таких законов изменения массы тела или точки, при к-рых кинематич. или динамич. характеристики их движения становятся наилучшими. Наиболее эффективный метод решения таких задач - вариационное исчисление.

Важной задачей механики тел переменной массы с твёрдой оболочкой является изучение движения этих тел при нек-рых дополнит, условиях, налагаемых на скорость центра масс. Такие задачи возникают, напр., при изучении движения телеуправляемых ракет и беспилотных самолётов, наводимых на цель автоматически или по радиокомандам с Земли. Большое число работ по М. т. п. м. относится к изучению движения небесных тел. Допуская, что увеличение массы небесного тела происходит за счёт налипания кос-мич. пыли, приходят к дополнит, условию о равенстве нулю абс. скорости налипающих частиц.

Лит.: Циолковский К. Э., Собр. соч., т. 2, М., 1954; Мещерский И. В., Работы по механике тел переменной массы, 2 изд., М., 1952; Космодемьянский А. А., Механика тел переменной массы, ч. 1, [М.], 1947; его же, Курс теоретической механики, 3 изд., ч. 2, М., 1966; М и е л е А., Механика полета (теория траекторий полёта), пер. с англ., М., 1965.

А. А. Космодемьянский.

МЕХАНИКИ УРАВНЕНИЯ КАНОНИЧЕСКИЕ, уравнения Гамильтона, дифференциальные ур-ния движения механич. системы, в к-рых переменными, кроме обобщённых косрдинат qi, являются обобщённые импульсы pi', совокупность qi и pt наз. канонич. переменными. М. у. к. имеют вид:

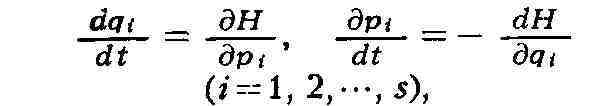
где H(qt, pi, t) - функция Гамильтона, равная (когда связи не зависят от времени, а действующие силы потенциальны) сумме кинетич. и потенциальной энергий системы, выраженных через канонич. переменные, s - число степеней свободы системы. Интегрируя эту систему обыкновенных дифференц. ур-ний 1-го порядка, можно найти все qt и pt как функции времени t и 2s постоянных, определяемых по начальным данным.

М. у. к. обладают тем важным свойством, что позволяют с помощью т. н. канонич. преобразований перейти от qi к pt к новым канонич. переменным Qi<,q_t,p_t,t)w.Pi(q_t,p_t,t), к-рые тоже удовлетворяют М. у. к., но с другой функцией H(Qt,Pi,t). Таким путем М. у. к. можно привести к виду, упрощающему процесс их интегрирования. М. у. к. используются, кроме классич. механики, в статистич. физике, квантовой механике, электродинамике и др. областях физики.

С. М. Торг.

МЕХАНИКО-МATEMATИЧЕСКОЕ ОБРАЗОВАНИЕ, система подготовки специалистов высшей квалификации для н.-и. и преподавательской работы в области математики, механики и смежных с ними отраслей науки, техники, экономики, пром-сти и с. х-ва. В СССР принято различать общее математич. образование, к-рое даёт средняя общеобразовательная школа, где основы математич. науки изучаются с 1-го класса, специальное и вспомогат. М.-м. о.

Специальное М.-м. о. дают механико-математич. и физико-математич. ф-ты (отделения) ун-тов и пед. ин-тов. В России спец. М.-м. о. впервые стало осуществляться в Академии, ун-те в Петербурге (осн. в 1726), затем в Моск. ун-те (1755) и Учительской гимназии в Петербурге (1803). Уже в 18 в. из ун-тов вышли видные деятели рус. математич. науки и просвещения: С. Е. Гурьев, С. Я. Румовский, Т. Ф. Осиповский и др.; на них большое влияние оказали пед. взгляды Л. Эйлера. В 19 в. спец. М.-м. о. получило развитие в Казанском, Харьковском, Киевском, Петербургском, Новороссийском (Одесском), Тартуском (Дерптском) и др. ун-тах, воспитанниками к-рых были Н. И. Лобачевский, М. В. Остроградский, П. Л. Чебышев, Н. Е. Жуковский, А. М. Ляпунов и др., ставшие основоположниками новых отраслей и разделов математики и механики и способствовавшие совершенствованию общего и спец. М.-м. о. в России. В нач. 20 в. отечественная математич. школа была представлена такими учёными, как А. М. Ляпунов, А. А. Марков, А. Н. Крылов (Петербург), Н. Е. Жуковский, Д. Ф. Егоров, Н. Н. Лузин, С. А. Чаплыгин (Москва), С. Н. Бернштейн (Харьков) и др. Физико-математич. ф-ты ун-тов готовили преим. преподавателей математики для гимназий, реальных уч-щ, высших и средних спец. уч. заведений. Университетские курсы достаточно полно отражали содержание и уровень развития математики и механики того времени. В этот период механика составляла естеств. часть спец. М.-м. о.

Уже в первые годы Сов. власти ун-ты стали крупнейшими уч. и науч. математич. центрами. Индустриализация страны потребовала приближения математич. подготовки специалистов к нуждам развивающейся пром-сти. В нач. 30-х гг. университетское М.-м. о. подверглось существ, реорганизации. Были выделены механич. специальности, в первую очередь по аэродинамике, гидродинамике, теории упругости, общей механике; в уч. планах нашли отражение совр. науч. идеи (в частности, функциональный анализ, тензорная геометрия и др.); во мн. ун-тах физико-математич. ф-ты разделены на механико-математич. и физические, в нек-рых - созданы н.-и. ин-ты механики и математики. В 50-60-е гг. в ун-тах были организованы ф-ты вычислит, математики, кибернетики, автоматич. систем управления, в ряде втузов - ф-ты прикладной математики. Ун-ты готовят математиков и механиков-теоретиков для различных отраслей нар. х-ва, преподавателей ср. и высшей школы, сотрудников н.-и. учреждений. Студенты-математики, помимо общенаучных (в т. ч. и математических - математич. анализ, высшая алгебра, аналитич. геометрия и др.) дисциплин, изучают теоретич. механику, теорию функций комплексного переменного, теорию функций действительного переменного и функциональный анализ, математич. логику, теорию вероятностей и математич. статистику, дифференциальные ур-ния, математич. физику и др. В 50-е гг. в уч. планы введены курсы программирования для ЭВМ, усилена подготовка по вычислит, математике; в большинстве ун-тов созданы вычислит, центры. Значительно расширилась подготовка специалистов в области механики, особенно в связи с исследованием космоса, развитием автоматики и автоматич. систем управления, необходимостью исследования механич. свойств как старых, так и новых синте-тич. материалов. Студенты-механики получают основат. математич. подготовку (близкую той, к-рую получают студенты-математики), изучают теорию упругости, теорию пластичности, гидро- и аэродинамику, сопротивление материалов и др. Учителей математики для ср. школы в основном готовят пед. ин-ты. В уч. планах значит, место занимают общема-тематич., общепед. и методич. дисциплины. Студенты изучают основания арифметики и геометрии, теорию вероятностей, математич. логику, курс математич. машин и программирование для ЭВМ, общую физику и астрономию. Большое внимание уделяется курсу элементарной математики, методике преподавания математики, пед. практике в школе. В нек-рых пед. ин-тах подготовка учителей ведётся по профилям: математика-физика, математика - программирование, математика - черчение. Сроки обучения на механико-математич. специальностях: 5-6 лет - в ун-тах, 4-5 лет -в пед. ин-тах. В 1974 подготовка специалистов с М.-м. о. велась по специальностям: математика (58 ун-тов-38,2 тыс. студентов, приём -8,8 тыс. чел., выпуск - 5,6 тыс. чел., и ок. 200 пед. ин-тов - 129,9 тыс. студентов, приём - 27,1 тыс. чел., выпуск - 23,3 тыс. чел.); механика (св. 20 ун-тов - 4,3 тыс. студентов, приём - ок. 1 тыс. чел., выпуск - 0,7 тыс. чел.); прикладная математика (св. 60 вузов различного профиля и ун-тов - 23,9 тыс. студентов, приём - 7,4 тыс. чел., выпуск - 1,9 тыс. чел.). В вузах, н.-и. Ин-те математики и механики АН СССР, в академиях союзных республик, АПН СССР организована аспирантура для подготовки науч. кадров в области математики и механики.

Вспомогательное М.-м. о. имеет целью дать студентам (уч-ся) математич. сведения, необходимые для изучения спец. дисциплин и использования математич. средств при проведении различных исследований и в повседневной работе. К вспомогат. М.-м. о. относятся курсы математики и механики, к-рые читаются во втузах, на экономич., химич., биологич., геологич. и др. ф-тах (отделениях) ун-тов, отраслевых ин-тов и в средних спец. уч. заведениях. Для подготовки математиков с инженерным, экономич., физич. образованием (для к-рых математика является средством глубокого проникновения в закономерности производственных, инженерных, экономич. и др. процессов) созданы Московский инженерно-физический институт и Московский физико-технический институт; ряд инженерно-математич. ф-тов во втузах, отделения математич. экономики и математич. лингвистики в Московском и Ленингр. ун-тах. В 50-60-е гг. в уч. планах втузов значительно увеличено количество часов на изучение математики; введены спец. математич. курсы; в программу общего курса включены теория вероятностей, математич. статистика, элементы программирования для ЭВМ, элементы линейного программирования и оптимального управления процессами. Во мн. втузах при дипломном и курсовом проектировании обязательно использование вычислит, техники. В 60-е гг. в крупнейших вузах страны организованы ф-ты повышения квалификации специалистов в области М.-м. о.

За рубежом подготовка математиков-исследователей, статистиков, вычислителей и программистов, преподавателей и др. осуществляется преим. в ун-тах В ряде стран Европы и в США организованы нац. комитеты по М.-м. о., к-рые занимаются его совершенствованием При ЮНЕСКО работает Междунар. комиссия по М.-м. о., в деятельности к-рой участвуют сов. математики. Раз в 4 года проводятся междунар. конгрессы по математич. образованию. С 1970 в Великобритании издаётся междунар. журнал, посвящённый М.-м. о., в CCCР выпускаются спец. сборники по вопросам преподавания математики в вузах.

Лит.: Гнеденко Б. В., Очерки по истории математики в России, М.- Л., 1946 Ланков А.В., К истории развития передовых идей в русской методике математики М., 1951; Прудников В. Е., Русские педагоги-математики XVIII-XIX веков, М., 1956; Колмогоров А. Н., О профессии математика, 3 изд., М., 1960; Вопросы истории физико-математических наук, М., 1963 разд. 1.

Б. В. Гнеденко.

"МЕХАНИСТЫ", термин, обозначавший в сер. 20-х - нач. 30-х гг. 20 в. группу сов. философов, стоявших на позициях отождествления диалектики с совр. механикой и создавших своеобразную "механистическую" концепцию теории познания, логики и историч. материализма. Группа включала И. И. Скворцова-Степанова, А. К. Тимирязева, Л. И. Аксельрод-Ортодокс, В. М. Сарабьянова, В. А. Петрова и др. К "М." примыкал Н. И. Бухарин, претендуя на руководство "социологич. школой". Концепция "М." была своеобразным воспроизведением в марксистской философии ряда идей позитивизма, в т. ч. отрицания самостоят. значения философии, подмены диалектики теорией "равновесия", отрицания объективной природы случайности и т. д. Взгляды "М." были подвергнуты критике на ряде науч. конференций и диспутов. В 1929 Всесоюзная конференция марксистско-ленинских науч. учреждении отметила, что механицизм является своеобразной ревизией диалектич. материализма (см. "Естествознание и марксизм", 1929, № 3, с. 211). В пост. ЦК ВКП(б) "О журнале „Под знаменем марксизма"" от 25 янв. 1931 механицизм охарактеризован как гл. опасность на теоретич. фронте тех лет.

В нач. 30-х гг. осн. представители этой группы отказались от своих ошибочных взглядов и подвергли их критике.

Лит.: О журнале "Под знаменем марксизма" [Из постановления ЦК ВКП(б)], в сб.: О партийной и советской печати, М., 1954; Нарский И. С., Суворов Л. Н., Позитивизм и механистическая ревизия, марксизма, М., 1962.

Л. Н. Суворов.

МЕХАНИЦИЗМ, односторонний метод познания и миропонимание, основывающиеся на представлении, будто механич. форма движения есть единственно объективная. Последоват. развитие этого взгляда приводит к отрицанию качеств, многообразия явлений в природе и обществе или к представлению о нём как лишь о субъективной иллюзии. В более широком смысле М. есть метод "сведения" сложных явлений к их более простым составляющим, метод разложения целого на части, неспецифичные для данного целого (на биологич. отношения, когда речь идёт о социальных явлениях, на физико-химические, когда речь идёт о биологии, и т. д.).

Исторически М. выступал в качестве господств, направления науч.-материалистич. мысли на протяжении 16-18 вв., когда механика была единств, развитой наукой и получившей применение в произ-ве, и потому казалась "наукой вообще", абс. наукой, располагающей соответственно абс. методом - математикой, понимаемой в основном механистически. Классич. представителями М. могут считаться Г. Галилей, И. Ньютон, П. С. Лаплас (в естествознании), Т. Гоббс, Ж. Ламетри, П. Гольбах ( в философии). Типичными представителями М. в 19 в. являлись Л. Бюхнер, К. Фохт, Я. Молешотт, Е. Дюринг. Односторонне механистич. подход к познанию природных и обществ, явлений подвергался критике Б. Спинозой, Г. В. Лейбницем, отчасти Д. Дидро. Как ограниченно оправданный метод мышления, он был преодолен ("снят") Г. Гегелем (ему принадлежит и сам термин "М.") в диалектич. понимании задач и природы мышления. Критикуя М., Гегель одновременно отождествлял его недостатки с природой материализма вообще. Гегель "... хотел унизить материализм эпитетом „механический". Но дело в том, что критикуемый Гегелем материализм - французский материализм XVIII века - был действительно исключительно механическим..." (Энгельс Ф., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20, с. 568-69).

М. есть пройденный историч. этап развития материалистич. философии, и всякая попытка возродить его в совр. условиях должна расцениваться как шаг назад в науч. отношении. Возможность рецидивов М. коренится в том, что любая, сколь угодно сложная и развитая форма движения материи заключает в своём составе механич. движение как одну из сторон. Поэтому с законами механики и могут быть согласованы не только различные, но и прямо противоположные процессы и явления. Как раз при таком "согласовании" совершается та нивелировка, в ходе к-рой подвергаются забвению их качеств, своеобразие и противоречивость. По отношению к любой форме движения, кроме чисто механической, М. приводит в конечном итоге к признанию принципиальной невозможности её познания. М. у Галилея, Гоббса, франц. материалистов ещё ни в малейшей степени не затронут агностицизмом. Но в 19 в. среди естествоиспытателей-механистов распространяются агностич. взгляды. В соответствии с принципом: что не механика, то не наука, всякое знание, раскрывающее природу надмеханич. областей движения, объявляется ненаучным. М. выдвигает понятие особых внешних "сил", в к-ром реальные моменты, абстрагированные от движения, превращаются в самостоятельно существующие механич. "причины" этого движения. "В механике причины движения принимают за нечто данное и интересуются не их происхождением, а только их действиями. Поэтому если ту или иную причину движения называют силой, то это нисколько не вредит механике как таковой; но благодаря этому привыкают переносить это обозначение также и в область физики, химии и биологии, и тогда неизбежна путаница" (там же, с. 407). Особенно наглядно несостоятельность М. проявляется в области проблем мышления, сознания, жизни. Здесь М. оказывается почвой для витализма, телеологии и идеализма.

М. как позиция в философии представляет собой типичное проявление метафизич. метода мышления, неспособного справиться с противоречием. Сталкиваясь с противоположными определениями предмета, М. всегда стремится зачеркнуть одно из них (напр., качество в угоду количеству) или же полагает только одно из них как истинное, в противоположность другому, принимаемому за неистинное: то абс. случайность, то столь же абс. необходимость, то дискретность, то непрерывность и т. д. М. мистифицирует и само понятие действующей причины, понимает движение не как самодвижение материи, а как результат действия внешней силы, поэтому и материя представляется ему инертной и косной массой.

Диалектич. материализм установил на основе обобщения данных науки, что механич. движение есть сторона, абстрактно-всеобщее условие всякого движения. В составе высших, надмеханич. процессов оно оказывается "побочной формой", необходимой, но далеко не достаточной для характеристики природы этих процессов.

Лит.: Энгельс Ф., Диалектика природы, Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20; его же, Анти-Дюринг, там же; Гегель Г. В. Ф., Энциклопедия философских наук, ч. 1, Логика, Соч., т. 1, М.-Л., 1929; его же, Наука логики, там же, т. 5-6, М., 1937 - 39; Самускевич А. В., Некоторые философские вопросы атомистики и борьба против механицизма в современной физике, в сб.: Научные труды по философии [Белорус, ун-та], в. 1, Минск, 1956; Вислобоков А. Д., Марксистская диалектика и современный механицизм, М., 1962.

А. В. Потёмкин.

МЕХАНИЧЕСКАЯ ЗАПИСЬ звука, система записи звука посредством изменения формы носителя при механич. воздействии на него. М. з. является первой практич. системой звукозаписи. Ещё в нач. 19 в. при исследовании звуковых сигналов физики стали записывать колебания нек-рых источников звука. Эти записи предназначались только для визуального изучения и не могли быть воспроизведены. В 1877 французский учёный Ш. Кро впервые научно обосновал принципы записи звука на барабан (или диск) и её последующего воспроизведения. Первым аппаратом механич. записи и воспроизведения звука был фонограф (заявка на изобретение 1877) амер. изобретателя Т. Эдисона. Его фонограф с восковым валиком не получил широкого распространения ввиду сложности копирования записи, быстрого изнашивания валиков и плохого качества воспроизведения. В 1888 немецкий инженер Э. Берлинер предложил использовать для записи носитель в форме диска. После записи с диска гальваническим способом получали матрицы, к-рые использовались для прессования граммофонных пластинок. До 50-х гг. 20 в. М. з. была монофонической (см. Монофоническая звукозапись). В дальнейшем получила распространение также стереофонич. М. з., обеспечивающая лучшее качество звучания (см. Стереофоническая звукозапись). В нач. 70-х гг. 20 в. предложена квадрофонич. М. з., в к-рой звуковые сигналы, передаваемые по 4 независимым каналам, записываются в одной канавке диска. Такая запись воспроизводится 4 громкоговорителями, располагаемыми по углам комнаты.

Станок для механической звукозаписи: 1 - микроскоп для контроля качества записи; 2 - трубка для отсоса воздуха из-под лакового диска с целью прижима его к планшайбе; 3 - вращающаяся планшайба со стробоскопическими метками по окружности, по которым контролируется скорость вращения; 4 - каретка, обеспечивающая передвижение рекордера 5 при записи.

Процесс М. з. делится на 3 этапа: перезапись с магнитной ленты на лаковый диск, изготовление матриц и прессование грампластинок. Установка для перезаписи на лаковый диск состоит из магнитофона, электронного устройства для усиления и коррекции электрич. сигналов и станка записи (рис.), имеющего движущий механизм, рекордер и устройство управления. Преобразование электрич. сигналов в механич. колебания осуществляется рекордером, резец к-рого вырезает на лаковом диске канавку, модулированную звуковым сигналом. Стереофонич. рекордер имеет две (по числу каналов) независимые динамич. системы, связанные с одним резцом. Сигналы каждого канала раздельно записываются на левую и правую стенки канавки. Для получения металлич. оригиналов и матриц, с к-рых затем будут изготавливаться грампластинки, запись с лакового диска переносится гальванопластич. способом на металлические диски. Для этого лаковый диск сначала покрывают тонким слоем серебра, а затем - никелевой плёнкой, на к-рую наращивают слой меди. После отделения лакового диска получают первый оригинал. Аналогичным образом получают вторые оригиналы, с к-рых изготавливают никелевые матрицы. Эти матрицы прикрепляются к подогреваемым пресс-формам. Прессование грампластинок из синтетич. материалов производится гидравлич. прессами.

Для воспроизведения М. з. служат электропроигрыватели. Преимущества М. з.- массовое тиражирование грампластинок, их относительная дешевизна и простота обращения, а также возможность надёжного хранения записи длит, время в металлич. оригиналах (матрицах), осн. недостатки - сравнительно быстрый износ грампластинки из-за непосредств. механич. контакта граммофонной иглы с ней, невозможность монтажа и стирания записи.

Лит.: Калашников Л. А., Очерк развития техники механической записи звука, "Тр. Ин-та истории естествознания и техники", 1959, т. 26; Аполлонова Л. П., Шумова Н. Д., Механическая звукозапись, М.- Л., 1964; Волков-Ланнит Л. Ф., Искусство запечатленного звука, М., 1964.

Ю. А. Вознесенский.

МЕХАНИЧЕСКАЯ ЛОПАТА, 1) вид одноковшового экскаватора, характеризуемый жёсткой связью между стрелой и ковшом. М. л. выполняется в виде прямой либо обратной лопаты. Прямая лопата (рис., а) применяется для земляных работ в строительстве, для вскрышных и добычных работ в карьерах, для выемки руды в камерах подземных рудников (крепкие горные породы предварительно рыхлятся взрывом). Строит. М. л. выпускаются обычно с ковшом ёмкостью до 3 м³, карьерные - с ковшом 2-22 м³, вскрышные - с ковшом до 150 м³, подземные - с ковшом до 3 м³. Прямая лопата выпускается в СССР с ковшами ёмкостью 0,25-35 м³; готовятся к выпуску М. л. с ковшом 100 м³. В зависимости от условий работ годовая выработка М. л. составляет на 1 м³ ёмкости ковша 120-250 тыс. м³, а расход энергии 0,4-0,8 квт-ч/м³. Обратная М. л. (рис., б) отличается от прямой направлением рабочего движения ковша и применяется для проходки канав, траншей и др. вспомогат. работ, когда забой расположен ниже уровня установки экскаватора. Обратная лопата выпускается в СССР с ковшами ёмкостью 0,15-2 м³. Производительность её примерно на 20% меньше, чем прямой при той же ёмкости ковша. 2) Канатно-скреперная установка для выгрузки из крытых вагонов сыпучих грузов (зерна, цемента и т. п.).

Механическая лопата: а - прямая; 6 - обратная; 1 - ковш; 2 - рукоять; 3 - стрела; 4 - кузов.

В. Г. Афонин.

МЕХАНИЧЕСКИЕ МУЗЫКАЛЬНЫЕ ИНСТРУМЕНТЫ, инструменты, снабжённые технич. приспособлениями для исполнения зафиксированных на дисках произведений или наигрышей без непосредств. участия музыкантов. М. м. и. бывают самых различных конструкций и форм - от маленьких примитивных табакерок, музыкальных шкатулок, часов-будильников до сложных по устройству стационарных напольных часов, полифонов, оркестрионов, башенных курантов, "озвученных" карет. Первые сведения о М. м. и. относятся к 16 в. Особенно много систем М. м. и. появилось, в т. ч. и в России, в кон. 19 - нач. 20 вв. Применялись они в трактирах, ресторанах, мещанско-купеч. быту. Широкое распространение в это время получила шарманка. С появлением граммофона, а затем радиомагнитофонной аппаратуры М. м. и. вышли из употребления. См. также Механическое фортепьяно.

МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ, совокупность показателей, характеризующих сопротивление материала воздействующей на него нагрузке, его способность деформироваться при этом, а также особенности его поведения в процессе разрушения. В соответствии с этим М. с. м. измеряют напряжениями (обычно в кгс/мм² или Мн/м²), деформациями (в %), уд. работой деформации и разрушения (обычно в кгс-м/см² или Маж/м²), скоростью развития процесса разрушения при статич. или повторной нагрузке (чаще всего в мм за 1 сек или за 1000 циклов повторений нагрузки, мм/кцикл). М. с. м. определяются при механич. испытаниях образцов различной формы.

Рис. 1. Схемы деформации при разных способах нагружения: а - растяжение, б - сжатие, в - изгиб, г - кручение (пунктиром показана начальная форма образцов).

В общем случае материалы в конструкциях могут подвергаться самым различным по характеру нагрузкам (рис. 1): работать на растяжение, сжатие, изгиб, кручение, срез и т. д. или подвергаться совместному действию неск. видов нагрузки, напр, растяжению и изгибу. Также разнообразны условия эксплуатации материалов и по темп-ре, окружающей среде, скорости приложения нагрузки и закону её изменения во времени. В соответствии с этим имеется много показателей М. с. м. и много методов механич. испытаний. Для металлов и конструкц. пластмасс наиболее распространены испытания на растяжение, твёрдость, ударный изгиб; хрупкие конструкц. материалы (напр., керамику, металлокерамику) часто испытывают на сжатие и статич. изгиб; механич. свойства композиц. материалов важно оценивать, кроме того, при испытаниях на сдвиг.

Диаграмма деформации. Приложенная к образцу нагрузка вызывает его деформацию. Соотношения между нагрузкой и деформацией описываются т. н. диаграммой деформации (рис. 2). Вначале деформация образца (при растяжении - приращение длины Дl) пропорциональна возрастающей нагрузке Р, затем в точке п эта пропорциональность нарушается, однако для увеличения деформации необходимо дальнейшее повышение нагрузки Р; при Дl > Дlв деформация развивается без приложения усилия извне, при постепенно падающей нагрузке. Вид диаграммы деформации не меняется, если по оси ординат откладывать напряжение

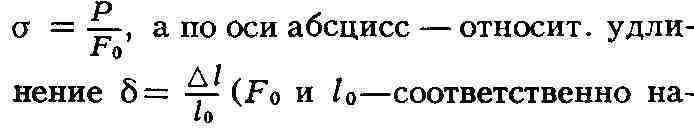
чальная площадь поперечного сечения и расчётная длина образца).

Сопротивление материалов измеряется напряжениями, характеризующими нагрузку, приходящуюся на единицу пло-

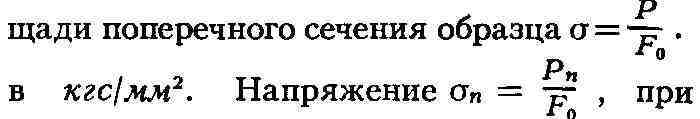
к-ром нарушается пропорциональный нагрузке рост деформации, наз. пределом пропорциональности. При нагрузке Р<Р_празгрузка образца приводит к исчезновению деформации, возникшей в нём под действием приложенного усилия; такая деформация наз. упругой. Небольшое превышение нагрузки относительно Рв может не изменить характера деформации - она по-прежнему сохранит упругий характер. Наибольшая нагрузка, к-рую выдерживает образец без появления остаточной пластич. деформации при разгрузке, определяет предел у п р у-

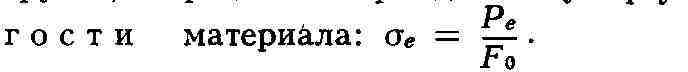
У конструкц. неметаллич. материалов (пластмассы, резины) приложенная нагрузка может вызвать упругую, высокоэластическую и остаточную деформации. В отличие от упругой, высокоэластич.деформация исчезает не сразу после разгрузки, а с течением времени. Высоко прочные армированные полимеры (стеклопластики, углепластики и др.) разрушаются при удлинении 1-3%. На по следних стадиях нагружения у нек-рых армированных полимеров появляется высокоэластич. деформация. Высокоэластич. модуль ниже модуля упругости поэтому диаграмма деформации в этом случае имеет тенденцию отклоняться к оси абсцисс.

Упругие свойства. В упругой области напряжение и деформация связаны ко эффициентом пропорциональности. При растяжении с = = Еб, где Е - т. н. модуль нормальной упругости, численно равный тангенсу угла наклона прямоли нейного участка кривой с - с(6) к oc. деформации (рис. 2). При испытании

Рис. 2. Типичная диаграмма деформации при растяжении конструкционных металлов.

напряженному состоянию соответствуе трёхосное деформированное состояние (приращение длины в направлении действия приложенных сил и уменьшение линейных размеров в двух других взаимно

в пределах упругости для осн. конструкций материалов колеблется в довольно узких пределах (0,27-0,3 для сталей, 0,3-0,3 для алюминиевых сплавов). Коэффициент Пуассона является одной из осн. рас чётных характеристик. Зная м и Е можно расчётным путём определить

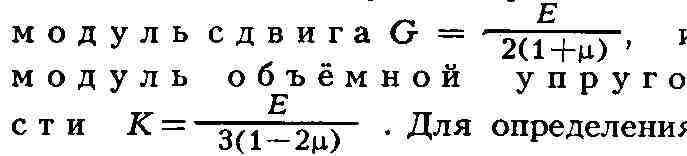
t, G и м пользуются тензометрами.

Сопротивление пластической деформации. При нагрузках Р>Р_е наряду со всё возрастающей упругой деформацией появляется заметная необратимая не исчезающая при разгрузке пластич. деформация. Напряжение, при к-ром остаточная относит, деформация (при растяжении - удлинение) достигает заданной величины (по ГОСТ-0,2% ), наз. условным пределом текучести и обозначается бо,2= Pт/Fв . Практически точность совр. методов испытания такова, что бп и бв определяют с заданными допусками соответственно на отклонение от закона пропорциональности [увеличение ctg (90 - а) на 25-50% и на величину остаточной деформации (0,003-0,05%) и говорят об условных пределах пропорциональности и

 

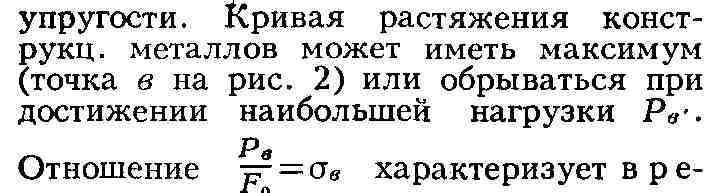
менное сопротивление (предел прочности) материала. При наличии максимума на кривой растяжения в области нагрузок, лежащих на кривой левее в, образец деформируется равномерно по всей расчётной длине /о, постепенно уменьшаясь в диаметре, но сохраняя начальную цилиндрич. или призматич. форму. При пластин, деформации металлы упрочняются, поэтому, несмотря на уменьшение сечения образца, для дальнейшей деформации требуется приклады-

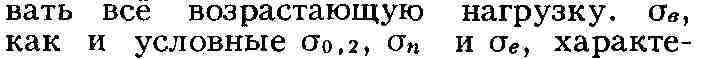
ризует сопротивление металлов пластической деформации. На участке диаграммы деформации правее в форма растягиваемого образца изменяется: наступает период сосредоточенной деформации, выражающейся в появлении "шейки". Уменьшение сечения в шейке "обгоняет" упрочнение металлов, что и обусловливает паде-

У многих конструкц. материалов сопротивление пластич. деформации в упруго-пластич. области при растяжении и сжатии практически одинаково. Для нек-рых металлов и сплавов (напр., магниевые сплавы, высокопрочные стали) характерны заметные различия по этой характеристике при растяжении и сжатии. Сопротивление пластич. деформации особенно часто (при контроле качества продукции, стандартности режимов термич. обработки и в др. случаях) оценивается по результатам испытаний на твёрдость путём вдавливания твёрдого наконечника в форме шарика (твёрдость по Бринеллю или Роквеллу), конуса (твёрдость по Роквеллу) или пирамиды (твёрдость по Виккерсу). Испытания на твёрдость не требуют нарушения целостности детали и потому являются самым массовым средством контроля механич. свойств. Твёрдость по Бринеллю (НВ) при вдавливании шарика диаметром D под нагрузкой Р характеризует среднее сжимающее напряжение, условно вычисляемое на единицу поверхности шарового отпечатка диаметром d:

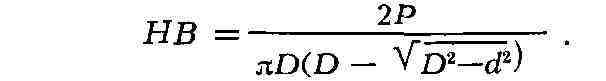
Характеристики пластичности. Пластичность при растяжении конструкц. материалов оценивается удлинен и-

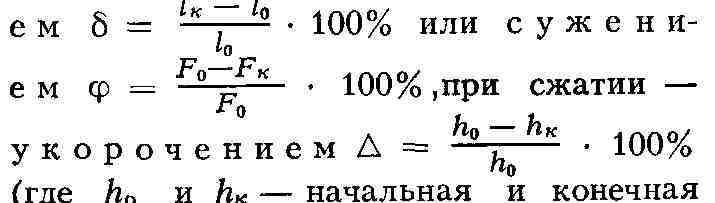
высота образца), при кручении - яв-

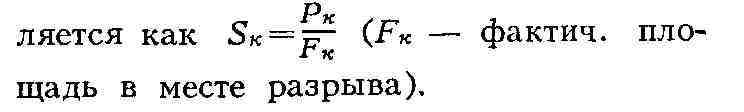
Характеристики разрушения. Разрушение происходит не мгновенно (в точке к), а развивается во времени, причём начало разрушения может соответствовать какой-то промежуточной точке на участке вк, а весь процесс заканчиваться при постепенно падающей до нуля нагрузке. Положение точки к на диаграмме деформации в значит, степени определяется жёсткостью испытат. машины и иннерционностью измерит, системы. Это делает величину S_Kв большой мере условной.

Многие конструкц. металлы (стали, в т. ч. высокопрочные, жаропрочные хромоникелевые сплавы, мягкие алюминиевые сплавы и др.) разрушаются при растяжении после значит. пластич. деформации с образованием шейки. Часто (напр., у высокопрочных алюминиевых сплавов) поверхность разрушения располагается под углом примерно 45° к направлению растягивающего усилия. При определ. условиях (напр., при испытании хладноломких сталей в жидком азоте или водороде, при воздействии растягивающих напряжений и коррозионной среды для металлов, склонных к коррозии под напряжением) разрушение происходит по сечениям, перпендикулярным растягивающей силе (прямой излом), без макропластической деформации.

Прочность материалов, реализуемая в элементах конструкций, зависит не только от механич. свойств самого металла, но и от формы и размеров детали (т. н. эффекты формы и масштаба), упругой энергии, накопленной в нагруженной конструкции, характера действующей нагрузки (статич., динамич., периодически изменяющаяся по величине), схемы приложения внешних сил (растяжение одноосное, двухосное, с наложением изгиба и др.), рабочей темп-ры, окружающей среды. Зависимость прочности и пластичности металлов от формы характеризуется т. н.чувствительностью к надрезу, оцениваемой обычно по отношению пределов прочности

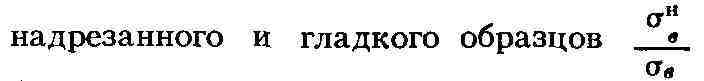
(у цилиндрич. ооразцов надрез ооычно выполняют в виде круговой выточки, у полос - в виде центр, отверстия или боковых вырезов). Для мн. конструкц. материалов это отношение при статич. нагрузке больше единицы, что связано со значит, местной пластич. деформацией в вершине надреза. Чем острее надрез, тем меньше локальная пластич. деформация и тем больше доля прямого излома в разрушенном сечении. Хорошо развитый прямой излом можно получить при комнатной темп-ре у большинства конструкц. материалов в лабораторных условиях, если растяжению или изгибу подвергать образцы массивного сечения (тем толще, чем пластичнее материал), снабдив эти образцы спец. узкой прорезью с искусственно созданной трещиной (рис. 3). При растяжении широкого, плоского образца пластич. деформация затруднена и ограничивается небольшой

штрихована), непосредственно примыкающей к кончику трещины. Прямой излом обычно характерен для эксплуатационных разрушений элементов конструкций.

Рис. 3. Образец со специально созданной в вершине надреза трещиной усталости для определения Kic. Испытания на внецентренное (а) и осевое (б) растяжение.

Широкое распространение получили предложенные амер. учёным Дж. Р. Ирвином в качестве констант для условий хрупкого разрушения такие показатели, как критический коэффициент интенсивности напряжений при плоской деформации Ki_c и вязкость разруше-

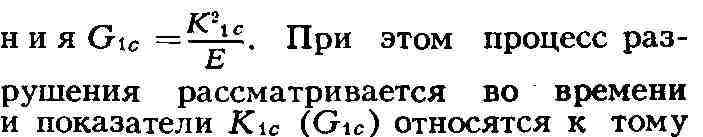
критич. моменту, когда нарушается устойчивое развитие трещины; трещина становится неустойчивой и распространяется самопроизвольно, когда энергия, необходимая для увеличения её длины, меньше энергии упругой деформации, поступающей к вершине трещины из соседних упруго напряжённых зон металла.

При назначении толщины образца t и размеров трещины 2/_тр исходят из

можно судить о склонности конструкц. материалов к хрупкому разрушению в условиях эксплуатации.

Для оценки качества металла весьма распространены испытания на ударный изгиб призматич. образцов, имеющих на одной стороне надрез. При этом оценивают ударную вязкость (в кгс-м/см² или Мдж/м²) - работу деформации и разрушения образца, условно отнесённую к поперечному сечению в месте надреза. Широкое распространение получили испытания на ударный изгиб образцов с искусственно полученной в основании надреза трещиной усталости. Работа разрушения таких образцов вту находится в целом в удовлетворительном соответствии с такой

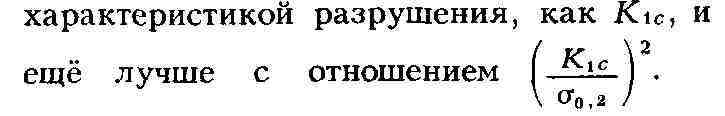
Временная зависимость прочности.

С увеличением времени действия нагрузки сопротивление пластич. деформации и сопротивление разрушению понижаются. При комнатной темп-ре у металлов это становится особенно заметным при воздействии коррозионной (коррозия под напряжением) или др. активной (эффект Ребиндера) среды. При высоких темп-рах наблюдается явление ползучести, т. е.

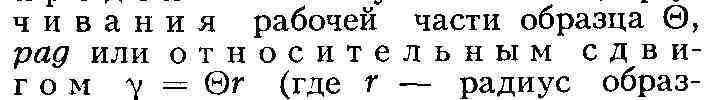
ца). Конечная ордината диаграммы деформации (точка к на рис. 2) характеризует сопротивление разрушению металла S_K, к-рое опреде прироста пластич. деформации с течением времени при постоянном напряжении (рис. 4,а). Сопротивление металлов ползучести оценивают условным пределом ползучести - чаще всего напряжением, при к-ром пластич. деформация за 100 ч достигает 0,2% , и обозначают его Сто,2/юо. Чем выше темп-pa t, тем сильнее выражено явление ползучести и тем больше снижается во времени сопротивление разрушению металла (рис. 4,6). Последнее свойство характеризуют т. н. пределом длительной прочности, т. е. напряжением, к-рое при данной темп-ре вызывает разрушение материала за заданное время (напр.,

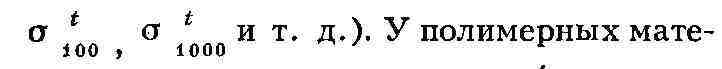
риалов температурно-временная зависимость прочности и деформации выражена сильнее, чем у металлов. При нагреве пластмасс наблюдается высокоэластич. обратимая деформация; начиная с нек-рой более высокой темп-ры развивается необратимая деформация, связанная с переходом материала в вязко-текучее состояние.

Рис. 4. Изменение механических свойств конструкционных материалов в функции времени (или числа циклов).

С ползучестью связано и др. важное механич. свойство материалов - склонность к релаксации напряжений, т. е. к постепенному падению напряжения в условиях, когда общая (упругая и пластическая) деформация сохраняет постоянную заданную величину (напр., в затянутых болтах). Релаксация напряжений обусловлена увеличением доли пластической составляющей общей деформации и уменьшением её упругой части.

Если на металл действует нагрузка, периодически меняющаяся по к.-л. закону (напр., синусоидальному), то с увеличением числа циклов N нагрузки его прочность уменьшается (рис. 4, в) - металл "устаёт". Для конструкц. стали такое падение прочности наблюдается до N = (2-5)-10⁶ циклов. В соответствии с этим говорят о пределе усталости конструкц. стали, понимая под ним обычно амплитуду напряжения

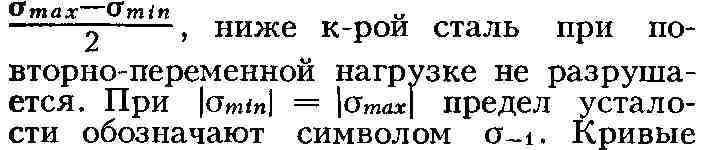
усталости алюминиевых, титановых и магниевых сплавов обычно не имеют горизонтального участка, поэтому сопротивление усталости этих сплавов характеризуют т. н. ограниченными (соответствующими заданному N) пределами усталости. Сопротивление усталости зависит также от частоты приложения нагрузки. Сопротивление материалов в условиях низкой частоты и высоких значений повторной нагрузки (медленная, или малоцикловая, усталость) не связано однозначно с пределами усталости. В отличие от статич. нагрузки, при повторно-переменных нагрузках всегда проявляется чувствительность к надрезу, т. е. предел усталости при наличии надреза ниже предела усталости гладкого образца. Для удобства чувствительность к надрезу при усталости выражают отношением

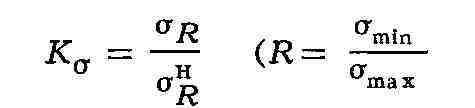
характеризует асимметрию цикла). В процессе уставания можно выделить период, предшествующий образованию очага усталостного разрушения, и следующий за ним, иногда довольно длительный, период развития трещины усталости. Чем медленнее развивается трещина, тем надёжнее работает материал в конструкции. Скорость развития трещины усталости dl/dN связывают с коэфф. интенсивности напряжений степенной функ-

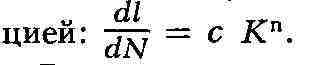
Различают сопротивление термической усталости, когда появляющиеся в материале напряжения обусловлены тем, что в силу тех или иных причин, напр, из-за формы детали или условий её закрепления, возникающие при циклич. изменении темп-ры тепловые перемещения не могут быть реализованы. Сопротивление термич. усталости зависит и от многих других свойств материала - коэффициентов линейного расширения и температуропроводности, модуля упругости, предела упругости и др.

Лит.: Давиденков Н. Н., Динамические испытания металлов, 2 изд., Л.- М., 1936; Ратнер С. И., Разрушение при повторных нагрузках, М., 1959; Сервисен С. В., Когаев В. П., Ш н е й д е р о в и ч P.M., Несущая способность и расчеты деталей машин на прочность, 2 изд., М., 1963; Прикладные вопросы вязкости разрушения, пер. с англ., М., 1968; Фридман Я. Б., Механические свойства металлов, 3 изд., М., 1974; Методы испытания, контроля и исследования машиностроительных материалов, под ред. А. Т. Туманова, т. 2, М., 1974.

С. И. Кишкина.