МАТРИЦА в математике, система элементов а_ij(чисел, функций или иных величин, над к-рыми можно производить алгебраич. операции), расположенных в виде прямоугольной схемы. Если схема имеет т строк и п столбцов, то говорят о (т X n)-матрице. Обозначения:

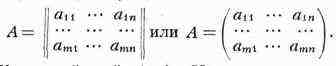
Короче: ||а_ij||, (a_ij) Наряду с конечными М. рассматриваются М. с бесконечным числом строк или столбцов.

М., состоящая из одной строки, наз. строкой, из одного столбца - столбцом. Если т = п, то М. наз. квадратной, а число п - её порядком. Квадратная М., у к-рой отличны от нуля лишь диагональные элементы a_i = a_ii, наз. диагональной и обозначается diag (a₁, ..., а_n). Если все a_i = а, получают скалярную М. При a = 1 М. наз. единичной и обозначается Е. М., все элементы к-рой равны нулю, наз. нулевой.

Переставив в М. строки со столбцами, получают транспонированную М. А', или Л^т. Если элементы М. заменяют на комплексно-сопряжённые, получают комплексно-сопряжённую М. Л. Если элементы транспонированной М. А' заменяют на комплексно-сопряжённые, то получают М. А*, наз. сопряжённой с А. Определитель квадратной М. А обозначается \А\ или detA. Минором k-то порядка М. А наз. определитель k-то порядка, составленный из элементов, находящихся на пересечении нек-рых k строк и k столбцов М. Л в их естеств. расположении. Рангом М. Л наз. максимальный порядок отличных от нуля миноров матрицы.

Действия над матрицами. Произведением прямоугольной (от X п)-матрицы Л на число а наз. М., элементы к-рой получены из элементов a_ij умножением на число а:

Сумма определяется для прямоугольных М. одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, т. е.

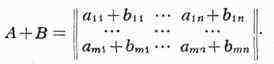
Умножение М. определяется только для прямоугольных М. таких, что число столбцов первого множителя равно числу строк второго. Произведением (т X р)-матрицы Л на (р X n)-матрицу В будет (т X n)-матрица С с элементами

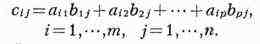
Введённые три действия над М. обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного закона при умножении М.: равенство АВ = В А может не выполняться. Матрицы А к В наз. перестановочными, если АВ = В А. Кроме того, произведение двух М. может равняться нулевой М., хотя каждый сомножитель отличен от нулевой.

Справедливы правила: (АВ)' = В'А', АВ = АВ, (АВ)* = В*А*.

Определитель произведения двух квадратных М. равен произведению определителей перемножаемых М.

Часто удобно разбивать М. на клетки, являющиеся М. меньших размеров, проводя разделит, линии через всю М. слева направо или сверху вниз. При умножении такой т. и. клеточной М. на число, нужно умножить все её клетки на то же число. При надлежащем согласовании разбиений действия сложения и умножения клеточных М. осуществляются так, как будто вместо клеток стоят числа.

Квадратная М. А = (ац) наз. неособенной, или невырожденной, если её определитель не равен нулю; в противном случае М. наз. особенной (вырожденной). М. Л"¹ наз. обратной к квадратной М. А, если AA^-1 = E; при этом а = А_ki/|А|. Неособенность т М. Л есть необходимое и достаточное условие существования обратной М., к-рая при этом оказывается единственной и перестановочной с исходной М. Верна формула:

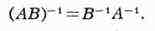
Болыной интерес приобретает обобщённая обратная (или псевдообратная) М. А⁺, определяемая как для любой прямоугольной М., так и для особенной квадратной. Эта М. определяется из четырёх равенств:
АА⁺А = А, А+АА⁺ = А, АА⁺ = (АА⁺)*, А+А = (А+А)*.

Квадратные матрицы. Степенью Aⁿ М. А наз. произведение п сомножителей, равных А. Выражение вида а₀А^п + + а₁А^п-1 + ... + а_nЕ,. Правила действий над полиномами от данной М. А ничем не отличаются от правил действий над алгебраич. многочленами. Можно рассматривать и аналитические функции от М. В частности, если

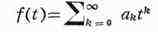
есть сходящийся на всей комплексной плоскости ряд (напр., f (t)=e^t).

Аналитич. функции от М. играют большую роль в теории дифференциальных уравнений. Так, система обыкновенных дифференциальных уравнений с постоянными коэффициентами, записанных в матричных обозначениях в виде

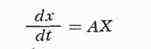
(здесь X - столбец из неизвестных функций), имеет решение х - е^AtС, где С - столбец из произвольных постоянных .

Ненулевой столбец X такой, что АХ=ЛХ, наз. собственным вектором М. А. В этом равенстве коэффициент X может быть лишь одним из корней многочлена к-рый наз. характеристич. многочленом М. А. Эти корни наз. собственными значениями, или характеристич. числами, М. А. Коэффициенты характеристич. многочлена выражаются через суммы нек-рых миноров М. А. В частности, p₁ = а₁₁ + • • • + a_1n = SрA (след A), р_n = (-1)^n-1|A|. Справедливо соотношение Кэли-Гамильтона: если ф(t) есть характеристич. многочлен М. А, то ф(A) = 0, так что М.Л является "корнем" своего характеристич. многочлена.

 

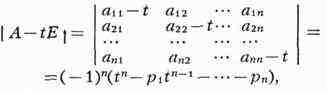
М. Л наз. подобной М. В, если существует такая неособенная М. С, что В=С^-1AC. Легко проверяется, что подобные М. имеют одинаковые характеристич. многочлены.

Исчисление матриц. М.-полезный аппарат для исследования многих задач тео-ретич. и прикладной математики. Одной из важнейших задач является задача нахождения решения систем линейных алгебраич. уравнений. В матричных обозначениях такие системы записываются в виде AX = F, где Л есть М. коэффициентов, X-искомое решение, записанное в виде столбца из п элементов, F - столбец свободных членов из т элементов. Если А-квадратная неособенная М., то система имеет единственное решение X = A^-1 F. Если А прямоугольная (га X п)-матрица ранга k, то решение может не существовать или быть не единственным. В случае несуществования решения имеет смысл обобщённое решение, дающее минимум сумме квадратов невязок (см. Наименьших квадратов метод). При отсутствии единственности точного или обобщённого решения часто выбирают нормальное решение, т. е. решение с наименьшей суммой квадратов компонент. Нормальное обобщённое решение находится по формуле X=A⁺F. Наиболее важен случай переопределённой системы: k=п<т. В этом случае обобщённое решение единственно. При k=m<n (недоопределённая система) точных решений бесконечно много и формула даёт нормальное решение.

Не менее важной для многочисленных приложений (в теории дифференциальных уравнений, в теории малых колебаний, в квантовой механике и т. д.) является задача решения полной или частичной проблемы собственных значений. Здесь ищутся все или часть собственных значений М. и принадлежащие им собственные или корневые (нек-рые обобщения собственных) векторы. К этой задаче близко примыкает и обобщённая проблема собственных значений, в к-рой ищутся числа и векторы такие, что AХ=ЛВХ (А и В- заданные М.), и многие родственные проблемы.

С полной проблемой непосредственно связана также задача о приведении преобразованиями подобия квадратной М. к канонич. форме. Такой формой будет diag (Л₁, ..., Л_n), если М. имеет п различных собственных значений Л₁, ..., Л_п, или форма Жордана [см. Нормальная (жорданова) форма матрицы] в общем случае.

Ввиду большой практич. важности поставленных задач для их численного решения имеется большое число различных методов. Наряду с нахождением численного решения важно оценивать качество найденного решения и исследовать устойчивость решаемой задачи.

Матрицы специального типа. Существует большое число различных типов М. в зависимости от выполнения различных соотношений между элементами.

Нек-рые типы естественно возникают в приложениях. Приведённая таблица даёт ряд важных типов квадратных М.

Следует отметить также ленточные М.-такие М., ненулевые элементы к-рых могут располагаться на главной диагонали и на диагоналях,соседних с главной, напр, двухдиагональные и трёх диагональные М.

Не менее важны специальные типы М., употребляемых в качестве вспомогательных. Это элементарные М.- М., отличающиеся от единичной одним элементом; М. вращения и отражения.

Имеются унитарные аналоги М. вращения иотражения; правые (левые)треугольные М.-М., у к-рых равны нулю элементы под (над) главной диагональю; правые (левые) почти треугольные М. (М. типа Хессенберга) - М., у к-рых равны нулю элементы под (над) диагональю, соседней снизу (сверху) с главной.

Преобразование матриц. Численные методы решения систем линейных уравнений основываются обычно на преобразовании систем посредством цепочки левых умножений на подходящие вспомогательные М. с тем, чтобы перейти к легко решаемой системе. В качестве вспомогательных для вещественных М. употребляются элементарные М., М. вращения или М. отражения. Система с неособенной М. приводится либо к системе с треугольной М., либо с ортогональной. В теоретич. аспекте это равносильно представлению М. коэффициентов в виде произведения двух треугольных М. (при выполнении нек-рых дополнит, условий) или в виде произведения треугольной на ортогональную (в том или другом порядке).

Для переопределённой системы умножением слева на цепочку М. вращения или отражения можно прийти к системе с треугольной М, порядка и, решение к-рой даёт обобщённое решение исходной системы.

Для решения проблемы собственных значений, раньше чем применять наиболее эффективные итерационные методы, целесообразно подобно преобразовать М. общего вида к М. типа Хессенберга или к трёхдиагональной в случае симметрии. Этого можно добиться за счёт цепочки подобных преобразований элементарными М., М. вращения или М. отражения.

Историческая справка. Понятие М. было введено в работах У. Гамильтона и А. Кэли в сер. 19 в. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я пол. 19 в. и нач., 20 в.). И. А. Лаппо-Данилевский разработал теорию аналитич. функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитич. коэффициентами. Матричные обозначения получили распространение в совр. математике и её приложениях. Исчисление М. развивается в направлении построения эффективных алгоритмов для численного решения основных задач.

Лит.: Смирнов В. И., Курс высшей математики, 9 изд., т. 3, ч. 1, М., 1967; Мальцев А. И., Основы линейной алгебры. 3 изд., М., 1970; Гантмахер Ф.Р., Теория матриц, 3 изд., М., 1967; Уилкинсон Дж. X., Алгебраическая проблема собственных значений, пер с англ М., 197-0: ф а д д е е в Д. К., Ф а д д е е в а В. Н-, Вычислительные методы линейной алгебры, 2 изд., М.-Л., 1963; Воеводин В. В., Численные методы алгебры. Теория и алгорифмы, М., 1966; Лаппо-Данилевский И. А., Применение функций от матриц к теории линейных систем обыкновенных дифференциальных уравнений, М., 1957; Ф р е з е р Р. А., Д у н к а н В., Коллар А., Теория матриц и её приложения к дифференциальным уравнениям и динамике, пер. с англ., М., 1950; В а з о в В., Форсайт Д ж., Разностные методы решения дифференциальных уравнений в частных производных, пер с англ., М., 1963.

В. Н. Фаддеева.

МАТРИЦА РАССЕЯНИЯ, S - м а т р и ц а, совокупность величин (матрица), описывающая процесс перехода кванто-вомеханич. систем из одних состояний в другие при их взаимодействии (рассеянии). Понятие "М. р." введено В. Гейзенбергом в 1943.

Если обозначить набор квантовых чисел, характеризующих начальное состояние, через г, а конечное - через f, то амплитуда рассеяния (квадрат модуля к-рой определяет вероятность данного рассеяния) может быть записана как Sft. Совокупность амплитуд рассеяния образует таблицу с двумя входами (i -номер строки, f - номер столбца), к - рая и наз. М. p. S. Каждая амплитуда является элементом этой матрицы (матричным элементом). Наборы квантовых чисел г, f могут содержать как непрерывные величины (энергию, угол рассеяния и др.), так и дискретные (орбитальное квантовое число, спин, изотопический спин, массу и т. д.). В простейшем случае системы двух бесспиновых частиц в нерелятивистской квантовой механике состояние определяется относит, импульсом частиц р; тогда ^амплитуда рассеяния представляет собой функцию двух переменных - энергии Е и угла рассеяния S_fi = F(E,Q).

В общем случае М. р. содержит элементы, отвечающие как упругому рассеянию, так и процессам превращения и рождения частиц. Квадрат модуля матричного элемента |S_fi|² определяет вероятность соответствующего процесса (или его эффективное поперечное сечение).

Нахождение М. р. - основная задача квантовой механики и квантовой теории поля. М. р. содержит всю информацию о поведении системы, если известны не только численные значения, но и аналитич. свойства (см. Аналитические функции) её элементов; в частности, её полюсы (см. Особая точка) определяют связанные состояния системы (а следовательно, дискретные уровни энергии). Из основных принципов квантовой теории следует важнейшее свойство М. р. - её унитарность. Оно выражается в виде соотношения SS⁺= 1[S⁺-матрица, эрмитово сопряжённая S, т. е. (S⁺)_fi= S*_if, где знак * означает комплексное сопряжение] или

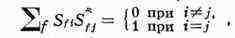
и отражает тот факт, что сумма вероятностей рассеяния по всем возможным каналам реакции должна равняться единице. Соотношение унитарности позволяет устанавливать важные соотношения между различными процессами, а в нек-рых случаях даже полностью решить задачу. В релятивистской квантовой механике существует направление, в к-ром М. р. считается первичной динамич. величиной; требования унитарности и аналитичности М. р. должны служить при этом основой построения полной системы ур-ний, определяющей матрицу S.

В. Б. Берестецкий.

МАТРИЦИРОВАНИЕ, полиграфич. операция для воспроизведения углублённого изображения графич. элементов (штриховых и полутоновых) с оригинальной печатной формы в листах матричного материала способом прессования для последующего изготовления стереотипов. В состав оригинальной рельефной формы входят текстовой набор, изготовленный на строко- и буквоотливных машинах или набранный вручную, цинкографские клише и пробельные элементы, вмонтированные в общую заключную раму. В качестве матричного материала для литых металлич. стереотипов используют термостойкий картон толщиной 0,5-1 мм, для гальваностереотипов - листы винипласта или калиброванного по толщине свинца (1-2 мм), а для пластмассовых и резиновых стереотипов - фильтровальный картон, пропитанный бакелитовым лаком и покрытый специальным слоем. При М. листы матричного материала, уложенные на оригинальную форму, покрывают сверху эластичной прокладкой из кирзы, резино-тканевого материала, или поропласта. М. производят чаще всего в прессах гидравлич. действия с различной степенью механизации и автоматизации. Рабочий пакет, состоящий из оригинальной формы, матричного материала и эластичного настила, укладывают на нижнюю плиту пресса и подъёмом этой плиты или опусканием верхней создают необходимое для прессования давление. Давление в зависимости от состава оригинальной печатной формы и характера матричного материала создаётся в широких пределах от 1 до 20 Ми/л² (от 10 до 200 кгс/см²), а для свинцовых матриц до 120 Ми/Л².

П. Я. Розенфельд.

МАТРИЧНЫЕ ИГРЫ, понятие игр теории. М. и. - игры, в к-рых участвуют два игрока (I и II) с противоположными интересами, причём каждый игрок имеет конечное число чистых стратегий. Если игрок I имеет т стратегий, а игрок II -п стратегий, то игра может быть задана (m x n)-матрицей А = || a_ij ||, где a_ij есть выигрыш игрока I, если он выберет стратегию i (z = 1, ...,т), а игрок II -стратегию j (j = 1, ..., га). Следуя общим принципам поведения в антагонистических играх (частным случаем к-рых являются М. и.), игрок I стремится выбрать такую стратегию i₀, на к-рой достигается

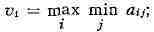игрок II стремится выбрать стратегию j₀, на к-рой достигается 
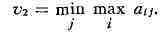
Если Vi = V2, то пара (i₀, j₀) составляет седловую точку игры, Т: е. выполняется двойное неравенство a_ij0< a_i0j0<a_i0j i=1,...,m; j=1,...,n Число ai₀j₀ наз. значением игры; стратегии i₀, j₀ наз. оптимальными чистыми стратегиями игроков I и II соответственно. Если v₁ не равно v₂, то всегда v₁ <v₂ в этом случае в игре седловой точки нет, а оптимальные стратегии игроков следует искать среди их смешанных стратегий (т. е. вероятностных распределений на множестве чистых стратегий). В этом случае игроки оперируют уже с матем. ожиданиями выигрышей.

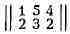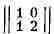Основная теорема теории М. и. (теорема Неймана о мини максе) утверждает, что в любой М. и. существуют оптимальные смешанные стратегии х*, у*, на к-рых достигаемые «минимаксы» равны (общее их значение есть значение игры). Напр., игра с матрицей  имеет седловую точку при i₀ =2 2, j₀ = 1, а значение игры равно 2: игра с матрицей  не имеет седловой точки. Для нее оптимальные смешанные стратегии суть х*= (3/4, 1/4), у* = (1/2, 1/2); значение игры равно 1/2.

Для фактич. нахождения оптимальных смешанных стратегий чаще всего используют возможность сведения М. и. к задачам линейного программирования. Можно использовать т. н. итеративный метод Брауна - Робинсон, состоящий в последовательном фиктивном разыгрывании» данной игры с выбором игроками в каждой данной партии своих чистых стратегий, наилучших против накопленных к этому моменту стратегий оппонента. Игры, в к-рых один из игроков имеет только две стратегии, просто решить графически.

М. и. могут служить математич. моделями многих простейших конфликтных ситуаций из области экономики, математич. статистики, воен. дела, биологии. Нередко в качестве одного из игроков рассматривают «природу», под к-рой понимается вся совокупность внешних обстоятельств, неизвестных принимающему решения лицу (другому игроку).

Лит.: Матричные игры. [Сб. переводов], под ред. Н. Н. Воробьева, М., 1961; Нейман Д ж. фон, Моргенштерн О., Теория игр и экономическое поведение, пер. с англ., М., 1970; Оуэн Г., Теория игр, пер. с англ., М., 1971.

А. А. Корбут.

МАТРИЧНЫЕ МОДЕЛИ в экономике, один из наиболее распространённых типов экономико-математич. моделей. Представляют собой прямоугольные таблицы (матрицы), элементы к-рых отражают взаимосвязи экономия, объектов и обладают определённым экономич. смыслом, значение к-рого вычисляется по установленным в теории матриц правилам. В М. м. отражается структура затрат на произ-во и распределение продукции и вновь созданной стоимости.

М. м. - балансово-нормативные, они объединяют в единой табличной форме балансы распределения продукции (по отд. её видам) и увязанные с ними балансы затрат на её произ-во, а также нормативы материальных и ден. затрат. М. м. используются для экономич. анализа и плановых расчётов с применением электронной вычислит, техники.

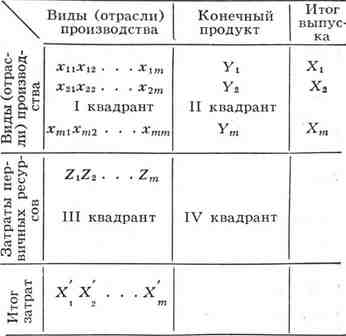
Представленная в графич. виде (см. схему) М. м. экономич. объекта имеет вид прямоугольной таблицы, разделённой на 4 четверти (квадранта).

X_i = X'j, если i тождественно j; тогда в этом равенстве итогов одноимённых строк и столбцов находит выражение закон стоимости: стоимость распределённых и накопленных благ и услуг равна стоимости производств, затрат плюс вновь созданная стоимость. Из этого основного равенства М. м. вытекает целый ряд др. производных уравнений, к-рые делают М. м. удобным расчётным плановым и аналитич. инструментом.

Т. о., каждый показатель имеет двоякое значение: с одной стороны, он выражает объём поставок одного производств, подразделения (отрасли) в другое, с другой стороны-объём производств, потребления вторым подразделением продукции первого. I квадрант М. м. отражает, следовательно, внутрипроизводств. связи моделируемой экономич. системы. Наиболее явное количеств, выражение производственная структура получает в коэффициентах прямых затрат, к-рые представляют собой частное от деления объёмов затрат продукции всех подразделений на объём выпуска определённого подразделения: a_ij=x_ij/X_i. Тогда I квадрант М. м. приобретает смысл таблицы нормативов затрат, рассчитанных на единицу валового выпуска каждого вида продукции. В результате обращения инверсированной квадратной матрицы I квадранта получают коэффициенту полных затрат, выражающие совокупность прямых и косвенных затрат в расчёте на единицу конечного выпуска В=(Е-А)¹. Во II квадранте отражаются результаты производств, и хоз. деятельности (конечная продукция); он рассматривается как выход модели. В III квадранте отражаются затраты первичных ресурсов, поступающих в систему извне, и вновь созданная стоимость (овеществлённый труд); он рассматривается в качестве входа модели. В IV квадранте, где пересекаются строки III квадранта с колонками IV квадранта, отражаются, т. о., транзитные процессы передачи материальных ресурсов и перераспределения стоимости: ресурсы, поступившие на вход данной экономич. системы, используются в качестве конечных продуктов на выходе, минуя производств, подразделения.

Принципиальная схема матричной модели

Благодаря простоте формы и богатому экономич. содержанию М. м. находят широкое применение в различных звеньях экономики для плановых и статистич. расчётов, организации нормативного х-ва, унификации документации и сокращения документооборота, организации внутрипроизводств. хозрасчёта и для экономич. анализа.

М. м., предназначенные для внутризаводского планирования и учёта произ-ва, представляют собой весьма крупноразмерные таблицы (до нескольких сотен позиций), включающие технологич. нормативы затрат сырья, материалов, комплектующих деталей, машинного и рабочего времени на произ-во каждого отд. вида продукции и составляющих его узлов, деталей и т. п. Свойства умножения матриц используются для одновременного отображения производственно-технологич. и организационной структуры. Особенностью М. м. является то, что плановый или аналитич. расчёт осуществляется за один приём по всей призводственно-экономич. системе; в результате достигается полное единство и взаимоувязка всех разделов плана (отчёта) - по произ-ву, снабжению, финансированию, труду и зарплате, себестоимости и т. д. Это позволяет также постоянно корректировать норма-типы различных типов и увязывать их между собой. В случае, если матрицы достигают слишком больших размеров, а расчёты производятся с помощью вычислит, техники, таблицы обычно не строят, а соответствующие данные фиксируют на перфокартах или магнитной ленте; матрица же служит' просто расчётной схемой.

Матричный техпромфинплан предприятия представляет собой серию унифицированных документов, главным из к-рых является М. м. экономики предприятия (в укрупнённых показателях по сравнению с "технологическими" матрицами). Сводный баланс экономики предприятия расшифровывается в ряде таблиц детальных показателей по материальному снабжению, труду, осн. фондам и оборудованию, финансам предприятия, имеющим также единообразную матричную форму. Матричный техпромфинплан является весьма совершенной формой унифицированной документации, приспособленной для машинной обработки. В нём число показателей и табличных форм сокращается в несколько раз при сохранении того же объёма информации, причём все показатели приводятся в сопоставимом и взаимоувязанном виде.

М. м. используются также для моделирования экономики отраслей нар. х-ва, экономики республик и территориально-производств. комплексов, нар. х-ва страны; матрицы этого типа носят название межотраслевого баланса и находят широкое применение в планировании и статистике.

М. м., с помощью к-рых моделируются последовательные звенья нар. х-ва, на основе использования правил сложения матриц образуют единый взаимосвязанный комплекс, наз. системой М. м. Так, М. м. экономики отрасли создаётся путём объединения М. м. предприятий с помощью т. н. вариантных матриц, отражающих разные технологич. варианты произ-ва продукции и услуг на разных предприятиях. Эти вариантные матрицы имеют самостоят, значение для межзаводского и межотраслевого анализа, организации нормативного х-ва отрасли. Вычитание и деление матриц обеспечивают процесс развёрстки плана отрасли по предприятиям, а представление их в виде систем линейных уравнений - применение методов математич. программирования для оптимального отраслевого планирования. Межотраслевые балансы экономики республики и нар. х-ва в целом могут строиться на основе объединения отраслевых матриц.

Система М. м. служит основой проектирования интегрированных схем обработки экономич. информации в автоматизированных системах управления предприятий, министерств и ведомств, плановых и статистич. органов. Сам процесс интегрированной обработки данных отображается в информационной М.м. В этом случае хи означает уже не взаимные поставки продукции и услуг, а передачу определённых сообщений, оцениваемых в к.-л. информационных единицах (документы, показатели, биты информации). С помощью матриц моделируются также транспортные потоки, процессы миграции населения и движение трудовых ресурсов, организационные структуры, процессы выработки решений и любые др. процессы, для к-рых имеет силу уравнение баланса.

М. м. удобна для анализа, поскольку в простой и наглядной форме отображает свойства объектов самой различной природы, где имеет место баланс поступления и расхода материальных ценностей, энергии, стоимости, информации и т. д., причём зависимость между ними имеет прямой, линейный характер. Матричный анализ даёт ряд новых возможностей по сравнению с др. методами экономич. анализа: интерполяция ненаблюдаемых элементов, выявление логич. структуры производств, и экономич. процессов, детальный учёт взаимного влияния факторов, применение методов математич. программирования для анализа оптимальности плана и т. д. Матричный анализ используется для изучения экономич. деятельности предприятий, производств, объединений, отраслей, экономич. р-нов, республик, нар. х-ва страны, процессов экономич. управления (анализ документооборота, движения показателей, взаимосвязи задач управления), а также отд. экономич. процессов (бухгалтерский баланс, движение ден. наличности и т. д.).

Свойства блочных матриц обеспечивают наглядность представления сложных взаимосвязей и делают матрицу удобным инструментом логич. анализа сложных структур, где отражаются одновременно технологический, организационно-производств. и экономич. аспекты деятельности нар.-хоз. объектов. Так, с помощью М. м. производств, процесса на предприятии выявляются производств, "петли" и нерациональные связи, исследуется загрузка оборудования и использование рабочей силы. иИнформационная матрица", отображающая движение документов и показателей, служит для анализа рациональности структуры, организации труда и загрузки отделов в заводоуправлении, учреждении, мин-ве. Экономич. М. м., т. е. модели экономич. объектов, построенные в сравнимых стоимостных показателях, служат для анализа взаимодействия различных видов деятельности на данном объекте, к-рые в целом формируют итог хоз. деятельности предприятия, производств, объединения, отрасли.

М. м. аналогичного типа, но построенные для более крупных экономич. систем - экономич. р-нов, республик служат для анализа сбалансированности и пропорциональности плана, степени полезного использования отд. видов ресурсов (производств, мощностей, трудовых, материальных и финанс. ресурсов), для анализа и проектировок комбинирования и специализации произ-ва.

Для динамич. анализа используется метод сравнения рядов М. м. за последовательные периоды времени или попарное сопоставление плановых и отчётных моделей.

Для развёрнутой системы аналитич. расчётов служат М. м. экономики республик, районов и нар. х-ва страны (межотраслевые балансы). С их помощью выявляются осн. нар.-хоз. пропорции, соотношения материального произ-ва с непроизводств, сферой, доля отраслей, районов, республик в создании нац. дохода и совокупного обществ, продукта страны и структура их образования и реализации, соотношения осн. элементов стоимости. Кроме того, на основе территориальных М. м. осуществляется анализ плановых проектировок стр-ва новых предприятий в республиках и районах, освоения новых с.-х. угодий, стр-ва новых городов. При этом рассчитывается комплексная эффективность этих мероприятий в целом по стране, республике, району, подсчитываются доходы населения, выявляется структура его спроса.

М. м. с помощью методов электронной иммитации дают возможность исследовать потоки материальных ценностей, услуг, финансов в динамике их развития. Система М. м. позволяет "проигрывать" плановые проектировки для анализа экономич. последствий реализации вариантов проектов строительства, трудно сопоставимых между собой. На основе системы М. м. могут также анализироваться потоки информации в органах экономич. управления в процессе составления нар.-хоз. плана и контроля за его реализацией.

Лит.: Немчинов В. С., Экономикс" математические методы и модели, М., 1962; Черняк Ю. И., Межотраслевой баланс и его использование в экономическом анализе и плановых расчётах, в I, M., 1962; его же, Единство планирования производства, снабжения и финансирования в системе матричных моделей, в сб.: Применение математики в экономических исследованиях, т. 3, М., 1965; Волошин Н. И., Система матричных моделей внутризаводского планирования, там же; Махров Н. В., Метод межотраслевого баланса - основа свода низовых планов, там же; Будрис В. А., Обработка деловой информации, представленной в матричной форме, в сб.: Математико-экономические проблемы. Труды межвузовской научной конференции, [Л.], 1966; Е р ш о в Э. Б., О выявлении и использовании структурных особенностей матриц в задачах планирования, -"Экономика и математические методы", 1966, т. 2, в. 2.

Ю. И. Черняк.

А. М. Матросов.

В. Матушевский.

МАТРИЧНЫЙ АНАЛИЗ в экономике, метод научного исследования свойств объектов на основе использования правил теории матриц, по к-рым определяется значение элементов модели, отображающих взаимосвязи экономич. объектов. Используется в тех случаях, когда гл. объектом исследования являются балансовые соотношения затрат и результатов производственно-хоз. деятельности и нормативы затрат и выпусков. (Подробнее см. в ст. Матричные модели.)

МАТРOНА (лат. matrona, от mater - мать), 1) в Др. Риме свободнорождённая, состоящая в законном браке женщина. В широком смысле М.- мать семейства, почтенная женщина. 2) Во мн. числе М. (matronae, matres) - женские божества в Др. Риме и провинциях (особенно в Галлии, Германии и Британии), считавшиеся покровителями данной местности или родо-плсменной общины.

МАТРOС (от голл. matroos), первое (младшее) воинское звание в ВМФ; соответствует званию солдат в др. видах вооруж. сил. В СССР введено в июле 1946 вместо звания краснофлотец; существует также звание старший М., к-рое соответствует званию ефрейтор. В рус. ВМФ имелись звания М. 2-й статьи и М. 1-й статьи. В торговом флоте М.- служащий в составе судовой команды.

МАТРOСОВ Александр Матвеевич (1924, Днепропетровск, - 23. 2. 1943, ок. дер. Чернушки Локнянского р-на Псковской обл.), Герой Сов. Союза (19. 6. 1943, посмертно). Чл. ВЛКСМ с 1942. Потерявший в детстве родителей, М. воспитывался в Ивановском детдоме Ульяновской обл. и в трудовой детской колонии в г. Уфе. В окт. 1942 призван в армию и направлен курсантом в пех. училище. В нояб. 1942 добровольно отправился на фронт и был зачислен рядовым в 254-й гвард. стрелк. полк 56-й гвард. стрелк. дивизии (Калининский фронт). 23 февр. 1943 в бою за дер. Чернушки прорвался к вражескому дзоту и, закрыв своим телом амбразуру, пожертвовал собой, чтобы обеспечить успех своему подразделению. 8 сент. 1943 имя М. было присвоено 254-му полку с зачислением погибшего героя навечно в списки 1-й роты полка. В Уфе М. поставлен памятник.

Лит.: Ульяновцы в боях за Родину, Ульяновск, 1962; Навечно в строю, кн. 1, М., 1957.

МАТРОСОВ Василий Иванович (р. 12. 4. 1909, дер. Красный Стан Можайского р-на Московской обл.), рабочий-новатор, закройщик моек, обувной ф-ки "Парижская Коммуна". Чл. КПСС с 1945.

Соревнуясь за досрочное выполнение 4-й пятилетки (1946 - 50), М. выполнил 4,5 нормы выработки при хорошем качестве кроя и значит, экономии кожи. По предложению М. в 1946 была организована бригада закройщиков, к-рой он передал свой опыт работы. Эта бригада в короткий срок более чем вдвое увеличила выпуск кроя. В 1947 М. выступил с предложением разработать цеховые и общефабричные планы внедрения стахановских методов труда. Эти планы предусматривали улучшение технологии произ-ва, организацию школ передовых методов труда. Гос. пр. СССР (1947) за внедрение новых высокопроизводит. методов работы, получивших широкое распространение в пром-сти.

Лит.: Ценное начинание закройщика В. Матросова, М.- Л., 1947.

МАТРОСОВ Владимир Евгеньевич (р. 15. 10. 1928, Ленинград), советский скульптор. Учился в Моск. художеств, ин-те им. В.И. Сурикова (1946-52). Произв.: портреты А. В. Ковалевского (гипс, 1958-59, Музей при Военно-воздушной академии имени Ю. А. Гагарина, Монино), Я. И. Алксниса, П. И. Баранова, К. В. Маслова (все три - бетон, 1965, Военно-воздушная академия имени Ю.А.Гагарина, Монино), К. Э. Циолковского, Н. И. Кибальчича, Ф. А. Цандера, С. П. Королёва (все четыре - гипс, 1967, Главный штаб ракетных войск); памятник В. И. Ленину в Анадыре (гранит, 1963-67). Участвовал в создании памятника-ансамбля героям Сталинградской битвы на Мамаевом кургане в Волгограде (1963-67, Ленинская пр., 1970; илл. см. т. 5, табл. XIII, стр. 448- 449).Награждён орденом Трудового Красного Знамени.

МАТРОСОВ Иван Константинович [16 (28). 6. 1886, с. Малые Соли, ныне Некрасовского р-на Ярославской обл.,- 30. 10. 1965, Москва], советский изобретатель, создатель неск. систем ж.-д. авто-матич. тормозов. В 1904-16 слесарь, затем пом. машиниста и машинист. В 1923 окончил уч-ще техников путей сообщения в Петрограде. В 1923-28 техник в управлении Сев.-Зап. жел. дороги. С 1928 работал на Моск. тормозном з-де. В 1926 предложил новую систему автотормоза для грузовых поездов. После сравнит, испытаний тормоз М. был принята 1931 в качестве типового для грузовых поездов на жел. дорогах СССР (см. Матросова тормоз). В 1935 разработал тормоз для поездов Моск. метрополитена, а в 1945 для пасс, поездов. Изобрёл ряд узлов тормозных устройств: концевой кран клапанного типа (1935), автоматич. регулятор грузовых режимов торможения поезда (1944, совм. с Е. В. Клыковым), кран машиниста и др. В 1950 создал электропневматич. тормоз для грузовых поездов; в 1959 усовершенствовал тормоз своей системы. Гос. пр. СССР (1941). Награждён орденом Ленина, 2 др. орденами, а также медалями.

С о ч.: Автотормоза. Устройство, управление, обслуживание и ремонт, 4 изд., М., 1951 (соавтор).

Лит.: Конструкции и изобретения И. К. Матросова, М., 1946; Смирнов С. С., Изобретатели тормозов, М., 1950.

И. А. Иванов.

МАТРОСОВА ТОРМОЗ, тормоз ж.-д. подвижного состава, в котором осн. прибором является воздухораспределитель конструкции И. К. Матросова (см. Тормоз железнодорожный). Новый тип воздухораспределителя был предложен в 1926, отличался оригинальным устройством по сравнению с воздухораспределителем Казанцева (см. Казанцева тормоз) и ценными эксплуатац. свойствами. С 1931 М. т. устанавливался в тормозных системах выпускаемых грузовых вагонов и локомотивов. В 1952 начато изготовление воздухораспределителя, предназначенного для эксплуатации на длинных и тяжеловесных поездах, к-рый позволил осуществлять бесступенчатый лёгкий отпуск тормозов в сочетании со ступенчатым отпуском, позволяющим улучшить управляемость движением поездов. С 1959 грузовые вагоны и локомотивы оборудуются усовершенствованным воздухораспределителем системы Матросова. Такой тормоз при сравнительно небольшой массе отличается высокой чувствительностью и простотой управления.

Лит.: К р ы л о в В. И., Клыков Е.В., Новый воздухораспределитель для грузовых поездов, М., 1960.

В. Г. Иноземцев, Е. В. Клыков.

МАТСАЛУ, залив Балтийского м. на зап. побережье Эст. ССР. Дл. 21 км, средняя шир. 4 км. Мелководен. В залив впадает р. Казари. Берега песчаные, покрыты камышом и тростником. М. и его окрестности - место обитания большого количества видов водоплавающих птиц (Матсалуский заповедник).

МАТСАЛУСКИЙ ЗАПОВЕДНИК, расположен в зап. части Эст. ССР, в ниж. течении р. Казари, прибрежной полосе зал. Матсалу Балтийского м. и на 50 о-вах Моонзундского прол. Пл. 13,5 тыс. га (1973). Основан в 1957 на базе орнитологич. заказника и охотоведч. уч.-опытного х-ва для охраны природных комплексов и разнообразной фауны птиц (ок. 250 видов, в т. ч. св. 160 гнездящихся). Орнитологич. исследования на терр. М. з. ведутся с 1870. Особенно многочисленны в заповеднике водоплавающие и болотные птицы. На пролёте - стаи лебедей-кликунов, сев. уток и куликов. В тростниках гнездятся лебеди-шипуны, серые гуси, линяют селезни крякв и красноголовых нырков. На травянистых лугах устраивают свои гнёзда речные утки, много куликов. На островах гнездятся гаги, хохлатые чернети, пеганки, крохали, турпаны, чайки и крачки.

МАТТЕЗОН (Mattheson) Иоганн (28.9. 1681, Гамбург,-17.4.1764, там же), немецкий музыкальный писатель, композитор, певец и дирижёр. Написал несколько опер, 24 оратории и кантаты, инструментальные пьесы. Осн. значение имели его муз.-теоретич. работы. М. был поборником нац. музыки, сторонником прогрессивного для того времени муз.-эстетич. учения об аффектах. Среди его трудов- "Вновь открытый оркестр" (ч. 1-3, 1713-21), "Музыкальная критика" (т. 1-2, 1722-25), "Современный капельмейстер..." (1739). Автор первой биографии Г. Ф. Генделя.

Лит.: Материалы и документы по истории музыки, под ред. М. В. Иванова-Борецкого, т. 2, М., 1934; WolffH. С h., Die Barockoper in Hamburg (1678-1738), Bd 1-2, Wolfenbtittel, 1957.

МАТТЕОТТИ (Matteotti) Джакомо (22.5.1885, Фратта-Полесине, пров. Ровиго, - 10. 6. 1924, Рим), один из лидеров Итал. социалистич. партии. По образованию юрист. Во время 1-й мировой войны 1914-18 за антивоен. деятельность был арестован и заключён в тюрьму. С 1919 деп. парламента. В окт. 1922 вместе с Ф. Турати и др. реформистами был исключён из Итал. социалистич. партии и участвовал в основании Унитарной социалистич. партии, являлся её политич. секретарём. В отличие от др. реформистов, выступал за решит, сопротивление фашизму. Во вновь избранной палате депутатов М. 30 мая 1924 разоблачал избирательные махинации и злоупотребления фаш. партии и потребовал аннулировать мандаты фаш. депутатов. Готовил новые разоблачения фаш. режима. Был похищен и убит фашистами. Убийство М. вызвало острый кризис фаш. режима (образование Авентинского блока и др.).

МАТТЕРХОРН (Matterhorn), горная вершина в Пеннинских Альпах, на границе Швейцарии и Италии. Вые. 4477 м. Имеет вид четырёхгранной пирамиды, возвышающейся почти на 1000 м над покрытым ледниками хребтом.

МАТТИНГЛИ (Mattingly) Томас (р. 17.3.1936, Чикаго, шт. Иллинойс), лётчик-космонавт США, капитан 3-го ранга ВМФ. Окончил высшую школу им. Т. Эдисона в Майами (шт. Флорида) и ун-т в Оберне (шт. Алабама) в 1958, получив степень бакалавра наук в области авиац. техники. В этом же году начал службу лётчиком в ВМФ США. До зачисления в 1966 в группу космонавтов Нац. управления по аэронавтике и исследованию космич. пространства США окончил школу по подготовке пилотов для аэрокосмич. исследований. 16-27 апр. 1972 совм. с Дж.Янгом и Ч. Дъюком совершил полёт к Луне в качестве пилота осн. блока .космич. корабля "Аполлон-16". Пробыв св. 5 сут на окололунной орбите, провёл работы по фотографированию Луны и зондированию её атмосферы. Находясь на расстоянии 300 тыс. км от Земли, выходил в открытый космос (62 мин).

МАТТИОЛА седая, растение сем. крестоцветных; то же, что левкой.

МАТТИСЕН (Matthiessen) Фрэнсис Отто (19.2. 1902, Пасадена, шт. Калифорния, - 1.4. 1950, Бостон), американский литературовед, публицист. Окончил Йельский ун-т (1923). Проф. Гарвардского ун-та (1929 - 50). От формализма ранних работ ("Свершения Т. С. Элиота", 1935, и др.) пришёл к социально-историч. пониманию лит. процесса, близкому к марксистскому (посмертно изданная кн. "Теодор Драйзер", 1951; "Ответственность критики", 1952). Работа М. "Американское Возрождение" (1941) посвящена проблемам амер. романтизма и творчеству Р. У. Эмерсона, Г. Торо, Н. Хоторна, Г. Мелвилла, У. Уитмена. В полемике с модернистской критикой М. одним из первых оценил реалистич. природу творчества Г. Джеймса и значение наследия Драйзера для амер. лит-ры. Ряд исследований М. поев, проблемам развития амер. поэзии в 20 в. и общим вопросам эстетики. В публицистич. кн. "Из сердца Европы" (1948) М. сочувственно отзывался о СССР, где побывал ещё в 1938, и европ. странах, строящих социализм. В годы маккартизма М. подвергся жестокой травле и покончил с собой.

Соч. в рус. пер.: Ответственность критики. [Предисл. Я. Засурского], М., 1972.

А. М. Зверев.

МАТТИССЕНА ПРАВИЛО, закономерность, к-рой подчиняется удельное электросопротивление твёрдого проводника, если оно определяется неск. механизмами. Согласно М. п., полное удельное

сопротивление равно сумме удельных сопротивлений, отвечающих каждому из механизмов в отдельности. Впервые было сформулировано нем. химиком А. Маттиссеном (A. Matthiessen) в 1862 применительно к металлам, у к-рых составляющая сопротивления, обусловленная рассеянием электронов на примесях и дислокациях (остаточное сопротивление), не зависит от темп-ры, а другая, связанная с рассеянием электронов на тепловых колебаниях кристаллической региётки (идеальное сопротивление), изменяется с темп-рой и становится малым при Т->ОК. М. п. является приближённым и может нарушаться вследствие корреляции между процессами рассеяния, а также под влиянием др. факторов. Тем не менее оно используется при приближённых оценках сопротивления металлов.

Лит.: Лифшиц И. М., Азбель М. Я., Каганов М. И., Электронная теория металлов, М., 1971; 3 а и м а н Д ж., Электроны и фононы, пер. с англ., М., 1962.

Э. М. Эпштейн.

МАТТЫ (от нем. Matte - горный луг, пастбище), альпийские ковры, низкотравные высокогорные луга. Распространены в Альпах, на Кавказе, Тянь-Шане, Камчатке и в др. местах, где выпадает большое количество снега. Травяной покров М. плотный, прижат к земле, изобилует яркими цветущими растениями. Различают М. разнотравные, осоково - разнотравные, кобрезиево - разнотравные, злаково-разнотравные. М. - хорошие летние пастбища. Иногда М. наз. альпийские луга и, в частности, низкотравные луга нек-рых островов умеренного и субарктич. поясов (на Алеутских о-вах, в Исландии).

МАТУА, остров в ср. части Курильских о-вов (Сахалинская обл. РСФСР). Дл. 12 км, шир. 6 км, пл. 52 км². Обособлен прол. Надежды и Головкина от о-вов Рас-шуа и Райкоке. Весь М. занят активно действующим вулканом Сарычева (выс. 1446 м), сложенным андезитами и андезито-базальтами (извержения 1946 и мн. др.). Берега обрывисты. Покрыт кустарником и стланиками.

МАТУАР (франц. matoir), инструмент для гравирования на металле, преим. пунктирной манерой. Имеет вид стального пестика с шаровидным или булавовидным утолщением с шипами, к-рыми наносятся на гравировальную доску углубления (точки и чёрточки).

МАТУ-ГРОСУ (Mato Grosso), плато на С.-З. Бразильского плоскогорья, в междуречье верховьев pp. Тапажос, Шингу и Парагвай. Ср. вые. 500-700 м, наибольшая-893 м. Сложено гл. обр. палеозойскими песчаниками, образующими крутые уступы (шапады). Климат субэкваториальный, жаркий, летневлажный. Покрыто низкодревесной саванной (кампос серрадос).

МАТУ-ГРОСУ (Mato Grosso), штат на 3. Бразилии, на Бразильском плоскогорье. Пл. 1231,5 тыс. км². Нас. 1623,6 тыс. чел. (1970). Адм. ц. - г. Куяба. На С. - влажный тропич. лес Амазонки, в центре и на Ю. - редколесье и саванна. Осн. отрасль х-ва - скотоводство. Сбор лесных продуктов, потребит, земледелие (рис, кукуруза, маниок, сах. тростник). Близ г. Корумба добыча марганцевой и железной руд. Имеются предприятия хл.-бум. и пищ. пром-сти. Гл. центры- Куяба, Корумба и Кампу-Гранди.

МАТУЛИС Юозас Юозович [р.7 (19). 3. 1899, Татконис, ныне Купишкского р-на Литов. ССР], советский физико-химик, чл.-корр. АН СССР (1946), акад. (1941) и президент (с 1946) АН Литов. ССР, Герой Социалистич. Труда (1965). Чл. КПСС с 1950. Окончил Каунасский ун-т (1929). Директор Ин-та химии и химич. технологии АН Литов. ССР (с 1956). Осн. труды посвящены фотохимии и электрохимии, теории электроосаждения металлов, разработке науч. основ технологии покрытий с заданными свойствами. Автор фундаментального курса коллоидной химии и руководства по физ. химии (изд. в Каунасе в 1947 и 1948). Награждён 4 орденами Ленина, 3 др. орденами, а также медалями.

МАТУРИН (Maturin), город на С.-В. Венесуэлы, адм. центр шт. Монагас. 97,3 тыс. жит. (1970). Центр с.-х. р-на (гл. обр. животноводство). Пищевая промышленность.

МАТУС (Matos) Грегориу ди (1633, Салвадор, - 1696, Ресифи), бразильский поэт. Окончил ун-т в Коимбре. Стихи М. распространялись в списках. Влияние испано-португ. барокко сказывается в контрастном сочетании бурлеска и религиозности, эротич. чувственности и платоники в его стихах. Особенно интересна сатирич. поэзия М., высмеивавшего колониальных чиновников и португальцев-нуворишей, обогащавшихся в Бразилии. М. впервые запечатлел в лит-ре реальные черты браз. действительности.

С о ч.: Obras completes, v. 1 - 2 Sao-Paulo, 1943.

Лит.: Araripe Tristao deAlencar (Junior), Gregorio de Matos, Rio de J., 1934; A literature no Brasil, v. 1, t. 1, Rio de J., 1956.

И.А. Тертерян.

МАТУСЕВИЧ Николай Николаевич [29.3(10. 4). 1879, Николаев, - 27. 5. 1950, Ленинград], советский гидрограф-геодезист, инженер - вице-адмирал, засл. деят. науки и техники РСФСР (1944). Окончил Морскую академию (1904) и Петерб. ун-т (1909). С 1931 проф. Воен. мор. академии. В 1911-31 руководил гидрографич. работами на Белом, Баренцевом, Карском морях. Именем М. названы залив острова Октябрьской Революции (Сев. Земля) и впадающая в него река. Награждён орденом Ленина, 2 др. орденами, а также медалями.

Лит.: Николай Николаевич Матусевич, "Изв. Всес. географического об-ва", 1950, т. 82, в. 5.

МАТУСОВСКИЙ Михаил Львович [р. 10(23).7. 1915, Луганск], русский советский поэт. Чл. КПСС с 1945. Род. в семье служащего. Окончил Лит. ин-т им. М. Горького (1939). В годы Великой Отечеств, войны 1941-45 воен. корреспондент фронтовых газет. Печататься начал в 1934. Первая книга стихов - "Луганчане" (1939, совм. с К. Симоновым). Автор сб-ков "Фронт" (1942), "Когда шумит Ильмень-озеро" (1944), "Слушая Москву" (1948), "Улица мира" (1951), "Тень человека. Книга стихотворений о Хиросиме, о её борьбе и её страданиях, о её людях н её камнях" (1968) и др. М. - известный поэт-песенник ("Школьный вальс", "Подмосковные вечера", песни к кинофильмам "Верные друзья", "Испытание верности","Неподдающиеся" и др.). Стихи ц песни М. отмечены серьёзностью обществ, звучания, они глубоко лиричны и мелодичны. Награждён 3 орденами, а также медалями.

С о ч.: Всё, что мне дорого, М., 1957; Подмосковные вечера, М., 1960; Это было недавно, это было давно. [Предисл. П. Антокольского], М., 1970.

Лит.: Азаров В., Чувство будущего, "Звезда", 1948, № 7; Кириллов И., "На Безымянной высоте", "Правда", 1966, 24 мая.

МАТУТЕ (Matute) Ана Мария (р. 26. 7. 1926, Барселона), испанская писательница. Представительница критического реализма в совр. исп. лит-ре. Творчество М., особенно раннее, окрашено в трагич. тона; ему свойственны социально-критич. направленность, углублённый психологизм. Многие её герои - жертвы франкистского режима (роман "Авели", 1948). В романе "Мёртвые сыновья" (1958, рус. пер. 1964) раскрыта трагедия исп. молодёжи в первые годы диктатуры. В трилогии "Торгаши", состоящей из романов "Первые воспоминания" (1960), "Солдаты плачут ночью" (1964, рус. пер. 1969), "Ловушка" (1969), сделана попытка критически осмыслить судьбу Испании последних десятилетий; носителем идеи борьбы и служения людям выступает коммунист-подпольщик. М. - автор книг для детей "Глупые дети" (1956), "Паулина, мир и звёзды" (I960) и др.

Соч.: Obra completa, t. I, Barcelona, [1971]; La torre vigia, [Barcelona, 1971]; в рус. пер.- Счастье. Рассказы, М., 1966; Гражданская война и писатели моего поколения, "Иностранная литература", 1966, № 9.

Лит.: Ясный В., Бегство в действительность. Современный испанский роман, М., '1971; Тертерян И., Современный испанский роман (1939 - 1969), М., [1972]; Fuentes V., Notas sobre el mundo noveles-co de A. M. Matute, "Revista nacional de cultura", 1963, № 160, p. 83-88; Jones M. E. W., The literary world of A. M. Matute, Lexington, 1970 (библ. с. 123-30).

В. К. Ясный.

МАТУШЕВСКИЙ (Matuszewski) Винценты (7. 7. 1870, Бжезины, - 5.10. 1918, Красноярск), деятель польского рабочего движения. Род. в крест, семье. По профессии - портной. С 1889 в Союзе польских рабочих, с 1900 в С.-д-тии Королевства Польского и Литвы (СДКПиЛ), в 1901-03 чл. её Главного правления. Делегат 3-го (1901), 4-го (1903), 5-го (1906), 6-го (1908) съездов СДКПиЛ и 5-го (1907) съезда РСДРП. Один из руководителей т. н. розламовцев, тесно сотрудничавших с большевиками. За революц. деятельность неоднократно арестовывался, в 1913 был сослан на вечное поселение в Сибирь. После Февр. бурж.-демократич. революции 1917 депутат Иркутского Совета рабочих и солдатских депутатов. С авг. 1917 - в Красноярске, где был членом парт, к-та, депутатом Совета рабочих и солдатских депутатов,адм. руководителем большевистской газ."Красноярский рабочий". Во время белогвардейского мятежа (янв. 1918) входил в подпольный К-т РСДРП(б). Был выдан провокатором и расстрелян. Портрет стр. 512.

МАТХУРА, М а т р а, город в Сев. Индии , в шт. Уттар-Прадеш, на р. Джамна. 140,5 тыс. жит. (1971). Трансп. узел. Произ-во растит, масел, текст, пром-сть, металлообработка. М. знаменита древними буддийскими памятниками (4-3 вв. до н. э.) и индуистскими храмами.

МАТЧ (англ, match), состязание между двумя или неск. спортсменами, командами. Со 2-й пол. 19 в. М. назывались регулярно проводившиеся традиционные спортивные соревнования, напр, встречи по крикету между командами Англии и Австралии. В этом значении термин получил широкое распространение в сер. 20 в., когда стали традиционными встречи спортсменов (легкоатлетов, конькобежцев, шахматистов и др.) разных стран, напр, легкоатлетич. М. СССР - США, конькобежные М. СССР - Норвегия.

В кон. 19 - нач. 20 вв. М. стали называть также состязания отд. спортсменов, в т. ч. за звание чемпиона мира (проф. бокс, шахматы), а затем и соревнования в спортивных играх (футбол, баскетбол, хоккей и др.).

МАТЧА, горный узел в системе Памиро-Алая (Тадж. ССР). Расположен в верховье р. Зеравшан (р. Матча), в месте стыка Туркестанского, Зеравшанского (обрамляющих с С. и Ю. долину Зеравшана) и Алайского горных хребтов. Выс. до 5621 м (в вост. оконечности Туркестанского хр.); крупные ледники.

МАТЧА, название верх, течения р. Зеравшан до устья р. Фандарья (Тадж. ССР).

МАТЧАНОВ Назар Маткаримович (р. 1. 1. 1923, Хива Хорезмской обл. Узб. ССР), советский гос. и парт, деятель, доктор вет. наук (1969), проф. (1971). Чл. КПСС с 1949. Род. в семье кустаря. В 1949 окончил Узбекский с.-х. ин-т. В 1949-59 работал гл. вет. врачом райсельхозотдела, нач. вет. отдела областного управления с. х-ва, нач. Вет. управления Мин-ва с. х-ва Узб. ССР. В 1959-60 зам. мин. с. х-ва Узб. ССР. В 1960-61 секретарь, в 1962-65 1-й секретарь Бухарского обкома КП Узбекистана. В 1961-62 зам. пред. Сов. Мин. Узб. ССР. В 1965-70 секретарь ЦК КП Узбекистана. С сент. 1970 пред. Президиума Верх. Совета Узб. ССР, с дек. 1970 зам. пред. Президиума Верх. Совета СССР. На 24-м съезде КПСС (1971) избран чл. ЦК КПСС. С 1966 чл. Бюро ЦК КП Узбекистана. Деп. Верх. Совета СССР 7-8-го созывов. Награждён орденом Ленина, 2 др. орденами, а также медалями.

МАТЫ (самоназвание - мады), в 17 в. этнографич. группа числ. ок. 600 чел., населявшая центр Тувы (правобережье р. Енисея и басе. р. Хемчик). М. занимались гл. обр. кочевым скотоводством. В их этногенезе принимали участие тюркоязычные и, по-видимому, самодийско-язычные племена. К 18 в. все М. были тюркоязычными. В процессе формирования тувинцев М. вошли в их состав. В 19-20 вв. потомки М. населяют гл. обр. сев. и сев.-вост. часть Тув. АССР.

MATЫPA, река в Тамбовской и Липецкой обл. РСФСР, лев. приток р. Воронеж (басс. Дона). Дл. 180 км, пл. басс. 5180 км². Берёт начало и протекает в пределах Окско - Донской равнины. Питание преим. снеговое. Ср. расход в 39 км от устья 11,7 м³/сек. Замерзает в ноябре - нач. декабря, вскрывается в кон. марта - 1-й пол. апреля. На реке - г. Грязи; водохранилище.

"МАТЬ-ГЕРОИНЯ", см. в статьях Ордена СССР н,Звания почётные.

МАТЬЁ Милица Эдвиновна [12 (24).7. 1899, с. Мартышкино, ныне Ленингр. обл., - 8. 4. 1966, Ленинград], советский историк-египтолог, искусствовед, филолог. Доктор историч. наук (1945), засл. деят. иск-в РСФСР (1964). В 1922 окончила Петроградский ун-т, где училась у Б. Л. Тураева, В. В. Струве, Н. Д. Флиттнер. Проф. Ленингр. ун-та (с 1947). С 1920 работала в Эрмитаже. Осн. труды М. разносторонне и глубоко освещают культуру Др. Египта. В работах о др.-егип. иск-ве М. решала вопросы его периодизации, формирования художеств, школ (в т. ч. фиванской), авторства.

С о ч.: Искусство Среднего царства, Л. 1941 (История искусства Древнего Востока т. 1, в. 2); Искусство Нового царства, Л. 1947 (История искусства Древнего Востока т. 1, в. 3); Роль личности художника в ис кусстве древнего Египта, в кн.: Труды Отдела Востока Государственного Эрмитажа, т. 4, Л., 1947. См. также лит. при ст. Египет Древний.

Лит.: К шестидесятилетию профессора М. Э. Матье. Список трудов М. Э. Матье, "Вестник древней истории", 1959, № 3.

МАТЬЕ ФУНКЦИИ, специальные функции, введённые франц. математиком Э. Матье (Е. Mathieu) в 1868 при решении задач о колебании эллиптич. мембраны. М. ф. применяются также при изучении распространения электромагнитных волн в эллиптич. цилиндре, при рассмотрении приливных волн в сосуде, имеющем форму эллиптич. цилиндра, и в ряде др. вопросов. М. ф. наз. чётные или нечётные функции, являющиеся периодич. решениями линейного дифференциального ур-ния второго порядка (у равнения Матье):

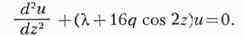
Условие периодичности решения этого ур-ния определяет ряд значений Л в зависимости от q. Если q = 0, то Л = п² (п = = 1,2,...), и М. ф. в этом случае являются cos nz и sin nz. При q не равным 0 М. ф., обозначаемые ce_n(z,q), se_n (г, q), представляются в виде

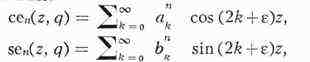
где a_k ⁿи b_kⁿзависят от q; e = 0 при п четном и Е = 1 при п нечётном.

Лит.: Уиттекер Э. Т. и Ватсон Д ж. Н., Курс современного анализа, пер. с англ., ч. 2, 2 изд., М., 1963; Мак-Лахлан Н. В., Теория и приложения функций Матье, пер. с англ., М., 1953.