МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины. Для случайной величины X, принимающей последовательность значений у₁, у₂, . . ., у_к, . . . с вероятностями, равными соответственно p₁, р₂, . . ., р_k, • . •, М. о. определяется формулой

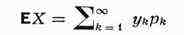
(в предположении, что ряд Сумма_k |у|р_к сходится). Так, напр., если Х - число очков, выпадающее на верхней грани игральной кости (X принимает каждое из значений 1, 2, 3, 4, 5, 6 с вероятностью ¹/₆), то

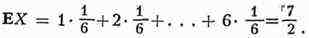
Для случайной величины, имеющей плотность вероятности р(у), М. о. определяется формулой

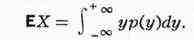
М. о. характеризует расположение значений случайной величины. Полностью эта роль М. о. разъясняется больших чисел законом. При сложении случайных величин их М. о. складываются, при умножении двух независимых случайных величин их М. о. перемножаются. М. о. случайной величины e^itx, то есть f (t) = Ее^itx, где t - действительное число, носит название характеристической функции.

Лит.: Гнеденко Б. В., Курс теории вероятностей, 4 изд., М., 1965.

Ю. В. Прохоров.

МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ, математическая дисциплина, посвящённая теории и методам решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами).

М. п.- раздел науки об исследовании операций (см. Операций исследование), охватывающий широкий класс задач управления, матем. моделями к-рых являются конечномерные экстремальные задачи. Задачи М. п. находят применение в различных областях человеческой деятельности, где необходим выбор одного из возможных образов действий, напр., при решении многочисл. проблем управления и планирования производств, процессов, в задачах проектирования и перспективного планирования.

Наименование "М. п." связано с тем, что целью решения задач является выбор программы действий.

Матем. формулировка задачи М.п.: минимизировать скалярную функцию ц>(х) векторного аргумента х на множестве

Х = {х:g_i(x)>=0, h_i(x) = 0, i=1, 2, ..., k}, где g_i(x) и h_i(x)- также скалярные функции; функцию ф(х) наз. целевой функцией, или функцией цели, множество X - допустимым множеством, решение х* задачи М. п.- оптимальной точкой (вектором).

В М. п. принято выделять следующие разделы. Линейное программирование: целевая функция ф(дг) и ограничения gt(x) и hi (х) линейны; выпуклое программирование: целевая функция и допустимое множество выпуклы; квадратичное программирование: целевая функция квадратична и выпукла, допустимое множество определяется линейными равенствами и неравенствами; дискретное программирование: решение ищется лишь в дискретных, напр., целочисленных, точках множества X; стохастическое программирование: в отличие от детерминированных задач, здесь входная информация носит элементы неопределённости; напр., в стохастич. задачах о минимизации линейной функции

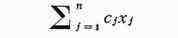
при линейных ограничениях

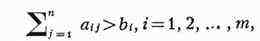
либо всё величины c_j, а_ij, b_i, либо часть из них случайны.

Задачи перечисленных разделов обладают общим свойством: всякая точка локального минимума является оптимальной точкой. Несколько в стороне находятся т. н. многоэкстремальные задачи - задачи, для к-рых указанное свойство не выполняется.

В основе теории выпуклого программирования и, в частности, линейного и квадратичного, лежит теорема Куна - Таккера о необходимых и достаточных условиях существования оптимальной точки х*: для того чтобы точка х* была оптимальной, то есть

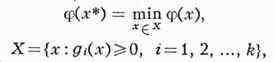
необходимо и достаточно, чтобы существовала такая точка у*= (у₁*, у₂*, ..., у_1k*), чтобы пара точек х*, у* образовывала седло функции Лагранжа

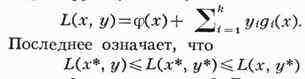
для любых х и всех у^О. Если ограничения g_i(x) нелинейны, то теорема справедлива при нек-рых дополнительных предположениях о допустимом множестве.

Если функции ф(х) и g_i(x) дифференцируемы, то следующие соотношения определяют седловую точку

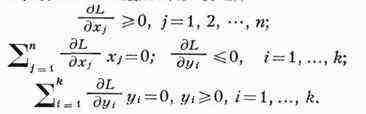
Таким образом, задача выпуклого программирования сводится к решению системы уравнений и неравенств.

На основе теоремы Куна - Таккера разработаны различные итерационные методы минимизации, сводящиеся к поиску седловой точки функции Лагранжа.

В М. п. одно из главных мест принадлежит вычислит, методам решения экстремальных задач. Широким классом таких методов являются методы проектирования. Идея этих методов состоит в следующем.

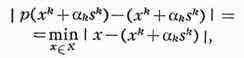
число а_k>0 выбирается при этом так, чтобы ф(x^k+1) < ф(х^k). Существуют различные варианты методов проектирования. Наиболее распространённым из них является метод проекции градиента, когда s^k= - grad ф(х^k). В М. п. доказано, что при определённых условиях на целевую функцию и допустимое множество, последовательность {х^k}, построенная методом проекции градиента, такова, что

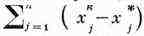
стремится к нулю со скоростью геометрич. прогрессии.

Характерной особенностью вычислит, стороны методов решений задач М. п. является то, что применение этих методов неразрывно связано с использованием электронных вычислит, машин, в первую очередь потому, что задачи М. п., связанные с ситуациями управления реальными системами, являются задачами большого объёма, недоступными для ручного счёта.

Важным направлением исследования в М. п. являются проблемы устойчивости. Здесь существ, значение имеет изучение класса устойчивых задач - задач, для к-рых малые возмущения (погрешности) в исходной информации влекут за собой малые возмущения и в решении. В случае неустойчивых задач большая роль отводится процедуре аппроксимации неустойчивой задачи последовательностью устойчивых задач - т. н. процессу регуляризации.

М. п. как наука сформировалось в 50-70-х гг. 20 в. Это обусловлено главным образом развитием электронных вычислит, машин, а следовательно, с возможностью проводить матем. обработку больших потоков информации, и на этой основе решать задачи управления и планирования, где применение матем. методов связано в первую очередь с построением матем. моделей и соответствующих им экстремальных задач, в том числе задач М. п.

Лит.: Зуховицкий С. И., Авдеева Л. И., Линейное и выпуклое программирование, 2 изд., М., 1967; Xедли Дж., Нелинейное и динамическое программирование, пер. с англ., М., 1967.

В. Г. Карманов.