ЛЯПУНОВА ТЕОРЕМА в теории вероятностей, теорема, устанавливающая нек-рые весьма общие достаточные условия для сходимости распределения сумм независимых случайных величин к нормальному закону. Сформулирована и доказана А. М. Ляпуновым в 1901. Л. т. завершает исследования П. Л. Чебышева, А. А. Маркова (старшего) и самого А. М. Ляпунова в этом основном для всей теории вероятностей направлении. Точная формулировка Л. т. такова: пусть независимые случайные величины X₁,..., Х_n, . . . имеют конечные математические ожидания ЕХ_k, дисперсии DX_k и при б > 0 абсолютные моменты Е|Х_k - ЕХ_k|^2+б и пусь В_n =

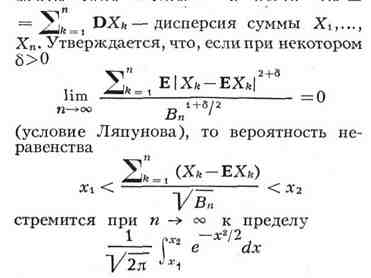
равномерно относительно всех значений х₁ и х₂ Ляпунов дал также оценку скорости сходимости в Л. т. В дальнейшем были установлены условия, расширяющие условие Ляпунова и являющиеся не только достаточными, но в нек-ром смысле необходимыми. См. Предельные теоремы теории вероятностей.

Лит.: Ляпунов А. М., Новая форма теоремы о пределе вероятности, Собр. соч., т. 1, М., 1954, с. 157; Бернштейн С. Н., Теория вероятностей, 4 изд., М.- Л., 1946, с. 275.

А. В. Прохоров.