ЛИШАЙНИКОВЫЕ КИСЛОТЫ, обширная группа органич. соединений, содержащихся в лишайниках. Встречаются во мн. родах лишайников (Ramalina, Evernia, Cladonia, Anzia и др.). Обычно для каждого вида лишайников характерно неск. определённых Л. к., что может служить систематич. (таксономич.) признаком. Водные экстракты из лишайников издавна применялись в нар. медицине, т. к. для большинства Л. к. характерна антибиотич. активность. Для химич. строения всех Л. к. характерно наличие двух остатков полизамещённых фенолов или фенолкарбоновых к-т, связанных друг с другом в различных комбинациях.

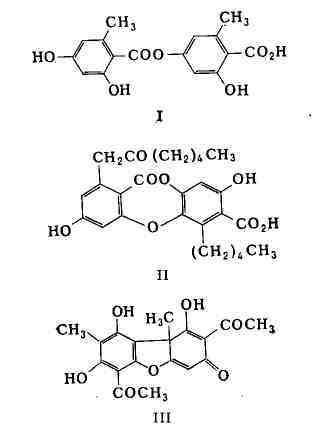
К структурному типу депсидов относятся антибиотики сферородин, леканоровая (I), акациевая, рамалиноловая и др. к-ты. Простейший представитель Л. к. структурного типа депсидонов - антибиотик физодовая к-та (И). К структурному типу дибензофурана относится широко распространённая в лишайниках усниновая к-та (III) - эффективный антибиотик, используемый при лечении кожных заболеваний и столбняка. Все эти типы Л. к. биосинтезируются целиком из остатков уксусной к-ты; большинство из них активно против микобактерий. К четвёртому структурному типу Л. к. (1,4-д ифенилбутадиена) относятся ядовитые вульпиновая, хризопетраровая и лепрариновая к-ты, а также эпанорин и ризокарповая к-та, содержащие остатки аминокислот лейцина и тирозина.

Лит.: Химия антибиотиков, 3 изд., т. 1, М., 1961, гл. 4 и 7; As a h i n a Y., S h i b a t a S., Chemistry of lichen substances, Tokyo, 1954.

Э. П. Серебряков.

ЛИШАЙНИЦЫ (Lithosiinae), подсемейство бабочек сем. медведиц. Крылья в размахе до 55 мм, обычно серые, жёлтые или чёрные; передние значительно уже задних. Большинство Л. ведёт ночной образ жизни. Гусеницы с волосистыми бородавками и часто с яркими пятнами на теле; питаются гл. обр. лишайниками, растущими на деревьях и скалах; окукливаются в коконах. Ок. 1000 видов. Наиболее богато представлены в тропич. лесах. В СССР - ок. 100 видов, преим. в лесной зоне.

ЛИ ШАН-ИНЬ (второе имя - Л и И ш а н ь) (813-858), китайский поэт. Оставил мн. стихов, превосходных по форме, но часто трудных для понимания, что отмечалось даже его современниками. Большое место в его творчестве занимают любовная и пейзажная лирика, послания друзьям, обличения чиновников, угнетающих простой народ. Интерес к человеку, его душевным переживаниям, описания быта, характерные для поэзии Л. III.-и., нашли ещё более яркое выражение в его прозаич. "Изречениях", к-рые были высоко оценены Лу Синем.

Соч. в рус. пер., в кн.: Антология китайской поэзии, т. 2, М., 1957; Цзацзуань. Изречения китайских писателей IX-XIX вв., М., 1969.

Лит.: Ф и ш м а н О., Из изречений Ли Шан-иня, "Советское востоковедение", 1956, № 4; Чжунго вэньсюэ ши. Бэйцзин Дасюэ, т. 2, Пекин, 1959, с. 254-64; L i n J. J. Y., The poetry of Li Shang-yin, Chi.- L., 1969.

ЛИШЕВ Всеволод Всеволодович [25.9 (7.10). 1877, Петербург,- 15.8.1960, Ленинград], советский скульптор, нар. худ. СССР (1957), действит. чл. АХ СССР (1949). Учился в АХ (1906-13) у Г. Р. Залемана и В. А. Беклемишева. Преподавал в АХ (1916-29; 1947-60; проф. с 1948). Ученики: Н. В. Томский, В. И. Ингал, М. Ф. Бабурин и др. В своём творчестве (тщательно моделированные портреты, памятники, жанровые композиции) Л. развивал традиции рус. академич. школы кон. 19 - нач. 20 вв. Произв.: портреты А. П. Ханжонкова (бронза, 1926) и Д. И. Менделеева (мрамор, 1952), "Мать" (бронза, 1945-46) - все три в Рус. музее в Ленинграде; пам. Н. Г. Чернышевскому в Ленинграде (бронза, открыт в 1947; модель фигуры для памятника - бронза, 1940, Третьяковская гал.; Гос. пр. СССР, 1942). Награждён орденом Ленина.

Лит.: Бойков В., В. В. Лишев, Л., 1960.

В. В. Лишев.

ЛИШЕНИЕ ПРАВА ЗАНИМАТЬ ОПРЕДЕЛЁННЫЕ ДОЛЖНОСТИ или заниматься определённой деятельностью, в сов. уголовном праве вид наказания, к-рый состоит в лишении осуждённого права занимать конкретно указанные в приговоре должности или заниматься определённой деятельностью в течение назначенного судом срока (не более 5 лет). Минимальный срок этой меры наказания установлен уголовным законодательством союзных республик по-разному: по УК РСФСР (ст. 29), а также по УК большинства др. союзных республик он составляет 1 год.

Такое наказание назначается судом в случаях, когда по характеру совершённых виновным преступлений он не может работать в прежней должности (напр., по ст. 116 УК РСФСР за незаконный аборт врач может быть приговорён к лишению свободы или к лишению права заниматься врачебной деятельностью). Лишение указанных прав может назначаться как в качестве основного, так и дополнительного наказания. Если лишение права назначено в качестве дополнительного к к.-л. другому осн. наказанию (напр., исправительным работам без лишения свободы), срок исчисляется с момента начала отбывания осн. наказания.

ЛИШЕНИЕ РОДИТЕЛЬСКИХ ПРАВ, см. в ст. Родительские права и обязанности.

ЛИШЕНИЕ СВОБОДЫ, вид уголовного наказания, заключающийся в принудит, изоляции преступника от общества. Отбывается в специально предназначенных для этого гос-вом местах заключения. По сов. уголовному праву Л. с. может назначаться только по приговору суда лицу, виновному в совершении преступления, на срок от 3 мес. до 10 лет, а в отд. случаях, предусмотренных законом, на срок не св. 15 лет (лицу, не достигшему до совершения преступления 18-летнего возраста, может быть назначено Л. с. на срок не более 10 лет). Л. с. связано с ограничениями прав осуждённых в соответствии с приговором суда и режимом отбывания данного вида наказания (напр., заключённые лишены свободы передвижения). Как правило, приговор суда о Л. с. отбывается в исправительно- трудовой колонии (несовершеннолетние - в воспитательно-трудовой колонии). Л. с. в виде тюремного заключения может быть назначено особо опасным рецидивистам либо лицам, совершившим по достижении 18-летнего возраста особо опасные гос. преступления или иные тяжкие преступления и осуждённым на срок св. 5 лет (см. Тюрьма, Тюремное заключение).

Законодательство зарубежных социалистич. гос-в устанавливает меру наказания в виде Л. с., исходя из тех же принципов, что и сов. законодательство. В законах социалистич. гос-в устанавливаются предельные сроки Л. с. (напр., в Болгарии, Венгрии, ГДР, Польше, Чехословакии - максимально 15 лет и лишь в нек-рых случаях, указанных в законе,- 20 лет), основания его применения и порядок исполнения. Л. с. назначается судом, как правило, за тяжкие преступления, а также злостным рецидивистам.

Законодательство большинства бурж. гос-в предусматривает в качестве меры наказания Л. с. в нескольких формах (тюремное заключение, арест и др.). Для бурж. права характерно установление длит, сроков Л. с., в т. ч. и бессрочное заключение (напр., бессрочное заключение во Франции, пожизненное заключение в США). Такие длит, сроки Л. с. соответствуют целям применения наказания в бурж. гос-вах - причинение физич. и моральных страданий осуждённым. Хотя бурж. гос-ва формально провозгласили принцип равенства всех граждан перед законом, для осуждённых из числа господствующего класса применяется особый режим Л. с. В США, напр., существует т. н. honor system - направление заключённых в спец. открытые места заключения со смягчённым режимом.

ЛИ ШИ-МИНЬ (храмовое имя - Т а й ц з у н) (23.1.599-10.7.649), китайский император (с 627) династии Таи. Отстранил от власти своего отца Ли Юаня. Сделал нек-рые уступки крестьянству, мелким и средним феодалам, купечеству. При Л. Ш.-м. завершается складывание феод, централизованного гос-ва. Этому способствовали реорганизация гос. аппарата, введение ооязат. гос. экзаменов для отбора на чиновничьи должности, укрепление армии, составление (с 631) кодекса законов. Л. Ш.-м. вёл завоеват. войны с Когурё, гос-вами к С.-З. от танских владений и др.

"ЛИШНИЙ ЧЕЛОВЕК", социально-психологич. тип, запечатленный в рус. лит-ре 1-й пол. 19 в.; его гл. черты: отчуждение от офиц. России, от родной среды (обычно - дворянской), чувство интеллектуального и нравств. превосходства над ней и в то же время - душевная усталость, глубокий скептицизм, разлад слова и дела. Наименование "Л. ч." вошло во всеобщее употребление после "Дневника лишнего человека" (1850) И. С. Тургенева; сам же тип сложился раньше: первое законченное воплощение - Онегин ("Евгений Онегин" А. С. Пушкина), затем Печорин ("Герой нашего времени" М. Ю. Лермонтова), Бельтов ("Кто виноват?" А. И. Герцена), тургеневские персонажи: Рудин ("Рудин"), Лаврецкий ("Дворянское гнездо") и др. Черты духовного облика "Л. ч." (подчас в усложнённом и изменённом виде) прослеживаются в лит-ре 2-й пол. 19 - нач. 20 вв. (в произв. М. Е. Салтыкова-Щедрина, Л. Н. Толстого, А. П. Чехова, вплоть до А. И. Куприна, В. В. Вересаева, М. Горького). Типология "Л. ч." сказалась в лирике (Лермонтов, Н. П. Огарёв). В зап.-европ. лит-ре "Л. ч." в известной мере близок герой, вызванный к жизни "длительным похмельем" (см. К, Маркс, в кн.: Маркс К. и Энгельс Ф., Соч., 2 изд., т. 8, с. 122) после бурж. революции 18 в., разочарованием в социальном прогрессе ("Адольф" Б. Констана, "Исповедь сына века" А. де Мюссе). Однако противоречия рус. действительности, контраст "цивилизации и рабства" (см. А. И. Герцен, Собр. соч., т. 7, 1956, с. 205), неразвитость обществ, жизни выдвинули "Л. ч." на более видное место, обусловили повышенный драматизм и интенсивность его переживаний. На рубеже 50-60-х гг. революц. демократы Н. Г. Чернышевский и Н. А. Добролюбов резко критиковали "Л. ч.", его нерешительность и пассивность, вместе с тем неправомерно сводя содержание проблемы "Л. ч." к теме либерализма. С переоценкой "Л. ч." выступил и Ф. М. Достоевский, осудив его индивидуализм и оторванность от нар. почвы. Лит. образ "Л. ч.", возникнув как переосмысление романтич. героя (Дж. Байрон, Пушкин), складывался под знаком реалистич. портретизации, выявления разности между персонажем и автором. Существенным в теме "Л. ч." был отказ от просветит, установок во имя беспристрастного анализа "истории души человеческой" (Лермонтов), что создавало почву для глубокого психологизма и последующих завоеваний реализма.

Лит.: Чернышевский Н. Г., Русский человек на rendez-vous, Полн. собр. соч., т. 5, М., 1950; Г о н ч а р о в И. А., "Мильон терзаний", Собр. соч., т. 8, М., 1952.

Ю. В. Манн.

ЛИ ЮАНЬ (храмовое имя - Гао-цзу) (566-25.6.635), китайский император в 618-626, основатель династии Тан. Крупный феодал, из провинции Шаньси. Воспользовавшись ослаблением власти династии Суй в результате многочисл. крест. восстаний и феод, междоусобиц, в 617 захватил столицу Чаньань, где был объявлен в 618 императором. Вёл вместе с сыном Ли Ши-минем войны за подчинение всей страны. Стремясь прекратить крест, восстания, объявил об уменьшении налогового бремени. Был отстранён от власти Ли Ши-минем.

ЛИ ЮАНЬ-ХУН (19.10.1864, у. Хуанпи, пров. Хубэй,- 3.6.1928, Тяньцзинь), китайский воен. и политич. деятель. Накануне бурж. Синьхайской революции (1911 -13) командир бригады кит. Новой армии, сформированной и обученной по европ. образцу. 11 окт. 1911, во время Учинского восстания, революц. солдаты и офицеры силой заставили Л. Ю.-х. возглавить воен.-революц. пр-во провинции Хубэй. Заняв этот пост, он проводил политику в интересах кит. контрреволюции. Был вице-президентом в пр-вах Сунь Ят-сена и Юань Ши-кая (3 янв. 1912-6 июня 1916). Президент Кит. республики с 7 июня 1916 до 1 июля 1917 и с 11 июня 1922 до 13 июня 1923. После 1923 отошёл от политической деятельности.

ЛИ ЮЙ (другие имена- Ли Хоучжу, Ли Чун-гуан) (937-15.8.978), китайский поэт. Последний император (961-976) династии Южная Тан. Мастер лирич. романсов малой формы - с ы. Лучшие из них ("Красавица Юй", "Смотрю на прибрежные розы", "Ночной крик ворона" и др.) были созданы в ссылке после того, как Л. Ю. лишился трона. В камерных по преимуществу стихах Л. Ю. простота нар. песни сочетается с меткими сравнениями и поэтич. параллелями.

Соч.: Ли Цзин Ли Юй цы, Пекин, 1958; в рус. пер., в кн.: Антология китайской поэзии, т. 3, М., 1957.

ЛИ ЮЙ (1611, Жугао, пров. Цзянсу,- 1679 или 1680, Ханчжоу), китайский писатель, теоретик театра. Автор сб. повестей "Немые пьесы" и "Двенадцать теремов", в к-рых нередко пародируются ср.-век. темы и сюжеты. В романе "Подстилка из плоти" Л. Ю. утверждает естественность человеческого поведения и чувства. Известен также как драматург (сб. "Десять пьес") и особенно как теоретик драмы и театр, иск-ва (главы трактата "Случайные заметки праздного", 1671). Призывал к освобождению драмы от традиционных трафаретов, подчёркивал подчинённость описываемого в пьесе её осн. идее, ратовал за доступность пьес для любого, в т. ч. необразованного, зрителя. Издал и прокомментировал Троецарствие и др. классич. эпопеи.

Соч.: Ли Юй цюань цзи, т. 1 - 15, Тайбэй, 1970; The before midnight scholar (Jou Pu Tuan), transl. by R. Martin from the german version by F. Kuhn, L., 1967.

Лит.: Martin H., Li Li-weng uber das Theater, Heidelberg, 1966.

ЛЛАНВИРНСКИЙ ЯРУС, лланвирн [от назв. нас. пункта Лланвирн (Llanvirn), Уэльс, Великобритания], третий снизу ярус ордовикской системы (периода). Выделен в 1881 англ, геологом Г. Гиксом в графстве Пембрукшир (Великобритания). В типовом разрезе сложен глинистыми сланцами и пепловыми туфами и расчленён по граптолитам на 2 зоны: Didymograptus bifidus и D.murchisoni. Верхняя часть последней содержит конодонты зоны Pygodus serrus. В США, Австралии и на Северо-Востоке СССР Л. я. расчленён на 3 зоны: 1) Didymoraptus bifidus, 2) Isograptus caduceus, 3) Paraglossograptus etheridgei. Отложения Л. я. распространены в ряде стран Зап. Европы (Великобритании, Франции, Швеции, Норвегии, Польше, Чехословакии), в СССР (Эст. ССР, Ленингр. обл., Казах. ССР, Кирг. ССР, на Урале, Северо-Востоке, в Алтае-Саянской обл.), в США, Юж. Америке (Аргентине и др.), КНР, Бирме, Австралии.

ЛЛАНДЕЙЛОВСКИЙ ЯРУС, л л а н д е и л о [от назв. нас. пункта Лландейло (Llandeilo), графство Кармартеншир, Уэльс, Великобритания], четвёртый снизу ярус ордовикской системы (периода). Выделен в 1829 Р. Мурчисоном. В типовом разрезе сложен плитняками, мергелями и известняками, охарактеризованными трилобитами, брахиоподами и конодонтами зон Pygodus anserinus и Amorphognathus tvaerensis. Отложения Л. я. распространены в ряде стран Зап. Европы (Великобритании, Франции, Чехословакии, Польше, Швеции, Норвегии), в СССР (Эст. ССР, Ленингр. обл., на Урале, в Казах. ССР, Кирг. ССР, Южной и Ср. Сибири, на Северо-Востоке), в США, Юж. Америке (Аргентине и др.), Австралии, КНР, Бирме.

ЛЛАНДОВЕРИЙСКИЙ ЯРУС, л л а н д о в е р и [от назв. нас. пункта Лландовери (Llandovery), графство Кармартеншир, Уэльс, Великобритания], первый снизу ярус силурийской системы (периода). Установлен в 1859 Р. Мурчисоном. В типовом разрезе представлен карбонатными осадками преим. с бентосной фауной и редкими граптолитами.

Расчленяется на нижний, средний и верхний лландовери и 11 граптолитовых зон, ограниченных снизу зоной Мопо- graptus persculptus, сверху - зоной М. crenulatus. Отложения Л. я. широко распространены в странах Зап. Европы (Франции, Швеции, ФРГ и др.), в Сев. Африке, Сев. Америке и на терр. СССР, где наиболее полно палеонтологически охарактеризован в Прибалтике, на Сибирской платформе, Урале, в Ср. Азии, Казахстане и на Северо-Востоке.

ЛЛОЙД (Lloyd) Гарольд (20.4.1893, Берчард,- 8.3.1971, Лос-Анджелес, Голливуд), американский киноактёр. Окончил драматич. школу в Сан-Диего. С 1913 снимался в кино. В 1915-17 стала популярна серия короткометражных фильмов с участием Л. об "одиноком Люке", в к-рой сказалось влияние Ч. Чаплина. Позднее сложился комедийный герой Л., получивший мировую известность,- изящный, воспитанный молодой человек, уверенный в себе, с упорством и невозмутимостью добивающийся цели. Наиболее характерные фильмы Л.: "Бабушкин внучек" (1922), "Наконец в безопасности" (1923), "Женобоязнь" (1924). В 1962 вышла на экран сборная программа кинокартин Л. под назв. "Мир комедий Гарольда Ллойда". Был также режиссёром и продюсером.

Лит.: Арнольд и Э., Гарольд Ллойд, в кн.: Комики мирового кино, М., 1966.

ЛЛОЙД (Lloyd) Генри (ок. 1720, Кумбихан, Мерионетшир, Уэльс,- 19.6.1783, Юи, Бельгия), воен. историк и теоретик. По национальности валлиец. С 40-х гг.- во франц. армии, во время Семилетней войны 1756-63 служил в австр., рус. и прус, армиях, во время рус.-тур. войны 1768-74 в рус. армии командовал дивизией; затем жил в Англии, Голландии и Бельгии. Обобщил и изложил в виде определённой системы стратегию совр. ему эпохи. Л.- один из первых воен. писателей, к-рый подчеркнул тесную связь войны с политикой, значение морально-политич. фактора и нац. особенностей. Теоретически обосновал господствовавшую в 18 в. стратегию, основанную на магазинной системе снабжения; ввёл понятия: базис воен. действий (пункт, где находятся гл. магазины) и операционная линия (путь от базиса до цели действий), предложил методы ведения наступат. и оборонит, войн. Теория Л. содержала значит, элемент догматизма и отличалась непоследовательностью.

Соч.; A political and military rhapsody on the invasion and defence of Great Britain and Ireland, L., 1.790; History of the late war in Germany between the King of Prussia and the empress of Germany and her allies, v. 1-2, L., 1781-90.

ЛЛОЙД (Corporation of Lloyd's), англ. страховое объединение, одна из важнейших англ, монополий, тесно связанная с крупными пром. монополиями и банками Великобритании и др. капиталистич. стран. Л. возник в кон. 17 в. и получил название от имени Э. Ллойда, владельца кофейной в Лондоне, где заключались сделки морского страхования. Устав Л. был утверждён в 1871 законом о Л. (Lloyd's Act). В дальнейшем он претерпел изменения, вызванные расширением операций. От проведения операций по мор. страхованию Л. с нач. 20 в. перешёл к проведению практически всех видов имущественного, а также личного страхования. В 1970 получил страховых платежей на сумму 786 млн. ф. ст. Л. в значит, степени определяет условия и конъюнктуру по мор. и авиац. страхованию на междунар. рынке. Юридически Л.- ассоциация отд. членов-страховщиков, к-рые объединены в страховые синдикаты. В 1973 насчитывалось св. 7 тыс. чл. Л., входивших в 261 синдикат. Во главе Л. стоит комитет, ведающий только орг. вопросами. Как объединение Л. не несёт ответственности перед страхователями по обязательствам отд. членов. Страхования заключаются от имени членов Л., каждый из к-рых несёт ответственность перед страхователем в пределах той суммы, к-рую принял на свой риск. В отличие от акционеров акц. страховых компаний, ответственность к-рых ограничена их долей в акц. капитале, члены Л. отвечают всем своим имуществом. Страхования могут заключаться только через посредников-брокеров Л. 75% всех операций Л. проводит за границей. Поступления от страховых операций в др. странах в 1972 составили 206 млн. ф. ст., или почти половину всех поступлений англ, страхового рынка от зарубежных операций.

Контакты с др. монополиями внутри страны и с междунар. орг-циями осуществляются через ассоциации Л. Старейшими являются: Ассоциация морских страховщиков Ллойда, Ассоциация страховщиков Ллойда, проводящих страхование от огня, и другие неморские страхования, Ассоциация страховых брокеров Ллойда и др. В нач. 18 в. Л. стал издавать список судов. Впоследствии на этой основе была создана самостоятельная орг-ция с представительством в ней комитета Л.- "Регистр судоходства Ллойда" (Lloyd's Register of Shipping), к-рый наблюдает за постройкой мор. судов, присваивает им класс и ежегодно издаёт список судов мор. торг, флота всех стран с указанием порта приписки. В 1856 Л. совместно с англ. страховыми компаниями создал Спасательную ассоциацию (Salvage Association), с 1867 - Ассоциация для защиты коммерческих интересов в отношении подвергнувшегося крушению и повреждённого имущества.

С. Г. Карпович.

ЛЛОЙД ДЖОРДЖ (Lloyd George) Дэвид (17.1.1863, Манчестер,- 26.3.1945, Лланистамдви, Карнарвоншир), гос. деятель Великобритании, лидер Либеральной партии. Род. в семье школьного учителя. Занимался юридич. практикой. В 1890 впервые избран в парламент. Стремясь завоевать популярность в массах, объявлял себя радикалом и сторонником широких реформ, действуя в то же время в соответствии с коренными интересами англ. империалистич. буржуазии. Л. Д. был наиболее ярким воплощением характерной для англ, политич. жизни системы демагогич. обмана нар. масс буржуазией с целью сохранения над ними её господства. "Я бы назвал эту систему,- писал В. И. Ленин,- ллойд-джорджизмом, по имени одного из самых передовых и ловких представителей этой системы в классической стране „буржуазной рабочей партии", английского министра Ллойд Джорджа. Первоклассный буржуазный делец и политический пройдоха, популярный оратор, умеющий говорить какие угодно, даже ррреволюционные речи перед рабочей аудиторией, способный проводить изрядные подачки послушным рабочим в виде социальных реформ (страхование и т. п.), Ллойд Джордж служит буржуазии великолепно и служит ей именно среди рабочих, проводит ее влияние именно в пролетариате, там, где всего нужнее и всего труднее морально подчинить себе массы" (Поли. собр. соч., 5 изд., т. 30, с. 176). После прихода к власти либералов Л. Д. в 1905-08 мин. торговли и в 1908-1915 мин. финансов. В 1909 с большим демагогич. шумом провёл бюджет, несколько повышавший налог на пустовавшие земли лендлордов и предусматривавший в то же время крупные ассигнования на воен.-мор. вооружения. Во время 1-й мировой войны 1914-18 выступал за ведение борьбы до решительного поражения Германии. В кон. 1916 путём интриг и сговора с консерваторами, ценой раскола Либеральной партии Л. Д. добился падения либерального пр-ва Асквита и возглавил коалиц. пр-во (премьер-мин. до окт. 1922). Л. Д.- один из гл. участников Парижской мирной конференции 1919-20 и творец Версальского мирного договора 1919. С его согласия и при его поддержке была развязана вооруж. интервенция англ, империализма против Сов. России. Однако, осознав вскоре бесперспективность такой политики, Л. Д. взял курс на установление отношений с Сов. Россией, рассчитывая вернуть её в дальнейшем на капиталистич. путь средствами экономич. и политич. давления. Провал политики пр-ва Л. Д. на Бл. Востоке, где оно организовало в 1919-20 войну против нац.-освободит, движения в Турции, позволил консерваторам устранить Л. Д. от власти и создать чисто консервативное пр-во. Упадок Либеральной партии привёл к падению политич. роли Л. Д., хотя он сохранял до конца жизни известное влияние в стране. После прихода Гитлера к власти в Германии Л. Д. полагал, что герм, нацизм может явиться безвредным для Великобритании антисоветским орудием. Убедившись в обратном, стал активно выступать за англо-советское соглашение в целях пресечения герм. агрессии. В 1945 получил титул графа. Портрет стр. 582.

Соч. в рус. пер.: Военные мемуары, т. 1-6, М., 1934-37; Правда о мирных договорах, т. 1 - 2, М., 1957.

Лит.: Виноградов К. Б., Д. Ллойд Джордж, М., 1970; Owen F., Tempestuous journey. Lloyd George, his life and times, L., 1954; Beaverbrook W. М. А., The decline and fall of Lloyd George, L., 1963.

В. Г. Трухановский.

ЛЛОЙДИЯ (Lloydia), род многолетних растений сем. лилейных. Небольшие луковичные травы с узколинейными листьями. Цветки мелкие, белые или жёлтые, одиночные, реже их 2-3; околоцветник воронковидный, из 6 неопадающих листочков. Плод - коробочка. Ок. 20 видов в арктической и умеренной обл. Сев. полушария. В СССР 3 вида, в т. ч. Л. поздняя (L. serotina) - арктоальпийский вид, встречающийся в Арктике, Карпатах, на Кавказе, в Сибири, Ср. Азии и на Д. Востоке. Растёт в тундрах, на альпийских лугах, по каменистым склонам.

"ЛЛОЙДС БАНК" (Lloyds Bank), один из крупнейших акц. коммерч. банков Великобритании. Входит в "Большую четвёрку", бывшую до 1968 ".Большой пятёркой*. Осн. в Бирмингеме в 1765, под наименованием "Тейлор энд Ллойд". С 1889 стал называться "Л. б.". За время своего существования поглотил более 50 банков. "Л. б." стоит во главе группы принадлежащих ему дочерних банков и финанс. компаний внутри страны и за её пределами ("Льюис банк", "Ллойде банк проперти компани", "Ллойде ассошиэйтед эйр лизинг" и т. д.). Участвует в капиталах ряда крупных банков и финанс. компаний. Непосредственно и через систему участия "Л. б." связан с металлургич. и машиностроит. пром-стью, в частности с автомобиле- и самолётостроением, с отраслями нефтеперерабатывающей пром-сти и пароходными компаниями. Через дочерний "Льюис банк" "Л. б." контролирует сеть крупнейших универсальных магазинов в стране. В 1970-71 в результате слияния принадлежавшего "Л. б." "Ллойде банк Юроп" с Банком Лондона и Южной Америки (в к-ром "Л. б." принадлежало ок. 25% капитала) был образован крупный междунар. банк "Ллойде энд Болса интернэшонал банк", в к-ром "Л. б." получил контрольный пакет акций, а вместе с ним и доступ в зап.-европ. и лат.-амер. страны. "Л. б." производит все виды банковских операций. Поддерживает корреспондентские отношения с осн. банками практически всех стран, в т. ч. и социалистических. Имеет (1972) в стране ок. 2,5 тыс. отделений. Общая сумма баланса "Л. б." на 1 янв. 1973 составляла (в млн. ф. ст.) 30/0, капитал и резервы 308, сумма депозитов и текущих счетов 2734.

С. Л. Аверина.

ЛО (Law) Джон (21.4.1671, Шотландия,- 21.3.1729, Венеция), шотландский финансист, создатель т. н. системы Ло, к-рая была основана на выпуске в обращение необеспеченных бум. денег. Считая, что бум. деньги сами по себе обладают определённой ценностью, Л. утверждал, что их усиленный выпуск благотворно скажется на деловой активности и увеличении богатства нации. Предложение Л. нашло поддержку в придворных кругах Франции, находившейся накануне финансового краха. В 1716 был создан частный банк (в 1718 преобразован в государственный), бумаги к-рого гарантировались именем короля, а Л. стал министром финансов Франции. Однако вследствие чрезмерного выпуска бум. денег, не обеспеченных золотом и серебром, в 1720 гос. банк лопнул, и Л. бежал за границу. "Система Ло" сыграла определённую роль в зарождении учения физиократов (см. Физиократы). "Возникновение физиократии было связано как с оппозицией против кольбертизма, так и, в особенности, со скандальным крахом системы Ло" (Маркс К., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 26, ч. 1, с. 31).

Соч.: Oeuvres completes, publ. par P. Harsin, v. 1 - 3, P., 1934.

Лит.: Аникин А. В., Юность науки, М., 1971.

В. И. Незнанов.

ЛО (Lot), река на Ю.-З. Франции, правый приток Гаронны. Дл. 480 км, пл. басс. 11,2 тыс. км². Берёт начало на зап. склонах Севенн, пересекает в узкой долине юж. часть Центр. Франц. массива, в низовьях течёт по Гароннской низм. Питание преим. дождевое, половодье в марте - апреле, межень в июле - сентябре. Подъём уровня при паводках 3-5 м. Ср. расход воды в устье 180 м³/сек. Судоходна ниже впадения р. Трюйер. На Л.- гг. Каор, Вильнёв.

К ст. Лишайники: 1 - ксантория постенная (Xanthoria parietma); 2 - фисция звёздчатая (Physcia stellaris); 3 - цетрария сосновая (Cetraria pinastri); 4 - графис письменный (Graphis scripta); 5 - кладония красноголовая (Cladonia сосcifera); 6 - гипогимния вздутая (Hypogymnia physodes); 7 - пармелия оливковая (Parmelia olivacea); 8 - псора обманчивая (Psora decipiens); 9 - ризокарпон географический (Rhizocarpon geographicum); 10 - леканора буроватая (Lecanora subfuscata); 11 - гематомма ветровая (Haematomma ventosum); 12 - хенотека золотистоголовая (Chaenotheca chrysocephala).

К ст. Лишайники: 1 - кладония оленья, "олений мох" (Cladonia rangiferina); 2 - кладония бахромчатая (С. fimbriata); 3 - пельтигера собачья (Peltigera canina); 4 - аспицилия блуждающая, "лишайниковая манна" (Aspicilia vagans); 5 - уснея цветущая (Usnea florida); 6 - лобария лёгочная (Lobaria pulmonaria); 7 - умбиликария цилиндрическая (Umbilicaria cylindrica); 8 - цетрария исландская, "исландский мох" (Cetraria islandica); 9 - веррукария известняковая (Verrucaria calciseda); 10 - пертузария гладкослоевищная (Pertusaria leioplaca); 11 - сферофор шаровидный (Sphaerophorus globosus); 12 - эверния сливовая, "дубовый мох" (Everma prunastri).

ЛО (Lot), департамент на Ю.-З. Франции, в басс. pp. Ло и Дордонь, частично на Центр. Франц. массиве, частично на плато Керси. Пл. 5,2 тыс. км². Нас. 150 тыс. чел. (1972). Адм. ц.- г. Каор (Кагор). Агр. р-н; овцеводство, плодоводство. Текст, и лесообрабат. пром-сть.

ЛО И ГАРОННА (Lot-et-Garonne), департамент на Ю.-З. Франции, на Гароннской низменности. Пл. 5,4 тыс. км². Нас. 292 тыс. чел. (1972). Адм. ц.- г. Ажен. Агр. р-н (посевы зерновых, табака; огородничество, садоводство и виноградарство). Пищевая пром-сть.

ЛОА (Loa), река в сев. части Чили. Дл. ок. 400 км. Берёт начало в Зап. Кордильере, в ср. течении пересекает пустыню Атакаму, впадает в Тихий ок. Питание преим. грунтовое. Колебания стока незначительны. Ср. расход воды по выходе из гор 6 м³/сек., в ниж. течении - 4 м³/сек. Используется для орошения. Воды родников в басс. Л.- осн. источник водоснабжения гг. Чукикамата, Калама, Антофагаста и др.

ЛОБАН (Mugil cephalus), рыба сем. кефалей. По бокам тела 12 буроватых полос. Дл. тела до 75 см, весит до 3,5 кг. Широко распространён в тропич. морях. В СССР обитает в Чёрном, Азовском, реже в Японском морях. Морская, стайная, подвижная рыба. Заходит в опреснённые участки моря (лиманы и лагуны). Половой зрелости достигает на 6-8-м году жизни. Нерест порционный в мае - сентябре, икра пелагическая. Питается обрастаниями, мелкими беспозвоночными. Промысловая рыба. Перспективный объект лиманного рыбоводства.

Лит.: Никольский Г. В., Морская ихтиология, 3 изд., М., 1971.

ЛОБАНОВ Андрей Михайлович [28.7 (10.8). 1900, Москва,- 18.2.1959, там же], советский режиссёр, нар. арт. РСФСР (1947. В 1922 окончил школу 2-й студии МХАТ. В 1924-25 актёр Театра им. В. Ф. Комиссаржевской в Москве. В 30-40-х гг. режиссёр Театра-студии под рук. Р. Н. Симонова, затем художеств. руководитель Моск. театра для детей; ставил спектакли в театрах Революции, Сатиры. В 1944-58 гл. режиссёр Театра им. М. Н. Ермоловой. Первая крупная режиссёрская работа Л. в Театре-студии - "Таланты и поклонники" Островского (1931). Спектакли Л. в Театре им. М. Н. Ермоловой - "Дачники" (1949), "Достигаев и другие" (1952) Горького, "Бешеные деньги" Островского (1945) и в Театре Сатиры - "На всякого мудреца довольно простоты" Островского (1958) - стали принципиальными завоеваниями сов. театра. Тяготение к точным жанровым зарисовкам сочеталось в них с подлинно современной трактовкой конфликта, сатирич., иногда гротескной заострённостью в передаче картин дореволюц. России. Большое внимание уделял Л. сов. драматургии. Одной из лучших режиссёрских работ Л. была "Таня" Арбузова (1939, Театр Революции). Великой Отечеств, войне и послевоен. периоду поев, спектакли "Старые друзья" Малюгина (1946), "Люди с чистой совестью" по Вершигоре, "Спутники" Пановой и Дара (оба в 1947), "Счастье" Павленко (1948). С 1933 вёл педагогич. работу в ГИТИСе (с 1948 - проф.). Гос. пр. СССР (1946). Награждён орденом Трудового Красного Знамени и медалями.

Соч.: Мысли о режиссуре, в сб.; Режиссёрское искусство сегодня, М., 1962.

Лит.: Блок В., Репетиции Лобанова, М., 1962.

И. В. Холмогорова.

ЛОБАНОВ Павел Павлович [р. 2(15).1902, дер. Старо, ныне Дмитровского р-на Моск. обл.], советский гос. деятель, учёный-экономист в области с. х-ва, акад. ВАСХНИЛ (1948), президент ВАСХНИЛ (1956-61 и с 1965). Герой Социалистич. Труда (1971). Чл. КПСС с 1927. В 1925 окончил Моск. с.-х. академию им. К. А. Тимирязева. В 1936-37 зав. кафедрой в Моск. ин-те землеустройства. В 1937 ректор Воронежского с.-х. ин-та. Зам. наркома (1937-38) и нарком (1938) земледелия РСФСР, нарком зерновых и животноводческих совхозов СССР (1938-46). 1-й зам. министра с. х-ва СССР (1947-53). 1-й зам. пред. Сов. Мин. РСФСР и министр с. х-ва РСФСР (1953-55). Зам. пред. Сов. Мин. СССР (1955-56). Зам. пред. Госплана СССР (1961).

На 18-м съезде КПСС избран членом Центр, ревизионной комиссии. Делегат 20, 23 и 24-го съездов КПСС. На 20-м съезде КПСС - канд. в члены ЦК КПСС. В 1956-62 пред. Совета Союза Верх. Совета СССР. Деп. Верх. Совета СССР 4, 5, 7, 8-го созывов и деп. Верх. Совета РСФСР 1-4-го созывов. Почётный акад. Академии с.-х. наук ГДР (1968) и Болгарской АН (1967), иностр. член Польской АН (1971). Почётный член Королевского с.-х. об-ва Великобритании (1968).

Осн. труды по системам ведения с. х-ва в различных природно-экономич. зонах, интенсификации с. х-ва нечернозёмной зоны, целинных и залежных земель. Награждён 2 орденами Ленина, орденом Октябрьской Революции, орденом Трудового Красного Знамени и медалями.

ЛОБАНОВА-ЯМАГАТА ПРОТОКОЛ 1896 по корейскому вопросу, подписан в Москве 28 мая (9 июня) министром иностр. дел России А. Б. Лобановым-Ростовским и представителем Японии А. Ямагата. Протокол подводил итоги рус.-япон. переговоров после убийства япон. агентами в окт. 1895 корейской королевы и бегства короля в здание рус. миссии. Обе стороны договорились о возвращении короля. Документ предусматривал в случае необходимости совместное рус.-япон. содействие Корее в получении иностр. займов, а также консультации между Россией и Японией по всем вопросам, к-рые могут возникнуть в будущем в Корее. По существу это соглашение отразило стремление царской России ограничить япон. влияние в Корее, ставшее преобладающим после японо-кит. войны 1894-95. Однако в 1898 соглашение было дополнено новым протоколом, согласно к-рому Россия обязалась не препятствовать развитию японо-корейских торг, и пром. связей.

ЛОБАНОВ-РОСТОВСКИЙ Алексей Борисович [18(30). 12.1824, Воронежская губ.,- 18 (30).8.1896, ст. Шепетовка, ок. Ровно, похоронен в Москве], князь, русский дипломат. На дипломатич. службе с 1844. Был послом в Турции (1859-63, 1878), Великобритании (1879-82), Австро-Венгрии (1882-95), Германии (1895), товарищем министра внутр. дел (1867- 1878); министром иностр. дел (1895-1896). Вместе с С. Ю. Витте - инициатор дипломатич. выступления России, Германии и Франции, заставивших Японию смягчить условия Симоносекского договора 1895, к-рым завершилась её война с Китаем. Участвовал в составлении рус.-кит. договора о союзе и строительстве Кит.-Вост. ж. д. и подписании соглашения с Японией (см. Лобанова-Ямагата протокол 1896). Занимался собиранием и изданием рус. архивных история, материалов 18-19 ъв , а также генеалогией рус. дворянских родов. Сотрудничал в журн. "Русская старина" и "Русский архив".

ЛОБАНЬ, река в Кировской обл. РСФСР, прав. приток р. Кильмезь (басс. р. Вятка). Дл. 169 км, пл. басс. 2810 км². Образуется при слиянии pp. Белая и Чёрная Л. Течёт на Ю.-Ю.-В. по заболоченной низменности. Питание преим. снеговое. Ср. расход в 56 км от устья 14,3 м³/сек, наибольший 625 м³/сек. Сплавная.

ЛОБАРИЯ (Lobaria), род лишайников сем. стиктовых. Имеют вид крупных листовидных, по краям выемчатых пластинок. Растут на коре деревьев, реже на др. субстратах, преим. в тёплых странах,. Известно ок. 80 видов; в СССР ок. 15 видов, встречаются гл. обр. на Д. Востоке. Наиболее распространена т. н. лёгочная Л. (L. pulmonaria) с сетчато-ямчатой верхней стороной, несколько напоминающей лёгкое. Используется в парфюмерной пром-сти.

ЛОБАСТЫЕ БЫКИ (Bibos), род (подрод) крупных жвачных млекопитающих сем. полорогих. Близки к настоящим быкам и буйволам. Холка приподнята. Лоб широкий плоский (отсюда назв.). Рога имеются у самцов и самок, слегка сплюснуты сверху вниз, направлены в стороны и назад. Окраска от рыжеватой до тёмно-бурой, почти чёрной; в отличие от остальных быков, у Л. б. ноги в нижней части белые. Распространены Л. б. в Индии, Индокитае и на Зондских о-вах. Обитают в равнинных лесах с полянами. Держатся небольшими группами. Питаются преим. травами, частично - листвой. Самки рождают по 1 телёнку. Численность Л. б. падает, нек-рые виды очень редки. 3 вида: гаур (одомашненная форма - гаял), бантенг (домашняя форма - балийский скот) и купрей.

Лит.: Жизнь животных, т. 6, М., 1971.

ЛОБАЧЕВСКИЙ Николай Иванович [20.11 (1.12).1792, Н. Новгород, ныне г. Горький,- 12 (24).2.1856, Казань], русский математик, создатель неевклидовой геометрии, мыслитель-материалист, деятель университетского образования и нар. просвещения. Род. в семье мелкого чиновника. Почти всю жизнь Л. провёл в Казани. Там он учился в гимназии (1802-07) на казённом содержании, затем в Казанском ун-те (1807-11). Рано обнаружил выдающиеся способности, по окончании ун-та получил степень магистра (1811) и был оставлен при ун-те; в 1814 стал адъюнктом, в 1816 - экстраординарным и в 1822 - ординарным профессором. Несмотря на реакционную обстановку, сложившуюся в годы попечительства М. Л. Магницкого, Л. вёл напряжённую научную и педагогич. работу (преподавал математику, физику и астрономию), закупил в столице оборудование для физ. кабинета и книги для библиотеки, а затем возглавлял её 10 лет (с 1825); Л. заведовал обсерваторией; избирался деканом физико-математич. факультета (1820-22, 1823-25). Но столкновения с попечителем обострились: Л. отстаивал в преподавании науч. материалистич. взгляды.

В эти годы Л. отыскивал пути строгого построения начал геометрии. Сохранились: студенческие записи его лекций (от 1817), где им делалась попытка доказать постулат параллельности Евклида, но в рукописи учебника "Геометрия" (1823) он уже отказался от этой попытки. В "Обозрениях преподавания чистой математики" на 1822/23 и 1824/25 Л. указал на "до сих пор непобедимую" трудность проблемы параллелизма и на необходимость принимать в геометрии в качестве исходных понятия, непосредственно приобретаемые из природы. Наконец, преодолев тысячелетние традиции, он приходит к созданию новой геометрии - т. н. геометрии Лобачевского. 7 февр. 1826 он представил для напечатания в Записках физ.-матем. отделения сочинение: "Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных" (на франц. яз.). 11 февр. оно было рассмотрено и назначены рецензенты. Сам Л. указывал, что он читал это рассуждение на заседании отделения 12 февр. Но издание не осуществилось. Рукопись и отзывы не сохранились, однако само сочинение было включено Л. в его труд "О началах геометрии" в журн. "Казанский вестник" (1829-30), явившийся первой в мировой литературе публикацией по неевклидовой геометрии. Исходя из поисков безусловной строгости и ясности в началах геометрии, Л. рассматривает аксиому параллельности Евклида как произвольное ограничение, как требование слишком жёсткое, ограничивающее возможности теории, описывающей свойства пространства. Он заменяет эту аксиому требованием более широким и общим, именно: на плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную (по существу не менее чем одна, если учесть предельный случай).

Разработанная Л. новая геометрия существенно отличается от евклидовой геометрии, но при больших значениях входящей в формулы нек-рой постоянной R (радиус кривизны пространства) отклонение становится незначительным (см. Лобачевского геометрия).

В соответствии со своим материалистич. подходом к изучению природы, Л. полагал, что только науч. опыт может выявить, какая из геометрий осуществляется в физ. пространстве. Используя новейшие астрономич. данные того времени, он пришёл к выводу, что число R очень велико и отклонения от евклидовой геометрии если и существуют, то заключены в пределах ошибок измерений. Т. о., была обоснована практич. пригодность евклидовой геометрии. Кроме того, Л. показал, как его геометрию можно применять в др. разделах математики, а именно в математич. анализе при вычислении определённых интегралов.

Доклад Л. совпал по времени с увольнением Магницкого. Л. был высоко оценён новым попечителем - М. Н. Мусиным-Пушкиным. Л. избрали ректором (1827) и за 19 лет руководства ун-том он добился его подлинного расцвета. Программа деятельности Л. отражена в его замечательной речи "О важнейших предметах воспитания" (1828, опубл. 1832), в к-рой обрисован идеал гармонич. развития личности, подчёркнуто обществ, значение воспитания и образования, освещена роль наук и долг учёного перед страной и народом.

В бытность Л. ректором было осуществлено в 1832-40 строительство целого комплекса вспомогательных зданий: библиотека, астрономич. обсерватория, физ. кабинет и хим. лаборатория, анатомич. театр, клиника и др. Он положил начало "Учёным запискам Казанского ун-та" (1834) и развил издательскую деятельность. Уровень научно-учебной работы повысился, контингент студентов возрос. Ун-т стал важным центром востоковедения. Немало сил Л. вкладывал и в улучшение постановки преподавания в гимназиях и училищах округа. В моменты стихийных бедствий (эпидемия холеры в 1830, пожар Казани в 1842) особенно ярко проявилась его забота, об ун-те. Но ректорство не отрывало Л. от преподавания: в разные годы он читал лекции по аналитич. механике, гидромеханике, интегральному исчислению, дифференциальным уравнениям, математич. физике, вариационному исчислению, а в 1838-40 - научно-популярные лекции по физике для населения. Студенты высоко ценили лекции Л.

Однако науч. идеи Л. не были поняты современниками. Его труд "О началах геометрии", представленный в 1832 советом ун-та в Академию наук, получил у М. В. Остроградского отрицательную оценку, а в 1834 в реакц. журн. "Сын отечества" появилась анонимная издевательская статейка. Но Л. не прекратил разработки своей геометрии. Его работы появлялись в 1835-38, а в 1840 в Германии вышла его книга "Геометрические исследования" (на нем. языке). Эта стойкая борьба за науч. истину отличает Л. от двух его современников, тоже пришедших к открытию неевклидовой геометрии. Венг. математик Я. Болъяй опубликовал свой труд позднее Л. (1832). Не встретив поддержки у современников, он не продолжил исследований. Нем. математик К. Ф. Гаусс также владел началами неевклидовой геометрии. Но из опасения встретить непонимание Гаусс не разрабатывал их далее и не опубликовал. Однако, не высказываясь в печати, он высоко оценил труды Л., и по его предложению Л. был в 1842 избран членом- корреспондентом Гёттингенского учёного общества.

Л. получил ряд ценных результатов и в др. разделах математики: так, в алгебре он разработал новый метод приближённого решения уравнений (Лобачевского метод), в математич. анализе получил ряд тонких теорем о тригонометрич. рядах, уточнил понятие непрерывной функции и др.

В 1846 Л. оказался фактически отстранённым от ун-та. Он был назначен помощником нового попечителя (без оплаты) и лишён ректорства. Здоровье его пошатнулось. Но семейное горе - смерть сына, материальные затруднения и развивавшаяся слепота не могли сломить мужества Л. Последнюю работу "Пан- геометрию" он создал за год до смерти, диктуя её текст.

Л. умер непризнанным. Большую роль в признании трудов Л. сыграли исследования Э. Белътрами (1868), Ф. Клейна (1871), А. Пуанкаре (1883) и др. Казанский ун-т и физико-математич. об-во провели большую работу по выявлению значения идей Л. и изданию его геометрич. сочинений. Широкое признание пришло к 100-летнему юбилею Л.- была учреждена международная премия, в Казани открыт памятник (1896).

Соч.: Поли. собр. соч., т. 1-5, М.- Л., 1946-51; Избр. труды по геометрии, М.- Л., 1956.

Лит.: Васильев А. В., Лобачевский, СПБ, 1914; Каган В. Ф., Лобачевский, 2 изд., М,- Л., 1948 (имеется библ.); Лаптев Б. Л., Великий русский математик, "Вестник высшей школы", 1967, № 12; Историко-математические исследования, в. 3, 4, 6, 11, М.- Л., 1950-58 (ряд статей); Модзалевский Л. Б., Материалы для биографии Н. И. Лобачевского, М.- Л., 1948.

Б. Л. Лаптев.

ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ, геометрическая теория, основанная на тех же осн. посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, к-рая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. В Л. г. вместо неё принимается след, аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Казалось бы, эта аксиома противоречит чрезвычайно привычным представлениям. Тем не менее как эта аксиома, так и вся Л. г. имеет вполне реальный смысл (о чём см. ниже). Л. г. была создана и развита Н. И. Лобачевским, к-рый впервые сообщил о ней в 1826. Л. г. наз. неевклидовой геометрией, хотя обычно термину "неевклидова геометрия" придают более широкий смысл, включая сюда и др. теории, возникшие вслед за Л. г. и также основанные на изменении осн. посылок евклидовой геометрии. Л. г. наз. специально гиперболической неевклидовой геометрией (в противоположность эллиптической геометрии Римана) (см. Неевклидовы геометрии, Римана геометрия).

Л. г. представляет теорию, богатую содержанием и имеющую применение как в математике, так и в физике. Историч. её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики вообще (см. Геометрия). С современной точки зрения можно дать, напр., следующее определение Л. г. на плоскости: она есть не что иное, как геометрия внутри круга на обычной (евклидовой) плоскости, лишь выраженная особым образом. Именно, будем рассматривать круг на обычной плоскости (рис. 1) и внутренность его, т. е. круг, за исключением ограничивающей его окружности, назовём "плоскостью". Точкой "плоскости" будет точка внутри круга. "Прямой" будем называть любую хорду (напр., a, b, b', MN) (с исключёнными концами, т. к. окружность круга исключена из "плоскости"). "Движением" назовём любое преобразование круга самого в себя, к-рое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрич. факт, описанный на таком языке, представляет теорему или аксиому Л. г. Иными словами, всякое утверждение Л. г. на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, т. к. через точку О, не лежащую на данной хорде а (т. е. "прямой"), проходит сколько угодно не пересекающих её хорд ("прямых") (напр., b, b'). Аналогично, Л. г. в пространстве может быть определена как геометрия внутри шара, выраженная в соответствующих терминах ("прямые" - хорды, "плоскости" - плоские сечения внутренности шара, "равные" фигуры - те, к-рые переводятся одна в другую преобразованиями, переводящими шар сам в себя и хорды в хорды). Т. о., Л. г. имеет совершенно реальный смысл и столь же непротиворечива, как геометрия Евклида. Описание одних и тех же фактов в разных терминах или, напротив, описание разных фактов в одних и тех же терминах представляет характерную черту математики. Она ясно выступает, напр., когда одна и та же линия задаётся в разных координатах разными уравнениями или, напротив, одно и то же уравнение в разных координатах представляет различные линии.

Возникновение геометрии Лобачевского. Источником Л. г. послужил вопрос об аксиоме о параллельных, к-рая известна также как V постулат Евклида (под этим номером утверждение, эквивалентное приведённой выше аксиоме о параллельных, фигурирует в списке постулатов в "Началах" Евклида). Этот постулат, ввиду его сложности в сравнении с другими, вызвал попытки дать его доказательство на основании остальных постулатов.

Вот неполный перечень учёных, занимавшихся доказательством V постулата до 19 в.: др.-греч. математики Птолемей (2 в.), Прокл (5 в.) (доказательство Прокла основано на предположении о конечности расстояния между двумя параллельными), Ибн аль-Хайсам из Ирака (кон. 10 - нач. 11 вв.) (Ибн аль- Хайсам пытался доказать V постулат, исходя из предположения, что конец движущегося перпендикуляра к прямой описывает прямую линию), тадж. математик Омар Хайям (2-я пол. 11 - нач. 12 вв.), азерб. математик Насирэддин Туей (13 в.) (Хайям и Насирэддин при доказательстве V постулата исходили из предположения, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения), нем. математик К. Клавий (Шлюссель, 1574), итал. математики П. Катальди (впервые в 1603 напечатавший работу, целиком поев, вопросу о параллельных), Дж. Борелли (1658), Дж. Витале (1680), англ, математик Дж. Валлис (1663, опубл. в 1693) (Валлис основывает доказательство V постулата на предположении, что для всякой фигуры существует ей подобная, но не равная фигура). Доказательства перечисленных выше геометров сводились к замене V постулата др. предположением, казавшимся более очевидным. Итал. математик Дж. Саккери (1733) сделал попытку доказать V постулат от противного. Приняв предложение, противоречащее постулату Евклида, Саккери развил из него довольно обширные следствия. Ошибочно признав нек-рые из этих следствий приводящими к противоречиям, Саккери заключил, что постулат Евклида доказан. Нем. математик И. Ламберт (ок. 1766, опубл. в 1786) предпринял аналогичные исследования, однако он не повторил ошибки Саккери, а признал своё бессилие обнаружить в построенной им системе логич. противоречие. Попытки доказательства постулата предпринимались и в 19 в. Здесь следует отметить работы франц. математика А. Лежандра; одно из его доказательств (1800) основано на допущении, что через каждую точку внутри острого угла можно провести прямую, пересекающую обе стороны угла, т. е., как и все его предшественники, он заменил постулат др. допущением. Довольно близко к построению Л. г. подошли нем. математики Ф. Швейкарт (1818)и Ф. Тауринус (1825), однако ясно выраженной мысли о том, что намечаемая ими теория будет логически столь же совершенна, как и геометрия Евклида, они не имели. Вопрос о V постулате Евклида, занимавший геометров более двух тысячелетий, был решён Лобачевским. Это решение сводится к тому, что постулат не может быть доказан на основе др. посылок евклидовой геометрии и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий. Лобачевский сделал об этом сообщение в 1826, а в 1829-30 напечатал работу "О началах геометрии" с изложением своей теории. В 1832 была опубликована работа венгерского математика Я. Болъяй аналогичного содержания. Как выяснилось впоследствии, немецкий математик К. Ф. Гаусс также пришёл к мысли о возможности существования непротиворечивой неевклидовой геометрии, но скрывал её, опасаясь быть непонятым. Хотя Л. г. развивалась как умозрительная теория и сам Лобачевский называл её "воображаемой геометрией", тем не менее именно Лобачевский рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации и тем полностью решён вопрос о её реальном смысле, логич. непротиворечивости.

Интерпретации (модели) геометрии Лобачевского. Л. г. изучает свойства "плоскости Лобачевского"(в планиметрии) и "пространства Лобачевского" (в стереометрии). Плоскость Лобачевского - это плоскость (множество точек), в к-рой определены прямые линии, а также движения фигур (вместе с тем - расстояния, углы и пр.), подчиняющиеся всем аксиомам евклидовой геометрии, за исключением аксиомы о параллельных, к-рая заменяется указанной выше аксиомой Лобачевского. Сходным образом определяется пространство Лобачевского. Задача выяснения реального смысла Л. г. состояла в нахождении моделей плоскости и пространства Лобачевского, т. е. в нахождении таких объектов, в к-рых реализовались бы соответствующим образом истолкованные положения планиметрии и стереометрии Л. г. (об интерпретации вообще см. Геометрия, раздел Истолкования геометрии). Итал. математик Э. Бельтрами в 1868 заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример к-рых представляет псевдосфера (рис. 2). Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, т. е. деформацией, сохраняющей длины, то всякой теореме Л. г. будет отвечать факт, имеющий место на псевдосфере. Т. о., Л. г. получает простой реальный смысл. При этом длины, углы, площади понимаются в смысле естеств. измерения их на псевдосфере. Однако здесь даётся интерпретация только геометрии на куске плоскости Лобачевского, а не на всей плоскости и тем более не в пространстве (в 1901 Д. Гильберт доказал даже, что вообще в евклидовом пространстве не может существовать регулярной поверхности, геометрия на к-рой совпадает с геометрией всей плоскости Лобачевского).

В 1871 Ф. Клейн указал ту модель как всей плоскости, так и пространства Лобачевского, к-рая была описана выше и в к-рой плоскостью служит внутренность круга, а пространством - внутренность шара. Между прочим, в этой модели расстояние между точками А и угол - ещё сложнее.

Позже А. Пуанкаре в связи с задачами теории функций комплексного переменного дал др. модель. За плоскость Лобачевского принимается внутренность круга (рис. 3), прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями - преобразования, получаемые комбинациями инверсий относительно окружностей, дуги к-рых служат прямыми. Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами. Исходя из таких соображений, можно строить модель Л. г. в пространстве.

Коротко модели Клейна и Пуанкаре можно определить так. В обоих случаях плоскостью Лобачевского может служить внутренность круга (пространством - внутренность шара), и Л. г. есть учение о тех свойствах фигур внутри круга (шара), к-рые в случае модели Клейна не изменяются при проективных, а в случае модели Пуанкаре - при конформных преобразованиях круга (шара) самого в себя (проективные преобразования есть те, к-рые переводят прямые в прямые, конформные - те, к-рые сохраняют углы).

Возможно чисто аналитич. определение модели Л. г. Напр., точки плоскости можно определять как пары чисел x, у, прямые можно задавать уравнениями, движения - формулами, сопоставляющими точкам (х, у) новые точки (x', у'). Это будет абстрактно определённая аналитич. геометрия на плоскости Лобачевского, аналогично аналитич. геометрии на плоскости Евклида. Т. к. Лобачевский дал основы своей аналитич. геометрии, то тем самым он уже фактически наметил такую модель, хотя полное её построение выяснилось уже после того, как на основе работ Клейна и других выявилось само понятие о модели. Другое аналитич. определение Л. г. состоит в том, что Л. г. определяется как геометрия риманова пространства постоянной отрицательной кривизны (см. Рима- новы геометрии). Это определение было фактически дано ещё в 1854 Б. Риманом и включало модель Л. г. как геометрии на поверхностях постоянной кривизны. Однако Риман не связал прямо своих построений с Л. г., а его доклад, в к-ром он о них сообщил, не был понят и был опубликован лишь после его смерти (в 1868).

Содержание геометрии Лобачевского. Лобачевский строил свою геометрию, отправляясь от осн. геометрич. понятий и своей аксиомы, и доказывал теоремы геометрич. методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, т. к. именно здесь начинается отличие Л. г. от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, общи обеим геометриям и образуют т. н. абсолютную геометрию, к к-рой относятся, напр., теоремы о равенстве треугольников. Вслед за теорией параллельных строились др. отделы, включая тригонометрию и начала аналитической и дифференциальной геометрии. Приведём неск. фактов Л. г., отличающих её от геометрии Евклида и установленных самим Лобачевским.

1) В Л. г. не существует подобных, но неравных треугольников; треугольники равны, если их углы равны. Поэтому существует абсолютная единица длины, т. е. отрезок, выделенный по своим свойствам, подобно тому как прямой угол выделен своими свойствами. Таким отрезком может служить, напр., сторона правильного треугольника с данной суммой углов.

2) Сумма углов всякого треугольника меньше я и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность я - (a -f- 3 + -у), где а, 3, 7 - углы треугольника, пропорциональна его площади.

3) Через точку О, не лежащую на данной прямой а, проходит бесконечно много прямых, не пересекающих а и находящихся с ней в одной плоскости; среди них есть две крайние b, b', к-рые и наз. параллельными прямой а в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) a общий конец (к-рый по определению модели исключается, так что эти прямые не имеют общих точек) (рис. 1,3). Угол а между прямой b (или b') и перпендикуляром из О на а - т. н. угол параллельности - по мере удаления точки О от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель b с одной стороны (а b' с противоположной) асимптотически приближается к а, а с другой - бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

4) Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, к-рые не достигают другой прямой.

5) Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.

6) Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

7) Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность - предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

8) Длина окружности не пропорциональна радиусу, а растёт быстрее.

9) Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрич. соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Напр., чем меньше треугольник, тем меньше сумма его углов отличается от я; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2я, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы Л. г. переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле "предельный" случай Л. г.

Л. г. продолжает разрабатываться многими геометрами; в ней изучаются: решение задач на построение, многогранники, правильные системы фигур, общая теория кривых и поверхностей и т. п. Ряд геометров развивали также механику в пространстве Лобачевского. Эти исследования не нашли непосредственных применений в механике, но дали начало плодотворным геометрич. идеям. В целом Л. г. является обширной областью исследования, подобно геометрии Евклида.

Приложения геометрии Лобачевского.

Сам Лобачевский применил свою геометрию к вычислению определённых интегралов. В теории функций комплексного переменного Л. г. помогла построить теорию автоморфных функций. Связь с Л. г. была здесь отправным пунктом исследований Пуанкаре, к-рый писал, что "неевклидова геометрия есть ключ к решению всей задачи". Л. г. находит применение также в теории чисел, в её геометрич. методах, объединённых под названием "геометрия чисел" (см. Чисел теория). Была установлена тесная связь Л. г. с кинематикой специальной (частной) теории относительности (см. Относительности теория). Эта связь основана на том, что равенство, выражающее закон распространения света

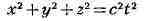
при делении на t², т. е. для скорости света, даёт - уравнение

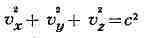
сферы в пространстве с координатами

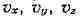
- составляющими скорости по осям x, у, z (в "пространстве скоростей"). Лоренца преобразования сохраняют эту сферу и, т. к. они линейны, переводят прямые пространства скоростей в прямые. Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с, т. е. для скоростей, меньших скорости света, имеет место Л. г.

Замечательное приложение Л. г. нашла в общей теории относительности (см. Тяготение). Если считать распределение масс материи во Вселенной равномерным (это приближение в космич. масштабах допустимо), то оказывается, что при определённых условиях пространство имеет Л. г. Т. о., предположение Лобачевского о его геометрии как возможной теории реального пространства оправдалось.

Лит.: Лобачевский Н. И.. Сочинения по геометрии, М.- Л., 1946-49 (Полн. собр. соч., т. 1-3); Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию ее идей, М., 1956; Александров П. С., Что такое неевклидова геометрия, М., 1950; Д е л о н е Б. Н., Элементарное доказательство непротиворечивости планиметрии Лобачевского, М., 1956; Широков П. А., Краткий очерк основ геометрии Лобачевского, М., 1955; Каган В. Ф., Лобачевский и его геометрия. Общедоступные очерки, М., 1955; его же. Геометрия Лобачевского и ее предистория, М.-Л., 1949 (Основания геометрии, ч. 1); Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971; Погорелов А. В., Основания геометрии, 3 изд., М., 1968; Розенфельд Б. А., Неевклидовы пространства, М., 1969; Нут Ю. Ю., Геометрия Лобачевского в аналитическом изложении, М., 1961; Андриевская М. Г., Аналитическая геометрия в пространстве Лобачевского, К., 1963.

А. Д. Александров.