ЛАПЛАСА АЗИМУТ, геодезич. азимут Л направления на наблюдаемую точку, полученный по его астрономич. азимуту а, исправленному с учётом влияния отклонения отвеса в пункте наблюдения. Астрономич. азимут направления на к.-л. точку в пространстве есть двугранный угол между плоскостью астрономич. меридиана пункта наблюдения и плоскостью, проходящей через отвесную линию в этом пункте и наблюдаемую точку. Л. а. (геодезич. азимут) пространственной точки равен двугранному углу между плоскостью геодезич. меридиана пункта наблюдения и плоскостью, проходящей через нормаль к поверхности референц-эллипсоида в этом пункте и наблюдаемую точку. Для перехода от астрономич. азимута к Л. а. служит формула 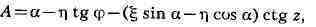в к-рой g и N - составляющие отклонения отвеса в пункте наблюдения в плоскостях меридиана и первого вертикала, Ф - широта этого пункта и z -зенитное расстояние наблюдаемой точки в пространстве. Эта формула при r, близком к 90°, приводит к уравнению Лапласа для определения Л. а.: 
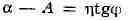
(назв. по имени П. Лапласа, установившего это соотношение ).

Лит.: Красовский Ф. Н., Руководство по высшей геодезии, 2 изд., ч. 2, М-, 1942.

А. А. Изотов.

ЛАПЛАСА ГИПОТЕЗА, космогоническая гипотеза об образовании Солнечной системы - Солнца, планет и их спутников из вращающейся и сжимающейся газовой туманности, высказанная П. Лапласом в 1796 в популярной книге "Изложение системы мира" (т. 1-2). Согласно Л. г., в результате ускорения вращения при сжатии разряженная внешняя часть туманности (протяжённая атмосфера образующегося Солнца) становится всё более сплюснутой, а когда центробежная сила на экваторе стала равной по величине силе тяготения, она приняла чечевице- образную форму. Вещество на остром ребре чечевицы перестало участвовать в дальнейшем сжатии, а оставалось на месте, образуя газовый диск. Затем он разделил- ся на отдельные кольца и вещество каждого кольца собралось в сгусток, превратившийся затем в планету. При сжатии этих сгустков процесс зачастую повторялся, приводя к образованию спутников планет. Центральный сгусток туманности превратился в Солнце.

Л. г. не смогла объяснить медленное вращение Солнца, прямое вращение планет, наличие спутников с обратным движением и спутников, период обращения к-рых меньше периода вращения планеты. Привлечение совр. астрофизич. данных позволило в сер. 20 в. по-новому развить идею Лапласа об отделении вещества от сжимающегося протосолнца в результате наступления ротационной неустойчивости. При этом механизм формирования планет оказался отличным от предполагавшегося Лапласом. Л. г. сыграла выдающуюся роль в истории науки. См. Космогония.

Б. Ю. Левин.

ЛАПЛАСА ЗАКОН, Зависимость перепада гидростатич. давления Дрна'поверх- ности раздела двух фаз (жидкость - жидкость, жидкость - газ или пар) от межфазного поверхностного натяжения а и средней кривизны поверхности е в рассматриваемой точке: Др = p1- р2 = ест, где р1-давление с вогнутой стороны поверхности, р2 - с выпуклой стороны, 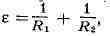 где R1 и R2- радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности в данной точке (см. рис.). Л. з., установленный в 1806 П. Лапласом, определяет величину капиллярного давления и позволяет тем самым записать условия механич. равновесия для подвижных (жидких) поверхностей раздела (см. Капиллярные явления).

Применение закона Лапласа к поверхности раздела вода - пар в капилляре: Др = р1 - р2 ; R1 и R2 - радиусы кривизны в точке О вогнутой поверхности (R1 = ОА и R2 = OB) определяются в двух взаимно перпендикулярных сечениях ACD и ВЕF.

ЛАПЛАСА НЕИЗМЕНЯЕМАЯ ПЛОСКОСТЬ, плоскость, проходящая через центр масс Солнечной системы перпендикулярно вектору момента количества движения. Понятие Л. н. п. было введено в 1789 П. Лапласом, указавшим на преимущества её использования в качестве осн. координатной плоскости при изучении движений тел Солнечной системы: в то время как положения плоскостей эклиптики и экватора непрерывно изменяются, Л. н. п. сохраняет своё положение в пространстве неизменным. Для того чтобы определить положение Л. н. п. относительно плоскости эклиптики, необходимо знать числовые значения масс всех планет. Поскольку с развитием астрономич. исследований эти величины постепенно уточняются, то и параметры, определяющие положение Л. н. п., несколько изменяются. Положение Л. н. п. относительно эклиптики в эпоху 1950,0 определяется след. элементами: эклиптич. долгота точки пересечения с эклиптикой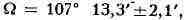 
наклон

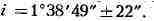
Г. А.Чеботарёв.

ЛАПЛАСА ОПЕРАТОР, лапласиан, дельта-оператор, Д - о п е р а  т о р, линейный дифференциальный оператор, к-рый функции cp(xi,xi,...,x_n) от n переменных Xi,x?,...,Xn ставит в соответствие функцию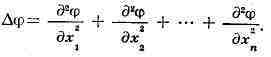 
В частности, для функции Ф(х,у) двух переменных

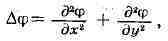
х, у Л. о. имеет вид а для функций одной переменной q>(x) Л. о. совпадает с оператором второй производной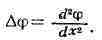
Л. о. встречается в тех задачах матем. физики, где изучаются свойства изотропной однородной среды (распространение света, тепла, движение идеальной несжимаемой жидкости и т. п.). Уравнение Дф = 0 обычно наз. Лапласа уравнением; отсюда и произошло название Л. о.

ЛАПЛАСА ПРЕОБРАЗОВАНИЕ, преобразование, переводящее функцию f(t) действительного переменного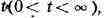
называемую "оригиналом", в функцию
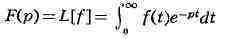(1)
комплексного переменного

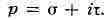
Под Л. п. понимают также не только само преобразование, но и его результат - функцию F(p). Интеграл в правой части формулы (1) наз. интегралом Лапласа. Он был рассмотрен П. Лапласом в ряде работ, к-рые объединены в его книге "Аналитическая теория вероятностей", вышедшей в 1812. Значительно раньше (в 1737) такие интегралы применял к решению дифференциальных уравнений Л. Эйлер. При нек-рых условиях, указанных ниже, Л. п. определяет функцию f(0 однозначно, в простейших случаях - rib формуле обращения: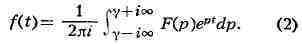 
Л. п. является линейным функциональным преобразованием. Из числа основных формул Л. п. можно отметить следующие: Л.

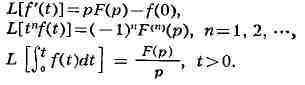
п. в сочетании с формулой (2) его обращения применяется к интегрированию дифференциальных уравнений. В частности, в силу свойства (1) и линейности, Л. п. решения обыкновенного линейного дифференциального уравнения с постоянными коэффициентами удовлетворяет алгебраич. уравнению 1-й степени и может быть, следовательно, легко найдено.Так, если, напр.,


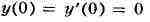
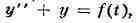
и

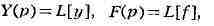
то

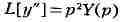
и

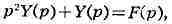
откуда
:
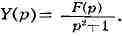Многочисл. задачи электротехники, гидродинамики, механики, теплопроводности эффективно решаются методами, использующими Л. п. Л. п. нашло особенно широкое применение в обосновании операционного исчисления, в к-ром обычно вместо Л. п. F(p) вводится "изображение" оригинала f(?)- функция pF(p).

Современная общая теория Л.п. строится на основе интегрирования в смысле Лебега (см. Интеграл). Для применимо* сти Л. п. к функции f(t) необходимо, чтобы f(t) была интегрируема в смысле Лебега на любом конечном интервале (0,?), ?>0 и интеграл (1) для неё сходился хотя бы в одной точке ро = оо + г'те. Если интеграл (1) сходится в точнее ро, то он сходится ве всех точках р, для к-рых Re (р-ро) >0. Т.о., если интеграл (1) сходится хотя бы в одной точке плоскости ро, то либо он сходится во всей плоскости, либо существует такое число а_с, что при Rej">a_c интеграл (1) сходится, а при Re р < а_с расходится. Число ov наз. абсциссой сходимости интеграла Лапласа. F(p) - аналитическая функция в полуплоскости Re p>a_c.

Лит.: Д и т к и н В. А. н Кузнецов П. И., Справочник по операционному исчислению. Основы теории и таблицы формул, М.-Л., 1951; Д и т к и н В. А. и Прудников А. П., Интегральные преобразования и операционное исчисление, М., 1961; Д ё ч Г., Руководство к практическому применению преобразования Лапласа, пер. с нем., М., 1965.

ЛАПЛАСА ТЕОРЕМА, простейшая из предельных теорем теории вероятностей, относящаяся к распределению отклонений частоты появления события при независимых испытаниях от его вероятности. В общем виде эта теорема доказана П. Лапласом в книге "Аналитическая теория вероятностей" (1812). Один частный случай Л. т. был известен А. Муавру (1730), в связи с чем Л. т. иногда наз. теоремой Муавра - Лапласа. Формулировка Л. т. такова. Пусть при каждом из n независимых испытаний вероятность появления нек-рого события Е равна р(0 < р << 1) и пусть т обозначает число испытаний, в к-рых событие Е фактически наступает; тогда вероятность неравенства

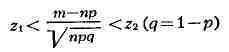
при достаточно большом числе испытаний п сколь угодно мало отличается от

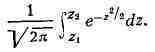
Если обозначить через Xk случайную величину, принимающую значение, равное 1, при появлении события Е в к-ом испытании и значение, равное 0, при его непоявлении, то т представляется как сумма независимых случайных величин т = Xi + ...+ Х„. Это позволяет рассматривать Л. т. как частный случай более общих предельных теорем теории вероятностей, в частности Ляпунова теоремы.

Приближённые значения вероятностей, даваемые Л. т., на практике используются как точные при npq порядка нескольких десятков и большем.

Лит. см. при ст. Предельные теоремы теории вероятностей.

Ю. В. Прохоров.

ЛАПЛАСА УРАВНЕНИЕ, дифференциальное уравнение с частными производными

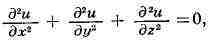
где х, у, 2 - независимые переменные, а и = u(x,y,z) - искомая функция. Это уравнение названо по имени П. Лапласа, рассмотревшего его в работах по теории тяготения (1782). К Л. у. приводит ряд задач физики и техники. Л. у. удовлетворяют температура при стационарных процессах, потенциал электростатич. поля в точках пространства, свободных от зарядов, потенциал поля тяготения в области, не содержащей притягивающих масс, и т. п. Функции, удовлетворяющие Л. у., наз. гармоническими функциями. О постановке задач для Л. у. см. в ст. Краевые задачи.