КУБИЧЕСКОЕ УРАВНЕНИЕ, алгебраическое уравнение третьей степени. Общий вид К. у.:

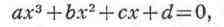
где а не равно 0. Заменяя в этом уравнении х новым неизвестным у, связанным с х равенством х = у - b/3а, К. у. можно привести к более простому (каноническому) виду: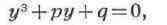

где

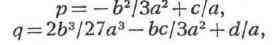
решение же этого уравнения можно получить с помощью Кардана формулы:

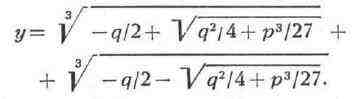
Если коэффициенты К. у.- действительные числа, то вопрос о характере его корней зависит от знака выражения q²/4+р³/27, стоящего под квадратным корнем в формуле Кардано. Если q²/4 + + Р³/27>0, то К. у. имеет три различных корня: один из них действительный, два других - сопряжённые комплексные; если q²/4 + р³/27=0, то все три корня действительны, два из них равны; если q²/4 + р³/27<0, то все три корня действительны и различны. Выражение q²/4 + + р³/27 только постоянным множителем отличается от дискриминанта К. у. D = - 4р³ - 27q².

Лит.: Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968; Энциклопедия элементарной математики, под ред. П. С. Александрова (и др.), кн. 2, М.- Л., 1951.