КООПЕРАТИВНАЯ ТЕОРИЯ ИГР, раздел игр теории, в к-ром игры рассматриваются без учёта стратегии. возможностей игроков (тем самым К. т. и. изучает нек-рый класс моделей общих игр). В частности, в К. т. и. входит исследование нестратегических (кооперативных) игр, лишённых с самого начала стратегич. аспекта. В кооперативной игре задаются возможности и предпочтения различных групп игроков (коалиций) и из них выводятся оптимальные (устойчивые, справедливые) для игроков ситуации, в т. ч. распределения между ними суммарных выигрышей: устанавливаются сами принципы оптимальности, доказывается их реализуемость в различных классах игр и находятся конкретные реализации. В терминах кооперативных игр поддаются описанию многие экономич. и социологич. явления.

Наиболее просто описание т. н. классич. кооперативных игр, состоящее в указании: 1) множества игроков J; 2) семейства R_n подмножеств J (коалиций интересов) и 3) функции v, заданной на R_n и принимающей вещественные значения. [v(K) можно понимать (иногда - с нек-рыми оговорками) как сумму, к-рую коалиция К может распределить между своими членами.] Обычно (не всегда) функцию v считают супераддитивной: v(K U L) >= v(K) +v(L) при К П L = 0 . Это отражает дополнительные возможности, возникающие у коллективов при их объединении. Для классич. кооперативных игр характерна возможность неогранич. передач выигрышей одними игроками другим и притом без изменения их полезности (ценности). Более общим типом игр являются игры без побочных платежей, где на такие передачи накладываются нек-рые ограничения.

Пусть J = {1,...,n}; вектор х= (x₁,...,x_n), для к-рого и х_i> v ({i})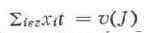 при всех i принадлежащих J, наз. дележом. Говорят, что делёж x доминирует над дележом у = (y₁, ...,y_n), если найдётся такая (предпочитающая его) коалиция К, что

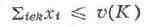
и x_i>yi для i принадлежащих К. Оптимальное поведение участников кооперативной игры может состоять в стремлении к множеству дележей, не доминирующих над др. дележами (с-ядро) или множеству не доминирующих друг над другом дележей, к-рые в совокупности доминируют над всеми остальными дележами (решения по Нейману - Моргенштерну) или к множеству дележей, в которых в нек-ром смысле минимизируется "недовольство" коалиций (n-ядро) и т. д. Нек-рые из принципов оптимальности не всегда реализуются; другие реализуются иногда неоднозначно. Нахождение реализаций часто затруднительно. Т. о., математич. проблема установления оптимального поведения в кооп. играх является весьма сложной как принципиально, так и технически.

Лит.: Нейман Дж., Морген-Штерн О., Теория игр и экономическое поведение, пер. с англ., М.. 1970; Воробьёв Н. Н., Современное состояние теории игр, "Успехи математических наук", 1970, т. 25, в. 2; Оуэн Г., Теория игр, пер. с англ., М., 1971; Rоsenmüller J,, Kooperative Spiele und Märkte, B.- Hdlb.,- N. Y., 1971.

H. H. Воробьёв.