КОЛЕБАНИЯ, движения (изменения состояния), обладающие той или иной степенью повторяемости. При К. маятника (рис. 1, а) повторяются отклонения его в ту и другую сторону от вертикального положения. При К. пружинного маятника - груза, висящего на пружине (рис. 1, б),- повторяются отклонения его вверх и вниз от нек-рого среднего положения. При К. в электрич. контуре, обладающем ёмкостью С и индуктивностью L (рис. 2), повторяются величина и знак заряда q на каждой пластине конденсатора. К. маятника происходят потому, что: 1) сила тяжести возвращает отклонённый маятник в положение равновесия; 2) вернувшись в положение равновесия, маятник, обладая скоростью, продолжает двигаться (по инерции) и снова отклоняется от положения равновесия в сторону, противоположную той, откуда он пришёл. К. груза (рис. 1, б) происходят потому, что: 1) упругая сила сжатой или растянутой пружины возвращает груз из смещённого вверх или вниз положения в положение равновесия; 2) вернувшись в положение равновесия, груз обладает скоростью и по инерции "проскакивает" через это положение, чем вызывается растяжение (или сжатие) пружины. К. в электрич. контуре происходят потому, что: 1) разность потенциалов между обкладками заряженного конденсатора вызывает появление тока i в катушке; 2) ток не прекращается в тот момент, когда конденсатор полностью разряжен: благодаря индуктивности катушки ток продолжает течь дальше, перезаряжая конденсатор (см. Электрические колебания).

Физика и техника имеют дело с К., весьма разнообразными по своей физич. природе, характеру и степени повторяемости, быстроте смены состояний, "механизму" возникновения. По своей физич. природе могут быть выделены, в частности, К.: а) механические, напр. К. маятника, моста, корабля на волне, струны; К. плотности и давления воздуха при распространении в нём упругих (акустических) волн, в частности слышимого звука; б) электромагнитные, напр. К. в колебательном контуре (рис. 2), объёмном резонаторе, волноводе. К. напряжённостей электрич. и магнитного полей в радиоволнах, волнах видимого света и любых др. электромагнитных волнах; в) электромеханические (К. мембраны телефона, пьезокварцевого или магнитострикционного излучателя ультразвука); г) химические (К. концентрации реагирующих веществ при т. н. периодич. химич. реакциях); д) термодинамические (напр., т. н. поющее пламя) и др. тепловые автоколебания, встречающиеся в акустике, а также в нек-рых типах реактивных двигателей. Большой интерес в астрофизике представляют К. яркости цефеид. Таким образом, К. охватывают огромную область физич. явлений и технич. процессов. В частности, К. имеют первостепенное значение в судостроении, самолётостроении, электротехнике, технике автоматич. регулирования. На их использовании основана вся радиотехника и технпч. акустика. К. встречаются также в метеорологии, химии, физиологии (напр., пульсации сердца) и в ряде др. естеств. наук.

К. присущи нек-рые характерные закономерности, одинаковые для К. различной физич. природы. Вследствие этого возникла область физики - теория К., занимающаяся исследованием общих закономерностей К. Математич. аппаратом теории К. являются гл. обр. дифференциальные уравнения. Существуют группы К. различной физич. природы, к-рым соответствуют аналогичные дифференциальные уравнения [напр., К. маятника, груза на пружине и электрич. контура (см. ниже); часов и лампового генератора; упругого стержня и электрич. кабеля]. Аналогичность этих уравнений отображает общность нек-рых объективно существующих закономерностей, присущих К. этой группы. Однако аналогии между К. различной физич. природы, как и всякие аналогии, ограничены определёнными рамками; они охватывают далеко не все существенные черты К.

Исследование К. маятника, предпринятое в нач. 17 в. итал. учёным Г. Галилеем, а затем голл. учёным X. Гюйгенсом, сыграло важнейшую роль в возникновении классич. механики. Изучение в кон. 19 в. электромагнитных К. англ. физиком У. Томсоном (Кельвином) имело большое значение для понимания электромагнитных явлений. Много важных сведений и результатов по теории К. содержится в трудах англ. физика Дж. Рэлея.

Рис. 1. а - колебания маятника; 6 - колебания груза на пружине.

Рис. 2. Электрический колебательный контур; С - ёмкость; L - индуктивность; q - заряд на обкладках конденсатора; I - ток в цепи.

Учение о К. многим обязано трудам русских учёных. Изобретение радио А. С. Поповым (1895) явилось важнейшим технич. применением электромагнитных колебаний. П. Н. Лебедев посвятил ряд выдающихся исследований получению электромагнитных К. очень высокой частоты, ультразвуковым К. и поведению вещества под действием быстроперемениых электрических полей. А. Н. Крылову принадлежат фундаментальные исследования по теории качки корабля. Большое значение в области изучения К., в частности нелинейных К., имели работы сов. учёных Л. И. Мандельштама, Н. Д. Папалекси, Н. М. Крылова, Н. Н. Боголюбова, А. А. Андронова и др. Работы А. Н. Колмогорова и А. Я. Хинчина содержат математич. основу теории случайных процессов в колебательных системах, получившей важное практич. значение.

Кинематика колебаний. С точки зрения кинематики можно выделить нек-рые важнейшие типы К. (рис. 3), где колеблющаяся величина s может быть любой физич. природы (механич. смещение твёрдого тела, уплотнение газа, сила тока и т. д.). Рис. 3,rt поясняет общий случай периодического К.; здесь каждое значение s повторяется неограниченное число раз через одинаковые промежутки времени t = Т:

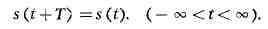
Т наз. периодом. Число К. в единицу времени v = 1/Т наз. частотой К.

Рис. 3. Различные виды колебаний: а - общий случай периодического колебания; 6 - прямоугольные колебания; в - пилообразные; г - синусоидальные; д -затухающие; е - нарастающие; ж - амплитудно-модулированные; з - частотно-модулированные; и - колебания, модулированные по амплитуде и по фазе; к - колебания, амплитуда и фаза к-рых - случайные функции; л - беспорядочные колебания; s - колеблющаяся величина; t - время.

Частными случаями периодич. К. являются К. прямоугольные (рис. 3, б), пилообразные (рис. 3, в), синусоидальные (или гармонические, рис. 3, г). В последнем случае

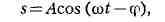
где А, со, Ф- постоянные. Величина А (макс, значение s) наз.  а м п л и т у д о й.  Т. к. значения cos(wt - ф) повторяются при возрастании аргумента на 2 л, то wТ = 2л и, следовательно,

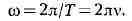
Величина со наз. круговой, или циклической, частотой, равна числу К. за 2я единиц времени. Функция времени cot - ф наз. фазой К., постоянная ф - начальной фазой (часто её наз. просто фазой). На рис. 3, д изображено затухающее К.

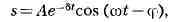
где А, 8, со, ф - постоянные. А наз. начальной амплитудой, Ае-^ы - мгновенным значением амплитуды, 6 - коэффициент затухания, т = = 1/6 - временной постоянной (см. также Декремент затухания). Величина о здесь положительна. При отрицат. знаке 8 К. является нарастающим (рис. 3, е). Величины cot - ф, to, ф имеют те же названия, что и в случае синусоидального К. Хотя затухающее К. не является точно периодическим, величина

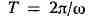
также наз. периодом.

В физике и радиотехнике большое значение имеют модулированные К., т. е. К. вида

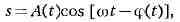
причём функции A(t), ф(t) меняются медленно по сравнению с cos tat (со - постоянная). Если cp(t) = const, то К. наз. амплитудно-модулированным (рис. 3, ж), если A(t) = const (рис. 3, з) - модулированным по фазе (или по частоте; см. Модуляция колебаний). В общем случае (рис. 3, и) К. модулированы как по амплитуде, так и по фазе. Рис. 3, ж, з, и соответствуют периодич. амплитудной и фазовой модуляции: A(t) и ср(?) - периодич. функции. Важное значение в технике (радиотелефония, телевидение) и в физике имеет случай, когда A(t) или ф(?), или же обе одновременно являются т. н. случайными функциями (рис. 3, к). Часто в природе и технике встречаются беспорядочные К. (рис. 3, л), напр, белый свет, акустич. и электрич. "белый" шум и т. п.

Ни в природе, ни в технике никогда не встречаются строго периодические (в частности, строго гармонические) К. Тем не менее гармонические К. весьма важны по двум причинам. 1) В природе и технич. устройствах часто возникают К., мало отличающиеся на протяжении достаточно большого времени от гармонических. 2) Многие физич. системы, принадлежащие к классу спектральных приборов в широком смысле этого слова или гармонич. анализаторов, преобразуют произвольные К. в набор К., близких к гармоническим. Когда говорят о гармонич. К., всегда имеют в виду К., лишь близкие к гармоническим. Гармонич. К. даже одинаковой физич. природы (К. давления воздуха, напряжённости электрич. поля), но различной частоты могут обладать (наряду с аналогичными) резко различающимися свойствами; они могут совершенно по-разному воздействовать на те или иные физич. системы и живые организмы и, в частности, на органы чувств человека и животных (см. Слух, Зрение).

Возникновение колебаний. Здесь рассматривается возникновение К. в системе, не получающей К. извне, а являющейся источником К. В случае, когда система приходит в К. под действием К., подводимых извне, говорят не о возникновении К., а о воздействии К. на систему и о преобразовании их системой. В пассивных (не содержащих источников энергии) системах такое воздействие вызывает вынужденные колебания. Существует 3 основных типа К. в системах, являющихся источниками К. 1) Свободные (или собственные) К., происходящие, когда система предоставлена самой себе после нарушения равновесия вмешательством извне, напр. К. пружинного маятника (рис. 1, б) и К. тока в электрич. контуре (рис. 2).

Свободные К. пружинного маятника и колебательного контура относятся к частному типу свободных К. в линейных колебательных системах (т. е. системах, обладающих параметрами, практически неизменными, и описываемых с достаточной точностью линейными дифференциальными уравнениями) с одной степенью свободы. В линейных системах с N степенями свободы (N > 1) свободные К. в каждой точке являются суперпозицией N К. (см. Нормальные колебания). В линейных распределённых системах (если отвлечься от атомистич. структуры вещества), напр. струне, стержне, трубе, а также в электрич. кабеле, объёмном резонаторе, свободные К. в каждой точке являются суперпозицией бесконечного числа К. Если восстанавливающая сила, т. е. сила, возвращающая систему к положению равновесия, не пропорциональна отклонению от него, свободные К. описываются нелинейным дифференциальным уравнением, напр, в случае маятника, когда амплитуду нельзя считать очень малой. Такие системы наз. нелинейными. Здесь, в отличие от линейных систем, свободные К. (даже если не учитывать затухания) не синусоидальны, и, кроме того, период их зависит от начальных условий, напр. у маятника период свободных К. тем больше, чем больше амплитуда. Лишь в пределе, когда она стремится к нулю, система становится линейной, а её К.изохронными: период не зависит от амплитуды.

2)Флуктуационные К., происходящие в результате теплового движения вещества. Поскольку маятник) груз, контур участвуют в тепловом движении материи, они совершают никогда не прекращающиеся флуктуационные К. (см. Флуктуации) - один из видов броуновского движения. Эти К. особенно легко обнаружить и наблюдать в случае колебательного контура, в к-ром происходят флуктуации напряжения и тока, применяя усилитель с большим коэфф. усиления и осциллограф. Флуктуационные К. в колебательных контурах, антеннах и т. д.- важнейший фактор, ограничивающий чувствительность радиоприёмников.

3) Автоколебания - незатухающие К., которые могут существовать при отсутствии переменного внеш. воздействия, причём амплитуда и период К. определяются только свойствами самой системы и в определённых пределах не зависят от начальных условий. Примерами являются: К. маятника или баланса часов, поддерживаемые опусканием гири или раскручиванием спиральной пружины, звучание духовых и смычковых муз. инструментов, К. всевозможных электронных ламповых генераторов, применяемых в радиотехнике, и др. Подробнее см. Автоколебания.

Распространение колебаний. Колеблющийся маятник (рис. 1) приводит в движение раму, на которой он подвешен; рама приводит в движение стол и т. д. Таким образом, К. не остаются локализованными, а распространяются, охватывая все окружающие тела. Явление распространения К. гораздо сильнее выражено в случае более быстрых механич. (звуковых) К.- струны, колокола, воздуха в трубах муз. духовых инструментов и т. п. Здесь распространение К. происходит гл. обр. через воздух. Вокруг источников электрич. К. возникают переменные электрич. и магнитные поля, распространяющиеся вдаль от точки к точке через диэлектрики (в т. ч. вакуум). Процессы распространения К. (а также всяких возмущений) наз. волнами.

Общий характер колебательных воздействий. Прогиб балки под действием постоянной нагрузки тем больше, чем больше нагрузка; сила тока, возникающего под действием постоянной эдс,тем больше, чем больше эдс, и т. д. В случае колеблющейся нагрузки, переменной эдс и др. колебательных воздействий дело обстоит гораздо сложнее - здесь имеют место вынужденные колебания. Результат воздействия в этом случае зависит не только от его интенсивности, но также в большой степени от его темпа, от того, как оно изменяется со временем. В этом состоит одна из основных и характерных черт К.

Пусть на груз пружинного маятника действует ряд периодически повторяющихся кратковременных толчков снизу вверх. В силу линейности системы для неё справедлив суперпозиции принцип: действия отд. толчков складываются. Вообще говоря, действие очередного толчка будет одинаково часто как усиливать, так и ослаблять действие всех предыдущих; амплитуда К. будет то увеличиваться, то уменьшаться, оставаясь сравнительно небольшой. Но если период толчков равен или кратен периоду собственных К., то каждый толчок, действуя "в такт" с К., будет усиливать действие предыдущих и пружинный маятник раскачается до очень большой амплитуды. Рост амплитуды прекратится только благодаря тому, что существенное значение при большой раскачке приобретает затухание К. за время между двумя толчками. Раскачка линейной колебательной системы под влиянием периодич. толчков, ограниченная только затуханием, представляет собой т. н. явление резонанса. Другой важный случай резонанса наступает при действии на такую систему непрерывной силы, изменяющейся по синусоидальному закону, если частота её изменения совпадает с частотой соо свободных К. системы.

При периодич. изменении параметра колебательной системы, напр., длины нити маятника, ёмкости колебательного контура и т. д., вообще говоря, маятник не будет раскачиваться, в контуре не будет возникать электрич. К. и т. д. Но и здесь при подходящем темпе воздействия (лучше всего, если параметр меняется с частотой, равной 2со) могут возникнуть К. В любой колебательной системе вследствие воздействия на неё различных случайных факторов всегда существуют флуктуационные К., к-рые имеют сплошной спектр со всевозможными фазами гармонич. составляющих. Поэтому периодич. изменения параметра системы всегда совпадут по фазе с одной из гармонич. составляющих и её амплитуда будет возрастать, при этом маятник начнёт раскачиваться около вертикали, в контуре появляются нарастающие электромагнитные К. (см. Параметрическое возбуждение колебаний).

Частоты некоторых важнейших К. Вращение есть суперпозиция двух взаимно перпендикулярных гармонич. К. Обращение планет вокруг Солнца совершается с частотами от 1,28-10-⁹ гц (Плутон, период 250 лет) до 1,32-10-⁷ гц (Меркурий, период 88 сут). Сутки - период обращения Земли вокруг её оси - соответствуют частоте около 1,16 10-⁵ гц. Морские приливы и отливы происходят с частотой того же порядка. Морские волны, возникающие под действием ветра, имеют частоту 10-¹ гц. К. сооружений, К. и вращение машин имеют частоты от долей до - 10⁴ гц. Механич. К., воспринимаемые нормальным человеческим ухом как звук, совершаются с частотами от 20 ги, до ~ 2-10⁴ гц. Более быстрые (неслышимые) упругие К. с частотой до 10⁹ гц наз. ультразвуковыми, а с частотами до 10¹² - 10¹³ гц наз. гиперзвуковыми. К. атомов, из к-рых складывается тепловое движение твёрдых и жидких тел, а также К. атомов в молекулах присущи частоты порядка 10¹³ гц.

Переменный ток, вырабатываемый электростанциями, имеет в СССР и большинстве др. стран стандартную частоту 50 гц. Радиотехника использует электромагнитные К. и волны с частотой от 10⁵ гц (длинные волны) до 10^й гц (миллиметровые волны). Оптика имеет дело с электромагнитными волнами, в к-рых К. напряжённости электрич. и магнитного полей происходит с частотой от 10¹² гц до 10" гц. К этому интервалу относится видимый свет (красный: 0,4-10¹⁴ гц, фиолетовый: 0,75-10¹⁴ гц). Интервал от 10¹² до 10¹⁴ гц соответствует инфракрасному, от 10¹⁵ до 10" гц - ультрафиолетовому излучениям. Далее в порядке повышения частоты идут рентгеновское излучение (10¹⁸ - 10¹⁹ гц), гамма-излучение (10²⁰гц), электромагнитное излучение, входящее в состав космических лучей (до 10²² гц и более).

Лит.: Элементарный учебник физики, под ред. Г. С. Ландсберга, 7 изд., т. 1, М., 1971; Красильников В. А., Звуковые волны в воздухе, воде и твердых телах. М.- Л., 1951; Стрэтт Д ж. В. (Рэлей), Теория звука, пер. с англ., т. 1 - 2, М.- Л., 1940 - 44; Андронов А. А. и Xайкин С. Э., Теория колебаний, ч. 1, М.-Л., 1937; Стрелков С. П., Введение в теорию колебаний, М.- Л., 1951; Горелик Г. С., Колебания и волны, 2 изд., М.- Л., 1959.

Г. С. Горелик.

КОЛЕБАНИЯ КОНСТРУКЦИЙ, многократно повторяющееся возвратно-поступательное или возвратно-вращательное движение элементов конструкций вследствие их упругих деформаций под действием сил, достаточно быстро меняющихся во времени. При К. к. элементы конструкций перемещаются относительно их устойчивого положения статич. равновесия (колебания мостов, высотных сооружений, фундаментов машин и т. п.) или общего движения (колебания летательных аппаратов, вагонов, автомобилей и т. п.). К. к. классифицируются по неск. признакам. По типу деформаций различают К. к. продольные (сжатия - растяжения), поперечные (изгибные, сдвиговые), крутильные и смешанные; по характеру перемещений во времени - периодические и непериодические (см. Колебания).

Значит, колебания опасны для прочности и устойчивости конструкций, примером чего служат многочисл. разрушения зданий и сооружений при землетрясениях, поломки валов двигателей, случай разрушения вследствие колебаний под действием ветра Такомского висячего моста, сооружённого в США в 1940. Систематические, даже умеренные К. к., безопасные для самой конструкции, могут вредно влиять на здоровье людей, а также на качество точных производств, процессов. Поэтому важное значение имеет борьба с К. к. путём расчёта конструкций на колебания при их проектировании и осуществление мероприятий с целью уменьшения К. к. Вопросы расчёта конструкций на колебания ц способы уменьшения К. к. рассматриваются в теории колебаний механич. систем. См. также Динамика сооружений, Виброизоляция.

Лит.: Тимошенко С. П., Колебания в инженерном деле, пер. с [англ.], 2 изд., М., 1967; Ден-Гартог Дж. П., Механические колебания, пер. с [англ.], М., 1960; Бабаков И. М., Теория колебании, М., 1968.

Е. С. Сорокин.

КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ, один из осн. видов внутр. движений твёрдого" тела, при к-ром составляющие его частицы (атомы или ионы) колеблются около положений равновесия - узлов кристаллич. решётки. К. к. р., напр., в виде стоячих или бегущих звуковых волн возникают всякий раз, когда на кристалл действует внешняя сила, изменяющаяся со временем. Однако и в отсутствие внешних воздействий в кристалле, находящемся в тепловом равновесии с окружающей средой, устанавливается стационарное состояние колебаний, подобно тому как в газе устанавливается стационарное распределение атомов или молекул по скорости их поступательного движения.

Характер этих колебаний зависит от симметрии кристалла, числа атомов в его элементарной ячейке, типа химической связи, а также от вида и концентрации дефектов в кристаллах. Смещения и атомов в процессе колебаний тем больше, чем выше температура, но они гораздо меньше постоянной решётки вплоть до температуры плавления, когда твёрдое тело превращается в жидкость. Силы, которые стремятся удержать атомы в положениях равновесия, пропорциональны их относит, смещениям так, как если бы они были связаны друг с другом пружинками (рис. 1). Представление кристалла в виде совокупности частиц, связанных идеально упругими силами, наз. гармоническим приближением.

Рис. 1. Представление объёмноцентрированного кубического кристалла в виде совокупности частиц с массой т, связанных друг с другом пружинами с жёсткостями Y₁ и Y₂

В кристалле, состоящем из N элементарных ячеек по n атомов в каждой, существует 3nN -б типов простейших колебаний в виде стоячих волн, наз. нормальными (либо собственными) колебаниями, или модами. Их число равно числу степеней свободы у совокупности частиц кристалла за вычетом трёх степеней свободы, отвечающих поступательному, и трёх - вращательному движению кристалла как целого (см. Степеней свободы число). Числом 6 можно пренебречь, т. к. 3nN - величина ~ 10²²-10²³ для 1 см³ кристалла.

В процессе нормального колебания все частицы кристалла колеблются около своих положений равновесия с одной и той же постоянной частотой со по закону и ~ sin w t подобно простому гармонич. осциллятору. В кристалле одновременно могут присутствовать все возможные нормальные колебания, причём каждое протекает так, как если бы остальных не было вовсе. Любое движение атомов в кристалле, не нарушающее его микроструктуру, может быть представлено в виде суперпозиции нормальных колебаний кристалла.

Каждую стоячую волну нормального колебания можно, в свою очередь, представить в виде двух упругих плоских бегущих волн, распространяющихся в противоположных направлениях (н о рмальные волны). Плоская бегущая волна, помимо частоты w, характеризуется волновым вектором At, определяющим направление движения фронта волны и длину волны X = 2л/k, а также поляризацией, к-рая определяет характер индивидуального движения частиц. В общем случае имеет место эллиптич. поляризация, когда каждый атом описывает эллипс около своего положения равновесия (рис. 2), при этом нормаль к плоскости эллипса не совпадает по направлению с k. Эллиптич. орбиты одинаковы для идентичных атомов, занимающих эквивалентные положения в решётке. В тех кристаллах, где каждый узел является центром симметрии (см. Симметрия кристаллов), все нормальные волны плоскополяризованы: атомы в любом нормальном колебании совершают возвратно-поступательные движения около своих положений равновесия.

Рис. 2. Эллиптическая поляризация упругих волн в кристалле; k - волновой вектор.

Дисперсия нормальных волн. При каждом значении k существует Зп типов нормальных волн с различной поляризацией. Они нумеруются целочисленной переменной а = 1, 2... 3 п и наз. ветвями нормальных колебаний. Для волн данного типа а величины со и k не могут быть произвольными, а связаны между собой определённым соотношением со = (О (k,a), наз. законом дисперсии. Напр., если представить кристалл в виде совокупности одинаковых атомов массы т, расположенных на равных расстояниях а друг от друга и связанных попарно пружинами с жёсткостью

у так, что они образуют бесконечную цепочку и могут смещаться только вдоль её оси (рис. 3,а), то элементарная ячейка состоит из одной частицы и существует одна ветвь частоты нормальных колебаний с законом дисперсии:

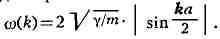
У двухатомной линейной цепочки (рис. 3,6) ячейка содержит 2 частицы с массами т и М и имеется 2 ветви с более сложным законом дисперсии (рис. 4):

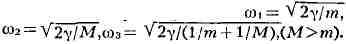
Рис. 3. Простейшие модели кристалла: а - линейная одноатомная цепочка; 6 - линейная двухатомная цепочка; m и Ммассы двух частиц, составляющих элементарную ячейку.

Рис. 4. Закон дисперсии двухатомной линейной цепочки:

1- акустическая ветвь; 2 - оптическая ветвь.

Упругие волны в кристалле всегда обладают дисперсией. В частности, их фазовая скорость, как правило, отличается от групповой, с к-рой по кристаллу переносится энергия колебаний. В то время как частота со упругих волн, распространяющихся в непрерывной среде, неограниченно возрастает с ростом k, в кристалле благодаря периодич. расположению атомов и конечной величине связывающих их сил существует нек-рая макс, частота колебаний w_макс (обычно ~10¹³ гц). Собств. частоты могут не сплошь заполнять интервал от w = = 0 до w= w_макс, в нём могут быть пустые участки (запрещённые зоны), разделяющие две следующие друг за другом ветви (рис. 4). Запрещённой зоны между соседними ветвями нет, если ветви перекрываются. Колебания, соответствующие запрещённым зонам и с частотой w > w_макс, не могут распространяться в кристалле, они быстро затухают.

Акустическая и оптическая ветви. Три первые ветви колебаний с а = 1,2,3 наз. акустическими. В случае, когда длина волны X значительно превышает наибольший из периодов пространств, решётки (k - мало), они характеризуются линейным законом диснерсии w = c k. Это обычные звуковые волны, ас - фазовая скорость их распространения, зависящая от направления распространения и поляризации. Они плоскополяризованы в одном из трёх взаимно перпендикулярных направлений соответственно трём значениям а = 1, 2, 3 и соответствуют колебаниям кристалла как сплошной среды. В анизотропном кристалле ни одно из этих направлений обычно не совпадает с направлением распространения волны, т. е. с k. Лишь в упругой изотропной среде звуковые волны имеют чисто продольную и чисто поперечную поляризации. Акустич. ветви охватывают диапазон частот от нуля до ~ 10¹³гц. Однако с уменьшением длины волны закон дисперсии становится более сложным.

Для остальных 3(n -1) ветвей частоты смещения атомов в процессе колебаний, соответствующих большой длине волны, происходят так, что центр масс отд. элементарной ячейки покоится. В ионных кристаллах, элементарная ячейка к-рых состоит из ионов противоположных знаков, движение такого типа можно возбудить переменным электрическим полем, напр, световой волной, с частотой, лежащей, как правило, в инфракрасной области. Поэтому эти ветви называются оптическими. Своё название акустич. ветвь получила по начальному участку (рис. 4), начальный участок акустич. ветви - обычный звук.

Фононы. Каждой ёегущей плоской волне с вектором k и частотой со можно поставить в соответствие совокупность движущихся квазичастиц с импульсом р = hk и энергией E= hw, где h - Планка постоянная (см. Корпускулярно-волновой дуализм). Эти квазичастицы являются квантами поля К. к. р. и наз. фононами по аналогии с фотонами - квантами электромагнитного поля.

Влияние К. к. р. на свойства кристаллов. Атомы осциллируют около положений равновесия тем интенсивнее, чем выше темп-pa кристалла. Когда амплитуда колебаний превышаетнек-рое критич. значение, наступает плавление и кристаллич. структура разрушается. С понижением тсмп-ры амплитуда уменьшается и становится минимальной при Т = О К. Полная остановка атомов с обращением их энергии в нуль, в силу законов квантовой механики, невозможна, и они при Т = = О К совершают "нулевые" колебания. Т. к. энергия "нулевых" колебаний обычно недостаточна, чтобы твёрдое тело расплавилось, то с понижением темп-ры все жидкости рано или поздно затвердевают. Единств, исключением является гелий, к-рый остаётся жидким вплоть до темп-ры О К и затвердевает лишь под давлением.

Количественной характеристикой способности кристалла запасать тепло в виде энергии колебаний служит решёточная теплоёмкость. Будучи отнесённой к одному атому, она оказывается приближённо равной Зk_Б (k_Б - Больцмана постоянная) при высоких темп-рах (Дюлонга и Пти закон) и пропорциональной Г³, когда Т приближается к О К.

В металлах и полупроводниках, помимо атомов или ионов, имеются также свободные электроны, к-рые в присутствии электрич. поля создают электрич. ток. Законы их движения таковы, что они беспрепятственно проходят сквозь идеальный кристалл из ионов, находящихся в состоянии "нулевых" колебаний. Поэтому сопротивление электрич. току при Т -> 0 К возникает лишь постольку, поскольку в кристаллах всегда имеются дефекты, рассеивающие электроны. Однако при темп-pax T > 0 К колебания хаотически нарушают идеальную периодичность решётки и создают дополнительное - решёточное, или фононное, электросопротивление. Сталкиваясь с осциллирующими атомами, электроны передают кристаллич. остову часть энергии своего направленного поступательного движения, к-рая выделяется в виде джоулева тепла.

Ангармонизм. В действительности возвращающие силы не строго пропорциональны смещениям атомов из положений равновесия и колебания кристалла не являются строго гармоническими (ангармонизм). Нелинейность междуатомных сил мала, поскольку малы амплитуды колебаний. Однако благодаря ей отд. нормальные колебания не являются независимыми, а оказываются связанными друг с другом и между ними возможен резонанс, как в системе связанных маятников.

В процессе установления термодинамич. равновесия в кристаллах энгармонизм играет ту же роль, что и столкновения частиц в газе. Он, в частности, объясняет тепловое расширение кристаллов, отклонение от Дюлонга и Пти закона в области высоких темп-р, а также отличие друг от друга изотермич. и адиабатич. упругих постоянных твёрдого тела и их зависимость от темп-ры и давления (см. Упругость).

При неравномерном нагревании твёрдого тела в нём возникают потоки тепла. В металлах большая часть его переносится электронами, а в диэлектриках - нормальными волнами (фоноиами). Поэтому если иметь в виду диэлектрики или решёточную часть теплопроводности металлов, то в отсутствии энгармонизма тепловой поток распространялся бы со скоростью нормальных волн, т. е. приблизительно со скоростью звука. Благодаря энгармонизму волны в тепловом потоке обмениваются энергией и интерферируют друг с другом. В процессе такой интерференции происходит потеря суммарного импульса теплового потока. В результате возникает теплосопротивлсние, а тепловая энергия переносится с диффузионной скоростью, гораздо меньшей скорости распространения упругой энергии, напр, звуковой волны. Ангармонизм является также одной из причин затухания ультразвука в кристаллах.

Локальные и квазилокальные колебания. На характер К. к. р. существенно влияют дефекты кристаллич. решётки. Жёсткость межатомных связей и массы частиц в области дефекта отличаются от таковых для идеального кристалла, наз. эталонным или матрицей. В результате этого нормальные волны не являются плоскими. Напр., если дефект - это примесный атом массы то, связанный с соседями пружинами, жёсткости -уо, то может случиться, что его собственная частота колебаний соо = №y/m попадёт в запрещённую область частот матрицы. В таком колебании активно участвует лишь примесный атом, поэтому оно и паз. локальным. Т. к. в реальном кристалле дефектов всегда много (см. Дефекты в кристаллах), то локальное колебание, будучи возбуждённым на одном дефекте, может перейти на другой, как при резонансе одинаковых слабо связанных маятников. Поэтому локальные колебания обладают целым спектром частот, которые образуют примесную зону частот К. к. р. - т Наряду с локальными колебаниями в области низких частот могут существовать т. н. квазилокальные колебания. В частности, такие колебания есть в кристалле с тяжёлыми примесными атомами. Квазилокальные колебания при низких темп-pax резко увеличивают решёточную теплоёмкость, коэфф. термич. расширения, тепло- и электросопротивления. Так, напр., 2-3% примесных атомов, в 10 раз более тяжёлых, чем атомы матрицы, способны при малых Т удвоить решёточную теплоёмкость и коэфф. термич. расширения.

Локальные колебания протяжённых дефектов, напр, дислокации, распространяются вдоль них в виде волн, но в матрицу, как и в случае точечных дефектов, не проникают. Частоты этих колебаний могут принадлежать как запрещённой, так и разрешённой области частот матрицы, отличаясь от них законом дисперсии. Таковы, напр., звуковые поверхностные волны, возникающие у плоской границы твёрдого тела (волны Рэлея).

Экспериментальные методы изучения К. к. р. разнообразны. Одним из методов изучения локальных и квазилокальных К. к. р. служит их возбуждение при помощи инфракрасного излучения. Оно сопровождается резонансным уменьшением прозрачности кристалла и позволяет не только обнаружить эти колебания, но и определить их частоты.

Исследования неупругого рассеяния нейтронов в кристаллах позволяют определить закон дисперсии и поляризацию нормальных колебаний. Закон дисперсии может быть также восстановлен с помощью диффузного рассеяния рентгеновских лучей. Мессбауэра эффект позволяет непосредственно определить среднеквадратичные смещения и импульсы атомов в процессе К. к. р.

Лит.: З а и м а н Дж., Электроны и фононы, пер. с англ., М., 1962; его же. Принципы теории твердого тела, пер. с англ., М., 1966; Лейбфрид Г., Микроскопическая теория механических и тепловых свойств кристаллов, пер. с англ., М., 1963: М а р а д уд и н А., Дефекты и колебательный спектр кристаллов, пер. с. англ., М., 1968: Ландау Л. Д., Л и ф ш и ц Е. М., Статистическая физика, 2 изд.. М.. 1964: их же, Теория упругости, 3 изд., М., 1965 (Теоретическая физика, т. 7); Киттель Ч., Введение в физику твердого тела, пер. с англ., М., 1963.

Я. А. Иосилевский.

КОЛЕБАНИЯ ШИРОТЫ, изменения географич. широт пунктов на земной поверхности вследствие движения полюсов Земли.

КОЛЕБАТЕЛЬНАЯ СКОРОСТЬ частиц (акустическая скорость), скорость v, с к-рой движутся по отношению к среде в целом частицы (бесконечно малые части среды), колеблющиеся около положения равновесия при прохождении звуковой волны. К. с. следует отличать как от скорости движения самой среды, так и от скорости распространения звуковой волны или скорости звука с. Величина v << с при распространении звуковых и ультразвуковых волн в любых средах (газах, жидкостях, твёрдых телах) и при любых достижимых в настоящее время интенсивностях звука.

КОЛЕБАТЕЛЬНОЕ СМЕЩЕНИЕ частиц (акустическое с м ещ е н и е), смещение ?; бесконечно малой части среды по отношению к среде в целом, обусловленное прохождением звуковой волны. Направление К. с. может совпадать или не совпадать с направлением распространения волны в зависимости от типа волны (см. Упругие волны). При всех достижимых интенсивностях звука К. с. g < X, где X - длина звуковой волны.

КОЛЕБАТЕЛЬНЫЕ ДВИЖЕНИЯ ЗЕМНОЙ КОРЫ, медленные поднятия и опускания земной коры, происходящие повсеместно и непрерывно. Благодаря им земная кора никогда не остаётся в покое; она всегда разделена на участки, одни из к-рых поднимаются, другие прогибаются. К. д. з. к. происходили на протяжении всех прошлых геологических периодов и продолжаются сейчас. Они определяют размещение и изменение очертаний суши и моря на поверхности Земли, лежат в основе образования и развития её рельефа.

Методы изучения К. д. з. к. различны для прошлых геол. периодов, антропогенового периода и совр. эпохи. Для выявления совр. движений, происходивших в историч. время и продолжающихся ныне, применяют геодезич. методы, осн. на длительных наблюдениях над уровнем моря или на повторных точных нивелировках. Эти наблюдения показывают, что обычная скорость совр. К. д. з. к. измеряется миллиметрами (до 2-3 см) в год. К. д. з. к., начавшиеся с неогена и создавшие совр. формы рельефа, наз. новейшими и изучаются гл. обр. методами геоморфологии (см.Неотектоника). К. д. з. к. более ранних геол. периодов запечатлены в составе, слоистости и мощности отложений.

Основные закономерности, связанные с К. д. з. к., разработал А. П. Карпинский. Его выводы получили развитие в работах А. Д. Архангельского. В дальнейшем проблему К. д. з. к. развивали М. М. Тетяев, Г. Ф. Мирчинк, Н. М. Страхов, В. В. Белоусов, А. Б. Ронов, В. Е. Хаин и др.

За рубежом К. д. з. к. были выделены в кон.19в. амер. геологом Г. Джильбертом под назв. эпейрогенических. В 20 в. изучением этих движений занимались франц. геолог Э. Or, нем. геологи X. Штилле, С. Бубнов и др. Исследованиями выявлены две разновидности К. д. з. к.: общие колебательные движения и волновыс. О бщ и е К.д.з. к. выражаются в одновременном поднятии или опускании обширных областей, охватывающих целый материк или значит, его часть. Благодаря общим колебательным движениям происходят трансгрессии и регрессии, меняются очертания суши и моря, изменяется состав морских осадков по вертикали, образуется их слоистость, возникают морские и речные террасы и т. д. Общие колебания состоят из движений многих порядков, наложенных друг на друга. Наиболее крупные общие колебания имеют период, измеряемый 200-300 млн. лет. Они лежат в основе тектонич. циклов, к-рые проявляются прежде всего в повторяемости крупных трансгрессий и регрессий. На их фоне происходят частные трансгрессии и регрессии с меньшим периодом. Самые короткие циклы трансгрессий и регрессий измеряются тысячами и даже сотнями лет. Чем короче период цикла, тем более локально он проявляется. Ср. скорость общих колебаний, измеренная за длительный геол. срок, обычно выражается в сотых и десятых долях мм в год. Отд. кратковременные колебания высших порядков происходят значительно быстрее, со скоростью, близкой к скорости совр. К.д.з.к.

В о л н о в ы е  К. д. з. к. накладываются на общие колебания и выражаются в длительном расчленении любого крупного участка поверхности на зоны поднятий и прогибаний. Эти движения фиксируются в рельефе земной поверхности и в распределении фаций и мощности осадочных отложений. Их амплитуда может достигать 15-20 км.

В развитии волновых К. д. з. к. наблюдаются различные режимы, из к-рых основные - геосинклинальный и платформенный. В геосинклиналях волновые К. д. з. к. очень контрастны и имеют большую амплитуду: узкие (в неск. десятков км) зоны поднятия и прогибания тесно примыкают друг к другу и часто разделены глубинными разломами. На платформах К. д. з. к. характеризуются малой амплитудой (до неск. км) и крайне слабой контрастностью: широкие (сотни и тысячи км), в плане округлые области медленного поднятия и опускания коры плавно и постепенно переходят друг в друга.

Поскольку в течение геол. истории материков в целом геосинклинальный режим постепенно уступал своё место платформенному, К. д. з. к. более поздних периодов суммарно менее интенсивны, чем те же движения в более ранние периоды. Однако в областях тектоыич. активизации (напр., в Тянь-Шане) К. д. з. к. снова приобретают чрезвычайно высокую интенсивность, хотя ранее там уже устанавливался на длительное время спокойный платформенный режим.

На поверхности островов и шельфового дна морей наблюдаются признаки древних, новейших и современных К. д. з. к. О К. д. з. к. на дне глубоких океанов известно очень мало.

Предполагается связь К. д. з. к. с изменениями плотности материала в верхней мантии и в глубине земной коры и с его перемещениями (см. Тектонические гипотезы).

Изучение К. д. з. к. имеет большой практич. интерес, поскольку оно помогает устанавливать закономерности распределения в земной коре таких формаций осадочных пород, с к-рыми связаны залежи полезных ископаемых (нефть, газ, уголь, осадочные руды Fe, Мn, фосфоритов, бокситов и др.).

Лит.: Карпинский А. П., Общий характер колебаний земной коры в пределах Европейской России, в кн.: Собр. соч., т. 2, М. -Л., 1939; Страхов Н. М., Основы исторической геологии, т. 1--2, М.-Л., 1948; Р о н о в А. Б., История осадконакопления и колебательных движений Европейской части СССР (по данным объемного метода), "Тр. Геофизического ин-та АН СССР", 1949, т. 3 (130); его же, Некоторые общие закономерности развития колебательных движений материков (по данным объемного метода), в кн.: Проблемы тектоники, М., 1961; Белоусов В. В., Основные вопросы геотектоники, 2 изд., М., 1962; X а и н В. Е., Общая геотектоника, М., 1964.

В. В. Белоусов.

КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ, физич. системы, в к-рых в результате нарушения состояния равновесия возникают собственные колебания, обусловленные свойствами самой системы.

С энергетич. стороны К. с. делятся: на консервативные системы, в которых нет потерь энергии или, вернее, к-рые можно с достаточной точностью считать лишёнными таких потерь (механич. системы без трения и без излучения упругих волн; электромагнитные системы без сопротивления и без излучения электромагнитных волн); д и с с и п а т и в н ы е системы, в к-рых первоначально сообщённая энергия не остаётся в процессе колебаний постоянной, а расходуется на работу, в результате чего колебания затухают; автоколебательные системы, в которых происходят не только потери энергии, но и пополнение её за счёт имеющихся в системе постоянных источников энергии (см. Автоколебания).

В общем случае параметры К. с. (масса, ёмкость, упругость и т. п.) зависят от происходящих в них процессов. Такие К.с. описываются нелинейными ур-ниями и относятся к классу нелинейных систем. К. с., параметры к-рых с достаточной точностью можно считать не зависящими от происходящих в них процессов и описывать линейными ур-ниями, наз. линейными. Осн. чертой линейных К. с. является выполнение суперпозиции принципа. Это позволяет представлять колебания в системе в виде суммы колебаний определённого типа.

К. с. различаются ещё по числу степеней свободы, т. е. по числу независимых параметров (обобщённых координат, определяющих состояние системы). Если число Л' таких параметров конечно, то К. с. наз. дискретными с N степенями свободы. Предельный случай при N -> °° составляют т. н. распределённые К. с. (струна, мембрана, электрич. кабель, сплошные объёмные системы и т. п.). Общие свойства К.с. и общие закономерности происходящих в них процессов составляют предмет теории колебаний.

КОЛЕБАТЕЛЬНЫЕ СПЕКТРЫ, вибрационные спектры, спектры, обусловленные колебаниями атомов в молекуле (см. Молекулярные спектры) и атомов, ионов и их групп в кристаллах (см. Спектры кристаллов) и жидкостях. К.с. обычно состоят из отд.спектральных полос. Наблюдаются К.с. поглощения и отражения в близкой инфракрасной области и К. с. комбинационного рассеяния в видимой области.

КОЛЕБАТЕЛЬНЫЙ КОНТУР, электрическая цепь, содержащая катушку индуктивности и конденсатор, в к-рой могут возбуждаться электрич. колебания (рис. 1). Если в нек-рый момент времени зарядить конденсатор до напряжения Vo, то энергия, сосредоточенная в электрич. поле конденсатора, равна

Е_с =(CV₀²)/2, где С - емкость конденсатора. При разрядке конденсатора в катушке потечёт ток I, к-рый будет возрастать до тех пор, пока конденсатор полностью не разрядится. В этот момент электрич. энергия К. к. Е_с = 0, а магнитная, сосредоточенная в катушке, E_L =( LI₀²)/2, где L - индуктивность катушки, I₀ - макс, значение тока. Затем ток в катушке начинает падать, а напряжение на конденсаторе возрастать по абс. величине, но с противоположным знаком. Спустя нек-рое время ток через индуктивность прекратится, а конденсатор зарядится до напряжения - V₀. Энергия К. к. вновь сосредоточится в заряженном конденсаторе. Далее процесс повторяется, но с противоположным направлением тока. Напряжение на обкладках конденсатора меняется по закону V = = V₀ cos w₀t, а ток в катушке индуктивности I = I₀ sin (w₀t, т. е. в К. к. возбуждаются собственные гармонич. колебания напряжения и тока с частотой соо = = 2л/Т₀, где Т₀ - период собств. колебаний, равный То = 2л№(LC). В К. к. дважды за период происходит перекачка энергии из электрич. поля конденсатора в магнитное поле катушки индуктивности и обратно.

В реальных К. к., однако, часть энергии теряется. Она тратится на нагрев проводов катушки, обладающих активным сопротивлением, на излучение электромагнитных волн в окружающее пространство и потери в диэлектриках (см. Диэлектрические потери), что приводит к затуханию колебаний. Амплитуда колебаний постепенно уменьшается, так что напряжение на обкладках конденсатора меняется уже по закону: V = V₀e-^бtcos wt, где коэфф. 8 = R/2L - показатель (коэфф.) затухания, а w = №(w₀²-б²⁾ - частота затухающих колебаний. T. о., потери приводят к изменению не только амплитуды колебаний, но и их периода Т = 2л/w. Качество К. к. обычно характеризуют его добротностью

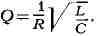
Величина Q определяет число колебаний, к-рое совершит К. к. после однократной зарядки его конденсатора, прежде чем амплитуда колебаний уменьшится в е раз (е - основание натуральных логарифмов).

Рис. 1. Колебательный контур.

Рис. 2. Колебательный контур с источником переменной эдс U=U₀ cos t.

Рис. 3. Резонансная кривая колебательного контура: w0 - частота собственных колебаний; Q - частота вынужденных колебаний; AQ -полоса частот вблизи w₀, на границах которой амплитуда колебаний V = 0,7 Vмакс. Пунктир - резонансная кривая двух связанных контуров.

Если включить в К. к. генератор с переменной эдс: U = U₀ cos Qt (рис. 2), то в К. к. возникнет сложное колебание, являющееся суммой его собств. колебаний с частотой w0 и вынужденных с частотой Q. Через нек-рое время после включения генератора собств. колебания в контуре затухнут и останутся только вынужденные. Амплитуда этих стационарных вынужденных колебаний определяется соотношением

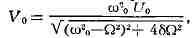
т. е. зависит не только от амплитуды внешней эдс Uo, но и от её частоты Q. Зависимость амплитуды колебаний в К. к. от частоты внешней эдс наз. резонансной характеристикой контура (рис. 3). Резкое увеличение амплитуды имеет место при значениях О, близких к собств. частоте wо К. к. При Q = wо амплитуда колебаний У_макс в Q раз превышает амплитуду внешней эдс U. Т. к. обычно 10 < Q < 100, то К. к. позволяет выделить из множества колебаний те, частоты к-рых близки к wо. Именно это свойство (избирательность) К. к. используется на практике. Область (полоса) частот AQ вблизи wо, в пределах которой амплитуда колебаний в К. к. меняется мало (рис. 3), зависит от его добротности Q. Численно Q равно отношению частоты соо собств. колебаний к ширине полосы частот ДО.

Для повышения избирательности К. к. необходимо увеличивать Q. Однако рост добротности сопровождается увеличением времени установления колебаний в К. к. Изменения амплитуды колебаний в контуре с высокой добротностью не успевают следовать за быстрыми изменениями амплитуды внешней эдс. Требование высокой избирательности К. к. противоречит требованию передачи быстро изменяющихся сигналов. Поэтому, напр., в усилителях телевизионных сигналов искусственно снижают добротность К. к. Часто используются схемы с двумя или несколькими связанными между собой К. к. Такие системы при правильно подобранных связях обладают почти прямоугольной резонансной кривой (пунктир, рис. 3).

Кроме описанных линейных К. к. с постоянными L и С, применяются нелинейные К. к., параметры к-рых L или С зависят от амплитуды колебаний. Напр., если в катушку индуктивности К. к. вставлен железный сердечник, то намагниченность железа, а с ним и индуктивность L катушки меняется с изменением тока, текущего через неё. Период колебания в таком К. к. зависит от амплитуды, поэтому резонансная кривая приобретает наклон, а при больших амплитудах становится неоднозначной (рис. 4). В последнем случае имеют место скачки амплитуды при плавном изменении частоты Q внешней эдс.

Рис. 4. Резонансная кривая нелинейного контура.

Нелинейные эффекты проявляются тем сильнее, чем меньше потери в К. к. В К. к. с низкой добротностью нелинейность вообще не сказывается на характере резонансной кривой.

К. к. обычно применяются в качестве резонансной системы генераторов и усилителей в диапазоне частот от 50 кгц до 250 Мгц. На более высоких частотах роль К. к. играют отрезки двухпроводных и коаксиальных линий, а также объёмные резонаторы.

Лит.: Стрелков С. П., Введение в теорию колебаний, М.- Л., 1951.

В. Н. Парыгин.