КИНЕМАТИКА (от греч. kinema, род. падеж kinematos - движение), раздел механики, посвящённый изучению геом. свойств движений тел без учёта их масс и действующих на них сил. Излагаемое ниже относится к К. движений, рассматриваемых в классич. механике (движения макроскопич. тел со скоростями, малыми по сравнению со скоростью света). О К. движений со скоростями, близкими к скоростям света, см. Относительности теория, а о движениях микрочастиц - Квантовая механика.

Устанавливаемые в К. методы и зависимости используются при кинематич. исследованиях движений, в частности при расчётах передач движений в различных механизмах, машинах и др., а также при решении задач динамики. В зависимости от свойств изучаемого объекта К. разделяют на К. точки, К. твёрдого тела и К. непрерывной изменяемой среды (деформируемого тела, жидкости, газа).

Движение любого объекта в К. изучают по отношению к нек-рому телу (тело отсчёта); с ним связывают т. н. систему отсчёта (оси х, у, z на рис. 1), с помощью к-рой определяют положение движущегося объекта относительно тела отсчёта в разные моменты времени. Выбор системы отсчёта в К. произволен и зависит от целей исследования. Напр., при изучении движения колеса вагона по отношению к рельсу систему отсчёта связывают с землёй, а при изучении движения того же колеса по отношению к кузову вагона - с кузовом и т. д. Движение рассматриваемого объекта считается заданным (известным), если известны ур-ния, наз. ур-ниями движения (или графики, таблицы), позволяющие определить положение этого объекта по отношению к системе отсчёта в любой момент времени.

Рис. 1.

Осн. задача К. заключается в установлении (при помощи тех или иных матем. методов) способов задания движения точек или тел и в определении по уравнениям их движений соответствующих кинематич. характеристик движения таких, как траектории, скорости и ускорения движущихся точек, угловые скороди и угловые ускорения вращающихся тел и др. Для задания движения точки пользуются одним из 3 способов: естественным, координатным или векторным:

а) естественный (или траекторный), применяемый, когда известна траектория точки по отношению к выбранной системе отсчёта. Положение точки опре-1еляется расстоянием s = O₁M от выбранного на траектории начала отсчёга O₁, измеренным вдоль дуги траектории и взятым с соответствующим знаком (рис. 1), а закон движения даётся уравнением S = f(t), выражающим зависимость s от времени t. Напр., если задано, что s - 3t² - 1, то в начальный момент времени to = О, s₀ = -1м (точка находится слева от начала О на расстоянии 1 м), в момент t₁= 1 сек, S₁ = 2 м (точка справа от O₁на расстоянии 2 м) и т. д. Зависимость s от t может быть также задана графиком движения, нa к-ром в выбранном масштабе отлокены вдоль оси t время, а вдоль оси s - расстояние (рис. 2), или таблицей, где в одном столбце даются значения f, а в другом соответствующие им знания s (подобный способ применяется, напр., в ж.-д. расписании движения поезда).

б) Координатный, при к-ром положеше точки относительно системы отсчёта определяется к.-н. тремя координатами, напр. прямоугольными декартовыми x, y, z, а закон движения задаётся 3 ур-ниями х = ft(t), у = f₂(0, z = f₃(t) Исключив из этих ур-ний время t, можно найти траекторию точки.

в) Векторный, при к-ром положение точки по отношению к системе отсчёта определяется её радиусом-вектором г, проведённым от начала отсчёта до двикущейся точки, а закон движения дается векторным ур-нием r = r(t). Траектория точки - годограф вектора r.

Осн. кинематич. характеристиками движущейся точки являются её скорость и ускорение, значения к-рых определяются по ур-ниям движения через первые и вторые производные по времени от s или от х, у, z, или от г (см. Скорсть, Ускорение).

Способы задания движения твёрдого тела зависят от вида его движения, и число ур-ний движения - от числа степеней свободы тела (см. Стегеней свободы число). простейшими являются поступательное движенue и вращательное движение твёрдого тела. При поступательном движении все точки тела движутся одинаково, и его движение задаётся и изучается так же, как движение одной точен. При вращательном движении вокруг неподвижной оси г (рис. 3) тело имеет одну степень свободы; его положение определяется углом поворота ф, а закон движения задаётся ур-нием ф =f(t). Осн. кинематич. характеристиками являются угловая скорость и угловое ускорение тела.

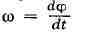
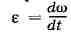
 Величины со и е изображаются в виде векторов, направленных вдоль оси вращения. Зная со и е, можно определить скорость и ускорение любой точки тела.

Более сложным является движение тела, имеющего одну неподвижную точку и обладающего 3 степенями свободы (напр., гироскоп, или волчок). Положение тела относительно системы отсчёта определяется в этом случае к.-н. 3 углами (напр., Эйлера углами: углами прецессии, нутации и собственного вращения), а закон движения - ур-ниями, выражающими зависимость этих углов от времени. Осн. кинематич. характеристиками являются мгновенная угловая скорость со и мгновенное угловое ускорение е тела. Движение тела слагается из серии элементарных поворотов вокруг непрерывно меняющих своё направление мгновенных осей вращения ОР, проходящих через неподвижную точку О (рис. 4).

Самым общим случаем является движение свободного твёрдого тела, имеющего 6 степеней свободы. Положение тела определяется 3 координатами одной из его точек, наз. полюсом (в задачах динамики за полюс принимается центр тяжести тела), и 3 углами, выбираемыми так же, как для тела с неподвижной точкой; закон движения тела задаётся 6 ур-ниями, выражающими зависимости названных координат и углов от времени. Движение тела слагается из поступательного вместе с полюсом и вращательного вокруг этого полюса, как вокруг неподвижной точки. Таким, напр., является движение в воздухе артиллерийского снаряда или самолёта, совершающего фигуры высшего пилотажа, движение небесных тел и др. Осн. кинематич. характеристиками являются скорость и ускорение поступательной части движения, равные скорости и ускорению полюса, и угловая скорость и угловое ускорение вращения тела вокруг полюса. Все эти характеристики (как и кинематич. характеристики для тела с неподвижной точкой) вычисляются по ур-ниям движения; зная эти характеристики, можно определить скорость и ускорение любой точки тела. Частным случаем рассмотренного движения является плосконаправленное (или плоское) движение твёрдого тела, при к-ром все его точки движутся параллельно нек-рой плоскости. Подобное движение совершают звенья мн. механизмов и машин.

В К. изучают также сложное движение точек или тел, т. е. движение, рассматриваемое одновременно по отношению к двум (и более) взаимно перемещающимся системам отсчёта. При этом одну из систем отсчёта рассматривают как основную (её еще наз. условно неподвижной), а перемещающуюся по отношению к ней систему отсчёта наз. подвижной; в общем случае подвижных систем отсчёта может быть несколько.

При изучении сложного движения точки её движение, а также скорость и ускорение по отношению к основной системе отсчёта наз. условно абсолютными, а по отношению к подвижной системе - относительными. Движение самой подвижной системы отсчёта и всех неизменно связанных с ней точек пространства по отношению к основной системе наз. переносным движением, а скорость и ускорение той точки подвижной системы отсчёта, с к-рой в данный момент совпадает движущаяся точка, наз. переносной скоростью и переносным ускорением. Напр., если осн. систему отсчёта связать с берегом, а подвижную с пароходом, идущим по реке, и рассмотреть качение шарика по палубе парохода (считая шарик точкой), то скорость и ускорение шарика по отношению к палубе будут относительными, а по отношению к берегу - абсолютными; скорость же и ускорение той точки палубы, к-рой в данный момент касается шарик, будут для него переносными. Аналогичная терминология используется и при изучении сложного движения твёрдого тела.

Осн. задачи К. сложного движения заключаются в установлении зависимостей между кинематич. характеристиками абс. и относит, движений точки (или тела) и характеристиками движения подвижной системы отсчёта, т. е. переносного движения. Для точки эти зависимости являются следующими: абс, скорость точки равна геом. сумме относительной и переносной скоростей, т. е.

v_a = v_отн+v_пер

а абс. ускорение точки равно геом. сумме трёх ускорений - относительного, переносного и поворотного, или кориолисова (см. Кориолиса ускорение), т. е.

w_а = w_отн + w_пер+w_кор.

Для твёрдого тела, когда все составные (т. е. относительные и переносные) движения являются поступательными, абс. движение также является поступательным со скоростью, равной геом. сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, напр., у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геом. сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений (см. Винтовое движение).

В К. непрерывной среды устанавливаются способы задания движения этой среды, рассматривается общая теория деформаций и определяются т. н. ур-ния неразрывности, отражающие условия непрерывности среды.

Лит. см. при ст. Механика.

С. М. Торг.

КИНЕМАТИКА ЗВЁЗДНЫХ СИСТЕМ, раздел звёздной астрономии; то же, что звёздная кинематика.

КИНЕМАТИКА МЕХАНИЗМОВ, раздел теории машин и механизмов, в к-ром изучают геом. сторону движения частей (звеньев) механизма, пренебрегая вызывающими его причинами. Исследования К. м. основываются на положении о том, что любой механизм состоит из подвижно соединённых твёрдых тел - звеньев, движения к-рых определяются движением одного или неск. звеньев, наз. ведущими.

К. м. решает задачи кинематич. анализа и кинематич. синтеза (см. Синтез механизмов). Осн. задачи кинематич. анализа: определение положений звеньев, траекторий отд. точек механизма, угловых скоростей и ускорений звеньев, лилейных скоростей и ускорений отд. точек механизма. Для решения каждой из этих задач должны быть заданы постоянные геом. параметры механизма, определяющие его кинематич. свойства и законы движения ведущих звеньев. Напр., для плоского шарнирного механизма (рис. 1) должны быть известны расстояния между центрами шарниров и закон движения ведущего звена АВ. Для кулачкового механизма (рис. 2) должны быть заданы профиль кулачка 1 и закон его движения, радиус ролика 3, расстояния между центрами шарниров С и D, А и D. Положения звеньев определяют графич. и аналитич. методами.

Рис. 1. Плоский шарнирный механизм.

Рис. 2. Кулачковый механизм.

Более простые графич. методы заключаются в следующем. Если для механизма (рис. 1) известно положение звена АВ и расстояния между центрами шарниров, можно положения всех остальных звеньев определить засечками циркуля. Т. о., задача для плоских механизмов всегда может быть сведена к определению точек пересечения плоских кривых. Графич. построения для пространств, механизмов усложняются, т. к. они связаны с определением линий и точек пересечения пространств. фигур. Однако в пределах точности графич. построений всегда можно построить положения всех звеньев плоских и пространств, механизмов любой сложности.

Аналитич. методы позволяют определять положения звеньев с заранее заданной точностью. Задача сводится к решению системы нелинейных ур-ний. Для типовых механизмов разработаны программы вычислений на ЭВМ.

Траектории отдельных точек механизма определяют обычно совместно с определением положений звеньев, причём выполняется графич. построение или аналитич. исследование только тех траекторий, от вида к-рых зависит движение рабочих органов механизма. Траектории, описываемые точками механизма, весьма разнообразны и в нек-рых случаях представляют собой сложные плоские или пространств, кривыс. Напр., траектория, описываемая точкой М (рис. 1), является алгебраич. кривой 6-го порядка. Траектории точек, лежащих на звене ME, представляют уже кривые 14-го порядка.

Определение скоростей звеньев и отдельных точек механизмов - наиболее разработанный раздел К. м., располагающий графич. методами кинематич. диаграмм и планов скоростей и аналитич. методом. Для определения скоростей к.-л. точки строят диаграмму изменения пути этой точки по времени, используя данные, полученные при определении положений звеньев, а затем, применяя графич. дифференцирование, строят диаграмму изменения скорости по времени (см. Графические вычисления). Это метод наиболее простой, однако характеризуется небольшой точностью. Метод планов скоростей применим для плоских и пространств, механизмов. При построении планов скоростей используют соотношения между векторами скоростей различных точек механизма. Точность метода планов скоростей, как и всякого графич. метода, ограничена, поэтому при исследовании механизмов, для к-рых требуется повышенная точность кинематич. расчёта, предпочтительно применение аналитич. методов, к-рые всегда можно свести к системе линейных ур-ний.

Ускорения точек механизма определяют по планам ускорений и аналитич. методом (решение систем линейных ур-ний). Метод кинематич. диаграмм для определения ускорений, как правило, не применяется, т. к. его точность зависит от точности графич. дифференцирования предварительно построенной диаграммы изменения скорости по времени, т. е. при решении возможно накопление ошибок. Для нек-рых быстроходных механизмов определяют не только ускорения 1-го порядка, но и ускорения 2-го порядка, к-рые иногда наз. рывками. Если точка совершает прямолинейное движение, то ускорение 2-го порядка равно первой производной от ускорения 1-го порядка по времени или третьей производной от пути по времени. Ускорение 2-го порядка находят по плану рывков или аналитическим методом (решение системы линейных уравнений).

Задачи кинематич. синтеза механизмов являются обратными рассмотренным задачам кинематич. анализа. Искомыми величинами в них являются постоянные параметры механизма, к-рые определяются по заданным кинематич. условиям, т. е. по траекториям нек-рых точек звеньев механизма, скорости и ускорению звеньев и отдельных точек. Задачи синтеза механизмов отличаются большей сложностью, чем задачи кинематич. анализа.

Лит.: Артоболевский И. И., Теория механизмов, 2 изд., М., 1967; Добровольский В. В., Теория механизмов, 2 изд., М., 1953.

И. И. Артоболевский, Н. И. Левитский.

КИНЕМАТИКА РЕЛЬЕФА, раздел геоморфологии, изучающий изменение взаимного положения точек земной поверхности во времени. В отличие от морфографии и морфометрии, наблюдающих рельеф в статике, К. р. изучает земную поверхность в движении, но вне зависимости от вызывающих движение сил и агентов. Это последнее ограничение отличает К. р. от динамики рельефа. Понятие "К. р." предложено сов. геоморфологом А. С. Девдариани.

Лит.: Девдариани А. С., Измерение перемещений земной поверхности, М., 1964.

КИНЕМАТИЧЕСКАЯ ВЯЗКОСТЬ,кинематический коэффициент вязкости, отношение обычного коэффициента вязкости л (называемого также динамическим) к плотности вещества р; обозначается v (см. Вязкость). Единицей К. в. в Международной системе единиц служит м²/сек. Дольная единица К. в. см²/сек наз. стоке. 1 м²/сек = 10⁴ ст.

КИНЕМАТИЧЕСКАЯ ПАРА, подвижное сопряжение двух твёрдых звеньев, налагающее ограничения на их относительное движение условиями связи. Каждое из условий связи устраняет одну степень свободы, т. е. возможность одного из 6 независимых относительных движений в пространстве. В прямоугольной системе координат возможно 3 постулат, движения (в направлении 3 осей координат) и 3 вращательных (вокруг этих осей). По числу условий связи S К. п. делятся на 5 классов. Число степеней свободы К. п. W = 6 - S. Внутри каждого класса К. п. делятся на виды по оставшимся возможным относительным движениям звеньев. По характеру соприкосновения звеньев выделяют низшие К. п.- с контактом по поверхностям, и высшие - с контактом по линиям или в точках, Высшие К, п, возможны всех 5 классов и мн. видов; низшие - только 3 классов и 6 видов (рис. 1). Различают также геометрически замкнутые и незамкнутые К. п. В первых постоянное соприкосновение поверхностей обеспечивается формой их элементов (напр., все К. п. на рис. 1), во вторых - для замыкания требуется прижимающая сила, т. н. силовое замыкание (напр., в кулачковом механизме). Условно к К. п. относят нек-рые подвижные сопряжения с неск. промежуточными телами качения (напр., шарико- и роликоподшипники) и с промежуточными деформируемыми элементами (напр., т. н. безлюфтовые шарниры приборов с плоскими пружинами; рис. 2).

Рис. 1. Кинематические пары: а - высшие, б - низшие.

Рис. 2. Схема безлюфтового шарнира: 1 -неподвижная деталь; 2 - деформируемые элементы (плоские пружины); 3 - рычаг.

Лит. см. при ст. Машин и механизмов теория.

Н. Я. Ниберг.

КИНЕМАТОГРАФИИ ИНСТИТУТ Всесоюзный государственный (ВГИК), готовит для кинематографии и телевидения сценаристов, режиссёров, актёров, операторов, киноведов-редакторов, художников по оформлению фильмов, экономистов. Осн. в 1919 как Гос. школа кинематографии, с 1925 - кинотехникум, с 1930 - Гос. ин-т кинематографии, с 1934 - ВГИК. В составе ин-та (1972): ф-ты - постановочный (с отделениями режиссёрским и актёрским), операторский, сценарно-киноведческий, художеств, и экономический; заочное отделение, аспирантура; 17 кафедр, н.-и. сектор, 10 уч. лабораторий, уч. киностудия, фильмотека (ок. 3,5 тыс. копий фильмов), в библиотеке св. 200 тыс. тт.

В 1972/73 уч. г. во ВГИКе обучалось ок. 1,5 тыс. студентов (в т. ч. студенты из 35 зарубежных гос-в); работало ок. 200 преподавателей, из них 26 профессоров, докторов наук и 130 доцентов, кандидатов наук. ВГИКу предоставлено право принимать к защите докторские п кандидатские диссертации. В работе ВГИКа принимали участие крупнейшие мастера и теоретики кино - С. М. Эйзенштейн, В. И. Пудовкин, А. П. Довженко, М. И. Ромм, Л. В. Кулешов и др. В ин-те преподают ведущие деятели сов. кинематографии - С. А. Герасимов, А. Д. Головня, Е. Л. Дзитан, А. Б. Столпер, И. П. Копалин, А. М. Згуриди, Л. В. Косматов, Б. И. Волчек, Л. А. Кулиджанов, Б. А. Бабочкин, Т. Ф. Макарова, С. Ф. Бондарчук, художники И. П. Иванов-Вано, М. А. Богданов, С. М. Каманин, киноведы Н. А. Лебедев, В. Н. Ждан, Р. Н. Юренев и др. Среди выпускников ВГИКа известные режиссёры Г. Н. Чухрай, С. И. Ростоцкий, Т. Е. Абуладзе, Р. Д. Чхеидзе, В. Г. Жалакявичюс, В. М. Шукшин, актёры Р. Д. Нифонтова, Т. П. Сёмина, В. В. Тихонов, Н. Н. Рыбников, В. С. Ивашов и др. За годы существования ВГИК подготовил ок. 5 тыс. специалистов. Ин-т издаёт (с 1965) сб. "Вопросы истории и теории кино", ежегодник "Кинематограф сегодня" (с 1967).

А.Н.Грошев.

КИНЕМАТОГРАФИЯ (от греч. kinema, род. падеж kinematos - движение и ...графия), отрасль культуры и хозяйства, осуществляющая произ-во кинофильмов и показ их зрителю. Как наиболее массовый вид иск-ва (см. Киноискусство) является важным средством политич. и науч. пропаганды. К. располагает средствами кинотехники. Произ-во фильмов сосредоточено на киностудиях. Изготовлением киноплёнки и аппаратуры занимается кинопромышленность. Фильмы демонстрируются в кинотеатрах, на кинопередвижках, по телевидению.

КИНЕСКОП (от греч. kinesis - движение и skopeo - смотрю), приёмная телевизионная трубка, электроннолучевая трубка для воспроизведения телевизионных изображений. К. применяется для наблюдений чёрнобелых и цветных изображений непосредственно или посредством проецирования изображений на большой экран, для съёмки изображений на фото- или киноплёнку, в качестве источника света и устройства разложения изображения на элементы при передаче по методу бегущего луча (см. Камера с бегущим лучом). В К. (рис. 1 и 2) сила тока электронного луча, выходящего из электронного прожектора, изменяется (модулируется) в соответствии с изменениями амплитуды сигналов, поступающих на управляющий электрод (модулятор). Под действием ускоряющего напряжения на аноде и отклоняющей системы промодулированный луч высвечивает с переменной яркостью на электролюминесцентном экране строку за строкой, воспроизводя кадр за кадром передаваемое изображение (см. Телевизионная развёртка). Экран изготовляется из порошкообразного люминофора определённого состава или смеси люминофоров, к-рые наносятся на внутр. поверхность дна колбы К. В местах падения электронного луча на экране появляется свечение, цвет к-рого зависит от состава люминофора. Во избежание размазывания изображения движущихся объектов выбираются люминофоры с малым временем послесвечения (менее 0,1 сек). У большинства К. обращённую внутрь колбы поверхность экрана покрывают тонкой (ок. 0,5-1,0 мкм), прозрачной для электронов, алюминиевой плёнкой, Отражая свет, возникающий при бомбардировке экрана электронами луча, плёнка увеличивает его светоотдачу на 30-50%, Она служит также защитой люминофора в центральной части экрана от разрушения потоком отрицат, ионов, т, е. от образования т. н. "ионного пятна". В отсутствие алюминиевого слоя для защиты люминофора применяется т. н. ионная ловушка. Осн. типы изготавливаемых в СССР К. для непосредств. наблюдения чёрно-белых изображений (рис. 1) имеют прямоугольную форму экрана с размерами по диагонали 6, 11, 16 и 23 см (для переносных транзисторных телевизоров), 35,43,47,59, 61, 65 и 67 см. Чаще всего фокусировка луча производится посредством электростатич. систем, отклонение - магнитных. Углы отклонения луча (полный "раствор") равны 70, 90 или 110°. Близкое к белому свечение экрана достигается применением порошкообразной смеси двух люминофоров, дающих (при свечении) дополнительные цвета. Обычно используют активированный серебром сульфид цинка (синее свечение) н активиров. серебром или медью шшко-кадмиевый сульфид (жёлтое свечение). Напряжение на аноде К. равно 12-20 кв, сила тока луча - 300-500 ма. У К. с диагональю экрана до 23 см яркость свечения равна 30-40 нт, от 35 до 67 см - 50 - 150 нт.

Рис. 1. Схематическое устройство кинескопа для чёрно-белого телевидения: 1 - нить подогревателя катода; 2 - катод; 3 - управляющий электрод; 4 - ускоряющий электрод; 5 - первый анод; 6 - второй анод; 7 - проводящее покрытие (акводаг); 8 - катушки вертикального отклонения луча; 9 - катушки горизонтального отклонения луча; 10 - электронный луч; 11 - экран; 12 - вывод второго анода.

Рис. 2. Схематическое устройство цветного кинескопа с теневой маской типа 59ЛКЗЦ: 1 - экран; 2- люминофорные точки (триады); 3 - мелкоструктурная цветоделительная маска; 4 - электронный прожектор; 5 - отклоняющая система; 6 - система радиального свечения; 7 - магнит чистоты цвета; 8 - магнит смещения луча.

Действие К. для непосредств. наблюдения цветных изображений основано на свойстве глаз человека воспринимать цвета как результат смешения в определённых количеств, соотношениях трёх осн. цветов: красного, зелёного и синего. В наиболее распространённом в СССР и зарубежных странах цветном К. с теневой маской (рис. 2) экран выполнен в виде мозаики (рис. 3). Она состоит из множества (ок. 1,5 млн.) люминофорных "точек", светящихся под действием трёх электронных лучей: красным (напр., из активиров. марганцем фосфата цинка), зелёным (напр., из активиров. серебром селенида цинка) и синим (напр., из активиров. серебром сульфида цинка) цветами. "Точки" люминофоров 3 видов образуют группы, систематически повторяющиеся вдоль строк мозаики. Каждая такая группа по размерам соответствует одному элементу телевиз. изображения (см. Телевизионный сигнал), Между прожектором и экраном, на нек-ром расстоянии от последнего, размещена тонкая металлич. пластина - теневая маска, имеющая ок. 500 000 отверстий диаметром, составляющим доли мм. 3 электронных луча из 3 прожекторов одновременно проходят через к.-л. отверстие.

Рис. 3. Мозаика (триады) экрана цветного кинескопа с теневой маской: К - красные, 3- зелёные, С-синие люминофорные "точки".

Один из лучей всегда попадает на точечный люминофор, светящийся красным цветом, второй - зелёным, третий - синим. Телевиз. развёртка изображения осуществляется общей магнитной отклоняющей системой, а одновременное сведение 3 лучей в к.-л. отверстие маски - 3 дополнит, индивидуальными системами отклонения. Для исключения засветки "чужого" люминофора служит магнит чистоты цвета. Поворотом его электронный луч направляют на "свой" люминофор. Лучи модулируются соответствующими телевизионными сигналами, несущими информацию о цветности и яркости отд. элементов передаваемого изображения (см. Цветное телевидение), На цветном К. можно получать также чёрно-белое изображение. Изготавливаемые в СССР К. с теневой маской имеют прямоугольную форму алюминиров. экрана с размерами по диагонали 40 и 59 см; напряжение на аноде 20-25 кв и яркость экрана (в белом цвете) 60 нт (при суммарной силе тока лучей 450-1250 мка). Однако К. с теневой маской достаточно сложны в изготовлении и эксплуатации. В Сов. Союзе и за рубежом разрабатываются (1972) более простые и надёжные цветные К. однопрожекторной системы с линейчатым экраном и фокусирующей сеткой (т. н. хроматрон). Экран хроматрона состоит из вертикальных полосок люминофоров красного, синего и зелёного цветов свечения, Против полосок люминофоров красного и синего свечения и параллельно им натянуты проволоки фокусирующей сетки, Вследствие разности потенциалов сетки и экрана между проволоками образуются цилиндрич. электронные линзы, дополнительно фокусирующие электронный луч, к-рый направляется на полосы люминофора зелёного свечения. При поочерёдном подведении к модулирующему электроду видеосигнала, содержащего информацию о красной, зелёной и синей составляющих изображения, и одновременной коммутации отклоняющего напряжения на сетке поочерёдно получаются все осн. цвета. Ввиду инерционности зрения эти цвета сливаются в одно цветное изображение. К достоинствам хроматрона относятся: применение одного прожектора и простой магнитной отклоняющей системы, отсутствие дополнит, магнитов сведения лучей и чистоты цвета. В отличие от хроматрона, в выпускаемом в Японии цветном К., но с тремя прожекторами (т. н. тринитроне), происходит одновременная передача цветов, что позволяет получить большую яркость изображения и лучшее качество цветовоспроизведения по сравнению с трёхпрожекторным К. с теневой маской, т. к. лучше используются токи лучей.

Для получения телевиз. изображений на большом экране (площадью 3-4 м²) выпускаются проекционные К. с диаметром экрана 6, 10, 13 см и высокой яркостью его свечения (25-30 тыс. нт) при силе тока луча 100-150 мка (для 6- и 10-см экранов) и 2000 мка (для 13-см экрана).

Лит.: Телевидение, под ред. П. В. Шмакова, 3 изд., М., 1970; Жигарев А. А., Электронная оптика и электроннолучевые приборы, М., 1972.

В. И. Баранов.

КИНЕТИКА (от греч. kinetikos - приводящий в движение), основная часть механики, включающая динамику - учение о движении тел под действием сил, и статику - учение о равновесии тел под действием сил.

"КИНЕТИКА И КАТАЛИЗ", научный журнал, орган Сибирского отделения АН СССР. Издаётся в Москве с 1960. Выходит 6 номеров в год. В журнале публикуются оригинальные теоретические и экспериментальные работы по кинетике хим. превращений в газах, растворах и твёрдых фазах, по исследованию промежуточных активных частиц (радикалов, ионов), горению, механизму гомогенного и гетерогенного катализа, по науч. основам подбора катализаторов, практически важным каталитич. процессам, влиянию процессов переноса вещества и тепла на кинетику хим. превращений, по методике расчёта и моделирования контактных аппаратов. Печатаются также обзоры по важнейшим вопросам катализа и кинетики хим. превращений. Тираж (1972) 1650 экз.

КИНЕТИКА ФИЗИЧЕСКАЯ, теория неравновесных макроскопич. процессов, т. е. процессов, возникающих в системах, выведенных из состояния теплового (термодинамического) равновесия. К К. ф. можно отнести термодинамику неравновесных процессов, кинетическую теорию газов (в том числе плазмы), теорию процессов переноса в твёрдых телах, а также общую статистич. теорию неравновесных процессов, к-рая начала развиваться лишь в 50-е гг.

Все неравновесные процессы в адиабатически изолированных системах (системах, не обменивающихся теплом с окружающими телами) являются необратимыми процессами - происходят с увеличением энтропии; в равновесном состоянии энтропия достигает максимума.

Как и в случае равновесных состояний, в К. ф. возможны два способа описания систем: феноменологический, или термодинамический (термодинамика неравновесных процессов), и статистический.

Термодинамический метод описания неравновесных процессов При термодинамич. описании неравновесных процессов рассматривается изменение в пространстве и времени таких макроскопических параметров состояния системы, как плотность массы i-го компонента pi (r, t), плотность импульса pu (r, t), локальная темп-ра Т (г, t), поток массы i-го компонента ji (r, t), плотность потока внутр. энергии q (r, t) [здесь r - координата, t - время, и- ср. массовая скорость, р - плотность массы]. В равновесном состоянии системы р, pi, Т постоянны, а потоки равны нулю.

Термодинамич. описание неравновесных процессов возможно лишь при достаточно медленном изменении параметров состояния в пространстве и во времени для состояний, близких к равновесным. Для газов это означает, что все термодинамич. параметры, характеризующие состояние системы, мало меняются на длине свободного пробега и за время, равное ср. времени свободного пробега молекул (ср. времени между двумя последоват. столкновениями молекул). Медленные процессы встречаются практически очень часто, т. к. установление равновесия происходит только после очень большого числа столкновений; к ним относятся: диффузия, теплопроводность, электропроводность и т. д. Отклонения от состояния термодинамич. равновесия характеризуются градиентами темп-ры, концентрации (рi/р) и массовой скорости (т. н. термодинамическими силами), а потоки энергии, массы i-го компонента и импульса связаны с термодинамич. силами линейными соотношениями. Коэффициенты в этих соотношениях наз. к инетическими коэффициентами.

Рассмотрим в качестве примера диффузию в бинарной смеси, т. е. процесс выравнивания концентрации компонентов в результате хаотического теплового движения молекул. Феноменологическое ур-ние, описывающее процесс диффузии, получают с помощью закона сохранения вещества и того опытного факта, что поток вещества одного из компонентов вследствие диффузии прямо пропорционален градиенту его концентрации (с обратным знаком). Коэфф. пропорциональности наз. коэффициентом диффузии. Согласно ур-нию диффузии, скорость изменения концентрации вещества со временем прямо пропорциональна дивергенции градиента концентрации с коэфф. пропорциональности, равным коэфф. диффузии.

Решение ур-ния диффузии позволяет определить время, в течение которого произойдёт выравнивание концентрации молекул в системе (напр., в сосуде с газом) за счёт диффузии (время релаксации). Время релаксации т_р имеет порядок: Тр ~ L²/D, где L - линейные размеры сосуда, a D-коэфф. диффузии. Это время тем больше, чем больше размеры сосуда и чем меньше коэфф. диффузии. Коэфф. диффузии пропорц. длине свободного пробега молекул X и их ср. тепловой скорости v. Поэтому время релаксации оказывается пропорциональным: т_р ~ L²/Xv = (L/X)²-X/v, где Xlv = т - ср. время свободного пробега. Очевидно, что Тр >>т при L >> X. Т. о., условие L >> X (размеры системы велики по сравнению с длиной свободного пробега молекул) является необходимым для того, чтобы процесс установления равновесного состояния можно было считать медленным.

Аналогичным образом устанавливаются ур-ния, описывающие теплопроводность, внутреннее трение, электропроводность и т, д, Коэфф. диффузии, теплопроводности и вязкости, а также уд. электропроводность в феноменология, теории должны быть определены экспериментально.

Перечисленные процессы наз. прямыми. Этим подчёркивается, что, напр., при диффузии градиент концентрации данного вещества вызывает поток этого же вещества; градиент темп-ры вызывает поток внутр. энергии, к-рая при постоянной концентрации молекул меняется только с темп-рой; электрич. ток вызывается градиентом потенциала и т. д.

Кроме прямых процессов, существуют ещё т. н. перекрёстные процессы. Примером перекрёстного процесса может служить термодиффузия - перенос вещества не вследствие градиента концентрации (это была бы обычная диффузия), а вследствие градиента темп-ры. Термодиффузия создаёт градиент концентрации, что приводит к появлению обычной диффузии. Если разность темп-р в системе поддерживается постоянной, то устанавливается стационарное состояние, при котором потоки вещества, вызванные градиентами темп-ры и концентрации, взаимно уравновешиваются. В смеси газов при этом концентрация молекул в местах повышенной темп-ры оказывается большей для молекул меньшей массы (данное явление используется для разделения изотопов).

Градиент концентрации в свою очередь создаёт поток внутренней энергии. В этом состоит процесс диффузионной теплопроводности. При наличии в теле заряженных частиц градиент темп-ры создаёт упорядоченное перемещение этих частиц - электрич. ток, наз. термоэлектрическим (см. Термоэлектрические явления).

В К. ф. важное значение имеет принцип симметрии кинетич. коэффициентов, установленный Л. Онсагером. В равновесном состоянии термодинамнч. параметры а. (давление, темп-pa и т. д.), характеризующие состояние макроскопич. системы, постоянны во времени: dai/dt = 0. Важнейшая функция состояния системы - энтропия S, зависящая от ai, в состоянии равновесия имеет максимум и, следовательно, её частные производные dS/dai = 0. При малом отклонении системы от равновесия производные dS/dat и dai/dt малы, но отличны от нуля, и между ними существуют приближённые линейные соотношения. Коэфф. пропорциональности в этих соотношениях и есть кинетич. коэффициенты. Если через y_ik обозначить коэфф., определяющий скорость изменения параметра системы at в зависимости от дS/да_k, то, согласно принципу Онсагера (в отсутствие магнитного поля и вращения системы как целого), имеет место равенство y_ik = у_ki. Принцип Онсагера вытекает из свойства микроскопич. обратимости, которая выражается в инвариантности ур-ний движения частиц системы относительно замены знака времени: t -> -t (см. Онсагера теорема). Из этого принципа, в частности, следует существование связи между коэфф., определяющим выделение током тепла из-за неравномерного нагрева проводника (Томсона эффект), и коэфф., определяющим выделение током тепла в спаях разнородных проводников или полупроводников (Пельтье эффект).

Статистический метод описания неравновесных процессов Статистическая теория неравновесных процессов является более детальной и глубокой, чем термодинамическая. В отличие от термодинамич. метода, статистич. теория на основе определённых представлений о строении вещества и действующих между молекулами силах позволяет вычислить кинетич. коэффициенты, определяющие интенсивность процессов диффузии, внутреннего трения (вязкости), электропроводности и т. д. Однако эта теория весьма сложна.

Статистич. метод описания систем как в равновесном, так и неравновесном состоянии основан на вычислении функции распределения. Для равновесных состояний имеются универсальные функции распределения координат и импульсов (или скоростей) всех частиц, определяющие вероятность того, что эти величины принимают фиксированные значения. Для систем, находящихся в тепловом контакте с окружающей средой, темп-pa к-рой постоянна, это - каноническое Гиббса распределение, а для изолированных систем - микроканоническое Гиббса распределение; оба распределения полностью определяются энергией системы.

Неравновесные состояния в гораздо большей степени (чем равновесные) зависят от микроскопических свойств систем: свойств атомов и молекул и сил взаимодействия между ними. Лишь в 1960-е гг. были разработаны общие методы построения функций распределения (по координатам и импульсам всех частиц системы), аналогичных канонич. распределению Гиббса, но описывающих неравновесные процессы.

С помощью функций распределения можно определить любые макроскопич. величины, характеризующие состояние системы, и проследить за их изменением в пространстве с течением времени. Это достигается вычислением статистич. средних (см. Статистическая физика). Нахождение функции распределения, зависящей от координат и импульсов всех частиц, является в общем случае неразрешимой задачей, т. к. оно эквивалентно решению ур-ний движения для всех частиц системы. Однако для практич. целей нет необходимости в знании точного вида этой функции распределения: она содержит слишком подробную информацию о движении отдельных частиц, к-рая не существенна для определения поведения системы в целом. В связи с этим используется приближённое статистич. описание с помощью более простых функций распределения, Для описания состояния газов ср. плотности достаточно знания т. н. одночастичной функции распределения f (p, r, t), дающей ср. число частиц с определёнными значениями импульсов р (или скоростей) и координат г. Для газов более высокой плотности необходимо знание двухчастичных (парных) функций распределения. Общий метод получения уравнений для одночастичных и более сложных функций (зависящих от координат и импульсов двух и более частиц) был разработан Н. Н. Боголюбовым, М. Борном, М. Грином и др. Эти уравнения наз. кинетическими. К их числу относится кинетическое уравнение Больцмана для разреженных газов, полученное Л. Больцманом из соображений, основанных на балансе частиц со скоростями в интервалах Av_x, Av_y, Av_z внутри объёма Ax Ay Az (v_x, v_y, v_z-проекции скорости v на координатные оси х, у, z). Разновидностями ур-ния Больцмана для ионизированного газа (плазмы) являются кинетич. ур-ния Л. Д. Ландау и А. А. Власова (см. Плазма).

Кинетич. ур-ния могут быть построены не только для газов, но и для малых возбуждений в конденсированных системах. Тепловое движение системы характеризуется различного рода возбуждениями. В газе это - поступат. движение составляющих его частиц и внутренние возбуждения атомов и молекул. В общем случае тепловое движение характеризуется возбуждениями более сложной природы. Так, в кристаллич. телах тепловое возбуждение можно представить в виде упругих волн, распространяющихся вдоль кристалла, точнее - волн, соответствующих нормальным колебаниям кристаллической решётки. В плазме коллективными возбуждениями являются колебания плотности электрич. заряда, вызванные дальнодействующими кулоновскими силами. В металлах возможны электронные возбуждения (переходы электронов из состояний внутри Ферми поверхности в состояния вне её), а в полупроводниках - ещё и дырочные возбуждения (появление свободных от электронов состояний в валентной зоне при переходе электронов в зону проводимости; см. Полупроводники), При низких температурах, в слабо возбуждённом состоянии, энергию возбуждения всегда можно представить в виде суммы нек-рых элементарных возбуждений, или, на квантовом языке, квазичастиц. Понятие о квазичастицах применимо не только для кристаллич. тел, но и для жидких, газообразных и аморфных, если темп-ра не слишком велика. Функции распределения для квазичастиц системы, находящейся в неравновесном состоянии, удовлетворяют кинетич. ур-нию.

В случае квантовых систем функция распределения зависит от спина частиц (или квазичастиц). В частности, для частиц с полуцелым спином равновесной функцией распределения служит распределение Ферми - Дирака, а для частиц (квазичастиц) с целым или нулевым спином - распределение Бозе - Эйнштейна (см. Статистическая физика).

В кинетич. ур-ниях наряду с внеш. воздействиями учитываются взаимодействия между частицами или квазичастицами, причём эти взаимодействия рассматриваются как парные столкновения. Именно эти взаимодействия приводят к установлению равновесных состояний. Во многих случаях функция распределения не зависит явно от времени. Такая функция наз. стационарной, она описывает процессы, течение к-рых не претерпевает изменений со временем, При стационарных процессах изменение функции распределения вследствие внешних воздействий компенсируется её изменением в результате столкновений.

В простых случаях можно грубо оценить изменение функции распределения f системы в результате столкновений, считая, что оно пропорционально величине отклонения от равновесной функции (т. к. только при отклонении от состояния равновесия столкновения меняют функцию распределения). Величина, обратная коэфф. пропорциональности в этом соотношении, называется временем релаксации. В общем случае учесть взаимодействие таким простым способом невозможно, и в кинетич. ур-ние входит т. н. интеграл столкновений, к-рый более точно учитывает результат изменения функции распределения вследствие взаимодействия частиц (квазичастиц).

Решая кинетич. ур-ние, находят неравновесную функцию распределения и вычисляют потоки энергии, массы и импульса, что позволяет получить ур-ния теплопроводности, диффузии и переноса импульса (ур-ние Навье - Стокса) с кинетич. коэффициентами, выраженными через молекулярные постоянные. [Однако кинетич. ур-ние можно построить лишь для газов (из частиц или квазичастиц)].

Основные принципы теории неравновесных процессов надёжно установлены. Разработаны методы построения ур-ний переноса энергии, массы и импульса в различных системах, не только в газах, а, напр., и в жидкостях. При этом получают выражения для кинетич. коэффициентов, входящих в эти ур-ния, через корреляционные функции (функции, описывающие корреляцию в пространстве и во времени) потоков этих физич. величин, т. е. в конечном счёте через молекулярные постоянные. Эти выражения очень сложны и могут быть вычислены лишь средствами совр. вычислит, математики.

Лит.: Гуревич Л. Э., Основы физической кинетики, М.- Л., 1940; Боголюбов Н. Н., Проблемы динамической теории в статистической физике, М. - Л.,, 1946; Гуров К. П., Основания кинетической теории. Метод Н. Н. Боголюбова, М., 1966; Ландау Л. Д., Лифшнц Е. М., Статистическая физика, М., 1964 (Теоретическая физика, т. 5); Климентович Ю. Л., Статистическая теория неравновесных процессов в плазме, М., 1964; Пригожий И. Р., Неравновесная статистическая механика, пер. с англ., М., 1964; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Гроот С., Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Честер Дж., Теория необратимых процессов, пер. с англ., М., 1966; Хаазе Р., Термодинамика необратимых процессов, пер. с нем., М., 1967.

Г. Я. Мякишев.

КИНЕТИКА ХИМИЧЕСКАЯ, кинетика химических реакций, учение о химических процессах - о законах их протекания во времени, скоростях и механизмах. С исследованиями кинетики хим. реакций связаны важнейшие направления совр. химии и хим. пром-сти: разработка рациональных принципов управления хим. процессами; стимулирование полезных и торможение и подавление нежелательных хим. реакций; создание новых и усовершенствование существующих процессов и аппаратов в хим. технологии; изучение поведения хим. продуктов, материалов и изделий из них в различных условиях применения и эксплуатации.

В реальных условиях, напр, в крупных пром. аппаратах, хим. процесс осложняется в связи с передачей тепла, выделяемого или поглощаемого в реакции, транспортом веществ в зону реакции, их искусств, или естеств. перемешиванием. Эти проблемы решает т. н. макрокинетика.

Вместе с тем мн. ур-ния, описывающие протекание во времени хим. реакций, пригодны и для описания ряда физ. процессов (распад радиоактивных ядер, деление ядерного горючего), а также для количеств, характеристики развития нек-рых биохим., в т. ч. ферментативных, и др. биол. процессов (нормальный и злокачественный рост тканей, развитие лучевого поражения, кинетич. критерии оценки эффективности лечения), К. х. лежит в основе исследования сложных процессов горения газов и взрывчатых веществ, помогает изучению процессов в двигателе внутр. сгорания. Т. о., можно говорить об общей кинетике, частным случаем к-рой является кинетика хим. реакций. Эти аналогии весьма удобны для практич. использования, но всегда следует иметь в виду принципиальные различия в природе рассматриваемых явлений.

Ввиду сложности реальных хим. систем и необходимости учёта большого числа факторов и условий проведения процесса, при выяснении оптимальных режимов получения нужных продуктов в совр. К. х. широко используются быстродействующие электронные вычислительные машины.

Историческая справка. Отдельные работы в области К. х. были выполнены ещё в середине 19 в. В 1850 нем. химик Л. Вильгельми изучил скорость инверсии тростникового сахара, в 1862-63 М. Бертло - скорость реакций этерификации. В работах Н. А. Меншуткина получили развитие (1882-90) такие осн. проблемы химии, как связь между строением веществ и их реакционной способностью, влияние среды на ход хим. превращения. В 80-х гг. 19 в. Я. Вант-Гофф и С. Аррениус сформулировали основные законы, управляющие простыми хим. реакциями, и дали трактовку этих законов, исходя из молекулярно-кинетич. теории. Дальнейшее развитие этих работ привело к созданию в 30-х гг. 20 в. Г. Эйрингом и М. Поляки на базе квантовой механики и статистич. физики теории абсолютных скоростей реакций, открывающей перспективы расчёта скоростей простых (элементарных) реакций, исходя из свойств реагирующих частиц (см. Активированный комплекс).

Параллельно развивались работы по изучению кинетики сложных реакций. Среди первых в этой области были исследования А. Н. Баха и Н. А. Шилова по реакциям окисления. Они включили в предмет К. х. представления о решающей роли промежуточных продуктов и промежуточных реакций в хим. превращении. Большую роль в разработке общих методов подхода к изучению сложных реакций сыграли работы М. Боденштейна. Выдающимся достижением теории сложных хим. процессов явилась созданная в 30-х гг. Н. Н. Семёновым общая теория цепных реакций. Широкие исследования механизма сложных кинетических процессов, особенно цепных реакций, были выполнены С. Н. Хингиелвудом.

Основные понятия и законы. Хим. реакция может протекать гомогенно, т. е. в объёме одной фазы, и гетерогенно, т. е. на границе раздела фаз. Наиболее полно разработана К. х. реакций в газовой фазе, т. к. она отправляется от хорошо развитой кинетич. теории газового состояния. В то же время интенсивно развивается кинетика реакций в жидкой фазе и в твёрдых телах. В зависимости от того, в какой форме подводится к реагирующей системе необходимая для реакций энергия (теплота, свет, электрич. ток, излучение, плазма, лазерные пучки, высокие и сверхвысокие давления, ударные волны), они подразделяются на тепловые, фотохимические, электрохимические, радиационно-химические и др.

В основе К. х. как учения о скоростях хим. превращений лежит действующих масс закон, согласно к-рому скорость реакции веществ А, В, С,... пропорциональна произведению их концентраций. Скорость реакции характеризуется обычно изменением за единицу времени концентрации к.-л. из исходных веществ или конечных продуктов реакции. Напр., скорость вступления в реакцию вещества А (уменьшение его концентрации в единицу времени) выражается ур-нием:

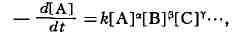
где k - константа скорости реакции, [А], [В], [С] ...-концентрации реагирующих веществ (в качестве действующих веществ могут выступать молекулы, радикалы и ионы, в зависимости от типа реакции); знак минус показывает, что концентрация вещества А убывает со временем. Сумма величин а, (3, у--- наз. порядком реакции. В зависимости от числа молекул, участвующих в элементарном акте хим. взаимодействия, различают реакции мономолекулярные, в к-рых реагируют отдельные молекулы одного вида, бимолекулярные - протекающие при двойном соударении (при встрече двух молекул), тримолекулярные - при тройном соударении. Реакции, требующие в элементарном акте встречи более трёх молекул, мало вероятны. Порядок простой гомогенной реакции совпадает с числом молекул, участвующих в элементарном акте реакции. Однако чаще всего такого совпадения не бывает. В частности, показатели а, (}, у... могут быть дробными величинами. Это говорит о том, что реакция имеет сложный механизм, т. е. протекает в несколько элементарных стадий, каждая из к-рых является строго моно-, би- или тримолекулярной реакцией. В тех случаях, когда сложная по существу реакция описывается простым кинетич. уравнением, говорят, что она имитирует простой закон протекания (см. Сложные реакции).

Температурная зависимость скорости реакции определяется ур-нием Аррениуса:

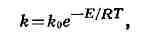
где k_oe - множитель, к-рый в ряде простейших случаев может быть предвычислен, исходя из молекулярно-кинетич. представлений о механизме элементарного акта, в - основание натуральных логарифмов, Е - энергия активации реакции, R - универсальная газовая постоянная, Т - абсолютная температура. На рис. 1 графически показано убывание со временем концентрации исходных веществ в случае реакций, удовлетворяющих простым законам. Кривые, показывающие изменение концентраций реагирующих веществ со временем, наз. кинетическими кривыми.

Рис. 1. Кинетические кривые химических реакций простых типов.

По механизму хим. процессы делятся на 3 основных типа: простые реакции между молекулами; радикальные, в т. ч. цепные реакции (протекающие через промежуточное образование свободных радикалов и атомов); ионные (идущие при участии ионов).

Кинетика реакций между молекулами. Реакции непосредственно между валентно-насыщенными молекулами весьмаредки, т. к. происходящая при этом перестройка молекул требует разрыва хим. связей, энергия к-рых достигает значительных величин (50-100 ккал/молъ, или 209,3418,7 кдж/моль). Поэтому в газовой фазе реакции идут чаще всего как цепные, а в жидкой фазе - и как цепные, и как ионные. Примерами реакций насыщенных молекул в газовой фазе могут служить:
1) мономолекулярная реакция распада азометана: CH₃N₂CH₃ -> С₂Н_б + N₂;
2) бимолекулярная реакция превращения йодистого нитрозила: NOI + NOI -> 2NO + I₂  и
3) тримолекулярная реакция окисления .окиси азота в двуокись азота: 2NO + О₂ -> 2NO₂.

Реакции, в к-рых превращение исходных веществ идёт по двум или нескольким направлениям, наз. параллельными; механизм и кинетич. закономерности реакций в разных направлениях могут быть самыми разнообразными - простыми и сложными (см. Параллельные реакции), Реакции, в к-рых превращение исходных веществ в конечные продукты происходит через несколько следующих друг за другом стадий с образованием промежуточных продуктов, наз. последовательными (см. Последовательные реакции).

На рис. 2 показаны кинетич. кривые для исходного, промежуточного и конечного веществ в последовательной реакции. Характерной особенностью этих кривых является наличие максимума у кривой промежуточного продукта и точки перегиба на кривой образования конечного продукта реакции. Однако эти особенности не могут служить однозначным признаком последовательной реакции. Известно много случаев, когда конечные продукты превращения ускоряют реакцию. Скорость таких автокаталитич. процессов вначале возрастает вследствие увеличения количества продукта, являющегося катализатором, а затем уменьшается вследствие израсходования исходных веществ (см. Автокатализ), Реакция, идущая под влиянием другой, протекающей одновременно и в том же участке пространства, наз. индуцированной, или сопряжённой (см. Сопряжённые реакции).

Кинетика цепных реакций. Реакции, в к-рых один первичный акт активации приводит к превращению большого числа молекул исходных веществ, наз. цепными. В реакции зарождения цепи образуется активная частица - свободный радикал или атом. Эта активная частица реагирует с молекулой исходного вещества, образуя молекулу продукта реакции и (вследствие неуничтожимости свободной валентности) регенерируя новую активную частицу; образовавшийся радикал в свою очередь реагирует с исходной молекулой и т. д. (неразветвлённая цепь). Энергия активации взаимодействия радикалов и атомов с молекулами не превышает 10 ккал/моль (41,86 кдж/моль), поэтому длина цепи из элементарных хим. реакций достигает тысяч и сотен тысяч звеньев. В нек-рых цепных реакциях увеличивается число свободных валентностей, что приводит к появлению новых активных центров, т. е. новых цепей. Т. о., цепь разветвляется и реакция ускоряется (становится нестационарной). Цепь обрывается в результате соединения (рекомбинации) двух радикалов, в случае реакции радикала с нек-рыми примесными частицами, соударения со стенкой сосуда. Скорость неразветвлённой цепной реакции вначале растёт, затем достигает постоянного значения и, наконец, медленно убывает. Скорость разветвлённой цепной реакции возрастает со временем, и при благоприятных условиях может произойти воспламенение реагирующей смеси. Достигнув максимального значения, скорость реакции уменьшается из-за расходования исходных веществ (подробнее см. Цепные реакции). В соответствии с этим кинетич. кривые цепных разветвлённых процессов имеют характерную S-образную форму (рис. 3). Точка перегиба на кривой отвечает максимуму скорости реакции.

Рис. 2. Изменение концентрации исходного 1, промежуточного 2 и конечного 3 веществ в последовательной реакции.

Рис. 3. Типичная кинетическая кривая цепного разветвлённого процесса. Формально аналогичный вид имеют и кривые автокаталитических реакций.

Основы теории цепных реакций разработаны и экспериментально подтверждены в исследованиях сов. учёного Н. Н. Семёнова и его школы. В СССР успешно изучаются скорость и механизм важнейших групп цепных процессов: полимеризации, крекинга, окисления. На базе цепной теории окислительных реакций разработаны новые высокоэффективные технологические процессы получения важных химических продуктов (в частности, мономеров для синтеза полимеров) путём окисления нефтяного сырья и углеводородных газов. Цепная теория процессов ингибированного окисления позволяет предотвращать окислительную порчу (старение) полимеров, смазочных масел и бензинов, пищевых продуктов и лекарственных препаратов. Ингибиторы окисления, или стабилизаторы окислит, процессов (см. Ингибиторы химические), - это важнейшие представители малотоннажных продуктов органич. синтеза.

Кинетика ионных реакций. Значительное число реакций в растворах протекает при участии ионов. Скорость ионных реакций сильно зависит от растворителей, т. к. в разных растворителях молекулы в разной степени диссоциированы на ионьт. Энергия активации реакции ионов с молекулами невелика: заряд иона снижает энергию активации. При изучении кинетики реакций в растворах учитывают влияние полярных групп, наличие большого межмолекулярного взаимодействия, влияние растворителя и т. п.

Кинетика гетерогенных каталитических реакций. Для реакций газов и жидкостей, протекающих у поверхности твёрдых тел (см. Катализ), по-видимому, имеют место те же 3 основных типа хим. превращений, к-рые были рассмотрены для гомогенных процессов, т. е. простые, радикально-цепные и ионные реакции. Различие заключается лишь в том, что в соответствующие кинетич. ур-ния входят концентрации реагирующих веществ в поверхностном адсорбционном слое (см. Адсорбция). Наблюдаются разные кинетич. зависимости, к-рые обусловлены характером адсорбции исходных веществ и продуктов реакции на поверхности. Основной суммарный кинетич. эффект катализатора заключается в снижении энергии активации реакции. Важной проблемой в области гетерогенного катализа является предвидение каталитич. действия. Представления и методы, свойственные теории гетерогенного катализа, всё больше сближаются с областью гомогенного катализа жидкофазных реакций, особенно при использовании в качестве катализаторов комплексных соединений переходных металлов. Выясняется механизм действия биол. катализаторов (ферментов), особенно с целью создания принципиально новых высокоэффективных катализаторов для хим. реакций.

Советскими и зарубежными учёными успешно разрабатываются и мн. др. актуальные проблемы К. х., напр., применение квантовой механики к анализу элементарного акта реакции; установление связей между строением веществ и кинетич. параметрами, характеризующими их реакционную способность; изучение кинетики и механизма конкретных сложных хим. реакций с применением новейших физ. экспериментальных методов и совр. вычислит. техники; использование кинетич. констант в инженерных расчётах в хим. и нефтехим. промышленности .

Лит.: Семенов Н. Н., О некоторых проблемах химической кинетики и реакционной способности, 2 изд., М., 1958; Кондратьев В. Н., Кинетика химических газовых реакций, М., 1958; Эмануэль Н. М., Кнорре Д. Г., Курс химической кинетики, 2 изд., М., 1969; Бенсон С., Основы химической кинетики, пер. с англ., М., 1964; Эмануэль Н. М., Химическая кинетика, в сб.: Развитие физической химии в СССР, М., 1967.

Н. М. Эмануэль.

КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ, раздел теоретич. физики, исследующий статистич. методами свойства газов на основе представлений о молекулярном строении газа и определённом законе взаимодействия между его молекулами. Обычно под К. т. г. понимается теория неравновесных процессов в газах, а теория равновесных состояний относится к равновесной статистич. механике. Область применения К. т. г.- собственно газы, газовые смеси и плазма. Основы К. т. г. были заложены во 2-й пол. 19 в. в работах Л. Болъцмана.

Газ представляет собой простейшую по сравнению с жидкостью и твёрдым телом систему. Среднее расстояние между молекулами газа много больше их размеров. Т. к. силы взаимодействия между электрически нейтральными атомами или молекулами являются короткодействующими (т. е. очень быстро убывают с увеличением расстояния между частицами и на расстояниях в неск. молекулярных диаметров практически уже не сказываются), то взаимодействие молекул происходит лишь при их непосредственном сближении - при столкновениях. Время столкновения гораздо меньше времени свободного пробега - времени между двумя последовательными столкновениями молекулы. Вследствие этого большую часть времени молекулы газа движутся свободно.

В К. т. г. наблюдаемые макроскопич. эффекты (давление, диффузия, теплопроводность и т. д.) рассматриваются как средний результат действия всех молекул исследуемого газа. Для вычисления этих средних Больцман ввёл функцию распределения f(c, r, t), зависящую от скоростей с и координат г молекул газа и времени t. Произведение f(v, r, t) Д"Дг даёт среднее число молекул со скоростями, лежащими в интервале от v до v + Ди, и координатами в интервале от г до г + Дг. Функция распределения f подчиняется кинетическому уравнению Больцман а. В этом ур-нии изменение f со временем рассматривается как результат движения частиц, действия на них внеш. сил и парных столкновений между частицами. Ур-ние Больцмана применимо лишь для достаточно разреженных газов. В состоянии статистического равновесия при отсутствии внеш. сил функция распределения зависит только от скоростей молекул и наз. Максвелла распределением.

Осн. задача К. т. г.- определение (из ур-ния Больцмана) вида функции распределения f, т. к. знание f(v, r, t) позволяет рассчитать средние величины, характеризующие состояние газа и процессы в нём, - среднюю скорость частиц, коэффициенты диффузии, вязкости, теплопроводности и др. (см. Кинетика физическая). Методы решения кинетич. ур-ния Больцмана были разработаны англ, учёными С. Чепменом и Д. Энскогом. Ур-ние Больцмана в частном случае отсутствия внеш. сил описывает эволюцию системы к состоянию равновесия.

В ионизированных газах (плазме) частицы взаимодействуют друг с другом посредством кулоновских сил, медленно убывающих с расстоянием. Для таких сил нельзя говорить о парных столкновениях, т.к. друг с другом взаимодействует сразу большое число частиц. Но и в этом случае можно получить кинетич. ур-ние (оно наз. ур-нием Ландау), если учесть, что в подавляющем числе случаев обмен импульсами (количеством движения) при столкновении частиц мал. Если столкновениями вообще можно пренебречь, то существенную роль будут играть кулоновские силы, действующие на данную частицу со стороны всех остальных частиц системы (т. н. приближение самосогласованного поля), В этом случае для плазмы справедливо кинетич. уравнение Власова (см. Плазма). Наиболее последовательные и эффективные методы вывода кинетич. ур-ний на основе динамики систем из большого числа частиц были разработаны Н. Н. Боголюбовым.

Лит.: Болъцман Л., Лекции по теории газов, пер. с нем., М., 1953; Ч е п м е н С., Каулинг Т., Математическая теория неоднородных газов, пер. с англ., М., 1960; Боголюбов Н. Н., Проблемы динамической теории в статистической физике, М, -Л., 1946; Силин В. П., Введение в кинетическую теорию газов, М., 1971; Коган М. Н., Динамика разреженного газа, М., 1967; Некоторые вопросы кинетической теории газов, пер. с англ., М., 1965; Климентович Ю. Л., Статистическая теория неравновесных процессов в плазме, М., 1964; Зоммерфель Д А., Термодинамика и статистическая физика, пер. с нем., М., 1955; Кикоин И. К., Кикоин А. К., Молекулярная физика, М., 1963, гл. 1 и 2.

Г. Я. Мякишев.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, энергия механич. системы, зависящая от скоростей движения её точек. К. э. Т материальной точки измеряется половиной произведения массы т этой точки на квадрат её скорости v, т. е. Т = 1/2 тv². К. э. механич. системы равна арифметич. сумме К. э. всех её точек: Т = 2½. mi,v²k. Выражение К. э. системы можно ещё представить в виде Т - ¹J2 Mv_c² + Тс, где М - масса всей системы, v_c - скорость центра масс, Тс - К. э. системы в её движении вокруг центра масс. К. э. твёрдого тела, движущегося поступательно, вычисляется так же, как К. э. точки, имеющей массу, равную массе всего тела. Формулы для вычисления К. э. тела, вращающегося вокруг неподвижной оси, см. в ст. Вращательное движение.

Изменение К. э. системы при её перемещении из положения (конфигурации) 1 в положение 2 происходит под действием приложенных к системе внеш. и внутр. сил и равно сумме работ A^e_kи Аⁱ_k этих сил на данном перемещении:

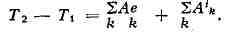
Это равенство выражает теорему об изменении К. э., с помощью к-рой решаются многие задачи динамики.

При скоростях, близких к скорости света, К. э. материальной точки

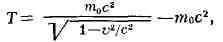
где т₀ - масса покоящейся точки, с - скорость света в вакууме (тос² - энергия покоящейся точки). При малых скоростях (v << с) последнее соотношение переходит в обычную формулу ½½ mv², См. также Энергия, Энергии сохранения закон.

Лит. см. при ст. Динамика.

С. М. Тарг.

КИНЕТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА, методы качественного и количественного хим. анализа, основанные на зависимости между скоростью реакции и концентрацией реагирующих веществ, К. м. а. можно применять для определения как сравнительно больших, так и малых количеств вещества; в последнем случае используют каталитич. реакции, в к-рых определяемое вещество может расходоваться в процессе реакции или служить её катализатором. Чувствительность К. м. а., основанных на таких реакциях, сравнима с чувствительностью активационного анализа. Напр., с помощью каталитич. реакций можно определить Мп и Со при концентрации их ионов соответственно 10-⁵ и 10-⁶ мкг/мл. Реакцию, по скорости к-рой определяют концентрацию, наз. индикаторной. Обычно применяют реакции следующих типов: окислительно-восстановительные (напр., окисление в щелочной среде Мn²+ в Мn⁴+ гипобромитом); реакции изотопного обмена между одноимённо заряженными ионами (напр., Се⁴⁺ - Се³⁺); реакции замещения во внутр. сфере комплексных соединений [напр., замещение CN- в Fe(CN) _б водой]; различные гетерогенно-каталитич. реакции и др. Скорость реакций измеряют титриметрическим, газоволюметрич., фотометрич., полярографич., потенциометрич. и др. методами. При выполнении измерений необходимо тщательно термостатировать реакционные сосуды и применять реагенты высокой чистоты, т. к. скорость каталитич. реакций сильно зависит от темп-ры, присутствия посторонних веществ и др. факторов. К. м. а. используют гл. обр. для определения содержания примесей в полупроводниковых элементах, микроэлементов в биол. объектах, грунтовых водах, а также при анализе высокочистых реактивов и материалов.

Лит.: Яцимирский К. Б., Кинетические методы анализа, М., 1963.

В. В .Краснощёков.

КИНЕТИЧЕСКИЙ МОМЕНТ, то же, что момент количества движения.

КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА, уравнение для функции распределения f(v, r, t) молекул газа по скоростям v и координатам г (в зависимости от времени f), описывающее неравновесные процессы в газах малой плотности. Функция f определяет среднее число частиц со скоростями в малом интервале от с до v + До и координатами в малом интервале от г до г + Дг (см. Кинетическая теория газов). Если функция распределения зависит только от координаты x и составляющей скорости v_x, К. у. Б. имеет вид:

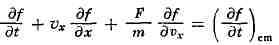
(т - масса частицы). Скорость изменения функции распределения со временем характеризуется частной производной df/dt; второй член в ур-нии, пропорциональный частной производной функции распределения по координате, учитывает изменение f в результате перемещения частиц в пространстве; третий член определяет изменение функции распределения, обусловленное действием внешних сил F. Стоящий в правой части ур-ния член, характеризующий скорость изменения функции распределения за счёт столкновений частиц, зависит от f и характера сил взаимодействия между частицами и равен

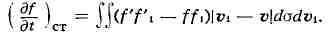
Здесь f, fi и f', fi-функции распределения молекул до столкновения и после столкновения соответственно, р, vi - скорости молекул до столкновения, da = odQ - дифференциальное эффективное сечение рассеяния в телесный угол dQ (в лабораторной системе координат), зависящее от закона взаимодействия молекул; для модели молекул в виде жёстких упругих сфер (радиуса R) о = = 4R²cos в, где dQ - угол между относит, скоростью v1 -v сталкивающихся молекул и линией, соединяющей их центры. К. у. Б. было выведено Л. Болъцманом в 1872.

Различные обобщения К. у. Б. описывают поведение электронного газа в металлах, фононов в кристаллич. решётке и т. д. (однако чаще эти ур-ния наз. просто кинетич. ур-ниями, или ур-ниями переноса). См. Кинетика физическая.

Г. Я. Мякишев

КИНЕТОКАРДИОГРАФИЯ (от греч. kinetos - движущийся,подвижный, кардио... и ...графия), метод электрич. регистрации низкочастотных вибраций грудной стенки, обусловленных сокращениями сердца. К. основана на преобразовании механич. колебаний в изменения к.-л. электрич. параметра датчика, приложенного к грудной клетке обследуемого. Полоса регистрируемых частот - в пределах 1-25 гц. Чаще регистрируют вибрации в двух точках грудной клетки, соответствующих проекции левого и правого желудочков (на 2 см левее грудины, на уровне 5-го ребра, и справа от грудины, у места прикрепления 4-5-го рёбер). Регистрируемая кривая состоит из серии зубцов, отражающих различные фазы сердечного цикла: систолу предсердий, периоды асинхронного и изометрического сокращений желудочков, быстрого и замедленного изгнания из них крови, быстрого и замедленного их наполнения. К. позволяет выявить изменения сердечной деятельности при нек-рых заболеваниях и оценить эффективность лечения.

КИНЕТОПЛАСТ (от греч. kinetos - движущийся, подвижный и plastos - вылепленный, сформированный), самовоспроизводящаяся клеточная органелла, расположенная у нек-рых простейших у основания жгутика; то же, что блефаропласт.

КИНЕТОСКОП (от греч. kinetps - движущийся, подвижный и skopeo - смотрю), аппарат для рассматривания быстро сменяющихся фотографич. снимков, что создаёт впечатление движения снятых объектов. Впервые модель К., предложенная амер. изобретателем Т. Эдисоном в 1891, демонстрировалась в апреле 1894 в Нью-Йорке. К. был одним из предшественников кинематографии.

КИНЕТОСОМА (от греч. kinetos - движущийся, подвижный и soma - тело), клеточная органелла, базальное зерно ресничек инфузорий. Происхождение К. связывают с центриолью, что подтверждается сходством ультраструктуры обеих органелл. Помимо белков, углеводов и липидов, К. содержит ДНК и РНК и способна к самостоят. биосинтезу белка и саморепродукции. К. могут давать начало ресничкам или трихоцистам. Тенденция называть К. все базальные тельца ошибочна.

КИНЕТОСТАТИКА (от греч. kinetos - движущийся и статика), раздел механики, в к-ром рассматриваются способы решения динамич. задач с помощью аналитич. или графич. методов статики. В основе К. лежит Д'Аламбера принцип, согласно к-рому ур-ния движения тел можно составлять в форме ур-ний статики, если к фактически действующим на тело силам и реакциям связей присоединить силы инерции. Методы К. находят применение при решении ряда динамич. задач, особенно в динамике машин и механизмов.

КИНЕТОСТАТИКА МЕХАНИЗМОВ, раздел теории машин и механизмов, в к-ром методом т. н. силового расчёта определяют реакции элементов кинематич. пар механизма при условии, что закон его движения известен (см. Машин и механизмов теория). Методами К. м. пользуются при проектировании новых машин для расчётов их на прочность.

Если ко всем внеш. силам, приложенным к звеньям механизма, добавить силы инерции, то на основании Д'Аламбера принципа весь механизм в целом и отд. его части условно можно рассматривать находящимися в состоянии равновесия. Поэтому при определении сил, действующих на механизм (реакций), пользуются ур-ниями статики (см. Статика механизмов). Системы ур-ний составляют для частей механизма - звеньев и кинематич. пар. Число неизвестных реакций равно числу ур-ний. Подобные системы в механике наз. статически определимыми. Силовой расчёт механизма ведут последовательно для кинематич. пар, начиная с группы, наиболее удалённой от начального звена механизма. Напр., механизм (рис., а) состоит из начального звена 1 и кинематич. пар, содержащих звенья 2-3 и 4-5. К звеньям приложены силы P₁, P₂, Р₃, Р₄, включая инерционные нагрузки, и моменты M₁, М₂, Ms. Для силового расчёта рассматривают вначале группу 4-5 механизма (рис., 6), Действие звеньев 6 и 2 на группу заменяют искомыми реакциями Р₂₄ и Р₆₅, к-рые разлагаются на нормальные составляющие Рⁿ₂₄ и Рⁿ₆₅ и тангенциальные составляющие Р^Т₂₄ и Рй . Тангенциальные составляющие определяются из ур-ний сумм моментов относительно точки Е для каждого из звеньев и 5. Нормальные составляющие Рⁿ₂₄ и Рⁿ₆₅, а следовательно, и полные реакции Р₂₄ и Р₆₅ определяют из векторного ур-ния равновесия группы

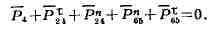
Для решения векторного ур-ния строят многоугольник сил (см. Верёвочный многоугольник). Реакцию Р₄5 = -Ps₄ определяют из векторного ур-ния равновесия сил на одном из звеньев 4 или 5. Затем рассматривают группу 2-3, на к-рую, кроме заданных сил, действует найденная реакция Р₄₂ = - Р₂₄.

Схема действия сил в механизме (а) и определение реакций в звене (б); Р,, Р₂, Р₃, Pt - действующие силы; М₁ М_г, М_ь - моменты сил; Р₂₄ и P_6S - искомые реакции.

При рассмотрении равновесия начального звена 1 определяют реакцию P_6i и уравновешивающий момент My, приложенный к этому звену, необходимый для обеспечения заданного закона движения начального звена.

При учёте сил трения в кинематич. парах к системе ур-ний добавляют ещё одно независимое ур-ние. После определения реакций вычисляют силы трения в парах и повторяют расчёт, принимая во внимание силы трения как внеш. силы, приложенные к звеньям, т. е. находят уточнённые реакции в первом приближении. Расчёт можно повторить с учётом определённых сил трения. Практически первого приближения бывает достаточно. При силовом расчёте многозвенных пространственных механизмов метод и последовательность кинетостатич. исследования сохраняются, однако решение получается более громоздким.

Лит. см. при ст. Машин и механизмов теория.

Н. И. Артоболевский, А. П. Бессонов.