КЕПЛЕРА ЗАКОНЫ, три закона движения планет, открытые И. Кеплером в нач. 17 в. Осн. труд Кеплера "Новая астрономия", напечатанный в 1609, содержал два первых закона. Третий закон был открыт позднее: в 3-й главе 5-й книги "Гармония Мира" (1619) Кеплер отметил, что идея нового закона блеснула у него внезапно 8 марта 1618 года, а 15 мая он закончил все необходимые вычисления, к-рые показали, что закон верен. В дальнейшем К. з. уточнялись и окончательно получили следующую формулировку. Первый К. з. В невозмущённом движении (т. е. в задаче двух тел) орбита движущейся точки есть кривая второго порядка, в одном из фокусов к-рой находится центр силы притяжения. Т. о., орбита материальной точки в невозмущённом движении - это нек-рое конич. сечение, т. е. окружность, эллипс, парабола или гипербола. Второй К. з. В невозмущённом движении площадь, описываемая радиусом вектором движущейся точки, изменяется пропорционально времени. Первые два К. з. имеют место только для невозмущённого движения, происходящего под действием силы притяжения, обратно пропорциональной квадрату расстояния до центра силы. Третий К. з. В невозмущённом эллиптич. движении двух материальных точек произведения квадратов времён обращения на суммы масс центральной и движущейся точек относятся как кубы больших полуосей их орбит, т. е.

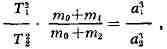
где Т1 и T 2 - периоды обращения двух точек, mi и т₂ - их массы, то - масса центральной точки, at, а₂ - большие полуоси орбит точек. Пренебрегая массами планет по сравнению с массой Солнца, получаем третий К. з. в его первоначальной форме: квадраты периодов обращений двух планет вокруг Солнца относятся, как кубы больших полуосей их эллиптич. орбит. Третий К. з. может быть применён только для случая эллиптич. орбит, а поэтому не имеет такого общего значения, как два первых закона. Однако, будучи применён к планетам, спутникам планет, компонентам двойных звёзд, движущимся по эллиптич. орбитам, он позволяет определить нек-рые характеристики небесных светил. Так, на основании третьего К. з. возможно подсчитать массы планет, принимая массу Солнца то = 1. Зная из наблюдений период обращения одного компонента двойной звезды относительно другого и измерив её параллакс, можно найти сумму их масс. Если параллаксы звёзд неизвестны, то на основании допущения, что массы компонентов соответствуют их физ. особенностям, по третьему К. з. можно вычислить расстояния до звёзд (это т. н. динамические параллаксы звёзд). Открыв первые два закона, Кеплер составил основанные на них таблицы движения планет, опубликованные в 1627 под назв. "Рудольфовых таблиц". Эти таблицы по своей точности далеко превзошли все прежние, ими пользовались в практич. астрономии на протяжении 17 и 18 вв. Успех Кеплера в объяснении движения планет обусловлен новым методологич. подходом к решению вопроса: впервые в истории астрономии была сделана попытка определить планетные орбиты непосредственно из наблюдений. Уже Кеплеру было ясно, что открытые им законы не являются совершенно строгими. Если для планет они выполняются с большой точностью, то для того, чтобы представить движение Луны, оказалось необходимым ввести эллипс с вращающейся линией апсид и добавить неравенства, называемые эвекцией и вариацией. Эти неравенства были открыты эмпирически ещё Птолемеем во 2 в. (эвекция) и Т. Браге в 16 в. (вариация) и объяснены только после открытия в 17 в. И. Ньютоном закона всемирного тяготения (см. Ньютона закон тяготения). К. з., найденные из наблюдений, были выведены Ньютоном как строгое решение задачи двух тел.

Лит.: Дубошин Г. Н., Небесная механика. Основные задачи и методы, 2 изд., М., 1968; Субботин М. Ф., Введение в теоретическую астрономию, М., 1968; Рябов Ю. А., К 350-летию открытия первых двух законов Кеплера, в кн.: Астрономический календарь на 1959, М., 1958.

Г. А. Чеботарёв.

КЕПЛЕРА УРАВНЕНИЕ, трансцендентное уравнение вида

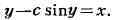
Для приложений важен случай | с | < 1, когда у определяется по заданным с и x единственным образом. К. у. впервые рассматривалось И. Кеплером ("Новая астрономия", 1609) в связи с задачей: на диаметре АВ полукруга АОВМ дана точка D; провести прямую DM так, чтобы она делила площадь полукруга в заданном отношении (см. рис.). К. у. играет важную роль в астрономии при определении элементов эллиптич. орбит планет. В небесной механике это уравнение обычно записывают в форме

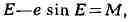
где е - эксцентриситет эллипса, М - средняя аномалия, Е - эксцентрическая аномалия (см. Орбиты небесных тел). Решением К. у. занимались также Ж. Лагранж (1771), П. Лаплас (1823), Ф. Бессель (1816-17), К. Гаусс (1809) и др.

Лит.: Субботин М. Ф., Курс небесной механики, 2 изд., т. 1, Л.- М., 1941.