КВАДРАТИЧНАЯ ФОРМА, форма 2-й степени от п переменных x1,
x2,..., xn, т. е. многочлен от этих
переменных, каждый член к-рого содержит либо квадрат одного из переменных, либо
произведение двух различных переменных. Общий вид К. ф. при п = 2:
ах12+bx22+ сх1х2,
при п = 3:
ах12 + bx22 + cx32
+ dx1x2 + ex1x3 + fx2x3,
где a, b, ...,f -к.-л. числа. Произвольная К. ф. записывается так:
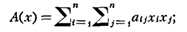
причем считают, что аij = aji. К. ф. от
2, 3 и 4 переменных непосредственно связаны с теорией линий (на плоскости) и
поверхностей (в пространстве) 2-го порядка: в декартовых координатах уравнение
линии и поверхности 2-го порядка, отнесённых к центру, имеет вид A(x) =1,
т. е. его левая часть является К. ф.; в однородных координатах левая часть
любого ур-ния линии и поверхности 2-го порядка является К. ф. При замене
переменных x1, x2, ..., хn др.
переменными y1, y2, ..., y_п, являющимися
линейными комбинациями старых переменных, К. ф. переходит в другую К. ф. Путём
соответствующего выбора новых переменных (невырожденного линейного
преобразования) можно привести К. ф. к виду суммы квадратов переменных,
умноженных на нек-рые числа. При этом ни число квадратов (ранг К. ф.), ни
разность между числом положительных и числом отрицательных коэффициентов при
квадратах (сигнатура К. ф.) не зависят от способа приведения К. ф. к сумме
квадратов (закон инерции). Указанное приведение можно осуществить даже
специальными (т. н. ортогональными) преобразованиями. Геометрически в этом
случае такое преобразование соответствует приведению линии или поверхности 2-го
порядка к главным осям.
При рассмотрении комплексных переменных изучаются К. ф. вида
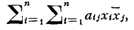
где xj - число, комплексно сопряжённое с xj.
Если, кроме того, такая К. ф. принимает только действительные значения (это
будет, когда aij = aji), то её наз.
эрмитовой. Для эрмитовых форм справедливы основные факты, относящиеся к
действительным К. ф.: возможность приведения к сумме квадратов, инвариантность
ранга, закон инерции.
Лит.: Мальцев А. И., Основы линейной алгебры, 3 изд., M., 1970.
КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ,квадратичное уклонение, стандартное
отклонение величин x1, x2, ..., хnот
а - квадратный корень из выражения
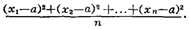
Наименьшее значение К. о. имеет при а= х, где х - среднее
арифметическое величин x1, x2, .., xn.
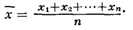
В этом случае К. о. может служить мерой рассеяния системы величин x1,
x2, .., xn.. Употребляют также более общее понятие
взвешенного К. о.
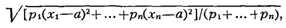
числа p1 , .. ., рп называют при этом весами,
соответствующими величинам x1, x2, .., xn. Взвешенное
К. о. достигает наименьшего значения при а, равном взвешенному среднему:
(p1x1
+···+ pnxn)/(p1
+···+pn).
В теории вероятностей К. о. 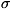 x случайной величины X (от
её математич. ожидания) называют квадратный корень из дисперсии
x случайной величины X (от
её математич. ожидания) называют квадратный корень из дисперсии
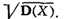
К. о. употребляют как меру качества статистич. оценок и наз. в этом случае
квадратичной ошибкой. См. Ошибок теория.
КВАДРАТИЧНОЕ СРЕДНЕЕ, число (S), равное корню квадратному из среднего
арифметического квадратов данных чисел a1, а2,
..., а„:
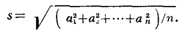
КВАДРАТИЧНЫЙ ВЫЧЕТ, понятие теории чисел. К. в.  о модулю т - число а,
для которого сравнение х2 = = a(mod т) имеет
решение: при нек-ром целом x число х2 - а делится на т;
если это сравнение не имеет решений, то а наз. квадратичным невычетом.
Напр., если m = 11, то число 3 будет К. в., так как сравнение х2
= 3 (mod H) имеет решения х = 5, х = 6, а число 2 будет
невычетом, т. к. не существует чисел х, удовлетворяющих сравнению х2 =
2 (mod H). К. в. являются частным случаем вычетов степени n для
n = 2. Если т равно простому нечётному числу р, то среди
чисел 1, 2, ..., p - 1 имеется (р - 1)/2 К. в. и (р - 1)/2 квадратичных
невычетов. Для изучения К. в. по простому модулю р вводится Лежандра
символ (a/p), определяемый так: если а взаимно просто с р, то
полагают (a/p) = 1, когда а - К. в., и (a/p)= -1, когда а- квадратичный
невычет. Основной теоремой в этом круге вопросов является т. н. закон
взаимности К. в.: если р и q - простые нечётные числа, то
о модулю т - число а,
для которого сравнение х2 = = a(mod т) имеет
решение: при нек-ром целом x число х2 - а делится на т;
если это сравнение не имеет решений, то а наз. квадратичным невычетом.
Напр., если m = 11, то число 3 будет К. в., так как сравнение х2
= 3 (mod H) имеет решения х = 5, х = 6, а число 2 будет
невычетом, т. к. не существует чисел х, удовлетворяющих сравнению х2 =
2 (mod H). К. в. являются частным случаем вычетов степени n для
n = 2. Если т равно простому нечётному числу р, то среди
чисел 1, 2, ..., p - 1 имеется (р - 1)/2 К. в. и (р - 1)/2 квадратичных
невычетов. Для изучения К. в. по простому модулю р вводится Лежандра
символ (a/p), определяемый так: если а взаимно просто с р, то
полагают (a/p) = 1, когда а - К. в., и (a/p)= -1, когда а- квадратичный
невычет. Основной теоремой в этом круге вопросов является т. н. закон
взаимности К. в.: если р и q - простые нечётные числа, то
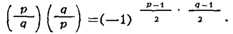
Эту закономерность открыл ок. 1772 Л. Эйлер, совр. формулировка дана
А. Лежандром, полное доказательство впервые дал в 1801 К. Гаусс. Удобным
обобщением символа Лежандра является Якоби символ. Закон взаимности К.
в. получил многочисленные обобщения в теории алгебр, чисел. И. M. Виноградовым
и др. учёными изучалось распределение К. в. и суммы значений символа
Лежандра.
Лит.: Виноградов И. M., Основы теории чисел, 8 изд., M., 1972.
КВАДРАТНО - ГНЕЗДОВОЙ ПОСЕВ, способ посева с.-х. культур, при к-ром
семена размещают по неск. штук в углах квадрата (прямоугольника). При К.-г. п.
растения на поле размещаются равномернее и лучше используют почв, и воз д.
питание и солнечный свет; сокращается расход семян; создаются условия для
механизированной обработки междурядий в продольном и поперечном направлениях,
позволяющей поддерживать почву рыхлой и чистой от сорняков; значительно
снижаются затраты ручного труда. К.-г. п. применяют для посева кукурузы,
подсолнечника, хлопчатника, клещевины, нек-рых овощных и др. культур. В СССР
К.-г. п. впервые начал применяться в 1932-35 для кукурузы (в УССР). Расстояние
между гнёздами и кол-во семян в гнезде устанавливают в зависимости от биол.
особенностей культуры, почв. условий и запасов влаги в почве. Напр., в
большинстве р-нов возделывания кукурузы на зерне и подсолнечника на семена
лучшие результаты получают при расстоянии между гнёздами 70 X 70 см и 2
растениях в гнезде. Для К.-г. п. сельскохозяйственных культур используют
навесные СКНК-4, СКНК-6, СКНК-8, СТХ-4А, СТХ-4Б и др. квадратно-гнездовые
сеялки. Для точного высева нужного числа растений в гнезде семена калибруют и
учитывают их полевую всхожесть. См. Посев.
С. А. Воробьёв.
КВАДРАТНОЕ ПИСЬМО (др.-евр.- кетаб мерубба), ответвление
западносемитского письма, восходит к арамейскому (с 3 в. до н. э.), в основном
сформировалось к 2-1 вв. до н. э. Письмо арамейских и др.-евр. надписей, лит-ры
на др.-евр. языке, совр. языков иврит, идиш и ладино (исп.-евр. язык
Средиземноморья). Курсивные разновидности: ашкенази (Вост. Европа), сефарди
(Средиземноморье), раши (раввинское письмо, в Италии, употребляется в религ.
текстах). Письмо первоначально чисто консонантное. В 6-8 вв. создаётся неск.
систем огласовок с помощью диакритик; основная, ныне принятая,- Тивериадская.
См. Еврейское письмо.
Лит.: Дирингер Д., Алфавит, пер. с англ., M., 1963, с. 311 - 319.
КВАДРАТНОЕ УРАВНЕНИЕ, уравнение вида ах2 + bх + с =
0, где а, b, с -
к.-л. числа, наз. коэффициентами уравнения. К. у. имеет два корня, к-рые
находятся по формулам:
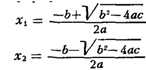
Выражение D = b2 - 4ас наз. дискриминантом К. у.
Если D > О, то корни К. у. действительные различные, если D < О, то корни
сопряжённые комплексные, если D = О, то корни действительные равные.
Имеют место формулы Виета: x1 + x2 = -b/a, x1x2
= с/а, связывающие корни и коэффициенты К. у. Левую часть К. у. можно
представить в виде а(х - x1)(x - x2). Функцию у
= ах2 + + bх + с наз. квадратным трёхчленом, её графиком служит парабола
с вершиной в точке М(-b/2а; с - b2/4a) и осью
симметрии, параллельной оси Oy; направление ветвей параболы совпадает со
знаком а. Решение К. у. было известно в геометрич. форме ещё математикам
древности.
КВАДРАТУРА (лат. quadratura - придание квадратной формы), 1) число
квадратных единиц в площади данной фигуры. 2) Построение квадрата, равновеликого
данной фигуре. 3) Вычисление площади или интеграла (см. Интегральное
исчисление).
КВАДРАТУРА в астрономии, одна из характерных конфигураций, т. е.
взаимных положений, Солнца, планет, Луны на небесной сфере. Подробнее см. Конфигурации
в астрономии.
КВАДРАТУРА КРУГА, задача о разыскании квадрата, равновеликого данному
кругу. Под К. к. понимают как задачу точного построения квадрата, равновеликого
кругу, так и задачу в ы-числения площади круга с тем или иным приближением.
Задачу о точной К. к. пытались решить первоначально с помощью циркуля и
линейки. Математика древности знала ряд случаев, когда с помощью этих
инструментов удавалось преобразовать криволинейную фигуру в равновеликую ей
прямолинейную (ем., напр., Гиппократовы. луночки). Попытки решения задачи
о К. к., продолжавшиеся в течение тысячелетий, неизменно оканчивались неудачей.
С 1775 Парижская АН, а затем и др. академии стали отказываться от рассмотрения
работ, посвящённых К. к. Лишь в 19 в. было дано науч. обоснование этого отказа:
строго установлена неразрешимость К. к. с помощью циркуля и линейки.
Если радиус круга равен г, то сторона равновеликого этому кругу
квадрата равна х = r( )1/2 . T. о., задача сводится к следующей:
осуществить построение, в результате к-рого данный отрезок (r) был бы
умножен на данное число (
)1/2 . T. о., задача сводится к следующей:
осуществить построение, в результате к-рого данный отрезок (r) был бы
умножен на данное число ( )1/2. Однако графич. умножение отрезка
на число осуществимо циркулем и линейкой, если упомянутое число - корень алгебр,
ур-ния с целыми коэффициентами, разрешимого в квадратных радикалах. T. о.,
окончательная ясность в вопросе о К. к. могла быть достигнута на пути изучения
арифметич. природы числа я. В кон. 18 в. нем. математиком И. Ламбертом и франц.
математиком А. Лежандром была установлена иррациональность числа л. В 1882 нем.
математик Ф. Линдеман доказал, что число я (а значит и у л) трансцендентно, т.
е. не удовлетворяет никакому алгебр, ур-нию с целыми коэффициентами. Теорема
Линдемана положила конец попыткам решения задачи о К. к. с помощью циркуля и
линейки. Задача о К. к. становится разрешимой, если расширить средства
построения. Уже греч. геометрам было известно, что К. к. можно осуществить,
используя трансцендентные кривые; первое решение задачи о К. к. было выполнено
Диностратом (4 в. до н. э.) при помощи спец. кривой - т. н. квадратрисы (см.
Линия).
О задаче нахождения приближённого значения числа я см. в ст. Пи.
)1/2. Однако графич. умножение отрезка
на число осуществимо циркулем и линейкой, если упомянутое число - корень алгебр,
ур-ния с целыми коэффициентами, разрешимого в квадратных радикалах. T. о.,
окончательная ясность в вопросе о К. к. могла быть достигнута на пути изучения
арифметич. природы числа я. В кон. 18 в. нем. математиком И. Ламбертом и франц.
математиком А. Лежандром была установлена иррациональность числа л. В 1882 нем.
математик Ф. Линдеман доказал, что число я (а значит и у л) трансцендентно, т.
е. не удовлетворяет никакому алгебр, ур-нию с целыми коэффициентами. Теорема
Линдемана положила конец попыткам решения задачи о К. к. с помощью циркуля и
линейки. Задача о К. к. становится разрешимой, если расширить средства
построения. Уже греч. геометрам было известно, что К. к. можно осуществить,
используя трансцендентные кривые; первое решение задачи о К. к. было выполнено
Диностратом (4 в. до н. э.) при помощи спец. кривой - т. н. квадратрисы (см.
Линия).
О задаче нахождения приближённого значения числа я см. в ст. Пи.
Лит.: О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). С
приложением истории вопроса, пер. с нем., 3 изд., М.-Л., 1936; Стройк Д. Я.,
Краткий очерк истории математики, пер. с нем., 2 изд., M., 1969.
КВАДРАТУРНЫЕ ФОРМУЛЫ, формулы, служащие для приближённого вычисления
определённых интегралов по значениям подинтегральной функции в конечном числе
точек. Наиболее распространённые К. ф. имеют вид
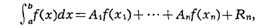
где
x1, x2, ..., xn - узлы К. ф., A1,
A2, ..., An - её коэффициенты и Rn- остаточный
член. Напр.,
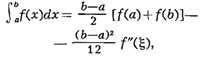
где а < 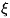 < b (формула трапеций). Иногда К. ф. наз. также
формулами механических, или численных, квадратур. См. также Ko-теса формулы,
Симпсона формула, Чебышева формула.
< b (формула трапеций). Иногда К. ф. наз. также
формулами механических, или численных, квадратур. См. также Ko-теса формулы,
Симпсона формула, Чебышева формула.
Лит.: Крылов В. И., Приближённое вычисление интегралов, 2 изд., M.,
1967.
КВАДРИВИУМ (лат. quadrivium. букв.- пересечение четырёх дорог),
повышенный курс светского образования в ср.-век. школе, состоявший из 4 предметов:
музыки, арифметики, геометрии и астрономии. Вместе с нач. курсом тривиумом К.
составлял т. н. "семь свободных искусств".
КВАДРИГА (лат. quadriga), античная (др.-греч., рим.) колесница на 2
колёсах, запряжённая четвёркой лошадей, расположенных в 1 ряд; возница управлял
ими стоя. Лёгкие К. применялись для конских состязаний, занимавших большое
место в Олимпийских и др. обществ, играх. Описания этих состязаний есть у
Гомера, Вергилия и др. античных авторов. Массивными К. пользовались императоры и
полководцы-победители для торжеств. процессий. Скульптурные изображения К. с
античными божествами или аллегорич. фигурами славы, счастья и т. п. в качестве
возниц служили украшением античных строений. Барельефы с изображением К. часто
встречаются на античных медалях, камеях и геммах. В России и Зап.
Европе 18-19 вв. К. украшались фронтоны монументальных зданий и триумфальные
арки.
КВАДРИЛЛИОН (франц. quadrillion), число, изображаемое единицей с 15
нулями, т. е. число 1015. Иногда К. наз. число 102".
КВАДРИРУЕМАЯ ОБЛАСТЬ, область, имеющая определённую площадь, или,
что то же, - определённую плоскую меру в смысле Жордана (см. Мера множества).
Отличительным свойством К. о. D является возможность заключить ее
"между" двумя многоугольниками так, чтобы один из них содержался
внутри данной К. о., другой, напротив, содержал её внутри, а разность их
площадей могла бы быть произвольно малой. В этом случае существует только одно
число, заключённое между площадями всех "охватывающих" и
"охватываемых" многоугольников; его и наз. площадью К. о. D. Свойства
квадрируемых областей: если К. о. D содержится в К. о. D1, то
площадь D не превосходит площади D1; область D. состоящая из двух
непересекающихся К. о. D1 и D2, квадрируема, и её
площадь равна сумме площадей областей D1 и D2; общая часть двух К.
о. D1 и D2 снова является К. о. Для того чтобы область D
была квадрируема, необходимо и достаточно, чтобы её граница имела площадь,
равную нулю; существуют области, не удовлетворяющие этому условию и,
следовательно, неквадрируемые.
КВАДРУПОЛЬ (от лат. quadrum - четырёхугольник, квадрат и греч. polos -
полюс), система заряженных частиц, полный электрич. заряд и электрич. диполь-ный
момент к-рой равны нулю. К. можно рассматривать как совокупность двух
одинаковых диполей с равными по величине и противоположными по
направлению дипольными моментами, расположенных на нек-ром расстоянии друг от
друга (см. рис.). На больших расстояниях R от К. напряжённость его
электрич. поля E убывает обратно пропорционально четвёртой степени R (E
~ 1/R4), а зависимость E от зарядов и их расположения описывается в
общем случае набором из пяти независимых величин, к-рые вместе составляют
квадрупольный момент системы. Квадрупольный момент определяет также энергию К.
во внешнем электрич. поле. В частном случае К., изображённых на рис.,
квадрупольный момент по абс. величине равен 2eIa, где е - заряд, l
- размер диполей, а - расстояние между центрами диполей. К. является мулътиполем
2-го порядка.
Примеры относительного расположения диполей в квадруполе.
Лит.: Ландау Л. Д. и Лифшиц E. M., Теория поля, 5 изд., M., 1967,
§ 41.
Г. Я. Мякишев.
КВАДРУПОЛЬНОЕ ВЗАИМОДЕЙСТВИЕ, взаимодействие систем заряженных частиц
на большом расстоянии друг от друга при условии, что полный электрич. заряд
каждой системы и её электрич. диполъный момент равны нулю. Если
электрич. заряд или дипольный момент системы отличны от нуля, то К. в. обычно
можно пренебречь. К.в. определяется наличием у систем т. н. квадрупольного
момента (см. Квадруполь). Энергия К. в. атомов (не обладающих дипольным
электрич. моментом) убывает с расстоянием R как 1/R5, в то
время как энергия взаимодействия дипольных моментов, наводимых в этих атомах
вследствие их взаимной поляризации, меняется с расстоянием как 1/R6.
Поэтому К. в. атомов на больших расстояниях оказывается доминирующим.
Квадрупольные моменты атомов могут быть рассчитаны с помощью квантовой
механики.
Квадрупольным моментом обладают многие атомные ядра, распределение электрич.
заряда в к-рых не обладает сферич. симметрией (см. Квадрупольный момент ядра,
Ядро атомное). К. в. играет большую роль в ядерной физике при
возбуждении ядер с нулевым дипольным моментом кулоновским полем налетающих на
ядра заряженных частиц. Квадрупольные моменты ядер определяются
экспериментально.
Г. Я. Мякишев.
КВАДРУПОЛЬНОЕ ИЗЛУЧЕНИЕ, излучение электромагнитных волн,
обусловленное изменением во времени квадрупольного момента излучающей системы
(см. Излучение).
КВАДРУПОЛЬНЫЙ МОМЕНТ ЯДРА, величина, характеризующая отклонение
распределения электрич. заряда в атомном ядре от сферически симметричного (см.
Ядро атомное). К.м. я. имеет размерность площади и обычно выражается в см2.
Для сферически симметричного ядра К. м. я. Q = О. Если ядро вытянуто
вдоль оси симметрии, то О - положительная величина, если ядро сплюснуто вдоль
оси, то отрицательная. К. м. я. изменяются в широких пределах, напр, для ядра 178ЪO
Q = -0,027-10-24 см2, для ядра 24193Am
Q = + 14,9-10-24 см2. Большие К. м. я., как
правило, положительны. Это означает, что при значительном отклонении от сферич.
симметрии ядро имеет форму вытянутого эллипсоида вращения.
Лит. см. при
ст. Ядро атомное.
В. П. Парфёнова.
КВАДЫ (лат. Ouadi), германское племя, жившее в 1 в. н. э. к С. от
среднего течения Дуная, а также по верховьям Эльбы и Одера. К. в 166-180
участвовали в Маркоманской войне с Римом, были разбиты и признали
господство Рима. Вскоре освободились, но в 375 были вновь покорены. В нач. 5 в.
часть К. вместе с вандалами переселилась в Испанию, основав на С.-З.
Испании своё королевство (в 585 завоёвано вестготами) (К. в Испании
иногда наз. квадосвевами, а их королевство - свевским).
КВАЗАРЫ (англ. quasar, сокр. от quasi-stellar radiosource), кваз и
звёздные объекты, квазизвёзды, сверхзвёзды, небесные объекты, имеющие сходство
со звёздами по оптическому виду и с газовыми туманностями по характеру
спектров, обнаруживающие, кроме того, значит, красные смешения (до 6 раз
превышающие наибольшие из известных у галактик). Последнее свойство определяет
важную роль К. в астрофизике и космологии. Открытие К. явилось результатом
повышения точности определения координат внегалактич. источников
радиоизлучения, позволившего значительно увеличить число радиоисточников,
отождествлённых с небесными объектами, видимыми в оптич. лучах. Первое
совпадение радиоисточника с звёздоподобным объектом было обнаружено в 1960, а в
1963, когда амер. астроном M. Шмидт отождествил сдвинутые вследствие эффекта
красного смещения линии в спектрах таких объектов, они были выделены в особый
класс космич. объектов - квазары. T. о., первоначально были обнаружены К.,
являющиеся сильными радиоисточниками, но впоследствии были найдены К. также и
со слабым радиоизлучением (ок. 98,8% всех К., доступных обнаружению). Эта многочисл.
разновидность К. наз. радиоспокойными К., квазигалактиками (квазагами),
интерлоперами, а иногда - голубыми звёздоподобными объектами. Полное число
доступных наблюдениям К. составляет ок. 10s; из них уже
отождествлено с оптич. объектами ок. 1000, но достоверная принадлежность к К.
по спектрам установлена лишь примерно для 200.
В спектрах К. обнаруживаются мощное ультрафиолетовое излучение и широкие
яркие линии, характерные для горячих газовых туманностей (темп-pa ок. 30 000 0C),
но значительно сдвинутые в красную область спектра. При красных смещениях,
превышающих 1,7, на снимках спектров К. становится видна даже резонансная линия
водорода La 1216 А. Изредка в спектрах К. наблюдаются узкие тёмные линии,
обусловленные поглощением света в окружающем К. меж-галактич. газе. На
фотографиях К. имеют вид звёзд, т. о. их угловые диаметры менее 1"; только
ближайшие К. обнаруживают оптич. особенности: эллиптич. форму звездообразного
изображения, газовые выбросы. По сильному ультрафиолетовому излучению, характеризуемому
голубыми показателями цвета, К. удаётся отличать на фотографиях от
нормальных звёзд, а по избыточному инфракрасному излучению - от белых карликов,
даже если К. не имеют радиоизлучения.
Вариации блеска многих К. являются, по-видимому, одним из фундаментальных
свойств К. (кратчайшая вариация с периодом 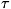 ~ 1 ч, максимальные
изменения блеска - в 25 раз). Поскольку размеры переменного по блеску объекта
не могут превышать Ct (с - скорость света), размеры К. не могут быть более 4-1012
м (менее диаметра орбиты Урана), и только при движении вещества со
скоростью, близкой к скорости света, эти размеры могут быть больше. В отличие
от непрерывного излучения, вариации интенсивности в спектральных линиях редки.
~ 1 ч, максимальные
изменения блеска - в 25 раз). Поскольку размеры переменного по блеску объекта
не могут превышать Ct (с - скорость света), размеры К. не могут быть более 4-1012
м (менее диаметра орбиты Урана), и только при движении вещества со
скоростью, близкой к скорости света, эти размеры могут быть больше. В отличие
от непрерывного излучения, вариации интенсивности в спектральных линиях редки.
Как радиоисточники, К. сходны с радиогалактиками: у К. часто наблюдаются
два, не обязательно одинаковых по интенсивности, протяжённых радиоисточника,
находящихся на значительном расстоянии по разные стороны от оптич. объекта.
Механизм радиоизлучения и тех и других синхротронный (см. Синхротроннов
излучение). Но в К., кроме того, обнаружены компактные радиоисточники,
порождающие вариации радиоизлучения на сантиметровых волнах; они представляют
собой расширяющиеся облака релятивистских частиц, существующие неск. лет.
Механизм их радиоизлучения связан, по-видимому, с плазменными колебаниями.
Природа К. изучена ещё мало. В зависимости от толкований природы красного
смещения в их спектрах обсуждаются три гипотезы (нач. 70-х гг. 20 в.). Наиболее
правдоподобна космологич. гипотеза, согласно к-рой большие красные смещения
свидетельствуют о том, что К. находятся на огромных расстояниях (до 10 гигапарсек)
и принимают участие в расширении Метагалактики. На этом предположении
основаны определения расстояний до К. (по красным смещениям) и оценки их масс и
светимостей. В космологич. гипотезе К. по абс. звёздным величинам (-27) и
массам (ок. 1038 кг, т. е. 108 масс Солнца)
являются действительно сверхзвёздами. Физич. природа К. в этом случае связывается
с гра-витац. коллапсом массы газа (см. Коллапс гравитационный), к-рый
остановлен вследствие магнитной турбуленции или вращения К.
Большой расход энергии на все виды электромагнитного излучения при этой
гипотезе ограничивает активную стадию К. 104 годами. По мощности
радиоизлучения (~1045 вт) K. сравнимы с радиогалактиками.
Предполагается, что К. являются сверхмассивными звёздами радиусом порядка 1012
м, плазма к-рых непрерывно, а также сильными взрывами выбрасывает потоки
частиц различных энергий. В радиусе порядка 1016м К. окружены
облаками ионизованного газа, создающими яркие линии в спектрах К., а на
расстояниях порядка 1019 м находятся облака релятивистских
частиц, запертых в слабых магнитных полях,- радиоизлучающие области К.
Ближайшие К. находятся далее 200 мегапарсек. Относительные редкость и
кратковременность их существования подтверждают предположение, что К.- это
стадия эволюции крупных космич. масс, напр, ядер галактик. T. о., оказывается
неслучайным сходство К. с N-галактиками, галактиками Сейферта и голубыми
компактными галактиками по характеру спектров, вариациям блеска и
радиоизлучения. Ближайшие К., у к-рых удалось рассмотреть на фотографиях
структуру, оказались N-галактиками, на основании чего их объединили в один
класс компактных сверхярких объектов. Загадочна привода объекта BL Ящерицы (и
ещё нескольких), к-рый по колебаниям блеска, радиоизлучению, показателям цвета
и оптич. структуре выглядит как типичный К., но в то же время не имеет в
спектре никаких линий.
Согласно другой гипотезе, К. со скоростями, близкими к скорости света,
разлетаются в результате взрыва в центре Галактики и выброса вещества массой
ок. 1040 кг, происшедших несколько млн. лет назад. По этой
гипотезе массы К. составляют 1031 кг (5 масс Солнца), а
расстояния до них 60-600 килопарсек. Однако неизвестны физич. процессы,
к-рые могли бы дать необходимую для взрыва энергию (1058 дж).
В третьей гипотезе предполагается, что К.- компактные газовые объекты
размерами 1016-10" м и массами 1042 - 1043 кг,
в спектрах к-рых линии имеют большие красные смещения гравитационного
характера.
Лит.: Б е р б и д ж Д ж. и Б е р 6 и д ж M., Квазары, пер. с англ.,
M., 1969.
Ю. П. Псковский.
КВАЗИ... (от лат. quasi - нечто вроде, как будто, как бы), составная
часть сложных слов, соответствующая по значению словам: "якобы",
"мнимый", "ложный" (напр., квазиучёный). См. Квазистационарный
процесс, Квазиупругая сила и др.
КВАЗИГЕОИД (от квази...), см. в ст. Геоид.
КВАЗИЗВЁЗДЫ, то же, что квазары.
КВАЗИИМПУЛЬС (от квази... и
импульс), векторная
величина, характеризующая состояние квазичастицы (напр., подвижного электрона в
периодическом поле кристаллич. решётки); подробнее см. Квазичастицы, Твёрдое
тело.
КВАЗИМОДО (Quasimodo) Сальваторе (20.8.1901, Сиракуза,-14.6.1968,
Неаполь), итальянский поэт. В 30-е гг. примыкал к направлению герметизма с
его мотивами тоски и одиночества (сб-ки "Вода и земля", 1930;
"Потонувший гобой", 1932; "Эрато и Аполлион", 1936;
"Стихи", 1938). В период антифашистского Сопротивления К. в своей
поэзии обратился к социальной действительности (сб. "День за днём",
1947). В послевоенном творчестве К. звучит гражд. и патриотич. тема
("Жизнь не сон", 1949; "Фальшивая и подлинная зелень",
1954), вера в народ, к к-рому поэт непосредственно обращается (сб. "Земля
несравненная", 1958). Чл. Всемирного Совета Мира (1950). Нобелевская пр.
(1959).
Соч.: Tutte Ie poesie, Verona, 1961: в рус. пер.- Моя страна - Италия. Пер.
с итал., под ред. К. Зелинского. [Вступит, ст. А. Суркова], M., 1961; [Стихи],
в кн.: Итальянская лирика. XX век, M., 1968.
Лит.: Tedescо N. S., Quasimodo е Ia condizione poetica del nostro
tempo, Palermo, [1959] (имеется библ.); Pento В., Lettura di Quasimodo, Mil.,
[1966]; Mazzamuto P., Salvatore Quasimodo, [Palermo, 1967]; Quasimodo e Ia
critica. A cura di G. Finzi,
[Mil., 1969].
P. И. Хлодовский.
КВАЗИОПТИКА (от квази... и оптика), область физики, в
к-рой изучается распространение электромагнитных волн с длиной волны  < 1-2 мм
(коротковолновая часть диапазона миллиметровых радиоволн - субмиллиметровые
волны и примыкающий к ней оптич. диапазон) в условиях, когда распространение
волн подчиняется законам геометрической оптики, но дифракционные явления также
играют существенную роль. Результатом этих исследований является создание
квазиоптических устройств - открытых резонаторов и квазиоптических линий, в
к-рых могут возбуждаться и распространяться волны указанного диапазона.
< 1-2 мм
(коротковолновая часть диапазона миллиметровых радиоволн - субмиллиметровые
волны и примыкающий к ней оптич. диапазон) в условиях, когда распространение
волн подчиняется законам геометрической оптики, но дифракционные явления также
играют существенную роль. Результатом этих исследований является создание
квазиоптических устройств - открытых резонаторов и квазиоптических линий, в
к-рых могут возбуждаться и распространяться волны указанного диапазона.
Для радиоволн короче 1-2 мм объемные резонаторы и волноводы (см. Радиоволновод)
с размерами порядка длины волны А, широко применяемые для сантиметоовых
волн, практически непригодны. Омические потери на этих длинах волн столь
велики, что волна почти полностью затухает в волноводах на расстояниях ~ 10-20 см
от источника, а добротность резонатора мала. В связи с этим были
созданы открытые резонаторы и открытые передающие тракты (линзовые и зеркальные
квазиоптич. линии).
Простейший открытый резонатор состоит из 2 параллельных зеркал,
расположенных друг против друга. Пучок света последовательно отражается от
каждого из зеркал и возвращается к противоположному. Ширина пучка гораздо
больше длины волны, но т. к. расстояние между зеркалами гораздо больше ширины
пучка, то существенной оказывается дифракционная расходимость пучка. Это
явление, а также дифракция на краях зеркал приводят к неоднородности в
распределении поля по сечению пучка и к появлению потерь энергии на излучение.
Для уменьшения потерь (увеличения добротности резонатора) применяются изогнутые
зеркала (в частности, конфокальный резонатор), к-рые фокусируют лучи.
Открытые разонаторы, хотя их размеры велики по сравнению с длиной
волны  , обладают достаточно редким (дискретным) спектром собственных
частот. Поэтому они оказались очень удобной резонансной системой не только для лазеров
(см. Оптический резонатор), но и для всей аппаратуры для
электромагнитных золн оптич. и субмиллиметрового диапазонов .
, обладают достаточно редким (дискретным) спектром собственных
частот. Поэтому они оказались очень удобной резонансной системой не только для лазеров
(см. Оптический резонатор), но и для всей аппаратуры для
электромагнитных золн оптич. и субмиллиметрового диапазонов .
В квазиоптич. линиях пучок (ширина к-рого >>  ) последовательно
проходит через ряд длиннофокусных линз или слабоизогнутых зеркал (корректоров).
Корректоры фокусируют пучок, компенсируя его дифракционное расширение при
распространении между ними. Такие линии могут применяться и в системах
оптической связи. Для субмиллиметровых и миллиметровых волн могут применяться
также радиоволноводы, широкие по сравнению с длиной волны
) последовательно
проходит через ряд длиннофокусных линз или слабоизогнутых зеркал (корректоров).
Корректоры фокусируют пучок, компенсируя его дифракционное расширение при
распространении между ними. Такие линии могут применяться и в системах
оптической связи. Для субмиллиметровых и миллиметровых волн могут применяться
также радиоволноводы, широкие по сравнению с длиной волны 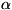 , в к-рых используются
зеркала, линзы и призмы.
, в к-рых используются
зеркала, линзы и призмы.
Лит.: Техника субмиллиметровых волн, под ред.
P. А. Валитова, M., 1969; Квазиоптика, пер. с англ. и нем., под ред. Б. З. Kaценеленбаума и В. В. Шевченко, M., 1966; Вайнштейн Л. A., Открытые
резонаторы и открытые волноводы, M., 1966; Каценеленбаум Б. З., Высокочастотная
электродинамика, M., 1966.
Б. З. Каценеленбаум.
КВАЗИСТАТИЧЕСКИИ ПРОЦЕСС, равновесный процесс, бесконечно медленный
переход термодинамич. системы из одного равновесного состояния в другое, при
к-ром в любой момент физ. состояние системы бесконечно мало отличается от
равновесного. Равновесие в системе при К. п. устанавливается во много раз
быстрее, чем происходит изменение физ. параметров системы. Всякий К. п.
является обратимым процессом. К. п. играют в термодинамике важную роль,
т. к. термодинамич. циклы, включающие одни К. п., дают макс. значения работы
(см. Карно цикл). Термин "К.п." предложен в 1909 К. Каратеодори.
КВАЗИСТАЦИОНАРНЫЙ ПРОЦЕСС, процесс, протекающий в ограниченной
системе и распространяющийся в ней так быстро, что за время распространения
этого процесса в пределах системы её состояние не успевает измениться. Поэтому
при рассмотрении процесса можно пренебречь временем его распространения в
пределах системы. Напр., если в к.-л. участке замкнутой электрич. цепи
действует переменная внешняя эдс, но время распространения электромагнитного
поля до наиболее удалённых точек цепи столь мало, что величина эдс не успевает
сколько-нибудь заметно изменяться за это время, то изменения напряжений и токов
в цепи можно рассматривать как К. п. В этом случае переменные электрич. и
магнитные поля, создаваемые движущимися в цепи электрич. зарядами
(распределение и скорости к-рых изменяются со временем), оказываются в каждый
момент времени такими же, какими были бы стационарные электрич. и магнитные
поля (поля стационарных зарядов и токов), распределение и скорости к-рых (не
изменяющиеся со временем) совпадают с распределением и скоростями зарядов,
существующими в системе в рассматриваемый момент времени. Однако в случае
нестационарных токов наряду с электрич. полями зарядов возникают вихревые
электрич. поля, обусловленные изменениями магнитных полей. Действие этих полей
может быть учтено путём введения эдс индукции (наряду со сторонними эдс
источников). Но введение эдс индукции не нарушает основной черты стационарных
токов - равенства сил токов во всех сечениях неразветвлённой цепи. В силу этого
для электрич. цепей, удовлетворяющих условиям квазистациодарности (квазистационарных
токов), справедливы Кирхгофа правила.
Условия квазистационарности наиболее просто формулируются для случая
периодич. процессов. Процессы можно считать квазистационарными в случае, если
время распространения между наиболее удалёнными друг от друга точками
рассматриваемой системы мало по сравнению с периодом процесса или, что то же
самое, когда расстояние между указанными точками мало по сравнению с
соответствующей длиной волны.
Понятие К. п. может быть применено и к др. системам - механич.,
термодинамическим. Если, напр., на один из концов упругого стержня действует
переменная внешняя сила, направленная вдоль стержня, и если условие
квазистационарности выполняется, т. е. за время распространения продольной
упругой волны от одного конца стержня до другого величина силы не успевает
измениться, то ускорения всех точек стержня в каждый момент времени
определяются значением силы в этот же момент времени. Процесс теплопроводности
можно считать К. п., если выравнивание темп-ры в теплопроводящем стержне
происходит значительно быстрее, чем изменение внешних условий: темп-р T1
и T2 концов стержня.
КВАЗИСТАЦИОНАРНЫЙ ТОК, относительно медленно изменяющийся переменный
ток, для мгновенных значений к-рого с достаточной точностью выполняются законы
постоянных токов (прямая пропорциональность между током и напряжением - Ома
закон, Кирхгофа правила и др.). Подобно постоянным токам, К. т. имеет
одинаковую силу тока во всех сечениях неразветвлённой цепи. Однако при расчёте
К. т. (в отличие от расчёта цепей постоянного тока) необходимо учитывать
возникающую при изменениях тока эдс индукции. Индуктивности, ёмкости,
сопротивления ветвей цепи К. т. могут считаться сосредоточенными параметрами.
Для того чтобы данный переменный ток можно было считать К. т., необходимо
выполнение условия квазистационарности (см. Квазистационарный процесс), к-рое
для синусоидальных переменных токов сводится к малости геометрич. размеров
электрической цепи по сравнению с длиной волны рассматриваемого тока. Токи
промышленной частоты, как правило, можно рассматривать как К. т. (частоте 50 гц
соответствует длина волны ~6000 км). Исключение составляют токи в линиях
дальних передач, в к-рых условие квазистационарности вдоль линии не
выполняется.
КВАЗИУПРУГАЯ СИЛА, направленная к центру О сила F, величина к-рой
пропорциональна расстоянию r от центра О до точки приложения силы;
численно F = cr, где с - постоянный коэффициент. Тело,
находящееся под действием К. с., обладает потенциальной энергией П = = 1/2 сr2.
Назв. "К. с." связано с тем, что аналогичным свойством обладают
силы, возникающие при малых деформациях упругих тел (т. н. силы упругости). Для
материальной точки, находящейся под действием К. с., центр О является
положением устойчивого равновесия. Выведенная из этого положения точка будет
совершать около О линейные гармонические колебания или описывать эллипс
(в частности, окружность).
КВАЗИЧАСТИЦЫ (от квази... и частицы), одно из фундаментальных
понятий теории конденсированного состояния вещества, в частности теории
твёрдого тела. Теоретич. описание и объяснение свойств конденсированных сред
(твёрдых тел и жидкостей), исходящее из свойств составляющих их частиц (атомов,
молекул), представляет большие трудности, во-первых, потому, что число частиц
огромно (~ 1022 частиц в 1 см3), и, во-вторых,
потому, что они сильно взаимодействуют между собой. Из-за взаимодействия частиц
полная энергия такой системы, определяющая многие её свойства, не является
суммой энергий отдельных частиц, как в случае идеального газа. Частицы
конденсированной среды подчиняются законам квантовой механики; поэтому свойства
совокупности частиц, составляющих твёрдое тело (или жидкость), могут быть
поняты лишь на основе квантовых представлений. Развитие квантовой теория
конденсированных сред привело к созданию специальных физ. понятий, в частности
к концепции К.- элементарных возбуждений всей совокупности взаимодействующих
частиц. Особенно плодотворные результаты концепция К. дала в теории кристаллов
и жидкого гелия.
Свойства квазичастиц. Оказалось, что энергию E кристалла (или
жидкого гелия) можно приближённо считать состоящей из двух частей: энергии
основного (невозбуждённого) состояния E0 (наименьшая энергия,
соответствующая состоянию системы при абс. нуле темп-ры) и суммы энергий E элементарных
(несводимых к более простым) движений (возбуждений):
E=E0+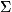 En
En
Индекс  характеризует тип элементарного возбуждения, п - целые
числа, показывающие число элементарных возбуждений типа
характеризует тип элементарного возбуждения, п - целые
числа, показывающие число элементарных возбуждений типа  .
.
T. о., энергию возбуждённого состояния кристалла (гелия) оказалось возможным
записать так же, как и энергию идеального газа, в виде суммы энергий. Однако в
случае газа суммируется энергия его частиц (атомов и молекул), а в случае
кристалла суммируются энергии элементарных возбуждений всей совокупности атомов
(отсюда термин "К."). В случае газа, состоящего из свободных частиц,
индекс  обозначает импульс p частицы, E - её энергию (E
= р2/2m, т - масса частицы), n - число частиц,
обладающих импульсом р. Скорость
обозначает импульс p частицы, E - её энергию (E
= р2/2m, т - масса частицы), n - число частиц,
обладающих импульсом р. Скорость  = p/m.
= p/m.
Элементарное возбуждение в кристалле также характеризуют вектором р, свойства
к-рого похожи на импульс, его называют квазиимпульсом. Энергия Л элементарного
возбуждения зависит от квазиимпульса, но эта зависимость E(р) носит не
такой простой характер, как в случае свободной частицы. Скорость
распространения элементарного возбуждения также зависит от квазиимпульса и от
вида функции E(р). В случае К. индекс  включает в себя обозначение типа
элементарного возбуждения, поскольку в конденсированной среде возможны
элементарные возбуждения, разные по своей природе (аналог - газ, содержащий
частицы различного сорта).
включает в себя обозначение типа
элементарного возбуждения, поскольку в конденсированной среде возможны
элементарные возбуждения, разные по своей природе (аналог - газ, содержащий
частицы различного сорта).
Введение для элементарных возбуждений термина "К" вызвано не
только внешним сходством в описании энергии возбуждённого состояния кристалла
(или жидкого гелия) и идеального газа, но и глубокой аналогией между свойствами
свободной (квантовомеханической) частицы и элементарным возбуждением
совокупности взаимодействующих частиц, основанной на корпускулярно-волновом
дуализме. Состояние свободной частицы в квантовой механике описывается
монохроматич. волной (см. Волны де Бройля), частота к-рой 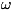 = E/h, а
длина волны
= E/h, а
длина волны  = 2
= 2 h/р (E и h - энергия и импульс свободной частицы, h -
Планка постоянная). В кристалле возбуждение одной из частиц (напр.,
поглощение одним из атомов фотона), приводящее из-за взаимодействия (связи)
атомов к возбуждению соседних частиц, не остаётся локализованным, а передаётся
соседям и распространяется в виде волны возбуждений. Этой волне ставится в
соответствие К. с квазиимпульсом p = hк и энергией E=h
h/р (E и h - энергия и импульс свободной частицы, h -
Планка постоянная). В кристалле возбуждение одной из частиц (напр.,
поглощение одним из атомов фотона), приводящее из-за взаимодействия (связи)
атомов к возбуждению соседних частиц, не остаётся локализованным, а передаётся
соседям и распространяется в виде волны возбуждений. Этой волне ставится в
соответствие К. с квазиимпульсом p = hк и энергией E=h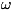 (k) (к - волновой
вектор, длина волны
(k) (к - волновой
вектор, длина волны  = 2
= 2 /k).
/k).
Зависимость частоты от волнового вектора к позволяет установить зависимость
энергии К. от квазиимпульса. Эта зависимость E = E(р) наз. законом
дисперсии, является основной ди-намич. характеристикой К., в частности
определяет ее скорость (v = dE/dp). Знание закона дисперсии К. позволяет
исследовать движение К. во внешних полях. К., в отличие от обычной частицы, не
характеризуется определённой массой. Однако, подчёркивая сходство К. и частицы,
иногда удобно вводить величину, имеющую размерность массы. Её наз. эффективной
массой mЭФ. (как правило, эффективная масса зависит от квазиимпульса
и от вида закона дисперсии).
Всё сказанное позволяет рассматривать возбуждённую конденсированную среду
как газ К. Сходство между газом частиц и газом К. проявляется также в том, что
для описания свойств газа К. могут быть использованы понятия и методы кинетич.
теории газов, в частности говорят о столкновениях К. (при к-рых имеют место
специфич. законы сохранения энергии и квазиимпульса), длине свободного пробега,
времени свободного пробега и т. п. Для описания газа К. может быть использовано
кинетическое уравнение Больцмана.
Одно из важных отличительных свойств газа К. (по сравнению с газом обычных
частиц) состоит в том, что К. могут появляться и исчезать, т. е. число их не
сохраняется. Число К. зависит от темп-ры. При T=0 K квазичастицы отсутствуют.
Для газа К. как квантовой системы можно определить энергетич. спектр
(совокупность энергетич. уровней) и рассматривать его как энергетич. спектр
кристалла или жидкого гелия. Разнообразие типов К. велико, т. к. их характер
зависит от атомной структуры среды и взаимодействия между частицами. В одной и
той же среде может существовать неск. типов К.
К., как и обычные частицы, могут иметь собственный механич. момент - спин.
В соответствии с его величиной (выражаемой целым или полуцелым числом h)
К. можно разделить на бозоны и фермионы. Бозоны рождаются и
исчезают поодиночке, фермионы рождаются и исчезают парами.
Для К.-фермионов распределение по энергетич. уровням определяется функцией
распределения Ферми, для К.-бозонов - функцией распределения Бозе. В энергетич.
спектре кристалла (или жидкого гелия), к-рый является совокупностью энергетич.
спектров всех возможных в них типов К., можно выделить фермиевскую и бозевскую
"ветви". В нек-рых случаях газ К. может вести себя и как газ,
подчиняющийся Больцмана статистике (напр., газ электронов проводимости и
дырок в невырожденном полупроводнике, см. ниже).
Теоретич. объяснение наблюдаемых ма-кроскопич. свойств кристаллов (или
жидкого гелия), основанное на концепции К., требует знания закона дисперсии К.,
а также вероятности столкновений К. друг с другом и с дефектами в
кристаллах. Получение численных значений этих характеристик возможно только
путём применения вычислит, техники. Кроме того, существенное развитие получил
полуэмпирич. подход: количеств, характеристики К. определяются из сравнения
теории с экспериментом, а затем служат для расчёта характеристик кристаллов
(или жидкого гелия).
Для определения характеристик К. используются рассеяние нейтронов, рассеяние
и поглощение света, ферромагнитный резонанс и антиферромагнитный
резонанс, ферроакустический резонанс, изучаются свойства металлов и
полупроводников в сильных магнитных полях, в частности циклотронный
резонанс, гальваномагнитные явления и т. д.
Концепция К. применима только при сравнительно низких темп-pax (вблизи
основного состояния), когда свойства газа К. близки к свойствам идеального
газа. С ростом числа К. возрастает вероятность их столкновений, уменьшается
время свободного пробега К. и, согласно неопределённостей соотношению, увеличивается
неопределённость энергии К. Само понятие К. теряет смысл. Поэтому ясно, что с
помощью К. нельзя описать все движения атомных частиц в конденсированных
средах. Напр., К. непригодны для описания самодиффузии (случайного блуждания
атомов по кристаллу).
Однако и при низких темп-pax с помощью К. нельзя описать все возможные
движения в конденсированной среде. Хотя, как правило, в элементарном
возбуждении принимают участие все атомы тела, оно микроскопично: энергия и
импульс каждой К.-атомного масштаба, каждая К. движется независимо от других.
Атомы и электроны в конденсированной среде могут принимать участие в движении
совершенно др. природы - макроскопическом по своей сути (гидродинамическом) и в
то же время не теряющем своих квантовых свойств. Примеры таких движений:
сверхтекучее движение в гелии-Н (см. Сверхтекучесть) и электрич. ток В
сверхпроводниках (см. Сверхпроводимость). Их отличительная черта -
строгая согласованность (когерентность) движения отдельных частиц.
Представление о К. получило применение не только в теории твёрдого тела и
жидкого гелия, но и в др. областях физики: в теории атомного ядра (см. Ядерные
модели), в теории плазмы, в астрофизике и т. п.
Фононы. В кристалле атомы совершают малые колебания, к-рые в виде
волн распространяются по кристаллу (см. Колебания кристаллической решётки). При
низких темп-pax T главную роль играют длинноволновые акустические
колебания - обычные звуковые волны: они обладают наименьшей энергией. К.,
соответствующие волнам колебаний атомов, наз. фононами. Фононы-бозоны;
их число при низких темп-pax растёт пропорционально T3. Это
обстоятельство, связанное с линейной зависимостью энергии фонона с?Ф от его
квазиимпульса 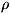 при достаточно малых квазиимпульсах (EФ = sp,
где s - скорость звука), объясняет тот факт, что теплоёмкость кристаллов
(неметаллических) при низких темп-pax пропорциональна Г3.
при достаточно малых квазиимпульсах (EФ = sp,
где s - скорость звука), объясняет тот факт, что теплоёмкость кристаллов
(неметаллических) при низких темп-pax пропорциональна Г3.
Фононы в сверхтекучем гелии. Основное состояние гелия напоминает
предельно вырожденный Бозе-газ. Как во всякой жидкости, в гелии могут
распространяться звуковые волны (волны колебаний плотности). Звуковые волны -
единств, тип микроскопич. движения, возможного в гелии вблизи основного
состояния. Так как в звуковой волне частота 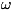 пропорциональна волновому вектору
k:
пропорциональна волновому вектору
k: 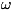 = sk (s - скорость звука), то соответствующие К.
(фононы) имеют закон дисперсии E = sp. По мере увеличения
импульса кривая E = E(р) отклоняется от линейного закона. Фононы гелия
также подчиняются статистике Бозе. Представление об энергетич. спектре гелия
как о фононном спектре не только описывает его термодинамич. свойства (напр.,
зависимость теплоёмкости гелия от темп-ры), но и объясняет явление
сверхтекучести.
= sk (s - скорость звука), то соответствующие К.
(фононы) имеют закон дисперсии E = sp. По мере увеличения
импульса кривая E = E(р) отклоняется от линейного закона. Фононы гелия
также подчиняются статистике Бозе. Представление об энергетич. спектре гелия
как о фононном спектре не только описывает его термодинамич. свойства (напр.,
зависимость теплоёмкости гелия от темп-ры), но и объясняет явление
сверхтекучести.
Магноны. В ферро- и антиферромагнетиках при T = 0 К спины
атомов строго упорядочены. Состояние возбуждения магнитной системы связано с
отклонением спина от "правильного" положения. Это отклонение не
локализуется на определённом атоме, а переносится от атома к атому.
Элементарное возбуждение магнитной системы представляет собой волну поворотов
спина (спиновая волна), а соответствующая ей К. наз. магноном. Магноны-бозоны.
Энергия магнона квадратично зависит от квазиимпульса (в случае малых
квазиимпульсов). Это находит отражение в тепловых и магнитных свойствах ферро-
и антиферромагнетиков (напр., при низких темп-pax отклонение магнитного
момента ферромагнетика от насыщения ~ T3/2). Высокочастотные свойства
ферро- и антиферромагнетиков описываются в терминах "рождения"
магнонов.
Экситон Френкеля представляет собой элементарное возбуждение
электронной системы отдельного атома или молекулы, к-рое распространяется по
кристаллу в виде волны. Экситон, как правило, имеет весьма значительную (по
атомным масштабам) энергию ~ неск. эв. Поэтому вклад экситонов в тепловые
свойства твёрдых тел мал. Экситоны проявляют себя в оптич. свойствах
кристаллов. Обычно среднее число экситонов очень мало. Поэтому их можно
описывать классич. статистикой Больцмана.
Электроны проводимости и дырки. В твёрдых диэлектриках и полупроводниках
наряду с экситонами существуют элементарные возбуждения, обусловленные
процессами, аналогичными ионизации атома. В результате такой
"ионизации" возникают две независимо распространяющиеся К.: электрон
проводимости и дырка (недостаток электрона в атоме). Дырка ведёт
себя как положительно заряженная частица, хотя её движение представляет собой
волну электронной перезарядки, а не движение положит, иона. Электроны проводимости
и дырки - фермионы. Они являются носителями электрич. тока в твёрдом теле.
Полупроводники, у к-рых энергия "ионизации" мала, всегда содержат
заметное кол-во электронов проводимости и дырок. Проводимость полупроводников
падает с понижением темп-ры, т. к. число электронов и дырок при этом
уменьшается.
Электрон и дырка, притягиваясь друг к другу, могут образовать э к с и т о н
Мотта (квазиатом), к-рый проявляет себя в оптич. спектрах кристаллов
водородоподобными линиями поглощения (см. Экситон).
Поляроны. Взаимодействие электрона с колебаниями решётки приводит к
её поляризации вблизи электрона. Иногда взаимодействие электрона с кристаллич.
решёткой настолько сильно, что движение электрона по кристаллу сопровождается
волной поляризации. Соответствующая К. наз. поляроном.
Электроны проводимости металла, взаимодействующие друг с другом и с
полем ионов кристаллич. решётки, эквивалентны газу К. со сложным законом
дисперсии. Заряд каждой К. равен заряду свободного электрона, а спин равен 1/2.
Их динамич. свойства, обусловленные законом дисперсии, существенно
отличаются от свойств обычных свободных электронов. Электроны проводимости -
фермионы. В пространстве квазиимпульсов при T = О К они заполняют
область, ограниченную Ферми поверхностью. Возбуждение электронов
проводимости означает появление пары: электрона "над" поверхностью
Ферми и свободного места (дырки) "под" поверхностью. Электронный газ
сильно вырожден не только при низких, но и при комнатных температурах (см.
Вырожденный газ). Это обстоятельство определяет температурную зависимость большинства
характеристик металла (в частности, линейную зависимость теплоёмкости от
темп-ры при T -> О).
Лит.: Ландау Л. Д., Лифшиц E. M., Статистическая физика, 2 изд.,
M., 1964; Займан Дж., Принципы теории твёрдого тела, пер. с англ., M., 1966; Л
и ф ш и ц И. M., Квазичастицы в современной физике, в сб.: В глубь атома, M.,
1964; Рейф Ф., Сверхтекучесть и "Квазичастицы", в сб.: Квантовая
макрофизика, пер. с англ., M., 1967.
M. И. Каганов.
КВАЗИЭЛЕКТРОННАЯ АВТОМАТИЧЕСКАЯ ТЕЛЕФОННАЯ СТАНЦИЯ, телефонная
станция, в к-рой установление соединения абонентов осуществляется
быстродействующими коммутационными устройствами на герконах, ферридах и
т. п. элементах, а управление ими - устройствами на электронных элементах (на интегральных
схемах и т. д.).
КВАИСИ, посёлок гор. типа в Джавском р-не Юго-Осет. АО Груз. CCP.
Расположен на р. Джеджора (приток Риони), в 60 км к С.-З. от г.
Цхинвали, с к-рым соединён автомоб. дорогой. Добыча свинцово-цинковых руд
(Кваисское месторождение). Обогатительная ф-ка.
КВАКВА (Nycticorax nycticorax), птица сем. цапель отряда голенастых.
Дл. тела 60 см. Окраска оперения гл. обр. чёрная (с металлич.
блеском), беловатая и серая. Распространена на Ю. Европы, Азии, Сев. Америки, а
также в Африке и Юж. Америке; в СССР населяет юг Европ. части и Cp. Азию; на
зиму улетает в Африку. Держится по берегам рек, прудов, озёр. Деятельна ночью.
Гнездится колониями, обычно на деревьях. В кладке 4-5 зеленоватых яиц,
насиживают оба родителя 21-22 суток. Питается рыбой, лягушками, а также мелкими
беспозвоночными животными.
Лит.: Птицы Советского Союза, под ред. Г. П. Дементьева и H. А.
Гладкова, т. 2, M., 1951.
КВАКЕРЫ (от англ. Quakers, букв.- трясущиеся; первоначально
употреблялось в нронич. смысле; самоназв. Society of Friends - общество
друзей), члены религ. христианской общины, осн. в сер. 17 в. в Англии
ремесленником Дж.Фоксом. К. отвергают институт священников и церковные таинства
(человек, согласно учению К., может вступать в непосредственный союз с богом),
проповедуют пацифизм, занимаются благотворительностью. Преследуемые англ,
пр-вом и англиканской церковью, многие общины К. начиная с 60-х гг. 17
в. эмигрировали в Сев. Америку. В 1689 положение англ, и амер. К. было
легализовано "Актом о терпимости". Вначале движение К. было чисто мелкобурж. по социальному составу участников; позже среди К. появились крупные
капиталистич. элементы. К нач. 70-х гг. 20 в. общины К. насчитывали ок. 200
тыс. членов (гл. обр. в США, Великобритании, странах Вост. Африки).
КВАКИУТЛИ, квакиютли, индейское племя в пров. Брит. Колумбия в
Канаде. Числ. ок. 4,5 тыс. чел. (1967, оценка). К. двуязычны: говорят на своём
языке, входящем в группу вакашских языков, и на англ. Ко времени прихода
европейцев (18 в.) насчитывалось ок. 25 тыс. чел. Занимались гл. обр.
рыболовством; зарождались отношения частной собственности, существовало
патриархальное наследственное рабство. К. создали своеобразную культуру и
иск-во. В наст, время живут в резервациях; осн. их масса - рабочие рыбной и
лесной пром-сти. Религия - протестантизм, сохраняются также нек-рые древние
верования и культы.
Лит.: Народы Америки, т. 1, M., 1959; Linguistic and cultural
affiliations of Canadian Indian Bands, Ottawa, 1967.
КВАКШИ (Hylidae), семейство бесхвостых земноводных. Дл. тела от 2,5
до 13,5 см. 31 род. Распространены во всех частях света, но гл. обр. в
Америке (в тропической части ) и в Австралии .Многие К. ведут древесный образ
жизни. Некоторые размножат ются на деревьях, откладывая икру в пазухах листьев
в накапливающуюся здесь дождевую воду; другие (филломедузы) откладывают икру
в свёрнутые листья, свешивающиеся над водой. У представителей сумчатых К., или сумчатых
лягушек, обитающих в тропической Америке, самки имеют на спине кожный
карман (сумку), где помещается оплодотворённая икра, которая у одних видов
находится здесь лишь на первых стадиях развития, у других - до превращения
головастиков в лягушек. Наиболее обширный род - настоящие К. (род HyIa),
содержит 350 видов. В СССР - 2 вида: обыкновенная К. (H. arborea) и
дальневосточная К. (H. japonica). Обыкновенная К., или древесница, встречается
на Украине (включая Крым) и на Кавказе. Дл. тела до 5 см; окраска может
меняться в зависимости от цвета окружающих предметов. У самцов на горле под
кожей голосовой мешок, раздувающийся при кваканий в виде пузыря. Весной самка
откладывает в воду до 1000 икринок.
П. В. Терентьев.
КВАЛИMETPИЯ (от лат. qualis - какой по качеству и
...метрия), научная
область, объединяющая методы количественной оценки качества продукции.
Осн. задачи К.: обоснование номенклатуры показателей качества, разработка
методов определения показателей качества продукции и их оптимизации,
оптимизация типоразмеров и параметрич. рядов изделий, разработка принципов
построения обобщённых показателей качества и обоснование условий их
использования в задачах стандартизации и управления качеством. К. использует
матем. методы: линейное, нелинейное и динамнч. программирование, теорию
оптимального управления, теорию массового обслуживания и т. п.
Лит.: "Стандарты и качество", 1970, № 11, с. 30-34.
КВАЛИТАТИВНОЕ (КАЧЕСТВЕННОЕ) СТИХОСЛОЖЕНИЕ (от лат. qualitas -
качество), тип стихосложения, в к-ром слоги соотносятся по ударности и
безударности, а не по долготе, как в квантитативном (количественном)
стихосложении. К. (к.) с. объединяет силлабич., силлабо-тонич. и тонич.
стихосложение. См. Стихосложение.
КВАЛИФИКАЦИЯ (от лат. qualis - какой по качеству и facio - делаю), 1)
степень и вид профессиональной обученностп работника, наличие v него знаний,
умения и навыков, необходимых для выполнения им определённой работы. К.
работников отражается в их тарификации (присвоении работнику в зависимости от
его К. того или иного тарифного разряда). Присвоение тарифного разряда
свидетельствует о пригодности работника к выполнению данного круга работ. В
СССР К. работников, как правило, устанавливается спец. квалификационной
комиссией в соответствии с требованиями тарифно-квалификационного справочника.
Показателем К. работника, помимо разряда, может быть также категория или
диплом, наличие звания и учёной степени. Занятие нек-рых должностей допускается
лишь при наличии диплома (должность врача, учителя). В СССР на предприятиях, в
учреждениях и opr-циях создана система подготовки и повышения квалификации
рабочих и служащих, где рабочие и служащие обучаются новым профессиям и
специальностям и проходят обучение по повышению своей квалификации (см.
Баланс трудовых ресурсов, Трудовые ресурсы). 2) Характеристика определённого вида
работы, устанавливаемая в зависимости от её сложности, точности и
ответственности. В СССР К. работы обычно определяется разрядом, к к-рому данный
вид работы отнесён тарифно-квалификационным справочником. Определение К. работ
важно при установлении тарифных ставок и должностных окладов работников. К.
инженерно-технич. работ и работ, выполняемых служащими и др. лицами, незанятыми
непосредственно на произ-ве, определяется требованиями, предъявляемыми к
занимаемой должности. 3) Характеристика предмета, явления, отнесение его к
к.-л. категории, группе, напр, квалификация преступления.
Л. Ф. Бибик.
КВАЛИФИКАЦИЯ ПРЕСТУПЛЕНИЯ, в уголовном праве установление и
закрепление в соответствующих процессуальных актах точного соответствия
признаков совершённого деяния тому или иному составу преступления,
предусмотренному уголовным законом. К. п. является основанием для назначения
меры наказания и для наступления иных правовых последствий совершённого
преступления. Советская правовая наука рассматривает правильную К. п. как
важный фактор соблюдения социалистич. законности в уголовном судопроизводстве.
Неправильная К. п., т. е. применение закона, не соответствующего фактич.
обстоятельствам дела, искажает представление о характере совершённых
преступлений и влечёт за собой вынесение неверного приговора. Ошибка в К. п.-
основание для отмены или изменения приговора.
КВАЛИФИЦИРОВАННОЕ БОЛЬШИНСТВО, в отличие от простого большинства в
50% + 1, большинство в ⅔, ¾ и т. д. голосов. Обычно
требуется для принятия наиболее важных решений (напр., для внесения изменений в
конституционные законы). Конституция СССР устанавливает, что изменение
Конституции производится по решению Верх. Совета СССР, принятому большинством
не менее ⅔ голосов в каждой из его палат. К. б.
требуется также при вынесении вердикта в суде присяжных.
КВАЛИФИЦИРОВАННОЕ ПРЕСТУПЛЕНИЕ, квалифицированный вид преступления, в
уголовном праве преступление, имеющее один или неск. предусмотренных в законе
признаков (отягчающих обстоятельств), к-рые указывают на его повышенную
общественную опасность по сравнению с неквалифицированным (простым) видом того
же преступления. Так, по сов. уголовному праву умышленное убийство из
хулиганских побуждений (УК РСФСР, ст. 102, п. "б") - К. п. по
сравнению с убийством без отягчающих обстоятельств (УК РСФСР, ст. 103). Закон в
статьях, устанавливающих наказание за отд. виды преступлений, признаками К. п.
считает повторность, наличие у виновного судимости, крупный размер
причинённого ущерба, совершение преступления организованной группой и др. За К.
п. устанавливается более строгое наказание.
КВАЛИФИЦИРОВАННЫЙ ТРУД, труд, требующий спец. предварительной
подготовки работника, наличия у него навыков, умения и знаний, необходимых для выполнения
определённых видов работ. В отличие от неквалифицированного (простого) труда,
К. т. выступает как сложный: один час его эквивалентен неск. часам простого
труда (см. Редукция труда). В соответствии с этим К. т. оплачивается
выше, чем неквалифицированный (см. Труд, Заработная плата, Квалификация).
КВАНГО, Куангу (Kwango, Cuango), река в Центр. Африке, в Анголе и
Респ. Заир. Крупнейший лев. приток р. Касаи (басс. р. Конго). Дл. ок. 1200 км.
Пл. басс. 263,5 тыс. км2. Берёт начало на плато Лунда, течёт
на С. в широкой и глубокой долине, образуя ряд порогов и водопадов. Гл. притоки
- Вамба и Квилу (справа). Подъём воды с сент.- окт. по апрель, в сезон дождей;
самые низкие уровни - в августе. Cp. годовой расход воды в ниж. течении - 2,7
тыс. м3/сек. Судоходна в низовьях (от устья до порогов Кингуши, 307
км) и частично в ср. течении (между Кингуши и водопадом
Франца-Иосифа, ок. 300 км). Рыболовство.
КВАНДЖУ, Кванчжу, город в Юж. Корее. Адм. ц. провинции Чолла-Намдо.
403,7 тыс. жит. (1966). Трансп. узел. Торг, центр с.-х. р-на
(равнина Йонсанган). Текст. пром-сть.
КВАНДО, Куанду (Kwando, Cuando), в ниж. течении - Линьянти, река в
Анголе (в ср. течении пограничная между Анголой и Замбией), Намибии и Ботсване,
прав, приток Замбези. Дл. ок. 800 км. Берёт начало на плато Бие, течёт в
порожистом русле по саванновым лесам; в низовьях протекает по болотистой
равнине, принимая справа один из рукавов р. Окаванго. Половодье в период дождей
(октябрь-ноябрь).
КВАНЗА, Куанзa (Kwanza, Cuanza), река в Анголе. Дл. 960 км. Пл.
басе. 147,7 тыс. км2. Берёт начало на плоскогорье Бие, течёт
на С., затем на С.-З. и 3. в глубоко врезанной долине, образуя многочисл.
пороги и водопады; в ниж. течении выходит на приморскую низм. и становится
судоходной (на 258 км от устья). Впадает в Атлантич. ок. к Ю. от г.
Луанда. Полноводна в период дождей. В ср. течении К.- ГЭС Камбамбе.
"КВАНТ", ежемесячный физико-математический
научно-популярный журнал АН СССР и АПН СССР. Издаётся с 1970 в Москве.
Рассчитан на преподавателей средних школ и учащихся старших классов. Тираж ок.
34 тыс. экз. (1972). Гл. редакторы (с 1970) академики И. К. Кикоин и A. H.
Колмогоров.
КВАНТ ДЕЙСТВИЯ, то же, что Планка постоянная.
КВАНТ СВЕТА (нем. Quant, от лат. quantum - сколько), количество
(порция) электромагнитного излучения, к-рое в единичном акте способен излучить
или поглотить атом или др. квантовая система; элементарная частица, то же, что фотон.
КВАНТИЛЬ, одна из числовых характеристик случайных величин,
применяемая в матем. статистике. Если функция распределения случайной величины X
непрерывна, то квантиль Kp порядка р определяется
как такое число, для к-рого вероятность неравенства X < КР равна
р. Из определения К. следует, что вероятность неравенства Кр
< X < Кр' равна р' - р. Квантиль K1, есть
медиана случайной величины X. Квантили K1, и K3/
наз. квартилями, a K0,1, K0,2, ..., К0,9
- децилями. Знание К. для подходяще выбранных значений р позволяет
составить представление о виде функции распределения.
Напр., для нормального распределения (рис.)
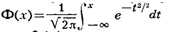
график функции Ф(x) можно вычертить по децилям: X0,1 = - 1,28; Х0,2
= -0,84; K0,3 = -0,52; X0,4 = -0,25; K0,5
= О; X0,б = 0,25; X0,7 = 0,52; X0,8
= 0,84; X0,9 = 1,28. Квартили нормального распределения Ф(x) равны X1/
= -0,67;
K=0,67.
КВАНТИТАТИВНОЕ (КОЛИЧЕСТВЕННОЕ) СТИХОСЛОЖЕНИЕ (от лат. quantitas -
количество), тип стихосложения, осн. на упорядоченном чередовании долгих и
кратких слогов; то же, что и метрическое стихосложение.
КВАНТИТАТИВНОЕ УДАРЕНИЕ, выделение ударных элементов слова или фразы
при помощи увеличения их относит, длительности. Как правило, ударение складывается
из взаимодействия неск. компонентов. Языки, в к-рых ударение было бы чисто
квантитативным, науке неизвестны; можно утверждать лишь, что в нек-рых языках
ударение является по преимуществу квантитативным. Напр., ударение в рус. языке,
в к-ром ударный слог (и особенно гласный в нём) обладает большей относительной
длительностью, чем безударный.
КВАНТОВАНИЕ ВТОРИЧНОЕ, метод, применяемый в квантовой механике и
квантовой теории поля для исследования систем, состоящих из мн. или из
бесконечного числа частиц (или квазичастиц). В этом методе состояние
квантовой системы описывается при помощи т. н. чисел заполнения - величин,
характеризующих среднее число частиц системы, находящихся в каждом из возможных
состояний.
Метод К. в. особенно важен в квантовой теории поля в тех случаях, когда
число частиц в данной физ. системе не постоянно, а может меняться при различных
происходящих в системе процессах. Поэтому важнейшей областью применения метода
К. в. является квантовая теория излучения, квантовая теория элементарных
частиц и систем различных квазичастиц. В теории излучения рассматриваются
системы, содержащие световые кванты (фотоны), число к-рых меняется в процессах
испускания, поглощения, рассеяния. В теории элементарных частиц необходимость
применения метода К. в. связана с возможностью взаимных превращений частиц;
таковы, напр., процессы превращения электронов и позитронов в фотоны и обратный
процесс (см. Аннигиляция и рождение пар). Наиболее эффективен метод К.
в. в квантовой электродинамике, квантовой теории электромагнитных процессов, а
также в теории твёрдого тела, базирующейся на представлении о
квазичастицах. Менее эффективно применение К. в. для описания взаимных
превращений частиц, обусловленных неэлектромагнитными взаимодействиями.
В математич. аппарате К. в. волновая функция системы рассматривается
как функция чисел заполнения. При этом осн. роль играют т. н. операторы "рождения"
и "уничтожения" частиц. Оператор уничтожения - это оператор, под
действием к-рого волновая функция к.-л. состояния данной физ. системы
превращается в волновую функцию другого состояния с числом частиц на единицу меньше.
Аналогично, оператор рождения увеличивает число частиц в этом состоянии на
единицу.
Принципиальная сторона метода К. в. не зависит от того, подчиняются ли
частицы, из к-рых состоит система, Бозе - Эйнштейна статистике (напр.,
фотоны) или Ферми - Дирака статистике (напр., электроны и позитроны).
Конкретный же матем. аппарат метода, в т. ч. осн. свойства операторов рождения
и уничтожения, в этих случаях существенно различен вследствие того, что в
статистике Бозе - Эйнштейна число частиц, к-рое может находиться в одном и том
же состоянии, ничем не ограничено (так что числа заполнения могут принимать
произвольные значения), а в статистике Ферми - Дирака в каждом состоянии может
находиться не более одной частицы (и числа заполнения могут иметь лишь значения
0 и 1).
Метод К. в. был впервые развит англ, физиком П. Дираком (1927) в его
теории излучения и далее разработан сов. физиком В. А. Фоком (1932).
Термин "К. в." появился вследствие того, что этот метод возник позже
"обычного", или "первичного", квантования, целью к-рого
было выявить волновые свойства частиц. Необходимость последовательного учёта и
корпускулярных свойств полей (поскольку корпускулярно-волновой дуализм присущ
всем видам материи) привела к возникновению методов К. в.
Лит. см. при ст. Квантовая теория поля.
КВАНТОВАНИЕ МАГНИТНОГО ПОТОКА, макроскопическое квантовое явление,
состоящее в том, что магнитный поток через кольцо из сверхпроводника с током
может принимать только дискретные значения (см. Сверхпроводимость). Минимальное
значение потока (квант потока) Ф0= ch/2e~2-10-7гс-см2,
где с - скорость света, h - Планка постоянная, е - заряд
электрона. Магнитный поток в сверхпроводнике может быть равен только целому
числу квантов потока. К. м. п. было теоретически предсказано Ф. Лондоном
(1950), к-рый получил для кванта потока значение ch/e. Эксперименты
(1961) дали для кванта потока вдвое меньшее значение. Это явилось прекрасным
подтверждением созданной к тому времени микроскопической теории
сверхпроводимости, согласно к-рой сверхпроводящий ток обусловлен движением пар
электронов.
Лит. см. при ст. Сверхпроводимость.
КВАНТОВАНИЕ ПРОСТРАНСТВА-ВРЕМЕНИ, общее название обобщений теории
элементарных частиц (квантовой теории поля), основанных на гипотезе о
существовании конечных минимальных расстояний и промежутков времени. Ближайшей
целью таких обобщений является построение непротиворечивой теории, в к-рой все
физич. величины получались бы конечными.
Представления о пространстве и времени, к-рые используются в совр. физич.
теории, наиболее последовательно формулируются в относительности теории А.
Эйнштейна и являются макроскопическими, т. е. они опираются на опыт изучения
макроскопич. объектов, больших расстояний и промежутков времени. При построении
теории, описывающей явления микромира,- квантовой механики и квантовой
теории поля,- эта классич. геометрич. картина, предполагающая непрерывность
пространства и времени, была перенесена на новую область без к.-л. изменений.
Экспериментальная проверка выводов квантовой теории пока прямо не указывает на
существование границы, за к-рой перестают быть применимыми классич. геометрич.
представления. Однако в самой теории элементарных частиц имеются трудности,
к-рые наводят на мысль, что, возможно, геометрич. представления, выработанные
на основе макроскопич. опыта, неверны для сверхмалых расстояний и промежутков
времени, характерных для микромира, что представления о физич. пространстве и
времени нуждаются в пересмотре.
Эти трудности теории связаны с т. н. проблемой расходимостей: вычисления
нек-рых физических величин приводят к не имеющим физического смысла бесконечно
большим значениям ("расходимостям"). Расходимости появляются
вследствие того, что в совр. теории элементарные частицы рассматриваются как
"точки", т. е. как материальные объекты без протяжённости. В
простейшем виде это проявляется уже в классич. теории электромагнитного поля
(классич. электродинамике), в к-рой возникает т. н. кулоновская
расходимость - бесконечно большое значение для энергии кулоновского поля
точечной заряженной частицы [из-за того, что на очень малых расстояниях г от
частицы (г -" О) поле неограниченно возрастает].
В квантовой теории поля не только остаётся кулоновская расходимость, но и
появляются новые расходимости (напр., для электрич. заряда), также в конечном
счёте связанные с точечностью частиц. (Условие точечности частиц в квантовой
теории поля выступает в виде требования т. н. локальности взаимодействий:
взаимодействие между полями определяется описывающими поля величинами, взятыми
в одной и той же точке пространства и в один и тот же момент времени.) Казалось
бы, расходимости легко устранить, если считать частицы не точечными, а
протяжёнными, "размазанными" по нек-рому малому объёму. Но здесь
существенные ограничения налагает теория относительности. Согласно этой теории,
скорость любого сигнала (т. е. скорость переноса энергии, скорость передачи
взаимодействия) не может превышать скорости света с. Предположение о
том, что взаимодействие может передаваться со сверхсветовыми скоростями,
приводит к противоречию с привычными (подтверждёнными всем общечеловеческим
опытом) представлениями о временной последовательности событий, связанных
причинно-следственными соотношениями: окажется, что следствие может
предшествовать причине. Конечность же скорости распространения взаимодействия
невозможно совместить с неделимостью частиц: в принципе нек-рой малой части
протяжённой частицы можно было бы очень быстро сообщить столь мощный импульс,
что данная часть улетела бы раньше, чем сигнал об этом дошёл бы до оставшейся
части.
T. о., требования теории относительности и причинности приводят к
необходимости считать частицы точечными. Но представление о точечности частиц
тесно связано с тем, какова геометрия, принимаемая в теории, в частности,
основывается ли эта геометрия на предположении о принципиальной возможности
сколь угодно точного измерения расстояний (длин) и промежутков времени. В
обычной теории явно или чаще неявно такая возможность предполагается.
Во всех вариантах изменения геометрии большая роль принадлежит т. н. фундаментальной
длине l, к-рая вводится в теорию как новая (наряду с Планка постоянной h
и скоростью света с) универсальная постоянная. Введение
фундаментальной длины l соответствует предположению, что измерение
расстояний принципиально возможно лишь с ограниченной точностью порядка
l (а
времени - с точностью порядка Uc). Поэтому l наз. также минимальной
длиной. Если считать частицы неточечными, то их размеры выступают в роли нек-рого минимального масштаба длины. T. о., введение фундаментальной
(минимальной) длины, в известном смысле, скрывает за собой неточечность частиц,
что и даёт надежду на построение свободной от расходимостей теории.
Одна из первых попыток введения фундаментальной длины была связана с
переходом от непрерывных координат х, у, z и времени t к
дискретным: х->n1l, у->2l, z -> п31,
t->n4/c, где n1, n2, n3,
n4 - целые числа, к-рые могут принимать значения от минус
бесконечности до плюс бесконечности. Замена непрерывных координат дискретными
несколько напоминает правила квантования Бора в первоначальной теории атома
(см. Атом) - отсюда и термин "К. п.-в."
Если рассматривать большие расстояния и промежутки времени, то каждый
"элементарный шаг" l или l/с можно считать бесконечно
малым. Поэтому геометрия "больших масштабов" выглядит как обычная.
Однако "в малом" эффект такого квантования становится существенным. В
частности, введение минимальной длины l исключает существование волн с
длиной  < l, т. е. как раз тех квантов бесконечно большой
частоты v = с/
< l, т. е. как раз тех квантов бесконечно большой
частоты v = с/ , а следовательно, и энергий е = hv, к-рые, как показывает
квантовая теория поля, ответственны за появление расходимостей. Здесь наглядно
проявляется то, как изменение геометрич. представлений влечёт за собой важные
физич. следствия.
, а следовательно, и энергий е = hv, к-рые, как показывает
квантовая теория поля, ответственны за появление расходимостей. Здесь наглядно
проявляется то, как изменение геометрич. представлений влечёт за собой важные
физич. следствия.
Введение указанным способом "ячеистого" пространства (с
"ячейками" размера l) связано с нарушением изотропии
пространства - равноправия всех направлений. Это один из существенных
недостатков данной теории.
Подобно тому, как на смену боровской теории (в которой условия квантования
постулировались) пришла квантовая механика (в к-рой квантование получалось как
естественное следствие осн. её положений), за первыми попытками К. п.-в.
появились более совершенные варианты. Их общей чертой (и здесь выступает
аналогия с квантовой механикой, в к-рой физич. величинам ставятся в
соответствие операторы) является рассмотрение координат и времени как
операторов, а не как обычных чисел. В квантовой механике формулируется важная
общая теорема: если нек-рые операторы не коммутируют между собой (т. е. в
произведении таких операторов нельзя менять порядок сомножителей), то
соответствующие этим операторам физич. величины не могут быть одновременно
точно определены. Таковы, напр ., операторы координаты х и импульса р_х
частицы (операторы принято обозначать теми же буквами, что и
соответствующие им физич. величины, но сверху со "шляпкой").
Некоммутативность этих операторов является математич. отражением того факта,
что для координаты и импульса частицы имеет место неопределённостей
соотношение:
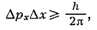
показывающее границы точностей, с которыми могут быть одновременно
определены p_X и х. Частица не может иметь одновременно точно
определённые координату и импульс: чем точнее определена координата, тем менее
определённым является импульс, и наоборот (с этим связано вероятностное
описание состояния частицы в квантовой механике).
При К. п.-в. некоммутирующими объявляются операторы, сопоставляемые
координатам самих точек пространства и моментам времени. Некоммутативность
операторов x и t, x и у и т. д. означает, что точное
значение, напр., координаты x в заданный момент времени t не
может быть определено, так же как не может быть задано точное значение неск.
координат одновременно. Это приводит к вероятностному описанию
пространства-времени. Вид операторов подбирается так, чтобы средние значения
координат могли принимать лишь целочисленные значения, кратные фундаментальной
длине l. Масштаб погрешностей (или неопределённость) координат
определяется фундаментальной длиной.
В нек-рых вариантах теории постулируется непереставимость операторов
координат и операторов, описывающих поле. Это равносильно предположению о
невозможности одновременного точного задания описывающих поле величин и точки
пространства, к к-рой эти величины относятся (такого рода варианты часто наз.
теориями нелокализуемых состояний).
В большинстве известных попыток К. п.-в. сначала вводятся постулаты,
касающиеся "микроструктуры" пространства-времени, а затем
получившееся пространство "населяется" частицами, законы движения
к-рых приводятся в соответствие с новой геометрией. На этом пути получен ряд
интересных результатов: устраняются нек-рые расходимости (однако иногда на их
месте появляются новые), в нек-рых случаях получается даже спектр масс
элементарных частиц, т. е. предсказываются возможные массы частиц. Однако
радикальных успехов получить пока не удалось, хотя методич. ценность
проделанной работы несомненна. Представляется правдоподобным, что возникающие
здесь трудности свидетельствуют о недостатках самого подхода к проблеме, при
к-ром построение новой теории начинается с постулатов, касающихся "пустого"
пространства (т. е. чисто геом. постулатов, независимых от материи, это
пространство "населяющей").
Пересмотр геометрич. представлений необходим - эта идея стала почти
общепризнанной. Однако такой пересмотр должен, по-видимому, в гораздо большей
мере учитывать неразрывность представлений о пространстве, времени и материи.
Лит.: Марков M. А., Гипероны и К-мезоны, M., 1958, §§ 33 и 34; Блохинцев Д. И., Пространство и время в микромире. M., 1970.
В. И.
Григорьев.
КВАНТОВАНИЕ ПРОСТРАНСТВЕННОЕ в квантовой механике, дискретность
возможных пространственных ориентации момента количества движения атома (или
др. частицы или системы частиц) относительно любой произвольно выбранной оси
(оси z). К. п. проявляется в том, что проекция Mz момента M на
эту ось может принимать только дискретные значения, равные целому (0, 1, 2, ...)
или полуцелому (½, 3/2,5/2, ...) числу т, помноженному
на Планка постоянную h, Mz = mh. Две другие
проекции момента Mx и Мy остаются при этом
неопределёнными, т. к., согласно осн. положению квантовой механики,
одновременно точные значения могут иметь лишь величина момента и одна из его
проекций. Для орбитального момента количества движения т (m1) может
принимать значения О, ± 1, ±2, ... ± l, где
l =0,1,2... определяет квадрат
момента Mi (т. е. его абс. величину): M2i=
l (l +1)h2. Для полного момента количества движения M (орбитального
плюс спинового) т (mi) принимает значения с интервалом в 1 от -j до
+j, где j определяет величину полного момента: M2 = j
(j + l)h2 и может быть целым или полуцелым числом. Если
атом помещается во внешнее магнитное поле H, то появляется выделенное
направление в пространстве - направление поля (к-рое и принимают за ось z). B
этом случае К. п. приводит к квантованию проекции 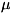 Н магнитного момента
атома
Н магнитного момента
атома 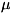 на направление поля, т. к. магнитный момент пропорционален механич. моменту
количества движения (отсюда название т - "магнитное квантовое
число"). Это приводит к расщеплению уровней энергии атома в магнитном поле
вследствие того, что к энергии атома добавляется энергия его магнитного
взаимодействия с полем, равная -
на направление поля, т. к. магнитный момент пропорционален механич. моменту
количества движения (отсюда название т - "магнитное квантовое
число"). Это приводит к расщеплению уровней энергии атома в магнитном поле
вследствие того, что к энергии атома добавляется энергия его магнитного
взаимодействия с полем, равная -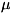 НН (см. Зеемана эффект).
НН (см. Зеемана эффект).
В. И. Григорьев.
КВАНТОВАНИЕ СИГНАЛА, дискретизация непрерывных сигналов,
преобразование электрического сигнала, непрерывного во времени и по
уровню, в последовательность дискретных (отдельных) либо дискретно-непрерывных
сигналов, в совокупности отображающих исходный сигнал с заранее установленной
ошибкой. К. с. осуществляется при передаче данных в телемеханике, при
аналого-цифровом преобразовании в вычислит, технике, в импульсных системах
автоматики и др.
При передаче непрерывных сигналов обычно достаточно передавать не сам
сигнал, а лишь последовательность его мгновенных значений, выделенных из
исходного сигнала по определённому закону. К. с. производится по времени,
уровню или по обоим параметрам одновременно. При К. с. по времени сигнал через
равные промежутки времени  ? прерывается (импульсный сигнал) либо
изменяется скачком (ступенчатый сигнал, рис.). Напр., непрерывный сигнал,
проходя через контакты периодически включаемого электрич. реле, преобразуется в
последовательность импульсных сигналов. При бесконечно малых интервалах
включения (отключения), т. е. при бесконечно большой частоте переключений
контактов, получается точное представление непрерывного сигнала. При К. с. по уровню
соответствующие мгновенные значения непрерывного сигнала заменяются ближайшими
дискретными уровнями, к-рые образуют дискретную шкалу квантования. Любое
значение сигнала, находящееся между уровнями, округляется до значения
ближайшего уровня.
? прерывается (импульсный сигнал) либо
изменяется скачком (ступенчатый сигнал, рис.). Напр., непрерывный сигнал,
проходя через контакты периодически включаемого электрич. реле, преобразуется в
последовательность импульсных сигналов. При бесконечно малых интервалах
включения (отключения), т. е. при бесконечно большой частоте переключений
контактов, получается точное представление непрерывного сигнала. При К. с. по уровню
соответствующие мгновенные значения непрерывного сигнала заменяются ближайшими
дискретными уровнями, к-рые образуют дискретную шкалу квантования. Любое
значение сигнала, находящееся между уровнями, округляется до значения
ближайшего уровня.
Квантование сигнала: а - по времени; 6 - по уровню; x0(t)
- исходный сигнал; x(t) - квантованный сигнал;  t - интервал
квантования;
t - интервал
квантования;  x - уровень квантования.
x - уровень квантования.
При бесконечно большом числе уровней квантованный сигнал превращается в
исходный непрерывный сигнал.
Лит.: Харкевич А. А., Борьба с помехами, 2 изд., M., 1965; Маркюс Ж.,
Дискретизация и квантование, пер. с франц., M., 1969.
M. M. Гельман.
КВАНТОВАЯ ЖИДКОСТЬ, жидкость, свойства к-рой определяются квантовыми
эффектами. Примером К. ж. является жидкий гелий при темп-ре, близкой к абс.
нулю. Квантовые эффекты начинают проявляться в жидкости при достаточно низких
темп-pax, когда длина волны де Бройля для частиц жидкости, вычисленная
по энергии их теплового движения, становится сравнимой с расстоянием между
ними. Для жидкого гелия это условие выполняется при темп-ре 3-2 К.
Согласно представлениям классич. механики, с понижением темп-ры кинетич.
энергия частиц любого тела должна уменьшаться. В системе взаимодействующих
частиц при достаточно низкой темп-ре последние будут совершать малые колебания
ок. положений, соответствующих минимуму потенциальной энергии всего тела. При
абс. нуле темп-ры колебания должны прекратиться, а частицы занять строго
определённые положения, т. е. любое тело должно превратиться в кристалл.
Поэтому самый факт существования жидкостей вблизи абс. нуля темп-ры связан с
квантовыми эффектами. В квантовой механике действует принцип: чем точнее
фиксировано положение частицы, тем больше оказывается разброс значений её
скорости (см. Неопределённостей соотношение). Следовательно, даже при
абс. нуле темп-ры частицы не могут занимать строго определённых положений, а их
кинетич. энергия не обращается в нуль, остаются т. н. нулевые колебания.
Амплитуда этих колебаний тем больше, чем слабее силы взаимодействия между
частицами и меньше их масса. Если амплитуда нулевых колебаний сравнима со ср.
расстоянием между частицами тела, то такое тело может остаться жидким вплоть до
абс. нуля темп-ры.
Из всех веществ при атмосферном давлении только два изотопа гелия (4He
и 3He) имеют достаточно малую массу и настолько слабое
взаимодействие между атомами, что остаются жидкими вблизи абс. нуля и позволяют
тем самым изучить специфику К. ж. Свойствами К. ж. обладают также электроны в
металлах.
К. ж. делятся на бозе-жидкости и фер-ми-жидкости, согласно различию в
свойствах частиц этих жидкостей и в соответствии с применяемыми для их описания
статистиками Бозе - Эйнштейна и Ферми - Дирака (см. Статистическая физика). Бозе-жидкость
известна только одна - жидкий 4He, атомы к-рого обладают равным нулю
спином (внутренним моментом количества движения). Атомы более редкого
изотопа 3He и электроны в металле имеют полуцелый спин (½), они
образуют ферми-жидкости.
Жидкий 4He был первой разносторонне исследованной К. ж. Теоретич.
представления, развитые для объяснения осн. эффектов в жидком гелии, легли в
основу общей теории К. ж. Гелий 4He при 2,171 К и давлении
насыщенного пара испытывает фазовый переход II рода в новое состояние Не
II со специфич. квантовыми свойствами. Само наличие точки перехода связывается
с появлением т. н. бозе-конденсата (см. Бозе-Эйнштейна конденсация), т.
е. конечной доли атомов в состоянии с импульсом, строго равным нулю. Это новое
состояние характеризуется сверхтекучестью, т. е. протеканием Не II без
всякого трения через узкие капилляры и щели. Сверхтекучесть была открыта П. Л. Капицей
(1938) и объяснена Л. Д. Ландау (1941).
Согласно квантовой механике, любая система взаимодействующих частиц может
находиться только в определённых квантовых состояниях, характерных для всей
системы в целом. При этом энергия всей системы может меняться только
определёнными порциями - квантами. Подобно атому, в к-ром энергия меняется
путём испускания или поглощения светового кванта, в К. ж. изменение энергии
происходит путём испускания или поглощения элементарных возбуждений,
характеризующихся определённым импульсом р, энергией 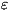 (
(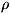 ), зависящей от
импульса, и спином. Эти элементарные возбуждения относятся ко всей жидкости в
целом, а не к отд. частицам и наз. в силу их свойств (наличия импульса, спина и
т. п.) квазичастицами. Примером квазичастиц являются звуковые
возбуждения в Не II - фононы, с энергией
), зависящей от
импульса, и спином. Эти элементарные возбуждения относятся ко всей жидкости в
целом, а не к отд. частицам и наз. в силу их свойств (наличия импульса, спина и
т. п.) квазичастицами. Примером квазичастиц являются звуковые
возбуждения в Не II - фононы, с энергией 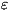 = hcр, где h -
Планка постоянная, делённая на 2
= hcр, где h -
Планка постоянная, делённая на 2 , с - скорость звука. Пока число квазичастиц
мало, что соответствует низким темп-рам, их взаимодействие незначительно и
можно считать, что они образуют идеальный газ квазичастиц. Рассмотрение свойств
К. ж. на основе этих представлений оказывается, в известном смысле, более
простым, чем свойств обычных жидкостей при высоких темп-pax, когда число
возбуждений велико и их свойства не аналогичны свойствам идеального газа.
, с - скорость звука. Пока число квазичастиц
мало, что соответствует низким темп-рам, их взаимодействие незначительно и
можно считать, что они образуют идеальный газ квазичастиц. Рассмотрение свойств
К. ж. на основе этих представлений оказывается, в известном смысле, более
простым, чем свойств обычных жидкостей при высоких темп-pax, когда число
возбуждений велико и их свойства не аналогичны свойствам идеального газа.
Если К. ж. течёт с нек-рой скоростью  через узкую трубку или щель, то её
торможение за счёт трения состоит в образовании квазичастиц с импульсом,
направленным противоположно скорости течения. В результате торможения энергия
К. ж. должна убывать, но не плавно, а определёнными порциями. Для образования
квазичастиц с требуемой энергией скорость потока должна быть не меньше, чем Vc
= min [
через узкую трубку или щель, то её
торможение за счёт трения состоит в образовании квазичастиц с импульсом,
направленным противоположно скорости течения. В результате торможения энергия
К. ж. должна убывать, но не плавно, а определёнными порциями. Для образования
квазичастиц с требуемой энергией скорость потока должна быть не меньше, чем Vc
= min [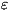 (
(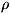 )/
)/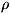 ]; эту скорость называют критической. К. ж., у к-рых vc
<> 0, будут сверхтекучими, т. к. при скоростях, меньших Vc,
новые квазичастицы не образуются, и, следовательно, жидкость не тормозится.
Предсказанный теорией Ландау и экспериментально подтверждённый энергетич.
спектр E(P) квазичастиц в Не II удовлетворяет этому требованию.
]; эту скорость называют критической. К. ж., у к-рых vc
<> 0, будут сверхтекучими, т. к. при скоростях, меньших Vc,
новые квазичастицы не образуются, и, следовательно, жидкость не тормозится.
Предсказанный теорией Ландау и экспериментально подтверждённый энергетич.
спектр E(P) квазичастиц в Не II удовлетворяет этому требованию.
Невозможность образования при течении с  < vc новых
квазичастиц в Не II приводит к своеобразной двухжидкостной
гидродинамике. Совокупность имеющихся в Не II квазичастиц рассеивается и
тормозится стенками сосуда, она составляет как бы нормальную вязкую часть
жидкости, в то время как остальная жидкость является сверхтекучей. Для
сверхтекучей жидкости характерно появление в нек-рых условиях (напр., при
вращении сосуда) вихрей с квантованной циркуляцией скорости сверхтекучей
компоненты. В Не II возможно распространение двух типов звука, из к-рых 1-й
звук соответствует обычным адиабатич. колебаниям плотности, в то время как 2-й
звук соответствует колебаниям плотности квазичастиц и, следовательно, темп-ры
(см. Второй звук).
< vc новых
квазичастиц в Не II приводит к своеобразной двухжидкостной
гидродинамике. Совокупность имеющихся в Не II квазичастиц рассеивается и
тормозится стенками сосуда, она составляет как бы нормальную вязкую часть
жидкости, в то время как остальная жидкость является сверхтекучей. Для
сверхтекучей жидкости характерно появление в нек-рых условиях (напр., при
вращении сосуда) вихрей с квантованной циркуляцией скорости сверхтекучей
компоненты. В Не II возможно распространение двух типов звука, из к-рых 1-й
звук соответствует обычным адиабатич. колебаниям плотности, в то время как 2-й
звук соответствует колебаниям плотности квазичастиц и, следовательно, темп-ры
(см. Второй звук).
Наличие газа квазичастиц одинаково характерно как для бозе-, так и для
ферми-жидкости. В ферми-жидкости часть квазичастиц имеет полуцелый спин и
подчиняется статистике Ферми - Дирака, это т. н. одночастичные возбуждения.
Наряду с ними в ферми-жидкости существуют квазичастицы с целочисленным спином,
подчиняющиеся статистике Бозе - Эйнштейна, из них наиболее интересен
"нуль-звук", предсказанный теоретически и открытый в жидком 3He
(см. Нулевой звук). Ферми-жидкости делятся на нормальные и сверхтекучие
в зависимости от свойств спектра квазичастиц .
К нормальным ферми-жидкостям относятся жидкий 3He и электроны в
несверхпроводящих металлах, в к-рых энергия одночастичных возбуждений может
быть сколь угодно малой при конечном значении импульса, что приводит к vc
= О. Теория нормальных ферми-жидкостей была развита Л. Д. Ландау (1956-58).
Единственной, но очень важной сверхтекучей ферми-жидкостью являются
электроны в сверхпроводящих металлах (см. Сверхпроводимость). Теория
сверхтекучей ферми-жидкости была развита Дж. Бароином, Л. Купером и
Дж. Шриффером (1957) и H. H. Боголюбовым (1957). Между
электронами в сверхпроводниках, согласно этой теории, преобладает притяжение,
что приводит к образованию из электронов с противоположными, но равными поабс.
величине импульсами связанных пар с суммарным моментом, равным нулю (см.
Купера эффект). Для возникновения любого одночастичного возбуждения - разрыва
связанной пары - необходимо затратить конечную энергию. Это приводит, в отличие
от нормальных ферми-жидкостей, к vc<>0, т. е. к
сверхтекучести электронной жидкости (сверхпроводимости металла). Существует
глубокая аналогия между сверхпроводимостью и сверхтекучестью. Как и в 4He,
в сверхпроводящих металлах имеется фазовый переход II рода, связанный с
появлением бозе-конденсата пар электронов. При определённых условиях в
магнитном поле в т. н. сверхпроводниках II рода появляются вихри с квантованным
магнитным потоком, являющиеся аналогом вихрей в Не II.
Кроме перечисленных выше К. ж., к ним относятся смеси 3He и 4He,
к-рые при постепенном изменении соотношения компонентов образуют непрерывный
переход от ферми- к бозе-жидкости. Согласно теоретич. представлениям, при
чрезвычайно высоких давлениях и достаточно низких темп-pax все вещества должны
переходить в состояние К. ж., что возможно, напр., в нек-рых звёздах.
Лит.: Ландау Л. Д. и Лифшиц E. M., Статистическая физика, 2 изд., M., 1964; Абрикосов А. А., Халатников И. M., Теория ферми-жидкости,
"Успехи физических наук", 1958, т. 66, в. 2, с. 177; Физика низких
температур, пер. с англ., M., 1959; Пайне Д., Нозьер Ф., Теория квантовых
жидкостей, пер. с англ., M., 1967.
С. В. Иорданский.
КВАНТОВАЯ МЕХАНИКА, волновая механика, теория, устанавливающая способ
описания и законы движения микрочастиц (элементарных частиц, атомов, молекул,
атомных ядер) и их систем (напр., кристаллов), а также связь величин,
характеризующих частицы и системы, с физ. величинами, непосредственно
измеряемыми в макроскопич. опытах.
Законы К. м. составляют фундамент изучения строения вещества. Они позволили
выяснить строение атомов, установить природу химической связи, объяснить
периодическую систему элементов, понять строение ядер атомных, изучать
свойства элементарных частиц. Поскольку свойства макроскопических тел
определяются движением и взаимодействием частиц, из которых они состоят, законы
К. м. лежат в основе понимания большинства макроскопич. явлений. К.м.
позволила, напр., объяснить температурную зависимость и вычислить величину теплоёмкости
газов и твёрдых тел, определить строение и понять многие свойства твёрдых
тел (металлов, диэлектриков, полупроводников). Только на основе К. м. удалось
последовательно объяснить такие явления, как ферромагнетизм, сверхтекучесть,
сверхпроводимость, понять природу таких астрофизич. объектов, как белые
карлики, нейтронные звёзды, выяснить механизм протекания термоядерных
реакций в Солнце и звёздах. Существуют также явления (напр., Джозефсона
эффект), в к-рых законы К. м. непосредственно проявляются в поведении
макроскопич. объектов.
Ряд крупнейших технических достижений 20 в. основан по существу на
специфических законах К.м. Так, квантово-механические законы лежат в основе
работы ядерных реакторов, обусловливают возможность осуществления в
земных условиях термоядерных реакций, проявляются в ряде явлений в металлах и
полупроводниках, используемых в новейшей технике, и т. д. фундамент такой бурно
развивающейся области физики, как квантовая электроника, составляет
квантовомеханич. теория излучения. Законы К. м. используются при
целенаправленном поиске и создании новых материалов (особенно магнитных,
полупроводниковых и сверхпроводящих). T. о., К. м. становится в значит, мере
"инженерной" наукой, знание к-рой необходимо не только
физикам-исследователям, но и инженерам.
Место квантовой механики среди других наук о движении. В нач. 20 в.
выяснилось, что классич. механика И. Ньютона имеет ограниченную область
применимости и нуждается в обобщении. Во-первых, она неприменима при больших
скоростях движения тел - скоростях, сравнимых со скоростью света. Здесь её
заменила релятивистская механика, построенная на основе специальной теории
относительности А. Эйнштейна (см. Относительности теория). Релятивистская
механика включает в себя Ньютонову (нерелятивистскую) механику как частный
случай. Ниже термин "классич. механика" будет объединять Ньютонову и
релятивистскую механику.
Для классич. механики в целом характерно описание частиц путём задания их
положения в пространстве (координат) и скоростей и зависимости этих величин от
времени. Такому описанию соответствует движение частиц по вполне определённым
траекториям. Однако опыт показал, что это описание не всегда справедливо,
особенно для частиц с очень малой массой (микрочастиц). В этом состоит второе
ограничение применимости механики Ньютона. Более общее описание движения даёт
К. м., к-рая включает в себя как частный случай классич. механику. К. м., как и
классическая, делится на нерелятивистскую, справедливую в случае малых
скоростей, и релятивистскую, удовлетворяющую требованиям спец. теории относительности.
В статье изложены основы нерелятивистской К. м. (Однако нек-рые общие положения
относятся к К. м. в целом.) Нерелятивистская К. м. (как и механика Ньютона для
своей области применимости) - вполне законченная и логически непротиворечивая
теория, способная в области своей компетентности количественно решать в
принципе любую физич. задачу. Релятивистская К.м. не является в такой степени
завершённой и свободной от противоречий теорией. Если в нерелятивистской
области можно считать, что движение определяется силами, действующими
(мгновенно) на расстоянии, то в релятивистской области это несправедливо.
Поскольку, согласно теории относительности, взаимодействие передаётся
(распространяется) с конечной скоростью, должен существовать физич. агент,
переносящий взаимодействие; таким агентом является поле. Трудности
релятивистской теории - это трудности теории поля, с к-рыми встречается как
релятивистская классич. механика, так и релятивистская К. м. В этой статье не
будут рассматриваться вопросы релятивистской К. м., связанные с квантовой
теорией поля.
Критерий применимости классической механики. Соотношение между Ньютоновой и
релятивистской механикой определяется существованием фундаментальной величины -
предельной скорости распространения сигналов, равной скорости света с (с~3-1010
см/сек). Если скорости тел значительно меньше скорости света (т. е. v/c
<<1, так что можно считать с бесконечно большой), то применима
Ньютонова механика.
Соотношение между классич. механикой и К.м. носит менее наглядный характер.
Оно определяется существованием другой универсальной мировой постоянной -
постоянной Планка h. Постоянная h (называемая также квантом
действия) имеет размерность действия (энергии, умноженной на время) и
равна h = 6,62·10-27 эрг*сек. (В теории чаще
используется величина ft = h/2 - = 1,0545919·10-27 эрг-сек, к-рую
также наз. постоянной Планка.) Формально критерий применимости классич.
механики заключается в следующем: если в условиях данной задачи физич. величины
размерности действия значительно больше H (так что h можно
считать очень малой), применима классич. механика. Более подробно этот критерий
будет разъяснён при изложении физических основ К. м.
- = 1,0545919·10-27 эрг-сек, к-рую
также наз. постоянной Планка.) Формально критерий применимости классич.
механики заключается в следующем: если в условиях данной задачи физич. величины
размерности действия значительно больше H (так что h можно
считать очень малой), применима классич. механика. Более подробно этот критерий
будет разъяснён при изложении физических основ К. м.
История создания квантовой механики. В начале 20 в. были обнаружены две
(казалось, не связанные между собой) группы явлений, свидетельствующих о
неприменимости обычной классич. механики Ньютона и классич. теории
электромагнитного поля (классич. электродинамики) к процессам
взаимодействия света с веществом и к процессам, происходящим в атоме. Первая
группа явлений была связана с установлением на опыте двойственной природы света
(дуализм света); вторая - с невозможностью объяснить на основе классич.
представлений устойчивое существование атома, а также спектральные
закономерности, открытые при изучении испускания света атомами. Установление
связи между этими группами явлений и попытки объяснить их на основе новой
теории и привели, в конечном счёте, к открытию законов К.м.
Впервые квантовые представления (в т. ч. квантовая постоянная
h) были
введены в физику в работе M. Планка (1900), посвящённой теории теплового
излучения (см. Планка закон излучения). Существовавшая к тому времени
теория теплового излучения, построенная на основе классич. электродинамики и статистической
физики, приводила к бессмысленному результату, состоявшему в том, что
тепловое (термодинамическою) равновесие между излучением и веществом не может
быть достигнуто, т. к. вся энергия рано или поздно должна перейти в излучение.
Планк разрешил это противоречие и получил результаты, прекрасно согласующиеся с
опытом, на основе чрезвычайно смелой гипотезы. В противоположность классич.
теории излучения, рассматривающей испускание электромагнитных волн как
непрерывный процесс, Планк предположил, что свет испускается определёнными
порциями энергии - квантами. Величина такого кванта энергии зависит от частоты
света  и
равна E = hv.
и
равна E = hv.
От этой работы Планка можно проследить две взаимосвязанные линии развития,
завершившиеся окончательной формулировкой К. м. в двух её формах к 1927. Первая
начинается с работы Эйнштейна (1905), в к-рой была дана теория фотоэффекта -
явления вырывания светом электронов из вещества. В развитие идеи Планка
Эйнштейн предположил, что свет не только испускается и поглощается дискретными
порциями - квантами излучения, но и распространение света происходит такими
квантами, т. е. что дискретность присуща самому свету - сам свет состоит из
отдельных порций - световых квантов (к-рые позднее были названы фотонами). Энергия
фотона E связана с частотой колебаний  волны соотношением Планка E=hv.
Ha основании этой гипотезы Эйнштейн объяснил закономерности фотоэффекта,
которые противоречили классической (базирующейся на классич. электродинамике)
теории света.
волны соотношением Планка E=hv.
Ha основании этой гипотезы Эйнштейн объяснил закономерности фотоэффекта,
которые противоречили классической (базирующейся на классич. электродинамике)
теории света.
Дальнейшее доказательство корпускулярного характера света было получено в
1922 А. Комптоном, показавшим экспериментально, что рассеяние света
свободными электронами происходит по законам упругого столкновения двух частиц
- фотона и электрона (см. Комптона эффект). Кинематика такого
столкновения определяется законами сохранения энергии и импульса, причём фотону
наряду с энергией E = hv следует приписать импульс p = h/ = hv/с, где
= hv/с, где  - длина
световой волны. Энергия и импульс фотона связаны соотношением E = ср, справедливым
в релятивистской механике для частицы с нулевой массой.
- длина
световой волны. Энергия и импульс фотона связаны соотношением E = ср, справедливым
в релятивистской механике для частицы с нулевой массой.
T. о., было доказано экспериментально, что наряду с известными волновыми
свойствами (проявляющимися, напр., в дифракции света) свет обладает и
корпускулярными свойствами: он состоит как бы из частиц - фотонов. В этом
проявляется дуализм света, его сложная корпускулярно-волновая природа. Дуализм
содержится уже в формуле E = hv, не позволяющей выбрать к.-л.
одну из двух концепций: в левой части равенства энергия E относится к
частице, а в правой - частота  является характеристикой волны. Возникло формальное
логич. противоречие: для объяснения одних явлений необходимо было считать, что
свет имеет волновую природу, а для объяснения других - корпускулярную. По
существу разрешение этого противоречия и привело к созданию физич. основ К.м.
является характеристикой волны. Возникло формальное
логич. противоречие: для объяснения одних явлений необходимо было считать, что
свет имеет волновую природу, а для объяснения других - корпускулярную. По
существу разрешение этого противоречия и привело к созданию физич. основ К.м.
В 1924 Л. де Бройль, пытаясь найти объяснение постулированным в 1913
H. Бором условиям квантования атомных орбит (см. ниже), выдвинул
гипотезу о всеобщности корпускулярно-волнового дуализма. Согласно де Бройлю,
каждой частице, независимо от её природы, следует поставить в соответствие
волну, длина к-рой  связана с импульсом частицы
связана с импульсом частицы 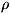 соотношением
соотношением
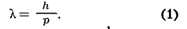
По этой гипотезе не только фотоны, но и все "обыкновенные частицы"
(электроны, протоны и др.) обладают волновыми свойствами, к-рые, в частности,
должны проявляться в явлении дифракции. В 1927 К. Дэвиссон и Л. Джермер
впервые наблюдали дифракцию электронов. Позднее волновые свойства были
обнаружены и у др. частиц, и справедливость формулы де Бройля была подтверждена
экспериментально (см. Дифракция частиц). В 1926 Э. Шрёдингер предложил
ур-ние, описывающее поведение таких "волн" во внешних силовых полях.
Так возникла волновая механика. Волновое ур-ние Шрёдингера является основным
ур-нием нерелятивистской К.м. В 1928 П. Дирак сформулировал
релятивистское ур-ние, описывающее движение электрона во внешнем силовом поле; Дирака
уравнение стало одним из основных ур-ний релятивистской К. м.
Вторая линия развития начинается с работы Эйнштейна (1907), посвящённой
теории теплоёмкости твёрдых тел (она также является обобщением гипотезы
Планка). Электромагнитное излучение, представляющее собой набор
электромагнитных волн различных частот, динамически эквивалентно нек-рому
набору осцилляторов (колебат. систем). Излучение или поглощение волн
эквивалентно возбуждению или затуханию соответствующих осцилляторов. Тот факт,
что излучение и поглощение электромагнитного излучс-ния веществом происходят
квантами энергии hv, можно выразить так: осциллятор поля не может
обладать произвольной энергией, он может иметь только определённые значения
энергии - дискретные уровни энергии, расстояние между к-рыми равно hv. Эйнштейн
обобщил эту идею квантования энергии осциллятора электромагнитного поля на
осциллятор произвольной природы. Поскольку тепловое движение твёрдых тел
сводится к колебаниям атомов, то и твёрдое тело динамически эквивалентно набору
осцилляторов. Энергия таких осцилляторов тоже квантованна, т. е. разность
соседних уровней энергии (энергий, к-рыми может обладать осциллятор) должна
равняться /zv, где  - частота колебаний атомов. Теория Эйнштейна, уточнённая П. Дебаем,
M. Борном и T. Карманом, сыграла выдающуюся роль в развитии
теории твёрдых тел.
- частота колебаний атомов. Теория Эйнштейна, уточнённая П. Дебаем,
M. Борном и T. Карманом, сыграла выдающуюся роль в развитии
теории твёрдых тел.
В 1913 H. Бор применил идею квантования энергии к теории строения атома,
планетарная модель к-рого следовала из результатов опытов Э. Резерфорда (1911).
Согласно этой модели, в центре атома находится положительно заряженное ядро, в
к-ром сосредоточена почти вся масса атома; вокруг ядра вращаются по орбитам
отрицательно заряженные электроны. Рассмотрение такого движения на основе
классич. представлений приводило к парадоксальному результату - невозможности
стабильного существования атомов: согласно классич. электродинамике, электрон
не может устойчиво двигаться по орбите, поскольку вращающийся электрич. заряд
должен излучать электромагнитные волны и, следовательно, терять энергию; радиус
его орбиты должен уменьшаться, и за время порядка 10-8 сек электрон
должен упасть на ядро. Это означало, что законы классич. физики неприменимы к
движению электронов в атоме, т.к. атомы существуют и чрезвычайно устойчивы.
Для объяснения устойчивости атомов Бор предположил, что из всех орбит,
допускаемых Ньютоновой механикой для движения электрона в электрич. поле
атомного ядра, реально осуществляются лишь те, к-рые удовлетворяют определённым
условиям квантования. T. е. в атоме существуют (как в осцилляторе) дискретные
уровни энергии. Эти уровни подчиняются определённой закономерности, выведенной
Бором на основе комбинации законов Ньютоновой механики с условиями квантования,
требующими, чтобы величина действия для классич. орбиты была целым кратным
постоянной Планка h. Бор постулировал, что, находясь на определённом
уровне энергии (т. е. совершая допускаемое условиями квантования орбитальное
движение), электрон не излучает световых волн. Излучение происходит лишь при
переходе электрона с одной орбиты на другую, т. е. с одного уровня энергии E_i
на другой с меньшей энергией Ek; при этом рождается квант
света с энергией, равной разности энергий уровней, между к-рыми осуществляется
переход:
hv = Ei-Ek (2) Так возникает линейчатый спектр
- основная особенность атомных спектров. Бор получил правильную формулу для
частот спектральных линий атома водорода (и водородоподобных атомов),
охватывающую совокупность открытых ранее эмпирич. формул (см. Спектральные
серии).
Существование уровней энергии в атомах было непосредственно подтверждено Франка-Герца
опытами (1913-14). Было установлено, что электроны, бомбардирующие газ,
теряют при столкновении с атомами только определённые порции энергии, равные
разности энергетич. уровней атома.
T. о., H. Бор, используя квантовую постоянную h, отражающую дуализм
света, показал, что эта величина определяет также и движение электронов в атоме
(и что законы этого движения существенно отличаются от законов классич.
механики). Этот факт позднее был объяснён на основе универсальности
корпус-кулярно-волнового дуализма, содержащегося в гипотезе де Бройля.
Успех теории Бора, как и предыдущие успехи квантовой теории, был достигнут
за счёт нарушения логич. цельности теории: с одной стороны, использовалась
Ньютонова механика, с другой - привлекались чуждые ей искусств, правила
квантования, к тому же противоречащие классич. электродинамике. Кроме того,
теория Бора оказалась не в состоянии объяснить движение электронов в сложных
атомах (даже в атоме гелия), возникновение молекулярной связи и т. д.
"Полуклассическая" теория Бора не могла также ответить на вопрос, как
движется электрон при переходе с одного уровня энергии на другой. Дальнейшая
напряжённая разработка вопросов теории атома привела к убеждению, что, сохраняя
классич. картину движения электрона по орбите, логически стройную теорию
построить невозможно. Осознание того факта, что движение электронов в атоме не
описывается в терминах (понятиях) классич. механики (как движение по
определённой траектории), привело к мысли, что вопрос о движении электрона
между уровнями несовместим с характером законов, определяющих поведение
электронов в атоме, и что необходима новая теория, в к-рую входили бы только
величины, относящиеся к начальному и конечному стационарным состояниям атома. В
1925 В. Гейзенбергу удалось построить такую формальную схему, в к-рой вместо
координат и скоростей электрона фигурировали некие абстрактные алгебраич.
величины - матрицы; связь матриц с наблюдаемыми величинами (энергетич.
уровнями и интенсивностями квантовых переходов) давалась простыми
непротиворечивыми правилами. Работа Гейзенберга была развита M. Борном и П.
Иорданом. Так возникла матричная механика. Вскоре после появления ур-ния
Шрёдингера была показана математич. эквивалентность волновой (основанной на
ур-нии Шрёдингера) и матричной механики. В 1926 M. Борн дал вероятностную
интерпретацию волн де Бройля (см. ниже).
Большую роль в создании К. м. сыграли работы Дирака, относящиеся к этому же
времени. Окончательное формирование К. м. как последовательной физич. теории с
ясными основами и стройным математич. аппаратом произошло после работы
Гейзенберга (1927), в к-рой было сформулировано неопределённостей
соотношение - важнейшее соотношение, освещающее физич. смысл ур-ний К. м.,
её связь с классич. механикой и другие как принципиальные вопросы, так и
качеств, результаты К. м. Эта работа была продолжена и обобщена в трудах Бора и
Гейзенберга.
Детальный анализ спектров атомов привёл к представлению (введённому впервые
Дж. Ю. Уленбеком и С. Гаудсмитом и развитому В. Паули) о
том, что электрону, кроме заряда и массы, должна быть приписана ещё одна внутр.
характеристика (квантовое число) - спин. Важную роль сыграл открытый В.
Паули (1925) т. н. принцип запрета (Паули принцип, см. ниже), имеющий
фундамент, значение в теории атома, молекулы, ядра, твёрдого тела.
В течение короткого времени К. м. была с успехом применена к широкому кругу
явлений. Были созданы теории атомных спектров, строения молекул, химич. связи,
периодич. системы Д. И. Менделеева, металлич. проводимости и
ферромагнетизма. Эти и мн. др. явления стали (по крайней мере качественно)
понятными. Дальнейшее принципиальное развитие квантовой теории связано гл.
обр. с релятивистской К. м. Нерелятивистская К. м. развивалась в основном в
направлении охвата разнообразных конкретных задач физики атомов, молекул,
твёрдых тел (металлов, полупроводников), плазмы и т. д., а также
совершенствования матем. аппарата и разработки количеств, методов решения
различных задач.
Вероятности и волны. Поскольку законы К. м. не обладают той степенью
наглядности, к-рая свойственна законам классич. механики, целесообразно
проследить линию развития идей, составляющих фундамент К. м., и только после
этого сформулировать её основные положения. Выбор фактов, на основе к-рых
строится теория, конечно, не единствен, поскольку К. м. описывает широчайший
круг явлений и каждое из них способно дать материал для её обоснования. Будем
исходить из требований простоты и возможной близости к истории.
Рассмотрим простейший опыт по распространению света (рис.1). На пути пучка
света ставится прозрачная пластинка S.
Рис. 1.
Часть света проходит через пластинку, а часть отражается. Известно, что свет
состоит из "частиц" - фотонов. Что же происходит с отдельным фотоном
при попадании на пластинку? Если поставить опыт (напр., с пучком света крайне
малой интенсивности), в к-ром можно следить за судьбой каждого фотона, то можно
убедиться, что фотон при встрече с пластинкой не расщепляется на два фотона,
его индивидуальность как частицы сохраняется (иначе свет менял бы свою частоту,
т. е. "цветность"). Оказывается, что нек-рые фотоны проходят сквозь
пластинку, а нек-рые отражаются от неё. В чем причина этого? Может быть,
имеется два разных сорта фотонов? Поставим контрольный опыт: внесём такую же
пластинку на пути прошедшего света, к-рый должен бы содержать только один из
двух "сортов" фотонов. Однако будет наблюдаться та же картина: часть
фотонов пройдёт вторую пластинку, а часть отразится. Следовательно, одинаковые
частицы в одинаковых условиях могут вести себя по-разному. А это означает, что
поведение фотона при встрече с пластинкой непредсказуемо однозначно.
Детерминизма в том смысле, как это понимается в классич. механике, при движении
фотонов не существует. Этот вывод является одним из отправных пунктов для
устранения противоречия между корпускулярными и волновыми свойствами частиц и
построения теории квантовомеханич. явлений.
Задача отражения света от прозрачной пластинки не представляет к.-л.
трудности для волновой теории: исходя из свойств пластинки, волновая оптика
однозначно предсказывает отношение интенсивностей прошедшего и отражённого
света. С корпускулярной точки зрения, интенсивность света пропорциональна числу
фотонов. Обозначим через N общее число фотонов, через N1 и N2
- число прошедших и число отражённых фотонов (N1 + N2
= N). Волновая оптика определяет отношение N1/N2,
и о поведении одного фотона, естественно, ничего сказать нельзя.
Отражение фотона от пластинки или прохождение через неё являются случайными
событиями: нек-рые фотоны проходят через пластинку, нек-рые отражаются от неё,
но при большом числе фотонов оказывается, что отношение N1/V2
находится в согласии с предсказанием волновой оптики. Количественно
закономерности, проявляющиеся при случайных событиях, описываются с помощью
понятия вероятности (см. Вероятностей теория). Фотон может с
вероятностью W1 пройти пластинку и с вероятностью W2
отразиться от неё. При общем числе фотонов N в среднем пройдёт
пластинку W1N частиц, а отразится W2N частиц.
Если N очень велико, то средние (ожидаемые) значения чисел частиц точно
совпадают с истинными (хотя флуктуации существуют, и классич. оптика их учесть
не может). Все соотношения оптики могут быть переведены с языка интенсивностей
на язык вероятностей и тогда они будут относиться к поведению одного фотона.
Вероятность того, что с фотоном произойдёт одно из двух альтернативных (взаимно
исключающих) событий - прохождение или отражение, равна W1 + W2
=1. Это закон сложения вероятностей, соответствующий сложению
интенсивностей. Вероятность прохождения через две одинаковые пластинки равна W21,
а вероятность прохождения через первую и отражения от второй - W1
W2 (это отвечает тому, что на второй пластинке свет, прошедший
первую пластинку, разделяется на прошедший и отражённый в том же отношении, как
и на первой). Это закон умножения вероятностей (справедливый для независимых
событий).
Рассмотренный опыт не специфичен для света. Аналогичные опыты с пучком
электронов или др. микрочастиц также показывают непредсказуемость поведения
отдельной частицы. Однако не только прямые опыты говорят в пользу того, что и в
самом общем случае следует перейти к вероятностному описанию поведения
микрочастиц. Теоретически невозможно представить, что одни микрочастицы
описываются вероятностно, а другие классически: взаимодействие
"классических" частиц с "квантовыми" с необходимостью
приводило бы к внесению квантовых неопределённостей и делало бы поведение
"классических" частиц также непредсказуемым (в смысле классич.
детерминизма).
Предсказание вероятностей различных процессов - такова возможная
формулировка задачи К. м., в отличие от задачи классической механики, состоящей
в предсказании в принципе только достоверных событий. Конечно, вероятностное
описание допустимо и в классической механике. Для получения достоверного
предсказания классич. механика нуждается в абсолютно точном задании нач.
условий, т. е. положений и скоростей всех образующих систему частиц. Если же
нач. условия заданы не точно, а с нек-рой степенью неопределённости, то и
предсказания будут содержать неопределённости, т. е. носить в той или иной
степени вероятностный характер. Примером служит классическая статистич. физика,
оперирующая с нек-рыми усреднёнными величинами. Поэтому дистанция между строем
мысли квантовой и классич. механики была бы не столь велика, если бы основными
понятиями К. м. были именно вероятности. Чтобы выяснить радикальное различие
между К. м. и классич. механикой, несколько усложним рассмотренный выше опыт по
отражению света.
Пусть отражённый пучок света (или микрочастиц) при помощи зеркала 3
поворачивается и попадает в ту же область А (напр., в тот же детектор,
регистрирующий фотоны), что и прошедший пучок (рис. 2). Естественно было бы
ожидать, что в этом случае измеренная интенсивность равна сумме интенсивностей
прошедшего и отражённого пучков.
Рис. 2.
Но хорошо известно, что это не так: интенсивность в зависимости от
расположения зеркала и детектора может меняться в довольно широких пределах и в
нек-рых случаях (при равной интенсивности прошедшего и отражённого света) даже
обращаться в ноль (пучки как бы гасят друг друга). Это - явление интерференции
света. Что же можно сказать о поведении отдельного фотона в
интерференционном опыте? Вероятность его попадания в данный детектор
существенно перераспределится по сравнению с первым опытом, и не будет равна
сумме вероятностей прихода фотона в детектор первым и вторым путями.
Следовательно, эти два пути не являются альтернативными (иначе вероятности
складывались бы). Отсюда следует, что наличие двух путей прихода фотона от
источника к детектору существ, образом влияет на распределение вероятностей, и
поэтому нельзя сказать, каким путём прошёл фотон от источника к детектору.
Приходится считать, что он одновременно мог придти двумя различными путями.
Необходимо подчеркнуть радикальность возникающих представлений.
Действительно, невозможно представить себе движение частицы одновременно по
двум путям. К. м. и не ставит такой задачи. Она лишь предсказывает результаты
опытов с пучками частиц. Подчеркнём, что в данном случае не высказывается
никаких гипотез, а даётся лишь интерпретация волнового опыта с точки зрения
корпускулярных представлений. (Напомним, что речь идёт не только о свете, но и
о любых пучках частиц, напр, электронов.) Полученный результат означает
невозможность классич. описания движения частиц по траекториям, отсутствие
наглядности квантового описания.
Попытаемся всё же выяснить, каким путём прошла частица, поставив на
возможных её путях детекторы. Естественно, что частица будет зарегистрирована в
одном, а не сразу во всех возможных местах. Но как только измерение выделит
определённую траекторию частицы, интерференционная картина исчезнет.
Распределение вероятностей станет другим. Для возникновения интерференции нужны
обе (все) возможные траектории. T. о., регистрация траектории частицы так
изменяет условия, что два пути становятся альтернативными, и в результате
получается сложение интенсивностей, к-рое было бы в случае "классич."
частиц, движущихся по определённым траекториям .
Для квантовых явлений очень важно точное описание условий опыта, в к-рых
наблюдается данное явление. В условия, в частности, входят и измерит, приборы.
В классич. физике предполагается, что роль измерит, прибора может быть в
принципе сведена только к регистрации движения и состояние системы при
измерении не меняется. В квантовой физике такое предположение несправедливо:
измерит, прибор наряду с др. факторами сам участвует в формировании изучаемого
на опыте явления, и эту его роль нельзя не учитывать. Роль измерит, прибора в
квантовых явлениях была всесторонне проанализирована H. Бором и В.
Гейзенбергом. Она тесно связана с соотношением неопределённостей, к-рое будет
рассмотрено позже.
Внимание к роли измерений не означает, что в К. м. не изучаются физич.
явления безотносительно к приборам, напр, свойства частиц "самих по
себе". Так, решаемые К. м. задачи об энергетич. уровнях атомов, о рассеянии
микрочастиц при их столкновениях друг с другом, об интерференционных
явлениях - это задачи о свойствах частиц и их поведении. Роль прибора выступает
на первое место тогда, когда ставятся специфич. вопросы, нек-рые из к-рых
лишены, как выяснилось, смысла (напр., вопрос о том, по какой траектории
двигался электрон в интерференционном опыте, т. к. либо нет траектории, либо
нет интерференции).
Вернёмся к интерференционному опыту. До сих пор было сделано лишь негативное
утверждение: частица не движется по определённому пути, и вероятности не
складываются. Конструктивное предложение для описания подобной ситуации можно
почерпнуть снова из волновой оптики. В оптике каждая волна характеризуется не
только интенсивностью, но и фазой (интенсивность пропорциональна квадрату
амплитуды). Совокупность этих двух действит. величин - амплитуды А и
фазы ф - принято объединять в одно комплексное число, к-рое наз. комплексной
амплитудой:  = Aeiф. Тогда интенсивность равна I = |
= Aeiф. Тогда интенсивность равна I = | |2
=
|2
=  *
* = A2,
где
= A2,
где  * -
функция, комплексно сопряжённая с ф. T. к. непосредственно измеряется именно
интенсивность, то для одной волны фаза никак не проявляется. В опыте с
прохождением и отражением света ситуация именно такая: имеется две волны
* -
функция, комплексно сопряжённая с ф. T. к. непосредственно измеряется именно
интенсивность, то для одной волны фаза никак не проявляется. В опыте с
прохождением и отражением света ситуация именно такая: имеется две волны  1
и
1
и  2,
ко одна из них существует только справа, а другая только слева (см. рис. 1);
интенсивности этих волн I1 = A12, I2
= A22, и фазы не фигурируют (поэтому можно
было обойтись только интенсивностями). В интерференционном опыте ситуация
изменилась: волна
2,
ко одна из них существует только справа, а другая только слева (см. рис. 1);
интенсивности этих волн I1 = A12, I2
= A22, и фазы не фигурируют (поэтому можно
было обойтись только интенсивностями). В интерференционном опыте ситуация
изменилась: волна  2 с помощью зеркала была направлена в область
нахождения волны
2 с помощью зеркала была направлена в область
нахождения волны  1 (см. рис. 2). Волновое поле в области существования
двух волн определяется в оптике с помощью принципа суперпозиции: волны
налагаются друг на друга, т. е. складываются с учётом их фаз. Суммарная волна ф
имеет комплексную амплитуду, равную сумме комплексных амплитуд обеих волн:
1 (см. рис. 2). Волновое поле в области существования
двух волн определяется в оптике с помощью принципа суперпозиции: волны
налагаются друг на друга, т. е. складываются с учётом их фаз. Суммарная волна ф
имеет комплексную амплитуду, равную сумме комплексных амплитуд обеих волн:
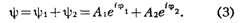
Интенсивность суммарной волны зависит от разности фаз 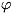 1 -
1 -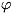 2
(пропорциональной разности хода световых пучков по двум путям):
2
(пропорциональной разности хода световых пучков по двум путям):
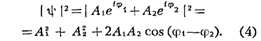
В частности, при A1= A2 и cos (]ph1
- 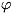 2)=
= -1 |
2)=
= -1 | |2
= О.
|2
= О.
В этом примере рассмотрен простейший случай сложения амплитуд. В более общем
случае из-за изменения условий (напр., из-за свойств зеркала) амплитуды могут
изменяться по величине и фазе, так что суммарная волна будет иметь вид
 = с1
= с1 1 + c2
1 + c2 2, где C1
и C2 - комплексные числа:
2, где C1
и C2 - комплексные числа:
Принципиальная суть явления при этом не изменяется. Характер явления не
зависит также от общей интенсивности. Если увеличить  в С раз, то интенсивность
увеличится в |С|2 раз, т. е. |С|2 будет общим множителем
в формуле распределения интенсивностей. Число С можно считать как комплексным,
так и действительным, физ. результаты не содержат фазы числа С - она
произвольна. Для интерпретации волновых явлений с корпускулярной точки зрения
необходимо перенесение принципа суперпозиции в К. м. Поскольку К. м. имеет дело
не с интенсивностями, а с вероятностями, следует ввести амплитуду
вероятности
в С раз, то интенсивность
увеличится в |С|2 раз, т. е. |С|2 будет общим множителем
в формуле распределения интенсивностей. Число С можно считать как комплексным,
так и действительным, физ. результаты не содержат фазы числа С - она
произвольна. Для интерпретации волновых явлений с корпускулярной точки зрения
необходимо перенесение принципа суперпозиции в К. м. Поскольку К. м. имеет дело
не с интенсивностями, а с вероятностями, следует ввести амплитуду
вероятности  = Aelф, полагая (по аналогии с оптич. волнами),
что вероятность w = |c
= Aelф, полагая (по аналогии с оптич. волнами),
что вероятность w = |c |2 = |с|2
|2 = |с|2 *
* ). Здесь с - число, паз.
нормировочным множителем, к-рый должен быть подобран так, чтобы суммарная
вероятность обнаружения частицы во всех возможных местах равнялась 1, т. е.
). Здесь с - число, паз.
нормировочным множителем, к-рый должен быть подобран так, чтобы суммарная
вероятность обнаружения частицы во всех возможных местах равнялась 1, т. е.
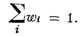
Множитель с определён только по модулю, фаза его произвольна. Нормировочный
множитель важен только для определения абс. вероятности; относит, вероятности
определяются амплитудами вероятности в произвольной нормировке. Амплитуда
вероятности наз. в К. м. также волновой функцией.
Амплитуды вероятности (как оптич. амплитуды) удовлетворяют принципу
суперпозиции: если  1 и
1 и  2 - амплитуды вероятности прохождения
частицы соответственно первым и вторым путём, то амплитуда вероятности для
случая, когда осуществляются оба пути, должна быть равна
2 - амплитуды вероятности прохождения
частицы соответственно первым и вторым путём, то амплитуда вероятности для
случая, когда осуществляются оба пути, должна быть равна  =
=  1 +
1 +  2. Тем
самым фраза: "частица прошла двумя путями" приобретает волновой
смысл, а вероятность то = |
2. Тем
самым фраза: "частица прошла двумя путями" приобретает волновой
смысл, а вероятность то = | 1 +
1 +  2|2
обнаруживает интерференционные свойства.
2|2
обнаруживает интерференционные свойства.
Следует подчеркнуть различие в смысле, вкладываемом в принцип суперпозиции в
оптике (и др. волновых процессах) и К. м. Сложение (суперпозиция) обычных волн
не противоречит наглядным представлениям, т. к. каждая из волн представляет
возможный тип колебаний и суперпозиция соответствует сложению этих колебаний в
каждой точке. В то же время квантовомеханич амплитуды вероятности описывают
альтернативные (с классич. точки зрения, исключающие друг друга) движения
(напр., волны  1 и
1 и  2 соответствуют частицам, приходящим в
детектор двумя различными путями). С классич. точки зрения, сложение таких
движений представляется совершенно непонятным. В этом проявляется отсутствие
наглядности квантовомеханич. принципа суперпозиции. Избежать формального логич.
противоречия квантовомеханич. принципа суперпозиции (возможность для частицы
пройти одновременно двумя путями) позволяет вероятностная интерпретация.
Постановка опыта по определению пути частицы (см. выше) приведёт к тому, что с
вероятностью |
2 соответствуют частицам, приходящим в
детектор двумя различными путями). С классич. точки зрения, сложение таких
движений представляется совершенно непонятным. В этом проявляется отсутствие
наглядности квантовомеханич. принципа суперпозиции. Избежать формального логич.
противоречия квантовомеханич. принципа суперпозиции (возможность для частицы
пройти одновременно двумя путями) позволяет вероятностная интерпретация.
Постановка опыта по определению пути частицы (см. выше) приведёт к тому, что с
вероятностью | 1|2 частица пройдёт первым и с вероятностью
|
1|2 частица пройдёт первым и с вероятностью
| 2|2
- вторым путём. Суммарное распределение частиц на экране будет определяться
вероятностью |
2|2
- вторым путём. Суммарное распределение частиц на экране будет определяться
вероятностью | 1|2 +|
1|2 +| 2|2, т. е.
интерференция исчезнет.
2|2, т. е.
интерференция исчезнет.
T. о., рассмотрение интерференционного опыта приводит к следующему выводу.
Величиной, описывающей состояние физ. системы в К. м., является амплитуда
вероятности, или волновая функция, системы. Осн. черта такого квантовомеханич.
описания - предположение о справедливости принципа суперпозиции состояний.
Принцип суперпозиции - осн. принцип К. м. В общем виде он утверждает, что
если в данных условиях возможны различные квантовые состояния частицы (или
системы частиц), к-рым соответствуют волновые функции  1,
1,  2,...,
2,...,  i,
..., то существует и состояние, описываемое волновой функцией
i,
..., то существует и состояние, описываемое волновой функцией
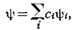
где Ci - произвольные комплексные числа. Если  1
описывают альтернативные состояния, то |сi|2 определяет
вероятность того, что система находится в состоянии с волновой функцией
1
описывают альтернативные состояния, то |сi|2 определяет
вероятность того, что система находится в состоянии с волновой функцией  1 , и
1 , и
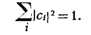
Волны де Бройля и соотношение неопределённостей. Одна из основных задач К.
м.- нахождение волновой функции, отвечающей данному состоянию изучаемой
системы. Рассмотрим решение этой задачи на простейшем (но важном) случае
свободно движущейся частицы. Согласно де Бройлю, со свободной частицей, имеющей
импульс р, связана волна с длиной  = h/p. Это означает, что
волновая функция свободной частицы
= h/p. Это означает, что
волновая функция свободной частицы  (
( ) - волна де Бройля - должна
быть такой функцией координаты х, чтобы при изменении
) - волна де Бройля - должна
быть такой функцией координаты х, чтобы при изменении 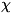 на
на  волновая
функция
волновая
функция  возвращалась к прежнему значению. Этим свойством обладает функция
еi2пч/x. Если ввести величину k = 2
возвращалась к прежнему значению. Этим свойством обладает функция
еi2пч/x. Если ввести величину k = 2 /
/ наз. волновым числом, то
соотношение де Бройля примет вид:
наз. волновым числом, то
соотношение де Бройля примет вид: 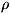 = (h/2
= (h/2 )k = hk. T. о., если частица имеет
определённый импульс р, то её состояние описывается волновой функцией
)k = hk. T. о., если частица имеет
определённый импульс р, то её состояние описывается волновой функцией
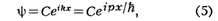
где С - постоянное комплексное число. Эта волновая функция обладает
замечательным свойством: квадрат её модуля | |2 не зависит от х, т.
е. вероятность нахождения частицы, описываемой такой волновой функцией, в любой
точке пространства одинакова. Др. словами, частица со строго определённым
импульсом совершенно нелокализована. Конечно, это идеализация - полностью
нелокализованных частиц не существует. Но в той же мере идеализацией является и
волна со строго определённой длиной волны, а следовательно, и строгая
определённость импульса частицы. Поэтому точнее сказать иначе: чем более
определённым является импульс частицы, тем менее определённо её положение
(координата). В этом заключается специфический для К. м. принцип
неопределённости. Чтобы получить количеств, выражение этого принципа - соотношение
неопределённостей, рассмотрим состояние, представляющее собой суперпозицию
некоторого (точнее, бесконечно большого) числа де-бройлевских волн с близкими
волновыми числами, заключёнными в малом интервале
|2 не зависит от х, т.
е. вероятность нахождения частицы, описываемой такой волновой функцией, в любой
точке пространства одинакова. Др. словами, частица со строго определённым
импульсом совершенно нелокализована. Конечно, это идеализация - полностью
нелокализованных частиц не существует. Но в той же мере идеализацией является и
волна со строго определённой длиной волны, а следовательно, и строгая
определённость импульса частицы. Поэтому точнее сказать иначе: чем более
определённым является импульс частицы, тем менее определённо её положение
(координата). В этом заключается специфический для К. м. принцип
неопределённости. Чтобы получить количеств, выражение этого принципа - соотношение
неопределённостей, рассмотрим состояние, представляющее собой суперпозицию
некоторого (точнее, бесконечно большого) числа де-бройлевских волн с близкими
волновыми числами, заключёнными в малом интервале  k Получающаяся в
результате суперпозиции волновая функция
k Получающаяся в
результате суперпозиции волновая функция  (x) (она называется волновым
пакетом) имеет такой характер: вблизи нек-рого фиксированного значения x0
все амплитуды сложатся, а вдали от x0 (|x-x0|>>
(x) (она называется волновым
пакетом) имеет такой характер: вблизи нек-рого фиксированного значения x0
все амплитуды сложатся, а вдали от x0 (|x-x0|>> ) будут гасить
друг друга из-за большого разнобоя в фазах. Оказывается , что практически такая
волновая функция сосредоточена в области шириной
) будут гасить
друг друга из-за большого разнобоя в фазах. Оказывается , что практически такая
волновая функция сосредоточена в области шириной  x, обратно
пропорциональной интервалу
x, обратно
пропорциональной интервалу  k, т. е.
k, т. е.  x~1/
x~1/ k, или
k, или  .x
.x p~h(где
p~h(где 
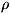 = h
= h k -
неопределённость импульса частицы). Это соотношение и представляет собой
соотношение неопределённостей Гейзенбепга.
k -
неопределённость импульса частицы). Это соотношение и представляет собой
соотношение неопределённостей Гейзенбепга.
Математически любую функцию  (x) можно представить как наложение простых периодич.
волн - это известное Фурье преобразование, на основании свойств к-рого
соотношение неопределённостей между
(x) можно представить как наложение простых периодич.
волн - это известное Фурье преобразование, на основании свойств к-рого
соотношение неопределённостей между  x и
x и  k получается
математически строго. Точное соотношение имеет вид неравенства
k получается
математически строго. Точное соотношение имеет вид неравенства  x
x  k>=1/2, или
k>=1/2, или
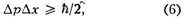
причём под неопределённостями  p и
p и  x понимаются дисперсии,
т. е. среднеквадратичные отклонения импульса и координаты от их ср. значений.
Физич. интерпретация соотношения (6) заключается в том, что (в
противоположность классич. механике) не существует такого состояния, в к-ром
координата и импульс частицы имеют одновременно точные значения. Масштаб
неопределённостей этих величин задаётся постоянной Планка h, в этом
заключён важный смысл этой мировой постоянной. Если неопределённости, связанные
соотношением Гейзенберга, можно считать в данной задаче малыми и пренебречь
ими, то движение частицы будет описываться законами классич. механики (как
движение по определённой траектории).
x понимаются дисперсии,
т. е. среднеквадратичные отклонения импульса и координаты от их ср. значений.
Физич. интерпретация соотношения (6) заключается в том, что (в
противоположность классич. механике) не существует такого состояния, в к-ром
координата и импульс частицы имеют одновременно точные значения. Масштаб
неопределённостей этих величин задаётся постоянной Планка h, в этом
заключён важный смысл этой мировой постоянной. Если неопределённости, связанные
соотношением Гейзенберга, можно считать в данной задаче малыми и пренебречь
ими, то движение частицы будет описываться законами классич. механики (как
движение по определённой траектории).
Принцип неопределённости является фундаментальным принципом К. м.,
устанавливающим физич. содержание и структуру её математич. аппарата. Кроме
этого, он играет большую эвристич. роль, т.к. многие результаты К.м. могут быть
получены и поняты на основе комбинации законов классич. механики с соотношением
неопределённостей. Важным примером является проблема устойчивости атома, о
к-рой говорилось выше. Рассмотрим эту задачу для атома водорода. Пусть электрон
движется вокруг ядра (протона) по круговой орбите радиуса 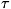 со скоростью v. По закону
Кулона сила притяжения электрона к ядру равна е2/r2, где е
- абс. величина заряда электрона, а центростремительное ускорение равно v2/r.
По второму закону Ньютона mv2/r=e2/r2, где т
- масса электрона. Отсюда следует, что радиус орбиты r = e2/mv2 может
быть сколь угодно малым, если скорость
со скоростью v. По закону
Кулона сила притяжения электрона к ядру равна е2/r2, где е
- абс. величина заряда электрона, а центростремительное ускорение равно v2/r.
По второму закону Ньютона mv2/r=e2/r2, где т
- масса электрона. Отсюда следует, что радиус орбиты r = e2/mv2 может
быть сколь угодно малым, если скорость  достаточно велика. Но в К. м. должно
выполняться соотношение неопределённостей. Если допустить неопределённость
положения электрона в пределах радиуса его орбиты г, а неопределённость
скорости - в пределах
достаточно велика. Но в К. м. должно
выполняться соотношение неопределённостей. Если допустить неопределённость
положения электрона в пределах радиуса его орбиты г, а неопределённость
скорости - в пределах  , т. е. импульса в пределах
, т. е. импульса в пределах  р - mv, то соотношение
неопределённостей примет вид: mvr>=h. Воспользовавшись связью
между
р - mv, то соотношение
неопределённостей примет вид: mvr>=h. Воспользовавшись связью
между  и r,
определяемой законом Ньютона, получим v<=e2lh и
r>=h2/mе2. Следовательно, движение электрона по орбите
с радиусом, меньшим r0 = h2/m2~0,5·
10-8 см, невозможно, электрон не может упасть на ядро - атом
устойчив. Величина r0 и является радиусом атома водорода
("боровским радиусом"). Ему соответствует максимально возможная
энергия связи атома E0 (равная полной энергии электрона в
атоме, т. е. сумме кинетич. энергии mv2/2 и потенциальной энергии - е2/r0,
что составляет E0 = -е2/2r0~ ~ - 13,6
эв), определяющая его минимальную энергию - энергию осн. состояния.
и r,
определяемой законом Ньютона, получим v<=e2lh и
r>=h2/mе2. Следовательно, движение электрона по орбите
с радиусом, меньшим r0 = h2/m2~0,5·
10-8 см, невозможно, электрон не может упасть на ядро - атом
устойчив. Величина r0 и является радиусом атома водорода
("боровским радиусом"). Ему соответствует максимально возможная
энергия связи атома E0 (равная полной энергии электрона в
атоме, т. е. сумме кинетич. энергии mv2/2 и потенциальной энергии - е2/r0,
что составляет E0 = -е2/2r0~ ~ - 13,6
эв), определяющая его минимальную энергию - энергию осн. состояния.
T. о., квантовомеханич. представления впервые дали возможность теоретически
оценить размеры атома (выразив его радиус через мировые постоянные h, т, е).
"Малость" атомных размеров оказалась связанной с тем, что
"мала" постоянная И.
Примечательно, что совр. представления об атомах, обладающих вполне
определёнными устойчивыми состояниями, оказываются ближе к представлениям
древних атомистов, чем основанная на законах классич. механики. планетарная
модель атома, позволяющая электрону находиться на любых расстояниях от ядра.
Строгое решение задачи о движении электрона в атоме водорода получается из
квантовомеханич. ур-ния движения - ур-ния Шрёдингера (см. ниже); решение
ур-ния Шрёдингера даёт волновую функцию  , к-рая описывает состояние
электрона, находящегося в области притяжения ядра. Но и не зная явного
вида
, к-рая описывает состояние
электрона, находящегося в области притяжения ядра. Но и не зная явного
вида  ,
можно утверждать, что эта волновая функция представляет собой такую суперпозицию
волн де Бройля, к-рая соответствует локализации электрона в области с размером
>> r0 и разбросу по импульсам
,
можно утверждать, что эта волновая функция представляет собой такую суперпозицию
волн де Бройля, к-рая соответствует локализации электрона в области с размером
>> r0 и разбросу по импульсам 
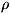 ~ h/r0.
~ h/r0.
Соотношение неопределённостей позволяет также понять устойчивость молекул и
оценить их размеры и минимальную энергию, объясняет существование вещества,
к-рое ни при каких темп-pax не превращается при нормальном давлении в твёрдое
состояние (гелий), даёт качеств, представления о структуре и размерах ядра и т.
д.
Существование уровней энергии - характерное квантовое явление, присущее всем
физич. системам, не вытекает непосредственно из соотношения неопределённостей.
Ниже будет показано, что дискретность уровней энергии связанной системы можно
объяснить на основе ур-ния Шрёдингера; отметим лишь, что возможные дискретные
значения энергии (энергетич. уровни) Eп > E0соответствуют
возбуждённым состояниям квантовомеханич. системы (см., напр., Атом).
Стационарное уравнение Шрёдингера. Волны де Бройля описывают состояние
частицы только в случае свободного движения. Если на частицу действует поле сил
с потенциальной энергией V (наз. также потенциалом), зависящей от
координат частицы, то волновая функция частицы  определяется дифференциальным
ур-нием, к-рое получается путём след, обобщения гипотезы де Бройля. Для случая,
когда движение частицы с заданной энергией & происходят в одном
измерении (вдоль оси х), ур-ние, к-рому удовлетворяет волна де Бройля
(5), может быть записано в виде:
определяется дифференциальным
ур-нием, к-рое получается путём след, обобщения гипотезы де Бройля. Для случая,
когда движение частицы с заданной энергией & происходят в одном
измерении (вдоль оси х), ур-ние, к-рому удовлетворяет волна де Бройля
(5), может быть записано в виде:
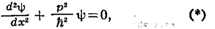
где p =(2тE)1/2 - импульс свободно движущейся
частицы (массы т). Если частица с энергией E движется в
потенциальном поле V(x), не зависящем от времени, то квадрат её импульса
(определяемый законом сохранения энергии) равен р2 = 2т[E -
V(x)]. Простейшим обобщением ур-ния (*) является поэтому ур-ние
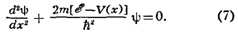
Оно наз. стационарным (не зависящим от времени) уравнением Шрёдингера и
относится к основным ур-ниям К. м. Решение этого ур-ния зависит от вида сил, т.
е. от вида потенциала V(x). Рассмотрим неск. типичных случаев.
1) V = const, E>V. Решением является волна де Бройля  = Ceikx,
где h2k2/2m = p2/2m =E-V -
кинетическая энергия частицы.
= Ceikx,
где h2k2/2m = p2/2m =E-V -
кинетическая энергия частицы.
Рис. 3.
2) Потенциальная стенка:
V = O при x < О, V = V1 > О при x > О.
Если полная энергия частицы больше высоты стенки, т. е.E > V1,
и частица движется слева направо (рис. 3), то решение ур-ния (7) в области х<0
имеет вид двух волн де Бройля - падающей и отражённой:
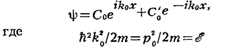
(волна с волновым числом k = - k0 соответствует движению
справа налево с тем же импульсом р0), а при x>0 -
проходящей волны де Бройля:
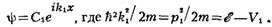
Отношения |C1/C0|2 и |C'0/0|2
определяют вероятности прохождения частицы над стенкой и отражения от неё. Наличие
отражения - специфически квантовомеханич. (волновое) явление (аналогичное
частичному отражению световой волны от границы раздела двух прозрачных сред):
"классич." частица проходит над барьером, и лишь импульс её
уменьшается до значения
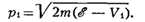
вели энергия частицы меньше высоты стенки, E < V (рис. 4,а), то
кинетич. энергия частицы E - V в области х>0 отрицательна. В
классич. механике это невозможно, и частица не заходит в такую область пространства
- она отражается от потенциальной стенки. Волновое движение имеет др. характер.
Отрицат. значение k2(p2/2m = h2k2/2m<0)
означает, что k - чисто мнимая величина, k = ix, где и
вещественно. Поэтому волна еikx превращается в е-kx,
т. е. колебат. режим сменяется затухающим (x>0,
Рис. 4.
иначе получился бы лишённый физ. смысла неограниченный рост волны с
увеличением х). Это явление хорошо известно в теории колебаний. Под
энергетич. схемой на рис. 4,а (и рис. 4,6) изображено качеств, поведение
волновой функции  (x), точнее её действит. части.
(x), точнее её действит. части.
3) Две области, свободные от сил, разделены прямоугольным потенциальным
барьером V, и частица движется к барьеру слева с энергией E<V
(рис. 4,6). Согласно классич. механике, частица отразится от барьера;
согласно К. м., волновая функция не равна нулю и внутри барьера, а справа будет
опять иметь вид волны де Бройля с тем же импульсом (т.е. с той же частотой, но,
конечно, с меньшей амплитудой). Следовательно, частица может пройти сквозь
барьер. Коэфф. (или вероятность) проникновения будет тем больше, чем меньше
ширина и высота (чем меньше разность V - E) барьера. Этот типично
квантовомеханич. эффект, называемый туннельным эффектом, имеет большое
значение в практич. приложениях К. м. Он объясняет, напр., явление альфа-распада
- вылета из радиоактивных ядер 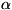 -частиц (ядер гелия). В
термоядерных реакциях, протекающих при темп-pax в десятки и сотни млн.
градусов, основная масса реагирующих ядер преодолевает
электростатич. (кулоновское) отталкивание и сближается на расстояния порядка
действия ядерных сил в результате туннельных (подбарьерных) переходов.
Возможность туннельных переходов объясняет также автоэлектронную эмиссию -
явление вырывания электронов из металла электрич. полем, контактные явления в
металлах и полупроводниках и мн. др. явления.
-частиц (ядер гелия). В
термоядерных реакциях, протекающих при темп-pax в десятки и сотни млн.
градусов, основная масса реагирующих ядер преодолевает
электростатич. (кулоновское) отталкивание и сближается на расстояния порядка
действия ядерных сил в результате туннельных (подбарьерных) переходов.
Возможность туннельных переходов объясняет также автоэлектронную эмиссию -
явление вырывания электронов из металла электрич. полем, контактные явления в
металлах и полупроводниках и мн. др. явления.
Рис. 5,
Уровни энергии. Рассмотрим поведение частицы в поле произвольной потенциальной
ямы (рис. 5). Пусть потенциал отличен от нуля в нек-рой ограниченной
области, причем V < О (силы притяжения). При этом и классическое, и
квантовое движения существенно различны в зависимости от того, положительна или
отрицательна полная энергия E частицы. При E>0
"классич." частица проходит над ямой и удаляется от неё. Отличие
квантовомеханич. движения от классического состоит в том, что происходит
частичное отражение волны от ямы; при этом возможные значения энергии ничем не
ограничены - энергия частицы имеет непрерывный спектр. При E < О
частица оказывается "запертой" внутри ямы. В классич. механике эта
ограниченность области движения абсолютна и возможна при любых значениях
E<0. В К. м. ситуация существенно меняется. Волновая функция должна затухать
по обе стороны от ямы, т. е. иметь вид е-x|x| . Однако
решение, удовлетворяющее этому условию, существует не при всех значениях E,
а только при определённых дискретных значениях. Число таких дискретных
значений Eпможет быть конечным или бесконечным, но оно всегда
счётно, т. е. может быть перенумеровано, и всегда имеется низшее значение E0
(лежащее выше дна потенциальной ямы); номер решения n наз. квантовым
числом. В этом случае говорят, что энергия системы имеет дискретный спектр.
Дискретность допустимых значений энергии системы (или соответствующих
частот 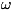 = En/h, где
= En/h, где 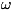 = 2
= 2
 - угловая частота) - типично
волновое явление. Его аналогии наблюдаются в классич. физике, когда волновое
движение происходит в ограниченном пространстве. Так, частоты колебаний струны
или частоты электромагнитных волн в объёмном резонаторе дискретны и
определяются размерами и свойствами границ области, в к-рой происходят
колебания. Действительно, ур-ние Шрёдингера математически подобно
соответствующим ур-ниям для струны или резонатора.
- угловая частота) - типично
волновое явление. Его аналогии наблюдаются в классич. физике, когда волновое
движение происходит в ограниченном пространстве. Так, частоты колебаний струны
или частоты электромагнитных волн в объёмном резонаторе дискретны и
определяются размерами и свойствами границ области, в к-рой происходят
колебания. Действительно, ур-ние Шрёдингера математически подобно
соответствующим ур-ниям для струны или резонатора.
Рис. 6.
Проиллюстрируем дискретный спектр энергии на примере квантового осциллятора.
На рис. 6 по оси абсцисс отложено расстояние частицы от положения равновесия.
Кривая (парабола) представляет потенциальную энергию частицы. В этом случае
частица при всех энергиях "заперта" внутри ямы, поэтому спектр
энергии дискретен. Горизонтальные прямые изображают уровни энергии частицы.
Энергия низшего уровня E0 = h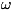 /2; это наименьшее значение
энергии, совместимое с соотношением неопределённостей: положение частицы на дне
ямы (E = О) означало бы точное равновесие, при к-ром и x = О, и p
= О, что невозможно, согласно принципу неопределённости. Следующие, более
высокие уровни энергии осциллятора расположены на равных расстояниях через интервал
h
/2; это наименьшее значение
энергии, совместимое с соотношением неопределённостей: положение частицы на дне
ямы (E = О) означало бы точное равновесие, при к-ром и x = О, и p
= О, что невозможно, согласно принципу неопределённости. Следующие, более
высокие уровни энергии осциллятора расположены на равных расстояниях через интервал
h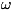 ;
формула для энергии n-го уровня:
;
формула для энергии n-го уровня:
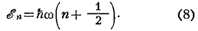
Над каждой горизонтальной прямой на рис. приведено условное изображение
волновой функции данного состояния. Характерно, что число узлов волновой
функции (т. е. число прохождений через О) равно квантовому числу n энергетич.
уровня. По др. сторону ямы (за точкой пересечения уровня с кривой потенциала)
волновая функция быстро затухает, в соответствии с тем, что говорилось выше.
В общем случае каждая квантовомеханич. система характеризуется своим
энергетическим спектром. В зависимости от вида потенциала (точнее, от характера
взаимодействия в системе) энергетич. спектр может быть либо дискретным (как у
осциллятора), либо непрерывным (как у свободной частицы,- её кинетич. энергия
может иметь произвольное положит, значение), либо частично дискретным, частично
непрерывным (напр., уровни атома при энергиях возбуждения, меньших энергии
ионизации, дискретны, а при больших энергиях - непрерывны).
Особенно важным является случай, имеющий место в атомах, молекулах, ядрах и
др. системах, когда наинизшее значение энергии, соответствующее осн. состоянию
системы, лежит в области дискретного спектра и, следовательно, осн. состояние
отделено от первого возбуждённого состояния энергетической щелью. Благодаря
этому внутр. структура системы не проявляется до тех пор, пока обмен энергией
при её взаимодействиях с др. системами не превысит определённого значения -
ширины энергетич. щели. Поэтому при ограниченном обмене энергией сложная
система (напр., ядро или атом) ведёт себя как бесструктурная частица
(материальная точка). Это имеет первостепенное значение для понимания, напр.,
теплового движения. Так, при энергиях теплового движения, меньших энергии
возбуждения атомных уровней, электроны атомов не могут участвовать в обмене
энергией и не дают вклада в теплоёмкость.
Временное уравнение Шрёдингера. До сих пор рассматривались лишь возможные
квантовые состояния системы и не рассматривалась эволюция системы во времени
(её динамика), определяемая зависимостью волновой функции от времени. Полное
решение задач К. м. должно давать волновую функцию  как функцию координат и
времени t . Для одномерного движения она определяется ур-нием
как функцию координат и
времени t . Для одномерного движения она определяется ур-нием
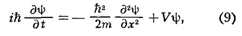
являющимся уравнением движения в К. м. Это ур-ние наз. временным уравнением
Шрёдингера. Оно справедливо и в том случае, когда потенциальная энергия зависит
от времени: V = V(x, t).
Частными решениями ур-ния (9) являются функции
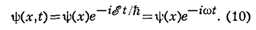
Здесь E - энергия частицы, а  (x) удовлетворяет
стационарному ур-нию Шрёдингера (7); для свободного движения
(x) удовлетворяет
стационарному ур-нию Шрёдингера (7); для свободного движения  (x) является
волной де Бройля еikx.
(x) является
волной де Бройля еikx.
Волновые функции (10) обладают тем важным свойством, что соответствующие
распределения вероятностей не зависят от времени, т. к. | (x,t)|2 = = |
(x,t)|2 = = | (x)|2.
Поэтому состояния, описываемые такими волновыми функциями, наз. стационарными;
они играют особую роль в приложениях К. м.
(x)|2.
Поэтому состояния, описываемые такими волновыми функциями, наз. стационарными;
они играют особую роль в приложениях К. м.
Общее решение временного ур-ния Шрёдингера представляет собой суперпозицию
стационарных состояний. В этом общем (нестационарном) случае, когда вероятности
существенно меняются со временем, энергия E не имеет определённого
значения. Так, если
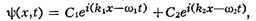
то E = h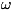 1 с вероятностью |C1|2 и E=
h
1 с вероятностью |C1|2 и E=
h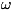 2
с вероятностью |С2|2. Для энергии и времени существует
соотношение неопределённостей:
2
с вероятностью |С2|2. Для энергии и времени существует
соотношение неопределённостей:  E
E t~h, (11) где
t~h, (11) где  E - дисперсия энергии,
а
E - дисперсия энергии,
а  t- промежуток времени, в течение к-рого энергия может быть
измерена.
t- промежуток времени, в течение к-рого энергия может быть
измерена.
Трёхмерное движение. Момент количества движения. До сих пор рассматривалось
(ради простоты) одномерное движение. Обобщение на движение частицы в трёх
измерениях не содержит принципиально новых элементов. В этом случае волновая
функция зависит от трёх координат х,y,z (и времени):  =
=  (x,y,z,t), а волна де
Бройля имеет вид
(x,y,z,t), а волна де
Бройля имеет вид
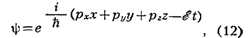
где рх, р_у, pг - три проекции импульса на оси
координат, а E = (р2х + p2y+"p2z)/2m.
Соответственно имеются три соотношения неопределённостей:
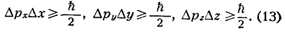
Временное ур-ние Шрёдингера имеет вид:
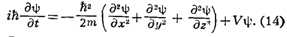
Это ур-ние принято записывать в символич. форме
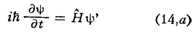
где
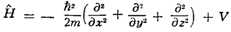
- дифференциальный оператор, наз. оператором Гамильтона, или гамильтонианом.
Стационарным решением ур-ния (14) является
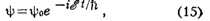
где  0
- решение ур-ния Шрёдингера для стационарных состояний:
0
- решение ур-ния Шрёдингера для стационарных состояний:
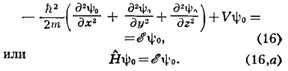
При трёхмерном движении спектр энергии также может быть непрерывным и
дискретным. Возможен и случай, когда неск. разных состояний имеют одинаковую
энергию; такие состояния наз. вырожденными. В случае непрерывного спектра
частица уходит на бесконечно большое расстояние от центра сил. Но, в отличие от
одномерного движения (когда были только две возможности - прохождение или
отражение), при трёхмерном движении частица может удалиться от центра под
произвольным углом к направлению первоначального движения, т. е. рассеяться.
Волновая функция частицы теперь является суперпозицией не двух, а бесконечного
числа волн де Бройля, распространяющихся по всевозможным направлениям.
Рассеянные частицы удобно описывать в сферич. координатах, т. е. определять их
положение расстоянием от центра (радиусом) r и двумя углами -
широтой 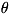 и азимутом
и азимутом 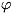 . Соответствующая волновая функция на больших
расстояниях r от центра сил имеет вид:
. Соответствующая волновая функция на больших
расстояниях r от центра сил имеет вид:
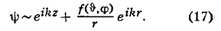
Первый член (пропорциональный волне це Бройля, распространяющейся вдоль. оси
z) описывает падающие частицы, а второй (пропорциональный
"радиальной волне де Бройля") - рассеянные. Функция f (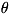 ,
, 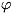 ) наз.
амплитудой рассеяния; она определяет т. н. дифференциальное сечение рассеяния d
) наз.
амплитудой рассеяния; она определяет т. н. дифференциальное сечение рассеяния d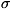 , характеризующее
вероятность рассеяния под данными углами:
, характеризующее
вероятность рассеяния под данными углами:
d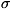 =|f(
=|f(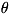 ,
,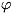 )|2d
)|2d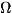 , (18)
, (18)
где d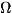 - элемент телесного угла , в к-рый происходит рассеяние.
- элемент телесного угла , в к-рый происходит рассеяние.
Дискретный спектр энергии возникает, как и при одномерном движении, когда
частица оказывается внутри потенциальной ямы. Энергетич. уровни нумеруют
квантовыми числами, причём, в отличие от одномерного движения, не одним, а
тремя. Наибольшее значение имеет задача о движении в поле центральных сил
притяжения. В этом случае также удобно пользоваться сферич. координатами.
Момент количества движения. Угловая часть движения (вращение) определяется в
К. м., как и в классич. механике, заданием момента количества движения, к-рый
при движении в поле центральных сил сохраняется. Но, в отличие от классич.
механики, в К. м. момент имеет дискретный спектр, т. е. может принимать только
вполне определённые значения. Это можно показать на примере азимутального
движения-вращения вокруг заданной оси (примем её за ось z). Волновая
функция в этом случае имеет вид "угловой волны де Бройля" e'm'f,
где 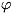 - азимут, а число т так же связано с моментом Mz, как
в плоской волне де Бройля волновое число k с импульсом р, т. е. т
= MzIh. T. к. углы
- азимут, а число т так же связано с моментом Mz, как
в плоской волне де Бройля волновое число k с импульсом р, т. е. т
= MzIh. T. к. углы 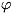 и
и 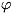 + 2
+ 2 описывают одно и то же положение, то и волновая
функция при изменении
описывают одно и то же положение, то и волновая
функция при изменении 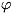 на 2
на 2 должна возвращаться к прежнему значению. Отсюда
вытекает, что т может принимать только целочисленные значения: т = О,
±1, ±2,..., т. е. момент может быть равен
должна возвращаться к прежнему значению. Отсюда
вытекает, что т может принимать только целочисленные значения: т = О,
±1, ±2,..., т. е. момент может быть равен
Мz = mh = 0, ±h, ±2h,··· (19)
Вращение вокруг оси z есть только часть углового движения (это проекция
движения на плоскость ху), a Mz - не полный момент, а
только его проекция на ось z. Чтобы узнать полный момент, надо
определить две остальные его проекции. Но в К. м. нельзя одновременно точно
задать все три составляющие момента. Действительно, проекция момента содержит
произведение проекции импульса на соответствующее плечо (координату,
перпендикулярную импульсу), а все проекции импульса и все плечи, согласно соотношениям
неопределённостей (13), одновременно не могут иметь точные значения.
Оказывается, что, кроме проекции Mz момента количества
движения на ось z (задаваемой числом т), можно одновременно точно
задать величину момента M, определяемую целым числом l:
M2 = h2/(/+l),
l = 0,1,2,... (20)
T. о., угловое движение даёт два квантовых числа -
l и т. Число l
наз. орбитальным квантовым числом, от него может зависеть значение энергии
частицы (как в классич. механике от вытянутости орбиты). Число т наз. магнитным
квантовым числом и при данном I может принимать значения т = 0,
±1, ±2, ..., ±1 - всего 21 + 1 значений; от т энергия не
зависит, т. к. само значение т зависит от выбора оси z, а поле
имеет сферич. симметрию. Поэтому уровень с квантовым числом I имеет (2l
+ 1)-кратное вырождение. Энергия уровня начинает зависеть от т лишь
тогда, когда сферич. симметрия нарушается, напр., при помещении системы в
магнитное поле (Зеемана эффект).
При заданном моменте радиальное движение похоже на одномерное движение с тем
отличием, что вращение вызывает центробежные силы. Их учитывают введением
(кроме обычного потенциала) центробежного потенциала, к-рый имеет вид М2/2тrг,
как и в классич. механике (здесь т - масса частицы). При этом
квадрат момента M2 следует заменить на величину h2l(l
+ 1). Решение ур-ния Шрёдингера для радиальной части волновой функции атома
определяет его уровни энергии и вводит третье квантовое число - радиальное пrили
главное п, к-рые связаны соотношением n = nr + 1 + 1, n, =
= 0, 1, 2, ..., 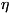 = 1, 2, 3,... В частности, для движения электрона в кулоновском
поле ядра с зарядом Ze (водородоподобный атом) уровни энергии
определяются формулой
= 1, 2, 3,... В частности, для движения электрона в кулоновском
поле ядра с зарядом Ze (водородоподобный атом) уровни энергии
определяются формулой
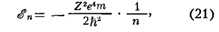
т. е. энергия зависит только от главного квантового числа п. Для
многоэлектронных атомов, в которых каждый электрон движется не только в поле
ядра, но и в поле остальных электронов, уровни энергии зависят также и от l.
На рис. 3 в статье Атом приведены радиальные и угловые распределения
электронной плотности (т.е. плотности вероятности или плотности заряда) вокруг
ядра. Видно, что задание момента (т. е. чисел l и т) полностью
определяет угловое распределение. В частности, при l=0 (M2 = 0) распределение
электронной плотности сферически симметрично. T. о., квантовое движение при
малых / совершенно непохоже на классическое. Так, сферически симметричное
состояние со ср. значением радиуса r<>0 в нек-рой степени, отвечает как
бы классич. движению по круговой орбите (или по совокупности круговых орбит,
наклонённых под разными углами), т. е. движению с ненулевым моментом (нулевой
момент в классич. механике соответствует нулевому плечу, а здесь плечо
r<>0). Это различие между квантовомеханическим и классическим движением
является следствием соотношения неопределённостей и может быть истолковано на
его основе. При больших квантовых числах (напр., при l>>1 1, пr>>1)
длина волны де Бройля становится значительно меньше расстояний L, характерных
для движения данной системы:
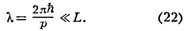
В этом случае квантовомеханич. законы движения приближённо переходят в
классич. законы движения по определённым траекториям, подобно тому, как законы
волновой оптики в аналогичных условиях переходят в законы геометрич. оптики
(описывающей распространение света с помощью лучей). Условие малости длины
де-бройлевской волны (22) означает, что pL >>h, где pL по
порядку величины равно классич. действию для системы. В этих условиях квант
действия h можно считать очень малой величиной, т. е. формально переход
квантовомеханич. законов в классические осуществляется при h -> 0. В
этом пределе исчезают все специфические квантовомеханич. явления, напр,
обращается в нуль вероятность туннельного эффекта.
Спин. В К. м. частица (как сложная, напр, ядро, так и
элементарная, напр., электрон) может иметь собственный момент количества
движения, наз. спином частицы. Это означает, что частице можно приписать
квантовое число (s), аналогичное орбитальному квантовому числу l.
Квадрат собств. момента количества движения имеет величину h2s(s+l),
а проекция момента на определённое направление может принимать 2s+1 значений от
- hs до +hs с интервалом h. T. о., состояние частицы (2s+
I) - кратно вырождено. Поэтому волна де Бройля частицы со спином аналогична
волне с поляризацией: при данной частоте и длине волны она имеет 2s+l поляризаций.
Число таких поляризаций может быть произвольным целым числом, т. е. спиновое
квантовое число s может быть как целым (0,1,2,...), так и полуцелым (½, 3/2,
5/2, ...) числом. Спин электрона, протона и нейтрона равен 4/2
(в единицах h). Спин ядер, состоящих из чётного числа нуклонов (протонов
и нейтронов), - целый или нулевой, а из нечётного - полуцелый. Отметим, что для
фотона соотношение между числом поляризаций и спином (к-рый равен 1) другое:
фотон не имеет массы покоя, а (как показывает релятивистская К. м.) для таких
частиц число поляризаций равно двум (а не 2s + 1 = 3).
Системы многих частиц. Тождественные частицы.
Квантовомеханич. ур-ние движения для системы N частиц получается
соответствующим обобщением ур-ния Шрёдингера для одной частицы. Оно содержит
потенциальную энергию, зависящую от координат всех N частиц, и включает
как воздействие на них внешнего поля, так и взаимодействие частиц между собой.
Волновая функция также является функцией от координат всех частиц. Её можно
рассматривать как волну в 3N-мерном пространстве; следовательно,
наглядная аналогия с распространением волн в обычном пространстве утрачивается.
Но это теперь несущественно, поскольку известен смысл волновой функции как
амплитуды вероятности .
Если квантовомеханич. системы состоят из одинаковых частиц, то в них
наблюдается специфическое явление, не имеющее аналогии в классич. механике. В
классич. механике случай одинаковых частиц тоже имеет нек-рую особенность.
Пусть, напр., столкнулись две одинаковые "классич." частицы (первая
двигалась слева, а вторая - справа) и после столкновения разлетелись в разные
стороны (напр., первая - вверх, вторая - вниз). Для результата столкновения не
имеет значения, какая из частиц пошла, напр., вверх, поскольку частицы
одинаковы,- практически надо учесть обе возможности (рис. 7,я и 7,6). Однако в
принципе в классич. механике можно различить эти два процесса, т. к. можно
проследить за траекториями частиц во время столкновения. В К. м. траекторий, в
строгом смысле этого слова, нет, и область столкновения обе частицы проходят с
нек-рой неопределённостью, с "размытыми траекториями" (рис. 7,в).
Рис. 7.
В процессе столкновения области размытия перекрываются и невозможно даже в
принципе различить эти два случая рассеяния. Следовательно, одинаковые частицы
становятся полностью неразличимыми - тождественными. Не имеет смысла говорить о
двух разных случаях рассеяния, есть только один случай - одна частица пошла
вверх, другая - вниз, индивидуальности у частиц нет.
Этот квантовомеханич. принцип неразличимости одинаковых частиц можно
сформулировать математически на языке волновых функций. Обнаружение частицы в
данном месте пространства определяется квадратом модуля волновой функции,
зависящей от координат обеих частиц, | (1,2)|2, где 1 и 2 означают совокупность
координат (включая и спин) соответственно первой и второй частицы.
Тождественность частиц требует, чтобы при перемене местами частиц 1 и 2
вероятности были одинаковыми, т. е.
(1,2)|2, где 1 и 2 означают совокупность
координат (включая и спин) соответственно первой и второй частицы.
Тождественность частиц требует, чтобы при перемене местами частиц 1 и 2
вероятности были одинаковыми, т. е.
| (1,2)|2=|
(1,2)|2=| (2,1)|2.
(23)
(2,1)|2.
(23)
Отсюда следует, что может быть два случая:
 (1,2)
=
(1,2)
=  (2,1),
(24,а)
(2,1),
(24,а)  (1,2)=-
(1,2)=- (2,1). (24,6)
(2,1). (24,6)
Если при перемене частиц местами волновая функция не меняет знака, то она
наз. симметричной [случай (24,а)], а если меняет,- антисимметричной [случай
(24,6)]. T. к. все взаимодействия одинаковых частиц симметричны относительно
переменных 1, 2, то свойства симметрии или антисимметрии волновой функции
сохраняются во времени.
В системе из произвольного числа тождеств, частиц должна иметь место
симметрия или антисимметрия относительно перестановки любой пары частиц.
Поэтому свойство симметрии или антисимметрии является характерным признаком
данного сорта частиц. Соответственно, все частицы делятся на два класса:
частицы с симметричными волновыми функциями наз. бозонами, с
антисимметричными - фермионами. Существует связь между значением спина
частиц и симметрией их волновых функций: частицы с целым спином являются
бозонами, с полуцелым - фермионами (т.н. связь спина и статистики; см. ниже).
Это правило сначала было установлено эмпирически, а затем доказано В. Паули
теоретически (оно является одной из основных теорем релятивистской К. м.). В
частности, электроны, протоны и нейтроны являются фермионами, а фотоны, пи-мезоны,
К-мезоны - бозонами. Сложные частицы, состоящие из фермионов, являются
фермионами, если состоят из нечётного числа частиц, и бозонами, если состоят из
чётного числа частиц; этими свойствами обладают, напр., атомные ядра.
Свойства симметрии волновой функции существенно определяют статистич.
свойства системы. Пусть, напр., невзаимодействующие тождеств, частицы находятся
в одинаковых внешних условиях (напр., во внешнем поле). Состояние такой системы
можно определить, задав числа заполнения - числа частиц, находящихся в
каждом данном (индивидуальном) состоянии, т. е. имеющих одинаковые наборы
квантовых чисел. Но если тождеств. частицы имеют одинаковые квантовые числа, то
их волновая функция симметрична относительно перестановки частиц. Отсюда
следует, что два одинаковых фермиона, входящих в одну систему, не могут
находиться в одинаковых состояниях, т. к. для фермионов волновая функция должна
быть антисимметричной. Это свойство наз. принципом запрета Паули. T. о., числа
заполнения для фермионов могут принимать лишь значения 0 или 1. T. к. электроны
являются фермионами, то принцип Паули существенно влияет на поведение
электронов в атомах, в металлах и т. д. Для бозонов (имеющих симметричную
волновую функцию) числа заполнения могут принимать произвольные целые значения.
Поэтому с учётом квантовомеханич. свойств тождеств, частиц существует два типа
статистик частиц: Ферми - Дирака статистика для фермионов и Базе-Эйнштейна
статистика для бозонов. Примером системы, состоящей из фермионов
(ферми-системы), является электронный газ в металле, примером бозе-системы -
газ фотонов (т. е. равновесное электромагнитное излучение), жидкий 4He
и др.
Принцип Паули является определяющим для понимания структуры перио-дич.
системы элементов Менделеева. В сложном атоме на каждом уровне энергии может
находиться число электронов, равное кратности вырождения этого уровня (числу
разных состояний с одинаковой энергией). Кратность вырождения зависит от
орбитального квантового числа и от спина электрона; она равна (21 + 1)
(2s + 1) = 2(2l + 1). Так возникает представление об электронных оболочках
атома, отвечающих периодам в таблице элементов Менделеева (см. Атом).
Обменное взаимодействие. Молекула. Молекула представляет собой систему ядер
и электронов, между к-рыми действуют электрич. (кулоновские) силы (притяжения и
отталкивания). Т.к. ядра значительно тяжелее электронов, электроны движутся
гораздо быстрее и образуют нек-рое распределение отрицат. заряда, в поле к-рого
находятся ядра. В классич. механике и электростатике доказывается, что такого
типа система не имеет устойчивого равновесия. Поэтому, даже если принять
устойчивость атомов (к-рую, как говорилось выше, нельзя объяснить на основе
законов классич. физики), невозможно без специфически квантовомеханич.
закономерностей объяснить устойчивость молекул. Особенно непонятным с точки
зрения классич. представлений является существование молекул из одинаковых
атомов, т. е. с т. н. ковалентной химич. связью (напр., простейшей молекулы -
H2). Оказалось, что свойство антисимметрии электронной волновой
функции так изменяет характер взаимодействия электронов, находящихся у разных
ядер, что возникновение такой связи становится возможным.
Рассмотрим для примера молекулу водорода H2, состоящую из двух
протонов и двух электронов. Волновая функция такой системы представляет собой
произведение двух функций, одна из к-рых зависит только от координат, а другая-
только от спиновых переменных обоих электронов. Если суммарный спин двух
электронов равен нулю (спины антипараллельны), спиновая функция антисимметрична
относительно перестановки спиновых переменных электронов. Следовательно, для
того чтобы полная волновая функция в соответствии с принципом Паули была
антисимметричной, координатная функция должна быть симметричной относительно
перестановки координат обоих электронов. Это означает, что координатная часть
волновой функции имеет вид:
 ~ [
~ [ a(1)
a(1) b(2) +
b(2) +  b(1)
b(1) a(2)], (25)
a(2)], (25)
где  a(i),
a(i),  b(i)
- волновые функции i-гo электрона (i = 1,2) соответственно у ядра а
и b.
b(i)
- волновые функции i-гo электрона (i = 1,2) соответственно у ядра а
и b.
Кулоновское взаимодействие пропорционально плотности электрического заряда
р=е| |2=е
|2=е *
* . При учёте свойств
симметрии координатной волновой функции (25), помимо плотности обычного вида
. При учёте свойств
симметрии координатной волновой функции (25), помимо плотности обычного вида
e| a(1)|2|
a(1)|2| b(2)|2, е|
b(2)|2, е| b(1)|2|
b(1)|2| a(2)Р,
a(2)Р,
соответствующих движению отдельных электронов у разных ядер, появляется
плотность вида
e a*(1)
a*(1) b(1)
b(1) b*(2)
b*(2) a(2), e
a(2), e b*(1)
b*(1) a(1)
a(1) a*(2)
a*(2) b(2)
b(2)
Она наз. обменной плотностью, потому что возникает как бы за счёт обмена
электронами между двумя атомами. Именно эта обменная плотность, приводящая к
увеличению плотности отрицат. заряда между двумя положительно заряженными
ядрами, и обеспечивает устойчивость молекулы в случае ковалентной химической
связи.
Очевидно, что при суммарном спине двух электронов, равном 1, координатная
часть волновой функции антисимметрична, т. е. в (25) перед вторым слагаемым
стоит знак минус, и обменная плотность имеет отрицательный знак; это означает,
что обменная плотность будет уменьшать плотность отрицат. электрич. заряда
между ядрами, т. е. приводить как бы к дополнит, отталкиванию ядер.
T. о., симметрия волновой функции приводит к "дополнительному" обменному
взаимодействию. Характерна зависимость обменного взаимодействия от спинов
электронов. Непосредственно спины не участвуют во взаимодействии - источником
взаимодействия являются электрич. силы, зависящие только от расстояния между
зарядами. Но в зависимости от ориентации спинов волновая функция,
антисимметричная относительно полной перестановки двух электронов (вместе с их
спинами), может быть симметричной или антисимметричной относительно перестановки
только положения электронов (их координат). А от типа симметрии координатной
части волновой функции зависит знак обменной плотности и, соответственно,
эффективное притяжение или отталкивание частиц в результате обменного
взаимодействия. Так, не участвуя непосредственно динамически во взаимодействии,
спины электронов благодаря квантовомеханической специфике свойств тождественных
частиц фактически определяют химическую связь.
Обменное взаимодействие играет существ, роль во
мн. явлениях. Оно объясняет,
напр., ферромагнетизм: благодаря обменному взаимодействию спиновые, а
следовательно, и магнитные моменты атомов ферромагнетика выстраиваются
параллельно друг другу. Огромное число явлений в конденсированных телах
(жидкости, твёрдом теле) тесно связано со статистикой образующих их частиц и с
обменным взаимодействием. Условие антисимметрии волновой функции для фермионов
приводит к тому, что фермионы при большой плотности как бы эффективно
отталкиваются друг от друга (даже если между ними не действуют никакие силы). В
то же время между бозонами, к-рые описываются симметричными волновыми
функциями, возникают как бы силы притяжения: чем больше бозонов находится в
к.-л. состоянии, тем больше вероятность перехода др. бозонов системы в это
состояние (подобного рода эффекты лежат, напр., в основе явлений сверхтекучести
и сверхпроводимости, принципа работы квантовых генераторов и квантовых
усилителей).
Математическая схема квантовой механики. Нерелятивистская К. м. может
быть построена на основе немногих формальных принципов. Математич. аппарат К.
м. обладает логич. безупречностью и изяществом. Чёткие правила устанавливают
соотношение между элементами математич. схемы и физич. величинами.
Первым основным понятием К. м. является квантовое состояние. Выбор
математич. аппарата К. м. диктуется физическим принципом суперпозиции квантовых
состояний, вытекающим из волновых свойств частиц. Согласно этому принципу,
суперпозиция любых возможных состояний системы, взятых с произвольными
(комплексными) коэффициентами, является также возможным состоянием системы.
Объекты, для к-рых определены понятия сложения и умножения на комплексное
число, наз. векторами. T. о., принцип суперпозиции требует, чтобы состояние
системы описывалось нек-рым вектором - вектором состояния (с к-рым тесно связано
понятие амплитуды вероятности, или волновой функции), являющимся элементом
линейного -"пространства состояний". Это позволяет использовать
математич. аппарат, развитый для линейных (векторных) пространств. Вектор
состояния обозначается по П. Дираку | >.
>.
Кроме сложения и умножения на комплексное число, вектор | > может подвергаться
ещё двум операциям. Во-первых, его можно проектировать на др. вектор, т. е.
составить скалярное произведение |
> может подвергаться
ещё двум операциям. Во-первых, его можно проектировать на др. вектор, т. е.
составить скалярное произведение | > с любым др. вектором состояния |
> с любым др. вектором состояния | '>; оно обозначается
как <
'>; оно обозначается
как < '|
'| > и является
комплексным числом, причём
> и является
комплексным числом, причём
< '|
'| >=<
>=< I
I '>*. (26)
'>*. (26)
Скалярное
произведение вектора | > с самим собой, <
> с самим собой, < |
| >, - положит, число; оно определяет длину (норму)
вектора. Длину вектора состояния удобно выбрать равной единице; его общий
фазовый множитель произволен. Различные состояния отличаются друг от друга
направлением вектора состояния в пространстве состояний.
>, - положит, число; оно определяет длину (норму)
вектора. Длину вектора состояния удобно выбрать равной единице; его общий
фазовый множитель произволен. Различные состояния отличаются друг от друга
направлением вектора состояния в пространстве состояний.
Во-вторых, можно рассмотреть операцию перехода от вектора | > к др. вектору |
> к др. вектору | '> (или
произвести преобразование |
'> (или
произвести преобразование | >->|
>->| '>· Символически эту операцию можно записать как
результат действия на вектор |
'>· Символически эту операцию можно записать как
результат действия на вектор | > нек-рого линейного оператора L:
> нек-рого линейного оператора L:
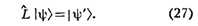
При этом вектор | '> может отличаться от |
'> может отличаться от | > "длиной" и
"направлением". Линейные операторы, в силу принципа суперпозиции
состояний, имеют в К. м. особое значение; в результате воздействия линейного
оператора на суперпозицию произвольных векторов |
> "длиной" и
"направлением". Линейные операторы, в силу принципа суперпозиции
состояний, имеют в К. м. особое значение; в результате воздействия линейного
оператора на суперпозицию произвольных векторов | 1> и |
1> и | 2>
получается суперпозиция преобразованных векторов:
2>
получается суперпозиция преобразованных векторов:
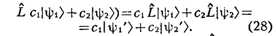
Важную роль для оператора L играют такие векторы | > = |
> = |
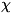 >, для к-рых |
>, для к-рых | '> совпадает по
направлению с I
'> совпадает по
направлению с I ),
), 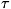 . е.
. е.
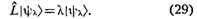
Векторы |
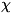 > наз.
собственными векторами оператора L, а числа
> наз.
собственными векторами оператора L, а числа  - его собственными
значениями. Собств. векторы |
- его собственными
значениями. Собств. векторы | х> принято обозначать просто |
х> принято обозначать просто | >, т. е. |
>, т. е. |
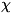 > = = |
> = = | >. Собств.
значения
>. Собств.
значения  образуют либо дискретный ряд чисел (тогда говорят, что оператор L
имеет дискретный спектр), либо непрерывный набор (непрерывный спектр), либо
частично дискретный, частично непрерывный.
образуют либо дискретный ряд чисел (тогда говорят, что оператор L
имеет дискретный спектр), либо непрерывный набор (непрерывный спектр), либо
частично дискретный, частично непрерывный.
Очень важный для К. м. класс операторов составляют линейные эрмитовы
операторы. Собств. значения  эрмитового оператора L вещественны.
Собств. векторы эрмитового оператора, принадлежащие различным собств.
значениям, ортогональны друг к другу, т.е. <
эрмитового оператора L вещественны.
Собств. векторы эрмитового оператора, принадлежащие различным собств.
значениям, ортогональны друг к другу, т.е. < |
| '> = 0. (30) Из них можно
построить ортогональный базис ("декартовы оси координат") в
пространстве состояний. Удобно нормировать эти базисные векторы на 1, <
'> = 0. (30) Из них можно
построить ортогональный базис ("декартовы оси координат") в
пространстве состояний. Удобно нормировать эти базисные векторы на 1, < |
| > = 1.
Произвольный вектор |
> = 1.
Произвольный вектор | > можно разложить по этому базису:
> можно разложить по этому базису:
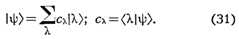
При этом:
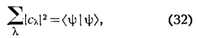
что эквивалентно теореме Пифагора; если | > нормирован на 1, то
> нормирован на 1, то
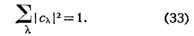
Принципиальное значение для построения математич. аппарата К. м. имеет тот
факт, что для каждой физич. величины существуют нек-рые выделенные состояния
системы, в которых эта величина принимает вполне определённое (единственное)
значение. По существу это свойство является определением измеримой (физической)
величины, а состояния, в к-рых физич. величина имеет определённое значение,
наз. собственными состояниями этой величины.
Согласно принципу суперпозиции, любое состояние системы может быть
представлено в виде суперпозиции собств. состояний к.-л. физич. величины.
Возможность такого представления математически аналогична возможности
разложения произвольного вектора по собств. векторам линейного эрмитового
оператора. В соответствии с этим в К. м. каждой физ. величине, или наблюдаемой,
L (координате, импульсу, моменту количества движения, энергии и т. д.)
ставится в соответствие линейный эрмитов оператор L. Собств.
значение  оператора L интерпретируются как возможные значения физич.
величины L проявляющиеся при измерениях. Если вектор состояния |
оператора L интерпретируются как возможные значения физич.
величины L проявляющиеся при измерениях. Если вектор состояния | > - собств.
вектор оператора L, то физич. величина L имеет определённое
значение. В противном случае L принимает различные значения
> - собств.
вектор оператора L, то физич. величина L имеет определённое
значение. В противном случае L принимает различные значения  с вероятностью |сх|2,
где сх - коэфф. разложения |
с вероятностью |сх|2,
где сх - коэфф. разложения | > по |
> по | >:
>:
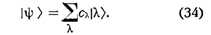
Коэфф. cx= < |
| > разложения |
> разложения | > в базисе |
> в базисе | > наз. также
волновой функцией в
> наз. также
волновой функцией в  -представлении. В частности, волновая функция
-представлении. В частности, волновая функция  (x) представляет
собой коэфф. разложения |
(x) представляет
собой коэфф. разложения | > по собственным векторам оператора координаты
> по собственным векторам оператора координаты
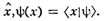
Среднее значение L наблюдаемой L в данном состоянии
определяется коэффициентами Cx, согласно общему соотношению между вероятностью
и средним значением
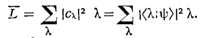
Значение L можно найти непосредственно через оператор L и вектор состояния | > (без
определения коэффициентов сх) по формуле:
> (без
определения коэффициентов сх) по формуле:
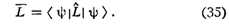
Вид линейных эрмитовых операторов, соответствующих таким физич. величинам, как
импульс, момент количества движения, энергия, постулируется на основе общих
принципов определения этих величин и соответствия принципа, требующего,
чтобы в пределе h->0 рассматриваемые физич. величины принимали
"классические" значения. Вместе с тем в К. м. вводятся нек-рые
линейные эрмитовы операторы (напр., отвечающие преобразованию векторов состояния
при отражении осей координат, перестановке одинаковых частиц и т. д.), к-рым
соответствуют измеримые физич. величины, не имеющие классич. аналогов (напр.,
чётность).
С операторами можно производить алгебраич. действия сложения и умножения.
Но, в отличие от обыкновенных чисел (к-рые в К. м. наз. с-числами), операторы
являются такими "числами" (q-числами), для к-рых операция
умножения некоммутативна. Если L и M - два оператора, то в общем
случае их действие на произвольный вектор | > в различном порядке даёт разные
векторы: LM|
> в различном порядке даёт разные
векторы: LM| ><>ML|
><>ML| >, т. е. LM
<> ML. Величина LM - ML обозначается как [L, M] и наз.
коммутатором. Только если два оператора переставимы (коммутируют), т. е. [L, M]
= О, у них могут быть общие собств. векторы и, следовательно, наблюдаемые L
и M могут одновременно иметь определённые (точные) значения
>, т. е. LM
<> ML. Величина LM - ML обозначается как [L, M] и наз.
коммутатором. Только если два оператора переставимы (коммутируют), т. е. [L, M]
= О, у них могут быть общие собств. векторы и, следовательно, наблюдаемые L
и M могут одновременно иметь определённые (точные) значения  и
и 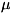 . В остальных
случаях эти величины не имеют одновременно определённых значений, и тогда они
связаны соотношением неопределённостей. Можно показать, что, если [L, M] = с,
то
. В остальных
случаях эти величины не имеют одновременно определённых значений, и тогда они
связаны соотношением неопределённостей. Можно показать, что, если [L, M] = с,
то  L
L М>|с|/2, где
М>|с|/2, где  L, и
L, и  М - среднеквадратичные
отклонения от средних для соответствующих величин.
М - среднеквадратичные
отклонения от средних для соответствующих величин.
Возможна такая математич. формулировка, в к-рой формальный переход от
классич. механики к К. м. осуществляется заменой с-чисел соответствующими
-числами. Сохраняются и ур-ния движения, но теперь это ур-ния для операторов.
Из этой формальной аналогии между К. м. и классич. механикой можно найти
основные коммутационные (перестановочные) соотношения. Так, для координаты и
импульса [х,р] =ih. Отсюда следует соотношение неопределённостей
Гейзенберга  p
p x>>h/2. Из перестановочных соотношений можно получить, в
частности, явный вид оператора импульса, в координатном (х-) представлении.
Тогда волновая функция есть
x>>h/2. Из перестановочных соотношений можно получить, в
частности, явный вид оператора импульса, в координатном (х-) представлении.
Тогда волновая функция есть  (x), а оператор импульса - дифференциальный
оператор
(x), а оператор импульса - дифференциальный
оператор
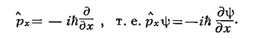
Можно показать, что спектр его собств. значений непрерывен, а амплитуда
вероятности <х|р> есть де-бройлевская волна (|р> - собств.
вектор оператора импульса р). Если задана энергия системы как функция
координат и импульсов частиц, Н(р, х), то знание коммутатора [х, р] достаточно
для нахождения [H, р], [H, х], а также уровней энергии как собств.
значений оператора полной энергии H.
На основании определения момента количества движения Мz = хрy
- урx, ... можно получить, что [Mx, Мy]
= ihMz. Эти коммутац. соотношения справедливы и при учёте
спинов частиц; их оказывается достаточно для определения собств. значения
квадрата полного момента: M2= h2j(j+1), где квантовое
число j-целое или полуцелое число, и его проекции Мг = тh,
т = -j, -j+1,..., +j·
Ур-ния движения квантовомеханич. системы могут быть записаны в двух формах:
в виде ур-ния для вектора состояния
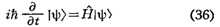
- шрёдингеровская форма ур-ния движения, и в виде ур-ния для операторов
(q-чисел)
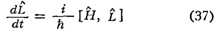
- гейзенберговская форма ур-ний движения, наиболее близкая классич. механике.
Из гейзенберговской формы ур-ний движения, в частности, следует, что ср.
значения физич. величин изменяются по законам классич. механики; это положение
наз. теоремой Эренфеста.
Для логич. структуры К. м. характерно присутствие двух совершенно
разнородных по своей природе составляющих. Вектор состояния (волновая функция)
однозначно определён в любой момент времени, если задан в начальный момент. В
этой части теория вполне детерминистична. Но вектор состояния не есть
наблюдаемая величина. О наблюдаемых на основе знания |ф> можно сделать лишь
статистические (вероятностные) предсказания. Результаты индивидуального
измерения над квантовым объектом в общем случае, строго говоря, непредсказуемы.
Предпринимались попытки восстановить идею полного детерминизма в классич.
смысле введением предположения о неполноте квантовомеханич. описания. Напр.,
высказывалась гипотеза о наличии у квантовых объектов дополнит, степеней
свободы-"скрытых параметров", учёт к-рых сделал бы поведение системы
полностью детерминированным в смысле классич. механики; неопределённость
возникает только вследствие того, что эти "скрытые параметры"
неизвестны и не учитываются. Однако Дж. Нейман доказал теорему о
невозможности нестатистич. интерпретации К. м. при сохранении её основного
положения о соответствии между наблюдаемыми (физич. величинами) и операторами.
Лит.: Классич. труды - Г е и з е н 6 е р г В., Физические принципы
квантовой теории, Л.- M., 1932; Дирак П., Принципы квантовой механики, пер. с
англ., M., 1960; Паули В., Общие принципы волновой механики, пер. с нем., М.-
Л., 1947; Нейман И., Математические основы квантовой механики, пер. с нем., M.,
1964. Учебники - Л а н д а у Л. Д., Л и ф ш и ц E. M., Квантовая механика, 2
изд., M., 1963 (Теоретическая физика, т. 3); Б л о х и н ц е в Д. И., Основы
квантовой механики, 4 изд., M., 1963; Давыдов А. С., Квантовая механика, M.,
1963; Соколов А. А., Лоскутов Ю. M., Тернов И. M., Квантовая механика, M.,
1962; Б о м Д., Квантовая теория, пер. с англ., M., 1961; Фейнман Р., Лейтон
Р., Сэндс M., Фейнмановские лекции по физике, пер. с англ., в. 8 и 9, M., 1966
-67; Шифф Л., Квантовая механика, пер. с англ,, 2 изд., M., 1959; Ферми Э.,
Квантовая механика, пер. с англ., M., 1965. Популярные книги - Б о р н M.,
Атомная физика, пер. с англ., 3 изд., M., 1970; Пайерлс P. E., Законы природы,
пер. с англ., 2 изд., M., 1962.
В. Б. Берестецкий.
КВАНТОВАЯ РАДИОФИЗИКА, то же, что и квантовая электроника.
КВАНТОВАЯ СТАТИСТИКА, раздел статистич. физики, исследующий системы
мн. частиц, подчиняющихся законам квантовой механики. См. Статистическая
физика.
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ. Содержание:
I. Частицы и поля в классической квантовой теории
II. Квантовая электродинамика
III. Метод возмущений в квантовой теории поля
IV. Трудности и проблемы квантовой теории поля
V. Некоторые новые методы в квантовой теории поля
Квантовая теория поля - квантовая теория систем с бесконечным числом
степеней свободы (полей физических). К. т. п., возникшая как обобщение квантовой
механики в связи с проблемой описания процессов порождения, поглощения и
взаимных превращений элементарных частиц, нашла затем широкое применение в
теории твёрдого тела, ядра атомного и др. и является теперь осн. теоретич.
методом исследования квантовых систем.
I. Частицы и поля в классической и квантовой теории
1. Двойственность классической теории.
В классич. теории, формирование к-рой в основном завершилось к нач. 20 в.,
физич. картина мира складывается из двух элементов - частиц и полей. Частицы -
маленькие комочки материи, движущиеся по законам классич. механики Ньютона.
Каждая из них имеет 3 степени свободы: её положение задаётся тремя
координатами, напр, х, у, z; если зависимость координат от времени
известна, то это даёт исчерпывающую информацию о движении частицы. Описание
полей значительно сложнее. Задать, напр., электрич. поле - значит задать его
напряжённость E во всех точках пространства. T. о., для описания поля
необходимо знать не 3 (как для материальной точки), а бесконечно большое число
величин в каждый из моментов времени; иначе говоря, поле имеет бесконечное
число степеней свободы. Естественно, что и законы динамики электромагнитного
поля, установление к-рых обязано в основном исследованиям M. Фарадея и
Дж. Максвелла, оказываются сложнее законов механики.
Указанное различие между полями и частицами является главным, хотя и не
единственным: частицы дискретны, а поля непрерывны; электромагнитное поле
(электромагнитные волны) может порождаться и поглощаться, в то время как
материальным точкам классич. механики возникновение и исчезновение чуждо;
наконец, электромагнитные волны могут, накладываясь, усиливать или ослаблять и
даже полностью "гасить" друг друга (интерференция волн), чего,
разумеется, не происходит при наложении потоков частиц. Хотя частицы и волны
переплетены между собой сложной сетью взаимодействий, каждый из этих объектов
выступает как носитель принципиально различных индивидуальных черт. Картине
мира в классич. теории присущи отчётливые черты двойственности. Открытие
квантовых явлений поставило на место этой картины другую, к-рую можно назвать
двуединой.
2. Кванты электромагнитного поля. В 1900 M. Планк для
объяснения закономерностей теплового излучения тел впервые ввёл в физику понятие
о порции, или кванте, излучения. Энергия E такого кванта пропорциональна
частоте  излучаемой электромагнитной волны, E = hv, где коэфф. пропорциональности
hz=6,62·10-27эрг/сек (позднее он был назван постоянной
Планка). А. Эйнштейн обобщил эту идею Планка о дискретности излучения,
предположив, что такая дискретность не связана с каким-то особым механизмом
взаимодействия излучения с веществом, а внутренне присуща самому
электромагнитному излучению. Электромагнитное излучение "состоит" из
таких квантов - фотонов. Эти представления получили экспериментальное
подтверждение - на их основе были объяснены закономерности фотоэффекта и
Комптона эффекта.
излучаемой электромагнитной волны, E = hv, где коэфф. пропорциональности
hz=6,62·10-27эрг/сек (позднее он был назван постоянной
Планка). А. Эйнштейн обобщил эту идею Планка о дискретности излучения,
предположив, что такая дискретность не связана с каким-то особым механизмом
взаимодействия излучения с веществом, а внутренне присуща самому
электромагнитному излучению. Электромагнитное излучение "состоит" из
таких квантов - фотонов. Эти представления получили экспериментальное
подтверждение - на их основе были объяснены закономерности фотоэффекта и
Комптона эффекта.
T. о., электромагнитному излучению присущи черты дискретности, к-рые прежде
приписывались лишь частицам. Подобно частице (корпускуле), фотон обладает
определённой энергией, импульсом, спином и всегда существует как единое
целое. Однако наряду с корпускулярными фотон обладает и волновыми свойствами,
проявляющимися, напр., в явлениях дифракции света и интерференции
света. Поэтому его можно было бы назвать " волно-частицей ".
3. Корпускулярно-волновой дуализм.
Двуединое, корпускулярно-волновое представление о кванте электромагнитного
поля - фотоне - было распространено Л. де Бройлем на все виды материи. И
электроны, и протоны, и любые др. частицы, согласно гипотезе де Бройля,
обладают не только корпускулярными, но и волновыми свойствами. Это
количественно проявляется в соотношениях де Бройля, связывающих такие
"корпускулярные" величины, как энергия E и импульс p частицы,
с величинами, характерными для волнового описания,- длиной волны  и
частотой
и
частотой  :
:
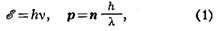
где n - единичный вектор, указывающий направление распространения
волны (см. Волны де Бройля).
Корпускулярно-волновой дуализм (подтверждённый экспериментально) потребовал
пересмотра законов движения и самих способов описания движущихся объектов.
Возникла квантовая механика (или волновая механика). Важнейшей чертой этой
теории является идея вероятностного описания движения микрообъектов.
Величиной, описывающей состояние системы в квантовой механике (напр., электрона,
движущегося в заданном поле), является амплитуда вероятности, или волновая
функция  (x, у, z, t). Квадрат модуля волновой функции, |
(x, у, z, t). Квадрат модуля волновой функции, | (х, у, z,
t)|2, определяет вероятность обнаружить частицу в момент ? в точке с
координатами, х, у, z. И энергия, и импульс, и все др.
"корпускулярные" величины могут быть однозначно определены, если
известна
(х, у, z,
t)|2, определяет вероятность обнаружить частицу в момент ? в точке с
координатами, х, у, z. И энергия, и импульс, и все др.
"корпускулярные" величины могут быть однозначно определены, если
известна  (
(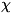 , у, z, t). При таком вероятностном описании можно говорить и
о "точечности" частиц. Это находит своё отражение в т. н. локальности
взаимодействия, означающей, что взаимодействие, напр., электрона с нек-рым
полем определяется лишь значениями этого поля и волновой функции электрона,
взятыми в одной и той же точке пространства и в один и тот же момент времени. В
классич. электродинамике локальность означает, что точечный заряд испытывает
воздействие поля в той точке, в к-рой он находится, и не реагирует на поле во
всех остальных точках.
, у, z, t). При таком вероятностном описании можно говорить и
о "точечности" частиц. Это находит своё отражение в т. н. локальности
взаимодействия, означающей, что взаимодействие, напр., электрона с нек-рым
полем определяется лишь значениями этого поля и волновой функции электрона,
взятыми в одной и той же точке пространства и в один и тот же момент времени. В
классич. электродинамике локальность означает, что точечный заряд испытывает
воздействие поля в той точке, в к-рой он находится, и не реагирует на поле во
всех остальных точках.
Являясь носителем информации о корпускулярных свойствах частицы, амплитуда
вероятности  (x, у, z, t) в то же время отражает и её волновые
свойства. Ур-ние, определяющее
(x, у, z, t) в то же время отражает и её волновые
свойства. Ур-ние, определяющее  (x, у, z, t), - Шрёдингера
уравнение - является уравнением волнового типа (отсюда назв.- волновая
механика); для
(x, у, z, t), - Шрёдингера
уравнение - является уравнением волнового типа (отсюда назв.- волновая
механика); для  (x, у, z, t) имеет место суперпозиции принцип, что
и позволяет описывать интерференционные явления.
(x, у, z, t) имеет место суперпозиции принцип, что
и позволяет описывать интерференционные явления.
T. о., отмеченная выше двуединость находит отражение в самом способе
квантовомеханич. описания, устраняющего резкую границу, разделявшую в классич.
теории поля и частицы. Это описание продиктовано Корпускулярно-волновой
природой микрообъектов, и его правильность проверена на огромном числе явлений.
4. Квантовая теория поля как обобщение квантовой механики. Квантовая
механика блестяще разрешила важнейшую из проблем - проблему атома, а
также дала ключ к пониманию мн. др. загадок микромира. Но в то же время самое
"старое" из полей - электромагнитное поле - описывалось в этой теории
классич. Максвелла уравнениями, т. е. рассматривалось по существу как
классическое непрерывное поле. Квантовая механика позволяет описывать движение
электронов, протонов и др. частиц, но не их порождение или уничтожение, т. е.
применима лишь для описания систем с неизменным числом частиц. Наиболее
интересная в электродинамике задача об испускании и поглощении электромагнитных
волн заряженными частицами, что на квантовом языке соответствует порождению или
уничтожению фотонов, по существу оказывается вне рамок её компетенции. При
квантовомеханич. рассмотрении, напр., атома водорода можно получить дискретный
набор значений энергии электрона, момента количества движения и др. физич.
величин, относящихся к различным состояниям атома, можно найти, какова
вероятность обнаружить электрон на определённом расстоянии от ядра, но переходы
атома из одного состояния в другое, сопровождающиеся испусканием или
поглощением фотонов, описать нельзя (по крайней мере, последовательно). T. о.,
квантовая механика даёт лишь приближённое описание атома, справедливое в той
мере, в какой можно пренебречь эффектами излучения.
Порождаться и исчезать могут не только фотоны. Одно из самых поразительных
и, как выяснилось, общих свойств микромира - универсальная взаимная
превращаемость частиц. Либо "самопроизвольно" (на первый взгляд),
либо в процессе столкновений одни частицы исчезают и на их месте появляются
другие. Так, фотон может породить пару электрон-позитрон (см. Аннигиляция и
рождение пар); при столкновении протонов и нейтронов могут рождаться пи-мезоны;
пи-мезон распадается на мюон и нейтрино и т. д. Для описания
такого рода процессов потребовалось дальнейшее развитие квантовой теории.
Однако новый круг проблем не исчерпывается описанием взаимных превращений частиц,
их порождения и уничтожения. Более общая и глубокая задача заключалась в том,
чтобы "проквантовать" поле, т. е. построить квантовую теорию систем с
бесконечным числом степеней свободы. Потребность в этом была тем более
настоятельной, что, как уже отмечалось, установление корпускулярно-волнового
дуализма обнаружило волновые свойства у всех "частиц". Решение
указанных проблем и является целью того обобщения квантовой механики, к-рое
наз. К. т. п.
Чтобы пояснить переход от квантовой механики к К. т. п., воспользуемся
наглядной (хотя далеко не полной) аналогией. Рассмотрим сначала один
гармонический осциллятор - материальную точку, колеблющуюся подобно маятнику.
Переход от классич. механики к квантовой при описании такого маятника выявляет
ряд принципиально новых обстоятельств: допустимые значения энергии оказываются
дискретными, исчезает возможность одновременного определения его координаты и
импульса и т. д. Однако объектом рассмотрения по-прежнему остаётся один маятник
(осциллятор), только величины, к-рые описывали его состояние в классич. теории,
заменяются, согласно общим положениям квантовой механики, соответствующими операторами.
Представим, что всё пространство заполнено такого рода осцилляторами. Вместо
того чтобы как-то "пронумеровать" эти осцилляторы, можно просто
указывать координаты точек, в к-рых каждый из них находится,- так
осуществляется переход к полю осцилляторов, число степеней свободы к-рого,
очевидно, бесконечно велико.
Описание такого поля можно производить различными методами. Один из них
заключается в том, чтобы проследить за каждым из осцилляторов. При этом на
первый план выступают величины, наз. локальными, т. е. заданными для каждой из
точек пространства (и момента времени), т. к. именно координаты
"помечают" выбранный осциллятор. При переходе к квантовому описанию
эти локальные классич. величины, описывающие поле, заменяются локальными
операторами, Ур-ния, к-рые в классич. теории описывали динамику поля,
превращаются в ур-ния для соответствующих операторов. Если осцилляторы не взаимодействуют
друг с другом (или с нек-рым др. полем), то для такого поля свободных
осцилляторов общая картина, несмотря на бесконечное число степеней свободы,
получается относительно простой; при наличии же взаимодействий возникают
усложнения.
Др. метод описания поля основан на том, что вся совокупность колебаний
осцилляторов может быть представлена как набор волн, распространяющихся в
рассматриваемом поле. В случае невзаимодействующих осцилляторов волны также
оказываются независимыми; каждая из них является носителем энергии, импульса,
может обладать определённой поляризацией. При переходе от классич. рассмотрения
к квантовому, когда движение каждого осциллятора описывается вероятностными
квантовыми законами, волны также приобретают вероятностный смысл. Но с каждой
такой волной (согласно корпускулярно-волновому дуализму) можно сопоставить
частицу, обладающую той же, что и волна, энергией и импульсом (а следовательно,
и массой) и имеющую спин (классич. аналогом к-рого является момент количества
движения циркулярно поляризованной волны). Эту "частицу", конечно,
нельзя отождествить ни с одним из осцилляторов поля, взятым в отдельности,- она
представляет собой результат процесса, захватывающего бесконечно большое число
осцилляторов, и описывает некое возбуждение поля. Если осцилляторы не
независимы (есть взаимодействия), то это отражается и на "волнах
возбуждения" или на соответствующих им "частицах возбуждения"-
они также перестают быть независимыми, могут рассеиваться друг на друге, порождаться
и исчезать. Изучение поля, т. о., можно свести к рассмотрению квантованных волн
(или "частиц") возбуждений. Более того, никаких др.
"частиц", кроме "частиц возбуждения", при данном методе
описания не возникает, т. к. каждая частица-осциллятор отдельно в нарисованную
общую картину квантованного осцилляторного поля не входит.
Рассмотренная "осцилляторная модель" поля имеет в основном
иллюстративное значение (хотя, напр., она довольно полно объясняет, почему в
физике твёрдого тела методы К. т. п. являются эффективным инструментом
теоретич. исследования). Однако она не только отражает общие важные черты
теории, но и позволяет понять возможность различных подходов к проблеме
квантового описания полей.
Первый из описанных выше методов ближе к т. н. гейзенберговской картине (или
представлению Гейзенберга) квантового поля. Второй - к
"представлению взаимодействия", к-рое обладает преимуществом большей
наглядности и поэтому, как правило, будет использоваться в дальнейшем
изложении. При этом, конечно, будут рассматриваться различные физич. поля, не
имеющие механич. природы, а не поле механич. осцилляторов. Так, рассматривая
электромагнитное поле, было бы неправильным искать за электромагнитными волнами
какие-то механич. колебания: в каждой точке пространства колеблются (т. е. изменяются
во времени) напряжённости электрич. E и магнитного H полей. В
гейзенберговской картине описания электромагнитного поля объектами тео-ретич.
исследования являются операторы E (х) и H (х) (и др. операторы,
к-рые через них выражаются), появляющиеся на месте классич. величин. Во втором
из рассмотренных методов на первый план выступает задача описания возбуждений
электромагнитного поля. Если энергия "частицы возбуждения" равна E,
а импульс р, то длина волны  и частота
и частота  соответствующей ей волны
определяются формулами (1). Носитель этой порции энергии и импульса - квант
свободного электромагнитного поля, или фотон. Т. о., рассмотрение свободного
электромагнитного поля сводится к рассмотрению фотонов.
соответствующей ей волны
определяются формулами (1). Носитель этой порции энергии и импульса - квант
свободного электромагнитного поля, или фотон. Т. о., рассмотрение свободного
электромагнитного поля сводится к рассмотрению фотонов.
Исторически квантовая теория электромагнитного поля начала развиваться
первой и достигла известной завершённости; поэтому квантовой теории
электромагнитных процессов - квантовой электродинамике - отводится в статье
основное место. Однако, кроме электромагнитного поля, существуют и др. типы
физич. полей: мезонные поля различных типов, поля нейтрино и антинейтрино,
нуклонные, гиперонные и т. д. Если физич. поле является свободным (т. е. не
испытывающим никаких взаимодействий, в т. ч. и самовоздействия), то его можно
рассматривать как совокупность невзаимодействующих квантов этого поля, к-рые
часто просто называют частицами данного поля. При наличии взаимодействий
(напр., между физич. полями различных типов) независимость квантов
утрачивается, а когда взаимодействия начинают играть доминирующую роль в
динамике полей, утрачивается и плодотворность самого введения квантов этих
полей (по крайней мере, для тех этапов процессов в этих полях, для к-рых нельзя
пренебречь взаимодействием). Квантовая теория таких полей недостаточно
разработана и в дальнейшем почти не обсуждается.
5. Квантовая теория поля и релятивистская теория. Описание частиц высоких
энергий должно проводиться в рамках релятивистской теории, т. е. в рамках
специальной теории относительности Эйнштейна (см. Относительности теория). Эта
теория, в частности, устанавливает важное соотношение между энергией E,
импульсом 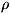 и массой т частицы:
и массой т частицы:
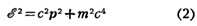
(с - универсальная постоянная, равная скорости света в пустоте, с =3·1010
см/сек). Из (2) видно, что энергия частицы не может быть меньше тс2.
Энергия, конечно, не возникает "из ничего". Поэтому минимальная
энергия, необходимая для образования частицы данной массы m (она наз. массой
покоя), равна mc2.
Если рассматривается система, состоящая из медленных частиц, то их энергия
может оказаться недостаточной для образования новых частиц. В такой
"нерелятивистской" системе число частиц может оставаться неизменным.
Это и обеспечивает возможность применения для её описания квантовой механики.
Всё изложенное выше относится к порождению частиц, имеющих отличную от нуля
массу покоя. Но у фотона, напр., масса покоя равна нулю, так что для его
образования совсем не требуется больших, релятивистских, энергий. Однако и
здесь невозможно обойтись без релятивистской теории, что ясно хотя бы из того,
что нерелятивистская теория применима лишь при скоростях, много меньших
скорости света с, а фотон всегда движется со скоростью с.
Кроме необходимости рассматривать релятивистскую область энергий, есть ещё
одна причина важности теории относительности для К. т. п.: в физике элементарных
частиц, изучение к-рых является одной из осн. (и ещё не решённых) задач К. т.
п., теория относительности играет фундаментальную роль. Это делает развитие
релятивистской К. т. п. особенно важным.
Однако и нерелятивистская К. т. п. представляет значит, интерес хотя бы
потому, что она успешно используется в физике твёрдого тела.
II. Квантовая электродинамика
1. Квантованное свободное поле. Вакуумное состояние поля, или физический
вакуум. Рассмотрим электромагнитное поле, или - в терминах квантовой теории -
поле фотонов. Такое поле имеет запас энергии и может отдавать её порциями.
Уменьшение энергии поля на hv означает исчезновение одного фотона
частоты  ,
или переход поля в состояние с уменьшившимся на единицу числом фотонов. В
результате последовательности таких переходов в конечном итоге образуется
состояние, в к-ром число фотонов равно нулю, и дальнейшая отдача энергии полем
становится невозможной. Однако, с точки зрения К. т. п., электромагнитное поле
не перестаёт при этом существовать, оно лишь находится в состоянии с наименьшей
возможной энергией. Поскольку в таком состоянии фотонов нет, его естественно
назвать вакуумным состоянием электромагнитного поля , или фотонным вакуумом.
Следовательно, вакуум электромагнитного поля - низшее энергетич. состояние
этого поля.
,
или переход поля в состояние с уменьшившимся на единицу числом фотонов. В
результате последовательности таких переходов в конечном итоге образуется
состояние, в к-ром число фотонов равно нулю, и дальнейшая отдача энергии полем
становится невозможной. Однако, с точки зрения К. т. п., электромагнитное поле
не перестаёт при этом существовать, оно лишь находится в состоянии с наименьшей
возможной энергией. Поскольку в таком состоянии фотонов нет, его естественно
назвать вакуумным состоянием электромагнитного поля , или фотонным вакуумом.
Следовательно, вакуум электромагнитного поля - низшее энергетич. состояние
этого поля.
Представление о вакууме как об одном из состояний поля, столь необычное с
точки зрения классич. понятий, является физически обоснованным.
Электромагнитное поле в вакуумном состоянии не может быть поставщиком энергии,
но из этого не следует, что вакуум вообще никак не может проявить себя. Физич.
вакуум - не "пустое место", а состояние с важными свойствами, к-рые
проявляются в реальных физич. процессах (см. ниже).
Аналогично, и для др. частиц можно ввести представление о вакууме как о
низшем энергетическом состоянии полей этих част и ц. При рассмотрении
взаимодействующих полей вакуумным наз. низшее энергетич. состояние всей системы
этих полей.
Если полю, находящемуся в вакуумном состоянии, сообщить достаточную энергию,
то происходит возбуждение поля, т.е. рождение частицы - кванта этого поля. T.
о., появляется возможность описать порождение частиц как переход из
"ненаблюдаемого" вакуумного состояния в состояние реальное. Такой подход
позволяет перенести в К. т. п. хорошо разработанные методы квантовой механики -
свести изменение числа частиц данного поля к квантовым переходам этих частиц из
одних состояний в другие.
Взаимные превращения частиц, порождение одних и уничтожение других, можно
количественно описывать при помощи т. н. метода вторичного квантования
[предложенного в 1927 П. Дираком и получившего дальнейшее развитие в
работах В. А. Фока (1932)].
2. Вторичное квантование. Переход от классич. механики к квантовой
называют просто квантованием, или реже - "первичным квантованием".
Как уже говорилось, такое квантование не даёт возможности описывать изменение
числа частиц в системе. Осн. чертой метода вторичного квантования является
введение операторов, описывающих порождение и уничтожение частиц. Поясним
действие этих операторов на простом примере (или модели) теории, в к-рой
рассматриваются одинаковые частицы, находящиеся в одном и том же состоянии
(напр., все фотоны считаются имеющими одинаковую частоту, направление распространения
и поляризацию). T. к. число частиц в данном состоянии может быть произвольным,
то этот случай соответствует бозе-частицам, или бозонам, подчиняющимся Базе
- Эйнштейна статистике.
В квантовой теории состояние системы частиц описывается волновой функцией
или вектором состояния. Введём для описания состояния с N частицами
вектор состояния  N; квадрат модуля
N; квадрат модуля  N, |
N, | N|2,
определяющий вероятность обнаружения N частиц, обращается, очевидно, в
1, если N достоверно известно. Это означает, что вектор состояния с
любым фиксированным N нормирован на 1. Введём теперь оператор уничтожения
частицы а- и оператор рождения частицы a+. По определению, а- переводит
состояние с N частицами в состояние с N - 1 частицей, т. е.
N|2,
определяющий вероятность обнаружения N частиц, обращается, очевидно, в
1, если N достоверно известно. Это означает, что вектор состояния с
любым фиксированным N нормирован на 1. Введём теперь оператор уничтожения
частицы а- и оператор рождения частицы a+. По определению, а- переводит
состояние с N частицами в состояние с N - 1 частицей, т. е.
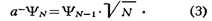
Аналогично, оператор порождения частицы а+ переводит
состояние  N в состояние с N + 1 частицей:
N в состояние с N + 1 частицей:
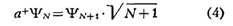
[множители N1/2 в (3) и (N + 1)½ в (4)
вводятся именно для выполнения условия нормировки: | N|2 = 1].
В частности, при N=O
N|2 = 1].
В частности, при N=O 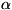 +
+ 0=
0=  1, где
1, где  0
- вектор состояния, характеризующий вакуум; т. е. одночастичное состояние
получается в результате порождения из "вакуума" одной частицы. Однако
a-
0
- вектор состояния, характеризующий вакуум; т. е. одночастичное состояние
получается в результате порождения из "вакуума" одной частицы. Однако
a- 0=0, поскольку невозможно уничтожить частицу
в состоянии, в к-ром частиц нет; это равенство можно считать определением
вакуума. Вакуумное состояние
0=0, поскольку невозможно уничтожить частицу
в состоянии, в к-ром частиц нет; это равенство можно считать определением
вакуума. Вакуумное состояние  0 имеет в К. т. п. особое значение, т.
к. из него при помощи операторов a+ можно получить любое состояние.
Действительно, в рассматриваемом случае (когда состояние всей системы
определяется только числом частиц)
0 имеет в К. т. п. особое значение, т.
к. из него при помощи операторов a+ можно получить любое состояние.
Действительно, в рассматриваемом случае (когда состояние всей системы
определяется только числом частиц)
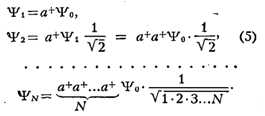
Легко показать, что порядок действия операторов а- и а+ не
безразличен. Действительно, а- (a+  0) = a-
0) = a- 1=
1= 0,
в то время как
0,
в то время как 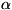 + (
+ (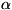 -
- 0) = 0. Т. о., (а-а+ -
0) = 0. Т. о., (а-а+ - 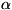 +
+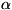 -)
-) 0
=
0
=  0,
или
0,
или
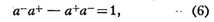
т. е. операторы а+ и a- являются непереставимыми
(некоммутирующими). Соотношения типа (6), устанавливающие связь между действием
двух операторов, взятых в различном порядке, наз. перестановочными
соотношениями, или коммутационными соотношениями, для этих операторов, а
выражения вида AB -BA = [А, В] - коммутаторами операторов А и В.
Если учесть, что частицы могут находиться в различных состояниях, то,
записывая операторы порождения и уничтожения, надо дополнительно указывать, к
какому состоянию частицы эти операторы относятся. В квантовой теории состояния
задаются набором квантовых чисел, определяющих энергию, спин и др.
физич. величины; для простоты обозначим всю совокупность квантовых чисел одним
индексом п: так, а+n обозначает оператор
рождения частицы в состоянии с набором квантовых чисел п. Средние числа
частиц, находящихся в состояниях, соответствующих различным п, называются
числами заполнения этих состояний.
Рассмотрим выражение а-пa+m 0.
Сначала на
0.
Сначала на  0 действует "ближайший" к нему оператор а+m;
это отвечает порождению частицы в состоянии т. Если п = т, то
последующее действие оператора а~п приводит опять к
0 действует "ближайший" к нему оператор а+m;
это отвечает порождению частицы в состоянии т. Если п = т, то
последующее действие оператора а~п приводит опять к  0,
т. е. а-пa+n
0,
т. е. а-пa+n 0=
0= 0· Если п<>т,
то а-пa+m
0· Если п<>т,
то а-пa+m 0=0, поскольку
невозможно уничтожение таких частиц, которых нет (оператор а-п описывает
уничтожение частиц в таких состояниях п, каких не возникает при действии
а+т на
0=0, поскольку
невозможно уничтожение таких частиц, которых нет (оператор а-п описывает
уничтожение частиц в таких состояниях п, каких не возникает при действии
а+т на  0. С учётом различных
состояний частиц перестановочные соотношения для операторов рождения и
уничтожения имеют следующий вид:
0. С учётом различных
состояний частиц перестановочные соотношения для операторов рождения и
уничтожения имеют следующий вид:
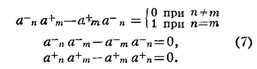
Однако существуют поля, для к-рых связь между произведением операторов
рождения и уничтожения, взятых в различном порядке, имеет др. вид: знак минус в
(7) заменяется на плюс (это наз. заменой коммутаторов на антикоммутатор ы),
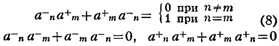
[эти соотношения также относят к классу перестановочных соотношений, хотя
они и не имеют вида (6)]. Операторы, подчиняющиеся соотношениям (8), необходимо
вводить для полей, кванты к-рых имеют полуцелый спин (т. е. являются
фермионами)
и вследствие этого подчиняются Паули принципу, согласно к-рому в
системе таких частиц (напр., электронов) невозможно существование двух или
более частиц в одинаковых состояниях (в состояниях с одинаковым набором всех
квантовых чисел). Действительно, построив вектор состояния, содержащего 2
частицы (двухчастичного состояния), а-пa+m 0,
нетрудно убедиться [учитывая (8)], что при n = m он равен самому
себе с обратным знаком; но это возможно только для величины, тождественно
равной нулю. T. о., если операторы рождения и уничтожения частиц удовлетворяют
перестановочным соотношениям (8), то состояния с двумя (или более) частицами,
имеющими одинаковые квантовые числа, автоматически исключаются. Такие частицы
подчиняются Ферми - Дирака статистике. Для полей же, кванты к-рых имеют
целый спин, операторы рождения и уничтожения частиц удовлетворяют соотношениям
(7); здесь возможны состояния с произвольным числом частиц, имеющих одинаковые
квантовые числа.
0,
нетрудно убедиться [учитывая (8)], что при n = m он равен самому
себе с обратным знаком; но это возможно только для величины, тождественно
равной нулю. T. о., если операторы рождения и уничтожения частиц удовлетворяют
перестановочным соотношениям (8), то состояния с двумя (или более) частицами,
имеющими одинаковые квантовые числа, автоматически исключаются. Такие частицы
подчиняются Ферми - Дирака статистике. Для полей же, кванты к-рых имеют
целый спин, операторы рождения и уничтожения частиц удовлетворяют соотношениям
(7); здесь возможны состояния с произвольным числом частиц, имеющих одинаковые
квантовые числа.
Наличие двух типов перестановочных соотношений имеет фундаментальное
значение, поскольку оно определяет два возможных типа статистик.
Необходимость введения некоммутирующих операторов для описания систем с
переменным числом частиц - типичная черта вторичного квантования.
Заметим, что "первичное квантование" также можно рассматривать как
переход от классич. механики, в к-рой координаты q и импульсы 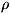 являются обычными
числами (т. е., конечно, qp =рq)> к такой теории, в к-рой q и
являются обычными
числами (т. е., конечно, qp =рq)> к такой теории, в к-рой q и 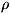 заменяются
некоммутирующими операторами: q->q, р->р, qp<>pq. Переход от
классич. теории поля к квантовой (напр., в электродинамике) производится
аналогичным методом, но только роль координат (и импульсов) должны при этом
играть величины, описывающие распределение поля во всём пространстве и во все
моменты времени. Так, в классич. электродинамике поле определяется значениями
напряжённостей электрического E и магнитного H полей (как функций координат и
времени). При переходе к квантовой теории E и H становятся операторами, к-рые
не коммутируют с оператором числа фотонов в поле.
заменяются
некоммутирующими операторами: q->q, р->р, qp<>pq. Переход от
классич. теории поля к квантовой (напр., в электродинамике) производится
аналогичным методом, но только роль координат (и импульсов) должны при этом
играть величины, описывающие распределение поля во всём пространстве и во все
моменты времени. Так, в классич. электродинамике поле определяется значениями
напряжённостей электрического E и магнитного H полей (как функций координат и
времени). При переходе к квантовой теории E и H становятся операторами, к-рые
не коммутируют с оператором числа фотонов в поле.
В квантовой механике доказывается, что если 2 к.-л. оператора не
коммутируют, то соответствующие им физ. величины не могут одновременно иметь
точные значения. Отсюда следует, что не существует такого состояния электромагнитного
поля, в к-ром были бы одновременно точно определёнными напряжённости поля и
число фотонов. Если, в силу физич. условий, точно известно число фотонов, то
совершенно неопределёнными (способными принимать любые значения) оказываются
напряжённости полей. Если же известны точно эти напряжённости, то
неопределённым является число фотонов. Вытекающая отсюда невозможность
одновременно положить равными нулю напряжённости поля и число фотонов и
является физич. причиной того, что вакуумное состояние не представляет собой
просто отсутствие поля, а сохраняет важные физич. свойства.
3. Полевые методы в квантовой теории многих частиц. Математич. методы К. т.
п. (как уже отмечалось) находят применение при описании систем, состоящих из
большого числа частиц: в физике твёрдого тела, атомного ядра и т. д. Роль
вакуумных состояний в твёрдом теле, напр., играют низшие энергетич. состояния,
в к-рые система переходит при минимальной энергии (т. е. при темп-ре Т->0).
Если сообщить системе энергию (напр., повышая её темп-ру), она перейдёт в
возбуждённое состояние. При малых энергиях процесс возбуждения системы можно
рассматривать как образование нек-рых элементарных возбуждений - процесс,
подобный порождению частиц в К. т. п. Отд. элементарные возбуждения в твёрдом теле
ведут себя подобно частицам - обладают определённой энергией, импульсом,
спином. Они наз. квазичастицами. Эволюцию системы можно представить как
столкновение, рассеяние, уничтожение и порождение квазичастиц, что и открывает
путь к широкому применению методов К. т. п. (см. Твёрдое тело). Одним из
наиболее ярких примеров, показывающих плодотворность методов К. т. п. в
изучении твёрдого тела, является теория сверхпроводимости.
4. Кванты - переносчики взаимодействия. В классич. электродинамике
взаимодействие между зарядами (и токами) осуществляется через поле: заряд
порождает поле и это поле действует на другие заряды. В квантовой теории
взаимодействие поля и заряда выглядит как испускание и поглощение зарядом
квантов поля - фотонов. Взаимодействие же между зарядами, напр, между двумя
электронами, в К. т. п. является результатом их обмена фотонами: каждый из
электронов испускает фотоны (кванты переносящего взаимодействие
электромагнитного поля), к-рые затем поглощаются др. электроном. Это
справедливо и для др. физич. полей: взаимодействие в К.т.п. - результат обмена
квантами поля.
В этой достаточно наглядной картине взаимодействия есть, однако, момент,
нуждающийся в дополнит, анализе. Пока взаимодействие не началось, каждая из
частиц является свободной, а свободная частица не может ни испускать, ни
поглощать квантов. Действительно, рассмотрим свободную неподвижную частицу
(если частица равномерно движется, всегда можно перейти к такой инерциальной
системе отсчёта, в к-рой она покоится). Запаса кинетич. энергии у такой
частицы нет, потенциальной - тоже, так что излучение энергетически невозможно.
Несколько более сложные рассуждения убеждают и в неспособности свободной
частицы поглощать кванты. Но если приведённые соображения справедливы, то,
казалось бы, неизбежен вывод о невозможности появления взаимодействий в К. т.
п.
Чтобы разрешить этот парадокс, нужно учесть, что рассматриваемые частицы
являются квантовыми объектами и что для них существенны неопределённостей
соотношения. Эти соотношения связывают неопределённости координаты частицы
( x) и
её импульса (
x) и
её импульса ( p):
p):
 x·
x· p>>h/2
(9) (где h = h/2
p>>h/2
(9) (где h = h/2 ). Имеется и второе соотношение - для неопределённостей
энергии
). Имеется и второе соотношение - для неопределённостей
энергии  E и специфич. времени
E и специфич. времени  ? данного физич. процесса (т.
е. времени, в течение к-рого процесс протекает):
? данного физич. процесса (т.
е. времени, в течение к-рого процесс протекает):
 E·
E· t~h. (10)
t~h. (10)
Если рассматривается взаимодействие между частицами посредством обмена
квантами поля (это поле часто наз. промежуточным), то за  t естественно
принять продолжительность такого акта обмена. Вопрос о возможности испускания
кванта свободной частицей отпадает: энергия частицы, согласно (10), не является
точно определённой; при наличии же квантового разброса энергий
t естественно
принять продолжительность такого акта обмена. Вопрос о возможности испускания
кванта свободной частицей отпадает: энергия частицы, согласно (10), не является
точно определённой; при наличии же квантового разброса энергий  E законы
сохранения энергии и импульса не препятствуют более ни испусканию, ни
поглощению переносящих взаимодействие квантов, если только эти кванты имеют
энергию ~
E законы
сохранения энергии и импульса не препятствуют более ни испусканию, ни
поглощению переносящих взаимодействие квантов, если только эти кванты имеют
энергию ~  Eи существуют в течение промежутка времени
Eи существуют в течение промежутка времени  t ~ h/
t ~ h/ E.
E.
Проведённые рассуждения не только устраняют указанный выше парадокс, но и
позволяют получить важные физич. выводы. Рассмотрим взаимодействие частиц в
ядрах атомов. Ядра состоят из нуклонов, т. е. протонов и нейтронов.
Экспериментально установлено, что вне пределов ядра, т. е. на расстояниях,
больших примерно 10-12 см, взаимодействие неощутимо, хотя в
пределах ядра оно заведомо велико. Это позволяет утверждать, что радиус
действия ядерных сил имеет порядок L ~ 10-12 см. Именно
такой путь пролетают, следовательно, кванты, переносящие взаимодействие между
нуклонами в атом-вых ядрах. Время пребывания квантов "в пути", даже
если принять, что они движутся с максимально возможной скоростью (со скоростью
света с), не может быть меньше, чем  t ~ L/C. Согласно
предыдущему, квантовый разброс энергии
t ~ L/C. Согласно
предыдущему, квантовый разброс энергии  E взаимодействующих
нуклонов получается равным
E взаимодействующих
нуклонов получается равным  E~ ~h/
E~ ~h/ t~hc/L. B пределах этого
разброса и должна лежать энергия кванта - переносчика взаимодействия. Энергия
каждой частицы массы т складывается из её энергии покоя, равной mc2,
и кинетич. энергии, растущей по мере увеличения импульса частицы. При не
слишком быстром движении частиц кинетич. энергия мала по сравнению с тс2,
так что можно принять
t~hc/L. B пределах этого
разброса и должна лежать энергия кванта - переносчика взаимодействия. Энергия
каждой частицы массы т складывается из её энергии покоя, равной mc2,
и кинетич. энергии, растущей по мере увеличения импульса частицы. При не
слишком быстром движении частиц кинетич. энергия мала по сравнению с тс2,
так что можно принять  E~mc2. Тогда из предыдущей
формулы следует, что квант, переносящий взаимодействия в ядре, должен иметь
массу порядка т~h/Lc. Если подставить в эту формулу численные значения
величин, то оказывается, что масса кванта ядерного поля примерно в 200-300 раз
больше массы электрона.
E~mc2. Тогда из предыдущей
формулы следует, что квант, переносящий взаимодействия в ядре, должен иметь
массу порядка т~h/Lc. Если подставить в эту формулу численные значения
величин, то оказывается, что масса кванта ядерного поля примерно в 200-300 раз
больше массы электрона.
Такое полукачествениое рассмотрение
привело в 1935 япон. физика-теоретика X.
Юкава к предсказанию новой частицы; позже эксперимент подтвердил
существование такой частицы, названной пи-мезоном. Этот блистательный результат
значительно укрепил веру в правильность квантовых представлений о
взаимодействии как об обмене квантами промежуточного поля, веру, сохраняющуюся
в значит. степени до сих пор, несмотря на то, что количественную мезонную
теорию ядерных сил построить всё ещё не удалось.
Если рассмотреть 2 настолько тяжёлые частицы, что их можно считать классич.
материальными точками, то взаимодействие между ними, возникающее в результате
обмена квантами массы т, приводит к появлению потенциальной энергии
взаимодействия частиц, равной
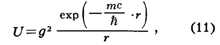
где r - расстояние между частицами, a g - т. н. константа
взаимодействия рассматриваемых частиц с полем квантов, переносящих
взаимодействие (или иначе - заряд, соответствующий данному виду
взаимодействия).
Если применить эту формулу к случаю, когда переносчиками взаимодействия
являются кванты электромагнитного поля - фотоны, масса покоя которых m = О, и
учесть, что вместо g должен стоять электрический заряд е, то
получится хорошо известная энергия кулоновского взаимодействия двух зарядов: Uэл
= е2/r.
5. Графический метод описания процессов. Хотя в К. т. п.
рассматриваются типично квантовые объекты, можно дать процессам взаимодействия
и превращения частиц наглядные графич. изображения. Такого рода графики впервые
были введены амер. физиком P. Фейнманом и носят его имя. Графики, или
диаграммы, Фейнмана, внешне похожи на изображение путей движения всех
участвующих во взаимодействии частиц, если бы эти частицы были классическими
(хотя ни о каком классич. описании не может быть и речи). Для изображения
каждой свободной частицы вводят нек-рую линию (к-рая, конечно, есть всего лишь
графич. символ распространения частицы): так, фотон изображают волнистой
линией, электрон - сплошной. Иногда на линиях ставят стрелки, условно
обозначающие "направление распространения" частицы. Ниже даны примеры
таких диаграмм.
На рис. 1 изображена диаграмма, соответствующая рассеянию фотона на
электроне: в начальном состоянии присутствуют один электрон и один фотон; в
точке l они встречаются и происходит поглощение фотона электроном; в точке 2
появляется (испускается электроном) новый, конечный фотон. Это - одна из
простейших диаграмм Комптон-эффекта.
Рис. 1.
Диаграмма на рис. 2 отражает обмен фотоном между двумя электронами: один
электрон в точке 1 испускает фотон, к-рый затем в точке 2 поглощается
вторым электроном. Как уже говорилось, такого рода обмен приводит к появлению
взаимодействия; т. о., данная диаграмма изображает элементарный акт
электромагнитного взаимодействия двух электронов. Более сложные диаграммы,
соответствующие такому взаимодействию, должны учитывать возможность обмена
неск. фотонами; одна из них изображена на рис. 3.
Рис, 2.
Рис. 3.
В приведённых примерах проявляется нек-рое общее свойство диаграмм,
описывающих взаимодействие между электронами и фотонами: все диаграммы
составляются из простейших элементов- вершинных частей, или вершин, одна из
к-рых (рис. 4) представляет испускание, а другая (рис. 5) - поглощение фотона
электроном.
Рис, 4.
Рис. 5.
Оба эти процесса в отдельности запрещены законами сохранения энергии и
импульса. Однако если такая вершина входит как составная часть в нек-рую более
сложную диаграмму, как это было в рассмотренных примерах, то квантовая
неопределённость энергии, возникающая из-за того, что на промежуточном этапе
нек-рая частица существует короткое время  t, снимает энергетич. запрет.
t, снимает энергетич. запрет.
Частицы, к-рые рождаются, а затем поглощаются на промежуточных этапах
процесса, наз. виртуальными (в отличие от реальных частиц, существующих
достаточно длительное время). На рис. 1 это - виртуальный электрон, возникающий
в точке l и исчезающий в точке 2, на рис. 2 - виртуальный фотон и т. д.
Часто говорят, что взаимодействие переносится виртуальными частицами. Можно
несколько условно принять, что частица виртуальна, если квантовая
неопределённость её энергии  E порядка ср. значения энергии частицы E
и её можно называть реальной, если
E порядка ср. значения энергии частицы E
и её можно называть реальной, если  E<<E (для
относительно медленно движущихся частиц с неравной нулю массой покоя т это
условие сведётся к неравенству
E<<E (для
относительно медленно движущихся частиц с неравной нулю массой покоя т это
условие сведётся к неравенству 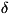 <<mc2).
<<mc2).
Диаграммы Фейнмана не только дают наглядное изображение процессов, но и
позволяют при помощи определённых математич. правил вычислять вероятности этих
процессов. Не останавливаясь детально на этих правилах, отметим, что в каждой
вершине осуществляется элементарный акт взаимодействия, приводящий к
превращению частиц (т. е. к уничтожению одних частиц и рождению других).
Поэтому каждая из вершин даёт вклад в амплитуду вероятности процесса, причём
этот вклад пропорционален константе взаимодействия тех частиц (или полей),
линии к-рых встречаются в вершине. Во всех приведённых выше диаграммах такой
константой является электрич. заряд е. Чем больше вершин содержит
диаграмма процесса, тем в более высокой степени входит заряд в соответствующее
выражение для амплитуды вероятности процесса. Так, амплитуда вероятности,
соответствующая диаграммам 1 и 2 с двумя вершинами, квадратична по заряду (~е2),
а диаграмма 3 (содержащая 4 вершины) приводит к амплитуде, пропорциональной
четвёртой степени заряда (~е4). Кроме того, в каждой вершине нужно
учитывать законы сохранения (за исключением закона сохранения энергии - его
применимость лимитируется квантовым соотношением неопределённостей для энергии
и времени): импульса (отвечающий каждой вершине акт взаимодействия может
произойти в любой точке пространства, т. е. неопределённость координаты  x=oo, и,
следовательно, импульс определён точно), электрич. заряда и т. д., а также
вводить множители, зависящие от спинов частиц.
x=oo, и,
следовательно, импульс определён точно), электрич. заряда и т. д., а также
вводить множители, зависящие от спинов частиц.
Выше были рассмотрены лишь простейшие виды диаграмм для нек-рых процессов.
Эти диаграммы не исчерпывают всех возможностей. Каждую из простейших диаграмм
можно дополнить бесконечным числом всё более усложняющихся диаграмм, включающих
всё большее число вершин. Напр., приведённую на рис. 1 "низшую"
диаграмму Комптон-эффекта можно усложнять, выбирая произвольно пары точек на
электронных линиях и соединяя эти пары волнистой фотонной линией (рис. 6), т.
к. число промежуточных (виртуальных) фотонных линий не лимитировано.
Рис. 6.
6. Взаимодействие частицы с вакуумом электромагнитного поля. Излучение
атома. На приведённых графиках взаимодействия двух электронов (рис. 2 и 3)
каждый из фотонов порождается одним и поглощается др. электроном. Однако
возможен и др. процесс (рис. 7):
Рис. 7.
фотон, испущенный электроном в точке
l, через нек-рое время поглощается им
же в точке 2. Поскольку обмен квантами обусловливает взаимодействие, то
такой график также является одной из простейших диаграмм взаимодействия, но
только взаимодействия электрона с самим собой, или, что то же самое, с
собственным полем. Этот процесс можно также назвать взаимодействием электрона с
полем виртуальных фотонов, или с фотонным вакуумом (последнее назв.
определяется тем, что реальных фотонов здесь нет). T. о., собственное
электромагнитное (электростатическое) поле электрона создаётся испусканием и
поглощением (этим же электроном) фотонов. Такие взаимодействия электрона с
вакуумом обусловливают экспериментально наблюдаемые эффекты (что свидетельствует
о реальности вакуума). Самый значит, из этих эффектов - излучение фотонов
атомами. Согласно квантовой механике, электроны в атомах располагаются на
квантовых энергетич. уровнях, а излучение фотона происходит при переходе
электрона с одного (высшего) уровня на другой, обладающий меньшей энергией.
Однако квантовая механика оставляет открытым вопрос о причинах таких переходов,
сопровождающихся т. н. спонтанным ("самопроизвольным") излучением;
более того, каждый уровень выглядит здесь как вполне устойчивый. Физ. причиной
неустойчивости возбуждённых уровней и спонтанных квантовых переходов, согласно
К. т. п., является взаимодействие атома с фотонным вакуумом. Образно говоря,
взаимодействие с фотонным вакуумом трясёт, раскачивает атомный электрон - ведь
при испускании и поглощении каждого виртуального фотона электрон испытывает
толчок, отдачу; без этого электрон двигался бы устойчиво по орбите (ради
наглядности, примем этот полуклассич. образ). Один из таких толчков заставляет
электрон "упасть" на более устойчивую, т. е. обладающую меньшей
энергией, орбиту; при этом освобождается энергия, к-рая идёт на возбуждение
электромагнитного поля, т. е. на образование реального фотона.
То, что взаимодействие электронов с фотонным вакуумом обусловливает саму
возможность переходов в атомах (и в др. излучающих фотоны системах), а значит,
и излучение,- это наибольший по масштабу и по значению эффект в квантовой
электродинамике. Однако есть и другие, гораздо более слабые, "вакуумные
эффекты", очень важные в принципиальном отношении; нек-рые из них будут
обсуждены в разделе III.
7. Электронно-позитронный вакуум. В 1928 англ. физик П. Дирак, решая
задачу о релятивистском квантовом ур-нии движения электрона, предсказал, что у
электрона должен быть "двойник" - античастица, отличающаяся от
электрона знаком электрич. заряда. Такая частица, названная позитроном, вскоре
была обнаружена экспериментально. Позитрон не может порождаться в одиночку -
это исключается, напр., законом сохранения электрич. заряда. Электроны и
позитроны могут появляться и исчезать (аннигилировать) лишь парами. Для
рождения электронно-позитронной пары необходима достаточно большая энергия (не
меньше удвоенной энергии покоя электрона), к-рую может поставить, напр.,
"жёсткий", т. е. имеющий большую энергию, фотон (гамма-квант),
налетающий на к.-л. заряженную частицу. Однако рождение пары может происходить
и виртуально. Тогда образовавшаяся пара, просуществовав очень недолгое
время  t, аннигилирует. Квантовый разброс энергий
t, аннигилирует. Квантовый разброс энергий  E~h/
E~h/ t,
если
t,
если  t очень мало, делает такой процесс энергетически разрешённым.
t очень мало, делает такой процесс энергетически разрешённым.
Графически процесс рождения и аннигиляции виртуальной
электронно-позитронной пары изображён на рис. 8:
фотон в точке
l исчезает, порождая пару, к-рая затем аннигилирует в точке 2,
в результате чего вновь образуется фотон. (Позитрон изображается такой же
сплошной линией, как и электрон, на к-рой условно стрелка направлена в
противоположную сторону, т. е. "вспять" во времени.)
То обстоятельство, что электроны и позитроны не могут появляться и исчезать
порознь, а возникают и уничтожаются только парами, показывает глубокое физ.
единство электронно-позитронного поля. Электронное и позитронное поля
выглядят как обособленные лишь до тех пор, пока не рассматриваются процессы,
связанные с изменением числа электронов и позитронов.
Античастицы есть не только у электронов. Установлено, что каждая частица
(кроме т. н. истинно нейтральных частиц, напр., фотона и нейтрального пи-мезона)
имеет свою античастицу. Процессы, подобные виртуальному рождению и аннигиляции
электронно-позитронных пар, существуют для любых пар частица-античастица.
III. Метод возмущений в квантовой теории поля
1. Математическая и физическая частица. Полевая масса. Перенормировка
массы. Для описания взаимодействующих полей часто применяется следующий метод
(к-рый фактически уже был использован выше). Сначала рассматриваются кванты
свободных полей (частицы). Это т. н. нулевое приближение, в к-ром
взаимодействие вообще не учитывается. Затем в рассмотрение вводится
взаимодействие - частицы перестают быть независимыми, появляется возможность их
рассеяния, порождения и уничтожения в результате взаимодействия. Последоват.
увеличение числа учитываемых процессов, обусловленных взаимодействием,
математически достигается применением т. н. метода возмущений. Ввиду большой
роли, к-рую играет этот метод в теории, обсудим его физич. смысл подробнее.
Процедура последоват. уточнения вклада от взаимодействий фактически
применяется и в классич. электродинамике. Поясним это на примере электрона н
создаваемого им электромагнитного поля. Электрон выступает в теории как
носитель определённой массы m0. Ho так как он порождает
электромагнитное поле, имеющее энергию Eэл, а следовательно
(согласно релятивистскому соотношению E = mc2), и массу Eэл/с2,
то, ускоряя электрон, нужно преодолевать и инерцию его электромагнитного (в
простейшем случае - кулоновского) поля.
T. о., вводя в рассмотрение взаимодействие между электроном и
электромагнитным полем, к "неполевой", или "затравочной",
массе m0 необходимо добавить "полевую" часть массы mпол
= Eэл/С2. Вычисление полевой массы для точечной
частицы (а именно такими приходится считать рассматриваемые в нулевом
приближении "затравочные" частицы) приводит к лишённому физического
смысла результату: mпол оказывается бесконечно большой. Действительно,
энергия кулоновского поля частицы, имеющей заряд е и протяжённость а,
равна Eкул = ke2/a (k - множитель порядка
единицы, численное значение к-рого зависит от распределения заряда); переход к
точечной частице (а -> О) приводит Eкул -> °° .
Бесконечное значение (расходимость) полевой массы (хотя и в несколько
изменённом, "ослабленном" виде) сохраняется и при переходе от
классич. теории к квантовой. Больше того, появляются и расходимости др. типов.
Анализ встречающихся здесь трудностей привёл к появлению идеи т.н.
перенормировок. Деление массы на полевую и неполевую возникает (как видно из
предыдущего) из-за принятого метода рассмотрения: вначале вводится свободная
"затравочная" частица, а затем "включается" взаимодействие.
В эксперименте, конечно, нет ни "затравочной", ни полевой массы, там
проявляется только общая масса частицы. В теории, что очень существенно, эти
массы также выступают лишь в сумме, а не порознь. Объединение полевой и
неполевой массы и использование для суммарной массы значения, получаемого не
теоретически, а из опыта, наз. перенормировкой массы.
Традиционный путь построения теории в рамках метода теории возмущений таков:
вначале формулируется теория свободных (не взаимодействующих) частиц, а затем
вводится в рассмотрение взаимодействие между ними. Так, напр., сначала строится
теория свободных электронов (или электронно-позитрон-ного поля), а затем
рассматривается взаимодействие этих "математических", или
"голых", электронов с электромагнитным полем. Однако реально
существующие в природе "физические" электроны, в отличие от
"математических", всегда взаимодействуют с фотонами (хотя бы с
виртуальными), и "выключить" это взаимодействие можно только
умозрительно. Важной частью идеи перенормировок является указание на
необходимость построения теории, в к-рой выступали бы не математические, а
физич. частицы.
Любопытно, что природа в какой-то мере даёт возможность увидеть различие
между частицей со "включённым" и "выключенным"
электромагнитным взаимодействием. Напр., известны три пи-мезона: с
положительным ( +), отрицательным (
+), отрицательным ( -) и нулевым (
-) и нулевым ( °) элект-рич. зарядами. Это различные
зарядовые состояния одной и той же частицы. Заряженные мезоны (
°) элект-рич. зарядами. Это различные
зарядовые состояния одной и той же частицы. Заряженные мезоны ( + и
+ и  -) имеют большую
массу, чем нейтральный (
-) имеют большую
массу, чем нейтральный ( °); очевидно, здесь проявляется добавка, обусловленная полевой
(электромагнитной) массой, хотя теория пока не может достаточно чётко объяснить
этого явления количественно.
°); очевидно, здесь проявляется добавка, обусловленная полевой
(электромагнитной) массой, хотя теория пока не может достаточно чётко объяснить
этого явления количественно.
В К. т. п. процесс "облачения" мате-матич. частицы, т. е. её
превращение в физическую, выглядит сложнее, чем в классич. электродинамике, где
всё сводится к "пристёгиванию" к частице кулоновского
"шлейфа". В квантовой теории физич. частица отличается от
математической "шубой", гораздо более сложной по своему строению: её
образуют "облака" рождаемых и вслед за тем поглощаемых частицей
виртуальных квантов. Это могут быть кванты любого из полей, с к-рыми частица
находится во взаимодействии (электромагнитного, электронно-позитронного,
мезонного и т. д.). "Шуба" не есть нечто застывшее,- образующие её
кванты непрерывно порождаются и поглощаются. "Шуба" пульсирует, т. е.
несущая её частица как бы проводит часть времени в "облачённом", а
часть - в "голом" состоянии. Какую именно часть - это определяется
степенью интенсивности взаимодействий. Напр., мезонные взаимодействия нуклонов
более чем в сто раз интенсивнее электромагнитных; это позволяет предполагать,
что мезонное "одеяние" протона более чем в сто раз "плотнее"
электромагнитного. Это, может быть, позволяет понять, почему квантовая теория
электромагнитных процессов даже при далеко не полном учёте вакуумных эффектов
блестяще согласуется с экспериментом, тогда как мезонная теория не добилась
таких успехов. В квантовой электродинамике можно ограничиться рассмотрением
процессов с малым числом виртуальных фотонов и виртуальных
электронно-позитронных пар, что соответствует учёту небольшого числа
"низших" поправок по методу теории возмущений; в мезон-ной теории это
не приводит к успеху, что и создаёт трудности, к-рые будут рассмотрены в
разделе IV.
Все приведённые выше рассуждения о "шубе" частиц являются, строго
говоря, полуинтуитивными и не могут быть пока переведены на язык точной теории.
Однако они могут быть полезными хотя бы потому, что помогают уяснить отличие
математической частицы от физической и понять, что описание последней является
далеко не простой задачей.
2. Поляризация вакуума. Перенормировка заряда. Электрическое (и в
первую очередь кулоновское) поле заряженной частицы оказывает влияние на
распределение виртуальных электронно-позитронных пар (и пар любых других
заряженных частиц-античастиц). Реальный электрон притягивает виртуальные
позитроны и отталкивает виртуальные электроны. Это должно приводить к явлениям,
напоминающим поляризацию среды, в к-рую вносится заряженная частица. Для
описания таких явлений опять применим метод возмущений.
Поляризация электронно-позитронного вакуума (принято использовать
подсказываемый приведённой аналогией термин) является чисто квантовым эффектом,
вытекающим из К. т. п. Эта поляризация приводит к тому, что электрон
оказывается окружённым плотным слоем позитронов из виртуальных пар, так что
эффективный заряд электрона должен существенно изменяться. Возникает
экранировка заряда, т. е. его эффективное уменьшение. Если рассматривать
"затравочные" частицы как точечные, то экранировка оказывается
полной, т. е. эффективный заряд нулевым (проблема "заряда нуль"). Для
преодоления этой трудности используется идея перенормировки заряда. Здесь почти
дословно повторяются приводившиеся.при обсуждении перенормировки массы
аргументы. Назовём "затравочным" заряд, к-рый был бы у частицы, если
бы исчезло взаимодействие с электронно-позитронным вакуумом (будем говорить
только о нём, хотя, конечно, нужно учитывать и влияние виртуальных пар др.
полей). Наличие такого взаимодействия приводит к появлению "поправки"
к заряду. Корректно вычислять её физики не умеют, как не умеют и определять
"затравочный" заряд. Но поскольку эти две части заряда ни в
эксперименте, ни в теории не выступают порознь, можно обойти трудность,
подставляя на место общего заряда величину, непосредственно взятую из опыта.
Эта процедура наз. перенормировкой заряда. Перенормировки заряда и массы не
решают проблем, возникающих в теории точечных частиц, они лишь изолируют эти
проблемы на нек-ром этапе теории и (что весьма важно) дают возможность выделить
конечные наблюдаемые части из бесконечных значений для нек-рых величин,
характеризующих физич. частицы.
3. Некоторые наблюдаемые "вакуумные"· эффекты. Существует
возможность экспериментально наблюдать влияние "вакуума" на частицы.
Оказывается, что "шуба" физич. частиц зависит от того, какие внешние
поля действуют на эту частицу. Иначе говоря, полевые добавки к энергии частицы
зависят от её состояния. Общая полевая энергия, как уже говорилось, получается
в теории точечных частиц бесконечно большой, но из этой бесконечно большой
величины можно выделить конечную часть, к-рая меняется в зависимости от
состояния частицы и поэтому может быть обнаружена на опыте.
Лэмбовский сдвиг уровня. В атоме водорода (и нек-рых др. лёгких
атомах) имеются два состояния - 2S½ и 2Р½, энергии
к-рых, согласно квантовой механике, должны совпадать. В то же время картина
движения электронов в этих состояниях различна. Образно говоря, S-электрон
(электрон в S-состоянии) проводит осн. часть своего времени вблизи ядра, а
Р-электрон в среднем находится на большем удалении от ядра. Поэтому S-электрон
в среднем находится в более сильном поле, чем Р-электрон. Это приводит к тому,
что добавки к энергии за счёт взаимодействия с фотонным вакуумом у Р-электрона
и у S-электрона оказываются разными, что можно пояснить наглядно. Как уже
говорилось, взаимодействие с вакуумом как бы раскачивает, трясёт электрон.
Вместо того чтобы двигаться по нек-рой устойчивой, напр., круговой, орбите
радиуса г (примем опять этот классич. образ), электрон начинает
хаотически отклоняться то в одну, то в другую сторону от этой орбиты. При
отклонении в каждую сторону на  r энергия меняется по-разному. Действительно,
кулоновская энергия электрона в поле ядра меняется по закону: Eпотенц.~1/r
; при увеличении r на
r энергия меняется по-разному. Действительно,
кулоновская энергия электрона в поле ядра меняется по закону: Eпотенц.~1/r
; при увеличении r на  r энергия изменяется на величину
r энергия изменяется на величину
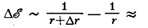
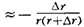
, а при уменьшении r на  r- на величину
r- на величину
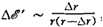
, т. е. абс. значение  E' больше, чем
E' больше, чем  E. Это
приводит к тому, что "вакуумное дрожание" электрона меняет значение
его потенциальной энергии. Особенно заметно это изменение там, где сама
потенциальная энергия велика и быстро меняется с изменением r, т. е. вблизи
ядра. T. о., для S-электронов вакуумные добавки к энергии (они наз.
радиационными поправками) должны быть больше, чем для Р-электронов, что и
"раздвигает" уровни их энергии, к-рые без этого совпадали бы.
Величина расщепления, называемая лэмбовским сдвигом уровней (впервые он был
теоретически объяснён X. Бете и обнаружен экспериментально в 1947 амер.
физиками У. Лэмбом и P. Ризерфордом), согласно К. т. п., оказывается
равной (если выражать её в единицах частоты
E. Это
приводит к тому, что "вакуумное дрожание" электрона меняет значение
его потенциальной энергии. Особенно заметно это изменение там, где сама
потенциальная энергия велика и быстро меняется с изменением r, т. е. вблизи
ядра. T. о., для S-электронов вакуумные добавки к энергии (они наз.
радиационными поправками) должны быть больше, чем для Р-электронов, что и
"раздвигает" уровни их энергии, к-рые без этого совпадали бы.
Величина расщепления, называемая лэмбовским сдвигом уровней (впервые он был
теоретически объяснён X. Бете и обнаружен экспериментально в 1947 амер.
физиками У. Лэмбом и P. Ризерфордом), согласно К. т. п., оказывается
равной (если выражать её в единицах частоты  ): для водорода 1057,77 Мгц, для
дейтерия 1058,9 Мгц, для гелия 14046,3 Мгц (переход к энергетич.
единицам - эргам - производится по формуле E = hv, где
): для водорода 1057,77 Мгц, для
дейтерия 1058,9 Мгц, для гелия 14046,3 Мгц (переход к энергетич.
единицам - эргам - производится по формуле E = hv, где  выражено в гц).
Эти значения находятся в таком хорошем соответствии с данными эксперимента,
что дальнейшее увеличение экспериментальной точности приведёт уже к обнаружению
эффектов, обусловленных не электромагнитными взаимодействиями, а т. н. сильными
взаимодействиями.
выражено в гц).
Эти значения находятся в таком хорошем соответствии с данными эксперимента,
что дальнейшее увеличение экспериментальной точности приведёт уже к обнаружению
эффектов, обусловленных не электромагнитными взаимодействиями, а т. н. сильными
взаимодействиями.
Аномальный магнитный момент. Не менее замечательна точность, с к-рой
вычисляется аномальный магнитный момент электрона, также отражающий
"вакуумные" (радиационные) влияния на эту частицу. Из квантовой
теории электрона П. Дирака следует, что электрон должен обладать магнитным
моментом

Но это относится к "голому" электрону. Процесс его
"облачения" меняет магнитный момент. Включив в рассмотрение
взаимодействие электрона с вакуумом, нужно прежде всего заменить заряд (е0)
и
массу (т0) идеализированной матем. частицы на физич. значения
этих величин:
m0 -> тфизич., e0 -> ефизич.
Однако этим не исчерпывается учёт наблюдаемых эффектов. Магнитный момент -
величина, обусловливающая взаимодействие покоящейся частицы с внешним магнитным
полем. Поправки, появляющиеся в выражении для энергии такого взаимодействия,
естественно интерпретировать как результат появления "вакуумных"
добавок к магнитному моменту (эти добавки, впервые теоретически исследованные
Ю. Швингером, и наз. аномальным магнитным моментом). Аномальный
магнитный момент электрона вычислен и измерен с высокой точностью, о чём можно
судить по следующим данным
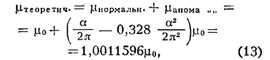
где 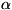 - т. н. постоянная тонкой структуры, равная
- т. н. постоянная тонкой структуры, равная
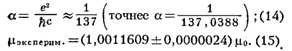
Здесь опять наблюдается поразительное совпадение измеренного магнитного
момента электрона и его значения, полученного на основе К. т. п.
Рассеяние света на свете. Существуют и др. описываемые К. т. п. эффекты.
Ограничимся рассмотрением ещё одного эффекта, к-рый предсказывается К. т. п.
Известно, что для электромагнитных волн справедлив принцип суперпозиции:
электромагнитные волны, накладываясь, не оказывают друг на друга никакого влияния.
Этот принцип наложения волн без взаимных искажений переходит из классич. теории
в квантовую, где он принимает форму утверждения об отсутствии взаимодействия
между фотонами. Однако положение меняется, если учесть эффекты, обусловленные
электронно-позитронным вакуумом.
Диаграмма, изображённая на рис. 9, соответствует след, процессу: в начальном
состоянии имеется два фотона; один из них в точке l исчезает, породив
виртуальную электронно-позитронную пару; второй фотон поглощается одной из
Рис. 9
частиц этой пары (на приведённой диаграмме - позитроном) в точке 2. Затем
появляются конечные фотоны: один из них рождается в точке 3 виртуальным
электроном, а другой возникает в результате аннигиляции пары в точке 4. Эта
диаграмма (и бесчисленное множество других, более сложных) показывает, что
благодаря виртуальным электронно-позитронным парам должно появляться
взаимодействие между фотонами, т. е. принцип суперпозиции должен нарушаться.
Нарушения должны проявляться в таких процессах, как рассеяние света на свете
(однако эффект этот настолько мал, что его ещё не удалось наблюдать на опыте).
Вне экспериментальных возможностей лежит пока и имеющий неск. большую
вероятность процесс рассеяния фотонов на внешнем электростатич. поле. Но успехи
квантовой электродинамики настолько велики, что не приходится сомневаться в
достоверности и этих её предсказаний.
Кроме указанных эффектов, "высшие" поправки, к-рые вычисляются по
методу возмущений (радиационные поправки), появляются в процессах рассеяния
заряженных частиц и в нек-рых др. явлениях.
IV. Трудности и проблемы квантовой теории поля
1. Успех, нуждающийся в объяснении. Успехи квантовой электродинамики, о к-рых говорилось выше, впечатляющи, но
не вполне объяснимы. Эти успехи связаны с анализом только простейших, низших
диаграмм Фейнмана, учитывающих лишь небольшое число виртуальных частиц, или -
на математич. языке - низшие приближения теории возмущений. К каждой из таких
диаграмм можно добавлять (рассматривая более высокие приближения) бесчисленное
число всё более усложняющихся диаграмм высших порядков, включающих всё большее
число внутр. линий (каждая такая внутр. линия отвечает виртуальной частице).
Правда, в такие усложнённые диаграммы будет входить всё увеличивающееся число
вершин, каждая же вершина вносит в выражение для амплитуды вероятности процесса
множитель е, точнее e/(hc)½. Поскольку внутренние
линии имеют два конца (две вершины), добавление каждой внутр. линии, грубо
говоря, изменяет амплитуду в е2/hс~1/137 раз. Если записать
амплитуду в виде суммы членов с возрастающими степенями величины 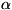 = e2/hc
(математически построение такой суммы, или ряда, и соответствует применению
метода теории возмущений), то каждому следующему члену будет соответствовать
диаграмма Фейнмана со всё большим числом внутр. линий. Каждый член ряда должен
быть поэтому примерно на два порядка (в сто раз) меньше предыдущего. Поэтому,
казалось бы, действительно, высшие диаграммы дают ничтожный вклад и могут быть
отброшены. Однако более внимательное рассмотрение показывает, что, поскольку
число таких отброшенных диаграмм бесконечно велико, оценка их вклада не проста
и не очевидна. Задача усложняется ещё и тем, что се выступает в комбинации с
множителем, пропорциональным логарифму энергии, так что при высоких энергиях
метод возмущений оказывается неэффективным.
= e2/hc
(математически построение такой суммы, или ряда, и соответствует применению
метода теории возмущений), то каждому следующему члену будет соответствовать
диаграмма Фейнмана со всё большим числом внутр. линий. Каждый член ряда должен
быть поэтому примерно на два порядка (в сто раз) меньше предыдущего. Поэтому,
казалось бы, действительно, высшие диаграммы дают ничтожный вклад и могут быть
отброшены. Однако более внимательное рассмотрение показывает, что, поскольку
число таких отброшенных диаграмм бесконечно велико, оценка их вклада не проста
и не очевидна. Задача усложняется ещё и тем, что се выступает в комбинации с
множителем, пропорциональным логарифму энергии, так что при высоких энергиях
метод возмущений оказывается неэффективным.
Если в квантовой электродинамике данная проблема может показаться не очень
актуальной, т. к. здесь теория блестяще описывает опыт, то в теориях др. полей
положение иное.
2. Проблема сильных взаимодействий. Теория сильных взаимодействий начала развиваться по аналогии с квантовой
электродинамикой, только роль переносчиков взаимодействия приписывалась, как
уже говорилось выше, пи-мезонам - частицам, обладающим массой покоя, примерно в
двести раз превосходящей массу покоя электрона. Однако здесь выявилось
обстоятельство, принципиально отличающее электродинамику от мезодинамики:
константа взаимодействия д, т. е. величина, играющая роль заряда в
сильных взаимодействиях, относительно велика, и вместо e2/hc ~
1/137 << 1 в мезодинамике появляется величина g2/hc>1. Поэтому
те аргументы, к-рые в электродинамике в какой-то степени оправдывают
отбрасывание высших диаграмм (т. е. использование низших приближений теории
возмущений), в мезодинамике теряют силу. Не удивительно, что учёт только низших
диаграмм в случае сильно взаимодействующих частиц не согласуется с опытом.
Иначе говоря, метод возмущений для вычисления амплитуды вероятности здесь
неприменим.
В К. т. п. сложилась довольно своеобразная ситуация: ур-ния для
взаимодействующих полей написаны уже много лет назад, найден, в принципе,
способ выделить то, что отвечает физич. частицам, и в то же время точно решать
эти ур-ния теоретики не умеют. Приближённые же методы, в первую очередь метод
теории возмущений, далеко не всегда пригодны. Но, не зная точного решения
ур-ний К. т. п., трудно судить с уверенностью, хороши ли эти уравнения, а
значит, и те физич. представления, на к-рых они основаны.
Трудности решения ур-ний К. т. п. порождают не только
"технические" проблемы. Метод решения в значит, мере определяет те
физич. образы, с к-рыми оперирует теория. Что такое, напр.,
"математические" частицы и процедура их "облачения", о
к-рой говорилось выше? Все эти представления продиктованы теорией возмущений: в
нулевом приближении взаимодействие вообще не учитывается (отсюда -
"голые" частицы), в следующих - взаимодействие учитывается введением
одной, двух и т. д. виртуальных частиц; так возникает картина постепенного
"обрастания" частицы облаком виртуальных квантов. Но в природе нет
никаких "математических" частиц, все частицы -
"физические",
именно их должна описывать теория. Хотя в теории перенормировок выдвигается
именно такая программа, конкретные вычисления заставляют возвращаться к теории
возмущений (отметим, что в электродинамике доказывается принципиальная
возможность провести перенормировки в любом приближении).
3. Проблема перенормируемости. Анализ трудностей теории. До появления идеи
перенормировок К. т. п. не могла рассматриваться как непротиворечивое
построение, поскольку в ней появлялись бессмысленные бесконечно большие
значения (расходимости) для нек-рых физич. величин и отсутствовало понимание
того, что же с ними делать. Идея перенормировок не только объяснила наблюдаемые
эффекты, но одновременно придала всей теории черты логич. замкнутости, устранив
из неё расходимости.
Образно говоря, был предложен метод учёта изменений "шубы" физич.
частиц в зависимости от внешних условий и количеств, исследования связанных с
этим эффектов. В то же время само "облачение" частицы выпадает из
рассмотрения. Частица рассматривается как целое в её внешних проявлениях, т. е.
во взаимодействии с др. частицами.
Далеко не всегда программа перенормировок может быть проведена успешно, т.
е. перенормировка конечного числа величин устраняет расходимости. В нек-рых
случаях рассмотрение диаграмм всё более высокого порядка приводит к появлению
расходимостей новых типов - тогда говорят, что теория непере-нормируема.
Такова, напр., теория слабых взаимодействий. Быть может, здесь теория
встречается с такими объектами, внутренняя структура к-рых сказывается в их
взаимодействиях.
T. о, метод возмущений, в к-ром в качестве отправного пункта используется
представление о свободных полях, а затем рассматривается всё более
усложняющаяся картина взаимодействий, оказывается эффективным в квантовой
электродинамике, т. к. в этой теории с помощью перенормировок можно получить
результаты, хорошо согласующиеся с экспериментом. Однако даже в этой теории
проблема расходимостей не может считаться решённой (расходимости не
устраняются, а только изолируются). В др. теориях положение ещё сложнее: в
теории сильных взаимодействий метод возмущений перестаёт быть применимым, в
теории слабых взаимодействий обнаруживается неперенормируемость. T. е.
существуют несомненные фундаментальные трудности К. т. п., не нашедшие пока
решения.
Есть неск. тенденций в объяснении причин возникновения этих трудностей.
Согласно одной из точек зрения, все затруднения обусловлены неправильным
методом решения ур-ний К. т. п. Действительно, метод возмущений имеет очевидные
минусы; больше того, именно он порождает, напр., проблему перенормировок. Если
пользоваться гейзенберговской картиной при описании полей, то можно избежать
необходимости вводить "математич." частицы и рассматривать их
последующее "облачение". Единственные частицы, к-рые при этом
фигурируют в теории,- "физические". Но, чтобы ввести такие частицы,
нужно принять, что все взаимодействия начинаются в нек-рый (хотя, возможно, и
очень отдалённый) момент, а затем, в будущем (к-рое также может быть очень
далёким) заканчиваются. Такое представление действительно близко к тому, что
выступает в эксперименте, где взаимодействие начинается, когда какие-то частицы
налетают на др. частицы-мишени, а продукты, образовавшиеся при столкновении, по
истечении нек-рого времени разлетаются так далеко, что взаимодействие между
ними прекращается. Возможность рассматривать асимптотически (т. е. в моменты
времени i=-°° и i=+oo) свободные поля, а следовательно, и частицы не снимает,
однако, всех трудностей, т. к. достаточно эффективных методов решения ур-ний
для гейзенберговских операторов пока найти не удалось. T. о., согласно
этой точке зрения, причина затруднений - именно в неумении достаточно корректно
решать ур-ния К. т. п.
Распространено также мнение, что и избавившись от всех недостатков метода
возмущений, теория не обретёт желаемого совершенства, т. е. что трудности имеют
не математическую, а физич. природу. Указывается, напр., что рассмотрение
ограниченного числа типов взаимодействующих полей неправомерно, т. к. все поля
взаимосвязаны. Возможно, последовательное рассмотрение всех полей в их
взаимодействии (включая и гравитационное поле) приведёт к правильному и
непротиворечивому описанию явлений.
Пересмотр представлений о взаимодействии типичен и для т. н. нелокальных
квантовых теорий поля, исходящих из предположения, что взаимодействие между
полями "размазано", т. е. определяется не только значениями этих
полей в одной и той же точке пространства и в одинаковые моменты времени.
Требования теории относительности налагают весьма жёсткие ограничения на
возможные типы "размазывания", что, в частности, приводит к
возникновению проблемы причинного описания в нелокальных теориях.
Ещё одна тенденция: причина затруднений усматривается в том, что совр.
теория пытается излишне детализировать описание явлений в микромире. Подобно
тому, как при переходе от классич. механики к квантовой теряют смысл такие
классич. представления, как траектория частицы, прослеживание её координаты во все
чередующиеся моменты времени, невозможно (и неправильно) пытаться описать в
принятых понятиях детальную картину эволюции поля во времени - можно лишь
ставить вопрос о вероятности перехода из начальных состояний поля, когда
взаимодействие ещё не началось, в конечные состояния, когда оно уже
закончилось. Задача заключается в нахождении законов, определяющих вероятности
таких переходов (заметим, что такая программа фактически выходит за рамки
традиционной К. т. п.). На первый план при этом выступает оператор (называемый
S-матрицей), устанавливающий связь между вектором состояния  (-°°) в
бесконечном прошлом (t= -°°) и вектором
(-°°) в
бесконечном прошлом (t= -°°) и вектором  (+°° ), относящимся к
бесконечному будущему (t=+оо):
(+°° ), относящимся к
бесконечному будущему (t=+оо):  (+оо) = S
(+оо) = S (-°°). Проблема заключается в нахождении законов,
определяющих S-матрицу, причём таких законов, к-рые не основывались бы на
детализированном описании эволюции системы во все промежуточные между t =
-оо и t =+oo моменты времени. Об открывающихся здесь возможностях могут, напр.,
свидетельствовать исследования, базирующиеся на рассмотрении зависимости
S-матрицы от заряда и приводящие к новым типам решений задач К. т. п.
(-°°). Проблема заключается в нахождении законов,
определяющих S-матрицу, причём таких законов, к-рые не основывались бы на
детализированном описании эволюции системы во все промежуточные между t =
-оо и t =+oo моменты времени. Об открывающихся здесь возможностях могут, напр.,
свидетельствовать исследования, базирующиеся на рассмотрении зависимости
S-матрицы от заряда и приводящие к новым типам решений задач К. т. п.
Нельзя не упомянуть, наконец, ещё об одном распространённом мнении, согласно
к-рому для устранения дефектов теории необходим радикальный шаг, принципиально
новая идея, в результате к-рой будет введена в рассмотрение новая универсальная
постоянная, напр., фундаментальная (элементарная) длина. Уже неоднократно
предпринимались попытки пересмотра представлений о пространстве и времени,
также использующие представление о такой фундаментальной длине (см.
Квантование пространства-времени).
Анализ причин, приводящих к появлению трудностей в теории, имеет большое
значение. Но едва ли не большую роль играют новые пути развития теории.
Некоторые из них рассматриваются ниже.
V. Некоторые новые методы в квантовой теории поля
Одним из важных примеров нового подхода к исследованию квантовых полей
является т. н. аксиоматический подход. Для него типичны тщательный анализ
положений, образующий математич. и физич. фундамент теории, и выделение из их
числа наиболее "надёжных". К числу таких положений
("аксиом") относятся: релятивистская инвариантность (т. е.
удовлетворение требованиям теории относительности); условие причинности, или
локальности взаимодействия, приводящее к требованию, чтобы коммутировали
операторы полей, относящиеся к различным точкам пространства и к таким моментам
времени, к-рые исключают возможность обмена сигналами со скоростью,
превосходящей скорость света (исключение сверхсветовых сигналов соответствует
требованию, чтобы причина всегда предшествовала во времени следствию); условие
т. н. спектральности, означающее требование, чтобы энергии всех допустимых
состояний физ. системы (спектр энергий) были положительными (если считать
энергию вакуумного состояния равной нулю). Очень важен вопрос о том, можно ли
на базе принимаемых аксиом получать экспериментально проверяемые предсказания,
относящиеся к взаимодействующим полям. Не менее важно понять, можно ли на
данной основе построить непротиворечивую теорию таких полей.
Одна из причин, обусловливающих интерес к аксиоматич. подходу, заключается в
том, что он должен указать доступные экспериментальному изучению следствия,
вытекающие из совр. представлений о пространстве и времени, и тем самым сделать
возможным прямую проверку этих представлений. Так, эксперименты, в к-рых
обнаружилось бы нарушение аксиомы локальности, служили бы доказательством
необходимости ревизии физической картины пространства-времени на сверхмалых
расстояниях.
Важнейшим примером того, что можно вывести из фундаментальных постулатов К.
т. п., является CPT-теорема. Оказывается, что из условия локальности и
релятивистской инвариантности вытекает, что теория должна быть инвариантной по
отношению к трём одновременно производимым операциям: пространственному отражению
P (замене координат r на -r), инверсии времени T (замене
времени t на - t), зарядовому сопряжению С (замене частиц на
античастицы); более наглядно, СРТ-теорема формулируется как утверждение об
инвариантности теории по отношению к замене в любом процессе падающих частиц на
уходящие античастицы. Нетривиальность СРТ-теоремы видна хотя бы из того, что,
напр., инвариантность только по отношению к пространств, отражению или (и) к
зарядовому сопряжению отсутствует.
И ещё одна особенность аксиоматич. подхода: проводимые в его рамках
тщательные исследования позволяют обнаруживать те исходные положения в
традиционной К. т. п., к-рые нуждаются в логич. и математич. уточнении.
Интенсивное развитие техники ускорителей заряженных частиц и
обязанное ему небывалое увеличение потока экспериментальной информации об
элементарных частицах заметно отразились на направлении теоретических поисков.
Особое внимание привлекает величина, имеющая непосредственный физ. смысл,- амплитуда
рассеяния (квадрат её модуля определяет вероятность процесса). Для каждого
процесса амплитуде рассеяния можно поставить в соответствие диаграмму,
напоминающую по виду диаграмму Фейнмана, но имеющую принципиально иной смысл.
Рассмотрим, напр., диаграмму, изображённую на рис. 10. Она похожа (рис. 4 и 5)
на график вершинной части (и наз. также вершинной), но теперь это не графич.
изображение приближённого (полученного при помощи теории возмущений) решения
нек-рого уравнения, - график просто фиксирует процесс, в к-ром принимают
участие частицы А, В и С. Если масса тА частицы А больше
суммы масс тв+тс частиц В и С, то диаграмма описывает
реальный распад А -> В + С. Если распад энергетически запрещён, то
хотя бы одна из линий диаграммы относится к виртуальной частице. Кружок на
рис.10 означает, что вершина является физической, т.е. непосредственно
соответствует тому, что выступает в эксперименте. Если линии А и В относятся к
реальным нуклонам (напр., протонам), а линия С изображает виртуальный фотон, то
такая вершинная часть зависит лишь от одной переменной. Требования теории
относительности заставляют выбрать в качестве такой переменной величину р2с
= E2c/с2-p2, т. к. только такая
комбинация из энергии Sc и импульса рc частицы не
меняется при переходе от одной инерц. системы отсчёта к другой; величина pc
наз. четырёхмерным импульсом частицы С. Для реальной частицы р2
= тс2, при этом говорят, что частица лежит на массовой
поверхности. Виртуальные частицы лежат "вне массовой поверхности";
это обусловлено наличием заметного квантового разброса энергии, или, что
эквивалентно, квантового разброса масс.
Зависимость амплитуды рассеяния от р2 описывает
наблюдаемое на опыте распределение электрич. заряда, магнитного момента и всех
высших электрич. и магнитных мультипольных моментов протона (т.н.
электромагнитный формфактор протона). В рамках методов, о к-рых шла речь выше и
которые типичны для квантовой электродинамики, такой формфактор в принципе
следовало бы искать, анализируя "шубу" протона; как уже отмечалось,
эффективных методов такого анализа не существует. Важная черта нового подхода -
активное использование данных эксперимента для заполнения тех
"брешей", к-рые возникают в теории.
Рис. 11.
Приведём ещё один важный пример "обобщённых" диаграмм - т.н.
"четырёххвостку" (рис. 11). Она изображает либо распад одной частицы
на три (А -> В + С + D), если такой процесс энергетически
разрешён, либо переходы типа "две частицы -> две частицы",
в частности, если частицы в начале и в конце процесса одинаковы,- упругое
рассеяние частиц. Рассмотрим этот последний процесс и, ради простоты, примем,
что все частицы имеют одинаковую массу и нулевой спин. Тогда амплитуда
рассеяния оказывается (если все 4 линии относятся к реальным частицам)
зависящей лишь от двух инвариантных переменных. Обычно используются такие
переменные: s = (рA + рB)2- величина,
равная квадрату энергии сталкивающихся частиц в системе центра инерции (т. е. в
системе, в к-рой общий импульс частиц Л и В равен нулю), и t = (pA
+ pC)2 - величина, определяющая передачу импульса при
рассеянии.
Приведённые на рис. 10 и 11 диаграммы не исчерпывают, разумеется, всех
возможностей. Однако они играют заметную роль и часто используются в качестве
"узлов" при построении более сложных диаграмм, описывающих процессы с
участием большего числа (более четырёх) частиц.
Для исследования амплитуды рассеяния f привлекается аппарат теории аналитических
функций. При этом s и t, от к-рых зависит амплитуда рассеяния
f (s,t), рассматривают как комплексные переменные. Такой подход
оправдывается тем, что поведение аналитических функций в значительной мере
определяется видом и положением т. н. особенностей функции (см. Особая точка). Один из важнейших видов особенностей - полюс функции f (z) в
нек-рой точке z0, отвечающий обращению функции f в
этой точке в бесконечность типа 1/(z-z0). Оказывается, что
полюсы в амплитуде рассеяния могут получить наглядную интерпретацию. Если,
напр., в амплитуде рассеяния, описывающей процесс A + В -> С + D, появляется
полюс вида l/(s - m2с4), то это означает, что процесс
идёт через промежуточную (виртуальную) частицу Q, А + В -> Q -> С + D,
причём масса промежуточной частицы mQ = т. Полюс
вида l/(t - m2c4 ) соответствует диаграмме, изображённой
на рис. 12; т есть масса промежуточной (виртуальной) частицы на этой
диаграмме. Особенности др. типов также могут интерпретироваться физически как
отражение неких важных процессов, проявляющихся на промежуточных этапах
рассеяния. Если все эти особенности найдены, то на базе общих теорем теории
аналитич. функций можно пытаться полностью восстановить вид амплитуды рассеяния
при всех значениях s и t, в частности при непосредственно интересующих
физиков действит. значениях этих величин. Для нахождения особенностей
используются как уже упоминавшиеся фундаментальные принципы реляти-
Рис. 12.
вистской квантовой механики, так и ряд других. Важную роль играет условие
унитарности; оно означает следующее: если процесс может происходить неск.
различными способами (протекать по различным "каналам"), напр.,
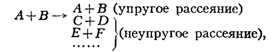
то полная вероятность всех возможных превращений равна единице. Несмотря на
кажущуюся тривиальность, такие требования, как унитарность и положительность
энергий физич. частиц, вносят довольно жёсткие ограничения на амплитуды
рассеяния.
Очень важную роль при построении амплитуды рассеяния для различных процессов
играют также требования симметрии (см. Симметрия в квантовой физике), в
частности то обстоятельство, что частицы можно разбить на группы, внутри каждой
из которых массы растут прямо пропорционально спинам. Необходимо, наконец,
учитывать те законы сохранения, которые важны для каждого из конкретных
рассматриваемых процессов (законы сохранения электрич. заряда, барионного
заряда, лептонного заряда и т. д.).
К. т. п. успешно использует также нек-рые методы, появившиеся впервые в
классич. электродинамике. Одним из них является метод, раскрывающий связь между
зависящими от частоты действительными и мнимыми частями диэлектрической
проницаемости диэлектрика. T. к. зависимость от частоты света показателя
преломления диэлектрика наз. дисперсией (а показатель преломления
определяется диэлектрич. проницаемостью), то указанная связь наз.
дисперсионными соотношениями. Оказывается, что, даже не делая никаких
конкретных предположений о строении диэлектрика, можно, исходя из требования
причинности [здесь оно предстаёт в виде требования, чтобы поляризация
диэлектрика в любой момент определялась лишь напряжённостями электрич. полей в
тот же или предшествующие (но не в последующие) моменты], получить выражение
для мнимой части диэлектрич. проницаемости, определяющей поглощение
электромагнитной волны, если известна её действит. часть во всём бесконечном
интервале частот (и наоборот). Дисперсионные соотношения позволяют сделать выводы,
непосредственно проверяемые экспериментально, напр, вывод о том, что в областях
прозрачности (т.е. при частотах, отвечающих малому поглощению) дисперсия
является нормальной: показатель преломления увеличивается при возрастании
частоты. Кроме того, из дисперсионных соотношений можно получить сведения об
асимптотическом (при очень больших частотах) поведении действительной и мнимой
частей диэлектрич. проницаемости.
Поскольку классич. задача о дисперсии, или о рассеянии электромагнитных волн
в веществе, решается в рамках дисперсионного подхода без использования к.-л.
конкретных моделей строения вещества, естественно ожидать, что такой подход
окажется плодотворным и при рассмотрении др. задач о рассеянии, в частности в
К. т. п. Здесь также можно выделить действительную и мнимую (отражающую вклад
от неупругих процессов, при к-рых в конечном состоянии появляются новые
частицы) части амплитуды рассеяния и установить соотношения между ними. Мнимая
часть амплитуды рассеяния учитывает все возможные (в т. ч. и упругие) процессы.
T. н. оптическая теорема утверждает, что мнимая часть амплитуды рассеяния по
направлению вперёд пропорциональна полной вероятности рассеяния.
Дисперсионный подход, получивший надёжное матем. обоснование и развитие в
работах H. H. Боголюбова и его школы, позволил получить ряд интересных
результатов. К ним относится, напр., определение точных значений констант
взаимодействия пи-мезонов с протонами и нейтронами (нуклонами), а также
констант взаимодействия К-мезонов, нуклонов и А-гиперонов. Представляют
значит, интерес и предсказания относительно асимптотич. поведения амплитуд
рассеяния.
Однако программа полного построения амплитуд процессов в рамках
дисперсионного подхода также не находит пока окончат, решения. Видимо, кроме
тех общих принципов, о к-рых говорилось выше, теория должна опираться на
какие-то более конкретные положения, играющие роль динамич. принципов. Иногда
такая новая динамика выступает в виде указания правил, по к-рым следует
определять особенности амплитуд; нахождение этих правил требует тщательного
использования экспериментальных данных. Однако такой "косвенный" учёт
динамики не является единственно возможным.
Нельзя не отметить возрождения интереса к теориям, в к-рых законы динамики
вновь приобретают традиционный вид ур-ний, описывающих детальную
пространственно-временную картину процессов. Толчком к этому послужили важные
исследования в области систематики элементарных частиц и установление новых
свойств симметрии (см. Элементарные частицы). За обнаруженными здесь
закономерностями естественно искать динамич. законы. Очень интересные, хотя и
предварительные результаты попыток согласовать динамику полей со свойствами
симметрии элементарных частиц, по-видимому, приводят к необходимости
рассмотрения нелинейных (т. е. испытывающих самовоздействие) полей (см.
Нелинейная квантовая теория поля). В известном смысле это направление близко к единой
К. т. п. (см. Единая теория поля), в к-рой делаются попытки
рассматривать материю в целом как некое единое фундаментальное поле (или неск.
основных типов фундаментальных полей), а отдельные частицы - как различные
проявления (состояния) этого поля.
Было бы преждевременно оценивать все имеющиеся попытки решения проблем,
возникающих в К. т. п. Однако сам факт многочисленности таких попыток свидетельствует
о серьёзности этих проблем и об усилиях, к-рые предпринимаются для решения осн.
вопроса физики - вопроса о строении материи.
Лит.: Ландау Л. Д., Л и ф ш и ц E. M., Теория поля,
M., 1967 (Теоретическая физика, т. 2); Швебер С., Введение в релятивистскую
квантовую теорию поля, [пер. с англ.], M., 1963; Боголюбов H. H., Ширков Д. В.,
Введение в теорию квантованных полей, M., 1957; Садам А., Фундаментальная
теория материи (результаты и методы), "Успехи физических наук", 1969,
т. 99, в. 4, с. 571 - 611; Ахиезер А. И., Берестецкий В. Б., Квантовая
электродинамика, 3 изд., M., 1969; З а и м а н Дж., Современная квантовая
теория, [пер. с англ.], M., 1971; Боголюбов H. H., Тодоров И.Т., Логунов А. А.,
Основы аксиоматического подхода в квантовой теории поля, M., 1969; Идеи Р.,
Соударения элементарных частиц при высоких энергиях, [пер. с англ.], M., 1970.
В. И. Григорьев.
КВАНТОВАЯ ХИМИЯ, область теоретической химии, в к-рой вопросы строения и
реакционной способности химич. соединений, химич. связи рассматриваются на
основе представлений и методов квантовой механики. Квантовая механика в
принципе позволяет рассчитывать свойства атомно-молекулярных систем, исходя
только из Шрёдингера уравнения, Паули принципа и универсальных физич.
постоянных. Различные физич. характеристики молекулы (энергия, элек-трич. и
магнитные дипольные моменты и др.) могут быть получены как собственные значения
операторов соответствующих величин, если известен точный вид волновой функции.
Однако для систем, содержащих 2 и более электронов, пока не удалось получить
точного аналитического решения уравнения Шрёдингера. Если же использовать функции
с очень большим числом переменных, то можно получить приближённое решение, по
числовой точности аппроксимирующее сколь угодно точно идеальное решение. Тем не
менее, несмотря на использование совр. ЭВМ с быстродействием порядка сотен
тысяч и даже миллионов операций в секунду, подобные "прямые" решения
уравнения Шрёдингера пока что осуществлены только для систем с неск.
электронами, напр, молекул H2 и LiH. Поскольку химиков интересуют
системы с десятками и сотнями электронов, приходится идти на упрощения. Поэтому
для описания таких систем были выдвинуты различные приближённые квантовохимич.
теории, более или менее удовлетворительные в зависимости от характера
рассматриваемых задач: теория валентных связей, заложенная в 1927 В. Гейтлером
и Ф. Лондоном в Германии, а в нач. 30-х гг. развитая Дж. Слейтером и Л.
Полингом в США; кристаллического поля теория, предложенная нем. учёным X. Бете
в 1929 и в последующие годы разрабатывавшаяся амер. учёным Ван Флеком (своё
применение в химии она получила в 1950-е гг. как теория поля лигандов благодаря
исследованиям англ. учёного Л. Оргела и датских учёных К. Йоргенсена и К.
Бальхаузена). В кон. 1920-х гг. появилась теория молекулярных орбиталей (МО),
разработанная Дж. Леннардом-Джонсом (Великобритания), P. Малликеном (США), Ф.
Хундом (Германия) и развивавшаяся затем мн. др. исследователями (см. Молекулярных
орбиталей метод). Долгое время эти приближённые теории сосуществовали и
даже дополняли друг друга. Однако теперь, когда достигнуты огромные успехи в
синтезе молекул и определении их структуры, а вычислит, техника получила
широкое развитие, симпатии исследователей склонились в сторону теории МО. Это
объясняется тем, что только теория МО выработала универсальный язык, в принципе
пригодный для описания любых молекул, строение к-рых отличается очень большим
разнообразием и сложностью. Теория МО включает наиболее общие физич.
представления об электронном строении молекул и (что не менее важно) использует
математич. аппарат, наиболее пригодный для проведения количеств, расчётов на
ЭВМ.
Теория МО исходит из того, что каждый электрон молекулы находится в поле
всех её атомных ядер и остальных электронов. Теория атомных орбиталей (АО),
описывающая электронное строение атомов, включается в теорию МО как частный
случай, когда в системе имеется только одно атомное ядро. Далее, теория МО
рассматривает все химич. связи как многоцентровые (по числу атомных ядер в
молекуле) и тем самым полностью делокализованные. С этой точки зрения всякого
рода преимущественная локализация электронной плотности около определённой
части атомных ядер есть приближение, обоснованность к-рого должна быть выяснена
в каждом конкретном случае. Представления В. Косселя о возникновении в
химических соединениях обособленных ионов (изоэлектронных атомам благородных
газов) или воззрения Дж. Льюиса (США) об образовании двухцентровых
двух-электронных химич. связей (выражаемых символикой валентного штриха)
естественно включаются в теорию МО как нек-рые частные случаи.
В основе теории МО лежит одноэлект-ронное приближение, при к-ром каждый
электрон считается квазинезависимой частицей и описывается своей волновой
функцией. Обычно вводится и др. приближение - одноэлектронные МО получаются как
линейные комбинации АО (приближение ЛКАО - МО).
Если принять указанные приближения, то, используя только универсальные
физич. постоянные и не вводя никаких экспериментальных данных (разве только
равновесные межъядерные расстояния, причём в последнее время всё чаще обходятся
и без них), можно проводить чисто теоретич. расчёты (расчёты ab initio, лат.
"от начала") по схеме метода самосогласованного поля (ССП; метода
Хартри - Фока). Такие расчёты ССП - ЛКАО - МО сейчас стали возможны уже для
систем, содержащих неск. десятков электронов. Здесь осн. трудности заключаются
в том, что приходится вычислять громадное кол-во интегралов. Хотя подобные
расчёты являются громоздкими и дорогостоящими, получающиеся результаты не
всегда удовлетворительны, во всяком случае, с количеств, стороны. Это
объясняется тем, что, несмотря на различные усовершенствования схемы ССП
(напр., введение конфигурационного взаимодействия и др. способов учёта
корреляции электронов), исследователи в конечном счёте ограничены возможностями
одноэлектронного приближения ЛКАО - МО.
В связи с этим большое развитие получили полуэмпирич. квантовохимич.
расчёты. Эти расчёты также восходят к уравнению Шрёдингера, но вместо того
чтобы вычислять огромное количество (миллионы) интегралов, большую часть из них
опускают (руководствуясь порядком их малости), а остальные упрощают. Потерю
точности компенсируют соответствующей калибровкой параметров, к-рые берутся из
эксперимента. Полуэмпирич. расчёты пользуются большой популярностью, ибо
оптимальным образом сочетают в себе простоту и точность в решении различных
проблем.
Описанные выше расчёты нельзя непосредственно сравнивать с чисто
теоретическими (неэмпирическими) расчётами, т. к. у них разные возможности, а
отсюда и разные задачи. Ввиду специфики используемых параметров при
полуэмпирич. подходе нельзя надеяться получить волновую функцию,
удовлетворительно описывающую различные (а тем более все) одноэлектронные
свойства. В этом состоит коренное отличие полуэмпирич. расчётов от расчётов
неэмпирических, к-рые могут, хотя бы в принципе, привести к универсальной
волновой функции. Поэтому сила и привлекательность полуэмпирич. расчётов
заключаются не в получении количественной информации как таковой, а в
возможности интерпретации получаемых результатов в терминах физико-химич.
концепций. Только такая интерпретация и приводит к действительному пониманию,
так. как без неё на основании расчёта можно лишь констатировать те или иные
количеств, характеристики явлений (к-рые надёжнее определить на опыте). Именно
в этой специфич. особенности полуэмпирич. расчётов и заключается их
непреходящая ценность, позволяющая им выдерживать конкуренцию с полными
неэмпирич. расчётами, к-рые по мере развития вычислит, техники становятся всё
более легко осуществимыми.
Что касается точности полуэмпирич. квантовохимич. расчётов, то она (как и
при любом полуэмпирич. подходе) зависит скорее от умелой калибровки параметров,
нежели от теоретич. обоснованности расчётной схемы. Так, если выбирать
параметры из оптич. спектров каких-то молекул, а затем рассчитывать оптич.
спектры родственных соединений, то нетрудно получить великолепное согласие с
экспериментом, но такой подход не имеет общей ценности. Поэтому осн. проблема в
полуэмпирич. расчётах заключается не в том, чтобы вообще определить параметры,
а в том, чтобы одну группу параметров (напр., полученных из оптических спектров)
суметь использовать для расчётов др. характеристик молекулы (напр.,
термодинамических). Только тогда появляется уверенность, что работа ведётся с
физически осмысленными величинами, имеющими некое общее значение и полезными
для концепционного мышления.
Кроме количеств, и полу количеств. расчётов, совр. К. х. включает ещё
большую группу результатов качеств, рассмотрения. Зачастую удаётся получать
весьма убедительную информацию о строении и свойствах молекул без всяких
громоздких расчётов, используя различные фундаментальные концепции, основанные
гл. обр. на рассмотрении симметрии.
Соображения симметрии играют важную роль в К. х., т. к. позволяют
контролировать физич. смысл результатов приближённого рассмотрения
многоэлектронных систем. Напр., исходя из точечной группы симметрии молекулы,
можно вполне однозначно решить вопрос об орбитальном вырождении электронных
уровней независимо от выбора расчётного приближения. Знание степени
орбитального вырождения часто уже достаточно для суждения о мн. важных свойствах
молекулы, таких как потенциалы ионизации, магнетизм, конфигурац. устойчивость
и ряд других. Принцип сохранения орбитальной симметрии лежит в основе совр.
подхода к механизмам протекания согласованных химич. реакций (правила Вудворда
- Гофмана). Указанный принцип может быть, в конечном счёте, выведен из общего
топологич. рассмотрения областей связывания и антисвязывания в молекуле.
Следует иметь в виду, что совр. химия имеет дело с миллионами соединений и
её научный фундамент не является монолитным. В одних случаях успех достигается
уже при использовании чисто качественных представлений К. х., в других - весь
её арсенал оказывается недостаточным. Поэтому, оценивая совр. состояние К. х.,
всегда можно привести много примеров, свидетельствующих как о силе, так и о
слабости совр. квантовохимич. теории. Ясно лишь одно: если раньше уровень
квантовохимич. работ ещё мог определяться технич. сложностью применённого
расчётного аппарата, то теперь доступность ЭВМ выдвигает на первый план
физико-химич. содержательность исследований. С точки зрения внутр. интересов К.
х. наибольшую ценность, вероятно, представляют попытки выйти за пределы
одноэлектронного приближения. В то же время для утилитарных целей в различных
областях химии рдноэлектронное приближение таит ещё много неиспользованных
возможностей. См. также Химическая связь, Валентность.
Лит. см. при ст. Валентность и Химическая связь.
E. M.
Шусторович,
КВАНТОВАЯ ЭВОЛЮЦИЯ, форма эволюции группы организмов, связанная с
резким переходом её из одной адаптивной зоны в другую. Термин "К.
э." введён амер. биологом Дж. Г. Симпсоном (1944). В этом смысле
"квант" - воздействие, к-рое, будучи ниже какого-то порога, не даёт
реакции, а, превысив этот порог, выводит группу из состояния равновесия и в
результате действия жёсткого естественного отбора приводит её либо к
гибели, либо к резким изменениям в строении организмов и к появлению новых
семейств, подотрядов, отрядов и т. д. К. э. объясняет взрывной характер
эволюции мн. крупных групп организмов, неожиданно достигавших бурного расцвета.
Так, образование к началу третичного периода обширных равнин и появление
травянистых покрытосеменных растений, особенно злаков, способствовали
прогрессивному изменению строения зубной системы и черепа, а также конечностей
у копытных млекопитающих, что привело к резкому увеличению их численности,
разнообразию форм и повсеместному расселению.
Лит.: Симпсон Дж. Г., Темпы и формы эволюции, пер. с англ., M., 1948.
А. В. Яблоков.
КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА, квантовая теория электромагнитных
процессов; наиболее разработанная часть квантовой теории поля. Классическая
электродинамика учитывает только непрерывные свойства электромагнитного поля, в
основе же К. э. лежит представление о том, что электромагнитное поле обладает
также и прерывными (дискретными) свойствами, носителями к-рых являются кванты
поля - фотоны. Фотоны обладают нулевой массой покоя, энергией E = hv и
импульсом р= (h/2 )k, где h - Планка постоянная,
)k, где h - Планка постоянная,  - частота электромагнитной
волны, k - волновой вектор, ориентированный по направлению
распространения волны и имеющий величину k = 2
- частота электромагнитной
волны, k - волновой вектор, ориентированный по направлению
распространения волны и имеющий величину k = 2
 /с, с - скорость света.
Взаимодействие электромагнитного излучения с заряженными частицами
рассматривается в К. э. как поглощение и испускание частицами фотонов .
/с, с - скорость света.
Взаимодействие электромагнитного излучения с заряженными частицами
рассматривается в К. э. как поглощение и испускание частицами фотонов .
К. э. количественно объясняет эффекты взаимодействия излучения с веществом
(испускание, поглощение и рассеяние), а также последовательно описывает
электромагнитные взаимодействия между заряженными частицами. К числу важнейших
проблем, которые не нашли объяснения в классической электродинамике, но успешно
разрешаются К. э., относятся тепловое излучение тел, рассеяние рентгеновских
лучей на свободных (точнее, слабо связанных) электронах (Комптона эффект), излучение
и поглощение фотонов атомами и более сложными системами, испускание фотонов при
рассеянии быстрых электронов во внешних полях (тормозное излучение) и т.
п. К. э. с высокой степенью точности описывает эти явления, а также любые др.
явления взаимодействия электромагнитного излучения с электронами и позитронами.
Меньший успех теории при рассмотрении др. процессов обусловлен тем, что в этих
процессах, кроме электромагнитных взаимодействий, играют определяющую роль и
взаимодействия иных типов (сильные взаимодействия, слабые взаимодействия).
Последовательное построение К. э. привело к пересмотру классич.
представлений о законах движения материи.
Лит. см. при ст. Квантовая
теория поля.
В. И. Григорьев.
КВАНТОВАЯ ЭЛЕКТРОНИКА, область физики, изучающая методы усиления и
генерации электромагнитных колебаний, основанные на использовании эффекта вынужденного
излучения, а также свойства квантовых усилителей и генераторов и их
применения. Практич. интерес к квантовым генераторам света (лазерам) обусловлен
прежде всего тем, что они, в отличие от др. источников света, излучают световые
волны с очень высокой направленностью и высокой монохроматичностью. Квантовые
генераторы радиоволн отличаются от др. радиоустройств высокой стабильностью
частоты генерируемых колебаний, а квантовые усилители радиоволн -
предельно низким уровнем шумов.
Физические основы квантовой электроники. Свет и радиоволны являются
электромагнитным излучением, порции которого кванты (или фотоны) могут
испускаться атомами, молекулами и др. квантовыми системами, обладающими нек-рой
избыточной внутренней энергией (возбуждёнными частицами). Внутренняя энергия
атома (или молекулы) может принимать только лишь нек-рые строго определённые
дискретные значения, наз. уровнями энергии. Уменьшение внутренней
энергии означает переход атома с более высокого уровня энергии на более низкий.
Если при этом избыток энергии отдаётся в виде кванта излучения, то частота
излучаемых волн  определяется условием Бора:
определяется условием Бора:
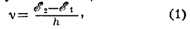
где h = 6,62-10-27 эрг-сек - Планка постоянная. Аналогично
увеличение внутренней энергии атома означает его переход с нижнего уровня
E1 на верхний E2. Если это увеличение
связано с поглощением кванта излучения, то . частота поглощаемого излучения
определяется тем же условием (1). T. о., условие (1) определяет частоту
спектральной линии поглощения или излучения, характерную для данных частиц.
Взаимодействие частиц с окружающими их частицами и полями, а также
"краткость их жизни на уровне" приводят к "размытию"
уровней энергии. В результате условие (1) выполняется не для одного
фиксированного значения частоты v, a для интервала значений частот, при этом
спектральные линии приобретают ширину (см. Ширина спектральных линий).
Возбуждённые частицы могут отдавать свою энергию в виде квантов излучения
двумя способами. Возбуждённые частицы неустойчивы, и для каждой из них
существует определённая вероятность самопроизвольно (спонтанно) испустить квант
излучения (рис. 1, в). Акты спонтанного испускания происходят случайно. Поэтому
спонтанное излучение носит хаотич. характер. Фотоны испускаются различными
частицами в различные моменты времени, имеют разную частоту, поляризацию и
направление распространения. Интенсивность спонтанного излучения
пропорциональна кубу частоты и поэтому резко падает при переходе от световых
волн к радиоволнам. Все не лазерные источники света (лампы накаливания,
газоразрядные лампы и т.п.) излучают свет в результате актов спонтанного
излучения. В радиодиапазоне такой же характер имеют шумы электронных устройств
и тепловое радиоизлучение нагретых тел. Возбуждённые частицы могут испускать
фотоны, переходя с верхнего уровня энергии E2 на нижний
уровень E1 не только самопроизвольно, но и под воздействием
внешнего излучения (вынужденно), если частота этого внешнего излучения
удовлетворяет условию (1) (рис. 1, б). Вероятность вынужденного
испускания, предсказанного А. Эйнштейном (1917), пропорциональна
интенсивности вынуждающего излучения и может превосходить вероятность
спонтанного процесса. T. о., в процесс вынужденного испускания вовлечены два
кванта излучения: первичный, вынуждающий, и вторичный, испущенный возбуждённым
атомом. Существенно, что вторичные кванты неотличимы от первичных. Они обладают
в точности такой же частотой, фазой, поляризацией и направлением
распространения. На эту особенность вынужденного излучения, имеющую
основополагающее значение для К. э., впервые указал П. Дирак (1927).
Тождественные кванты формируют электромагнитную волну, являющуюся точной
усиленной копией исходного излучения. С ростом числа актов вынужденного
испускания в 1 сек интенсивность волны возрастает, а её частота, фаза,
поляризация и направление распространения остаются неизменными. Происходит
когерентное усиление электромагнитного излучения (см. Когерентность).
Для одной частицы вынужденные переходы с верхнего уровня E2
энергии на нижний E1 (испускание фотона, рис. 1,6) и с
нижнего на верхний (поглощение фотона, рис. 1, в) одинаково вероятны.
Поэтому когерентное усиление волны возможно только при превышении числа
возбуждённых частиц над невозбуждёнными. В условиях равновесия
термодинамического число возбуждённых частиц меньше числа невозбуждённых,
т. е. верхние уровни энергии населены частицами меньше, чем нижние, в
соответствии с распределением Больцмана частиц по уровням энергии (рис. 2; см.
Больцмана статистика). При взаимодействии излучения с таким веществом произойдёт
поглощение излучения.
Рис. 1. а - спонтанное излучение фотона; б - вынужденное
излучение; 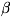 - резонансное поглощение; E1 и E2
-уровни энергии атома.
- резонансное поглощение; E1 и E2
-уровни энергии атома.
Рис. 2. Распределение частиц по уровням энергии E0, E1,
E2, E3, E4,E5 в соответствии
со статистикой Больцмана; N - число частиц на уровне.
Чтобы получить эффект усиления, необходимо принимать спец. меры для того,
чтобы число возбуждённых частиц превышало число невозбуждённых. Состояние
вещества, при к-ром хотя бы для двух уровней энергии частиц верхний уровень
оказался более населённым, чем нижний, наз. состоянием с инверсией
населённостей. Такое вещество в К.э. наз. активным (активной средой). B K.э.
используется вынужденное излучение в активной среде для усиления (квантовый
усилитель) и генерации (квантовый генератор) электромагнитных волн. Необходимая
для генерации обратная связь осуществляется помещением активной среды в объёмный
резонатор, в к-ром могут возбуждаться стоячие электромагнитные волны. В
какой-то точке резонатора неизбежно происходит спонтанный переход частицы
активной среды с верхнего уровня на нижний, т. е. самопроизвольно испускается
фотон. Если резонатор настроен на частоту этого фотона, то фотон не выходит из
резонатора, а, многократно отражаясь от его стенок, порождает множество себе
подобных фотонов, к-рые, в свою очередь, воздействуют на активное вещество,
вызывая всё новые акты вынужденного испускания таких же фотонов (обратная
связь). В результате такого "размножения" фотонов в резонаторе
накапливается электромагнитная энергия, часть к-рой выводится наружу с помощью
специальных устройств (напр., полупрозрачного зеркала для световых волн). Если
в какой-то момент мощность вынужденного излучения превышает мощность потерь
энергии на нагрев стенок резонатора, рассеяние излучения и т. п., а также
на полезное излучение во внешнее пространство (т. е. если выполнены условия
самовозбуждения), то в резонаторе возникают незатухающие колебания, т. е.
возбуждается генерация (см. Генерирование электрических колебаний).
В силу свойств вынужденного излучения эти колебания монохроматичны. Все
частицы активного вещества работают синфазно. Их заставляет работать син-фазно
обратная связь. Значение частоты такого генератора с высокой степенью точности
совпадает с частотой излучения возбуждённых частиц, хотя оно существенно
зависит также от расстройка частоты резонатора относительно частоты излучения
частиц. Интенсивность генерации определяется числом возбуждаемых частиц в сек
в каждом см3 активной среды. Если число таких
частиц 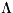 , то максимально возможная мощность P непрерывного
излучения в см3 среды составляет:
, то максимально возможная мощность P непрерывного
излучения в см3 среды составляет:
P = Лhv. (2)
Исторический очерк. Несмотря на то что положения Эйнштейна и Дирака о
вынужденном излучении формировались применительно к оптике, развитие К.э.
началось в радиофизике. В условиях термодинамич. равновесия оптич. (верхние)
уровни энергии практически не заселены, возбуждённых частиц в веществе очень
мало и на нижние уровни энергии они переходят спонтанно, т. к. при малых
плотностях световой энергии спонтанные переходы более вероятны, чем
вынужденные. Поэтому, хотя понятие монохроматичности возникло в оптике (см.
Монохроматический свет), именно в оптике отсутствовали строго гармонич. колебания и волны, т.
е. колебания с постоянными амплитудой, частотой и фазой. В радиофизике,
наоборот, вскоре после создания первых искровых радиопередатчиков развивается
техника получения гармонич. колебаний, создаваемых генераторами с
колебательными контурами и регулируемой положит, обратной связью.
Немонохроматичность излучений оптич. диапазона и отсутствие в оптике методов и
концепций, хорошо развитых в радиофизике, в частности понятия обратной связи,
послужили причиной того, что мазеры появились раньше лазеров.
В 1-й пол. 20 в. радиофизика и оптика развивались разными
путями. В оптике развивались квантовые представления, в радиофизике - волновые.
Общность радиофизики и оптики, обусловленная общностью квантовой природы
электромагнитных волновых процессов, не проявлялась до тех пор, пока не
возникла радиоспектроскопия, изучающая спектры молекул, атомов, ионов,
попадающие в диапазон СВЧ (1010 - 1011 гц). Важной
особенностью радиоспектроскопич. исследований (в отличие от оптич.)
было использование источников монохроматич. излучения. Это привело к гораздо
более высокой чувствительности, разрешающей способности и точности
радиоспектроскопов по сравнению с оптич. спектроскопами. Не менее важным
явилось и то обстоятельство, что в радио диапазоне, в отличие от оптич.
диапазона, возбуждённые уровни в условиях термодинамич. равновесия сильно
населены, а спонтанное излучение гораздо слабее. В результате вынужденное
излучение непосредственно сказывается на величине наблюдаемого резонансного
поглощения радиоволн исследуемым веществом. Причиной заселения возбуждённых
уровней является тепловое движение частиц. При комнатных темп-pax тепловому
движению соответствует энергия ~4·10-14 эрг. Для видимого
света с длиной волны  = 0,5 мкм частота колебаний
= 0,5 мкм частота колебаний  = 6·1014 гц,
а энергия кванта hv = I-10-12 эрг. Для радиоизлучения с
длиной волны
= 6·1014 гц,
а энергия кванта hv = I-10-12 эрг. Для радиоизлучения с
длиной волны  = 0,5 см частота колебаний
= 0,5 см частота колебаний  = 6·1010 гц, энергия
квантов hv = 4-10-16 эрг. Следовательно, тепловое
движение может сильно населять возбуждённые радиоуровни и не может населять
возбуждённые оптич. уровни.
= 6·1010 гц, энергия
квантов hv = 4-10-16 эрг. Следовательно, тепловое
движение может сильно населять возбуждённые радиоуровни и не может населять
возбуждённые оптич. уровни.
Перечисленные факторы привели к тому, что радиоспектроскопия стала базой
работ по К. э. В СССР работы по радиоспектроскопии газов были начаты в
лаборатории колебаний Физического ин-та АН СССР (A. M. Прохоров), где
наряду с решением чисто спектроскопич. задач исследования шли также и в
направлении использования спектральных линий СВЧ для создания стандартов
частоты.
Точность стандарта частоты, основанного на измерении положения резонансной
линии поглощения, зависит от ширины спектральной линии. Чем уже линия, тем выше
точность. Наиболее узкими линиями обладают газы, так как в газах частицы слабо
взаимодействуют друг с другом. Вместе с тем тепловое хаотич. движение
частиц газа вызывает в силу Доплера эффекта т. н. доплеровское уширение
спектральных линий. Эффективным методом устранения влияния этого уширения
является переход от хаотич. движения к упорядоченному движению, напр, переход
от газов к молекулярным пучкам. Но в этом случае возможности
радиоспектроскопа сильно ограничены малой интенсивностью резонансных линий. В
пучке мало частиц и, следовательно, разница в числе возбуждённых и
невозбуждённых частиц незначительна. На этом этапе работы возникла мысль о том,
что, искусственно изменив соотношение между числом возбуждённых и
невозбуждённых частиц, можно существенно повысить чувствительность
радиоспектроскопа. Более того, создав инверсию населённостей в пучке, вместо
поглощения радиоволн можно получить их усиление. Если же нек-рая система
усиливает радиоизлучение, то при соответствующей обратной связи она может
генерировать это излучение. В радиофизике теория генерирования была хорошо
разработана. Существенными элементами радиотехнич. генераторов являются
колебательные контуры. В области СВЧ роль контуров играют объёмные резонаторы,
особенно удобные для работы и с пучками частиц. T. о., именно в радиофизике
существовали все необходимые элементы и предпосылки для создания первого
квантового генератора. В первом приборе К. э.- молекулярном генераторе,
созданном в 1955 одновременно в СССР (H. Г. Басов, A. M. Прохоров) и в
США (Дж. Гордон, Г. Зейгер, Ч. Таунс), активной средой являлся пучок
молекул аммиака NH3. Для создания инверсии населённостей применялся
метод электростатической пространственной сортировки. Из пучка молекул NH3
выбирались более возбуждённые молекулы и отбрасывались в сторону молекулы,
обладавшие меньшей энергией. Отсортированный пучок пропускался через объёмный
резонатор, в к-ром при выполнении условий самовозбуждения возникала
генерация (см. Молекулярный генератор). Частота генератора с высокой
степенью точности совпадала с частотой излучения возбуждённых молекул NH3 и
поэтому была чрезвычайно стабильна. Относительная стабильность частоты
составляет 10-11 - 10-12. Появление молекулярных
генераторов открыло новые возможности в создании сверхточных часов и точных
навигационных систем. Их погрешность ~1 сек за 300 000 лет. Аналогичные
по принципу действия, созданные позднее водородные генераторы имеют ещё большую
стабильность частоты ~10-13 (см. Квантовые стандарты частоты,
Квантовые часы).
То обстоятельство, что К. э. родилась в радиодиапазоне, объясняет возникновение
термина "квантовая радиофизика", иногда используемого вместо термина
"К. э.", к-рый имеет более общий смысл, охватывая и оптич. диапазон.
Получение инверсии населённостей путём отбора возбуждённых частиц не всегда
возможно, в частности это невозможно в твёрдых телах. Кроме того, на высоких
оптич. уровнях при не слишком высоких темп-pax возбуждённых частиц практически
нет. Поэтому уже в 1955 был предложен новый метод создания инверсии
населённостей (H. Г. Басов, A. M. Прохоров), в к-ром возбуждённые частицы не
отбираются из имеющегося количества, а создаются. Этот метод, известный под
назв. метода трёх уровней, состоит в том, что на частицы, в энергетич. спектре
к-рых есть три уровня E1, E2,E3 (рис.
3, а), воздействуют мощным вспомогательным излучением (накачка), к-рое,
поглощаясь частицами, "перекачивает" их с уровня E1на
уровень E3. Накачка должна быть достаточно интенсивной, тогда
на верхний уровень E3 с нижнего E1перебрасывается
столько частиц, что их количество может стать практически одинаковым (рис. 3,
6).
При этом на уровне E2 может оказаться больше частиц, чем
на уровне E1 (либо на уровне E3 больше, чем
на уровне E2), т. е. для уровней E_2, E1(или
E3 и E2) будет иметь место инверсия
населённостей. Частота VH излучения накачки соответствует резонансным условиям
поглощения, т. е.
vH = (E3-E1)/h.
Рис. 3. Метод трёх уровней: а - населённости уровней при отсутствии
накачки; б - мощное вспомогательное излучение накачки уравнивает населённости
уровней E1 и E3, создавая тем самым
инверсию населённостей уровня E2 по отношению к уровню E1.
Метод трёх уровней был применён по предложению H. Бломбергена (1956, США)
для создания квантовых усилителей радиодиапазона на парамагнитных кристаллах.
Квантовые усилители обычно работают при темп-ре жидкого гелия (4,2K), когда
практически все частицы находятся на самом нижнем уровне энергии. При
накачке половина всех имеющихся в кристалле частиц переводится на верхний
уровень E2 и участвует в когерентном усилении. Если
молекулярный генератор удовлетворил потребность электроники в высокостабильном
источнике монохроматич. колебаний, то квантовый усилитель решил др. важнейшую
проблему радиофизики - проблему резкого уменьшения шумов, т. е. увеличения
чувствительности радиоприёмников СВЧ. Поэтому квантовые усилители нашли
применение в радиоастрономии, радиолокации, линиях глобальной и космич.
связи.
Успехи К. э. поставили вопрос о её продвижении в сторону более коротких
волн. При этом существенную трудность представляла разработка резонаторов. В
диапазоне СВЧ применяют закрытые полости с проводящими стенками, размеры к-рых
сравнимы с длиной волны. Для оптич. излучения резонаторы такого типа изготовить
невозможно. В 1958 был предложен открытый резонатор (A. M. Прохоров). В
субмиллиметровом диапазоне резонатор представлял собой два параллельных, хорошо
отражающих металлич. диска, между к-рыми возникает система стоячих волн. Для
света этот резонатор сводился к двум параллельным зеркалам и подобен интерферометру
Фабри - Перо.
Первым достижением К. э. в оптич. диапазоне явилось создание в 1960 лазера
(T. Мейман, США). В качестве рабочего вещества в нём использовался монокристалл
рубина, а для получения инверсии населённости был применён метод трёх
уровней. Отражающими зеркалами резонатора служили хорошо отполированные и
посеребрённые торцы кристалла рубина. Источником накачки была лампа - вспышка.
Рубиновые лазеры наряду с лазерами на стекле с примесью неодима дают рекордные
энергии и мощности. В режиме свободной генерации большие кристаллы рубина при
мощной накачке дают в импульсе энергию до 1000 дж (мощность до 106
em). Другой режим рубиновых лазеров достигается включением зеркал резонатора
лишь в определённые моменты времени, когда инверсия населённостей достигает
максимальной величины. Тогда все накопленные на метастабильном уровне частицы
излучают практически сразу, и генератор выдаёт гигантский импульс излучения
очень короткой длительности (10-8 - 10-9 сек) со
сравнительно небольшой энергией (ок. 3 дж). Но так как эта энергия
излучается в очень короткое время, то пиковая мощность импульса достигает
значений 3-106 - 3-109 вт.
Вскоре после рубинового лазера был разработан первый газовый лазер· (А.
Джаван, У.Беннетт, Д. Гарриот; 1960, США) на смеси атомов неона и гелия. Затем
появился полупроводниковый инжекционный лазер (P. Хол, а также· У. Думке с
сотрудниками; 1962, США). В газовых лазерах получение инверсии
населённости достигается не световой накачкой, а при соударениях атомов или
молекул рабочего газа с электронами: или ионами, имеющимися в электрич.
разряде. Среди газовых лазеров выделяются гелий-неоновый лазер и лазер на смеси
углекислого газа, азота и гелия: (CO2 - лазер), к-рые могут
работать, как в импульсном, так и в непрерывном: режимах. С помощью гелий-неонового
лазера получены световые колебания очень высокой стабильности (~ 10-13)
и высокой монохроматичности (
 = 1 гц при частоте 1014 гц). Хотя
кпд этого лазера крайне невелик ( 0,01%), именно высокая монохроматичность и
направленность его излучения (обусловленные, в частности, однородностью его
активной среды) сделали этот лазер незаменимым при всякого рода котировочных и
нивелировочных работах. Мощный CO2 - лазер (К. Пател, 1964, США)
генерирует инфракрасное излучение (
= 1 гц при частоте 1014 гц). Хотя
кпд этого лазера крайне невелик ( 0,01%), именно высокая монохроматичность и
направленность его излучения (обусловленные, в частности, однородностью его
активной среды) сделали этот лазер незаменимым при всякого рода котировочных и
нивелировочных работах. Мощный CO2 - лазер (К. Пател, 1964, США)
генерирует инфракрасное излучение ( = 10,6 мкм). Его кпд, достигающий 30%,
превосходит кпд всех существующих лазеров, работающих при комнатной темп-ре.
Особенно перспективен газодинамический лазер на СО2. С его
помощью можно получить в непрерывном режиме мощность в десятки кет. Монохроматичность,
направленность и высокая мощность делают его весьма перспективным для целого
ряда технологич. применений.
= 10,6 мкм). Его кпд, достигающий 30%,
превосходит кпд всех существующих лазеров, работающих при комнатной темп-ре.
Особенно перспективен газодинамический лазер на СО2. С его
помощью можно получить в непрерывном режиме мощность в десятки кет. Монохроматичность,
направленность и высокая мощность делают его весьма перспективным для целого
ряда технологич. применений.
В полупроводниковых лазерах инверсия достигается гл. обр. при
инжекции носителей тока через электронно-дырочный переход соответствующим
образом легированного полупроводника. Имеется довольно много
полупроводниковых материалов, из к-рых изготовляются лазеры в широком диапазоне
длин волн. Наиболее распространённым из них является арсенид галлия (GaAs),
к-рый при темп-ре жидкого азота может излучать в непрерывном режиме в ближней
инфракрасной области мощность до 10 вт при кпд = 30% . Изменяя ток
инжекции, можно достаточно безынерционно управлять мощностью, генерируемой
инжекционными лазерами. Это делает перспективным их применение в
быстродействующих вычислительных машинах и в системах связи.
Для получения инверсии населённости в парамагнитном квантовом усилителе, в
рубиновом лазере, в газовых и полупроводниковых лазерах и др. используются
совершенно различные физич. явления. Но единым и главным фактором для всех
методов создания инверсии населённости является необходимость преодоления
процессов, направленных к восстановлению равновесной населённости.
Препятствовать процессам восстановления равновесной населённости можно, только
затрачивая энергию, поступающую от внешнего источника питания. При этом в
лазерное излучение преобразуется, как правило, малая доля энергии накачки. В
режиме свободной генерации кпд рубинового лазера меньше 1 % , в режиме
гигантских импульсов ещё меньше. Однако "проигрыш" в количестве
энергии излучения компенсируется в К. э. выигрышем в его "качестве",
монохроматичности и направленности излучения, обусловленных свойствами
вынужденного излучения.
Монохроматичность и высокая направленность позволяют сфокусировать всю энергию
лазерного излучения в пятно с размерами, близкими к длине волны излучения. В
этом случае электрич. поле световой волны достигает значений, близких к
внутриатомным полям. При взаимодействии таких полей с веществом возникают
совершенно новые явления.
Применения К. э. революционизировали радиофизику СВЧ и оптику.
Наиболее глубокие преобразования К. э. внесла в оптику. В радиофизике создание
мазеров означало появление радиоустройств хотя принципиально и новых, но вместе
с тем обладающих привычными для радиоинженера свойствами. И до появления К. э.
в радиофизике существовали когерентные усилители и монохроматич. генераторы.
К. э. лишь резко улучшила чувствительность усилителей (в 103 раз) и
стабильность частоты генераторов (в десятки тысяч раз). В оптике же все
источники света до появления лазеров не обладали ни сколько-нибудь заметной
направленностью, ни монохроматичностью. Создание лазеров означало появление
источников света, обладающих совершенно новыми свойствами. Это дало невиданную
ранее в оптике возможность концентрировать энергию излучения как в
пространстве, так и в узком частотном интервале.
Пром-сть выпускает различные типы лазеров, к-рые используются не только как
эффективный инструмент научных исследований, но и для решения разного рода практич.
задач. Осн. преимущества лазерного воздействия - малая область распространения
тепла, отсутствие переноса электрич. зарядов и механич. контакта, возможность
работать внутри вакуумных баллонов и в агрессивных газах. Одним из первых
применений лазеров было измерение расстояния до Луны с большей точностью, чем
это было сделано радиофизич. методом. После того как на Луне был установлен уголковый
отражатель, расстояние до неё было измерено с точностью до 1,5 м. Существует
лазерная локационная служба расстояния Земля - Луна.
Новые возможности открыло применение лазеров в оптич. линиях связи. Развитие
оптич. линий связи с их задачами модуляции колебаний, детектирования, гетеродинирования,
преобразования частоты световых колебаний потребовало переноса в оптику методов
радиофизики и теории колебаний.
Возникла нелинейная оптика, изучающая нелинейные оптич. эффекты,
характер к-рых зависит от интенсивности света (самофокусировка света, генерация
оптич. гармоник, вынужденное рассеяние света, параметрическая генерация
света, самопросветление или самозатемнения света). Методами нелинейной оптики
создан новый класс перестраиваемых по частоте источников когерентного излучения
в ультрафиолетовом диапазоне. Нелинейные явления в оптике существуют только в
узком диапазоне интенсивностей лазерного излучения. При малых интенсивностях
нелинейные оптич. эффекты отсутствуют, затем по мере роста интенсивности они
возникают, возрастают, но уже при потоках интенсивности 1014 вт/см2
все известные вещества разрушаются лазерным лучом и превращаются в плазму.
Получение и исследование лазерной плазмы является одним из наиболее
интересных применений лазеров. Осуществлён термоядерный синтез, инициируемый лазерным
излучением.
Благодаря высокой концентрации электромагнитной энергии в пространстве и по
спектру лазеры находят широкое применение в микробиологии, фотохимии, химич.
синтезе, диссоциации, катализе. К. э. привела к развитию голографии - метода
получения объёмных изображений предметов восстановлением структуры световой
волны, отражённой предметом.
Работы по К.э. были отмечены Нобелевской премией 1964 по физике (H. Г.
Басов, A. M. Прохоров, СССР, и Ч. Taунс, США).
Лит.: Квантовая электроника. Маленькая энциклопедия, M., 1969;
Фабрикант В., Классика, кванты и квантовая электроника, "Наука и
жизнь", 1965, № 10; Прохоров A. M., Квантовая электроника, "Успехи
физических наук", 1965, т. 85, в. 4; Басов H. Г., Полупроводниковые
квантовые генераторы, там же, 1965, т. 85, в. 4; Шавлов А., Современные
оптические квантовые генераторы, там же, 1963, т. 81, в. 4; T а у н с Ч.,
Получение когерентного излучения с помощью атомов и молекул, там же, 1966, т.
88, в. 3.
H. В. Карлов.
КВАНТОВЫЕ ПЕРЕХОДЫ, скачкообразные переходы квантовой системы (атома,
молекулы, атомного ядра, твёрдого тела) из одного состояния в другое. Наиболее
важными являются К. п. между стационарными состояниями, соответствующими
различной энергии квантовой системы, - К. п. системы с одного уровня энергии
на другой. При переходе с более высокого уровня энергии Ekна
более низкий Ei система отдаёт энергию Ek -
Ei, при обратном переходе - получает её (рис.). К. п.
Часть уровней квантовой системы: E1 - основной уровень
(уровень с наименьшей возможной энергией), E_2, E3,E_4 -
возбуждённые уровни. Стрелками показаны квантовые переходы с поглощением
(направление вверх) и с отдачей энергии (направление вниз). могут быть
излучательными и безызлу-чательными. При излучательных К. п. система испускает
(переход Ek->Ei) или поглощает (переход Ei->Ek)
квант электромагнитного излучения - фотон - энергии hv (v -
частота излучения, h - Планка постоянная), удовлетворяющей
фундаментальному со-отношению Ek-Ei = hv
(1) (к-рое представляет собой закон сохранения энергии при таком
переходе). В зависимости от разности энергий состояний системы, между к-рыми
происходит К. п., испускаются или поглощаются фотоны радиоизлучения,
инфракрасного, видимого, ультрафиолетового, рентгеновского излучения, 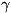 -излучения.
Совокупность излучательных К. п. с нижних уровней энергии на верхние образует
спектр поглощения данной квантовой системы, совокупность обратных переходов -
её спектр испускания (см. Спектры оптические).
-излучения.
Совокупность излучательных К. п. с нижних уровней энергии на верхние образует
спектр поглощения данной квантовой системы, совокупность обратных переходов -
её спектр испускания (см. Спектры оптические).
При безызлучательных К. п. система получает или отдаёт энергию при
взаимодействии с др. системами. Напр., атомы или молекулы газа при
столкновениях друг с другом или с электронами могут получать энергию
(возбуждаться) или терять её.
Важнейшей характеристикой любого К. п. является вероятность перехода,
определяющая, как часто происходит данный К. п. Вероятность перехода измеряют
числом переходов данного типа в рассматриваемой квантовой системе за единицу
времени (1 сек); поэтому она может принимать любые значения от О до °°
(в отличие от вероятности единичного события, которая не может превышать 1).
Вероятности переходов рассчитываются методами квантовой механики.
Ниже будут рассмотрены К. п. в атомах и молекулах (о К. п. в твёрдом
теле, ядре атомном см. в этих ст.).
Излучательные квантовые переходы могут быть спонтанными
("самопроизвольными"), не зависящими от внешних воздействий на
квантовую систему (спонтанное испускание фотона), и вынужденными,
индуцированными - под действием внешнего электромагнитного излучения
резонансной [удовлетворяющей соотношению (I)] частоты  (поглощение и вынужденное
испускание фотона). Поскольку спонтанное испускание возможно, квантовая система
находится на возбуждённом уровне энергии Ek некоторое конечное
время, а затем скачкообразно переходит на к.-н. более низкий уровень. Средняя
продолжительность
(поглощение и вынужденное
испускание фотона). Поскольку спонтанное испускание возможно, квантовая система
находится на возбуждённом уровне энергии Ek некоторое конечное
время, а затем скачкообразно переходит на к.-н. более низкий уровень. Средняя
продолжительность 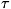 k пребывания системы на возбуждённом уровне Ek
наз. временем жизни на уровне. Чем меньше
k пребывания системы на возбуждённом уровне Ek
наз. временем жизни на уровне. Чем меньше 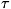 k, тем больше вероятность
перехода системы в состояние с низшей энергией. Величина Ak = 1/
k, тем больше вероятность
перехода системы в состояние с низшей энергией. Величина Ak = 1/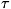 k,
определяющая среднее число фотонов, испускаемых одной частицей (атомом,
молекулой) в 1 сек (
k,
определяющая среднее число фотонов, испускаемых одной частицей (атомом,
молекулой) в 1 сек (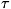 k выражается в сек), наз.
вероятностью спонтанного испускания с уровня Ek . Для
простейшего случая спонтанного перехода с первого возбуждённого уровня E_2
на осн. уровень E1 величина А2 = l/
k выражается в сек), наз.
вероятностью спонтанного испускания с уровня Ek . Для
простейшего случая спонтанного перехода с первого возбуждённого уровня E_2
на осн. уровень E1 величина А2 = l/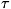 2
определяет вероятность этого перехода; её можно обозначить A21. С
более высоких возбуждённых уровней возможны К. п. на различные нижние уровни
(рис.). Полное число А/k фотонов, испускаемых в среднем одной
частицей с энергией
2
определяет вероятность этого перехода; её можно обозначить A21. С
более высоких возбуждённых уровней возможны К. п. на различные нижние уровни
(рис.). Полное число А/k фотонов, испускаемых в среднем одной
частицей с энергией 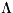 за 1 сек, равно сумме чисел Aki
фотонов, испускаемых при отдельных переходах:
за 1 сек, равно сумме чисел Aki
фотонов, испускаемых при отдельных переходах:
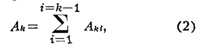
т. е. полная вероятность Ak спонтанного испускания с
уровня Ek равна сумме вероятностей Akiотдельных
спонтанных переходов Ek -> Ei ; величина
Akiназ. коэффициентом Эйнштей-н а для спонтанного испускания
при таком переходе. Для атома водорода Aki ~ (107
- 108) сек-1.
Для вынужденных К. п. число переходов пропорционально плотности 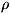
 излучения частоты
излучения частоты  =(Ek-Ei)/h,
т. е. энергии фотонов частоты
=(Ek-Ei)/h,
т. е. энергии фотонов частоты  , находящихся в 1 см3. Вероятности
поглощения и вынужденного испускания характеризуются соответственно коэфф.
Эйнштейна Вikи Bki, равными числам фотонов,
поглощаемых и соответственно вынужденно испускаемых в среднем одной частицей за
1 сек при плотности излучения, равной единице. Произведения Bik
, находящихся в 1 см3. Вероятности
поглощения и вынужденного испускания характеризуются соответственно коэфф.
Эйнштейна Вikи Bki, равными числам фотонов,
поглощаемых и соответственно вынужденно испускаемых в среднем одной частицей за
1 сек при плотности излучения, равной единице. Произведения Bik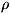 v и Bki
v и Bki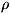 v
определяют вероятности вынужденного поглощения и испускания под действием
внешнего электромагнитного излучения плотности pv и, так же как Aki,
выражаются в сек ~4.
v
определяют вероятности вынужденного поглощения и испускания под действием
внешнего электромагнитного излучения плотности pv и, так же как Aki,
выражаются в сек ~4.
Коэффициенты Aki, Bik и Bkiсвязаны
между собой соотношениями (впервые полученными А. Эйнштейном и строго
обоснованными в квантовой электродинамике):
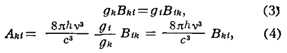
где gi(g_к) - кратность вырождения уровня Ei(Ek),
т. е. число различных состояний системы, имеющих одну и ту же энергию Ei(соответственно
Ek), с - скорость света. Для переходов между
невырожденными уровнями (gi = = gk= 1) Bki=
Вik, т. е. вероятности вынужденных К. п.- прямого и обратного
- одинаковы. Если один из коэфф. Эйнштейна известен, то по соотношениям (3) и
(4) можно определить остальные.
Вероятности излучательных переходов различны для разных К. п. и зависят от
свойств уровней энергии Ei и Ek, между
к-рыми происходит переход. Вероятности К. п. тем больше, чем сильнее изменяются
при переходе электрич. и магнитные свойства квантовой системы, характеризуемые
её электрическими и магнитными моментами. Возможность излучательиых К. п. между
уровнями Ei и Ek с заданными
характеристиками определяется отбора правилами. (Подробнее см. Излучение
электромагнитное.)
Безызлучательные квантовые переходы также характеризуются
вероятностями соответствующих переходов Сki и Сik
- средними числами процессов отдачи и получения энергии Ek
- Ei в 1 сек, рассчитанными на одну частицу с энергией
Ek (для процесса отдачи энергии) или энергией Ek
(для процесса получения энергии). Если возможны как излучательные, так и
безызлучательные К. п., то полная вероятность перехода равна сумме вероятностей
переходов обоих типов. Учёт безызлучательных К. п. играет существенную роль,
когда его вероятность того же порядка или больше соответствующего К. п. с
излучением. Напр., если с первого возбуждённого уровня E2 возможен
спонтанный излучательный переход на осн. уровень E1 с
вероятностью A21 и безызлучательный переход на тот же уровень
с вероятностью C21, то полная вероятность перехода равна A21+
C21, а время жизни на уровне равно 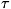 '2 = 1/(A21 +
C21) вместо
'2 = 1/(A21 +
C21) вместо 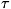 2 = 1/A2 при отсутствии
безызлучат. перехода. T. о., за счёт безызлучат. К. п. время жизни на уровне
уменьшается. При C21>>A21 время
2 = 1/A2 при отсутствии
безызлучат. перехода. T. о., за счёт безызлучат. К. п. время жизни на уровне
уменьшается. При C21>>A21 время 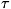 '2 очень
мало по сравнению с
'2 очень
мало по сравнению с 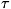 2, и подавляющее большинство частиц будет терять
энергию возбуждения E2 - E1 при
безызлучательных процессах - будет происходить тушение спонтанного испускания.
2, и подавляющее большинство частиц будет терять
энергию возбуждения E2 - E1 при
безызлучательных процессах - будет происходить тушение спонтанного испускания.
Лит. см. при ст. Атом, Молекула, Спектры оптические.
M. А. Ельяшевич.
КВАНТОВЫЕ СТАНДАРТЫ ЧАСТОТЫ, устройства, в к-рых для точного
измерения частоты колебаний или для генерирования колебаний с весьма стабильной
частотой используются квантовые переходы частиц (атомов, молекул, ионов)
из одного энергетич. состояния в другое. К. с. ч. позволяют измерять частоту
колебаний, а следовательно, и их период, т. е. время, с наибольшей точностью по
сравнению с др. стандартами частоты (см. Частоты стандарт, Время). Это
привело к их внедрению в метрологию. К. с. ч. служат основой
национальных эталонов частоты и времени и вторичных эталонов частоты, к-рые по
классу точности и метрологич. возможностям приближаются к нац. эталону, но
подлежат калибровке по нему. К. с. ч. применяются как лабораторные стандарты
частоты, имеющие широкий набор выходных частот и снабжённые устройством для
сравнения измеряемой частоты с частотой стандарта, а также как 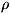 е-перы частоты,
к-рые позволяют наблюдать выбранную спектральную линию, не внося в неё
существенных искажений, И сравнивать (с высокой точностью) измеряемую частоту с
частотой, фиксируемой спектральной линией. Качество К. с. ч. характеризуется их
стабильностью - способностью сохранять выбранное значение частоты неизменным в
течение длительного промежутка времени.
е-перы частоты,
к-рые позволяют наблюдать выбранную спектральную линию, не внося в неё
существенных искажений, И сравнивать (с высокой точностью) измеряемую частоту с
частотой, фиксируемой спектральной линией. Качество К. с. ч. характеризуется их
стабильностью - способностью сохранять выбранное значение частоты неизменным в
течение длительного промежутка времени.
Квантовые законы накладывают весьма жёсткие ограничения на состояние атомов.
Под действием внешнего электромагнитного поля определённой частоты атомы могут
либо возбуждаться, т. е. скачком переходить из состояния с меньшей энергией E1
в состояние с большей энергией E2, поглощая при этом порцию
(квант) энергии электромагнитного поля, равную:
hv =E2-E1 ,
либо переходить в состояние с меньшей энергией, излучая электромагнитные волны
той же частоты (см. Атом, Квантовая электроника).
К. с. ч. принято разделять на два класса. В активных К. с. ч. квантовые
переходы атомов и молекул непосредственно приводят к излучению электромагнитных
волн, частота к-рых служит стандартом или опорной частотой. Такие приборы наз.
также квантовыми генераторами. В пассивных К. с. ч. измеряемая частота
колебаний внешнего генератора сравнивается с частотой колебаний,
соответствующих определённому квантовому переходу выбранных атомов, т. е. с
частотой спектральной линии. Первыми достигли технич. совершенства и стали
доступными пассивные К. с. ч. на пучках атомов цезия (цезиевые стандарты
частоты). В 1967 междунар. соглашением длительность секунды определена как
9.192.631.770,0 периодов колебаний, соответствующих определённому энергетич.
переходу атомов единственного стабильного изотопа цезия 133Cs. Нуль
после запятой означает, что это число не подлежит дальнейшему изменению. В
цезиевом стандарте частоты наблюдается контур спектральной линии 133Cs,
соответствующей переходу между 2 выбранными уровнями энергии E1
и E2. Частота, соответствующая вершине этой линии,
фиксируется и с ней при помощи спец. устройств сравниваются измеряемые частоты.
Гл. частью К. с. ч. с пучком атомов Cs является атомнолучевая трубка, в
к-рой поддерживается высокий вакуум. В одном конце трубки расположен
источник пучка атомов Cs - полость, в к-рой находится небольшое кол-во жидкого
Cs (рис. 1). Полость соединена с остальной трубкой узким каналом или набором
параллельных каналов. Источник поддерживается при темп-ре ок. 100 0C,
когда Cs находится в жидком состоянии (темп-pa плавления Cs 29,5 0C),
но давление его паров ещё мало, и атомы Cs, вылетая из источника, пролетают
через каналы достаточно редко, не сталкиваясь друг с другом. В результате этого
в трубке формируется слабо расходящийся пучок атомов Cs.
В противоположном конце трубки расположен чрезвычайно чувствительный
приёмник (детектор) атомов Cs, способный зарегистрировать ничтожные изменения в
интенсивности пучка атомов.
Рис. 1. Схема атомнолучевой трубки: / -источник пучка Cs; 2 и 4-отклоняющие
магниты, создающие неоднородные магнитные поля H1 и H2;
3 - объёмный резонатор, в котором возбуждаются электромагнитные волны,
находящийся в постоянном и однородном магнитном поле H; 5 - раскалённая
вольфрамовая проволочка; 6 - коллектор ионов Cs; 7 - измерительный прибор; 8
- область постоянного однородного магнитного поля H (ограничена
пунктиром).
Детектор состоит из раскалённой вольфрамовой проволочки 5 и коллектора 6,
между к-рыми включён источник напряжения (положительный полюс присоединён к
проволочке, а отрицательный - к коллектору). Как только атом Cs касается
раскалённой вольфрамовой проволочки, он отдаёт ей свой внешний электрон
(энергия ионизации Cs равна 3,27 эв, а работа выхода электрона из
вольфрама составляет 4,5 эв; см. Поверхностная ионизация). Ион Cs
притягивается к коллектору. Если на раскалённый вольфрам попадает достаточно
много атомов Cs, то в цепи между коллектором и вольфрамовой проволочкой
возникает электрич. ток, измеряя к-рый, можно судить об интенсивности цезиевого
пучка, попавшего на детектор.
По пути от источника к детектору пучок атомов Cs проходит между полюсными
наконечниками двух сильных магнитов. Неоднородное магнитное поле Hi первого
магнита расщепляет пучок атомов Cs на неск. пучков, в к-рых летят атомы,
обладающие различными энергиями (находящиеся на разных энергетич. уровнях).
Второй магнит (поле H2) направляет (фокусирует) на детектор только
атомы, принадлежащие к одной паре энергетич. уровней E1 и E2,
отклоняя в стороны остальные.
В промежутке между магнитами атомы пролетают через объёмный резонатор 3 -
полость с проводящими стенками, - в к-ром возбуждаются (с помощью
стабильного кварцевого генератора) электромагнитные колебания
определённой частоты. Если под влиянием этих колебаний атом Cs с энергией E1
перейдёт в энергетич. состояние E2, то поле второго магнита
отбросит его от детектора, т. к. для атома, перешедшего в состояние E2,
поле второго магнита уже не будет фокусирующим и этот атом минует детектор. T.
о., ток через детектор окажется уменьшенным на величину, пропорциональную числу
атомов, совершивших энергетич. переходы под влиянием электромагнитного
резонатора. Таким же образом будут зафиксированы переходы атомов Cs из
состояния E_2 в состояние E1.
Число атомов, совершающих вынужденный переход в ед. времени под действием
электромагнитного поля, максимально, если частота действующего на атом
электромагнитного поля точно совпадает с резонансной частотой V0
= (E2 - E1)/n. По мере увеличения
несовпадения (расстройки) этих частот число таких атомов уменьшается. Поэтому,
плавно меняя частоту поля вблизи v0 и откладывая по
горизонтальной оси частоту  , а по вертикали изменение тока детектора, получим
контур спектральной линии, соответствующий переходу E_1->E2
и обратно E_2->E1 (рис. 2, а).
, а по вертикали изменение тока детектора, получим
контур спектральной линии, соответствующий переходу E_1->E2
и обратно E_2->E1 (рис. 2, а).
Частота v0, соответствующая вершине спектральной линии, и
является опорной точкой (репером) на шкале частот, а соответствующий ей период
колебаний принят равным 1/9 192 631,0 сек,
Точность определения частоты, соответствующей вершине спектральной линии,
как правило, составляет неск. процентов, а в лучшем случае - доли процента от
ширины линии. Она тем выше, чем уже спектральная линия. Этим объясняется
стремление устранить или по крайней мере ослабить все причины, приводящие к
уширению используемых спектральных линий.
В цезиевых стандартах уширение спектральной линии (рис. 2,
а) обусловлено
временем взаимодействия атомов с электромагнитным полем резонатора: чем меньше
это время, тем шире линия (см. Неопределённостей соотношение). Время
взаимодействия совпадает со временем пролёта атома через резонатор. Оно
пропорционально длине резонатора и обратно пропорционально скорости атомов.
Рис. 2. Форма спектральной линии в цезиевых стандартах частоты: а - с
обычным резонатором; 6 - в случае П-образного резонатора;  - резонансная
частота,
- резонансная
частота, 
 -
ширина спектральной линии.
-
ширина спектральной линии.
Но длина резонатора не может быть сделана очень большой (увеличивается
рассеяние атомного пучка). Существенно уменьшить скорость атомов, понижая
темп-ру, также невозможно, т. к. при этом падает интенсивность пучка.
Увеличение размеров резонатора затруднено и тем, что он должен располагаться в
весьма однородном по величине и направлению магнитном поле H. Последнее
необходимо потому, что используемые энергетич. переходы в атомах Cs обусловлены
изменением ориентации магнитного момента ядра атома Cs относительно магнитного
момента его электронной оболочки (см. Электронный парамагнитный резонанс). Переходы
такого типа не могут наблюдаться вне магнитного поля, причём частота,
соответствующая таким переходам, зависит (хотя и слабо) от величины этого поля.
Создавать такое поле в большом объёме затруднительно.
Получение узкой спектральной линии достигается применением резонатора
П-образной формы (рис. 3). В этом резонаторе пучок пролетает через отверстие
вблизи его концов и только там взаимодействует с высокочастотным
электромагнитным полем. Поэтому только в двух этих небольших областях
необходимы однородность и стабильность магнитного поля H. При этом перед
вторым влётом в резонатор атомы "сохраняют" результат первого
взаимодействия с полем. В случае П-образного резонатора спектральная линия
приобретает более сложную форму (рис. 2,6), отражающую и время пролёта в
электромагнитном поле внутри резонатора (широкий пьедестал), и полное время
пролёта между обоими концами резонатора (узкий центральный пик). Именно узкий
центральный пик служит для фиксации частоты.
Рис. 3. Схема атомнолучевой трубки с П-образным резонатором (обозначения те
же, что и на рис. 1).
В К. с. ч. с пучком атомов Cs погрешность в значении частоты v0
имеет место лишь в 13-м знаке для уникальных устройств (эталонов частоты) и в
12-м знаке для серийных приборов высокой точности (вторичных эталонов или
стандартов частоты).
В состав К. с. ч. с пучком атомов Cs наряду с атомнолучевой трубкой и
кварцевым генератором входят спец. радиосхемы, позволяющие с высокой точностью
сравнивать измеряемую частоту внешних генераторов с частотой, определяемой К.
с. ч. Кроме того, обычно цезиевый стандарт дополняют устройствами,
вырабатывающими набор "целых" стандартных частот, стабильность к-рых
равна стабильности эталона. Иногда эти системы вырабатывают и сигналы точного
времени. В таких случаях К. с. ч. превращается в квантовые часы.
Уникальные лабораторные образцы К. с. ч. на пучках атомов Cs, входящие в
состав нац. эталонов частоты и времени, обеспечивают воспроизведение
длительности секунды, а следовательно всей системы измерения частоты и времени
с относительной погрешностью, меньшей чем 10-11. Эта относительная
погрешность практически не превышает 10-12, но для фиксации этого
значения междунар. соглашением необходимо проведение длительных наблюдений.
Существенным преимуществом К. с. ч. на пучках атомов цезия является то, что их
пром. конструкции обеспечивают воспроизведение номинального значения частоты
(времени) с погрешностью 10-11, т. е. не уступают по точности
эталону. Даже малогабаритные приборы этого типа, пригодные для применения в
условиях обычных лабораторий и на подвижных объектах, работают с погрешностью
не более 10-10, а нек-рые образцы и 10-11.
Наиболее важным активным К. с. ч. является водородный квантовый генератор
(рис. 4). В водородном генераторе пучок атомов водорода выходит из источника 1,
где при низком давлении под влиянием электрич. разряда молекулы водорода
расщепляются на атомы. Размеры каналов, сквозь к-рые атомы вылетают из
источника 1 в вакуумную камеру, меньше, чем расстояние, пролетаемое атомами
водорода между их столкновениями. При этом условии атомы водорода вылетают из
источника в виде узкого лучка. Этот пучок проходит между полюсными
наконечниками многополюсного магнита 2. Действие поля, создаваемого
таким магнитом, таково, что оно фокусирует вблизи оси пучка атомы, находящиеся
в возбуждённом состоянии, и разбрасывает в стороны атомы, к-рые находятся в
основном (невозбуждённом) состоянии.
Рис. 4. Устройство водородного генератора:
1 - источник атомного пучка; 2
- сортирующая система (многополюсный магнит); 3 - резонатор; 4 - накопительная
колба.
Возбуждённые атомы пролетают через маленькое отверстие в кварцевую колбу 4,
находящуюся внутри объёмного резонатора 3, настроенного на частоту,
соответствующую переходу атомов водорода из возбуждённого состояния в основное.
Под действием электромагнитного поля атомы водорода излучают, переходя в основное
состояние. Фотоны, излучаемые атомами водорода в течение сравнительно большого
времени, определяемого добротностью резонатора, остаются внутри него, вызывая
снова вынужденное испускание таких же фотонов атомами водорода, влетающими
позже. T. о., резонатор создаёт обратную связь, необходимую для самовозбуждения
генератора (см. Генерирование электрических колебаний). Однако
достижимая интенсивность пучков атомов водорода всё же недостаточна для того,
чтобы обеспечить самовозбуждение такого генератора, если используется обычный
объёмный резонатор. Поэтому в резонатор помещают кварцевую колбу 4, стенки
к-рой покрыты изнутри тонким слоем фторопласта (тефлона). Возбуждённые
атомы водорода могут удариться о плёнку тефлона более десяти тысяч раз, не
потеряв при этом свою избыточную энергию. Благодаря этому в колбе скапливается
значит, число возбуждённых атомов водорода и среднее время пребывания каждого
из них в резонаторе увеличивается примерно до 1 сек. Этого достаточно
для того, чтобы условия самовозбуждения были выполнены и водородный генератор
начал работать, излучая электромагнитные волны с чрезвычайно стабильной
частотой.
Колба, размеры к-рой выбираются меньшими, чем генерируемая длина волны,
играет ещё одну, чрезвычайно важную роль. Хаотичное движение атомов водорода
внутри колбы должно было бы привести к уширению спектральной линии вследствие
эффекта Доплера (см. Доплера эффект). Однако если движение атомов
ограничено объёмом, размеры к-рого меньше длины волны, то спектральная линия
приобретает вид узкого пика, возвышающегося над широким низким пьедесталом. В
результате этого в водородном генераторе, генерирующем излучение с длиной
волны  = 21 см, ширина спектральной линии составляет всего 1 гц.
= 21 см, ширина спектральной линии составляет всего 1 гц.
Именно чрезвычайно малая ширина спектральной линии обеспечивает малую
погрешность частоты водородного генератора, также лежащую в пределах 13-го
знака. Погрешность обусловлена взаимодействием атомов водорода с фторпластовым
покрытием колбы. Значение этой частоты, измеренное при помощи К. с. ч. на пучке
атомов Cs (см. выше), равно 1.420.405.751,7860 + 0,0046 гц. Мощность
водородного генератора чрезвычайно мала (~10-12вт). Поэтому
К. с. ч. на основе водородного генератора включает в себя, помимо схем сравнения
и формирования сетки стандартных частот, чрезвычайно чувствительный приёмник.
Оба описанных К. с. ч. работают в диапазоне сверхвысоких радиочастот (СВЧ).
Известен ряд др. атомов и молекул, спектральные линии к-рых позволяют создавать
активные и пассивные К. с. ч. радиодиапазона. Однако они пока не нашли практич.
применения. Лишь К. с. ч. на атомах рубидия, основанные на методе оптической
накачки, широко применяются в качестве вторичного стандарта частоты в
лабораторной практике, а также в системах радионавигации и в квантовых часах.
К. с. ч. оптич. диапазона представляют собой лазеры, в к-рых приняты
спец. меры для стабилизации частоты их излучения. В оптич. диапазоне
доплеровское уширение спектральных линий очень велико и из-за малой длины
световых волн подавить его так, как это сделано в водородном генераторе, не
удаётся. Создать же эффективный лазер на пучках атомов или молекул пока также
не удаётся. T. к. в пределах доплеровской ширины спектральной линии помещается
неск. относительно узких резонансных линий оптич. резонатора, то частота
генерации подавляющего большинства лазеров определяется не столько частотой
используемой спектральной линии, сколько размерами оптич. резонатора,
определяющими его резонансные частоты. Но эти частоты не остаются постоянными,
а изменяются под влиянием изменений темп-ры, давления, под действием вибраций,
старения и т. п.
Наименьшая относительная погрешность частоты у оптич. К. с. ч.(~ 10-13)
достигнута с помощью гелий-неонового лазера, генерирующего на волне 3,39 мкм
(см. Газовый лазер). Внутрь резонатора лазера помещена трубка,
наполненная метаном при низком давлении. Метановая ячейка деформирует форму
спектральной линии лазера, образуя на ней чрезвычайно узкий и стабильный по
частоте резонансный пик. Именно на вершине этого пика происходит
самовозбуждение лазера, а частота его излучения определяется гл. обр.
положением вершины пика. Для повышения максимальной стабильности вся
конструкция помещается в термостат, стабилизируются источники питания, длина
резонатора и т. п.
К. с. ч. оптич. диапазона пока ещё не связаны (в метрологич. смысле) с К. с.
ч. радиодиапазона, а следовательно, с единицей частоты (гц) и единицей
времени (сек). Непосредственное измерение частоты (сравнение с эталоном)
возможно только в длинноволновом участке инфракрасного диапазона (3,39 мкм и
длиннее).
Лит.: Квантовая электроника, Маленькая энциклопедия, M., 1969, с. 35;
Григорьянц В. В., Ж а б о т и н с к и й M. E., Золин В. Ф., Квантовые стандарты
частоты, M., 1968, с. 164, 194; Басов H. Г., Беленов Э. M., Сверхузкие
спектральные линии и квантовые стандарты частоты, "Природа",
1972, № 12.
M. E. Жаботинский.
КВАНТОВЫЕ ЧАСЫ, устройство для точного измерения времени, основной
частью к-рого является квантовый стандарт частоты. Роль
"маятника" в К. ч. играют атомы. Частота, излучаемая или поглощаемая
атомами при их квантовых переходах из одного энергетич. состояния в
другое, регулирует ход К. ч. Эта частота настолько стабильна, что К. ч.
позволяют измерять время точнее, чем астрономич. методы (см. Время). К.
ч. часто наз. атомными часами.
К. ч. применяются в системах радионавигации, в астрономич.
обсерваториях, в исследовательских и контрольно-измерит. лабораториях и т. п.,
заменяя собой менее совершенные кварцевые часы.
Сигналы квантовых стандартов частоты сами по себе не могут быть использованы
для вращения часового механизма, т. к. мощность этих сигналов ничтожно мала, а
частота колебаний, как правило, весьма высока и имеет нецелочисленное значение
(напр., мощность атомного водородного генератора составляет 10-11
-10-12 вт, а частота равна 1420,406 Мгц). Это
затрудняет непосредственное использование квантовых стандартов частоты в службе
времени, в различных навигационных системах, а также в лабораторной
практике. В этих случаях более удобно иметь набор (сетку) стандартных
высокостабильных частот: 1 кгц, 10 кгц, 100 кгц, 1 Мгц и
т. д. при высокой мощности выходного сигнала. Поэтому К. ч., помимо квантового
стандарта частоты, содержат спец. радиотехнич. устройства, формирующие такую
сетку частот и обеспечивающие вращение стрелок часов (или смену цифр на их
циферблате) и выдачу сигналов точного времени.
Большинство К. ч. содержит вспомогательный кварцевый генератор. Из-за
изменения частоты кварцевого генератора во времени (старения) точность базирующихся
на нём кварцевых часов была бы сама по себе недостаточно высока. В К. ч.
частота кварцевого генератора контролируется с помощью квантового стандарта
частоты, благодаря чему точность часов повышается до уровня точности самого
квантового стандарта. Однако введение периодич. поправок оператором не всегда
удобно. Для нек-рых устройств, в частности навигационных, более рационально
повышение стабильности частоты кварцевого генератора с помощью автоматич.
подстройки его частоты к частоте квантового стандарта.
В одном из вариантов такой подстройки (фазовая автоподстройка частоты, рис.
1) частота vKB кварцевого генератора (обычно ~10-20 Мгц) умножается
радиотехнич. средствами в нужное число (и) раз и в смесителе вычитается из
частоты квантового стандарта vCT. Подбором конкретных
значений  кв
и n разностную частоту
кв
и n разностную частоту  = (vCT - n
= (vCT - n КВ) можно сделать
приблизительно равной частоте кварцевого генератора:
КВ) можно сделать
приблизительно равной частоте кварцевого генератора:  КВ = (vCT
- n
КВ = (vCT
- n  КВ).
КВ).
Рис. 1. Блок-схема квантовых часов с фазовой автоматической подстройкой
частоты.
После усиления сигнал разностной частоты ( ст - n
ст - n КВ) подаётся
на один вход фазового детектора, а на другой его вход подаются колебания
кварцевого генератора. Фазовый детектор вырабатывает напряжение, величина и
знак к-рого зависят от отклонения разностной частоты Д и частоты кварцевого
генератора vKВ друг от друга. Это напряжение подаётся затем
на блок управления частотой кварцевого генератора и вызывает сдвиг частоты
генератора, к-рый компенсирует отклонение vKВ от разностной
частоты Д. T. о., любое изменение частоты кварцевого генератора вызывает
появление на выходе блока управления напряжения соответствующей величины и
знака, сдвигающего частоту в обратном направлении. Поэтому частота кварцевого
генератора автоматически поддерживается неизменной. В результате стабильность
его частоты становится практически равной стабильности частоты квантового
стандарта. Синтезатор частот формирует из сигнала кварцевого генератора сетки
столь же точных стандартных частот. Одна из них служит для питания электрич.
часов, а остальные используются для метрологических и др. целей. Погрешность
хода лучших К. ч. такого типа при тщательном изготовлении и настройке
составляет не более 1 сек за неск. тыс. лет. Первые К. ч. были созданы в
1957 (рис. 2). Стандартом частоты в них служил молекулярный генератор на
пучке молекул аммиака. Созданные позднее К. ч., в к-рых используется квантовый
стандарт частоты с пучком атомов цезия, не нуждаются в калибровке по эталону,
т. к. номинальное значение опорной частоты может быть установлено на основе
манипуляций в самом приборе.
КВ) подаётся
на один вход фазового детектора, а на другой его вход подаются колебания
кварцевого генератора. Фазовый детектор вырабатывает напряжение, величина и
знак к-рого зависят от отклонения разностной частоты Д и частоты кварцевого
генератора vKВ друг от друга. Это напряжение подаётся затем
на блок управления частотой кварцевого генератора и вызывает сдвиг частоты
генератора, к-рый компенсирует отклонение vKВ от разностной
частоты Д. T. о., любое изменение частоты кварцевого генератора вызывает
появление на выходе блока управления напряжения соответствующей величины и
знака, сдвигающего частоту в обратном направлении. Поэтому частота кварцевого
генератора автоматически поддерживается неизменной. В результате стабильность
его частоты становится практически равной стабильности частоты квантового
стандарта. Синтезатор частот формирует из сигнала кварцевого генератора сетки
столь же точных стандартных частот. Одна из них служит для питания электрич.
часов, а остальные используются для метрологических и др. целей. Погрешность
хода лучших К. ч. такого типа при тщательном изготовлении и настройке
составляет не более 1 сек за неск. тыс. лет. Первые К. ч. были созданы в
1957 (рис. 2). Стандартом частоты в них служил молекулярный генератор на
пучке молекул аммиака. Созданные позднее К. ч., в к-рых используется квантовый
стандарт частоты с пучком атомов цезия, не нуждаются в калибровке по эталону,
т. к. номинальное значение опорной частоты может быть установлено на основе
манипуляций в самом приборе.
Рис. 2. Первые квантовые часы, построенные в Национальном бюро стандартов
США, с молекулярным аммиачным генератором в качестве квантового стандарта
частоты.
Недостатки этих К. ч.- большой вес и чувствительность к вибрациям. В К. ч.
другого типа (наиболее распространённых) применяется рубидиевый стандарт
частоты с оптич. накачкой. Они легче, компактнее, не боятся вибраций, но
нуждаются в калибровке, после чего они поддерживают установленное значение
частоты с погрешностью порядка 10-11 в течение года. Осн. частью
рубидиевых К. ч. является спец. радиоспектроскоп с оптич. накачкой и оптич.
индикацией, фиксирующий спектральную линию изотопа 87Rb, лежащую в
диапазоне СВЧ. Спектроскоп содержит объёмный резонатор 3, в к-ром
находится колба 2 с парами изотопа 87Rb (рис. 3) при давлении
~ 10-6 мм рт. ст.
Рис. 3. Схема рубидиевого стандарта частоты с оптической накачкой: / -
лампа, освещающая колбу 2, наполненную парами 87Rb; 3 -
объёмный резонатор; 4 - фото детектор; 5 - усилитель низкой
частоты; 6 - фазовый детектор; 7 - генератор низкой частоты; 8 - кварцевый
генератор; 9 - умножитель частоты.
Резонатор настроен на частоту спектральной линии 87Rb, равную
6835 Мгц. Чувствительность обычного радиоспектроскопа недостаточна для
того, чтобы зафиксировать радиочастотную линию 87Rb. Для увеличения
чувствительности используются оптич. накачка паров 87Rb и оптич.
индикация спектральной линии. На атомы 87Rb направляется свет,
частота к-рого совпадает с частотой др. спектральной линии 87Rb,
лежащей в оптич. диапазоне. Газоразрядная лампа 1 низкого давления с парами 87Rb
освещает колбу. Свет, прошедший сквозь колбу, попадает на фотоприёмник (напр.,
фотоэлектронный умножитель). Под действием света рубидиевой лампы (накачка) атомы 87Rb
возбуждаются, т. е. переходят из состояния с энергией E_2 в состояние с
энергией E3 (рис. 4). Если интенсивность света достаточно
высока, то наступает насыщение - число атомов, находящихся в состояниях E2и
E3, становится одинаковым. При этом поглощение света в парах
уменьшается (т. к. число невозбуждённых частиц на уровне E_2 способных
поглощать кванты света, уменьшается) и пары 87Rb становятся
прозрачнее, чем они были бы при воздействии на них накачки. Если одновременно с
накачкой пары 87Rb облучить радиоволной, частота к-рой равна частоте
спектральной линии, лежащей в диапазоне СВЧ и соответствующей переходам атомов 87Rb
между уровнями E1 и E2, то, поглощаясь, она
переводит атомы 87Rb с уровня E1 на уровень E2
(рис. 4). Такая радиоволна будет препятствовать насыщающему действию световой
волны, в результате чего поглощение света в парах 87Rb увеличится.
T. о., измеряя при помощи фотоприёмника интенсивность света, прошедшего через
колбу с парами 87Rb, можно точно определить, действуют ли
одновременно на эти пары свет с частотой, соответствующей переходу E2
-> E3, и радиоволна с частотой перехода E1->E2.
Рис. 4. Уровни энергии атомов 87Rb, используемые в рубидиевых
часах.
Источником радиоволны служит кварцевый генератор, возбуждающий в резонаторе
электромагнитное поле резонансной частоты. Если плавно изменять частоту
генератора, то в момент её совпадения с частотой радиоспектральной линии 87Rb
интенсивность света, попадающего на фотоприёмник, резко уменьшится.
Зависимость интенсивности света, прошедшего через пары 87Rb, от
частоты радиоволны используется для автоматич. подстройки частоты колебаний
кварцевого генератора по частоте радиоспектральной линии. Колебания кварцевого
генератора модулируются по фазе при помощи вспомогат. генератора низкой частоты
(см. Модуляция колебаний. Фазовая модуляция). Поэтому свет, проходящий
через колбу, оказывается модулированным по интенсивности той же низкой
частотой. Модуляция света тем сильнее, чем точнее совпадает частота
электромагнитного поля в резонаторе с частотой радиоспектральной линии 87Rb.
Электрич. сигнал фотоприёмника после усиления подаётся на фазовый детектор, на
к-рый поступает также сигнал непосредственно от низкочастотного генератора.
Амплитуда выходного сигнала фазового детектора тем больше, чем меньше разность
частот (расстройка) частоты спектральной линии и поля резонатора. Этот сигнал
подаётся на элемент, изменяющий частоту кварцевого генератора, и поддерживает
её значение таким, чтобы оно точно совпадало с вершиной спектральной линии 87Rb.
Точность рубидиевых К. ч. определяется гл. обр. шириной радиоспектральной
линии 87Rb. Осн. причиной, приводящей к уширению спектральных линий
газов (паров) при низких давлениях, является Доплера эффект. Для уменьшения
его влияния в колбу с парами 87Rb добавляется буферный газ (при
давлении неск. мм рт. ст.). Атомы 87Rb, сталкиваясь с атомами
буферного газа, оказываются как бы зажатыми между ними и совершают быстрые
хаотич. движения, оставаясь в среднем почти на одном месте, лишь медленно
диффундируя внутри колбы. В результате спектральная линия приобретает вид
узкого пика на широком низком пьедестале. Ширина и положение этого пика зависят
от состава буферного газа. Напр., смесь из 50% неона и 50% аргона позволяет
свести ширину спектрального пика примерно до 100 гц, причём его
положение смещается лишь на 0,02 гц при изменении темп-ры на 1 0C
или давления на 1 мм рт. ст.
Точность рубидиевых К. ч. обусловлена также постоянством интенсивности света
лампы накачки, поэтому применяются системы автоматич. регулирования
интенсивности. Возможно создание рубидиевых К.ч., в к-рых вместо описанной
системы оптич. индикации используется квантовый генератор с парами рубидия. В
этих К. ч. применяются настолько интенсивная оптич. накачка и резонатор со
столь высокой добротностью, что в нём выполняются условия самовозбуждения. При
этом пары 87Rb, наполняющие колбу внутри резонатора, излучают
электромагнитные волны на частоте 6835 Мгц. Радиосхема таких К. ч. также
содержит кварцевый генератор и синтезатор, но в отличие от предыдущего частота
кварцевого генератора управляется системой фазовой автоподстройки, в к-рой
опорной является частота сигнала рубидиевого генератора.
Лит.: Квантовая электроника, Маленькая энциклопедия, M., 1969, с. 35,
241; Григорьянц В. В., Ж а б о т и н с к и й M. E., Золин В. Ф., Квантовые
стандарты частоты, M., 1968, с. 171.
М. E. Жаботинский.
КВАНТОВЫЕ ЧИСЛА, целые (0,1,2,...) или полуцелые
½, 3/2, 5/2, ...)числа,
определяющие возможные дискретные значения физич. величин, к-рые характеризуют
квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные
частицы. Применение К. ч. в квантовой механике отражает черты
дискретности процессов, протекающих в микромире, и тесно связано с
существованием кванта действия, или Планка постоянной h. К. ч. были
впервые введены в физику для описания найденных эмпирически закономерностей
атомных спектров (см. Атом), однако смысл К. ч. и связанной с ними
дискретности нек-рых величин, характеризующих динамику микрочастиц, был раскрыт
лишь квантовой механикой.
Набор К. ч., исчерпывающе определяющий состояние квантовой системы, наз.
полным. Совокупность состояний, отвечающих всем возможным значениям К. ч. из
полного набора, образует полную систему состояний. Состояние электрона в атоме
определяется четырьмя К. ч. соответственно четырём степеням свободы электрона
(3 степени свободы связаны с тремя координатами, определяющими пространственное
положение электрона, а четвёртая, внутренняя, степень свободы - с его спином).
Для атома водорода и водородоподобных атомов эти К. ч., образующие полный
набор, следующие.
Главное К. ч. и = 1, 2, 3, ... определяет уровни энергии электрона.
Азимутальное (или орбитальное) К. ч. / = О, 1, 2, ..., 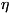 -1 задаёт спектр
возможных значений квадрата орбитального момента количества движения электрона:
Ml2 - h2l(l + 1).
-1 задаёт спектр
возможных значений квадрата орбитального момента количества движения электрона:
Ml2 - h2l(l + 1).
Магнитное К. ч. m1 характеризует возможные значения
проекции M12 орбитального момента Ml на
нек-рое, произвольно выбранное, направление (принимаемое за ось z): Mlz=
hml; может принимать целые значения в интервале от -l
до +l (всего 2l + 1 значений).
Магнитное спиновое К. ч., или просто спиновое К. ч., ms
характеризует возможные значения проекции спина электрона и может принимать 2
значения:
ms = ±1/2.
Задание состояния электрона с помощью К. ч. п, I, ml и msне
учитывает т. н. тонкой структуры энергетич. уровней - расщепления уровней с
данным n (при n=>2) в результате влияния спина на орбитальное
движение электрона (см. Спин-орбитальное взаимодействие). При учёте
этого взаимодействия для характеристики состояния электрона вместо mlи
ms применяют К. ч. j и mj.
К. ч. j полного момента количества движениям электрона (орбитального
плюс спинового) определяет возможные значения квадрата полного момента: M2=
h2j(j+1) и при заданном l может принимать 2 значения:
j =l / ±1/2.
Магнитное квантовое число полного момента mj определяет
возможные значения проекции полного момента на ось z, Mz =
hmj; может принимать 2j + 1 значений: mj = -j, -j
+ 1, ..., +j.
Те же К. ч. приближённо описывают состояния отдельных электронов в сложных
(многоэлектронных) атомах (а также состояния отдельных нуклонов - протонов и
нейтронов - в атомных ядрах). В этом случае n нумерует последовательные
(в порядке возрастания энергии) уровни энергии с заданным l. Состояние
же многоэлектронного атома в целом определяется след. К. ч.: К. ч. полного
орбитального момента атома L, определяемого движением всех электронов, L
= O, 1, 2, ...; К. ч. полного момента атома ], к-рое может принимать значения
с интервалом в 1 от j = |L - S| до J = L+S, где S - полный спин атома (в
единицах И); магнитным квантовым числом mJ определяющим
возможные значения проекции полного момента атома на ось z, Mz, =
mjh, и принимающим 1J+1 значений.
Для характеристики состояния атома и вообще квантовой системы вводят ещё
одно К. ч.- чётность состояния P, к-рое принимает значения +1 или -1 в
зависимости от того, сохраняет волновая функция, определяющая состояние
системы, знак при отражении координат r относительно начала координат
(т. е. при замене r->-r) или меняет его на обратный. Чётность
P для атома водорода равна (-1)l, а для многоэлектронных атомов (-1)L.
К. ч. оказались также удобными для формулировки отбора правил, определяющих
возможные типы квантовых переходов.
В физике элементарных частиц и в ядерной физике вводится ряд др. К.
ч. Квантовые числа элементарных частиц - это внутренние характеристики частиц,
определяющие их взаимодействия и закономерности взаимных превращений. Кроме
спина s, к-рый может быть целым или полуцелым числом (в единицах h), к
ним относятся: электрический заряд Q - у всех известных элементарных
частиц равен либо О, либо целому числу, положительному или отрицательному (в
единицах величины заряда электрона е); барионный заряд В - равен О или 1
(для античастиц О, -1); лептонные заряды, или. лептон-ные числа,
- электронное Le и мюонное Lm, равны О или +1 (для
античастиц О, -1); изотопический спин T - целое или полуцелое число; странность
S или гиперзаряд Y (связанный с S соотношением Y = S+B) - все
известные элементарные частицы (или античастицы) имеют S = O или ±1, ±2, ±3;
внутренняя чётность П - К. ч., характеризующее свойства симметрии элементарных
частиц относительно отражений координат, может быть равна +1 (такие частицы
наз. чётными) и -1 (нечётные частицы), и нек-рые др. К. ч. Эти К. ч.
применяются и к системам из неск. элементарных частиц, в т. ч. к атомным ядрам.
При этом полные значения электрич., барионного и лептонного зарядов и
странности системы частиц равны алгебраич. сумме соответствующих К. ч.
отдельных частиц, полный спин и изото-пич. спин получаются по квантовым
правилам сложения моментов, а внутр. чётности частиц перемножаются.
В широком смысле К. ч. часто называют физич. величины, определяющие движение
квантовомеханич. частицы (или системы), сохраняющиеся в процессе движения, но
не обязательно принадлежащие к дискретному спектру возможных значений. Напр.,
энергию свободно движущегося электрона (имеющую непрерывный спектр значений)
можно рассматривать как одно из его К. ч.
Лит. см. при ст. Атомная физика, Элементарные частицы.
Д. В. Гальцов.
КВАНТОВЫЙ ГЕНЕРАТОР, генератор электромагнитных волн, в к-ром
используется явление вынужденного излучения (см.Квантовая электроника). К.г. радиодиапазона сверхвысоких частот (СВЧ), так же как и квантовый
усилитель этого диапазона, часто наз. мазером. Первый К. г. был
создан в диапазоне СВЧ в 1955 одновременно в СССР (H. Г. Басов и A. M.
Прохоров)
и в США (Ч. Таунс). В качестве активной среды в нём использовался
пучок молекул аммиака. Поэтому он получил назв. молекулярного генератора. В
дальнейшем был построен К. г. СВЧ на пучке атомов водорода. Важная особенность
этих К. г.- высокая стабильность частоты генерации, достигающая 10-13,
в силу чего они используются как квантовые стандарты частоты.
К. г. оптич. диапазона - лазеры (оптические квантовые генераторы,
ОКГ) появились в 1960. Лазеры работают в широком диапазоне длин волн от
ультрафиолетовой до субмиллиметровой областей спектра, в импульсном и
непрерывном режимах. Существуют лазеры на кристаллах и стёклах, газовые,
жидкостные и полупроводниковые. В отличие от др. источников света, лазеры
излучают высококогерентные монохроматические световые волны, вся энергия к-рых
концентрируется в очень узком телесном угле.
Лит. см. при ст. Квантовая электроника.
КВАНТОВЫЙ ГИРОСКОП, прибор, позволяющий обнаруживать вращение тела и
определять его угловую скорость, основанный на гироскопич. свойствах
электронов, атомных ядер или фотонов.
Лазерный (оптический) г и р о с к о п. Датчиком оптич. гироскопа служит
кольцевой лазер, генерирующий две бегущие навстречу друг другу световые
волны, к-рые распространяются по общему световому каналу в виде узких
монохроматич. световых пучков. Резонатор кольцевого лазера (рис. 1) состоит из
трёх (или больше) зеркал 1,2,3, смонтированных на жёстком
основании и образующих замкнутую систему. Часть света проходит через
полупрозрачное зеркало 3 и попадает на фотодетектор 5. Длина волны,
генерируемая кольцевым лазером (в пределах ширины спектральной линии рабочего
вещества), определяется условием, согласно к-рому бегущая волна, обойдя контур
резонатора, должна прийти в исходную точку с той же фазой, к-рую имела вначале.
Рис. 1. Схема лазерного гироскопа:
1, 2, 4 - непрозрачные зеркала; 3
- полупрозрачное зеркало; 5 - фотодетектор.
Если прибор неподвижен, то это имеет место, когда в периметре P контура
укладывается целое число n длин волн  o, т. е. P = n
o, т. е. P = n 0.
В этом случае лазер генерирует 2 встречные волны, частоты которых одинаковы и
равны:
0.
В этом случае лазер генерирует 2 встречные волны, частоты которых одинаковы и
равны:
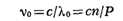
(с - скорость света).
Если же весь прибор вращается с угловой скоростью 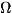 вокруг направления,
составляющего угол
вокруг направления,
составляющего угол 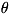 с перпендикуляром к его плоскости (рис. 2), то за
время обхода волной контура последний успеет повернуться на нек-рый угол. В
зависимости от направления распространения волны путь, проходимый ею до
совмещения фазы, будет больше или меньше P (см. Доплера эффект). В
результате этого частоты встречных волн становятся неодинаковыми. Можно
показать, что эти частоты
с перпендикуляром к его плоскости (рис. 2), то за
время обхода волной контура последний успеет повернуться на нек-рый угол. В
зависимости от направления распространения волны путь, проходимый ею до
совмещения фазы, будет больше или меньше P (см. Доплера эффект). В
результате этого частоты встречных волн становятся неодинаковыми. Можно
показать, что эти частоты  - и v+ не зависят от формы контура и связаны с
частотой
- и v+ не зависят от формы контура и связаны с
частотой 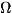 вращения прибора соотношением:
вращения прибора соотношением:
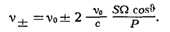
Здесь S -площадь, охватываемая контуром резонатора. Фотодетектор,
чувствительный к интенсивности света, в этом случае зарегистрирует биения с
разностной частотой:
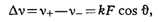
где
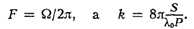
Напр., для квадратного гелий-неонового К. г. (см.
Газовый лазер) со
стороной 25 см  0 = 6-10-5 см, откуда
k = 2,5-106. При этом суточное вращение Земли, происходящее с
угловой скоростью
0 = 6-10-5 см, откуда
k = 2,5-106. При этом суточное вращение Земли, происходящее с
угловой скоростью 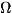 = 15 град/ч, на широте € = 60° должно
приводить к частоте биений
= 15 град/ч, на широте € = 60° должно
приводить к частоте биений 
 = 15 гц. Если ось К. г. направить на Солнце,
то, измеряя частоту биений и считая угловую скорость
= 15 гц. Если ось К. г. направить на Солнце,
то, измеряя частоту биений и считая угловую скорость 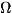 вращения
вращения
Земли известной, можно с точностью до долей град определить
широту 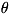 места, на к-рой расположен К. г.
места, на к-рой расположен К. г.
Интегрирование угловой скорости вращающегося тела по времени (к-рое может
выполняться автоматически) позволяет определить угол поворота, как функцию
времени. Предел чувствительности оптич. К. г. теоретически определяется спонтанным
излучением атомов активной среды лазера. Если частоте биений 
 = 1 гц соответствует
угол поворота в 1 град/ч, то предел точности К. г. равен 10-3
град/ч. В существующих оптич. К. г. этот предел ещё далеко не достигнут.
= 1 гц соответствует
угол поворота в 1 град/ч, то предел точности К. г. равен 10-3
град/ч. В существующих оптич. К. г. этот предел ещё далеко не достигнут.
Ядерные и электронные гироскопы. В ядерных К. г. используются вещества с
ядерным парамагнетизмом (вода, органич. жидкости, газообразный гелий,
пары ртути). Атомы или молекулы таких веществ в основном (невозбуждённом)
состоянии обладают моментами количества движения, обусловленными только спинами
ядер (электронные же спиновые моменты у них скомпенсированы, т. е. все
электроны спарены). Со спинами ядер связаны их магнитные моменты. Если
ориентировать магнитные моменты ядер, напр, при помощи внешнего магнитного
поля, а затем ориентирующее поле выключить, то в отсутствие др; магнитных полей
(напр., земного) возникший суммарный магнитный момент M будет нек-рое
время сохранять своё направление в пространстве, независимо от изменения
ориентации датчика. Такой статический К. г. позволяет определить изменение
положения тела, связанного с датчиком гироскопа.
T. к. величина момента M будет постепенно убывать благодаря релаксации,
то для К. г. выбирают вещества с большими временами релаксации, напр,
некоторые органич. жидкости, для к-рых время релаксации 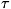 составляет неск. мин, жидкий
3He (ок. 1 ч) или раствор жидкого 3He (10-3% ) в 4He
(около года).
составляет неск. мин, жидкий
3He (ок. 1 ч) или раствор жидкого 3He (10-3% ) в 4He
(около года).
В К. г., работающем по методу ядерной индукции, вращение с угловой
скоростью 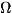 датчика К. г., к-рый содержит ядра с ориентированными магнитными
моментами, эквивалентно действию на ядра магнитного поля с напряжённостью H
=
датчика К. г., к-рый содержит ядра с ориентированными магнитными
моментами, эквивалентно действию на ядра магнитного поля с напряжённостью H
= 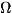 /
/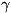 я, где
я, где 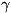 я - гиромагнитное отношение для
ядер. Прецессия магнитных моментов ядер вокруг направления поля H приводит
к появлению переменной эдс в катушке L, охватывающей рабочее вещество К.
г. (рис. 3). Определение частоты
я - гиромагнитное отношение для
ядер. Прецессия магнитных моментов ядер вокруг направления поля H приводит
к появлению переменной эдс в катушке L, охватывающей рабочее вещество К.
г. (рис. 3). Определение частоты 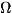 вращения тела, связанного с датчиком К. г.,
сводится к измерению частоты электрич. сигнала, к-рая пропорциональна
вращения тела, связанного с датчиком К. г.,
сводится к измерению частоты электрич. сигнала, к-рая пропорциональна 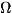 (см.
Ядерный магнитный резонанс).
(см.
Ядерный магнитный резонанс).
В динамическом ядерном гироскопе суммарный ядерный магнитный момент M датчика
прецессирует вокруг постоянного магнитного поля H, жёстко связанного с
устройством. Вращение датчика вместе с полем H с угловой скоростью 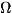 приводит к
изменению частоты прецессии магнитного момента M, приблизительно равному
проекции вектора
приводит к
изменению частоты прецессии магнитного момента M, приблизительно равному
проекции вектора 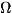 на Н. Это изменение регистрируется в виде
электрич. сигнала. Для получения высокой чувствительности и точности в этих
приборах требуется высокая стабильность и однородность магнитного поля H. Напр.,
для обнаружения изменения частоты прецессии, вызванного суточным вращением
Земли, необходимо, чтобы
на Н. Это изменение регистрируется в виде
электрич. сигнала. Для получения высокой чувствительности и точности в этих
приборах требуется высокая стабильность и однородность магнитного поля H. Напр.,
для обнаружения изменения частоты прецессии, вызванного суточным вращением
Земли, необходимо, чтобы  Н/Н<=I0-9. Для экранировки прибора
от действия внешних магнитных полей применяются сверхпроводники (см.
Сверхпроводимость).
Напр., если поворот датчика обусловлен суточным вращением Земли, то
остаточное поле в экране не должно превышать 3· 10-9 э.
Н/Н<=I0-9. Для экранировки прибора
от действия внешних магнитных полей применяются сверхпроводники (см.
Сверхпроводимость).
Напр., если поворот датчика обусловлен суточным вращением Земли, то
остаточное поле в экране не должно превышать 3· 10-9 э.
Электронные К. г. аналогичны ядерным, но в них применяются вещества, атомы
или молекулы к-рых содержат неспаренные электроны (напр., устойчивые свободные
радикалы, атомы щелочных металлов). Хотя времена релаксации электронных спинов
малы, электронные К. г. перспективны, т. к. гиромагнитное отношение 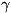 эл
Для электронов в сотни раз больше, чем для ядер, и, следовательно, выше частота
прецессии, что важно для многих применений.
эл
Для электронов в сотни раз больше, чем для ядер, и, следовательно, выше частота
прецессии, что важно для многих применений.
Несмотря на то что К. г., особенно оптические, непрерывно совершенствуются,
их точность и чувствительность ещё уступают лучшим образцам механич. гироскопов.
Однако К. г. обладают рядом существенных преимуществ перед механич.
гироскопами: они не содержат движущихся частей (безынерционны), не требуют
арретирования, обладают высокой надёжностью и стабильностью, приводятся в
действие в течение короткого промежутка времени, могут выдержать значит,
ускорения и работать при низких темп-pax. Нек-рые типы К. г. уже применяются не
только как высокочувствительные индикаторы вращения, ориентаторы и гирометры,
но и как гирокомпасы, гиробуссоли и секстанты.
Лит.: Привалов В. E., Фридрихов С. А., Кольцевой газовый лазер,
"Успехи физических наук", 1969, т. 97, в. 3, с. 377; Померанцев H.
M., Скроцкнй Г. В., Физические основы квантовой гироскопии, там же, 1970, т.
100. в. 3, с. 361.
Г. В. Скроцкий.
КВАНТОВЫЙ МАГНИТОМЕТР, прибор для измерения напряжённости магнитных
полей, основанный на квантовых явлениях. Такими явлениями служат свободная
упорядоченная прецессия ядерных или электронных магнитных моментов (см.
Магнитный резонанс), квантовые переходы между магнитными подуровнями атомов, а также
квантовые изменения магнитного потока в сверхпроводящем контуре (см.
Сверхпроводимость).
К. м. применяются гл. обр. для измерения напряжённости слабых магнитных
полей и, в частности, магнитного поля Земли и его аномалий как на её
поверхности, так и на больших высотах, соответствующих орбитам баллистич. ракет
и искусственных спутников Земли, для измерения магнитных полей планет Солнечной
системы в космич. пространстве. К. м. применяются также для разведки полезных
ископаемых, для магнитного каротажа, поиска затонувших судов и т. п.
Уровни энергии атомных ядер, электронов атомов или молекул, обладающих
магнитными моментами, в магнитном поле расщепляются на несколько подуровней,
разность энергий между которыми  E зависит от величины напряжённости H магнитного
поля и во многих случаях пропорциональна H (см. Зеемана эффект).
E зависит от величины напряжённости H магнитного
поля и во многих случаях пропорциональна H (см. Зеемана эффект).
Рис. 2.
Частицы могут переходить с одного магнитного подуровня на другой, поглощая
или излучая порцию (квант) электромагнитной энергии, равную: h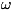 , Где h - Планка
постоянная,
, Где h - Планка
постоянная, 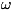 - частота электромагнитного поля. Частота
- частота электромагнитного поля. Частота 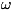 точно равна частоте
прецессии магнитного момента вокруг направления магнитного поля, т. е.
точно равна частоте
прецессии магнитного момента вокруг направления магнитного поля, т. е. 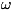 =
= 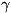 Н, где
Н, где 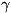 -
гиромагнитное отношение (см. Магнитомеханическое отношение, Лармора
прецессия, Ядерный магнитный резонанс). Частота со лежит в радиодиапазоне.
Измеряя её, напр, по резонансному поглощению веществом радиоволн (см. Радиоспектроскопия),
можно определить напряжённость магнитного поля H. Так как
коэффициент пропорциональности между частотой
-
гиромагнитное отношение (см. Магнитомеханическое отношение, Лармора
прецессия, Ядерный магнитный резонанс). Частота со лежит в радиодиапазоне.
Измеряя её, напр, по резонансному поглощению веществом радиоволн (см. Радиоспектроскопия),
можно определить напряжённость магнитного поля H. Так как
коэффициент пропорциональности между частотой 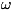 и полем H выражается через
атомные константы, характеризующиеся чрезвычайно высокой стабильностью и
воспроизводимостью, то чувствительность таких К. м. высока. Наиболее
совершенные К. м. этого типа обладают чувствительностью до 10-8 э
или 10-3 гамм (1 гамма = 10-5 э).
и полем H выражается через
атомные константы, характеризующиеся чрезвычайно высокой стабильностью и
воспроизводимостью, то чувствительность таких К. м. высока. Наиболее
совершенные К. м. этого типа обладают чувствительностью до 10-8 э
или 10-3 гамм (1 гамма = 10-5 э).
Протонный магнитометр. Датчиком магнитометра является ампула с диамагнитной жидкостью,
молекулы к-рой содержат атомы водорода (напр., воду или бензол). Магнитные
моменты молекул обусловлены только магнитными моментами ядер атомов водорода -
протонами (электронные магнитные моменты в молекулах таких жидкостей
скомпенсированы; см. Диамагнетизм). Ампулу помещают в катушку L, через
к-рую пропускают в течение неск. секунд ток, создавая в ней вспомогательное
магнитное поле H0 напряжённостью в неск. сот э (рис. 1). Под
действием поля H0 магнитные моменты протонов ориентируются и
жидкость приобретает суммарный магнитный момент M.
Рис. 1. Схема протонного магнитометра: L - катушка, создающая
вспомогательное намагничивающее поле H0; П - катушка, в
которой возникает эдс, обусловленная прецессией ядерных моментов вокруг
измеряемого магнитного поля H; У - усилитель сигнала; Ч -
частотомер, градуированный в э.
После выключения тока магнитные моменты протонов начинают прецессировать
вокруг направления измеряемого магнитного поля H с частотой 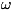 =
= 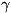 РН,
где
РН,
где 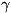
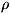 = (2,67513 ± ±0,00002)
104гс-1сeк-1 - магнитомеханич. отношение для
протонов. Прецессия суммарного магнитного момента M приводит к появлению
в катушке П переменной эдс с частотой, равной частоте прецессии
= (2,67513 ± ±0,00002)
104гс-1сeк-1 - магнитомеханич. отношение для
протонов. Прецессия суммарного магнитного момента M приводит к появлению
в катушке П переменной эдс с частотой, равной частоте прецессии 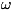 . В магнитном
поле Земли H3 ~0,6 э,
. В магнитном
поле Земли H3 ~0,6 э, 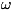 = 2,55 кгц. Прецессия
постепенно затухает благодаря процессу релаксации, обусловленному слабым
взаимодействием между протонами и атомами парамагнитных примесей, растворимых в
рабочей жидкости. Для чистой воды время релаксации ~3 сек. Для
повторного измерения поля цикл повторяют. Цикличность работы датчика устраняют,
напр., с помощью системы из 2 датчиков, работающих поочерёдно.
= 2,55 кгц. Прецессия
постепенно затухает благодаря процессу релаксации, обусловленному слабым
взаимодействием между протонами и атомами парамагнитных примесей, растворимых в
рабочей жидкости. Для чистой воды время релаксации ~3 сек. Для
повторного измерения поля цикл повторяют. Цикличность работы датчика устраняют,
напр., с помощью системы из 2 датчиков, работающих поочерёдно.
Электронный К.м. аналогичен протонному. В нём используется прецессия в
магнитном поле магнитных моментов неспаренных электронов парамагнитных атомов,
частота к-рой в несколько сот раз больше частоты прецессии протонов (см.
Электронный парамагнитный резонанс). Частота прецессии для электронов в поле H ~ 1 э
равна 2,8 Мгц. Изменение поля на 1 гамму приводит к изменению
частоты прецессии на 28 гц, что в 660 раз больше, чем для протонных
магнитометров.
Для получения достаточно больших эдс применяют методы динамической
поляризации ядер. При этом ориентация магнитных моментов протонов
осуществляется благодаря их взаимодействию с электронными моментами
парамагнитных ионов (в воде растворяют парамагнитную соль). Таким способом
ядерную намагниченность удастся увеличить в неск. сот раз. Применение вещества,
содержащего радикалы нитрозодисульфоната калия, позволяет увеличить
намагниченность ещё примерно в 40 раз.
Оптический магнитометр (магнитометр с оптической накачкой; рис.2). Датчиком
прибора является стеклянная колба, наполненная парами щелочного металла (напр.,
Rb), атомы к-рого парамагнитны, т. к. содержат один неспаренный электрон (см.
Парамагнетик).
Рис. 2. Схема оптического квантового магнитометра: Л - источник
света; СФ - светофильтр; П, - поляроид; Я2 - пластинка ( /4), создающая
разность фаз 90° для получения циркулярно поляризованного света; К - колба, наполненная
парами щелочного металла;
/4), создающая
разность фаз 90° для получения циркулярно поляризованного света; К - колба, наполненная
парами щелочного металла; 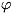 - фотоприёмник; II - измеряемое поле.
- фотоприёмник; II - измеряемое поле.
При пропускании через колбу, помещённую в измеряемое поле H, циркулярно
поляризованного света, частота к-рого равна частоте оптического квантового
перехода между основным состоянием атома и одним из его возбуждённых состояний,
происходит резонансное рассеяние света. При этом момент количества движения
квантов рассеиваемого света передаётся атомам, к-рые таким образом
"оптически ориентируются", скапливаясь на одном из магнитных
подуровней основного состояния. Если в объёме колбы датчика создать переменное
магнитное поле, частота к-рого равна частоте квантового перехода между
магнитными подуровнями основного состояния, то населённость атомов на магнитных
подуровнях выравнивается, атомы теряют приобретённую преимущественную
ориентацию магнитных моментов и приходят в исходное состояние. При этом пары
металла, наполняющие колбу, вновь начинают сильно поглощать и рассеивать свет.
Измеряя частоту переменного поля 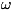 , можно определить напряжённость магнитного поля H,
в к-ром находится колба датчика.
, можно определить напряжённость магнитного поля H,
в к-ром находится колба датчика.
Оптич. К. м. особенно удобны для измерения слабых полей, < 1 э.
Чувствительность, к-рая может быть достигнута при помощи таких приборов, ~ 10-6-10-7
э, что позволяет измерять очень слабые поля, в частности в космич.
пространстве. Сверхпроводящий магнитометр основан на квантовании магнитного
потока, захваченного сверхпроводящим кольцом. Величина захваченного потока
кратна кванту магнитного потока Ф0= 2·10-7 э-см2.
Полный ток, протекающий через параллельные соединения двух переходов
Джозефсона (сверхпроводящее кольцо, разделённое по диаметру очень тонким слоем
изолятора; см. Джозефсона эффект) в результате сложения токов,
проходящих по каждой из ветвей (рис. 3), изменяется пропорционально Cos е/hФ,
где Ф - магнитный поток, охватываемый кольцом, е - заряд электрона.
Рис. 3. Схема сверхпроводящего магнитометра: С - сверхпроводящее кольцо с
двумя переходами Джозефсона (а и б); T - согласующий трансформатор; У, -
узкополосный усилитель с детектором: У, - усилитель постоянного тока; P
- самописец. Магнитный поток через кольцо (перпендикулярный плоскости
рисунка - сверху вниз) изображён крестиками. Его изменение приводит к появлению
периодической эдс на входе усилителя У1 .
Этот ток достигает максимума всякий раз, когда Ф=nФ0 (n
- целое число). Наблюдая за изменениями тока, проходящего через двойной переход
Джозефсона, можно измерять магнитный поток Ф и, зная площадь сечения перехода,
определить напряжённость измеряемого магнитного поля. Если площадь,
охватываемая двумя переходами, равна 1 мм2·, то максимумы
тока разделены интервалом в 2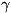 . Таким методом можно регистрировать десятую часть
этого интервала. Чувствительность метода составляет в этом случае 0,2 гаммы.
Для рассмотренного примера наиболее сильное поле, которое можно измерить,
составляет ок. 20 гамм.
. Таким методом можно регистрировать десятую часть
этого интервала. Чувствительность метода составляет в этом случае 0,2 гаммы.
Для рассмотренного примера наиболее сильное поле, которое можно измерить,
составляет ок. 20 гамм.
Все К. м. не боятся вибраций; их показания не зависят от ориентации прибора
относительно измеряемого поля H, слабо зависят от изменения темп-ры,
давления, влажности и т. п.
Лит.: Померанцев H. M., Рыжков В. M., Скроцкий Г. В., Физические
основы квантовой магнитометрии, M., 1972; Абрагам А., Ядерный магнетизм, пер.
с англ., M., 1963.
Г. В. Скроцкий.
КВАНТОВЫЙ УСИЛИТЕЛЬ, устройство для усиления электромагнитных волн за
счёт вынужденного излучения возбуждённых атомов, молекул или ионов. Эффект
усиления в К. у. связан с изменением энергии внутриатомных (связанных)
электронов, движение которых описывается квантовой механикой. Поэтому, в
отличие, напр., от ламповых усилителей, в которых используются потоки свободных
электронов, движение к-рых хорошо описывается классич. механикой, эти усилители
получили название квантовых (см. Квантовая электроника).
T. к. кроме вынужденных квантовых переходов возбуждённых атомов в
состояние с меньшей энергией возможны их самопроизвольные (спонтанные)
переходы, в результате к-рых излучаются волны, имеющие случайные амплитуду,
фазу и поляризацию, то они добавляются к усиливаемой волне в виде шумов. Спонтанное
излучение является единственным, принципиально неустранимым источником шумов К.
у. Мощность спонтанного излучения очень мала в радиодиапазоне и резко растёт
при переходе к оптич. диапазону. В связи с этим К. у. радиодиапазона (мазеры)
отличаются исключительно низким уровнем собственных шумов [в них
отсутствуют шумы, связанные с неравномерностью электронного потока, неизбежные
в радиолампах (см. Дробовой шум); кроме того, К. у. радиодиапазона
работают при температурах, близких к абсолютному нулю, и шумы, связанные с
тепловым движением электронов в цепях усилителя, очень малы]. Благодаря
чрезвычайно низкому уровню шумов чувствительность К. у., т. е. способность
усиливать очень слабые сигналы, велика. К. у. применяются в качестве входных
ступеней в самых высокочувствительных радиоприёмных устройствах в диапазоне
длин волн от 4 мм до 50 см. К. у. радиодиапазона значительно
увеличили дальность действия космических линий связи с межпланетными станциями,
планетных радиолокаторов и радиотелескопов.
В оптич. диапазоне К. у. широко используются как усилители мощности
лазерного излучения. К. у. света имеют много общего по принципу действия и
конструкции с квантовыми генераторами света (см. Лазер).
Вынужденный переход атома из состояния с энергией E2 в
состояние с меньшей энергией E1, сопровождающийся испусканием
кванта электромагнитной энергии E2-E1=hv (v
- частота вынуждающей и испускаемой волн, h - Планка постоянная), приводит
к усилению колебаний. Усиление, создаваемое одним атомом, очень мало. Но если
колебание частоты  распространяется в веществе, содержащем большое число одинаковых
возбуждённых атомов, находящихся на уровне E2, то усиление
может стать достаточно большим. Атомы же, находящиеся на нижнем уровне E1,
в результате вынужденного поглощения, наоборот, ослабляют волну. В результате
вещество будет ослаблять или усиливать волну в зависимости от того, каких
атомов в ней больше, невозбуждённых или возбуждённых, или, как говорят, какой
из уровней энергии более населён атомами.
распространяется в веществе, содержащем большое число одинаковых
возбуждённых атомов, находящихся на уровне E2, то усиление
может стать достаточно большим. Атомы же, находящиеся на нижнем уровне E1,
в результате вынужденного поглощения, наоборот, ослабляют волну. В результате
вещество будет ослаблять или усиливать волну в зависимости от того, каких
атомов в ней больше, невозбуждённых или возбуждённых, или, как говорят, какой
из уровней энергии более населён атомами.
Если вещество находится в состоянии равновесия термодинамического, то
распределение частиц по уровням энергии определяется его темп-рой, причём
уровень с меньшей энергией более населён, чем уровень с большей энергией (рис.
1; см. также Болъцмана статистика). Такое вещество всегда поглощает
электромагнитные волны. Вещество начинает усиливать - становится активным, лишь
тогда, когда равновесие нарушается и возбуждённых атомов становится больше, чем
невозбуждённых (инверсия населённостей). Чем больше число атомов на
верхнем уровне превышает число атомов, находящихся на нижнем уровне, т. е. чем
больше инверсная разность населённости  NИ=N2-N1,
тем эффективней усиление.
NИ=N2-N1,
тем эффективней усиление.
Однако инверсное состояние вещества не может существовать сколь угодно
долго. После прекращения внешнего воздействия в результате теплового движения
частиц и взаимодействия между ними через нек-рое время снова устанавливается
равновесное распределение населённостей уровней (рис. 1). Этот процесс (релакса-
Рис. 1. Распределение частиц по уровням энергии в условиях
термодинамического равновесия: а - при температуре T1; б- при
температуре T2<T1; N - населённость
уровней энергии,  N - равновесная разность населённостей уровней
энергии E1 и E2
N - равновесная разность населённостей уровней
энергии E1 и E2
ция) происходит и во время действия внешнего возмущения, стремясь
восстановить тепловое равновесие в веществе. Поэтому внешнее воздействие должно
быть достаточно сильным, чтобы привести вещество в состояние с инверсией
населённостей и не должно быть однократным.
Существуют различные методы создания активной среды. Для К. у. наиболее
удобным оказался метод, основанный на использовании 3 уровней энергии,
предложенный H. Г. Басовым и A. M. Прохоровым. Частицы (атомы
молекулы или ионы), в энергетич. спектре к-рых есть 3 уровня энергии E1,
E2,E3 (рис. 2), подвергаются воздействию
сильного электромагнитного излучения (накачки). Частота этого излучения  соответствует
частоте перехода между нижним E1 и верхним E3уровнями
(hv = E3-E1). Интенсивность накачки должна быть
достаточно велика, чтобы переходы E1->E3 происходили
гораздо чаще, чем обратные релаксационные переходы. В этом случае населённости
уровней E1 и E3выравниваются. При этом для
одной из пар уровней E1 и E2 или E2
и E3 будет иметь место инверсия населённости. Инверсия
населённостей образуется для пары уровней с более медленной релаксацией и с
меньшей разностью энергии.
соответствует
частоте перехода между нижним E1 и верхним E3уровнями
(hv = E3-E1). Интенсивность накачки должна быть
достаточно велика, чтобы переходы E1->E3 происходили
гораздо чаще, чем обратные релаксационные переходы. В этом случае населённости
уровней E1 и E3выравниваются. При этом для
одной из пар уровней E1 и E2 или E2
и E3 будет иметь место инверсия населённости. Инверсия
населённостей образуется для пары уровней с более медленной релаксацией и с
меньшей разностью энергии.
С понижением темп-ры T увеличивается как равновесная разность
населённостей  N уровней (рис. 1), так и инверсная разность населённостей
N уровней (рис. 1), так и инверсная разность населённостей  Nи
(рис. 2). Кроме того, понижение темп-ры сильно замедляет релаксацию и тем самым
снижает требуемую мощность накачки. Поэтому инверсию населённостей, достаточную
для создания эффективных К. у. радиодиапазона, удаётся получить при охлаждении
вещества до темп-ры кипения гелия (4,2 К). Существуют конструкции К. у., к-рые
могут работать при темп-pax до 77 К (точка кипения азота) и даже 190 К, но они
менее эффективны.
Nи
(рис. 2). Кроме того, понижение темп-ры сильно замедляет релаксацию и тем самым
снижает требуемую мощность накачки. Поэтому инверсию населённостей, достаточную
для создания эффективных К. у. радиодиапазона, удаётся получить при охлаждении
вещества до темп-ры кипения гелия (4,2 К). Существуют конструкции К. у., к-рые
могут работать при темп-pax до 77 К (точка кипения азота) и даже 190 К, но они
менее эффективны.
Рис. 2. Возникновение инверсии населённостей для уровней энергии E2
и E3 в системе 3 уровней E1,E2,E3под
действием накачки: а - при температуре вещества T1; 6
- при температуре Т2>T1.. Пунктир
показывает распределение частиц по уровням энергии при термодинамическом
равновесии.
Наиболее подходящим материалом для К. у. радиодиапазона оказались
диамагнитные кристаллы с небольшой примесью парамагнитных ионов. Обычно
применяются рубин (Al2O3 с примесью ионов хрома Cr3+),
рутил (TiO2 с примесью ионов Cr3+ и Fe3+),
изумруд [Be3Al2 (SiO3)6 с примесью
окиси хрома Cr2O3]. Для К. у. необходимы кристаллы
объёмом в неск. см3, выращенные искусственно из очень чистых
материалов со строго дозированной примесью парамагнитных ионов.
В отсутствии внешних магнитных полей магнитные моменты ионов ориентированы
хаотически. В постоянном магнитном поле магнитный момент может располагаться
только под неск. определёнными углами к магнитному полю H, энергия иона
в этих положениях различна (см. Зеемана эффект). Образуется ряд уровней
энергии (магнитные подуровни), расстояние между к-рыми зависит от величины
постоянного магнитного поля H. Число магнитных подуровней определяется спином
иона (рис. 3). Разность энергии между ними при обычных магнитных полях
соответствует радиодиапазону и может быть легко изменена изменением магнитного
поля. Такое вещество может усиливать радиоволны нужной частоты.
Рис. 3. Энергетические уровни парамагнитного иона во внешнем магнитном поле H
расщепляются на несколько магнитных подуровней, число которых зависит от
величины спина иона S; a) S - ½; 6) S = 1; в) S = 3/2.
Основная характеристика всякого усилителя электрич. колебаний - его коэффициент усиления К, показывающий, во сколько раз амплитуда колебаний
на выходе усилителя больше амплитуды на входе. Чем больше путь, к-рый волна
проходит в активном веществе, тем больше коэфф. усиления К. у. В кристалле
рубина волна, распространяясь на расстояние, равное её длине  , увеличивает
свою амплитуду незначительно. T. о., для получения достаточного усиления
необходимы монокристаллы больших размеров, выращивание к-рых связано с
серьёзными трудностями. Для К. у. с коэфф. усиления 10 потребовались бы
кристаллы (а, следовательно, в магниты) длиной в неск. м. Такой усилитель был
бы очень громоздким и дорогим.
, увеличивает
свою амплитуду незначительно. T. о., для получения достаточного усиления
необходимы монокристаллы больших размеров, выращивание к-рых связано с
серьёзными трудностями. Для К. у. с коэфф. усиления 10 потребовались бы
кристаллы (а, следовательно, в магниты) длиной в неск. м. Такой усилитель был
бы очень громоздким и дорогим.
Усиление можно увеличить, заставив волну многократно проходить через
активное вещество. Для этого активное вещество помещают в объёмный резонатор
(полость, ограниченную металлич. стенками). Волна, попавшая из антенны в
резонатор через отверстие в его стенке (отверстие связи), многократно
отражается от стенок резонатора и длительно взаимодействует с активным
веществом (рис. 4). Усиление будет эффективным, если при каждом отражении
от стенки фаза отражённой волны совпадает с фазой падающей волны. Это
условие выполняется при определённых размерах резонатора, т. е. резонатор так
же, как и само вещество, должен быть настроен на частоту усиливаемой волны. При
каждом отражении от стенки с отверстием часть электромагнитной, энергии
излучается наружу в виде усиленного сигнала. Для разделения входа и выхода
резо-наторного К. у. применяется циркуляmop (рис. 5). Такой К. у. наз.
отражательным.
Рис. 4. Объёмный резонатор с активным веществом.
Рис. 5. Схематическое изображение отражательного квантового
усилителя с одним резонатором.
Для получения оптимальных характеристик К. у. необходимо подобрать размер
отверстия связи, т. к., кроме требуемого коэфф. усиления, К. у. должен иметь
нужную полосу пропускания, которая определяет его способность усиливать
сигналы, быстро меняющиеся во времени Чем быстрее во времени меняется сигнал,
тем больший частотный интервал он занимает (см., напр., Модуляция колебаний). Если полоса пропускания усилителя 
 меньше полосы частот,
занимаемой сигналом, то произойдёт сглаживание быстрых изменений сигнала в
усилителе. T о , введение резонатора в конструкцию К. у. с одной стороны
увеличивает его коэфф. усиления, а с другой - во столько же раз уменьшает его
полосу пропускания. Последнее значительно сужает область применения усилителя.
Однорезонаторные К. у. не получили широкого распространения из-за
невозможности обеспечить одновременно большой коэфф. усиления и широкую полосу
пропускания. Оказалось, что можно сохранить широкую полосу пропускания при
большом коэфф. усиления, применив неск. резонаторов. Существует два типа многорезонаторных
К. у.- усилители отражательного типа с циркулятором (рис. 6) и усилители
проходного типа (рис. 7). В проходных К. у. волна распространяется вдоль
цепочки резонаторов, заполненных активным веществом. В каждом резонаторе при
значит, полосе пропускания усиление невелико, но полное усиление всей цепочки
может быть достаточно большим. Резонаторы проходного К. у. соединены друг с
другом ферритовыми невзаимными элементами. Под действием постоянного магнитного
поля ферриты приобретают свойство пропускать волну, распространяющуюся в
одном направлении, поглощая встречную волну. Осн. недостатком
многорезонаторных К. у. является сложность перестройки частоты усилителя, т к.
при этом необходимо одновременно с изменением магнитного поля менять
собственную частоту большого числа резонаторов, что технически трудно.
меньше полосы частот,
занимаемой сигналом, то произойдёт сглаживание быстрых изменений сигнала в
усилителе. T о , введение резонатора в конструкцию К. у. с одной стороны
увеличивает его коэфф. усиления, а с другой - во столько же раз уменьшает его
полосу пропускания. Последнее значительно сужает область применения усилителя.
Однорезонаторные К. у. не получили широкого распространения из-за
невозможности обеспечить одновременно большой коэфф. усиления и широкую полосу
пропускания. Оказалось, что можно сохранить широкую полосу пропускания при
большом коэфф. усиления, применив неск. резонаторов. Существует два типа многорезонаторных
К. у.- усилители отражательного типа с циркулятором (рис. 6) и усилители
проходного типа (рис. 7). В проходных К. у. волна распространяется вдоль
цепочки резонаторов, заполненных активным веществом. В каждом резонаторе при
значит, полосе пропускания усиление невелико, но полное усиление всей цепочки
может быть достаточно большим. Резонаторы проходного К. у. соединены друг с
другом ферритовыми невзаимными элементами. Под действием постоянного магнитного
поля ферриты приобретают свойство пропускать волну, распространяющуюся в
одном направлении, поглощая встречную волну. Осн. недостатком
многорезонаторных К. у. является сложность перестройки частоты усилителя, т к.
при этом необходимо одновременно с изменением магнитного поля менять
собственную частоту большого числа резонаторов, что технически трудно.
Время взаимодействия волны с веществом можно увеличить, применяя вместо
системы резонаторов замедляющие системы. Скорость распространения волны
вдоль такой структуры во много раз меньше скорости распространения волны в
радиоволноводе или в свободном пространстве. Соответственно увеличивается и
усиление при прохождении волной единицы длины кристалла. Существенно, что
замедляющие структуры широкополосны. Это даёт возможность перестраивать частоту
К. у. изменением только магнитного поля. Полоса пропускания таких усилителей, а
также многорезонаторных К. у. определяется шириной спектральной линии. К.
у. с замедляющей структурой получили назв. К. у. бегущей волны. В них также
применяются ферриты. Они пропускают волну, распространяющуюся вдоль замедляющей
структуры в нужном направлении, и поглощают встречные, отраженные волны.
Мощность шумов К. у. удобно измерять, сравнивая её с мощностью теплового
излучения абсолютно чёрного тела. Спектр теплового излучения включает
оптический и радиодиапазоны. T. о., мощность шумов можно выражать через абс.
температуру (см. Шумовая температура). Предельная низкая темп-ра шума К
у, обусловленная спонтанным излучением для  =3 см, составляет 0,5 К
Для большинства активных веществ, используемых в К. у., мощность шума
колеблется в пределах от 1 К до 5 К. В реальных К. у. к этим ничтожно малым
шумам добавляется гораздо более мощное тепловое излучение подводящих радиоволноводов
и др. конструктивных деталей. Мощность шумов, излучаемую волноводом, можно
характеризовать величиной
=3 см, составляет 0,5 К
Для большинства активных веществ, используемых в К. у., мощность шума
колеблется в пределах от 1 К до 5 К. В реальных К. у. к этим ничтожно малым
шумам добавляется гораздо более мощное тепловое излучение подводящих радиоволноводов
и др. конструктивных деталей. Мощность шумов, излучаемую волноводом, можно
характеризовать величиной 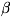 T, где
T, где 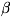 - коэфф. поглощения волны, а Т
- его абс. темп-pa. Для уменьшения шумов необходимо охладить возможно
большую часть входных деталей. Но охладить весь входной тракт до темп-ры
жидкого гелия невозможно. Поэтому не удаётся снизить шумы К. у. с антенной до
величины ниже 15-30 К. Это приблизительно в 100 раз меньше уровня шумов лучших
усилителей, имевшихся до появления К. у.
- коэфф. поглощения волны, а Т
- его абс. темп-pa. Для уменьшения шумов необходимо охладить возможно
большую часть входных деталей. Но охладить весь входной тракт до темп-ры
жидкого гелия невозможно. Поэтому не удаётся снизить шумы К. у. с антенной до
величины ниже 15-30 К. Это приблизительно в 100 раз меньше уровня шумов лучших
усилителей, имевшихся до появления К. у.
Рис. 6. Отражательный усилитель с 3 резонаторами.
Рис 7. Схема квантового усилителя проходного типа с 3 резонаторами.
Охлаждение К. у. производится жидким гелием в криостатах. Трудности,
связанные со сжижением, транспортировкой и переливкой жидкого гелия из
транспортных сосудов в криостаты, ограничивают возможность применения К. у.,
осложняют и удорожают их эксплуатацию. Разработаны небольшие холодильные машины
с замкнутым циклом движения охлаждающего вещества. Масса такой машины,
рассчитанной на охлаждение К. у. до 40 К, составляет 10-20 кг. Машина,
рассчитанная на получение 4 К, весит более чем 200 кг и потребляет
мощность в неск. квт.
Лит.: Карлов H. В., Маненков А. А., Квантовые усилители, M., 1966; Сигмен А., Мазеры, пер. с англ., M., 1966; Квантовая электроника. Маленькая
энциклопедия, M., 1969; Штейншлейгер В. Б., M и с е ж н и к о в Г. С., Лифанов
П. С., Квантовые усилители СВЧ (мазеры), M., 1971.
А. В. Францессон.
КВАНТОР (от лат. quantum - сколько), логическая операция, дающая
количественную характеристику области предметов, к к-рой относится выражение,
получаемое в результате её применения. В обычном языке носителями таких
характеристик служат слова типа "все", "каждый",
"некоторый", "существует", "имеется",
"любой", "всякий", "единственный",
"несколько", "бесконечно много", "конечное
число", а также все количественные числительные. В формализованных
языках, составной частью к-рых является исчисление предикатов, для выражения
всех подобных характеристик оказывается достаточным К. двух видов: К. (в с е) о
б щ н о с т и (оборот "для всех x", обозначается через Vx, (Vx), (х),
(Ax), П, 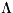 , П) и К. с у щ е с т в о в а н и я ("для некоторых x",
обозначения: Ex, (Ex), (Ex), U,
, П) и К. с у щ е с т в о в а н и я ("для некоторых x",
обозначения: Ex, (Ex), (Ex), U, 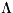 ,
, 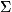 ). С помощью К можно записать четыре основных
формы суждений традиционной логики: "все А суть В"
записывается в виде Vх[_А(х)=э =>В(х)], "ни одно А не есть
В" - в виде Vx[A(X)·=> -В(х)], "некоторые А суть
В" - в виде Eх[А(х)&В(x)], "некоторые A не суть В" -в
виде Ex[A(х)&-B(X)] (здесь A(X) означает, что
). С помощью К можно записать четыре основных
формы суждений традиционной логики: "все А суть В"
записывается в виде Vх[_А(х)=э =>В(х)], "ни одно А не есть
В" - в виде Vx[A(X)·=> -В(х)], "некоторые А суть
В" - в виде Eх[А(х)&В(x)], "некоторые A не суть В" -в
виде Ex[A(х)&-B(X)] (здесь A(X) означает, что 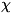 обладает
свойством А, 13 - знак импликации, - - отрицания, & - конъюнкции).
обладает
свойством А, 13 - знак импликации, - - отрицания, & - конъюнкции).
Часть формулы, на к-рую распространяется действие к.-л. К., наз. областью
действия этого К. (ее можно указать с помощью скобок). Вхождение к -л. переменной
в формулу непосредственно после знака К. или в область действия К., после
к-рого стоит эта переменная наз. её связанным вхождением. Все остальные
вхождения переменных наз. свободными. Формула, содержащая свободные вхождения
переменных, зависит от них (является их функцией); связанные же
вхождения переменных можно "переименовывать"; напр., записи Ex(x =
3y) и 3z(z = 2y) означают одно и то же, чего нельзя сказать о Eх(х =
2у) и E(х)(х = 2t). Применение К уменьшает число свободных
переменных в логич. выражении и превращает (если К. не "фиктивный",
т. е. относится к переменной, действительно входящей в формулу) трёхместный
предикат в двухместный, двухместный - в одноместный, одноместный - в
высказывание. Употребление К. кодифицируется спец. "постулатами
квантификации" (присоединение к-рых к исчислению высказываний по
существу и означает расширение его до исчисления предикатов), напр., следующими
"постулатами Бернайсак аксиомами A(t) => EхА(х) и EхА(х)з
^>A(t) и правилами вывода "если доказано C^A(X), то
можно считать доказанным и C^VfxA(x)" и "если доказано А(х)^>С,
то можно считать доказанным и EхА(х)оС" (здесь x не
входит свободно в С).
К К. общности и существования сводятся и др. виды К., напр, вместо т. н. К.
единственности E!x ("существует единственный 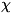 такой, что") можно писать
"обычные" К., заменяя E! хА(х) на
такой, что") можно писать
"обычные" К., заменяя E! хА(х) на
ExA(x)&VyVz[A(y)&A(z )=>y = z].
Аналогично, К., "ограниченный" к-л. одноместным предикатом Р(x)(Exp(x),
читается как "существует х, удовлетворяющий свойству P и такой,
что", a VxP(x)- "для всех х, удовлетворяющих
свойству P, верно, что"), легко выразить через К. общности и существования
и операторы импликации и конъюнкции:
EХр(x)А(х) = Ex[P(x)&A(x)] и Vxp(x)A(x)
= Vx[P(x) => A(x)].
Лит.: К л и н и С. К., Введение в метаматематику, пер. с англ., M.,
1957, с. 72 - 80, 130 - 138; Ч ё р ч А., Введение в математическую логику, пер. с англ.,
т. 1, M., 1960, с. 42 - 48.
Ю. А. Гастев.
KBAHTУH, встречающееся в лит-ре на рус. яз. название юго-зап.
оконечности Ляодунского п-ова в Китае; см. Гуаньдун.
КВАНТУНСКАЯ АРМИЯ, группировка японских войск, предназначавшаяся для
агрессии против Китая, СССР и мн.. Создана в 1931 на базе войск, расположенных
на терр. Квантунской обл. (юго-зап. оконечности Ляодунского п-ова до зал.
Гуаньдун), откуда и получила своё название. 18 сент. 1931 К. а. вероломно
напала на Китай и к нач. 1932 оккупировала его сев.-вост. провинцию -
Маньчжурию, где было создано 9 марта 1932 марионеточное гос-во Маньчжоу-Го,
ставшее фактически колонией япон. империалистов и плацдармом для их последующей
агрессии. Это событие положило начало серии вооружённых конфликтов с соседними
странами, спровоцированных япон. военщиной. Расширяя агрессию в Китае, япон.
империалисты одновременно стремились проверить прочность советских дальневосточных
границ и овладеть выгодными плацдармами для последующего вторжения на терр.
СССР и мн.. Численность К. а. постепенно увеличивалась и к 1938 достигла 8
дивизий (ок. 200 тыс. чел.), а в 1940-12 дивизий (ок. 300 тыс. чел.). Летом
1938 войска К. а. вторглись в пределы СССР у оз. Хасан; в 1939 была
организована более крупная провокация против Сов. Союза и мн. нар. Халхин-Гол,
но в обоих конфликтах К. а. потерпела поражение. В 1941, когда сов. народ
вёл тяжёлую борьбу с фаш. Германией, К. а. в соответствии с япон. планом "Кантокуэн"
развернулась на маньчжурской границе и в Корее для нападения на СССР,
выжидая удобного момента для начала боевых действий в зависимости от исхода
борьбы на сов.-герм, фронте.
В 1941-43 в Маньчжурии и Корее насчитывалось 15-16 япон. дивизий (ок. 700
тыс. чел.).
К началу кампании Сов. Вооруж. Сил на Дальнем Востоке (9 авг. 1945) К. а.
имела в своём составе: 1-й фронт (3-я и 5-я армии), 3-й фронт (30-я и 44-я
армии), 17-й фронт (34-я и 59-я армии), отдельную (4-ю) армию, две (2-я и 5-я)
воздушные армии и Сунгарийскую воен. флотилию. Кроме того, ей были оперативно
подчинены армия Маньчжоу-Го, войска Внутренней Монголии (князя Де Вана) и
Суйюаньская армейская группа. В составе К. а. и подчинённых ей войск
насчитывалось 37 пехотных и 7 кав. дивизий, 22 пехотных, 2 танк, и 2 кав.
бригады (всего 1 млн. 320 тыс. чел.), 1155 танков, 6260 орудий, 1900 самолётов
и 25 кораблей. К. а. располагала также бактериологич. оружием, к-рое
предназначалось для применения против Сов. Вооруж. Сил. После разгрома К. а. в Маньчжурской
операции 1945 Япония лишилась реальных сил и возможностей для продолжения
войны и 2 сент. 1945 подписала акт о безоговорочной капитуляции.
Лит.: Финал, 2 изд., M., 1969; X а я с и С а б у р о, Японская армия
в военных действиях на Тихом океане, [пер. с англ.], M., 1964.
H. В. Еронин.
КВАПИЛОВА (Kvapilova, урожд. Ky б е ш о в a, Kubesova) Гана
(29.11.1860, Прага,- 8.4.1907, там же), чешская актриса. Родилась в семье
ремесленника. В 1886 дебютировала в труппе Э. Вояна. С 1888 актриса Нац.
театра в Праге. С начала творч. деятельности К. восставала против сценич.
рутины. В 1906 была инициатором гастролей MXT в Праге. Активный протест против
социального бесправия, мечта о свободе и лучшей жизни - гл. тема её творчества.
Актриса утверждала на чеш. сцене иск-во глубокого переживания, её деятельность
способствовала развитию нац. драматургии, для К. писали пьесы Я. Врхлицкий, Ю.
Зейер, А. Ирасек и др. чеш. драматурги. Среди ролей: Офелия, леди Макбет
("Гамлет", "Макбет" Шекспира), Йемена ("Антигона"
Софокла), Войнарка ("Войнарка" Ирасека), Мария Стюарт ("Мария
Стюарт" Шиллера), Маша ("Три сестры" Чехова) и др.
Соч.: Literarni pozustalost, 3 vyd., Praha, 1946.
Лит.: Horacek J., Hanna Kvapilova, Praha, 1911; С е г п у F., Hanna Kvapilova,
2 vyd., Praha, 1963.
Л. П. Солнцева.
KBAPA (Kwara), штат в зап. Нигерии. Пл. 74,3 тыс. км2. Нас.
2,4 млн. чел. (1963, перепись), гл. обр. йоруба, игала, игбира. Адм. ц. - г.
Илорин. Расположен в осн. по правобережью р. Нигер. Климат экваториально-муссонный;
влажный сезон продолжается 7 мес. Осадков преим. 1000-1300 мм в
год. Cp. мес. темп-ры от 25 0C до 30 0C. Растительность -
саванные леса и саванна. Потребительское земледелие (просо и сорго);
мелкотоварные х-ва производят в небольшом кол-ве ямс, рис, хлопок, сах.
тростник, какао, кунжут, пальмовые масло и ядра. Месторождения жел. руды (близ
Локоджи), слюды, угля, талька. Предприятия по произ-ву сахара, сигарет, спичек,
бумаги и картона. Хлопкоочистит., маслоб., лесопил. з-ды. Ремесленное произ-во
гончарных изделий.
КВАРЕЛИ, город (до 1964-посёлок), центр Кварельского р-на Груз. CCP.
Расположен в долине р. Алазани (приток Куры), в 19 км к С. от ж.-д.
станции Мукузани (на ветке Тбилиси - Телави). 9,5 тыс. жит. (1970). З-ды:
винные, коньячного спирта, эфирномасличный, кирпичный; виноградарские совхозы.
В К. Музей И. Г. Чавчавадзе, Дом-музей К. А. Марджанишвили. Народный
театр.
КВАРЕНГИ, Гваренги (итал. К у а р е н г и, Ouarenghi) Джакомо [20 или
21.9.1744, Валле-Иманья, близ Бергамо, Италия,-18.2(2.3).1S17, Петербург],
архитектор, представитель русского классицизма кон. 18 - нач. 19 вв. Итальянец
по происхождению. С 1761 учился в Риме живописи у А. Р. Менгса и С. Поцци;
изучал античную архитектуру, работы Пал-ладио. В России работал с 1780. Первая значит,
работа К.- Английский дворец в Петергофе (ныне Петродворец; 1781 - 1794;
полностью разрушен нем. фашистами в 1942), классически ясное монументальное
здание, с мощными колоннадами коринфского ордера. Среди крупнейших работ:
здания Академии наук (1783-89), Ассигнационного банка (1783-90), Эрмитажного
театра (1783-1787), корпус Обуховской больницы (1782-87, перестроен),
Екатерининский ин-т (1804-07), Конногвардейский манеж (1804-07), Смольный ин-т
(1806-1808) - все в Ленинграде. Они отличаются ясностью планировочных решений,
простотой и чёткостью объёмных композиций, монументальной пластичностью форм, к-рая достигается введением торжественных колоннад, выделяющихся на фоне
гладких поверхностей стен. Среди дворцовых загородных построек - Александровский
дворец (1792-96) в Царском Селе (ныне г. Пушкин), центр гл. фасада к-рого
подчёркнут парадным двориком, пространственно связанным с парком открытой
торжественной колоннадой. К. был умелым строителем-практиком, тщательно
следившим за высоким качеством осуществления своих работ в натуре.
Многочисленные рисунки К. скрупулёзно изображают памятники др.-рус.
зодчества, постройки совр. ему архитекторов, жанровые сцены ("Теремной дворец в
Кремле", "Михайловский замок", "Коломенское" - все тушь, акварель, Эрмитаж,
Ленинград; "Катание по льду на Неве", тушь, акварель, Музей изобразит. иск-в имени А. С. Пушкина, Москва;
"Панорама Кремля", акварель, тушь, Музей архитектуры им. А. В.
Щусева, Москва). К. издал гравированные альбомы со своих проектов Эрмитажного
театра и Ассигнационного банка (1787 и 1791) и первый том собрания своих
проектов (1810).
Лит.: Талепоровский В. H., Кваренги, Л.- M., 1954; Гримм Г. Г.,
Кваренги, Л., 1962; Архитектурные проекты и рисунки Д. Кваренги из музеев и
хранилищ СССР, Л., 1967.
KBAPKEH СЕВЕРНЫЙ, Hорра-Kваркен (Norra Kvarken), пролив в Балтийском
м., в зап. части Васийских шхер. Соединяет сев. (Боттенвик) и южную (Боттенхав)
части Ботнического зал. Шир. 75 км. Группой о-вов разделяется на два
пролива - Вост. Кваркен и Зап. Кваркен. Глуб. Вост. Кваркена 6-7 м, Зап.-
до 29 м. Течения зависят от ветров и атм. давления. Зимой замерзает.
КВАРКЕН ЮЖНЫЙ, Сёдра-Кваркен (Sodra Kvarken), пролив между Аландскими
о-вами и Скандинавским п-овом, соединяет Ботнический зал. с Балтийским м. Шир.
ок. 40 км, максимальная глуб. 244 м. Течения обычно направлены на
Ю. В суровые зимы замерзает, в менее холодные и мягкие - покрыт плавучими
льдами.
КВАРКИ, гипотетич. частицы, из к-рых, как предполагается, могут
состоять все известные элементарные частицы, участвующие в сильных
взаимодействиях (адроны). Гипотеза о существовании К. была высказана в 1964
независимо амер. физиком M. Гелл-Маном и австр. физиком Г. Цвейгом с
целью объяснения закономерностей, установленных для адронов. У назв.
"кварк" нет точного перевода, оно имеет лит. происхождение (было
заимствовано M. Гелл-Маном из романа Дж. Джойса "Поминки по
Финегану", где означало нечто неопределённое, мистическое). Такое назв.
для частиц, очевидно, было выбрано потому, что К. необходимо приписать ряд
необычных свойств, выделяющих их из всех известных элементарных частиц (напр.,
дробный электрич. заряд).
Предположение о существовании К. возникло в связи с открытием большого числа
адронов и их успешной систематизацией. Было установлено, что адроны могут быть
сгруппированы в нек-рые семейства частиц, близких по своим осн. характеристикам
(одинаковые барионные заряды, спины, внутренние чётности, близкие
массы). Так, напр., 8 частиц: протон (р), нейтрон (п) и гипероны 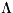 °,
°, 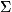 +,
+, 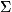 °,
°, 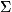 -,
-,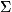 -
-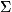 ° могут
быть объединены в одно семейство барионов (октет) со спином
½ и
положительной чётностью. Такие семейства частиц получили назв.
супермультиплетов (см. Элементарные частицы). Число частиц в каждом
супермультиплете и их осн. свойства можно объяснить, если предположить, что
адроны являются составными частицами - состоят из трёх типов фундаментальных
частиц, т. н. р, n-и
° могут
быть объединены в одно семейство барионов (октет) со спином
½ и
положительной чётностью. Такие семейства частиц получили назв.
супермультиплетов (см. Элементарные частицы). Число частиц в каждом
супермультиплете и их осн. свойства можно объяснить, если предположить, что
адроны являются составными частицами - состоят из трёх типов фундаментальных
частиц, т. н. р, n-и  -K. (а также из античастиц
-K. (а также из античастиц 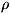 ,
, 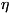 ,
, ). При этом К. необходимо
приписать характеристики, указанные в табл. (в т. ч. дробные электрические и
барионные заряды).
). При этом К. необходимо
приписать характеристики, указанные в табл. (в т. ч. дробные электрические и
барионные заряды).
Барионы, согласно указанной гипотезе, состоят из трёх К., напр, протон (Q =
1, B = 1) - из двух р-К. и одного п-К., нейтрон (Q = O, B = I) -
из двух п-К. и одного р-К., 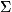 +(Q = 1, B = 1) -
из двух р-К. и одного
+(Q = 1, B = 1) -
из двух р-К. и одного  -К.,
-К., 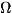 - (Q = -1, B = 1) - из трёх
- (Q = -1, B = 1) - из трёх  -К. и т.д. Антибарионы
состоят из трёх антикварков, а мезоны - из одного К. и одного антикварка
(напр.,
-К. и т.д. Антибарионы
состоят из трёх антикварков, а мезоны - из одного К. и одного антикварка
(напр.,  +-
из
+-
из 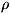 и
и 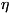 , К°
- из
, К°
- из  и n и т. д.). В состав странных частиц обязательно
входят
и n и т. д.). В состав странных частиц обязательно
входят  -К.- носители странности.
-К.- носители странности.
Поиски К. проводились в космических лучах, на ускорителях высокой энергии,
а также физико-химич. способами в окружающей среде. Все они оказались
безуспешными. Однако нельзя считать, что результаты этих опытов окончательно
опровергают гипотезу о существова-
Характеристики кварков
нии К.- они лишь устанавливают пределы для величины возможной массы К. и
вероятности рождения К. в процессах сильного взаимодействия. Так, в опытах на
Серпуховском ускорителе протонов с энергией 70 Гэв, в к-рых при
столкновении протонов с нуклонами (протонами и нейтронами) мишени могли бы
рождаться К., если бы их масса не превышала примерно 5 протонных масс (в
энергетич. единицах ~ 5 Гэв), не было зарегистрировано ни одной частицы с
зарядом - ⅓ или - ⅔. Это означает, что масса К., если
они существуют, больше 5 Гэв или что вероятность рождения К., если их
масса меньше 5 Гэв, по крайней мере в 1010 раз меньше
вероятности рождения л-мезонов (к-рых за время опыта было зарегистрировано
>1010). Поиски К. в окружающей среде показали, что если К. и
существуют, то концентрация их в веществе не превышает 10-18-10-20
от числа нуклонов, а по нек-рым данным, этот предел может быть ещё меньше (10-24
-10-30).
Наряду с гипотезой существования фундаментальных частиц с дробными зарядами выдвигалось
предположение о существовании фундаментальных частиц с целыми зарядами (их
называют иногда К. с целыми зарядами). Для объяснения закономерностей
систематики адронов необходимо считать, что имеется неск. супермультиплетов
фундаментальных частиц с целыми зарядами (напр., 3 семейства по 3 частицы).
Попытки их экспериментального обнаружения также оказались безрезультатными.
Лит.: Коккедэ Я., Теория кварков, пер. [с англ.], M., 1971; Физика
высоких энергий и теория элементарных частиц, К., 1967.
Л. Г. Ландсберг.
KBAPKУШ, горный хребет на Сев. Урале, в басе. р. Вишера, в Пермской
обл. РСФСР. Дл. 60 км, выс. до 800-850 м, высшая точка 1065 м (г.
Вогульский Камень). Сложен кварцевыми конгломератами, кварцито-песчаниками и
кристаллич. сланцами. Склоны глубоко изрезаны речными долинами и покрыты
таёжным лесом из ели, кедра, берёзы с примесью пихты. На вершине - горная
тундра, каменные россыпи, много останцов, горные луга.