ЕВКЛИД (Eukleides), древнегреческий математик, автор первого из дошедших до нас теоретич. трактатов по математике. Биографич. сведения об Е. крайне скудны. Достоверным можно считать лишь то, что его науч. деятельность протекала в Александрии в 3 веке до н. э. Е.- первый математик александрийской школы. Его гл. работа "Начала" (в латинизиров. форме - "Элементы") содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел (см., напр., Евклида алгоритм); в ней он подвёл итог предшествующему развитию греч. математики и создал фундамент дальнейшего развития математики (см. "Начала" Евклида, Евклидова геометрия). Из др. соч. по математике надо отметить "О делении фигур", сохранившееся в араб. переводе, 4 кн. "Конические сечения", материал к-рых вошёл в произведение того же названия Аполлония Пергского, а также "Поризмы", представление о к-рых можно получить из "Математического собрания". Паппа Александрийского. Е. - автор работ по астрономии, оптике, музыке и др. Дошедшие до нас произв. Е. собраны в издании "Euclidis opera omnia", ed. J. L. Heibert et H. Menge, v. 1-9, 1883-1916, дающем их греч. подлинники, лат. переводы и комментарии позднейших авторов.

Соч.: Начала Евклида, кн. 1-6, 7 - 10, 11 - 15, пер. с греч. и комментарии Д. Д. Мордухай-Болтовского, т. 1 - 3, М.- Л., 1948 - 50.

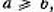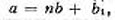ЕВКЛИДА АЛГОРИТМ, способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков. Описан в геометрич. форме в "Началах" Евклида. Для случая положит. чисел а и Ь, причём этот способ состоит в следующем. Деление с остатком числа а на число Ъ всегда приводит к результату где частное  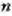- целое положит. число, а остаток 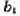 - либо 0, либо положит. число, меньшее  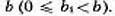Будем производить последоват. деление:

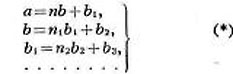
где все 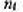- положит. целые числа и  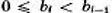до тех пор, пока не получится остаток, равный нулю. Этот последний остаток 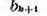 можно не писать, так что ряд равенств (*) закончится так:

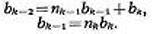
Последний положит. остаток 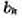 в этом процессе и является наибольшим общим делителем чисел а и b. Е. а. служит не только для нахождения наибольшего общего делителя, но и для доказательства его существования. В случае многочленов или отрезков поступают сходным образом. В случае несоизмеримых отрезков (см. Соизмеримые и несоизмеримые величины) Е. а. оказывается бесконечным.

ЕВКЛИДОВА ГЕОМЕТРИЯ, геометрия,систематич. построение к-рой было впервые дано в 3 в. до н. э. Евклидом. Система аксиом Е. г. опирается на следующие осн. понятия: точка, прямая, плоскость, движение и след. отношения: "точка лежит на прямой на плоскости", "точка лежит между двумя другими". В совр. изложении систему аксиом Е. г. разбивают на следующие пять групп.

I. Аксиомы сочетания.

1) Через каждые две точки можно провести прямую и притом только одну.

2) На каждой прямой лежат по крайней мере две точки. Существуют хотя бы три точки, не лежащие на одной прямой.

3) Через каждые три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну. 4) На каждой плоскости есть по крайней мере три точки и существуют хотя бы четыре точки, не лежащие в одной плоскости. 5) Если две точки данной прямой лежат на данной плоскости, то и сама прямая лежит на этой плоскости. 6) Если две плоскости имеют общую точку, то они имеют ещё одну общую точку (и, следовательно, общую прямую).

II. Аксиомы порядка. 1) Если точка В лежит между А и С, то все три лежат на одной прямой. 2) Для каждых точек А, В существует такая точка С, что В лежит между А и С. 3) Из трёх точек прямой только одна лежит между двумя другими. 4) Если прямая пересекает одну сторону треугольника, то она пересекает ещё другую его сторону или проходит через вершину (отрезок АВ определяется как множество точек, лежащих между А и В; соответственно определяются стороны треугольника).

III. Аксиомы движения. 1) Движение ставит в соответствие точкам точки, прямым прямые, плоскостям плоскости, сохраняя принадлежность точек прямым и плоскостям. 2) Два последоват. движения дают опять движение, и для всякого движения есть обратное. 3) Если даны точки 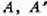 и полуплоскости 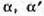, ограниченные продолженными полупрямыми 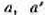, которые исходят из точек 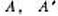, то существует движение, и притом единственное, переводящее 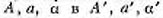 (полупрямая и полуплоскость легко определяются на основе понятий сочетания и порядка).

IV. Аксиомы непрерывности. 1) Аксиома Архимеда: всякий отрезок можно перекрыть любым отрезком, откладывая его на первом достаточное число раз (откладывание отрезка осуществляется движением). 2) Аксиома Кантора: если дана последовательность отрезков, вложенных один в другой, то все они имеют хотя бы одну общую точку.

V. Аксиома параллельности Евклида. Через точку А вне прямой а в плоскости, проходящей через А и а, можно провести лишь одну прямую, не пересекающую а.

Возникновение Е. г. тесно связано с наглядными представлениями об окружающем нас мире (прямые линии - натянутые нити, лучи света и т. п.). Длит. процесс углубления наших представлений привёл к более абстрактному пониманию геометрии. Открытие Н. И. Лобачевским геометрии, отличной от Е. г., показало, что наши представления о пространстве не являются априорными. Иными словами, Е. г. не может претендовать на роль единственной геометрии, описывающей свойства окружающего нас пространства. Развитие естествознания (гл. обр. физики и астрономии) показало, что Е. г. описывает структуру окружающего нас пространства лишь с определённой степенью точности н не пригодна для описания свойств пространства, связанных с перемещениями тел со скоростями, близкими к световой. Т. о., Е. г. может рассматриваться как первое приближение для описания структуры реального физич. пространства. См. Пространство, Геометрия, Лобачевского геометрия, Неевклидовы геометрии.

Э. Г. Позняк.

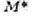ЕВКЛИДОВО ПРОСТРАНСТВО (в математике), пространство, свойства к-рого описываются аксиомами евклидовой геометрии. В более общем смысле Е. п. наз. n-мерное векторное пространство, в к-ром возможно ввести нек-рые спец. координаты (декартовы) так, что метрика его будет определена след. образом: если точка М имеет координаты  а точка - координаты 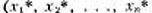), то расстояние между этими точками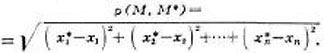

См. Пространство, Многомерное пространство.