ДИСПЕРСИОННЫЕ ПРИЗМЫ, призмы для пространственного разделения излучений различных длин волн; применяются гл. обр. в спектральных приборах. Разделение излучений в Д. п. является результатом зависимости угла отклонения 8 луча, прошедшего через призму (см. рис.), от показателя преломления п, различного для лучей разных длин волн X (см. Дисперсия света).

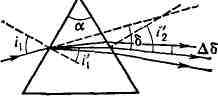
Качество Д. п. характеризуется угловой дисперсией Дб/ДХ, к-рая зависит от материала призмы (величин п и Дn/ДХ), преломляющего угла а и угла падения i₁:

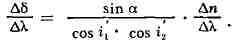
В зависимости от исследуемой области спектра применяются Д. п. из различных материалов: стекла (флинта) - для видимой области; кристаллич. кварца, флюорита и др. - для ультрафиолетовой; фтористого лития, каменной соли и др. - для инфракрасной.

Лит.: Ландсберг Г. С., Оптика, 4 изд., М.- Л., 1957 (Общий курс физики).

ДИСПЕРСИОННЫЙ АНАЛИЗ в математике, статистический метод выявления влияния отдельных факторов на результат эксперимента. Первоначально Д. а. был предложен англ, статистиком Р. Фишером (1925) для обработки результатов агрономич. опытов по выявлению условий, при к-рых испытываемый сорт с.-х. культуры даёт максимальный урожай. Современные приложения Д. а. охватывают широкий круг задач экономики, биологии и техники и трактуются обычно в терминах статистич. теории выявления систематич. различий между результатами непосредств. измерений, выполненных при тех или иных меняющихся условиях. Если значения неизвестных постоянных a₁, ..... а_n„ могут быть измерены с помощью различных методов или измерительных средств M₁,..., М_т и в каждом случае систематическая ошибка может зависеть как от выбранного метода, так и от неизвестного измеряемого значения at, то результаты измерений хц представляют собой суммы вида

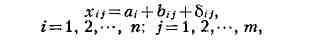
где bij - систематич. ошибка, возникающая при измерении at по методу Mj, бij - случайная ошибка. Такая модель наз. двухфакторной схемой Д. а. (первый фактор - измеряемая величина, второй-метод измерения). Дисперсии эмпирических распределений, соответствующих множествам случайных величин к-рое и объясняет происхождение названия Д. а.

Если величины систематич. ошибок не зависят от метода измерений (т. е. между методами измерений нет систематич. расхождений), то отношение s²₂/s²₀ близко к единице. Это свойство лежит в основе критерия для статистич. выявления систематич. расхождений: если s²₂/s²₀ значимо отличается от единицы, то гипотеза об отсутствии систематич. расхождений отвергается. Значимость отличия определяется в согласии с законом распределения вероятностей случайных ошибок измерений. В частности, если все измерения равноточны и случайные ошибки подчиняются нормальному распределению, то критич. значения для отношения s²₂/s²₀определяются с помощью таблиц т. н. F-распределения (распределения дисперсионного отношения).

Изложенная схема позволяет лишь обнаружить наличие систематич. расхождений и, вообще говоря, непригодна для их численной оценки с последующим исключением из результатов наблюдений. Эта цель может быть достигнута только при многократных измерениях (при повторных реализациях указанной схемы).

Лит.: Шеффе Г., Дисперсионный анализ, пер. с англ., М., 1963: Смирнов Н. В., Дунин - Барковскиq И. В., Курс теории вероятностей и математической статистики для технических приложений, 2 изд., М., 1965.

Л. Н. Большев.

ДИСПЕРСИОННЫЙ АНАЛИЗ в химии, совокупность методов определения дисперсности, т. е. характеристики размеров частиц в дисперсных системах. Д. а. включает различные способы определения размеров свободных частиц в жидких и газовых средах, размеров каналов-пор в тонкопористых телах (в этом случае вместо понятия дисперсности используют равнозначное понятие пористости), а также удельной поверхности. Одни из методов Д. а. позволяют получать полную картину распределения частиц (пор) по размерам (объёмам), а другие дают лишь усреднённую характеристику дисперсности (пористости).

К первой группе относятся, напр., методы определения размеров отд. частиц непосредственным измерением (ситовой анализ, оптич. и электронная микроскопия) или по косвенным данным: скорости оседания частиц в вязкой среде (седиментационный анализ в гравитац. поле и в центрифугах), величине импульсов электрич. тока, возникающих при прохождении частиц через отверстие в непроводящей перегородке (кондуктометрич. метод, см. Коултера прибор), или др. показателям.

Вторая группа методов объединяет оценку средних размеров свободных частиц и определение удельной поверхности порошков и пористых тел. Средний размер частиц находят по интенсивности рассеянного света (нефелометрия), с помощью ультрамикроскопа, методами диффузии и т. д.; удельную поверхность - по адсорбции газов (паров) или растворённых веществ, по газопроницаемости, скорости растворения и др. способами. Ниже приведены границы применимости различных методов Д. а. (размеры частиц в м):
 

Ситовой анализ	10-2-10-4
Седиментационный анализ в гравитационном поле	10-4-10-6
Кондуктометрический метод	10-4-10-6
Микроскопия	10-4-10-7
Метод фильтрации	10-5-10-7
Центрифугирование	10-7-10-9
Ультрацентрифугирование	10-7-10-9
Ультрамикроскопия	10-7-10-9
Нефелометрия	10-7-10-9
Электронная микроскопия	10-7-10-9
Метод диффузии	10-7-10-10

Д. а. широко используют в различных областях науки и пром. произ-ва для оценки дисперсности систем (суспензий, эмульсий, золей, порошков, адсорбентов и т. д.) с величиной частиц от нескольких миллиметров (10^-3м) до нескольких нанометров (10^-9л).

Лит.: Фигуровский Н. А., Седиментометрический анализ, М.- Л., 1948; Ходаков Г. С., Основные методы дисперсионного анализа порошков, М., 1968; Коузов П. А., Основы анализа дисперсного состава промышленных пылей и измельченных материалов, Л., 1971; Рабинович Ф. М., Кондуктометрический метод дисперсионного анализа, Л., 1970; Irani R. R., С all is С. F., Particle size, Measurement, interpretation and application, N. Y.-L., 1963.

ДИСПЕРСИЯ (от лат. dispersio - рассеяние), в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. В статистич. понимании Д.

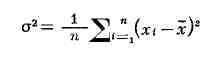
есть среднее арифметическое из квадратов отклонений величин x_i от их среднего арифметического

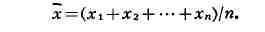
В теории вероятностей Д. случайной величины X наз. математическое ожидание Е(Х - mx)² квадрата отклонения X от её математич. ожидания т_х = Е(Х). Д. случайной величины X обозначается через D(X) или через о²х. Квадратный корень из Д. (т. е. а, если Д. есть о²) наз. средним квадратичным отклонением (см. Квадратичное отклонение).

Для случайной величины X с непрерывным распределением вероятностей, характеризуемым плотностью вероятности р(х), Д. вычисляется по формуле

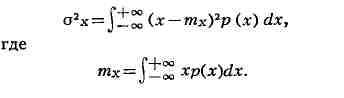
Об оценке Д. по результатам наблюдения см. Статистические оценки.

В теории вероятностей большое значение имеет теорема: Д. суммы независимых слагаемых равна сумме их Д. Не менее существенно Чебышева неравенство, позволяющее оценивать вероятность больших отклонений случайной величины X от её математич. ожидания.

Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969.

ДИСПЕРСИЯ волн, зависимость фазовой скорости гармонич. волн от их частоты. Д. определяется физич. свойствами той среды, в к-рой распространяются волны. Напр., в вакууме электромагнитные волны распространяются без дисперсии, в вещественной же среде, даже в такой разреженной, как ионосфера Земли, возникает Д. волн. Ультразвуковые волны также обнаруживают дисперсию (см. Дисперсия звука).

Наличие Д. волн приводит к искажению формы сигналов при распространении их в среде. Это объясняется тем, что гармонич. волны разных частот, на к-рые может быть разложен сигнал, распространяются с различной скоростью (подробнее см. Волны, Групповая скорость). Д. света при его распространении в прозрачной призме приводит к разложению белого света в спектр (см. Дисперсия света).

ДИСПЕРСИЯ ЗВУКА, зависимость фазовой скорости монохроматических звуковых волн от частоты. Д. з. является причиной изменения формы звуковой волны (звукового импульса) при распространении его в среде. Различают Д. з., обусловленную физич. свойствами среды, и Д. з., обусловленную наличием границ тела, в к-ром звуковая волна распространяется, и от свойств тела не зависящую.

Д. з. первого типа может вызываться различными причинами. Наиболее важны случаи Д. з., связанной с релаксационными процессами (см. ниже), происходящими в среде при прохождении звуковой волны. Механизм возникновения релаксационной Д. з. можно выяснить на примере многоатомного газа. При распространении звука в газе молекулы газа совершают постулат, движение. Если газ одноатомный, то никаких других движений, кроме поступательных, атомы газа совершать не могут. Если же газ многоатомный, то при столкновениях молекул между собой могут возникать вращат. движения молекул, а также колебат. движения атомов, составляющих молекулу. При этом часть энергии звуковой волны тратится на возбуждение этих колебат. и вращат. движений. Переход энергии от звуковой волны (т. е. от по-ступат. движения) к внутр. степеням свободы (т. е. к колебат. и вращат. движениям) происходит не мгновенно, а за нек-рое время, к-рое наз. временем релаксации т. Это время определяется числом соударений, к-рое должно произойти между молекулами для перераспределения энергии между всеми степенями свободы. Если период звуковой волны мал по сравнению с г (высокие частоты), то за период волны внутр. степени свободы не успеют возбудиться и перераспределение энергии не успеет произойти. В этом случае газ будет вести себя так, как будто никаких внутр. степеней свободы вовсе нет. Если же период звуковой волны много больше, чем t (низкие частоты), то за период волны энергия постулат, движения успеет перераспределиться на внутр. степени свободы. При этом энергия постулат, движения будет меньше, чем в случае, когда внутр. степеней свободы не было бы. Поскольку упругость газа определяется энергией, приходящейся на постулат, движения молекул, то, следовательно, упругость газа, а значит и скорость звука, также будет меньше, чем в случае высоких частот. Иными словами, в нек-рой области частот, близких к частоте релаксации, равной w_р=1/t, скорость звука увеличивается с ростом частоты, т. е. имеет место т. н. положит, дисперсия. Если Со - скорость звука при малых частотах (wt << 1), а с_{БЕСКОНЕЧНОСТЬ} - при очень больших частотах (wt >>1), то скорость звука для произвольной частоты описывается формулой

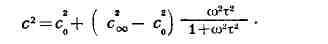
Вследствие необратимости процессов перераспределения энергии в той области частот, где имеет место Д. з., наблюдается повышенное поглощение звука.

Релаксационная Д. з. может быть не только в газах, но и в жидкостях, где она связана с различными межмолекулярными процессами, в растворах электролитов, в смесях, в к-рых под действием звука возможны химич. реакции между компонентами, в эмульсиях, а также в нек-рых твёрдых телах.

Величина Д. з. может быть весьма различной в разных веществах. Так, напр., в углекислом газе величина дисперсии порядка 4%, в бензоле ~ 10% , в морской воде меньше чем 0,01%, а в сильно вязких жидкостях и в высокополимерных соединениях скорость звука может измениться на 50%. Однако в большинстве веществ Д. з. весьма малая величина и измерения её довольно сложны. Частотный диапазон, в к-ром имеет место Д. з., также различен для разных веществ. Так, в углекислом газе при норм, давлении и темп-ре 18 °С частота релаксации равна 28 кгц, в морской воде 120 кгц. В таких соединениях, как четырёх-хлористый углерод, бензол, хлороформ и др., область релаксации попадает в область частот порядка 10⁹-10¹⁰гц, где обычные ультразвуковые методы измерений не применимы и Д. з. можно измерить, только используя оптич. методы.

К Д. з. 1-го же типа, но не носящей релаксационного характера, приводят теплопроводность и вязкость среды. Эти виды Д. з. обусловлены обменом энергией между областями сжатий и разрежений в звуковой волне и особенно существенны для микронеоднородных сред. Д. з. может проявляться также в среде с вкрапленными неоднородностями (резонаторами), напр, в воде, содержащей пузырьки газа. В этом случае при частоте звука, близкой к резонансной частоте пузырьков, часть энергии звуковой волны идёт на возбуждение колебаний пузырьков, что приводит к Д. з. и к возрастанию поглощения звука.

Вторым типом Д. з. является "геометрическая" дисперсия, обусловленная наличием границ тела или среды распространения. Она появляется при распространении волн в стержнях, пластинах, в любых волноводах акустических. Дисперсия скорости наблюдается для изгиб-ных волн в тонких пластинах и стержнях (толщина пластины или стержня должна быть много меньше, чем длина волны). При изгибании тонкого стержня упругость на изгиб тем больше, чем меньше изгибаемый участок. При распространении изгибной волны длина изгибаемого участка определяется длиной волны. Поэтому с уменьшением длины волны (с повышением частоты) увеличивается упругость, а следовательно, и скорость распространения волны. Фазовая скорость такой волны пропорциональна корню квадратному из частоты, т. е. имеет место положит, дисперсия.

При распространении звука в волноводах звуковое поле можно представить как суперпозицию нормальных волн, фазовые скорости к-рых для прямоугольного волновода с жёсткими стенками имеют вид

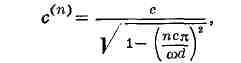
где п - номер нормальной волны (n = = 1, 2, 3, ...), с-скорость звука в свободном пространстве, d - ширина волновода. Фазовая скорость нормальной волны всегда больше скорости звука в свободной среде и уменьшается с ростом частоты ("отрицательная" дисперсия).

Д. з. обоих типов приводит к расплы-ванию формы импульса при его распространении. Это особенно важно для гидроакустики, атмосферной акустики к геоакустики, где имеют дело с распространением звука на большие расстояния.

Лит.: Бергман Л., Ультразвук и его применение в науке и технике, пер. с нем., 2 изд., М., 1957; Михайлов И. Г., Соловьёв В. А. и Сырников Ю. П., Основы молекулярной акустики, М., 1964; Физическая акустика, под ред. У. Мэзона, пер. с англ., т. 2, ч. А, М., 1968; Фабелинский И. Л., Молекулярное рассеяние света, М., 1965.

Л. Л. Полякова.

ДИСПЕРСИЯ СВЕТА, зависимость показателя преломления п вещества от частоты v (длины волны X) света или зависимость фазовой скорости световых Волн от частоты. Следствие Д. с. - разложение в спектр пучка белого света при прохождении сквозь призму (см. Спектры оптические). Изучение этого спектра привело И. Ньютона (1672) к открытию Д. с. Для веществ, прозрачных в данной области спектра, п увеличивается с увеличением v (уменьшением К), чему и соответствует распределение цветов в спектре; такая зависимость га от X наз. нормальной Д. с.

Вблизи полос поглощения вещества ход изменения га с длиной волны значительно сложнее. Так, для тонкой призмы из красителя цианина (рис. 1) в области поглощения красные лучи преломляются сильнее фиолетовых, а наименее преломляемым будет зелёный, затем синий (т. н. аномальная Д. с.).

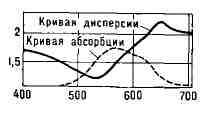
Рис. 1. Зависимость показателя преломления (сплошная линия) и поглощения (пунктирная линия) от длины волны в m и- для тонкой призмы из красителя цианина.

У всякого вещества имеются свои полосы поглощения, и общий ход показателя преломления обусловлен распределением этих полос по спектру. На рис. 2 показан вид интерференционных полос в области аномальной дисперсии паров натрия.

Рис. 2. Аномальная дисперсия в парах натрия (фотография Д. С. Рождественского).

Преломление света в веществе возникает вследствие изменения фазовой скорости света; показатель преломления п = с_о/с, где с_о - скорость света в вакууме, с - фазовая скорость его в данной среде. По электромагнитной теории света

е от частоты. Эта зависимость связана с взаимодействием электромагнитного поля световой волны с атомами и молекулами, приводящим к поглощению; показатель преломления при этом становится комплексной величиной n~ = п + ix, где и характеризует поглощение. В видимой и ультрафиолетовой областях спектра основное значение имеют колебания электронов, а в инфракрасной - колебания ионов.

Согласно классич. представлениям, под действием электрич. поля световой волны электроны атомов или молекул совершают вынужденные колебания с частотой, равной частоте приходящей волны. При приближении частоты световой волны к частоте собств. колебаний электронов возникает явление резонанса, обусловливающее зависимость Е от частоты, а также поглощение света. Эта теория хорошо объясняет связь Д. с. с полосами поглощения. Для того чтобы получить количественное совпадение с опытом, в классич. теории приходилось вводить для каждой линии поглощения нек-рые эмпирич. константы ("силы осцилляторов"). Согласно электронной теории, справедливы приближённые формулы:

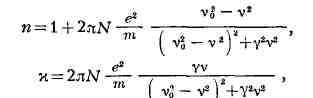
где N - число частиц в единице объёма, е и т - заряд и масса электрона, y - коэфф. затухания. На рис. 3 приведены графики зависимости n и х от v/v_0.

Квантовая теория подтвердила качественные результаты классич. теории и, кроме того, дала возможность связать эти константы с другими характеристиками электронных оболочек атомов (их волновыми функциями в разных энер-гетич, состояниях). Квантовая теория объяснила также особенности Д. с., наблюдающиеся в тех случаях, когда имеется значит, число атомов в возбуждённых состояниях (т. н. отрицательная Д. с.).

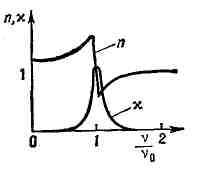
Рис. 3. Графики зависимостей n и x от v/n₀.

Д. с. в прозрачных материалах, применяемых в оптич. приборах, имеет большое значение при расчёте спектральных приборов в целях получения хороших спектров, при расчёте ахроматич. линз или призм, для уничтожения Д. с., вызывающей хроматическую аберрацию, и др.

Вращательная дисперсия-изменение угла вращения плоскости поляризации ср в зависимости от длины волны X. В прозрачных веществах угол ср обычно возрастает с уменьшением X, причём для нек-рых сред приближённо выполняется закон Био: ф = К/Х² (К -постоянная для данного вещества). Вращательная Д. с. такого типа наз. нормальной. В области поглощения света ход вращательной Д. с. значительно сложнее, причём угол ф может достигать огромных величин (аномальная вращательная дисперсия). См. Вращение плоскости поляризации.

Лит.: Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Горелик Г. С., Колебания и волны, 2 изд., М.-Л., 1959.

М. Д. Галанин.

ДИСПЕРСНАЯ СТРУКТУРА, неупорядоченная пространственная сетка в дисперсной системе (каркас), образованная частицами дисперсной фазы, соединёнными молекулярными силами различной природы. Формирование Д. с. сопровождается загущением (возрастанием структурной вязкости) или отвердеванием первоначально жидкой системы. Структурная сетка может занимать при этом от неск. сотых долей % до неск. десятков % от объёма системы, а в нек-рых случаях заполнять практически весь объём. По характеру связи между частицами различают коагуляционные и конденсационные Д. с. Коагуляц. Д. с. возникают в процессе коагуляции частиц дисперсной фазы или при увеличении степени объёмного заполнения ими дисперсной системы. В коагуляц. Д. с. соединение частиц осуществляется через тонкую прослойку жидкой дисперс. среды вследствие действия слабых межмолекулярных (ван-дер-ваальсовых) сил притяжения. Такие Д. с. обладают малой прочностью, пластичностью, нек-рой эластичностью и тиксотропией, т. е. способностью самопроизвольно и обратимо восстанавливаться после механич. разрушения - в результате столкновения частиц в броуновском движении. Лиогели (см. Гели) и различного рода пасты имеют Д. с. типично коагуляц. типа.

Конденсац. Д. с. формируются в процессе выделения новой фазы из пересыщенных паров, расплавов и растворов. Мельчайшие частицы новой (дисперсной) фазы, возникнув в недрах гомогенной среды, увеличиваются в размерах, срастаются и образуют структурную сетку с прочными фазовыми, или когезионными (см. Когезия), контактами. Такая Д. с. может быть упруго-хрупкой или эластичной (в зависимости от механич. свойств составляющей её фазы), но она лишена пластичности и тиксотропии, т. е. разрушается необратимо. Если новая фаза выделяется в виде кристаллов, к-рые в процессе роста срастаются или переплетаются, то образованная ими Д. с. наз. кристаллизационной или конденсационно - кристаллизационной. Таковы, напр., Д. с., возникающие при взаимодействии минеральных вяжущих веществ - цементов - с водой. Керамика и металлокерамика (керметы) также относятся к Д. с. конденсациошю - кристаллизационного типа. К ним причисляют и предельно плотные Д. с. мелкозернистых твёрдых тел, закристаллизовавшихся из расплава, напр, ситаллы - закристаллизованные стёкла. Возникновение конденсац. Д. с. из пересыщенных растворов полимеров может идти двумя путями: через промежуточную стадию образования коацерватных капель (см. Коацервация) с повышенным содержанием полимера и через образование в эластичном полимерном студне капелек разбавленного раствора, подобных вакуолям. В 1-м случае обеднение растворителем и частичная коалесценция капель, перешедших в высоко-эластическое состояние, приводят к возникновению сетчатой структуры срастания. Аналогичные структуры образуются из шаровидных полимерных частиц при желатинизации латекса, напр, в производстве губчатых резин, или из частиц молочного жира при получении сливочного масла. Во 2-м случае разрастание и слияние друг с другом "вакуолей" создаёт систему связных каналов; одновременно в результате синерезиса происходит обеднение растворителем фазы студня и возникает структурная сетка ячеистого типа. Удаление растворителя из полимерной Д. с. конденсационного типа (т. н. псевдогеля) даёт полимерные ксерогели, представляющие практич. интерес в производстве тонкопористых материалов: мембранных фильтров, искусственной кожи, макропористых ионообменных смол и т. д.

Природные и искусственные материалы, напр, нек-рые горные породы, наполненные пластмассы и резины, могут иметь и сложную коагуляционно-конденсацион-ную структуру. Исследование и направленный синтез Д. с. с заданными свойствами - предмет специальной отрасли науки - физико-химической механики.

Лит.: Ребиндер П. А., Влодавец И. Н., Физико-химическая механика пористых и волокнистых Дисперсных структур, в кн.: Проблемы физико-химической механики волокнистых и пористых дисперсных структур и материалов, Рига, 1967, с. 5-40; Воюцкий С. С., Курс коллоидной химии, М., 1964, с. 334-40, 533-44.

Л. А. Шиц.

ДИСПЕРСНАЯ ФАЗА, совокупность мелких однородных твёрдых частиц, капелек жидкости или пузырьков газа, равномерно распределённых в окружающей (дисперсионной) среде. Д. ф. и дисперсионная среда образуют дисперсные системы. См. также Коллоидные системы.

ДИСПЕРСНОСТЬ (от лат. dispersus -рассеянный, рассыпанный), характеристика размеров частиц в дисперсных системах. Д. обратно пропорциональна среднему диаметру частиц и определяется удельной поверхностью, т. е. отношением общей поверхности частиц к единице объёма (или иногда массы) дисперсной фазы.

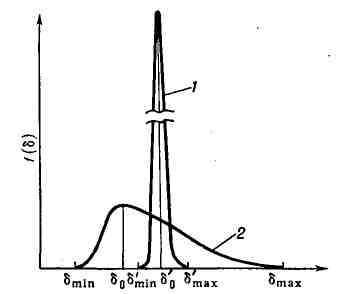
Кривые распределения объёма (массы) час-тиц по размерам: 1 - монодисперсная система: 2 - полидисперсная система. б_min, б_max, б₀ - соответственно минимальный, максимальный и вероятнейший размер частиц: f(б) - функция распределения, доля объёма (или массы) дисперсной фазы, к-рая приходится на частицы с данным интервалом размеров, делённая на величину интервала.

Удельная поверхность - усреднённый показатель Д. Более полное представление о Д. даёт кривая распределения объёма или массы дисперсной фазы по размерам частиц (рис.). С ростом полидисперсности системы, т. е. с увеличением разницы в размерах частиц, максимум на кривой распределения снижается и становится более широким, но площадь, ограниченная кривой и осью абсцисс, сохраняется постоянной. В редком случае монодисперсной системы, когда частицы имеют почти одинаковый размер, кривая имеет вид острого пика с узким основанием. Встречаются системы, дающие на кривой распределения два и большее число максимумов. Для тонкопористых тел, напр. адсорбентов и катализаторов, понятие Д. заменяется равнозначным понятием пористости, т. е. характеристикой размеров каналов-пор, пронизывающих эти тела.

В химии высокомолекулярных соединений Д. часто наз. характеристику размеров линейных или разветвлённых (цепочечных) полимерных молекул, определяемую мол. массой. Полн. дисперсность полимеров может быть выражена функцией распределения молекул по их мол. массам (т. н. молекулярно массовое распределение). Графически эта функция изображается кривой типа приведённых на рис.; по оси абсцисс откладывают мол. массы, а по оси ординат - доли полимерных фракций с соответствующими мол. массами.

Д. как технологич. показатель имеет важное значение в произ-ве и применении пигментов, различных наполнителей для пластмасс, минеральных вяжущих веществ, удобрений, пестицидов, фармацевтич. препаратов и мн. других порошкообразных и мелкозернистых продуктов. Определяется Д. методами дисперсионного анализа.

Лит. см. при ст. Дисперсионный анализ.

ДИСПЕРСНОУПРОЧНЁННЫЕ МАТЕРИАЛЫ, металлы или сплавы, упрочнённые дисперсными частицами тугоплавких соединений, гл. обр. окислов, не растворяющихся и не коагулирующих в матрице (основе) сплава при высоких рабочих темп-pax. Д. м. отличаются от широко используемых в технике дисперсионно-твердеющих сплавов (см. Старение металлов) структурой, составом, методами изготовления, а также более высокой структурной и термич. стабильностью, проявляющейся в сохранении длительной прочности Д. м. при высоких темп-рах. В распространённых жаропрочных дис-персионно-твердеющих никелевых сплавах наибольшее влияние на повышение жаропрочности оказывают интерметаллидные упрочнители (Ni₃Al, Ni₃Ti). Однако при темп-pax выше 1000-1100 °С последние растворяются и коагулируют в основе сплава, что приводит к его разупрочнению. Повышенная жаропрочность Д.м. на никелевой основе достигается введением в никель 2-5% тугоплавких кислородных соединений (ThO₂, НfO₂, Y₂O₃). Оптимальная дислокационная структура матрицы формируется при строгом соблюдении дисперсности частиц (100-600 А), расстояния между ними (0,5-0,8 мкм), а также в результате применения термо-механич. режимов обработки - холодной деформации и высокотемпературного отжига. На рис. приведены графики зависимости длительной прочности дисперсноупрочнённых и дисперсионно-твердеющих никелевых сплавов от времени и темп-ры.

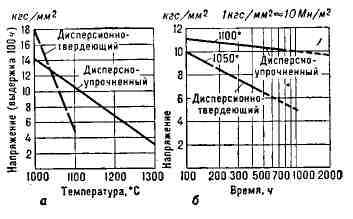
Зависимость длительной прочности дисперсноупрочнённых и дисперсионно-твер-деющих никелевых сплавов от температуры (а) и времени (б).

Изделия из Д. м. получают, как правило, в три стадии: подготовка исходных порошков гл. обр. путём совместного химич. осаждения основы и упрочнителя из водных растворов их солей, формование заготовок и обработка их давлением - экструзией, волочением, прокаткой и т. д. Применение дисперсного упрочнения позволяет повысить жаропрочность и расширить температурные области использования практически всех металлов и сплавов на основе меди, никеля, кобальта, железа, циркония, титана, молибдена и др.

Лит.: Современные композиционные материалы, под ред. Л. Браутмана и Р. Крока, пер. с англ., М., 1970; Портной К. И., Туманов А. Т., Композиционные и дисперсно-упрочненные жаропрочные никелевые сплавы, в кн.: Сборник научных докладов на совещании по проблеме: "Структура и свойства жаропрочных металлических материалов", М., 1970; Туманов А. Т., Портной К. И., Новые пути повышения жаропрочности никелевых сплавов, "Докл. АН СССР", 1971, т. 197, № 1.

К. И. Портной, А. Т. Туманов.

ДИСПЕРСНЫЕ КРАСИТЕЛИ, группа плохо растворимых в воде красителей, применяемых для окрашивания полиамидных, полиэфирных, полиакрило-нитрильных и ацетатных волокон. Д. к. характеризуются отсутствием кислотных групп SO₃H и СООН, мол. массой не более 350; в процессе производства диспергируются до размеров 0,2-2 мкм. См. Крашение.

ДИСПЕРСНЫЕ СИСТЕМЫ, образования из двух или большего числа фаз (тел) с сильно развитой поверхностью раздела между ними. В Д. с. по крайней мере одна из фаз - дисперсная фаза -распределена в виде мелких частиц (кристалликов, нитей, плёнок или пластинок, капель, пузырьков) в другой, сплошной, фазе - дисперсионной среде. Д. с. по основной характеристике - размерам частиц или (что то же самое) дисперсности (определяемой отношением общей площади межфазной поверхности к объёму дисперсной фазы) - делятся на грубо (низко) дисперсные и тонко (высоко) дисперсные, или коллоидные системы (коллоиды). В грубодисперсных системах частицы имеютразмер от 10^-4 см и выше, в коллоидных - от 10^-4-10^-5 до 10^-7 см. По агрегатному состоянию дисперсионной среды различают газодисперсные системы - аэрозоли (туманы, дымы), пыль; жидкодисперсные - золи, суспензии, эмульсии, пены, твёрдо дисперсные -стеклообразные или кристаллич. тела с включениями мельчайших твёрдых частиц, капель жидкости или пузырьков газа (см. табл.). Пыль, суспензии, лио-

Классификация дисперсных систем по агрегатному состоянию фаз фобные эмульсии (см. Лиофилъные и лиофобные коллоиды) - грубодисперсные системы; как правило (при наличии разности плотностей), они седиментационно неустойчивы, т. е. их частицы оседают под действием силы тяжести или всплывают.
 

Дисперсионная среда	Дисперсная фаза
	газовая	жидкая	твёрдая
Газовая	Дисперсные системы не образуются	Туманы	Дымы, пыль
Жидкая	Пены	Эмульсии	Суспензии
		Золи (коллоидные "растворы")*
Твёрдая	Аэрогели (пористые тела)	Жидкие включения в твёрдых телах	Твёрдые золи (рубиновое стекло)

* Предельно высокодисперсные системы (золи) иногда трудно классифицировать по агрегатному состоянию дисперсной фазы.

Золи - типичные высокодисперсные коллоидные системы, частицы дисперсной фазы к-рых (мицеллы) участвуют в броуновском движении и потому седиментационно устойчивы. Жидкие и твёрдые пены, состоящие из газовых ячеек-пузырьков, разделённых тонкими прослойками непрерывной фазы, представляют особую группу структурированных ячеистых систем (см. ниже).

По интенсивности молекулярного взаимодействия фаз различают лиофильные и лиофобные Д. с. В лиофильных системах молекулярное взаимодействие между фазами достаточно велико и удельная свободная поверхностная энергия (поверхностное натяжение) на меж фазной границе очень мала. Лиофильные системы образуются самопроизвольно (спонтанно) и имеют предельно высокую дисперсность. В лиофобных системах взаимодействие между молекулами различных фаз значительно слабее, чем в случае лиофильных систем; межфазное поверхностное натяжение велико, вследствие чего система проявляет тенденцию к самопроизвольному укрупнению частиц дисперсной фазы (см. Коагуляция и Коалесценция). Обязательное условие существования лиофобных Д. с.- наличие стабилизаторов, веществ, к-рые адсорбируются на поверхности раздела фаз и образуют защитные слои, препятствующие сближению частиц дисперсной фазы.

Д. с. могут быть бесструктурными (свободно дисперсными) и структурированными (связнодисперсными). Структурированные Д. с. пронизаны сеткой-каркасом из соединённых между собой частиц (капель, пузырьков) дисперсной фазы, вследствие чего обладают нек-рыми механич. свойствами твёрдых тел (подробнее см. Дисперсная структура, Гели). Характерная особенность Д. с.- высокая свободная энергия как следствие сильно развитой межфазной поверхности; поэтому Д. с. обычно (кроме лиофильных Д. с.) термодинамически неустойчивы. Они обладают повышенной адсорбционной способностью, химической, а иногда и биологич. активностью. Д. с.- основной объект изучения коллоидной химии.

Д. с. широко распространены в природе, технике и быту. Примерами Д. с. могут служить горные породы, грунты, почвы, дымы, облака, атмосферные осадки, растительные и животные ткани; строительные материалы, краски, моющие средства, волокнистые изделия, важнейшие пищевые продукты и мн. др.

Лит. см. при ст. Коллоидная химия.

ДИСПЕТЧЕРИЗАЦИЯ, централизация (концентрация) оперативного контроля и координация управления производств, процессами с целью обеспечения согласованной работы отд. звеньев предприятия или группы предприятий для достижения наивысших технико-экономич. показателей, выполнения графиков работ и производственной программы. Д. направлена на обеспечение равномерности загрузки всех звеньев предприятия, непрерывности, ритмичности и экономичности выполнения всех процессов осн. производственного цикла, бесперебойной работы вспомогательных и обслуживающих участков. Вследствие изменения состава производимой продукции, корректив, вносимых в методы и технологию её изготовления, разного уровня выполнения программы различными рабочими и производств. участками, а также в связи с перебоями из-за ремонта оборудования, нарушения графика поставки материалов и т. п. нарушаются предварительно установленные пропорции и ритм. В задачу Д. входит регулирование процесса произ-ва с целью восстановления действующих или установления новых пропорций и ритма работы предприятия. Д. охватывает контроль и управление технологич. процессами, контроль и оперативное распределение материальных и энергетич. ресурсов, транспортных средств, учёт работы машин и механизмов, повышает безопасность и точность движения транспорта. Способствуя предотвращению простоев оборудования и потерь рабочего времени и выполнению заказов в срок, Д. оказывает положит. влияние на экономику произ-ва.

Простейшая форма диспетчерской службы возникла в период пром. революции 18-19 вв. в связи с переходом от кустарного и полукустарного к фабрично-заводскому произ-ву. Первоначально осн. функцией диспетчерской службы было распределение рабочей силы, сырья и материалов и учёт готовой продукции. С развитием крупносерийного и поточно-массового произ-в, с возникновением производств. связей между смежными предприятиями, созданием крупных пром. и энергетич. объединений, а также быстрым совершенствованием транспорта Д. стала необходимой для оперативного руководства сложным комплексом технологич. процессов, взаимодействия отд. звеньев транспортных систем. Примитивная диспетчерская служба уступила место совр. Д., основанной на совершенных методах управления и контроля с применением новейших средств связи, автоматики, пром. телевидения, телемеханики и вычислительной техники. Д. стала одним из важнейших средств управления в пром-сти, энергетике, на транспорте, в строительстве, с. х-ве, торговле и др. (см. Автоматизация производства).

Структура Д. зависит от характера и масштаба объекта управления. Простейшая в совр. понимании Д. осуществляется гл. обр. с помощью диспетчерской двусторонней телефонной связи с объектами. Небольшие предприятия, строит. площадки располагают обычно одним диспетчерским пунктом. На крупных объектах с разветвлённой или многоступенчатой структурой (напр., энергосистема) действуют неск. местных диспетчерских пунктов и один центральный, координирующий их деятельность.

Д. в энергетике осуществляет оперативное управление электростанциями, подстанциями, линиями электропередачи и отд. крупными установками потребителей. Диспетчерская служба призвана обеспечить бесперебойность и надёжность работы энергосистемы, распределение электроэнергии в соответствии с графиком нагрузки, поддержание установленных для энергосистемы параметров (напряжение, частота в электросети, темп-pa и давление пара и темп-pa воды в тепловых сетях), максимальную экономичность работы энергосистемы в результате оптимального использования различных источников энергии: тепловых, гидроэлектрич., атомных и др. электростанций, теплоэлектроцентралей, центральных котельных и т. д. Диспетчер энергосистемы контролирует и координирует совместную работу нескольких электростанций и электрических сетей в рамках одной энергосистемы. В зависимости от масштаба системы управление ею может быть сосредоточено на одном диспетчерском пункте либо на нескольких, деятельность к-рых координируется с центрального диспетчерского пункта (см. Единая электроэнергетическая система). Любые изменения режима и состояния элементов энергосистемы (включение и отключение линий электропередачи, остановка и пуск агрегатов на электростанциях, покрытие пиковых нагрузок, доставка топлива, проведение профилактич. работ и т. п.) возможны только с ведома и по указанию соответствующего диспетчера. Информация о состоянии объектов поступает к диспетчеру от дежурных операторов, инженеров, техников-смотрителей, контролёров либо собирается, регистрируется и обрабатывается автоматизированными системами сбора и обработки данных (см. Автодиспетчер). Полученная информация отображается различными средствами индикации и сигнализации на пульте диспетчера, на экранах контрольных телевизионных установок и специализиров. устройств отображения. Диспетчерские пункты крупных энергосистем, как правило, оснащаются электронными управляющими машинами.

Пром. предприятия (группы предприятий) с непрерывным производств. процессом, ход к-рого может быть описан математически, используют логич. устройства или управляющие вычислит. машины для автоматич. обработки поступающей информации. Несколько иные задачи Д. предприятий с дискретным производств. процессом, гл. обр. потому что даже изделие средней сложности содержит десятки, а иногда и тысячи деталей с различной технологией изготовления. Математическое описание таких процессов с целью автоматизации всего производств. цикла очень сложно. В этом случае в задачу диспетчерской службы входит не только контроль работы конвейеров и поточных линий (выпуск конечного продукта), но и обязательно координация деятельности всех участков, цехов, отделов, лабораторий, складов, вплоть до вспомогат. служб, обеспечивающих ритмичную, высокопроизводит. работу главного конвейера.

При производстве особо сложной продукции, представляющей собой крупные агрегаты и пром. комплексы, в изготовлении к-рых участвуют несколько самостоят. предприятий (смежных, кооперированных), часто разных отраслей пром-сти при участии научно-исследовательских и проектных организаций, возникла новая форма Д.- межзаводская. Такая диспетчерская служба широко использует, наряду с обычной документацией и техникой, метод сетевого планирования и управления. Одно из направлений развития Д. предусматривает сочетание регулирования процессов с выбором оптимального распределения операций по станкам, агрегатам, линиям, что позволяет снизить время переналадки оборудования и повысить производительность труда. Любой перебой в произ-ве фиксируется средствами Д., и ответственность за потери, связанные с нарушением производств. процесса, возлагается на звенья, по вине к-рых возник этот перебой. Дальнейшее совершенствование Д. позволит освободить руководителей произ-ва (мастеров, начальников цехов) от трудоёмкой работы по обеспечению произ-ва сырьём, материалами и полуфабрикатами, регулированию хода изготовления продукции и т. п. и сосредоточить их внимание на работе с коллективом трудящихся, решении технич., организационных и экономич. задач.

Структура и организация диспетчерской службы на автомобильном, воздушном, водном и ж.-д. транспорте вследствие специфики отд. видов транспорта и различия в их технич. оснащённости значительно отличаются от диспетчерской службы на пром. предприятии; имеет общую для всех видов транспорта цель: обеспечить надёжность и бесперебойность перевозок пассажиров и грузов. Особенность Д. на транспорте - непрерывное изменение обстановки на линиях, на начальных и конечных пунктах, значит. изменяемость графиков движения и загруженности транспортных средств в течение суток, месяца, года, что связано с сезонностью в работе отд. отраслей пром-сти, продолжительностью рабочего дня, периодом отпусков, дачным сезоном, загородными поездками в выходной день, состоянием погоды на трассе и т. д. Осн. задачи Д. на транспорте: непрерывный контроль состояния подвижного состава, его технич. готовности, состояния графиков погрузочно-разгрузочных работ и соблюдения расписания движения; обеспечение пассажиров билетами и необходимой путевой информацией. На крупных ж.-д. узлах, в аэропортах, речных и морских портах Д. предусматривает создание неск. диспетчерских пунктов, работа к-рых координируется гл. диспетчером с центрального пункта, оснащённого совр. средствами радио- и телефонной связи, автоматики, телемеханики и вычислительной техники. Отд. диспетчерские пункты, как правило, организуют в районе погрузочно-разгрузочных работ, при билетных кассах, в депо, гаражах, на стоянках автобусов, при вспомогат. службах на пунктах связи и т. п.

Д. в строительстве осуществляется при помощи совр. средств связи, автоматич. учёта и контроля. В задачи строит. диспетчерской службы входят: контроль выполнения оперативных планов строительства и своевременного обеспечения строительства рабочими, материалами, конструкциями, строит. машинами, транспортом; согласование работы строит. участков и устранение простоев рабочих и машин и др. неполадок. Диспетчерская система управления строительством охватывает все элементы строит. произ-ва и его обслуживания. Общая схема диспетчерской службы в строит. тресте включает гл. диспетчера в центральном аппарате треста, участкового диспетчера в строит.-монтажных управлениях и на участках, цеховых диспетчеров на производств. предприятиях, трансп. и др. диспетчеров в обслуживающих хозяйствах. Каждый диспетчер действует в пределах своего участка, общее оперативное руководство и контроль в объёме всего треста осуществляются гл. диспетчером. Диспетчерские пункты оборудованы совр. средствами связи, контроля, сбора и регистрации информации. Здесь же сосредоточиваются все оперативно-учётные данные и имеется ряд оперативных графиков и таблиц, по к-рым диспетчер может судить о состоянии произ-ва на любой момент, комплексно охватывая весь ход работ по отд. строит. участкам, управлениям и по тресту в целом.

Д. в сельском хозяйстве осуществляется диспетчерской службой совхоза или колхоза и охватывает все производственные участки х-ва, включая оперативное планирование, сбор и обработку производств. информации, решение конкретных задач по материально-тех-нич. обеспечению, устранение причин, нарушающих режим работы на полевых станах, фермах, в звеньях и отделениях. В отд. крупных х-вах (отделениях, фермах, гаражах и т. д.) в период напряжённых полевых работ могут создаваться диспетчерские посты. Диспетчерский пункт обычно располагается в центральной конторе. Д. в с. х-ве может охватывать целые р-ны и даже области для централизов. контроля и управления с.-х. производством.

Лит.: Малов В. С., Мешков В. К., Диспетчерские пункты энергетических систем, М.- Л., 1955; Эйхенвальд А. В., Сочинений А. Р., Оперативно-производственное планирование и диспетчирование на машиностроительном заводе, М., 1957; Буданцев Ю., Электронные помощники диспетчера, М., 1963; Бабенко А. С., Диспетчерская служба в сельском хозяйстве, М., 1967; Железные дороги, под ред. М. М. Филиппова, М., 1968; Технология и организация строительного производства, под ред. И. Г. Галкина, М., 1969; Вальденберг Ю. С., Белостоцкий А. А., Абизов P.M., Вычислительная техника на промышленном транспорте, М., 1970.

Г. И. Белов, С. Е. Каменицер, Г. И. Попов.

ДИСПЕТЧЕР-ПРОГРАММА (англ, dispatcher, от dispatch - отправлять по назначению, быстро выполнять), программа, предназначенная для организации и управления ходом работы вычислительной системы. Д.-п. является одной из составных частей системы математического обеспечения ЭВМ и представляет собой большую программу (десятки тысяч команд) со сложной логикой взаимодействия отдельных частей. Обеспечивая работу ЦВМ в режиме пакетной (одновременной) обработки неск. задач, Д.-п. устанавливает порядок ввода исходных данных, распределяет программы и массивы информации по памяти, координирует работу устройств ЦВМ при одновременном выполнении участков одной или неск. программ, обеспечивает автоматич. защиту программ и информационных массивов в памяти от неразрешённого вмешательства, случайного наложения или взаимного влияния. При работе ЦВМ в режиме разделения времени Д.-п. обслуживает десятки и более математич. пультов потребителей, иногда находящихся на значит, расстоянии от машины, выделяя для решения задачи, задаваемой с каждого пульта, небольшой интервал машинного времени. Д.-п. также анализирует отказы и сбои в машине и вырабатывает решения по продолжению вычислений.

Лит.: Труды 2-ой Всесоюзной конференции по программированию, Новосиб., 1970.

А. В. Гусев.

ДИСПЕТЧЕРСКАЯ СВЯЗЬ, проводная (телефонная, реже телеграфная), в некоторых случаях радиосвязь, используемая для переговоров диспетчера с руководителем работ на местах. Применяется в пром-сти, энергетике, на всех видах транспорта для непрерывного оперативного руководства (см. Оргасвязь). Во многих случаях для Д. с. используется аппаратура избирательной (селекторной) телефонной связи. См. также Диспетчеризация.

ДИСПЕТЧЕРСКАЯ ЦЕНТРАЛИЗАЦИЯ, система регулирования движения поездов на блок-участках ж. д. из одного пункта управления с применением средств телемеханики. Д. ц. представляет собой сочетание автоблокировки на перегонах с электрич. централизацией стрелок и сигналов станций участка и располагает аппаратурой телеуправления и телесигнализации, устройствами местного управления стрелками и сигналами на станциях, центральным диспетчерским аппаратом, пультом управления со световым табло, устройством для автоматич. регистрации движения поездов (поездо-графом) и т. д. (см. Железнодорожная автоматика и телемеханика). Все операции по приёму и отправлению поездов на станциях участка производит поездной диспетчер, находящийся в пункте управления, а следование поездов по перегонам регулируется автоматически по сигналам проходных светофоров.

Д. ц. гл. обр. распространена на однопутных линиях, позволяет повысить их пропускную способность на 25-30% и уменьшить число работающих (50-60 чел. на каждые 100 км пути).

Лит.: Пенкин Н. Ф., Диспетчерская централизация, М., 1963.

ДИСПЕТЧЕРСКИЙ ПУЛЬТ, ряд панелей с органами управления, контроля, сигнализации и средствами диспетчерской связи, с помощью к-рых диспетчер контролирует и координирует ход рабочего процесса на объекте управления. Автоматизиров. средства сбора, учёта, регистрации и частичной обработки информации, к-рыми оснащаются Д. п., облегчают контроль и регистрацию данных. С применением специализиров. вычислительных машин и методов математич. оптимизации Д. п. становится автоматизированным. Д. п. обычно входит в состав диспетчерского пункта. В зависимости от условий и специфики объекта диспетчирования Д. п. часто конструктивно объединяют с диспетчерским щитом, либо располагают в непосредственной близости от него.

ДИСПЕТЧЕРСКИЙ ПУНКТ, центр системы диспетчерского управления, где сосредоточивается информация о состоянии произ-ва, движении транспорта, энергоснабжении, ходе строительства и др. (см. Диспетчеризация). В состав Д. п. входят: операторская (зал дежурств, кабинет), где находится рабочее место диспетчера; аппаратная с вспомогат. оборудованием ; контрольно-ремонтная мастерская с дежурным персоналом, обслуживающим оборудование Д. п.; вспомогат. помещения. Рабочее место диспетчера (оператора), диспетчерский пульт и диспетчерский щит размещают так, чтобы диспетчеру одинаково хорошо были видны все контрольные приборы, элементы сигнализации, экраны (табло), устройства отображения информации и пром. телевидения.

Размеры и оснащённость Д. п. зависят от вида и характера контролируемых процессов и объектов управления. Напр., для Д. п. пром. предприятия характерно преобладание графич. способов отражения хода производства с помощью диаграмм, планограмм, сетевых графиков и т. д., к-рые находятся непосредственно над столом диспетчера; контрольно-учётная и сигнальная аппаратура размещается в надстройке стола. На Д. п. энергосистемы осн. значение имеют автоматич. сигнализация и измерения, требующие непрерывного наблюдения; это обусловливает размещение соответствующих устройств и приборов на диспетчерском щите перед диспетчерским пультом. Число одновременно занятых диспетчеров зависит от сложности системы управления и объёма поступающей информации. На совр. предприятиях с развитым автоматизиров. производством, с большим объёмом поступающей на Д. п. информации, где управленческие работы ведутся с помощью ЭВМ, Д. п. располагается в непосредств. близости от информационно-вычислительного центра предприятия, часто представляя с ним единое звено автоматизированной системы управления (АСУ)

ДИСПЕТЧЕРСКИЙ ЩИТ, устройство для оперативного визуального контроля и автоматич. регистрации информации о состоянии объектов, входящих в систему диспетчерского управления. Устанавливается в диспетчерских пунктах энергетич. систем, пром. предприятий, на транспорте. Д. щ. обычно выполняется в виде панели, с расположенными на ней контрольными приборами, световыми индикаторами, мнемоническими схемами, отражающими состояние объекта, а также его реакцию на действия диспетчера. Д. щ. могут включать также экраны радиолокаторов при оценке воздушной обстановки в аэропорту или пром. телевидения на предприятиях. С развитием автоматики и вычислительной техники появилась возможность создания компактных Д. щ., оснащённых автоматич. устройствами для приёма и обработки информации и более наглядной индикацией. Такие Д. щ. наиболее часто применяются в автоматизированных системах управления.

В. М. Зуев.

ДИСПНОЭ (греч. dyspnoia, от dys... -приставка, означающая затруднение, нарушение, и рnоё" - дыхание), затруднённое дыхание, расстройство его ритма, частоты и глубины; то же, что одышка.

ДИСПОЗИТИВНАЯ НОРМА (воспол-нительная), норма права, предоставляющая сторонам регулируемого ею правоотношения известную самостоятельность в определении их взаимных прав и обязанностей. Д. н. наиболее часто являются нормы гражд. права, содержащие указания на права и обязанности сторон в общей форме, или несколько вариантов этих прав (на усмотрение сторон) и т. д. См. также Норма права.

ДИСПОЗИТИВНОСТЬ (от позднелат. dispositivus - распоряжающийся, от лат. dispono - располагаю, устраиваю), принцип гражд. судопроизводства, согласно к-рому стороны в гражд. процессе свободно распоряжаются своими материальными и процессуальными правами. В сов. гражд. процессе принцип Д. закреплён в Основах гражданского судопроизводства СССР и союзных республик 1961. Напр., ст. 24 устанавливает право истца изменить основание или предмет иска, увеличить или уменьшить размер исковых требований или отказаться от иска. Основы предоставляют право всякому заинтересованному лицу обратиться в суд за защитой нарушенного или оспариваемого права или охраняемого законом интереса, а также устанавливают обязанность суда приступить к рассмотрению гражд. дела по такому заявлению. Вместе с тем принцип Д. ограничен известными пределами, чтобы исключить неблагоприятные последствия, к-рые могут наступить в силу юридич. неосведомлённости сторон либо по иным причинам. Поэтому Д. сочетается с обязанностью прокуратуры и нек-рых других органов выступать в защиту прав и законных интересов граждан, с активной ролью суда и т. д. Напр., суд обязан, не ограничиваясь представленными ему материалами и объяснениями, принимать все предусмотренные законом меры для всестороннего, полного и объективного выяснения обстоятельств дела, прав и обязанностей сторон, разъяснить лицам, участвующим в деле, их права и обязанности, предупреждать их о последствиях процессуальных действий и т. д.

Принцип Д. действует в известной мере и в уголовном судопроизводстве. Напр., по сов. праву дела т. н. частного и частнопубличного обвинения (см. Частное обвинение) возбуждаются, как общее правило, только по жалобе потерпевшего, дела частного обвинения могут быть прекращены в результате примирения потерпевшего и обвиняемого.

Принцип Д. является одним из важнейших в гражд.процессе социалистич. стран. Этот принцип провозглашён в законодательстве большинства бурж. гос-в.

И. Д. Перлов.

ДИСПОЗИЦИЯ (от лат. dispositio -размещение, расположение), 1) в ВМФ план расположения кораблей на рейде, в базе, а также на якоре в открытом море. Составляется с расчётом удобства выхода в море отдельных соединений или флота в целом. 2) В сухопутных войсках 18-19 вв. письменный приказ командира (командующего), в к-ром подчинённым частям (соединениям) ставились боевые задачи. В рус. армии с нач. 20 в. вместо термина "Д." стал применяться термин "боевой приказ".

ДИСПОЗИЦИЯ (в праве), структурная часть правовой нормы; см. Норма права.

ДИСПРОЗИЙ (лат. Dysprosium), Dy, химич. элемент с ат. номером 66, редкоземельный металл, относится к лантаноидам.

ДИСПРОПОРЦИИ экономические, нарушения пропорций в развитии отд. отраслей нар. х-ва, экономич. подразделений (произ-ва средств произ-ва и произ-ва предметов потребления) и отделов внутри каждого из них, взаимосвязанных фаз произ-ва (процесса произ-ва и обращения), других различных сторон и частей нар. х-ва, в результате чего возникают перебои в ходе воспроизводства на отд. участках или в экономике в целом. Следует различать частные и общие Д. Первые носят локальный и кратковременный характер. Вторые связаны с потрясениями всей экономики и продолжаются длительное время. Большое значение для возникновения и развития диспропорциональности имеет состояние потребления в данном обществе, его увязка с произ-вом и платёжеспособным спросом, что обусловлено отношениями собственности. Д. проявляются как нарушения объективно необходимой связи между произ-вом и потреблением.

Д. - одна из наиболее характерных черт развития капиталистич. экономики, заключающаяся в постоянном нарушении в ходе капиталистич. воспроизводства необходимых соотношений между отд. отраслями и элементами произ-ва. Д. являются результатом господства частно-капиталистич. собственности на средства произ-ва, обострения конкуренции и анархии произ-ва. Общие Д. принимают форму периодич. экономических кризисов перепроизводства.

В отличие от капиталистич. экономики, социалистич. экономика развивается планомерно и ей присуща тенденция к согласованному и гармоничному развитию, т. е. к всеобъемлющей пропорциональности. Но такое состояние социалистич. экономики создаётся не автоматически, а в результате целенаправленного преодоления различного рода Д., природа к-рых принципиально иная, чем при капитализме. При переходе от капитализма к социализму новое общество на первых порах неизбежно наследует нек-рые экономия. Д., присущие старому обществу. Напр., в СССР долгое время преодолевались и в результате социалистич. индустриализации страны были ликвидированы как Д., связанные с общей отсталостью экономики страны, унаследованной от царизма, так и Д. внутри пром-сти (преобладание лёгкой и пищевой пром-сти над тяжёлой и отсутствие многих важных отраслей последней).

В социалистич. странах Д. могут быть связаны со стихийными бедствиями, неурожаями и т. д. Д. в развитии социалистич. экономики могут возникнуть в связи с относительным недостатком ресурсов при быстром росте многообразных потребностей общества. Поэтому важное значение для поддержания необходимой пропорциональности и недопущения Д. имеет повышение науч. уровня планирования.

В. И. Кац.

ДИСПРОПОРЦИОНИРОВАНИЯ РЕАКЦИЯ, перераспределение атомов или их группировок между молекулами одного и того же вещества, в результате чего вещество превращается в два или более других, из к-рых одни содержат меньше, а другие - больше этих атомов или группировок, чем исходное. Большинство Д. р. представляет собой окислительно-восстановительные процессы и связано с перераспределением атомов кислорода или водорода. Напр., закись ртути при нагревании превращается в металлич. ртуть и окись ртути:

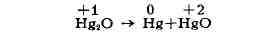
Альдегиды в присутствии щёлочи дают соответствующие спирты и карбоновые кислоты (Канниццаро реакция):

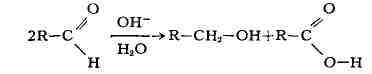
К этому же типу Д. р. относится необратимый катализ по Зелинскому:

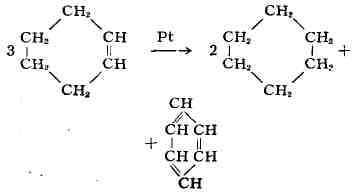
а также превращение свободных алкильных радикалов в алкены и алканы:

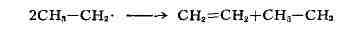
Примером Д. р., сопровождающейся перераспределением алкильных групп, является переход алкилбензолов в смесь бензола и полиалкилбензолов при действии хлористого алюминия:

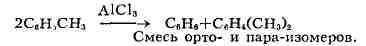
Д. р. широко используется в химии и во многих случаях имеет важное препаратив-ное значение. Б. Л. Дяткин.

ДИСПРОПОРЦИЯ (от due... и пропорция), несоразмерность, несоответствие частей чего-либо, отсутствие пропорциональности.

ДИССЕКТОР (от лат. disseco - рассекаю), передающая телевизионная трубка без накопления электрич. заряда. Д. применяют гл. обр. во вспомогат. автоматич. системах телевидения (напр., для определения положения источника света и др.). При освещении фотокатод Д. (рис.) испускает с поверхности электроны, плотность к-рых соответствует распределению освещённости на поверхности.

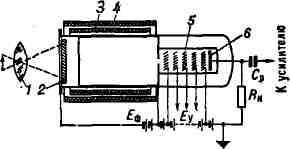
Диссектор. 1 - объектив; 2 - фотокатод; 3 - отклоняющая катушка; 4 - фокусирующая катушка; 5 - электронный умножитель; 6 - коллектор электронного умножителя; Е_Ф - источник постоянного напряжения, подаваемого на фокусирующую катушку; Еу - источник постоянного напряжения, подаваемого на электроды электронного умножителя; Rн - резистор в качестве сопротивления нагрузки, на концах к-рого образуется напряжение сигналов; Ср - конденсатор, разделяющий электрические цепи по постоянному току.

Созданное таким образом на фотокатоде электронное изображение переносится электрич. полем в однородном магнитном поле, фокусирующем это изображение, к электронному умножителю (ЭУ). Разложение электронного изображения на отд. электрич. сигналы осуществляется магнитным полем отклоняющих катушек, изменяющемся в двух взаимно перпендикулярных направлениях относительно оси входного отверстия ЭУ. Затем с коллектора ЭУ эти сигналы поступают в усилитель автоматической системы. Д. имеет низкую чувствительность.

В. И. Баранов.

ДИССЕМИНАЦИЯ (лат. disseminatio, от dissemino - рассеиваю, распространяю), распространение возбудителя из инфекционного и изолированного очага или клеток опухоли из основного узла в пределах органа или по всему организму через кровеносную и лимфатич. системы. Вслед за Д. обычно наступает генерализация патологич. процесса: развитие новых, часто многочисленных, очагов (метастазов).

ДИССЕНТЕРЫ (англ. dissenters, от лат. dissentio - не соглашаюсь), одно из распространённых в Англии (в 16-17 вв.) названий лиц, отступающих от официального вероисповедания.

ДИССЕПИМЕНТЫ (лат. dissaepimentum, от dissaepio - разгораживаю), тонкие поперечные перегородки вторичной полости тела у метамерных беспозвоночных животных, напр. у кольчатых червей.

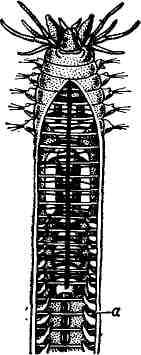
Вскрытый Nereis; а - диссепименты.

Д. образуются путём слияния примыкающих друг к другу стенок парных целомич. полостей, расположенных друг за другом. Сокращением мышц Д. и кожно-мускульного мешка осуществляется изменение давления полостной жидкости. У полихет и олигохет Д. выражены наиболее полно (рис.), у пиявок - отсутствуют.

ДИССЕРТАЦИЯ (от лат. dissertatio -рассуждение, исследование), научная работа, подготовленная с целью её публичной защиты для получения учёной степени. Система публичной защиты обязательных письменных сочинений на науч. и лит. темы для получения учёной степени или звания стала складываться в ср. века в ун-тах стран, говорящих на нем. языке. В 16-17 вв. эта система распространилась в др. странах. В России защита печатных Д. была введена после учреждения Московского ун-та (1755). "Положением 1819 г. о производстве в учёные степени" при экзамене (устные и письменные испытания) на звание магистра и доктора была утверждена публичная защита Д. Магистерская Д. представлялась на лат., рус. или ином языках, докторская - на лат., причём требовались при ней ещё "тезы" - прообраз авторефератов.

В СССР защита Д. на соискание учёных степеней кандидата наук и доктора наук была учреждена в 1932. Учёные степени по результатам защиты Д. до 1938 присуждались квалификационными комиссиями, организованными при наркоматах, АН СССР, республиканских и отраслевых академиях. В 1937 определён перечень отраслей наук, по к-рым производится защита Д., и право утверждения докторских Д. передано Высшей аттестационной комиссии (ВАК). В 1945 для защитивших Д. введены единые дипломы, выдаваемые только ВАКом.

К защите кандидатской Д. допускаются лица, имеющие высшее образование, окончившие аспирантуру или сдавшие кандидатские экзамены в установленном порядке (см. Кандидатский минимум). Кандидатская Д. должна содержать новые науч. и практич. выводы и рекомендации, обнаружить у соискателя способность к самостоят. науч. исследованию, глубокие теоретич. знания в области данной дисциплины. Докторская Д. является самостоятельной исследовательской работой, в к-рой содержится теоретич. обобщение и решение крупной науч. проблемы, представляющей значительный вклад в науку и практику.

Публичная защита докторских и кандидатских Д. осуществляется в совете вуза и научного учреждения, к-рому решением ВАКа при Мин-ве высшего и ср. спец. образования СССР предоставлено право приёма к защите Д. по данным специальностям.

Основное содержание представленной к защите Д. должно быть опубликовано в виде монографий или статей в науч. или спец. журналах, сборниках, учёных записках или трудах вузов, н.-и. учреждений и др. платных изданиях (в т. ч. и работы, написанные в соавторстве). Вместо Д. для защиты могут быть представлены опубликованные работы, изобретения и открытия, зарегистрированные в Комитете по делам изобретений и открытий при Совете Министров СССР, завершённые работы по созданию новых машин, систем управления, приборов, сооружений и технологич. процессов, выполненные индивидуально и коллективно, а также учебники, написанные без соавторов. Перед защитой Д. публикуется автореферат, отражающий осн. содержание и выводы Д.

На Д. даются отзывы официальных оппонентов (не менее трёх по докторской и двух по кандидатской) и ведущего предприятия, н.-и. учреждения, вуза. Официальными оппонентами по докторской Д. должны быть доктора наук соответствующей специальности, по кандидатской - кандидаты наук и не менее одного доктора наук.

После публичной защиты Д. (к-рая проходит в обстановке диспута между соискателем учёной степени и официальными, а также неофициальными оппонентами) совет тайным голосованием принимает решение о присуждении степени кандидата наук или о представлении в ВАК ходатайства о присуждении степени доктора наук (кандидатские Д. рассматриваются ВАКом в порядке контроля).

В 1937-71 по результатам защиты ВАКом утверждено 33 992 доктора и 325 197 кандидатов наук, в т. ч. по разделам наук:
 

Разделы наук	Докторов наук	Кандидатов наук
Физико-математические	2497	22 343
Химические	1693	17 871
Биологические	2824	21 787
Геолого-минералогические	1388	11 676
Технические	8016	103 437
Сельскохозяйственные	1456	17 919
Исторические	1748	15 691
Экономические	1188	18 330
Философские	580	6 180
Филологические	1222	12207
Географические	450	3 674
Юридические	521	3 835
Педагогические	357	8 189
Медицинские	8840	51 628
Фармацевтические	60	780
Ветеринарные	659	3 926
Искусствоведение	237	1 816
Архитектура	80	1 130
Военные науки	84	2080
Военно-морские	51	552
Психологические (с 1968)	41	246

Д. (в т. ч. и дореволюционные) хранятся в отраслевых б-ках, учреждениях и архивах. Общесоюзный фонд Д. организован в Гос. б-ке СССР им. В. И. Ленина (за исключением медицинских, к-рые передаются в Гос. центральную мед. б-ку). Библиографич. регистрация Д. начата Всесоюзной книжной палатой в 1938-40 и продолжена Гос. б-кой СССР им. В. И. Ленина. В СССР и др. странах изданы многочисленные библиографии Д. по отдельным ун-там и ин-там, по отраслям знания и отдельным темам.

Лит.: Кричевский Г. Г., Библиография диссертаций, [М.- Л., 1948]; его же, Общие библиографии зарубежных стран, М., 1962 (см. Библиография диссертаций, с. 177-183, 249-251). Библиографии диссертаций СССР: Ежегодник диссертаций, 1936 - 37, М., 1938 -1940; Библиография диссертаций. Докторские диссертации за 1941 - 1945, М., 1946-47 (Гос. б-ка СССР им. В. И. Ленина); Диссертации, защищённые в Ленинградском ордена Ленина Государственном университете им. А. А. Жданова, 1934-1960 гг. (Библиогр. указ.), [Л.], 1955-62; Каталог кандидатских диссертаций, поступивших в Библиотеку им. В. И. Ленина [начиная с 1956, М., 1956-]; Докторские и кандидатские диссертации, защищённые в Московском государственном университете с 1934 по 1954 г. Библиогр. указ., под ред. П. А. Зайончковского [и др.], в. 1 -3, [M.]_, 1956-60; Каталог докторских диссертаций, поступивших в Библиотеку им. В. И. Ленина в 1956 г., М., 1957; Докторские диссертации по педагогическим наукам. Библиогр. указ., под ред. Н. К. Гончарова, М., 1961. Международная библиография диссертаций: Catalogue des dissertations et ecrits academiques..., recu par la Bibliotheque Nationale en 1882-1924, [t. 1-37], P., 1884-1925; Walt her С h. F., Catalogue methqdique des dissertations 911 theses academiques, imprimees par les Elzevirs de 1616 a 1712, Brux.,

М. Н. Волков, В. Г. Панов, П. К. Колмаков.

ДИССИДЕНТЫ (от лат. dissidens -несогласный), в западноевропейских гос-вах в средние века все "отступники" от католицизма, к-рых церковь рассматривала как еретиков; со времени Реформации - верующие-христиане, к-рые не придерживаются господствующего в данной стране вероисповедания (католич. или протестантского). Вопрос о гражд. правах Д. был особенно острым в 16-17 вв. в Англии (диссентеры) и Франции (гугеноты), в 17-18 вв.- в Польше.

ДИССИМИЛЯЦИЯ (от лат. dissimilis - несходный) в биологии, противоположная ассимиляции сторона обмена веществ, заключающаяся в разрушении органич. соединений с превращением белков, нуклеиновых к-т, жиров, углеводов (в т. ч. введённых в организм с пищей) в простые вещества. Ряд процессов Д.- дыхание, брожение и гликолиз - занимает центральное место в обмене веществ. В результате этих процессов происходит освобождение энергии, заключённой в молекулах сложных органич. соединений, к-рая частично трансформируется в энергию аденозинфосфорных кислот (преим. АТФ). Осн. конечные продукты Д. во всех организмах - вода, углекислый газ и аммиак. У животных эти продукты по мере накопления выделяются наружу. В растит, организмах СО₂ частично, a NH₃ полностью используются для биосинтеза органич. веществ, являясь, т. о., исходным материалом для ассимиляции.

Неразрывная связь Д. с ассимиляцией обеспечивает постоянное обновление тканей организма. Так, в крови человека половина существующего альбумина обменивается на новые молекулы альбумина за 10 дней; продолжительность жизни эритроцитов - ок. 4 мес. Соотношение интенсивности ассимиляции и Д. изменяется в зависимости от стадии развития, возраста и физиологич. состояния организма. Рост и развитие организма характеризуются преобладанием ассимиляции, что проявляется в образовании новых клеток, тканей и органов, в их росте и дифференциации, в общем увеличении массы тела. При нек-рых патологич. состояниях и при голодании Д. обычно преобладает над ассимиляцией, что ведёт к уменьшению массы тела.

С. Е. Северин, Г. А. Соловьёва.

ДИССИМИЛЯЦИЯ в языкознании, один из видов комбинаторного изменения звуков в потоке речи, когда один из двух тождественных или сходных звуков речи (смежных или несмежных) заменяется другим звуком, отличным или менее сходным с ним. Напр., лат. peregrinum, рус. "пилигрим", лат. februaris, рус. "февраль".

ДИССИПАТИВНЫЕ СИСТЕМЫ, механические системы, полная механическая энергия которых (т. е. сумма кинетической и потенциальной энергий) при движении убывает, переходя в другие формы энергии, напр. в теплоту. Этот процесс наз. процессом диссипации (рассеяния) механич. энергии; он происходит вследствие наличия различных сил сопротивления (трения), к-рые наз. также диссипативными силами. Примеры Д. с.: твёрдое тело, движущееся по поверхности другого при наличии трения; жидкость или газ, между частицами к-рых при движении действуют силы вязкости (вязкое трение), и т. п.

Движение Д. с. может быть как замедленным, или затухающим, так и ускоренным. Напр., колебания груза, подвешенного к пружине (рис., а), будут затухать вследствие сопротивления среды и внутреннего (вязкого) сопротивления, возникающего в материале самой пружины при её деформациях. Движение же груза вдоль шероховатой наклонной плоскости, происходящее, когда скатывающая сила больше силы трения (рис., б).

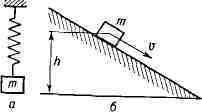
будет ускоренным. При этом его скорость v, а следовательно, и кинетич. энергия Т = mv²/2, где т -масса груза, всё время возрастают, но это возрастание происходит медленнее, чем убывание потенциальной энергии П = mgh (g -ускорение силы тяжести, h - высота груза). В результате полная механич. энергия груза Т + П всё время убывает.

Понятие Д. с. употребляют в физике также и к немеханическим системам во всех случаях, когда энергия упорядоченного процесса переходит в энергию неупорядоченного процесса, в конечном счёте - в тепловую. Так, система контуров, в к-рой происходят колебания электрич. тока, затухающие из-за наличия омич. сопротивления, будет также Д. с.; в этом случае электрич. энергия переходит в джоулево тепло.

Практически в земных условиях из-за неизбежного наличия сил сопротивления все системы, в к-рых не происходит притока энергии извне, являются Д. с. Рассматривать их как консервативные, т. е. такие, в к-рых имеет место сохранение механич. энергии, можно лишь приближённо, отвлекаясь от учёта сил сопротивления. Однако и неконсервативная система может не быть Д. с., если в ней диссипация энергии компенсируется притоком энергии извне. Напр., отдельно взятый маятник часов из-за наличия сопротивлений трения будет Д. с. и его колебания (как и груза на рис., в) будут затухать. Но при периодич. притоке энергии извне за счёт заводной пружины или опускающихся гирь диссипация энергии компенсируется и маятник будет совершать автоколебания.

С. М. Тарг.

ДИССИПАЦИЯ атмосфер планет (от лат. dissipatio - рассеяние) (ускользание, улетучивание), рассеивание атмосферы планет вследствие улетучивания составляющих их газов в космическое пространство. Беспорядочное тепловое движение частиц газа приводит их тому, что часть их, находящаяся во внешних слоях атмосферы, приобретает скорость, лежащую выше критич. скорости ускользания, при к-рой тело преодолевает силу тяжести и может уйти за пределы поля тяготения планеты. Таким образом, Д. зависит от силы тяготения планеты, темп-ры её экзосферы, определяющей кинетич. энергию молекул и молекулярной массы частиц, от к-рой, согласно кинетической теории газов, зависит их скорость. Каждой темп-ре соответствует средняя скорость движения молекул определённого вида, от к-рой имеются заметные отступления для части молекул (по закону Максвелла). Поэтому в астрономич. время устойчивой является атмосфера, средняя скорость молекул к-рой не превышает 0,2 критической. При средней тепловой скорости, равной 0,25 критической, атмосфера рассеивается за 50 000 лет, а при скорости в 0,33 критической - всего за несколько недель.

Соотношение между средними тепловыми скоростями молекул при 0 °С (табл. 1) и критич. скоростями Д. (табл. 2) можно видеть из сопоставления этих таблиц:

Таблица 1
 

Газ	Молекулярная масса	Средняя квадратичная скорость молекул при 0°С, км/сек
Водород	2	1,84
Гелий	4	1,31
Пар водяной	18	0,62
Азот	28	0,49
Кислород	32	0,46
Углекислый газ	44	0,39

Таблица 2
 

Планета	Скорость диссипации, км/сек
Луна	2,4
Меркурий	3,8
Марс	5,1
Венера	10,4
Земля	11,2
Сатурн	36,7
Юпитер	61,0

Поэтому Луна и Меркурий не могут иметь устойчивой атмосферы, на Марсе устойчивы только тяжёлые газы, с планет типа Земли диссипируют только водород и гелий, а малые планеты и большая часть спутников совсем лишены атмосферы. Реальное состояние атмосфер планет зависит от соотношения между процессами формирования и уничтожения атмосферы.

Лит.: Мороз В. И., Физика планет, М., 1967; Атмосфера Земли и планет. Сб. статей, пер. с англ., М., 1951; Введение в физику Луны, М., 1969.
К. П. Флоренский.

ДИССИПАЦИЯ ЭНЕРГИИ, у физических систем переход части энергии упорядоченного процесса (напр., электрич. энергии) в энергию неупорядоченного процесса - в конечном счёте в тепловую (напр., в джоулево тепло). У механич. систем переход части её механич. энергии в др. формы (напр., в теплоту) происходит за счёт наличия сил сопротивления; Д. э. в атмосфере - переход части кинетич. энергии ветра в теплоту под воздействием внутр. трения. См. Диссипативные системы.

ДИССОГОНИЯ (от греч. dissos - двойной и ...гония), способность к половому размножению сначала в личиночной стадии, а затем во взрослом состоянии, характерная для нек-рых гребневиков. Напр., личинки Bolina hydatina образуют способные к оплодотворению половые продукты (яйца и сперматозоиды); в дальнейшем их половые железы исчезают. Взрослые гребневики, у к-рых гонады развиваются вторично, также способны давать потомство.

ДИССОНАНС (франц. dissonance, от лат. dissono - нестройно звучу) в стихосложении, вид рифмующего созвучия, в к-ром не совпадают ударяемые гласные, напр.: слово - слева - слава. Звуковой повтор в Д. строится на согласных звуках, поэтому его иногда наз. консонансом (от франц. consonne - согласная). Д. вошёл в поэтич. практику лишь в 20 в. как редкий, но выразит, приём. Например:

На побережье после бури

Твоих камней я слышу хруст,

О, море, самый умный в мире

Художник-абстракционист.

(Л. Н.Мартынов).

ДИССОНАНС в музыке, звучание тонов, "не сливающихся" друг с другом (не следует отождествлять с неблагозвучием как эстетически неприемлемым звучанием, см. Какофония). Понятие Д. противостоит понятию консонанса. К Д. относят большие и малые секунды и септимы, увеличенные и уменьшенные интервалы, а также все аккорды, включающие хотя бы один из этих интервалов; условно к Д. относят и кварту по отношению к басу. С математико-акустич. точки зрения Д. представляет более сложное отношение чисел колебаний (длин струн); различие между консонансом и Д. оказывается только количественным, а граница между ними - условной. С точки зрения муз. психологии Д. сравнительно с консонансом является созвучием более напряжённым, неустойчивым; в системе мажора и минора качеств. различие консонанса и Д. достигает степени противоположности, контраста и представляет большую эстетич. ценность. Учение о композиции всегда учитывало это различие в восприятии диссонирующих и консонирующих созвучий. До 17 в. условием применения Д. было полное его подчинение консонансу - правильное приготовление и разрешение (переход) в консонанс; в 17-19 вв. обязательным правилом было лишь разрешение Д.; с конца 19 в. и в особенности в 20 в. диссонанс всё чаще применяется самостоятельно - без приготовления и без разрешения.

Лит.: Гарбузов Н. А., О консонирующих и диссонирующих интервалах, "Музыкальное образование", 1930, № 4-5; Клещов С. В., К вопросу о различии диссонирующих и консонирующих созвучий, "Труды физиологических лабораторий академика И. П. Павлова", 1941, т. 10; Т ю л и н Ю. Н., Современная гармония и ее историческое происхождение, в кн.; Вопросы современной музыки, Л., 1963; Гельмгольц Г., Учение о слуховых ощущениях как физиологическая основа для теории музыки, пер. с нем., СПБ, 1875; S t u m p f С., Konsonanz und Dissonanz, Lpz., 1898; Riemann H., Zur Theorie der Konsonanz und Dissonanz, в его сб.: Praludien und Studien, Bd 3, Lpz., 1901.

Ю. Н. Холопов.

ДИССОЦИАЦИЯ (от лат. dissociatio - разделение, разъединение), процесс, заключающийся в распаде молекул на несколько более простых частиц - молекул, атомов, радикалов или ионов. Обычно различают три вида Д.: термическая диссоциация, происходящая при повышении темп-ры (напр., N₂O₄-><-2NO₂), электролитическая диссоциация, происходящая при растворении электролитов (расщепление молекул электролитов на ионы, напр. КОН-><-K⁺ + ОН^-), и фотохимическая диссоциация, наблюдающаяся при действии света (напр., Сl₂ + hv-> -> 2С1, где hv - квант света). Количественной характеристикой Д. служит степень диссоциации - отношение числа распавшихся молекул к общему числу молекул. О константе диссоциации см. Равновесие химическое.

ДИССОЦИАЦИЯ БАКТЕРИЙ, одно из проявлений изменчивости микроорганизмов, в результате чего бактерии, образующие на плотных питательных средах крупные, гладкие, блестящие колонии и обычно обозначаемые как S-формы (от англ, smooth - гладкий), дают мутанты - R-формы (от англ, rough-шероховатый), образующие складчатые матовые колонии. Д. б. может возникать самопроизвольно или под влиянием физ. и хим. факторов. При Д. б. изменяются также мн. физиологич., биохимич. и иммунологич. свойства культуры. Поэтому складчатые формы патогенных бактерий не применяют для изготовления вакцин.

ДИСТАЛЬНЫЙ (отлат. disto - отстою), в анатомии животных и человека пункт, участок тела, более отдалённый от его центра или срединной (медианной) плоскости, в противоположность ближе лежащему пункту - проксималъному, напр., кисть занимает Д. положение по отношению к предплечью.

ДИСТАНЦИОННАЯ ГРАНАТА, артиллерийский снаряд осколочного действия с дистанционным взрывателем, обеспечивающим разрыв снаряда в заданной точке траектории. Называется также бризантной гранатой. Применяется для стрельбы по живой силе противника и воздушным целям. Д. г. входят в боекомплект совр. зенитных арт. орудий средних и крупных калибров и ряда наземных арт. систем.

ДИСТАНЦИОННАЯ ТРУБКА, один из видов взрывателей.

ДИСТАНЦИОННОЕ ИЗМЕРЕНИЕ, измерение физич. величин на расстоянии. Применяется в случаях, когда по тем или иным причинам трудно или невозможно измерять с помощью приборов, установленных в непосредственной близости от точки замера. См. также Телеизмерение.

ДИСТАНЦИОННОЕ УПРАВЛЕНИЕ, управление технич. системами на расстоянии. Д. у. применяется преимущественно при централизации управления производств, установкой, а также в условиях, когда недопустимо пребывание оператора вблизи объекта управления, напр, из-за высокой температуры, загрязнения воздушной среды, опасных излучений и т. п. (см. также Телеуправление).

ДИСТАНЦИОННЫЙ ВВОД, автоматич. ввод в счётно-решающее устройство (вычислительную систему) информации, полученной от удалённого объекта (источника) и переданной по каналу связи.

Источниками информации могут быть различные датчики, вычислительные устройства, устройства автоматич. регулирования и контроля. Перед выдачей в канал связи информация кодируется, т. е. преобразуется в сигналы, удобные для передачи. На входе счётно-решающего устройства принятые сигналы автоматически декодируются. Д. в. информации может осуществляться как по мере её поступления, так и с предварительным накоплением и запоминанием. В случае ввода информации от неск. источников применяют параллельную или циклическую систему Д. в. При параллельной системе для каждого источника предусматривается автономный канал для одновременного и независимого Д. в. данных, но эта система сложна и требует больших аппаратурных затрат. При циклической системе ввода каналы связи через коммутирующее устройство поочерёдно подключаются к одной, общей цепи ввода.

М. М. Гельман.

ДИСТАНЦИЯ (от лат. distantia - расстояние) (воен.), расстояние по глубине между военнослужащими, орудиями, машинами, подразделениями или частями (кораблями) в строю, на марше (походе) или в боевом порядке, а также между самолётами при полёте в строю или в боевом порядке.

ДИСТАНЦИЯ (на железной дороге), хозяйств, единица, входящая в отделение дороги, к-рое подчиняется соответствующей службе дороги (пути, сигнализации и связи, грузовой и т. д.). На ж.-д. транспорте имеются Д.: пути, сигнализации и связи, погрузочно-разгрузочных работ, контактной сети (входящая в энергоучасток). Д. осуществляют надзор за исправным состоянием технич. средств и производят соответствующие их назначению работы (ремонт пути, погрузку грузов и т. д.).

ДИСТЕН (от ди... и греч. sthenos - сила), минерал состава Al₂OSiO₄; см. Кианит.

ДИСТЕРВЕГ (Diesterweg) Фридрих Адольф Вильгельм (29.10.1790, Зиген, Вестфалия,- 7.7.1866, Берлин), немецкий педагог-демократ. В 1812-20 преподавал физику и математику в ср. школах в Вормсе, Франкфурте-на-Майне и Эльберфельде, затем - директор учит, семинарии в Мерсе (1820-32) и Берлине (1832-47). Д. стремился к объединению нем. учительства: в 1831-41 создал в Берлине 4 учительских об-ва, в 1848 избран председателем "Всеобщего немецкого учительского союза". Д. издавал пед. журнал "Rheinische Blatter fur Erziehung und Unterricht" (1827-66) и ежегодник "Padagogisches Jahrbuch" (1851-66). Выступал в нём против сословных и нац. ограничений в области образования, против конфессионального обучения и опеки церкви над школой, против воспитания юношества в духе религиозной нетерпимости. После подавления Революции 1848 был уволен прусским правительством в отставку за "опасное вольнодумство", но продолжал лит. и общественно-политич. деятельность. В печати и с трибуны палаты депутатов, куда он был избран от берлинского учительства, Д. боролся с изданными прусским правительством в 1854 реакц. школьными законами.

Д.- автор учебников и руководств по математике, нем. яз., естествознанию, географии, астрономии. Наиболее известная работа Д. - "Руководство к образованию немецких учителей" (2 тт., 1835).

Последователь Песталоцци, Д. творчески развил его пед. учение и популяризировал его среди нем. учительства. Осн. принципами воспитания Д. считал природосообразность, культу росообразность, самодеятельность. Под природосообразностью он понимал возбуждение врождённых задатков ребёнка в соответствии с заложенным в них стремлением к развитию. Д. не понимал социальной сущности воспитания, его зависимости от политики господствующего класса. Но выдвинутый им принцип культуросообразности означал, что воспитание должно считаться не только с природой ребёнка, но и с уровнем культуры данного времени и страны, т. е. с изменяющимися социально-историч. условиями. Самодеятельность Д. считал решающим фактором, определяющим личность человека, всё его поведение. В развитии детской самодеятельности он видел непременное условие всякого образования.

Д. разработал дидактику развивающего обучения, сформулировав её осн. требования в виде 33 законов и правил. Выдвинул ряд требований, касающихся наглядного обучения, установления связи между родственными учебными предметами, систематичности преподавания, прочности усвоения знаний, воспитывающего характера обучения.

Пед. идеи Д., его учебники оказали положительное влияние на развитие нар. образования в Германии и получили распространение далеко за её пределами. Передовые рус. педагоги 60-х гг. 19 в. П. Г. Редкий, Н.Ф.Бунаков, Н.А. Корф, И. И. Паульсон высоко оценивали учение Д.

В ГДР учреждена медаль имени Д., к-рой награждаются заслуженные учителя.

Соч.: Samtliche Werke, Bd 1-1 0 (издание продолжается), В., 1956-69; Schriften und Reden, Bd 1 - 2, В.-Lpz., 1950; в рус. пер.- Руководство для немецких учителей, М., 1913; Избранные педагогические сочинения, М., 1956.

Лит.: Пискунов А. И., Дидактические взгляды Адольфа Дистервега, "Советская педагогика", 1956, №1; Соколова М. А., Борьба А. Дистервега за единую школу и за освобождение школы от надзора церкви, там же, 1960, № 10; Siebert H. Adolf Diesterweg. Seine Bedeutung fur die Entwicklung der Erziehung und Bildung in Deutschland. В., 1953.

В. А. Ротенберг.

ДИСТИЛЛИРОВАННАЯ ВОДА, вода, очищенная от растворённых в ней минеральных солей, органических веществ, аммиака, двуокиси углерода и других примесей путём перегонки. Д. в. применяют как растворитель в хим. и физ. лабораториях и в мед. практике. Качество Д. в. контролируют по электрич. проводимости [не более 10^-6 сим (ом^-1)] и сухому остатку (не более 0,1 мг при выпаривании 1 л Д. в.). В нек-рых случаях, напр. при использовании Д. в. для подкожных вливаний, её дополнительно стерилизуют. Хранят Д. в. в закрытых оловянных сосудах или в бутылях из химически стойкого стекла.

ДИСТИЛЛЯЦИЯ (от лат. distillatio-стекание каплями), перегонка, разделение жидких смесей на отличающиеся по составу фракции. Процесс основан на различии температур кипения компонентов смеси. В зависимости от физич. свойств компонентов разделяемых жидких смесей применяют различные способы Д.

Простая Д. (рис. 1) проводится частичным испарением кипящей жидкой смеси, непрерывным отводом и последующей конденсацией образовавшихся паров. Так как пары над кипящей жидкой смесью содержат низкокипящих компонентов больше, чем жидкость, то конденсат (наз. дистиллятом) обогащается, а неиспарившаяся жидкость (кубовый остаток) обедняется ими. В дистилляционном кубе / кипит исходная жидкая смесь. Образующиеся пары непрерывно отводятся в конденсатор 2, где образуется дистиллят, к-рый стекает в приёмник 3. При простой Д. содержание низкокипящих компонентов в паровой и жидкой фазах непрерывно падает. Поэтому состав дистиллята меняется во времени. Простая Д., осуществляемая по описанной схеме,- периодич. процесс.

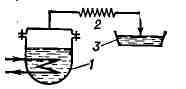
Рис. 1.

Для ускорения процесса применяют полунепрерывную Д., при к-рой в дистилляционный куб непрерывно поступает исходная смесь, равная массе уходящих паров.

Фракционная Д., наз. также дробной перегонкой (рис. 2),- одна из разновидностей простой Д. Такую Д. применяют для разделения смеси жидкостей на фракции, кипящие в узких интервалах температур. При этом дистилляты разных составов отводят (последовательно во времени) в несколько сборников. В сборник 1 поступает первая по времени порция дистиллята, наиболее богатая низкокипящими компонентами, в сборник 2-менее богатая, в сборник 3 - ещё менее богатая и т. д.

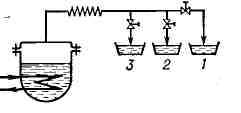
Рис. 2.

В каждом из этих дистиллятов (фракциях) преобладает один или несколько компонентов исходной смеси с близкими темп-рами кипения. Простую Д. для улучшения разделения смесей часто комбинируют с противоточной дефлегмацией (рис. 3). При этом образующиеся в кубе

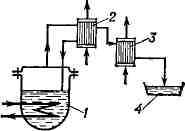
Рис. 3.

1 пары частично конденсируются в дефлегматоре 2, конденсат (флегма) непрерывно возвращается в куб, а остаток паров после дефлегматора поступает в конденсатор 3, откуда дистиллят стекает в сборник 4. Этим способом достигается большее обогащение дистиллята низкокипящими компонентами, т. к. при частичной конденсации (дефлегмации) паров преимущественно конденсируются высококипящие компоненты.

Равновесная Д. (однократное испарение) характеризуется испарением части жидкости и продолжительным контактом паров с неиспарившейся жидкостью до достижения фазового равновесия (рис. 4). Разделяемая смесь проходит по трубам /, обогреваемым снаружи топочными газами. Образовавшаяся при этом парожидкостная смесь, близкая к равновесному состоянию, поступает в сепаратор 2 для механич. отделения жидкости от пара. Пары (П) из сепаратора поступают в конденсатор, откуда дистиллят стекает в приёмник, а оставшаяся в сепараторе жидкость отводится в сборник. В этом процессе соотношение между паром и жидкостью определяется материальным балансом и условиями фазового равновесия. Равновесная Д. редко применяется для двухкомпонентных смесей; хорошие результаты получают в основном в случае многокомпонентных смесей, из к-рых можно получить фракции, сильно различающиеся по составу.

Рис. 4.

Д. в токе водяного пара или инертных газов применяют, когда необходимо понизить темп-ру процесса отгонки, в случае разделения нетермостойких компонентов, а также для отгонки веществ с низкой темп-рой испарения от компонентов с высокой темп-рой испарения. Пузырьки водяного пара или инертного газа барботируют через слой жидкости (см. Барботирование). При Д. с водяным паром образовавшаяся смесь паров воды и летучего компонента отводится из аппарата и подвергается конденсации и охлаждению. Состав образующихся в кубе паров не зависит от состава жидкости, а температура кипения смеси всегда ниже температуры кипения каждого из компонентов при данном давлении. При Д. с инертным газом компоненты раствора испаряются в поток газа, даже если раствор не кипит, а парообразование при испарении может происходить при любых температурах, вне зависимости от внешнего давления, что позволяет вести процесс при низких температурах.

Молекулярная Д. основана на разделении жидких смесей свободным их испарением в высоком вакууме 133-13,3 мн/м² (10^-3-10^-4мм рт.ст.) при темп-ре ниже точки их кипения. Процесс проводят при взаимном расположении поверхностей испарения и конденсации на расстоянии, меньшем длины свободного пробега молекул перегоняемого вещества. Благодаря вакууму молекулы пара движутся от испаряющей поверхности к конденсирующей с минимальным числом столкновений. При молекулярной Д. изменение состава пара по сравнению с составом жидкости определяется различием скоростей испарения компонентов. Поэтому этим способом можно разделять смеси, компоненты к-рых обладают одинаковым давлением паров. При данной темп-ре жидкости и соответствующем ей давлении паров скорость молекулярной Д. растёт с понижением давления в аппарате.

Для уменьшения времени диффузии молекул летучего компонента из глубины слоя жидкости к поверхности испарения процесс в современных молекулярных кубах проводят в очень тонких плёнках жидкости, что позволяет, кроме того, уменьшить время нахождения вещества на поверхности испарения и опасность его термич. разложения.

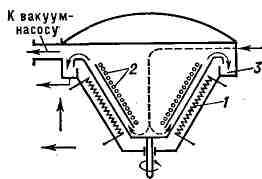
Рис. 5.

Для молекулярной Д. применяют аппараты с горизонтальными и вертикальными поверхностями испарения, а также получившие наибольшее пром. применение центробежные аппараты. В последних процесс характеризуется наименьшими толщиной жидкой плёнки (в среднем 0,05 мм) и временем её пребывания на поверхности нагрева (0,03-1,2 сек). В центробежных аппаратах (рис. 5) на испаритель 1, представляющий собой быстровращающийся конус (иногда диск), подаётся разделяемая смесь. Центробежная сила перемещает жидкость от центра к периферии (вверх). Пары перегоняемого вещества собираются на неподвижном конденсаторе 2, расположенном параллельно поверхности испарителя, откуда дистиллят непрерывно отводится. Остаток после перегонки сбрасывается в кольцевой жёлоб 3 и выводится из куба. Для увеличения эффекта разделения устанавливают несколько аппаратов последовательно.

Молекулярную Д. применяют для разделения и очистки высокомолекулярных и термически нестойких органич. веществ, напр. для очистки эфиров себациновой, стеариновой, олеиновой и др. кислот, для выделения витаминов из рыбьего жира и различных растительных масел, при производстве медицинских препаратов, вакуумных масел и др.

В металлургии понятие Д. объединяет пирометаллургич. процессы (см. Пирометаллургия), основанные на переводе восстанавливаемого металла (см. Восстановление металлов) в парообразное состояние с последующей конденсацией. Металлургич. Д.- сочетание химич. (окислительно-восстановит. реакции) и физич. (испарения и конденсации) процессов. Восстановление проводят с использованием углеродистых восстановителей (см. Карботермия) или металло-термич. способом (см. Металлотермия). Возможно выделение свободного металла при окислит. обжиге сульфидных концентратов. Степень разделения при Д. определяется различием состава перегоняемой смеси и её пара. Полнота перехода металла в газовую фазу при Д. определяется восстановлением металлов при темп'рах и давлениях, обеспечивающих получений восстановленного металла в парообразном агрегатном состоянии.

Лит.: Касаткин А. Г., Основные процессы и аппараты химической технологии, 8 изд., М., 1971; Гельперин Н. И., Дистилляция и ректификация, М.- Л., 1947; Багатуров С. А., Теория и расчет перегонки и ректификации, М., 1961; Циборовский Я., Процессы химической технологии, пер. с польск., Л., 1958; Матрозов В. И., Аппаратура для молекулярной дистилляции, М., 1954; Чижиков Д. М., Металлургия тяжелых цветных металлов, М.-Л., 1948; Лакерник М. М., Электротермия в металлургии меди, свинца и цинка, М., 1964.

В. Л. Пебалк.

ДИСТИМИЯ (от дне... и греч. thymos -душа, чувства, настроение), нарушение настроения, характеризующееся унынием, подавленностью, печалью.

ДИСТИНКЦИЯ (от лат. distinctio - различение), термин, обозначающий познавательный акт, в процессе к-рого фиксируется различие между предметами и явлениями действительности или между элементами сознания. В совр. формальной логике под Д. подразумевается один из логич. приёмов, заменяющих определение (см. Различие).

ДИСТОМАТОЗЫ, глистные заболевания, вызываемые трематодами (сосальщиками); то же, что трематодозы.

ДИСТОРЗИЯ (лат. distorsio, distortio, от distorqueo - выворачиваю, искривляю), повреждение связочного аппарата сустава; то же, что растяжение.

ДИСТОРСИЯ (от лат. distorsio - искривление), погрешность изображения в оптич. системах, при которой нарушается геометрич. подобие между объектом и его изображением; одна из аберраций оптических систем. Д. возникает в результате того, что линейное увеличение разных частей изображения различно. Характерный пример искажений, даваемых системой, обладающей Д.,- приведённое на рис. изображение квадрата. Слева изображена подушкообразная, или положительная, Д., справа - бочкообразная, или отрицательная. Д. не нарушает резкости изображения. Д. оптич. системы количественно характеризуется т. н. относительной Д. v = В/В₀-1, где

В₀- линейное увеличение идеальной системы без Д., а 0 - увеличение, имеющее место в действительности. Относительная Д. выражается в %.

Д. особенно вредна в фотографич. объективах, применяемых в геодезии или фотограмметрии. Для хороших фотообъективов v близка к 0,5%. В объективах, применяемых при аэрофотосъёмке, Д. равна ~0,01%. В отдельных случаях (симметричные фотообъективы или зрительные трубы) Д. можно уничтожить.

ДИСТРИБУТИВНОСТЬ (от лат. distributivus - распределительный), распределительность, распределительный закон, свойство умножения, выражаемое тождествами с (а + b) - са + cb и (а + b)с = ас + bc. В более общем смысле говорят о Д. оператора F(x) относительно нек-рого действия х * у как о свойстве, выражаемом равенством F(x * у) = F(x) * F(y). Напр., равенство (аb)" = аⁿbⁿ показывает, что оператор возведения в степень дистрибутивен относительно операции умножения [но не относительно операции сложения, т. к., вообще говоря, (а + b)ⁿ не= аⁿ +b^п].

ДИСТРИБУТИВНЫЙ АНАЛИЗ, метод лингвистич. исследования, при к-ром классификация языковых единиц и изучение их свойств производятся исключительно на основе распределения (дистрибуции) рассматриваемых единиц в потоке речи, т. е. на основе их сочетаемости с другими единицами, к-рые называются окружением, или контекстом, рассматриваемых единиц. Д. а. был разработан представителями т. н. дескриптивной лингвистики.

ДИСТРИБУЦИЯ, термин, употребляемый в структурном языкознании, особенно в американской дескриптивной лингвистике. Под Д. данного элемента обычно понимают сумму всех окружений, в которых он встречается, т. е. сумму всех (различных) позиций элемента относительно позиций других элементов. Понятие Д. отражает тот факт, что каждая языковая единица (за исключением предложения) обладает ограниченной в большей или меньшей степени способностью сочетаться с другими подобными единицами. Различают следующие типы Д.: 1) два элемента никогда не встречаются в одинаковой позиции; этот тип, называемый - "дополнительной (комплементарной) Д.", характерен для вариантов одной и той же единицы (так, более открытый и более закрытый гласный в словах "дед" и "деть"), первый из к-рых встречается в рус. речи перед твёрдыми, а второй - перед мягкими согласными; являются вариантами фонемы [е]; 2) два элемента встречаются в одинаковых окружениях - в этом случае речь идёт либо о "контрастной Д.", характеризующей функционально различные единицы (напр., два звука, замена одного из к-рых другим влечёт за собой различие в значении), принадлежащие к одному классу, либо о "свободном чередовании" факультативных вариантов одной и той же единицы (напр., вибрирующее и трассированное г во франц. яз., окончания "-ой" и "-ою" в творит, падеже ед. числа в рус. яз.); 3) множество окружений, в к-рых встречается один элемент, включает в себя множество окружений, в к-рых встречается другой элемент,- эта разновидность "контрастной Д." характерна для функционально противопоставленных единиц, одна из к-рых обычно описывается как обладающая положительным признаком (маркированная), а другая - отрицательным (немаркированная) (так, Д. рус. глухих согласных шире Д. звонких, т. к. последние не встречаются в финальной позиции); 4) множества окружений двух единиц или двух классов единиц частично пересекаются (так, напр., в чеш. яз. Д. фонем г и 1, относящихся к классу согласных, частично пересекается с Д. гласных, т. к. они могут быть центральным элементом слога, ср. vlk - "волк", prst -"палец").

Лит.: Глисон Г., Введение в дескриптивную лингвистику, пер. с англ., М., 1959.

Т. В. Булыгина.

ДИСТРИКТ (англ, district, от позднелат. districtus), в ряде бурж. гос-в (напр., в США, Великобритании) название низшей адм. единицы судебного или избират. округа.

ДИСТРОФИЯ (от дис... и греч. trophe - питание), дегенерация, перерождение, патологический процесс, возникающий в связи с нарушением обмена веществ и характеризующийся появлением в тканях продуктов обмена веществ, изменённых количественно и качественно. Д.- процесс, лежащий в основе развития мн. заболеваний. Среди механизмов развития Д. различают инфильтрацию (пропитывание) (напр., инфильтрация белком эпителия канальцев почек при нефрозах, инфильтрация липоидами внутренней оболочки артерий при атеросклерозе), извращённый синтез (напр., синтез гемомеланина при малярии), трансформацию (жиров и углеводов в белки или белков и углеводов в жиры) и декомпозицию, фанероз (распад липопротеидов клеточных мембран, напр, эластич. волокон аорты при сифилитич. мезаортите). К Д. приводят расстройства крово- и лимфообращения или иннервации, гипоксия, инфекции, интоксикации, нарушения гормонального (эндокринные расстройства) и энзимного (ферментопатии) баланса и др. нарушения обмена веществ. В зависимости от преобладания нарушений того или иного вида обмена веществ различают белковые, жировые, углеводные и минеральные Д. Морфологич. проявления нарушенного обмена могут обнаруживаться преимущественно в клетках или вне их, или в равной мере в клетках и межклеточном веществе. В связи с этим Д. делят на клеточные, внеклеточные и смешанные. Д. могут иметь общий (системный) и местный характер.

Развитие белковых Д., или диспротеинозов, связано с поступлением патологич. белков в клетки или межклеточное вещество, с извращённым синтезом белков или же с распадом тканевых структур; белок при этом изменяется физико-химически и морфологически. К клеточным диспротеинозам относят зернистую, или паренхиматозную (изменения функциональной ткани печени, почек, мышечных волокон сердца), гиалиново-капельную (образование гиалина внутри клеток в виде шаров или капель), водяночную (появление в цитоплазме или ядре капелек жидкости, приводящих к распаду клетки) и роговую Д. К внеклеточным Д. принадлежит мукоидное набухание, фибриноидные изменения (отложение неоднородного вещества - фибриноида, в формировании к-рого принимают участие все элементы соединительной ткани и белки крови; отмечается при аллергич. заболеваниях, коллагенозах, нек-рых инфекционных болезнях), гиалиноз и амилоидоз. К смешанным диспротеинозам относят большую группу Д., возникающих при нарушении обмена хромопротеидов (гемосидероз, меланоз, гемомеланоз, желтухи, порфирии), нуклеопротеидов (подагра, мочекислый инфаркт) и гликопротеидов (слизистая и коллоидная Д.). Слизистая Д. развивается в эпителии и в соединительной ткани. Эпителиальные клетки начинают усиленно продуцировать слизеподобное вещество (мукойд) и слизь (муцин), гибнут и отторгаются; отмечается при воспалениях слизистых оболочек. В соединительной ткани наиболее выражена при опухолях (хондромах, миксомах и др.). Коллоидная Д. развивается в железах (щитовидной железе, гипофизе); характеризуется избыточным продуцированием коллоида, растяжением им фолликулов, гибелью клеток и пропитыванием коллоидом ткани железы.

Жировые Д., или липидозы, характеризуются изменением количества жира в жировых депо, появлением липидов там, где их обычно нет, и в изменении количества и качества липидов в клетках и тканях. Нарушение обмена нейтрального жира проявляется в уменьшении или увеличении его запасов и может быть общим или местным. Общее уменьшение количества жировой ткани характерно для истощения (кахексии), местное - для регионарной липодистрофии (липоатрофии) - атрофия жировой ткани отдельных областей тела. Особой формой является прогрессирующая липодистрофия - болезнь Барракера - Симондса, выражающаяся в исчезновении жира на голове, шее, грудной клетке. Общее увеличение запасов жира ведёт к ожирению (тучности), местное -наблюдается при атрофии функциональной ткани или органа (жировое замещение) и при болезни Деркума - развитие жировых отложений в виде отдельных узлов (липом) или диффузное. Нарушение обмена липоидов (фосфатидов) цитоплазмы (клеточные ли-поидозы) наиболее часто встречается в паренхиматозных органах (миокард, печень, почки), реже оно характеризуется отложением в ретикуло-эндотелиальной системе различных видов липоидов (системные липоидозы): цереброзида и керазина - при болезни Гоше, лецитина - при болезни Нимана - Пика, холестерина - при болезни Хенда - Шюллера - Крисчена. Внеклеточная жировая Д. (внеклеточный липоидоз) кровеносных сосудов лежит в основе атеросклероза.

Углеводные Д. касаются нарушения обмена полисахаридов, мукополисахаридов и гликопротеидов. Наибольшее значение имеет нарушение обмена гликогена. Эти нарушения наиболее ярко выражены при диабете сахарном, когда тканевые запасы гликогена резко уменьшаются, и при гликогенозах - болезни Гирке и др., при к-рых в избыточных количествах гликоген откладывается в печени, сердце, почках, скелетных мышцах.

Среди минеральных Д. наибольшее значение имеют нарушения обмена калия, кальция, железа и меди. Увеличение количества калия в крови и тканях отмечается при аддисоновой болезни; дефицитом калия объясняют возникновение наследственной болезни -периодического паралича (миоплегия семейная, пароксизмальный паралич; характеризуется внезапными приступами вялых параличей скелетной мускулатуры). Нарушения обмена кальция - известковые Д., или тканевые обызвествления,- характеризуются выпадением извести в тканях в виде плотных масс. Различают метастическое (известковые метастазы), дистрофическое (петрификация) и метаболическое (известковая подагра, кальциноз) тканевое обызвествление. При известковых метастазах, сопровождающих гиперкальциемию (повышенное содержание кальция в крови), наблюдается распространённое обызвествление органов и тканей (лёгкие, желудок, почки, сердце, артерии), при дистрофич. обызвествлении известь отлагается в тканях, находящихся в состоянии некробиоза или некроза; метаболич. обызвествление может быть как универсальным, так и локальным. Железо содержится в основном в гемоглобине. Нарушения его обмена связаны с гемоглобиногенными пигментами (хромопротеидами) и выражаются гемосидерозом (отложением в коже в виде буро-коричневатых пятен и во внутренних органах пигмента гемосидерина) и гемохроматозом (меланодермия, пигментный цирроз, бронзовый диабет, характеризующийся отложением пигментов - гемосидерина, гемофусцина, меланина - в печени, поджелудочной железе, лимфатич. узлах, миокарде и др.; одновременно с выпадением пигментов функциональная ткань замещается соединительной). Болезнью нарушенного обмена меди является гепато-церебралъная дистрофия, при к-рой медь депонируется в печени, почках, мозге, роговице.

Механизмы развития Д. изучаются с применением методов гистохимии, электронной микроскопии, ауторадиографии, гистоспектрографии и др.

Лит.: Серов В. В., Дистрофия, в кн.: Струков А. И., Патологическая анатомия, М., 1967; Давыдовский И. В., Общая патология человека, 2 изд., М., 1969.

В. В. Серов.

ДИСТРОФИЯ АДИПОЗО-ГЕНИТАЛЬНАЯ, заболевание, связанное с нарушением функции желез внутренней секреции (гипофиза) и межуточного мозга и характеризующееся ожирением, задержкой роста и недоразвитием или атрофией половых желез и вторичных половых признаков. В основе Д. а.-г. лежат поражения (чаще всего опухоли, кровоизлияния или инфекции) области турецкого седла, гипоталамуса или третьего желудочка мозга. Недоразвитие полового аппарата особенно резко проявляется в период полового созревания. Ожирение при Д. а.-г. придаёт мальчикам женоподобный, а девочкам-зрелый вид. Д. а.-г. сопровождается головокружением, головными болями, ослаблением полового влечения и потенции, нарушениями зрения. Иногда происходят изменения в области эмоций, быстрая смена настроений, ослабление способности концентрировать внимание на одном виде деятельности, понижение способности к запоминаниям. Возможно семейное предрасположение к заболеванию. Лечение: хирургич., рентгеновыми лучами, гормонами; при Д. а.-г. инфекционного происхождения - специфическое.

Л. М. Гольбер.

ДИСТРОФИЯ АЛИМЕНТАРНАЯ, голодная болезнь, отёчная болезнь, голодные отёки, болезненное состояние, развивающееся в результате недостаточного поступления питательных веществ (особенно полноценного белка) в организм, т. е. с голоданием, к-рым определяются все проявления Д. а. Термин "Д. а." предложен врачами, работавшими в Ленинграде во время немецко-фашистской блокады (1941-42). Усугубляющими факторами в развитии Д. а. являются холод, физич. и нервно-психич. перенапряжение, инфекционные заболевания. Д. а. встречается в сухой и отёчной формах. В первом случае быстро прогрессирует похудание, а во втором -на фоне истощения постепенно развиваются отёки всего тела. При Д. а. довольно часто встречаются такие осложнения, как воспаление лёгких, дизентерия, туберкулёз. На фоне Д. а. отмечаются симптомы авитаминоза, в частности недостаточность витаминов С, B₁, B₂.

Проявляется Д. а. слабостью, быстрой утомляемостью, похуданием, доходящим до потери 50% общей массы тела, вялостью и мышечными болями. Частое мочеиспускание иногда является одним из ранних признаков болезни. Понижается температура тела. Изменяется сердечнососудистая деятельность (замедляются сокращения сердца, снижается артериальное давление). Появляются отёчность лица, сухость и шелушение кожи, выпадение волос. По мере развития болезни возникают частые рвоты и тошноты. Появляется безразличное отношение к окружающему, апатия, ослабление памяти и внимания, реже наступает возбуждение, галлюцинации и острые психозы. У женщин обычно прекращаются менструации.

Лечение: полное освобождение от работы; полноценное питание с 5-6-разовыми приёмами легкоусвояемой высокопитательной, витаминизированной пищи, с повышенным количеством животных белков; вливания растворов глюкозы, хлорида натрия, переливание крови или плазмы; при поносах - пепсин, соляная кислота.

Лит.: Свечников В. А., Болезнь голодания (алиментарная дистрофия), Л., 1947; Алиментарная дистрофия в блокированном Ленинграде. Сб. статей, под ред. М. В. Черноруцкого, Л., 1947.

И. С. Савощенко.

ДИСТРОФИЯ ДЕТСКАЯ, хронич. расстройство питания ребёнка, сопровождающееся нарушением процессов обмена, функций мн. органов и систем, роста и развития ребёнка. Д. д. может протекать с избыточным (паратрофия), пониженным (гипотрофия) и нормальным весом тела ребёнка; чаще наблюдается гипотрофия (в зависимости от дефицита веса различают 1, 2 и 3-ю степени), при к-рой нередко происходит задержка психофизич. и моторного развития, возникают диспепсич. расстройства и снижение иммунитета, приводящие к развитию различных заболеваний.

Д. д. могут быть алиментарного происхождения (качественные и количественные нарушения питания), инфекционного (острые и хронич. инфекции), а также возникать вследствие нарушения режима и ухода. В основе "конституциональной", или врождённой, дистрофии лежит действие внутриутробных вредностей, нарушающих питание и развитие плода; причиной Д. д., развивающейся с первых недель жизни, могут быть врождённая патология обмена веществ, нарушение активности ферментов, гормональные расстройства, пороки развития. Проявляется пониженной упитанностью, малой активностью, сниженным аппетитом; иногда присоединяются рвота, поносы, нарушение функции почек. Лечение: рациональное питание повышенной калорийности, витаминотерапия; тщательный уход и правильный гигиенич. режим; стимулирующая терапия (переливание крови, плазмы, апилак, метандростенолон и т. п.), массаж, леч. гимнастика. Профилактика: правильная организация режима питания и ухода, закаливание, предупреждение и своевременное лечение различных заболеваний.

Лит.: М а с л о в М. С., Хронические расстройства питания или дистрофии (гипотрофии) у детей раннего возраста, в кн.: Многотомное руководство по педиатрии, под ред. Ю. Ф. Домбровской, т. 4, М., 1963.

М. Я. Студеникин, Р. Н. Рылеева.

ДИСУЛЬФИДНЫЕ СВЯЗИ, -S-S-связи, образующиеся в результате соединения атомов серы двух сульфгид-рильных групп. С образованием Д. с. происходит, напр., "сшивание" полипеп-тидных цепей, содержащих остатки аминокислоты цистеина.

ДИСУЛЬФОРМИН, лекарственное средство из группы сульфаниламидных препаратов. Применяют в таблетках и порошках при лечении острых и хронич. энтеритов и бациллярной дизентерии.

ДИСФАГИЯ (от дис... и греч. phagein -есть, глотать), расстройство акта глотания. Причины Д. - воспалит, процессы полости рта, глотки, пищевода, гортани, средостения, инородные тела, руёцовые сужения и опухоли, нек-рые нервные заболевания. Проявляется затруднением или невозможностью глотания, болями в момент глотания, попаданием пищи или жидкости в нос, гортань, трахею. Лечение: устранение основной причины, вызвавшей Д.

ДИСФОРИЯ (от греч. dysphoreo - тяжело переношу, раздражён), расстройство настроения, характеризующееся напряжённым, злобно-тоскливым аффектом с выраженной раздражительностью, доходящей до взрывов гнева с агрессивностью. Наблюдается при эпилепсии, а также при нек-рых психопатич. (см. Психопатия) состояниях.

ДИСЦИПЛИНА (лат. discipline) общественная, определённый порядок поведения людей, отвечающий сложившимся в обществе нормам права и морали или требованиям к.-л. организации. Д. является необходимым условием нормального существования общества; благодаря Д. поведение людей принимает упорядоченный характер, что обеспечивает коллективную деятельность и функционирование социальных организаций. В обществе всегда существует общеобязательная Д. и специальная Д. -обязательная только для членов определённой орг-ции (трудовая, партийная, воинская и т. д.). Д. всегда определяется господствующими обществ, отношениями и служит для их поддержания. Различают внутр. Д., или самодисциплину, Д. из соображений выгоды и Д. по принуждению. Внутр. Д. предполагает глубокое усвоение (интериоризацию) членами общества норм, регулирующих поведение людей. Такая Д. поддерживается без внешних санкций и принудит. мер. "... Подчинение может, при идеальной сознательности и дисциплинированности участников общей работы, напоминать больше мягкое руководство дирижера" (Ленин В. И., Полн. собр. соч.., 5 изд., т. 36, с. 200). Дисциплинированный человек испытывает внутр. потребность следовать принятым нормам поведения и в случае их несоблюдения испытывает угрызения совести, чувство вины и т. д. В отличие от внутр. Д., Д. из соображений выгоды и Д. по принуждению опираются на внешние санкции - положительные или отрицательные. Член общества или организации может следовать нормам и распоряжениям только в расчёте на материальное или к.-л. иное поощрение или стремясь избежать наказания. В конечном счёте Д. определяется степенью сочетания личных интересов членов общества, их потребностей и выполняемых ими социально обусловленных норм поведения. Если эти нормы не становятся внутр. пружинами действий индивидов, возникают разного рода отклонения в поведении, к-рые либо регулируются с помощью механизмов социального контроля, либо могут привести к изменениям и ломке существующих норм и институтов. Однако общественно вредной может ока-.заться и чрезмерно жёсткая Д., т. к. в этих условиях члены общества лишаются творческой инициативы, а общественная система утрачивает необходимую гибкость.

В различных обществ, системах ни один из видов Д. не встречается в изолированном виде; речь может идти лишь об удельном весе того или иного вида Д. В обществах, основанных гл. обр. на традициях, в периоды их устойчивого существования преобладало морально-религ. регулирование поведения людей, дополняемое принудительной (личная зависимость) Д. Роль материальных интересов и Д. из соображений выгоды преобладают в бурж. обществе с его отношениями "голого чистогана" и господством индивидуалистической морали. Вместе с тем в качестве регулятивного механизма выступает нормативная Д. в форме "деловой этики", "профессионального долга" и т. п.

В социалистич. обществе постепенно утверждается сознательная Д. трудящихся. В. И. Ленин характеризовал социалистич. Д. как"... дисциплину товарищескую, дисциплину всяческого уважения, дисциплину самостоятельности и инициативы в борьбе" (там же, с. 500). Социалистич. Д. развивается в процессе сознательного строительства новых обществ, отношений, в результате процесса ком-мунистич. воспитания. Важным средством её укрепления является социальный контроль, материальное и моральное стимулирование.

На совр. этапе социалистического и коммунистического строительства усложнившаяся организация общества и научно-технич. революция предъявляют повышенные требования к Д., организованности, ответственности, сознательности каждого члена общества. Нормы Д. периода коммунистического строительства сформулированы в Программе КПСС, в моральном кодексе строителя коммунизма.

Лит.: Энгельс Ф., Об авторитете, Маркс К. иЭнгельс Ф., Соч., 2 изд., т. 18; Ленин В. И., Государство и революция, Полн. собр. соч.., 5 изд., т. 33; его ж е, Очередные задачи Советской власти, там же, т. 36; его же, Как организовать соревнование?, там же, т. 35; его же, Великий почин, там же, т. 39; Программа КПСС, М., 1961; Макаренко А. С., Соч., [2 изд.], т. 5, М., 1958, с. 36 - 43, 130-44.

Л. А. Седов.

ДИСЦИПЛИНА ВОИНСКАЯ, строгое и точное соблюдение всеми военнослужащими порядка и правил, установленных законами и воинскими уставами. Д. в. присуща всем армиям, но в различных армиях отличается по своему характеру и зависит от характера обществ, строя гос-ва. В Сов. Вооруж. Силах дисциплина основывается не на страхе наказания и принуждении, а на сознании каждым военнослужащим воинского долга и личной ответственности за защиту своей Родины - Союза Советских Социалистических Республик. Дисциплина содействует чёткому управлению войсками, преодолению трудностей в боевой обстановке и является важнейшим условием высокой боеспособности и постоянной боевой готовности войск. Победы Сов. Вооруж. Сил в период Гражд. войны 1918-20 и во время Великой Отечественной войны 1941-45 были возможны лишь при высокой сознательности и железной воинской дисциплине сов. воинов. Общие положения и конкретные правила дисциплинарной практики излагаются в Дисциплинарном уставе Вооружённых Сил СССР, утверждаемом Указом Президиума Верх. Совета СССР и имеющем силу закона. Д. в. обязывает каждого военнослужащего строго соблюдать законы и точно выполнять требования воен. присяги (см. Присяга военная), воинских уставов (см. Уставы воинские), приказы и приказания начальников, стойко переносить все тяготы и лишения воен. службы, не щадить своей крови и самой жизни при выполнении воинского долга, строго хранить воен. и государственную тайну, быть честным, правдивым, добросовестно изучать воен. дело и всемерно беречь воен. и народное имущество, оказывать уважение начальникам и старшим, строго соблюдать правила воинской вежливости и отдания чести, с достоинством и честью вести себя вне расположения части, не допускать самому и удерживать других от нарушений общественного порядка и всемерно содействовать защите чести и достоинства граждан. Интересы защиты Родины обязывают всех командиров (начальников) наряду с постоянной заботой о подчинённых и их воспитанием решительно и твёрдо требовать соблюдения дисциплины и порядка, не оставлять без воздействия ни одного проступка подчинённых, строго взыскивать с нерадивых и поощрять достойных за проявленную разумную инициативу, усердие, подвиги и отличия по службе. Правильное сочетание мер убеждения и принуждения в отношении тех, кто нерадиво относится к исполнению своего воинского долга, составляет основу дисциплинарной практики. Решающую роль в поддержании сознательной Д. в. в Вооруж. Силах имеет политич. воспитание военнослужащих, осуществляемое командирами (начальниками), политорганами, парт, и комсомольскими организациями.

И. Н. Миненко.

ДИСЦИПЛИНА ГОСУДАРСТВЕННАЯ, в СССР точное соблюдение всеми организациями и гражданами установленного Сов. государством порядка деятельности гос. органов, предприятий и учреждений по выполнению возложенных на них гос. обязанностей. Д. г. в социалистич. обществе основывается на высокой сознательности широких масс трудящихся, объективном выражении в требованиях и предписаниях гос. органов интересов абсолютного большинства трудящихся. Д. г. требует строгого соблюдения законности, плановых заданий, договорных обязательств; она несовместима сведомств. или местническим подходом к решению общегос. задач, с противопоставлением личных интересов государственным. Д. г. опирается на демократич. принципы организации управления, неразрывно связана с укреплением обществ, дисциплины, дисциплины труда, с требованиями коммунистической морали и нравственности.

Составными частями Д. г. являются плановая, финансовая, договорная, тех-нологич., служебная и др. виды дисциплины. В области хоз. деятельности гл. элементом Д. г. является договорная дисциплина - установл. законом обязанность социалистич. организаций точного и своеврем. исполнения их договорных обязательств, а также своеврем. заключения договоров на базе плановых актов, обязат. для обеих сторон. В СССР

Основы гражд. законодательства 1961 содержат ряд норм, направленных на обеспечение своевременности заключения договоров и гарантирующих соблюдение договорной дисциплины при их исполнении. Особое внимание уделяется соблюдению дисциплины в договорах между социалистич. организациями, основанных на обязательном для обеих сторон плановом задании. Закон устанавливает, что разногласия, возникающие между гос., кооп. (кроме колхозов) и иными обществ. организациями при заключении договора, основанного на плановом задании, разрешаются соответствующим арбитражем (третейским судом), если законом не предусмотрен иной порядок их рассмотрения. В тех случаях, когда разногласия между названными организациями возникают при заключении договора, не основанного на обязательном для обеих сторон плановом задании, стороны могут обратиться в арбитраж, если речь идёт о поставке продукции, не распределённой в плановом порядке, и если стороны договорились о предмете и сроках поставки; обращение в арбитраж возможно также при длит. хоз. связях сторон. Укреплению договорной дисциплины служат устанавливаемые гражд. законодательством или самим договором условия взыскания убытков, санкции на случай неисполнения или ненадлежащего исполнения договора, санкции, налагаемые Госбанком СССР на предприятия и организации, нарушающие свои договорные обязательства, а также гражданско-правовые способы обеспечения обязательств. Умышленное нарушение договорной дисциплины в случаях, предусмотренных законом, может повлечь уголовную ответственность. Важным элементом Д. г. является финансовая дисциплина. Её требования определяются спецификой финансовой деятельности Сов. гос-ва, стремящегося к устойчивости и прочности гос. финансов, что возможно только при точном и всестороннем регулировании финансовых отношений, их детальной регламентации и упорядоченности финансовой работы. Эти требования распространяются не только на гос. бюджет, но и на все звенья сов. финансовой системы: на финансы социалистич. предприятий, гос. страхование, гос. и банковский кредит, финансовая дисциплина включает: бюджетную дисциплину (внесение всеми гос. органами, предприятиями, учреждениями, организациями и гражданами платежей в бюджет в установл. размерах ив предусмотр. сроки; расходование бюджетных средств, строго по целевому назначению, в пределах утверждённых ассигнований и в меру фактич. выполнения производств, и финансовых планов); кредитную дисциплину (строгое соблюдение правил использования полученных кредитов, своевременное погашение долгосрочных и краткосрочных ссуд банковских учреждений и процентов по ним). Важным требованием финанс. дисциплины является обязанность всех предприятий, учреждений и организаций хранить свои денежные средства на соответств. счетах банковских учреждений или сберегательных касс и вести расчёты с контрагентами, как правило, в. безналичном порядке (см. Безналичные расчёты).

Законодательство устанавливает систему нормативов, в соответствии с к-рыми могут планироваться и расходоваться денежные средства (численность штатов, ставки заработной платы и др.).

Д. г. направлена на обеспечение чёткой работы гос. аппарата, она требует от каждого работника глубокого понимания возложенных на него служебных функций, ответственности за порученное дело, инициативы и деловитости.

КПСС придаёт особое значение соблюдению Д. г. В Программе КПСС 1961, в решениях съездов и пленумов ЦК КПСС подчёркивается, что Д. г. - одно из важнейших условий успешного строительства коммунистич. общества, а следовательно, необходима решит, борьба с любыми проявлениями расхлябанности, ведущей к нарушению Д. г. Устав КПСС требует от всех членов партии строгого соблюдения парт.и гос. дисциплины.

Соблюдение требований Д. г. обеспечивается организаторской и воспитат. работой парт. и гос. органов, обществ, организаций. Особая ответственность за соблюдение Д. г. возлагается на руководителей гос. органов, обществ, организаций, учреждений и предприятий.

Советское законодательство предусматривает материальную, а в нек-рых случаях и уголовную ответственность за нарушение требований Д. г. Особое внимание уделяется контролю и надзору за точным соблюдением требований Д. г., привлечению к этому делу обществ, организаций и общественности. Ответств. задачи по обеспечению Д. г. в деятельности гос. аппарата возложены на органы народного контроля.

М. И. Пискотин, Н. Г. Салищева, Н. О. Татищева.

ДИСЦИПЛИНА ПАРТИЙНАЯ, непременное условие организованности и боеспособности марксистско-ленинских партий, решающее условие выполнения коммунистами и парт, организациями требований Программы, Устава, решений парт, органов и парт, морали. Д. п., как одна из организац. основ пролетарской партии нового типа, тесно связана с её руководящим организац. принципом -демократическим централизмом.

Важнейшие принципы Д. п. разработал и обосновал В. И. Ленин. "Принципиально мы уже не раз определяли, - говорил он, - наш взгляд на значение дисциплины и на понятие дисциплины в рабочей партии. Единство действий, свобода обсуждения и критики, - вот наше определение. Только такая дисциплина достойна демократической партии передового класса. Сила рабочего класса - организация. Без организации масс пролетариат - ничто. Организованный, он - все. Организованность есть единство действия, единство практического выступления" (Полн. собр. соч.., 5 изд., т. 14, с. 125-26). Ленин подчёркивал, что особое значение приобретает железная Д. п. в период вооруж. борьбы рабочего класса за власть, за её отстаивание и упрочение. Коммунистич. партия может успешно выполнить свою роль вождя трудящихся масс в том случае, если в ней господствует крепкая сознательная Д. п. и когда её руководящий центр является властным авторитетным органом с широкими полномочиями, пользующимися всеобщим доверием членов партии и беспартийных трудящихся масс. Говоря о причинах победы Сов. республики над интервентами и белогвардейцами в 1918-1920, Ленин особо подчёркивал роль Д. п. Он писал, что "... большевики не продержались бы у власти не то что 2½ года, но и 2⅓ месяца без строжайшей, поистине железной дисциплины в нашей партии, без самой полной и беззаветной поддержки ее всей массой рабочего класса, т. е. всем, что есть в нем мыслящего, честного, самоотверженного, влиятельного, способного вести за собой или увлекать отсталые слои" (там же, т. 41, с. 5-6). Монолитное единство и железная Д. п. правящей компартии являются рещающим условием осуществления руководящей роли коммунистич. партии в системе диктатуры пролетариата, сыграли решающую роль в обеспечении победы социализма в СССР и продолжают играть такую же роль в условиях общенар. гос-ва в борьбе за построение коммунистич. общества. Железная Д. п. не исключает, а предполагает критику и самокритику внутри партии, сознательность и добровольность подчинения (см. Демократия внутрипартийная). Д. п. неразрывно связана с идейным единством пролетарской партии. Только сознательная дисциплина может быть действительно железной, идейной и принципиальной дисциплиной. Д. п. является одинаково обязательной для всех коммунистов - рядовых и руководителей. Ленин подвергал критике меньшевиков, насаждавших барские нравы в рядах РСДРП, деливших членов партии на "избранных" и "неизбранных". Большевистская партия выковала Д. п. в непримиримой борьбе с меньшевиками, троцкистами, бухаринцами и другими оппортунистич. группами и течениями, посягавшими на единство партии. Огромное значение в борьбе против антипарт. группировок и течений в укреплении сознательной дисциплины и единства партии сыграла ленинская резолюция "О единстве партии", принятая Десятым съездом РКП(б) (1921).

Принципы Д. п. КПСС воплощены в Уставе КПСС. "Нерушимый закон жизни КПСС, - говорится в Уставе партии, -идейное и организационное единство, монолитность ее рядов, высокая сознательная дисциплина всех коммунистов. Всякое проявление фракционности и групповщины несовместимо с марксистско-ленинской партийностью, с пребыванием в партии" (1971, с. 5). Член партии обязан всемерно охранять единство партии как главное условие силы и могущества партии, соблюдать Д. п. и гос. дисциплину. Партия привлекает к ответственности виновных в нарушении Программы и Устава партии, парт., гос. дисциплины, а также нарушителей партийной морали. Коммунист - активный и самоотверженный боец за выполнение партийных и гос. решений. Для члена партии недостаточно только согласия с парт, решениями, он обязан бороться за претворение этих решений в жизнь.

Братские коммунистич. и рабочие партии крепят дисциплину и единство своих рядов, учитывая историч. опыт КПСС. Отступление от марксистско-ленинских требований Д. п., как этого добиваются правые и "левые" ревизионисты, приводит в конечном счёте к перерождению партии в орг-цию реформистско-анархистского или военизированного типа.

Лит.: Ленин В. И., Полн. собр. соч.., 5 изд. (см. Справочный том, ч. 1, с. 144); Устав КПСС, М., 1971.

ДИСЦИПЛИНА ТРУДОВАЯ, закреплённая правом и другими социальными нормами система организационных отношений, в рамках к-рой происходит совместная трудовая деятельность. Характер Д. т. определяется типом производственных отношений. При феодализме Д. т. основывалась на прямом принуждении. В бурж. обществе, где рабочий вынужден продавать капиталисту свою рабочую силу, Д. т. носит подневольный характер. Постоянная угроза увольнения и само увольнение используются в качестве осн. меры поддержания Д. т.

Социалистич. строй создаёт новую Д. т. "Коммунистическая организация общественного труда, к которой первым шагом является социализм, держится и чем дальше, тем больше будет держаться на свободной и сознательной дисциплине самих трудящихся..." (Ленин В. И., Полн. собр. соч.., 5 изд., т. 39, с. 14). В. И. Ленин укрепление Д. т. ставил в прямую связь с возможностью построения социализма, он отмечал, что "... только строжайшая организация и трудовая дисциплина приведут нас к социализму" (там же, т. 36, с. 258). Сочетание обществ. и личных интересов, подчинение личных интересов общественным - такова основа социалистич. Д. т.

Требования Д. т. в социалистич. обществе обязательны для всех трудящихся. В СССР обязанность соблюдать Д. т. закреплена Конституцией 1936 (ст. 130); содержание этой обязанности конкретизируется в трудовом законодательстве, в правилах внутреннего трудового распорядка, в уставах о дисциплине, в коллективных договорах, в должностных и технич. инструкциях.

В период строительства коммунизма укрепление Д. т. в СССР имеет огромное значение для правильной организации труда и воспитания сознательности граждан. Нарушение Д. т. даже отдельными работниками наносит материальный ущерб производству, нар. х-ву СССР в целом. Воспитание нового коммунистич. отношения к труду, формирование и укрепление сознат. Д. т. - сложный и длит. процесс. "Строить новую дисциплину труда, строить новые формы общественной связи между людьми, строить новые формы и приемы привлечения людей к труду, это - работа многих лет и десятилетий" (Ленин В. И., там же, т. 40, с. 316). В СССР наряду с высокой организованностью большинства трудящихся, для к-рых характерно социалистич. отношение к труду, встречаются ещё серьёзные нарушения Д. т., связанные с сохранившимися пережитками прошлого в сознании нек-рых работников, проявляющиеся в недобросовестном отношении к труду. Социалистич. характер Д. т. в СССР предопределяет и методы её укрепления: осн. из них является метод убеждения, развитие социалистич. соревнования, последовательное проведение социалистич. принципа материальной заинтересованности, установление льгот и преимуществ для работников, добившихся успехов в труде, а также меры морального поощрения (благодарности, награды и т. п.). К нарушителям Д. т. применяются меры обществ. и дисциплинарного воздействия. Широко используются коллективные средства воздействия на нарушителей Д. т. - обсуждение на рабочих собраниях, товарищеских судах и т. д.

Повседневная, упорная борьба за повышение социалистич. Д. т. сочетается с постоянной заботой об улучшении условий труда работников, рациональной организацией труда, производства и управления, с быстрым внедрением достижений науки и техники в производство, что создаёт условия для укрепления Д. т. См. также Взыскания дисциплинарные, Ответственность дисциплинарная, Товарищеский суд.

Е. М. Тершанов, В. И. Никитинский.

ДИСЦИПЛИНАРНАЯ ОТВЕТСТВЕННОСТЬ, см. Ответственность дисциплинарная.

ДИСЦИПЛИНАРНЫЕ ЧАСТИ, батальоны, рот ы, особые воинские части, предназначенные для отбывания наказания осуждёнными военнослужащими. По сов. праву наказание в виде направления в Д. ч. предусматривается У К союзных республик (напр., УК РСФСР, ст. ст. 21, 22, 34, 41 и др.). Назначается за совершение отдельных воинских преступлений сержантами и солдатами срочной службы (напр., за самовольную отлучку), а также за совершение ими воинских и иных преступлений, если суд приговорил их к лишению свободы на срок до 2 лет (назначив такую меру наказания, суд имеет право заменить её направлением в Д. ч.). Приговаривая осуждённого военнослужащего к направлению в Д. ч., суд учитывает возможность оставления осуждённого на военной службе.

Порядок и условия содержания осуждённых военнослужащих в Д. ч. определяются "Положением о дисциплинарном батальоне в Вооружённых Силах СССР" 1966. Время нахождения осуждённого в Д. ч. в срок военной службы не включается, но осуждённые остаются военнослужащими, носят погоны рядовых (матросов). По отбытии не менее половины срока наказания осуждённый может быть представлен к условно-досрочному освобождению.

Д. ч. существовали также в дореволюц. рус. армии (учреждены в 1878 для содержания осуждённых нижних чинов со сроком от 1 до 3 лет); имеются в армиях многих иностр. гос-в.

ДИСЦИПЛИНАРНЫЙ АРЕСТ, мера дисциплинарного взыскания. В Союзе ССР Д. а. предусмотрен Дисциплинарным уставом Вооружённых Сил Союза ССР и некоторыми другими уставами о дисциплине лиц, приравненных к военнослужащим. Налагается на срок до 15 суток, при этом военнослужащие, подвергнутые Д. а., как правило, содержатся на гауптвахте. Порядок наложения и отбывания Д. а. регламентируется соответствующими уставами.

ДИСЦИПЛИНАРНЫЙ УСТАВ, 1)один из общевоинских уставов Вооруж. Сил СССР. В нём излагаются основы советской воинской дисциплины (см. Дисциплина воинская), обязанности и права военнослужащих по поддержанию и укреплению воинской дисциплины, виды поощрений и дисциплинарных взысканий по отношению к военнослужащим и права начальников по их применению к подчинённым, а также порядок подачи и рассмотрения жалоб и заявлений. В России первый Д. у. под названием "Воинский устав о наказаниях" был принят в мае 1867 и заменил собой воинский уголовный устав 1839. В Красной Армии в янв. 1919 был утверждён Дисциплинарный устав, разработанный с учётом особенностей РККА как армии нового типа. В дальнейшем были приняты: Временный дисциплинарный устав РККА (1925), Дисциплинарный устав Красной Армии (1940) и Дисциплинарный устав Военно-Морского Флота Союза ССР (1940), Дисциплинарный устав (1946)- единый для всех Вооруж. Сил СССР, Дисциплинарный устав Вооружённых Сил Союза ССР (1960), к-рый был утверждён Указом Президиума Верх. Совета СССР.

Д. у. имеются в армиях социалистич. стран - членов Варшавского договора, а также в армиях нек-рых капиталистич. гос-в (Франция, ФРГ и др.). В вооруж. силах США поддержание воинской дисциплины основывается на "Едином кодексе военной юстиции" 1951, уточнённом в 1963, в англ. вооруж. силах - на "Акте об армии" (1957).

Лит.: Дисциплинарный устав Вооружённых Сил Союза ССР, М., 1967.

И. П. Лябик.

2) В СССР нормативный акт, регулирующий в пределах отрасли нар. х-ва основные обязанности работников, меры поощрения и дисциплинарного взыскания. Д. у. действуют в тех отраслях, где соблюдение трудовой дисциплины имеет особо важное значение: на ж.-д. транспорте (СП СССР, 1964, № 13, ст. 91), морском транспорте, речном транспорте, в гражд. авиации и в авиации ДОСААФ, на предприятиях связи, во флоте рыбной пром-сти (СП СССР, 1966, № 13, ст. 124) и др. Д. у. утверждаются Советом Министров СССР (иногда - Советами Министров союзных республик). Большинство Д. у. распространяется не на всех рабочих и служащих соответствующей отрасли нар. х-ва, а лишь на тех, кто выполняет основные, профилирующие работы. Напр., Д. у. работников ж.-д. транспорта распространяется на работников железных дорог, заводов по ремонту подвижного состава, станций связи и центрального аппарата Министерства путей сообщения. Д. у. устанавливают более строгие меры дисциплинарных взысканий по сравнению с правилами внутреннего трудового распорядка; жалобы работников по поводу наложения дисциплинарных взысканий по Д. у. не рассматриваются в комиссиях по трудовым спорам, а только вышестоящими в порядке подчинённости органами.

Р. З. Лившиц.

ДИТЕРИХС Михаил Константинович [5(17).4. 1874, Петербург, - 9. 10. 1937, Шанхай], один из руководителей контрреволюции в Сибири и на Д. Востоке, ген.-лейтенант (1919). Род. в семье офицера - чеха по национальности. Окончил Пажеский корпус (1894) и Академию Генштаба (1900). Во время 1-й мировой войны 1914-18 с сент. 1917 ген.-квартирмейстер Ставки верх, главнокомандующего А. ф. Керенского, а с 3 (16) нояб. нач. штаба Ставки у ген. Н. Н. Духонина. 8 (21) нояб. 1917 бежал на Украину и вскоре стал нач. штаба Чехословацкого корпуса; один из организаторов его мятежа в мае 1918. В июле -авг. 1919 командовал колчаковской Сибирской армией, в авг.- сент. 1919 - нач. штаба и воен. министр, в окт.- нояб.- командующий Вост. фронтом. В 1922 избран т. н. "Земским собором" при поддержке япон. интервентов "единоличным правителем и воеводой земской рати" и объявил крестовый поход против Сов. России за восстановление монархии. После разгрома белогвардейцев на Д. Востоке бежал в Шанхай.

ДИТЕРЛЕ (Dieterle) Уильям (р. 15.7. 1893, Людвигсхафен), амер. кинорежиссёр. По национальности немец. Был актёром театра М. Рейнхардта (Берлин). В 1913 дебютировал в кино. В 1923-29 снимал незначит. игровые фильмы в Германии, в 1930 переехал в Голливуд, где ставил мелодрамы и псевдоисторич. фильмы. Во 2-й пол. 30-х гг. поставил серию историко-биографич. картин, в к-рых воссоздал образы передовых людей, преодолевавших фанатизм, невежество, узость человеческого мышления в борьбе за научный и социальный прогресс. Эти фильмы - "Повесть о Луи Пастере" (1936), "Жизнь Эмиля Золя" (1937), "Хуарес" (1939) - характеризовались современным звучанием намеренно подчёркнутых параллелей между реакционными силами 19 и 20 вв., антифашистской направленностью. Демократич. взгляды проявились и в его обращении к теме войн: в Испании - "Блокада" (1938) - и в фильме "Собор Парижской богоматери" (1939, по роману В. Гюго). В 50-е гг. ставил коммерч. фильмы в Голливуде, Италии, ФРГ.

ДИТМАРШЕН (Dithmarschen), область, расположенная между Северным м., р. Эльба и Кильским каналом, часть земли Шлезвиг-Гольштейн (ФРГ). Пл. 1360 км². В раннее средневековье Д. был заселён вост. саксами, с 13 в.- также фризами. Находясь с кон. 12 в. в номинальной ленной зависимости от архиепископов Бременских, Д. в 13 в. фактически приобрёл независимость, стал своеобразной "крестьянской республикой" (состоявшей из совокупности соседских общин-марок); крестьянство Д. сохранило личную свободу. В 1559 был завоёван дат. феодалами. После дат. войны 1864 перешёл к Пруссии.

ДИТРИХ (Dietrich) (наст, имя и фам. -Мария Магдалена фон Лош; Losch) Марлен (р. 27. 12. 1904, Берлин), американская актриса. По национальности немка. Училась в Муз. академии и Школе драматич. иск-ва М. Рейнхардта (Берлин). В 1922 дебютировала в театре и в кино. Первую значит, роль сыграла в фильме"Голубой ангел" (1930, по роману Т. Манна). Уехав в 1930 в Голливуд, снималась в экзотич. фильмах реж. Дж. Штернберга "Марокко" (1930), "Шанхайский экспресс" (1932), "Красная императрица" (1934), "Дьявол - это женщина" (1935) в амплуа женщины-"вамп" и стала одной из самых популярных "звёзд" амер. кино 30-х гг. В годы 2-й мировой войны 1939-45 Д. принимала активное участие в антифашистской пропаганде, выступала как певица перед амер. солдатами. В фильмах послевоенного времени играла роли прежнего амплуа. В 50-е гг. с переходом на роли немолодых героинь показала себя как одарённая актриса, создавшая яркие, сложные характеры в фильмах "Свидетель обвинения" (1957), "Процесс в Нюрнберге" (1962) и др. Известна также как эстрадная певица.

Лит.: Grifftib R., Marlene Dietrich, N. Y., 1959; Kobal J., Marlene Dietrich, [L.- N. Y., 1968].

В. А. Утилов.

ДИТХАПНИ, Дитхапри, Читхапни, Читхапри, остатки древнего поселения в провинции Хванхэ-Пукто (КНДР). Открыто в 1957 (археолог Хун Цин Юй). Осн. слои относятся к неолиту. Обнаружены землянки и полуземлянки квадратных очертаний с ямами и крупными сосудами для хранения пищи; различные каменные орудия и оружие: топоры (прямоугольные и линзовидные в сечении), наконечники стрел и копий, зернотёрки, грузила. Керамика - круглодонная, с гребенчатым орнаментом ("ёлочка" и ряды штрихов). Находки зёрен проса, кам. лемехов и серпов свидетельствуют о занятии земледелием. В слоях эпохи бронзы найдены гладкие сосуды с ручками, фрагменты кам. кинжалов и звёздчатых палиц.

Лит.: Воробьев М. В., Древняя Корея, М., 1961, с. 16.

ДИТЦ Отто Германович [17(29). 11.1876, Вышний Волочёк,-17.12.1957, Ленинград], советский геодезист. Окончил Геодезич. отделение Академии Генштаба (1909). Преподавал в Военно-топографич. уч-ще и в Петербургском (Ленинградском) политехнич. ин-те (с 1910), где заведовал кафедрой геодезии. Принимал участие в геодезич. работах при постройке гидростанций на Днепре, Свири, Туломе, Вуоксе, Беломорско-Балтийском канале. Способствовал внедрению в практику геодезич. работ фотограмметрии и точных измерений методом интерференции света. Награждён орденом Трудового Красного Знамени и медалями.

Лит.: Отто Германович Дитц (к восьмидесятилетию со дня рождения), "Геодезия и картография", 1957, № 3, с. 69 - 72; там же, 1958, № 4, с. 58 - 59.

ДИТЯТИН Иван Иванович [1847, Петербург,- 29.10(10.11).1892, Дерпт, ныне Тарту], русский историк права и государствовед. Окончил Петерб. ун-т (1870). За 1-й т. труда "Устройство и управление городов России" - "Города России в XVIII ст." (1875)- Д. присвоена степень магистра гос. права, т. 2 - "Городское самоуправление до 1870г." (1877) - защищён Д. как докторская диссертация. В 1875-78 проф. Ярославского лицея, в 1878-87 проф. Харьковского ун-та, в 1889 Дерптского ун-та. Исходя из концепции государственной школы, воспринятой от А. Д. Грановского, утверждал определяющую роль надклассового гос-ва и в возникновении, и существовании городов, что приводило к недооценке роли городов и уровня их развития в России, а также к ложному тезису об искусств, насаждении городов гос. властью. В защите идеи самоуправления, в противовес бюрократич. регламентированию, проявились прогрессивные взгляды Д. Заслуга Д. состоит в самой постановке науч. вопросов, связанных с историей городов 18-19 вв.

ДИУ (Diu), низменный остров в Аравийском м., у юж. оконечности п-ова Катхиявар. Дл. ок. 13 км, пл. 52 км². На вост. берегу - город и порт Диу. С 1535 по 1961 терр. Д. была колонией Португалии. С 1962- часть территории центр. подчинения Гоа, Даман и Диу в Индии.

ДИУРБЕЛЬ (Diourbel), город на 3. Сенегала. 28,5 тыс. жит. (1965). Произ-во растит, масла. Центр с.-х. р-на (гл. обр. посевы арахиса, а также проса, сорго, маниока; кр. рог. скот).

ДИУРЕТИН, лекарственный препарат; то же, что темисал.

ДИУРОН, хим. препарат для борьбы с сорными растениями в посевах хлопчатника; см. Гербициды.

ДИФЕНИЛ, С₆Н₃-С₆Н₅, бесцветные кристаллы; t_пл71 °С, t_киn 254-255 °С. Д. нерастворим в воде, хорошо растворим в органических растворителях; содержится в антраценовом масле, выделяемом из кам.-уг. смолы. В пром-сти его получают дегидрированием бензола при 750-800 "С.

Д.- полупродукт в произ-ве нек-рых красителей; в смеси с дифениловым эфиром (73,5%) применяется как высокотемпературный теплоноситель, известный под названием "даутерм"

ДИФЕНИЛАМИН, ароматич. амин, С₆Н₅МНС6Н₅; бесцветные, темнеющие на свету кристаллы со слабым характерным запахом; t_пл 54 °С, t_кип, 302 °С. Д. нерастворим в воде, растворим в большинстве органических растворителей. В пром-сти Д. получают при нагревании анилина С₆Н₅NН₂ и солянокислого анилина при 200-230 °С. Д. применяют в произ-ве красителей и многих органич. полупродуктов (акридина, карбазола и др.), как стабилизатор пироксилиновых порохов, для колориметрич. определения нек-рых окислителей (напр., азотной и азотистой кислот).

ДИФЕНИЛОВЫЙ ЭФИР, дифенилоксид, простой ароматич. эфир, С₆Н₃-О-С₆Н₅; бесцветные кристаллы с запахом герани; t_пл 26-27 °С, t_кип 259 °С. Д. э. нерастворим в воде, растворим в органич. растворителях. В пром-сти Д. э. получают при нагревании хлорбензола с фенолятом калия в присутствии порошкообразной меди при 210 °С.

Д. э. применяют для составления парфюмерных композиций и отдушек мыла; в смеси с дифенилом (26,5% ) используют как высокотемпературный теплоноситель под назв. "даутерм".

ДИФЕНИЛХЛОРАРСИН, хлорангидрид дифенилмышъяковистой кислоты, (C₆H₃)2AsCl; бесцветные кристаллы; t_пл ~38 °С, t_кип 333 °С, плотность 1,3870 г/см³ (42 °С), показатель преломления n⁵⁶_D 1,6332. Д. нерастворим в воде, хорошо растворяется в большинстве органич. растворителей; легко реагирует с водой и щелочами, достаточно легко окисляется. Д. получают восстановлением дифенил-мышьяковой к-ты (C₆H₅)₂AsO(OH) сернистым газом в растворе концентрированной соляной к-ты.

Д. в виде дыма или паров раздражает верхние дыхательные пути, вызывая неудержимое чихание и кашель (непереносимая концентрация 1 мг/м³). Его широко использовала Германия во время 1-й мировой войны как отравляющее вещество под шифром "Кларк I".

Лит. см. при ст. Дифосген.

ДИФЕНИЛЦИАНАРСИН, цианангидрид дифенилмышьяковистой кислоты, (СиНзЪАзСМ; бесцветные кристаллы; t_пл 31,5 °С, t_кип 346 °С, плотность 1,3160 г/см³ (52 °С), показатель преломления n⁵⁶_D 1,6153. Д. нерастворим в воде, хорошо растворяется в органич. растворителях; довольно быстро гидролизуется горячей водой; сравнительно легко окисляется. Д. получают гл. обр. из дифенилхлорарсина (обменная реакция с цианистым натрием).

Д. в виде паров или дыма сильно раздражает верхние дыхательные пути (непереносимая концентрация 0,25 мг/м³). Его применяла Германия во время 1-й мировой войны как отравляющее вещество под шифром "Кларк II".

Лит. см. при ст. Дифосген.

ДИФЕНИН, дилантин, лекарственное средство из группы противосудорожных средств. Назначают в таблетках при лечении эпилепсии и при нарушении сердечного ритма.

ДИФИЛЛОБОТРИОЗ, глистное заболевание, вызываемое паразитированием в организме человека и нек-рых животных ленточных червей (Diphyllobothrium).

Д. человека. Человека наиболее часто поражает т. н. лентец широкий, достигающий 10-12 м длины. Половозрелые гельминты паразитируют в тонком кишечнике; при нек-рых Д. личинки - плероцеркоиды, обитают в подкожной клетчатке и внутр. органах, вызывая заболевание - спарганоз. Заражение происходит при употреблении в пищу свежепосоленной икры, сырой или полусырой рыбы, в мускулатуре и внутр. органах к-рой паразитируют плероцеркоиды. При Д. в организме происходят механич. и токсич. раздражения нервных окончаний кишечника; в результате поступления в кровь больного продуктов обмена лентецов развиваются аллергич. реакции. Иногда при Д. может развиться пернициозная анемия.

Д. проявляется слабостью, сердцебиением, потерей аппетита, болями в животе, поносами, головной болью, головокружением, бессонницей. Профилактика: не допускать загрязнение водоёмов фекалиями; запрещается употреблять в пищу сырую, плохо прожаренную или проваренную рыбу, а также свежепосоленную икру пресноводных рыб. Лечение: противоглистные препараты.

А. И. Кротов.

Д. животных. Д. наблюдается у пушных зверей, домашних и диких плотоядных; на территории СССР регистрируется в Прибалтике, Ленинградской, Архангельской, Тюменской обл., Карельской и Якутской АССР, на Чукотке, о. Сахалин и нек-рых др. р-нах. Продолжительность паразитирования лентеца широкого у собак, лисиц и песцов - от 1 месяца до 1,5 лет. Повреждая кишечную стенку, паразиты нарушают работу желудочно-кишечного тракта. У щенков пушных зверей часто при Д. наблюдаются различные расстройства нервной системы (сонливость, припадки и др.). В основе развития дифиллоботриоэной анемии лежит эндогенный авитаминоз - дефицит в организме больных животных витамина Bt2 и, возможно, фолиевой к-ты. При лечении применяютареколин, экстракт мужского папоротника, семена тыквы и др. Профилактика: возможность заражения Д. исключается при варке, вакуумной сушке, промораживании в холодильниках и посоле рыбы, употребляемой для кормления животных.

ДИФИОДОНТИЗМ (от ди... и греч. phyo - произвожу, возникаю и odiis, род. падеж odontos - зуб), однократная смена зубов в течение жизни организма, наблюдаемая у большинства млекопитающих и человека. См. Зубы.

ДИФИРАМБ (греч. dithyrambos), жанр античной лирики; возник, по-видимому, в Др. Греции как хоровая песнь, гимн в честь бога виноградной лозы и виноделия Диониса, или Вакха (позднее - др. богов и героев); сопровождался оргиастич. (исступлённым) танцем; имел зачатки диалога (между запевалой и хором), способствовал возникновению греч. драмы. Литературно оформился в 7 в. до н. э. (у Ариона-поэта и музыканта с о. Лесбос). Расцвет Д. - 6-5 вв. до н. э. (поэзия Симонида Кеосского, Пин дара, Бакхилида); Д. сохранились лишь в отрывках. В новой европ. лит-ре встречаются подражания древнему Д. (у ф. Шиллера, В. Мюллера, И. Гердера, сатирическому Д.- у Ф. Ницше и др.).

В переносном смысле Д. - чрезмерная похвала.

Лит.: Голосовкер Я. Э., Лирика древней Эллады, [пер. с древнегреч.], М.- Л., 1935 (есть перевод Д. "Тезей" Бакхилида); Радциг С. И., История древнегреческой литературы, 2 изд., М., 1959.

ДИФИЦЕРКНЫЙ, дифицеркальный (от ди... и греч. phyo - произвожу, возникаю и kerkos - хвост), хвостовой плавник кистепёрых и двоякодышащих рыб, в к-ром осевой скелет проходит до заднего края плавниковой пластинки, разделяя её на симметричные верхнюю и нижнюю лопасти. В филогенезе возникает путём вторичного выпрямления скелетной оси гетероцеркного плавника и усиления его верхней лопасти.

ДИФМАНОМЕТР, дифференциальный манометр, прибор для измерения разности (перепада) давлений; применяется также для измерений уровня жидкостей и расхода жидкости, пара или газа по методу перепада давлений. По принципу действия различают Д.: жидкостные, в к-рых измеряемое давление или разрежение уравновешивается столбом жидкости, и механические, в к-рых давление уравновешивается силами упругости различных чувствит. элементов -мембраны, пружины, сильфона. Упругая деформация чувствит. элемента - величина, пропорциональная измеряемому давлению.

Жидкостные Д. разделяются на трубные, поплавковые, кольцевые и колокольные. Трубные Д. бывают двухтрубные (U-ооразные) и однотрубные (с сосудом и вертикальной трубкой и с сосудом и наклонной трубкой, служащей для увеличения точности отсчёта при измерении малых величин). Действие двухтрубного Д. (рис. 1) основано на использовании сообщающихся сосудов, заполненных жидкостью, столб к-рой одновременно является гидравлич. затвором и создаёт гидростатич. давление, противодействующее измеряемому. Один конец U-образной трубки, заполненной жидкостью, соединяют с замкнутым пространством, в к-ром надо измерить избыточное давление, а второй остаётся открытым (под барометрич. давлением). Разность уровней жидкости в трубках показывает избыточное давление р_изб = р_абс - Р_бар = р; р = hpg, где h - разность уровней жидкости, р - плотность заполняющей жидкости, д - ускорение свободного падения. Уравнение для однотрубного Д. с сосудом и вертикальной трубкой (рис. 2) аналогично уравнению для двухтрубного Д. Величина перемещения жидкости в трубке однотрубного Д. прямо пропорциональна измеряемому перепаду давлений и зависит от соотношения квадратов диаметров или площадей сечения трубки и сосуда: f/F = d²/D² .

Рис. 1. Двухтрубный U-образный дифманометр.

Рис. 2. Дифманометр с сосудом и вертикальной трубкой.

Чтобы упростить измерения, обычно принимают соотношение, при к-ром h₂ будет отличаться от h₁не более чем на 1%; поэтому величиной h₁ пренебрегают и отсчёт производят только по уровню жидкости в трубке. Для исключения погрешности шкала изготовляется с делениями, равными не 1 мм, а меньше (0,9 мм). Диапазон измерений U-образных Д. до 93 кн/м² (700 мм рт. ст.) при давлении среды до 15 Мн/м² (150 кгс/см²). Точность отсчёта в двух трубках ±1 мм.

Поплавковый Д. по принципу действия аналогичен однотрубному Д. с сосудом и вертикальной трубкой, только для измерения служит поплавок, передающий изменение уровня жидкости в сосуде на стрелку прибора. Диапазон измерения перепадов давления от 0 до 133 кн/м² (от 0 до 1000 мм рт. ст.), при давлении среды до 16 Мн/м² (160 кгс/см²). Осн. приведённая погрешность ± 1,5-2% .

Кольцевой Д., или "кольцевые весы", имеет чувствит. элемент в виде полого кольца с перегородкой (рис. 3). В нижней части кольца, заполненного жидкостью (вода, масло, ртуть), укреплён компенсационный груз. При p₁ = p% уровень жидкости в обеих частях кольца одинаков, а центр тяжести груза находится на вертикальной оси, проходящей через центр кольца. При p₁ > p₂ жидкость в левой части опустится, а в правой поднимется. Усилие, создаваемое действием разности давлений на перегородку, вызывает момент, стремящийся повернуть кольцо по часовой стрелке. Диапазон измерения перепадов давлений: для низкого давления (с водяным заполнением) до 1,6 кн/м² (160 кгс/м²) при давлении среды до 150 кн/м² (15 000 кгс/м²); для среднего (с ртутным заполнением) - до 33 кн/м² (250 мм рт. ст.) при давлении среды 3,2 Мн/м² (32 кгс/см²). Осн. приведённая погрешность ± 0,5-1,5%.

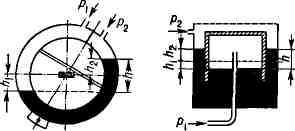
Рис. 3. Схема кольметра. Рис. 4. Схема кольцевого колокольного дифманометра.

Колокольный Д. (рис. 4) представляет собой колокол, погружённый в жидкость и перемещающийся под влиянием разности давлений внутри (большее) и снаружи (меньшее) колокола. Противодействующая измеряемому давлению сила создаётся утяжелением колокола (гидростатич. уравновешивание) или деформацией пружины, на к-рой подвешивается колокол (механич. уравновешивание). Диапазон измерения перепада давлений от 40 н/м²до 4 кн/м² (от 4 до 400 кгс/м²) при давлении среды от 10 кн/м² до 0,3 Мн/м² (от 1000 кгс/м² до 3 кгс/см²).

Механические Д. разделяются на мембранные с плоской упругой металлич. мембраной (рис. 5) и с неметаллич. мембраной и сильфонные. В мембранных Д. упругая металлич. мембрана прогибается под влиянием измеряемого давления, по величине прогиба определяют давление. В нек-рых конструкциях Д. мембрана служит только для разделения камер. Противодействующую силу при деформации создаёт тарированная цилиндрич. спиральная пружина, к-рая разгружает мембрану. Нек-рые мембранные Д. имеют защиту от односторонней перегрузки и могут применяться для измерения не только перепадов, но и избыточных давлений. Диапазон измерения давления от 0 до 6,3 кн/м² (0-630 кгс/м²) и от 0,16 до 0,63 Мн/м² (1,6-6,3 кгс/см²); диапазон перепада давлений до 133 кн/м² (1000 мм рт. ст.) при макс, давлении среды до 60 Мн/м² (600 кгс/см²). Основная приведённая погрешность ± 1,5%. Д. с неметаллич. мембранами (из резины и т. п. материалов) имеют только цилиндрич. спиральную пружину, не воспринимают изгибающих моментов и сжимающих усилий и работают только на растяжение. Для увеличения перемещения они изготовляются гофрированными и имеют жёсткий центр, образованный двумя металлическими дисками. Диапазон измерений перепада давлений до 133 кн/м² (1000 мм рт. ст.) при давлении среды до 6,4 Мн/м² (64 кгс/см²). Осн. приведённая погрешность ± 1-2% .

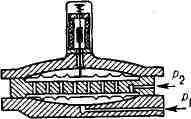
Рис. 5. Дифманометр с упругой мембраной и электрической передачей показаний.

Сильфонные Д. имеют чувствит. элемент - гофрированную металлич. коробку (сильфон) с тарированной цилиндрич. спиральной пружиной. Сильфон разделяет полость Д. на две камеры. Большее давление подводится в полость над сильфоном, а меньшее - внутрь. Под действием разности давлений сильфон прогибается на величину, пропорциональную измеряемому давлению. Диапазон измерений до 25 хн/м² (2500 кгс/м²) при давлении среды до 32 Мн/м² (320 кгс/см²). Осн. приведённая погрешность ±0,5-1% .

Поплавковые, кольцевые, колокольные и механич. Д. изготовляются показывающими, самопишущими и бесшкальными (с электрич. или пневматич. дистанционной передачей показаний), с электрич. контактным устройством. Д. для измерения расхода по методу переменного перепада выпускаются с интегрирующими и суммирующими устройствами. Дальнейшее развитие конструирования Д. идёт по пути усовершенствования механического Д.

Лит.: Кремлевский П. П., Расходомеры, 2 изд., М.- Л., 1963; Автоматизация, приборы контроля и регулирования производственных процессов в нефтяной и нефтехимической промышленности. Справочник, кн. 2, М., 1964.

Г. Г. Мирзабеков.

ДИФОСГЕН, трихлорметиловый эфир хлоругольной кислоты,

движная жидкость, слегка дымящая на воздухе, с характерным запахом прелого сена; t_пл -57 ^оС, t_кип 128 ^оС, d¹⁵₄ 1,644, показатель преломления n²⁰_D 1,4566. Д. плохо растворим в воде, очень хорошо - в органич. растворителях; медленно гидролизуется водой (гидролиз значительно ускоряется при нагревании и в присутствии щелочей). Д. энергично взаимодействует с аммиаком и аминами, образуя мочевину или её производные. Эта реакция может служить для дегазации Д. При 300-350 °С, а также в присутствииFеС1₃, А1С1₃ и др. галогенидов металлов Д. разлагается с образованием СОС1₂, СО, ССl₄ и др. Д. получают исчерпывающим хлорированием (при освещении) метилхлорформиата.

Д. обладает сильным удушающим и заметным раздражающим действием. Непереносимая концентрация 0,075 мг/л, смертельная 0,25 мг/л (при экспозиции 30 мин). При отравлении Д. характерно наличие скрытого периода действия (до 6-8 ч). Очень опасно длит, воздействие малых концентраций Д., суммарное действие к-рых может привести к тяжёлым поражениям организма (т. н. кумулятивный эффект). Д. использовался во время 1-й мировой войны как отравляющее вещество.

Лит.: Соборовский Л. З., Эпштейн Г. Ю., Химия и технология боевых химических веществ, М.-Л., 1939;Флюри Ф., Церник Ф., Вредные газы, М., 1938.

Р. Н. Стерлин.

ДИФОСФОПИРИДИНДИНУКЛЕОТИД (ДПН), кофермент ряда дегидрогеназ, рациональное хим. название - никотинамидадениндинуклеотид (НАД).

ДИФРАКЦИОННАЯ РЕШЁТКА, оптический прибор, представляющий собой совокупность большого числа параллельных, равноотстоящих друг от друга штрихов одинаковой формы, нанесённых на плоскую или вогнутую оптич. поверхность. Таким образом, Д. р. представляет собой периодич. структуру: штрихи с определённым и постоянным для данной решётки профилем повторяются через строго одинаковый промежуток d, наз. периодом Д. р. (рис.). В Д. р. происходит дифракция света.

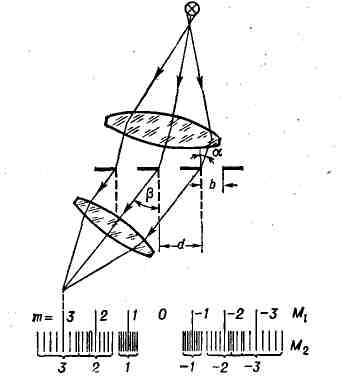
Схема образования спектров прозрачной дифракционной решётки, состоящей из щелей, при освещении её монохроматическим светом (M₁j) и светом сложного спектрального состава (М₂).

Осн. свойство Д. р.- способность разлагать падающий на неё пучок света по длинам волн, т. е. в спектр, что используется в спектральных приборах. Если штрихи нанесены на плоскую поверхность, то Д. р. наз. плоскими, если на вогнутую (обычно сферическую) поверхность - вогнутыми. Различают отражательные и прозрачные Д. р. У отражательных штрихи наносятся на зеркальную (обычно металлич.) поверхность и наблюдение ведётся в отражённом свете. У прозрачных штрихи наносятся на поверхность прозрачной (обычно стеклянной) пластинки (или вырезаются в виде узких щелей в непрозрачном экране) и наблюдение ведётся в проходящем свете. В совр. спектральных приборах применяются гл. обр. отражат. Д. р.

Наиболее наглядно описание действия Д. р. в случае прозрачной Д. р. При падении монохроматич. параллельного пучка света с длиной волны X под углом а на Д. р., состоящую из щелей ширины b, разделённых непрозрачными промежутками, происходит интерференция волн, исходящих от разных щелей. В результате после фокусировки положения максимумов на экране (рис.) определяются уравнением: d (sin a + sin В) = mX, где Р - угол между нормалью к решётке и направлением распространения пучка (угол дифракции); целое число т = 0, ±1, ± 2, ± 3, ... равно кол-ву длин волн, на к-рое волна от нек-рого элемента данной щели Д. р.отстаёт от волны, исходящей от такого же элемента соседней щели (или опережает её). Монохроматич. пучки, относящиеся к различным значениям га, наз. порядками спектра, а даваемые ими изображения входной щели - спектральными линиями. Все порядки, соответствующие положит. и отри-цат. значениям т, лежат симметрично относительно нулевого. По мере возрастания числа щелей Д. р. спектральные линии становятся более узкими и резкими. Если на Д. р. падает излучение сложного спектрального состава, то для каждой длины волны получится свой набор спектральных линий и, следовательно, излучение будет разложено в спектры по числу возможных значений т. Относит, интенсивность линий определяется функцией распределения энергии от отдельной щели.

Основными характеристиками Д. р. являются угловая дисперсия и разрешающая способность. Угловая дисперсия, определяющая угловую ширину спектра, зависит от отношения разности углов дифракции для двух длин волн:

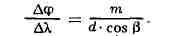
Т. о., угловая ширина спектров изменяется приблизительно пропорционально номеру порядка спектра. Разрешающая способность R измеряется отношением длины волны к наименьшему интервалу длин волн, к-рый ещё может разделить решётка:

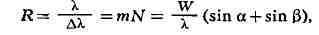
где N - число щелей Д. p., a W - ширина заштрихованной поверхности. При заданных углах разрешающая способность может быть повышена только за счёт увеличения ширины Д. р.

Д. р., применяемые для работы в различных областях спектра, отличаются частотой и профилем штрихов, размерами, формой, материалом поверхности и др. Для ультрафиолетовой и видимой областей наиболее типичны Д. р., имеющие от 300 до 1200 штрихов на 1 мм. Штрихи этих Д. р. выполняют в слое алюминия, предварительно нанесённом на стеклянную поверхность испарением в вакууме. Д. р. для вакуумной ультрафиолетовой области изготавливаются преим. на стеклянных поверхностях. В этой области незаменимы Д. р., изготовленные на вогнутых (в большинстве случаев - сферических) поверхностях, обладающих способностью фокусировать спектр. В инфракрасной области применяются Д. р., наз. эшелеттами, к-рые имеют от 300 до 0,3 штрихов на 1 мм и выполняются на различных мягких металлах.

Кроме спектральных приборов, Д. р. применяются также в качестве оптич. датчиков линейных и угловых перемещений (измерительные Д. р.), поляризаторов и фильтров инфракрасного излучения, делителей пучков в интерферометрах и для др. целей. В СССР изготовляются все известные виды Д. р. Макс, количество штрихов на 1 мм составляет 2400, а макс, размер заштрихованной поверхности равен 300 X 300 мм.

Лит.: Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Курс общей физики, т. 3); Тарасов К. И., Спектральные приборы. Л., 1968. См. также лит. при ст. Дифракция света.

Ф. М. Герасимов .

ДИФРАКЦИЯ (от лат. diffractus - разломанный) волн, явления, наблюдаемые при прохождении волн мимо края препятствия, связанные с отклонением волн от прямолинейного распространения при взаимодействии с препятствием. Из-за Д. волны огибают препятствия, проникая в область геометрич. тени. Именно Д. звуковых волн объясняется возможность слышать голос человека, находящегося за углом дома. Дифракцией радиоволн вокруг поверхности Земли объясняется приём радиосигналов в диапазоне длинных и средних радиоволн далеко за пределами прямой видимости излучающей антенны.

Д. волн - характерная особенность распространения волн независимо от их природы. Объяснить Д. в первом приближении можно, применив Гюйгенса - Френеля принцип. Согласно этому принципу, рассматривая распространение к.-л. волны, можно каждую точку среды, к-рой достигла эта волна, считать источником вторичных волн. Поэтому, поставив на пути волн экран с малым отверстием (диаметр порядка длины волны), получим в отверстии экрана источник вторичных волн, от которого распространяется сферическая волна", попадая и в область геометрич. тени. Если имеется экран с двумя малыми отверстиями или щелями, дифрагирующие волны накладываются друг на друга и в результате интерференции волн дают чередующееся в пространстве распределение максимумов и минимумов амплитуды результирующей волны с плавными переходами от одного к другому. С увеличением количества щелей максимумы становятся более узкими. При большом количестве равноотстоящих щелей (дифракционная решётка) получают резко разделённые направления взаимного усиления волн.

Д. волн существенно зависит от соотношения между длиной волны X и размером объекта, вызывающего Д. Наиболее отчётливо Д. обнаруживается в тех случаях, когда размер огибаемых препятствий соизмерим с длиной волны. Поэтому легко наблюдается Д. звуковых, сейсмических и радиоволн, для к-рых это условие обычно всегда выполняется (Х~от м до км), и гораздо труднее наблюдать без спец. устройств дифракцию света (Х~400-750 нм). Эта же причина приводит к многим технич. трудностям при изучении волновых свойств др. объектов. Так, поскольку рентгеновские лучи имеют длину волны от сотен до 0,0001 А, дифракц. решётку с таким расстоянием между щелями изготовить невозможно, поэтому нем. физик М. Лауэ для изучения дифракции рентгеновских лучей использовал в качестве дифракционной решётки кристалл, в к-ром атомы (ионы) расположены в правильном порядке.

Д. волн сыграла большую роль в изучении природы микрочастиц. Экспериментально было установлено, что при прохождении микрочастиц (напр., электронов) через среду (газ, кристалл) наблюдается Д. Дифракция частиц является следствием того, что микрочастицы обладают двойственной природой (т. н. корпускулярно-волновым дуализмом): в одних явлениях поведение микрочастиц может быть объяснено на основе представления о частицах, в других, как, напр., в явлениях Д., на основе представления о волнах. Согласно квантовой механике, каждой частице соответствует т. н. волна де Бройля, длина к-рой зависит от энергии частицы. Так, электрону с энергией 1 эв соответствует волна де Бройля длиной того же порядка, что и размер атома. Д. электронов и нейтронов широко пользуются для изучения строения вещества.
В. Н. Парыгин.

ДИФРАКЦИЯ АТОМОВ И МОЛЕКУЛ, см. Дифракция частиц.

ДИФРАКЦИЯ НЕЙТРОНОВ, см. Дифракция частиц.

ДИФРАКЦИЯ РАДИОВОЛН, явления, возникающие при встрече радиоволн с препятствиями. Радиоволна, встречая при распространении в однородной среде препятствие, изменяется по амплитуде и фазе и проникает в область тени, отклоняясь от прямолинейного пути. Это явление, аналогичное дифракции света, называется Д. р. В реальных случаях распространения радиоволн препятствия могут иметь произвольную форму и быть как непрозрачными, так и полупрозрачными для радиоволн.

Д. р. на сферич. поверхности Земли является одной из причин приёма радиосигналов за пределами прямой видимости, когда передатчик и приёмник разделены выпуклостью земного шара. Эффект дифракционного проникновения радиоволны в область тени, как и в оптич. случае, зависит от соотношения между размером препятствия и длиной волны и выражен тем сильнее, чем больше длина волны. С другой стороны, радиоволны, распространяясь вблизи полу проводящей поверхности Земли, затухают вследствие частичного поглощения энергии волны Землёй тем сильнее, чем короче волна. Поэтому дальность распространения т. н. земной волны существенно зависит от её длины. Достаточно длинные волны могут распространяться за счёт Д. р. на значит, расстояния, достигающие иногда неск. тысяч км.

Д. р. на отдельно стоящих зданиях и выпуклостях рельефа, расположенных вдоль трассы (горы и др.), также может играть полезную роль. Она вызывает перераспределение энергии волны и может привести к "усилению" радиосигнала за препятствием.

Особую роль играет дифракция при распространении радиоволн в средах, содержащих локальные неоднородности, напр. в ионосфере, где радиоволна встречает множество хаотически расположенных препятствий - облаков различной формы, отличающихся электрич. свойствами. Непрерывно происходящие изменения и движения неоднородностей вызывают изменения энергии сигнала в точке приёма - т. н. дифракционные замирания радиоволны.

Дифракционные явления могут быть существенными при излучении радиоволн направленными антеннами и при радиолокации сложных объектов.

Лит. см. при ст. Распространение радиоволн.

ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ, рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при к-ром из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта. Дифрагированные пучки составляют часть всего рассеянного веществом рентгеновского излучения. Наряду с рассеянием без изменения длины волны наблюдается рассеяние с изменением длины волны -т. н. комптоновское рассеяние (см. Комптона эффект). Явление Д. р. л., доказывающее их волновую природу, впервые было экспериментально обнаружено на кристаллах нем. физиками М. Лауэ, В. Фридрихом и П. Книппингом в 1912. Кристалл является естественной трёхмерной дифракционной решёткой для рентгеновских лучей, т. к. расстояние между рассеивающими центрами (атомами) в кристалле одного порядка с длиной волны рентгеновских лучей (~ 1А= = 10^-8 см). Д. р. л. на кристаллах можно рассматривать как избирательное отражение рентгеновских лучей от систем атомных плоскостей кристаллич. решётки (см. Брэгга - Вульфа условие). Направление дифракционных максимумов удовлетворяет одновременно трём условиям:

a (cos а - cos а₀) = НX,
b(cosВ--cosВ₀) = KX,
с (cos у-cos y₀) = LX

Здесь а, b, с-периоды кристаллической решётки по трём её осям; а₀, В₀, y₀ -углы, образуемые падающим, а а, В, y -рассеянным лучами с осями кристалла; Х - длина волны рентгеновских лучей, Н, К, L - целые числа. Эти уравнения наз. уравнениями Лауэ. Дифракционную картину получают либо от неподвижного кристалла с помощью рентгеновского излучения со сплошным спектром (т. н. лауэграмма; рис. 1), либо от вращающегося или колеблющегося кристалла (углы а_с, Зо меняются, a yo остаётся постоянным), освещаемого монохроматич. рентгеновским излучением (X - постоянно), либо от поликристалла, освещаемого мс~ нохроматич. излучением. В последнем случае, благодаря тому что отд. кристаллы в образце ориентированы произвольно, меняются углы а₀, В₀, y_0.

Рис. 1. Лауэграмма берилла.

Интенсивность дифрагированного луча зависит в первую очередь от т. н. структурного фактора, к-рый определяется атомными факторами атомов кристалла, их расположением внутри элементарной ячейки кристалла, а также характером тепловых колебаний атомов. Структурный фактор зависит от симметрии расположения атомов в элементарной ячейке. Интенсивность дифрагированного луча зависит также от размеров и формы объекта, от совершенства кристалла и пр.

Д. р. л. от поликристаллич. тел приводит к возникновению резко выраженных конусов вторичных лучей. Осью конуса является первичный луч, а угол раствора конуса равен 4 О (О - угол между отражающей плоскостью и падающим лучом). Каждый конус соответствует определённому семейству кристаллич. плоскостей. В создании конуса участвуют все кристаллики, семейство плоскостей к-рых расположено под углом ft к падающему лучу. Если кристаллики малы и их приходится очень большое количество на единицу объёма, то конус лучей будет сплошным. В случае текстуры, т. е. наличия предпочтительной ориентировки кристалликов, дифракционная картина (рентгенограмма) будет состоять из неравномерно зачернённых колец (см. также Дебая - Шеррера метод).

Метод Д. р. л. на кристаллах дал возможность определять длину волны рентгеновских лучей, если известна структура кристаллич. решётки, благодаря чему возникла рентгеновская спектроскопия, сыгравшая важную роль при установлении строения атома. Наблюдения Д. р. л. известной длины волны на кристалле неизвестной структуры позволяют установить характер этой структуры (расположение ионов, атомов и молекул, составляющих кристалл), что послужило основой рентгеновского структурного анализа.

Д. р. л. наблюдается также при рассеянии их аморфными твёрдыми телами, жидкостями и газами. В этом случае на кривой зависимости интенсивности от угла рассеяния вокруг центрального пятна появляются широкие кольца типа гало (рис. 2). Положение этих колец (угол в) определяется средним расстоянием между молекулами или расстояниями между атомами в молекуле. Из зависимости интенсивности от угла рассеяния можно определить распределение плотности вещества.
 

Рис. 2. Рентгенограмма воды.

Д. р. л. можно наблюдать также на обычной оптической дифракционной решётке при скользящем падении (меньше угла полного отражения) рентгеновских лучей на решётку. С помощью этого метода можно непосредственно и с большой точностью измерять длины волн рентгеновских лучей.

Лит.: Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Боровский И. Б., Физические основы рентгеноспектральных исследований, М., 1956.

В. И. Иверонова.

ДИФРАКЦИЯ СВЕТА, явления, наблюдающиеся при распространении света мимо резких краёв непрозрачных или прозрачных тел, сквозь узкие отверстия. При этом происходит нарушение прямолинейности распространения света, т. е. отклонение от законов геометрической оптики. Вследствие Д. с. при освещении непрозрачных экранов точечным источником света на границе тени, где, согласно законам геометрич. оптики, должен был бы происходить скачкообразный переход от тени к свету, наблюдается ряд светлых и тёмных дифракционных полос (рис. 1
и 2). Поскольку дифракция свойственна всякому волновому движению, открытие Д. с. в 17 в. итальянским физиком и астрономом Ф. Гримальди и её объяснение в начале 19 в. французским физиком О. Френелем явились одним из основных доказательств волновой природы света.

Рис. 1. Тень винта, окружённая дифракционными полосами.

Приближённая теория Д. с. основана на применении Гюйгенса-Френеля принципа. Для качественного рассмотрения простейших случаев Д. с. может быть применено построение зон Френеля. При прохождении света от точечного источника через небольшое круглое отверстие в непрозрачном экране (рис. 2, а) или вокруг круглого непрозрачного экрана (рис. 2, б) наблюдаются дифракционные полосы в виде концентрич. окружностей.
 

Рис. 2. Дифракционные кольца при прохождении света: а - через круглое отверстие; б - вокруг круглого экрана.

Если отверстие оставляет открытым чётное число зон, то в центре дифракционной картины получается тёмное пятнышко, при нечётном числе зон - светлое. В центре тени от круглого экрана, закрывающего не слишком большое число зон Френеля, получается светлое пятнышко.

Различают 2 случая Д. с. - дифракция сферич. волны, при к-рой размер отверстия сравним с размером зоны Френеля, т. е. b~КОРЕНЬ(zX), где b -размер отверстия, z - расстояние точки наблюдения от экрана, X - длина волны (дифракция Френеля), и Д. с. в параллельных лучах, при к-рой отверстие много меньше одной зоны Френеля, т. е. b<<КОРЕНЬ(zX) (дифракция Фраунгофера). В последнем случае при падении параллельного пучка света на отверстие пучок становится расходящимся с углом расходимости ф ~ Х/b (дифракционная расходимость).

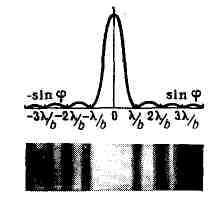
Рис. 3. Дифракция Фраунгофера на щели.

Большое практич. значение имеет случай Д. с. на щели. При освещении щели параллельным пучком монохроматич. света на экране получается ряд тёмных и светлых полос, быстро убывающих по интенсивности. Если свет падает перпендикулярно к плоскости щели, то полосы расположены симметрично относительно центральной полосы (рис. 3), а освещённость меняется вдоль экрана периодически с изменением ф, обращаясь в нуль при углах ср, для к-рых sin ф = m Х/b (m = = 1,2,3,...). При промежуточных значениях освещённость достигает макс, значений. Главный максимум имеет место при m=0, при этом sin ф = 0, т. е. ф = 0. Следующие максимумы, значительно уступающие по величине главному, соответствуют значениям ф, определённым из условий: sin = l,43X/b; 2.46Х/6b; 3,47 Х/b и т. д.

С уменьшением ширины щели центральная светлая полоса расширяется, а при данной ширине щели положение минимумов и максимумов зависит от X, т. е. расстояние между полосами тем больше, чем больше X. Поэтому в случае белого света имеет место совокупность соответствующих картин для разных цветов. При этом главный максимум будет общим для всех X и представится в виде белой полоски, переходящей в цветные полосы с чередованием цветов от фиолетового к красному.

Если имеются 2 идентичные параллельные щели, то они дают одинаковые накладывающиеся друг на друга дифракционные картины, вследствие чего максимумы соответственно усиливаются, а кроме того, происходит взаимная интерференция волн от первой и второй щелей, значительно осложняющая картину. В результате минимумы будут на прежних местах, т. к. это те направления, по к-рым ни одна из щелей не посылает света. Кроме того, возможны направления, в к-рых свет, посылаемый двумя щелями, взаимно уничтожается. Т. о., прежние минимумы определяются условиями: b sin ф = X, 2Х, ЗХ, . ., добавочные минимумы d sin ф = = Х/2, ЗХ/2, 5Х/2, ... (d - размер щели b вместе с непрозрачным промежутком а), главные максимумы d sin ф = 0,Х, 2Х, ЗХ, ..., т. е. между двумя главными максимумами располагается один добавочный минимум, а максимумы становятся более узкими, чем при одной щели. Увеличение числа щелей делает это явление ещё более отчётливым (см. Дифракционная решётка).

Д. с. играет существенную роль при рассеянии света в мутных средах, напр. на пылинках, капельках тумана и т. п. На Д. с. основано действие спектральных приборов с дифракционной решёткой (дифракционных спектрометров). Д. с. определяет предел разрешающей способности оптич. приборов (телескопов, микроскопов и др.). Благодаря Д. с. изображение точечного источника (напр., звезды в телескопе) имеет вид кружка с диаметром Xf/D, где D - диаметр объектива, a f - его фокусное расстояние. Расходимость излучения лазеров также определяется Д. с. Для уменьшения расходимости лазерного пучка его преобразуют в более широкий пучок при помощи телескопа, и тогда расходимость излучения определяется диаметром D объектива по формуле ф~Х/О.

Лит.: Ландсберг Г. С.. Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Горелик Г. С., Колебания и волны, 2 изд., М., 1959, гл. 9.

ДИФРАКЦИЯ ЧАСТИЦ, рассеяние микрочастиц (электронов, нейтронов, атомов и т. п.) кристаллами или молекулами жидкостей и газов, при к-ром из начального пучка частиц данного типа возникают дополнит, отклонённые пучки этих частиц; направление и интенсивность таких отклонённых пучков зависят от строения рассеивающего объекта.

Д. ч. может быть понята лишь на основе квантовой теории. Дифракция - явление волновое, оно наблюдается при распространении волн различной природы: дифракция света, звуковых волн, волн на поверхности жидкости и т. д. Дифракция при рассеянии частиц, с точки зрения классич. физики, невозможна.

Квантовая механика устранила абс. грань между волной и частицей. Осн. положением квантовой механики, описывающей поведение микрообъектов, является корпускулярно-волновой дуализм, т. е. двойственная природа микрочастиц. Так, поведение электронов в одних явлениях, напр. при наблюдении их движения в камере Вильсона или при измерении электрич. заряда в фотоэффекте, может быть описано на основе представлений о частицах, в других же, особенно в явлениях дифракции,- только на основе представления о волнах. Идея "волн материи" была высказана франц. физиком Л. де Бройлем в 1924 и вскоре получила блестящее подтверждение в опытах по Д. ч.

Согласно квантовой механике, свободное движение частицы с массой т и импульсом р = mv (где v - скорость частицы) можно представить как плоскую монохроматич. волну w₀ (волну де Бройля) с длиной волны Х = h/p, (1) распространяющуюся в том же направлении (напр., в направлении оси x), в к-ром движется частица (рис. 1). Здесь h - Планка постоянная. Зависимость w₀от координаты х даётся формулой

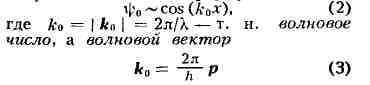
направлен в сторону распространения волны, или вдоль движения частицы.

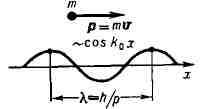
Рис. 1. Сопоставление волны и свободно движущейся частицы. Вверху показано прямолинейное движение частицы с массой m и импульсом p=mv (v - скорость частицы), внизу - распространение соответствующей ей "материальной волны" w₀ ~COS k₀x с длинной волны X = h/p.

Т. о., волновой вектор монохроматич. волны, связанной со свободно движущейся микрочастицей, пропорционален её импульсу или обратно пропорционален длине волны.

Поскольку кинетич. энергия сравнительно медленно движущейся частицы Е = mv²/2, длину волны можно выразить и через энергию:

При взаимодействии частицы с нек-рым объектом - с кристаллом, молекулой и т. п. - её энергия меняется: к ней добавляется потенциальная энергия этого взаимодействия, что приводит к изменению движения частицы. Соответственно меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений. Поэтому основные геометрич. закономерности Д. ч. ничем не отличаются от закономерностей дифракции любых волн (см. Дифракция волн). Общим условием дифракции волн любой природы является соизмеримость длины падающей волны X с расстоянием d между рассеивающими центрами: X~<d. Опыты по дифракции частиц и их квантовомеханическая интерпретация. Первым опытом по Д. ч., блестяще подтвердившим исходную идею квантовой механики - корпускулярно-волновой дуализм, явился опыт амер. физиков К. Дэвиссона и Л. Джермера (1927) по дифракции электронов на монокристаллах никеля (рис. 2). Если ускорять электроны электрич. полем с напряжением V, то они приобретут кинетич. энергию Е = eV (е - заряд электрона), что после подстановки в равенство (4) числовых значений лает

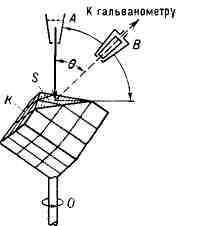
Рис. 2. Схема впыта Дэвиссона - Джермера: К-монокристалл никеля; Л - источник электронов; В - приёмник электронов; О-угол отклонения электронных пучков. Пучок электронов падает перпендикулярно отшлифованной плоскости кристалла S. При поворотах кристалла вокруг оси О гальванометр, присоединённый к приёмнику В, даёт периодически возникающие максимумы.

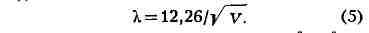
Здесь V выражено в в, а X - в А (1А = = 10-⁸с.м). При напряжениях V порядка 100 в, к-рые использовались в этих опытах, получаются т. н. "медленные" электроны с X порядка lA. Эта величина близка к межатомным расстояниям d в кристаллах, к-рые составляют неск. А и менее, и соотношение X~<d, необходимое для возникновения дифракции, выполняется. Кристаллы обладают высокой степенью упорядоченности. Атомы в них располагаются в трёхмерно-периодической кристаллич. решётке, т. е. образуют пространственную дифракционную решётку для соответствующих длин волн. Дифракция волн на такой решётке происходит в результате рассеяния на системах параллельных кристаллографич. плоскостей, на к-рых в строгом порядке расположены рассеивающие центры. Условием наблюдения дифракционного максимума при отражении от кристалла является Брэгга - Вулъфа условие:

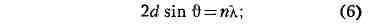
здесь 6 - угол, под к-рым падает пучок электронов на данную кристаллографич. плоскость (угол скольжения), a. d - расстояние между соответствующими кристаллографич. плоскостями.

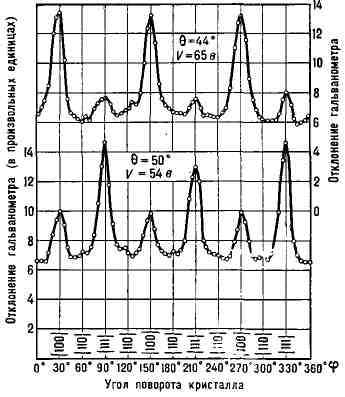
Рис. 3. Запись дифракционных максимумов в опыте Дэвиссона-Джермера по дифракции электронов при различных углах поворота кристалла ф для двух значений угла отклонения электронов в и двух ускоряющих напряжений V. Максимумы отвечают отражению от различных кристаллографич. плоскостей, индексы которых указаны в скобках.

В опыте Дэвиссона и Джермера при "отражении" электронов от поверхности кристалла никеля при определённых углах отражения возникали максимумы (рис. 3). Эти максимумы отражённых пучков электронов соответствовали формуле (6), и их появление не могло быть объяснено никаким другим путём, кроме как на основе представлений о волнах и их дифракции; т. о., волновые свойства частиц - электронов - были доказаны экспериментом.

При более высоких ускоряющих электрич. напряжениях (десятках кв) электроны приобретают достаточную кинетич. энергию, чтобы проникать сквозь тонкие плёнки вещества (толщиной порядка 10-⁵см, т. е. тысячи А). Тогда возникает т. н. дифракция быстрых электронов на прохождение (рис. 4), к-рую на поликристаллич. плёнках алюминия и золота впервые исследовали английский учёный Дж. Дж. Томсон и советский физик П. С. Тартаковский.

Рис. 4. Дифракционная картина, образованная пучком электронов (ускоряющее напряжение 60 кв, Х=0,05 А) при прохождении через монокристальную плёнку моногидрата, хлористого бария. Центральное пятно-след начального пучка, остальные пятна-следы пучков, дифрагированных различными системами плоскостей кристалла.
 

Вскоре после этого удалось наблюдать и явления дифракции атомов и молекул. Атомам с массой М, находящимся в газообразном состоянии в сосуде при абс. темп-ре Т, соответствует, по формуле (4), длина волны

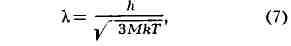
где k - Больцмана постоянная (т. к. средняя кинетическая энергия атома Е =³/₂kT). Для лёгких атомов и молекул (Н, Н₂, Не) и темп-р в сотни градусов Кельвина длина волны X также составляет около lA. Дифрагирующие атомы или молекулы практически не проникают в глубь кристалла; поэтому можно считать, что их дифракция происходит при рассеянии от поверхности кристалла, т. е. как на плоской дифракционной решётке.

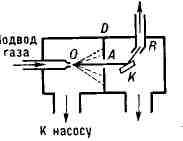
Рис. 5. Принципиальная схема прибора для исследования дифракции атомных или молекулярных пучков: А - атомный или молекулярный пучок; К - кристалл; О - капилляр, подводящий газ; D - диафрагма; R - приёмник, соединённый с манометром. Манометр измеряет давление, созданное дифрагированным пучком.

Выпущенный из сосуда и сформированный с помощью диафрагм молекулярный или атомный пучок (см. Молекулярные пучки) направляют на кристалл и тем или иным способом фиксируют "отражённые" дифракционные пучки (рис. 5). Таким путём немецкие учёные О. Штерн и И. Эстерман, а также др. исследователи на рубеже 30-х гг. наблюдали дифракцию атомных и молекулярных пучков (рис. 6).

Позже наблюдалась дифракция протонов, а также дифракция нейтронов (рис. 7), получившая широкое распространение как один из методов исследования структуры вещества.

Так было доказано экспериментально, что волновые свойства присущи всем без исключения микрочастицам.

В широком смысле слова дифракционное рассеяние всегда имеет место при упругом рассеянии различных элементарных частиц атомами и атомными ядрами, а также друг другом. С другой стороны, представление о корпускулярно-волновом дуализме материи укрепилось при анализе явлений, всегда считавшихся типично волновыми, напр, дифракции рентгеновских лучей - коротких электромагнитных волн с длиной волны X ~ "0,5-5А. В то же время начальный и рассеянный пучки рентгеновских лучей можно рассматривать и регистрировать как поток частиц - фотонов, определяя с помощью счётчиков фотонов число фотонов рентгеновского излучения в этих пучках.

Следует подчеркнуть, что волновые свойства присущи каждой частице в отдельности. Это было подтверждено опытом В. А. Фабриканта (1947) по дифракции электронов, поочерёдно летящих через образец.

 

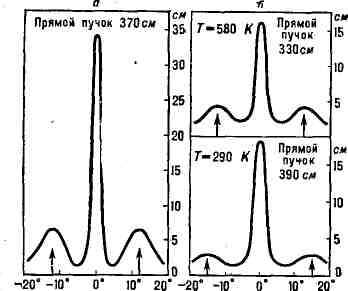
Рис. 6. Дифракция на кристалле фтористого лития атомов гелия (a) и молекул водорода при двух значениях абсолютной температуры Т (6). По оси абсцисс отложен угол дифракции O, а по оси ординат-интенсивность дифрагированных пучков (в сантиметрах отклонения стрелки измерительного прибора). Кроме пика при 9 = 0°, обязанного зеркальному отражению начального пучка, наблюдаются два боковых дифракционных лика. При Т = 580 К боковые пики лежат несколько ближе к центральному, чем при Т=290 К, что соответствует уменьшению длины волны X с повышением температуры [см. формулу (7)].

Рис. 7. Дифракция при рассеянии нейтронов на монокристалле NaCl.

При этом постепенно, по истечении нек-рого времени, возникала обычная картина дифракции. Это означало, что каждый из электронов подчиняется всем законам волновой оптики, а дифракционный эффект обязан взаимодействию волны де Бройля каждого электрона со всем объёмом кристалла. Начальная волна wo [см. формулу (2)], описывающая движение начального электрона, при прохождении через кристалл превращается в рассеянную волну ф.

Образование дифракционной картины при рассеянии частиц интерпретируется в квантовой механике след, образом. Прошедший через кристалл электрон в результате взаимодействия с кристаллич. решёткой образца отклоняется от своего первоначального движения и попадает в некоторую точку фотопластинки, установленной за кристаллом для регистрации электронов. Войдя в фотографич. эмульсию, электрон проявляет себя как частица и вызывает фотохимич. реакцию. На первый взгляд попадание электрона в ту или иную точку пластинки носит совершенно произвольный характер. Но при длительной экспозиции постепенно возникает упорядоченная картина дифракционных максимумов и минимумов в распределении электронов, прошедших через кристалл.

Точно предсказать, в какое место фотопластинки попадёт данный электрон, нельзя, но можно указать вероятность его попадания после рассеяния в ту или иную точку пластинки. Эта вероятность определяется волновой функцией электрона w, точнее квадратом её модуля (т. к. w - комплексная функция) |w|². Однако, поскольку вероятность при больших числах испытаний реализуется как достоверность, при многократном прохождении электрона через кристалл или, как это имеет место в реальных дифракционных экспериментах, при прохождении через образец пучка электронов, содержащего громадное кол-во частиц, величина |w|² определяет уже распределение интенсивности в дифрагированных пучках. Т. о., результирующая волновая функция электрона ф, к-рую можно рассчитать, зная ф₀ и потенциальную энергию взаимодействия электрона с кристаллом, даёт полное описание дифракц. опыта в статистическом смысле.

Специфика дифракции различных частиц. Атомная амплитуда рассеяния. Вследствие общности геометрич. принципов дифракции теория Д. ч. многое заимствовала из развитой ранее теории дифракции рентгеновских лучей. Однако взаимодействие разного рода частиц -электронов, нейтронов, атомов и т. п. -с веществом имеет различную физич. природу. Поэтому при рассмотрении Д. ч. на кристаллах, жидкостях и т. д. существенно знать, как рассеивает различные частицы изолированный атом вещества. Именно в рассеянии частиц отдельными атомами проявляется специфика дифракции различных частиц. Напр., рассеяние электронов определяется взаимодействием его электрич. заряда с электро-статич. потенциалом атома ф (r) (r - расстояние от атома), к-рый складывается из потенциала положительно заряженного ядра и потенциала электронной оболочки атома; потенциальная энергия этого взаимодействия U = еa(r). Рассеяние нейтронов определяется потенциалом их сильного взаимодействия с атомным ядром, а также взаимодействием магнитного момента нейтрона с магнитным моментом атома (магнитное рассеяние нейтронов; см. Нейтронография).

Количественно рассеивающую способность атома характеризуют величиной, к-рая наз. атомной амплитудой рассеяния f(O), где в - угол рассеяния, и определяется потенциальной энергией взаимодействия частиц данного сорта с атомами рассеивающего вещества. Интенсивность рассеяния частиц пропорциональна f² (O).

Если атомная амплитуда известна, то, зная взаимное расположение рассеивающих центров - атомов вещества в образце (т. е. зная структуру рассеивающего образца), можно рассчитать общую картину дифракции (к-рая образуется в результате интерференции вторичных волн, исходящих из рассеивающих центров).

Теоретич. расчёт, подтверждённый экспериментальными измерениями, показывает, что атомная амплитуда рассеяния электронов f_э максимальна при O =0 и спадает с увеличением O. Величина f_э зависит также от заряда ядра (атомного номepa) Z и от строения электронных оболочек атома, в среднем возрастая с увеличением Z приблизительно как Z ^1/3 для малых О и как Z ^2/3 при больших значениях в, но обнаруживая колебания, связанные с периодич. характером заполнения электронных оболочек.

Атомная амплитуда рассеяния нейтронов f_н для тепловых нейтронов (нейтронов с энергией в сотые доли эв) не зависит от угла рассеяния, т. е. рассеяние таких нейтронов ядром одинаково во всех направлениях (сферически симметрично). Это объясняется тем, что атомное ядро с радиусом порядка 10^-13 см является "точкой" для тепловых нейтронов, длина волны к-рых составляет 10^-8 см. Кроме того, для рассеяния нейтронов нет явной зависимости от заряда ядра Z. Вследствие наличия у нек-рых ядер т. н. резонансных уровней с энергией, близкой к энергии тепловых нейтронов, f_н для таких ядер отрицательны.

Атом рассеивает электроны значительно сильнее, чем рентгеновские лучи и нейтроны: абсолютные значения амплитуды рассеяния электронов f_э - это величины порядка 10^-8см, рентгеновских лучей -fp~l0-¹¹ см, нейтронов - f_н ~ 10^-12см. Т. к. интенсивность рассеяния пропорциональна квадрату амплитуды рассеяния, электроны взаимодействуют с веществом (рассеиваются) примерно в миллион раз сильнее, чем рентгеновские лучи (и тем более нейтроны). Поэтому образцами для наблюдения дифракции электронов обычно служат тонкие плёнки толщиной 10^-6 - 10^-5см, тогда как для наблюдения дифракции рентгеновских лучей и нейтронов нужно иметь образцы толщиной в несколько мм.

Дифракцию на любой системе атомов (молекуле, кристалле и т. п.) можно рассчитать, зная координаты их центров f_i и атомные амплитуды f_i для данного сорта частиц.

Наиболее ярко эффекты Д. ч. выявляются при дифракции на кристаллах. Однако тепловое движение атомов в кристалле несколько изменяет условия дифракции, и интенсивность дифрагированных пучков с увеличением угла в в формуле (6) уменьшается. При Д. ч. жидкостями, аморфными телами или молекулами газов, упорядоченность к-рых значительно ниже кристаллической, обычно наблюдается несколько размытых дифракционных максимумов.

Д. ч., сыгравшая в своё время столь большую роль в установлении двойственной природы материи - корпускулярно-волнового дуализма (и тем самым послужившая экспериментальным обоснованием квантовой механики), давно уже стала одним из главных рабочих методов для изучения строения вещества. На Д. ч. основаны два важных совр. метода анализа атомной структуры вещества -электронография и нейтронография.

Лит.: Блохинцев Д. И., Основы квантовой механики, 4 изд., М., 1963, гл. 1, §7, 8; Пинскер З. Г., Дифракция электронов, М.- Л., 1949; Вайнштейн Б. К., Структурная электронография, М., 1956; Бэкон Дж., Дифракция нейтронов, пер. с англ., М., 1957; Рамзе и Н., Молекулярные пучки, пер. с англ., М., 1960.

Б. К. Вайнштейн.

ДИФРАКЦИЯ ЭЛЕКТРОНОВ, см. Дифракция частиц.

ДИФТЕРИЯ (от греч. diphtherion - кожица, плёнка), острое инфекционное заболевание, характеризующееся воспалением с образованием плотных плёнчатых налётов на месте внедрения возбудителя болезни и тяжёлым общим отравлением (интоксикацией) организма. Возбудитель Д. - Corynobacterium diphteriae - открыт нем. бактериологом Э. Клебсом в 1883 и выделен в чистой культуре нем. бактериологом Ф. Лёфлером; имеет форму палочки и образует дифтерийный экзотоксин. Источник инфекции при Д. - больной или бактерионоситель (здоровый или переболевший Д.). Дифтерийные палочки выделяются в окружающую среду с каплями слизи при разговоре, чихании, кашле. Заражение происходит при попадании микроба в организм через слизистые оболочки зева, носа и верхних дыхат. путей, реже - конъюнктивы глаз, повреждённую кожу и т. д. (воздушно-капельный путь); возможно попадание возбудителя через рот с пищей и через различные предметы - бельё, одежду, книги, игрушки и т. п. Дифтерийная палочка, попав на слизистые оболочки (или кожу), выделяет токсин, к-рый вызывает некроз (омертвение) эпителия и поражение кровеносных сосудов с выпадением сетки фибрина (белок крови) и образованием плёнки; при поступлении токсина в кровь развивается общая интоксикация; при этом преим. поражаются нервная и сердечно-сосудистая системы, надпочечники, почки. Инкубац. период -2-10 дней.

По локализации процесса различают Д. зева (наиболее частая форма), дыхат. путей, носа, глаз, уха, наружных половых органов (у девочек), кожи, пупка у новорождённых, Д. ран и др.

Д. зева. При локализованной форме плёнчатые налёты покрывают миндалины, не переходя за их пределы, лимфатич. узлы увеличены умеренно, темп-ра тела повышается до 38,5-39 °С. Недомогание, понижение аппетита, головная боль выражены незначительно. При распространённой форме налёты переходят с миндалин на слизистую оболочку нёбных дужек, язычка, глотки; общее недомогание выражено достаточно ярко. Токсич. форма характеризуется обширным поражением зева; миндалины отёчны, поверхность их покрыта толстыми налётами грязно-белого цвета. Процесс может распространиться на носоглотку и полость носа. Обычно развивается отёк подкожной клетчатки вокруг увеличенных верхнешейных лимфатич. узлов; явления интоксикации прогрессивно нарастают: нарушается сердечный ритм, глотание затруднено, при переходе процесса на органы дыхания нарушается дыхание, при явлениях миокардита в остром периоде отмечаются носовые кровотечения; боли в животе, понос, может наступить коллапс.

Д. дыхательных путей. При локализации процесса на слизистой оболочке гортани или трахеи вследствие образования плёнок, отёка, инфильтрации слизистой оболочки и спазм гортанной мускулатуры прогрессивно нарастают расстройства дыхания - дифтерийный круп. Круп проявляется "лающим" кашлем, сиплым голосом, вплоть до полной афонии (отсутствие голоса), резким затруднением вдоха. При переходе процесса на бронхи возникает тяжёлая форма Д.- распространённый круп.

Д. носа встречается у детей младшего возраста, интоксикация обычно не наблюдается; проявляется односторонним насморком с кровянистыми выделениями, склонна к затяжному течению.

Д. глаз, уха, наружных половых органов, пищеварит. тракта, кожи и ран, в т. ч. пупочной раны у новорождённых, в совр. мед. практике почти не встречается.

Осложнения отмечаются в основном лишь при токсич. форме Д., особенно при запоздалом начале сывороточного лечения. Коллапс развивается на 2-3-4-й день болезни и тяжёлый миокардит на 5-6-й день болезни; иногда возникают периферич. параличи, параличи черепно-мозговых нервов, токсич. нефроз; при дифтерийном крупе - пневмония.

Лечение. Возможно раннее введение антитоксич. противодифтерийной сыворотки; витаминотерапия; антибактериальная терапия. При дифтерийном крупе при нарастании явлений нарушения дыхания и кислородном голодании -срочная операция (интубация или трахеотомия).

Профилактика. Осн. роль в борьбе с Д. играет активная иммунизация. В СССР противодифтерийные прививки обязательны для всего детского населения (в период с 5-6 мес до 12-летнего возраста проводятся 1 вакцинация и 3 ревакцинации). Иммунизация проводится адсорбированным дифтерийным анатоксином. С 1958 в СССР прививки осуществляются ассоциированным препаратом (АКДС), в к-рый, кроме дифтерийного анатоксина, входят коклюшная вакцина и столбнячный анатоксин. В связи с активной иммунизацией заболеваемость Д. в СССР резко снизилась (с 1959 по 1966 - в 30,7 раза).

Как можно раньше выявляется и изолируется (госпитализируется) заболевший. После госпитализации больного проводится дезинфекция помещения. Все лица, находившиеся в контакте с больным, подлежат многократному бактериологич. обследованию и мед. наблюдению в течение 7 дней. Детям, контактировавшим с больным, на этот срок запрещено посещать детские учреждения (ясли, детсады, школы и др.); у них проверяют состояние специфич. иммунитета - реакция Шика (по им. австр. врача Б. Шика).

Лит.: Молчанов В. И., Дифтерия, 2 изд., М., 1960; Титова А. И. и Флексер С. Я., Дифтерия, М., 1967.

Р. Н. Рылеева, М. Я. Студеникин.

ДИФТЕРОИДЫ, бактерии, обладающие сходством с дифтерийными палочками -возбудителями дифтерии. Различают парадифтерийные и ложнодифтерийные Д., имеющие вид коротких, толстых, неподвижных палочек. Парадифтерийные Д., в отличие от ложнодифтерийных, имеют 1-2 маленьких полярных зерна и не разлагают мочевину.

ДИФТОНГ (от греч. diphthongos -двугласный), сочетание двух гласных (слогового и неслогового) в одном слоге. Напр., франц. [oi]. Различаются: Д. восходящий, у к-рого слогообразующим элементом является второй из составляющих его гласных. Напр., франц. [ie], [ui]; Д. нисходящий, у к-рого слогообразующим является первый из составляющих его гласных. Напр., англ, [ai], Гаи].

ДИФФАМАЦИЯ (от лат. diffamo - порочу), в уголовном праве нек-рых бурж. гос-в распространение порочащих сведений. В отличие от клеветы, при Д. порочащие сведения могут и не носить клеветнич. характера.

ДИФФЕРДАНЖ (Differdange), город в Люксембурге, в округе Люксембург, близ границы с Францией. 17,8 тыс. жит. (1970). Центр металлургич. пром-сти; произ-во хим. удобрений. В р-не Д.- добыча жел. руды (продолжение Лотарингского железорудного бассейна).

ДИФФЕРЕНТ СУДНА (от лат. dif-ferens, род. падеж differentis - разница), наклон судна в продольной плоскости. Д. с. характеризует посадку судна и измеряется разностью его осадок (углублений) кормой и носом. Если разность равна нулю, говорят, что судно "сидит на ровный киль", при положит, разности - судно сидит с дифферентом на корму, при отрицат. - с дифферентом на нос. Д. с. влияет на поворотливость судна, условия работы гребного винта, проходимость во льдах и пр. Д.с. бывает статический и ходовой, возникающий при больших скоростях движения. Д. с. обычно регулируют приёмом или удалением водяного - балласта.

ДИФФЕРЕНЦИАЛ (от лат. differentia - разность, различие) в математике, главная линейная часть приращения функции. Если функция y=f(x) одного переменного х имеет при х=х₀ производную, то приращение

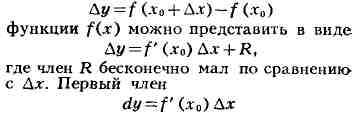
в этом разложении и называется дифференциалом функции f(x) в точке х₀. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Дх, а равенство Дy = dy +R показывает, в каком смысле Д. dy является главной частью приращения Дy.
Подробнее о Д. функций одного и нескольких переменных см. Дифференциальное исчисление.

Обобщение понятия дифференциала. Обобщение понятия Д. на вектор-функции, начало к-рому положили в начале 20 в. франц. математики Р. Гато и М. Фреше, позволяет лучше выяснить смысл понятия "дифференциал" для функций нескольких переменных, а в применении к функционалам приводит к понятию вариации, лежащему в основе вариационного исчисления.

Важную роль в этом обобщении играет понятие линейной функции (линейного отображения). Функция L(x) векторного аргумента х наз. л и-н е и н о и, если она непрерывна и удовлетворяет равенству

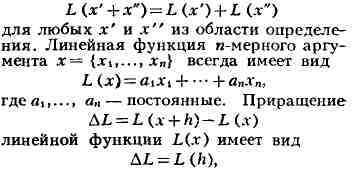
т. е. зависит только от векторного приращения h, и притом линейно, функция f(x) наз. дифференцируемой при значении аргумента .г, если её приращение Дf = f(x + h) - f(x), рассматриваемое как функция от h, имеет главную линейную часть L(h), т. е. выражается в виде Дf = L(h) + R(h),
где остаток R(h) при h->0 бесконечно мал по сравнению с h. Главная линейная часть L(h) приращения Дf и наз. дифференциалом df функции f в точке х. При этом в зависимости от того, в каком смысле понимается бесконечная малость R(h) по сравнению с h, различают слабый дифференциал, или дифференциал Гато, и сильный дифференциал, или дифференциал фреше. Если существует сильный Д., то существует и слабый Д., равный сильному Д. Слабый Д. может существовать и тогда, когда сильный не существует.

В случае f(x) = x из общего определения следует, что df = h, т. е. можно приращение h считать Д. аргумента х и обозначать dx.

Если сделать теперь переменной точку х, в к-рой определяется Д. df, то он будет функцией двух переменных: df(x;h)

Далее, считая h = h₁ постоянным, можно найти Д. от дифференциала df(x; h₁) как главную часть приращения df(x+h₂;h₁)-df(x;h₁), где h₂ - нек-рое второе, не связанное с h₁приращение х. Получаемый таким образом второй дифференциал d²f=d²f(x; h₁,h₂) является функцией трёх векторных аргументов х, h₁ и h₂, линейной по каждому из двух последних аргументов. Если d²f непрерывно зависит от х, то он симметричен относительно h₁ и h₂: d*f(x; h₁, h₂) = d²f(x; h₂, h₁). Аналогично определяется дифференциал dⁿf=dⁿf(x; h₁,...,h_n) любого порядка п. В вариационном исчислении сам векторный аргумент х является функцией x(t), а дифференциалы df и d²f функционала f[x(t)] наз. его первой и второй вариациями и обозначаются бf и б²f.

Всюду выше речь шла об обобщении понятия Д. на числовые функции векторного аргумента. Существует обобщение понятия Д. и на случай вектор-функций, принимающих значения в банаховых пространствах.

Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., М., 1967; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964.

А. Н. Колмогоров.

ДИФФЕРЕНЦИАЛ, дифференциальный механизм в приводе ведущих колёс автомобиля, трактора или др. транспортных машин. Д. обеспечивает вращение ведущих колёс с разными относит, скоростями при прохождении кривых участков пути.

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ, раздел геометрии, в к-ром геометрич. образы изучаются методами математич. анализа. Главными объектами Д. г. являются произвольные достаточно гладкие кривые (линии) и поверхности евклидова пространства, а также семейства линий и поверхностей. Обычно в Д. г. исследуются локальные свойства геометрич. образов, к-рые присущи сколь угодно малой их части. Рассматриваются также и свойства геометрич. образов в целом (напр., свойства замкнутых выпуклых поверхностей).

Геометрические объекты, изучаемые в Д. г., обычно подчинены нек-рым требованиям гладкости. Как правило, эти требования выражаются в том, что функции, задающие указанные объекты, не менее двух раз непрерывно дифференцируемы.

Сущность методов Д. г., применяемых для выяснения локальных свойств геометрич. объектов, проще всего уяснить на примере локального исследования формы кривых.

В каждой точке М достаточно гладкой кривой L можно построить касательную прямую МТ и соприкасающуюся плоскость л (рис. 1). При этом касательная МТ является пределом секущей MN при неограниченном приближении точки N к М по кривой L, а соприкасающаяся плоскость есть предел переменной плоскости, проходящей через касательную МТ и точку N при приближении N к М по L. Касательную МТ можно рассматривать также как прямую, наиболее тесно прилегающую к L вблизи точки М. Соприкасающаяся же плоскость представляет собой плоскость, наиболее тесно прилегающую к L вблизи М.

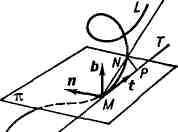
Рис. 1.

Для геометрич. характеристики искривлённости кривой L вблизи данной точки М рассматривается соприкасающаяся окружность, представляющая собой окружность, проходящую через М и наиболее тесно прилегающую к L, вблизи М. Это свойство выражается в том, что если учитывать величины только 1-го и 2-го порядка малости по сравнению с длиной дуги MN, то участок кривой L вблизи М можно считать дугой соприкасающейся окружности. Соприкасающаяся окружность касается L в точке М и расположена в соприкасающейся плоскости. Её центр наз. центром кривизны кривой L в точке М, а радиус - радиусом кривизны L в М.

Для численной характеристики искривлённости L в точке М используется кривизна k кривой, равная обратной величине радиуса R соприкасающейся окружности: k=1/R. Кривизну k можно рассматривать и как меру отклонения L от касательной МТ (рис. 1):

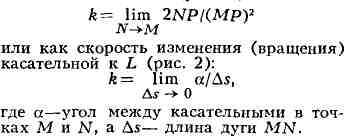
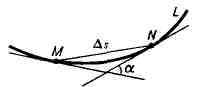
Рис. 2.

Мерой отклонения кривой от соприкасающейся плоскости я в точке М служит т. н. кручение а, к-рое определяется как предел отношения угла (3 между соприкасающимися плоскостями в точках М и N к длине Дs дуги MN при Дs->О:

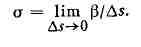
При этом угол р берётся со знаком +, если для наблюдателя в М вращение соприкасающейся плоскости в N при приближении N к М происходит против часовой стрелки, и со знаком - в противном случае. Кручение кривой можно рассматривать как скорость изменения (вращения) соприкасающейся плоскости. В частности, для плоской кривой соприкасающаяся плоскость во всех точках совпадает с плоскостью кривой и поэтому кручение такой кривой во всех точках равно нулю. Кривизна k и кручение а достаточно гладкой кривой L, определены в каждой её точке и представляют собой функции параметра, определяющего точки этой кривой. Для вычисления k и а используется к.-л. способ задания кривой. Чаще всего кривая L задаётся параметрич. уравнениями в прямоугольных координатах: x = ф (t), y= w(t) , z = х(t)- (1) При изменении параметра t точка М с координатами (x, у, z) описывает кривую L. Иными словами, параметрич. уравнения кривой связаны с представлением о кривой как траектории движущейся точки. Правые части (1) могут рассматриваться и как проекции на оси координат радиуса-вектора r переменной точки М кривой L. Вектор г' с координатами {ф'(0, w'(t), Х'(t)} наз. производной вектор-функции r(t) и направлен по касательной к L в точке М.

Кривизна и кручение вычисляются по формулам

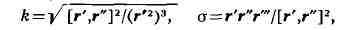
в к-рых [r', r"] - векторное, а r'r"r'" - смешанное произведение (см. Векторное исчисление).

С каждой точкой М кривой L связаны три единичных вектора: касательной (t), главной нормали (n) и бинормали (b) (рис. 1). При этом вектор (га) расположен в соприкасающейся плоскости и направлен от точки М к центру кривизны L в М, а вектор Ь ортогонален t и и и направлен так, что векторы г, н и b образуют правую тройку. Указанная тройка векторов образует т. н. основной, или сопровождающий, триедр кривой L. Плоскости векторов (n,b) и (t, b) наз. соответственно нормальной и спрямляющей плоскостями L в М.

Формулы для производных векторов t, п, b по длине s дуги L наз. формулами френе. Они играют фундаментальную роль как в теории кривых, так и в приложениях этой теории (в механике, теоретич. физике и т. д.). Эти формулы имеют вид

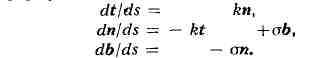
Если кривизна и кручение не равны нулю в точке М, то можно сделать определённые заключения о форме L вблизи М: проекции L на соприкасающуюся и нормальную плоскости в М имеют вид, изображённый соответственно на рис. 3 и 4. Форма проекции на спрямляющую плоскость зависит от знака кручения. На рис. 5 и 6 изображены проекции L на спрямляющую плоскость для o>0 и o <0. Кривизна и кручение вполне определяют кривую. Именно, если между точками двух кривых установлено соответствие так, что соответствующие дуги этих кривых имеют одинаковую длину и в соответствующих точках кривые имеют равные кривизны и равные кручения, то эти кривые могут быть совмещены посредством движения.

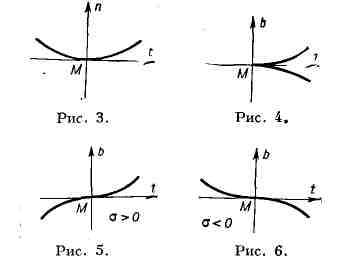
По аналогии с кривыми исследуется локальное строение формы поверхностей. В каждой точке М достаточно гладкой поверхности S можно построить касательную плоскость у и однозначно определённый соприкасающийся параболоид л (рис. 7), к-рый может выродиться в параболич. цилиндр или плоскость. При этом касательную плоскость можно рассматривать как плоскость, наиболее тесно прилегающую к S вблизи М.

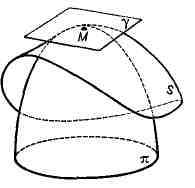
Рис. 7

Соприкасающийся же параболоид характеризуется тем, что в окрестности точки М он совпадает с S с точностью до величин третьего порядка малости по сравнению с размерами этой окрестности. С помощью соприкасающихся параболоидов точки М поверхностей классифицируются следующим образом: эллиптическая (рис. 8) (соприкасающийся параболоид - эллиптический), гиперболическая (рис. 9) (соприкасающийся параболоид - гиперболический), параболическая (рис. 10) (соприкасающийся параболоид - параболический цилиндр), точка уплощения (рис. 11) (соприкасающийся параболоид - плоскость).

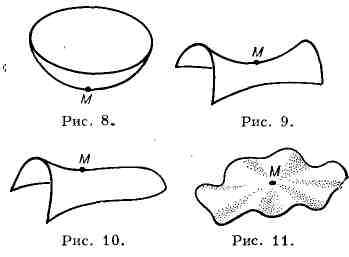
Обычно для исследования строения поверхности используются т. н. первая и вторая основные квадратичные формы поверхности.

Пусть поверхность S определена пара-метрич. уравнениями: x= ф(u, v), y = w(u,v), z = x(u,v). (2) При фиксированном значении v уравнения (2) определяют на S линию, называемую координатной линией и. Аналогично определяется линия v. Координатные линии и и v образуют на S параметрическую сеть (если, напр., сферу радиуса 1 задать параметрич. ур-ниями х = cos и cos v, у =cos и sin v, z = sin u, то параметрич. сетью линий и и v будут меридианы и параллели этой сферы). Величины и и v наз. также внутренними координатами, т. к. точка на поверхности есть точка пересечения проходящих через неё координатных линий, т. е. может быть найдена путём построений на поверхности без обращения к объемлющему пространству.

Радиус-вектор г произвольной точки М на S определяется уравнениями (2) как функция и и V. Частные производные r_u и r_v этой функции суть векторы, касательные соответственно к линиям и и и. Эти векторы в точке М лежат в касательной плоскости к S в М. Векторное произведение [r_u,r_v] определяет нормаль к S в точке М.

Пусть s - длина дуги линии L на S и пусть и = f(t), v = g(t) - параметрич. ур-ния во внутр. координатах. Тогда, вдоль Lr и s будут функциями от г, причём дифференциал s определяется равенством ds² = dx² + dy² + dz², правая часть к-рого есть скалярный квадрат вектора dr= r_udu + r_vdv, т. е. ds² = dr². Поэтому ds²= r_udu² + 2r_u r_v dudv + r²_v,dv С помощью обозначений r²_u== Е, r_ur_v= F, г²_v = G выражение для ds² можно записать в виде ds² = Edu² + 2Fdudv + Gdv². (3) Правая часть соотношения (3) наз. первой основной квадратичной формой поверхности S. С помощью этой формы можно измерять длины дуг на поверхности путём интегрирования выражения

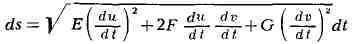
вдоль рассматриваемой дуги. Поэтому форма (3) наз. также метрической формой поверхности. Первая форма определяет также внутреннюю геометрию поверхности, т. е. совокупность фактов, к-рые могут быть получены путём измерений на поверхности, без обращения к объемлющему пространству. Внутр. геометрия поверхности не меняется при её изгибании - деформации поверхности как абсолютно гибкой и нерастяжимой плёнки.

Вторая основная квадратичная форма поверхности представляет собой выражение Ldu² + 2Mdudv + Ndv², в котором L = r_uun, М = r_uun, N = r_vvп (п - единичный вектор нормали к S в точке М). С помощью второй формы можно получить представление о пространственной форме поверхности. Напр., кривизны 1/К нормальных сечений поверхности в данной точке М (т. е. линий пересечения S с плоскостями, проходящими через нормаль в М) вычисляются по формуле

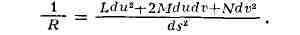
Две основные формы поверхности, заданные в к.-л. внутр. координатах, определяют поверхность с точностью до положения в пространстве. Если заданы две формы

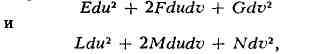
первая из к-рых положительная, а коэфф. L, M и N второй удовлетворяют нек-рой системе уравнений, из к-рых одно (полученное К. Гауссом) алгебраическое, а два других (полученные К. М. Петерсоном) -линейные дифференциальные уравнения с частными производными первого порядка, то найдётся поверхность, для к-рой эти формы являются соответственно первой и второй основными формами.

Отмеченные уравнения Гаусса - Петерсона играют фундаментальную роль в теории поверхностей.

Подробнее о поверхностях см. Поверхностей теория.

Одним из объектов исследований в Д.г. являются семейства кривых и поверхностей. Такие семейства задаются посредством уравнений, содержащих параметры. Напр., ур-ние (х - а)² + у² = 1, содержащее параметр а, определяет семейство окружностей радиуса 1 с центрами в точках (а, 0), т. е. на оси Оx (рис. 12).

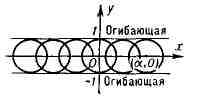
Рис. 12.

С семейством кривых (поверхностей) связано понятие огибающей - такой кривой (поверхности), к-рая касается всех кривых (поверхностей) семейства. В рассмотренном выше примере огибающей будет пара параллельных оси Ох прямых, отстоящих от неё на расстоянии 1. Особенно детально в Д. г. исследованы двупараметрич. семейства прямых b в пространстве, называемые конгруэнция м и. Простейший пример конгруэнции - семейство параллельных прямых в пространстве. Истоком теории конгруэнции является геометрическая оптика.

Различные разделы Д. г. посвящены изучению во всевозможных аспектах т. н. дифференциально-геометрических многообразий. Примерами таких многообразий могут служить кривые (одномерные многообразия), поверхности (двумерные многообразия), обычное евклидово пространство (трёхмерное многообразие). Более сложным примером может служить четырёхмерное многообразие, элементами к-рого являются прямые обычного "евклидова пространства (прямая в декартовых координатах определяется ур-ниями вида z = ах + b, z ~ су + d, числа а, b, с, d можно рассматривать как координаты этой прямой).

Изучение дифференциально-геометрич. многообразий ведётся по след. основным направлениям. 1) Геометрия транзитивной группы отображений многообразия на себя, или геометрия "локальной группы" отображений. В тематику этих вопросов входят обычная классич. локальная Д. г. (изучение инвариантов группы движений евклидова пространства), аффинная, проективная и конформная геометрии (изучение инвариантов соответствующей группы преобразований). 2) Геометрия многообразий с римановой метрикой (римановых пространств), представляющая собой обобщение на многомерный случай внутренней геометрии поверхностей, к-рое можно рассматривать как двумерные римановы пространства. Геометрия римановых пространств играет важную роль в теории относительности. 3) Геометрия т. н, финслеровых пространств, являющихся обобщением римановых пространств. 4) Геометрия многообразий со связностью, т. е. многообразий, в к-рых указан способ, с помощью к-рого можно сравнивать геометрии, образы, расположенные в касательных пространствах в разных точках.

Возникновение Д. г. связано с именами Л. Эйлера и Г. Монжа. Ими к концу 18 в. были получены важные факты теории поверхностей. Значит, вклад в развитие Д. г. сделан в нач. 19 в. К .Гауссом, к-рый ввёл обе основные квадратичные формы. Им же была доказана теорема об инвариантности полной кривизны относительно изометрич. преобразований, фактически им были заложены основы внутр. геометрии поверхностей. Построение основ классич. теории поверхностей было завершено в сер. 19 в. основателем моек, геометрич. школы К. М. Петерсоном. В сер. и во 2-й пол. 19 в. много глубоких и общих результатов по классич. теории поверхностей было получено Ф. Миндингом, Ж. Лиувиллем, Э. Бельтрами, Ж. Г. Дарбу, Л. Бианки. Ряд замечат. результатов по классич. Д. г. был получен рус. учёными Д. Ф. Егоровым, Н. Н. Лузиным, С. П. Финиковым и др.

Развитие др. направлений в Д. г. связано с именами Б.Римана, Г. Ламе, Ф. Клейна, Г. Вейля, Э. Картона.

В СССР разрабатывались различные направления Д. г.; наибольшие успехи относятся к области проблем "в целом" (А. Д. Александров, А.В. Погорелое и др.).

Лит.: Монж Г., Приложение анализа к геометрии, пер. с франц., М.- Л., 1936; Стройк Д. Д ж., Очерк истории дифференциальной геометрии до XX столетия, пер. с англ., М. -Л., 1941; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Рашевский П. К., Курс дифференциальной геометрии, 3 изд., М., 1950; Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; Рашевский П. К., Риманова геометрия и тензорный анализ, 2 изд., М., 1964; Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М.- Л., 1948; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969.

Э. Г. Лозняк.

ДИФФЕРЕНЦИАЛЬНАЯ ПСИХОЛОГИЯ, отрасль психологии, изучающая индивидуальные различия между людьми. Предпосылкой возникновения Д. п. на рубеже 19 и 20 вв. явилось введение в психологию эксперимента, а также генетич. и математич. методов. Пионером разработки Д. п. был Ф. Гальтон (Великобритания), к-рый изобрёл ряд приёмов и приборов для изучения индивидуальных различий. В. Штерн (Германия) ввёл самый термин "Д. п." (1900). Первыми крупными представителями Д. п. были А. Бине (Франция), А. Ф. Лазурский (Россия), Дж. Кеттел (США) и др.

В Д. п. широко применяются тесты -как индивидуальные, так и групповые; они используются для определения умственных различий, а с изобретением т. н. проективных тестов - для определения интересов, установок, эмоциональных реакций. С помощью тестов методами факторного анализа выявляются факторы, характеризующие общие свойства (параметры, измерения) интеллекта или личности. На этом основании определяются количеств, вариации в психология, свойствах отд. индивидов.

Вопрос о причинах психологич. различий явился предметом острейших дискуссий на протяжении всей истории Д. п. и прежде всего - проблема соотношения биол. и социально-культурных факторов в формировании индивидуальных особенностей человека. В 50-60-х гг. 20 в. для Д. п. характерно интенсивное развитие новых подходов и методов - как экспериментальных, так и математических. Совершенствуется техника статис-тич. анализа тестов (Дж. Гилфорд, США; Р. Кеттел, Великобритания), изучается роль ценностной ориентации личности, детально выявляются психологич. аспекты возрастных и половых различий.

Наряду с различиями между индивидами в умств. отношении широко исследуются различия в творч. и организаторских способностях, общей структуре личности, сфере мотивации. Изучаются корреляции между психологич. свойствами, с одной стороны, и физиологическими - с другой (У. Шелдон, Г. Айзенк - Великобритания). В СССР работа в этом направлении ведётся в ряде лабораторий - в Ин-те психологии АПН СССР (исследования, проводившиеся Б. М. Тепловым и его сотрудниками на основе учения И. П. Павлова о типах высшей нервной деятельности), Ленингр. и Пермском ун-тах и др.

Факты и выводы Д. п. важны для решения мн. практич. задач (отбор и обучение персонала, диагностика и прогностика развития отд. свойств, склонностей, способностей индивидов и др.).

Лит.: Теплов Б. М., Проблемы индивидуальных различий, М., 1961; Рiёron Н., La psychologic differentielle, 2 ed., P., 1962; Anastasi A., Differential psychology, 3 ed., N.Y., 1958.

М. Г. Ярошевский.

ДИФФЕРЕНЦИАЛЬНАЯ РЕНТА, При капитализме добавочная прибыль, возникающая в результате затрат труда на средних и лучших земельных участках или при повышающейся производительности добавочных вложений капитала, присваивается собственником земли; одна из форм земельной ренты, к-рая порождается монополией на землю как объект капиталистич. х-ва. Источник её - излишек прибавочной стоимости, создаваемой трудом с.-х. наёмных рабочих над средней прибылью, возникающий вследствие более высокой производительности труда на относительно лучших земельных участках (более плодородных или ближе расположенных к месту сбыта либо таких, в к-рые вложен дополнит, капитал). Различают Д. р. I и Д. р. И. Д. р. I связана с различиями в плодородии и местоположении зем. участков. Индивидуальная цена производства единицы земледельч. продукта с лучших участков оказывается более низкой, т. к. труд, приложенный к более плодородной почве, при прочих равных условиях более производителен или расходы по доставке на рынок с.-х. товаров с ближе расположенных к нему зем. участков ниже, чем с более отдалённых. Реализуются же с.-х. товары по общественной цене произ-ва, к-рая в с. х-ве выражает общественную стоимость этих товаров и определяется условиями произ-ва на худших зем. участках. Это обусловливается тем, что количество земли ограничено, а с.-х. продуктов, производимых только на относительно лучших участках, недостаточно для покрытия общественного спроса на них, рынок предъявляет спрос также на продукты, производимые на средних и худших участках. Капиталистич. фермеры, ведущие х-во на лучших и средних землях, реализуя продукцию по рыночным ценам, получают добавочную прибыль, к-рая в форме Д. р. на основе права собственности на землю присваивается землевладельцем (независимо от того, является им частное лицо или капиталистич. гос-во). Д. р. I исторически возникла раньше Д. р. II, растёт с развитием экстенсивного земледелия, а также по мере развития сети путей сообщения и пром. центров.

Д. р. II представляет собой добавочную прибыль, возникающую в результате последовательных вложений капитала в землю. Она неразрывно связана с интенсификацией с. х-ва, является её важнейшим экономия, результатом. Повышение массы и нормы Д. р. II выражает рост производительности добавочных вложений капитала, тенденция к к рому, вопреки т. н. закону убывающего плодородия почвы (см. "Убывающего плодородия почвы закон"), в условиях научно-технич. прогресса становится главной и определяющей. Получаемая в результате добавочных вложений капитала сверхприбыль до окончания арендного договора достаётся фермеру-арендатору. Но при заключении нового арендного договора землевладелец, в силу господства монополии частной собственности на землю, присваивает себе эту добавочную прибыль путём повышения арендной платы, т. е. получает часть Д. р. II. Это является основой борьбы капиталистов-арендаторов с землевладельцами за сроки аренды земли.

Д. р. и рентные отношения сохраняются и при социализме. Материальную основу Д. р. составляет дополнит, чистый доход, образующийся на относительно лучших и удобно расположенных землях или при повышающейся производительности добавочных вложений. Наличие при социализме товарно-ден. отношений и монопольное пользование землёй как объектом х-ва обусловливают превращение этого дохода в Д. р. и ведут к возникновению рентных отношений. Однако социально-экономич. содержание Д. р. в условиях господства социалистич. собственности на средства произ-ва коренным образом меняется. Социалистич. строй устраняет социально-классовые антагонизмы в рентных отношениях, неизбежные между собственником земли, капиталистом-предпринимателем и наёмным рабочим в условиях капиталистич. способа произ-ва.

Источником Д. р. I является дополнит. чистый доход, получаемый в результате более высокой производительности труда на лучших по плодородию и местоположению зем. участках. Т. к. для удовлетворения общественного спроса приходится вовлекать в с.-х. оборот и относительно худшие земли, плановое ценообразование необходимо осуществлять с учётом возмещения затрат и получения необходимой прибыли х-вами, располагающими такими землями, иначе будут подорваны хозрасчётные стимулы их возделывания. Колхозы и совхозы, использующие средние и лучшие земли, получают дополнит. доход в виде разницы между общественной ценой и индивидуальной стоимостью единицы продукта. А т. к. образование этого дохода обусловлено не трудовыми усилиями отд. коллективов, а общественными факторами воспроизводства, то на основе права общенар. собственности на землю он изымается гос-вом в форме Д. р. I. При этом совершенно снимается антагонистич. характер изъятия, поскольку Д. р. I не становится достоянием класса зем. собственников, а поступает в общенар. фонд и используется в интересах всего общества, в т. ч. для планомерного подъёма с. х-ва. Д. р. I изымается гос-вом через закупочные цены, дифференциацию планов закупок и подоходный налог.

Д. р. II возникает в результате различной производительности добавочных вложений: её масса и норма планомерно возрастают в условиях интенсификации, науч.-технич. прогресса в с.-х. произ-ве; она почти полностью остаётся у с.-х. предприятий.

Сложившиеся в социалистич. странах различные отношения зем. собственности обусловливают и разные конкретные формы распределения Д. р. Однако сущность рентных отношений и общие принципы распределения Д. р. остаются едиными независимо от того, вся земля национализирована или часть её находится в собственности кооперативов. В правильном экономич. регулировании рентных отношений при социализме важное значение имеет эффективное применение механизма распределения Д. р., прежде всего научно обоснованное ценообразование, учитывающее специфику с. х-ва.

Д. р. существует не только в с. х-ве, но и в добывающей пром-сти, строительстве, образуется в результате различий в производительности труда, обусловленных неравенством естественных условий разработки и использования полезных ископаемых, лесных угодий и т. д. При социализме Д. р. в добывающей пром-сти принадлежит всему обществу и используется в его интересах, в т. ч. для развития угольной, рудной и др. отраслей. Как стоимостная категория Д. р. перестанет существовать с отмиранием товарного произ-ва.

Лит. см. при ст. Земельная рента.

И. Н. Буздалов.

 

ДИФФЕРЕНЦИАЛЬНО-ДИАГНОСТИЧЕСКИЕ СРЕДЫ, специальные смеси питат. веществ (см. Питательные среды), на к-рых выращивают микроорганизмы для определения их видовой принадлежности. К Д.-д. с. относятся белковые среды, применяемые для определения гемолитич. и протеолитич. способности микробов; среды, содержащие углеводы и индикаторы изменения кислотности (в результате утилизации микробами этих соединений); среды, содержащие вещества, служащие источником питания только для определ. видов бактерий, и др.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ, раздел математики, в к-ром изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную матем. дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 в.). Они сформулировали осн. положения Д. я. и чётко указали на взаимно обратный характер операций дифференцирования и интегрирования. С этого времени Д. и. развивается в тесной связи с интегральным исчислением, вместе с к-рым оно составляет осн. часть матем. анализа (или анализа бесконечно малых). Создание дифференциального и интегрального исчислений открыло новую эпоху в развитии математики. Оно повлекло за собой появление ряда матем. дисциплин: теорий рядов, теории дифференциальных уравнений, дифференциальной геометрии и вариационного исчисления. Методы матем. анализа нашли применение во всех разделах математики. Неизмеримо расширилась область приложений математики к вопросам естествознания и техники. "Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только состояния, но и процессы: движение" (Энгельс Ф., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20, с. 587).

Д. и. зиждется на следующих важнейших понятиях математики, определение и исследование к-рых составляют предмет введения в матем. анализ: действительные числа (числовая прямая), функция, предел, непрерывность. Все эти понятия выкристаллизовались и получили совр. содержание в ходе развития и обоснования дифференциального и интегрального исчислений. Осн. идея Д. и. состоит в изучении функций в малом. Точнее: Д. и. даёт аппарат для исследования функций, поведение к-рых в достаточно малой окрестности каждой точки близко к поведению линейной функции или многочлена. Таким аппаратом служат центральные понятия Д. и.: производная и дифференциал. Понятие производной возникло из большого числа задач естествознания и математики, приводящихся к вычислению пределов одного и того же типа. Важнейшие из них -определение скорости прямолинейного движения точки и построение касательной к кривой. Понятие дифференциала является матем. выражением близости функции к линейной в малой окрестности исследуемой точки. В отличие от производной, оно легко переносится на отображения одного евклидова пространства в другое и на отображения произвольных линейных нормированных пространств и является одним из осн. понятий совр. нелинейного функционального анализа.

Производная. Пусть требуется определить скорость прямолинейно движущейся материальной точки. Если движение равномерно, то пройденный точкой путь пропорционален времени движения; скорость такого движения можно определить как путь, пройденный за единицу времени, или как отношение пути, пройденного за нек-рый промежуток времени, к длительности этого промежутка. Если же движение неравномерно, то пути, пройденные точкой в одинаковые по длительности промежутки времени, будут, вообще говоря, различными. Пример неравномерного движения даёт тело, свободно падающее в пустоте. Закон движения такого тела выражается формулой s= gt²/2, где s -пройденный путь с начала падения (в метрах), t - время падения (в секундах), g - постоянная величина, ускорение свободного падения, g ~~ 9,81 м/сек². За первую секунду падения тело пройдёт ок. 4,9 м, за вторую - ок. 14,7 м, а за десятую - ок. 93,2 м, т. е. падение происходит неравномерно. Поэтому приведённое выше определение скорости здесь неприемлемо. В этом случае рассматривается средняя скорость движения за нек-рый промежуток времени после (или до) фиксированного момента t; она определяется как отношение длины пути, пройденного за этот промежуток времени, к его длительности. Эта средняя скорость зависит не только от момента t, но и от выбора промежутка времени. В нашем примере средняя скорость падения за промежуток времени от t до t + Дt равна

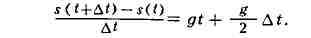
Это выражение при неограниченном уменьшении промежутка времени Дt приближается к величине gt, к-рую называют скоростью движения в момент времени t. Таким образом, скорость движения в к.-л. момент времени определяется как предел средней скорости, когда промежуток времени неограниченно уменьшается.

В общем случае эти вычисления надо проводить для любого момента времени t, промежутка времени от t до t + At и закона движения, выражаемого формулой s = f(t). Тогда средняя скорость движения за промежуток времени от t aot + At даётся формулой Дs/Дt, где Дs = - f(t + Дt) - f(t), а скорость движения в момент времени t равна

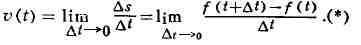
Осн. преимущество скорости в данный момент времени, или мгновенной скорости, перед средней скоростью состоит в том, что она, как и закон движения, является функцией времени t, а не функцией интервала (f,t + Дt). С другой стороны, мгновенная скорость представляет собой некоторую абстракцию, поскольку непосредственному измерению поддаётся средняя, а не мгновенная скорость.

К выражению типа (*) приводит и задача (см. рис.) построения касательной к плоской кривой в нек-рой её точке М. Пусть кривая Г есть график функции у = f(x). Положение касательной будет определено, если будет найден её угловой коэффициент, т. е. тангенс угла а, образованного касательной с осью Ох. Обозначим через х<, абсциссу точки М, а через х₁= х_а + Дх - абсциссу точки M1. Угловой коэффициент секущей MM1 равен

 

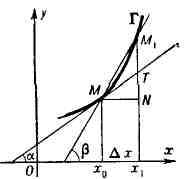
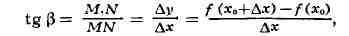
где Ду = М1N = f(x₀ + Дх) - f(x₀) -приращение функции на отрезке [х₀,х1]. Определяя касательную в точке М как предельное положение секущей MM1, когда х1 стремится к х₀, получаем

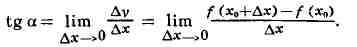
Отвлекаясь от механич. или геом.содержания приведённых задач и выделяя общий для них приём решения, приходят к понятию производной. Производной функции у = f(x) в точке х наз. предел (если он существует) отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, так что

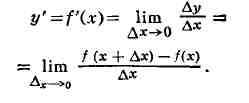
С помощью производной определяется, кроме уже рассмотренных, ряд важных понятий естествознания. Напр., сила тока

менение количества вещества за время Д?; вообще, производная по времени есть мера скорости процесса, применимая к самым разнообразным физ. величинам.

Производную функции у = f (х) обозначают f'(х), у', dy/dx, df/dx или Df (x). Если функция y = f(x) имеет в точке х₀ производную, то она определена как в самой точке Ха, так и в нек-рой окрестности этой точки и непрерывна в точке х_а. Обратное заключение было бы, однако, неверным. Напр., непрерывная в каждой точке функция у =|х| = + КОРЕНЬ(х²⁾, графиком к-рой служат биссектрисы первого и второго координатных углов, при х = 0 не имеет производной, т. к. отношение Дy//Дx не имеет предела при Дх->0: если Дх> 0, это отношение равно + 1, а если Дx<0, то оно равно -1. Более того, существуют непрерывные функции, не имеющие производной ни в одной точке (см. Непрерывная функция).

Операцию нахождения производной называют дифференцированием. На классе функций, имеющих производную, эта операция линейна.

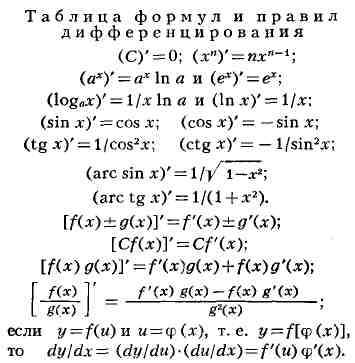
Здесь С, п и а - постоянные, я>0. Эта таблица, в частности, показывает, что производная от всякой элементарной функции есть снова элементарная функция.

Если производная f'(x), в свою очередь, имеет производную, то её называют второй производной функции у = f(x) и обозначают

у", f"(x), d²y/dx², d²f/dx² или D²f(x). Для прямолинейно движущейся точки вторая производная характеризует её ускорение.

Аналогично определяются и производные.более высокого (целого) порядка. Производная порядка п обозначается уⁿ, fⁿ(x), dⁿy/dxⁿ, dⁿf/dxⁿили Dⁿf(x).

Дифференциал. Функция у = f(x), область определения к-рой содержит нек-рую окрестность точки х₀, наз. дифференцируемой в точке х₀, если её приращение

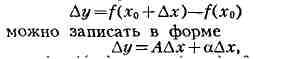
где А=А(х₀), а= a(x,х₀)->0 при х->хо. В этом и только в этом случае выражение АДх наз. дифференциалом функции f(x) в точке х_а и обозначается dy или df(xo). Геометрически дифференциал (при фиксированном значении -г₀ и меняющемся приращении Дх) изображает приращение ординаты касательной, т. е. отрезок NT (см. рис.). Дифференциал dy представляет собой функцию как от точки х₀, так и от приращения Дх. Говорят, что дифференциал есть главная линейная часть приращения функции, понимая под этим, что, при фиксированном х₀, dy есть линейная функция от Дх; и разность Дy - dy есть бесконечно малая относительно Дх. Для функции f(x) = х имеем dx = Дх, т. е. дифференциал независимого переменного совпадает с его приращением. Поэтому обычно пишут dy = Adx. Имеется тесная связь между дифференциалом функции и её производной. Для того чтобы функция от одного п е-ременного y= f(x) имела в точке х₀дифференциал, необходимо и достаточно, чтобы она имела в этой точке (конечную) производную f'(х₀), и справедливо равенство dy = f (х₀)dx. Наглядный смысл этого предложения состоит в том, что касательная к кривой y - f(x) в точке с абсциссой х₀ как предельное положение секущей является также такой прямой, к-рая в бесконечно малой окрестности точки х₀ примыкает к кривой более тесно, чем любая другая прямая. Таким образом, всегда А(х₀) = f'(xa), запись dy/dx можно понимать не только как обозначение для производной f'(х₀), но и как отношение дифференциалов зависимого и независимого переменных. В силу равенства dy = f'(х₀)dx правила нахождения дифференциалов непосредственно вытекают из соответствующих правил нахождения производных.

Рассматриваются также дифференциалы высших порядков. На практике с помощью дифференциалов часто производят приближённые вычисления значений функции, а также оценивают погрешности вычислений. Пусть, напр., надо вычислить значение функции f(x) в точке х, если известны f(xo) и f'(xo). Заменяя приращение функции её дифференциалом, получают приближённое равенство f(x₁)~~f(х₀)+df(х₀)=f(х₀)+f'(х₀)+(х₁-х₀)

Погрешность этого равенства приближённо равна половине второго дифференциала функции, т. е.

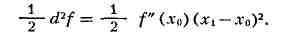
Приложения. В Д. и. устанавливаются связи между свойствами функции и её производных (или дифференциалов), выражаемые основными теоремами Д. и. К их числу относятся Ролля теорема, формула Лагранжа f(a) - f(b) = f'(c) (b-а), где a < с < b (подробнее см. Конечных приращений формула), и Тейлора формула.

Эти предложения позволяют методами Д. и. провести подробное исследование поведения функций, обладающих достаточной гладкостью (т. е. имеющих производные достаточно высокого порядка). Таким путём удаётся исследовать степень гладкости, выпуклость и вогнутость, возрастание и убывание функций, их экстремумы, найти их асимптоты, точки перегиба (см. Перегиба точка), вычислить кривизну кривой, выяснить характер её особых точек и т. д. Напр., условие f'(x)>0 влечёт за собой (строгое) возрастание функции у = f(x), а условие f"(x) >0 -её (строгую) выпуклость. Все точки экстремума дифференцируемой функции, принадлежащие внутренности её области определения, находятся среди корней уравнения f'(x) = 0.

Исследование функций при помощи производных составляет основное приложение Д. и. Кроме того, Д. и. позволяет вычислять различного рода пределы функций, в частности пределы вида О/С и БЕСКОНЕЧНОСТЬ/БЕСКОНЕЧНОСТЬ (см. Неопределённое выражение, Лопиталя правило). Д. и. особенно удобно для исследования элементарных функций, т. к. в этом случае их производные выписываются в явной форме.

Д. и. функций многих переменных. Методы Д. и. применяются для изучения функций нескольких переменных. Для функции двух независимых переменных z = f (х,у) частной производной по х наз. производная этой функции по .г при постоянном у. Эта частная производная обозначается z'_x, f'_x(x,y), dz/dx или df(x,y)/dx, так что

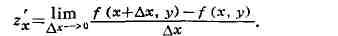
Аналогично определяется и обозначается частная производная z по у. Величина

Дz = f(x + Дx,y + Дy) - f(x,y) наз. полным приращением функции z= f(x,y). Если его можно представить в виде

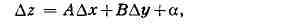
где а - бесконечно малая более высокого порядка, чем расстояние между точками (х,у) и (x + Дx,у + Дy), то говорят, что функция z=f(x,y) дифференцируема. Слагаемые АДх + ВДу образуют полный дифференциал dz функции z = f(x,y), причём А = z'_x, B = z'_y. Вместо Д.Т и Ду обычно пишут dx и dy, так что

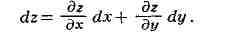
Геометрически дифференцируемость функции двух переменных означает существование у её графика касательной плоскости, а дифференциал представляет собой приращение аппликаты касательной плоскости, когда независимые переменные получают приращения dx и dy. Для функции двух переменных понятие дифференциала является значительно более важным и естественным, чем понятие частных производных. В отличие от функций одного переменного, для функций двух переменных существование обеих частных производных первого порядка ещё не гарантирует дифференцируемости функции. Однако, если частные производные кроме того ещё непрерывны, то функция дифференцируема.

Аналогично определяются частные производные высших порядков. Частные производные d²f/dx² и d²f/dy², в которых дифференцирование ведётся по одному переменному, называют чистыми, а частные производные d²f/dxdy и d²f/dydx - смешанными. Если смешанные частные производные непрерывны, то они между собой равны. Все эти определения и обозначения переносятся на случай большего числа переменных.

Историческая справка. Отдельные задачи об определении касательных к кривым и о нахождении максимальных и минимальных значений переменных величин были решены ещё математиками Древней Греции. Напр., были найдены способы построения касательных к коническим сечениям и нек-рым другим кривым. Однако разработанные античными математиками методы были применимы лишь в весьма частных случаях и далеки от идей Д. и.

Эпохой создания Д. и. как самостоят, раздела математики следует считать то время, когда было понято, что указанные специальные задачи вместе с рядом других (в особенности с задачей определения мгновенной скорости) решаются при помощи одного и того же математич. аппарата - при помощи производных и дифференциалов. Это понимание было достигнуто И. Ньютоном и Г. Лейбницем.

Ок. 1666 И. Ньютон разработал метод флюксий (см. Флюксий исчисление). Осн. задачи Ньютон формулировал в терминах механики: 1) определение скорости движения по известной зависимости пути от времени; 2) определение пройденного за данное время пути по известной скорости. Непрерывную переменную Ньютон называл флюентой (текущей), её скорость -флюкcиеq. Т. о., у Ньютона главными понятиями были производная (флюксия) и неопределённый интеграл как первообразная (флюента). Он стремился обосновать метод флюксий с помощью теории пределов, хотя последняя была им лишь намечена.

В сер. 70-х гг. 17 в. Г. Лейбниц разработал очень удобный алгоритм Д. и. Осн. понятиями у Лейбница явились дифференциал как бесконечно малое приращение переменного и определённый интеграл как сумма бесконечно большого числа дифференциалов. Лейбницу принадлежат обозначения дифференциала dx и интеграла ИНТЕГРАЛ (ydx), ряд правил дифференцирования, удобная и гибкая символика и, наконец, сам термин "дифференциальное исчисление". Дальнейшее развитие Д. и. шло сначала по пути, намеченному Лейбницем; большую роль на этом этапе сыграли работы братьев Я. и И. Бернулли, Б. Тейлора и др.

Следующим этапом в развитии Д. и. были работы Л. Эйлера и Ж. Лагранжа (18 в.). Эйлер впервые стал излагать его как аналитич. дисциплину, независимо от геометрии и механики. Он вновь выдвинул в качестве основного понятия Д. и. производную. Лагранж пытался строить Д. и. алгебраически, пользуясь разложением функций в степенные ряды; ему, в частности, принадлежит введение термина -"производная" и обозначения у' или f'(x). В нач. 19 в. была удовлетворительно решена задача обоснования Д. и. на основе теории пределов. Это было выполнено гл. обр. благодаря работам О. Коши, Б. Больцано и К. Гаусса. Более глубокий анализ исходных понятий Д. и. был связан с развитием теории множеств и теории функций действительного переменного в кон. 19 -нач. 20 вв.

Лит.: История-Вилейтнер Г., История математики от Декарта до середины 19 столетия, пер. с нем., 2 изд., М., 1966; Строик Д. Я., Краткий очерк истории математики, пер. с нем., 2 изд., М., 1969; Cantor М., Vorlesungen uber Geschichte der Mathematik, 2 Aufl., Bd 3-4, Lpz.- В., 1901-24.

Работы основоположников и классиков Д. и. Ньютон И., Математические работы, пер. с латин., М.- Л., 1937; Леибниц Г., Избранные отрывки из математических сочинений, пер. с латин., "Успехи математических наук", 1948, т. 3, в. 1; Л'Опиталь Г. Ф. де, Анализ бесконечно малых, пер. с франц., М.-Л., 1935; Эйлер Л., Введение в анализ бесконечных, пер. с латин., 2 изд., т. 1, М., 1961; его же, Дифференциальное исчисление, пер. с латин., М.- Л., 1949; Коши О. Л., Краткое изложение уроков о дифференциальном и интегральном исчислении, пер. с франц., СПБ, 1831; его же, Алгебраический анализ, пер. с франц., Лейпциг, 1864.

Учебники и учебные пособия по Д. и. Xинчин А. Я., Краткий курс математического анализа, 3 изд., М., 1957; его ж е, Восемь лекций по математическому анализу, 3 изд., М.- Л., 1948; Смирнов В. И., Курс высшей математики, 22 изд., т. 1, М., 1967; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969; Ла Валле-Пуссен Ш. Ж. де, Курс анализа бесконечно малых, пер. с франц., т. 1, Л. -М., 1933; Курант Р., Курс дифференциального и интегрального исчисления, пер. с нем. и англ., 4 изд., т. 1, М., 1967; Банах С., Дифференциальное и интегральное исчисление, пер. с польск., 2 изд., М., 1966; Рудин У., Основы математического анализа, пер. с англ., М., 1966.

Под редакцией С. Б. Стечкина.

ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫЕ УРАВНЕНИЯ, уравнения, связывающие аргумент, искомую функцию, её производные и приращения (раз:п-сти). Напр., у' = kДy, где у = у(х), Дy = y(x + h) - у(х). Подстановка последнего выражения в исходное уравнение показывает, что Д.-р.у. - это частный случай дифференциальных уравнений с отклоняющимся аргументом, поэтому Д.-р. у. изучаются в рамках этого более широкого класса уравнений.

ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ, раздел матем. теории управления, в к-ром изучается управление объектом в конфликтных ситуациях (см. Игр теория). В Д. и. возможности игроков описываются дифференциальными уравнениями, содержащими управляющие векторы, к-рыми распоряжаются игроки. Для выбора своего управления каждый игрок может использовать лишь текущую информацию о поведении игроков. Различают Д. и. двух игроков и многих игроков. Наиболее исследованными являются Д. и. преследования, в к-рых количество игроков равно 2, одного называют догоняющим, другого убегающим. Цель догоняющего - приведение вектора z(t) на заданное множество М за возможно короткое время; цель убегающего - по возможности оттянуть момент прихода вектора z(t) на М. Основополагающие результаты в Д. и. получены в 60-е гг. 20 в. в СССР Л. С. Понтрягиным, Н. Н. Красовским, Е. Ф. Мищенко, Б. Н. Пшеничным и др., в США - Р. Айзексом, Л. Берковицем, У. Флемингом и др. М. С. Никольский.

ДИФФЕРЕНЦИАЛЬНЫЕ ПOШЛИНЫ, см. Пошлины дифференциальные.

ДИФФЕРЕНЦИАЛЬНЫЕ ПРИЗНАКИ, определённые свойства языковых единиц, противопоставляющие эти единицы другим единицам того же уровня, к-рые либо не обладают данными свойствами, либо обладают противопоставленными им свойствами. Напр., рус. звук "ль" противопоставлен звуку "л" по палатализованности (наличие - отсутствие свойства), словоформа чстол" - словоформе "столы" по числу (ед. число и мн. число), значение слова "человек" - значению слова "камень" по одушевлённости (одушевлённое - неодушевлённое). Понятие Д. п. более всего разработано в фонологии, где оно является основополагающим. Различаются релевантные и нерелевантные (иррелевантные) признаки. Данный Д. п. является релевантным для данной фонологич. системы, если по этому Д. п. противопоставляются к.-л. фонемы данного языка (так, признак "звонкости -глухости" согласных релевантен для рус., нем., франц., англ. и нек-рых других языков). Однако и релевантный Д. п. может оказаться нерелевантным при нек-рых условиях, напр. если он обусловлен позицией звука (глухость согласных на конце слов в рус. языках нерелевантна) или особенностями фонологич. системы.

Амер. учёные Р. Якобсон, Г. Фант, М. Халле предложили список из 12 универсальных двоичных акустич. Д. п., достаточный, по их мнению, для исчерпывающего описания фонологич. системы любого языка. Понятие Д. п. используется и на других уровнях языковой структуры и является одним из осн. понятий совр. лингвистики.

Лит.: Трубецкой Н.С., Основы фонологии, пер. с нем., М., 1960; Блумфилд Л., Язык, пер. с англ., М., 1968; Jakоbsоn R., Fant С. G. М., Halle M., Preliminaries to speech analysis, Camb., 19Г5 (рус. пер. 2 части - в кн.: Новое в лингвистике, в. 2, М., 1962); Jakobson R., Halle M., Fundamentals of language, VGravenhage, 1956.

В. В. Раскин.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, уравнения, содержащие искомые функции, их производные различных порядков и независимые переменные. Теория Д. у. возникла в кон. 17 в. под влиянием потребностей механики и других естественнонауч. дисциплин, по существу одновременно с интегральным, исчислением и дифференциальным исчислением.

Простейшие Д. у. встречались уже в работах И. Ньютона и Г. Лейбница, термин "Д. у." принадлежит Лейбницу. Ньютон при создании исчисления флюксий и флюент (см. Флюксий исчисление) ставил две задачи: по данному соотношению между флюентами определить соотношение между флюксиями; по данному ур-нию, содержащему флюксии, найти соотношение между флюентами. С совр. точки зрения, первая из этих задач (вычисление по функциям их производных) относится к дифференциальному исчислению, а вторая составляет содержание теории обыкновенных Д. у. Задачу нахождения неопределённого интеграла F(x) функции f(x) Ньютон рассматривал просто как частный случай его второй задачи. Такой подход был для Ньютона как создателя основ матем. естествознания вполне оправданным: в очень большом числе случаев законы природы, управляющие теми или иными процессами, выражаются в форме Д. у., а расчёт течения этих процессов сводится к решению Д. у.

Следующие два простых примера могут служить иллюстрацией к сказанному.

1) Если тело, нагретое до темп-ры Т, помещено в среду, темп-pa к-рой равна нулю, то при известных условиях можно считать, что приращение ДГ (отрицательное в случае T>0) его темп-ры за малый промежуток времени Дt с достаточной точностью выражается формулой ДT= -kTДt, где k - постоянный коэффициент. При матем. обработке этой физ. задачи считают, что выполняется точно соответствующее предельное соотношение между дифференциалами dT=-kTdt, (1) т. е. имеет место Д. у. T'=-kT, где Т' обозначает производную по t. Решить полученное Д. у., или, как выражаются иначе, проинтегрировать его, значит найти функции, обращающие его в тождество. Для ур-ния (1) все такие функции (т. е. все его частные решения) имеют вид T = Ce-^kt, (2) где С постоянно. Сама формула (2) с произвольной постоянной С наз. общим решением ур-ния (1).

2) Пусть, напр., груз р массы т подвешен к пружине и находится в положении равновесия (рис. 1, а). Отклоняя его от положения равновесия с помощью растяжения пружины (рис. 1, б), приводят груз в движение.

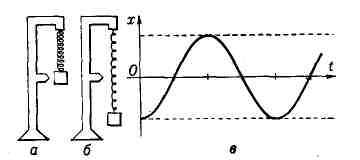
Рис. 1.

Если x(t) обозначает величину отклонения тела от положения равновесия в момент времени t, то ускорение тела выражается 2-й производной x"(t). Сила mx"(t), действующая на тело, при небольших растяжениях пружины по законам теории упругости пропорциональна отклонению x(t). Т. о., получается Д. у. mx"(t)=-kx(t). (3) Его решение имеет вид:

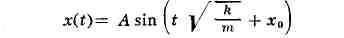
и показывает, что тело будет совершать гармонические колебания (рис. 1, в).

Теория Д. у. выделилась в самостоятельную детально разработанную науч. дисциплину в 18 в. (труды Д. Бернулли, Ж. Д'Аламбера и особенно Л. Эйлера).

Д. у. делятся на "обыкновенные", содержащие производные одной или нескольких функций одного независимого переменного, и -"уравнения с частными производными", содержащие частные производные функций нескольких независимых переменных. Порядком Д. у. наз. наибольший порядок входящих в него производных. Так,

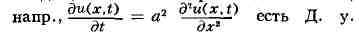
с частными производными 2-го порядка.

Обыкновенные дифференциальные уравнения. Уравнения 1-го порядка. Обыкновенным Д. у. 1-го порядка с одной неизвестной функцией (только такие пока будут рассматриваться) наз. соотношение F(x, у, у') = О (А) между независимым переменным х, искомой функцией у и её производной . Если ур-ние (А) может быть разрешено относительно производной, то получается ур-ние вида у'=f(x, у)- (Б) Многие вопросы теории Д. у. проще рассматривать для таких разрешённых относительно производной ур-ний, предполагая функцию f(x,y) однозначной.

Ур-ние (Б) можно записать в виде соотношения между дифференциалами f(x, y)dx-dy = 0, тогда оно становится частным случаем ур-ний вида

Р (х, y)dx + Q (х,у) dy = 0. (В) В ур-ниях вида (В) естественно считать переменные х и у равноправными, т. е. не интересоваться тем, какое из них является независимым.

Геометрическая интерпретация дифференциальных уравнений. Пусть у = у(х) есть решение ур-ния (Б). Геометрически это значит, что в прямоугольных координатах касательная к кривой у = у(х) имеет в каждой лежащей на ней точке М (х,у) угловой коэффициент k = f(x,y). Т. о., нахождение решений у = у(х) геометрически сводится к такой задаче: в каждой точке нек-рой области на плоскости задано "направление", требуется найти все кривые, к-рые в любой своей точке М имеют направление, заранее сопоставленное этой точке. Если функция f(x,y) непрерывна, то это направление меняется при перемещении точки М непрерывно, и можно наглядно изобразить поле направлений, проведя в достаточно большом числе достаточно густо расположенных по всей рассматриваемой области точек короткие чёрточки с заданным для этих точек направлением. На рис. 2 это выполнено для

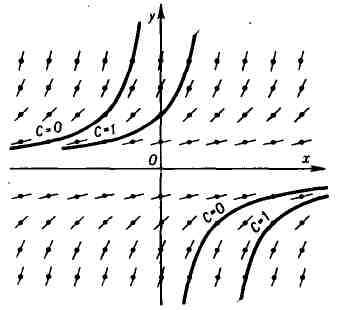
Рис. 2.

уравнения у' = у². Рисунок позволяет сразу представить себе, как должны выглядеть графики решения - т. н. интегральные кривые Д. у. Вычисление показывает, что общее ре-

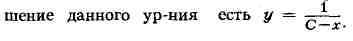
На рис. 2 вычерчены интегральные кривые, соответствующие значениям параметра С = 0 и С = 1.

График любой однозначной функции у = у(х) пересекает каждую прямую, параллельную оси Оу, только один раз. Таковы, следовательно, интегральные кривые любого ур-ния (Б) с однозначной непрерывной функцией в правой части. Новые возможности для вида интегпаль-ных кривых открываются при переходе к ур-ниям (В). При помощи пары непрерывных функций Р(х, у) и О (х, у) можно задать любое непрерывное "поле направлений". Задача интегрирования ур-ний (В) совпадает с чисто геометрической (не зависящей от выбора осей координат) задачей разыскания интегральных кривых по заданному на плоскости полю направлений. Следует заметить, что тем точкам (x₀, уо), в к-рых обе функции Р (х, у) и Q (х, у) обращаются в нуль, не соответствует к.-л. определённое направление. Такие точки наз. особыми точками уравнения (В).

Пусть, напр., задано уравнение ydx + xdy = 0, к-рoe можно записать в виде

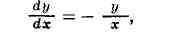
хотя, строго говоря, правая часть этого последнего уравнения теряет смысл при х = 0 и у = 0. Соответствующие поле направлений и семейство интегральных кривых, являющихся в этом случае окружностями х² + у² = С, изображены на рис. 3.

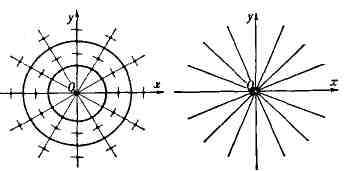
Рис. 3. Рис. 4.

Начало координат (х = 0, у = 0) - особая точка данного уравнения. Интегральными кривыми уравнения ydx - xdy = 0, изображёнными на рис. 4, являются всевозможные прямолинейные лучи, выходящие из начала координат; начало координат является особой точкой и этого ур-ния.

Начальные условия. Геом. интерпретация Д. у. 1-го порядка приводит к мысли, что через каждую внутр. точку М области G с заданным непрерывным полем направлений можно провести одну вполне определённую интегральную кривую.

В отношении существования интегральной кривой сформулированная гипотеза оказывается правильной. Доказательство этого предложения принадлежит Дж. Пеано. В отношении же единственности интегральной кривой, проходящей через заданную точку, высказанная выше гипотеза оказывается, вообще говоря, ошибочной. Уже для такого простого ур-ния, как

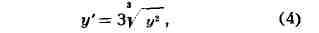
у к-рого правая часть непрерывна во всей плоскости, интегральные кривые имеют вид, изображённый на рис. 5. Единственность интегральной кривой, проходящей через заданную точку, нарушается здесь во всех точках оси Ох.

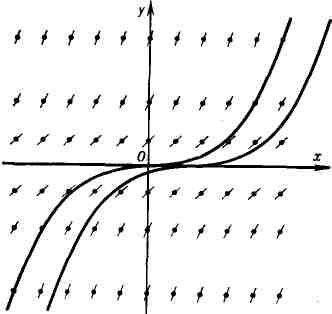
Рис. 5.

Единственность, т. е. однозначное определение интегральной кривой условием её прохождения через заданную точку, имеет место для ур-ний (Б) с непрерывной правой частью при том дополнительном условии, что функция f (x,y) имеет в рассматриваемой области ограниченную производную по у.

Это требование является частным случаем следующего, несколько более широкого условия Липшица: существует такая постоянная L, что в рассматриваемой области всегда |f(x, у₁)-f(x, у₂)| <L | у₂ - у₁ |. Это условие чаще всего приводится в учебниках как достаточное условие единственности.

С аналитич. стороны теоремы существования и единственности для уравнения вида (Б) обозначают следующее: если выполнены надлежащие условия [напр., функция f (x, у) непрерывна и имеет ограниченную производную по у], то задание для "начального" значения Хо независимого переменного х "начального" значения у₀ = у (х₀) функции у(х) выделяет из семейства всех решений у(х) одно определённое решение. Напр., если для рассмотренного выше уравнения (1) потребовать, чтобы в начальный момент времени t₀ = 0 темп-pa тела была равна "начальному" значению Т₀, то из бесконечного семейства решений (2) выделится одно определённое решение, удовлетворяющее заданным начальным условиям: T(t) = T₀e^-kT.

Этот пример типичен: в механике и физике Д. у. обычно определяют общие законы течения к.-л. явления; однако, чтобы получить из этих законов определённые количеств, результаты, надо присоединить к ним сведения о начальном состоянии изучаемой физ. системы в нек-рый определённый выбранный в качестве "начального" момент времени t₀.

Если условия единственности выполнены, то решение у(х), удовлетворяющее условию у(х₀) = y₀, можно записать в виде:
y(x) = ф(x; х₀, y₀), (5)

где х₀ и y₀ входят как параметры, функция же ф (х; х₀, y₀) трёх переменных х, х₀ и y₀ однозначно определяется самим уравнением (Б). Важно отметить, что при достаточно малом изменении поля (правой части Д. у.) функция Ф (х; х₀, y₀) меняется сколь угодно мало на конечном промежутке изменения переменного х - имеется непрерывная зависимость решения от правой части Д. у. Если правая часть f(x, у) Д. у. непрерывна и её производная по у ограничена (или удовлетворяет условию Липшица), то имеет место также непрерывность ф (х; x_о, у₀) по х₀ y₀.

Если в окрестности точки (х_а, у₀) для уравнения (Б) выполнены условия единственности, то все интегральные кривые, проходящие через достаточно малую окрестность точки (х₀, у₀), пересекают вертикальную прямую х = х₀ и определяются ординатой у = С своей точки пересечения с этой прямой (см. рис. 6). Т. о., все эти решения содержатся в семействе с одним параметром С: y(x) = F(x,C), к-рое является общим решением Д- у. (Б).

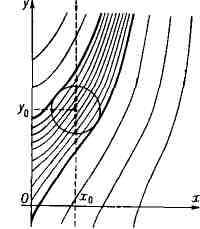
Рис. 6.

В окрестности точек, в к-рых нарушаются условия единственности, картина может быть сложнее. Весьма сложен и вопрос о поведении интегральных кривых "в целом", а не в окрестности точки (х₀, у о).

Общий интеграл. Особые решения. Естественно поставить обратную задачу: задано семейство кривых, зависящих от параметра С, требуется найти Д. у., для к-рого кривые заданного семейства служили бы интегральными кривыми. Общий метод для решения этой задачи заключается в следующем: считая семейство кривых на плоскости хОу заданным при помощи соотношения F(x,y,C) = 0, (6) дифференцируют (6) при постоянном С и получают

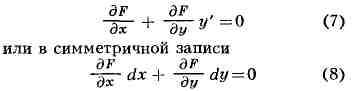
и из двух уравнений (6) и (7) или (6) и (8) исключают параметр С. Если данное Д. у. получается таким образом из соотношения (6), то это соотношение наз. общим интегралом заданного Д. у. Одно и то же Д. у. может иметь много различных общих интегралов. После нахождения для заданного Д. у. общего интеграла оказывается необходимым, вообще говоря, ещё исследовать, не имеет ли Д. у. дополнительных решений, не содержащихся в семействе интегральных кривых (6).

Пусть, напр., задано семейство кривых (x-С)³-y= 0. (9)

Дифференцируя (9) при постоянном С, получают 3(x-С)²-y' = 0, после же исключения С приходят к Д у 27y²-(y)³ = 0, (10) равносильному ур-нию (4). Легко видеть, что, кроме решений (9), ур-ние (10) имеет решение y= 0. (11) Решение уравнения (10) самого общего вида таково:

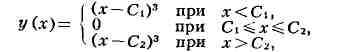
где - БЕСКОНЕЧНОСТЬ =<C1=<C2=< + БЕСКОНЕЧНОСТЬ (рис. 7). Оно зависит от двух параметров С1 и С2, но составляется из кусков кривых однопараметрич. семейства (9) и куска особого решения (11).

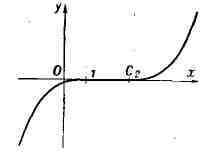
Рис. 7.

Решение (11) уравнения (10) может служить примером особого решения Д. у. В качестве другого примера можно рассмотреть семейство прямых 4(y-Сx) + С² = 0. (12) Эти прямые являются интегральными кривыми Д. у. 4(у-ху') + (у') = 0.

Особой же интегральной кривой этого Д. у. служит парабола x²-y=0 огибающая прямые (12) (рис. 8). Картина, наблюдавшаяся в рассмотренном примере, типична; особые интегральные кривые обычно являются огибающими семейства интегральных кривых, получаемых из общего решения.

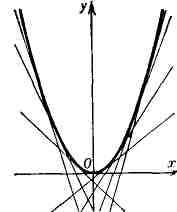
Рис. 8.

Дифференциальные у р-ния высших порядков и системы дифференциальных ур-ний. Д. у. и-го порядка с одной неизвестной функцией у(х) независимого переменного х записывают так: F(x,y, y', у", ... , y^(n-1), yⁿ) = 0.(13) Если ввести дополнительные неизвестные функции y1 = y', y2 = y",..., y_n-1 = y^n-1, (14) то уравнение (13) можно заменить системой из п уравнений с п неизвестными функциями, но зато 1-го порядка. Для этого достаточно к п-1 ур-ниям (14) присоединить ур-ние F(x, у, y1, y2,..., y_n-1, y_n-1') = 0.

Аналогичным образом сводятся к системам ур-ний 1-го порядка и системы ур-ний высших порядков. В механике сведение систем ур-ний 2-го порядка к системе из удвоенного числа ур-ний 1-го порядка имеет простой механич. смысл. Напр., система трёх ур-ний движения материальной точки тх" = р(х, у, z), my" = Q(x, у, z), mz" = R(x, у, z), где х, у, z - координаты точки, зависящие от времени t, сводится к системе шести ур-ний: ти'=р(х, у, z), mv' = Q(x, у, z), mw' = R(x, у, z), и = х', v = y', w = z' при помощи введения в качестве новых переменных составляющих и, v, w скорости.

Наибольшее значение имеют системы, в к-рых число ур-ний равно числу неизвестных функций. Система из п ур-ний 1-го порядка с п неизвестными функциями, разрешённая относительно производных, имеет вид:

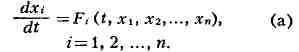
Решением системы Д. у. (а) наз. система функций xt(t), *₂(t),..., x_n(t), к-рая при подстановке в уравнения (а) обращает их в тождества. Часто встречаются системы вида (а), в к-рых правые части не зависят от f. В этом случае изучение системы (а) в основном сводится к изучению системы из (и - 1)-го уравнения, к-рую целесообразно записывать в симметричной форме

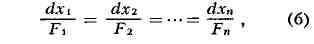
не предрешая вопроса о том, от какого из переменных х₁, х₂, ...,х_п мыслятся зависящими остающиеся п - 1 переменных. Считая х = (х₁, х₂, ..., х_п) вектором, можно записать систему (а) в виде одного векторного ур-ния:

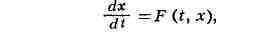
что позволяет широко пользоваться при изучении систем (а) аналогией с теорией одного ур-ния 1-го порядка вида (Б). В частности, оказывается, что для систем (а) сохраняют силу основные результаты относительно существования и единственности решения задачи с начальными условиями: если в окрестности точки (t₀, х⁰₁ , х⁰₂ ,..., х⁰_n ) все функции F1 непрерывны по совокупности переменных t, x₁, х₂, ..., х_п и имеют ограниченные производные по переменным x₁, x₂, ..., х_п, то задание начальных значений xi (t_o) = х⁰_i, i = 1,2,..., п, определяет одно, вполне определённое, решение системы (а). Этим объясняется то, что, вообще говоря, решение систем из п уравнений 1-го порядка с п неизвестными функциями зависит от п параметров.

Для приведённых выше конкретных примеров Д. у. их общее решение удаётся выразить при помощи элементарных функций. Типы Д. у., допускающие такого рода решение, детально изучаются. Часто придерживаются более общей точки зрения, считая Д. у. "решённым", если искомая зависимость между переменными (и входящими в общее решение параметрами C₁, С₂,...) может быть выражена при помощи элементарных функций и одной или нескольких операций взятия неопределённого интеграла ("решение выражено в квадратурах").

Большой общностью обладают способы нахождения решений при помощи разложения их в степенные ряды. Напр., если правые части ур-ний (а) в окрестности точки (t₀, х⁰₁ , х⁰₂ ,..., х⁰_n) голоморфны (см. Аналитические функции), то решение соответствующей начальной задачи выражается функциями xi (t), разлагающимися в степенные ряды:

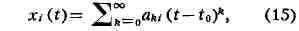
коэффициенты к-рых можно найти последовательным дифференцированием правых частей Д. у. (а) и сопоставлением коэффициентов при одинаковых степенях в левых и правых частях этих ур-ний.

Из специальных типов Д. у. особенно хорошо разработана теория линейных Д. у. и систем линейных Д. у. (см. Линейные дифференциальные уравнения).

Для линейных Д. у. сравнительно просто решаются также вопросы "качественного" поведения интегральных кривых, т. е. их поведение во всей области задания Д. у. Для нелинейных Д. у., где нахождение общего решения особенно сложно, вопросы качеств, теории Д. у. приобретают иногда даже доминирующее значение. После классич. работ А. М. Ляпунова ведущую роль в качеств, теории Д. у. играют работы сов. математиков, механиков и физиков. В связи с этой теорией см. Динамическая система, Особая точка, Устойчивость, Предельный цикл.

Большое значение имеет аналитич. теория Д. у., изучающая решения Д. у. с точки зрения теории аналитич. функций, т. е. интересующаяся, напр., расположением их особых точек в комплексной плоскости и т. п.

Наряду с рассмотренной выше начальной задачей, в к-рой задаются значения искомых функций (а в случае ур-ний старших порядков и их производных) в одной точке (при одном значении независимого переменного), находят широкое применение краевые задачи.

Дифференциальные уравнения с частными производными. Типичной особенностью Д. у. с частными производными и систем Д. у. с частными производными является то, что для однозначного определения частного решения здесь требуется задание не значений того или иного конечного числа параметров, а нек-рых функций. Напр., общим решением уравнения

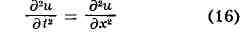
является выражение u(t,x) = f(x + t) + g(x-t), где f и g - произвольные функции. Т. о., Д. у. (16) лишь в той мере ограничивает произвол в выборе функции двух переменных и(х,у), что её удаётся выразить через две функции f(z) и g(v) от одного переменного, к-рые остаются [если в дополнение к ур-нию (16) не дано к.-л. "начальных" или "краевых" условий] произвольными.

Типичной задачей с начальными условиями для системы Д. у. с частными производными 1-го порядка

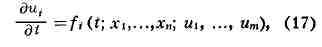
где независимыми переменными являются t, x₁, ..., х_п, a u₁, ..., u_m суть функции от этих независимых переменных, может служить задача Коши: по заданным при к.-л. t = to значениям ui(t0,x1,...,х_п)-фi(x1,..., х_п) i=1, 2,..., т, найти функции т (t, xi, ..., х_п).

В теории Д. у. с частными производными порядка выше первого и систем Д. у. с частными производными рассматриваются как задачи типа Коши, так и ряд краевых задач.

При постановке и решении краевых задач для Д. у. с частными производными порядка выше первого существенное значение имеет тип ур-ния. В качестве примера можно привести классификацию Д. у. с частными производными 2-го порядка с одной неизвестной функцией z (х, у) от двух переменных: F(x, у, z, р, q, r, s, t) = 0, (18) где

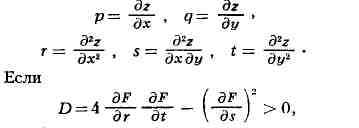
то (18) есть эллиптическое ур-ние. Примером может служить ур-ние Лапласа:

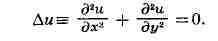
Если D<0, то (18) есть гиперболическое у р - н и е. Примером может служить ур-ние колебания струны:

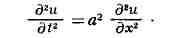
Если D = 0, то (18) есть параболическое у р - н и е. Примером может служить ур-ние распространения тепла:

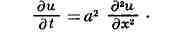
О краевых задачах для этих различных типов ур-ний см. Уравнения математической физики.

Лит.: Обыкновенные Д. у. Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959; Петровский И. Г., Лекции по теории обыкновенных дифференциальных уравнений, 5 изд., М., 1964; Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 2 изд., М., 1965; Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 3 изд., М., 1965; Филиппов А. Ф., Сборник задач по дифференциальным уравнениям, 2 изд., М., 1965.

Д. у. с частными производными. Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961; Тихонов А.Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966; Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; Смирнов М. М., Задачи по уравнениям математической физики, 5 изд., М., 1968.

По материалам одноимённой статьи из 2-го издания БСЭ.

"ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ", ежемесячный научный математич. журнал, осн. в 1965, издаётся в Минске. Публикует результаты исследований в области дифференциальных, интегро-дифференциальных и интегральных ур-ний, а также ур-ний в конечных разностях. Переводится в США на англ. яз. и изд. под назв. "Differential equations".

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ, уравнения, связывающие аргумент, а также искомую функцию и её производные, взятые, вообще говоря, при различных значениях этого аргумента (в отличие от обычных дифференциальных уравнений). Примерами могут служить ур-ния

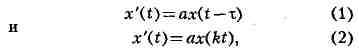
где постоянные а, т, k заданы; t = t -- (t - t) в ур-нии (1) и t - kt в ур-нии (2) - отклонения аргумента. Такие ур-ния появились в кон. 18 в. Неоднократно рассматривались сами по себе и в связи с решением геом. задач, а позднее -в связи с различными приложениями, прежде всего к теории регулирования. Построение систематич. теории Д. у. с о. а. было начато в 50-х гг. 20 в., а уже с 60-х гг. эта теория представляет собой значительный отдел матем. анализа.

Наиболее хорошо изучены линейные однородные автономные (т. е. с постоянными коэффициентами и постоянными отклонениями аргумента) Д. у. со. а.; к таким ур-ниям относится, напр., (1). Здесь имеется достаточно полная система решений вида х = е^pt, причём для отыскания р получается трансцендентное характеристическое ур-ние вида Р(р) = 0, где Р(р) - сумма членов вида Aр^т е^aр, m>0- целое [напр., для (1) имеем Р(р) = р - aе^-tр]. Это ур-ние имеет, вообще говоря, бесконечное число комплексных корней. Прочие решения рассматриваемого Д. у. с о. а. разлагаются в ряды по указанным простейшим решениям, и поэтому об основных свойствах совокупности решений, в частности об их устойчивости, можно судить по расположению нулей функции Р(р).

Важнейший и наиболее изученный класс Д. у. с о. а. образуют дифференциальные ур-ния с запаздывающим аргументом, в к-рых старшая производная от искомой функции при к.-л. значении аргумента определяется через саму эту функцию и её младшие производные, взятые при меньших либо равных значениях аргумента. Примеры: ур-ние (1) при t=>0(t- запаздывание); ур-ние (2) при k=<1 и t=>0. Эти ур-ния и их системы, если аргументом служит время, описывают процессы с последействием, скорость к-рых в любой момент определяется их состоянием не только в тот же момент (как для обычных дифференциальных ур-ний), но и в предшествующие моменты. Такая ситуация возникает, в частности, в системах автоматич. управления при наличии запаздывания в органе управления. Уравнения с запаздывающим аргументом во многом напоминают обыкновенные дифференциальные ур-ния, однако в ряде отношений отличаются от них. Напр., если решение ур-ния (1) строится при t=>t₀, то в качестве начального условия х (t) должно быть задано при t₀-t=<t=<t₀, решение можно строить последовательно на интервалах t₀=<t=<t₀+t, t₀ + t=<t₀+2t, пользуясь на каждом шаге результатом вычислений с предыдущего шага. В линейном автономном случае к таким ур-ниям можно применять методы операционного исчисления.

Лит.: Пинни Э., Обыкновенные дифференциально-разностные уравнения, пер. с англ., М., 1961; Беллман Р., Кук К., Дифференциально-разностные уравнения, пер. с англ., М., 1967; Мышкис А. Д., Эльсгольц Л. Э., Состояние и проблемы теории дифференциальных уравнений с отклоняющимся аргументом, "Успехи математических наук", 1967, т. 22, в. 2 (134) (библ.): Эльсгольц Л. Э., Норкин С. Б., Введение в теорию дифференциальных уравнений с отклоняющимся аргументом, 2 изд., М., 1971.

А. Д. Мышкис.

ДИФФЕРЕНЦИАЛЬНЫЙ БИНОМ, биномиальный дифференциал, выражение вида x^m(a + bxⁿ)^pdx, где а и b - постоянные, отличные от нуля, т, п и р - рациональные числа. Интеграл от Д. 6. ИНТЕГРАЛ х^т (а + bⁿ)^p dx выражается в конечном виде через элементарные функции лишь в трёх случаях: 1) если р - целое число; 2) если (т +1)/n-целое число; 3) если [(m + 1)/n] + р-целое число. Эти три случая интегрируемости Д. б. были известны ещё Л. Эйлеру. П. Л. Чебышев в 1853 показал, что во всех остальных случаях интеграл от Д. б. в конечном виде через элементарные функции не выражается. Это один из первых случаев, когда вопрос об интегрируемости в конечном виде к.-л. достаточно общего класса аналитич. выражений был решён до конца. Результат Чебышева может быть поставлен в ряд с классич. теоремами о невозможности алгебраич. решения различных классов алгебраич. уравнений и о неразрешимости при помощи циркуля и линейки задачи о квадратуре круга.

ДИФФЕРЕНЦИАЛЬНЫЙ МАНОМЕТР, то же, что дифманометр.

ДИФФЕРЕНЦИАЛЬНЫЙ МЕТОД ИЗМЕРЕНИЙ, разностный метод, метод измерений, в к-ром определяют разность между измеряемой и известной физическими величинами. Известную величину чаще всего воспроизводят с помощью меры. Если разность между измеряемой и известной величинами мала, то погрешность измерения в основном определяется точностью знания известной величины. Напр., если разность не превышает 0,01 части измеряемой величины, измерение её с погрешностью 0,1% внесёт в общий результат погрешность не более 0,001%. Д. м. и. имеет большое значение при поверке средств измерений - сличении поверяемой меры с образцовой (напр., нормальных элементов при встречно-последовательном их включении), а также при испытаниях материалов и изделий сравнением их с образцами. В области линейных измерений Д. м. и. называют относительным методом. Д. м. и. превращается в нулевой метод измерений, если разность между измеряемой и известной величинами доводят до нуля (для этого известная величина должна быть регулируемой).

К. П. Широков.

ДИФФЕРЕНЦИАЛЬНЫЙ МЕХАНИЗМ, устройство, позволяющее получать результирующее движение как сумму или разность составляющих движений. В Д. м. с одной степенью свободы составляющие движения кинематически связаны и осуществляются одним приводом, а результирующее получается как разность этих движений. Д. м. с одной степенью свободы применяют для получения малых точных перемещений или больших сил (напр., в приборах, металлорежущих станках и т. п.).

В Д. м. с двумя и более степенями свободы составляющие движения независимы и выполняются каждое своим звеном. Известны разные типы таких Д. м., но наибольшее распространение получил Д. м. с коническими зубчатыми колёсами (обычно называемый просто дифференциалом), применяемый в автомобилях и др. транспортных машинах, механич. приводах и т. п. Зависимость между действительными скоростями звеньев Д. м. выражается формулой (w₁ + w₂= 2w_в или n₁ + n₂ = 2n_в, где w₁, w₂, w_в и n₁ п₂ и п_всоответственно угловые скорости и частоты вращения центральных колёс и водила. В вариаторе, работающем по замкнутой схеме, Д. м. позволяет расширить диапазон регулирования и осуществить реверсивное вращение выходного вала. В металлорежущих станках Д. м. применяется с целью упрощения настройки и уменьшения числа необходимых для этого сменных зубчатых колёс. В счётно-решающих машинах Д. м. используется для выполнения матем. операции сложения параметров.

Конический дифференциал: 1 и 2 - центральные колёса; 3 - сателлит; 4 - водило; w_1,, w₂ и w_в - угловые скорости центральных колёс и водила.

Н. Я. Ниберг.

ДИФФЕРЕНЦИАЦИЯ (франц. differentiation, от лат. differentia - разность, различие), разделение, расчленение, расслоение целого на различные части, формы и ступени.

ДИФФЕРЕНЦИАЦИЯ (биол.), 1) Д. филогенетическая, расчленение в процессе эволюции единой группы организмов на две или несколько - одна из характерных особенностей эволюции организмов. Наиболее важная филогенетич. Д. - процесс видообразования, приводящий к возникновению нового вида. Филогенетическая Д. неизбежно сопровождается возникновением иерархической системы форм (популяция, вид, род, семейство, отряд, класс и т. д.). Д. связана с интеграцией: целое становится в своих жизненных проявлениях более сложным, отдельные его части гармонично дополняют друг друга, что ведёт к более дифференцированному использованию среды обитания (возрастанию "суммы жизни", по Ч. Дарвину) и возникновению новых возможностей в эволюции. Д. носит адаптивный характер; в процессе эволюции происходит аккумуляция Д. общего значения, замена частных приспособлений общими. 2) Д. онтогенетическая - см. Дифференцировка. 3) Д. половая - см. Пол, Половое размножение.

Лит.: Шмальгаузен И. И., Организм как целое в индивидуальном и историческом развитии, М. - Л., 1942; его же, Проблемы дарвинизма, 2 изд.. Л., 1969.

Л. В. Яблоков.

ДИФФЕРЕНЦИАЦИЯ социальная, расчленение социального целого или его части на взаимосвязанные элементы; Д. обозначает как процесс расчленения, так и его результаты. В немарксистской социологии разрабатывались преим. формальные аспекты Д. Теорию Д. в кон. 19 в. выдвинул англ. философ Г. Спенсер, к-рый заимствовал этот термин из биологии и провозгласил Д. всеобщим законом эволюции материи от простого к сложному, проявляющуюся в обществе как разделение труда. Франц. социолог Э. Дюрк-гейм рассматривал Д. в результате разделения труда как закон природы и связывал Д. функций в обществе с ростом плотности населения и интенсивности межличностных и межгрупповых контактов. Нем. философ и социолог М. Вебер видел в Д. следствие процесса рационализации ценностей, норм и отношений между людьми. Совр. структурно-функциональная школа в немарксистской социологии (амер. социолог Т. Парсонс и др.) рассматривает Д. как наличное состояние социальной структуры и как процесс, ведущий к возникновению различных видов деятельности, ролей и групп, специализирующихся в выполнении отд. функций, необходимых для самосохранения социальной системы. Однако в рамках этой школы вопрос о причинах и типах Д. остаётся не решённым (см. Структурно-функциональный анализ). Наряду с функциональными, существуют таксономич. определения Д., когда термин обозначает просто различия социальных ролей, статусов, групп и орг-ций. В. И. Ленин подверг критике абстрактную трактовку процесса Д. в буржуазной социологии, не учитывающую того главного, что связано с разделением общества на антагонистические классы (см. Полн. собр. соч., 5 изд., т. 33, с. 10).

Основоположники марксизма-ленинизма проанализировали процесс Д. в обществе, связывая его с развитием производит. сил, разделением труда и усложнением обществ. структуры. Важнейшие стадии Д. - разделение земледельческого и скотоводческого труда, ремесла и земледелия, сферы произ-ва и семьи возникновение гос-ва. Марксизм требует конкретного изучения процессов Д. в обществе в целом - возникновения и формирования классов, социальных слоев и групп, выделения отд. сфер общества (производства, науки и др.), а также Д. внутри классов, обществ, сфер. Такой конкретный анализ показывает, напр., что если Д. при капитализме связана с ростом социального неравенства, то в условиях социализма происходит движение общества к социальной однородности, преодоление классовых различий.

Л. А. Седов.

ДИФФЕРЕНЦИАЦИЯ ДОХОДОВ НАСЕЛЕНИЯ, один из важнейших социально-экономич. показателей, характеризующий степень неравномерности распределения материальных и духовных Олаг между членами общества. Количества или доли, в к-рых общественный продукт распределяется между группами населения, и сам принцип распределения определяются господствующими производственными отношениями. В капиталистич. обществе Д. д. н. выражает отношения эксплуатации и классового неравенства и связана прежде всего с разными источниками доходов у представителей анта-гонистич. классов: зарплата, с одной стороны, прибыль на капитал ("незаработанный доход") - с другой. Будучи одной из форм проявления всеобщего закона капиталистического накопления, Д. д. н. отражает диаметрально противоположные тенденции динамики доли трудящихся и доли капиталистов в общественном богатстве. Бурж. официальная статистика, как правило, не даёт полной картины существующей дифференциации: она оперирует т. н. потребительским доходом, не охватывающим всей суммы капиталистич. прибыли. Но даже по этим неполным источникам, Д. д. н. в большинстве капиталистич. стран относительно велика. Так, по материалам Департамента торговли США за 1967, 12,5% амер. семей (не считая одиночек) получало годовой доход менее 3 тыс. долл. Эти семьи, находящиеся на нижней ступени материальной обеспеченности, занимали всего 2,6% в общей сумме доходов населения. В то же время высокообеспеченные семьи с годовым доходом на одну семью 15 тыс. долл. и более, имея примерно такую же долю в общем числе семей, занимали в фонде доходов населения 25%. Крайней неравномерностью отличается также распределение доходов в Великобритании. Данные, публикуемые Министерством труда, показывают, что в 1960-х гг. десятую часть всех доходов присваивали 2,4% семей с доходом св. 60 ф. ст. в неделю, тогда как равные им по численности семьи с недельным доходом до 4 фунтов получали лишь ок. 0,4% общей суммы доходов. В Дании и Швеции в том же году на долю 10% наименее состоятельных семей приходилось 1,3-1,7% доходов, а на долю 10% богатейших семей - 27-34% . Во Франции нижняя 10-процентная группа населения получала 0,5% дохода, а верхняя-36,8% , в ФРГ - соответственно 2,1 и 41,4%, причём св. 23% доходов присваивали богатейшие семьи, к-рые составляли 1,25% в общем числе семей ("Incomes in Postwar Europe: A Study of Policies, Growth and Distribution. United Nations Economic Commission for Europe", Gen., 1967, ch. 6, p. 15). В социалистич. обществе, где основу распределения материальных и духовных благ составляет труд, меняются и существо, и размеры Д. д. н. В СССР доходы населения складываются из зарплаты рабочих и служащих, оплаты труда колхозников, поступлений от личных подсобных х-в, выплат из общественных фондов потребления (пенсий, стипендий, пособий) и т. д. К этому нужно добавить бесплатные услуги населению, оказываемые за счёт обществ. фондов потребления и увеличивающие размер совокупных доходов семей.

Поскольку в СССР и в других социалистич. странах главный источник жизненных благ подавляющего большинства населения - трудовой доход, ликвидируется сама основа существования чрезмерно больших различий в доходах. Однако производств. отношения социализма порождают определённое, неизбежное на данном этапе, неравенство в экономич. положении трудящихся -дифференциацию их доходов и потребления. Эта дифференциация, не носящая классового характера, обусловлена различиями в оплате труда и неодинаковым составом и размером семей работников. Дифференциация зарплаты (составляющей основную часть доходов рабочих и служащих), а также оплаты труда колхозников объясняется качественной неоднородностью и разным количеством труда, вкладываемого работниками в общественное произ-во.

Зарплата, попадая в бюджет семьи, принимает форму семейного дохода, на величину к-рого оказывают большое влияние демографич. факторы (соотношение числа работающих и иждивенцев, число детей и их возраст, наличие в семье учащихся-стипендиатов, стариков-пенсионеров и т. п.). В результате Д. д. н. может количественно отличаться от дифференциации зарплаты, и доля работника в потреблении оказывается не той, к рую он получил в порядке распределения по труду. В связи с этим возникает задача устранения влияния на Д.д.н. факторов, не имеющих отношения к труду и заслугам людей перед обществом. Главная роль здесь принадлежит общественным фондам потребления, средства к-рых направляются в первую очередь на материальную помощь и содержание нетрудоспособных.

Наиболее полное представление о сложившихся соотношениях в зарплате и доходах дают статистич. ряды распределения рабочих и служащих по размерам зарплаты, и их семей - по величине совокупного или душевого дохода. Для получения таких рядов статистич. органы периодически проводят спец. обследования. Данные о доходах населения по союзным республикам (экономич. группировки семей по доходам на душу) представляет также бюджетная статистика. Ряды распределения и исчисляемые на их основе статистич. характеристики отражают весь комплекс различий в величине рассматриваемого признака. Если исследованию подлежит совершенно однородная статистич. совокупность (напр., рабочие одной и той же квалификации, работающие в одинаковых условиях), то для измерения разброса их зарплаты могут быть использованы показатели отклонения от средней (дисперсия, среднеквадратич. отклонение, коэффициент вариации). Но эти показатели целесообразно применять только в случаях, когда вариация признака носит более или менее случайный характер. Если же различия между отд. элементами совокупности внутренне обусловлены, закономерны и задача состоит именно в том, чтобы установить величину этих различий, т. е. речь идёт о дифференциации признака, а не о простой колеблемости (вариации), то приходится прибегать к другим измерительным средствам. Так, построив группы семей в порядке возрастания их доходов, нужно взять для сравнения уровень дохода, ниже к-рого получают 25% семей, и уровень, выше к-рого получают 25% семей, и исчислить отношение этих уровней (соответственно можно принять за основу 10- и 5-процентные группы с относительно низкими и относительно высокими доходами). Подобные показатели носят название квантильных (квартальных, децильных и т. д.) коэффициентов дифференциации.

Существуют также показатели, измеряющие Д. д. н. степенью концентрации доходов. Они отвечают на вопрос: какая доля доходов сосредоточена в руках той или иной группы населения с данной численностью или уд. весом. Следовательно, место каждой группы характеризуется двумя величинами: долей в общей численности и долей присваиваемых доходов. Чем глубже расслоение, экономич. неравенство членов общества, тем большая часть богатства концентрируется в руках немногих, тем больше разница между первой и второй долями. Соотношение между ними является показателем неравномерности распределения и может быть представлено графически (т. н. кривая Лоренца).

При статистич. анализе рядов распределения зарплаты и доходов применяют различные математич. функции. Так, в кон. 19 в. пользовалась большой популярностью формула, предложенная итал. статистиком В. Парето. Ур-ние Парето, представляющее степенную функцию, было возведено бурж. экономистами в ранг "вечного закона", общего для всех стран и времён. Однако для социалистич. х-ва формула Парето совершенно неприменима: она не отвечает фактич. данным и противоречит самой природе распределения при социализме, исключающей крайности нищеты и богатства. По мнению ряда авторов, проводивших соответствующие исследования в СССР и др. социалистич. странах, наиболее подходящей для матем. описания распределения зарплаты и доходов в условиях социализма является логарифмически-нормальная функция. Согласно этой гипотезе, распределение логарифмов признака имеет вид нормальной кривой Гаусса (см. Нормальное распределение). На обычной шкале такое распределение принимает характерную форму кривой с умеренной правосторонней скошенностью.

Дифференциация зарплаты и Д. д. н. в условиях социализма обнаруживают тенденцию к сокращению. Сокращение дифференциации - процесс закономерный, обусловленный постепенным уменьшением качественной неоднородности труда по мере технич. прогресса. К этому направлена и политика Сов. гос-ва в области зарплаты и доходов: периодич. пересмотр минимальных тарифных ставок и уменьшение ставок налогов; введение ден. пособий на детей в многодетных семьях; увеличение длительности оплачиваемых декретных отпусков; улучшение пенсионного обеспечения престарелых, инвалидов и семей, потерявших кормильца; увеличение размеров стипендий и т. д. Мероприятия, осуществляемые за счёт общественных фондов потребления, касаются прежде всего наименее обеспеченных слоев, и это, в свою очередь, способствует выравниванию различий в доходах отдельных групп трудящихся.

Лит.: Маркс К., Капитал, т. 1, Маркс К. и Энгельс Ф., Соч., 2 изд., т. 23, отд. 5, 6, 7, гл. 23; его же, Капитал, т. 3, там же, т. 25, ч. 1 и 2, гл. 14 и 51; его же, Критика Готской программы, там же, т. 19, с. 19; Ленин В. И., Развитие капитализма в России, Полн. собр. соч., 5 изд., т. 3, гл. 12, с. 140-64; его же, Империализм, как высшая стадия капитализма, там же, т. 27; Аганбегян А. Г. и Майер В. Ф., Заработная плата в СССР, М., 1959; Кац А. И., Положение пролетариата США при империализме, М., 1962; Ланге О., Введение в эконометрику, пер. с польск., М., 1964; Маслов П. П., Показатель дифференциации в кн.: Доклады советских ученых на XXXV сессии международного статистического института, М., 1965; Римашевская Н. М., Экономический анализ доходов рабочих и служащих, М., 1965; Рабкина Н. Е., Римашевская Н. М., Экономические основы дифференциации заработной платы, "Вопросы экономики", 1966, № 12; их ж е, Дифференциация заработной платы и её прогнозирование, "Экономика и математические методы", 1965. в. 6; Фигурнов С. П., Строительство коммунизма и рост благосостояния народа, М., 1962; Жизненный уровень. Сб. статей, пер. с венг., М., 1964; Математические методы в экономике труда. Сб. статей, М., 1966.

Н. Е. Рабкина.

ДИФФЕРЕНЦИАЦИЯ ЗАРАБОТНОЙ ПЛАТЫ при социализме, установление неодинаковых уровней заработной платы для различных категорий работников в отд. отраслях нар. х-ва и р-нах страны. Отражает различие в продолжительности и интенсивности (напряжённости) труда работников, в сложности условий их труда, в квалификации работников, а также в обществ, значимости того или иного вида труда. В отд. периоды стимулируются те виды труда, к-рые приобретают особое значение для нар. х-ва. Осн. принципы построения заработной платы в СССР, разработанные В. И. Лениным и сформулированные в первых правительств, декретах по тарифному вопросу (1918-20), исключали уравнительность в оплате труда. Ленин подчёркивал, что создание материальной заинтересованности работников в результатах своего труда - ключ к всемерному повышению его производительности и росту на этой основе обществ, произ-ва. Именно этими принципами организации заработной платы, находившими отражение в её дифференциации, руководствовалось социалистич. гос-во на различных этапах своего развития. Разработанный 23-м и 24-м съездами КПСС курс на усиление роли экономия, стимулов в развитии произ-ва требует, чтобы при оплате труда наиболее полно учитывались затраты труда каждого работника и коллектива в целом. Совершенствование оплаты труда в соответствии с его количеством и качеством - один из определяющих моментов повышения жизненного уровня народа в девятой пятилетке 1971-75. Директивами 24-го съезда КПСС, наряду с увеличением минимальных размеров заработной платы, предусмотрено увеличение ставок и окладов среднеоплачиваемых категорий работников, совершенствование соотношений в оплате труда по отраслям нар. х-ва и категориям работников с учётом условий их труда и квалификации.

Для закрепления кадров в экономически перспективных (преим. удалённых) р-нах СССР предусмотрено повышение оплаты труда рабочих и служащих, а также расширение для них нек-рых льгот.

В общей системе Д. з. п. выделяются внутриотраслевая, межотраслевая и межрайонная. Внутриотраслевые и межотраслевые различия в уровнях заработной платы обеспечивают тарифная система и применение поощрительных систем оплаты.

Внутриотраслевая Д. з. п. устанавливает различия в оплате по квалификационным и проф. группам работников в соответствии со сложностью выполненных трудовых функций, а также по видам произ-ва и условиям труда. Напр., разрыв в уровнях тарифных ставок по квалификации (диапазон тарифной сетки рабочих) установлен в 75-80% ; на подземных работах ставки 1-го разряда на 15-20% выше по сравнению со ставками рабочих, занятых на поверхности шахт и рудников добывающих отраслей пром-сти; на работах с тяжёлыми и вредными условиями труда ставки 1-го разряда установлены на 8-15% выше, чем в нормальных условиях труда. Ставки рабочих-сдельщиков, учитывая большую напряжённость их труда, установлены на более высоком уровне, чем ставки рабочих-повременщиков.

Как в СССР, так и в др. социалистич. странах по мере повышения технич. уровня и совершенствования организации произ-ва, ведущих к общему повышению сложности работ с одновременным сокращением диапазона сложности, а также в связи с уменьшением различий в значимости отд. видов труда, разрыв в уровнях оплаты по сложности и нар.-хоз. значимости (т. е. Д. з. п.) сокращается. Так, в пром-сти СССР превышение среднемесячной заработной платы инженерно-технич. работников над зарплатой рабочих уменьшилось с 78% (1950) до 36% (1970).

Д. з. п. по условиям труда (при постоянном их улучшении) увеличивается, что вызвано потребностью усиливать материальные стимулы для привлечения трудящихся на работы в условиях труда, отклоняющихся от нормальных.

Межотраслевая Д. з. п. складывается прежде всего под влиянием особенностей трудового процесса в отд. отраслях (содержание трудовых функций, общеотраслевые условия труда, профессионально-квалификационная структура работающих и т. п.), а также под влиянием роли и значения различных отраслей в технич. прогрессе и развитии всего нар. х-ва. Межотраслевые соотношения уровней заработной платы в связи с этим весьма динамичны. Так, если в 1940 ср. уровень заработной платы рабочих и служащих пром-сти СССР (промышленно-производств. персонал) по отношению к ср. уровню заработной платы в нар. х-ве был выше на 3%, то в 1970 это превышение составляло 9%. Ср. уровень оплаты работников транспорта к ср. уровню оплаты работников нар. х-ва составил 112% в 1970 против 105% в 1940, соответственно ср. уровень оплаты работников строительства составил 123% в 1970 против 110% в 1940. За эти же годы значительно возрос уровень оплаты труда работников совхозов, подсобных и др. с.-х. предприятий, приблизившись к среднему уровню оплаты труда в нар. х-ве.

Межрайонная Д. з. п. определяется отраслевой структурой произ-ва по р-нам, важностью экономич. р-нов и перспективой их развития, а также их природно-климатич. условиями. Цель установленных гос-вом различий в уровнях заработной платы по р-нам страны состоит в том, чтобы обеспечить равные условия для воспроиз-ва рабочей силы в связи с разницей в структуре потребления и уровнем цен на ряд потребительских товаров. Установление различий в оплате по р-нам диктуется также необходимостью привлечения и закрепления кадров в тех р-нах, к-рые испытывают недостаток в рабочей силе. Гос. регулирование заработной платы по р-нам страны осуществляется через систему районных коэффициентов к заработной плате. Максимальный размер действующих коэффициентов (1970) составляет к заработку 2,0, минимальный - 1,1.

Лит.: Баткаев Р. А., Марков В. И., Дифференциация заработной платы в промышленности СССР, М., 1964; Майер В. Ф., Заработная плата в период перехода к коммунизму, М., 1963; Капустин Е. И., Качество труда и заработная плата, М., 1964.

Ю. П. Кокин.

ДИФФЕРЕНЦИАЦИЯ МАГМЫ, совокупность физико-хим. процессов, вследствие к-рых из магмы возникают разные по хим. составу породы или породы с различными количеств, соотношениями одних и тех же минералов. См. также Магма.

ДИФФЕРЕНЦИАЦИЯ ЯЗЫКОВ, один из основных процессов, характеризующих развитие родственных языков, противоположный по своей направленности интеграции языков. Хотя процесс обусловлен не лингвистическим, а обществ, факторами (с ростом консолидации общества его темпы замедляются), он сводится к материальному и структурному расхождению языков путём постепенной утраты элементов общего качества и приобретения специфич. черт. Напр., рус., белорус, и укр. языки на основе древнерусского. Процесс Д. я. затрагивает все стороны языковой структуры. Системные тенденции расхождения, выражающиеся в наличии регулярных звуко-соответствий в общем материале родственных языков, позволяют констатировать самый факт языковой дифференциации. Общий ход Д. я. в пределах языковой семьи моделируется схемой т. и. "родословного дерева", исходный пункт к-рой обозначает праязык, а конечные точки -совокупность родственных языков.

Г. А. Климов.

ДИФФЕРЕНЦИРОВАНИЕ в математике, операция отыскания производной. См. Дифференциальное исчисление.

ДИФФЕРЕНЦИРОВАНИЕ ЦЕН, установление различных уровней действующих в СССР цен на одинаковую продукцию в связи с экономич., природными, территориальными и др. независящими от предприятий различиями в затратах на сё произ-во, а также в зависимости от качества продукции (сортности, класса, типа и пр.).

В пром-сти особенно широко дифференцируются оптовые цены предприятий. Часто различный уровень себестоимости одинаковых изделий на разных предприятиях не зависит от хоз. деятельности самих предприятий, а связан с их геогр. размещением, природными факторами и др. объективными причинами. Прежде всего это относится к таким отраслям пром-сти, как угольная, торфяная, лесозаготовительная, цементная и др., где оптовые цены должны отражать разницу в затратах предприятий на произ-во продукции, вытекающую из различных естеств. условий отд. р-нов, бассейнов, месторождений и пр. Для потребителей продукции этих отраслей пром-сти устанавливаются единые оптовые отпускные цены (иногда с учётом поясных различий), а для предприятий-производителей -дифференцированные расчётные цены, исходя из плановой себестоимости продукции на данном предприятии или у группы однородных по условиям произ-ва предприятий. В ряде добывающих отраслей (угольная, железорудная и др.) применяется зональная дифференциация оптовых цен, отражающая различия в уровнях общественно необходимых затрат в отд. зонах (р-нах).

В с. х-ве вследствие больших различий в почвенно-климатич. и экономич. условиях произ-ва важнейших с.-х. продуктов - зерна, подсолнечника, сах. свёклы, картофеля, овощей, продуктов животноводства - закупочные цены дифференцированы по союзным республикам, геогр. р-нам или зонам, исходя из средне-зональных затрат на произ-во продукции. Дифференцирование закупочных цен -один из важных инструментов выравнивания экономич. условий и доходов колхозов и совхозов, находящихся в неравных природно-экономич. условиях. Кроме того, закупочные цены дифференцированы в зависимости от качества продукции. Так, учитывая высокие мукомольные, хлебопекарные качества твёрдых пшениц, закупочные цены на них установлены на 40% выше, чем на сорта мягких пшениц; пивоваренный ячмень оценивается на 20% дороже кормового; на молоко закупочные цены дифференцируются (с помощью наценок и скидок) в зависимости от жирности, кислотности и др. показателей, влияющих на его качество. На картофель, овоще-бахчевые культуры, фрукты, мясо и нек-рые др. продукты закупочные цены дифференцированы также с учётом сезонных условий произ-ва и реализации продукции.

Важной особенностью гос. розничных цен на товары нар. потребления является их стабильность, единство на одинаковые товары, что обеспечивает единую покупательную силу рубля. На большинство пром. товаров (ткани, обувь, часы, холодильники, радиоприёмники, стиральные, швейные машины, фотоаппараты и пр.) действуют единые розничные цены для всей страны. Однако по нек-рым товарам необходимо учитывать различный уровень издержек произ-ва в отд. р-нах, а также различие в затратах на транспорт, если они составляют значит. долю в стоимости товара. Поэтому наряду с едиными общесоюзными применяются поясные розничные цепы (дифференцированные по поясам страны) гл. обр. на прод. товары - хлебопродукты, мясопродукты, рыботовары, сахар, кондитерские изделия, соль, консервы и пр. и на нек-рые мало-транспортабельные пром. товары -мебель, лесоматериалы, оконное стекло. Для большинства этих товаров на терр. СССР установлено 3 пояса цен. Наиболее низкие цены устанавливаются для 1-го пояса, к к-рому относятся р-ны массового произ-ва данного товара, с низким уровнем издержек на его произ-во и транспортировку. Поясная дифференциация цен изменяется с изменением размещения, условий произ-ва и сбыта товаров в отд. р-нах страны. См. также ст. Ценообразование.

Г. И. Кабко.

ДИФФЕРЕНЦИРОВАННОЕ ОБУЧЕНИЕ, см. Обучение.

ДИФФЕРЕНЦИРОВАННОЙ СВЯЗИ ТЕОРИЯ, в буржуазной (гл. обр. в амер.) криминологии одна из социально-психологич. теорий причин преступного поведения. Была сформулирована амер. криминологом Сатерлендом в 1939, её придерживаются криминологи Кресси, Глейзер, Сайке и Матза и др. В соответствии с Д. с. т. человек становится преступником, если в процессе его общения с людьми, к-рых он считает для себя образцом, а также при оценке собственной личности он вступает в преимуществ, контакт с людьми, определениями, понятиями, благоприятствующими нарушению закона. В свою очередь преимуществ. влияние одних контактов по сравнению с другими и возникающие в результате этих контактов связи зависят от их интенсивности, частоты, длительности, их "значимости" для человека. Д. с. т. была дополнена теорией т. н. дифференцированного отождествления, согласно к-рой реакции человека на оказываемое воздействие зависят от того, каково его представление о самом себе, его самооценка (с образцом какого человека, с какими нормами поведения, а следовательно, с какой из социальных групп он отождествляет себя). Здесь Д. с. т. близка к имеющей более общий характер т. н. социокультурной теории.

Авторы, стоящие на позициях Д. с. т., пытаются охарактеризовать психологич. "механизм" подготовки к преступлению. Они полагают, что в сознании такого лица ещё до совершения правонарушения "нейтрализуется" (отбрасывается) социальное неодобрение противоправного поступка, напр. путём поиска оправдания их нарушения для себя. В частности, правонарушитель нередко трактует себя как жертву исключит. обстоятельств. дурного влияния и т. д. и поэтому считает, что не может нести ответственности за правонарушение; он совершает правонарушение, не изменяя представления о самом себе.

Эти положения раскрывают ключевой пункт Д. с. т. - обусловленность преступления представлением лица о самом себе, о том соотношении, в к-ром оно находится с другими, предварит, снятие социально-психологич. сдерживания. Д. с. т. - полностью научно несостоятельна, т. к. её представители пытаются объяснить причины преступности вне классового анализа осн. экономич., социальных и идеологич. предпосылок, порождающих преступность в совр. капиталистич. обществе.

А. М. Яковлев.

ДИФФЕРЕНЦИРОВКА, дифференциация онтогенетическая (биол.), возникновение различий между однородными клетками и тканями, их изменения в ходе развития, приводящие к специализации.

Д. происходит в основном в процессе зародышевого развития, когда из одинаковых неспециализированных эмбриональных клеток образуются органы и ткани с различными по форме и функции клетками. Развивающийся зародыш дифференцируется сначала на зародышевые листки, затем на зачатки осн. систем и органов, далее - на большое число специализированных тканей и органов, характерных для взрослого организма. Д. происходит также в нек-рых органах взрослого организма (напр., из клеток костного мозга дифференцируются различные клетки крови). Часто Д. наз. и ряд последовательных изменений, претерпеваемых клетками одного типа в процессе их специализации (напр., в ходе Д. красных клеток крови эритробласты преобразуются в ретикулоциты, а те - в эритроциты). Д. выражается в изменении как формы клеток, их внутреннего и внешнего строения и взаимосвязей (напр., миобласты вытягиваются, сливаются друг с другом, в них образуются миофибриллы и т. д.; у нейробластов увеличивается ядро, появляются отростки, соединяющие нервные клетки с различными органами и между собой), так и их функциональных свойств (мышечные волокна приобретают способность сокращаться, нервные клетки - передавать нервные импульсы, железистые - секретировать соответствующие вещества и т. д.).

Гл. факторы Д. - различия цитоплазмы ранних эмбриональных клеток, обусловленные неоднородностью цитоплазмы яйца, и специфич. влияния соседних тканей - индукция. На ход Д. оказывает влияние ряд гормонов. Мн. факторы, определяющие Д., ещё неизвестны. Д. может происходить только в клетках, к ней подготовленных. Действие фактора Д. вызывает сначала состояние латентной (скрытой) Д., или детерминации, когда внешние признаки Д. ещё не проявляются, но дальнейшее развитие ткани уже Может происходить независимо от побудительного фактора. Напр., Д. нервной ткани вызывается зачатком хордомезодермы. Индукция же Д. возможна и совершается только в эктодерме зародыша на определённой стадии его развития. Обычно состояние Д. необратимо, т. е. дифференцированные клетки уже не могут утратить своей специализации. Однако в условиях повреждения ткани, способной к регенерации, а также при злокачественном её перерождении происходит частичная дедифференцировка, когда клетки утрачивают мн. признаки, приобретённые в процессе Д., и внешне напоминают малодифференцированные клетки зародыша. Возможны случаи приобретения дедифференцированными клетками Д. в ином направлении (метаплазия).

Молекулярно-генетич. основа Д. -активность специфических для каждой ткани генов. В каждой клетке, в т. ч. и дифференцированной, сохраняется весь генетич. аппарат (все гены). Однако активна в каждой ткани лишь часть генов, ответственных за данную Д. Роль факторов Д. сводится, т. о., к строго избират. активации (включению) этих генов. Механизм такого включения интенсивно изучается. Активность определённых генов приводит к синтезу соответствующих белков, определяющих Д. Так, в эритробластах синтезируется специфич. белок красных кровяных клеток - гемоглобин, в мышечных клетках -миозин, в дифференцирующихся клетках поджелудочной железы - инсулин, трипсин, амилаза и др.; при Д. хрящевой или костной ткани синтезируются ферменты, обеспечивающие образование и накопление вокруг клеток мукополисахаридов хряща и солей кости. Предполагается, что решающую роль в определении формы клеток, их способности к соединению друг с другом, их движениях в ходе Д. играют белки клеточной поверхности.

А. А. Нейфах.

ДИФФЕРЕНЦИРОВОЧНОЕ ТОРМОЖЕНИЕ, форма внутр. торможения, развивающегося у животного при неподкреплении раздражителя, близкого к подкрепляемому условному (см. Условные рефлексы). Скорость развития Д. т. зависит от аналитич. способности нервной системы, степени близости дифференцируемых раздражителей, силы возбуждения, развиваемого условным сигналом, тренировки и др.

ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ в точке (матем.), функция, имеющая дифференциал в этой точке. Для функций одного переменного это требование равносильно существованию производной. См. Дифференциальное исчисление.

ДИФФЕРЕНЦИРУЮЩЕЕ УСТРОЙСТВО, устройство для получения производной по времени от входной величины, поступающей на Д. у. Входной величиной может быть меняющийся угол поворота вала, переменная электрич. величина и др. Выходной сигнал Д. у.

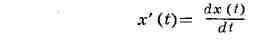
характеризует скорость изменения входной величины (являясь производной входной величины). Д. у. применяются в вычислительных устройствах, а также в системах автоматич. регулирования для повышения их качества. Различают Д. у. механические (фрикционные Д. у., центробежные и др.), электрические (дифференцирующие цепи, активные электронные дифференцирующие элементы), электромеханические (тахогенераторы пост, и перем. тока и др.).

Лит.: Теория автоматического регулирования, под ред. В. В. Солодовникова, кн. 2, М., 1967.

ДИФФЛЮГИЯ (Difflugia), род простейших отряда раковинных амёб класса саркодовых (Sarcodina).

"ДИФФУЗИИ ВЛАСТИ" ТЕОРИЯ, одна из совр. буржуазно-реформистских концепций, согласно к-рой наличие в совр. капиталистич. обществе значит, числа политич. организаций разных классов (партии, профсоюзы, предпринимательские союзы и др.) ведёт к распылению (диффузии) политич. власти в этом обществе. Его политич. организация изображается как нечто вроде коллективного властвования этих организаций, уравновешивающих друг друга и в равной мере воздействующих на потерявшее вследствие этого классовый характер гос-во. В своём реформистском варианте "Д. в." т. (особенно широко используемая англ. лейбористами - Дж. Стрейчи и др.) отражает процесс врастания правой с.-д-тии в капиталистич. государственность. В действительности никакой "Д. в." в совр. капиталистич. обществе не происходит; политич. власть принадлежит монополистич. капиталу, занимающему господствующее положение в экономике, а осуществляется им с помощью системы политич. организаций, основное место среди которых занимает гос. механизм, тесно сросшийся с монополиями. Коммунистич. и рабочие партии и другие прогрессивные организации трудящихся капиталистич. стран ведут последовательную борьбу с системой власти монополистич. буржуазии.

ДИФФУЗИОНИЗМ (от лат. diffusio - распространение, растекание), направление в буржуазной этнографии и археологии, объединяющее ряд сходных школ. Д. объясняет развитие культур не их самостоятельной эволюцией, а гл. обр. или даже исключительно заимствованиями культурных достижений и миграциями народов. Д. возник в кон. 19-нач. 20 вв. как реакция на позитивистский эволюционизм, противопоставив упрощённой идее полного единообразия в развитии культур идею их абсолютного различия, нарушающегося лишь там, где заимствования или миграции обусловливают культурное сходство. Для последовательного Д. характерны подмена развития во времени перемещением в пространстве (нем. учёные Л. Фробениус, Ф. Гребнер), отрицание единства историч. процесса (австр. учёные В. Шмидт, В. Копперс); делались попытки использовать Д. для построения расистских теорий, приписывавших отдельным народам или расам исключительную культурную роль (австр. учёный О. Менгин, нем. учёный Г. Коссинна). Марксистская этнография, археология и социология рассматривают культурные влияния и миграции как важный, но не определяющий фактор культурно-историч. процесса.

Лит.: Артановский С.Н., Историческое единство человечества и взаимное влияние культур, Л., 1967.

А. И. Першиц.

ДИФФУЗИОННАЯ КАМЕРА, прибор, в к-ром можно наблюдать видимые следы (треки) заряженных частиц. Как и в Вильсона камере, треки в Д. к. создаются каплями жидкости в пересыщенном паре, а центрами конденсации являются ионы, образующиеся вдоль траектории заряженной частицы. Пересыщение газа в Д. к. достигается за счёт непрерывного потока пара от более горячей поверхности у крышки камеры к холодной поверхности у её дна. В отличие от камеры Вильсона, в Д. к. пересыщение существует постоянно, поэтому Д. к. чувствительна к ионизирующим частицам непрерывно. Д. к. впервые осуществлена американским физиком А. Лангсдорфом в 1936.

Металлич. дно камеры, заполненной газом, охлаждается твёрдой углекислотой до темп-ры -60-70 °С (рис.). Вследствие теплопроводности газа и конвективного теплообмена между газом и стенками камеры в камере устанавливается большой перепад темп-ры по высоте. Верхняя часть камеры заполняется парами метилевого спирта с упругостью, близкой к насыщению (при темп-ре от 10 до 20 °С).
 

Рис. Схема диффузионной камеры: 1 - верхнее стекло; 2 - металлическое корытце с метиловым спиртом 9; 3 - стеклянный цилиндр (боковая поверхность камеры); 4 -металлическое дно камеры, охлаждаемой твёрдой углекислотой 5; 6 - поршень из термоизолирующего материала; 7 - сжатая пружина; 8 - параболическое зеркало; 10 - фотоаппарат; 11 - металлическое кольцо с редкой сеткой из тонкой проволоки для создания очищающего от ионов электрического поля; S-источник света.

Пары спирта диффундируют вниз и конденсируются на дне камеры. Т. к. темп-pa газа в области, прилегающей ко дну камеры, значительно ниже, чем темп-pa у крышки, внизу образуется слой с пересыщением парами спирта, в к-ром формируются треки частиц. Высота чувствительного к ионизирующим частицам слоя в Д. к. достигает 50-70 мм. Чёткие следы частиц в Д. к. образуются при температурных перепадах в чувствительном слое ~ 50-10 град/см.

Д. к. высокого давления наполняют водородом до 3-4 Мн/м² (30-40 атм) и гелием до 20 Мн/м² (20 атм). Они применяются для изучения процессов взаимодействия частиц высокой энергии с ядрами водорода, дейтерия и гелия. Помещая Д. к. в магнитное поле (~10-20 000 э), можно с большой точностью измерять импульсы частиц. С помощью Д. к. было исследовано образование пи-мезонов при столкновениях протонов, нейтронов и других частиц с ядрами водорода и гелия; наблюдалось парное рождение лямбда-пи-мезонов с К-мезонами при соударениях я-мезонов с протонами и др.

Лит.: Ляпидевский В. К., Диффузионная камера, "Успехи физических наук", 1958, т. 66, в. 1.

ДИФФУЗИОННАЯ МЕТАЛЛИЗАЦИЯ, процесс, основанный на диффузионном насыщении поверхностных слоев изделий из металлов и сплавов различными металлами (см. Диффузия). Д. м. проводят, чтобы придать поверхности металлич. деталей специальные физико-хим. и механич. свойства. В зависимости от диффундирующего элемента различают: алитирование, диффузионное хромирование, молибденирование; марганценирование, хромоалитирование, хромотитанирование и другие виды. Диффузионное насыщение возможно из различных фаз: твёрдой, паровой, газовой и жидкой.

Насыщение из твёрдой фазы применяют для железа, никеля, кобальта, титана и др. металлов. В этом случае Д. м. осуществляют различными тугоплавкими металлами (Mo, W, Nb, U и др.), упругость паров к-рых меньше упругости паров основного металла. Процесс протекает в герметизир. контейнере, в к-ром обрабатываемые детали засыпаются порошкообразным металлом, в вакууме или в нейтральной среде при 1000-1500°С. Насыщение из паровой фазы применяют для сплавов на основе железа, никеля, молибдена, титана и др. металлов такими элементами, к-рые имеют более высокую упругость паров, чем насыщаемый металл, напр. Zn, Al, Cr, Ti и др. Процесс происходит в герметичных контейнерах при разрежении ~ 10¹-10~² и/л², или 10^-1-10^-4 мм рт. ст., и 850-1600 °С, контактным или неконтактным способом. В первом случае паровая фаза возникает при сублимации металла и генерируется вблизи мест контактирования порошкообразного или кускообразного металла с обрабатываемой поверхностью; во втором - генерация паровой фазы происходит на нек-ром расстоянии от поверхности. Насыщение из газовой фазы производят при Д.м.различных металлов элементами: А1, Cr, Mn, Mo, W, Nb, Ti и др. Диффузии металла предшествуют реакции взаимодействия газообразных хим. соединений диффундирующего элемента с осн. металлом. Газовой фазой служат галогениды диффундирующих металлов. Газовое насыщение осуществляется в муфельных печах или в печах спец. конструкции при 700-1000 °С. Газовая фаза может генерироваться на расстоянии от насыщаемой поверхности (неконтактный способ) и в зоне контакта источника активной фазы с поверхностью металла (контактный способ). Насыщение из жидкой фазы применяют при алитировании, хромировании, цинковании, меднении. Процесс протекает в печах-ваннах, в к-рых расплав диффундирующего металла или его соли взаимодействуют с поверхностью обрабатываемых изделий при 800-1300 °С. Этим методом осуществляют также комплексную Д. м., напр, хромоалитирование, хромотитанирование, хромоникелирование и т. д.

Д. м. можно получать диффузионный слой толщиной от 10 мкм до 3 мм. Процессы Д. м. позволяют повысить жаростойкость сплавов (напр., алитированная сталь имеет жаростойкость до 900 °С), абразивную износостойкость (напр., хромирование стали У12 увеличивает её износостойкость в 6 раз), сопротивление термоудару, быстрой смене темп-р, коррозионную стойкость и кислотоупорность и улучшить другие свойства металлов и сплавов.

Лит.: Дубинин Г. Н., Диффузионное хромирование сплавов, М., 1964; Минкевич А. Н., Химико-термическая обработка металлов и сплавов, 2 изд., М., 1965.

Г. Н. Дубинин.

ДИФФУЗИОННАЯ СВАРКА, способ сварки без расплавления основного металла за счёт нагрева и сдавливания соединяемых деталей. В месте сварки деталей происходит диффузия одного металла в другой. Детали с тщательно зачищенными и пригнанными поверхностями помещают в закрытую сварочную камеру с разрежением до ~0,01-0,001 н/м², т. е. до 10^-5 мм рт. ст. Детали сдавливают небольшим постоянным усилием, для повышения пластичности и ускорения диффузии нагревают до 600-800 °С. Через неск. минут после окончания сварки детали охлаждаются, и их выгружают из камеры. При нагреве в вакуумной камере происходит интенсивная очистка поверхностей от органич. загрязнений и окислов. Д. с. позволяет получать сварные швы высокого качества без внутр. напряжений и без перегрева металла в околошовной зоне. Этим способом можно соединять детали из одинаковых твёрдых и хрупких или разнородных материалов: из стали, твёрдых сплавов, титана, меди, никеля и их сплавов и т. д. Возможна сварка деталей из нек-рых неметаллич. материалов, напр, двух керамических или керамич. с металлической Д. с. применяется в основном в электронной пром-сти, машиностроении, при произ-ве металлорежущего инструмента, штампов и др. Применение Д. с. ограничивается необходимостью иметь сложную и дорогую аппаратуру. Производительность Д. с. не очень высока из-за наличия таких операций, как вакуумирование камеры, нагрев деталей, выдержка для проведения диффузии.

К. К. Хренов.

ДИФФУЗИОННЫЕ ПРОЦЕССЫ, процессы, протекающие при перемещении мельчайших частиц вещества (атомов, ионов, молекул) или их комплексов вследствие стремления к равновесному распределению концентрации мигрирующих частиц в данном объёме (см. Диффузия). При Д. п. возможен обмен частицами между веществами, находящимися в различных агрегатных состояниях, т. е. возможны явления адсорбции и десорбции, растворение и кристаллизация, сушка и т. п. Д. п. лежат в основе таких технологич. операций, как спекание порошков (напр., в порошковой металлургии), термическая обработка металлов и химико-термическая обработка металлов (цементация, азотирование и т. п.), гомогенизация сплавов, диффузионная металлизация и т. д. Значение Д. п. возрастает в связи с необходимостью создания спец. материалов для развивающихся областей техники (атомной энергетики, космонавтики и т. д.). Знание законов, управляющих Д. п., позволяет предупреждать нежелательные изменения в изделиях, происходящие под влиянием повышенных темп-р, больших нагрузок, облучения и т. п.

Лит.: Л ю б о в Б. Я., Кинетическая теория фазовых превращений, М., 1969.

Б. Я. Любое.

ДИФФУЗИОННЫЙ АППАРАТ, аппарат для извлечения методом экстракции растворимых веществ из измельчённого твёрдого материала. Д. а. широко применяются в пищ. пром-сти, гл. обр. в сахарной, где они являются одним из осн. видов технологич. оборудования. В этих аппаратах осуществляется водная экстракция сахара из свекловичной стружки или из измельчённого сахарного тростника.

Различают Д. а. периодич. и непрерывного действия. К первому типу относятся диффузионные батареи, состоящие из чётного количества (12-16) диффузоров и такого же количества промежуточных подогревателей, соединённых в кольцевую систему. Батареи работают по принципу противотока: вода поступает в последний диффузор, в к-ром находится уже обессахаренная свекловичная стружка, постепенно обогащаясь сахаром, она последовательно прокачивается через все диффузоры снизу вверх и отводится из последнего диффузора в виде сока. Такие Д. а. весьма громоздки и требуют значительных затрат труда на обслуживание и ремонт.

Около половины з-дов СССР оснащено Д. а. непрерывного действия. Наиболее распространены вертикальные одно- и многоколонные, наклонные корытные, горизонтальные ротационные. В первых стружка перемещается снизу вверх шнековым, лопастным или цепным транспортёром и выгружается из верх. части аппарата в виде жома, а вода непрерывно протекает сквозь столб стружки сверху вниз, диффузионный сок отводится через сито из нижней части колонны. В наклонных Д. а. стружка перемещается снизу вверх парой параллельных ленточных шнеков и выгружается в виде жома при помощи лопастного колеса. Аппарат полностью автоматизирован. В горизонтальных Д. а. к внутренним стенкам вращающегося барабана жёстко прикреплены одно- или двухлоточные винтовые перегородки, разделяющие его на ряд секций, и решётки, перебрасывающие стружку из секции в секцию, навстречу протекающей вдоль винтовой перегородки воде.

Существуют Д. а. с бесконечной горизонтальной перфорированной лентой, перемещающей стружку, и системой насосов, последовательно противоточно перекачивающих воду (сок) через отдельные участки транспортёра. Перспективно использование для извлечения сахара из свекловичной стружки серии гидроциклонов. Применение Д. а. непрерывного действия позволяет полностью автоматизировать процесс, в 5-8 раз сократить затраты труда, снизить потери сахара в жоме, повысить общую культуру произ-ва. Производительность Д. а. от 1500 до 3000 т свёклы в сутки.

Лит.: Силин П. М., Технология сахара, 2 изд., [М., 1967]; Гребевюк С. М., Технологическое оборудование сахарных заводов, М., 1969.

Н. М. Петренко.

ДИФФУЗИОННЫЙ НАСОС, то же, что пароструйный вакуумный насос. Откачивающее действие Д. н. основано на диффузии молекул откачиваемого газа в струю пара рабочего вещества (ртуть, масло).

ДИФФУЗИЯ (от лат. diffusio - распространение, растекание), взаимное проникновение соприкасающихся веществ друг в друга вследствие теплового движения частиц вещества. Д. происходит в направлении падения концентрации вещества и ведёт к равномерному распределению вещества по всему занимаемому им объёму (к выравниванию химического потенциала вещества).

Д. имеет место в газах, жидкостях и твёрдых телах, причём диффундировать могут как находящиеся в них частицы посторонних веществ, так и собственные частицы (самодиффузия).

Д. крупных частиц, взвешенных в газе или жидкости (напр., частиц дыма или суспензии), осуществляется благодаря их броуновскому движению. В дальнейшем, если специально не оговорено, имеется в виду молекулярная Д.

Наиболее быстро Д. происходит в газах, медленнее в жидкостях, ещё медленнее в твёрдых телах, что обусловлено характером теплового движения частиц в этих средах. Траектория движения каждой частицы газа представляет собой ломаную линию, т. к. при столкновениях частицы меняют направление и скорость своего движения. Неупорядоченность движения приводит к тому, что каждая частица постепенно удаляется от места, где она находилась, причём её смещение по прямой гораздо меньше пути, пройденного по ломаной линии. Поэтому диффузионное проникновение значительно медленнее свободного движения (скорость диффузионного распространения запахов, напр., много меньше скорости молекул). Смещение частицы меняется со временем случайным образом, но средний квадрат его L² за большое число столкновений растёт пропорционально времени t. Коэфф. пропорциональности D в соотношении: L² ~ Dt наз. коэфф. Д. Это соотношение, полученное А. Эйнштейном, справедливо для любых процессов Д. Для простейшего случая самодиффузии в газе коэфф. Д. может быть определён из соотношения D ~ L²/t, применённого к средней длине свободного пробега молекулы l. Для газа l = ст, где с - средняя скорость движения частиц, t - среднее время между столкновениями. Т. о., D ~ l²/t ~ lс (более точно D = ⁴/₃ lс). Коэфф. Д. обратно пропорционален давлению р газа (т. к. l ~ 1/p), с ростом темп-ры Т (при постоянном объёме) Д. увеличивается пропорционально Т ^1/2(т. к. с ~ КОРЕНЬ Т). С увеличением молекулярной массы коэфф. Д. уменьшается.

В жидкостях, в соответствии с характером теплового движения молекул, Д. осуществляется перескоками молекул из одного временного положения равновесия в другое. Каждый скачок происходит при сообщении молекуле энергии, достаточной для разрыва её связей с соседними молекулами и перехода в окружение др. молекул (в новое энергетически выгодное положение). В среднем скачок не превышает межмолекулярного расстояния. Диффузионное движение частиц в жидкости можно рассматривать как движение с трением, к нему применимо второе соотношение Эйнштейна: D ~ ukT. Здесь k - Больц-мана постоянная, и - подвижность диффундирующих частиц, т. е. коэфф. пропорциональности между скоростью частицы с и движущей силой F при стационарном движении с трением (с = uF). Если частицы сферически симметричны, то и = ¹/6пnr, где n) - коэфф. вязкости жидкости, r - радиус частицы (см. Стокса закон).

Коэфф. Д. в жидкости увеличивается с темп-рой, что обусловлено "разрыхлением" структуры жидкости при нагреве и соответствующим увеличением числа перескоков в единицу времени.

В твёрдом теле могут действовать неск. механизмов Д.: обмен местами атомов с вакансиями (незанятыми узлами кристаллич. решётки), перемещение атомов по междоузлиям, одновременное циклич. перемещение нескольких атомов, прямой обмен местами двух соседних атомов и т. д. Первый механизм преобладает, напр., при образовании твёрдых растворов замещения, второй - твёрдых растворов внедрения.

Коэфф. Д. в твёрдых телах крайне чувствителен к дефектам кристаллич. решётки, возникшим при нагреве, напряжениях, деформациях и др. воздействиях. Увеличение числа дефектов (гл. обр. вакансий) облегчает перемещение атомов в твёрдом теле и приводит к росту коэфф. Д. Для коэфф. Д. в твёрдых телах характерна резкая (экспоненциальная) зависимость от темп-ры. Так, коэфф. Д. цинка в медь при повышении темп-ры от 20 до 300 °С возрастает в 10¹⁴ раз.

Значение коэффициента диффузии (при атмосферном давлении)
 

Диффундирующее вещество	Основной компонент	Темп-pa , °С	Коэфф. диффузии, мг/сек
Водород (газ)	Кислород (газ)	0	0,70-10-4
Пары воды	Воздух	0	0,23-10-4
Пары этилового спирта	Воздух	0	0,10-10-4
Соль (NaCl)	Вода	20	1,1-10-9
Сахар	Вода	20	0,3-10-9
Золото (тв.)	Свинец (ТВ.)	20	4-10-14
Самодиффузия	Свинец	285	7-10-15

Для большинства науч. и практич. задач существенно не диффузионное движение отдельных частиц, а происходящее от него выравнивание концентрации вещества в первоначально неоднородной среде. Из мест с высокой концентрацией уходит больше частиц, чем из мест с низкой концентрацией. Через единичную площадку в неоднородной среде проходит за единицу времени безвозвратный поток вещества в сторону меньшей концентрации - диффузионный поток j. Он равен разности между числами частиц, пересекающих площадку в том и др. направлениях, и потому пропорционален градиенту концентрации V С (уменьшению концентрации С на единицу длины). Эта зависимость выражается законом Фика (1855): j= -DvC.

Единицами потока j в Международной системе единиц являются 1/м² сек или кг!м²сек, градиента концентрации - 1/л⁴ или кг/м⁴, откуда единицей коэфф. Д. является м²/сек. Математически закон Фика аналогичен ур-нию теплопроводности Фурье. В основе этих явлений лежит единый механизм молекулярного переноса: в 1-м случае переноса массы, во 2-м - энергии (см. Переноса явления).

Д. возникает не только при наличии в среде градиента концентрации (или химического потенциала). Под действием внешнего электрического поля происходит Д. заряженных частиц (электродиффузия), действие поля тяжести или давления вызывает бародиффузию, в неравномерно нагретой среде возникает термодиффузия.

Все экспериментальные методы определения коэфф. Д. содержат два осн. момента: приведение в контакт диффундирующих веществ и анализ состава веществ, изменённого Д. Состав (концентрацию продиффундировавшего вещества) определяют химически, оптически (по изменению показателя преломления или поглощения света), масс-спектроскопически, методом меченых атомов и др.

Д. играет важную роль в хим. кинетике и технологии. При протекании хим. реакции на поверхности катализатора или одного из реагирующих веществ (напр., горении угля) Д. может определять скорость подвода др. реагирующих веществ и отвода продуктов реакции, т. е. являться определяющим (лимитирующим) процессом.

Для испарения и конденсации, растворения кристаллов и кристаллизации определяющей оказывается обычно Д. Процесс Д. газов через пористые перегородки или в струю пара используется для изотопов разделения. Д. лежит в основе многочисленных технологич. процессов - адсорбции, цементации и др. (см. Диффузионные процессы); широко применяются диффузионная сварка, диффузионная металлизация.

В жидких растворах Д. молекул растворителя через полупроницаемые перегородки (мембраны) приводит к возникновению осмотического давления (см. Осмос), что используется в физико-хим. методе разделения веществ - диализ.  Д. А. Франк-Каменецкий.

Д. в биологических системах. Д. играег важную роль в процессах жизнедеятельности клеток и тканей животных и растений (напр., Д. кислорода из лёгких в кровь и из крови в ткани, всасывание продуктов пищеварения из кишечника, поглощение элементов минерального питания клетками корневых волосков, Д. ионов при генерировании биоэлектрич. импульсов нервными и мышечными клетками). Различная скорость Д. ионов через клеточные мембраны - один из физ. факторов, влияющих на избират. накопление элементов в клетках организма. Проникновение растворённого вещества в клетку может быть выражено законом Фика, в к-ром значение коэфф. Д. заменено коэфф. проницаемости мембраны, а градиент концентрации - разностью концентраций вещества по обе стороны мембраны. Диффузионное проникновение в клетку газов и воды (см. Осмос) также описывается законом Фика; при этом значения разности концентраций заменяются значениями разности давлений газов и осмотич. давлений внутри и вне клетки.

Различают простую Д.- свободное перемещение молекул и ионов в направлении градиента их химич. (электро-химич.) потенциала (так могут перемещаться лишь вещества с малыми размерами молекул, напр. вода, метиловый спирт); ограниченную Д., когда мембрана клетки заряжена и ограничивает Д. заряженных частиц даже малого размера (напр., слабое проникновение в клетку анионов); облегчённую Д.- перенос молекул и ионов, самостоятельно не проникающих или очень слабо проникающих через мембрану, др. молекулами ("переносчиками"); так, по-видимому, проникают в клетку сахара и аминокислоты. Через мембрану, вероятно, могут диффундировать и переносчик, и комплекс переносчика с веществом. Перенос вещества, определяемый градиентом концентрации переносчика, наз. обменной Д.; такая Д. отчётливо проявляется в экспериментах с изотопными индикаторами. Различную концентрацию веществ в клетке и окружающей её среде нельзя объяснить только Д. их через мембраны за счёт имеющихся электрохимических и осмотических градиентов. На распределение ионов влияют также процессы, которые могут вызывать перераспределение веществ против их электрохимического градиента с затратой энергии,- т. н. активный транспорт ионов.

Л. Н. Воробьёв, И. А. Воробьёва,

Лит.: Френкель Я. И., Собр. избр. трудов, т. 3 -Кинетическая теория жидкостей, М. -Л.,1959; Гиршфельдер Дж., Кертисс Ч., Берд Р., Молекулярная теория газов и жидкостей, пер. с англ., М., 1961; Шьюмон П., Диффузия в твердых телах, пер. с англ., М., 1966; Франк-Каменецкий Д. А., Диффузия и теплопередача в химической кинетике, 2 изд., М., 1967; Булл Г., Физическая биохимия, пер. с англ., М., 1949; Руководство по цитологии, т. 1, М. -Л., 1965; Ходоров Б. И., Проблема возбудимости, Л., 1969.

ДИФФУЗИЯ нейтронов, распространение нейтронов в веществе, сопровождающееся многократным изменением направления и скорости движения в результате их столкновений с атомными ядрами. Д. нейтронов аналогична Д. в газах и подчиняется тем же закономерностям (см. Диффузия). Быстрые нейтроны, т. е. нейтроны с энергией, во много раз большей, чем средняя энергия теплового движения частиц среды, при Д. отдают энергию среде и замедляются. В слабо поглощающих средах нейтроны приходят в тепловое равновесие со средой (тепловые нейтроны). В неограниченной среде тепловой нейтрон диффундирует до тех пор, пока не поглотится одним из атомных ядер. Д. тепловых нейтронов характеризуется коэфф. диффузии D и средним квадратом расстояния от точки образования теплового нейтрона до точки его поглощения, равным L²_T = 6 Dt, где t - среднее время жизни теплового нейтрона в среде.

Для характеристики Д. быстрых нейтронов употребляют средний квадрат расстояния L²_Б между точкой образования быстрого нейтрона (в ядерной реакции, напр., реакции деления) и точкой его замедления до тепловой энергии. В табл. приведены для некоторых сред значения L²_Т для тепловых нейтронов и L²_Б для нейтронов, испускаемых при делении урана.

ЗначенияL²_Т и L²_Б для некоторых веществ
 

Вещество	L2Т см2	L2Б , см2	КОРЕНЬ (L2Т +L2Б)
Вода Н2,О	44	186	15
Тяжёлая вода D2O	1,5 105	750	390
Берилий Be	2600	516	56
Графит С	20000	1880	150

При Д. в ограниченной среде нейтрон с большой вероятностью вылетает за её пределы, если полуразмер (радиус) системы мал по сравнению с величиной

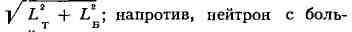
шой вероятностью поглотится в среде, если её радиус велик по сравнению с этой величиной.

Д. нейтронов играет существенную роль в работе ядерных реакторов. В связи с этим разработка ядерных реакторов сопровождалась интенсивным развитием теории Д. нейтронов и методов её экспериментального изучения.

Лит.: Бекурц К., Виртц К., Нейтронная физика, пер. с англ., М., 1968.

ДИФФУЗНЫЕ ТУМАННОСТИ, туманные объекты, принадлежащие к числу туманностей галактических. Различают: светлые эмиссионные Д. т. (их спектр в основном состоит из линий излучения); светлые отражательные Д. т.; тёмные туманности, видимые как тёмные пятна на светлом фоне Млечного Пути. Д. т. наблюдаются также и в др. галактиках.

ДИФФУЗОР, в аэрогидродинамике часть канала (трубы), в к-рой происходят замедление (расширение) потока и возрастание давления. При скоростях, не превышающих скорости звука, площадь поперечного сечения Д. вдоль потока возрастает, а при сверхзвуковых скоростях уменьшается. Д. применяется в устройствах, в к-рых осуществляется перемещение жидкостей и газов (водопроводах, воздуховодах, газопроводах, нефтепроводах, аэродинамич. трубах, реактивных двигателях и др.). В электроакустике часть механич. колебательной системы громкоговорителя, предназнач. для возбуждения звуковых волн в окружающем воздухе. Обычно изготовляется из спец. сортов бумаги и гибко крепится к металлич. корпусу громкоговорителя. В фототехнике приспособление для получения фотографич. изображения мягкого рисунка. Представляет собой: а) плоскопараллельную стеклянную пластинку с квадратной сеткой или концентрич. кругами, нанесёнными алмазом на расстоянии 2-3 мм; б) узкие полоски стекла шириной 0,1 диаметра объектива и толщиной 0,8-1 мм. Полоски и пластинки укрепляются в оправу, к-рая надевается на объектив фотоаппарата или фотографич. увеличителя после наводки на резкость. В производстве глинозёма аппарат для проточного выщелачивания дроблёного бокситового спека. Обычно 12-14 таких аппаратов соединяются последовательно, образуя батарею. Особенность проточного выщелачивания в Д. состоит в том, что спек в них остаётся всё время неподвижным на решётчатом днище, а раствор последовательно в каждом Д. просачивается через толщу спека. Омывая каждую отдельную частицу, а также проникая по порам внутрь её, раствор выщелачивает растворимые составляющие. В один конец батареи подаётся горячая вода, из др. сливается концентриров. раствор алюмината натрия. Все Д. соединены трубопроводами; с помощью кранов можно отключить любой из них, не нарушая работы остальных. Д. с выщелоченным спеком периодически отключают, а в др. конце батареи вместо него включают Д. со свежим спеком. Обычно в батарее из 14 Д. 12 находятся в работе, 1 под загрузкой и 1 под разгрузкой. Д. в пищевой промышленности - см. Диффузионный аппарат.

Лит.: Лайнер А. И., Производство глинозема, М., 1961; Беляев А. И., Металлургия легких металлов, 6 изд., М., 1970.

А. И. Лайнер.

ДИХАЗИЙ (от греч. dichazd - делю надвое, разделяю), двулучевой верхоцветник, полузонтик, развилина, соцветие растений цимозного типа. Главная ось в Д. заканчивается одним верхушечным цветком; из пазух 2 супротивных листьев, находящихся под этим цветком, развиваются 2 боковые ветви, к-рые перерастают главную ось и тоже заканчиваются цветками, распускающимися позднее; на каждой из них, в свою очередь, развиваются по 2 супротивные боковые ветви, перерастающие их и заканчивающиеся цветками, распускающимися ещё позднее, и т. д. Д. характерны для мн. растений семейства гвоздичных и др.Иногда ветвление и рост у Д. несколько нарушаются и образуются соцветия, внешне непохожие на Д. (напр., т. н. ложные мутовки у растений сем. губоцветных).

ДИХАНГ, участок р. Брахмапутры в месте прорыва ею Гималаев (на терр. Китая), где река течёт в глубоком ущелье. Дл. ок. 400 км. Пороги, невысокие водопады. Несудоходна.

ДИХЛОРАЛЬМОЧЕВИНА, химическое соединение, применяемое для борьбы с однодольными сорными растениями (см. Гербициды).

ДИХЛОРФЕНОКСИУКСУСНАЯ КИСЛОТА - 2,4 (2,4-Д), С1₂С₆Н₃ОСН₂СООН, гербицид для борьбы с двудольными (широколистными) сорными растениями в посевах зерновых культур, на лугах и т. д. В чистом виде Д. к.- белые кристаллы без запаха, с t_пл 140,5 °С; при 20 °С в 1 л воды растворяется 540 мг кислоты. Технич. препарат имеет неприятный фенольный запах, обусловленный примесью 2,4-дихлорфенола. В пром-сти Д. к. получают взаимодействием солей монохлоруксусной к-ты с 2,4-дихлорфе-нолятом натрия и хлорированием феноксиуксусной к-ты. По масштабам производства и применения Д. к. среди гербицидов занимает первое место. Применяют Д. к. в виде растворимых в воде солей с алифатич. аминами (диметиламин, диэтиламин, этаноламины и др.), в виде натриевой соли, эфиров с различными спиртами (изопропиловый, бутиловый, октиловый и др.) и амидов (напр., о-хлоранилида).

При нормах расхода 0,5-2 кг/га с помощью Д. к. могут быть уничтожены почти все виды двудольных сорных растений (бодяк полевой, борщевик обыкновенный, василёк и др.). Обработку зерновых культур проводят в фазе кущения.

К действию Д. к. чувствительны мн. культурные растения, такие, как хлопчатник, подсолнечник, плодовые (яблоня, груша, слива, вишня, абрикос, персик), ягодные (смородина, земляника, крыжовник, малина и др.), а также лиственные древесные и кустарниковые породы. Действие гербицида на бедных почвах и в засушливый период слабее; наоборот, растения, выросшие на богатых и влажных почвах, погибают быстрее. Д. к. умеренно токсична для животных и человека.

Механизм действия Д. к. окончательно не изучен. Известно, что она быстро всасывается листьями растений и вызывает разрастание меристематич. клеток, вследствие чего происходит разрыв тканей, скручивание и гибель растения. В почве Д. к. под влиянием микроорганизмов сравнительно быстро разрушается и не накапливается.

Лит.: Мельников Н. Н., Баскаков Ю. А., Химия гербицидов и регуляторов роста растений, М., 1962; Крафтс А., Роббинс У., Химическая борьба с сорняками, пер. с англ., М., 1964; Мельников Н. Н., Химия пестицидов, М., 1968.

Н. Н. Мельников.

ДИХЛОРЭТАН, хлористый этилен, СlСН₂СН₂Сl, бесцветная подвижная жидкость с запахом, напоминающим запах хлороформа; t_пл - 35,9 "С, t_кип 83,5 °С, плотность 1,2600 г/см³ (15 °С), п ¹⁵_D 1,4476; темп-pa вспышки 21,1 °С (в открытой чашке); пределы взрываемости в воздухе 6,20-15,90% (по объёму). Д. плохо растворим в воде (0,81% при 25 °С), образует азеотропную смесь с водой (t_кип 71,5 °С, 82,9% Д.). Гидролиз Д. приводит к этиленгликолю НОСН₂СН₂ОН. Пиролиз или взаимодействие Д. со щёлочью даёт винилхлорид, реакция с аммиаком - этилендиамин и т. д. При нагревании с полисульфидами натрия Д. образует полисульфидный каучук. Д. получают при взаимодействии этилена и хлора.

Д. токсичен. Предельно допустимая концентрация паров в воздухе 0,01%. Д. широко применяют как растворитель в различных произ-вах, как компонент антидетонационных смесей, фумигант, сырьё для получения полисульфидного каучука.

ДИХОГАМИЯ (от греч. dicha - на две части, отдельно и gamos - брак), неодновременное созревание в цветках пыльников и рылец. Д. имеет значение для перекрёстного опыления, что впервые отметил А. Т. Болотов (1780). У одних цветков сначала созревают пыльники (протандрия), у других - рыльца (протогиния). Д. наблюдается не только в обоеполых, но и в однополых цветках однодомных и двудомных растений. Д. наз. совершенной, если рыльца созревают после увядания тычинок (или наоборот); чаще встречается Д. несовершенная - половозре-лость позднее созревающих органов наступает при ещё неутраченной функции органов противоположного пола. Протандрия наблюдается почти у всех растений сем. сложноцветных, зонтичных и мн. др. Протогиния встречается реже, напр, у растений сем. крестоцветных, розовых, лютиковых (анемоны) и нек-рых др. Д. наз. также неодновременное созревание органов разного пола у споровых растений.

ДИХОТОМИЧЕСКОЕ ДЕЛЕНИЕ, деление объёма понятия (класса, множества) на два соподчинённых (производных) класса по формуле исключённого третьего: "А или не-А" (см. Исключённого третьего принцип). Иначе говоря, только такое деление на два будет дихотомическим, в к-ром производные классы определяются парой логически противоречивых свойств (терминов), одно из к-рых служит основанием деления. Так, деление множества всех людей на мужчин и не-мужчин (по признаку -"быть мужчиной") является дихотомическим, но деление того же множества на класс мужчин и класс женщин (по признаку пола) не является Д. д.- основания деления здесь разные, а свойство "быть мужчиной" логически не противоречит свойству " быть женщиной". Последний тип деления (в виду аналогии "деление на два") называют иногда псевдодихотомическим. С точки зрения результата оба типа деления могут совпадать; в этом смысле отнесение нек-рого "деления на два" к типу дихотомического (если "абсолютно"- с точки зрения определения -оно не является таковым) зависит в ряде случаев от принимаемых допущений. Так, в рамках двузначности принципа псевдодихотомическое деление высказываний на истинные и ложные (основание деления - значение истинности высказывания) равнозначно их Д. д. на класс истинных и класс неистинных высказываний (основание деления - свойство высказывания "быть истинным"). Но если принцип двузначности не принимать, то очевидно, что, с точки зрения результата, эти два деления явно различны: в числе неистинных высказываний могут быть и такие, к-рые у нас нет оснований считать ложными. Любое псевдодихотомич. деление может быть преобразовано в Д. д., но не наоборот. Это связано, в частности, с тем, что при Д. д. один из производных классов - дополнительный - определяется всегда только отрицательно (посредством отрицательного термина), тогда как в псевдодихотомич. делении оба класса определяются положительно, заменить же отрицательное определение положительным не всегда возможно. Напр., поскольку нет положительного определения понятия "трансцендентная функция", для Д. д. функций на алгебраические и трансцендентные (неалгебраические) нет и соответствующего псевдодихотомич. деления.

М. М. Новосёлов.

ДИХОТОМИЯ (греч. dichotomia, от dicha - на две части и tome - разрез, сечение), тип ветвления растений, при к-ром ось разделяется на 2 новые, обычно одинаково развитые ветви (см. Ветвление). Д. свойственна и некоторым беспозвоночным животным (напр., дихотомическое деление кишечнополостных).

ДИХРОИЗМ (от греч. dichroos - двухцветный), различная окраска одноосных кристаллов (обладающих двойным лучепреломлением) в проходящем свете при взаимно перпендикулярных направлениях наблюдения - вдоль оптич. оси и перпендикулярно к ней. Напр., кристалл апатита, освещаемый белым светом, кажется на просвет светло-жёлтым, если смотреть по направлению оптич. оси, и зелёным - в перпендикулярном направлении. Окраску кристалла в указанных условиях наблюдения называют, соответственно, "осевой" и "базисной". При др. направлениях наблюдения кристалл также виден окрашенным (в к.-л. из промежуточных цветов), т. е. Д. представляет собой частный случай плеохроизма (многоцветности). Д. обусловлен различием спектров поглощения кристалла для лучей, имеющих разное направление и поляризацию (подробнее см. в ст. Плеохроизм).

ДИХРОМАТЫ, бихроматы, двухромовокислые соли, соли двухромовой кислоты Н₂Сr₂О₇, напр. К₂Сr₂О₇. Большинство Д. имеет оранжево-красную окраску. Растворимость их, как правило, выше, чем соответствующих хроматов (солей хромовой кислоты Н₂СrО₄). Д., как и хроматы, в кислой среде являются сильными окислителями (6-валентный Сг восстанавливается до 3-валентного, напр. К₂Сr₂О₇ + 14НС1 =
= 2КС1 + 2СrС1₃ + 3Сl₂ + 7Н₂O). Обладающая очень сильным окислительным действием смесь равных объёмов насыщенного на холоду раствора К₂Сr₂О₇ и концентрированной H₂SO₄ (хромовая смесь) применяется в лабораториях для мытья химической посуды.

ДИХУА, второе название г. Урумчи, в сев.-зап. Китае.

ДИЦ (Diez) Фридрих Кристиан (15.3.1794, Гисен,-29.5.1876, Бонн), немецкий филолог-романист. Основоположник сравнительного изучения романских языков. Проф. ун-та в Бонне (с 1823). Осн. труды -грамматика и этимологич. словарь романских языков. Известен также исследованиями в области старопровансальской лит-ры, поэзии трубадуров.

Соч.: Etymologisches Worterbuch der romanischen Sprachen, 3 Ausg., Tl 1 - 2, Bonn, 1869-70; Grammatik der romanischenSprachen, Tl 1-3, Bonn, 1836-44; Leben und Werke der Troubadours, 2 Aufl., Amst., 1965; Die Poesie der Troubadours, 2 Aufl., Lpz., 1883.

ДИЦГЕН (Dietzgen) Иосиф (9.12.1828, Бланкенберг, -15.4.1888, Чикаго), немецкий рабочий-кожевник, философ, самостоятельно пришедший к идее материалистич. диалектики. Преследуемый за революц. деятельность, Д. в 1848 эмигрировал в США; жил в России (1864-1869), где работал мастером на кожевенном заводе в Петербурге. В 1869 вернулся в Германию. Филос. эрудицию приобрёл самообразованием. Материализм и атеизм Д. формировались гл. обр. под влиянием Л. Фейербаха, а после 1867 - под воздействием К. Маркса и Ф. Энгельса. С 1869 Д. чл. С.-д. партии, организатор одной из секций 1-го Интернационала в Германии. В 1870-88 сотрудничал в с.-д. газетах Германии и США. Первый филос. опыт Д.- "Сущность головной работы человека" (1869, рус. пер. 1902) - получил высокую оценку Маркса и Энгельса. Д. принадлежит ряд работ по философии и политэкономии (см. "Мелкие философские статьи", 2 изд., 1913). Последние годы жизни Д. посвятил разработке гл. обр. теории познания. В своих произв. Д. выступал как воинствующий материалист, противник филос. метафизики и религии. Однако филос. построения Д. не всегда были последовательными, что в обстановке теоретич. борьбы внутри 2-го Интернационала дало философам махистского толка основание противопоставить "дицгенизм" марксистской философии (см. В. И. Ленин, Полн. собр. соч., 5 изд., т. 18, с. 261). Так, в ряде случаев Д. формулировал тождество материи и сознания, априоризм отд. понятий, преувеличивал степень относительности знания, что приводило его к агностицизму. Диалектика Д. не сложилась в целостную систему; Д. не удалось раскрыть диалектику как теорию познания. Критикуя ошибки Д., Ленин высоко ценил его как одного из "...выдающихся социал-демократических писателей-философов Германии" (там же, т. 23, с. 117).

Соч.: Samtliche Schriften, Bd 1-3, Stuttg., 1920; Ausgewählte Schriften, В., 1954; в рус. пер.-Избранные философские сочинения, М., 1941.

Лит.: М а р к с К. и Энгельс Ф., Соч., 2 изд., т. 1, 2, 3 (см. указатель имен); Андреев Н., Диалектический материализм и философия Иосифа Дицгена, "Современный мир", 1907, № 11; Волкова В., Иосиф Дицген, М., 1961.

ДИЦЕНТРА, диклитра, сердечки (Dicentra), род многолетних травянистых корневищных растений сем. дымянковых. Листья трижды тройчато - или перисторассечённые или сложные. Цветки сердцевидные, собраны в кисти, лепестков 4, из к-рых 2 наружных со шпорцем. Ок. 20 видов в Вост. Азии и Сев. Америке; в СССР 1 вид - Д. бродяжная (D. peregrina), встречающаяся на гольцах и обнажениях Вост. Сибири и Д. Востока. В цветоводстве используются Д. великолепная (D. spectabilis) с односторонней кистью крупных розовато-красных цветков, а также Д. красивая (D. formosa) и Д. исключительная (D. eximia).

ДИЦИНОДОНТЫ (Dicynodontia), подотряд (или надсемейство) ископаемых зверообразных пресмыкающихся. Были широко распространены в конце пермского и начале триасового периодов. Размеры - от крысы до носорога. Череп массивный, зубы редуцированы, за исключением двух клыков; челюсти имели форму клюва, как у черепах. Вероятно, Д. были растительноядны. Остатки Д. найдены па всех материках (кроме Австралии); особенно обильны они в верхнепермских отложениях Юж. Африки.

Лит.: Основы палеонтологии. Земноводные, пресмыкающиеся и птицы, М., 1964.

ДИЧЕНКО Михаил Петрович [27. 1 (8.2). 1863, г. Боярка, ныне Киевской обл.,- 4.12.1932], советский астроном, специалист по астрометрии и теоретич. астрономии. С 1891 по 1898 астроном Пулковской обсерватории, где определил на меридианном круге положения 125 околополярных звёзд. С 1898 Д. астроном-наблюдатель Киевской обсерватории. В результате 34-летних наблюдений положений звёзд на меридианном круге Д. составил каталог зодиакальных звёзд. Кроме того, на основе произведённого им вновь наблюдения звёзд зоны Аргеландера исследовал движение Солнца.

ДИЧКИ, 1) в плодоводстве выращенные из семян молодые деревца (наз. сеянцами), используются для прививки в качестве подвоев. 2) В лесоводстве молодые 2-3-летние деревца, появившиеся из семян (т. н. самосев).

ДИЧЬ, добываемые охотой птицы и звери, мясо к-рых употребляется в пищу. Кроме мяса, Д. даёт пух, перо, шкуры, рога. По охотничьей классификации птицы считаются пернатой, а звери четвероногой Д. Пернатую Д. по месту обитания делят на лесную, или боровую (рябчик, белая куропатка, тетерев, глухарь, фазан и др.), полевую и степную (серая и даурская куропатки, перепел, стрепет, дрофа, журавль-красавка, саджа и др.), водоплавающую (утки, гуси, лебеди и др.), болотную (кулики: вальдшнеп, бекас, дупель, гаршнеп и др.), горную (кам. куропатка, горная индейка, или улар, и др.). К четвероногой Д. относятся зайцы и многочисленные виды диких копытных (олени, степные и горные антилопы, горные козлы, бараны, кабаны и др.).

В СССР ежегодно добывается ок. 50 млн. шт. различной Д. В добыче пернатой Д. первостепенное значение имеет водоплавающая Д., широко распространённая на внутр. водоёмах страны и на о-вах Северного Ледовитого и Тихого океанов. Ежегодная (60-е гг. 20 в.) добыча этой Д. 25-30 млн. шт., осн. районы добычи - Зап. Сибирь, Казахстан, прибрежные районы и заливы Белого, Балтийского, Чёрного, Каспийского и Аральского морей. В лесной и лесостепной зонах Европ. части СССР, Зап. и Вост. Сибири ежегодно добывается 12-15 млн. шт. боровой Д. В Европ. части СССР, Зап. Сибири и Казахстане ежегодно отстреливают ок. 3 млн. болотных птиц (куликов); в целинных степях Казахстана и Забайкалья ок. 1 млн. шт. степной Д. Небольшое кол-во горной Д. (кам. куропаток и уларов) отстреливают в горах Кавказа, Копетдага, Тянь-Шаня и Алтая. Многие редкие виды пернатой Д. (лебеди, краснозобая казарка, фламинго, чёрный и белый журавли, дрофа и др.) находятся под охраной, охота на них временно запрещена. Мясо пернатой Д.- высокопитательный диетич. продукт.

Из четвероногой Д. объектами охоты в СССР являются зайцы и многие виды диких парнокопытных. Ежегодно в стране добывают 5-6 млн. зайцев. Дикие парнокопытные - первоклассная (т. н. красная) Д. В результате мероприятий по установлению рациональных сроков охоты и норм отстрела, а также работ по акклиматизации и реакклиматизации численность диких копытных возросла к 1972 до 5-6 млн. голов (из к-рых ок. 400 тыс. голов - ежегодная добыча охотников). В тундре, лесотундре и значит, части тайги охотятся на дикого сев. оленя, ежегодная добыча к-рого до 30 тыс. голов. В лесной и лесостепной зонах добывают лося (ежегодная добыча 30-35 тыс. голов), благородных оленей - европ. оленя в Европ. части СССР, марала на Алтае и юге Вост. Сибири, марала и изюбра на Д. Востоке; косулю -в лесной зоне Европ. части СССР, в Сибири и на Д. Востоке; в горах Алтая, Саян, Вост. Сибири, в юж. Приморье успешно разводят безрогого маленького оленя кабаргу; в юж. Приморье успешно разводят пятнистых оленей, охота на к-рых временно запрещена (общее поголовье этих оленей в СССР ок. 40 тыс. голов). В степях и пустынях Ср. Азии и Казахстана охотятся на сайгака; в результате мер охраны численность его возросла до 1,2 млн. голов (ежегодная добыча 200-250 тыс. голов). Другие виды антилоп - горал, обитающий в горах Приморья, дзерен (степи Забайкалья), джейран (степи Ср. Азии и Закавказья), серна (Кавказ) являются довольно редкой Д. и охота на них временно запрещена. На кабанов охотятся в центр, обл. Европ. части СССР, в Прибалтике, на Украине, Кавказе, в Ср. Азии, Казахстане, на Д. Востоке, на Алтае, в Саянах и Приморском крае; ежегодная добыча кабанов 30-35 тыс. Из диких козлов осн. объектом охоты является сибирский козерог, обитающий в горах Тянь-Шаня, Алтая, Саян. Охота на др. виды козлов (кавказский тур, дагестанский тур, бе-зоаровый козёл, винторогий козёл) в большинстве районов временно запрещена. На диких баранов охотятся в горах Ср. Азии, Алтая, Камчатки, Закавказья; охота на них также временно запрещена до восстановления численности.

Мясо диких оленей, антилоп и др. копытных по питательности превосходит мясо домашних животных. Шкуры - отличное сырьё для выделки кож, замши. Из неокостеневших рогов пятнистого оленя, марала и изюбра (пантов) вырабатывают пантокрин. "Кабарожью струю" используют для изготовления различных препаратов в медицине и парфюмерии. Рога диких копытных идут на поделку украшений и сувениров.

По запасам Д. СССР занимает первое место в мире. Во всех странах мира Д. считается общенациональным достоянием, охрана к-рого, рациональное использование и расширенное воспроизводство контролируются гос-вом. Добывание Д. регулируется сроками и правилами охоты, устанавливаемыми гос. органами управления охотничьим х-вом. С целью обогащения охотничьей фауны проводится расселение различных видов Д.

В странах Зап. Европы из массовых видов Д. ежегодно добывают: св. 70 тыс. лосей, 140-150 тыс. благородных оленей, св. 1 млн. косуль, св. 100 тыс. кабанов, до 10 млн. зайцев, до 2 млн. серых куропаток, св. 5 млн. фазанов, св. 15 млн. уток и др. В США и Канаде, кроме ежегодно добываемых массовых видов Д. (белохвостые и чернохвостые амер. олени, вапити, дикий кролик, воротничковый рябчик, виргинский перепел, фазан, серая куропатка и др.), как и в европ. странах, широко практикуется пром. разведение пернатой Д. на фермах (фазан, каменная куропатка - кеклик, серая куропатка, кряква и др.) с последующим выпуском молодняка птиц в естественные угодья для доращивания. Проблемы дичеразведения и охраны Д. ставятся в программу Междунар. конгрессов биологов-охотоведов (10-й конгресс в 1971, Париж). См. также статьи об отдельных видах Д.

В. Ф. Гаврин.

ДИЭЛЕКТРИКИ, вещества, плохо про водящие электрич. ток. Термин "Д." (от греч. dia - через и англ, electric - электрический) введён М. Фарадеем для обозначения веществ, через к-рые проникают электрич. поля. В любом веществе, помещённом в электрич. поле, составляющие его электрич. заряды (электроны, атомные ядра) испытывают силы со стороны этого поля. В результате часть зарядов направленно перемещается, образуя электрический ток. Остальные же заряды перераспределяются так, что "центры тяжести" положительных и отрицательных зарядов смещаются друг относительно друга. В последнем случае говорят о поляризации вещества. В зависимости от того, какой из этих двух процессов - электропроводность или поляризация - преобладает, принято деление веществ на изоляторы (Д.) и проводники (металлы, электролиты, плазма). Электропроводность Д. по сравнению с металлами очень мала. Их удельное сопротивление р порядка 10⁸-10¹⁷ ом*см, а у металлов р ~ 10^-6-10^-4ом*см. Существует и промежуточный класс - полупроводники, свойства к-рых определяются процессами как электропроводности, так и поляризации.

Количеств, различие в электропроводности твёрдых Д. и металлов классич. физика пыталась объяснить тем, что в металлах есть свободные электроны, а в Д. все электроны связаны, т. е. принадлежат отдельным атомам, и электрич. поле не отрывает, а лишь слегка смещает их. Однако такое объяснение неточно. Как показывает совр. квантовомеханич. теория, твёрдое тело представляет собой как бы гигантскую "молекулу", где каждый электрон принадлежит всему кристаллу в целом. Это в одинаковой степени справедливо и для Д., и для металлов. Причиной различного поведения электронов в металле и в Д. является различный характер распределения электронов по уровням энергии.

Энергия электронов в твёрдом теле не может иметь произвольного значения. Области энергий, к-рыми электрон может обладать (разрешённые зон ы), чередуются с интервалами энергий, к-рые электрон не может принимать (запрещённые зон ы). Т. к., с одной стороны, электроны стремятся занять уровни с наименьшей энергией, а с др. стороны, в одном состоянии может находиться только один электрон, то электроны заполняют энергетич. уровни от нулевого до нек-poro максимального. В Д. верхний заполненный электронами энергетич. уровень совпадает с верх, границей одной из разрешённых зон (рис. 1). В металлах же верхний заполненный электронами энергетич. уровень лежит внутри разрешённой зоны (см. Твёрдое тело).

Для того чтобы в твёрдом теле под действием электрич. поля возник электрич. ток (направленное движение электронов), необходимо, чтобы часть электронов могла увеличивать свою энергию под действием поля, т. е. переходить с нижних энергетич. уровней на более высокие. В металле такой переход возможен, т. к. к заполненным уровням непосредственно примыкают свободные. В Д. же ближайшие свободные уровни отделены от заполненных запрещённой зоной, к-рую электроны под действием обычных не слишком сильных электрич. полей преодолеть не могут. В Д. действие электрич. поля сводится к перераспределению электронной плотности, к-рое приводит к поляризации Д. Распределение электронов по уровням энергии в полупроводниках и Д. сходно. Полупроводник отличается от Д. лишь более узкой запрещённой зоной. Поэтому при низких темп-pax свойства полупроводников и Д. близки, а при повышении темп-ры электропроводность полупроводников возрастает и становится заметной. Резкой грани между Д. и полупроводниками провести нельзя. Вещества с шириной запрещённой зоны ДЕ < 2-3 эв относят к полупроводникам, а с ДЕ > 2-3 эв - к Д.

Выше шла речь о твёрдых Д. Однако Д. могут быть также жидкости (см. Жидкие диэлектрики) и газы. В обычных условиях все газы состоят в основном из нейтральных атомов и молекул и поэтому не проводят электрич. тока, т. е. являются Д. С повышением темп-ры атомы и молекулы ионизируются и газ постепенно превращается в плазму, хорошо проводящую электрич. ток. Ниже речь будет идти о твёрдых Д.

Поляризация Д. Механизмы поляризации Д. могут быть различными. Они зависят от характера химической связи, т. е. распределения электронных плотностей в Д. Напр., в ионных кристаллах (каменная соль NaCl и др.), где электроны распределены так, что можно выделить отдельные ионы, поляризация является результатом сдвига ионов друг относительно друга (ионная поляризация, рис. 2, я), а также деформации электронных оболочек отдельных ионов (электронная поляризация). Иными словами, поляризация в этом случае является суммой ионной и электронной поляризаций. В кристаллах с ковалентной связью (напр., в алмазе), где электронные плотности равномерно распределены между атомами, поляризация обусловлена гл. обр. смещением электронов, осуществляющих хим. связь (рис. 2, 6). В полярных Д. (напр., твёрдый сероводород) группы атомов - молекулы или радикалы представляют собой электрич. диполи, к-рые в отсутствии электрич. поля ориентированы хаотически, а под действием поля эти диполи ориентируются вдоль него (рис. 2, в). Такая ориентационная (дипольная) поляризация типична для полярных жидкостей и газов. Сходный механизм поляризации связан с перескоком под действием электрич. поля

Рис. 1. Уровни энергии электронов твёрдого тела группируются в разрешённые зоны (валентная зона и зона проводимости), разделённые запрещёнными зонами.

отдельных ионов из одних возможных положений равновесия в решётке в другие. Особенно часто такой механизм поляризации наблюдается в веществах с водородной связью (напр., у льда), где ионы водорода имеют неск. положений равновесия.

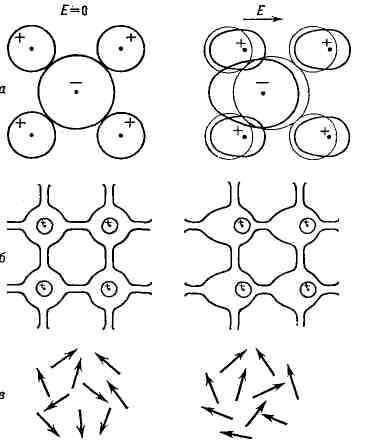
Рис. 2. Поляризация диэлектриков в поле Е: а - ионная и электронная поляризации ионных кристаллов; б - электронная поляризация ковалентных кристаллов; в - ориентационная поляризация полярных диэлектриков.

Поляризацию Д. характеризуют вектором поляризации P, к-рый представляет собой дипольный момент единицы объёма Д. Дипольный момент нейтральной в целом системы зарядов есть вектор, равный произведению расстояния между центрами тяжести положительных и отрицательных зарядов на величину заряда одного знака. Направлен этот вектор от центра тяжести отрицательных к центру тяжести положительных зарядов. Вектор P зависит от напряжённости электрич. поля Е. Поскольку сила, действующая на заряд, пропорциональна Е, то, естественно, что при малых полях величина P пропорциональна Е. Коэфф. пропорциональности x в соотношении P = xЕ наз. диэлектрической восприимчивостью Д. Часто оказывается удобным вместо вектора P пользоваться вектором электрич. индукции D = Е + 4пP.

Коэфф. пропорциональности Е в соотношении D = еЕ наз. диэлектрической проницаемостью. Ясно, что е = 1 + 4пx.

В вакууме х = 0 и е = 1 (в системе единиц СГСЕ). Значение е (или и) является основной характеристикой Д.

В анизотропных Д. (напр., в некуби ческих кристаллах) направление вектора поляризации P определяется не только направлением поля Е, но также выделенными направлениями среды, напр, осями симметрии кристалла. Поэтому вектор P будет составлять различные углы с вектором Е в зависимости от ориентации Е по отношению к осям симметрии. В результате вектор D будет определяться через вектор Е с помощью не одной величины е, а неск. величинами (в общем случае - шестью), образующими тензор диэлектрич. проницаемости (см. Анизотропия).

Д. в переменном поле. Если электрич. поле Е изменяется во времени, то величина поляризации в заданный момент времени t не определяется значением поля Е в тот же момент времени t. Поляризация Д. не успевает следовать за вызывающим её электрич. полем, т. к. смещения зарядов не могут происходить мгновенно (рис. 3).

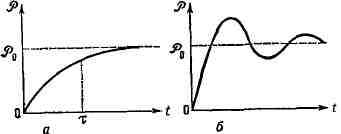
Рис. 3 а, 6. Две характерные зависимости поляризации диэлектрика Р от времени t. Постоянное электрическое поле Е включается в момент времени t=0.

Т. к. любое переменное поле можно представить в виде совокупности полей, меняющихся по гармонич. закону (см. Фурье ряд, Фурье интеграл), то достаточно изучить поведение Д. в поле Е =Е₀Х X cos wt, где w - частота переменного поля. Под действием такого поля величины D и P будут колебаться также гармонически с той же частотой со. Однако между колебаниями D и E будет существовать разность фаз, что вызвано отставанием поляризации P от поля Е.

Гармонический закон можно представить в комплексном виде: Е = Е₀е^iwt (см. Комплексная амплитуда). Тогда D = D₀e^iwt, причём амплитуды колебаний D к Е связаны соотношением: D₀ = е (w) Е₀. Диэлектрич. проницаемость е (со) в этом случае является комплексной величиной: е (w) = e1+ie2, и характеризуется двумя величинами e1 и e2, зависящими от частоты со пе-ременного поля. Абс. величина |е(w)| =КОРЕНЬ(е²+е²)= определяет амплитуду колебания D, а отношение (e1 / e2) = tg б определяет разность фаз б между колебаниями D к Е. Величина б наз. углом диэлектрических потерь. Это назв. связано с тем, что наличие разности фаз 8 приводит к поглощению энергии электрич. поля в Д. Действительно, работа, совершаемая полем Е в единице объёма Д., выражается интегралом ИНТЕГРАЛ EdР. Взятый за один период колебания, этот интеграл обращается в ноль, если Р и Е колеблются синфазно (б = 0) или в противофазе (б = п). В остальных случаях интеграл отличен от нуля. Доля энергии, теряемой за один период, равна e₂. В постоянном электрич. поле (w = 0) е₂ = 0, a e₁ совпадает с е.

В переменных электрич. полях очень высоких частот (напр., электромагнитные волны оптич. диапазона) свойства Д. принято характеризовать преломления показателем п и поглощения показателем k (вместо e₁ и e₂). Коэфф. преломления п равен отношению скоростей распространения электромагнитных волн в Д. и в вакууме. Коэфф. поглощения k характеризует затухание элект-

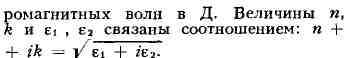
Дисперсия диэлектрической проницаемости. Зависимость диэлектрич. проницаемости от частоты со переменного поля е (w) = e₁ (w) + ie₂ (w) наз. дисперсией диэлектрич. проницаемости. Характер дисперсии определяется процессом установления поляризации во времени. Если процесс установления поляризации - релаксационный (рис. 3, а), то дисперсия будет иметь вид, изображённый на рис. 4, а. Когда период колебания электрич. поля велик по сравнению с временем релаксации т (частота со мала по сравнению с 1/t), поляризация успевает следовать за полем и поведение Д. в переменном электрич. поле не будет существенно отличаться от его поведения в постоянном поле (т. е. e₁ = e, e₂= 0, как на рис. 3, а). При частотах w >> 1/t Д. не будет успевать поляризироваться, т. е. амплитуда P будет очень мала по сравнению с величиной поляризации Л в постоянном поле. Это значит, что е1 ~~ 1, а e₂ ~ 0. Т. о., e₁ с ростом частоты изменяется от е до 1. Наиболее резкое изменение e₁ происходит как раз на частотах w ~ 1/t. На этих же частотах e₂ проходит через максимум. Такой характер дисперсии Е (w) наз. релаксационным. Если поляризация в процессе установления испытывает колебания, как показано на рис. 3, б, то дисперсия Е (w) будет иметь вид, изображённый на рис. 4, 6. В этом случае характер дисперсии наз. резонансным.

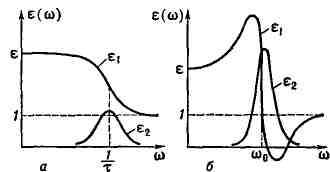
Рис. 4. а - релаксационный характер дисперсии диэлектрической проницаемости е (w), соответствующий зависимости P(t), изображённой на рис. 3, а; б - резонансный характер дисперсии диэлектрической проницаемости e(w), - соответствующий зависимости, изображённой на рис. 3, б.

В реальном веществе дисперсия e (w) имеет более сложный характер, чем на рис. 4. На рис. 5 изображена зависимость Е (w), характерная для широкого класса твёрдых Д. Из рис. 5 видно, что можно выделить неск. областей дисперсии в разных диапазонах частот. Наличие этих, обычно чётко разграниченных, областей указывает на то, что поляризация Д. обусловлена различными механизмами. Напр., в ионных кристаллах поляризацию можно представить как сумму ионной и электронной поляризаций. Типичные периоды колебаний ионов ~ 10^-13 сек. Поэтому дисперсия e (w), обусловленная ионной поляризацией, приходится на частоты ~ 10¹³ гц (инфракрасный диапазон). Характер дисперсии обычно резонансный. При более высоких частотах ионы уже не успевают смещаться и весь вклад в поляризацию обусловлен электронами. Характерные периоды колебаний электронов определяются шириной запрещённой зоны Д. Когда энергия фотона hw (h - Планка постоянная) становится больше ширины запрещённой зоны, фотон может поглотиться, вызвав переход электрона через запрещённую зону. В результате электромагнитные волны на таких частотах (w ~ 10¹⁵гц - ультрафиолетовый диапазон) сильно поглощаются, т. е. резко возрастает величина e₂. При меньших частотах (в частности, для видимого света) чистые однородные Д., в отличие от металлов, обычно прозрачны. В полярных Д. под действием электрического поля происходит ориентация диполей. Характерные времена установления поляризации при таком ориентационном механизме сравнительно велики: t ~ 10^-6-10^-8 сек (диапазон сверхвысоких частот). Характер дисперсии при этом обычно релаксационный. Т. о., изучая зависимость Е (w), можно получить сведения о свойствах Д. и выделить вклад в поляризацию от различных механизмов поляризации.

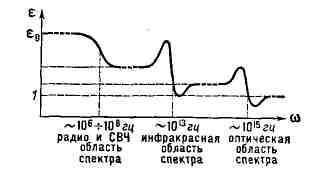
Рис. 5. Зависимость e₁ твёрдого диэлектрика от частоты to поля Е.

Диэлектрическая проницаемость разных веществ. Статическое значение диэлектрич. проницаемости Е существенно зависит от структуры вещества и от внеш. условий (напр., от темп-ры), обычно меняясь в пределах от 1 до 100-200 (у сегнетоэлектриков до 10⁴-10³, табл. 1).

Табл. 1. - Диэлектрическая проницаемость Е некоторых твёрдых диэлектриков
 

Диэлектрик	e 6,3
Рутил, TiO2 (вдоль оптич. оси)	170
Алмаз, С	5,7
Кварц, SiO2	4,3
Лёд, Н2О(при -5°С)	73
Титанат бария, ВаТiO3(при 20 °С перпендикулярно оптич. оси)	4000

Такой разброс значений е объясняется тем, что в разных веществах осн. вклад в Ё на низких частотах дают различные механизмы поляризации. В ионных кристаллах наиболее существенна ионная поляризация. На высоких частотах (w => 10¹⁴ гц) значения е (w) для разных ионных кристаллов близки к 1. Это обусловлено тем, что вклад от электронной поляризации, к-рая для этих частот только и имеет место, невелик. В ковалентных кристаллах, где основной вклад в поляризацию даёт перераспределение валентных электронов, статич. проницаемость Е мало отличается от высокочастотной e₁(w). При этом величина Е зависит от жёсткости ковалентной связи, к-рая тем меньше, чем уже запрещённая зона Д. Напр., для алмаза (Д = 5,5 эв) e = 5,7. Для кремния (Д = 1,1 эв) e = 12. Большой вклад в EI даёт ориентационная поляризация.

Поэтому в полярных Д. е сравнительно велика, напр, для воды е = 81.

Методы измерения диэлектрич. проницаемости различны для разных частот (см. Диэлектрические измерения).

Поляризация диэлектриков в отсутствии электрического поля. До сих пор рассматривались Д., в к-рых поляризация возникала под действием внеш. электрич. поля. Однако в ряде твёрдых Д. наличие поляризации может быть вызвано др. причинами. В пироэлектриках поляризация существует и без электрич. поля. В таких кристаллах заряды располагаются столь несимметрично, что центры тяжести зарядов противоположного знака не совпадают, т. е. Д. спонтанно (самопроизвольно) поляризован. В пьезоэлектриках поляризация возникает при деформировании кристалла. Это связано с особенностями строения кристаллич. решётки таких веществ (см. Пьезоэлектричество).

Большой интерес представляют сегнетоэлектрики, к-рые являются особой разновидностью пироэлектриков. Спонтанная поляризация сегнетоэлектриков существенно меняется, в отличие от обычных пироэлектриков, под влиянием внешних воздействий (темп-ры, электрич. поля). Сегнетоэлектрики поэтому характеризуются очень большими значениями Е, сильной нелинейной зависимостью P от Е, доменной структурой (см. Домены) и наличием спонтанной поляризации лишь в определённом интервале температур. В этом смысле диэлектрич. свойства сегнетоэлектриков аналогичны магнитным свойствам ферромагнетиков.

Поляризация в отсутствии электрич. поля может наблюдаться также в нек-рых веществах типа смол и стёкол, наз. электретами. Поляризованные при высоких темп-pax, а затем охлаждённые, электреты сохраняют достаточно долгое время поляризацию без поля.

Электропроводность Д. мала, однако всегда отлична от нуля (табл. 2). Носителями тока в Д. могут быть электроны и ионы. Электронная проводимость Д. обусловлена теми же причинами, что и электропроводность полупроводников. В обычных условиях, однако, электронная проводимость Д. мала по сравнению с ионной. Ионная проводимость может быть обусловлена перемещением как собств. ионов, так и примесных. Возможность перемещения ионов по кристаллу тесно связана с наличием дефектов в кристаллах. Если, напр., в кристалле есть вакансии (незанятые узлы кристаллич. решётки), то под действием поля ион может перескочить на соседнее с ним вакантное место. Во вновь образовавшуюся вакансию может перескочить следующий ион и т. д. В итоге происходит движение вакансий, к-рое приводит к переносу заряда через весь кристалл. Перемещение ионов может происходить и в результате перескоков ионов по междоузлиям. С ростом темп-ры ионная проводимость сильно возрастает. Заметный вклад в электропроводность Д. может вносить поверхностная проводимость.

Пробой. Электрич. ток в Д. пропорционален напряжённости электрич. поля Е (Ома закон). Однако в достаточно сильных полях ток нарастает быстрее, чем по закону Ома. При нек-ром критич. поле Епр наступает электрич. пробой Д. Величина Епр наз. электрической прочностью Д. (табл. 2). При пробое однородное токовое состояние становится неустойчивым и почти весь ток начинает течь по узкому каналу. Плотность тока в этом канале достигает очень больших значений, что приводит к необратимым изменениям в Д.

Табл. 2. - Удельное сопротивление р и электрическая прочность Е_пр некоторых твёрдых диэлектриков, используемых в качестве изоляционных материалов
 

Диэлектрический материал	р, ом* см	Епр, в/см
Кварцевое стекло	1016-1018	2-3*105
Полиэтилен	1015-1016	4*105
Слюда	1014- 1 016	1-2*10"
Электрофарфор	1013-1014	3*105
Мрамор	108- 109	2-3*105

На рис. 6 приведена зависимость плотности тока j от напряжённости электрич. поля Е, рассчитанная в предположении, что ток однороден по сечению образца. Эта зависимость может быть описана соот-

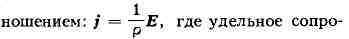
тивление р не постоянная величина, как в законе Ома, а зависит от j. Дифференцируя это соотношение, получим выражение:

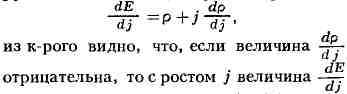
может стать отрицательной (дифференциальное отрицательное сопротивление). Состояние с отрицательным дифференциальным сопротивлением является неустойчивым и приводит к образованию канала тока при Е = Е_пр.

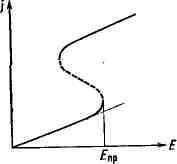
Рис. 6. Зависимость плотности тока j от напряжённости электрич. поля Е в диэлектрике; пунктир соответствует неустойчивым состояниям.

В твёрдых Д. различают тепловой и электрич. пробой. При тепловом пробое с ростом j растёт джоулево тепло и, следовательно, темп-pa Д., что приводит к увеличению числа носителей тока п. В результате р падает. При электрич. пробое с ростом j также возрастает число носителей и, а р с увеличением п падает.

В реальных Д. большую роль при пробое играют всегда присутствующие неоднородности. Они способствуют пробою, т. к. в местах неоднородности Е может локально возрасти. Необратимые изменения в Д., связанные с образованием токового канала при пробое, могут быть разного характера. Напр., в Д. образуется сквозное отверстие или Д. проплавляется по каналу. В канале могут протекать хим. реакции, напр, в органич. Д. осаждается углерод, в ионных Д. выпадает металл (металлизация канал а).

Электрич. прочность жидких Д. в сильной степени зависит от чистоты жидкости. Наличие примесей и загрязнений существенно понижает Епр. Для чистых, однородных жидких Д. Е_ПР близка к Е_ПР твёрдых Д.

Пробой в газах связан с механизмом ударной ионизации и проявляется в виде электрического разряда в газах.

Нелинейные свойства Д. Поляризация Д., как указывалось выше, пропорциональна напряжённости электрич. поля. Однако такая линейная зависимость справедлива только для электрич. полей, значительно меньших внутрикристаллических полей Е_кр ~ 10⁸в/см (см. Кристаллическое поле). Т. к. обычно Е_ПР" "Е_кр, то в большинстве Д. не удаётся наблюдать нелинейную зависимость Р(Е) в постоянном электрич. поле. Исключение составляют Сегнетоэлектрики, где в определённом интервале темп-р (в сегнетоэлектрич. области и вблизи точек фазовых переходов) наблюдается сильная нелинейная зависимость Р(Е).

При высоких частотах электрич. прочность Д. повышается, поэтому нелинейные свойства любых Д. проявляются в высокочастотных полях больших амплитуд. В луче лазера могут быть созданы электрич. поля напряжённости 10⁸ в/см. В таких полях становятся очень существенными нелинейные свойства Д., что позволяет осуществить преобразование частоты света, самофокусировку света и др. нелинейные эффекты (см. Нелинейная оптика).

Д. в науке и технике используются прежде всего как электроизоляционные материалы. Для этого необходимы Д .с большим удельным сопротивлением, высокой электрической прочностью и малым углом диэлектрических потерь. Д. с высоким значением е используются как конденсаторные материалы. Ёмкость конденсатора, заполненного Д., возрастает в е раз. Пьезоэлектрики широко применяются для преобразований звуковых колебаний в электрические и наоборот (приёмники и излучатели ультразвука, звукосниматели и др., см. Пьезоэлектрический датчик). Пироэлектрики служат для индикации и измерения интенсивности инфракрасного излучения. Сегнетоэлектрики применяют в радиотехнике для создания нелинейных элементов, входящих в состав различных схем (усилители, стабилизаторы частоты и преобразователи электрических сигналов, схемы регулирования и др.).

Д. используются и в оптике. Чистые Д. прозрачны в оптич. диапазоне. Вводя в Д. примеси, можно окрасить его, сделав непрозрачным для определённой области спектра (фильтры). Диэлектрические кристаллы используются в квантовой электронике (в квантовых генераторах света - лазерах и квантовых усилителях СВЧ). Ведутся работы по использованию Д. в вычислительной технике и т. п.

Лит.: Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, [в. 5] - Электричество и магнетизм, пер. с англ., М., 1966; Калашникове. Г., Электричество, 2 изд., М., 1964; физический энциклопедический словарь, т. 1, М., 1960; Сканави Г. И., Физика диэлектриков (Область слабых полей), М. -Л., 1949; его же. Физика диэлектриков (Область сильных полей), М.,1958; Фрёлих Г., Теория диэлектриков, М., 1960; Xиппeль А. Р., Диэлектрики и волны, пер. с англ., М., 1960; Же л у дев И. С., Физика кристаллических диэлектриков, М., 1968.

А. П. Леванюк, Д. Г. Санников.

ДИЭЛЕКТРИЧЕСКАЯ АНТЕННА, антенна в виде отрезка диэлектрич. стержня, возбуждённого радиоволноводом или штырём коаксиального кабеля. В стержне Д. а. (рис.) возбуждается волна особой структуры (т. н. поверхностная волна), распространяющаяся вдоль его оси, и, как следствие, на поверхности стержня возникают тангенциальные (касательные к поверхности) составляющие электрич. и магнитного полей, фаза к-рых меняется ло закону бегущей волны.

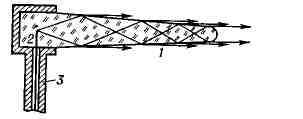
Диэлектрическая антенна: 1 - конусообразный стержень; 2 - штырь, излучающий радиоволны в стержень; 3 -коаксиальный кабель. Стрелками показано направление излучения антенны.

По существу Д. а. представляет собой бегущей волны антенну, состоящую из элементарных электрич. и магнитных вибраторов. Её максимум излучения, как и всякой антенны бегущей волны, совпадает с осью стержня. Характер излучения Д. а. зависит от фазовой скорости распространения поверхностной волны. С увеличением диаметра стержня и диэлектрич. проницаемости материала, из к-рого он выполнен, фазовая скорость уменьшается. Чем меньше фазовая скорость, тем больше длина стержня, при к-рой коэфф. направленного действия (КНД)антенны максимален (т. н. оптимальная длина), и больше максимально возможный КНД. По мере уменьшения фазовой скорости или приближения её к скорости света в окружающей среде (воздухе) диэлектрич. стержень теряет волноводные свойства. Это приводит к резкому спаданию поля к концу стержня, увеличению излучения в окружающую Д. а. среду непосредственно из открытого конца радиоволновода и уменьшению эффективности Д. а. Диаметр и материал стержня обычно выбирают так, чтобы фазовая скорость была не очень близкой к скорости света (не более 0,95-0,96 скорости света). При такой фазовой скорости оптимальная длина равна 12 длинам излучаемой волны и КНД равен ~ 100. Стержень Д. а. изготовляют из диэлектрич. материалов с малым затуханием электромагнитных волн в них - полистирол, фторопласт и др. Д. а. применяют преим. на летательных аппаратах в радиоустройствах, работающих на сантиметровых и дециметровых волнах.

О. Н. Терёшин, Г. К. Галимов.

ДИЭЛЕКТРИЧЕСКАЯ ВОСПРИИМЧИВОСТЬ, величина, характеризующая способность диэлектриков к поляризации. Количественно Д. в. - коэфф. пропорциональности х в соотношении Р = хE, где Е - напряжённость электрич. поля, Р - поляризация диэлектрика (дипольный момент единицы объёма диэлектрика). Д. в. характеризует диэлектрич. свойства вещества так же, как и диэлектрическая проницаемость е, с к-рой она связана соотношением: 8= 1 + 4пх. Лит. см. при ст. Диэлектрики.

ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ, устаревшее название диэлектрической проницаемости.

ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ, величина, характеризующая диэлектрические свойства среды - её реакцию на электрическое поле. В соотношении D = еЕ, где Е - напряжённость электрич. поля, D - электрич. индукция в среде, Д. п. - коэффициент пропорциональности Е. В большинстве диэлектриков при не очень сильных полях Д. п. не зависит от поля Е. В сильных электрич. полях (сравнимых с внутриатомными полями), а в нек-рых диэлектриках (напр., сегнетоэлектриках) в обычных полях зависимость D от Е - нелинейная (см. Нелинейная, оптика).

Величина Д. п. существенно зависит от типа вещества и от внешних условий (темп-ры, давления и т. п.). В переменных электрических полях Д. п. зависит от частоты поля Е (см. Диэлектрики). О методах измерения Д. п. см. Диэлектрические измерения.

Лит. см. при ст. Диэлектрики, Электроизоляционные материалы.

ДИЭЛЕКТРИЧЕСКАЯ ЭЛЕКТРОНИКА, область физики, занимающаяся исследованием и практич. применением явлений, связанных с протеканием электрич. токов в диэлектриках. Концентрация электронов проводимости или к.-л. других свободных носителей заряда в диэлектриках (дырок, ионов) пренебрежимо мала. Поэтому до недавнего времени диэлектрики в электро- и радиотехнике использовались только как изоляторы (см. Электроизоляционные материалы). Исследования тонких диэлектрич. плёнок показали, что при контакте с металлом в диэлектрик переходят электроны или дырки, в результате чего у контакта в тонком слое диэлектрика появляются в заметном количестве свободные носители заряда. Если диэлектрик массивный, то весь его остальной объём действует по-прежнему как изолятор, и поэтому в системе металл-диэлектрик - металл ток ничтожно мал. Если же между двумя металлич. электродами поместить тонкую диэлектрич. плёнку (обычно 1-10 мкм), то эмитируемые из металла электроны заполнят всю толщу плёнки и напряжение, приложенное к такой системе, создаст ток через диэлектрик.

Теоретически возможность протекания управляемых эмиссионных токов через диэлектрик была предсказана англ. физиками Н. Моттом и Р. Гёрни в 1940. Д. э. изучает протекание токов, ограниченных пространственным зарядом в диэлектриках, при термоэлектронной эмиссии из металлов и полупроводников, при туннельной эмиссии и т. д.

Простейший прибор Д. э. - диэлектрич. диод представляет собой сандвич-структуру металл - диэлектрик - металл (рис. 1). Он во многом аналогичен электровакуумному диоду и поэтому наз. аналоговым.

Его выпрямляющее действие обусловлено различием работы выхода электронов из электродов, изготовленных из разных металлов. Для одного из электродов - истока (аналог катода) применяется металл, у к-рого работа выхода электронов в данный диэлектрик мала (доли эв); для второго (сток - аналог анода) - металл с большой работой выхода (1-2 эв). Поэтому в одном направлении возникают значительные токи, а в обратном направлении токи исчезающе малы. Коэффициент выпрямления диэлектрического диода достигает значений 10⁴ и выше.

Создание диэлектрич. триода связано с технологич. трудностями размещения управляющего электрода - затвора (аналог сетки в электровакуумном триоде) в тонком слое диэлектрика между истоком и стоком. В одном типе триода эмиссия происходит из полупроводника п, обладающего электронной проводимостью, в высокоомный полупроводник р с дырочной проводимостью, который играет роль диэлектрика (рис. 2). Низкоомные области, образованные из полупроводника Р⁺с высокой дырочной проводимостью, исполняют роль, во многом сходную с ролью металлич. ячеек сетки электровакуумного триода. Подаваемое на эти области внешнее напряжение управляет величиной тока, протекающего между истоком и стоком.

Рис. 2. Горизонтальный разрез диэлектрического триода со встроенной сеткой; п - полупроводник, обладающий электронной проводимостью; р - диэлектрик (высокоомный полупроводник с дырочной проводимостью), в к-рый происходит эмиссия электронов; Р⁺ - низкоомные области полупроводника с дырочной проводимостью, через к-рые электроны не проходят.

В другом типе триода (рис. 3) затвор помещён вне диэлектрика CdS; его роль сводится к изменению распределения потенциала в диэлектрике, от чего существенно зависит величина тока. физ. картина явлений в этих триодах значительно сложнее и существенно отличается от протекания эмиссионных токов в вакууме. Распространение получили триоды с изолированным затвором МОП (металл - окисел - полупроводник) или МДП (металл - диэлектрик - полупроводник).

Рис. 3. Структура триода с изолированным затвором.

В приборах Д. э. удачно сочетаются достоинства полупроводниковых и электровакуумных приборов и отсутствуют многие их недостатки. Приборы Д. э. микроминиатюрны. Создание эмиссионных токов в диэлектриках не требует затрат энергии на нагрев эмитирующего электрода и не сталкивается с проблемой отвода тепла. Диэлектрич. приборы малоинерционны, обладают хорошими частотными характеристиками, низким уровнем шумов, мало чувствительны к изменениям температуры и радиации.

Лит.: Мотт Н., Герни Р., Электронные процессы в ионных кристаллах, пер. с англ., М., 1950; Адирович Э. И., Электрические поля и токи в диэлектриках, "Физика твердого тела", 1960, т. 2, в. 7, с. 1410; его же, Эмиссионные токи в твердых телах и диэлектрическая электроника, в сб.: Микроэлектроника, под ред. Ф. В. Лукина, в. 3, М., 1969, с. 393.

Э. И. Адирович.

ДИЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ, измерения величин, характеризующих свойства диэлектриков в постоянном и переменном электрич. полях. К Д. и. относятся измерения диэлектрич. проницаемости е в постоянных и переменных полях, диэлектрич. потерь, удельной электропроводности в постоянном электрич. поле, электрич. прочности.

В случае твёрдых диэлектриков Д. и. часто сводятся к измерению ёмкости С плоского электрич. конденсатора, между пластинами к-рого помещён исследуемый

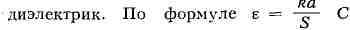
(d - толщина диэлектрич. образца, S -площадь его боковой грани, k - коэфф. пропорциональности) находят диэлектрич. проницаемость е. В случае жидкостей и газов измеряют ёмкость системы электродов в вакууме (С₀) и в данном веществе (С_е), а затем определяют е из соотношения: е = С_е/С_о.

Методы измерения ёмкости и диэлектрич. потерь различны для разных частот электрич. поля. В постоянном поле и при низких частотах (десятые доли гц) ёмкость, как правило, определяют путём измерений зарядного или разрядного токов конденсатора с помощью баллистического гальванометра (рис. 1).

В области частот от десятых гц до 10⁷ гц, помимо С, существенно измерение диэлектрических потерь, мерой к-рых является тангенс угла диэлектрических потерь tgб. С и tgб измеряют с помощью мостовых схем, в частности мостов Шеринга.

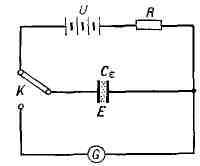
Рис. 1. Измерения диэлектрической проницаемости при помощи баллистического гальванометра G.

В высокочастотной области (от 10⁵ до 10⁸ гц) для измерения ёмкости С_е и диэлектрической проницаемости е применяют гл. обр. резонансные методы (рис. 2). Колебательный контур, содержащий образцовый конденсатор (см. Емкости меры), настраивается в резонанс, и определяется соответствующая резонансу величина ёмкости С'. Затем параллельно образцовому конденсатору присоединяют конденсатор с диэлектриком Се, и контур снова настраивается в резонанс. Во втором случае ёмкость С" образцового конденсатора будет меньше. Ёмкость конденсатора, заполненного диэлектриком Се, определяется по формуле: С_е = С'-С". (1)

Различные резонансные методы отличаются друг от друга по способу определения tgб. В методе замещения диэлектрик заменяется эквивалентной схемой, состоящей из ёмкости и сопротивления.

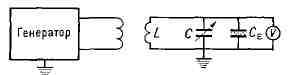
Рис. 2. Измерения ёмкости С_е и диэлектрической проницаемости е резонансным методом. Катушка индуктивности L и образцовый конденсатор С образуют замкнутый контур, слабо связанный с генератором переменного тока.

Подбирается такое сопротивление R, к-рое, будучи включено последовательно или параллельно образцовому конденсатору С, ёмкость к-рого берётся равной ёмкости диэлектрика С_е, даёт такой же резонансный ток в контуре, как и образец диэлектрика. Метод расстройки контура основан на том, что ширина резонансной кривой контура определяется его добротностью Q, связанной с тангенсом угла потерь диэлектрика соотношением:

Ёмкость и диэлектрич. потери определяют также методом куметра. В данной области частот можно применять также метод биений.

В области сверхвысоких частот (от 10⁸ до 10¹¹ гц) Д. и. основаны на использовании объёмных резонаторов и радиоволноводов, а также на закономерностях распространения электромагнитных волн в свободном пространстве. В случае газообразных диэлектриков измеряют резонансную частоту w₀ и добротность Qo объёмного резонатора (рис. 3), когда в нём создан вакуум, и те же величины w_е и Q_е, когда он целиком заполнен диэлектриком.

Рис. 3. Волноводные установки для измерения е и tgS газов.

При этом имеют место соотношения:

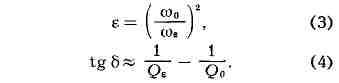
В случае жидких и твёрдых диэлектриков, если они целиком заполняют резонатор, получаются гораздо большие изменения резонансной частоты и добротности. Кроме того, если диэлектрич. потери велики, то добротность резонатора становится весьма малой величиной. Это нарушает справедливость формул (3) и (4). Поэтому применяют частичное заполнение резонатора диэлектриком, чаще всего имеющим форму диска или стержня.

Другой метод Д. и. в области СВЧ состоит в том, что в радиоволноводе устанавливаются бегущая или стоячая электромагнитные волны. Для волновода, заполненного диэлектриком, длина волны Х_е равна:

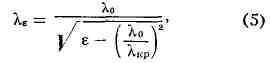
где Х₀ - длина волны в свободном пространстве, Хкр - критич. (предельная) длина волны, зависящая от типа волн и размеров поперечного сечения волновода. Из формулы (5) можно определять Е. При введении диэлектрика в волновод изменяются условия распространения волн и происходит поглощение энергии электромагнитного поля. Это позволяет определить tgб.

Существуют два основных метода измерения е и tg6 с помощью волновода. Первый основан на наблюдении картины стоячих волн в волноводе, нагружённом известным сопротивлением. Второй - на наблюдении поглощения волн, проходящих через диэлектрик. В случае газов, к-рые имеют е~~1 и малые диэлектрич. потери, Е и tgб определяют с помощью установки, схематически изображённой на рис. 3. В среднем участке волновода, отгороженном слюдяными окнами, создаётся вакуум, а затем туда вводится газ. При этом в согласии с формулой (5) длина волны уменьшается и положение минимумов стоячей волны смещается. Д. и. жидкостей и твёрдых тел, имеющих е не= 1, осложняются отражением волн на границе воздух - диэлектрик. В этих условиях наблюдают картину стоячих волн на входе заполненного диэлектриком волновода с помощью измерительной линии. В области миллиметровых, инфракрасных и световых волн измеряют коэфф. отражения или преломления и коэфф. поглощения диэлектрика, откуда находят е и tgб.

Методы измерения удельной электропроводности диэлектриков а в постоянном поле существенно не отличаются от аналогичных методов для металлов и полупроводников. Для точных измерений очень малых а используют постоянного тока усилитель.

Измерения электрич. прочности Е_пр основаны на измерении напряжения Е_пp, к-рое соответствует наступлению диэлектрич. пробоя:

где d - расстояние между электродами.

Лит.: Сканави Г. И., Диэлектрическая поляризация и потери в стеклах и керамических материалах с высокой диэлектрической проницаемостью, М.-Л., 1952; Карандеев К. Б., Мостовые методы измерений, К., 1953; Xиппель А. Р., Диэлектрики и их применение, пер. с англ., М.-Л., 1959; Браун В., Диэлектрики, пер. с англ., М., 1961; Измерения на сверхвысоких частотах, пер. с англ., под ред. В. Б. Штейншлейгера, М., 1952.

А. Н. Губкин.

ДИЭЛЕКТРИЧЕСКИЕ ПОТЕРИ, часть энергии переменного электрич. поля в диэлектрич. среде, к-рая переходит в тепло. При изменении значения и направления напряжённости Е электрич. поля диэлектрич. поляризация также меняет величину и направление (см. Диэлектрики); за время одного периода переменного поля поляризация дважды устанавливается и дважды исчезает. Если диэлектрик построен из молекул, к-рые представляют собой диполи (полярные молекулы) или содержит слабо связанные ионы, то ориентация таких частиц или смещение в электрич. поле (ориентационная поляризация) требуют определённого времени (время релаксации). В результате максимум поляризации не совпадает во времени с максимумом напряжённости поля, т. е. имеется сдвиг фаз между напряжённостью поля и поляризацией. Благодаря этому имеется также сдвиг фаз между напряжённостью электрического поля Е и электрич. индукцией D, к-рый и обусловливает потери энергии W_e. Переходя к векторному изображению величин, можно сказать, что вектор электрич. индукции отстаёт' от вектора электрич. поля на нек-рый угол 6, к-рый носит назв. угла диэлектрических потерь. Когда молекулы или ионы ориентируются полем, они испытывают соударения с др. частицами, при этом рассеивается энергия. Если время релаксации г во много раз больше, чем период Т изменения приложенного поля, то поляризация почти не успевает развиться и Д. п. очень малы. При малых частотах, когда время релаксации т значительно меньше периода Т, поляризация следует за полем и Д. п. также малы, т. к. мало число переориентации в единицу времени. Д. п. имеют макс. значение, когда выполняется равенство w = ^l/t, где w - круговая

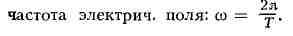
Описанный механизм релаксац. Д. п. имеет место в твёрдых и жидких диэлектриках, содержащих полярные молекулы или слабо связанные ионы. Величина релаксационных Д. п. в жидкости зависит от её вязкости, от темп-ры и от частоты приложенного поля. Для невязких жидкостей (вода, спирт) эти потери проявляются в сантиметровом диапазоне длин волн. В полимерах, содержащих полярные группы, возможна ориентация как отдельных полярных радикалов, так и более или менее длинных цепочек молекул.

В диэлектриках с ионной и электронной поляризацией вещество можно рассматривать как совокупность осцилляторов, к-рые в переменном электрич. поле испытывают вынужденные колебания, сопровождающиеся рассеянием энергии (рис. 1). Однако если частота электрич. поля гораздо больше или меньше собственной частоты осцилляторов, то рассеяние

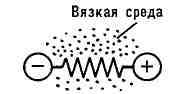
Рис. 1. Модель диэлектрика, состоящего из осцилляторов - упруго связанных электрических зарядов.

энергии и, следовательно, Д. п. незначительны. При частотах, сравнимых с собственной частотой осцилляторов, рассеяние энергии и Д. п. W_e велики и имеют максимум при равенстве этих частот со = w₀ (рис. 2). При электронной поляризации максимум потерь соответствует оптич. диапазону частот. В диэлектриках, построенных из ионов (напр., щёлочно-галоидные кристаллы), поляризация обусловлена упругим смещением ионов и максимум потерь имеет место в инфракрасном диапазоне частот (10¹²-10¹³ гц).

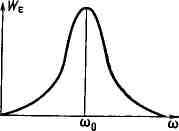
Рис. 2. Зависимость We^(w) для диэлектрика, состоящего из одинаковых осцилляторов, изображённых на рис. 1.

Т. к. реальные диэлектрики обладают нек-рой электропроводностью, то имеются потери энергии, связанные с протеканием в них электрич. тока (джоулевы потери), величина к-рых не зависит от частоты.

Величина Д. п. в диэлектрике, находящемся между обкладками конденсатора, определяется соотношением:

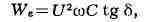
где U - напряжение на обкладках конденсатора, С - ёмкость конденсатора, tgS - тангенс угла диэлектрических потерь. Д. п. в 1 см³ диэлектрика в однородном поле Е равны:

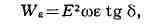
где Е - диэлектрическая проницаемость.

Произведение Е tg б наз. коэфф. Д. п. Уменьшение величины Д. п. имеет большое значение в производстве конденсаторов и электроизоляционной технике. Большие Д. п. используются для диэлектрического нагрева в электрич. поле высокой частоты.

Лит.: Сканави Г. И., Физика диэлектриков (Область слабых полей), М.-Л., 1949; Браун В., Диэлектрики, пер. с англ., М., 1961; Хиппель А. Р., Диэлектрики и их применение, пер. с англ., М., 1959; физический энциклопедический словарь, т. 1, М., 1960, с. 643.

Е. А. Конорова.

ДИЭЛЕКТРИЧЕСКИЙ ВОЛНОВОД, радиоволновод, состоящий целиком из диэлектрич. материалов (полиэтилена, полистирола и др.).

ДИЭЛЕКТРИЧЕСКИЙ НАГРЕВ, нагрев диэлектриков в переменном электрич. поле. При наложении переменного электрич. поля в диэлектриках появляется ток смещения, вызванный их поляризацией, и ток проводимости, обусловленный наличием в диэлектрике свободных электрически заряженных частиц. Протекание суммарного тока приводит к выделению тепла. Выделяющаяся удельная мощность пропорциональна напряжённости (Е) и частоте (f) электрич. поля, а также диэлектрич. постоянной (Е) и тангенсу угла потерь (tg б) диэлектрика. При частотах 0,3-300 Мгц Д. н. осуществляется в поле конденсатора (источник энергии - ламповые генераторы), при сверхвысоких частотах - в поле объёмного резонатора или излучателя (источник -магнетроны). Напряжённость электрич. поля в промышленных установках Д. н. 5-3000 кв/м. Достоинства установок Д. н.: высокая скорость нагрева; равномерный нагрев материалов с низкой теплопроводностью; осуществление местного и избирательного нагрева и др. Области применения Д. н. - сушка материалов (древесины, бумаги, керамики и др.); нагрев пластмасс перед прессованием; сварка пластмасс; склеивание древесины и т. д.

Лит.: Высокочастотный нагрев диэлектриков и полупроводников, 2 изд., М.-Л., 1959; Высокочастотная электротермия. Справочник, М.-Л., 1965; Брицын Н. Л., Нагрев в электрическом поле высокой частоты, 3 изд., М. -Л., 1965.

А. Б. Кувалдин.

ДИЭЛЕКТРИЧЕСКИЙ УСИЛИТЕЛЬ, усилитель электрич. колебаний, в к-ром усиление создаётся изменением ёмкости конденсатора с сегнетоэлектриком при изменении подводимого к нему напряжения. В типовом каскаде усиления Д. у. (рис.) подводимые электрич. колебания изменяют ёмкость конденсатора С и, следовательно, его реактивное сопротивление, что вызывает модуляцию колебаний, создаваемых генератором Г. Полученные на концах сопротивления нагрузки Z, модулированные колебания затем детектируются диодом D. В результате детектирования на выходе Д. у. возникают колебания, совпадающие по форме с подводимыми, но большей амплитуды.

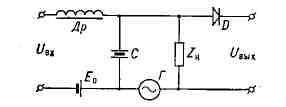
Схема каскада усиления диэлектрического усилителя: Uвх - подводимое напряжение сигнала; Др - высокочастотный дроссель, защищающий источник усиливаемого сигнала от проникновения в него высокочастотных колебаний генератора Г; Е₀ - источник постоянного напряжения для установления рабочего режима на конденсаторе С; С - конденсатор с сегнетоэлектриком; Г - генератор высокочастотных колебаний; Z_H - сопротивление нагрузки; - D - диод; Uвых - усиленное выходное напряжение сигнала.

Часто в каскаде усиления Д. у. конденсаторы с сегнетоэлектриком включаются по схеме электрич. моста. Усиление по мощности низкочастотных (сотни гц - десятки кгц) электрич. колебаний, даваемое одним каскадом Д. у., достигает 100. U повышением частоты (до неск. Мгц) усиление существенно уменьшается (до 10 и менее). Для получения большего усиления в Д. у., как в ламповых и транзисторных усилителях, отд. каскады усиления могут быть включены один за другим. Д. у., аналогично магнитному усилителю, с к-рым он сходен по принципу действия, применяют гл. обр. для усиления низкочастотных колебаний в устройствах автоматики, сигнализации и т. п.

ДИЭТИЛЕНГЛИКОЛЬ, В,В' - диоксиди-этиловыйэфир, НОСН₂СН₂ОСН₂СН₂ОН, густая бесцветная жидкость; tпл-8°С, tкип 245°С, плотность 1,1197 г/см³(15°С), показатель преломления n²⁰_D 1,4472. Д. смешивается с водой, спиртом, ацетоном, плохо растворим в эфире, бензоле; его химические свойства сходны со свойствами этиленгликоля. Последний вместе с окисью этилена

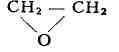
и этиленхлоргидрином (С1СН₂СН₂ОН) служит сырьём для пром. получения Д. Д. широко применяют как растворитель нитроцеллюлозы, масел, смол, как пластификатор, компонент антифризов и поглотительных смесей, как осушитель (в газовой пром-сти) и т. д. Практич. значение имеют нек-рые производные Д.: диэтиленгликольдинитрат, моноэфиры (карбитолы) и диэфиры (напр., диглим, СН₃ОСН₂СН₂ОСН₂СН₂ОСН₃).

ДИЭТИЛЕНГЛИКОЛЬДИНИТРАТ, дигликольдинитрат, нитродигликоль,

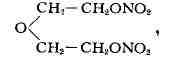
вторичное взрывчатое вещество, бесцветная сиропообразная жидкость, плотность 1390 кг/л³; кристаллизуется в двух модификациях: стабильной с t_3атв 2°С и лабильной с t_3атв -10,9°С. Д. почти нерастворим в воде, хорошо растворяется в ацетоне, метаноле, нитрогликоле и нитроглицерине, пластифицирует нитроцеллюлозу. Теплота взрыва (~4,18Мдж/кг) близка к теплоте взрыва тротила. Получают этерификацией диэтиленгликоля смесью серной и азотной к-т. Применяется в смеси с нитроглицерином для изготовления динамитов, баллиститных порохов (см. Баллиститы) и др. взрывчатых веществ.

Б. Н. Кондриков.

ДИЭТИЛСТИЛЬБЭСТРОЛ, синтетический лекарственный препарат из группы гормональных препаратов (женских половых гормонов). Применяют внутрь в таблетках и в масляном растворе внутримышечно при недостаточной функции яичников и др.

ДИЯЛА, Диала, река в Ираке (истоки составляющих в Иране), лев. приток Тигра. Дл. 231 км (от слияния составляющих Сирван и Эльвенд), пл. басс. св. 30 тыс. км². Верховья - в горах Загрос, низовья - на Месопотамской низм., где Д. образует обширную плодородную дельту. Весеннее половодье, летняя межень, повышенная водность зимой. Ср. годовой расход воды в низовьях -130 м^3/сек. Воды широко используются для орошений.

ДИЯРБАКЫР (Diyarbakir), город на Ю.-В. Турции, на р. Тигр; адм. ц. вилайета Диярбакыр. 138,7 тыс. жит. (1970).

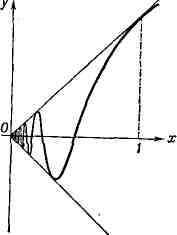
Ж.-д. станция. Узел шоссейных дорог. Предприятия пищ. и текст, пром-сти. Автосборка. Ремёсла (изготовление тканей, сафьяна). К С.-З. от Д. - добыча хромовой и медной руд.

ДЛИНА, числовая характеристика протяжённости линий. В разных случаях понятие Д. определяется различно. 1) Д. отрезка прямой - расстояние между его концами, измеренное к.-л. отрезком, принятым за единицу Д. 2) Д. ломаной -сумма Д. её звеньев. 3) Д. простой дуги -предел Д. вписанных в эту дугу ломаных, когда число звеньев неограниченно увеличивается и макс. Д. звеньев стремится к нулю. 4) Д. непрерывной кривой, состоящей из конечного числа простых дуг, равна сумме Д. этих дуг. Напр., Д. окружности может. быть получена как предел периметров правильных вписанных многоугольников при неограниченном удвоении числа их сторон и равна 2пR, где R - радиус окружности. Всякая непрерывная кривая имеет Д. - конечную или бесконечную. Если её Д. конечна, то кривая наз. спрямляемой. График функции (см. рис.)

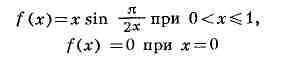
даёт пример неспрямляемой кривой; здесь Д. вписанных ломаных неограниченно растут, когда Д. звеньев стремятся к нулю. Если уравнение плоской кривой в прямоугольных координатах имеет вид у = = f(x) (а =<x<=b), причём функция f(x) имеет непрерывную производную f'(x), то Д. кривой выражается интегралом

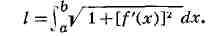
Аналогично выражается Д. кривой, заданной параметрически, и Д. пространственной кривой.

К вычислению Д. кривой при помощи предельного перехода из Д. ломаных прибегали по существу ещё математики древности. Для них, однако, этот предельный переход был лишь способом вычисления Д. кривой, а не определения понятия Д. кривой, т. к. последнее им представлялось, по-видимому, одним из первоначальных математич. понятий. Необходимость определения Д. кривой стала ясной лишь в 1-й пол. 19 в. Полное выяснение вопроса было достигнуто К. Жорданом. В дифференциальной геометрии определяется также Д. кривой на поверхности или в произвольном римановом пространстве. О единицах и технике измерения Д. см. Меры, длины, Измерение.

Лит.: Лебег А., Об измерении величин, пер. с франц., 2 изд., М., 1960; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.

С. Б. Стечкин.

ДЛИНА ВОЛНЫ, расстояние между двумя ближайшими точками волны, находящимися в одинаковой фазе колебания. Д. в. \ связана с периодом колебания Т и скоростью с распространения волны соотношением X = сТ.

ДЛИНА СВОБОДНОГО ПРОБЕГА (точнее - средняя длина свободного пробега, l), средняя длина пути, проходимого частицей между двумя последоват. соударениями с др. частицами. Понятием Д. с. п. широко пользуются при расчётах различных процессов переноса, напр, вязкости, теплопроводности, диффузии, электропроводности и др.

Согласно кинетич. теории газов, молекулы от столкновения до столкновения движутся равномерно и прямолинейно. Если за 1 сек молекула проходит в среднем путь v, испытывая при этом v упругих соударений с такими же молекулами, то

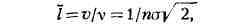
где п - число молекул в единице объема (плотность газа), а - эффективное поперечное сечение молекулы. С повышением плотности газа (его давления) Д. с. п. уменьшается, т. к. растёт число столкновений v в 1 сек. Повышение темп-ры (интенсивности движения молекул) приводит к нек-рому уменьшению о и, следовательно, к росту l. Для обычных молекулярных газов в нормальных условиях (при атм. давлении и 20°С) l ~ ~ 10^-5 см, что примерно в 100 раз больше ср. расстояния между молекулами. К частицам, движение и взаимодействие к-рых подчиняется законам квантовой механики, понятие Д. с. п. в ряде случаев также применимо (напр., электроны проводимости в твёрдом теле, нейтроны в слабо поглощающих средах, фотоны в звёздах), но расчёт Д. с. п. для таких частиц более сложен.

ДЛИННАЯ ЛИНИЯ, электрич. линия, образованная двумя параллельными проводниками тока, длина к-рых превышает длину волны передаваемых электромагнитных колебаний, а расстояние между проводниками значительно меньше длины волны. Д. л. является системой с распределёнными постоянными (параметрами), т. к. каждый элемент её длины обладает одновременно нек-рыми значениями индуктивности L и активного сопротивления R проводов, ёмкости С и проводимости тока G между проводами. Через эти параметры определяют осн. характеристики Д. л.- волновое сопротивление W и скорость распространения v электромагнитных волн вдоль неё. Мгновенные значения силы переменного тока и напряжения в любой точке Д. л. математически связаны между собой т. н. телеграфными ур-ниями. Д. л. наз. однородной, если значения её параметров неизменны на всём протяжении; при отсутствии в ней электрич. потерь, т. е. R = G = 0 (обычно

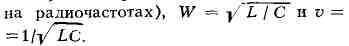
Входное сопротивление Д. л. имеет в общем случае комплексный характер (содержит активную и реактивную составляющие) и зависит от длины линии и характера электрич. нагрузки на её конце (выходе). Входное сопротивление Д. л. бесконечной длины равно W. Для макс. передачи энергии от источника линии её входное сопротивление должно быть активным и равным внутр. сопротивлению источника, т. е. согласованным с ним. Различают 3 режима работы Д. л.: режим бегущей волны, когда передаваемая энергия полностью поглощается нагрузкой (сопротивление нагрузки активное и равное W); режим стоячей волны, когда передаваемая энергия полностью отражается от конца линии к источнику (короткозамкнутая или разомкнутая на конце Д. л.), и промежуточный режим (сопротивление нагрузки комплексное и не равное W). Д. л. применяют для передачи информации в дальней телеграфно-телефонной связи, телевидении, радиолокации, а также для передачи энергии по проводам на далёкие расстояния (см. Линия электропередачи).

Лит.: Гарновский Н. Н., Теоретические основы электропроводной связи, ч. 2, М., 1959; Гоноровский И. С., Радиотехнические цепи и сигналы, ч. 2, М., 1967.

Ю. Б. Любченко.